Un modello probabilistico per quantificare i risultati delle ricerche sulla Sindone di Torino
|
|
|
- Vittorio Bellini
- 8 anni fa
- Visualizzazioni
Transcript
1 Congresso nternazionale di Studi sulla Sindone, Torino, 5-7 giugno 998 Un odello probabilistico per quantificare i risultati delle ricerche sulla Sindone di Torino Giulio Fanti, Eanuela Marinelli + CSAS G. Colobo (Centro nterdipartientale Studi ed Attività Spaziali), Dipartiento di ngegneria Meccanica, Università di Padova, Via Venezia, 3537 Padova - taly tel , fax , e-ail: <fanti@ail.di.unipd.it> + Collegaento pro Sindone, Via dei Brusati 84, 0063 Roa tel , fax , e-ail: <cpshroud@tin.it>. (*) Soario Viene proposto un odello probabilistico, di eventi utuaente escludentisi, capace di sintetizzare i olteplici ed anche contrastanti risultati delle ricerche sulla Sindone di Torino. l odello si basa sulla definizione di tre alternative possibili (A= autentica, F= falsa, N= non autentica) per l origine del lenzuolo e sulla valutazione di ciascuna alternativa sulla base dell assegnazione di opportune probabilità, con relativa incertezza, a ciascun risultato delle ricerche copiute. A ciascuna afferazione vengono quindi assegnati 7 coefficienti di cui tre relativi alle probabilità di verificarsi delle alternative A, F e N, tre relativi alle corrispondenti incertezze ed un peso relativo all iportanza del risultato. Coe esepio applicativo vengono confrontati i risultati ottenuti da un analisi probabilistica eseguita su sole 7 afferazioni, con quelli già elaborati più seplicisticaete in bibliografia. Abstract To synthetize the variety of the contrasting results coing fro the researches done on the Turin Shroud, a probabilistic odel capable of consider utually excluding events, is proposed. t is based on the definition of three possible alternatives (A=true, F=fake, N=not A or F) regarding the cloth origin. Each alternative is then evaluated fro the assignent of the corresponding probability, with relative uncertainty, to each stateent, relative to the results of the Shroud investigations. Each stateent is coposed by 7 coefficients: 3 relative to the corresponding alternative (A, F and N) probability, 3 relative to the corresponding uncertainty and one to evaluate the result iportance. As an exaple, results obtained fro a very siple probabilistic analysis that considers only 7 stateents, are copared with that published by other authors. Abbreviazioni: ST = Sindone di Torino; UST = Uoo delle Sindone di Torino. (*) Per fini puraente accadeici, il contributo individuale dei singoli autori è specificato coe segue: G. Fanti (40%) ha sviluppato la forulazione probabilistica; ha inoltre definito le 00 afferazioni con E. Marinelli (60%) che ha garantito l attendibilità delle stesse fornendo i corrispondenti riferienti bibliografici.
2 ) ntroduzione La necessità di costruire un odello probabilistico per valutare i risultati delle ricerche eseguite sulla ST nasce dalla difficoltà di riuscire a giudicare in odo globale e oggettivo la notevole quantità di prove o afferazioni portate a favore o contro una tesi di autenticità o di falsità. Molti studiosi continuano tutt oggi a sostenere tesi diaetralente opposte [,2,3] portando a favore solo un nuero liitato di afferazioni. Una volta costruito un odello interpretativo capace di analizzare olte afferazioni, ciascuno studioso dovrebbe essere in grado di forulare giudizi più obiettivi. n questo studio si prevede di analizzare le 00 afferazioni ritenute più significative, siano esse a favore o contro una particolare tesi. Poiché alcune di esse sono scientificaente accertate, altre sono più dubbie, sorge la necessità di potere pesare ciascuna afferazione in funzione del suo grado di attendibilità. D altra parte, dalle nuerosissie ricerche effettuate a livello ondiale, non è risultata un unica afferazione così copleta e significativa da diostrare l autenticità o falsità della ST. É opinione degli scriventi che forse la prova più significativa potrà risultare dall analisi globale di tutti i risultati finora ottenuti. Sono state eseguite già in passato diverse analisi di questo tipo [4,5]. Tali analisi però, liitate ad un nuero più ridotto di prove (cinque o sette), non considerano le probabilità condizionate. Questi risultati vengono rivisti alla luce della nuova ipostazione proposta. 2) Considerazioni generali sul odello probabilistico Si utilizza la statistica inferenziale o induttiva che si occupa del controllo di ipotesi statistiche e della stia di grandezze non note a priori. É necessario che l ipotesi da controllare sia di natura statistica. La stia della grandezza sconosciuta viene eseguita applicando la forula di Bayes (vedi Appendice e 3.3). Si può dire che la probabilità finale di un ipotesi subordinataente all esito ottenuto è proporzionale al prodotto della probabilità iniziale per la verosiiglianza dell esito subordinataente all ipotesi, essendo la costante di proporzionalità le probabilità dell esito. Si considera coe spazio capione 2 l insiee di tutte le sindoni inclusa quella che avvolse Gesù; tale insiee coprende oltre alla ST anche quelle false e quelle esistenti, o non più disponibili perché distrutte, che hanno avvolto corpi di uoini. Nota : Per esepio nel lancio di un dado a 6 facce, per ogni tiro ci sono 6 alternative corrispondenti al nuero della faccia che risulta dal lancio. Se il dado non ha difetti, l alternativa corrispondente al nuero ha una probabilità su 6 di verificarsi; le altre alternative hanno uguale probabilità. Se si lancia il dado due volte, ci sono (6x6=) 36 diverse alternative: per esepio l alternativa che esca la pria volta e 6 la seconda ha una probabilità su (6x6=) 36 di verificarsi. Anche l alternativa che esca la pria e la seconda volta ha una probabilità su 36 di verificarsi. n tale caso gli eventi non sono utuaente escludentisi perché sono aessi anche i casi isti e la probabilità risultante è data dal prodotto delle probabilità di ciascuna alternativa. Nel caso invece del calcolo probabilistico della ST, non si può considerare un alternativa ista, in parte favorevole ed in parte contraria ad una particolare tesi. n analogia col doppio tiro del dado è coe accettare le sole alternative coincidenti, cioè,, 2,2, etc.: si tratta di probabilità condizionate dall evento precedente. n tale caso la probabilità che esca sia la pria che la seconda volta non è più /36, a /6 (eq. A.5) perché vengono esclusi dall analisi i casi isti,2,,3,.., 6,,.., 6,5. Nota 2 : per chiarire eglio la definizione di alcuni concetti probabilistici e di statistica inferenziale, si riporta un esepio applicativo che spiega per analogia il procediento logico applicato alla ST. Si fa riferiento ad un azzo di 52 carte da bridge che sia stato preventivaente segnato da un baro ed alla distribuzione ad un giocatore di 3 carte da gioco. 2
3 Dallo spazio capione si considera l evento E consistente nell estrazione della ST; scopo principale del lavoro non è quello di valutare la corrispondente probabilità di estrazione a priori, a quello di valutare la probabilità a posteriori che la ST sia appartenuta ad un particolare uoo, Gesù, sulla base di inforazioni ottenute da ricerche effettuate sul lenzuolo. Per fare ciò è necessario innanzitutto definire le possibili alternative dell evento e successivaente, traite l analisi dei risultati di ricerche, definire un grado di probabilità a posteriori per ciascuna alternativa. Lo sviluppo del odello è basato sulla concezione soggettivistica della statistica, secondo la quale la probabilità di un evento è definita coe la isura del grado di fiducia che un individuo coerente 3 attribuisce al verificarsi dell evento stesso. Essa perette di pesare i diversi coefficienti assegnati in funzione dell attendibilità dell afferazione. La valutazione dei diversi coefficienti verrà eseguita dal singolo individuo secondo l ipostazione soggettivistica della probabilità intesa coe isura del grado di fiducia attribuito al verificarsi di una certa alternativa. l odello viene poi integrato da una valutazione dell incertezza dei paraetri assegnati. Esistono diverse perplessità sull accettazione di un atteggiaento soggettivistico nei riguardi di problei scientifici e tali perplessità auentano nel caso si tratti di problei con iplicazioni di tipo religioso che possono influenzare in odo non trascurabile il giudizio dell individuo che in tale caso rischia di essere poco coerente. Secondo gli autori, un giudizio soggettivo dell assegnazione potrà tuttavia essere reso sufficienteente significativo se il risultato finale sarà ottenuto dalla sintesi di risultati espressi da olti ricercatori aventi anche diverse linee di pensiero. Per questo otivo la ricerca si sviluppa in tre fasi diverse: la pria, oggetto del presente lavoro, consiste nella forulazione di un odello interpretativo di tipo probabilistico delle prove e delle afferazioni; la seconda, riguarda la sintesi, in un centinaio di prove, delle innuerevoli analisi significative, più o eno scientifiche, eseguite sulla ST; la terza, eseguibile da ognuno che sia interessato, consiste nell assegnare a ciascuna afferazione gli opportuni paraetri richiesti dal odello e nel giungere quindi a diversi risultati. Dovrà poi essere eseguita una sintesi finale dei risultati forniti. 3) Forulazione del odello probabilistico a) Lo spazio capione è l insiee di tutte le possibili ani che possono essere distribuite ad un giocatore ed esse sono in totale 52. = b) l evento consiste nell avere estratto dallo spazio capione quel particolare azzo di 3 carte. c) Si possono definire per esepio le seguenti 3 alternative utuaente escludentisi che possono essere iportanti per il giocatore: A= avere in ano 4 re, F= avere in ano 4 assi, N= non avere in ano 4 re o 4 assi. n questa sede non interessa solo la valutazione della probabilità a priori di avere in ano una delle 3 alternative, a interessa anche la valutazione da parte del baro delle probabilità che l avversario abbia in ano una delle tre alternative, a partire dalla conoscenza di alcuni dettagli. Per esepio il baro sa che () tutte le figure hanno un segno rosso, (2) tutte le carte di valore dispari hanno un segno verde, (3) il fante, il re e l asso di cuori hanno un segno blu, etc. Si suppone poi che il baro riesca a leggere il colore dei segni di tutte le carte dell avversario. A partire da questi dati si deve quindi valutare la probabilità a posteriori che l avversario abbia in ano l alternativa A, F o N. Nota 3 : Per esepio la probabilità di un evento può essere intesa coe la quota di scoessa che un individuo coerente è disposto a pagare per ricevere l iporto di una unità se l evento si verifica. Si tratta di individuo coerente nel senso che egli deve accettare la scoessa della quota prescelta sia da giocatore che da banco. 3
4 3.) Definizione delle alternative. Si considerano 3 diverse alternative che hanno causato l evento E; esse coprendono le ipotesi più plausibili riguardanti l origine della ST; esse sono possibili, a tra loro escludentisi, e vengono noinate A, F, N: -) Alternativa A: la ST è autentica; essa ha avvolto il corpo di Gesù; -2) Alternativa F: la ST è falsa, edievale o post-edievale: può essere un dipinto o l opera di un cosiddetto geniale falsario assassino ; -3) Alternativa N: la ST non è autentica, a non è neeno falsa, edievale o postedievale; non sono quindi verificata le alternative A ed F ; in tale alternativa sono coprese tutte le altre possibili cause della forazione della ST, non escluso il iracolo. Ovviaente il odello è adatto anche all analisi di 2 sole alternative, per esepio la ST è o non è un dipinto ; in tale caso si dovranno porre nulli tutti i coefficienti relativi alla terza alternativa. 3.2) Assegnazione dei valori probabilistici All alternativa A si assegna una probabilità a priori P (A) ed una incertezza assoluta i A, all alternativa F una probabilità a priori P (F) ed una incertezza assoluta i F, all alternativa N una probabilità a priori P (N) ed una incertezza assoluta i N. n un altro lavoro [6] vengono assegnate e discusse le seguenti probabilità a priori con le corrispondenti incertezze: P (A)=0.05; i A =0.02; P (F)=0.35; i F =0.05; P (N)=0.60; i N =0.05 A ciascuna afferazione j-esia, devono essere assegnati i seguenti paraetri: - a j = probabilità che si verifichi l alternativa A in seguito all afferazione in esae, - f j = probabilità che si verifichi l alternativa F in seguito all afferazione in esae, - n j = probabilità che si verifichi l alternativa N in seguito all afferazione in esae, - i aj = incertezza assoluta assegnata alla probabilità a j dell afferazione in esae, - i fj = incertezza assoluta assegnata alla probabilità f j dell afferazione in esae, - i nj = incertezza assoluta assegnata alla probabilità n j dell afferazione in esae, - p j = peso assegnato all afferazione in esae. l peso p j può venire valutato in base a diversi fattori legati alla scientificità dell afferazione, alla sua significatività ed all eventuale dipendenza da altre prove: p j = p j p 2j p 3j () essendo: -p j : peso correlato alla scientificità dell afferazione; può essere utilizzato uno schea del tipo: - afferazione pubblicata su rivista internazionale: p j = - afferazione pubblicata: p j =0.8 - afferazione poco docuentata o ipotesi non verificata: p j =0. - afferazione avente incertezza relativa i aj /a j, i fj /f j o i nj /n j superiori al 50%: p j =0; -p 2j : peso correlato all iportanza dell afferazione secondo lo schea: - afferazione di estreo interesse: p 2j =3 - afferazione interessante: p 2j =2 - afferazione standard: p 2j = - afferazione di scarso interesse: p 2j =0.5; 4
5 -p 3j effetto di un possibile grado di correlazione con altre afferazioni con valori copresi fra 0 e. Per esepio se esistessero due afferazioni identiche si deve assegnare a ciascuna il valore p 5j =0,5. Le afferazioni soggette ad analisi sono per ipotesi seplificativa tra loro utuaente indipendenti; l eventuale dipendenza che potrà essere riscontrata, verrà considerata traite il peso p che viene proposto in questo lavoro per potere confrontare fra loro afferazioni di diversa iportanza. n [6] le afferazioni sono suddivise per argoenti per potere più facilente assegnare tali valori. Per esepio il non credente potrà assegnare p 3j =0 alle afferazioni riguardanti l Antico e Nuovo Testaento se non le riterrà significative. l credente invece potrà assegnare valori di p 3j copresi fra 0,5 e alle stesse afferazioni perché, in alcune di esse, potrebbe essere individuata una correlazione con la definizione dell alternativa A o con altre afferazioni considerate. l caso p j = non ha alcuna influenza nel prodotto (eq. 3a,b,c) e quindi una tipica afferazione deve avere tale coefficiente. l caso p j =2 eleva al quadrato il coefficiente probabilistico e quindi è coe considerare due volte nell analisi la stessa l afferazione; si applica quindi ad afferazioni di elevata significatività. Nel caso p j =0,5 si calcola la radice quadrata del coefficiente a j, f j, n j ; si ipone quindi che la afferazione sia pari a ezza afferazione tipica. Per il principio delle probabilità totali (o dell addizione, eq. A.3), per ogni afferazione j-esia, deve essere verificata la condizione relativa alla cobinazione di alternative utuaente escludentisi: a j + f j + n j = (2) cioè le probabilità assegnate per una certa afferazione devono essere in totale il 00%. 3.3) Costruzione del odello. Si tratta di accettare o eno un alternativa fra le possibili escludentisi a vicenda. l criterio probabilistico di accettazione si basa sull analisi delle afferazioni ricavate da vari esperienti o da studi eseguiti sulla ST. l risultato dell analisi consiste nell assegnare valori di probabilità alle alternative sviluppando i seguenti punti: -a) FASE. Vengono assegnate le probabilità a priori P (A), P (F), P (N), delle tre alternative ignorando copletaente i risultati delle ricerche eseguite. -b) FASE. Si calcolano le probabilità a posteriori P (A), P (F), P (N) o probabilità subordinate, di seguito indicate coe P (), essendo l indice corrispondente alle tre alternative A, F, N e P(E) la probabilità dell evento E subordinata al verificarsi dell alternativa. Sono date afferazioni da valutare traite l assegnazione dei coefficienti a j, f j, n j, p j (di indice j variabile da a ). Le probabilità P () risultano dalla coposizione delle singole probabilità (a j, f j, n j ) assegnate, per il principio delle probabilità coposte (vedi eq. A.4): P (A) = p j a j j= ; P (F) = p j f j j= ; P (N) = p j n j j= (3a, b, c) 5
6 Tenendo conto dei pesi p j assegnati alle varie afferazioni, il nuero effettivo di casi considerati, in genere diversi da, diviene quindi:. (4) = p j j= É auspicabile che sia verificata la condizione che sia uguale a, nuero di prove; in tale odo si può fare un riferiento probabilistico diretto al nuero di prove considerate. -c) Si calcolano le probabilità finali P*() a eno della costante di Bayes: P*() = P () P (), =A, F, N (5) -d) Si calcolano le probabilità P(E) dell evento E date le tre alternative che risultano, per il principio delle probabilità totali (vedi eq. A.3): P(E) = Σ (=A,F,N) P * () = P (A) P (A) + P (F) P (F) + P (N) P (N) (6) -e) FASE. Essendo le alternative A, F, N dell evento considerato possibili, a tra loro escludentisi, sono da scartare le possibilità iste. Si calcolano quindi le probabilità finali P (A), P (F), P (N) in base all applicazione della forula di Bayes: P ( ) P ( ) P ( ) =, =A, F, N (7) P( E) 4) Analisi dell incertezza Nonostante il soggettiviso dell ipostazione probabilistica, si ritiene necessario valutare l ordine di grandezza dell incertezza del risultato, in riferiento alla Guida per l espressione dell incertezza [7], ipotizzando distribuzioni di probabilità rettangolari dell incertezza, convertite in equivalenti gaussiane dividendo i valori per,7. Sono da intendersi, ove non specificato diversaente incertezze assolute. Vengono assegnate le incertezze i A, i F, i N delle probabilità a priori e le incertezze i aj, i fj, i nj, (j =,) delle probabilità delle afferazioni considerate. Scopo dell analisi è la deterinazione delle incertezze i A, i F, i N delle probabilità finali. Si assue l ipotesi seplificativa che il grado di correlazione sia nullo e che quindi non copaiano le coponenti iste di incertezza nelle forule di propagazione. 4. Regole pratiche per l applicazione del odello Vengono elencati alcuni criteri proposti per ottenere risultati attendibili. -) Se le probabilità finali P (A), P (F), P (N), fossero affette da incertezza troppo elevata, è necessario che per ogni afferazione l incertezza relativa i /P() sia inferiore ad un prefissato valore. L incertezza relativa liite nel presente lavoro viene assunta 4 pari al 50%. 4 L incertezza relativa liite è funzione sia del nuero di afferazioni oggetto di analisi, sia del risultato in quanto (eq. 7) risultati probabilistici percentualente olto diversi perettono in alcuni casi di accettare anche incertezze relativaente elevate. Per definire l incertezza liite i l, si può assuere una relazione del tipo: K i l = % essendo il nuero di afferazioni in esae e K un coefficiente scelto pari a 500 nel presente lavoro. 6
7 Se l incertezza supera il valore liite si assue che la afferazione sia poco significativa e la si scarta assegnando un peso p=0. -2) Dato che nessuna afferazione, in riferiento alle ricerche eseguite [6], è in grado di diostrare con assoluta certezza una delle alternative (in caso contrario sarebbe inutile applicare il odello probabilistico proposto!), si ipone che il valore inio assegnato alle alternative a j, f j, n j sia superiore o uguale a Ciò equivale a supporre di non disporre di afferazioni così certe da assegnare probabilità igliori di su ) Si ottiene (eq. 2): a j = - f j - n j ; f j = - a j - n j ; n j = - a j - f j (8a, b, c) e quindi, assegnate due incertezze assolute, si valuta la terza secondo una delle relazioni derivanti dall applicazione dell eq. (A2. 0): i = i 2 + i 2 ; i = i 2 + i 2 ; i = i + i aj fj nj fj aj nj 2 2 nj aj fj (9a,b,c) 4.2) Propagazione dell incertezza al risultato. Per deterinare le incertezze i A, i F, i N delle probabilità P (), si applica l eq. (A2. 0) alle equazioni (3a,b,c) e si ottiene: i a p i pj a j A = j j j j a = = j i f p i pj f j F = j j j j f = = j i n p i pj n j N = j j j j n = = j (0a) (0b) (0c) Per deterinare le incertezze i A, i F, i N delle probabilità finali P (), si applica l eq. (A2. 0) all eq. (7) e si ottiene: i = P ( A) A A i = P ( F) F F i = P ( N) N N i i i A P E + P A + P A ( ) ( ) ( ) P( E) i i i F P E + P F + P F ( ) ( ) ( ) P( E) i i i N P E + P N + P N ( ) ( ) ( ) P( E) (a) (b) (c) essendo i P(E) l incertezza sulla probabilità dell evento E: 7
8 ip ( E) = ( P ( A) i A ) + ( P ( A) i A ) + ( P ( F) i F ) + ( P ( F) i F ) + ( P ( N) i N ) + ( P ( N) i N ) (2) Estendendo alle probabilità finali l eq. (2), si ha: P (A) + P (F) + P (N) = (3) e quindi: P (A) = - P (F) - P (N); P (F) = - P (N) - P (A); P (N) = - P (A) - P (F) (4) Assegnate due incertezze assolute si può valutare la terza secondo una delle relazioni derivanti dall applicazione dell eq. (A2. 0): ( ) ( ) ; i f = ( i n ) + ( i a ) ; i n = ( i a ) + ( i f ) i = i + i a f n 2 2 (5a,b,c) 5) Risultati Coe esepio, si applica il odello proposto, alle afferazioni discusse in [4] : vengono considerate 7 afferazioni supponendo l esistenza di due sole alternative: - alternativa A: la ST è autentica; - alternativa F: la ST è falsa, alle quali l autore può avere assegnato iplicitaente le seguenti probabilità a priori: - P (A)=0.5; P (F)=0.5. Non essendo considerata l alternativa N ed il peso p, si pone: - P (N) = 0; P (N) = 0; P (N) = 0; p j =; non viene inoltre valutata l incertezza nella pria fase dell esepio; nella seconda fase gli autori assegneranno a titolo di esepio alcuni valori indicativi. 5. Esepio applicativo parte Le afferazioni oggetto dell analisi sono le seguenti: ) L UST ha avuto un lenzuolo [a =0.667, f =0.333]; 2) L UST è riasto poco tepo nel lenzuolo [a 2 =0.95, f 2 =0.05]; 3) l sangue dell UST risulta perfettaente separato dalla tela senza sbavature o striature [a 3 =0.98, f 3 =0.02]; 4) L UST è stato fissato alla croce con chiodi [a 2 =0.333, f 2 =0.667]; 5) Sull UST appaiono le ferite di un casco di spine: [a 2 =0.999, f 2 =0.00]; 6) L UST ha ricevuto un colpo di lancia al costato destro [a 2 =0.80, f 2 =0.20]; 7) l volto dell UST presenta un espressione aestosa e triste, e nello stesso tepo, nobilente serena [a 2 =0.9999, f 2 =0.000]; Applicando le eq. (3a,b), si ottengono le seguenti probabilità P (): - P (A) = 0.653; P (F) = = / Dall eq. (6) si ottiene P(E): 8
9 - P(E) = P (A) P (A) + P (F) P (F) = Dall eq. (7) si ottengono le probabilità finali P (A), P (F): - P (A) = ; P (F) = = / Anziché una probabilità su 225 iliardi risulterebbe quindi una probabilità su circa 8 iliardi Esepio applicativo parte Si assue [6] : P (A)=0.05; i A =0.02; P (F)=0.95; i F =0.02. Dall eq. (9a,b), risulta i a =i f =i; si assegnano quindi le seguenti incertezze: ) i=0,; 2) i=0,02; 3) i=0,0; 4) i=0,; 5) i=0,0003; 6) i=0,08; 7) i=0,00003 Risulta quindi: P (A) = 0.65; P (F) = ; =7; P(E) = ; P (A) = ; P (F) = =/ ; i = Risulta quindi che la probabilità che la ST sia falsa è: P (F) = pari a circa / con un incertezza del 00%. L elevata incertezza del risultato è dovuta alle incertezze, percentualente di entità elevata, che sono state assegnate. l risultato P (F) può quindi variare, con un grado di confidenza del 95%, tra 0 e / Secondo le afferazioni considerate e le probabilità con relative incertezze assegnate, questo significa che la probabilità che la ST sia falsa, anziché essere pari a una su 225 iliardi [4], essa oscilla tra zero ed una probabilità su un iliardo. 6) Discussione A questo punto può sorgere un dubbio sul significato fisico del risultato dell indagine probabilistica proposta; il dubbio riguarda l interpretazione del risultato in terini di accettazione o eno di una possibile alternativa. Si può ricondurre il problea alla definizione di una probabilità liite oltre la quale il risultato non sia scientificaente accettabile. n riferiento ad un esepio pratico, si consideri la seguente afferazione Ogni anno, un cubo in granito di di lato, non sollecitato da forze esterne, si solleva di aleno un etro da terra. Chiunque è sicuro che tale afferazione sia assolutaente falsa perché si descrive un fenoeno fisicaente ipossibile. Tuttavia questo non risulterebbe così chiaraente da una dettagliata indagine probabilistica. Si dovrebbe considerare la cobinazione probabilistica di tutte le forze indotte dagli urti casuali delle olecole costituenti sia il blocco in granito che l abiente circostante. 5 Nota: Se non venissero considerate le probabilità P (), si giungerebbe alle seguenti probabilità finali: P (A) = ; P (F) = = /
10 l calcolo delle probabilità fornirebbe un risultato possibile con una probabilità di uno diviso un nuero seguito da qualche decina di iliardi di zeri. Se dal punto di vista teorico il risultato è estreaente iprobabile a possibile, dal punto di vista pratico il risultato è invece da considerarsi effettivaente ipossibile. Non è ancora copletaente definita quale possa essere la probabilità liite oltre la quale considerare ipossibile un fenoeno fisico. Si può pensare all esepio del gioco della roulette. La probabilità che esca il nuero 36 dopo una giocata è /37 (esistono tutte le possibilità coprese tra lo zero ed il nuero 36); la probabilità che esca due volte consecutive il nuero 36 è /37 2 =/369; la probabilità che esca cento volte consecutive il nuero 36 è /37 00 cioè un uno diviso un nuero seguito da 56 zeri. Secondo gli autori, potrebbe essere definita ipossibile un alternativa che abbia una probabilità di verificarsi dell ordine di /0 30 che corrisponderebbe alla probabilità di ottenere 9 volte consecutive 6 l uscita del nuero 36 alla roulette. Secondo questa ipostazione la probabilità P (F), variabile tra zero e su un iliardo fornisce la seguente inforazione: anche se è olto iprobabile che la ST sia falsa, tale alternativa non è da escludersi. Risulterebbe però più probabile che esca il nuero 36 per 5 volte consecutive al gioco della roulette che la ST sia falsa. 7) Conclusioni l odello probabilistico proposto, per eventi utuaente escludentisi, è capace di sintetizzare i olteplici ed anche contrastanti risultati delle ricerche sulla ST. Esso si basa sulla definizione di tre alternative possibili (A= autentica, F= falsa, N= non autentica) per l origine del lenzuolo e sulla valutazione di ciascuna alternativa sulla base dell assegnazione di opportune probabilità, con relativa incertezza, a ciascun risultato delle ricerche copiute. L esepio applicativo considerato confronta i risultati ottenuti da un analisi probabilistica eseguita su sole 7 afferazioni, con quelli già elaborati più seplicisticaete in bibliografia indicando che l alternativa (F) può variare, con un grado di confidenza del 95%, tra 0 e / La probabilità che la ST sia falsa, secondo le afferazioni considerate, anziché essere di una su 225 iliardi, coe proposto in bibliografia [4], oscilla quindi tra zero ed una probabilità su un iliardo. Se vengono rispettate tutte le condizioni di applicabilità, il odello può essere utilizzato per sintetizzare un nuero assai più elevato di risultati scientifici (anche 00): questo è l oggetto di un altro studio [6]. Bibliografia ) P. Baia Bollone: La Sindone, la prova, ed. Mondadori ) O. Petrosillo, E. Marinelli: La Sindone: storia di un eniga, ed. Rizzoli 998 3) C. Papini: Sindone: una sfida alla scienza e alla fede, ed. Claudiana, Torino, ) P. DeGail: Le visage de Jesus Christ et son linceul Éditions France-Epire, Paris 972 5) B. Barberis, P. Savarino: Sindone, radiodatazione e calcolo delle probabilità, ed Elle Di Ci, 997 Nota 6 : Per ottenere il risultato si applica la relazione : n = [log ] / [log 0 (/37)] = 30 /,568 = 9 essendo n il nuero di volte consecutive che esce il nuero 36. 0
11 6) G. Fanti, E. Marinelli Risultati di un odello probabilistico applicato alle ricerche eseguite sulla Sindone di Torino, Congresso nternazionale di Studi sulla Sindone, Torino, Giugno ) SO-GUM Guide to expression of Uncertainty in Measureent, SO 993 8) B. de Finetti: La logica dell incerto, l Saggiatore, Milano ) D. Costantini: ntroduzione alla probabilità Boringhieri, Torino 977. APPENDCE : Richiai di probabilità e di stia statistica Si consideri un qualsiasi insiee Ω di eleenti ω; l insiee Ω è noinato spazio capione e gli eleenti ω punti capione. Evento casuale è un insiee E di punti capione e quindi un sottoinsiee dello spazio capione Ω. L insiee forato da un solo punto capione è detto seplice, se è forato da più punti è detto coposto. Si ricorda dall algebra degli eventi che, dati due eventi E ed E 2, l evento E E 2 (intersezione) si verifica se e solo se si verificano congiuntaente E ed E 2, entre l evento E E 2 (unione) si verifica se e solo se si verificano aleno uno dei due eventi E ed E 2, Un evento è detto totale se si può realizzare in diversi odi escludentisi a vicenda ed ha per probabilità la soa delle probabilità delle diverse alternative. Si chiaa isura di probabilità o distribuzione di probabilità su un insiee Ω una funzione P definita per tutti gli eventi di Ω con le seguenti proprietà: -a) ad ogni evento è associato un nuero reale non negativo P(E) detto probabilità dell evento E -b) se si hanno 2 eventi E ed E 2 di Ω utuaente esclusivi, tali che P(E E 2 ) =0, si ha: P(E E 2 ) = P(E )+P(E ) (A.) -c) la probabilità che si verifichi Ω è pari a uno: P(Ω)=. Due eventi A e B si dicono indipendenti se la probabilità di intersezione di A e B è uguale al prodotto 7 delle probabilità di A e di B: P(A B) = P(A) P(B) (A.2) Si considerano eventi indipendenti nel senso che i diversi punti capione considerati non sono tra loro correlati. La probabilità totale che si verifichi aleno uno di più eventi escludentisi a vicenda o utuaente incopatibili è pari alla soa delle probabilità dei singoli eventi (principio delle probabilità totali o dell addizione). La probabilità dell evento unione di n eventi utuaente esclusivi è la soa delle probabilità 8 dei singoli eventi, P( E) = P( E i ) n i= (A.3) La probabilità coposta che si verifichino più eventi utuaente copatibili è pari al prodotto delle probabilità dei singoli eventi (principio delle probabilità coposte o della oltiplicazione): P( E) = P( E i ) n i= (A.4) Nota 7 : L indipendenza è verificata se il risultato del prio evento non condiziona la probabilità del secondo. Per esepio si consideri un dado a 6 facce senza difetti lanciato 2 volte: la probabilità che la pria volta esca 4 e la seconda esca 6 corrisponde ad (/6)(/6)=/36. Nota 8 : Per esepio la probabilità che esca oppure 3 oppure 6 in un lancio di un dado senza difetti è (/6 + /6 + /6) = 0,50.
12 che è valida se gli eventi sono utuaente indipendenti; se gli eventi sono dipendenti, la probabilità dell evento i-esio è calcolata tenendo conto che tutti gli eventi precedenti si sono verificati. Eventi condizionati o subordinati si hanno nel caso non sia verificata l indipendenza statistica fra due eventi A e B. Se l evento A non è indipendente da B, si denota con il sibolo A B e si legge A condizionato a B. La probabilità dell evento A condizionata all evento B è: P(A B) P(A B) = (A.5) P(B) che si può scrivere, secondo il principio delle probabilità coposte coe 9 : P(A B) = P(B) P(A B) = P(A) P(B A) (A.6) l ultia uguaglianza essendo verificata se P(A) 0. Eventi indipendenti: se invece gli eventi A e B sono indipendenti, cioè se la probabilità di intersezione di A e B è uguale al prodotto delle probabilità di A e di B, si ha: P(A B) = P(A) (A.7) cioè non è di nessun rilievo il fatto che si verifichi B ai fini dell evento A. n tale caso secondo il principio delle probabilità coposte si ha 0 : P(A B) = P(A)P(B) (A.8) Si tratta di accettare o eno un alternativa A, F, N fra le possibili a priori, ciascuna delle quali si esclude a vicenda, in base all analisi delle afferazioni ricavate da diversi esperienti e studi sulla ST. Si consideri la probabilità che l evento E che si verifica ad una ed una sola delle tre alternative A, F, N. Per il principio delle probabilità totali, la probabilità dell evento E è: P( E) = P( E ) (A.9) = A, F, N Per il principio delle probabilità coposte, P( E ) è la probabilità che si verifichi sia l evento E che l alternativa e corrisponde all equazione (A.6) avendo sostituito A e B a ed E. APPENDCE 2: Richiai di analisi dell incertezza Siano date una variabile x e una variabile dipendente y=f(x). Si suppone di valutare x un certo nuero di volte, per stabilirne il valore edio e la relativa ripetibilità (t σ) data dal prodotto dello scarto quadratico edio per il fattore di copertura t che dipende dal grado di confidenza stabilito. Nota 9 : Per esepio nel lancio di un dado senza difetti a 6 facce, l evento A sia l uscita della faccia col 4 e l evento B sia l uscita di una faccia col nuero pari. La probabilità di A è /6 e la probabilità di B è /2. La probabilità di A condizionata a B, è aggiore e risulta P(A B) =/3 poiché dall eq. (A.5) si ha P(B)=/2 e P(A B)=/6. Nota 0 : Per esepio da un urna con 0 dischetti di cui 3 rossi e 7 neri, si estraggano due dischetti senza riettere il prio nell urna e si supponga che ogni dischetto abbia uguale probabilità di essere estratto. Si considerano i seguenti eventi: A: al prio colpo si estrae un dischetto rosso ; B: al prio ed al secondo colpo si estrae un dischetto rosso ; C: al secondo colpo si estrae un dischetto rosso. Lo spazio capione Ω è costituito da (0x9=90) risultati. A è forato da (3x9= 27) punti perché ci sono 3 possibili scelte per il prio dischetto e 9 per il secondo; B è forato da (3x2=6) punti. Le probabilità degli eventi A, B, C sono: P(A) =(3x9):(0x9) = 0.3 ; P(B) = (3x2):(0x9) = :5 = P(C) =(7x3 + 3x2 perché è possibile pescare o uno dei 7 dischetti neri la pria volta e uno dei 3 rossi la seconda volta, oppure uno dei 3 dischetti rossi la pria volta e uno dei 2 riasti la seconda volta):(0x9) = 0.3 La probabilità condizionata di C dato A, cioè la probabilità di C supponendo verificato l evento A è: P(C A) P(B) P(C A) = = = (6/90)/ (27/90) = 20/90 = P(A) P(A) Se invece si riettesse il dischetto pescato nell urna si avrebbero eventi indipendenti e quindi la probabilità P (B) che si verifichi l evento C subordinato ad A (e quindi l evento B) sarebbe: P (B) = P(A) P(C) = 0.3x0.3 = 0.09 > P(B) = essendo P(A)=(3x0=30), P(B)=(3x3=9), P(C)=(0x3=30). 2
13 n generale si adotta il grado di confidenza (P= 95%) in tutti i calcoli dell incertezza a cui corrisponde un fattore di copertura t=2 se il capione è sufficienteente nueroso. l valore di x sarà copreso entro l intervallo x ±tσ, e si suppone che il valore di y cada entro l intervallo definito da: y ±δ y = f ( x ±tσ ) (A2.) Sviluppando la (4.) in serie di Taylor, si ottiene: dy y ±δ y = f ( x )± tσ + 2 d y ( t σ) dx 2 x = x ] (A2.2) 2 dx x= x l valore edio di y sarà pari a f ( x ). l terine fra parentesi quadra sarà quindi la stia di δ y. Facendo un approssiazione lineare diδ y, si ottiene: δ y dy. t σ (A2.3) dx x = x ove il terine dy è l indice della sensibilità di y ai cabiaenti di x. L incertezza i y di y dipende dx x = x dall incertezza i x di x, secondo la relazione: i y = dy i x (A2.4) dx x = x Estendendo il odello a relazioni ultivariabili, si considera un risultato q deterinato dalla relazione: q=f (x, x 2,..., x L ); (x,..., x L, = variabili indipendenti) (A2.5) La igliore stia del valore isurato q sarà: q =q ± i q (P%) (A2.6) ove il valore edio è ricavato da: q=f ( x, x,..., x ) 2 L (A2.7) e l incertezza i q è ottenuta da: i q = f 2 ( i,i,...,i ) x x2 xl (A2.8) Definito l indice di sensibilità coe: ϑ i = q x = x i =, 2,..., L (A2.9) x i in riferiento ai cabiaenti di ogni x i riguardo q; il contributo quindi dell incertezza di x i al risultato q è stiato dal terine ( ϑ i i xi ). La stia più probabile di i q è data dalla forula: L i q = ± ( i ) 2 ϑ i xi (P%) (A2.0) i= 3
Confronto fra valore del misurando e valore di riferimento (1 di 2)
 Confronto fra valore del isurando e valore di riferiento (1 di 2) Talvolta si deve espriere un parere sulla accettabilità o eno di una caratteristica fisica del isurando ediante il confronto fra il valore
Confronto fra valore del isurando e valore di riferiento (1 di 2) Talvolta si deve espriere un parere sulla accettabilità o eno di una caratteristica fisica del isurando ediante il confronto fra il valore
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Corso di Matematica. Corso di Laurea in Farmacia, Facoltà di Farmacia. Università degli Studi di Pisa. Maria Luisa Chiofalo.
 Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Capitolo 4 Probabilità
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Sistemi di Numerazione
 Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
STATISTICA IX lezione
 Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti. Enrico Saltari Università di Roma La Sapienza
 MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Un gioco con tre dadi
 Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
PRINCIPIO DI INDUZIONE. k =. 2. k 2 n(n + 1)(2n + 1) 6
 PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn. 2 Esercizio 2. Diostrare che per ogni n si ha 2 2 nn 2n. Soluzione Procediao per induzione: la 2 è ovviaente vera per
PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn. 2 Esercizio 2. Diostrare che per ogni n si ha 2 2 nn 2n. Soluzione Procediao per induzione: la 2 è ovviaente vera per
LAVORO ED ENERGIA Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
 Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
PROGETTO INDAGINE DI OPINIONE SUL PROCESSO DI FUSIONE DEI COMUNI NEL PRIMIERO
 PROGETTO INDAGINE DI OPINIONE SUL PROCESSO DI FUSIONE DEI COMUNI NEL PRIMIERO L indagine si è svolta nel periodo dal 26 agosto al 16 settembre 2014 con l obiettivo di conoscere l opinione dei residenti
PROGETTO INDAGINE DI OPINIONE SUL PROCESSO DI FUSIONE DEI COMUNI NEL PRIMIERO L indagine si è svolta nel periodo dal 26 agosto al 16 settembre 2014 con l obiettivo di conoscere l opinione dei residenti
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9
 Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9 19 Carte di colore Blu che vanno dallo 0 al 9 19 Carte di colore Giallo che
Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9 19 Carte di colore Blu che vanno dallo 0 al 9 19 Carte di colore Giallo che
Statistica 1. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Test statistici di verifica di ipotesi
 Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Il mercato assicurativo: selezione avversa, fallimenti del mercato, menù di contratti, assicurazione obbligatoria
 Il mercato assicurativo: selezione avversa, fallimenti del mercato, menù di contratti, assicurazione obbligatoria Esercizio 1 Ci sono 2000 individui ciascuno con funzione di utilità Von Neumann-Morgestern
Il mercato assicurativo: selezione avversa, fallimenti del mercato, menù di contratti, assicurazione obbligatoria Esercizio 1 Ci sono 2000 individui ciascuno con funzione di utilità Von Neumann-Morgestern
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Inferenza statistica. Statistica medica 1
 Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
La teoria dell utilità attesa
 La teoria dell utilità attesa 1 La teoria dell utilità attesa In un contesto di certezza esiste un legame biunivoco tra azioni e conseguenze: ad ogni azione corrisponde una e una sola conseguenza, e viceversa.
La teoria dell utilità attesa 1 La teoria dell utilità attesa In un contesto di certezza esiste un legame biunivoco tra azioni e conseguenze: ad ogni azione corrisponde una e una sola conseguenza, e viceversa.
La probabilità di avere non più di un maschio, significa la probabilità di averne 0 o 1: ( 0) P( 1)
 Esercizi sulle distribuzioni binoiale e poissoniana Esercizio n. Una coppia ha tre figli. Calcolare la probabilità che abbia non più di un aschio se la probabilità di avere un aschio od una feina è sepre
Esercizi sulle distribuzioni binoiale e poissoniana Esercizio n. Una coppia ha tre figli. Calcolare la probabilità che abbia non più di un aschio se la probabilità di avere un aschio od una feina è sepre
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Rappresentazione dei numeri in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi di calcolo combinatorio
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Incompatibilità ed indipendenza stocastica. Probabilità condizionate, legge della probabilità totale, Teorema
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 7 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Incompatibilità ed indipendenza stocastica. Probabilità condizionate, legge della probabilità totale, Teorema
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
Esercizi di Ricerca Operativa II
 Esercizi di Ricerca Operativa II Raffaele Pesenti January 12, 06 Domande su utilità 1. Determinare quale è l utilità che un giocatore di roulette assegna a 100,00 Euro, nel momento che gioca tale cifra
Esercizi di Ricerca Operativa II Raffaele Pesenti January 12, 06 Domande su utilità 1. Determinare quale è l utilità che un giocatore di roulette assegna a 100,00 Euro, nel momento che gioca tale cifra
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
LEZIONE 3. Ing. Andrea Ghedi AA 2009/2010. Ing. Andrea Ghedi AA 2009/2010
 LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
1. Scopo dell esperienza.
 1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
VERIFICA DELLE IPOTESI
 VERIFICA DELLE IPOTESI Nella verifica delle ipotesi è necessario fissare alcune fasi prima di iniziare ad analizzare i dati. a) Si deve stabilire quale deve essere l'ipotesi nulla (H0) e quale l'ipotesi
VERIFICA DELLE IPOTESI Nella verifica delle ipotesi è necessario fissare alcune fasi prima di iniziare ad analizzare i dati. a) Si deve stabilire quale deve essere l'ipotesi nulla (H0) e quale l'ipotesi
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA REGIMI DI FUNZIONAMENTO DEI CIRCUITI ELETTRICI: CORRENTE CONTINUA
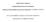 APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURZZA RGIMI DI FUNZIONAMNTO DI CIRCUITI LTTRICI: CORRNT CONTINUA SOLO ALCUNI SMPI DI ANALISI DI UN CIRCUITO LTTRICO FUNZIONANTI IN CORRNT CONTINUA APPUNTI DL
APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURZZA RGIMI DI FUNZIONAMNTO DI CIRCUITI LTTRICI: CORRNT CONTINUA SOLO ALCUNI SMPI DI ANALISI DI UN CIRCUITO LTTRICO FUNZIONANTI IN CORRNT CONTINUA APPUNTI DL
Statistiche campionarie
 Statistiche campionarie Sul campione si possono calcolare le statistiche campionarie (come media campionaria, mediana campionaria, varianza campionaria,.) Le statistiche campionarie sono stimatori delle
Statistiche campionarie Sul campione si possono calcolare le statistiche campionarie (come media campionaria, mediana campionaria, varianza campionaria,.) Le statistiche campionarie sono stimatori delle
15. Antico gioco russo
 15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
REGOLAMENTO ROULETTE 3D
 REGOLAMENTO ROULETTE 3D La Roulette 3D appartiene alla famiglia dei Giochi di sorte a quota fissa. Il gioco della Roulette 3D prevede una pallina che, lanciata in direzione opposta rispetto ad una ruota
REGOLAMENTO ROULETTE 3D La Roulette 3D appartiene alla famiglia dei Giochi di sorte a quota fissa. Il gioco della Roulette 3D prevede una pallina che, lanciata in direzione opposta rispetto ad una ruota
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
Corso di. Dott.ssa Donatella Cocca
 Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico
 Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico 1.1 Lo schema di misurazione Le principali grandezze elettriche che caratterizzano un bipolo in corrente continua, quali per esempio
Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico 1.1 Lo schema di misurazione Le principali grandezze elettriche che caratterizzano un bipolo in corrente continua, quali per esempio
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
COMPITO DI SCIENZE NATURALI 23 gennaio 2012. Modulo di probabilità e statistica
 COMPITO DI SCIENZE NATURALI 23 gennaio 2012 Modulo di probabilità e statistica 1. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza annuale.
COMPITO DI SCIENZE NATURALI 23 gennaio 2012 Modulo di probabilità e statistica 1. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza annuale.
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 14 marzo 2013 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2013.html IL PARI O DISPARI I II S T S (-1, 1) (1, -1)
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 14 marzo 2013 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2013.html IL PARI O DISPARI I II S T S (-1, 1) (1, -1)
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
Pro e contro delle RNA
 Pro e contro delle RNA Pro: - flessibilità: le RNA sono approssimatori universali; - aggiornabilità sequenziale: la stima dei pesi della rete può essere aggiornata man mano che arriva nuova informazione;
Pro e contro delle RNA Pro: - flessibilità: le RNA sono approssimatori universali; - aggiornabilità sequenziale: la stima dei pesi della rete può essere aggiornata man mano che arriva nuova informazione;
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Teoria della probabilità Assiomi e teoremi
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Assiomi e teoremi A.A. 2008-09 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Assiomi e teoremi A.A. 2008-09 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento
Operatori logici e porte logiche
 Operatori logici e porte logiche Operatori unari.......................................... 730 Connettivo AND........................................ 730 Connettivo OR..........................................
Operatori logici e porte logiche Operatori unari.......................................... 730 Connettivo AND........................................ 730 Connettivo OR..........................................
I.T.I. Modesto PANETTI B A R I
 I.T.I. Modesto PAETTI B A R I Via Re David, 86-705 BARI 080-54.54. - Fa 080-54.64.3 Intranet http://0.0.0. - Internet http://www.itispanetti.it eail : BATF05000C@istruzione.it Introduzione Analisi statistica
I.T.I. Modesto PAETTI B A R I Via Re David, 86-705 BARI 080-54.54. - Fa 080-54.64.3 Intranet http://0.0.0. - Internet http://www.itispanetti.it eail : BATF05000C@istruzione.it Introduzione Analisi statistica
