Probabilità discreta
|
|
|
- Simone Elia
- 9 anni fa
- Visualizzazioni
Transcript
1 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che può avere diversi esiti, alcuni dei quali consideriamo favorevoli e altri sfavorevoli (per esempio un lancio di dado dal quale vogliamo ottenere un certo punteggio), ed è possibile contare questi esiti, allora è anche possibile calcolare la probabilità di ottenere un esito favorevole. Il principio basilare è che la probabilità di ottenere un esito favorevole è uguale al numero di esiti favorevoli diviso per il numero di esiti possibili. (Ricordiamo che nel calcolo delle probabilità, la probabilità di un evento è un numero compreso tra 0 e 1: in prima approssimazione, 0 corrisponde all impossibilità e 1 alla certezza.) Un esempio semplice è dato dal lancio di un dado a sei facce numerate da 1 a 6. Poniamo di considerare favorevole un punteggio di 5 o 6. Allora gli esiti favorevoli sono due, mentre gli esiti possibili sono sei (tutti i possibili risultati che può dare il lancio del dado). Quindi la probabilità di un esito favorevole è pari a /6, cioè 1/3. Chiaramente qui stiamo assumendo che il dado sia bilanciato, cioè che ogni risultato sia ugualmente probabile. Più formalmente, chiamiamo X l insieme di tutti gli esiti possibili, detto anche spazio campione. Qualsiasi sottoinsieme Y X è detto evento; in quello che abbiamo detto finora fissiamo la nostra attenzione su un particolare evento, e consideriamo i suoi elementi come esiti favorevoli. Allora la probabilità P(Y ) che si realizzi un certo evento (cioè che un dato fenomeno abbia esito favorevole) è data da: P(Y ) = Y X. Quindi, in questi casi, il problema di calcolare una probabilità si riconduce a quello di calcolare le cardinalità di due insiemi: quella di tutto lo spazio campione e quella dell evento che ci interessa. E la combinatoria ci dà numerosi strumenti per calcolare le cardinalità di opportuni insiemi. Esempio: Ottenere k teste su n lanci di moneta. Supponiamo di voler tirare per quattro volte di seguito una moneta, e di voler ottenere testa almeno tre 1
2 volte. Qual è la probabilità che ciò accada? Descriviamo i risultati di una serie di lanci con una stringa di 1 e 0, in cui 1 rappresenta testa e 0 rappresenta croce. Quindi un serie di lanci in cui si ottenga testa-croce-testa-testa verrebbe rappresentata con la stringa Tutte le possibili serie di quattro lanci (o equivalentemente, tutte le possibili stringhe di lunghezza 4 composte da due simboli) sono 16 = 4 ; il nostro spazio campione X ha quindi cardinalità 16. Quante di queste serie di lanci compongono l evento che ci interessa, quello delle serie con almeno tre teste? Facendo il conto a mano, si vede che o tutti e quattro i lanci hanno devono dare come risultato testa, o ci deve essere un unica croce che può trovarsi in una qualsiasi delle quattro posizioni: quindi gli eventi favorevoli corrispondono alle cinque stringhe 1111, 0111, 1011, 1101 e Perciò la probabilità di ottenere il risultato richiesto è pari a 5/16. Generalizziamo questa situazione. Qual è la probabilità di ottenere almeno, o esattamente, k teste lanciando una moneta n volte? I possibili esiti di n lanci di una moneta sono n : infatti, ci sono due possibilità per il risultato del primo lancio; ce ne sono di nuovo due per il risultato del secondo, che è indipendente dal primo, e così via. Come detto sopra, stiamo semplicemente contando le stringhe di lunghezza n, o n-ple, composte da due simboli, per esempio 0 e 1. Quindi lo spazio campione X ha cardinalità n. Ricordiamo che queste n-ple, a loro volta, descrivono ognuna un sottoinsieme dell insieme {1,,...,n}: infatti la presenza di un 1 nella i-esima posizione corrisponde a dire che l elemento i appartiene al sottoinsieme. Per esempio, per n = 5, la stringa corrisponde alla presenza del secondo e quinto elemento, cioè al sottoinsieme {, 5} dell insieme {1,, 3, 4, 5}. Consideriamo prima i lanci in cui testa compare esattamente k volte. Dobbiamo cioè contare le n-ple contenenti esattamente k cifre 1. Per contarle, dobbiamo contare tutti i modi in cui possiamo scegliere esattamente k posizioni tra le n a nostra disposizione. Per definizione di coefficiente binomiale, queste scelte sono esattamente ( n k), che è quindi la cardinalità dell evento Yk che stiamo considerando. Di nuovo, le n-ple con esattamente k cifre 1 corrispondono ai sottoinsieme con esattamente k elementi. Per esempio, le ( 5 ) = 10 stringhe di lunghezza 5 con due cifre 1 corrispondono ai 10 sottoinsiemi di cardinalità di {1,,3,4,5}: la stringa corrisponde a {1, }, corrisponde a {1, 3} e così via. Quindi la probabilità di ottenere esattamente k risultati testa su n lanci è pari a Y k / X, cioè a ( n k) / n. E se ci interessa sapere qual è la probabilità di ottenere almeno k teste, basterà considerare come nuovo evento l unione degli eventi Y k, Y k+1,..., Y n : chiamiamo Y questo nuovo evento. Osserviamo che Y k, Y k+1,..., Y n sono disgiunti tra loro (per esempio, se in una serie di lanci si sono
3 ottenute esattamente 3 teste non se ne sono ottenute anche esattamente 4). Quindi la cardinalità di Y è uguale alla somma delle cardinalità di Y k, Y k+1,..., Y n, cioè: n n ( ) n Y = Y i =. i In conclusione, la probabilità di ottenere almeno k teste in n lanci è: ( n i) i=k P(Y ) = n i=k i=k n. Attenzione, se gli eventi che stiamo studiando non sono disgiunti, cioè se hanno qualche elemento in comune, non è più sufficiente sommare le loro cardinalità: bisogna invece calcolare la cardinalità della loro unione. Per esempio, se in un lancio di dado vogliamo ottenere un numero dispari oppure un numero minore di 4, l evento A che ci interessa è dato dall unione di B = {numeri dispari compresi tra 1 e 6} = {1, 3, 5} e di C = {numeri compresi tra 1 e 6 minori di 4} = {1,,3}. Ora, B ha cardinalità 3, C ha cardinalità 3, ma A = B C non ha cardinalità 3+3 = 6, bensì 4, perché A = {1,,3,5}. Quindi la probabilità di ottenere un risultato favorevole, in questo caso, è pari a 4/6. Vari problemi analoghi a questo si possono affrontare nello stesso modo. In particolare, finché consideriamo problemi sugli esiti di lanci di monete e chiediamo che probabilità ci sia che una serie di n lanci abbia una certa proprietà, la risposta sarà sempre data da una frazione il cui denominatore sarà n e rimarrà solo da calcolare quante successioni di lanci abbiano la proprietà richiesta. Per esempio, la probabilità che, su n lanci, in tutti gli ultimi k si ottenga testa si può ottenere calcolando quante sono le successioni di n cifre 0 e 1 tali che le ultime k siano uguali a 1. Ovviamente, visto che non abbiamo vincoli sulle prime n k cifre mentre le ultime k sono fissate, otteniamo n k possibili successioni. Dividendo per il solito denominatore n, otteniamo una probabilità pari a n k / n, cioè 1/ k. Esempio: Poker. Nel gioco del poker, si distribuiscono le carte da un mazzo in modo che ogni giocatore riceva una mano di cinque carte; deve fare in modo, eventualmente cambiando alcune delle carte in mano, di avere la combinazione di maggior valore possibile. In una delle varianti del poker (negli esercizi verranno prese in considerazione altre varianti), si gioca con tutte e 5 le carte di un mazzo completo di carte francesi (con quattro semi, per ognuno dei quali ci sono 13 carte, di valore crescente dal al 10, più fante, regina, re e asso). Il numero di mani possibili per un giocatore, cioè di possibili 5-sottoinsiemi dell insieme di 5 carte di tutto il mazzo, è naturalmente uguale al coefficiente binomiale ( ) 5 5 = Ora calcoleremo la probabilità di ottenere alcune delle combinazioni del poker che, come negli esempi precedenti, si troverà dividendo il 3
4 numero di mani che realizzano la combinazione voluta per il numero di tutte le mani possibili. (In quello che segue considereremo solo la probabilità di ottenere una data combinazione servita, cioè senza considerare la possibilità di cambiare alcune carte.) Un poker, inteso come combinazione di carte, è composto da quattro carte di uguale valore, più una quinta carta qualsiasi. Quanti sono i poker possibili? Ci sono 13 possibilità per il comune valore di queste quattro carte, e la quinta carta può essere una qualsiasi delle 48 (= 5 4) carte rimanenti. Quindi ci sono = 64 poker possibili. La probabilità di ottenere un poker servito, giocando con tutte le 5 carte, è quindi pari a 64/ ( ) 5 5 cioè circa, Un full è composto da tre carte di valore uguale e da due carte che abbiano a loro volta valore uguale (e diverso dal primo!). Per esempio, tre assi e due 7 costituiscono un full. Per contare i possibili full, possiamo fare così: 1. consideriamo i 13 possibili valori per la carta ripetuta tre volte e ne scegliamo uno;. fisstao questo valore, scegliamo i tre semi che compariranno nel full: questo si può fare in ( 4 3), cioè 4, modi possibili; 3. ora rimangono 1 scelte possibili per la carta ripetuta due volte; 4. quali due carte compariranno, tra le quattro con quel valore, si può scegliere in ( 4 ) = 6 modi. Complessivamente, ci sono = 3744 possibili full. Ne segue che la probabilità che una mano scelta a caso sia un full è 3744/ ( ) 5 5, che è dell ordine di grandezza di 1 su Una doppia coppia, come suggerisce il nome, è costituita da due carte di un certo valore, due carte di un altro valore e una quinta carta di una valore diverso dai primi due. Quindi il numero di possibili doppie coppie si può calcolare facilmente: dobbiamo scegliere un insieme di due valori tra i tredici possibili, quelli delle due carte che compaiono due volte; poi per ognuno dei due valori bisogna scegliere i due semi su quattro; infine si deve scegliere ancora un valore tra gli undici rimanenti e il relativo seme (per la carta spaiata). In tutto ci sono quindi ( ) ( 13 4 ) 11 4 doppie coppie, cioè (Si verifica quindi che la probabilità che una mano a caso sia una doppia coppia è dell ordine di grandezza di 1 su 0.) Notiamo che se avessimo scelto per primo la carta il cui valore compare una volta sola, e poi avessimo costruito la doppia coppia considerando solo i 1 valori rimanenti, avremmo ottenuto ovviamente lo stesso risultato, ma espresso diversamente: 5 (1 ) ( 4. ) Senza svolgere esplicitamente i calcoli, possiamo concludere 4
5 quindi che ( ) 13 ( ) 4 44 = 5 oppure che ( ) = 13 ( ) 1 ( ) 1. ( ) 4, Questo tipo di ragionamento, applicato in casi più generali (cioè dipendenti da alcune variabili anziché riferiti a un caso specifico con valori fissati), è alla base del cosiddetto doppio conteggio : calcolando in due modi diversi la cardinalità di un certo insieme otteniamo un uguaglianza tra due numeri o tra due espressioni. Che probabilità c è che succeda più volte o mai...? Consideriamo il seguente problema relativo ad alcuni lanci di un normale dado a sei facce. Abbiamo visto prima che la probabilità di ottenere 5 o 6 in un dato lancio è uguale a 1/3. Qual è la probabilità di ottenere 5 o 6 in ognuno di tre lanci consecutivi? I possibili esiti di tre lanci, cioè le possibili terne (a, b, c) di numeri compresi tra 1 e 6, sono 16 (cioè 6 3 ). Al solito, ora ci basta contare quante di queste terne sono composte solo di 5 e 6: tali terne sono 8 (per ogni posizione abbiamo due scelte). La probabilità cercata è quindi 8/16, cioè 1/7. C è un altro modo per ricavare la stessa probabilità. Ricordiamo che la probabilità che si verifichino vari eventi tra loro indipendenti (cioè, informalmente, i cui esiti non si influenzano a vicenda) è data semplicemente dal prodotto delle probabilità dei singoli eventi. Quindi, visto che la probabilità di ottenere 5 o 6 in un singolo lancio è 1/3, la probabilità di ottenerli in tre lanci consecutivi è (1/3) 3 = 1/7, riottenendo il risultato appena trovato. E che probabilità abbiamo che in almeno un lancio su tre si ottenga un risultato di 5 o 6? Stavolta dobbiamo contare le terne (a, b, c) in cui almeno uno dei tre valori sia pari a 5 o a 6. Il modo più semplice è contare quelle in cui nessuno dei valori è 5 o 6, e sottrare questo numero da 16, il numero di tutte le terne. Se nessun valore deve essere 5 o 6, possiamo prendere in considerazione solo i numeri da 1 a 4, e quindi abbiamo 4 3 = 64 terne; quindi quelle in cui compare almeno una volta un 5 o un 6 sono = 15, e la probabilità di ottenere una di queste è quindi 15/16 = 19/7, poco più di 0,7. Come prima, possiamo ottenere questa probabilità complessiva (quella di ottenere almeno un 5 o 6 su tre lanci) a partire dalla probabilità di un singolo lancio; ma non basta ovviamente prenderne la terza potenza, altrimenti riotterremmo il risultato di 1/7. 5
6 Ricordiamo che se p è la probabilità che un certo evento si verifichi, dove p è un numero compreso tra 0 e 1, allora la probabilità che non si verifichi è uguale a 1 p. Questa semplice considerazione è utile in circostanze in cui ci interessa che si verifichi almeno una tra varie circostanze, come qui. La probabilità di non ottenere mai l esito cercato (nel nostro caso il risultato di 5 o 6) in k lanci è uguale a (1 p) k ; quindi la probabilità di ottenerlo almeno una volta è 1 (1 p) k. Nel nostro caso troviamo 1 (1 1/3) 3 = 1 8/7 = 19/7, come sopra. 3 Esercizi 1. Lanciamo una moneta n volte: ogni volta che otteniamo testa guadagniamo un punto e ogni volta che otteniamo croce ne perdiamo uno. Qual è la probabilità di totalizzare 0 punti? Di totalizzarne uno? Di totalizzarne k?. Qual è la probabilità di lanciare una moneta n volte e ottenere sempre la stessa faccia? E di lanciarla 10 volte e ottenere 8 o più volte la stessa faccia? 3. Considerate tutte le possibili combinazioni del poker e calcolate la probabilità di ottenerle: è vero che il valore stabilito dalle regole del poker è tanto maggiore quanto minore è la loro probabilità? (Chiaramente, considerando la possibilità di cambiare alcune carte e i fattori psicologici del gioco, il valore delle varie combinazioni nella pratica può essere diverso da quello che suggeriscono le sole probabilità.) 4. Nella variante più diffusa in Europa, anziché con tutte le carte si gioca solo con quelle da 11 (numero di giocatori) all asso (per esempio, in cinque si usano le carte dal 6 in poi). Come cambiano le probabilità di ottenere le varie combinazioni? Nel gioco all americana con 5 carte il full ha valore maggiore del colore (cinque carte dello stesso seme), al contrario di quello che accade nel gioco all europea. Che cosa succede per le rispettive probabilità? 5. Qual è la probabilità di ottenere 7 lanciando due dadi a sei facce e sommando i risultati? Qual è la probabilità di ottenere k (k =, 3,..., 1)? 6. Che probabilità c è che k persone prese a caso compiano gli anni tutte il 1 gennaio? (Si consideri ugualmente probabile nascere qualsiasi giorno dell anno e si ignori il 9 febbraio.) E che probabilità c è che k persone compiano gli anni lo stesso giorno, se non fissiamo a priori questa data? 7. In un gruppo di n persone, qual è la probabilità che almeno due siano nate lo stesso giorno dell anno? Ultimo aggiornamento:
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
COEFFICIENTI BINOMIALI
 COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 9 giugno 006 Spazi di probabilità finiti e uniformi Esercizio Un urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare
Esercizi di Probabilità e Statistica Samuel Rota Bulò 9 giugno 006 Spazi di probabilità finiti e uniformi Esercizio Un urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare
Ancora sull indipendenza. Se A e B sono indipendenti allora lo sono anche
 Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Corso di Matematica. Corso di Laurea in Farmacia, Facoltà di Farmacia. Università degli Studi di Pisa. Maria Luisa Chiofalo.
 Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Capitolo 4 Probabilità
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
LEZIONE 5: CALCOLO COMBINATORIO
 LEZIONE 5: CALCOLO COMBINATORIO e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 31 Ottobre 2012 Cos è il calcolo combinatorio?
LEZIONE 5: CALCOLO COMBINATORIO e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 31 Ottobre 2012 Cos è il calcolo combinatorio?
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado
 Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Poker tradizionale a 5 carte
 Poker tradizionale a 5 carte Il poker tradizionale anche denominato poker a 5 carte o 5 card draw è la variante del gioco di carte più conosciuta e diffusa. Le regole e le modalità di gioco variano a seconda
Poker tradizionale a 5 carte Il poker tradizionale anche denominato poker a 5 carte o 5 card draw è la variante del gioco di carte più conosciuta e diffusa. Le regole e le modalità di gioco variano a seconda
8. Qual è la probabilità di estrarre da un mazzo di 40 carte napoletane una figura?
 www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea
 Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
Università di Milano Bicocca. Esercitazione 6 di Matematica per la Finanza. 14 Maggio 2015
 Università di Milano Bicocca Esercitazione 6 di Matematica per la Finanza 14 Maggio 2015 Esercizio 1 Un agente presenta una funzione di utilitá u(x) = ln(1 + 6x). Egli dispone di un progetto incerto che
Università di Milano Bicocca Esercitazione 6 di Matematica per la Finanza 14 Maggio 2015 Esercizio 1 Un agente presenta una funzione di utilitá u(x) = ln(1 + 6x). Egli dispone di un progetto incerto che
24 : 3 = 8 con resto 0 26 : 4 = 6 con resto 2
 Dati due numeri naturali a e b, diremo che a è divisibile per b se la divisione a : b è esatta, cioè con resto 0. In questo caso diremo anche che b è un divisore di a. 24 : 3 = 8 con resto 0 26 : 4 = 6
Dati due numeri naturali a e b, diremo che a è divisibile per b se la divisione a : b è esatta, cioè con resto 0. In questo caso diremo anche che b è un divisore di a. 24 : 3 = 8 con resto 0 26 : 4 = 6
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
VINCERE AL BLACKJACK
 VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Probabilità e Statistica Esercitazioni. a.a. 2006/2007
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Appunti ed esercizi di combinatoria. Alberto Carraro
 Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
PROBABILITA MISURARE L INCERTEZZA Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere?
 Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere? Abbiamo visto nella lezione precedente che lo spazio degli eventi più idoneo a rappresentare l esperimento
Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere? Abbiamo visto nella lezione precedente che lo spazio degli eventi più idoneo a rappresentare l esperimento
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Dagli insiemi al calcolo combinatorio
 Dagli insiemi al calcolo combinatorio Il calcolo combinatorio è una parte della matematica che si occupa di contare gli elementi di un insieme finito, ottenuto a partire da altri insiemi, dei quali si
Dagli insiemi al calcolo combinatorio Il calcolo combinatorio è una parte della matematica che si occupa di contare gli elementi di un insieme finito, ottenuto a partire da altri insiemi, dei quali si
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
CARTE. Regolamento Belote. Regole del gioco: Determinazione del seme di briscola (Belote classico):
 CARTE aggiornato al 25/06/2014 Entrambe le gare di carte si svolgeranno presso il salone Polivalente di Pinasca. Entrambe le gare saranno giocate da giocatori in coppia, la coppia può essere diversa nelle
CARTE aggiornato al 25/06/2014 Entrambe le gare di carte si svolgeranno presso il salone Polivalente di Pinasca. Entrambe le gare saranno giocate da giocatori in coppia, la coppia può essere diversa nelle
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
IL CALCOLO COMBINATORIO
 IL CALCOLO COMBINATORIO Giochiamo a dadi Nel XVII secolo il cavaliere De Meré, forte giocatore, come spesso accadeva fra la nobiltà di quel tempo, si pose questo quesito: Che cosa è più conveniente, scommettere
IL CALCOLO COMBINATORIO Giochiamo a dadi Nel XVII secolo il cavaliere De Meré, forte giocatore, come spesso accadeva fra la nobiltà di quel tempo, si pose questo quesito: Che cosa è più conveniente, scommettere
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Calcolo combinatorio
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Uguali? Diversi! Addomesticare l infinito Varese, ottobre 2009 M. Dedò
 Uguali? Diversi! Addomesticare l infinito Varese, ottobre 2009 M. Dedò Che cosa c entra l idea di uguali e diversi con l infinito? Tantissimi è uguale a infinito? Tutti gli infiniti sono uguali? O ci sono
Uguali? Diversi! Addomesticare l infinito Varese, ottobre 2009 M. Dedò Che cosa c entra l idea di uguali e diversi con l infinito? Tantissimi è uguale a infinito? Tutti gli infiniti sono uguali? O ci sono
COMPITO DI SCIENZE NATURALI 23 gennaio 2012. Modulo di probabilità e statistica
 COMPITO DI SCIENZE NATURALI 23 gennaio 2012 Modulo di probabilità e statistica 1. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza annuale.
COMPITO DI SCIENZE NATURALI 23 gennaio 2012 Modulo di probabilità e statistica 1. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza annuale.
1 Probabilità condizionata
 1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
Un gioco con tre dadi
 Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
Un metodo per il rilevamento degli errori: la tecnica del Bit di Parità
 Appunti: Tecniche di rilevazione e correzione degli errori 1 Tecniche di correzione degli errori Le tecniche di correzione degli errori sono catalogabili in: metodi per il rilevamento degli errori; metodi
Appunti: Tecniche di rilevazione e correzione degli errori 1 Tecniche di correzione degli errori Le tecniche di correzione degli errori sono catalogabili in: metodi per il rilevamento degli errori; metodi
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Scelte in condizioni di rischio e incertezza
 CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
Vincere a testa o croce
 Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
b. Che cosa succede alla frazione di reddito nazionale che viene risparmiata?
 Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
4. Operazioni aritmetiche con i numeri binari
 I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
ARRAY. ARRAY a 3 DIMENSIONI
 Prof. Claudio Maccherani a.s. 2005 / 2006 ARRAY 1 TRESSETTE 2 BRISCOLA 4 POKER 6 ARRAY Una VARIABILE SEMPLICE è una scatola che può contenere un oggetto alla volta. La variabile è caratterizzata dal proprio
Prof. Claudio Maccherani a.s. 2005 / 2006 ARRAY 1 TRESSETTE 2 BRISCOLA 4 POKER 6 ARRAY Una VARIABILE SEMPLICE è una scatola che può contenere un oggetto alla volta. La variabile è caratterizzata dal proprio
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
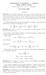 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
Soluzioni del giornalino n. 16
 Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
PROVE D'ESAME DI CPS A.A. 2009/2010. 0 altrimenti.
 PROVE D'ESAME DI CPS A.A. 009/00 0/06/00 () (4pt) Olimpiadi, nale dei 00m maschili, 8 nalisti. Si sa che i 4 atleti nelle corsie centrali hanno probabilità di correre in meno di 0 secondi. I 4 atleti delle
PROVE D'ESAME DI CPS A.A. 009/00 0/06/00 () (4pt) Olimpiadi, nale dei 00m maschili, 8 nalisti. Si sa che i 4 atleti nelle corsie centrali hanno probabilità di correre in meno di 0 secondi. I 4 atleti delle
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
I SISTEMI DI NUMERAZIONE
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA I SISTEMI DI NUMERAZIONE Prof. G. Ciaschetti Fin dall antichità, l uomo ha avuto il bisogno di rappresentare le quantità in modo simbolico. Sono nati
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA I SISTEMI DI NUMERAZIONE Prof. G. Ciaschetti Fin dall antichità, l uomo ha avuto il bisogno di rappresentare le quantità in modo simbolico. Sono nati
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
