Teoremi per la prima prova. Dimostrazioni. Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
|
|
|
- Vito Salvadori
- 5 anni fa
- Visualizzazioni
Transcript
1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria ederico.lastaria@polimi.it Teoremi per la prima prova. Dimostrazioni. 24 Ottobre 2018 Indice 1 Teoremi per la prima prova in itinere. Dimostrazioni Unicità del limite Successioni monotòne limitate Permanenza del segno Radici n-esime Continuità della unzione composta Teorema degli Zeri Teorema dei Valori Intermedi Derivabilità implica continuità Teorema di Fermat Teorema del Valore Medio (di Lagrange) Funzioni derivabili strettamente monotòne Funzioni con derivata nulla su un intervallo Teorema di de l Hospital Formula di Taylor con il resto di Peano Pag. 1
2 1 Teoremi per la prima prova in itinere. Dimostrazioni. 1.1 Unicità del limite Teorema 1.1 (Unicità del limite). Una successione in R ha al più un limite. Prima dimostrazione. Supponiamo che L e L siano limiti della successione (a n ). Allora, per deinizione di limite, per ogni ε > 0 esistono K, K N tali che n > K = a n L < ε, n > K = a n L < ε Poniamo K = max{k, K }. Allora, per ogni n K abbiamo (acendo uso della disuguaglianza triangolare): L L = L a n + a n L L a n + a n L < ε + ε = 2ε (1.1) Dal momento che ε è un numero positivo arbitrario, concludiamo che L = L. Osservazione 1. Unicità del limite signiica che il limite, ammesso che esista, è unico. Nel linguaggio matematico l unicità non implica l esistenza. L unicità del limite vale (e si dimostra in modo del tutto analogo) anche per i limiti di unzioni. Osservazione 2. Se analizziamo la dimostrazione dell unicità del limite per successioni in R, vediamo che, al ine di dimostrare l unicità del limite, la struttura di campo ordinato completo di R non gioca alcun ruolo. Inatti, l unicità del limite vale, più in generale, per successioni in un qualunque spazio metrico. Ricordiamo le deinizioni. Uno spazio metrico (X, dist) consiste in un insieme X e in una unzione X X dist R detta distanza in X, che soddisa le proprietà seguenti. Per ogni scelta di p, q, r X: dist(p, q) 0 e dist(p, q) = 0 se e solo se p = q. (Simmetria) dist(p, q) = dist(q, p) (Disuguaglianza triangolare) dist(p, q) dist(p, r) + dist(r, q) Esempi di spazi metrici sono: R (se x, y R, si deinisce dist(x, y) = x y ), il piano R 2, lo spazio R 3 (e più in generale ogni R n ), la supericie di una sera S immersa in R 3 (come si può deinire una distanza su S?), il piano complesso C eccetera. Se (a n ), n N, è una successione in uno spazio metrico X, si dice che (a n ) tende a L X se dist(a n, L) 0, cioè se: ε > 0 n 0 N n N n > n 0 = dist(a n, L) < ε Pag. 2
3 L unicità del limite di una successione vale in qualunque spazio metrico: Teorema (Unicità del limite in uno spazio metrico) Una successione in uno spazio metrico (X, dist) ha al più un limite. Dimostrazione. Supponiamo che la successione (a n ) nello spazio metrico X converga a L X e a L X, cioè supponiamo che si abbia, al tempo stesso: dist(a n, L ) 0 e dist(a n, L ) 0 Per la proprietà triangolare, si ha, qualunque sia n: 0 dist(l, L ) dist(l, a n ) + dist(a n, L ) (1.2) Poiché, per n +, dist(l, a n ) 0 e dist(l, a n ) 0, anche la successione (costante) dist(l, L ) tende a zero, e questo è possibile se, e solo se, dist(l, L ) = 0, cioè se, e solo se, L = L. Pag. 3
4 1.2 Successioni monotòne limitate Teorema 1.2 (Successioni monotòne limitate). Ogni successione in R che sia crescente a 1 < a 2 < a 3 < < a n < a n+1 < (1.3) e (superiormente) limitata è convergente. superiore dell insieme dei suoi termini. Precisamente, converge all estremo Se invece una successione è decrescente e limitata, convergerà all estremo ineriore dell insieme dei suoi termini. Dimostrazione. Sia (a n ), n N, una successione crescente e limitata. Chiamiamo A = {a n, n N} l insieme dei suoi elementi. Per ipotesi l insieme A è (non vuoto e) limitato. Pertanto (qui si usa la completezza dei reali) A ha un estremo superiore. Poniamo L = sup A. Ricordiamo che, per deinizione, l estremo superiore L di A è la minima limitazione superiore di A, cioè l unico numero L R che soddisa queste due proprietà: 1. L è una limitazione superiore per A, cioè: a n L per ogni n N 2. Nessun numero L < L è una limitazione superiore per A, cioè: Per ogni L < L esiste un a k A per il quale L < a k. Dimostriamo che a n converge a L. Sia ε > 0 arbitrario. Siccome L ε < L, il numero L ε non è una limitazione superiore dell insieme A = {a n, n N}. Dunque esiste un intero k per il quale L ε < a k. Poiché la successione è crescente, per tutti gli n > k si ha a k < a n e quindi L ε < a n, deinitivamente (cioè, per tutti gli n maggiori di k). Ma per ogni n si ha a n L. Riassumendo, si ha L ε < a n L per tutti gli n > k. Per la stessa deinizione di limite di una successione, si conclude allora che lim n + a n = L. Osservazione. Si dimostra che in un campo ordinato K, la proprietà delle successioni monotòne limitate ( Ogni successione monotòna limitata converge in K ) è equivalente alla proprietà dell estremo superiore ( Ogni sottoinsieme di K non vuoto e superiormente limitato ha una minima limitazione superiore ). Pag. 4
5 1.3 Permanenza del segno Teorema 1.3 (Permanenza del segno). Se (a n ), n N, è una successione convergente in R al numero L > 0 (L < 0), allora i termini della successione sono deinitivamente 1 positivi (negativi). Dimostrazione. Vediamo il caso L > 0. (Il caso L < 0 si tratta in modo del tutto simile). Fissiamo ε = L 3. (Per la nostra dimostrazione, va bene issare un qualunque ε che soddisi L ε > 0.) Per deinizione di limite, issato tale ε = L 3, esiste un numero naturale n 0 tale che, per ogni n N soddisacente n > n 0, si ha: 2 L ε < a n < L + ε ossia 3 L < a n < 4 3 L Dunque, per ogni n > n 0, vale la disuguaglianza a n > 2 3 L > 0, e quindi gli a n sono deinitivamente positivi.. Osservazione. Il teorema di permanenza del segno vale anche per i limiti di unzioni: in breve, se lim x x0 (x) = L > 0, allora esiste un intorno U di x 0 tale che (x) > 0 per ogni x U dom(). La dimostrazione è del tutto analoga a quella vista sopra. 1 L espressione: I termini della successione sono deinitivamente positivi signiica: Esiste un intero positivo n 0, tale che a n è positivo per ogni n > n 0. Pag. 5
6 1.4 Radici n-esime Teorema 1.4 (Radici n-esime di un numero complesso). Sia z = r(cos ϑ+i sin ϑ) un numero complesso non nullo e sia n un intero positivo. Esistono esattamente n numeri complessi che elevati alla potenza n-esima danno come risultato z. Tali numeri sono: ( ϑ + 2kπ z k = n r [ cos ( ϑ + 2kπ n ) + i sin n )], k = 0, 1,..., n 1 (1.4) Ciascuno di tali numeri z 0,..., z n 1 si chiama una radice n-esima di z. Quindi il teorema dice che ogni numero complesso (non nullo) ha esattamente n radici n-esime. (Nel caso z = 0, le n radici n-esime sono coincidenti.) Dimostrazione. Un numero complesso w = w (cos α + i sin α) (1.5) è una radice n-esima di z se w n = z, ossia (per la ormula di De Moivre) se w n (cos nα + i sin nα) = r(cos ϑ + i sin ϑ) (1.6) Ora due numeri complessi, scritti in orma polare, sono uguali se e solo se hanno i moduli uguali, e gli argomenti uguali a meno di multipli interi di 2π: w n = r, nα = ϑ + 2kπ, k Z Ma si vede acilmente che si ottengono n radici distinte soltanto per gli n valori k = 0, 1,..., (n 1), mentre dando a k un qualunque altro valore, si riottiene una delle radici z 0,..., z n 1. Quindi tutte le n radici n-esime distinte hanno modulo e argomento rispettivamente dati da n r, ϑ + 2kπ n k = 0, 1,..., n 1 Osservazione. Si noti che le radici n-esime si trovano tutte sulla circonerenza di centro l origine e raggio n r e sono equidistanziate tra loro, cioè sono i vertici di un poligono regolare di n lati. Pag. 6
7 1.5 Continuità della unzione composta Teorema 1.5 (Composizione di unzioni continue). Se X g Y e Y Z sono unzioni continue (X, Y, Z sottoinsiemi di R, oppure, più in generale, spazi metrici), allora anche la unzione composta X g Z è continua. X Y g g Z Dimostrazione Sia x 0 X, poniamo (x 0 ) = y 0, e sia W un qualunque intorno X Y Z g x (U) V 0 (x0 ) = y 0 g(y 0 ) = g((x 0 )) U V g(v ) W W di g((x 0 )) = g(y 0 ). Per la continuità di g in y 0, esiste un intorno V di y 0 tale che g(v ) W. Del resto, poiché è continua in x 0, esiste un intorno U di x 0 per il quale (U) V. Poiché da (U) V segue g((u)) g(v ), si ha (g )(U) = g((u)) g(v ) W Pag. 7
8 Questo prova la continuità della unzione composta in x 0. Poiché x 0 è un punto arbitario di X, abbiamo dimostrato la continuità della unzione composta g. Pag. 8
9 1.6 Teorema degli Zeri Teorema 1.6 (Teorema degli Zeri). Siano I R un intervallo e I R una unzione continua. Siano a, b due punti appartenenti a I, con a < b. Supponiamo che i valori (a) e (b) abbiano segni opposti ((a) < 0 e (b) > 0, o viceversa). Allora esiste almeno un punto α (a, b) in cui si ha (α) = 0. Dimostrazione La dimostrazione del Teorema degli Zeri è costruttiva, cioè presenta un algoritmo (detto metodo di bisezione o metodo dicotomico) per mezzo del quale è possibile trovare un punto in cui si annulla. Per issare le idee supponiamo (a) < 0 e (b) > 0 e consideriamo il punto medio c = a + b 2 dell intervallo [a, b]. Possono presentarsi due casi. Se (c) = 0 il problema è risolto (abbiamo trovato uno zero di ). Se invece (c) 0, scegliamo tra i due intervalli [a, c] e [c, b] quello in cui la unzione assume valori discordi agli estremi. Tenuto conto delle nostre scelte iniziali ((a) < 0 e (b) > 0), si tratta di scegliere l intervallo in cui la unzione assume valore negativo nell estremo di sinistra e valore positivo nell estremo di destra. Quindi se (c) 0, scegliamo l intervallo I 1 = [i 1, j 1 ] nel modo seguente : [a, c] se (c) > 0 I 1 = [i 1, j 1 ] = (1.7) [c, b] se (c) < 0 Operiamo ora sull intervallo I 1 = [i 1, j 1 ] nello stesso modo in cui abbiamo operato sull intervallo [a, b]. Precisamente: sia c 1 il punto medio di [i 1, j 1 ]. Se (c 1 ) = 0 il problema è risolto (c 1 è uno zero di ). Altrimenti scegliamo tra i due intervalli [i 1, c 1 ] e [c 1, j 1 ] quello in cui la unzione assume valore negativo nell estremo di sinistra e positivo nell estremo di destra. Iterando questo procedimento, si possono avere due casi: 1. Esiste un intero positivo k tale che la unzione si annulla nel punto medio c k dell intervallo [i k, j k ]. In questo caso abbiamo trovato un punto c k nel quale la unzione si annulla, e la tesi del teorema è dimostrata. 2. La unzione non si annulla in nessun punto medio c k. In questo caso otteniamo una successione ininita di intervalli compatti inscatolati con le due seguenti proprietà: [i 1, j 1 ] [i 2, j 2 ] [i 3, j 3 ] [i n, j n ] (a) nell estremo di sinistra di ogni intervallo la unzione assume valore negativo, mentre nell estremo di destra assume valore positivo, cioè per ogni k (0 k n) abbiamo (i k ) < 0 e (j k ) > 0. (b) gli intervalli hanno ampiezza j k i k = b a 2 k Abbiamo dunque costruito una successione di intervalli compatti inscatolati le cui ampiezze tendono a zero. Per il teorema sugli intervalli inscatolati (conseguenza della completezza di R) esiste un unico numero reale α che appartiene a tutti gli intervallini [i n, j n ], per ogni n N. A tale numero α convergono le due successioni i n e j n : lim i n = α = n + lim n + j n Pag. 9
10 Poiché è continua in x = α ( commuta con lim, nel senso che lim = lim ), abbiamo ( ) ( ) lim (i n) = lim i n = (α) e lim (j n) = lim j n = (α) n + n + n + n + Ma poiché (i n ) < 0 (per ogni n), risulta (α) = lim (i n) 0 n + (perché il limite di una successione di termini (i n ) < 0 è certamente 0). Analogamente, poiché (j n ) > 0 per ogni n, si deve avere (α) = lim (j n) 0 n + Poichè le due ultime disuguaglianze devono valere contemporaneamente, abbiamo (α) = 0 e quindi α è uno zero di. Pag. 10
11 1.7 Teorema dei Valori Intermedi Teorema 1.7 (Teorema dei Valori Intermedi. Una unzione continua trasorma connessi in connessi). Sia I un intervallo di R e sia I R una unzione continua. Se a e b appartengono a I, la unzione assume ogni valore compreso tra (a) e (b). Detto altrimenti, l immagine J = (I) di è un intervallo. In breve: Le unzioni continue da R a R trasormano intervalli in intervalli. Dimostrazione Siano a = (a) e b = (b) due punti di (I); supponiamo a < b. Sia w un numero tale che a < w < b. Dobbiamo dimostrare che w (I). Consideriamo la unzione g(x) = (x) w, x [a, b] Tale unzione è ovviamente continua sull intervallo [a, b] e si ha: g(a) = (a) w = a w < 0 g(b) = (b) w = b w > 0 (1.8) Dunque la unzione g soddisa le ipotesi del Teorema degli Zeri (1.6) sull intervallo [a, b]. Allora esiste un punto c (a, b) per il quale g(c) = (c) w = 0, ossia (c) = w, come si voleva dimostrare. Commento. Deiniamo la seguente proprietà, detta di Darboux: Proprietà (di Darboux). Una unzione I R, I intervallo di R, soddisa la proprietà di Darboux se per ogni x 1, 2 I, assume sull intervallo [x 1, x 2 ] ogni valore compreso tra (x 1 ) e (x 2 ). Il teorema dei Valori Intermedi 1.7 si può allora enunciare dicendo che le unzioni continue su un intervallo soddisano la proprietà di Darboux. Non è però vero il viceversa. Un controesempio è ornito dalla unzione seguente: { sin 1 (x) = x x 0 (1.9) 0 x = 0 Si vede acilmente che questa unzione soddisa la proprietà di Darboux. Ma non è continua su R, perché in x 0 = 0 presenta una discontinuità non eliminabile. Pag. 11
12 1.8 Derivabilità implica continuità Teorema 1.8 (Derivabilità implica continuità). Se è derivabile in x 0, allora è continua in x 0. Dimostrazione. Partiamo dall identità (valida per x x 0 ) Allora 2 : lim (x) = (x 0 )+ x x 0 ( (x) = (x 0 ) + (x) (x 0) x x 0 (x x 0 ) (x) (x 0 ) lim x x 0 x x 0 ) ( ) lim (x x 0 ) x x 0 = (x 0 )+ (x 0 ) 0 = (x 0 ) Questo prova che è continua in x 0. Un altra dimostrazione è la seguente. Poiché è dierenziabile in x 0, si scrive Passando al limite: (x 0 + h) = (x 0 ) + (x 0 ) h + o(h) (per h 0) lim (x [ 0 + h) = lim (x0 ) + (x 0 )h + o(h) ] h 0 h 0 = (x 0 ) + lim h 0 (x 0 )h + lim h 0 o(h) = (x 0 ) + lim (x 0 )h + lim h o(h) h 0 h 0 h = (x 0 ) = (x 0 ) 2 Si ricordi che se esistono i limiti di g 1(x) e g 2(x) per x x 0, allora il limite della somma g 1(x) + g 2(x) è la somma dei limiti. Si noti che, a secondo membro, (x 0) è una costante e quindi lim x x0 (x 0) = (x 0) Pag. 12
13 1.9 Teorema di Fermat Teorema 1.9 (Fermat). Sia D R una unzione a valori reali deinita su un insieme D R. Supponiamo che: 1. x 0 sia un punto di massimo (o di minimo) locale per ; 2. x 0 sia interno a D; 3. sia derivabile in x 0. Allora x 0 è un punto stazionario di, cioè (x 0 ) = 0. Dimostrazione. Per issare le idee, supponiamo che x 0 sia un punto di massimo locale per. Poiché, per ipotesi, x 0 è al tempo stesso un punto interno al dominio D di e un punto di massimo locale, esiste un intorno suicientemente piccolo I di x 0 con le due proprietà seguenti 3 : (perché x 0 è interno a D) e I D (1.10) x I (x) (x 0 ) 0 (1.11) (perché x 0 è punto di massimo locale). Per ogni x I, x x 0, si ha allora se x > x 0 e (x) (x 0 ) x x 0 0 (1.12) (x) (x 0 ) x x 0 0 (1.13) si ricava 4 rispettivamente (x 0 ) 0 e (x 0 ) 0. Di conseguenza (x 0 ) = 0. Osservazione. Si noti che nel teorema dimostrato è essenziale l ipotesi che x 0 sia interno a D. (Non basta che il punto x 0 appartenga a D). Ad esempio, la unzione (x) = x nell intervallo D = [0, 1] ha un punto di massimo locale in x 0 = 1, anche se la derivata (sinistra) di in x 0 non è nulla (è uguale a 1). Naturalmente questo non contaddice il teorema di Fermat. Semplicemente non sono soddisatte le ipotesi di tale teorema, perché il punto x 0 = 1 non è interno a D = [0, 1]. 3 Sappiamo che esiste un intorno U di x 0 che soddisa la condizione U D e esiste un intorno V di x 0 su cui vale (x) (x 0). Allora sull intersezione I = U V (che è ancora un intorno di x 0) sono soddisatte entrambe le condizioni. 4 Qui si usa il teorema di Permanenza del Segno: Sia g una unzione deinita su un intorno U di un punto x 0 (con la possibile eccezione del punto x 0). Supponiamo che, per ogni x U \x 0, si abbia g(x) 0 e supponiamo che esista (inito) il limite lim x x0 g(x) = L. Allora si ha L 0. Pag. 13
14 1.10 Teorema del Valore Medio (di Lagrange) Teorema 1.10 (del Valore Medio, o di Lagrange). Sia [a, b] R una unzione continua sull intervallo compatto [a, b] e derivabile sull intervallo aperto (a, b). Allora esiste un punto γ (a, b) per il quale si ha (b) (a) = (γ)(b a) (1.14) Dimostrazione. Si consideri la unzione g(x) = (x) (a) (b) (a) (x a) (1.15) b a deinita sull intervallo [a, b]. Tale unzione è continua su [a, b], derivabile su (a, b) e assume lo stesso valore agli estremi: g(a) = g(b) = 0 Quindi g soddisa le ipotesi del teorema di Rolle. Per tale teorema, esiste un punto γ in (a, b) in cui g (γ) = 0. La derivata di g(x) è Quindi si ha che equivale a g (x) = (x) 0 = g (γ) = (γ) (b) (a) b a (b) (a) b a (b) (a) = (γ)(b a) Osservazione. Il teorema di Lagrange ha la seguente interpretazione geometrica. Si noti che il numero (b) (a) b a è il coeiciente angolare della retta (secante) che passa per (a, (a)) e (b, (b)), di equazione y = (a) + (b) (a) (x a) (1.16) b a Quindi il teorema aerma che esiste almeno un punto (γ, (γ)) appartenente al graico della unzione in cui la retta tangente (il cui coeiciente angolare è (γ)) è parallela alla retta secante che unisce i due punti estremi (a, (a)) e (b, (b)). Si noti che la unzione ausiliaria (1.15) è la dierenza tra l ordinata del punto (x, (x)) sul graico di e l ordinata del punto di coordinate (x, (a) + (b) (a) b a (x a)) sulla retta secante. Pag. 14
15 1.11 Funzioni derivabili strettamente monotòne Teorema 1.11 (Funzioni derivabili strettamente monotòne). Sia I R una unzione derivabile su un intervallo aperto I di R. Se (x) > 0 (oppure < 0) in ogni punto x I, allora è strettamente crescente (strettamente decrescente) su I. Dimostrazione. Dimostriamo il teorema per il caso di unzioni con derivata positiva in ogni punto. (L altro caso si tratta in modo analogo). Siano x 1, x 2 due punti di I, con x 1 < x 2. Per il teorema di Lagrange esiste un punto c, compreso tra x 1 e x 2, per il quale si ha: (x 1 ) (x 2 ) = (c)(x 1 x 2 ) Poiché per ipotesi (c) > 0 e x 1 x 2 < 0, si deve avere (x 1 ) (x 2 ) < 0. Abbiamo allora dimostrato che, per ogni x 1, x 2 I, x 1 < x 2 = (x 1 ) < (x 2 ) Dunque è strettamente crescente su I. Osservazione. Il teorema non si inverte: se una unzione è strettamente crescente su un intervallo I ed è derivabile in I, allora si avrà senz altro (x) 0 per ogni x I, ma in qualche punto la derivata potrebbe annullarsi. Ad esempio, la unzione (x) = x 3, x R, è strettamente crescente su R, ma (0) = 0. Osservazione. L implicazione > 0 = strettamente crescente non vale se il dominio di non è un intervallo. Ad esempio, la unzione (x) = 1/x, deinita su D = (, 0) (0, + ) (che non è un intervallo) ha derivata positiva su D, ma non è strettamente crescente sul suo dominio D. Ovviamente è crescente sulla semiretta (, 0) ed è crescente sulla semiretta (0, + ), ma non è crescente sul suo dominio D = (, 0) (0, + ) (che non è un intervallo). Pag. 15
16 1.12 Funzioni con derivata nulla su un intervallo Teorema 1.12 (Funzioni con derivata nulla su un intervallo). Una unzione deinita su un intervallo aperto I = (a, b) e con derivata nulla in ogni punto di tale intervallo è costante. Dimostrazione. Prendiamo due punti qualunque x 1, x 2 in (a, b), x 1 < x 2. Per il teorema di Lagrange applicato all intervallo [x 1, x 2 ] esiste un punto c, compreso tra x 1 e x 2, per il quale si ha: (x 2 ) (x 1 ) = (c)(x 2 x 1 ) = 0 (x 2 x 1 ) = 0 Ne segue (x 1 ) = (x 2 ). Quindi è costante. Osservazione. Si noti che in questo teorema è essenziale l ipotesi che il dominio della unzione sia un intervallo (un sottoinsieme connesso di R). Esempio 1. La unzione (x) = R \ {0} R { 1 se x (, 0) 1 se x (0, + ) ha derivata nulla in ogni punto del suo dominio (, 0) (0, + ), ma non è costante. (Si noti che (, 0) (0, + ) non è un intervallo di R, cioè non è connesso). Esempio 2. La unzione R \ {0} R (x) = arctan x + arctan 1 x ha derivata nulla in ogni punto del suo dominio (come si veriica acilmente calcolando la derivata), ma non è costante. Precisamente, arctan x + arctan 1 x = π/2 per x > 0 e arctan x + arctan 1 x = π/2 per x < 0 Pag. 16
17 1.13 Teorema di de l Hospital Teorema 1.13 (de L Hospital. Caso 0 0.). Siano e g due unzioni continue sull intervallo [x 0, b] (x 0 R) e derivabili in (x 0, b). Supponiamo che valgano le seguenti condizioni: 1. (x 0 ) = g(x 0 ) = g (x) 0 per ogni x (x 0, b). 3. Esiste (inito o ininito) il limite Allora esiste anche il limite lim x x + 0 lim x x + 0 lim x x + 0 (x) g (x) = L (1.17) (x) g(x) ed è uguale al precedente: (x) g(x) = L (1.18) Dimostrazione. (Per il caso L inito). Premettiamo un osservazione. Sia x un qualunque punto in (x 0, b). Allora si può scrivere (x) g(x) = (γ) g (γ) per un opportuno γ compreso tra x 0 e x, cioè soddisacente: x 0 < γ < x. Per dimostrarlo, applichiamo il teorema di Cauchy alla coppia di unzioni,g sull intervallo [x 0, x]. Poiché (x 0 ) = g(x 0 ) = 0, per il teorema di Cauchy si ha (x) g(x) = (x) (x 0) = (γ) g(x) g(x 0 g (γ) per un opportuno γ soddisacente x 0 < γ < x, come si voleva dimostrare. A questo punto possiamo concludere, in modo un po sbrigativo ma sostanzialmente corretto, nel modo seguente. Quando x tende a x 0, il punto γ, compreso tra x e x 0, deve tendere a x 0. Quindi, poiché (x) g(x) = (γ) g (γ) (x) (x) e lim x x + g = L, anche il limite lim deve esistere, e deve essere uguale a (x) 0 x x + g(x) 0 L. Commento. Se vogliamo essere più rigorosi, possiamo arrivare alla tesi usando la ε-δ deinizione di limite. Prendiamo allora un arbitrario ε > 0. (x) Poiché, per ipotesi, lim x x + g = L, esiste un δ > 0 tale che (x) 0 t (x 0, x 0 + δ) (t) g (t) L < ε (1.19) Pag. 17
18 Ora prendiamo un qualunque x in (x 0, x 0 + δ). Per quanto abbiamo visto sopra, (x) g(x) = (γ) g (γ) per un opportuno γ soddisacente x 0 < γ < x < x 0 +δ. Siccome tale γ è compreso tra x 0 e x 0 + δ, per la 1.19 si ha (γ) g (γ) L < ε e quindi (x) g(x) L = (γ) g (γ) L < ε Questo prova, per deinizione di limite, che anche lim x x + 0 (x) g(x) = L (1.20) Osservazione. Ovviamente il teorema di de L Hospital vale anche per i limiti da sinistra (x x 0 ) e quindi per il limite (ordinario) per x x 0. Pag. 18
19 1.14 Formula di Taylor con il resto di Peano Teorema 1.14 (Formula di Taylor locale, con il resto di Peano). Sia una unzione con derivate di ogni ordine su un intervallo aperto I dell asse reale. Fissiamo un punto x 0 in I e un intero positivo n. Deiniamo il resto R n (x) come la dierenza tra (x) e il polinomio di Taylor di di ordine n nel punto x 0 : (x) = (x 0 )+ (x 0 )(x x 0 )+ (x 0 ) (x x 0 ) ! n! (n) (x 0 )(x x 0 ) n +R n (x) Allora il resto R n (x) è o((x x 0 ) n ) per x x 0, cioè lim x x0 R n(x) (x x 0 ) n = 0. Dimostrazione. Per semplicità, vediamo il caso n = 2. (Il caso generale si dimostra nello stesso modo). Dobbiamo allora dimostrare che (x) (x 0 ) (x 0 )(x x 0 ) (x 0 ) (x x 0 ) lim 2! x x 0 (x x 0 ) 2 = 0 (1.21) Si controlla acilmente che sono soddisatte le condizioni per potere usare la regola di de L Hospital. (Inatti, numeratore e denominatore sono derivabili in tutto un intorno di x 0, sono nulli in x 0, e la derivata del denominatore è diversa da zero per x x 0 ) Il rapporto tra le derivate del numeratore e del denominatore è dato da (x) (x 0 ) (x 0 )(x x 0 ) 2(x x 0 ) Applichiamo ancora una volta la regola di de L Hospital, e otteniamo: (x) (x 0 ) 2 Poiché la unzione (x) è continua (se una unzione ha derivate di ogni ordine, tutte le derivate devono essere continue), si ha lim x x0 (x) = (x 0 ), e quindi (x) (x 0 ) lim x x 0 2 (Nel caso di n arbitrario, iterando n volte la regola di de l Hospital, si arriva a lim (n) (x) (n) (x 0 ) x x0 n!, che vale zero, perché (n) è continua in x 0.) Dunque, per il teorema di de L Hospital, anche il limite iniziale (1.21) esiste e vale 0, come volevamo dimostrare. Commento. Abbiamo dimostrato il teorema di Taylor (locale) 1.14 nell ipotesi che sia ininitamente derivabile. Non è diicile dimostrare che la stessa tesi vale anche in ipotesi meno restrittive. Vale inatti il seguente Teorema [Formula di Taylor locale] Supponiamo che sia derivabile n volte in un punto x 0 (n intero positivo). Poniamo (x) = (x 0 )+ (x 0 )(x x 0 )+ (x 0 ) (x x 0 ) ! n! (n) (x 0 )(x x 0 ) n +R n (x) Allora, il resto R n (x) è o((x x 0 ) n ) per x x 0. Pag. 19
Teoremi per la prima prova. Dimostrazioni. Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Teoremi per la prima prova. Dimostrazioni. 16 Ottobre 2017 Indice 1 Teoremi per la prima prova in itinere.
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Teoremi per la prima prova. Dimostrazioni. 16 Ottobre 2017 Indice 1 Teoremi per la prima prova in itinere.
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria 2. Le funzioni continue.
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria ederico.lastaria@polimi.it 2. Le unzioni continue. Settembre 2012 Indice 1 Funzioni reali continue 1 1.1 Deinizione di unzioni continua..........................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria ederico.lastaria@polimi.it 2. Le unzioni continue. Settembre 2012 Indice 1 Funzioni reali continue 1 1.1 Deinizione di unzioni continua..........................
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
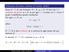 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria Formule di Taylor Ottobre 2012
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Teoremi per appelli e orali. Dimostrazioni. Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Teoremi da studiare per gli appelli e per le prove orali. 18 Dicembre 2018 Indice 1 Teoremi per gli appelli
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Teoremi da studiare per gli appelli e per le prove orali. 18 Dicembre 2018 Indice 1 Teoremi per gli appelli
Limiti e continuità. Limiti di funzioni
 Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Indice. Calcolo differenziale Parte seconda. Mauro Saita Versione provvisoria. Novembre
 Calcolo differenziale Parte seconda Mauro Saita maurosaita@tiscalinet.it Versione provvisoria. Novembre 214. 1 Indice 1 Funzioni derivabili su un intervallo 2 1.1 Punti di massimo o minimo locale per una
Calcolo differenziale Parte seconda Mauro Saita maurosaita@tiscalinet.it Versione provvisoria. Novembre 214. 1 Indice 1 Funzioni derivabili su un intervallo 2 1.1 Punti di massimo o minimo locale per una
Il Metodo di Newton, o delle Tangenti Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
I TEOREMI DEL CALCOLO DIFFERENZIALE
 I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
Calcolo differenziale. Parte seconda. CALCOLO DIFFERENZIALE Parte Seconda. Mauro Saita. Versione provvisoria. Gennaio 2016.
 CALCOLO DIFFERENZIALE Parte Seconda maurosaita@tiscalinet.it Versione provvisoria. Gennaio 2016. 1 Indice 1 Funzioni derivabili su un intervallo 3 1.1 Punti di massimo o minimo locale per una funzione...............
CALCOLO DIFFERENZIALE Parte Seconda maurosaita@tiscalinet.it Versione provvisoria. Gennaio 2016. 1 Indice 1 Funzioni derivabili su un intervallo 3 1.1 Punti di massimo o minimo locale per una funzione...............
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Limiti. Funzioni continue. Federico Lastaria, Analisi e Geometria 1
 Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Limiti. Continuità. Ottobre 2015 Indice 1 Prime nozioni di topologia dell asse reale
Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Limiti. Continuità. Ottobre 2015 Indice 1 Prime nozioni di topologia dell asse reale
LA DERIVATA DI UNA FUNZIONE. Prof Giovanni Ianne
 LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
I teoremi del calcolo differenziale
 I teoremi del calcolo dierenziale Ora che le regole di derivazione e il concetto di derivata sono stati arontati è possibile passare ad analizzare alcuni risultati importanti. Deinizione: data una unzione
I teoremi del calcolo dierenziale Ora che le regole di derivazione e il concetto di derivata sono stati arontati è possibile passare ad analizzare alcuni risultati importanti. Deinizione: data una unzione
CALCOLO DEL RAGGIO DI CURVATURA DI UNA CURVA REGOLARE DI E Q UAZI O NE y = f (x ), ivi derivabile almeno due volte, e che la derivata seconda
 ALOLO DEL RAGGIO DI URVATURA DI UNA URVA REGOLARE DI E Q UAZI O NE Supponiamo che b sia una unzione deinita in, ivi derivabile almeno due volte, e che in la derivata seconda sia diversa da zero, e indichiamo
ALOLO DEL RAGGIO DI URVATURA DI UNA URVA REGOLARE DI E Q UAZI O NE Supponiamo che b sia una unzione deinita in, ivi derivabile almeno due volte, e che in la derivata seconda sia diversa da zero, e indichiamo
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Analisi e Geometria 1 Politecnico di Milano Ingegneria
 Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Introduzione ai numeri complessi. Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16
 Introduzione ai numeri complessi Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16 Definizione (Campo complesso C. Prima definizione.) Il campo complesso C è costituito da tutte le espressioni
Introduzione ai numeri complessi Federico Lastaria. Analisi e Geometria 1. Numeri Complessi 1/16 Definizione (Campo complesso C. Prima definizione.) Il campo complesso C è costituito da tutte le espressioni
Il differenziale ed i teoremi sulle funzioni derivabili. Appunti delle lezioni di Analisi A. Pisani A.S Liceo Classico Dante Alighieri (GO)
 Il dierenziale ed i teoremi sulle unzioni derivabili Appunti delle lezioni di Analisi A. Pisani A.S. 22-3 Liceo Classico Dante Alighieri (GO Nota bene Questi appunti sono da intendere come guida allo studio
Il dierenziale ed i teoremi sulle unzioni derivabili Appunti delle lezioni di Analisi A. Pisani A.S. 22-3 Liceo Classico Dante Alighieri (GO Nota bene Questi appunti sono da intendere come guida allo studio
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica), a.a. 2007/08. Insiemi numerici: sup A, inf A
 Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
CONTINUITA E DERIVABILITA
 CONTINUITA E DERIVABILITA La continuità e la derivabilità di una unzione sono proprietà dierenti. TEOREMA: CONTINUITA DELLE FUNZIONI DERIVABILI Se è una unzione derivabile in un punto, allora è continua
CONTINUITA E DERIVABILITA La continuità e la derivabilità di una unzione sono proprietà dierenti. TEOREMA: CONTINUITA DELLE FUNZIONI DERIVABILI Se è una unzione derivabile in un punto, allora è continua
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Teoria Es. 1 Es. 2 Totale Analisi e Geometria 1 Primo compito in itinere 6 novembre 2018-Compito E (II turno) Cognome: Nome: Matricola:
 Teoria Es. 1 Es. 2 Totale Analisi e Geometria 1 Primo compito in itinere 6 novembre 2018-Compito E (II turno) Docente: Numero di iscrizione all appello: Cognome: Nome: Matricola: Istruzioni: Tutte le risposte
Teoria Es. 1 Es. 2 Totale Analisi e Geometria 1 Primo compito in itinere 6 novembre 2018-Compito E (II turno) Docente: Numero di iscrizione all appello: Cognome: Nome: Matricola: Istruzioni: Tutte le risposte
Proprietà globali delle funzioni continue
 Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Il teorema di Lusin (versione )
 G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
Analisi Matematica 1+2
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
Il campo ordinato completo R dei numeri reali. Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13
 Il campo ordinato completo R dei numeri reali Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13 Cosa significa campo? Significa che sono definite due operazioni: somma e prodotto,
Il campo ordinato completo R dei numeri reali Federico Lastaria. Analisi e Geometria 1. Il campo ordinato completo R 1/13 Cosa significa campo? Significa che sono definite due operazioni: somma e prodotto,
DERIVATA di una funzione
 DERIVATA di una unzione Sia e * A punto di accumulazione di A : A R * è il RAPPORTO INCREMENTALE * Il rapporto incrementale di calcolato in * rappresenta il coeiciente angolare della secante passante per
DERIVATA di una unzione Sia e * A punto di accumulazione di A : A R * è il RAPPORTO INCREMENTALE * Il rapporto incrementale di calcolato in * rappresenta il coeiciente angolare della secante passante per
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Capitolo 5. Calcolo infinitesimale
 Capitolo 5 Calcolo ininitesimale 5 Derivazione a b R ed ] a, Siano ( :(, DEFINIZINE Diremo che ( è derivabile nel punto se esiste inito il seguente ite ( ( e porremo per deinizione ( ( ( La unzione : (
Capitolo 5 Calcolo ininitesimale 5 Derivazione a b R ed ] a, Siano ( :(, DEFINIZINE Diremo che ( è derivabile nel punto se esiste inito il seguente ite ( ( e porremo per deinizione ( ( ( La unzione : (
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
CAP. VII FUNZIONI DERIVABILI
 C Boccaccio Appunti di Analisi Matematica CAP VII CAP VII FUNZIONI DERIVABILI In molti problemi di varia natura (isica, economica, matematica, ecc ) si ha a che are con unzioni, delle quali importa determinare
C Boccaccio Appunti di Analisi Matematica CAP VII CAP VII FUNZIONI DERIVABILI In molti problemi di varia natura (isica, economica, matematica, ecc ) si ha a che are con unzioni, delle quali importa determinare
( ) ( ) DERIVATE. $ ed è finito lim
 DERIVATE La derivata di una unzione in un punto c, quando esiste, rappresenta il coeiciente angolare della retta tangente al graico della unzione nel suo punto di ascissa c: ( c) = D ( c) = m tg = tanα,
DERIVATE La derivata di una unzione in un punto c, quando esiste, rappresenta il coeiciente angolare della retta tangente al graico della unzione nel suo punto di ascissa c: ( c) = D ( c) = m tg = tanα,
10 - Massimi, minimi e flessi
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 10 - Massimi, minimi e flessi Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 10 - Massimi, minimi e flessi Anno Accademico 2015/2016
Docente Dipartimento di Ingegneria Industriale Ore didattica assegnate 2016/17 Registro del docente BAGAGIOLO FABIO. Ore didattica assegnate
 Docente Dipartimento di Ingegneria Industriale Ore didattica assegnate 2016/17 Registro del docente BAGAGIOLO FABIO Tipo copertura: docente strutturato Attività didattica: Attività didattica [codice] Corso
Docente Dipartimento di Ingegneria Industriale Ore didattica assegnate 2016/17 Registro del docente BAGAGIOLO FABIO Tipo copertura: docente strutturato Attività didattica: Attività didattica [codice] Corso
Matematica generale CTF
 Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
f (x) = f(x 2) f(x 1 ) x 2 x 1
 Lezioni 29-30 86 Il Teorema di Lagrange o del Valor Medio Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto
Lezioni 29-30 86 Il Teorema di Lagrange o del Valor Medio Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria. Curve nello spazio Gennaio Lunghezza d arco
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Funzioni implicite e teorema del Dini
 Funzioni implicite e teorema del Dini Il succo dell argomento può essere presentato così. Sia f una funzione a valori reali, definita in un aperto G del piano euclideo R 2 e sufficientemente buona; consideriamo
Funzioni implicite e teorema del Dini Il succo dell argomento può essere presentato così. Sia f una funzione a valori reali, definita in un aperto G del piano euclideo R 2 e sufficientemente buona; consideriamo
Diario del corso di Analisi Matematica 1 (a.a. 2017/18)
 Diario del corso di Analisi Matematica 1 (a.a. 2017/18) 22 settembre 2017 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 25 settembre
Diario del corso di Analisi Matematica 1 (a.a. 2017/18) 22 settembre 2017 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 25 settembre
1 Note ed esercizi risolti a ricevimento
 1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
Esercizio 1. Per quali valori di h e k le seguenti funzione sono derivabili? x 3 sin 1 x 0. 0 x = 0. x cos 1 x > 0
 Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
A.A. 2016/17 - Analisi Matematica 1
 A.A. 2016/17 - Analisi Matematica 1 Argomenti svolti, libro di testo di riferimento: P. Marcellini, C. Sbordone: Elementi Calcolo. Liguori Editore. O. Bernardi: Temi d esame senza tema. Ed. Libreria Progetto.
A.A. 2016/17 - Analisi Matematica 1 Argomenti svolti, libro di testo di riferimento: P. Marcellini, C. Sbordone: Elementi Calcolo. Liguori Editore. O. Bernardi: Temi d esame senza tema. Ed. Libreria Progetto.
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Integrali definiti secondo Riemann
 Analisi matematica ntegrali deiniti secondo Riemann Calcolo integrale ntegrali deiniti secondo Riemann Trapezoide di una unzione Funzione a scala ntegrale deinito 2 2006 Politecnico di Torino 1 Analisi
Analisi matematica ntegrali deiniti secondo Riemann Calcolo integrale ntegrali deiniti secondo Riemann Trapezoide di una unzione Funzione a scala ntegrale deinito 2 2006 Politecnico di Torino 1 Analisi
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale
 Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
Esercizi sulle Funzioni
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Funzioni Esercizio svolto. Trovare i domini di definizione delle seguenti funzioni: a) f) sin + cos ; b) g) log ) ; c) h) sin + e sin. Soluzione. a) La
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Funzioni Esercizio svolto. Trovare i domini di definizione delle seguenti funzioni: a) f) sin + cos ; b) g) log ) ; c) h) sin + e sin. Soluzione. a) La
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Successioni numeriche (II)
 Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Limiti. Funzioni continue. Federico Lastaria, Analisi e Geometria 1
 Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Limiti. Continuità. 13 Settembre 2018 Indice 1 Prime nozioni di topologia dell asse reale
Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Limiti. Continuità. 13 Settembre 2018 Indice 1 Prime nozioni di topologia dell asse reale
Il teorema di Lagrange e la formula di Taylor
 Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
Diario del corso di Analisi Matematica 1 (a.a. 2016/17)
 Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Limiti di funzioni. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Sappiamo che una funzione definita in un intervallo aperto I ed ivi derivabile è anche differenziabile, ossia che, fissato x 0 I, si ha.
 La formula di Taylor Sappiamo che una funzione definita in un intervallo aperto I ed ivi derivabile è anche differenziabile, ossia che, fissato x 0 I, si ha dove f(x) = f(x 0 ) + f (x 0 )(x x 0 ) + ω(x)(x
La formula di Taylor Sappiamo che una funzione definita in un intervallo aperto I ed ivi derivabile è anche differenziabile, ossia che, fissato x 0 I, si ha dove f(x) = f(x 0 ) + f (x 0 )(x x 0 ) + ω(x)(x
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
29 ESERCIZI SUI POLINOMI DI TAYLOR
 9 ESERCIZI SUI POLINOMI DI TAYLOR Calcolare i seguenti polinomi di Taylor con centro in 0, usando ove possibile i polinomi di Taylor noti e le operazioni su polinomi di Taylor Calcolare T 3( cos x Usiamo
9 ESERCIZI SUI POLINOMI DI TAYLOR Calcolare i seguenti polinomi di Taylor con centro in 0, usando ove possibile i polinomi di Taylor noti e le operazioni su polinomi di Taylor Calcolare T 3( cos x Usiamo
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Primi elementi di topologia dell asse reale. Intorni
 Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
