Complementi di Fisica. 1 Equazioni di Maxwell nei corpi materiali (unità Gauss)

Transcript

1 Università degli Studi di Perugia - Corso di Laurea Triennale in Fisia Corso di Prof. Gianlua Grignani 1 Equazioni di Maxwell nei orpi materiali unità Gauss) Introdotti due tensori elettromagnetii F λµ e H λµ definiti ome 0 D x D y D z 0 E x E y E z F λµ D x 0 H z H y D y H z 0 H x, E x 0 B z B y Hλµ E y B z 0 B x, D z H y H x 0 E z B y B x 0 le equazioni di Maxwell si srivono in forma ovariante F µν x µ = 4π J ν ν = 1,, 3) roth 1 ν = 0) div D = 4πρ ; D t = 4π j ; 1) H µν x λ + H λµ x ν + H νλ x µ = 0 0, 1, ) λ, µ, ν) =, 3, 0) 3, 0, 1) rot E + 1 λ, µ, ν) = 1,, 3) div B = 0 ; B t = 0 ; ) J µ ρ, j). La densità di forza he si eserita su di un elemento di aria in movimento è ) f µ = 1 E j Hµν J ν, f = ρe 1 + j B. Deomponiamo ora la orrente J µ in orrente di onduzione J µ e di onvezione J k µ, in modo tale he nel sistema di quiete del onduttore la prima possegga solo la omponente spaziale e la seonda la omponente spaziale diverse da zero: J µ = J µ + J k µ, J k µ = 1 u µj λ u λ, u µ γ, γ v). Allora la legge di Ohm mirosopia) assume la forma Jµ = σ H µνu ν ρ = v j, j = σγ E + 1 ) ) v B e le equazioni di ollegamento sono F λµ u µ = ɛh λµ u µ, H λµ u ν + H µν u λ + H νλ u µ = µ F λµ u ν + F µν u λ + F νλ u µ ), orrispondenti a D + 1 v H = ɛ E + 1 ) v B, B 1 v E = µ H 1 ) v D 3) - 1 -

2 Equazioni di Maxwell nei orpi materiali unità Gauss) o, risolvendo rispetto a D e B, D = B = 1 1 ɛµβ 1 1 ɛµβ { ɛ E1 β ) + ɛµ 1) { µ H1 β ) ɛµ 1) v H ɛ 1 } v E) v [ 1 v E + µ 1 } v H) v Si vede immediatamente he nel vuoto ɛ = µ = 1) si ha D = E e B = H ed i tensori F λµ e H λµ oinidono. Una onnessione tra F λµ e H λµ si ha tramite il tensore dei momenti H λµ = F λµ + 4πM λµ, [ 1 0 P x P y P z M λµ P x 0 M z M y P y M z 0 M x, 4) P z M y M x 0 dove P e M sono, rispettivamente, l intensità di polarizzazione e di magnetizzazione. La relazione sritta, eq.4), equivale alle equazioni della teoria di Maxwell: E = D 4π P, B = H + 4π M. Dalle proprietà di trasformazione di M λµ segue, in partiolare, he un orpo he nel suo sistema di quiete sia polarizzato elettriamente, ma non magnetizzato, appare ad un osservatore in moto anhe magnetizzato. Vieversa, un orpo he nel sistema di quiete sia solo magnetizzato, sembra possedere un momento elettrio quando è in movimento. Proprietà di trasformazione dei ampi per un boost lungo la direzione x ad esempio per H λµ ): E x = E x, E y = γ E y βb z ), E z = γ E z + βb y ), ovvero, per un boost in una direzione generia B x = B x, B y = γ B y + βe z ), B z = γ B z βe y ) ;,. 5) { E = E, E = γ E + β B ), { B = B, B = γ B β E ). 6) Dalle regole di trasformazione del tensore dei momenti, per un boost lungo la direzione x, si ha P x = P x, P y = γ P y βm z ), P z = γ P z + βm y ), M x = M x, M y = γ M y + βp z ), M z = γ M z βp y ). Nel aso in ui il orpo nel sistema in quiete non sia magnetizzato M = 0), nel limite di piole veloità, si ha P = P M = P v. 7) - -

3 Equazioni di Maxwell nei orpi materiali unità Gauss) La prima terna delle equazioni di Maxwell, eq.1), per orpi in movimento lento, si può quindi srivere nella forma rot B 4πP v ) = 1 E t + 4π P ) + 4π t j, osì he il sistema ompleto delle equazioni di Maxwell per i mezzi in moto, nel aso di piole veloità e di mezzi non magnetizzabili, è il seguente rote = 1 B t, 8) divb = 0, 9) rotb = 1 [ E t + 4π j + P ) t + rot P v, 10) ) div E + 4πP = 4πρ. 11) 1.1 Esperienza di Fizeau Se u 0 è la veloità di propagazione della lue in un mezzo materiale in quiete, la sua veloità di propagazione u in un mezzo he si muove on veloità v sarà data da per la propagazione nel senso del moto e da u = u 0 + kv u = u 0 kv per la propagazione in senso opposto. Il oeffiiente k viene detto oeffiiente di trasinamento, se k fosse uguale ad uno, la veloità della lue e del mezzo si omporrebbero vettorialmente. Il primo tentativo di misurare sperimentalmente il valore del oeffiiente di trasinamento fu fatto da Fizeau nel 1851 e il risultato dell esperienza di Fizeau fu: k = 1 1 n Cerhiamo ora di spiegare questo risultato in base alle formule ottenute nel paragrafo preedente 8)-11). Le equazioni fondamentali del ampo elettromagnetio in un isolante non magnetizzabile sario, he si muove on veloità v j = 0, ρ = 0, µ = 1), seondo le 8)-11), sono rotb = 1 D t + 4πrot P v ), divd = 0 1) rote = 1 B t, div B = 0, 13) D = E + 4πP, 4πP = ɛ 1) E + v ) B. 14) - 3 -

4 Equazioni di Maxwell nei orpi materiali unità Gauss) L ultima delle 14) segue dalle equazioni di ollegamento 3). Confrontiamo queste equazioni on le usuali equazioni di Maxwell per un mezzo in quiete: roth = rotb = 1 D t, div D = 0 15) rote = 1 B t, div B = 0, 16) D = E + 4πP, 4πP = ɛ 1) E. 17) Esistono due differenze essenziali tra questi due sistemi di equazioni. Primo, il termine 4π rot P v), he esprime il trasinamento onvettivo dello stato di polarizzazione. È la ausa per ui l induzione magnetia B nei mezzi in movimento, nonostante l ipotesi µ = 1, non oinide on l inetnsità del ampo magnetio H, ome nel aso dei mezzi in quiete. Un altra differenza onsiste nel fatto he la polarizzazione P non dipende più eslusivamente dall intensità del ampo elettrio, ma anhe dall induzione magnetia; infatti su di una aria in movimento agise la forza di Lorentz: F = e E v ) + B. Vogliamo ora erare una soluzione delle equazioni he orrisponda ad un onda piana; faiamo a questo sopo e titolo tentativo la seguente posizione: B = B r ˆn iωt 0 e u ), r ˆn E = E0 iωt e u ) 18) da ui segue P = P r ˆn iωt 0 e u ), r ˆn D = D0 iωt e u ) 19) Qui ω india la frequenza, u la veloità ed ˆn la direzione di propagazione dell onda. Dobbiamo ora determinare i valori ostanti E 0, B0, P 0, D0 e la veloità dell onda u in modo he siano soddisfatte le equazioni 1)-14). Nel aso di un mezzo in quiete l introduzione di 18) e 19) nel sistema di equazioni 15)-17) dà le note formule: ˆn B 0 = u D 0, ˆn D 0 = ɛˆn E 0 = 0, ˆn E 0 = u B 0, ˆn B 0 = 0, 0) he indiano he in questo aso i vettori E e B e quindi anhe D e P sono diretti normalmente alla direzione di propagazione ˆn e he inoltre l induzione B è normale ai vettori elettrii. Inoltre dalle equazioni 0) segue he la veloità dell onda è legata alla ostante dielettria ɛ dalla formula u = u 0 = ɛ. Le ose vanno altrimenti nel aso di un mezzo in movimento. L introduzione di 18) e 19) nel sistema di equazioni 1)-14) porta alle seguenti relazioni: ˆn B 0 = u D 0 4π ˆn P 0 v), ˆn D 0 = 0, ˆn E 0 = u B 0, ˆn B 0 = 0, 4πP 0 = ɛ 1) E0 + v ) B 0, 1) D 0 = ɛ E 0 + ɛ 1) v B

5 Invarianza di gauge ed equazioni per i potenziali Da queste si dedue he D e B sono normali ad ˆn non però in generale al vettore elettrio E; infatti dall equazione: ˆn D 0 = ɛˆn E 0 + ɛ 1)ˆn v B 0 = 0, si vede he ˆn E è diverso da zero quando i tre vettori ˆn, v, B, non giaiono sullo stesso piano. Analogamente per l intensità del ampo magnetio H = B 4π P v. Ciò mostra he generalmente quando la direzione del moto e la direzione di propagazione non oinidono il vettore di Poynting non ha la direzione di propagazione dell onda. Per i aloli he seguono, onviene esprimere E 0 e P 0 nelle equazioni 1) per mezzo di D 0 e B 0 ; evidentemente si ha: E 0 = 1 D ɛ 0 ɛ 1 v ɛ B 0, 4πP 0 = ɛ 1 D0 + v ) ɛ B 0. Limitiamoi a piole veloità in modo da poter trasurare i termini dell ordine di β in onfronto all unità; allora sostituendo le ) nelle prime due equazioni 1), tenendo onto he è ˆn B 0 = ˆn D 0 = 0 si ha: ) ˆn B u ˆn v 0 = D 0, 1 ɛ ˆn D 0 = ɛ 1 ɛ u ɛ 1 ɛ ˆn v ) B 0. Dalla 3) risulta he nel aso β 1, anhe B 0 è perpendiolare a D 0. Eliminando ora B 0 e D 0 per sostituzione, si ottiene, essendo ˆn B 0 = ˆn D 0 = 0, l equazione: u ɛ 1 ) ˆn v = 1 ɛ ɛ oppure, risolvendola u = + ɛ 1 ˆn v ɛ ɛ Essendo poi l indie di rifrazione del mezzo n dato da n = ɛ e n = u 0, si ha: u = u n ) ˆn v ome legge generale per il movimento della lue in una direzione qualsiasi. Questo risultato si può interpretare intuitivamente diendo he la lue nella sua propagazione in un mezzo in movimento viene trasinata nella direzione del moto e preisamente la grandezza di questo trasinamento è determinata dal oeffiiente di trasinamento k = 1 1 n. ) 3) Invarianza di gauge ed equazioni per i potenziali Limitiamoi d ora in poi al vuoto ɛ = µ = 1, H λµ = F λµ ). Le equazioni di Maxwell omogenee sono soddisfatte automatiamente se si pone F µν = A ν x µ A µ x ν, B = rota, E 1 ) A = gradϕ, t - 5 -

6 Invarianza di gauge ed equazioni per i potenziali on A µ = ϕ, A) definito a meno di una trasformazione di gauge A µ A µ = A µ Λ x µ. Il gruppo di equazioni di Maxwell non omogeneo diventa A µ A ν x ν x µ = 4π J µ. Sfruttando l arbitrarietà dei potenziali si può imporre la ondizione di Lorentz A µ x µ = 0. Le equazioni di Maxwell sono allora sostituite da A µ = 4π J A µ µ, x µ = 0. 4) Questa è la gauge di Lorentz. A µ è definito ora a meno di una trasformazione speiale di gauge Λ = 0). Gauge di Coulomb. Esiste un altra gauge ed è quella definita in un dato sistema di riferimento) da: diva = 0, allora l equazione per il potenziale ϕ è ϕ = 4πρ, ioè la stessa he per il ampo statio; la soluzione è ϕ r, t) = dr ρ r, t) r r. Il potenziale vettore soddisfa l equazione Si ha A = 4π j 1 grad ϕ t. grad ϕ t = grad L ultima uguaglianza segue dalla deomposizione 1 d r div j r, t) r r = 4π j l. j = j l + j t, rot j l = 0, div j t = 0. Allora si ha A = 4π j t da ui il nome di gauge trasversa per la gauge di Coulomb. La gauge di Coulomb si usa spesso in assenza di sorgenti, allora ϕ = 0 e A = 0. 1 Dato un ampo vettoriale v tale he div v = 4πρ e rot v = 4π lo si può deomporre nel modo seguente v = v 1 + v dove rot v 1 = 0, div v 1 = 4πρ e rot v = 4π, div v = 0. Per v 1 si ha immediatamente ρ r ) v 1 = gradχ, dove χ = r r d r. Per v si può porre v = rot u on div u = 0). Per ui rot rot u = 4π, ioè: grad div u u = 4π, ovvero u = 4π. Allora r ) u = r r d r

7 Teoremi di onservazione 3 Tensore energia-impulso Nel vuoto la densità di forza diventa e si può srivere f µ = 1 F µν J ν f µ = 1 4π F F ρν ν µν x ρ = T µ x ν, 5) dove il tensore energia-impulso è dato da T µν = 1 F µλ F νλ 4π 14 ) gµν F λσ F λσ, ioè u S x T µν = S y S y S x S y S z T 11 T 1 T 13 T 1 T T 3 T 31 T 3 T 33, T µ µ = 0. 6) T µν è un tensore di rango due, simmetrio, a traia nulla, le ui omponenti sono ostituite dal tensore di Maxwell, o degli sforzi elettromagnetii T ik = 1 [ E i E k B i B k + 1 4π δ ik E + B ) 7) dalla densità di energia e dal vettore di Poynting u = 1 E + B 8π ) S = 4π E B. 4 Teoremi di onservazione Dalla espressione della densità di forza ome quadridivergenza di T µν, 5), seguono le due leggi di onservazione seguenti la prima orrisponde alla prima equazione ardinale della dinamia in ui si tiene onto anhe dei ampi): d dt d dt P m) i ) + P ) i = T m) + U )) = σ σ T ik n k dσ, 8) S ˆndσ, 9) dove P m) e T m) sono le quantità di moto e l energia delle masse arihe) ontenute nel volume V rahiuso nella superfiie σ e P ) = 1 S dv, U ) = u dv, V V

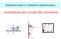
8 Teoremi di onservazione y x ˆn θ E dσ Figura 1: Elemento di superfiie. sono, onseguentemente, la quantità di moto e l energia del ampo ontenuto in V. Il teorema dell energia prende il nome di teorema di Poynting. Per illustrare meglio il signifiato del tensore di Maxwell supponiamo he sia presente solo il ampo E. Consideriamo un elemento di superfiie dσ, ed una selta degli assi in modo he E sia diretto lungo l asse x ome in figura 1: ˆn os θ, sin θ, 0), E E, 0, 0), le omponenti spaziali del tensore di Maxwell 7) sono 1 8π E 0 0 T ik = 1 0 8π E π E Definiamo T, un vettore di omponenti T 1 8π E os θ, ) 1 8π E sin θ, 0, T i T ik n k Quindi quando E indipendentemente dal segno) è perpendiolare a dσ il tensore eserita soltanto una trazione, quando E giae nel piano di dσ il tensore eserita una pressione. Per θ = 45 esiste una tensione pura. Applihiamo quanto detto, ome esempio al aso di due arihe puntiformi sull asse x a distanze +a e a dall origine, figura. y r b +e a +e x Figura : Dipolo. Come volume del sistema prendiamo la semisfera limitata dal piano yz) e dalla metà di sinistra di una superfiie sferia di entro l origine e di raggio tendente all infinito he non ontribuise perhé su di essa T va ome 1/r 4 )

9 Soluzione ritardata dei potenziali Nel aso di arihe di segno onorde si ha E = 0, e y r r, e z ) r, r T dσ = e 0 T = 1 8π E = 1 π b b db a + b ) 3 = e Infine per arihe opposte T dσ = e π 0 a E = πdb b a + b ) 3 = e e b r 6 y + z ) = e π a + b ) 3, 0 dλ λ a + λ) 3 = e a e r a r, 0, 0 ) a T = e π a + b ) 3, a 0 dλ, 0 λ a + λ) 3 = e a dµ 0 µ 1 + µ) 3 = e a). dµ µ) 3 = e a). 5 Soluzione ritardata dei potenziali Nella gauge di Lorentz le equazioni dei potenziali sono 4) A µ = 4π J µ, A µ x µ = 0. Una soluzione partiolare di queste equazioni, valida nel aso in ui J µ è diversa da zero in una zona finita dello spazio si ottiene ome segue. Si onsideri l equazione fx) = gx), indiando brevemente on x le tre oordinate spaziali e il tempo e on gx) una funzione nota. Se riusiamo a determinare una funzione Gx, x ) funzione di Green) tale he Gx, x ) = δ 4) x x ), on δ 4) x x ) δx x )δy y )δz z )δx 0 x 0) in ui x 0 = t) si può srivere una soluzione partiolare per f nella forma fx) = d 4 x Gx x )gx ) on d 4 x dx dy dz dx 0. Consideriamo gli integrali di Fourier Gx x ) = 1 π) 4 d 4 k G 0 k) e ikµx x ) µ, 30) δ 4) x x ) = 1 π) 4 d 4 k e ikµx x ) µ. 31) Si ha: G 0 k) = 1 k µ k µ = 1 k k 0 Se desideriamo una soluzione ritardata di Gx x ), ioè tale he G = 0 per t < t ed onde usenti per t > t, dobbiamo prendere un ammino omplesso R nel piano omplesso k 0 ome indiato in figura 3. La soluzione ritardata quindi è

10 Potenziali di Liénard -Wiehert Im[k 0 k 0 R k k Re[k 0 Figura 3: Cammino di integrazione. G R x x ) = 1 π) 4 d 4 k e ikµx x ) µ R k µ k µ si ha per suessive integrazioni usando il teorema dei residui) avendo posto G R x x ) = 1 π) 3 = 1 π R 1 = π) R = 1 8π R Quindi la soluzione ritardata per fx) è: fx) = 1 4π = 1 4π d 3 k e i k r r ) sin[ k t t ) k 0 dk sink t) sinkr) dk sink t) sinkr) dk [e ikr t) e ikr+ t) = 1 δr t), 3) 4πR k k, R r r, e t t t. 6 Potenziali di Liénard -Wiehert d 4 x gx ) δr t) R d r [g r, t ) t =t R/ R Supponiamo he la sorgente dei ampi sia ostituita da una aria puntiforme, +e, in moto vario. Sia r e t) la sua posizione al tempo t e v = d r e /dt la sua veloità. Il quadrivettore J λ r, t ) è dato da J µ r, t ) = eβ µ δ 3) r r e t)), β µ 1, β), essendo β = v/. Notare he β µ non è un quadrivettore, bensì β µ δ 3) r r e t)). Sostituendo questa espressione di J µ nella formula dei potenziali ritardati sritta ome integrale quadruplo,

11 Potenziali di Liénard -Wiehert si ha A µ = 1 d 4 x J µ x ) R δ R t + t ) = e dt βµ t ) Rt ) δ t + 1 ) Rt ) t eβ µ = R R β dove, d ora in poi, Rt ) = r r e t ) e l apie alle varie grandezze india he vanno prese al tempo ritardato t definito da t = t 1 Rt ). Nell uguaglianza preedente si è fatto uso inoltre di t t + 1 ) Rt ) t = R R t = 1 β R. Separando le omponenti spaziali e temporali di A µ si ha A r, t) = e β R R β, ϕ r, t) = e R R β, 33) questi sono i potenziali di Liénard e Wiehert. Da questi potenziali si possono ottenere i ampi mediante le usuali equazioni E = gradϕ 1 A t, B = rota, dove ompaiono derivate rispetto al tempo t attuale e rispetto alle oordinate del punto potenziato r. I potenziali di Liénard e Wiehert, 33), sono espressi però in termini di r e di t ed il tempo ritardato t risulta essere funzione di r e t tramite la relazione impliita t = t 1 Rt ). Periò bisogna alolare derivate di t rispetto a x, y, z e t. Prima abbiamo, derivando rispetto a t l equazione t = t 1 Rt ) da ui segue t t = 1 1 Rt ) t t t = 1 + R β t R t, Per trovare le derivate di t rispetto a x, y, z notiamo he grad t = grad t 1 ) Rt ) = 1 gradrt ) = 1 da ui segue grad t = 1 R R R β Usando queste formule si trova per i ampi E r, t) = e 1 β ) R R β ) R R β ) 3 t t = R R R β 34) + e R R t gradt + ) R [ R R R β ) β R R β ) 3, 35) B r, t) = 1 R R E. 36)

12 Campi reati da una aria in moto uniforme Il ampo magnetio è sempre perpendiolare a E. Il ampo elettrio è omposto da un primo termine he non ontiene l aelerazione e he per grandi distanze va ome 1/R e un seondo termine he ontiene β e he va ome 1/R per grandi R. Quest ultimo termine è relativo alle onde elettromagnetihe irradiate dalla partiella. 7 Campi reati da una aria in moto uniforme Supponiamo ora he v = ost.. Cerhiamo di esprimere tutto in termini di funzioni del tempo attuale t. Dalla figura 7 abbiamo he P R R R β = vt t ) v Figura 4: Punto potenziato e raggi vettori attuali e ritardati. R = R + R β 37) e risolvendo l equazione di seondo grado he si ottiene per R quadrando la 39), R = β R + β R ) + 1 β ) R 1 β, dove la radie è stata selta on il segno positivo poihè R > 0 e β < 1. Abbiamo anhe Allora i ampi si srivono R R β = 1 β ) R R β = β R ) + 1 β ) R s E = e 1 β ) R s 3, B = β E, he si possono naturalmente ottenere in modo più immediato operando on una trasformazione di Lorentz sul ampo Coulombiano esistente nel sistema in ui la aria è in quiete. Analogamente per i potenziali si ottiene A = e β s = ϕ β, ϕ = e s. Indiando on θ l angolo he R forma on β, possiamo srivere il modulo di E ome E = e R 1 β ) 1 β sin θ) 3/

13 Effetto Cěrenkov L intensità del ampo, rispetto al valore statio, risulta rimpiiolita di un fattore 1/γ lungo la direzione del moto θ = 0), mentre perpendiolarmente ad esso θ = π ) viene moltipliata per un fattore γ. Si onseguenza, via via he la veloità della aria si avviina alla veloità della lue, l intero suo ampo tende a onentrarsi su di un diso piatto perpendiolare alla traiettoria. Considerando ora la forza di Lorentz F = E + 1 v B = E + β β E) = 1 β ) E + β E) β = grad [ 1 β )ϕ, essendo ϕ il potenziale salare. ψ 1 β )ϕ è detto talvolta potenziale di onvenzione. Esso ha valori ostanti sull ellissoide di rotazione x + 1 β )y + z ) = ost., avendo selto l origine on la posizione istantanea della aria e β lungo l asse x. Questo ellissoide si ottiene ontraendo una sfera in direzione x per un fattore 1/γ. Riordare il aso di una sfera onduttrie aria e l assurdo he si avrebbe se anhe la sfera subisse la ontrazione di Lorentz. 8 Effetto Cěrenkov Nel aso di una aria in moto uniforme nel vuoto, nel risolvere l equazione di seondo grado, allo sopo di esprimere R in termini delle grandezze alolate al tempo attuale t, si è potuto esludere una delle soluzioni poihé, R > 0 e β < 1. Quando la aria si muove in un mezzo aratterizzato da un indie di rifrazione n, tutte due le soluzioni sono aettabili, quando sia verifiata la ondizione β m = nv > 1, 38) dove β m nella materia prende il posto di β. La ondizione 38) die he la veloità della partiella deve essere maggiore della veloità della lue nel mezzo. In questo aso si ha βm β m R R) ± β m 1) R R = βm = t t ), 1 ovvero esistono due posizione ritardate della aria he ontribuisono a reare i ampi al tempo attuale t ome rappresentato in figura 5. Il aso in ui la veloità della aria è minore della veloità della lue nel mezzo è rappresentato dalla figura 6. Possiamo alolare ora l apertura del ono inviluppo delle onde sferihe partendo dai diversi punti oupati suessivamente dalla aria. I potenziali saranno diversi da zero dentro questo ono. Indiando on θ l angolo tra R e β, e poihé R > 0, dovremo avere tenuto onto anhe della realtà di R ) le due ondizioni seguenti. βm R ) β m 1 ) R 0, β m R 0 da ui seguono ovvero os θ 1 1 β m 1 os θ, os θ 0, 1 1 β m

14 Effetto Cěrenkov Figura 5: Veloità della partiella superiore alla veloità della lue nel mezzo. Figura 6: Veloità della partiella minore della veloità della lue nel mezzo. β m Quindi l apertura del ono, entro ui sono diversi da zero i potenziali è π θ dove os θ = 1 1. Da iò segue he il ono di emissione della radiazione Cěrenkov ono perpendiolare a quello preedentemente desoitto) ha un apertura θ uguale a osθ = os π ) θ = sin θ = 1 = β m nv. I ampi sono quasi eslusivamente onentrati sulla superfiie del ono di apertura θ, e quindi anhe l energia. Ciøostituise un onda d urto l effetto fu soperto sperimentalmente da Cěrenkov nel 1937 e interpretato teoriamente da Frank e Tamm nello stesso anno si veda la sezione 10). R = R + R β 39)

15 Potenza irradiata da una aria puntiforme P R π θ +e θ β Figura 7: Angoli effetto Cěrenkov. 9 Potenza irradiata da una aria puntiforme In approssimazione non relativistia β 0) la parte radiativa di E è data da E e ˆn ˆn β) R, ˆn = R R, nella stessa approssimazione si è posto t = t poihé dalla 34) [ t t = R 1 β 1 R 1. Il vettore di Poynting è dato da S = 4π E B = 4π Eˆn, quindi la potenza irradiata per unità di angolo solido è dw dω = 4π E R = e 4π ˆn ˆn e [ β) = β ˆn β) = 4π e v 4π 3 sin Θ, essendo Θ l angolo tra i vettori ˆn e β. Integrando su tutto l angolo solido on la selta della direzione di β ome asse polare) si ha la potenza totale irradiata W = e v 3 3, formula di Larmor. Un alolo relativistio esatto avrebbe dato per la potenza totale irradiata l espressione di Liénard W = e [ 3 γ6 β) β β), 40) la quale si ottiene integrando sulle direzioni di ˆn l espressione relativistia di dw/dω data da dw dω = 4π E t R t = e ˆn [ˆn β) β 4π 1 ˆn β) 41) 5 Il fattore t/ t = 1 ˆn β è neessario per riferire la potenza al tempo t della aria; nell ultima espressione è stato omesso, per sempliità, l apie

16 Spettro in frequenza dell energia irradiata Vediamo espliitamente ome si ottiene la 40) dalla 41). Omettendo gli apii, il prodotto vettore in 41) si espande seondo la [ ˆn ˆn β) β = β) 1 + β ) β β) ˆn β β) + β β ˆn β ˆn β) ˆn β β) Prendendo l asse z nella direzione di β, le integrazioni sull angolo ϕ sono semplii e gli integrali neessari per trovare la potenza totale irradiata sono del tipo x = os θ) e danno i risultati e 4π e 4π e 4π e 4π dω β) 1 + β ) β β) 1 ˆn β) 5 = dω ˆn β β) + β β ˆn β 1 ˆn β) 5 = dω ˆn β) 1 ˆn β) 5 = e 1 β ) 4 dω ˆn β β) 1 ˆn β) 5 = Sommando le 4) si ottiene ioè appunto la 40). W = = = e 1 β ) 4 1 dx 1 βx) 5 = 1 + β ) 1 β ) 4, x dx 1 βx) 5 = β5 + β ) 31 β ) 4, x dx 1 βx) 5 = β1 + 5β ) 31 β ) 4, e [ 1 β ) 4 β) 1 + β ) β β) 1 + β ), e [ 1 β ) 4 3 β) β 5 + β ) + 3 β β) 5 + β ) [ β β) 1 3 β 1 β ) [ β )[β β) β β) e [ β 31 β ) 4 1 β ) + β β) 1 β ) e [ β 31 β ) 3 1 β ) + β β),. 4) e 31 β ) 3 [ β β β), 43), 10 Spettro in frequenza dell energia irradiata Caloliamo ora lo spettro di frequenza della energia irradiata in tutto il tempo in ui la aria è aelerata, supponendo he l aelerazione duri per un tempo finito o he vada a zero nel passato e nel futuro in modo he l energia irradiata sia finita. Riferendoi ora al tempo dell osservatore in modo he si abbia lo spettro di frequenze visto da lui, abbiamo, per la potenza irradiata ed inoltre dw dω = gt), dove gt) = 4π R E [ R E e ˆn ˆn β ) β = 1 ˆn β. )

17 Spettro in frequenza dell energia irradiata Per l energia totale irradiata abbiamo de dω = + gt) dt = + dove g 0 ω) è la trasformata di Fourier di gt) g 0 ω) dω g 0 ω) = 1 + gt)e iωt dt, π + 0 diω) dω dω ed è stato fatto uso del teorema di Parseval. Inoltre, l ultima uguaglianza definise diω) dω ovviamente per frequenze positive) e si ha usando g 0 ω) = g 0ω)): solo diω) dω = g 0ω) + g 0 ω) = g 0 ω). diω) dω è lo spettro di frequenza erato. Caloliamo g 0ω) g 0 ω) = = e 8π e 8π e + + 8π e i ωr [ dt e iωt ˆn ˆn β ) β 1 ˆn β ) 3 [ ) dt e iω ˆn ˆn β ) t + β R 1 ˆn β ) [ˆn β) β + ˆn re iωt dt e ) ˆn 1 ˆn β). dove si è fatto un ambiamento di variabili da t a t = t R, riordando he t/ t = 1 ˆn β, e si è approssimato R on r ˆn r e onsiderando inoltre ˆn quasi uguale al versore di r e indipendente dal tempo. e + g 0 ω) = 8π e i ωr ˆn re iωt dt e ) d ˆn ˆn ) β dt 1 ˆn β). Quindi = e 8π iω e i ωr diω) dω = e ω 4π + + ˆn re iωt dt e ) ˆn ˆn β ) ˆn re iωt dt e ) ˆn ˆn β ) Questa formua può essere usata nel aso dell effetto Cěrenkov sostituendo /n a e e/n ad e), ioè diω) dω = e ω n + ˆn re iωt 4π 3 dt e ) ˆn ˆn v). Poihé il moto è uniforme si ha r e = vt e, indiando on θ l angolo tra ˆn e v, abbiamo e n β sin θ ω π + dt e iωt1 nβ os θ) = e n β sin θ δ1 β m os θ)

18 Spettro in frequenza dell energia irradiata Questa energia è infinita perhé la aria irradia per un tempo infinito. Se il tempo fosse stato T allora: diω) dω = e n β sin θ ω T dt e iωt1 nβ m os θ) π = e n β sin θ ω T π T sin [ωt 1 β m os θ) [ωt 1 β m os θ). 44) La funzione sin [.../[... ha un massimo molto stretto per ωt >> 1 intorno all angolo θ. Integrando ora sull angolo solido e ponendo sin θ sin θ si ha Iω) = ue β sin θ = ue β sin θ = ue β sin θ ω T π π +1 1 ω T π π 1 ωt β m ω T π dx sin [ωt 1 β m x) [ωt 1 β m x) + dy sin y y π π = βt ) e ω ωt β m sin θ, 45) e si vede he Iω) è proporzionale a T. Si può ottenere l energia irradiata per intervalli unitari di frequenza e per unità di perorso dividendo la preedente formula per il perorso L = βt [ diω) dx = e ω sin θ = e ω 1 1 β n, ω) dove ω è tale he nω) > 1/β. Il numero di quanti on frequenza ompresa tra ω e ω + dω emessi per unità di perorso da una partiella di aria e è dunque ) dω 1 e v n = 1 ) 1 dω 137 v n e dipende da ω solo attraverso nω). Per un elettrone molto rapido v ) he passi attraverso l aqua n 1.33) vi sono ira 30 quanti emessi per entimetro di perorso nella regione visibile 4000Å λ 7500Å)