1. Calcolare l insieme delle soluzioni della seguente equazione differenziale: y y y y x cos x P t t t t t t 2
|
|
|
- Graziana Giordani
- 5 anni fa
- Visualizzazioni
Transcript
1 EQUAZIONI DIFFERENZIALI A COEFFICIENTI COSTANTI Callare l insieme delle sluzini della seguente equazine differenziale: y y y y s P t t t t t t, n radii, i Plinmi aratteristi: Sluzine generale dell equazine mgenea assiata:,, Sluzine partilare dell equazine mpleta: derivate s sin sin s y a b d d e e sin s s sin y a d d e e s sin sin s y d d e e y e s sin, n y a b d s esin n Sstituend la sluzine e le sue derivate nell equazine mpleta abbiam: a b a 0 a b 8 a b 0 y 8 s sin 5 5 d e d 5 d e 0 e 5 Sluzine generale:,, y e s sin 8 s sin, n 5 5 Si determini la sluzine del seguente prblema di Cauhy:
2 Plinmi aratteristi: Pt t t t y y y e y 0 0 y 0 0 y 0 0 n radii 0, e y e e Sluzine generale dell equazine mgenea,,, y a b e Sluzine partilare dell equazine mpleta nella frma: y e e e,,, 4 4 Sluzine generale: Impnend le ndizini del prblema abbiam: y e e e Quindi la sluzine del prblema di Cauhy è: Per gni numer reale k 0 si determini l insieme delle sluzini (dett anhe integrale generale) dell equazine differenziale yky s Plinmi aratteristi Ptt k n radii ki y s k sen k, n Sluzine generale dell equazine mgenea assiata, Se k erhiam una sluzine partilare dell equazine mpleta della frma y a b n derivata senda y as bsen e sstituend funzine e s sen
3 derivata nell equazine tteniam a ka a s k y b kb 0 k b 0 s y k sen k, n, k generale è s e la sluzine Se k erhiam una sluzine partilare dell equazine mpleta della frma y a b y b a s b a sen e s sen n derivata senda a 0 a 0 sen sstituend funzine e derivata nell equazine tteniam y e b b sen la sluzine generale è y s sen, n, 4 Si alli l integrale generale dell equazine differenziale rdinaria y y y sene Plinmi aratteristi: Pt t t t t n radii, y e e n, Sluzine generale dell equazine mgenea assiata: Cerhiam una sluzine partilare dell equazine mpleta nella frma y e e e rislvend il sistema sen s s sen e e 0 e e e e e sin e e sen e e e e y s e e e s e sen e e e sen e n, La sluzine generale pertant è: y e e e sen e 5 Si alli la sluzine del seguente prblema di Cauhy y y y 0 0 y 0 0 e
4 y e La sluzine dell equazine mgenea assiata è: Cn un ambi di variabile u y, n, pssiam erare una sluzine partilare dell equazine mpleta della frma u e n La sstituzine di queste due funzini nell equazine mpleta i prta a u e e e e e quindi integrand abbiam e lg e Quindi u lg e e e e y u d e e lg e lg e e La sluzine generale quindi è: lg lg, y e e e e e n La sluzine del prblema di Cauhy i prta le ndizini lg 0 lg 0 e sì tteniam: lg lg lg lg y e e e e e 6 Determinare al variare di l integrale generale y dell equazine differenziale Dire per quali valri di il lim y y sin y dal valre della stante he mltiplia la sluzine (attenzine he questa ndizine dipende anhe e dell mgenea) Dire per quali valri di la sluzine del seguente prblema di Cauhy è peridia y y sin y 0 0 y 0 4
5 Plinmi aratteristi: Pt t t t t n radii 0, y e L integrale generale dell equazine mgenea assiata: Integrale partilare dell equazine mpleta: s sin, n, y a b n sin s e 4 s 4 sin y a b y a b Sstituend le derivate nell equazine mpleta tteniam: 4a s 4bsin a sin b s sin a a 4b b 4 4a b 0 4 periò y s sin 4 L integrale generale dell equazine mpleta è:, s sin y e 4 n Per rispndere alla senda rihiesta dbbiam determinare per quali valri del parametr s sin lim e 4 A ausa della limitatezza dell integrale partilare dell equazine mpleta, per valri finiti del parametr il limite diverge psitivamente sl a ausa del termine espnenziale Si deve periò imprre he 0 e 0 Per rispndere all ultim punt ntiam he la sluzine generale dell equazine mpleta si riava s sin da quella preedente, per, è: y e 0 Le ndizini pste dal prblema di Cauhy e dalla rihiesta he la sluzine sia peridia, iè he il termine espnenziale sia sppress, i permettn di srivere le equazini: 0 0 s sin 0 y
6 7 Si determini l integrale generale dell equazine differenziale y 4y s Plinmi aratteristi Pt t 4t t t 4 n radii 0, i y s sin, n Integrale generale dell equazine mgenea assiata:,, Cerhiam un integrale partilare dell equazine mpleta nella frma y a b y a b s b sin, s sin n derivate 4 s 4 sin, y b b Sstituend le derivate nell equazine tteniam Integrale generale dell equazine:,, y 4 b s 4 b sin 4a 8b y s y s sin s n Si alli l insieme delle sluzini dell equazine differenziale: y y y e s Plinmi aratteristi: Pt t t t n radii 0, i Sluzine generale dell equazine mgenea y e s sen Sluzine partilare dell equazine mpleta nella frma: s sen y a b e Sstituend le derivate di questa funzine nell equazine tteniam:,,, 6
7 a 4 4a 4a b 0 b y e s sen e s sen 4 4 4, Sluzine generale:,, 9 Si determini la sluzine del seguente prblema di Cauhy: y y y e y 0 0 y 0 0 y 0 0 Plinmi aratteristi: Pt t t t n radii 0, e y e e,,, Sluzine generale dell equazine mgenea y a b e Sluzine partilare dell equazine mpleta nella frma: y e e e,,, 4 4 Sluzine generale: Impnend le ndizini del prblema abbiam:
8 9 7 y e e e Quindi la sluzine del prblema di Cauhy è: 0 Si determini la sluzine del seguente prblema di Cauhy: y y 4y e y 0 0 y 0 0 y 0 0 Plinmi aratteristi P t t t 4 t t n radii e di mltepliità dppia y e e e n Sluzine generale dell equazine mgenea assiata:,, y a e Cerhiam una sluzine partilare dell equazine mpleta nella frma n derivate y e 4a 8a a e y 8 4 e a a a Sstituend funzine e derivate nell equazine tteniam: e 6a y 6 Sluzine generale dell equazine: : e y e e e n,, 6 Impnend le ndizini del prblema di Cauhy abbiam: Sluzine del prblema di Cauhy: e e e e y
9 Si alli la sluzine del seguente prblema di Cauhy: y y 4y 8y s sin y 0 0 y 0 0 y 0 0 n radii e i Plinmi aratteristi Pt t t 4t 8 t t 4 y s sin e n Sluzine generale dell equazine mgenea assiata:,, y a b, n Cerhiam una sluzine dell equazine mpleta nella frma s sin derivate y b as b asin, e y 4b 4a s 4b 4a sin y 8b a s 8a b sin Sstituend la funzine e le derivate nell equazine abbiam: a 0 8a8b sin y 8a 8b b 8 8 sin y s sin e n,, 8 Sluzine generale Impnend le ndizini del prblema di Cauhy abbiam: Sluzine del prblema di Cauhy: s sin e sin y
10 Si determini la sluzine del seguente prblema di Cauhy: y y y e sen y 0 0 y 0 0 Plinmi aratteristi P t t t n radii i Sluzine generale dell equazine mgenea assiata: y e s sen, n Cerhiam una sluzine dell equazine mpleta nella frma y e a s bsen Sstituend la funzine e le sue derivate nell equazine abbiam: y e e s sen s n,, Sluzine generale Impnend le ndizini del prblema di Cauhy abbiam: 0 0 y e e Sluzine del prblema di Cauhy: sen s a a b0 b0 0
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA Si determini la soluzione del seguente problema di Cauchy: x.
 Si dtrmini la sluzin dl sgunt prblma di Cauh: 0 d Si tratta di un quazin a variabili sparabili Si risriv dp avr sparat l d variabili si intgran sparatamnt l du funzini d da ui d, lg, Cn la ndizin 0 dtrminiam
Si dtrmini la sluzin dl sgunt prblma di Cauh: 0 d Si tratta di un quazin a variabili sparabili Si risriv dp avr sparat l d variabili si intgran sparatamnt l du funzini d da ui d, lg, Cn la ndizin 0 dtrminiam
Analisi 1 e 2 - Quarto compitino Soluzioni proposte
 Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
Testo della prova d'esame (A) con gli assi, eventuali asintoti, monotonia ed eventuali estremi. Dopo aver verificato che
 PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
Gli integrali indefiniti
 Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
ESERCIZI SULLO STUDIO DI FUNZIONE. Esercizi per il corso di Analisi Matematica 1, DTG, Università degli Studi di Padova
 ESERCIZI SULLO STUDIO DI FUNZIONE FRANCESCA ALBERTINI, LAURA CARAVENNA, MONICA MOTTA Esercizi per il crs di Analisi Matematica 1, DTG, Università degli Studi di Padva Per le seguenti funzini determinare:
ESERCIZI SULLO STUDIO DI FUNZIONE FRANCESCA ALBERTINI, LAURA CARAVENNA, MONICA MOTTA Esercizi per il crs di Analisi Matematica 1, DTG, Università degli Studi di Padva Per le seguenti funzini determinare:
Giustificare adeguatamente tutti i passaggi. + EX. 1 Si studi la convergenza (semplice, assoluta, totale) della serie 6 2
 Prva scritta di Analisi Matematica II - 4 giugn 013 Cmpit A COGNOME...... NOME. Matr... Crs di Laurea Ambiente Territri e Risrse Infrmazine Meccanica firma Giustificare adeguatamente tutti i passaggi +
Prva scritta di Analisi Matematica II - 4 giugn 013 Cmpit A COGNOME...... NOME. Matr... Crs di Laurea Ambiente Territri e Risrse Infrmazine Meccanica firma Giustificare adeguatamente tutti i passaggi +
A + B C + D A + B (A B) C + D (A B) Cinetica Chimica
 Cinetia Chimia termdinamia : desrizine dei fenmeni energetii nsiderand sl stat iniziale e stat finale inetia himia : studi della velità e dei meanismi di reazine A + B C + D A e B devn urtarsi urt effiae
Cinetia Chimia termdinamia : desrizine dei fenmeni energetii nsiderand sl stat iniziale e stat finale inetia himia : studi della velità e dei meanismi di reazine A + B C + D A e B devn urtarsi urt effiae
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi.
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA
 INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
Equazioni. Prerequisiti. Definizioni e concetti generali. Incognita Lettera (di solito X) alla quale è possibile sostituire dei valori numerici
 Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
SEGNALI PERIODICI, SEQUENZE, TRASFORMATA DISCRETA DI FOURIER. 1 Fondamenti Segnali e Trasmissione
 SEGALI PERIODICI, SEQUEZE, RASFORMAA DISCREA DI FOURIER Fndamenti Segnali e rasmissine Rappresentazine dei segnali peridii () Un segnale peridi n perid pu essere rappresentat me smma di espnenziali mplessi
SEGALI PERIODICI, SEQUEZE, RASFORMAA DISCREA DI FOURIER Fndamenti Segnali e rasmissine Rappresentazine dei segnali peridii () Un segnale peridi n perid pu essere rappresentat me smma di espnenziali mplessi
ASINTOTI di una funzione
 LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Trovare l interno di N (rispetto allo spazio topologico R. [2]. (E) Calcolare il seguente integrale indefinito (5x 2 + 3x + 1) 4 (10x + 3) dx. [3]. (E)
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Trovare l interno di N (rispetto allo spazio topologico R. [2]. (E) Calcolare il seguente integrale indefinito (5x 2 + 3x + 1) 4 (10x + 3) dx. [3]. (E)
Soluzione Es.1- In generale, le equazioni orarie del moto lungo l'asse orizzontale x e quello verticale y si possono scrivere come: (1a) (1b) (1c)
 Sluzine Es.1- In generale, le equazini rarie del mt lung l'asse rizzntale x e quell verticale si pssn scrivere cme: ( t) h + v (csα) t gt / h + v t / gt / (1a) v ( t) v csα gt v / gt (1b) x( t) v (sinα
Sluzine Es.1- In generale, le equazini rarie del mt lung l'asse rizzntale x e quell verticale si pssn scrivere cme: ( t) h + v (csα) t gt / h + v t / gt / (1a) v ( t) v csα gt v / gt (1b) x( t) v (sinα
Il processo inverso della derivazione si chiama integrazione.
 Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a
 MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a. 2008.09 Crs inegra cn Teria dei Segnali Maredì 8,30-11,30 Mercledì 8,30-10,30 Givedì 8,30-10,30 Esame del crs inegra: è cmplea quand si è supera sia sia Maemaica
MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a. 2008.09 Crs inegra cn Teria dei Segnali Maredì 8,30-11,30 Mercledì 8,30-10,30 Givedì 8,30-10,30 Esame del crs inegra: è cmplea quand si è supera sia sia Maemaica
Equazioni differenziali lineari
 Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Fondamenti di Automatica
 Fndamenti di Autmatica Allievi in Ingegneria Elettrica - Prf. P. Claneri Appell del Lugli 4 Cgnme Nme N di Matricla Firma Durante la prva nn è cnsentita la cnsultazine di libri, dispense e quaderni. Quest
Fndamenti di Autmatica Allievi in Ingegneria Elettrica - Prf. P. Claneri Appell del Lugli 4 Cgnme Nme N di Matricla Firma Durante la prva nn è cnsentita la cnsultazine di libri, dispense e quaderni. Quest
approfondimento Lezione 4. Scomposizione canonica di Kalman F. Previdi - Controlli Automatici - Lez. 4 1
 Lezine. Scmpsizine cannica di Kalman F. Previdi - Cntrlli utmatici - Lez. Schema della lezine. Intrduzine alle scmpsizini canniche. Scmpsizine di raggiungibilità. Scmpsizine di sservabilità. Scmpsizine
Lezine. Scmpsizine cannica di Kalman F. Previdi - Cntrlli utmatici - Lez. Schema della lezine. Intrduzine alle scmpsizini canniche. Scmpsizine di raggiungibilità. Scmpsizine di sservabilità. Scmpsizine
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del terzo appello, 19 febbraio 2018 Testi 1
 Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
INTRODUZIONE AI SEGNALI
 INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
Le disequazioni di primo grado
 ) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 24 luglio 2017 Testi 1
 Scritto del sesto appello, luglio 7 Testi Prima parte, gruppo.. Determinare i punti di massimo e minimo assoluti della funzione f( := 3 e relativamente alla semiretta, specificando se non ne esistano..
Scritto del sesto appello, luglio 7 Testi Prima parte, gruppo.. Determinare i punti di massimo e minimo assoluti della funzione f( := 3 e relativamente alla semiretta, specificando se non ne esistano..
( ) ( ) d x = ω. dsenθ dθ. d 2 senθ dθ 2. = d dθ. = sen θ. = d cosθ dθ. d 2 cosθ dθ. dcosθ dθ. = cosθ dθ. = d( senθ) = d sen θ dθ
 Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
Equazioni differenziali ordinarie del primo ordine
 Equazini differenziali rdinarie del rim rdine DEFINIZIONE Dicesi equazine differenziale rdinaria del rim rdine una equazine nella quale figura cme incgnita una funzine stabilisca un legame fra la variabile,
Equazini differenziali rdinarie del rim rdine DEFINIZIONE Dicesi equazine differenziale rdinaria del rim rdine una equazine nella quale figura cme incgnita una funzine stabilisca un legame fra la variabile,
a ), la (34) diventa: Senza perdita di generalità si può omettere il valore assoluto e quindi la soluzione generale dell equazione omogenea è:
 Appunti dlla lzin dl Prf. Stfan D Marchi dl 9/0/6 a cura dl Prf. Frnand D Angl. Equazini diffrnziali linari dl prim rdin. Un quazin diffrnzial linar dl prim rdin si scriv:, () a + b, I I R cn b a, funzini
Appunti dlla lzin dl Prf. Stfan D Marchi dl 9/0/6 a cura dl Prf. Frnand D Angl. Equazini diffrnziali linari dl prim rdin. Un quazin diffrnzial linar dl prim rdin si scriv:, () a + b, I I R cn b a, funzini
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del TEMA log x. f(x) = e
 Esercizio 1 [6 punti] Sia ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione Appello del 8.07.019 TEMA 1 f) = e +log. a) Determinare il dominio D di f; determinare i limiti di f agli estremi di
Esercizio 1 [6 punti] Sia ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione Appello del 8.07.019 TEMA 1 f) = e +log. a) Determinare il dominio D di f; determinare i limiti di f agli estremi di
TRE SISTEMI DI RIFERIMENTO O O' O'' IN MOTO RELATIVO TRA LORO Z'' Z'' Z Z ' O' Z Z ' O' O'' O (SISTEMA RIFERIMENTO DEL LABORATORIO) O''
 Z Z Z Z ' ' ' ' v v V Z'' Z'' '' '' X' X' x'' x'' TRE SISTEMI DI RIFERIMENT ' '' IN MT RELATIV TRA LR (SISTEMA RIFERIMENT DEL LABRATRI) ' SI MUVE CN VELCITA' UNIFRME v (DIREZINE IDENTIFICATA CN L'ASSE
Z Z Z Z ' ' ' ' v v V Z'' Z'' '' '' X' X' x'' x'' TRE SISTEMI DI RIFERIMENT ' '' IN MT RELATIV TRA LR (SISTEMA RIFERIMENT DEL LABRATRI) ' SI MUVE CN VELCITA' UNIFRME v (DIREZINE IDENTIFICATA CN L'ASSE
Equazioni differenziali del II ordine. y 5y + 6y = 0 y(0) = 0 y (0) = 1
 Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
Analisi I - IngBM COMPITO B 22 Febbraio 2014 MATRICOLA... VALUTAZIONE =...
 Analisi I - IngBM - 03-4 COMPITO B Febbraio 04 COGNOME... NOME... MATRICOLA... VALUTAZIONE... +... =.... Istruzioni. Il compito è composto di due parti. La prima parte deve essere svolta preliminarmente.
Analisi I - IngBM - 03-4 COMPITO B Febbraio 04 COGNOME... NOME... MATRICOLA... VALUTAZIONE... +... =.... Istruzioni. Il compito è composto di due parti. La prima parte deve essere svolta preliminarmente.
SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1
 www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
Analisi e Geometria 1 Politecnico di Milano Ingegneria Industriale
 Analisi e Geometria Politecnico di Milano Ingegneria Industriale Docenti: P Antonietti, F Cipriani, F Colombo, F Lastaria G Mola, E Munarini, P Terenzi, C Visigalli Terzo appello, Settembre 9 Compito A
Analisi e Geometria Politecnico di Milano Ingegneria Industriale Docenti: P Antonietti, F Cipriani, F Colombo, F Lastaria G Mola, E Munarini, P Terenzi, C Visigalli Terzo appello, Settembre 9 Compito A
1) D0MINIO. x x 4x + 3 Determinare il dominio della funzione f (x) = x Deve essere
 ) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
Compito di Analisi Matematica II del 28 giugno 2006 ore 11
 Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
2. Circuiti Lineari con Amplificatori Operazionali
 . Circuiti Lineari cn Amplificatri Operazinali iferimenti di Tensine Generatri di Crrente Amplificatre a Transimpedenza Cnvertitri - ad alta sensibilità Cnvertitri - Amplificatre di crrente differenziale
. Circuiti Lineari cn Amplificatri Operazinali iferimenti di Tensine Generatri di Crrente Amplificatre a Transimpedenza Cnvertitri - ad alta sensibilità Cnvertitri - Amplificatre di crrente differenziale
INTRODUZIONE AI SEGNALI. 1 Fondamenti di segnali e trasmissione
 INRODUZIONE AI SEGNALI Fndameni di segnali e rasmissine Classificazine dei segnali () I segnali rappresenan il cmpramen di grandezze fisiche (ad es. ensini, emperaure, pressini,...) in funzine di una piu
INRODUZIONE AI SEGNALI Fndameni di segnali e rasmissine Classificazine dei segnali () I segnali rappresenan il cmpramen di grandezze fisiche (ad es. ensini, emperaure, pressini,...) in funzine di una piu
Compito di Istituzioni di Matematica 1 Prima parte, Tema ALFA COGNOME: NOME: MATR.:
 Compito di Istituzioni di Matematica 1 Prima parte, Tema ALFA 6 settembre 2017 COGNOME: NOME: MATR.: 1) L applicazione lineare f : R 3 R 4 data da f(x, y, z) = (x kz, 3x + 2y + z, x + z, 2x + y + z) è
Compito di Istituzioni di Matematica 1 Prima parte, Tema ALFA 6 settembre 2017 COGNOME: NOME: MATR.: 1) L applicazione lineare f : R 3 R 4 data da f(x, y, z) = (x kz, 3x + 2y + z, x + z, 2x + y + z) è
Es. 1: 6 punti Es. 2: 12 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti Totale. sin x arctan x lim. 4 x 2. f(x) = x 2
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo appello, 1 Luglio 010 Cognome: Nome: Matricola: Compito A Es. 1: 6 punti Es. : 1 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo appello, 1 Luglio 010 Cognome: Nome: Matricola: Compito A Es. 1: 6 punti Es. : 1 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti
SIE (Ing. Edile) Fila A 15-gennaio-2007
 Prova scritta di I e SIE (Ing. Edile) Fila A 15-gennaio-2007 3 1 1 1 1 1 1 1 0 1 0 0 h 1 h 2 2 2h h 1 h 2 6 3 1 h determinare il rango di A al variare del parametro reale h. 3. (3 pt) Sia V = ( 1 0) e
Prova scritta di I e SIE (Ing. Edile) Fila A 15-gennaio-2007 3 1 1 1 1 1 1 1 0 1 0 0 h 1 h 2 2 2h h 1 h 2 6 3 1 h determinare il rango di A al variare del parametro reale h. 3. (3 pt) Sia V = ( 1 0) e
INTRODUZIONE AI SEGNALI. Fondamenti Segnali e Trasmissione
 INRODUZIONE AI SEGNALI Fndameni Segnali e rasmissine Classificazine dei segnali ( I segnali rappresenan il cmpramen di grandezze fisiche (ad es. ensini, emperaure, pressini,... in funzine di una piu variabili
INRODUZIONE AI SEGNALI Fndameni Segnali e rasmissine Classificazine dei segnali ( I segnali rappresenan il cmpramen di grandezze fisiche (ad es. ensini, emperaure, pressini,... in funzine di una piu variabili
LICEO SCIENTIFICO SESSIONE STRAORDINARIA PROBLEMA 2
 www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 218 - PROBLEMA 2 Consideriamo la funzione f: R R, osì definita: f(x) = ln(a e bx + ) al variare di a, b, parametri reali positivi. 1) Verifia he,
www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 218 - PROBLEMA 2 Consideriamo la funzione f: R R, osì definita: f(x) = ln(a e bx + ) al variare di a, b, parametri reali positivi. 1) Verifia he,
Le due fenditure dell interferometro si comportano come piccole sorgenti, di intensità rispettivamente pari a I 1 = α 2 I o ; I 2 = β 2 I o.
 Prva i stituzini i Fisica ella Materia 7.06.06 sercizi Un na M piana ce prcee nel vut, in irezine ẑ, è escritta al camp elettric (figura ): r z,t r r ep i kz t cn ˆ ( ) [ ( )] a) Determinare la lungezza
Prva i stituzini i Fisica ella Materia 7.06.06 sercizi Un na M piana ce prcee nel vut, in irezine ẑ, è escritta al camp elettric (figura ): r z,t r r ep i kz t cn ˆ ( ) [ ( )] a) Determinare la lungezza
1) D0MINIO FUNZIONE. Determinare il dominio della funzione f (x) = 4 x 2 4x + 3 x 2 6x + 8 Deve essere. x 2 6x + 5 (x 1) (x 5)
 ) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 5 febbraio 2018 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
SEGNALI NON PERIODICI: LA TRASFORMATA DI FOURIER
 SEGNALI NON PERIODICI: LA RASFORMAA DI FOURIER Fndameni di Segnali e rasmissine Inrduzine Se il segnale d ingress di un sisema Lineare emp-invariane LI e un espnenziale cmpless, l uscia sara ancra un espnenziale
SEGNALI NON PERIODICI: LA RASFORMAA DI FOURIER Fndameni di Segnali e rasmissine Inrduzine Se il segnale d ingress di un sisema Lineare emp-invariane LI e un espnenziale cmpless, l uscia sara ancra un espnenziale
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Dire il comportamento della serie n=0 n+2n n 3 +n! motivando la risposta. [2]. (E) Dire il comportamento della serie n=0 n+2n n 3 +3 n motivando la risposta.
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (E) Dire il comportamento della serie n=0 n+2n n 3 +n! motivando la risposta. [2]. (E) Dire il comportamento della serie n=0 n+2n n 3 +3 n motivando la risposta.
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quinto appello, 25 giugno 2018 Testi 1
 Scritto del quinto appello, 25 giugno 208 Testi Prima parte, gruppo. a) x = 2, y = 2; r = α = b) x = 0, y = 3; r = α = c) r = 2 3, α = 2π/3; x = y = 2. Trovare i punti di minimo e massimo assoluti della
Scritto del quinto appello, 25 giugno 208 Testi Prima parte, gruppo. a) x = 2, y = 2; r = α = b) x = 0, y = 3; r = α = c) r = 2 3, α = 2π/3; x = y = 2. Trovare i punti di minimo e massimo assoluti della
Nome e cognome: Matricola: Si prega inoltre di compilare i seguenti campi, in base alla scelta che si intende fare.
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Parziale di MATEMATICA (A) San Flrian, //07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Parziale di MATEMATICA (A) San Flrian, //07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
lim β α e detto infinitesimo una qualsiasi quantita tendente a zero quando una dati due infinitesimi α e β non esiste
 Infinitesimi e detto infinitesimo una qualsiasi quantita tendente a zero quando una opportuna variabile tende ad assumere un determinato valore dati due infinitesimi α e β α e β non sono paragonabili tra
Infinitesimi e detto infinitesimo una qualsiasi quantita tendente a zero quando una opportuna variabile tende ad assumere un determinato valore dati due infinitesimi α e β α e β non sono paragonabili tra
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
a) usando la formula (x-x C ) 2 +(y-y C ) 2 +(z-z C ) 2 =r 2 Esercizi vari - Esercitazioni di Algebra e Geometria - Anno Accademico 2009-2010 1
 Esercizi di riepilg Esercizi In E 3 (R) si determinin: [(a)] una rappresentazine cartesiana della sfera di centr C=(,,) e raggi R=5; [(b)] una rappresentazine cartesiana della retta passante per C e rtgnale
Esercizi di riepilg Esercizi In E 3 (R) si determinin: [(a)] una rappresentazine cartesiana della sfera di centr C=(,,) e raggi R=5; [(b)] una rappresentazine cartesiana della retta passante per C e rtgnale
SOMMATORI. Il circuito di figura, detto sommatore invertente, fornisce in uscita una combinazione lineare dei segnali d ingresso, del tipo V
 SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE
 1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Raccolta esami di Analisi II
 Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
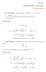 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Equazioni differenziali Problema di Cauchy
 Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
ESERCIZI DI ANALISI MATEMATICA II. sin(tv) v. f(v) dv = (1 + t) (e 1/t + 1)
 ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2006
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 6 PRBLEMA Si considerino le funzioni f e g determinate da f () log e g () a, essendo a un parametro reale e il logaritmo di base e.. Si discuta,
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 6 PRBLEMA Si considerino le funzioni f e g determinate da f () log e g () a, essendo a un parametro reale e il logaritmo di base e.. Si discuta,
Appello di Matematica II Corso di Laurea in Chimica / Scienze Geologiche 19 Giugno ( 1) n sin 1. n 3
 Appello di Matematica II Corso di Laurea in Chimica / Scienze Geologiche 9 Giugno 203 TRACCIA A. Studiare il carattere della seguente serie numerica + n= ( ) n sin. Si tratta di una serie a termini di
Appello di Matematica II Corso di Laurea in Chimica / Scienze Geologiche 9 Giugno 203 TRACCIA A. Studiare il carattere della seguente serie numerica + n= ( ) n sin. Si tratta di una serie a termini di
Cosa vedremo. Lezione 4. Dati. Tipo di dato. Tipo di dato. I Dati: Gli oggetti che conosce il computer
 Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 16 giugno 1999
 assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE.
 PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
DERIVATE pag Calcolo della derivata prima [ ] [ ] [ ] ( ) ( 1. ( x x 1) f () x = x. xcos
![DERIVATE pag Calcolo della derivata prima [ ] [ ] [ ] ( ) ( 1. ( x x 1) f () x = x. xcos DERIVATE pag Calcolo della derivata prima [ ] [ ] [ ] ( ) ( 1. ( x x 1) f () x = x. xcos](/thumbs/95/125308067.jpg) Calcolo della derivata prima.0. f = 5 + 5 7.0. f sin +.0. f = log.0. f = log DERIVATE pag. = 5 ] 6 = f ' = cos + 7 [ ] f ' = f ' = f ' = cos sin = cos [ ].0.5 f = sin cos.0.6 ( f = )( + ) = 0 + 6 ].0.7
Calcolo della derivata prima.0. f = 5 + 5 7.0. f sin +.0. f = log.0. f = log DERIVATE pag. = 5 ] 6 = f ' = cos + 7 [ ] f ' = f ' = f ' = cos sin = cos [ ].0.5 f = sin cos.0.6 ( f = )( + ) = 0 + 6 ].0.7
INTEGRALI IMPROPRI. Esercizi svolti
 INTEGRALI IMPROPRI Esercizi svolti. Usando la definizione, calcolare i seguenti integrali impropri: a c d e f / + 5 d arctan + d 8 + 4 5/ + e + d 9 + 8 + + d 4 d. d. Usando la definizione di integrale
INTEGRALI IMPROPRI Esercizi svolti. Usando la definizione, calcolare i seguenti integrali impropri: a c d e f / + 5 d arctan + d 8 + 4 5/ + e + d 9 + 8 + + d 4 d. d. Usando la definizione di integrale
La buca di potenziale di altezza infinita.
 La buca di potenziale di altezza infinita. Un caso semplice, ma interessante per le implicazioni, anche intuitive, che ne derivano, è quello della particella quantistica in una buca di potenziale. Consideriamo
La buca di potenziale di altezza infinita. Un caso semplice, ma interessante per le implicazioni, anche intuitive, che ne derivano, è quello della particella quantistica in una buca di potenziale. Consideriamo
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo?
 Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
y 3y + 2y = 1 + x x 2.
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
B Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
TAVOLA DEGLI INTEGRALI INDEFINITI
 Integrazione di funzioni elementari c c ln c arc tan c arc tan c a a a e e c TAVOLA DEGLI INTEGRALI INDEFINITI Integrazione di funzioni composte f( ) f ( ) f '( ) C ' f ln f ( ) c f( ) f '( ) arctan( f
Integrazione di funzioni elementari c c ln c arc tan c arc tan c a a a e e c TAVOLA DEGLI INTEGRALI INDEFINITI Integrazione di funzioni composte f( ) f ( ) f '( ) C ' f ln f ( ) c f( ) f '( ) arctan( f
REALTÀ E MODELLI SCHEDA DI LAVORO
 RELTÀ E MODELLI SCHED DI LVORO La rampa di access Per accedere a un edifici pubblic ci sn 6 gradini alti 6 cm e prfndi 0 cm; è necessari cstruire una rampa di access per carrzzine. La nrmativa prevede
RELTÀ E MODELLI SCHED DI LVORO La rampa di access Per accedere a un edifici pubblic ci sn 6 gradini alti 6 cm e prfndi 0 cm; è necessari cstruire una rampa di access per carrzzine. La nrmativa prevede
ANALISI MATEMATICA 1. (Ingegneria Industriale, corsi A e B) Esempi di prove scritte
 ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
LE FUNZIONI REALI DI VARIABILE REALE
 LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi.
 Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
APPELLO C AM1C 19 Gennaio f(x) = log( x + 2) x
 Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea (quadriennale) in Fisica a.a. 2002/03
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
Cognome: Nome: Matr. (e x 1 x)(1 x) 2/3 x (sin x) a
 Es. 1 Es. 2 Es. 3 Es. 4 T. Totale Analisi e Geometria 1 Docente: Gianluca Mola 27/1/29 Ing. Industriale Cognome: Nome: Matr. Nello spazio sottostante gli esercizi devono essere riportati sia i risultati
Es. 1 Es. 2 Es. 3 Es. 4 T. Totale Analisi e Geometria 1 Docente: Gianluca Mola 27/1/29 Ing. Industriale Cognome: Nome: Matr. Nello spazio sottostante gli esercizi devono essere riportati sia i risultati
PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016
 PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016 LE DISEQUAZIONI 1. Le disequazioni di primo e secondo grado 2. Le disequazioni di grado superiore al secondo e le disequazioni fratte
PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016 LE DISEQUAZIONI 1. Le disequazioni di primo e secondo grado 2. Le disequazioni di grado superiore al secondo e le disequazioni fratte
Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati siano stati dimostrati a lezione.
 Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quarto appello, 12 giugno 2017 Testi 1. n a + n 2a n 4 log(1 + 1/n 2 )
 Scritto del quarto appello, giugno 07 Testi Prima parte, gruppo. cartesiane: a) (, ); b) (0, ); c) (, 3). + sin(e ); b) lim log(); c) lim 0 + + sin(/ ). 3. Scrivere lo sviluppo di Talor di ordine 6 (in
Scritto del quarto appello, giugno 07 Testi Prima parte, gruppo. cartesiane: a) (, ); b) (0, ); c) (, 3). + sin(e ); b) lim log(); c) lim 0 + + sin(/ ). 3. Scrivere lo sviluppo di Talor di ordine 6 (in
1 a Prova parziale di Analisi Matematica I (1) 22/11/2006 (civili + ambientali)
 a Prova parziale di Analisi Matematica I () ) Data la funzione f ( ) = tg + ln( cos ) a) determinare il campo di esistenza, b) calcolare il limite lim f ( ) π ) Definizione di limite finito: lim f ( )
a Prova parziale di Analisi Matematica I () ) Data la funzione f ( ) = tg + ln( cos ) a) determinare il campo di esistenza, b) calcolare il limite lim f ( ) π ) Definizione di limite finito: lim f ( )
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 15 gennaio 2018 Testi 1
 Secondo compitino e primo appello, 5 gennaio 8 Testi Prima parte, gruppo.. Calcolare la velocità (intesa come vettore) e il modulo della velocità di un punto che si muove nel piano con la seguente legge
Secondo compitino e primo appello, 5 gennaio 8 Testi Prima parte, gruppo.. Calcolare la velocità (intesa come vettore) e il modulo della velocità di un punto che si muove nel piano con la seguente legge
Argomento 9 Suggerimenti
 Argomento 9 Suggerimenti E. 9. ) Integrare per parti scegliendo log come fattore finito. ) Se D indica la derivata, osservare che D (e ) = e. ) Integrare per parti scegliendo e come fattore differenziale.
Argomento 9 Suggerimenti E. 9. ) Integrare per parti scegliendo log come fattore finito. ) Se D indica la derivata, osservare che D (e ) = e. ) Integrare per parti scegliendo e come fattore differenziale.
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 12 giugno 2000
 assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
PROGRAMMA DI MATEMATICA APPLICATA
 PROGRAMMA DI MATEMATICA APPLICATA Classe II A Turismo A.S. 2014/2015 Prof.ssa RUGGIERO ANGELA ISABELLA I NUMERI REALI Radicali: - Riduzione allo stesso indice e semplificazione - Alcune operazioni fra
PROGRAMMA DI MATEMATICA APPLICATA Classe II A Turismo A.S. 2014/2015 Prof.ssa RUGGIERO ANGELA ISABELLA I NUMERI REALI Radicali: - Riduzione allo stesso indice e semplificazione - Alcune operazioni fra
, α N, quando f è una delle seguenti
 . Determinare lim 0 + α f, α R, e lim 0 α f funzioni: f = ln 8 cos4+, f = ln f = sin sine., α N, quando f è una delle seguenti, f = ln ln, sin sin. Calcolare la derivata della funzione f definita da f
. Determinare lim 0 + α f, α R, e lim 0 α f funzioni: f = ln 8 cos4+, f = ln f = sin sine., α N, quando f è una delle seguenti, f = ln ln, sin sin. Calcolare la derivata della funzione f definita da f
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO COGNOME: NOME: MATR.: 1) 7; C: x sin(x) dx è A: π ; B:2 ; C: 0 ; D: π/2; E: N.A.
 Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il
Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il

