Mtr Mtr Mtr Mtr Mtr Mtr Mtr. Mtr. 2. Limiti di successioni i,t". Ssr,:* (1+50) :7275 FolruÌa[3.3jcor n 5C:,o i,a..,, -5:;
|
|
|
- Agnella Festa
- 8 anni fa
- Visualizzazioni
Transcript
1 ES E M P! O Somma dei termini di una progressione aritmetica := I primi 50 numeri naturali, escludendo lo zero: 1, 2, 3,4, 5,..., 50 umeri naturali (escluso lo zero). si possono pensare come i primi 50 termini di una progressione aritmetica il cui primo termine è a1 : 1 e la cui ragione è r/ : 1. È In base alla formula [3.3] abbiamo allora: ftì Ssr,:* (1+50) :7275 FolruÌa[3.3jcor n 5C:,o i,a..,, -5:; z E 5 E M P lo Somma dei termini di una proqressione qeometrica ' D"t"rriniamo la somma dei primi 6 termini della progressione geometrica definita da an:,, 3 fl) n.t,.on n > 1. \2/ La ragione della progressione è q: +, e a1 :3. In base alla formula [3.a] abbiamo allora: ESERCIZI ap.'t72 Vero o falso? a. la successi orre an : ;nè strettamente crescente b. data ta successione definita,^ {::;t:, * ro,, rísutta at : 29 c. la successiorre an : Jn +4 è hmitata d. la successioîe an -- t - 2-" è limitata superiormente ma non inferiormente e. la successione an : nz l1 è una progressione aritmetica /3\,. f. la successiorre an : l; ) è una progressione geometrica g. la somma dei primi dieci termini della progressione aritmetica definita da an :2 + 3n, con r? > 1, è 185 h. la somma dei primi cinque termini della progressione geometrica definita da an : (+)' t,. 211 con/r>1,e g1 2. Limiti di successioni i,t".
2 CD Oetermina il termine generale della progressione geometrica il cui primo termine è ay :3 e la cui ragione è 5. fa':3 ' 5"-rl CI) Oetermina il termine generale della progressione geometrica ii cui primo termine è a1 : 8 e la cui ragione è -4. la,: g(-+)" rl CD Oetermina il termine generale della progressione geometrica in ani a1 : 4 e a2: /Q. lar: 4' 5"-1f :6eat:3.,2 D Oetermina il termine generale della progressione geometrica di ragione positiva in cui ar [".:.(+)' '] CD Oefinisci ricorsivamente la progressione aritrnetica il cui primo termine è a1 :5 e la cui ragione è -2. CE) Definisci ricorsivamente la progressione aritrnetica il cui termine generale è an - 3n - 4. CD Oefinisci ricorsivamente la progressiong geometrica il cui primo termine è 4 e la cui ragione è -2. CD Oefinisci ricorsivamente la progressione geometrica il cui termine generale è an: -3-2"-2. CD Oetermlna il termine generale della successione definita ricorsivamente da q : 2, an :2 t an-t. CD Oetermina il termine generale della successione definita ricorsivamenteda q :3, clr: I * an-t. (D Oetermina il termine generale della successione definita ricorsivamenteda h : L, an:3an-r. (D Determina il termine generale della successione definita ricorsivamen te da q : 4, an : ior-r. QD Calcolala somma dei primi 8O numeri pari, escluso lo zero. Calcola la somma dei primi 10OO numeri naturali, escluso lo zero. [soo Calcolala somma dei primi 100 termini della progressione aritmetica definita ricorsivamente da: lar:t ì. or*t : [10 000] an 12 (E) Calcola la somma dei primi 50 termini della progressione definita da: an:3n I 5, n > O. l3ezsl (D Calcolala somma: 1, ". ptr*'- rl] (D Cdcola la somma: n. (D calcola Ia somma: t *+*I* *#. (D calcola ta somma: t * +* * * lírn'- 'r] 12-2t-"1 l, - (+)'l 2. Limiti di successioni I Esercizipreliminari Test GD Quale delle seguenti successioni è convergente? Ban: na+t n2 CD Quale delle seguenti successioni è divergente? Ear: t - e-n Ean:1-lnn Ban:1 - sin n Ear: I _1 n CD Quale delle seguenti successioni non è irregolare? Ean: sinn P)a": cos n n - E (-1)'(1- e-')
3 @ Vero o falso? a. se una successione è superiormente limitata e strettamente decrescente, allora è convergente b. se a, < 100 per ogni n N e a, è strettamente crescente, allota anè convergente c. se an è limitata e monotona, allora non può essere divergente d. se liqf(x) : 1 e en ---+ Oper /! + *oo, allota,\y,, f(a"1 : t e. se4n ---+Oebn ---+0pern++cr:einoltre,-lim n++@ f(ar):1, lim f(b"): -l,alloranonpuòesistereil limite per x - 0 della funzione n.+ f f. se la successione an è irregolate, allora, qualsiasi sia il caratter e di bn, anche la succession e anbn è irregolare ','.r:i':i '::l:.:io--ì r.,lr:.: Inventa tu. Fornisci l'esempio: a. di una successione divergente e superiormente limitata; b. di una successione convergente e inferiormente limitata; c. di una successione convergente non monotona; d. di una successione divergente non monotona. I Calcolo di limitidisuccessioni Verifica, in base alla definizione, i seguenti limiti. Nelle soluzioni è riportata la condizione che definisce i valori di n per cui è soddisfatta la tim 3:o n++@ n,!**(2,.t_ 3) 1; tim (r*!\:,,_+_\ rim 'l= :, n-+q fil I.r+r(*)': o,itl(3 - t) : *- Calcola i seguenti limiti di successioni.!b lim 'n, =' n-+a nl Z # tim 3n2-+-Zn - 3 n++6 Zn + /,qîl(s - t") ti -- rl> "'!.-l a '';7 ; 1/it"l i ii > ("í. ;! > @ tim e& 11^ L n++@ rim$ n-+@ e't' ri- l1)' tim tim lim sin lim cos n++ 7On / rn+2\ (a;s; (t-,)
4 lim ln (r*a\ n-+m \ n / h- {11 n-+q. l nm +!, n_+@ \/n + i0l t0j t- 1l l1l [+ -'l (ID CD qe (fd,. 1 1 llfil n-*q -COS 11 - nz,itl[i" (nz + 5) - tn(n2 - +)] -.{ lllll n-+q - 3n 4n Irmn-+q tfl t1l Trt iri - "rjîl ",(,1;l_r) 1ip --nln-+q \n @ n^ (r *a* t) n-+@\n \/n n^'{--i n-+@ n "I+L(J"'+z-") (@ nm_?4tl-- n-+x \/tlz+3n+2-5n GD,lim n(l-eiy (EE) lim ntn n'+m lt *1) \ n/ GD lim nzlt -.o,?l n-f@ \ n) GD,ITLn sin a GD,rim rotr("+) pl l; -l i0l [1] lr) L- l t1l l0l l0l 1l -l,) -_1 l2l!31 i2l ["j i3i ì-l qd CE fd fd (D fd fe).. 3-3n lrm _ n-+* 4 * 2n,\T*JT *m.':+r (' * +)'",tt+*(t/ii - {n1,tit*" (t.í).. 7-e* llltt n-+rc Z sln -_ ṉ,\+-(#)" }ly*(ffi)" lim n2ú -.o, 1\ n-+ \ n/ (D ti^ n+f= n-+@ n * ln5 (@,\iry,*n* ce ti^ (tl?\",-+*\n+s/ (gl ri- (4)" "z ag - n) [-ì til letl Lz) I 3l l- t) t0j [+-] i1l L2l i0ì t1j lctl [e't'j 18 i ll L.) l GD nrim "t,(ftr) GD,ti.r, +# ::l iir ili {T + tsl l0l (sussni**to: ricorda.n" ( i ) : "#*,)
5 ! Successioni e funzioni Dimostra Dimostra che lim x sinx non esiste. x++@ lim cos x2 non esiste. x-+@ s^éè, Dimostra che limcos l non esiste. r-0 X 11 Dimostra che lim- sin -l non esiste. x+ox X Progressioni aritmetiche e geometriche e limiti di successioni Q Fornisci l'esempio: a. di una successione limitata e irregolare; b. di una progressione geometrica limitata; c. di una progressione aritmetica strettamente decrescente; d. di una successione monotona non convergente. G) catcota:,lim cos (#*l O Stabilisci se ciascuna delle seguenti successioni è convergente, divergente o Consideralasuccessionecosìdefinitaperricorrentut {1t:'^, <, conn > 1. Stabiliscisesitrattadiuna t 4n : an-'r _5' progressione aritmetica o geometrica, esprimi il termine generale an in funzione di n e determina se la successione a, è convergente, divergente o irregolare. Quanto vale lim h -l ':,,-l an, n-+a n CD Calcola: lim n++ ) StaUitisci se le seguenti affermazioni relative a una successiotte an sono vere o false. Se sono vere giustificale, altrimenti esibisci un controesempio. a. se an è convergente, allora anche an+7- arèconvergente b. se aral - a, è convergente, alloraanè convergente (n+2)t-(n+1)! (n + 2)l G) Sia s, la somma dei primi n multipli di 3 diversi sn dazero; calcola lim n++ú nz' M tr M tr c. se an è convergente a un numero non nullo, allora anche o'l' èconvergente M tr an d. se a1*1 è convergente, allora anche a, è an convergente M Considera la progressione aritmetica c, tale che at :3? a Determina il termine generale an e calcola lim L. n++e Considera la progressione geometrica a, Il cui primo termine è a1 : 9 e la cui ragione è ]. Oetermi na il termine generale di a, e il termine generale di sn: at I + ar. Quindi calcola: a' nrlyt-a' b.,4+l" (p Considera la successione così definita per ricor- (a,:4 rcnza: \ -^' i,- r\_, conn> 1 e k e R. Per quali 4, : (r - t)qn t valori di k è convergente? I FUNTO PER OGNI ESERCIZIO RISOLTO CORR,ETTAMEhITE; suffrctenza: ALMENo 6 pururl Le soluzioni sono in fondo al volume 177
6 Frazioni generatrici. Esprimi i seguenti numeri periodici come somma di una opportuna serie geometrica, quindi ricava la ftazione generatrice: a. 0,6 b. O,2I c.7,234 Determina per quali valori di r le seguenti serie sono convergenti e, per tali valori di x, calcolane la somma S. In=O + tn=o lm t n:0 *rc t n:o +N t n:0 (+)' xzn (7 + 2x)" (#)' (2 sin x)', con0( x 12n /,, a, í:' A partire da un quadrato Q1 il cui lato misura 4, costruiamo una successione di quadrati Qz, Qs,,, Q, ciascuno avente il lato di misura uguale alla metà del precedente. Siano Ir, lz,...,1, rispettivamente le lunghezze dei lati dei quadrati a1, a2,, an le loro aree. Esprimi In e a, in funzione di n; supponi quindi che il processo di costruzione dei quadrati continui indefinitamente e calcola: a. la somma delle lunghezze dei lati degli infiniti quadrati che si ottengono; b. la somma delle aree degli infiniti quadrati che si ottengono. 'r..),ì 6/'\ '.,"1-l;il Considera la figura qui sotto. Il lato del quadrato A1B1C1D1 misura 21. Sia ar, a2,, an la successione delle aree dei cerchi inscritti nei quadrati AtBtCrDr, A2B2C2D2,..., ArBnCnDr. Esprimi an in funzione di n; supponi quindi che il processo di costruzione dei quadrati e dei cerchi continui indefinitamente e calcola la somma delle aree degli infiniti cerchi che si ottengono. Sia AeBsCg un triangolo rettangolo in cui l'altezza AsAl relativa all'ipotenusa misura h e A()QBs : e. Costruiamo una poligonale AyA1A2...A, in cui Az èla proiezione di.a1 su AsBs, As è la proiezione di,4,2 su BsCs, e così via, come indicato in figura. Siano /e, 11,..., l, le lunghezze di AsA1, A1A2, A2A3,..., An-tAn. a. Calcola lalunghezza della poligonaleasaya2. An quando n + foo. b. Calcola la somma delle aree dei triangoli AsA1A2, AtAzAz,,An-2An-1An quandon + *oo. Ao A2 A4 A
7 Considera la successione così definita: an: 1 l1 a.dimostrache, < Zr-Tperognin>1. -L-I-I 11 7t ' zl' +1,conn>1. nt b. Tenendo conto di quanto dimostrato al punto a, dimostra che an < 3 per ogni n > 1. c. Dimostra che a, è convergente. Calcola il seguente limite:,{15 i,,, ttt :,),i t:,ttlt., di matematica e in Esprimi in funzione dinla seguente somma: ', t:ì, ':r' ' ',, r':,r, l)')-\, s : r(0) + r(1) + f(2) r(100) l ''',i Let f be the function given by f (*) : 3x + 4 for all real.x. Compute the sum: List the first nine terms of the sequenc e an - t- (+). Does this have a limit? Is the sequence bounded? Is the sequence monotonic? sequence Use induction principle to prove that2n < nl f.or n > 4. Find the values of x for which the series f n'r" converges. í:u I Problemi ed Considera la progressione geometrica an, il cuiprimo termine è a1 : 2 e la cui ragione è -3. a. Determina il termine generale a, della progressione e stabilisci se è convergente. b.determinaiterminigeneralidellesuccessionipneqnlcoírn)l,talichel'equazionex2+pnx+qn:oabbia come soluzioni a, e en+t-. Stabilisci se si tratta di progressioni aritmetiche o geometriche e, in caso affermativo, individuane il primo termine e la ragione. c. Determina il termine generale della successione c, definita da cn :Za e calcola lim cn. CIn n-ià d.stabilisci se la successione d, avente termine generale dr:logslcnl è una progressione aritmetica o geometrica e calcola,l:y_a". e. Esprimi in funzione di n il termine generale della successione s, definita da sn : ct I cz t I Cn. f. Calcola,lj+Lr,. Q) Sia aolocodo un quadrato. Tracciamo i quattro segmenti così definiti: il segmento che congiunge A0 con il punto medio di BeCs, il segmento che congiunge Be con il punto medio di CeDe, il segmento che congiunge Ce con il punto medio di AsDe e il segmento che congiunge Ds con il punto medio diaobo. Questi quattro segmenti, intersecandosi a due a due, individuano quattro puntial, Bt, Ct, D1, vertici del quadrilateroalblcldl. a. Dimostra che A1B1C1D1 è un quadrato. b. Supposto che il lato del quadrato AoBsCsDo misuri 2, determina la misura del lato dia1b1c1d1.
8 c. Ripetendo sul quadrato AútCtDt la stessa costruzione effettuata su AsBsCsDs si ottiene un nuovo quadrato, A2B2C2D2. Sul quadrato A2B2C2D2 può essere nuovamente dpetuta la costruzione, ottenendo così un quadrato A3B3CyD3, e così via. Sia as, a1,, 4n la successione delle aree dei quadrati AsBsCsDs, A1B1C1D1,.., AnBnCnDr. Dimostra che è una progressione geometrica e determina il suo termine generale. d. Determina il minimo valore di n per cui l'area dianbncndnè minore Ot,h- dell'area diaobocodo. e. Sia sn la somma delle aree dei quadrati AsBsCsDs, ArBtCtDt,, AnBrCnDr. Determina il limite di s, per 4 + *oo. r Quesiti C) Considera la progressione aritmetica i cui primi due termini Sorlo 41 : 6 e az:8. Sia s, : at i az +. + an.calcola l, 'tx Sn GD Considera la progressione geometrica aricttiprimi due termini Sorlo 41 : -2 e or:!. 3' Sia s, : at + az + + ar. calcolu nlly*o" ",U+L r,. (E) Stabilisci per quali valori di x la successione definita da a, : ( " =\t', \x+5/ a. è convergente; b. è irregolare. G) calcola' tr- (n - 1)l sin n n++@ ) sia sn: r * n; calcola: ''m $' n'+q fiz G) Dimostra per induzione che n3 - (E Stabitisci se le seguenti affermazioni sono vere o false; se sono vere, giustificale, se sono false fornisci un controesempio. a. se una successione è strettamente cfescente, allora è convergente M tr b. seunasuccessionearèstrettamentedecrescentee ar)operognit4 N, alloraarèconvergente M tr c. se an e b, sono due successioni convergenti, allora an * bn è convergente M tr d. se an e b, sono due successioni divergenti, allora an I b, è divergente M tr e. se una successione diverge a *oo, allora è definitivamente crescente M E (D Risolvi l'equazione nell'incognita x: 7+2x+4xz +8x3 + +(2x\ro: 2, I t \4^t _ l_2x nl n è divisibile per 3 per ogni n N, conn ) 2. Q) Dimostra che la successione così definita ricorsivamente: { :t :t- o 7 è convergente e calcola il suo limitepern+*oo. lon-t:+-- (D tndividua quale delle seguenti successioni, di cui è dato il termine generale, è irregolare, giustificando esaurientemente la risposta. t?r)' (-7)" n î.an_(-t)'(;) b. an: C. An: ^ d.an:r# n+z "
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Anna Montemurro. 2Geometria. e misura
 Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Esame di Analisi Matematica prova scritta del 23 settembre 2013
 Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
Prove d'esame a.a. 20082009
 Prove d'esame aa 008009 Andrea Corli settembre 0 Sono qui raccolti i testi delle prove d'esame assegnati nell'aa 00809, relativi al Corso di Analisi Matematica I (trimestrale, 6 crediti), Laurea in Ingegneria
Prove d'esame aa 008009 Andrea Corli settembre 0 Sono qui raccolti i testi delle prove d'esame assegnati nell'aa 00809, relativi al Corso di Analisi Matematica I (trimestrale, 6 crediti), Laurea in Ingegneria
VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 25 NOVEMBRE 2010 DURATA ORE 2:00
 VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 5 NOVEMBRE 010 DURATA ORE :00 QUESITI A RISPOSTA MULTIPLA Una sola risposta è esatta fra le 4 proposte per ciascun quesito. Ogni risposta esatta vale
VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 5 NOVEMBRE 010 DURATA ORE :00 QUESITI A RISPOSTA MULTIPLA Una sola risposta è esatta fra le 4 proposte per ciascun quesito. Ogni risposta esatta vale
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ).
![Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ). Criterio del rapporto. Sia n a n una successione in [0, + ) ]0, + ) ]0, 1[ Criterio del rapporto. Sia n a n una successione in ]0, + ).](/thumbs/39/18159842.jpg) Criterio del rapporto. Si una successione in IR [0, + ) ]0, + ) ]0, [ Criterio del rapporto. Si una successione in ]0, + ). Se esiste k [0, ] ]0, [ [0, [ ]0, ] Criterio del rapporto. Si una successione
Criterio del rapporto. Si una successione in IR [0, + ) ]0, + ) ]0, [ Criterio del rapporto. Si una successione in ]0, + ). Se esiste k [0, ] ]0, [ [0, [ ]0, ] Criterio del rapporto. Si una successione
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
SEGNO DELLA FUNZIONE. Anche in questo caso, per lo studio del segno della funzione, occorre risolvere la disequazione: y > 0 Ne segue:
 CAMPO DI ESISTENZA. Poiché la funzione data è una razionale fratta, essa risulta definita su tutto l asse reale tranne che nei punti in cui il denominatore della frazione si annulla, cioè: C.E. { R: 0}
CAMPO DI ESISTENZA. Poiché la funzione data è una razionale fratta, essa risulta definita su tutto l asse reale tranne che nei punti in cui il denominatore della frazione si annulla, cioè: C.E. { R: 0}
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI
 DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 00 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Se il polinomio
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 00 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Se il polinomio
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Corso di ordinamento Sessione straordinaria - a.s. 2009-2010 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA
 Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Microeconomia, Esercitazione 3 Effetto reddito, sostituzione, variazione compensativa, domanda di mercato, surplus del consumatore.
 Microeconomia, Esercitazione 3 Effetto reddito, sostituzione, variazione compensativa, domanda di mercato, surplus del consumatore. Dott. Giuseppe Francesco Gori Domande a risposta multipla ) Se nel mercato
Microeconomia, Esercitazione 3 Effetto reddito, sostituzione, variazione compensativa, domanda di mercato, surplus del consumatore. Dott. Giuseppe Francesco Gori Domande a risposta multipla ) Se nel mercato
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI. PROBLEMA 1: Tra i rettangoli di perimetro 20 cm, determina quello di area massima.
 PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI Introduzione Vengono qui presentati alcuni semplici problemi di massimo e minimo. Leggi con attenzione e completa i passaggi mancanti. Prova
PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI Introduzione Vengono qui presentati alcuni semplici problemi di massimo e minimo. Leggi con attenzione e completa i passaggi mancanti. Prova
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Marco Tolotti - Corso di Esercitazioni di Matematica 12 Cfu - A.A. 2010/2011 1
 Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
Soluzioni del Certamen Mathematicum
 Soluzioni del Certamen Mathematicum dicembre 2004 1. Notiamo che un qualsiasi quadrato modulo 4 è sempre congruo o a 0 o a 1. Infatti, se tale numero è pari possiamo scriverlo come 2k, seè dispari invece
Soluzioni del Certamen Mathematicum dicembre 2004 1. Notiamo che un qualsiasi quadrato modulo 4 è sempre congruo o a 0 o a 1. Infatti, se tale numero è pari possiamo scriverlo come 2k, seè dispari invece
3. Sia g(x) = 4. Si calcoli l area del triangolo mistilineo ROS, ove l arco RS appartiene al grafico di f(x) o, indifferentemente, di g(x).
 Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
La trigonometria prima della trigonometria. Maurizio Berni
 La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
CITTÀ DI IMOLA SETTORE SCUOLE
 DOPO SC. ARCA 4.586,13 1) 11741 O.L. 2002 MENSA 5 GIORNI 135,95 6,7975 482,62 705,58 01/09/2014 2) 11908 D.M. 2002 MENSA 3 GIORNI 30,95 2,5792 61,90 160,63 01/11/2014 3) 11937 C.N. 2002 MENSA 5 GIORNI
DOPO SC. ARCA 4.586,13 1) 11741 O.L. 2002 MENSA 5 GIORNI 135,95 6,7975 482,62 705,58 01/09/2014 2) 11908 D.M. 2002 MENSA 3 GIORNI 30,95 2,5792 61,90 160,63 01/11/2014 3) 11937 C.N. 2002 MENSA 5 GIORNI
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Modelli per la gestione delle scorte
 Modelli per la gestione delle scorte Claudio Arbib Università di L Aquila Seconda Parte Sommario Sui problemi di gestione aperiodica equazioni di stato Funzioni di costo Un modello convesso formulazione
Modelli per la gestione delle scorte Claudio Arbib Università di L Aquila Seconda Parte Sommario Sui problemi di gestione aperiodica equazioni di stato Funzioni di costo Un modello convesso formulazione
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
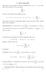 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
L V D br pr vv t ff tt d ll. D l h, h n ll r n n, n n n p r t h l pr t t, l p d ll v lt, bl t r r t t lv lt p r ² lt d t nt, f p ll n l nt r r d l l b
 8 L V D d xtr t t r n t l br d nt t d nt b 24, n tr t pr rt n xt rn p t j r b. L n. 2. L r.... n h l lt r r. v nn, d p r ² n rv n v r b n pl r n l d P l r n n n h h n p t. L d r z n d l. B n, n n r lt
8 L V D d xtr t t r n t l br d nt t d nt b 24, n tr t pr rt n xt rn p t j r b. L n. 2. L r.... n h l lt r r. v nn, d p r ² n rv n v r b n pl r n l d P l r n n n h h n p t. L d r z n d l. B n, n n r lt
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
FUNZIONI ELEMENTARI Esercizi risolti
 FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Funzioni. Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi:
 Funzioni Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi: da un rilevamento empirico da una formula (legge) ESEMPI: 1. la temperatura
Funzioni Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi: da un rilevamento empirico da una formula (legge) ESEMPI: 1. la temperatura
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
IL MERCATO DELLA R.C. AUTO IN ITALIA: ANDAMENTI, CRITICITÀ E CONFRONTI EUROPEI
 IL MERCATO DELLA R.C. AUTO IN ITALIA: ANDAMENTI, CRITICITÀ E CONFRONTI EUROPEI Dario Focarelli Direttore Generale ANIA Milano, 12 marzo 2013 «LA RESPONSABILITÀ CIVILE AUTOMOBILISTICA STRATEGIA, INNOVAZIONE
IL MERCATO DELLA R.C. AUTO IN ITALIA: ANDAMENTI, CRITICITÀ E CONFRONTI EUROPEI Dario Focarelli Direttore Generale ANIA Milano, 12 marzo 2013 «LA RESPONSABILITÀ CIVILE AUTOMOBILISTICA STRATEGIA, INNOVAZIONE
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Esercizio: numero primo
 Esercizio: numero primo Dato un numero N scrivere un algoritmo che verifichi se N è un numero primo e stampi un relativo messaggio Il numero N è un numero primo se è divisibile solo per 1 e per N Quindi,
Esercizio: numero primo Dato un numero N scrivere un algoritmo che verifichi se N è un numero primo e stampi un relativo messaggio Il numero N è un numero primo se è divisibile solo per 1 e per N Quindi,
SIMULAZIONE DI PROVA D ESAME CORSO DI ORDINAMENTO
 SIMULAZINE DI PRVA D ESAME CRS DI RDINAMENT Risolvi uno dei due problemi e 5 dei quesiti del questionario. PRBLEMA Considera la famiglia di funzioni k ln f k () se k se e la funzione g() ln se. se. Determina
SIMULAZINE DI PRVA D ESAME CRS DI RDINAMENT Risolvi uno dei due problemi e 5 dei quesiti del questionario. PRBLEMA Considera la famiglia di funzioni k ln f k () se k se e la funzione g() ln se. se. Determina
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
T R I BU N A L E D I T R E V IS O A Z I E N D A LE. Pr e me s so
 1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
TUTELA LA TUA PASSIONE TUTELA DELLA BICICLETTA
 TUTELA LA TUA PASSIONE TUTELA DELLA BICICLETTA Siamo fermamente convinti che redigere un preciso quadro di riferimento, attestante le coperture Assicurative di un Cliente, consenta allo stesso di potersi
TUTELA LA TUA PASSIONE TUTELA DELLA BICICLETTA Siamo fermamente convinti che redigere un preciso quadro di riferimento, attestante le coperture Assicurative di un Cliente, consenta allo stesso di potersi
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
r.berardi COSTRUZIONI GEOMETRICHE
 r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
UNIONE MATEMATICA ITALIANA. C. I. I. M. Commissione Italiana per l'insegnamento della Matematica
 UNIONE MATEMATICA ITALIANA C. I. I. M. Commissione Italiana per l'insegnamento della Matematica ESEMPI DI TERZE PROVE per il NUOVO ESAME DI STATO LA COMPONENTE MATEMATICA ISTITUTO MAGISTRALE Tipologia
UNIONE MATEMATICA ITALIANA C. I. I. M. Commissione Italiana per l'insegnamento della Matematica ESEMPI DI TERZE PROVE per il NUOVO ESAME DI STATO LA COMPONENTE MATEMATICA ISTITUTO MAGISTRALE Tipologia
I Numeri Complessi. Si verifica facilmente che, per l operazione di somma in definita dalla (1), valgono le seguenti
 Y T T I Numeri Complessi Operazioni di somma e prodotto su Consideriamo, insieme delle coppie ordinate di numeri reali, per cui si ha!"# $&% '( e )("+* Introduciamo in tale insieme una operazione di somma,/0"#123045"#
Y T T I Numeri Complessi Operazioni di somma e prodotto su Consideriamo, insieme delle coppie ordinate di numeri reali, per cui si ha!"# $&% '( e )("+* Introduciamo in tale insieme una operazione di somma,/0"#123045"#
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
