LA GEOMETRIA NELLO SPAZIO
|
|
|
- Alessio Spano
- 7 anni fa
- Visualizzazioni
Transcript
1 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio in due regioni, dette SEMISPAZI, di cui i piano stesso si dice origine o frontiera, tai che: a) i segmento che ha per estremi due punti A e B deo stesso semispazio non interseca i piano; ) i segmento che ha per estremi due punti C e D appartenenti a semipiani diversi interseca i piano in un punto. Da questo assioma discendono immediatamente due importanti considerazioni: a) un piano ed un semispazio sono figure convesse; ) una retta avente in comune con un piano α un soo punto P è divisa da P in due semirette che appartengono a semispazi opposti rispetto ad α. n.2 Un atro eemento primitivo: i piano I piano neo spazio è caratterizzato dai seguenti assiomi: Per tre punti deo spazio, non aineati, passa sempre uno ed un soo piano. Una retta passante per due punti di un piano giace interamente in que piano. Una retta giacente in un piano o divide in due regioni diverse, dette SEMIPIANI, di cui a retta stessa si dice origine o contorno, tai che: a) ogni segmento che congiunge due punti appartenenti ad uno stesso semipiano giace interamente in esso; ) ogni segmento che congiunge due punti appartenenti a semipiani diversi incontra a retta in un punto. Dai primi due assiomi discendono immediatamente due importanti considerazioni: a) se due piani hanno in comune tre punti non aineati, essi coincidono; ) per una retta ed un punto fuori di essa passa un piano ed uno soo; c) per due rette che si incontrano in un punto passa sempre un piano ed uno soo. n.3 La posizione di una retta rispetto ad un piano Un piano ed una retta che non gi appartiene possono avere un soo punto in comune e a RETTA si dice INCIDENTE IL PIANO. Se una retta ed un piano hanno due punti in comune aora a RETTA GIACE SUL PIANO e appartenendo ad esso ha infiniti punti in comune. Se una retta ed un piano non hanno punti in comune aora a RETTA si dice PARALLELA AL PIANO. n.4 La posizione reciproca di due rette. Due rette si dicono COMPLANARI quando appartengono ad uno stesso piano, SGHEMBE quando non c è acun piano che e contiene e quindi appartengono a piani diversi.
2 Si dice STELLA DI CENTRO P insieme di tutte e rette deo spazio che passano per i punto P che viene detto SOSTEGNO DELLA STELLA. L intersezione di una stea con un piano passante per i suo sostegno è un fascio di rette proprio. Due rette di una stea, dato che appartengono ad uno ed un soo piano, individuano uno ed un soo fascio. n.5 La posizione reciproca di due piani Se due piani hanno in comune tre punti non aineati, aora sono o stesso piano. Se due piani hanno in comune due punti A e B (oppure tre punti aineati), aora hanno anche in comune tutti i punti dea retta AB Se due piani distinti hanno in comune un punto, aora hanno in comune i punti di una ed una soa retta che passa per que punto. In conseguenza di ciò si può dire che due PIANI o sono COINCIDENTI, o si intersecano ungo una retta e sono INCIDENTI o non hanno punti in comune e sono PARALLELI. Per una retta passano infiniti piani. L insieme di tai piani si dice FASCIO PROPRIO DI PIANI e a retta ASSE DEL FASCIO. L insieme dei piani che passano per un punto si dice STELLA DI PIANI. n.6 Perpendicoarità tra retta e piano Ne piano esiste un'unica perpendicoare passante per un punto ad una retta data. Neo spazio questo è vero soo se i punto è a di fuori di essa. Per i punto P che appartiene aa retta r si possono condurre infinite perpendicoari ad r, una per ciascun piano de fascio di centro r. Se una retta r è perpendicoare in un suo punto P ad atre due rette a e, aora è perpendicoare a tutte e soe e rette de fascio di centro P generato da a e. Pertanto si può dire che una RETTA r incidente un piano α in un punto P è PERPENDICOLARE AL PIANO α se è perpendicoare a tutte e rette di α che passano per P. I punto P viene detto PIEDE dea perpendicoare. I piano passante per un punto di una retta e perpendicoare aa retta stessa è unico. Affinché una retta sia perpendicoare ad un piano asta che sia perpendicoare a due rette quasiasi de piano passanti per i punto d intersezione dea retta con i piano. TEOREMA DELLE TRE PERPENDICOLARI Se una retta r è perpendicoare ad un piano α in un suo punto P e da questo punto si conduce una retta s perpendicoare ad una retta t di α, quest utima è perpendicoare a piano β individuato da r ed s. Si osservi che una quaunque retta de piano β incidente s e t ne punto che hanno in comune risuta perpendicoare a t. P r t s
3 n.7 paraeismo fra rette Due RETTE neo spazio si dicono PARALLELE se sono companari e non hanno punti d intersezione. Due rette perpendicoari ad uno stesso piano sono paraee e viceversa, se due rette sono paraee, un piano che è perpendicoare a una è perpendicoare anche a atra. Se due rette sono paraee, ogni piano che incontra una incontra anche atra. Due rette paraee ad una terza sono paraee fra oro. Siano r ed s due rette paraee. Sia t intersezione di due piani passanti rispettivamente per e rette r ed s. Aora t risuta paraea sia ad r che ad s. n.8 paraeismo tra rette e piani Una RETTA si dice PARALLELA ad un PIANO se non ha acun punto in comune con esso oppure se appartiene interamente ad esso. Se una retta passante per un punto esterno ad un piano è paraea ad una retta de piano, essa è paraea a piano. Se una retta r è paraea a due piani che si intersecano ungo una retta s aora risuta r//s. Una retta ed un piano perpendicoari ad una medesima retta, in due punti distinti, sono paraei. Se per una retta paraea ad un piano si conduce un piano quaunque che interseca i primo, a retta d intersezione dei due piani è paraea aa retta data. Una retta ed un piano paraei determinano su due rette paraee segmenti congruenti. L utimo risutato permette di giustificare a seguente definizione: Data una retta paraea ad un piano, si dice DISTANZA DELLA RETTA DAL PIANO a distanza di un punto quasiasi dea retta da piano. n.9 paraeismo tra piani Due PIANI distinti ridicono PARALLELI quando non hanno acun punto in comune. Due piani perpendicoari ad una stessa retta sono paraei Se due rette che s intersecano sono paraee ad un piano, i piano individuato dae due rette è paraeo a primo. Le intersezioni di due piani paraei con un terzo piano sono rette paraee. Se due piani sono paraei, ogni retta che incontra uno dei due piani incontra anche atro. Se due piani sono paraei, ogni retta perpendicoare a primo è pure perpendicoare a secondo. Due piani paraei ad un terzo sono paraei tra oro. Per un punto esterno ad un piano si può condurre un ed un soo piano paraeo a queo dato. Se due piani sono paraei e distanze di ciascun punto di uno da atro sono congruenti. Si dice DISTANZA DI DUE PIANI PARALLELI a distanza di un punto quaunque di uno di essi da atro. Due angoi, comunque situati neo spazio, aventi i ati rispettivamente paraei e concordi,sono congruenti ed i oro piani paraei.
4 Se un piano incontra due piani paraei, e rette intersezione sono fra oro paraee. Se due piani sono paraei, ogni retta paraea a primo è paraea anche a secondo. Se due piani paraei intersecano due rette paraee, i segmenti che si vengono a determinare sono congruenti. TEOREMA DI TALETE un fascio di piani paraei individua su due rette trasversai insiemi di segmenti direttamente proporzionai. Viceversa se un fascio di piani individua su due rette segmenti in proporzione, tae fascio risuta costituito da piani paraei. n.10 diedri Due semipiani aventi a retta origine in comune dividono o spazio in due regioni opposte che hanno in comune soo i punti dei due semipiani. Si dice ANGOLO DIEDRO o più sempicemente DIEDRO ciascuna dee due parti in cui due semipiani aventi a stessa origine dividono o spazio, incusi i semipiani stessi. La retta origine dei due semipiani si dice SPIGOLO de diedro, i due semipiani si dicono FACCE e costituiscono a SUPERFICE de diedro. Dee due parti quea che contiene i proungamenti dee facce si dice DIEDRO CONCAVO atra si dice DIEDRO CONVESSO. Un diedro è soitamente convesso e se α e β sono e facce esso si indica con. ˆ I punti di un diedro che non appartengono ae facce si dicono interni, tutti i punti che non stanno sue facce e non sono interni si dicono esterni. Si dice poi che: - un DIEDRO è PIATTO se e due facce sono una i proungamento de atra, cioè i semipiani di un medesimo piano; un diedro piatto è un semispazio e una quaunque retta sceta su di esso costituisce o spigoo. Due diedri a cui somma è un diedro piatto si dicono SUPPLEMENTARI. - Un DIEDRO è GIRO quando e due facce sono semipiani coincidenti e contiene tutti i punti deo spazio; un diedro giro è o spazio stesso. Due diedri a cui somma è un diedro giro si dicono espementari. - Un DIEDRO è NULLO quando e due facce sono semipiani coincidenti e contiene soo i punti dee facce. - Due diedri si dicono consecutivi se hanno in comune una faccia e o spigoo. - Due diedri si dicono adiacenti se sono consecutivi e e facce non comuni sono i proungamento una de atra. La SEZIONE NORMALE DI UN DIEDRO è angoo ottenuto intersecando i diedro stesso con un piano perpendicoare ao spigoo. Tutte e sezioni normai di uno stesso diedro sono congruenti. Se due diedri hanno sezioni normai congruenti, sono congruenti e viceversa. La MISURA di un diedro si può identificare con a misura di una sua sezione normae e perciò si esprime in gradi o radianti.
5 Osservazione: se a sezione normae di un diedro è un angoo giro, piatto, retto,. aora i diedro è rispettivamente giro, piatto, retto,. e viceversa. Due DIEDRI si dicono OPPOSTI ALLO SPIGOLO se hanno o stesso spigoo e e facce sono una i proungamento de atra. Due diedri opposti ao spigoo sono congruenti. Si dice SEMIPIANO BISETTORE i semipiano che uscendo de diedro o divide in due diedri congruenti. - Ciascuna dee due parti in cui i piano isettore divide un diedro piatto si dice DIEDRO RETTO. Due diedri a cui somma è un diedro retto si dicono COMPLEMENTARI. n.11 perpendicoarità Due PIANI si dicono PERPENDICOLARI se, incontrandosi, formano quattro diedri congruenti e quindi retti. L esistenza di piani perpendicoari è assicurata da seguente teorema: se una retta è perpendicoare ad un piano, quaunque piano passante per essa è perpendicoare a piano dato. Per una retta perpendicoare ad un piano si possono condurre infiniti piani perpendicoari a piano dato. Se due piani sono perpendicoari, quaunque retta appartenente a uno di essi e perpendicoare aa oro intersezione è pure perpendicoare a atro, questa perpendicoare giace ne primo piano. Se due piani che si intersecano sono perpendicoari ad uno stesso piano, anche a oro intersezione è perpendicoare a questo piano. Due piani perpendicoari a rette perpendicoari, sono perpendicoari tra oro. Dato un piano e una retta, non perpendicoare ad esso, esiste uno ed un soo piano che contiene a retta data ed è perpendicoare a piano dato. Infine i seguente teorema permette di definire a distanza tra due rette sgheme. Date due rette sgheme,esiste una ed una soa retta perpendicoare ad entrame. I segmento, compreso tra e due rette date, è minore di quaunque atro segmento compreso tra esse. Tae segmento si dice DISTANZA TRA DUE RETTE SGHEMBE. Si dice ANGOLO DI DUE RETTE SGHEMBE angoo acuto o retto, formato da due rette, paraee ae date condotte da un punto quaunque deo spazio. Se angoo di due rette sgheme è retto e RETTE si dicono ORTOGONALI. Se due rette sono rispettivamente perpendicoari a due piani perpendicoari tra oro, esse sono ortogonai. n.12 angooidi Siano F un poigono e P un punto che non appartiene a piano su cui i poigono poggia. La SUPERFICIE descritta da tutte e semirette uscenti da P, detto VERTICE, che intersecano i ati de poigono F è detta PIRAMIDALE. Le semirette che partono da P e passano per i vertici di F si dicono SPIGOLI, gi angoi con vertice P e ati due spigoi consecutivi si dicono FACCE. Una superficie piramidae divide o spazio in due regioni distinte una interna ed una esterna. P La regione di spazio costituita daa superficie piramidae e da tutti i suoi punti interni è detta ANGOLOIDE ed è una figura soida. I vertici, gi spigoi e e facce dea superficie piramidae sono anche i vertice, gi spigoi e e facce de angooide. L insieme dee facce costituisce a superficie
6 de angooide. I diedri formati dai semipiani contenenti due facce consecutive si dicono diedri de angooide. Se a,, c, d, sono gi spigoi e O i vertice, angooide si indica con Ô acd.. Un angooide si dice TRIEDRO, TETRAEDRO, PENTAEDRO,.. a seconda che aia tre, quattro, cinque, facce. Se e facce di un angooide sono tutte uguai fra oro esso si dice REGOLARE. Un angooide si dice CONCAVO o CONVESSO a seconda che i poigono F sia concavo o convesso. In ogni triedro ogni faccia è minore dea somma dee atre due e maggiore dea oro differenza. In ogni angooide ciascuna faccia è minore dea somma di tutte e atre. La somma dee facce di un angooide è minore di quattro angoi retti. Due triedri sono direttamente o inversamente congruenti se hanno rispettivamente congruenti: due facce e i diedro compreso, due diedri e a faccia comune, e tre facce, i tre diedri. n.13 poiedri Si dice SUPERFICIE POLIEDRICA a figura formata da più poigoni convessi situati in piani diversi e disposti in modo che ciascun ato sia comune a due di essi e che i piano di ogni poigono asci tutti gi atri da una medesima parte. Si dice POLIEDRO a figura formata da una superficie poiedrica e da tutti i suoi punti interni. Ovvero un poiedro è una regione finita deo spazio deimitata da poigoni, detti facce, giacenti in piani diversi e tai che ogni ato sia comune a due poigoni. Si dice DIAGONALE i segmento congiungente due vertici non appartenenti aa stessa faccia. Un poiedro ha ameno quattro facce e in questo caso si dice TETRAEDRO, se ne ha cinque si dice PENTAEDRO, sei ESAEDRO, otto OTTAEDRO, dodici DODECAEDRO, venti ICOSAEDRO. n.14 poiedri regoari Un poiedro si dice regoare quando e sue facce sono poigoni regoari tutti congruenti tra oro e i suoi angooidi sono pure tutti congruenti tra oro. Esistono soo i seguenti cinque poiedri regoari: TETRAEDRO REGOLARE: si ottiene facendo concorrere in un vertice tre triangoi equiateri; ha 4 facce triangoari, 4 vertici e 6 spigoi e angooidi triedri; OTTAEDRO REGOLARE: si ottiene facendo concorrere in un vertice quattro triangoi equiateri; ha 8 facce triangoari, 6 vertici,12 spigoi, angooidi tetraedri; ICOSAEDRO REGOLARE: si ottiene facendo concorrere in un vertice cinque triangoiequiateri; ha 20 facce triangoari, 12 vertici, 30 spigoi e angooidipentaedri; ESAEDRO o CUBO: si ottiene facendo concorrere in un vertice tre quadrati; ha sei facce, 8 vertici, 12 spigoi e angooiditriedri; DODECAEDRO che si ottiene facendo concorrere in un vertice tre pentagoni regoari; ha 12 facce pentagonai, 20 vertici, 30 spigoi e angooidi triedri. I 5 poiedri regoari prendono i nome di soidi patonici per i significato simoico attriuito ad essi da fiosofo Patone. L icoesaedro è da disegnare. I paone da cacio è un poiedro semiregoare perché si aternano pentagoni ad esagoni.
7 TEOREMA DI EULERO: se s è i numero degi spigoi, f queo dee facce, v queo dei vertici di un poiedro convesso, è vaida a reazione f+v=s+2. Le conseguenze sono che non esistono poiedri in cui tutte e facce aiano più di cinque spigoi e che i poiedri in cui e facce aiano ugua numero di ati e gi angooidi ugua numero di spigoi possono essere soo quei patonici. n.15 atri poiedri: prismi e piramidi Siano F un poigono e d una retta non appartenente a piano su cui giace F. si dice SUPERFICIE PRISMATICA INDEFINITA insieme dee rette aventi a direzione di d passante per i vertici e per i punti dei ati di F. La parte di spazio deimitata daa superficie prismatica e contenente i poigono F si dice PRISMA INDEFINITO. Le sezioni di un prisma indefinito con piani paraei sono poigoni congruenti e quindi è possiie dare a seguente definizione. Si dice PRISMA a parte di prisma indefinito deimitato da una coppia di piani paraei. I poigoni individuati dai due piani paraei si dicono BASI, i paraeogrammi che o deimitano si dicono FACCE LATERALI, a distanza tra i piani dee asi si dice ALTEZZA. In definitiva un prisma è un poiedro che ha come asi due poigoni giacenti su piani paraei diversi e come facce aterai tanti paraeogrammi quanti sono i ati di ase. Se gi spigoi aterai sono perpendicoari ai piani di ase aora i PRISMA si dice RETTO atrimenti oiquo. Se in un prisma retto i poigoni di ase sono regoari aora si dice che i PRISMA è REGOLARE. Ne disegno è rappresentato un prisma esagonae. Nei prismi regoari e facce aterai sono rettangoi tutti congruenti. La superficie aterae S si cacoa motipicando i perimetro di ase per atezza S 2 p h La superficie di ase S è quea de poigono regoare (per i pentagono, esagono, si cacoa come semiperimetro per apotema) La superficie ae S si cacoa sommando quea aterae con e due di ase S S 2S I voume si cacoa V A h Un caso particoare di prisma è i PARALLELEPIPEDO: prisma che ha per asi due paraeogrammi. Se gi spigoi di un PARALLELEPIPEDO sono perpendicoari ae asi aora esso diventa RETTO. Se a ase di un PARALLELEPIPEDO retto è un rettangoo aora si dice che è RETTANGOLO. e se a e sono e dimensioni de rettangoo di ase e h atezza si ha: superficie aterae S =2h(a+) superficie di ase S =a superficie ae S =2h(a+2)+2a Diagonae = a h I voume si cacoa V A h= ah
8 Se e dimensioni di un paraeepipedo rettangoo sono tutte uguai tra oro, cioè a==h= ato, aora esso si dice CUBO. superficie aterae S = 4 2 superficie di ase S = 2 superficie ae S = 6 2 Diagonae = 3 I voume V 3 Se si considera un angooide di vertice V ed un piano α non passante per V che incontra tutti i suoi spigoi si dice PIRAMIDE intersezione de semispazio individuato da α contenente V con angooide. La sezione de angooide con i piano è un poigono che si dice BASE dea piramide, i vertice e gi spigoi de angooide compresi tra i vertice e a ase sono i VERTICE e gi SPIGOLI LATERALI dea piramide, a distanza de vertice da piano si dice ALTEZZA. L intersezione determina sue facce de angooide dei triangoi che si dicono FACCE LATERALI e a oro unione si dice SUPERFICE LATERALE. L unione dea superficie aterae con quea di ase si dice SUPERFICIE TOTALE. Come per i prismi e piramidi prendono i nome da numero dei ati dea ase. Così si hanno piramidi triangoari, quadrangoari,.. a piramide triangoare è un TETRAEDRO. Ciascuna faccia si può considerare ase e si dicono opposti gi spigoi che non hanno vertici in comune. Una PIRAMIDE si dice RETTA se ha per ase un poigono circoscriviie ad un cerchio, i cui centro coincide con a proiezione de vertice sua ase. I segmenti congiungenti i vertice con i punti di contatto dei ati dea ase con a circonferenza inscritta sono e atezze dee facce aterai e sono congruenti fra oro. L atezza comune dee facce aterai si dice APOTEMA. Se p indica i semiperimetro de poigono di ase e a apotema si ha: superficie aterae S =p a superficie di ase S superficie ae S S S voume V 1 3 A h Se una piramide ha per ase un poigono regoare si dice PIRAMIDE REGOLARE. Se si tagia con un piano paraeo aa ase una piramide si ottiene un poigono simie a poigono di ase e i ati e i perimetri di questi due poigoni sono proporzionai ae distanze de oro piano da vertice e e aree ai quadrati di queste distanze. n.16 soidi di rotazione: ciindro, cono e sfera Facendo compiere una rotazione competa ad un semipiano α intorno aa sua retta origine r, ossia a ASSE DI ROTAZIONE r, a inea giacente su di esso genera una superficie detta SUPERFICIE DI ROTAZIONE e viene detta GENERATRICE. Ogni punto dea generatrice descrive una circonferenza, detta PARALLELO, che giace su un piano perpendicoare a asse di rotazione ed ha i centro su esso.
9 L intersezione di un piano quaunque contenente asse di rotazione è una inea congruente aa generatrice e si dice MERIDIANO. Se si considera una figura F su semipiano α e si compie una rotazione competa si descrive un soido detto SOLIDO DI ROTAZIONE o SUPERIFICIE ROTONDA e i contorno dea figura genera a sua superficie. I caso dea rotazione di rette paraee a asse: ciindri. Si dice SUPERFICIE CILINDRICA CIRCOLARE INDEFINITA a superficie generata daa rotazione di una retta paraea a asse di rotazione. Si dice CILINDRO INDEFINITO i soido ottenuto daa rotazione dea striscia di piano individuata da asse di rotazione e da una sua paraea. La parte di spazio de ciindro indefinito deimitata da due piani distinti perpendicoari a asse di rotazione si dice CILINDRO CIRCOLARE RETTO o CILINDRO. I ciindro può essere visto come i soido generato daa rotazione competa di un rettangoo attorno ad un suo ato. I cerchi individuati dai piani secanti sono e BASI, i segmenti di generatrice compresa tra i piani dee asi si dicono LATI, a distanza tra i piani dee asi ALTEZZA. Un CILINDRO è EQUILATERO se i ato e quindi atezza è congruente a diametro di ase. La superficie aterae di un ciindro è equivaente ad un rettangoo che ha per ati atezza h de ciindro e a circonferenza, di raggio r, rettificata di ase. Quindi si ha: superficie aterae S =2πrh 2 superficie di ase S = 2 πr S S 2S 2πr hr superficie ae voume V r 2 h I caso dea rotazione di rette incidenti asse: coni. Si dice SUPERFICIE CONICA CIRCOLARE INDEFINITA a superficie generata daa rotazione di una semiretta avente origine V su asse di rotazione. Si dice CONO INDEFINITO i soido ottenuto daa rotazione de angoo individuato da asse di rotazione e daa semiretta. Tutte e generatrici sono uguamente incinate rispetto a asse. I raggi dei paraei sono cono proporzionai sia ae distanze dei rispettivi piani da vertice, sia ae distanze dei punti dei paraei da vertice stesso. Le sezioni di un cono indefinito con i piani perpendicoari a asse sono cerchi, e cui aree stanno tra oro come i quadrati dee rispettive distanze da vertice. La parte di spazio de cono indefinito contenente i vertice e deimitata da un piano perpendicoare a asse di rotazione si dice CONO CIRCOLARE RETTO o CONO. I cono può essere visto come i soido generato daa rotazione competa di un triangoo rettangoo attorno ad un suo cateto. I cerchio sezione è a BASE, i segmento di generatrice compreso fra i vertice e a circonferenza di ase si dice APOTEMA, i segmento che unisce i vertice con i centro dea circonferenza di ase si dice ALTEZZA ed è a distanza de vertice daa ase. Un CONO è EQUILATERO se apotema è congruente a diametro di ase. La superficie aterae è equivaente ad un settore di circonferenza che ha per arco a circonferenza de cono e per raggio apotema. superficie aterae S =πra
10 superficie di ase S = πr 2 S S superficie ae S πra r voume si cacoa V 1 3 A h Superficie di una SFERA S 4r 2 Voume di una SFERA: V 4 3 r3 Esercizi di geometria deo spazio: Quesito Proema Quesito 2 e Quesito
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
DIEDRI. Un diedro è convesso se è una figura convessa, concavo se non lo è.
 DIEDRI Si definisce diedro ciascuna delle due parti di spazio delimitate da due semipiani che hanno la stessa origine, compresi i semipiani stessi. I due semipiani prendono il nome di facce del diedro
DIEDRI Si definisce diedro ciascuna delle due parti di spazio delimitate da due semipiani che hanno la stessa origine, compresi i semipiani stessi. I due semipiani prendono il nome di facce del diedro
APPUNTI DI GEOMETRIA SOLIDA
 APPUNTI DI GEOMETRIA SOLIDA Geometria piana: (planimetria) studio delle figure i cui punti stanno tutti su un piano Geometria solida: (stereometria) studio delle figure i cui punti non giacciono tutti
APPUNTI DI GEOMETRIA SOLIDA Geometria piana: (planimetria) studio delle figure i cui punti stanno tutti su un piano Geometria solida: (stereometria) studio delle figure i cui punti non giacciono tutti
LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI
 LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI SPAZIO: l insieme di tutti i punti. PUNTI ALLINEATI: punti che appartengono alla stessa retta PUNTI COMPLANARI: punti che appartengono allo stesso
LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI SPAZIO: l insieme di tutti i punti. PUNTI ALLINEATI: punti che appartengono alla stessa retta PUNTI COMPLANARI: punti che appartengono allo stesso
Le figure solide. Due rette nello spaio si dicono sghembe se non sono complanari e non hanno alcun punto in comune.
 Le figure solide Nozioni generali Un piano nello spazio può essere individuato da: 1. tre punti A, B e C non allineati. 2. una retta r e un punto A non appartenente ad essa. 3. due rette r e s incidenti.
Le figure solide Nozioni generali Un piano nello spazio può essere individuato da: 1. tre punti A, B e C non allineati. 2. una retta r e un punto A non appartenente ad essa. 3. due rette r e s incidenti.
Geometria euclidea dello spazio Presentazione n. 5 Poliedri Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia
 Geometria euclidea dello spazio Presentazione n. 5 Poliedri Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Poliedri Un poliedro è un solido delimitato da una superficie formata da
Geometria euclidea dello spazio Presentazione n. 5 Poliedri Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Poliedri Un poliedro è un solido delimitato da una superficie formata da
Superfici e solidi di rotazione. Cilindri indefiniti
 Superfici e solidi di rotazione Consideriamo un semipiano α, delimitato da una retta a, e sul semipiano una curva g; facendo ruotare il semipiano in un giro completo attorno alla retta a, la curva g descrive
Superfici e solidi di rotazione Consideriamo un semipiano α, delimitato da una retta a, e sul semipiano una curva g; facendo ruotare il semipiano in un giro completo attorno alla retta a, la curva g descrive
Geometria nello spazio
 Geometria nello spazio Def. Lo spazio è l insieme di infiniti elementi A, B, C detti punti; esso è dotato di sottoinsiemi non vuoti a, b, c detti rette e α, β, γ detti piani.. POSTULATI DI INCIDENZA. Dati
Geometria nello spazio Def. Lo spazio è l insieme di infiniti elementi A, B, C detti punti; esso è dotato di sottoinsiemi non vuoti a, b, c detti rette e α, β, γ detti piani.. POSTULATI DI INCIDENZA. Dati
LA GEOMETRIA DELLO SPAZIO
 LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 12
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 12 PARTE SECONDA GEOMETRIA SOLIDA UNA PREMESSA Diversi esperti di Didattica della Matematica ritengono che l approccio migliore, per la
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 12 PARTE SECONDA GEOMETRIA SOLIDA UNA PREMESSA Diversi esperti di Didattica della Matematica ritengono che l approccio migliore, per la
SOLIDI DI ROTAZIONE. Superficie cilindrica indefinita se la generatrice è una retta parallela all asse di rotazione
 SOLIDI DI ROTAZIONE Dato un semipiano α limitato dalla retta a, sia g una linea qualunque appartenente al semipiano α; ruotando il semipiano α di un angolo giro attorno alla retta a, la linea g genera
SOLIDI DI ROTAZIONE Dato un semipiano α limitato dalla retta a, sia g una linea qualunque appartenente al semipiano α; ruotando il semipiano α di un angolo giro attorno alla retta a, la linea g genera
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea dello spazio Presentazione n. 6 Solidi di rotazione Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia
 Geometria euclidea dello spazio Presentazione n. 6 Solidi di rotazione Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Solidi di rotazione Un solido di rotazione è generato dalla rotazione
Geometria euclidea dello spazio Presentazione n. 6 Solidi di rotazione Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Solidi di rotazione Un solido di rotazione è generato dalla rotazione
I solidi. Un solido è una parte di spazio delimitata da una superficie chiusa. I solidi delimitati da poligoni vengono chiamati poliedri.
 I solidi Un solido è una parte di spazio delimitata da una superficie chiusa. I solidi delimitati da poligoni vengono chiamati poliedri. I solidi che hanno superfici curve vengono chiamati solidi rotondi.
I solidi Un solido è una parte di spazio delimitata da una superficie chiusa. I solidi delimitati da poligoni vengono chiamati poliedri. I solidi che hanno superfici curve vengono chiamati solidi rotondi.
I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e spigoli del poliedro.
 1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
Prontuario di geometria euclidea nello spazio. Per la scuola secondaria di I grado
 Prontuario di geometria euclidea nello spazio Per la scuola secondaria di I grado N. B. Gli argomenti presentati sono una sintesi di quelli trattati in classe e non sostituiscono ma integrano il libro
Prontuario di geometria euclidea nello spazio Per la scuola secondaria di I grado N. B. Gli argomenti presentati sono una sintesi di quelli trattati in classe e non sostituiscono ma integrano il libro
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
Il Tetraedro regolare
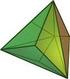 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
Teoremi di geometria piana
 la congruenza teoremi sugli angoli γ teorema sugli angoli complementari Se due angoli sono complementari di uno stesso angolo α β In generale: Se due angoli sono complementari di due angoli congruenti
la congruenza teoremi sugli angoli γ teorema sugli angoli complementari Se due angoli sono complementari di uno stesso angolo α β In generale: Se due angoli sono complementari di due angoli congruenti
LA PERPENDICOLARITA NELLO SPAZIO. Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani.
 1 LA PERPENDICOLARITA NELLO SPAZIO Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani. 2.1 La perpendicolarità retta piano Nel piano la perpendicolarità tra
1 LA PERPENDICOLARITA NELLO SPAZIO Nello spazio si definiscono la perpendicolarità sia tra una retta e un piano sia tra due piani. 2.1 La perpendicolarità retta piano Nel piano la perpendicolarità tra
Le caratteristiche dei poligoni. La relazione tra i lati e gli angoli di un poligono. Definizioni
 Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
ELEMENTI DI GEOMETRIA DELLO SPAZIO
 ELEMENTI DI GEOMETRIA DELLO SPAZIO Lo spazio euclideo è un insieme infinito di elementi detti punti e contiene sottoinsiemi propri ed infiniti detti piani. In ogni piano valgono gli assiomi del piano euclideo.
ELEMENTI DI GEOMETRIA DELLO SPAZIO Lo spazio euclideo è un insieme infinito di elementi detti punti e contiene sottoinsiemi propri ed infiniti detti piani. In ogni piano valgono gli assiomi del piano euclideo.
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 17-24 Ottobre 2005 INDICE 1. GEOMETRIA EUCLIDEA........................ 2 1.1 Triangoli...............................
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 17-24 Ottobre 2005 INDICE 1. GEOMETRIA EUCLIDEA........................ 2 1.1 Triangoli...............................
GEOMETRIA EUCLIDEA. segno lasciato dalla punta di una matita appena appoggiata sul foglio. P
 GEOMETRIA EUCLIDEA 1) GLI ENTI FONDAMENTALI: PUNTO, RETTA E PIANO Il punto, la retta e il piano sono gli ELEMENTI ( o ENTI ) GEOMETRICI FONDAMENTALI della geometria euclidea; come enti fondamentali non
GEOMETRIA EUCLIDEA 1) GLI ENTI FONDAMENTALI: PUNTO, RETTA E PIANO Il punto, la retta e il piano sono gli ELEMENTI ( o ENTI ) GEOMETRICI FONDAMENTALI della geometria euclidea; come enti fondamentali non
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
Postulati e definizioni di geometria piana
 I cinque postulati di Euclide I postulato Adimandiamo che ce sia concesso, che da qualunque ponto in qualunque ponto si possi condurre una linea retta. Tra due punti qualsiasi è possibile tracciare una
I cinque postulati di Euclide I postulato Adimandiamo che ce sia concesso, che da qualunque ponto in qualunque ponto si possi condurre una linea retta. Tra due punti qualsiasi è possibile tracciare una
4.1 I triedri Def triedro vertice spigoli facce triedro
 1 FIGURE NELLO SPAZIO Rette, piani, semispazi, di cui abbiamo visto le prime proprietà, delimitano le figure solide che si sviluppano nello spazio. Introduciamo gradualmente le figure solide e le loro
1 FIGURE NELLO SPAZIO Rette, piani, semispazi, di cui abbiamo visto le prime proprietà, delimitano le figure solide che si sviluppano nello spazio. Introduciamo gradualmente le figure solide e le loro
Rette, piani e figure nello spazio
 Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Principali Definizioni e Teoremi di Geometria
 Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
LA CIRCONFERENZA DEFINIZIONI. Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro.
 LA CIRCONFERENZA DEFINIZIONI Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro. Un cerchio è una figura piana formata dai punti di una circonferenza
LA CIRCONFERENZA DEFINIZIONI Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro. Un cerchio è una figura piana formata dai punti di una circonferenza
1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza
 Terzo modulo: Geometria Obiettivi 1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza e cerchio, ecc.). calcolare perimetri e aree di figure elementari nel
Terzo modulo: Geometria Obiettivi 1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza e cerchio, ecc.). calcolare perimetri e aree di figure elementari nel
GEOMETRIA. Studio dei luoghi /relazioni tra due variabili. Studio delle figure (nel piano/spazio) Problemi algebrici sulle figure geometriche
 GEOMETRIA ANALITICA EUCLIDEA Studio dei luoghi /relazioni tra due variabili Studio delle figure (nel piano/spazio) Funzioni elementari Problemi algebrici sulle figure geometriche Grafici al servizio dell
GEOMETRIA ANALITICA EUCLIDEA Studio dei luoghi /relazioni tra due variabili Studio delle figure (nel piano/spazio) Funzioni elementari Problemi algebrici sulle figure geometriche Grafici al servizio dell
1 I solidi a superficie curva
 1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
Principali Definizioni e Teoremi di Geometria
 Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
COS È UN PRISMA. Due POLIGONI congruenti e paralleli, come basi. È UN POLIEDRO DELIMITATO DA
 PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
Il punteggio totale della prova è 100/100. La sufficienza si ottiene con il punteggio di 60/100.
 ISI Civitali - Lucca CLASSE, Data Nome: Cognome: Nei test a scelta multipla la risposta esatta è unica Ad ogni test viene attribuito il seguente punteggio: 4 punti risposta corretta 1 punto risposta omessa
ISI Civitali - Lucca CLASSE, Data Nome: Cognome: Nei test a scelta multipla la risposta esatta è unica Ad ogni test viene attribuito il seguente punteggio: 4 punti risposta corretta 1 punto risposta omessa
01. Se il raggio di un cerchio dimezza, la sua area diventa: a) 1/3 b) 1/4 c) 3/2 d) 1/5
 GEOMETRIA 01. Se il raggio di un cerchio dimezza, la sua area diventa: 1/ b) 1/4 c) / d) 1/5 0. Quanto misura il lato di un quadrato la cui area è equivalente a quella di un triangolo che ha la base di
GEOMETRIA 01. Se il raggio di un cerchio dimezza, la sua area diventa: 1/ b) 1/4 c) / d) 1/5 0. Quanto misura il lato di un quadrato la cui area è equivalente a quella di un triangolo che ha la base di
Dato un triangolo ABC, è il segmento che partendo dal vertice opposto al lato, incontra il lato stesso formando due angoli retti.
 Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
Anno 2014 1 Sommario Altezze, mediane, bisettrici dei triangoli... 2 Altezze relativa a un vertice... 2 Mediane relative a un lato... 2 Bisettrici relativi a un lato... 2 Rette perpendicolari... 3 Teorema
N. Domanda A B C D. circonferenza in quattro parti la base del triangolo isoscele che genera il cono
 1 Se in un triangolo circocentro e incentro coincidono allora esso come è? 2 Un angolo di un triangolo misura 50 gradi. Quanto misrano gli altri due angoli? 3 In un trapezio avente l'area di 320 m^2 le
1 Se in un triangolo circocentro e incentro coincidono allora esso come è? 2 Un angolo di un triangolo misura 50 gradi. Quanto misrano gli altri due angoli? 3 In un trapezio avente l'area di 320 m^2 le
Scopri come utilizzare i nostri servizi:
 Geometria CONCORSO AGENTI POLIZIA PENITENZIARIA 2015 Link utili Link utili Esercitati con il Simulatore Quiz Gratuito di Concorsando.it: http://www.concorsando.it/fb.php Scopri come utilizzare i nostri
Geometria CONCORSO AGENTI POLIZIA PENITENZIARIA 2015 Link utili Link utili Esercitati con il Simulatore Quiz Gratuito di Concorsando.it: http://www.concorsando.it/fb.php Scopri come utilizzare i nostri
CONCETTI e ENTI PRIMITIVI
 CONCETTI e ENTI PRIMITIVI Sono Concetti e Enti primitivi ciò che non può essere definito in modo più elementare, il significato è noto a priori, cioè senza alcun'altra specificazione. es. es. movimento
CONCETTI e ENTI PRIMITIVI Sono Concetti e Enti primitivi ciò che non può essere definito in modo più elementare, il significato è noto a priori, cioè senza alcun'altra specificazione. es. es. movimento
Matematica Introduzione alla geometria
 Matematica Introduzione alla geometria prof. Vincenzo De Felice 2014 Problema. Si mostri che un triangolo con due bisettrici uguali è isoscele. La matematica è sfuggente. Ziodefe 1 2 Tutto per la gloria
Matematica Introduzione alla geometria prof. Vincenzo De Felice 2014 Problema. Si mostri che un triangolo con due bisettrici uguali è isoscele. La matematica è sfuggente. Ziodefe 1 2 Tutto per la gloria
La circonferenza e il cerchio
 La circonferenza e il cerchio Def. Circonferenza Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una
La circonferenza e il cerchio Def. Circonferenza Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una
1) Sono dati quattro punti non complanari, tre di essi possono essere allineati?
 1 Nuovi assiomi 1) Sono dati quattro punti non complanari, tre di essi possono essere allineati? ) Sono dati quattro punti non complanari a tre a tre non allineati, quanti piani generano? ) Quante coppie
1 Nuovi assiomi 1) Sono dati quattro punti non complanari, tre di essi possono essere allineati? ) Sono dati quattro punti non complanari a tre a tre non allineati, quanti piani generano? ) Quante coppie
Test di Matematica di base
 Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Alcuni Elementi di Geometria Euclidea Schemi di lezione di Margherita Motteran
 Scuola Interateneo di Specializzazione per la Formazione degli Insegnanti della Scuola Secondaria del Veneto Indirizzo Tecnologico ANNO ACCADEMICO 2006-2007 DIDATTICA DELLA MATEMATICA Alcuni Elementi di
Scuola Interateneo di Specializzazione per la Formazione degli Insegnanti della Scuola Secondaria del Veneto Indirizzo Tecnologico ANNO ACCADEMICO 2006-2007 DIDATTICA DELLA MATEMATICA Alcuni Elementi di
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
Indice del vocabolario della Geometria euclidea
 Indice del vocabolario della Geometria euclidea 1 Postulati di appartenenza: piano, retta e punto nello spazio Punto, retta, piano nello spazio Punto, retta nel piano Punto nella retta Punto esterno alla
Indice del vocabolario della Geometria euclidea 1 Postulati di appartenenza: piano, retta e punto nello spazio Punto, retta, piano nello spazio Punto, retta nel piano Punto nella retta Punto esterno alla
Introduzione. Al termine della lezione sarai in grado di:
 Anno 4 Prismi 1 Introduzione In questa lezione parleremo di un particolare poliedro detto prisma. Ne daremo una definizione generale e poi soffermeremo la nostra attenzione su alcuni prismi particolari.
Anno 4 Prismi 1 Introduzione In questa lezione parleremo di un particolare poliedro detto prisma. Ne daremo una definizione generale e poi soffermeremo la nostra attenzione su alcuni prismi particolari.
CONGRUENZE TRA FIGURE DEL PIANO
 CONGRUENZE TRA FIGURE DEL PIANO Appunti di geometria ASSIOMI 15. La congruenza tra figure è una relazione di equivalenza 16. Tutte le rette del piano sono congruenti tra loro; così come tutti i piani,
CONGRUENZE TRA FIGURE DEL PIANO Appunti di geometria ASSIOMI 15. La congruenza tra figure è una relazione di equivalenza 16. Tutte le rette del piano sono congruenti tra loro; così come tutti i piani,
Problemi di geometria
 criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
C7. Circonferenza e cerchio
 7. irconferenza e cerchio 7.1 Introduzione ai luoghi geometrici Un luogo geometrico è l insieme dei punti del piano che godono di una proprietà detta proprietà caratteristica del luogo geometrico. Esempio
7. irconferenza e cerchio 7.1 Introduzione ai luoghi geometrici Un luogo geometrico è l insieme dei punti del piano che godono di una proprietà detta proprietà caratteristica del luogo geometrico. Esempio
Poliedri regolari. - Le condizioni (a), (b) e (c) della definizione data non sono sovrabbondanti: Riferimenti bibliografici: (a) e (c) non (b)
 Riferimenti bibliografici: Poliedri regolari - Forme Maria Dedò Ed. Zanichelli - Le condizioni (a), (b) e (c) della definizione data non sono sovrabbondanti: (a) e (c) non (b) Definizione: Un poliedro
Riferimenti bibliografici: Poliedri regolari - Forme Maria Dedò Ed. Zanichelli - Le condizioni (a), (b) e (c) della definizione data non sono sovrabbondanti: (a) e (c) non (b) Definizione: Un poliedro
In un triangolo qualsiasi, la semiretta che, uscendo dal vertice di un angolo, lo divide in due parti uguali prende il nome di: a) mediana
 66 08 09 10 11 1 13 14 In un triangolo qualsiasi, la semiretta che, uscendo dal vertice di un angolo, lo divide in due parti uguali prende il nome di: a) mediana b) bisettrice c) asse d) ortogonale Un
66 08 09 10 11 1 13 14 In un triangolo qualsiasi, la semiretta che, uscendo dal vertice di un angolo, lo divide in due parti uguali prende il nome di: a) mediana b) bisettrice c) asse d) ortogonale Un
CAP. 1 - GLI ELEMENTI PRIMITIVI
 CP. 1 - GLI ELEMENTI PRIMITIVI 1 Geometria e realtà 2 Elementi primitivi della geometria 3 Punto 4 Figura geometrica 5 Figure congruenti 6 Linea 7 Retta 8 Proprietà della retta 9 Punti allineati 10 Semiretta
CP. 1 - GLI ELEMENTI PRIMITIVI 1 Geometria e realtà 2 Elementi primitivi della geometria 3 Punto 4 Figura geometrica 5 Figure congruenti 6 Linea 7 Retta 8 Proprietà della retta 9 Punti allineati 10 Semiretta
Le sezioni piane del cubo
 Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
I PARALLELOGRAMMI Si dice PARALLELOGRAMMA un quadrilatero avente i lati opposti paralleli a due a due.
 I PARALLELOGRAMMI Si dice PARALLELOGRAMMA un quadrilatero avente i lati opposti paralleli a due a due. A D B H C K Una particolarità del parallelogramma è che mantiene le sue caratteristiche anche quando
I PARALLELOGRAMMI Si dice PARALLELOGRAMMA un quadrilatero avente i lati opposti paralleli a due a due. A D B H C K Una particolarità del parallelogramma è che mantiene le sue caratteristiche anche quando
Esercizi sul cubo. Prisma e cilindro
 Esercizi sul cubo 1. Dimostra la formula della diagonale del cubo. 2. Ein würfelförmiger Kasten hat eine Kantenlänge von 16cm. Er wird mit Würfeln von 4cm Kantenlänge ganz gefüllt. Wie viele Würfel kann
Esercizi sul cubo 1. Dimostra la formula della diagonale del cubo. 2. Ein würfelförmiger Kasten hat eine Kantenlänge von 16cm. Er wird mit Würfeln von 4cm Kantenlänge ganz gefüllt. Wie viele Würfel kann
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 10
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
COMUNICAZIONE N.4 DEL
 COMUNICAZIONE N.4 DEL 7.11.2012 1 1 - PRIMO MODULO - COSTRUZIONI GEOMETRICHE (4): ESEMPI 10-12 2 - SECONDO MODULO - APPLICAZIONI DI GEOMETRIA DESCRITTIVA (4): ESEMPI 19-25 PRIMO MODULO - COSTRUZIONI GEOMETRICHE
COMUNICAZIONE N.4 DEL 7.11.2012 1 1 - PRIMO MODULO - COSTRUZIONI GEOMETRICHE (4): ESEMPI 10-12 2 - SECONDO MODULO - APPLICAZIONI DI GEOMETRIA DESCRITTIVA (4): ESEMPI 19-25 PRIMO MODULO - COSTRUZIONI GEOMETRICHE
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA
 Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
Due rette si dicono INCIDENTI se hanno esattamente un punto in comune, altrimenti si dicono PARALLELE.
 Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
N. Domanda Risposta. Quinto postulato di Euclide. 30 cm. 11 dm. 14 cm. 6 cm^2
 418 "Per un punto passa una sola retta parallela ad una retta data". Questo è l'enunciato del: 8 0,201 km corrispondono a: 201 m 199 10 dm^3 corrispondono a: 10000 cm^3 55 20 15' corrispondono a: 20,25
418 "Per un punto passa una sola retta parallela ad una retta data". Questo è l'enunciato del: 8 0,201 km corrispondono a: 201 m 199 10 dm^3 corrispondono a: 10000 cm^3 55 20 15' corrispondono a: 20,25
Angoli formati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, corrispondenti, coniugati).
 ppunti di geometria.s. 013-014 1 Prof. Luigi ai PPUNTI ngoli formati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, corrispondenti, coniugati). In un triangolo l angolo
ppunti di geometria.s. 013-014 1 Prof. Luigi ai PPUNTI ngoli formati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, corrispondenti, coniugati). In un triangolo l angolo
Risposte ai quesiti D E H D
 Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Istituto Statale d Arte Max Fabiani di Gorizia DISEGNO GEOMETRICO
 Istituto Statale d Arte Max Fabiani di Gorizia ANNO SCOLASTICO 2009-2010 CLASSE : 1^ e 2^ SEZIONE : A - B DISEGNO GEOMETRICO DISPENSA N 1 GEOMETRIA - DEFINIZIONI GLOSSARIO GEOMETRIA = La G. è quella parte
Istituto Statale d Arte Max Fabiani di Gorizia ANNO SCOLASTICO 2009-2010 CLASSE : 1^ e 2^ SEZIONE : A - B DISEGNO GEOMETRICO DISPENSA N 1 GEOMETRIA - DEFINIZIONI GLOSSARIO GEOMETRIA = La G. è quella parte
N. Domanda Risposta. 266 Dati due angoli acuti allora: la loro differenza è un angolo acuto
 199 "Per un punto passa una sola retta parallela ad una retta data". Questo è l'enunciato del: 233 0,201 km corrispondono a: 201 m 139 1 m corrisponde a: 0,001 km 263 10 dm^3 corrispondono a: 10000 cm^3
199 "Per un punto passa una sola retta parallela ad una retta data". Questo è l'enunciato del: 233 0,201 km corrispondono a: 201 m 139 1 m corrisponde a: 0,001 km 263 10 dm^3 corrispondono a: 10000 cm^3
N. Domanda Risposta. 32 cm
 1 L'area di un rombo misura 320 cm^2 e la diagonale minore 20 cm. Quanto misura la diagonale maggiore? 2 Se tagliamo una piramide con un piano parallelo alla base otteniamo: un'altra piramide e un tronco
1 L'area di un rombo misura 320 cm^2 e la diagonale minore 20 cm. Quanto misura la diagonale maggiore? 2 Se tagliamo una piramide con un piano parallelo alla base otteniamo: un'altra piramide e un tronco
Conoscenze. 2. Segna il completamento esatto. a. L area della superficie laterale di un prisma si calcola utilizzando la seguente formula:
 Conoscenze 1. Completa. a. Un prisma è un...poliedro... limitato da due...poligoni congruenti...e...paralleli... e da tanti...parallelogrammi...quanti sono i lati del...poligono di base... b. Un prisma
Conoscenze 1. Completa. a. Un prisma è un...poliedro... limitato da due...poligoni congruenti...e...paralleli... e da tanti...parallelogrammi...quanti sono i lati del...poligono di base... b. Un prisma
CONCETTI DI GEOMETRIA
 LA GEOMETRIA EUCLIDEA SI BASA SU TRE CONCETTI INTUITIVI: IL PUNTO, LA RETTA, IL PIANO IL PUNTO E' UN ENTE GEOMETRICO PRIVO DI DIMENSIONI. LA RETTA E' UN INSIEME DI PUNTI ALLINEATI. IL PIANO E' UN INSIEME
LA GEOMETRIA EUCLIDEA SI BASA SU TRE CONCETTI INTUITIVI: IL PUNTO, LA RETTA, IL PIANO IL PUNTO E' UN ENTE GEOMETRICO PRIVO DI DIMENSIONI. LA RETTA E' UN INSIEME DI PUNTI ALLINEATI. IL PIANO E' UN INSIEME
LA CIRCONFERENZA e IL CERCHIO
 LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
GEOMETRIA CLASSE IV B A.S.
 GEOMETRIA CLASSE IV B A.S. 2014/15 Insegnante: Stallone Raffaella RETTA, SEMIRETTA E SEGMANTO La retta è illimitata, non ha né inizio né fine. Si indica con una lettera minuscola. La semiretta è ciascuna
GEOMETRIA CLASSE IV B A.S. 2014/15 Insegnante: Stallone Raffaella RETTA, SEMIRETTA E SEGMANTO La retta è illimitata, non ha né inizio né fine. Si indica con una lettera minuscola. La semiretta è ciascuna
FIGURE SOLIDE OSSERVANDO LE FIGURE DELLO SPAZIO CHE CI CIRCONDANO NOTIAMO CHE:
 FIGURE SOLIDE OSSERVANDO LE FIGURE DELLO SPAZIO CHE CI CIRCONDANO NOTIAMO CHE: IL CUBO IL PARALLELEPIPEDO LA PIRAMIDE HANNO LA SUPERFICIE COSTITUITA DA POLIGONI (QUADRATO, RETTANGOLO, TRIANGOLO) E PRENDONO
FIGURE SOLIDE OSSERVANDO LE FIGURE DELLO SPAZIO CHE CI CIRCONDANO NOTIAMO CHE: IL CUBO IL PARALLELEPIPEDO LA PIRAMIDE HANNO LA SUPERFICIE COSTITUITA DA POLIGONI (QUADRATO, RETTANGOLO, TRIANGOLO) E PRENDONO
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 11
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 11 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 11 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
I TRIANGOLI AB < AC + BC
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
A B C D E F G H I L M N O P Q R S T U V Z
 IL VOCABOLARIO GEOMETRICO A B C D E F G H I L M N O P Q R S T U V Z A A: è il simbolo dell area di una figura geometrica Altezza: è la misura verticale e il segmento che parte da un vertice e cade perpendicolarmente
IL VOCABOLARIO GEOMETRICO A B C D E F G H I L M N O P Q R S T U V Z A A: è il simbolo dell area di una figura geometrica Altezza: è la misura verticale e il segmento che parte da un vertice e cade perpendicolarmente
December 16, solidi_generalità e prisma_sito scuola.notebook. da studiare solo sul file. La geometria solida. nov
 da studiare solo sul file La geometria solida nov 20 8.33 1 I SOLIDI SI SUDDIVIDONO IN DUE GRANDI CATEGORIE POLIEDRI SOLIDI ROTONDI nov 20 8.40 2 POLIEDRI Cos'è un poligono? E' una parte di spazio delimitata
da studiare solo sul file La geometria solida nov 20 8.33 1 I SOLIDI SI SUDDIVIDONO IN DUE GRANDI CATEGORIE POLIEDRI SOLIDI ROTONDI nov 20 8.40 2 POLIEDRI Cos'è un poligono? E' una parte di spazio delimitata
GEOMETRIA SOLIDA PIRAMIDE. Prof.ssa M. Rosa Casparriello
 GEOMETRIA SOLIDA PIRAMIDE Prof.ssa M. Rosa Casparriello Scuola media di Cervinara 2007/2008 DEFINIZIONE La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati
GEOMETRIA SOLIDA PIRAMIDE Prof.ssa M. Rosa Casparriello Scuola media di Cervinara 2007/2008 DEFINIZIONE La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati
Unità Didattica N 22 I triangoli. U.D. N 22 I triangoli
 10 Unità Didattica N 22 I triangoli U.D. N 22 I triangoli 01) Il triangolo ed i suoi elementi 02) Uguaglianza di due triangoli 03) Primo criterio di uguaglianza dei triangoli 04) Secondo criterio di uguaglianza
10 Unità Didattica N 22 I triangoli U.D. N 22 I triangoli 01) Il triangolo ed i suoi elementi 02) Uguaglianza di due triangoli 03) Primo criterio di uguaglianza dei triangoli 04) Secondo criterio di uguaglianza
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI
 LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
LA CIRCONFERENZA, I POLIGONI INSCRITTI E CIRCOSCRITTI 1. La circonferenza e il cerchio ESERCIZI 1 A Disegna un triangolo ABC di altezza CH relativa ad AB. Fissa un segmento ED minore di CH. Determina il
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Misura dei volumi dei solidi
 Geometria euclidea dello spazio Presentazione n. 8 Misura dei volumi dei solidi Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Richiamo di geometria piana: misura delle aree Per misurare
Geometria euclidea dello spazio Presentazione n. 8 Misura dei volumi dei solidi Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia Richiamo di geometria piana: misura delle aree Per misurare
U. A. 1 GLI INSIEMI CONOSCENZE
 U. A. 1 GLI INSIEMI Acquisire il significato dei termini,dei simboli e caratteristiche dell'insieme delle parti, dell'insieme differenza e complementare della partizione di un insieme e del prodotto cartesiano.
U. A. 1 GLI INSIEMI Acquisire il significato dei termini,dei simboli e caratteristiche dell'insieme delle parti, dell'insieme differenza e complementare della partizione di un insieme e del prodotto cartesiano.
Una proposizione che si pone alla base di una teoria matematica senza darne una giustificazione. Sono le «regole del gioco».
 Ripasso Scheda per il recupero Il metodo assiomatico-deduttivo OMNE he cos è un assioma? he cos è un concetto primitivo? he cos è un teorema? he cosa significa affrontare lo studio della geometria secondo
Ripasso Scheda per il recupero Il metodo assiomatico-deduttivo OMNE he cos è un assioma? he cos è un concetto primitivo? he cos è un teorema? he cosa significa affrontare lo studio della geometria secondo
Circonferenza e cerchio
 Cerchio e circonferenza - 1 Circonferenza e cerchio La circonferenza è il luogo geometrico dei punti del piano equidistanti da un unico punto detto centro. Il cerchio è l insieme costituito dai punti appartenenti
Cerchio e circonferenza - 1 Circonferenza e cerchio La circonferenza è il luogo geometrico dei punti del piano equidistanti da un unico punto detto centro. Il cerchio è l insieme costituito dai punti appartenenti
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Corso di Matematica - Geometria. Geometria - 0. Ing. L. Balogh
 Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI
 Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI LATI: equilatero, isoscele, scaleno CLASSIFICAZIONE RISPETTO
Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI LATI: equilatero, isoscele, scaleno CLASSIFICAZIONE RISPETTO
LAVORO ESTIVO di MATEMATICA Classi Terze Scientifico Moderno N.B. DA CONSEGNARE ALLA PRIMA LEZIONE DI MATEMATICA DI SETTEMBRE
 LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
MATEMATICA: Compiti delle vacanze Estate 2015
 MATEMATICA: Compiti delle vacanze Estate 2015 Classe II a PRIMA PARTE Ecco una raccolta degli esercizi sugli argomenti svolti quest anno: risolvili sul tuo quaderno! Per algebra ho inserito anche una piccola
MATEMATICA: Compiti delle vacanze Estate 2015 Classe II a PRIMA PARTE Ecco una raccolta degli esercizi sugli argomenti svolti quest anno: risolvili sul tuo quaderno! Per algebra ho inserito anche una piccola
Problemi di geometria
 1 2 3 applicazioni al triangolo rettangolo Calcola il perimetro e l area di un triangolo rettangolo sapendo che l ipotenusa e l altezza ad essa relativa sono lunghe rispettivamente 3 cm e 16,8 cm. [8 cm;
1 2 3 applicazioni al triangolo rettangolo Calcola il perimetro e l area di un triangolo rettangolo sapendo che l ipotenusa e l altezza ad essa relativa sono lunghe rispettivamente 3 cm e 16,8 cm. [8 cm;
NR Argomento TESTO RISP1 RISP2 RISP3 RISP4 1 GEM Quanti centimetri misura una circonferenza di diametro pari a 8 centimetri?
 NR Argomento TESTO RISP1 RISP2 RISP3 RISP4 1 GEM Quanti centimetri misura una di diametro pari a 8 64 16π 8 8π 2 GEM Dato un parallelepipedo con perimetro di base pari a 33 centimetri e altezza pari a
NR Argomento TESTO RISP1 RISP2 RISP3 RISP4 1 GEM Quanti centimetri misura una di diametro pari a 8 64 16π 8 8π 2 GEM Dato un parallelepipedo con perimetro di base pari a 33 centimetri e altezza pari a
descrivere le caratteristiche della sfera utilizzare le formule inerenti. Introduzione
 Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Scuola Secondaria di 1 Grado Via MAFFUCCI-PAVONI Via Maffucci 60 Milano PROGETTO STRANIERI GEOMETRIA 2 CERCHIO SIMMETRIA GEOMETRIA SOLIDA
 Scuola Secondaria di 1 Grado Via MAFFUCCI-PAVONI Via Maffucci 60 Milano PROGETTO STRANIERI GEOMETRIA CERCHIO SIMMETRIA GEOMETRIA SOLIDA A cura di Maurizio Cesca PROGETTO STRANIERI SMS Maffucci-Pavoni -
Scuola Secondaria di 1 Grado Via MAFFUCCI-PAVONI Via Maffucci 60 Milano PROGETTO STRANIERI GEOMETRIA CERCHIO SIMMETRIA GEOMETRIA SOLIDA A cura di Maurizio Cesca PROGETTO STRANIERI SMS Maffucci-Pavoni -
N. Domanda A B C D. Quinto postulato di Euclide. Secondo teorema di. Euclide. 3 0,201 km corrispondono a: 3,01 m 201 m 20,1 m 0,201 m
 1 «Il rapporto tra i segmenti tagliati su una trasversale da un fascio di rette parallele è uguale al rapporto tra i segmenti corrispondenti tagliati su un'altra trasversale». Questo è l'enunciato: 2 "Per
1 «Il rapporto tra i segmenti tagliati su una trasversale da un fascio di rette parallele è uguale al rapporto tra i segmenti corrispondenti tagliati su un'altra trasversale». Questo è l'enunciato: 2 "Per
Elementi di Geometria euclidea
 Elementi di Geometria euclidea Proprietà dei triangoli isosceli Il triangolo isoscele ha almeno due lati congruenti, l eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati
Elementi di Geometria euclidea Proprietà dei triangoli isosceli Il triangolo isoscele ha almeno due lati congruenti, l eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati
Problemi di geometria
 equivalenza fra parallelogrammi 1 2 3 4 Dimostra che, fra tutti i rettangoli equivalenti, il quadrato è quello che ha perimetro minimo. Dimostra che ogni quadrato è equivalente alla metà del quadrato costruito
equivalenza fra parallelogrammi 1 2 3 4 Dimostra che, fra tutti i rettangoli equivalenti, il quadrato è quello che ha perimetro minimo. Dimostra che ogni quadrato è equivalente alla metà del quadrato costruito
Costruzioni inerenti i triangoli
 Costruzioni inerenti i triangoli D ora in poi indicheremo con a, b e c i tre lati del triangolo di vertici A, B e C, in modo che a sia opposto al vertice A, b al vertice B e c al vertice C Costruzione
Costruzioni inerenti i triangoli D ora in poi indicheremo con a, b e c i tre lati del triangolo di vertici A, B e C, in modo che a sia opposto al vertice A, b al vertice B e c al vertice C Costruzione
N. Domanda Risposta. 7 L'angolo è una figura piana delimitata da: due semirette con l'origine in comune
 1 Il perimetro di un triangolo equilatero misura 36 cm. Il suo lato sarà: 12 cm 2 La somma degli angoli interni di un triangolo è: un angolo piatto 3 Conoscendo un lato e la diagonale di un rettangolo,
1 Il perimetro di un triangolo equilatero misura 36 cm. Il suo lato sarà: 12 cm 2 La somma degli angoli interni di un triangolo è: un angolo piatto 3 Conoscendo un lato e la diagonale di un rettangolo,
