Spazi di Hilbert. Spazi pre-hilbertiani ([H]-Cap. 1.1) - Esercizi ([E]-Cap. 1.1) NASTASI Antonella
|
|
|
- Emma Giacinta Pellegrino
- 5 anni fa
- Visualizzazioni
Transcript
1 Spazi di Hilbert Spazi pre-hilbertiani ([H]-Cap. 1.1) - Esercizi ([E]-Cap. 1.1) Def1.1-Def1.2-T1.1-Def1.3-T1.2-T1.3-T1.4-T1.5- Oss1.1-Def1.4-Def1.4-Def1.5- Esempio1.5-T1.6-T1.7-C1.1-C1.2-T1.8-T1.9 Esempio1.1-Esempio1.2-Esempio1.3-Esempio1.4- Esercizio1.1 Spazi lineari normati ([H]-Cap. 1.2) - Esercizi ([E]-Cap. 1.2) DI CARA PUPELLA DICARA Laurea Def2.1-T2.1-CNS2.1-T2.2-Def.2.2-Esempio2.2- Def2.3-Oss2.1-T2.3-T2.4-Def2.4-Def2.5- T2.6-Def2.6-Oss.2.2-T2.6 PUPELLA Esempio2.1-Esempio2.2-Esercizio2.1-Esercizio2.2-T2.5-Esempio2.3- Esempio2.4- Esempio2.5-Esempio2.6 T3.1-T3.3-Oss3.2 Lo Spazio di Hilbert l 2 ([H]-Cap. 1.3) - Esercizi ([E]-Cap. 1.3) T3.2-T3.4-T3.5-Oss3.1-Oss3.2- Esercizio3.1 Lo Spazio di Hilbert L 2 ([H]-Cap. 1.4) - Esercizi ([E]-Cap. 1.4) DE BIASE DE BIASE T4.1-T4.2-T4.4-T4.5(skeck)-T4.6-Oss4.1-Oss4.2 C4.1-T4.3-T4.4
2 Sottospazi ([H]-Cap. 2.1) - Esercizi ([E]-Cap. 2.1) Def1.1- Esempio1.1-Esempio1.2-T1.1-T1.2-T1.3-Def1.2-T1.4-Def1.3-Esercizio1.1 Esempio1.3-Esempio1.4- Oss1.1-Oss1.2-T1.5-Esercizio1.1 Sottospazi ortogonali ([H]-Cap. 2.2) - Esercizi ([E]-Cap. 2.2) Def.2.1-Oss2.1-Oss2.2-T2.1-T2.2- T2.3-T2.4- T2.5-C2.1-T2.6-T2.7- C2.2-C2.3 T2.8-T2.9-Oss2.3-C2.4-Esempio2.1-T2.10-Esercizio2.1 Basi ([H]-Cap. 2.3) - Esercizi ([E]-Cap. 2.3) Def3.1-Esempio3.1-Esempio3.2-Esempio3.3-T3.1 Oss3.1-Oss3.2-C3.2-C3.3-Def3.2 Esempio3.4-C3.1-T3.2-T3.3-Esempio3.5-T3.4 Isomorfismi ([H]-Cap. 2.4) - Esercizi ([E]-Cap. 2.4) DI CARA T4.1-Def4.1-Def4.2-Def4.3-Oss4.1-Def4.4-C4.1-C4.2 Applicazioni (operatori) lineari e limitati ([H]-Cap. 3.1) - Esercizi ([E]-Cap. 3.1) CAMMARATA Def1.1-Def1.2-Def1.3-Oss1.1-Oss1.2-T1.1-Oss1.3-T1.2-Esempio1.1- Esempio1.2- Esempio1.3- Def1.4-T1.3-T1.4 CAMMARATA T1.5- T1.6- Def1.5- Esempio1.4-T1.7-Teorema di Pavone
3 Operatori lineari ([H]-Cap. 3.2) - Esercizi ([E]-Cap. 3.2) PUPELLA Def2.1-Esempio2.1-T2.2-Def2.3-Oss2.2-Def2.4-T2.3-T2.4-Esempio2.2-Esempio2.3 PUPELLA T2.1- Def2.2-Oss2.1--Def2.5-Oss2.3-C2.1-T2.5 Forme bilineari ([H]-Cap. 3.3) - Esercizi ([E]-Cap. 3.3) Def3.1-Def3.2-Oss3.1-T3.1-C3.1-C3.2-T3.2-T3.3 T3.4-T3.5-C3.3-C3.4 Operatori aggiunti ([H]-Cap. 3.4) - Esercizi ([E]-Cap. 3.4) T4.1-Def4.1-T4.3-Def4.2-Oss4.1-Oss4.2-Oss4.3-Oss4.4-T4.4-Oss4.5-C4.1-T4-6-T4.7 Esempio4.1-Esempio4.2-T4.2-T4.5 Operatori di proiezione ([H]-Cap. 3.5) - Esercizi ([E]-Cap. 3.5) Def5.1-T5.1-Oss5.1-Esempio5.1-T5.2-Oss5.2-T5.3-T5.4-C5.1-T5.5 C5.2-Oss5.3-T5.6-C5.3
4 Spazi di Banach Spazi lineari normati ([B]-Cap. 4.1) X Operatori lineari ([B]-Cap. 4.2) X Funzionali lineari ([B]-Cap. 4.3) X DE BIASE Operatori e Funzionali lineari su spazi di dimensione finita ([B]-Cap. 4.4) X PUPELLA Spazi normati di operatori - Spazio duale ([B]-Cap. 4.5) X Teorema di Hahn-Banach (fino al Teorema 6.1 compreso) ([B]-Cap. 4.6) X DE BIASE Il teorema di Hahn-Banach (Teorema 6.2) ([B]-Cap. 4.6) X Il teorema di Hahn-Banach (dal Teorema 6.3 in poi) ([B]-Cap. 4.6) X CAMMARATA X Spazi riflessivi ([B]-Cap. 4.7) Teorema di categoria e di uniforme limitatezza ([B]-Cap. 4.8) X CAMMARATA X Forte e debole convergenza ([B]-Cap. 4.9) Convergenza di successioni di operatori ([B]-Cap. 4.10) X
5 Spazi di Sobolev ([SB]-Cap. 5.1) Da Motivazione a Riassumendo ([SB]-Cap. 5.1-p.1/6) X Da Passaggio alla formulazione variazionale a Proprieta di W 1,p (I) ([SB]-Cap. 5.1-p.7/12) X CAMMARATA Da Gli spazi di Sobolev W m,p (I) e H m (I) a Soluzione del problema debole ([SB]-Cap. 5.1-p.13/17) X X DE BIASE Problemi ai limiti ([SB]-Cap. 5.1-p.18/19) Da Lo spazio di Sobolev W 1,p (Ω) e H 1 (Ω) a Lo spazio di Sobolev W 1,p 0 (Ω) e H 1 0 (Ω) ([SB]-Cap. 5.1-p.20/23) X Da Problema di Dirichlet Omogeneo a Problema di Neumann omogeneo ([SB]-Cap. 5.1-p.24/28) X PUPELLA
ANALISI non Lineare. Diego Averna
 ANALISI non Lineare Ovvero: presentazione di Analisi non Lineare Diego Averna Dipartimento di Matematica e Informatica Facoltà di Scienze MM.FF.NN. Via Archirafi, 34-90123 Palermo (Italy) diego.averna@unipa.it
ANALISI non Lineare Ovvero: presentazione di Analisi non Lineare Diego Averna Dipartimento di Matematica e Informatica Facoltà di Scienze MM.FF.NN. Via Archirafi, 34-90123 Palermo (Italy) diego.averna@unipa.it
Chiusura lineare. N.B. A può essere indifferentemente un insieme, finito o no, o un sistema. Es.1. Es.2
 Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
Indice. Notazioni generali
 Indice Notazioni generali XIII 1 Derivati e arbitraggi 1 1.1 Opzioni 1 1.1.1 Finalità 3 1.1.2 Problemi 4 1.1.3 Leggi di capitalizzazione 4 1.1.4 Arbitraggi e formula di Put-Call Parity 5 1.2 Prezzo neutrale
Indice Notazioni generali XIII 1 Derivati e arbitraggi 1 1.1 Opzioni 1 1.1.1 Finalità 3 1.1.2 Problemi 4 1.1.3 Leggi di capitalizzazione 4 1.1.4 Arbitraggi e formula di Put-Call Parity 5 1.2 Prezzo neutrale
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Grazie ai Colleghi di Geometria del Dipartimento di Matematica dell Università degli Studi di Torino per il loro prezioso contributo. Grazie al Prof.
 A01 178 Grazie ai Colleghi di Geometria del Dipartimento di Matematica dell Università degli Studi di Torino per il loro prezioso contributo. Grazie al Prof. S.M. Salamon per tanti utili suggerimenti e
A01 178 Grazie ai Colleghi di Geometria del Dipartimento di Matematica dell Università degli Studi di Torino per il loro prezioso contributo. Grazie al Prof. S.M. Salamon per tanti utili suggerimenti e
Forme bilineari e prodotti scalari. Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione. b :
 Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Elementi Finiti: stime d errore e adattività della griglia
 Elementi Finiti: stime d errore e adattività della griglia Elena Gaburro Università degli studi di Verona Master s Degree in Mathematics and Applications 05 giugno 2013 Elena Gaburro (Università di Verona)
Elementi Finiti: stime d errore e adattività della griglia Elena Gaburro Università degli studi di Verona Master s Degree in Mathematics and Applications 05 giugno 2013 Elena Gaburro (Università di Verona)
Principi generali di normativa per il Disegno Tecnico e introduzione alle Proiezioni Ortogonali
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
Operatori non limitati con domini densi in spazi di Hilbert.
 Capitolo 5 Operatori non limitati con domini densi in spazi di Hilbert. In questo capitolo estenderemo la teoria degli operatori in spazi di Hilbert considerando operatori non limitati (in particolare
Capitolo 5 Operatori non limitati con domini densi in spazi di Hilbert. In questo capitolo estenderemo la teoria degli operatori in spazi di Hilbert considerando operatori non limitati (in particolare
Richiami di algebra lineare e geometria di R n
 Richiami di algebra lineare e geometria di R n combinazione lineare, conica e convessa spazi lineari insiemi convessi, funzioni convesse rif. BT.5 Combinazione lineare, conica, affine, convessa Un vettore
Richiami di algebra lineare e geometria di R n combinazione lineare, conica e convessa spazi lineari insiemi convessi, funzioni convesse rif. BT.5 Combinazione lineare, conica, affine, convessa Un vettore
Appunti di Analisi convessa. Paolo Acquistapace
 Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
CORSO DI MACROECONOMETRIA. Oggetto del corso, testo e orari di ricevimento. Programma. Facoltà di Economia. prof. Mario Forni
 prof. Mario Forni 1 2 Oggetto del corso, testo e orari di ricevimento Programma Analisi statistica delle serie temporali Applicazioni economiche (previsione, scomposizione ciclo-trend) Ma le applicazioni
prof. Mario Forni 1 2 Oggetto del corso, testo e orari di ricevimento Programma Analisi statistica delle serie temporali Applicazioni economiche (previsione, scomposizione ciclo-trend) Ma le applicazioni
Introduzione alla formulazione debole dei problemi ai limiti per EDP per il Corso di Metodi Matematici per
 Introduzione alla formulazione debole dei problemi ai limiti per EDP per il Corso di Metodi Matematici per l Ingegneria Marco Bramanti Politecnico di Milano 3 maggio Indice Derivate deboli e spazi di Sobolev.
Introduzione alla formulazione debole dei problemi ai limiti per EDP per il Corso di Metodi Matematici per l Ingegneria Marco Bramanti Politecnico di Milano 3 maggio Indice Derivate deboli e spazi di Sobolev.
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Informatica Grafica. Un introduzione
 Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Prova scritta di Geometria 2 Prof. M. Boratynski
 10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Esame di Geometria - 9 CFU (Appello del 28 gennaio 2013 - A)
 Esame di Geometria - 9 CFU (Appello del 28 gennaio 23 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Nello spazio R 3, siano dati il piano e i punti P = (, 2, ), Q = (2,, ). π : x + 2y 3
Esame di Geometria - 9 CFU (Appello del 28 gennaio 23 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Nello spazio R 3, siano dati il piano e i punti P = (, 2, ), Q = (2,, ). π : x + 2y 3
1 Regole generali per l esame. 2 Libro di Testo
 FACOLTÀ DI INGEGNERIA Corso di GEOMETRIA E ALGEBRA (mn). (Ing. per l Ambiente e il Territorio, Ing. Informatica - Sede di Mantova) A.A. 2008/2009. Docente: F. BISI. 1 Regole generali per l esame L esame
FACOLTÀ DI INGEGNERIA Corso di GEOMETRIA E ALGEBRA (mn). (Ing. per l Ambiente e il Territorio, Ing. Informatica - Sede di Mantova) A.A. 2008/2009. Docente: F. BISI. 1 Regole generali per l esame L esame
1.11.3 Distribuzione di carica piana ed uniforme... 32
 Indice 1 Campo elettrico nel vuoto 1 1.1 Forza elettromagnetica............ 2 1.2 Carica elettrica................ 3 1.3 Fenomeni elettrostatici............ 6 1.4 Legge di Coulomb.............. 9 1.5 Campo
Indice 1 Campo elettrico nel vuoto 1 1.1 Forza elettromagnetica............ 2 1.2 Carica elettrica................ 3 1.3 Fenomeni elettrostatici............ 6 1.4 Legge di Coulomb.............. 9 1.5 Campo
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
FONDAMENTI MATEMATICI DELLA FISICA
 FONDAMENTI MATEMATICI DELLA FISICA MACROSCOPICA: UN PERCORSO GEOMETRICO C. LO SURDO 2 INDICE 0.0 PRESENTAZIONE 0.0.1 CONSIDERAZIONI GENERALI E PIANO DI LAVORO 0.0.2 I CONTENUTI CAPITOLO PER CAPITOLO: SINTESI
FONDAMENTI MATEMATICI DELLA FISICA MACROSCOPICA: UN PERCORSO GEOMETRICO C. LO SURDO 2 INDICE 0.0 PRESENTAZIONE 0.0.1 CONSIDERAZIONI GENERALI E PIANO DI LAVORO 0.0.2 I CONTENUTI CAPITOLO PER CAPITOLO: SINTESI
Corso di Laurea in Ingegneria Informatica Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Lezioni del corso di Geometria e Algebra. prof. Michele Mulazzani dott. Alessia Cattabriga
 Lezioni del corso di Geometria e Algebra prof Michele Mulazzani dott Alessia Cattabriga AA 20001/2002 Indice 1 Equazioni e sistemi lineari 4 11 Alcune strutture algebriche 4 12 Operazioni standard su K
Lezioni del corso di Geometria e Algebra prof Michele Mulazzani dott Alessia Cattabriga AA 20001/2002 Indice 1 Equazioni e sistemi lineari 4 11 Alcune strutture algebriche 4 12 Operazioni standard su K
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Ingegneria Meccanica
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Ingegneria Meccanica Esame di Geometria (Prof. F. Tovena) Argomenti: Proprietà di nucleo e immagine di una applicazione lineare. dim V = dim
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Ingegneria Meccanica Esame di Geometria (Prof. F. Tovena) Argomenti: Proprietà di nucleo e immagine di una applicazione lineare. dim V = dim
Morte di un gatto e splitting del Multiverso
 http://www.extrabyte.info Monografia 001 February 04th, 2015 Morte di un gatto e splitting del Multiverso Marcello Colozzo Dedicato a un gatto che non c è più Sommario Keywords: many worlds interpretation,meccanica
http://www.extrabyte.info Monografia 001 February 04th, 2015 Morte di un gatto e splitting del Multiverso Marcello Colozzo Dedicato a un gatto che non c è più Sommario Keywords: many worlds interpretation,meccanica
f(x, y, z) = (x + ky + z, x y + 2z, x + y z) f(x, y, z) = (x + 2y z, x + y z, x + 2y) F (f(x)) = (f(0), f(1), f(2))
 Algebra Lineare e Geometria Analitica Politecnico di Milano Ingegneria Applicazioni Lineari 1. Sia f : R 3 R 3 l applicazione lineare definita da f(x, y, z) = (x + ky + z, x y + 2z, x + y z) per ogni (x,
Algebra Lineare e Geometria Analitica Politecnico di Milano Ingegneria Applicazioni Lineari 1. Sia f : R 3 R 3 l applicazione lineare definita da f(x, y, z) = (x + ky + z, x y + 2z, x + y z) per ogni (x,
TECNICHE DI CONTROLLO
 TECNICHE DI CONTROLLO Richiami di Teoria dei Sistemi Dott. Ing. SIMANI SILVIO con supporto del Dott. Ing. BONFE MARCELLO Sistemi e Modelli Concetto di Sistema Sistema: insieme, artificialmente isolato
TECNICHE DI CONTROLLO Richiami di Teoria dei Sistemi Dott. Ing. SIMANI SILVIO con supporto del Dott. Ing. BONFE MARCELLO Sistemi e Modelli Concetto di Sistema Sistema: insieme, artificialmente isolato
Miglioramento dell analisi di immagine in GRASS tramite segmentazione
 Segmentazione in GRASS Miglioramento dell analisi di immagine in GRASS tramite segmentazione Alfonso Vitti e Paolo Zatelli Dipartimento di Ingegneria Civile ed Ambientale Università di Trento Italy FOSS4G-it
Segmentazione in GRASS Miglioramento dell analisi di immagine in GRASS tramite segmentazione Alfonso Vitti e Paolo Zatelli Dipartimento di Ingegneria Civile ed Ambientale Università di Trento Italy FOSS4G-it
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Indice. Ringraziamenti 1. Introduzione 3
 Indice Ringraziamenti 1 Introduzione 3 1 Moltiplicazione fra distribuzioni 9 1.1 Definizione e proprietà........................ 9 1.1.1 Commutatività ed associatività............... 10 1.1.2 Alcune proprietà
Indice Ringraziamenti 1 Introduzione 3 1 Moltiplicazione fra distribuzioni 9 1.1 Definizione e proprietà........................ 9 1.1.1 Commutatività ed associatività............... 10 1.1.2 Alcune proprietà
Parte 2. Metodi Matematici per la Meccanica Quantistica. Spazi di pre-hilbert e spazi di Hilbert. Gianpiero CATTANEO
 Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
ANALISI ISOGEOMETRICA (IgA) Un'introduzione. Maria Lucia Sampoli. Universita' degli Studi di Siena
 ANALISI ISOGEOMETRICA (IgA) Un'introduzione Maria Lucia Sampoli Universita' degli Studi di Siena PDE Equazione differenziale nella funzione incognita u = u(t, x 1,..., x d ) F (x, t, u, u t, u x 1,...,
ANALISI ISOGEOMETRICA (IgA) Un'introduzione Maria Lucia Sampoli Universita' degli Studi di Siena PDE Equazione differenziale nella funzione incognita u = u(t, x 1,..., x d ) F (x, t, u, u t, u x 1,...,
REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE)
 REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE) 30/09/2013 ore 3 I numeri naturali, relativi, razionali e loro proprieta'. Incompletezza del campo dei numeri razionali. I numeri reali come allineamenti
REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE) 30/09/2013 ore 3 I numeri naturali, relativi, razionali e loro proprieta'. Incompletezza del campo dei numeri razionali. I numeri reali come allineamenti
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
OPERATORI NON LIMITATI
 Capitolo 13 OPERATORI NON LIMITATI La teoria degli operatori limitati negli spazi di Hilbert è soddisfacente per molti versi, ma non cattura diversi esempi che sono pervasivi nella Fisica Matematica: gli
Capitolo 13 OPERATORI NON LIMITATI La teoria degli operatori limitati negli spazi di Hilbert è soddisfacente per molti versi, ma non cattura diversi esempi che sono pervasivi nella Fisica Matematica: gli
DIARIO DEL CORSO TEORIA GEOMETRICA DELLA MISURA A.A. 08/09
 DIARIO DEL CORSO TEORIA GEOMETRICA DELLA MISURA A.A. 08/09 SILVANO DELLADIO 18/02/09 (1-1). Presentazione generale del corso. Richiami di teoria astratta della misura. Definizione di misura. Monotonia
DIARIO DEL CORSO TEORIA GEOMETRICA DELLA MISURA A.A. 08/09 SILVANO DELLADIO 18/02/09 (1-1). Presentazione generale del corso. Richiami di teoria astratta della misura. Definizione di misura. Monotonia
ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura
 Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile
 Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2015-2016 A. Ponno (aggiornato al 19 gennaio 2016) 2 Ottobre 2015 5/10/15 Benvenuto, presentazione
Programma dettagliato del corso di MECCANICA RAZIONALE Corso di Laurea in Ingegneria Civile Anno Accademico 2015-2016 A. Ponno (aggiornato al 19 gennaio 2016) 2 Ottobre 2015 5/10/15 Benvenuto, presentazione
Geometria Superiore. A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno. March 2, 2015
 Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano March 2, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano March 2, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
ANALISI NUMERICA. Elementi finiti bidimensionali. a.a. 2014 2015. Maria Lucia Sampoli. ANALISI NUMERICA p.1/23
 ANALISI NUMERICA Elementi finiti bidimensionali a.a. 2014 2015 Maria Lucia Sampoli ANALISI NUMERICA p.1/23 Elementi Finiti 2D Consideriamo 3 aspetti per la descrizione di elementi finiti bidimensionali:
ANALISI NUMERICA Elementi finiti bidimensionali a.a. 2014 2015 Maria Lucia Sampoli ANALISI NUMERICA p.1/23 Elementi Finiti 2D Consideriamo 3 aspetti per la descrizione di elementi finiti bidimensionali:
Introduzione a FreeFem++
 Introduzione a FreeFem++ Manolo Venturin EnginSoft, Padova 14 maggio 2012 M. Venturin (EnginSoft) Introduzione a FreeFem++ 14 maggio 2012 1 / 35 Indice della presentazione Indice 1 Introduzione Caratteristiche
Introduzione a FreeFem++ Manolo Venturin EnginSoft, Padova 14 maggio 2012 M. Venturin (EnginSoft) Introduzione a FreeFem++ 14 maggio 2012 1 / 35 Indice della presentazione Indice 1 Introduzione Caratteristiche
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Autovalori e Autovettori
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
3 Applicazioni lineari e matrici
 3 Applicazioni lineari e matrici 3.1 Applicazioni lineari Definizione 3.1 Siano V e W dei K spazi vettoriali. Una funzione f : V W è detta applicazione lineare se: i u, v V, si ha f(u + v = f(u + f(v;
3 Applicazioni lineari e matrici 3.1 Applicazioni lineari Definizione 3.1 Siano V e W dei K spazi vettoriali. Una funzione f : V W è detta applicazione lineare se: i u, v V, si ha f(u + v = f(u + f(v;
LE FIBRE DI UNA APPLICAZIONE LINEARE
 LE FIBRE DI UNA APPLICAZIONE LINEARE Sia f:a B una funzione tra due insiemi. Se y appartiene all immagine di f si chiama fibra di f sopra y l insieme f -1 y) ossia l insieme di tutte le controimmagini
LE FIBRE DI UNA APPLICAZIONE LINEARE Sia f:a B una funzione tra due insiemi. Se y appartiene all immagine di f si chiama fibra di f sopra y l insieme f -1 y) ossia l insieme di tutte le controimmagini
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI
 DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
PAOLA GERVASIO RISOLUZIONE DI EQUAZIONI ALLE DERIVATE PARZIALI CON METODI SPETTRALI IN REGIONI PARTIZIONATE IN SOTTODOMINI
 PAOLA GERVASIO RISOLUZIONE DI EQUAZIONI ALLE DERIVATE PARZIALI CON METODI SPETTRALI IN REGIONI PARTIZIONATE IN SOTTODOMINI Tesi di Dottorato in Matematica Relatore: Ch.mo Prof. ALFIO QUARTERONI Università
PAOLA GERVASIO RISOLUZIONE DI EQUAZIONI ALLE DERIVATE PARZIALI CON METODI SPETTRALI IN REGIONI PARTIZIONATE IN SOTTODOMINI Tesi di Dottorato in Matematica Relatore: Ch.mo Prof. ALFIO QUARTERONI Università
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Spazi lineari - PARTE II - Felice Iavernaro. Dipartimento di Matematica Università di Bari. 9 e 16 Marzo 2007
 Spazi lineari - PARTE II - Felice Iavernaro Dipartimento di Matematica Università di Bari 9 e 16 Marzo 2007 Felice Iavernaro (Univ. Bari) Spazi lineari 9-16/03/2007 1 / 17 Condizionamento dei sistemi lineari
Spazi lineari - PARTE II - Felice Iavernaro Dipartimento di Matematica Università di Bari 9 e 16 Marzo 2007 Felice Iavernaro (Univ. Bari) Spazi lineari 9-16/03/2007 1 / 17 Condizionamento dei sistemi lineari
LEZIONE 14. a 1,1 v 1 + a 1,2 v 2 + a 1,3 v 3 + + a 1,n 1 v n 1 + a 1,n v n = w 1
 LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
Programma Svolto. Tecnologie dell Informazione e Comunicazione. Classe IA
 ISTITUTO STATALE DI ISTRUZIONE SUPERIORE ALESSANDRO VOLTA Via Volta, 1 - Tel. : 0785/53024 fax: 0785/52654 - e-mail: isisghilarza@tiscalinet.it - C.M. ORIS00100L - C.F.90027890954 09074 GHILARZA (Oristano)
ISTITUTO STATALE DI ISTRUZIONE SUPERIORE ALESSANDRO VOLTA Via Volta, 1 - Tel. : 0785/53024 fax: 0785/52654 - e-mail: isisghilarza@tiscalinet.it - C.M. ORIS00100L - C.F.90027890954 09074 GHILARZA (Oristano)
Il polo magnetico: simulazione nel tempo
 Corso di Elettrotecnica Industriale Professore Paolo Di Barba Il polo magnetico: simulazione nel tempo Anno Accademico 2013/2014 Lo scopo dell esercizio è quello di valutare l andamento del campo magnetico
Corso di Elettrotecnica Industriale Professore Paolo Di Barba Il polo magnetico: simulazione nel tempo Anno Accademico 2013/2014 Lo scopo dell esercizio è quello di valutare l andamento del campo magnetico
Bando per l ammissione al Corso di laurea magistrale in. MATEMATICA (classe LM-40)
 Area Studenti Anno Accademico 2014-2015 Bando per l ammissione al Corso di laurea magistrale in MATEMATICA (classe LM-40) Dipartimento di Matematica e Fisica Sommario art. 1 Premessa... 2 art. 2 Posti
Area Studenti Anno Accademico 2014-2015 Bando per l ammissione al Corso di laurea magistrale in MATEMATICA (classe LM-40) Dipartimento di Matematica e Fisica Sommario art. 1 Premessa... 2 art. 2 Posti
Se x* e punto di minimo (locale) per la funzione nell insieme Ω, Ω = { x / g i (x) 0 i I, h j (x)= 0 j J } lo e anche per F(x) = f o (x) + c x x 2
 NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
Metodo degli elementi finiti per l approssimazione numerica del problema delle correnti parassite
 UNIVERSITÀ DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Metodo degli elementi finiti per l approssimazione numerica del problema delle correnti
UNIVERSITÀ DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Metodo degli elementi finiti per l approssimazione numerica del problema delle correnti
1 scheda informativa. Sede didattica: Genova Via Dodecaneso 35 (Valletta Puggia) Classe delle lauree specialistiche in: matematica (n.
 Corso di Laurea Specialistica in Matematica (classe 45/S) 1 scheda informativa 2 norme didattiche e propedeuticità 3 piano di studi 4 attività formative: contenuti/obiettivi specifici. 1 scheda informativa
Corso di Laurea Specialistica in Matematica (classe 45/S) 1 scheda informativa 2 norme didattiche e propedeuticità 3 piano di studi 4 attività formative: contenuti/obiettivi specifici. 1 scheda informativa
sezioni incluso Espandi tutto 0. Elementi di matematica elementare (parzialmente incluso) Sezione 0.1: I numeri reali Sezione 0.2: Regole algebriche.
 sezioni incluso Espandi tutto 0. Elementi di matematica elementare (parzialmente incluso) Sezione 0.1: I numeri reali Sezione 0.2: Regole algebriche. Potenze e percentuali Sezione 0.3: Disuguaglianze Sezione
sezioni incluso Espandi tutto 0. Elementi di matematica elementare (parzialmente incluso) Sezione 0.1: I numeri reali Sezione 0.2: Regole algebriche. Potenze e percentuali Sezione 0.3: Disuguaglianze Sezione
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
Università degli Studi di Roma La Sapienza Laurea in Ingegneria Energetica A.A. 2014-2015 Programma del corso di Geometria Prof.
 Università degli Studi di Roma La Sapienza Laurea in Ingegneria Energetica A.A. 2014-2015 Programma del corso di Geometria Prof. Antonio Cigliola Prerequisiti Logica elementare. Principio di Induzione.
Università degli Studi di Roma La Sapienza Laurea in Ingegneria Energetica A.A. 2014-2015 Programma del corso di Geometria Prof. Antonio Cigliola Prerequisiti Logica elementare. Principio di Induzione.
Sviluppo Applicazioni Mobile Lezione 7. Dr. Paolo Casoto, Ph.D - 2011
 + Sviluppo Applicazioni Mobile Lezione 7 Dr. Paolo Casoto, Ph.D - 2011 + Credits I lucidi di questa lezione sono stati preparati da: Professor Stefano Mizzaro Professor Paolo Coppola e sono stati modificati
+ Sviluppo Applicazioni Mobile Lezione 7 Dr. Paolo Casoto, Ph.D - 2011 + Credits I lucidi di questa lezione sono stati preparati da: Professor Stefano Mizzaro Professor Paolo Coppola e sono stati modificati
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
Ricerca Operativa (Compito A) Appello del 16/06/2014 Andrea Scozzari
 Ricerca Operativa (Compito A) Appello del 16/06/2014 Andrea Scozzari Esercizio n.1 Un agenzia finanziaria deve investire 1000000 di euro di un suo cliente in fondi di investimento. Il mercato offre cinque
Ricerca Operativa (Compito A) Appello del 16/06/2014 Andrea Scozzari Esercizio n.1 Un agenzia finanziaria deve investire 1000000 di euro di un suo cliente in fondi di investimento. Il mercato offre cinque
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 1 INTRODUZIONE
 2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
Analisi funzionale. Riccarda Rossi Lezione 9
 Riarda Rossi Lezione 9 Caratterizzazione della onvergenza debole in L p (Ω) Siano 1 < p < e {f n}, f L p (Ω): allora f n f in L p (Ω) Teorema di ompattezza debole in L p (Ω) Teorema Siano 1 < p < e {f
Riarda Rossi Lezione 9 Caratterizzazione della onvergenza debole in L p (Ω) Siano 1 < p < e {f n}, f L p (Ω): allora f n f in L p (Ω) Teorema di ompattezza debole in L p (Ω) Teorema Siano 1 < p < e {f
Approssimazione di PDE con il metodo della decomposizione di domini (DD)
 Capitolo 4 Approssimazione di PDE con il metodo della decomposizione di domini (DD) Prof. Alfio Quarteroni 4.1 Introduzione Sia Ω un dominio di dimensione d, per d = 2, 3, con frontiera Lipschitziana Ω;
Capitolo 4 Approssimazione di PDE con il metodo della decomposizione di domini (DD) Prof. Alfio Quarteroni 4.1 Introduzione Sia Ω un dominio di dimensione d, per d = 2, 3, con frontiera Lipschitziana Ω;
Problemi al contorno per equazioni e sistemi di equazioni ellittiche, paraboliche ed iperboliche in domini a frontiera non regolare.
 Prof.ssa Diomeda Lorenza Maria Professore Ordinario Dipartimento di Scienze Economiche Area Matematica Facoltà di Economia, Via C.Rosalba 53- Bari Tel. 080-5049169 Fax 080-5049207 E-mail diomeda@matfin.uniba.it
Prof.ssa Diomeda Lorenza Maria Professore Ordinario Dipartimento di Scienze Economiche Area Matematica Facoltà di Economia, Via C.Rosalba 53- Bari Tel. 080-5049169 Fax 080-5049207 E-mail diomeda@matfin.uniba.it
Teoremi di rigidità per funzioni di Sobolev e applicazioni.
 Università degli Studi di Roma La Sapienza A.A. 01-013 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea Specialistica in Matematica Teoremi di rigidità per funzioni di Sobolev e applicazioni.
Università degli Studi di Roma La Sapienza A.A. 01-013 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea Specialistica in Matematica Teoremi di rigidità per funzioni di Sobolev e applicazioni.
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Note integrative ed Esercizi consigliati
 - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Note integrative ed consigliati Laura Poggiolini e Gianna Stefani Indice 0 1 Convergenza uniforme 1 2 Convergenza totale 5 1 Numeri
- a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Note integrative ed consigliati Laura Poggiolini e Gianna Stefani Indice 0 1 Convergenza uniforme 1 2 Convergenza totale 5 1 Numeri
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Sistemi di
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Sistemi di
Corso di Disegno di Macchine + Abilità Informatiche. Test di autovalutazione 14 marzo 2012 / A
 Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
FONDAMENTI DI ANALISI SUPERIORE 1
 FONDAMENTI DI ANALISI SUPERIORE 1 Docente: LUCIO CADEDDU SSD: MAT/05 Codifica dell Ateneo: Tipologia: Integrato: NO Anno di corso 1 magistrale Semestre 1 Sede lezioni: Dipartimento di Matematica e Informatica,
FONDAMENTI DI ANALISI SUPERIORE 1 Docente: LUCIO CADEDDU SSD: MAT/05 Codifica dell Ateneo: Tipologia: Integrato: NO Anno di corso 1 magistrale Semestre 1 Sede lezioni: Dipartimento di Matematica e Informatica,
TEMA 1. 1. Della seguente matrice, calcolare i complementi algebrici e il determinante: a + b 1 a 2 S = a + b + 3 a + 2b. x = t. f = x 2 + 2xy 3y 2,
 Prova scritta di MATEMATICA B1 Vicenza, 17 marzo 008 TEMA 1 1 1 A = 1 0 1. 3 0 1. Stabilire se il seguente sottoinsieme di M(, R): {( ) a + b 1 a S = a, b R}, a + b + 3 a + b è un sottospazio di M(, R).
Prova scritta di MATEMATICA B1 Vicenza, 17 marzo 008 TEMA 1 1 1 A = 1 0 1. 3 0 1. Stabilire se il seguente sottoinsieme di M(, R): {( ) a + b 1 a S = a, b R}, a + b + 3 a + b è un sottospazio di M(, R).
Corso di Grafica Computazionale
 Corso di Grafica Computazionale Premesse Teoriche Docente: Massimiliano Corsini Laurea Specialistica in Ing. Informatica Università degli Studi di Siena Overview Premesse Teoriche Mini-ripasso geometria
Corso di Grafica Computazionale Premesse Teoriche Docente: Massimiliano Corsini Laurea Specialistica in Ing. Informatica Università degli Studi di Siena Overview Premesse Teoriche Mini-ripasso geometria
Graduatoria simulazione test di accesso per l ammissione al corso di Laurea delle Professioni Sanitarie
 Graduatoria simulazione test di accesso per l ammissione al corso di Laurea delle Professioni Sanitarie 1 0004689 47,5 18,75 12,75 9 7 2 0002098 45,5 24,75 10,75 4 6 3 0002099 44,5 23,75 11,75 3 6 4 0002264
Graduatoria simulazione test di accesso per l ammissione al corso di Laurea delle Professioni Sanitarie 1 0004689 47,5 18,75 12,75 9 7 2 0002098 45,5 24,75 10,75 4 6 3 0002099 44,5 23,75 11,75 3 6 4 0002264
EQUAZIONI non LINEARI
 EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica Nome N. Matricola Ancona, 14 luglio 2015 1. Tre macchine producono gli stessi pezzi
Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica Nome N. Matricola Ancona, 14 luglio 2015 1. Tre macchine producono gli stessi pezzi
Si basano sul seguente Teorema: S = A sse S { A} è insoddisfacibile.
 Deduzione automatica La maggior parte dei metodi di deduzione automatica sono metodi di refutazione: anziché dimostrare direttamente che S A, si dimostra che S { A} è un insieme insoddisfacibile (cioè
Deduzione automatica La maggior parte dei metodi di deduzione automatica sono metodi di refutazione: anziché dimostrare direttamente che S A, si dimostra che S { A} è un insieme insoddisfacibile (cioè
POLITECNICO di BARI - A.A. 2012/2013 Corso di Laurea in INGEGNERIA Informatica e dell Automazione
 POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
Siano V e W due spazi vettoriali. La definizione seguente é è tra quelle basilari per il corso di Matematica B. L : V W
 Matematica B - a.a 2006/07 p. 1 Siano V e W due spazi vettoriali. La definizione seguente é è tra quelle basilari per il corso di Matematica B. Definizione 1. La funzione L : V W si dice una applicazione
Matematica B - a.a 2006/07 p. 1 Siano V e W due spazi vettoriali. La definizione seguente é è tra quelle basilari per il corso di Matematica B. Definizione 1. La funzione L : V W si dice una applicazione
Note sulla teoria dei campi e del potenziale
 Note sulla teoria dei campi e del potenziale Claudio Serpico Corso di Elettrotecnica per Ingegneria Elettronica Anno Accademico 2001-2002 7 gennaio 2002 1 Solenoidalità, Indivergenza, Conservatività e
Note sulla teoria dei campi e del potenziale Claudio Serpico Corso di Elettrotecnica per Ingegneria Elettronica Anno Accademico 2001-2002 7 gennaio 2002 1 Solenoidalità, Indivergenza, Conservatività e
SISTEMI LINEARI QUADRATI: METODI ITERATIVI
 SISTEMI LINEARI QUADRATI: METODI ITERATIVI CALCOLO NUMERICO e PROGRAMMAZIONE SISTEMI LINEARI QUADRATI:METODI ITERATIVI p./54 RICHIAMI di ALGEBRA LINEARE DEFINIZIONI A R n n simmetrica se A = A T ; A C
SISTEMI LINEARI QUADRATI: METODI ITERATIVI CALCOLO NUMERICO e PROGRAMMAZIONE SISTEMI LINEARI QUADRATI:METODI ITERATIVI p./54 RICHIAMI di ALGEBRA LINEARE DEFINIZIONI A R n n simmetrica se A = A T ; A C
Aspetti Matematici della Meccanica Quantistica
 Appunti del corso Aspetti Matematici della Meccanica Quantistica (FM450 A.A. 04/5) Michele Correggi Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, L.go San Leonardo Murialdo,, 0046,
Appunti del corso Aspetti Matematici della Meccanica Quantistica (FM450 A.A. 04/5) Michele Correggi Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, L.go San Leonardo Murialdo,, 0046,
I polinomi 1; x;x 2 ;x 3 sono linearmente indipendenti; infatti. 0= 1 1+ 2 x+ 3 x 2 + 4 x 3 =) 1 = 2 == 4 =0
 ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
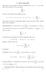 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
+ t v. v 3. x = p + tv, t R. + t. 3 2 e passante per il punto p =
 5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
Foglio1. Da 15 a 24 contenuto socioassistenziale. regionale a. previdenziale. previdenziale. Da 24 a sanitaria e. 35 + file organizzazione dei servizi
 CALENDARIO FAD 1 CORSO OSS SEDE DI CB -TERMINUS data modulo unità didattica pag. libro ore data test 1.1. Elementi di CULTURALE legislazione ISTITUZIONALE E nazionale e Da 15 a 25-nov-15 regionale a 6
CALENDARIO FAD 1 CORSO OSS SEDE DI CB -TERMINUS data modulo unità didattica pag. libro ore data test 1.1. Elementi di CULTURALE legislazione ISTITUZIONALE E nazionale e Da 15 a 25-nov-15 regionale a 6
Rango: Rouchè-Capelli, dimensione e basi di spazi vettoriali.
 CAPITOLO 7 Rango: Rouchè-Capelli, dimensione e basi di spazi vettoriali. Esercizio 7.1. Determinare il rango delle seguenti matrici al variare del parametro t R. 1 4 2 1 4 2 A 1 = 0 t+1 1 A 2 = 0 t+1 1
CAPITOLO 7 Rango: Rouchè-Capelli, dimensione e basi di spazi vettoriali. Esercizio 7.1. Determinare il rango delle seguenti matrici al variare del parametro t R. 1 4 2 1 4 2 A 1 = 0 t+1 1 A 2 = 0 t+1 1
EFFETTO MAGNETICO DELLA CORRENTE
 IL CAMPO MAGNETICO E GLI EFFETTI MAGNETICI DELLA CORRENTE 1 EFFETTO MAGNETICO DELLA CORRENTE Ogni conduttore percorso da corrente crea intorno a sé un campo magnetico (H), cioè una perturbazione di tipo
IL CAMPO MAGNETICO E GLI EFFETTI MAGNETICI DELLA CORRENTE 1 EFFETTO MAGNETICO DELLA CORRENTE Ogni conduttore percorso da corrente crea intorno a sé un campo magnetico (H), cioè una perturbazione di tipo



