Le isometrie nel piano
|
|
|
- Marino Serafini
- 7 anni fa
- Visualizzazioni
Transcript
1 CAPITOLO 4 Le isometrie ne piano 1. ISOMETRIE CON GEOGEBRA Gi strumenti per eseguire trasformazioni geometriche si trovano nea nona icona. Nee esercitazioni che seguono cercheremo di riconoscere e principai proprietaá dee isometrie, con particoare riguardo ae simmetrie assiai. Esercitazione 1. Simmetrie, trasazioni e rotazioni Disegniamo un triangoo ABC ne piano eucideo e troviamo: 1. i suo simmetrico rispetto a un punto O de piano; 2. i suo simmetrico rispetto a una retta a che assumiamo come asse di simmetria; 3. i suo corrispondente nea trasazione di un vettore ~v assegnato; 4. i suo corrispondente in una rotazione di ampiezza attorno a un punto P. Punto 1. Simmetria centrae Disegniamo un triangoo ABC e un punto O; mediante i Menu contestuae visuaizziamo poi e ettere in corrispondenza dei vertici. Per costruire i triangoo simmetrico di ABC rispetto ad O usiamo o strumento 9-Simmetrico rispetto a un punto; a breve guida a ato dea barra degi strumenti grafici ci dice che dobbiamo ciccare prima su'oggetto da trasformare, ne nostro caso i triangoo ABC, e poi su centro di simmetria, ne nostro caso i punto O. Subito viene disegnato i triangoo A 0 B 0 C 0 ; notiamo che i punti che si corrispondono vengono indicati con a stessa ettera munita di un apice. Per megio evidenziare a procedura di costruzione, tracciamo e rette che passano per i punti simmetrici: tai rette evidentemente passano tutte per O (in figura abbiamo modificato o stie de tratto scegiendo a rappresentazione a puntini). Scegiendo adesso un punto quasiasi su ato AB e troviamo i suo simmetrico rispetto ad O; da menu contestuae di questi due punti spuntiamo a voce Traccia attiva. Se adesso facciamo scorrere i primo punto su AB, anche i suo simmetrico scorre su A 0 B 0 e dee successive posizioni dei due punti rimane traccia su fogio di avoro. Evidenziamo adesso gi angoi dei due triangoi con o strumento 8-Angoo, ciccando prima su un triangoo e Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO 1
2 poi su'atro (degi angoi viene indicata anche a misura in gradi e da essa possiamo giaá anticipare a congruenza degi angoi corrispondenti). Individuiamo e proprietaá di questa trasformazione usando i comando 10-reazione tra due oggetti: ciccando su una coppia di angoi corrispondenti, per esempio su quei di vertici A e A 0 ci viene comunicato che i due angoi sono uguai (non viene usato in GeoGebra i termine "congruenti"); ciccando su una coppia di segmenti corrispondenti, per esempio su AB e A 0 B 0 ci viene comunicato che i due segmenti hanno a stessa unghezza (nea versione attuae viene detto che i due segmenti non sono uguai ma che hanno a stessa unghezza, versioni successive potrebbero aver corretto questo errore); ciccando sui due triangoi, ci viene comunicato che sono uguai. In modo de tutto anaogo si deve procedere per soddisfare ae atre richieste; diamo soo acuni cenni sui passi da seguire, ricordando che si deve poi mostrare, tracciando opportuni segmenti, a procedura di costruzione. Punto 2. Simmetria rispetto a una retta a Si disegna a retta a asse di simmetria. Si attiva o strumento 9-Simmetrico rispetto a una retta e si cicca prima su triangoo ABC e poi sua retta a. Punto 3. Trasazione di vettore ~v Si disegna un vettore con o strumento 3-Vettore tra due punti. Si attiva o strumento 9-Trasa di un vettore e si cicca prima su triangoo ABC e poi su vettore. Punto 4. Rotazione di ampiezza attorno a un punto P Si attiva o strumento 9-Ruota intorno a un punto di un angoo. Si cicca su triangoo ABC e poi su punto P centro dea rotazione. Nea finestra di diaogo che si apre, si indica 'ampiezza de'angoo e si scegie i verso di rotazione orario oppure antiorario. Esercitazione 2. Prodotto di isometrie Dopo aver disegnato un triangoo ABC studiamo a che cosa equivae i prodotto di: 1. due simmetrie assiai con gi assi perpendicoari 2. due simmetrie assiai con gi assi paraei 3. due simmetrie assiai con gi assi fra oro incidenti in modo quasiasi 4. due simmetrie centrai. Punto 1. Prodotto di simmetrie assiai con gi assi perpendicoari Disegnato i triangoo ABC e due rette a e b tra oro perpendicoari che si intersecano in O, troviamo i simmetrico di ABC rispetto aa retta a; successivamente i simmetrico de triangoo A 0 B 0 C 0 ottenuto rispetto aa retta b. Tracciamo adesso i segmenti che uniscono i punti A e A 00, B e B 00, C e C 00 ; tutti questi segmenti passano per O che eá anche i oro punto medio (si puoá verificare con o strumento 2-Punto medio). I due triangoi ABC e A 00 B 00 C 00 sono quindi simmetrici rispetto a punto O. Questo conferma che: i prodotto di due simmetrie assiai con gi assi perpendicoari equivae ad una simmetria centrae avente centro ne punto di intersezione degi assi. 2 Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
3 Punto 2. Prodotto di simmetrie assiai con gi assi paraei In una nuova finestra grafica disegniamo un atro triangoo ABC e due rette a e b tra oro paraee; troviamo poi i triangoo simmetrico di ABC rispetto ad a e poi i simmetrico di quest'utimo rispetto a b. Tracciamo ora i vettori che congiungono i punti omooghi A e A 00, B e B 00, C e C 00. Usiamo o strumento 10-Reazione tra due oggetti e cicchiamo prima su vettore AA 00 e poi su BB 00 ; a finestra di diaogo che si apre ci comunica che i due vettori sono uguai. La stessa cosa capita quando cicchiamo su BB 00 e poi su CC 00. Possiamo aora concudere che ABC e A 00 B 00 C 00 si corrispondono in una trasazione di vettore AA 00. Per comprendere se esiste una reazione fra questo vettore e i due assi di simmetria, tracciamo i vettore che esprime a distanza tra e due rette paraee: da un punto di a tracciamo a perpendicoare ad a e determiniamo i punto di intersezione con b tracciamo i vettore ~z che unisce questi due punti con verso daa retta a aa retta b. Costruiamo adesso un vettore ~s che sia uguae a doppio de vettore ~z: nea barra di inserimento scriviamo s ˆ 2 z confermiamo con INVIO. Nea Vista Grafica viene visuaizzato i vettore ~s. Usando o strumento 10-Reazione tra due oggetti confrontiamo i vettore ~s con uno quaunque dei vettori AA 00, BB 00, CC 00 : i due vettori sono uguai. Dunque: i prodotto di due simmetrie assiai con gi assi paraei equivae ad una trasazione di vettore perpendicoare agi assi e di moduo doppio dea oro distanza. Punto 3. Prodotto di simmetrie assiai con gi assi fra oro incidenti in modo quasiasi Disegniamo due rette a e b incidenti in un punto O ma non perpendicoari ed eseguiamo e due simmetrie, prima rispetto aa retta a e poi aa retta b. Definiamo adesso 'angoo fra e due rette (orientato da a verso b) ed eseguiamo una rotazione de triangoo ABC attorno ad O di ampiezza pari a 2 (i verso di rotazione eá orario oppure antiorario a seconda di come si sono scete e rette a e b; nea figura i verso eá orario). Nea rotazione i triangoo ABC corrisponde di nuovo a triangoo A 00 B 00 C 00. Abbiamo cosõá verificato che: i prodotto di due simmetrie assiai con gi assi incidenti in O e che formano un angoo di ampiezza eá equivaente a una rotazione di ampiezza 2 e centro O. Punto 4. Prodotto di simmetrie centrai Dopo aver di nuovo costruito un triangoo ABC, fissiamo due punti P e Q che rappresentano i centri dee due simmetrie. Costruiamo i simmetrico di ABC rispetto a punto P e poi i simmetrico di quest'utimo rispetto a punto Q. Per evidenziare e due simmetrie tracciamo anche i segmenti che uniscono i punti omooghi dei triangoi che si corrispondono e, per evitare possibii confusioni, usiamo i Menu contestuae per modificare o stie de tratto (nea figura che segue abbiamo sceto a inea a puntini). Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO 3
4 Per capire in quae trasformazione si corrispondono i triangoo ABC e i triangoo A 00 B 00 C 00, usando o strumento 3-Vettore tra due punti, tracciamo i vettore ƒ! ƒ! PQ e i vettore AA 00 (nea figura abbiamo modificato o stie attraverso i Menu contestuae e i abbiamo evidenziati rispettivamente in rosso e in verde con un tratto di spessore piuá marcato). Troviamo poi i punto medio M de segmento AA 00 e definiamo i vettore AM ƒ!. Mediante o strumento 10-reazione tra due oggetti verifichiamo che i due vettori ƒ! PQ e AM ƒ! sono uguai. Abbiamo cosõá verificato che: i prodotto di due simmetrie centrai equivae a una trasazione di vettore doppio dea distanza tra i due centri. 2. ISOMETRIE CON CABRI Gi strumenti per eseguire trasformazioni ne piano si trovano ne'icona Trasforma riportata a ato. Quei che ci servono in questo capitoo sono soo i primi quattro ed eá immediato capire a quae isometria si riferiscono. Vediamo dunque come utiizzare questi strumenti. Esercitazione 1. La simmetria assiae Per trovare i simmetrico di un oggetto geometrico rispetto a una retta occorre eseguire in sequenza ordinata queste operazioni: seezionare o strumento Simmetria assiae indicare 'oggetto da trasformare indicare 'asse di simmetria. In genere 'asse di simmetria eá una retta o una sua parte, vae a dire che si puoá trovare i simmetrico di un oggetto rispetto a un segmento o a un ato di un poigono; in questi casi viene assunta come asse di simmetria a retta a cui appartiene que segmento o que ato. Per renderti conto di come funzionano e cose, disegna ne fogio di avoro un triangoo ABC e una retta r ed esegui poi queste operazioni dopo aver attivato o strumento Simmetria assiae: cicca prima su triangoo (quando avvicini i cursore compare i messaggio Simmetrico di questo triangoo) e poi sua retta (compare i messaggio Rispetto a questa retta); trovi cosõá i simmetrico di ABC rispetto a r cicca prima sua retta (compare i messaggio Simmetrica di questa retta) e poi su un ato de triangoo, per esempio AB (compare i messaggio Rispetto a questo ato de triangoo); trovi cosõá a retta simmetrica di r rispetto ad AB. Nea figura di pagina seguente, a sinistra eá rappresentato i risutato dea prima operazione, a destra i risutato dea seconda, dove eá a retta de ato AB che viene considerata asse di simmetria. Devi quindi prestare attenzione a'ordine con cui seezioni gi oggetti: prima 'oggetto di cui si vuoe trovare i simmetrico, poi 'asse di simmetria; in ogni caso i messaggio che compare quando avvicini i cursore ti guida nea sceta. Verifichiamo adesso e proprietaá dea simmetria assiae riferendoci iniziamente aa trasformazione di sinistra de'immagine: n nascondi i triangoo ABC (rimangono in evidenza i suoi vertici) e poi, con a stessa procedura, determina i simmetrico di A 0 B 0 C 0 rispetto ao stesso asse r : ottieni di nuovo i triangoo ABC di partenza; a simmetria assiae eá quindi invoutoria 4 Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
5 n disegna una retta s perpendicoare a'asse di simmetria e trova a sua trasformata: apparentemente non accade nua percheâ a retta trasformata coincide con se stessa. In reataá se ti poni nea modaitaá Puntatore e sposti i mouse sua retta, compare i messaggio "Quae oggetto?" percheâ e rette sono due, sovrapposte. Possiamo aora dire che s eá una retta unita n prendi adesso un punto P su s e trova i suo trasformato: tae punto appartiene ancora a s ma non coincide con P, cioeá non eá unito: e rette perpendicoari a'asse sono dunque rette unite ma non sono rette di punti uniti. Esercitazione 2. Le atre isometrie Con procedure anaoghe si eseguono e atre isometrie; vediamo quai sono e operazioni da eseguire. n Simmetria centrae Si seeziona o strumento Simmetria centrae, si indica per primo 'oggetto da trasformare, si indica per secondo i centro dea simmetria. Se i centro eá un punto giaá rappresentato ne fogio di avoro, basta avvicinare i cursore (compare i messaggio Rispetto a questo punto) e ciccare; se i centro non eá ancora stato disegnato, si deve ciccare ne punto desiderato. n Trasazione Per eseguire una trasazione occorre assegnare i vettore di trasazione mediante o strumento Vettore de'icona Rette; i vettore viene disegnato ciccando ne'ordine ne punto origine e ne secondo estremo de vettore. Si seeziona poi o strumento Trasazione e si indica 'oggetto da trasformare e poi i vettore dea trasazione. n Rotazione Per eseguire una rotazione occorre assegnare un punto (i centro dea rotazione) e un angoo. L'angoo deve essere disegnato prima di utiizzare questo strumento e puoá essere dato in diversi modi: ciccando su un angoo giaá rappresentato; in questo caso i verso dea rotazione eá orario se 'arco eá stato definito prendendo i punti in senso antiorario, eá antiorario in caso contrario. indicando 'ampiezza in gradi de'angoo mediante o strumento Numeri de'icona Visuaizza: scrivendo un numero positivo a rotazione eá in verso antiorario, scrivendo un numero negativo eá in verso orario. Fissati i centro e 'ampiezza, per eseguire una rotazione si deve procedere come per e atre trasformazioni: indicare per primo 'oggetto a cui appicare a rotazione, per secondo i centro e per utimo 'angoo. Verifichiamo adesso e proprietaá di queste isometrie: disegna un segmento AB che useremo come oggetto da trasformare ed esegui queste operazioni. n Trova i simmetrico A 0 B 0 di AB rispetto ad un punto O e, usando gi opportuni strumenti, verifica che: AB ed i suo trasformato sono paraei AB ed A 0 B 0 hanno a stessa unghezza a simmetria centrae eá invoutoria. n Disegna un vettore ~v ed appica ad AB a trasazione de vettore sceto; verifica che: AB ed i suo corrispondente nea trasazione sono paraei e hanno a stessa unghezza a trasazione non eá invoutoria. n Dopo aver indicato e seguenti ampiezze di angoi: 180, 60, fissa un punto O ne fogio di avoro e, considerando sempre AB come oggetto iniziae, esegui e seguenti rotazioni di centro O: di ampiezza 180 e verifica che A 0 B 0 si ottiene anche mediante a simmetria di centro O di ampiezza 60 e verifica che a rotazione non eá invoutoria. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO 5
6 Esercitazione 3. I prodotto di trasformazioni Con Cabri eá facie anche vedere che cosa si ottiene eseguendo un prodotto di trasformazioni; verifichiamo per esempio che i prodotto di due simmetrie assiai con gi assi incidenti eá una rotazione di ampiezza uguae a doppio de'angoo formato dai due assi. Disegna dunque due rette r e s (gi assi di simmetria) e un segmento AB; esegui poi queste operazioni: trova i simmetrico di AB rispetto a r e chiamao CD trova i simmetrico di CD rispetto a s e chiamao EF definisci 'angoo formato dae due rette r e s e trova a sua ampiezza definisci 'angoo di rotazione uguae a doppio de'angoo (puoi usare a cacoatrice di Cabri e trascinare i risutato ne fogio di avoro in modo che a variare de'ampiezza di vari in corrispondenza anche ; ricorda poi di attribuire i segno corretto a'ampiezza ottenuta) nascondi i segmento EF (rimane a traccia dei suoi estremi) e trova i corrispondente di AB nea rotazione di ampiezza. Savo errori di approssimazione, 'utimo segmento trovato si sovrappone a segmento EF. ESERCIZI 1. Verifica che i prodotto di due rotazioni di centro O rispettivamente di ampiezza e equivae a una rotazione deo stesso centro e ampiezza. 2. Disegna un quaunque triangoo ABC e costruisci i suo simmetrico rispetto aa retta de ato AC; indicato con B 0 i corrispondente de vertice B, costruisci i simmetrico de triangoo ottenuto rispetto aa retta de ato B 0 C. Individua: a. gi eementi uniti nea prima e nea seconda simmetria b. in quae trasformazione si corrispondono i primo ed i terzo triangoo. 3. Verifica che a simmetria assiae eá una trasformazione invoutoria, mentre a rotazione non o eá. 4. Disegna un triangoo e due vettori ~v e! w ; appica a triangoo a trasazione di vettore ~v e, a suo trasformato, a trasazione di vettore! w. Verifica che i prodotto dee due trasazioni equivae a una trasazione che ha come vettore ~v! w. 5. Disegna un triangoo ABC isoscee sua base BC e traccia a retta de'atezza AH; individua i suo corrispondente nea simmetria avente per asse AH. Quai osservazioni puoi fare? Ci sono punti e rette unite? 6. Disegna un triangoo ABC e appica ad esso a simmetria avente per asse a retta di AB; a triangoo ottenuto appica a simmetria avente per asse a retta di BC. Individua a trasformazione nea quae si corrispondono ABC e 'utimo triangoo ottenuto. 7. Disegna due segmenti congruenti e paraei AB e CD e individua e simmetrie nee quai essi si corrispondono. 6 Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
7 Approfondimento La topoogia e 'aneo di MoÈbius Nee isometrie moti sono gi invarianti: e unghezze dei segmenti, e ampiezze degi angoi, 'aineamento dei punti, 'incidenza e i paraeismo; vi sono peroá trasformazioni in cui ben poco si conserva. Anche se questo tipo di trasformazioni sembra piuá compesso a prima vista da descrivere e da studiare, esso eá tuttavia i primo che si usa. Un bambino di 3-4 anni, in effetti, disegna a figura umana mettendo un ovae a posto dea testa, quacosa che ricorda un triangoo o un rettangoo a posto de corpo e dee inee piuá o meno unghe a posto dee gambe e dea braccia; eá interessante poi notare che egi disegna due piccoi cerchi e una specie di arco a'interno de'ovae dea testa per disegnare occhi e bocca. Un bambino possiede quindi giaá e reazioni di inea aperta/chiusa e di interno/esterno. Uno dei piuá recenti ed interessanti rami dea matematica, nato nea seconda metaá de XIX secoo, eá a topoogia, a quae studia appunto e proprietaá dee figure geometriche sottoposte a deformazioni che ne modificano radicamente forma e dimensioni. La topoogia, in atre paroe, si occupa di un particoare tipo di trasformazioni geometriche, dette appunto trasformazioni topoogiche, in cui sussistono particoari invarianti quai ad esempio a distinzione interno/esterno, a percorribiitaá continua, etc. In figura 1 puoi vedere un esempio di come un oggetto che presenta due fori puoá essere trasformato senza che e sue proprietaá topoogiche si modifichino: a figura finae, seppur diversa per forma e dimensioni, puoá essere ottenuta daa prima per deformazioni continue, senza strappi. Figura 1 Lo studio dea topoogia ha portato a considerare moti aspetti curiosi dea reataá, che, pur rispondendo a una formuazione teorica rigorosa, possono essere visti come piacevoi giochi. Se prendi una striscia di carta e chiedi a un tuo amico quante "facce" ha, egi ti risponderaá sicuramente due. Puoi scommettere peroá che sei in grado di costruire una superficie con una soa faccia. Come? Prendi una striscia rettangoare e, dopo aver fatto compiere ad uno degi estremi un mezzo giro, incoa e due estremitaá ottenendo in questo modo un aneo come in figura 2. Se ora provi a percorrere con un pennareo a striscia a partire da un suo punto, ti accorgerai che ritorni a punto di partenza dopo aver percorso tutte e due e facce de rettangoo iniziae. La superficie che hai costruito ha quindi una soa faccia. Figura 2 Una superficie di questo tipo eá detta nastro o aneo di MoÈbius, in quanto venne studiata da'astronomo tedesco Augustus MoÈbius ( ), i quae fu i primo ad anaizzare e sorprendenti proprietaá di questo nuovo aspetto dea geometria. Sebbene una superficie come 'aneo di MoÈbius possa apparire soo un divertente gioco matematico, essa ha trovato appicazioni in atri campi, ad esempio in fisica come modeo dea ricerca sue particee subatomiche. PiuÁ in generae possiamo dire che a topoogia eá utiissima nei piuá diversi settori, daa pianificazione dea viabiitaá su un territorio a disegno dei circuiti integrati dei computer. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO 7
8 1 La figura B si ottiene daa figura A tramite: a. a simmetria di centro P b. una rotazione di centro Q c. a simmetria rispetto aa retta ` d. una trasazione e. a simmetria rispetto a una retta de piano non tracciata in figura. a: Š 2 I diagramma a fianco viene ruotato attorno a'origine. Quae fra e seguenti eá a figura che eá stata ottenuta? a. b. c. d. e. e: Š 3 Quanti assi di simmetria possiede a figura a ato? a. 2 b. 4 c. 6 d. 8 e. nessuna dee precedenti e: Š 4 Fissiamo un punto O ne'intersezione di due inee di un fogio a quadretti e indichiamo e quattro direzioni paraee ae inee come Nord, Sud, Est, Ovest (i Nord in ato). Muoviamoci, partendo da O, di un quadretto verso Est, poi due verso Nord, tre verso Ovest, quattro verso Sud, cinque verso Est e cosõávia. Dopo 1997 passi, in che punto ci troviamo rispetto a punto iniziae O? a quadretti a Nord di O b. 998 quadretti a Sud e 999 quadretti a Est di O c. 999 quadretti a Ovest e 998 quadretti a Nord di O d. 999 quadretti a Nord e 999 quadretti a Ovest di O e. 998 quadretti a Est e 998 quadretti a Sud di O. b: Š 5 Ci sono cinque sagome di cartoncino identiche che sono bianche da un ato e nere da'atro ato. Poste su un tavoo esse si trovano nee posizioni in figura, quattro mostrano a faccia nera e una quea bianca. Qua eá a sagoma bianca? a. b. c. d. e. d: Š 8 Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
9 6 Si consideri una retta r ed un triangoo ABC che giace in uno dei due semipiani individuati da r. Detti A 0, B 0, C 0 i punti simmetrici di A, B, C rispetto a r, si conduca da A 0 a paraea a BC, dab 0 a paraea ad AC edac 0 a paraea ad AB. Si dimostri che queste tre rette passano per uno stesso punto. 7 Dato un triangoo scaeno ABC, sia C 0 i punto simmetrico di C rispetto aa retta AB. Siano: a a retta simmetrica dea retta C 0 A rispetto aa retta CC 0, M i punto intersezione di a con a retta CB. Anaogamente, sia b a retta simmetrica di C 0 B rispetto a CC 0, e sia N i punto intersezione di b con a retta CA.Si dimostri che e rette CC 0, AB, MN passano per uno stesso punto. 8 Ne Far West due fiumi rettiinei scorrono paraeamente aa distanza di 10km. Lo stregone di un viaggio indiano, che si trova nea sua capanna, deve raccogiere un'ampoa d'acqua da ciascuno dei due fiumi e portare e ampoe a viaggio per a cerimonia dea preghiera a ManituÁ. Qua eá a minima distanza de percorso che deve compiere, sapendo che a capanna e i viaggio sono equidistanti dai due fiumi e distano fra oro 48km? a. 48 b. 52 c. 53 d. 58 e. p b: Š I geotista, ovvero i geometra artista Le isometrie sono e trasformazioni che piuá vengono usate ne'arte in genere, daa pittura, a'architettura, aa scutura. Si possono reaizzare simpatiche costruzioni appicando i concetti imparati a questo proposito; basta avere quache specchio, dee pietruzze coorate, sagome di cartone, coori a tempera, un po'di coa e... tanta fantasia. Pitture simmetriche I bambini amano usare i coori e, con a fantasia che soo un bimbo puoá avere, riconoscono ne risutato dee oro opere immagini e figure fantastiche: draghi, fiori dae forme inconsuete, ciei sconfinati pieni di nuvoe, fiamme che si innazano fino a imite de disegno. Ma tutte queste immagini sono spesso gemee, non esiste un drago senza i suo compagno, un fiore soitario, una nuvoa spaiata, una fiamma che brucia in soitudine. Probabimente anche tu, da piccoo, stendevi dei grumi di coore a'interno di un fogio piegato a metaá, bianco, giao, bu, rosso, arancio; poi chiudevi ben bene i fogio e premevi con e mani su coore che si espandeva a'interno dea piegatura. Quando riaprivi i fogio, a magia era compiuta: nee due metaá, perfettamente simmetriche, e tue figure fantastiche. La camera a specchi Prepara un piano di cartone su quae disegnare una serie di angoi tutti con un ato in comune come in figura: un angoo retto, un angoo di 60 e uno di 45. Procura poi due specchi piani rettangoari uguai e disponii ad angoo ungo i ato piuá corto; uniscii su retro con un pezzo di nastro adesivo, in modo peroá che sia possibie modificare 'ampiezza de'angoo di apertura. Q Re Fraschini - Grazzi, Atas SpA Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO 9
10 Appoggia i due specchi su piano e aprii a 90. Metti un oggetto quasiasi, per esempio una pietruzza coorata, una moneta o un disegno geometrico coorato, a'interno deo spazio deimitato dagi specchi. Se ti metti di fronte aa struttura cosõá preparata, quanti sono gi oggetti che vedi riprodotti? Ripeti 'esperienza modificando 'angoo di apertura a 60. Questa vota quanti sono gi oggetti? Che cosa succede quando 'angoo diventa di 45? Modifichiamo adesso a camera mettendo i due specchi a 60 e ponendo un terzo specchio davanti ai primi due. Nea precedente esperienza 'oggetto che hai posto fra i due specchi si era riprodotto per 5 vote formando, insieme a'oggetto reae, un esagono. L'aggiunta de terzo specchio riproduce 'esagono coprendo interamente a superficie deimitata dai tre specchi eseguendo una caratteristica pavimentazione. Muovendo 'oggetto a pavimentazione cambia di continuo creando effetti di simmetria moto piacevoi e in continua evouzione. Un'utima domanda: sai spiegare percheâ abbiamo considerato angoi di apertura di 90, 60 e 45? I caeidoscopio I principi dea camera a specchi descritta ne'esercizio precedente si appica nea costruzione dei caeidoscopi. Puoi costruirne uno procurandoti i seguente materiae: - un tubo di cartone, puoá andare bene anche queo che avanza dai rotoi di carta per a cucina - acuni specchi, oppure, moto piuá pratica da utiizzare, dea pastica adesiva a specchio che si puoá comprare in un quasiasi coorificio - de cartone da ritagiare - pezzetti di pastica coorata - dischi di pastica trasparente che si puoá ricavare dae scatoe di confezioni dee camicie. Come prima cosa costruisci un cerchio di cartone in modo da chiudere una dee estremitaá de tubo. Inserisci i pezzetti di pastica coorata su fondo e poi appoggia i dischi trasparenti in modo peroá che i pezzetti coorati si possano muovere anche scorrendo gi uni sugi atri. Ritagia poi tre strisce uguai di pastica a specchio e accostai in modo da formare un triangoo equiatero; a dimensione dee strisce deve essere tae da poter essere inserita ne tubo di cartone. Se i diametro de tubo eá di 5cm, quanto deve essere ungo i ato che va a formare i triangoo equiatero? Una vota inserita questa struttura ne tubo (e facce a specchio devono risutare a'interno de soido a base triangoare), richiudio con un atro disco di pastica trasparente e appoggia su di esso un secondo disco di cartone a quae avrai fatto un foro de diametro di circa 1cm. I caeidoscopio eá pronto; guardando a'interno de tubo attraverso i foro de disco superiore e ruotandoo otterrai immagini ogni vota diverse che pavimentano 'intera superficie osservata, conservando sempre una struttura simmetrica. 10 Tema 5 - Cap. 4: LE ISOMETRIE NEL PIANO Q Re Fraschini - Grazzi, Atas SpA
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
Parallelogrammi, trapezi e poligoni regolari
 CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
Luoghi di punti e funzioni non lineari
 CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
RAPPRESENTARE LA TERRA
 CPIA 1 FOGGIA VOLUME MODULO D 2 LE VENTI CAPITOLO REGIONI ITALIANE 0 RAPPRESENTARE LA TERRA 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: panisfero...... paraeo......
CPIA 1 FOGGIA VOLUME MODULO D 2 LE VENTI CAPITOLO REGIONI ITALIANE 0 RAPPRESENTARE LA TERRA 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: panisfero...... paraeo......
ISTRUZIONI PER INIZIARE
 1 ISTRUZIONI PER INIZIARE Questa è la barra di menu: serve per dare tutte le informazioni sui file che devi creare, salvare, ecc. Questa icona serve per chiudere a bordo pagina il file e poi riaprirlo
1 ISTRUZIONI PER INIZIARE Questa è la barra di menu: serve per dare tutte le informazioni sui file che devi creare, salvare, ecc. Questa icona serve per chiudere a bordo pagina il file e poi riaprirlo
Le affinità. Una affinità è una corrispondenza biunivoca fra i punti di un piano che ha come invarianti l allineamento dei punti e il parallelismo.
 A Le affinità Trasazioni, simmetrie assiai o centrai, omotetie e diatazioni, di cui abbiamo già fatto argo uso neo studio dea geometria anaitica, insieme ad atre trasformazioni quai e rotazioni, sono egate
A Le affinità Trasazioni, simmetrie assiai o centrai, omotetie e diatazioni, di cui abbiamo già fatto argo uso neo studio dea geometria anaitica, insieme ad atre trasformazioni quai e rotazioni, sono egate
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
Le funzioni goniometriche
 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
I grafici derivati e la periodicità
 A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
I poligoni e la circonferenza
 CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA. LEZIONE n 13
 METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
IL MIO ORMULARIO. Capitolo 1: Gli insiemi N e Z. Capitolo 2: Gli insiemi Q e R
 IL MIO F ORMULARIO Compia i tuo formuario per ricordare e informazioni più importanti. Puoi descrivere a paroe, usare formue, fare disegni, a seconda di come riesci a ricordare megio. La prima vota che
IL MIO F ORMULARIO Compia i tuo formuario per ricordare e informazioni più importanti. Puoi descrivere a paroe, usare formue, fare disegni, a seconda di come riesci a ricordare megio. La prima vota che
IL PENDOLO REVERSIBILE DI KATER
 IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...) che caratterizzano la trasformazione
 LE TRASFORMAZIONI IN CABRI Per ottenere la figura immagine di una figura data in una trasformazione Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...)
LE TRASFORMAZIONI IN CABRI Per ottenere la figura immagine di una figura data in una trasformazione Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...)
Parallelismo e perpendicolaritaá nel piano
 CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
Le isometrie Capitolo
 Le isometrie Capitolo Simmetria centrale e assiale erifica per la classe prima COGNOME............................... NOME............................. Classe.................................... Data...............................
Le isometrie Capitolo Simmetria centrale e assiale erifica per la classe prima COGNOME............................... NOME............................. Classe.................................... Data...............................
TRASFORMAZIONE PRIMA SELEZIONE SELEZIONE SUCCESSIVA
 Come ottenere la figura immagine di una figura data Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...) che caratterizzano la trasformazione Clicca sul
Come ottenere la figura immagine di una figura data Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...) che caratterizzano la trasformazione Clicca sul
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
þ k Þy ¼ ð 1 3k Þx 2 þ 21 k
 A I fasci di paraboe Come equazione di un fascio di rette è a combinazione ineare di due particoari rette, e sue generatrici, anche un fascio di paraboe è a combinazione ineare di due particoari di esse.
A I fasci di paraboe Come equazione di un fascio di rette è a combinazione ineare di due particoari rette, e sue generatrici, anche un fascio di paraboe è a combinazione ineare di due particoari di esse.
La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli relativi.
 orso di Laurea in Matematica Prova scritta di Fisica Prof. E. Santovetti) 8 gennaio 016 Nome: La risposta numerica deve essere scritta ne apposito riquadro e giustificata accudendo i cacoi reativi. Probema
orso di Laurea in Matematica Prova scritta di Fisica Prof. E. Santovetti) 8 gennaio 016 Nome: La risposta numerica deve essere scritta ne apposito riquadro e giustificata accudendo i cacoi reativi. Probema
Grafico della funzione y = sen x
 G Grafico della funzione y = sen x Utilizzare GeoGebra per costruire il grafico della funzione y ¼ sen x a partire dalla sua definizione mediante la circonferenza goniometrica. Come sai, il valore della
G Grafico della funzione y = sen x Utilizzare GeoGebra per costruire il grafico della funzione y ¼ sen x a partire dalla sua definizione mediante la circonferenza goniometrica. Come sai, il valore della
GRANDEZZE FISICHE. Le grandezze fisiche si possono distinguere in grandezze scalari e grandezze vettoriali.
 GRANDEZZE FISICHE Le grandezze fisiche si possono distinguere in grandezze scalari e grandezze vettoriali. Le grandezze scalari sono completamente determinate da un numero che né esprime la misura. Esempio:
GRANDEZZE FISICHE Le grandezze fisiche si possono distinguere in grandezze scalari e grandezze vettoriali. Le grandezze scalari sono completamente determinate da un numero che né esprime la misura. Esempio:
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09
 NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
Triangolo rettangolo
 Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
Modelli di secondo grado
 MATEMATICAperTUTTI ESERCIZIO SVOLTO Le equazioni di secondo grado incompete. Un equazione di secondo grado si può sempre scrivere nea sua forma normae ax þ bx þ c 0 dove a, b, c sono numeri reai con a
MATEMATICAperTUTTI ESERCIZIO SVOLTO Le equazioni di secondo grado incompete. Un equazione di secondo grado si può sempre scrivere nea sua forma normae ax þ bx þ c 0 dove a, b, c sono numeri reai con a
Somma degli angoli di un triangolo
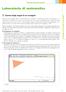 G Somma degli angoli di un triangolo Disegna un triangolo ABC e una semiretta r di origine O. Costruisci quindi le semirette s, t, u anch esse di origine O in modo che gli angoli rs, st, tu siano rispettivamente
G Somma degli angoli di un triangolo Disegna un triangolo ABC e una semiretta r di origine O. Costruisci quindi le semirette s, t, u anch esse di origine O in modo che gli angoli rs, st, tu siano rispettivamente
I vettori CAPITOLO 2 1. I VETTORI CON GEOGEBRA. Ci sono due comandi selezionabili dai menu di disegno che operano sui vettori:
 CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
Nicola De Rosa, Liceo scientifico di ordinamento sessione straordinaria 2012, matematicamente.it
 Nicoa De Rosa, Liceo scientifico di ordinamento sessione straordinaria, matematicamente.it PROBLEMA I triangoo ABC, rettangoo in A, ha ipotenusa BC a ; sia P i punto medio di AC, Q a sua proiezione ortogonae
Nicoa De Rosa, Liceo scientifico di ordinamento sessione straordinaria, matematicamente.it PROBLEMA I triangoo ABC, rettangoo in A, ha ipotenusa BC a ; sia P i punto medio di AC, Q a sua proiezione ortogonae
Cosa puoi dire del quadrilatero ABCD? Come sono i lati, le diagonali, gli angoli?
 Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati
 LABORATORIO DI GEOMETRIA COSTRUZIONI DI BASE DI POLIGONI 1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati Si costruisce un segmento AB, base del triangolo, ed un segmento CD, lato obliquo. Si
LABORATORIO DI GEOMETRIA COSTRUZIONI DI BASE DI POLIGONI 1. costruzione di un TRIANGOLO ISOSCELE di assegnati lati Si costruisce un segmento AB, base del triangolo, ed un segmento CD, lato obliquo. Si
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Rette, piani e figure nello spazio
 CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
Sfruttando le considerazioni appena fatte come misureresti il coefficiente di attrito statico μ s?
 MISURA DEL COEFFICIENTE DI ATTRITO STATICO Materiae occorrente: piano incinato monete Nota a unghezza de piano, qua è a reazione che sussiste fra i coefficiente di attrito statico μ s e a configurazione
MISURA DEL COEFFICIENTE DI ATTRITO STATICO Materiae occorrente: piano incinato monete Nota a unghezza de piano, qua è a reazione che sussiste fra i coefficiente di attrito statico μ s e a configurazione
IL PIANO CARTESIANO. Preparazione. Esercizi
 IN CLASSE IL PIANO CARTESIANO Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
IN CLASSE IL PIANO CARTESIANO Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
LE TRASFORMAZIONI GEOMETRICHE
 pag. 1 LE TRASFORMAZIONI GEOMETRICHE Trasformazione geometrica Movimento rigido Traslazione Simmetria Costruzione di due punti simmetrici rispetto ad una retta Poligoni aventi assi di simmetria Rotazione
pag. 1 LE TRASFORMAZIONI GEOMETRICHE Trasformazione geometrica Movimento rigido Traslazione Simmetria Costruzione di due punti simmetrici rispetto ad una retta Poligoni aventi assi di simmetria Rotazione
LE TRASFORMAZIONI GEOMETRICHE
 Lezione 8 3/11/2017 LE TRASFORMAZIONI GEOMETRICHE Narciso di Caravaggio I sette tipi di fregi TRASFORMARE Ogni giorno facciamo esperienza di trasformazioni nello spazio: ci si sposta nello spazio si
Lezione 8 3/11/2017 LE TRASFORMAZIONI GEOMETRICHE Narciso di Caravaggio I sette tipi di fregi TRASFORMARE Ogni giorno facciamo esperienza di trasformazioni nello spazio: ci si sposta nello spazio si
Il primo criterio di congruenza
 G Il primo criterio di congruenza Costruire un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza dei triangoli. Prima di iniziare a tracciare gli oggetti che fanno parte
G Il primo criterio di congruenza Costruire un triangolo congruente a un triangolo dato sfruttando il primo criterio di congruenza dei triangoli. Prima di iniziare a tracciare gli oggetti che fanno parte
l B 1. la velocità angolare dell asta un istante prima dell urto; 2. la velocità v 0 ; 3. l energia cinetica dissipata nell urto;
 1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
Scheda di lavoro 1. Isometrie: come ottenerle con GeoGebra
 Scheda di lavoro 1. Isometrie: come ottenerle con GeoGebra Esercizio 1. Traslazioni. Per traslare un oggetto di un vettore, bisogna prima definire l oggetto ed il vettore. Consideriamo la retta y = 2x
Scheda di lavoro 1. Isometrie: come ottenerle con GeoGebra Esercizio 1. Traslazioni. Per traslare un oggetto di un vettore, bisogna prima definire l oggetto ed il vettore. Consideriamo la retta y = 2x
Due rette si dicono INCIDENTI se hanno esattamente un punto in comune, altrimenti si dicono PARALLELE.
 Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Riepilogo di Geometria: Assioma A1 Per tutte le coppie di punti P,Q dell insieme S è assegnato un numero reale (=)> 0, che si dice distanza di P da Q e si indica don d(p,q) 1- Se i punti P,Q sono distinti
Capitolo IV - Iperbole
 Capitolo IV - Iperbole 1 Proprietà focali dell iperbole Gli argomenti che ora esponiamo sono analoghi a quelli già usati per lo studio dell ellisse (cfr. Cap. III, 1) 1 Teorema. Sia H un iperbole. Nel
Capitolo IV - Iperbole 1 Proprietà focali dell iperbole Gli argomenti che ora esponiamo sono analoghi a quelli già usati per lo studio dell ellisse (cfr. Cap. III, 1) 1 Teorema. Sia H un iperbole. Nel
Lavoro individuale: leggi attentamente il testo e completa il testo che trovi al termine del stesso. (10 )
 Testo 1: Lavoro individuale: leggi attentamente il testo e completa il testo che trovi al termine del stesso. (10 ) Lavoro di gruppo T1: discuti assieme ai tuoi compagni il significato di quanto hai letto
Testo 1: Lavoro individuale: leggi attentamente il testo e completa il testo che trovi al termine del stesso. (10 ) Lavoro di gruppo T1: discuti assieme ai tuoi compagni il significato di quanto hai letto
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
PROBLEMA 1 RISOLUZIONE. Punto 1
 PROBLEMA Data una circonerenza di centro O e raggio unitario, si prendano su di essa tre punti A, B, C, tai che AB = BC.. Si cacoi, in unzione de angoo AÔB =, a quantità: AB BC CA controando che risuti:
PROBLEMA Data una circonerenza di centro O e raggio unitario, si prendano su di essa tre punti A, B, C, tai che AB = BC.. Si cacoi, in unzione de angoo AÔB =, a quantità: AB BC CA controando che risuti:
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Nicola De Rosa, Liceo scientifico sperimentale sessione straordinaria 2012, matematicamente.it
 Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
La composizione di isometrie
 La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
Risoluzione di una trave iperstatica soggetta a cedimento vincolare col metodo delle forze
 Risouzione di una trave iperstatica soggetta a cedimento vincoare co metodo dee forze Compemento aa ezione 44/: Cedimenti vincoari e distorsioni termiche Per a trave in figura, determinare () i diagrammi
Risouzione di una trave iperstatica soggetta a cedimento vincoare co metodo dee forze Compemento aa ezione 44/: Cedimenti vincoari e distorsioni termiche Per a trave in figura, determinare () i diagrammi
Corso di Meccanica, Macchine e Impianti Termici CAPITOLO 3 DIAGRAMMA DELLE SOLLECITAZIONI INTERNE
 Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Istituto Professionae Statae per 'Industria e 'rtigianato "L.. berti" Rimini nno Scoastico 009/010 orso di Meccanica, Macchine e Impianti Termici PITOLO 3 DIGRMM DELLE SOLLEITZIONI INTERNE Prof. Matteo
Un approccio costruttivo alle trasformazioni geometriche del piano
 Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
4^C - FISICA compito n b. Determina modulo, direzione e verso del campo elettrico nel centro del quadrato.
 4^C - FISICA compito n 1-2017-18 1. Ai vertici di un quadrato di ato sono disposte quattro cariche, come +q - q 4 3 indicato in figura. a. Determina moduo, direzione e verso dea forza agente sua carica
4^C - FISICA compito n 1-2017-18 1. Ai vertici di un quadrato di ato sono disposte quattro cariche, come +q - q 4 3 indicato in figura. a. Determina moduo, direzione e verso dea forza agente sua carica
Esercitazione 4 - Forze distribuite
 Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
1 Congruenza diretta e inversa
 1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
LA CIRCONFERENZA. Preparazione. Esercizi
 IN CLASSE LA CIRCONFERENZA Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi sempre le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
IN CLASSE LA CIRCONFERENZA Preparazione Per questi esercizi con GeoGebra dovrai utilizzare i seguenti pulsanti. Leggi sempre le procedure di esecuzione nella zona in alto a destra, accanto alla barra degli
Equilibrio del corpo rigido
 Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
x -x-2 =3 x 2 x-2 lim
 G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
Soluzione della prova scritta di Fisica 1 del 10/09/2013. Figura 1: Quesito 1
 Souzione dea prova scritta di Fisica de 0/09/0 Quesito ) O M, L m v 0 Figura : Quesito Durante urto tra proiettie e sbarra non si conserva a quantità di moto a causa dee presenza dee reazioni vincoari
Souzione dea prova scritta di Fisica de 0/09/0 Quesito ) O M, L m v 0 Figura : Quesito Durante urto tra proiettie e sbarra non si conserva a quantità di moto a causa dee presenza dee reazioni vincoari
I TRIANGOLI. Geogebra l Triangoli COSTRUZIONE DEL TRIANGOLO ISOSCELE
 I TRIANGOLI COSTRUZIONE DEL TRIANGOLO ISOSCELE Come sai il triangolo isoscele ha due lati della stessa lunghezza. Costruiamo il triangolo isoscele a partire dal lato disuguale. 1. Apri il programma Geogebra
I TRIANGOLI COSTRUZIONE DEL TRIANGOLO ISOSCELE Come sai il triangolo isoscele ha due lati della stessa lunghezza. Costruiamo il triangolo isoscele a partire dal lato disuguale. 1. Apri il programma Geogebra
Costruzione di un triangolo simile a un triangolo dato
 C Costruzione di un triangolo simile a un triangolo dato Disegna un triangolo ABC e un segmento A 0 B 0. Costruisci poi un punto C 0 in modo che il triangolo A 0 B 0 C 0 sia simile ad ABC. Verifica quindi
C Costruzione di un triangolo simile a un triangolo dato Disegna un triangolo ABC e un segmento A 0 B 0. Costruisci poi un punto C 0 in modo che il triangolo A 0 B 0 C 0 sia simile ad ABC. Verifica quindi
1 Prodotto cartesiano di due insiemi 1. 5 Soluzioni degli esercizi 6
 1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
Laboratorio di informatica
 GEOMETRIA ANALITICA CON GEOGEBRA Oltre che per lo studio della geometria euclidea, come abbiamo fatto lo scorso anno, il software Geogebra (geometria + algebra) può essere utilizzato per lo studio della
GEOMETRIA ANALITICA CON GEOGEBRA Oltre che per lo studio della geometria euclidea, come abbiamo fatto lo scorso anno, il software Geogebra (geometria + algebra) può essere utilizzato per lo studio della
Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece
 Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece ha lasciato inalterato. Si chiama trasformazione geometrica un
Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece ha lasciato inalterato. Si chiama trasformazione geometrica un
Le disequazioni CAPITOLO 2 1. LE DISEQUAZIONI CON DERIVE
 CAPITOLO Le disequazioni 1. LE DISEQUAZIONI CON DERIVE Le disequazioni si risovono con o stesso comando che abbiamo imparato ad usare per risovere e equazioni, sia che si tratti di disequazioni intere
CAPITOLO Le disequazioni 1. LE DISEQUAZIONI CON DERIVE Le disequazioni si risovono con o stesso comando che abbiamo imparato ad usare per risovere e equazioni, sia che si tratti di disequazioni intere
Costruzione dell immagine prospettica di un parallelepipedo.
 Costruzione dell immagine prospettica di un parallelepipedo. La difficoltà di costruzione dell immagine prospettica di un parallelepipedo equivale, tutto sommato, a quella che si incontra nella costruzione
Costruzione dell immagine prospettica di un parallelepipedo. La difficoltà di costruzione dell immagine prospettica di un parallelepipedo equivale, tutto sommato, a quella che si incontra nella costruzione
Laboratorio di informatica
 Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
Rette, piani e figure nello spazio
 Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
1 Prodotto cartesiano di due insiemi 1. 5 Soluzioni degli esercizi 6
 1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
Compito scritto di Elettricità e Magnetismo ed Elettromagnetismo 24 Giugno 2004
 Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
Il Tetraedro regolare
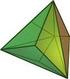 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
GUIDA ALL UTILIZZO DELLA WEBAPP "ESERCIZIARIO DI MATEMATICA"
 GUIDA ALL UTILIZZO DELLA WEBAPP "ESERCIZIARIO DI MATEMATICA" Questa appicazione web (d ora in poi WebApp) consente di seezionare numerosissimi esercizi per creare raccote personaizzate da proporre agi
GUIDA ALL UTILIZZO DELLA WEBAPP "ESERCIZIARIO DI MATEMATICA" Questa appicazione web (d ora in poi WebApp) consente di seezionare numerosissimi esercizi per creare raccote personaizzate da proporre agi
Geogebra Triangoli Simili
 TRIANGOLI SIMILI 1. Apri il programma Geogebra geometria, in basso a sinistra, un segmento orizzontale lungo 4. 3. Vai nella finestra di inserimento e digita: α 50 e premi Invio 5. Nascondi il segmento
TRIANGOLI SIMILI 1. Apri il programma Geogebra geometria, in basso a sinistra, un segmento orizzontale lungo 4. 3. Vai nella finestra di inserimento e digita: α 50 e premi Invio 5. Nascondi il segmento
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
1 L'omotetia. 2 Il teorema del rapporto dei perimetri e delle aree di due triangoli simili
 1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
Ricordiamo. 1. Disegna una retta orientata, prendi un unità di misura e posiziona i seguenti punti: 1
 Geometria Analitica Piano Cartesiano Sistema di coordinate su una retta Presa una retta r orientata, su cui sono stati fissati un origine O e un unità di misura, definiamo sistema di coordinate su una
Geometria Analitica Piano Cartesiano Sistema di coordinate su una retta Presa una retta r orientata, su cui sono stati fissati un origine O e un unità di misura, definiamo sistema di coordinate su una
OPERAZIONI SU SPAZI DI HILBERT. Nel seguito introdurremo i concetti di prodotto diretto e somma diretta di due spazi di Hilbert.
 2/7 OPERAZIONI SU SPAZI DI HILBERT 08/09 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hibert H (1) e H (2) si possono definire su di essi operazioni i cui risutato è un nuovo spazio di Hibert H che
2/7 OPERAZIONI SU SPAZI DI HILBERT 08/09 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hibert H (1) e H (2) si possono definire su di essi operazioni i cui risutato è un nuovo spazio di Hibert H che
C C B B. Fig. C4.1 Isometria.
 4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
LIMITI E CONTINUITA. 1. Sul concetto di limite
 LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
kx 1 cos 2 ax 3 kx 2 cos 2 ax 3 ak 2 (x2 1 + x2 2 ) sin 2ax 3
 1 Souzioni Tutorato 1 1/3/17) Esercizio 1 Si consideri a forza posizionae F : R 3 R 3 definita come segue: Fx) = kx 1 cos ax 3 kx cos ax 3, ak x 1 + x ) sin ax 3 dove k e a sono parametri positivi. Si
1 Souzioni Tutorato 1 1/3/17) Esercizio 1 Si consideri a forza posizionae F : R 3 R 3 definita come segue: Fx) = kx 1 cos ax 3 kx cos ax 3, ak x 1 + x ) sin ax 3 dove k e a sono parametri positivi. Si
4.3 PROBLEMI TIPO. 1. Determinare l asse di simmetria, data una figura e la sua simmetrica. (scheda 2)
 4.3 PROBLEMI TIPO Le situazioni descritte rappresentano alcuni problemi standard che riguardano lo studio della simmetria assiale. Considerata la potenzialità del software Cabrì Geometre e la possibilità
4.3 PROBLEMI TIPO Le situazioni descritte rappresentano alcuni problemi standard che riguardano lo studio della simmetria assiale. Considerata la potenzialità del software Cabrì Geometre e la possibilità
ELABORATO 1 TEORIA DEI VETTORI
 ELABOATO 1 TEOIA DEI VETTOI DATI q 1 = 5 kn/m q = 7 kn/m q 3 = 1 kn/m q 4 = 14 kn/m q 5 = 5 kn/m L = 1 m F 1 = 10 kn F = 15 kn M = -35 knm Anaisi dea parte superiore dea struttura Si assegna un sistema
ELABOATO 1 TEOIA DEI VETTOI DATI q 1 = 5 kn/m q = 7 kn/m q 3 = 1 kn/m q 4 = 14 kn/m q 5 = 5 kn/m L = 1 m F 1 = 10 kn F = 15 kn M = -35 knm Anaisi dea parte superiore dea struttura Si assegna un sistema
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Meccanica dei Manipolatori. Corso di Robotica Prof. Davide Brugali Università degli Studi di Bergamo
 Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Problemi di scelta. y ˆ 5x 800 y ˆ 1500
 A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
1) Scrivere le espressioni lagrangiane delle energie cinetica e potenziale e usarle per scrivere le equazioni di Lagrange per il sistema.
 7 si può discutere come quea di un pendoo sempice con punto di equiibrio stabie ϕ e α quando δ < e come quea di un pendoo inverso cioè con a gravità verso ato invece che verso i basso e punto di equiibrio
7 si può discutere come quea di un pendoo sempice con punto di equiibrio stabie ϕ e α quando δ < e come quea di un pendoo inverso cioè con a gravità verso ato invece che verso i basso e punto di equiibrio
