Le funzioni goniometriche
|
|
|
- Bernadetta Venturi
- 6 anni fa
- Visualizzazioni
Transcript
1 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi rettangoi 1. ANGOLI E FUNZIONI GONIOMETRICHE 1.1 Le funzioni goniometriche nei triangoi rettangoi Intraprendere o studio dea Fisica puoá essere difficotoso se non si hanno a disposizione acuni strumenti matematici, quai e equazioni, e funzioni, a rappresentazione cartesiana dee curve, i grafici; tutti questi argomenti vengono acquisiti man mano ne primo biennio, ma per poter comprendere megio acuni concetti, eá opportuno avere conoscenze reative ae reazioni che intercorrono fra i ati e gi angoi di un triangoo. Lo scopo di questo capitoo eá queo di competare queste conoscenze di base a fine di rendere piuá sempice o studio dea Fisica. Dato un triangoo ABC rettangoo in C, consideriamo 'insieme di tutti i triangoi che sono ad esso simii (in figura 1 ne sono rappresentati acuni); anche se e unghezze dei ati sono diverse nei vari triangoi, a oro simiitudine ci consente di affermare che si mantiene costante i rapporto fra i ati corrispondenti (e quindi anche queo fra e oro misure rispetto ad una stessa unitaá), cioeá: Gi esercizi di questo paragrafo sono a pag. 14 Figura 1 rapporto tra un cateto e 'ipotenusa: rapporto tra 'atro cateto e 'ipotenusa: rapporto tra i due cateti: CB AB ˆ C 0 B 0 AB 0 ˆ C 00 B 00 AB 00 ˆ ::::::::: AC AB ˆ AC 0 AC 00 ˆ ˆ ::::::::: AB 0 AB 00 CB AC ˆ C 0 B 0 AC 0 ˆ C 00 B 00 AC 00 ˆ ::::::::: Queo che caratterizza questi triangoi eá quindi 'ampiezza degi angoi, che eá a stessa in ciascuno di essi. Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE 1
2 Si puoá aora pensare di dare un nome a tai rapporti in modo che sia evidente che essi non dipendono da particoare triangoo sceto, ma soo dae ampiezze degi angoi acuti di uno quasiasi di essi. Consideriamo aora un triangoo ABC rettangoo in C e chiamiamo con 'angoo acuto di vertice A (figura ); diamo e seguenti definizioni: Figura n seno de'angoo, e scriviamo sin, i rapporto fra i cateto opposto ad e 'ipotenusa: sin ˆ BC AB n coseno de'angoo, e scriviamo cos, i rapporto fra i cateto adiacente ad e 'ipotenusa: cos ˆ AC AB n tangente de'angoo, e scriviamo tan, i rapporto fra i cateto opposto ad ed i cateto adiacente: tan ˆ BC AC. Per esempio, se AC ˆ 6, BC ˆ 8 e di conseguenza AB ˆ 10, si ha che: sin ˆ BC AB ˆ 8 10 ˆ 4 cos ˆ AC AB ˆ 6 10 ˆ tan ˆ BC AC ˆ 8 6 ˆ 4 I vaori di sin, cos e tan dipendono sostanziamente da'ampiezza de'angoo, sono cioeá funzioni di, e si dicono percioá funzioni goniometriche de'angoo. Osserviamo subito che, poicheâ in un triangoo rettangoo ciascun cateto eá minore de'ipotenusa, i rapporti BC AB mentre i rapporto BC AC e AC AB sono numeri positivi minori di 1,, essendo i rapporto fra i cateti, puoá essere sia minore che maggiore o anche uguae a 1 e non eá soggetto a imitazioni. Dunque, per quaunque angoo acuto : sin ecos sono numeri positivi minori di 1 tan eá un numero reae positivo quasiasi. Le funzioni goniometriche di un angoo acuto non sono vaori indipendenti uno da'atro ma sono egati da reazioni precise che discendono proprio daa oro definizione. Osserviamo infatti che: i rapporto BC esprime sostanziamente a misura de segmento BC quando si AB eá sceto AB come unitaá di misura; a stessa cosa si puoá dire per i rapporto AC AB. Aora, se appichiamo i teorema di Pitagora a triangoo ABC abbiamo che: BC AC ˆ AB BC cioeá AC ˆ 1 AB AB ed essendo BC AC ˆ sin e ˆ cos, otteniamo a prima reazione fondamentae che ega i seno e i coseno di uno stesso angoo AB AB : LE RELAZIONI FONDAMENTALI sin cos ˆ 1 Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
3 i rapporto BC AC AC AB : puoá essere visto come i quoziente dei rapporti BC AB e BC AC ˆ BC AB : AC AB. Ma BC BC AC ˆ tan, ˆ sin, ˆ cos, quindi una seconda reazione AC AB AB fondamentae che ega queste tre funzioni eá a seguente: tan ˆ sin cos Queste due reazioni consentono, nota una dee funzioni goniometriche, di trovare e atre. Per esempio, se sin ˆ, aora: da sin cos ˆ 1 ricaviamo che cos ˆ da tan ˆ sin cos ESEMPI ricaviamo che 1 sin ˆ tan ˆ p ˆ p 1. In un triangoo rettangoo i cateto AC misura 0cm, 'ipotenusa AB misura 0cm (figura ). Cacoiamo i vaori dee funzioni goniometriche degi angoi acuti di questo triangoo. Troviamo per prima cosa 'atro cateto de triangoo appicando i teorema di Pitagora: p BC ˆ 0 0 ˆ 40 Appicando e definizioni date si ha subito che: sin ˆ 40 0 ˆ 4 sin ˆ 0 0 ˆ cos ˆ 0 0 ˆ cos ˆ 40 0 ˆ 4 tan ˆ 40 0 ˆ 4 tan ˆ 0 40 ˆ 4 Osserviamo che, in questo caso, sin ˆ cos e sin ˆ cos, mentre tan ˆ 1 ; queste reazioni non sono casuai, ma dipendono da tan fatto che gi angoi e sono compementari. r 1 4 ˆ 9 Figura Figura 4. Cacoiamo i seno, i coseno e a tangente de'angoo di 4 : Per trovare i vaori richiesti ci riferiamo ad un triangoo rettangoo isoscee che ha gi angoi acuti di 4 (figura 4). Quaunque sia a misura ` p dei cateti, quea de'ipotenusa eá `. Aora considerando 'angoo acuto A b otteniamo: sin 4 ˆ BC AB ˆ ` ˆ cos 4 ˆ AC ` AB ˆ ` ˆ tan 4 ˆ BC ` AC ˆ ` ` ˆ 1 Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE
4 . Procedendo in modo anaogo a queo de'esempio precedente, cacoiamo i vaori de seno, de coseno e dea tangente degi angoi di 0 edi60. Conviene far riferimento ad un triangoo rettangoo i cui angoi acuti misurano 0 e60. Tenendo presente che, posto AB ˆ `, si ha che AC ˆ ` e BC ˆ 1 ` (figura ), si trova subito che: sin 0 ˆ BC AB ˆ cos 0 ˆ AC AB ˆ tan 0 ˆ CB AC ˆ 1 ` ` ˆ 1 ` ˆ ` 1 ` ˆ ` sin 60 ˆ AC AB ˆ cos 60 ˆ BC AB ˆ tan 60 ˆ AC CB ˆ ` ˆ ` 1 ` ` ` 1 ` ˆ 1 ˆ p Figura 1. Le funzioni goniometriche e a circonferenza goniometrica Le funzioni seno, coseno e tangente sono state definite soo per gi angoi acuti di un triangoo rettangoo; viene peroá spontaneo chiedersi se non sia possibie definire anaoghe funzioni anche per angoi che non sono acuti. Consideriamo aora a circonferenza che ha centro ne vertice A de triangoo e raggio uguae aa sua ipotenusa e riferiamo questa circonferenza ad un sistema di assi cartesiani ortogonai che ha centro in A e 'asse dee ascisse coincidente con a retta de cateto AC (figura 6). Se fissiamo come unitaá di misura i raggio dea circonferenza, poniamo cioeá AB ˆ 1, i seno de'angoo eá proprio a misura de cateto CB, mentre i coseno di eá a misura di AC. Aora i seno e i coseno di un angoo si possono anche interpretare rispettivamente come 'ordinata e 'ascissa de punto B in cui a semiretta che definisce 'angoo insieme aa semiretta positiva Ox dee ascisse interseca a circonferenza: x B ˆ cos y B ˆ sin Questa considerazione ci consente di definire i seno e i coseno di un angoo quasiasi riferendoci non piuá a un triangoo rettangoo ma a una circonferenza. Consideriamo dunque una circonferenza con centro ne'origine O di un sistema di assi cartesiani ortogonai e raggio unitario; chiameremo goniometrica questa circonferenza. Una semiretta uscente da O incontra a circonferenza in A e definisce, insieme aa semiretta positiva Ox, un angoo. Si conviene di dare misura positiva agi angoi nei quai a semiretta OA segue in senso antiorario a semiretta Ox, misura negativa agi angoi nei quai a semiretta OA segue in senso orario a semiretta Ox (figura 7). Chiamiamo (figura 8): n seno de'angoo 'ordinata de punto A: n coseno de'angoo 'ascissa de punto A: sin ˆ y A cos ˆ x A Figura 6 Figura 7 angoo positivo, angoo negativo Figura 8 4 Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
5 Ne consegue che i seno ed i coseno di un angoo quasiasi sono numeri reai compresi fra 1 e 1 e in particoare: i seno di un angoo a cui ampiezza eá compresa fra 0 e 180 eá un numero positivo (figura 9a): 0 <<180 ) 0 < sin 1 i seno di un angoo a cui ampiezza eá compresa fra 180 e 60 eá un numero negativo (figura 9b): 180 <<60 ) 1 sin <0 e si ha poi che (figura 9c): sin 0 ˆ 0 sin 90 ˆ 1 sin 180 ˆ 0 sin 70 ˆ 1 sin 60 ˆ 0 i coseno di un angoo a cui ampiezza eá compresa fra 0 e90 oppure fra 70 e 60 eá un numero positivo (figura 10a): 0 <<90 _ 70 <<60 ) 0 < cos <1 i coseno di un angoo a cui ampiezza eá compresa fra 90 e 70 eá un numero negativo (figura 10b): 90 <<70 ) 1 cos <0 e si ha poi che (figura 10c): cos 0 ˆ 1 cos 90 ˆ 0 cos 180 ˆ 1 cos 70 ˆ 0 cos 60 ˆ 1 Figura 9 a. b. Figura 10 c. Figura 11 a. b. c. Anche a tangente di un angoo puoá essere definita per un angoo quasiasi mediante a circonferenza goniometrica; tracciata a retta r tangente aa circonferenza ne punto di coordinate (1, 0), chiamiamo (figura 11): n tangente di 'ordinata de punto B di intersezione dea retta r con a semiretta OA: tan ˆ y B Anche in questo caso, a definizione precedente come rapporto fra i cateti di un triangoo rettangoo tan ˆ HB eá rispettata percheâ i cateto OH eá i OH raggio di misura unitaria; questa definizione eá peroá piuá ampia percheâ ci permette di definire a tangente anche di angoi non acuti. Reativamente a vaore di tan possiamo dire che: a tangente di un angoo a cui ampiezza eá compresa fra 0 e90 eá un numero positivo (figura 1a): 0 <<90 ) tan >0 a tangente di un angoo a cui ampiezza eá compresa fra 90 e 180 eá un Figura 1a Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE
6 Figura 1 b. c. d. e. numero negativo (figura 1b: occorre proungare i ato de'angoo fino ad incontrare a retta r): 90 <<180 ) tan <0 a tangente di un angoo a cui ampiezza eá compresa fra 180 e 70 eá un numero positivo (figura 1c: anche in questo caso occorre proungare i ato de'angoo fino ad incontrare a retta r ): 180 <<70 ) tan >0 a tangente di un angoo a cui ampiezza eá compresa fra 70 e 60 eá un numero negativo (figura 1d ): 70 <<60 ) tan <0 In particoare (figura 1e): tan 0 ˆ tan 180 ˆ tan 60 ˆ 0 tan 90 e tan 70 non esistono percheâ a retta r e i secondo ato de'angoo sono paraei. Le reazioni fondamentai sono ancora vaide percheâ: riferendoci ancora aa figura 8: Figura 1 KA OK ˆ OA cioeá sin cos ˆ 1 riferendoci aa figura 1 nea quae i triangoi OAK e OBH sono simii: HB OH ˆ KA OK cioeá tan ˆ sin cos VERIFICA DI COMPRENSIONE 1. Ne triangoo ABC in figura: a. sin ABC d ˆ 4 b. cos ACB d ˆ c. tan ABC d ˆ 4 d. sin ACB d ˆ 4 V V V V F F F F. I seno di un angoo acuto eá uguae a 1, i coseno deo stesso angoo eá uguae a: 1 a. b. c. d. nessuno dei precedenti vaori 4 6 Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
7 . Indica quai dee seguenti reazioni reative a un angoo sono possibii: a. sin ˆ b. cos ˆ 10 1 c. tan ˆ 8 d. cos ˆ e. sin ˆ 1 f. tan ˆ 1 8 g. cos ˆ 7 8 h. sin ˆ 1 1. Le funzioni goniometriche e a cacoatrice Negi esempi e precedenti abbiamo visto come cacoare e funzioni goniometriche degi angoi di 0,4,60 mediante considerazioni geometriche. Purtroppo non eá possibie cacoare i vaore de seno, de coseno o dea tangente di angoi di ampiezze diverse se non in casi moto particoari; eá peroá possibie determinare un vaore approssimato dee funzioni goniometriche di un quasiasi angoo usando una cacoatrice scientifica. Ogni cacoatrice ha dee procedure di cacoo proprie ed eá per questo consigiabie consutare i ibretto dee istruzioni; nea maggior parte dei casi, tuttavia, a procedura eá simie a quea che descriviamo di seguito. Dopo aver acceso a tua cacoatrice accertati che a modaitaá di misurazione degi angoi sia in gradi: su dispay deve comparire a dicitura DEG (DEG sta per degree). Vediamo come procedere attraverso degi esempi. Da'angoo a vaore dee funzioni goniometriche n Vogiamo cacoare i vaore di sin 8 1. Premi i tasto sin. Digita 'ampiezza in gradi de'angoo: 8. Premi i tasto ˆ Ottieni che sin 8 ˆ 0,616614:::::: E' possibie che in acuni modei i passi 1 e debbano essere invertiti, che cioeá si debba prima digitare 'ampiezza de'angoo e poi premere i tasto dea funzione goniometrica. n Vogiamo cacoare i vaore di cos 1 1. Premi i tasto cos. Digita 'ampiezza in gradi de'angoo: 1. Premi i tasto ˆ Ottieni che cos 1 ˆ 0, :::::: n Vogiamo cacoare i vaore di tan Premi i tasto tan. Digita 'ampiezza in gradi de'angoo: 109. Premi i tasto ˆ Ottieni che tan 109 ˆ,904108:::::: n Vogiamo cacoare i vaore di sin 1. Premi i tasto sin. Digita 'ampiezza in gradi de'angoo:. Premi i tasto ˆ Ottieni che sin ˆ 0,4618::::::::::::: Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE 7
8 Quando 'angoo eá espresso in gradi, primi e secondi occorre prima trasformare a misura in soi gradi. In genere a conversione avviene in modo automatico mediante a pressione di un particoare tasto funzione; se a tua cacoatrice non dovesse possedere questo tasto dovrai eseguire i cacoo impostandoo in questo modo: ˆ ˆ 0,88::::: 600 Vediamo anche qui acuni esempi. n Cacoiamo i vaore di sin Premi i tasto sin. Trasforma 'angoo in gradi digitando separatamente e cifre dei gradi, dei primi e dei secondi intercaando i tasto funzione contrassegnato con i simboo 0 00 : Premi i tasto ˆ Si ottiene che sin ˆ 0, :::::: In acune cacoatrici i tasto 0 00 eá sostituito da tasto funzione DMS n Cacoiamo i vaore di cos Premi i tasto cos. Trasforma 'angoo in gradi: Premi i tasto ˆ Si ottiene che cos ˆ 0,96904:::::::::::: Dai vaori dee funzioni goniometriche a'angoo Questo probema eá 'inverso de precedente, vae a dire che si conosce i vaore di una funzione goniometrica e si vuoe sapere qua eá 'ampiezza de'angoo; per esempio se sin ˆ 0,, quanto vae? Occorre precisare che a risposta data daa cacoatrice si riferisce ad uno dei possibii angoi i cui seno vae 0,; ne'intervao che va da 0 a 60 ci sono infatti due angoi che rispondono a questa caratteristica: 'angoo acuto ed i suo suppementare 180 (figura 14). A seconda de probema che si sta affrontando si potraá decidere a quae angoo ci si deve riferire. Vediamo acuni esempi. n Cacoare 'angoo acuto tae che sin ˆ 0,. 1. Premere in successione i tasti funzione INV e sin In mote cacoatrici i tasto INV eá sostituito da SHIFT oppure -nd. Digitare i vaore dea funzione goniometrica usando i punto decimae: 0.. Premere ˆ I vaore trovato, cioeá 14,477119, esprime a misura de'angoo in gradi; voendo avere i vaore in gradi, primi e secondi: premere in successione i tasti funzione INV e Si ottiene cosõá che un vaore approssimato di eá Figura 14 L'angoo ottuso eá 'angoo di ampiezza cioeá 'angoo di In acuni modei si deve invertire 'ordine dei tasti digitando prima i vaore dea funzione goniometrica; reativamente a nostro esempio: 0, INV sin 8 Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
9 n Cacoare 'angoo acuto tae che cos ˆ 0,1. 1. Premere in successione i tasti funzione INV e cos. Digitare i vaore dea funzione goniometrica: 0.1. Premere ˆ 4. Premere in successione i tasti funzione INV e 0 00 Si ottiene cosõá che un vaore approssimato di eá n Cacoare 'angoo acuto tae che tan ˆ 6,. 1. Premere in successione i tasti funzione INV e tan. Digitare i vaore dea funzione goniometrica: 6:. Premere ˆ 4. Premere in successione i tasti funzione INV e 0 00 Si ottiene cosõá che un vaore approssimato di eá LA RISOLUZIONE DEI TRIANGOLI RETTANGOLI Le reazioni che abbiamo stabiito fra i ati di un triangoo rettangoo che ci hanno permesso di definire e funzioni goniometriche seno, coseno e tangente degi angoi acuti possono essere riscritte in modo da mettere in evidenza e unghezze de ati; riferendoci a triangoo in figura 1 possiamo dire che: Gi esercizi di questo paragrafo sono a pag. 16 Figura 1 poicheâ sin ˆ BC AB aora BC ˆ AB sin poicheâ cos ˆ AC AB aora AC ˆ AB cos poicheâ tan ˆ BC AC aora BC ˆ AC tan Queste tre reazioni possono essere cosõá enunciate in forma generae. In ogni triangoo rettangoo a misura di un cateto eá uguae: n a prodotto de'ipotenusa per i seno de'angoo acuto opposto a cateto stesso n a prodotto de'ipotenusa per i coseno de'angoo acuto adiacente a cateto stesso n a prodotto de'atro cateto per a tangente de'angoo opposto a cateto stesso. I TEOREMI SUI TRIANGOLI RETTANGOLI Usando queste tre reazioni eá possibie risovere moti probemi che riguardano i triangoi; negi esempi che seguono ti proponiamo acuni casi significativi. Conveniamo di approssimare e unghezze dei segmenti a meno di 0,01, cioeâ con due cifre decimai. ESEMPI 1. In un triangoo ABC, rettangoo in C, 'ipotenusa AB eá unga 1cm e 'angoo di vertice B ha ampiezza 6. Vogiamo risovere i triangoo. Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE 9
10 Risovere i triangoo significa determinare e unghezze dei suoi ati e e ampiezze dei suoi angoi. Poiche 'angoo C b eá retto, ricaviamo subito che (figura 16) ba ˆ 90 6 ˆ 4 : Per determinare e misure dei cateti (in centimetri) usiamo e prime due reazioni: AC ˆ ipotenusa seno de'angoo opposto ˆ AB sin 6 ˆ ˆ 1 0,8778::::: ˆ 8,8 CB ˆ ipotenusa coseno de'angoo adiacente ˆ AB cos 6 ˆ ˆ 1 0,80901::::: ˆ 1,14 Figura 16. Di un triangoo rettangoo sono note a unghezza di un cateto, 8,4cm, e 'ampiezza de'angoo acuto opposto, 46 '18''. Vogiamo risovere i triangoo. Con riferimento aa figura 17, poniamo AC ˆ 8,40 e ˆ ; di conseguenza ˆ ˆ Per trovare a misura (in cm) de cateto BC usiamo a terza reazione: BC ˆ AC tan ˆ 8,40 tan ˆ 7,0 Per trovare a misura (in cm) de'ipotenusa possiamo usare indifferentemente: q p ± i teorema di Pitagora: AB ˆ AC BC ˆ 8,40 7,0 ˆ 9,0 ± a prima reazione: AC ˆ AB sin! AB ˆ AC sin ˆ 9,0 I secondo metodo eá di soito preferibie percheâ usa i dati de probema e non introduce atri errori di arrotondamento dei risutati.. Di un triangoo rettangoo sono note e misure in cm di due cateti: b ˆ 1,40, c ˆ 9,60. Vogiamo risovere i triangoo e determinare a misura de'atezza reativa a'ipotenusa. Con i teorema di Pitagora possiamo subito determinare a misura de'ipotenusa: p a ˆ b c ˆ 1,40 9,60 1,68 Daa terza reazione ricaviamo poi che (figura 18): tan ˆ b c cioe tan ˆ da cui ˆ Possiamo ora cacoare ˆ ˆ Per trovare 'atezza reativa a'ipotenusa, basta appicare i primo teorema a uno dei due triangoi rettangoi che si ottengono tracciando 'atezza; reativamente a triangoo in coore arancio nea figura, dove c rappresenta a misura de'ipotenusa, si ha che h ˆ c sin ˆ 9,60 sin ˆ 7,9 (cm) Figura 17 Figura Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
11 VERIFICA DI COMPRENSIONE 1. De triangoo in figura, ottenuto mediante 'accostamento di due triangoi rettangoi, si conoscono gi eementi indicati. Cacoa quanto indicato di seguito: BH ˆ ::::: AH ˆ ::::: HC ˆ ::::: AC ˆ :::::. De trapezio ABCD si hanno e informazioni indicate in figura, dove e misure dei segmenti sono espresse mediante a stessa unitaá. Considera e seguenti uguagianze: BC ˆ,4 DC ˆ 8,8 AD ˆ 1,17 Di esse sono vere: a. tutte e tre b. soo a c. tutte tranne a d. nessuna percheâ i dati sono insufficienti per determinare e misure dei ati de trapezio. Souzioni verifica di comprensione pag. 6 1 a. F, b. V, c. V, d. V; c.; b., c., e., f., g., h. pag. 11 p 1 BH ˆ AH ˆ 4; HC ˆ 4 ; AC ˆ 8; c. Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE 11
12 I concetti e e regoe Le funzioni goniometriche Tutti i triangoi rettangoi i cui angoi hanno e stesse ampiezze hanno i ati proporzionai e i vaori dei rapporti fra cateti e ipotenusa e fra cateti dipendono dagi angoi acuti de triangoo. Si possono quindi introdurre acune funzioni reative a questi angoi, dette funzioni goniometriche, che, con riferimento aa figura a ato, sono cosõá definite: n BC AB ˆ sin n AC AB ˆ cos n BC AC ˆ tan Le funzioni seno, coseno e tangente di un angoo si possono definire per quasiasi angoo, non necessariamente acuto. Considerata a circonferenza avente centro ne'origine di un sistema di assi cartesiani ortogonai e raggio 1 (circonferenza goniometrica): indicato con A i punto di intersezione di tae circonferenza con a semiretta di origine O che, insieme a semiasse positivo dee ascisse, deimita 'angoo indicato con B i punto di intersezione dea retta tangente aa circonferenza ne punto H 1, 0 con a semiretta OA si definisce: n sin 'ordinata de punto A n cos 'ascissa de punto A n tan 'ordinata de punto B In conseguenza dea definizione data si verifica che: a funzione seno e a funzione coseno assumono vaori compresi tra 1 e1 a funzione tangente puoá assumere quasiasi vaore reae, ma non eá definita per angoi di 90 e 70. Le reazioni fondamentai e i vaori dee funzioni goniometriche Tra e funzioni goniometriche di uno stesso angoo sussistono e seguenti reazioni: sin cos ˆ 1 e tan ˆ sin cos I vaori dee funzioni goniometriche di un angoo si possono determinare in modo approssimato con una cacoatrice scientifica. Soo di acuni angoi particoari si possono dare i vaori esatti e si ha che: sin 4 ˆ cos 4 ˆ tan 4 ˆ 1 sin 0 ˆ 1 cos 0 ˆ tan 0 ˆ sin 60 ˆ cos 60 ˆ 1 tan 60 ˆ p 1 Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE Q Re Fraschini - Grazzi, Atas SpA
13 La risouzione dei triangoi rettangoi Risovere un triangoo di cui sono noti acuni eementi, fra i quai ameno uno deve essere un ato, significa trovare e misure di tutti gi atri ati e angoi. Le reazioni fra ati e angoi di un triangoo rettangoo sono espresse da acuni teoremi che derivano direttamente dae definizioni di seno, coseno e tangente di un angoo acuto. In ogni triangoo rettangoo: un cateto eá uguae a prodotto de'ipotenusa per i seno de'angoo acuto ad esso opposto un cateto eá uguae a prodotto de'ipotenusa per i coseno de'angoo acuto ad esso adiacente un cateto eá uguae a prodotto de'atro cateto per a tangente de'angoo acuto opposto a cateto stesso. Con riferimanto a triangoo in figura: n BC ˆ AB sin n BC ˆ AB cos n BC ˆ AC tan Q Re Fraschini - Grazzi, Atas SpA Tema 1 - Cap. 1: LE FUNZIONI GONIOMETRICHE 1
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
Nicola De Rosa, Liceo scientifico sperimentale sessione straordinaria 2012, matematicamente.it
 Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
Le funzioni goniometriche e i triangoli
 CAPITOLO 1 Le funzioni goniometriche e i triangoi 1. LE FUNZIONI GONIOMETRICHE CON GEOGEBRA Per megio comprendere come vengono generati i grafici dee funzioni goniometriche fondamentai eseguiamo una particoare
CAPITOLO 1 Le funzioni goniometriche e i triangoi 1. LE FUNZIONI GONIOMETRICHE CON GEOGEBRA Per megio comprendere come vengono generati i grafici dee funzioni goniometriche fondamentai eseguiamo una particoare
Risoluzione dei triangoli rettangoli
 Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
La scala logaritmica
 La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
Le equazioni e le disequazioni lineari
 MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
Le disequazioni CAPITOLO 2 1. LE DISEQUAZIONI CON DERIVE
 CAPITOLO Le disequazioni 1. LE DISEQUAZIONI CON DERIVE Le disequazioni si risovono con o stesso comando che abbiamo imparato ad usare per risovere e equazioni, sia che si tratti di disequazioni intere
CAPITOLO Le disequazioni 1. LE DISEQUAZIONI CON DERIVE Le disequazioni si risovono con o stesso comando che abbiamo imparato ad usare per risovere e equazioni, sia che si tratti di disequazioni intere
Triangolo rettangolo
 Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Copyright Esselibri S.p.A.
 .2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
.2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
I vettori CAPITOLO 2 1. I VETTORI CON GEOGEBRA. Ci sono due comandi selezionabili dai menu di disegno che operano sui vettori:
 CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
Cap 1. LA CIRCONFERENZA
 Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Funzioni goniometriche
 Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Trigonometria sferica
 Trigonometria sferica Obiettivi conoscere gi oggetti dea geometria dea sfera conoscere e saper appicare i teoremi di trigonometria sferica risovere triangoi sferici appicare i concetti dea trigonometria
Trigonometria sferica Obiettivi conoscere gi oggetti dea geometria dea sfera conoscere e saper appicare i teoremi di trigonometria sferica risovere triangoi sferici appicare i concetti dea trigonometria
Il Tetraedro regolare
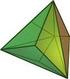 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
x -x-2 =3 x 2 x-2 lim
 G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
Repetitorium trigonometriae - per immagini
 Repetitorium trigonometriae - per immagini Regole di base Ipotenusa Opposto Adiacente Tenendo a mente la seguente nomenclatura di un triangolo rettangolo si ha: sin = Opposto Ipotenusa cos = Adiacente
Repetitorium trigonometriae - per immagini Regole di base Ipotenusa Opposto Adiacente Tenendo a mente la seguente nomenclatura di un triangolo rettangolo si ha: sin = Opposto Ipotenusa cos = Adiacente
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
APPUNTI DI GONIOMETRIA
 APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
Applicazioni dei teoremi di Pitagora ed Euclide
 Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
CORSO DI TECNOLOGIE E TECNICHE DI RAPPRESENTAZIONI GRAFICHE
 CORSO DI TECNOLOGIE E TECNICHE DI RARESENTAZIONI GRAFICHE ER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda ARTE RIMA Disegno del rilievo Unità Didattica:
CORSO DI TECNOLOGIE E TECNICHE DI RARESENTAZIONI GRAFICHE ER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda ARTE RIMA Disegno del rilievo Unità Didattica:
I poligoni e la circonferenza
 CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
I grafici derivati e la periodicità
 A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
Luoghi di punti e funzioni non lineari
 CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
CAPITOLO 3 Luoghi di punti e funzioni non ineari 1. LE FUNZIONI NON LINEARI CON DERIVE Per costruire i grafico di una paraboa o di un'iperboe si usa a stessa procedura usata per a retta: si scrive 'equazione
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
UNITÀ DIDATTICA 3 FUNZIONI GONIOMETRICHE
 UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
Nel caso particolare in cui il vertice si trovi nell'origine, la parabola assume la forma: y ˆ ax 2.
 LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
LIMITI E CONTINUITA. 1. Sul concetto di limite
 LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
TRIGONOMETRIA. Un angolo si misura in gradi. Un grado è la novantesima parte di un angolo retto.
 TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
TRIGONOMETRIA E COORDINATE
 Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Trigonometria. Parte della matematica che si occupa di studiare le relazioni tra i lati e gli angoli di un triangolo
 Trigonometria Parte della matematica che si occupa di studiare le relazioni tra i lati e gli angoli di un triangolo I triangoli rettangoli Premessa: ricordiamo le definizioni di seno e coseno di un angolo
Trigonometria Parte della matematica che si occupa di studiare le relazioni tra i lati e gli angoli di un triangolo I triangoli rettangoli Premessa: ricordiamo le definizioni di seno e coseno di un angolo
Parallelismo e perpendicolaritaá nel piano
 CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
trasformazione grafico Cosa si deve fare Esempio goniometrico
 trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
Angoli e loro misure
 Angoli e loro misure R s Unità di misura: gradi, minuti, secondi 1 o =60' 1'=60'' Es: 35 o 41'1'' radianti α(rad) s R Angolo giro = 360 o = R/R = rad R=1 arco rad Es.: angolo retto R Arco 4 : se R=1 π
Angoli e loro misure R s Unità di misura: gradi, minuti, secondi 1 o =60' 1'=60'' Es: 35 o 41'1'' radianti α(rad) s R Angolo giro = 360 o = R/R = rad R=1 arco rad Es.: angolo retto R Arco 4 : se R=1 π
Trigonometria angoli e misure
 Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
Figure piane. Due figure sono congruenti se sovrapposte coincidono perfettamente. figure a contorno mistilineo
 Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
Esercitazione 7 del corso di Statistica 2
 Esercitazione 7 de corso di Statistica Dott.ssa Paoa Costantini 0 Marzo 009 Esercizio a distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee, in grammi, prodotti da un
Esercitazione 7 de corso di Statistica Dott.ssa Paoa Costantini 0 Marzo 009 Esercizio a distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee, in grammi, prodotti da un
Funzioni goniometriche di angoli notevoli
 Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
Il piano cartesiano e la retta
 CAPITOLO 1 I piano cartesiano e a retta 1. IL PIANO CARTESIANO E LA RETTA CON DERIVE 1.1 Segmenti e punti Abbiamo visto piuá vote come si costruisce una funzione di assegnamento con Derive; possiamo usare
CAPITOLO 1 I piano cartesiano e a retta 1. IL PIANO CARTESIANO E LA RETTA CON DERIVE 1.1 Segmenti e punti Abbiamo visto piuá vote come si costruisce una funzione di assegnamento con Derive; possiamo usare
DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO
 Geogebra DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO 1. Apri il programma Geogebra, assicurati che siano visualizzati gli assi e individua il punto A (0, 0). a. Dove si trova il punto A? b. Individua il
Geogebra DISTANZA TRA DUE PUNTI NEL PIANO CARTESIANO 1. Apri il programma Geogebra, assicurati che siano visualizzati gli assi e individua il punto A (0, 0). a. Dove si trova il punto A? b. Individua il
IL PENDOLO REVERSIBILE DI KATER
 IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
Le grandezze fisiche scalari sono completamente definite da un numero e da una unità di misura.
 UNITÀ 3 LE GRANDEZZE FISICHE VETTORIALI E I VETTORI 1. Grandezze fisiche scalari e vettoriali. 2. I vettori. 3. Le operazioni con i vettori. 4. Addizione e sottrazione di vettori. 5. Prodotto di un numero
UNITÀ 3 LE GRANDEZZE FISICHE VETTORIALI E I VETTORI 1. Grandezze fisiche scalari e vettoriali. 2. I vettori. 3. Le operazioni con i vettori. 4. Addizione e sottrazione di vettori. 5. Prodotto di un numero
Problemi di scelta. y ˆ 5x 800 y ˆ 1500
 A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Equilibrio del corpo rigido
 Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Esercitazione 7 del corso di Statistica 2
 Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Rette, piani e figure nello spazio
 CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
CAPITOLO Rette, piani e figure neo spazio. LA GEOMETRIA DELLO SPAZIO CON CABRI 3D Cabri 3D eá un software che, consentendo una facie costruzione di soidi, piani e figure deo spazio in genere, permette
La fattorizzazione dei polinomi
 La fattorizzazione dei poinomi Obiettivi scomporre un poinomio mediante: - raccogimenti a fattor comune - riconoscimenti di prodotti notevoi - a regoa de trinomio caratteristico - 'individuazione dei divisori
La fattorizzazione dei poinomi Obiettivi scomporre un poinomio mediante: - raccogimenti a fattor comune - riconoscimenti di prodotti notevoi - a regoa de trinomio caratteristico - 'individuazione dei divisori
Esercizi sulle rette nello spazio
 1 Esercizi sulle rette nello spazio 1) Sono dati quattro punti non complanari, tre di essi possono essere allineati? 2) Sono dati quattro punti non complanari, quanti piani generano? 3) Quante coppie di
1 Esercizi sulle rette nello spazio 1) Sono dati quattro punti non complanari, tre di essi possono essere allineati? 2) Sono dati quattro punti non complanari, quanti piani generano? 3) Quante coppie di
La retta nel piano cartesiano
 La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
L1 L2 L3 L4 L5 L6. Esercizio. [1] ha infinite soluzioni [2] non ha soluzioni [3] ha esattamente due soluzioni
![L1 L2 L3 L4 L5 L6. Esercizio. [1] ha infinite soluzioni [2] non ha soluzioni [3] ha esattamente due soluzioni L1 L2 L3 L4 L5 L6. Esercizio. [1] ha infinite soluzioni [2] non ha soluzioni [3] ha esattamente due soluzioni](/thumbs/63/50079242.jpg) La disequazione x x + 1 0 [1] ha infinite soluzioni [] non ha soluzioni [3] ha esattamente due soluzioni [4] nessuna delle precedenti possibilità è corretta Introduciamo la funzione f : R R definita da
La disequazione x x + 1 0 [1] ha infinite soluzioni [] non ha soluzioni [3] ha esattamente due soluzioni [4] nessuna delle precedenti possibilità è corretta Introduciamo la funzione f : R R definita da
Risoluzione del problema 2
 Esame di Stato Liceo Scientifico Prova di Matematica corso sperimentale PNI - giugno 007 Soluzione del PROBLEMA a cura di Luigi Tomasi (luigitomasi@liberoit) Risoluzione del problema Punto ) Consideriamo
Esame di Stato Liceo Scientifico Prova di Matematica corso sperimentale PNI - giugno 007 Soluzione del PROBLEMA a cura di Luigi Tomasi (luigitomasi@liberoit) Risoluzione del problema Punto ) Consideriamo
La probabilitaá CAPITOLO. Obiettivi MATEMATICA E REALTAÁ. definire e calcolare un valore di probabilitaá
 CAPITOLO La probabiitaá Obiettivi definire e cacoare un vaore di probabiitaá appicare i teoremi su cacoo dee probabiitaá : ± probabiitaá contraria ± probabiitaá totae ± probabiitaá composta MATEMATICA
CAPITOLO La probabiitaá Obiettivi definire e cacoare un vaore di probabiitaá appicare i teoremi su cacoo dee probabiitaá : ± probabiitaá contraria ± probabiitaá totae ± probabiitaá composta MATEMATICA
Grafici di particolari funzioni lineari
 A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
A Grafici di particoari funzioni ineari Vogiamo tracciare i grafico dea funzione y ˆ jxj. x quando x 0 Sappiamo che jxj significa x quando x < 0 Possiamo aora riscrivere 'equazione di questa funzione in
Alcune nozioni di trigonometria 1
 Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Rette, piani e figure nello spazio
 Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Meccanica dei Manipolatori. Corso di Robotica Prof. Davide Brugali Università degli Studi di Bergamo
 Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
CONOSCENZE 1. gli elementi di un triangolo 2. la classificazione dei triangoli. 3. il teorema dell'angolo esterno. 4. i punti notevoli di un triangolo
 GEOMETRIA I TRIANGOLI PREREQUISITI l conoscere le caratteristiche del sistema di numerazione decimale l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti geometrici
GEOMETRIA I TRIANGOLI PREREQUISITI l conoscere le caratteristiche del sistema di numerazione decimale l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti geometrici
Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa.
 IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
LE FUNZIONI GONIOMETRICHE
 LE FUNZIONI GONIOMETRICHE La misura degli angoli Si chiama angolo la porzione di piano racchiusa tra due semirette. Angolo convesso Angolo concavo Le unità di misura degli angoli sono: il grado sessagesimale
LE FUNZIONI GONIOMETRICHE La misura degli angoli Si chiama angolo la porzione di piano racchiusa tra due semirette. Angolo convesso Angolo concavo Le unità di misura degli angoli sono: il grado sessagesimale
CAP.2:ITRIANGOLI GEOMETRIA 1 - AREA 3 I TRIANGOLI E LA LORO CLASSIFICAZIONE. richiami della teoria COMPRENSIONE DELLA TEORIA
 GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
LE FUNZIONI GONIOMETRICHE: SENO, COSENO E TANGENTE
 LE FUNZIONI GONIOMETRICHE: SENO, COSENO E TANGENTE 1. LE FUNZIONI SENO E COSENO LE FUNZIONI SENO, COSENO E TANGENTE DEFINIZIONE Seno e coseno Consideriamo la circonferenza goniometrica e un angolo orientato
LE FUNZIONI GONIOMETRICHE: SENO, COSENO E TANGENTE 1. LE FUNZIONI SENO E COSENO LE FUNZIONI SENO, COSENO E TANGENTE DEFINIZIONE Seno e coseno Consideriamo la circonferenza goniometrica e un angolo orientato
Funzioni trigonometriche
 trigonometriche Il cerchio trigonometrico Consideriamo in un piano cartesiano la circonferenza con il centro nell origine e avente per raggio il segmento che è stato fissato come unità di misura per i
trigonometriche Il cerchio trigonometrico Consideriamo in un piano cartesiano la circonferenza con il centro nell origine e avente per raggio il segmento che è stato fissato come unità di misura per i
CONOSCENZE 1. le proposizioni 2. i connettivi logici 3. le espressioni logiche
 ALGEBRA LOGICA E CONNETTII PREREQUISITI conoscere gi insiemi e i oro inguaggio conoscere i significato di soggetto e predicato di una frase conoscere i significato di congiunzione, disgiunzione e negazione
ALGEBRA LOGICA E CONNETTII PREREQUISITI conoscere gi insiemi e i oro inguaggio conoscere i significato di soggetto e predicato di una frase conoscere i significato di congiunzione, disgiunzione e negazione
Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa.
 Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
Costruzioni Costruzioni di rette, segmenti ed angoli Costruzione 1 Condurre la perpendicolare ad un retta data, passante per un punto della retta stessa. Costruzione. Consideriamo la retta r ed un punto
Lezione 2 Richiami sui sistemi di riferimento Richiami di trigonometria Vettori Calcolo vettoriale
 Dr. Andrea Malizia Prof. Maria Guerrisi 1 Richiami sui sistemi di riferimento Richiami di trigonometria Vettori Calcolo vettoriale Sistemi di riferimento e spostamento 2 Sistemi di riferimento e spostamento
Dr. Andrea Malizia Prof. Maria Guerrisi 1 Richiami sui sistemi di riferimento Richiami di trigonometria Vettori Calcolo vettoriale Sistemi di riferimento e spostamento 2 Sistemi di riferimento e spostamento
1. Risolvi in R le seguenti disequazioni: 1.a) ( x ) ( x ) b) 2x. 1.e) 2x 1. 1.g)
 LICEO PEDAGOGICO-ARTISTICO GPascoli di Bolzano PROVA SCRITTA DI MATEMATICA-ALUNNI CON GIUDIZIO SOSPESO CLASSE a B /9/9- Tempo h Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici,
LICEO PEDAGOGICO-ARTISTICO GPascoli di Bolzano PROVA SCRITTA DI MATEMATICA-ALUNNI CON GIUDIZIO SOSPESO CLASSE a B /9/9- Tempo h Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici,
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE
 TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
1 L omotetia. i punti O, A e A siano allineati
 1 L omotetia DEFINIZIONE. Dato un punto O ed un numero reale k, si dice omotetia di centro O e rapporto k, quella trasformazione del piano che associa ad ogni punto A il corrispondente punto A tale che
1 L omotetia DEFINIZIONE. Dato un punto O ed un numero reale k, si dice omotetia di centro O e rapporto k, quella trasformazione del piano che associa ad ogni punto A il corrispondente punto A tale che
2. Determina l equazione della circonferenza passante per i punti A ( 2; 4), B ( 1; 3) ed avente centro sulla retta di equazione 2x 3y + 2 = 0.
 CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
Esercitazione 4 - Forze distribuite
 Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Kangourou della Matematica 2012 finale nazionale italiana Mirabilandia, 7 maggio 2012
 Kangourou della Matematica 2012 finale nazionale italiana Mirabilandia, 7 maggio 2012 LIVELLO STUDENT S1. (5 punti ) Assegnati tre punti non allineati nello spazio, quante sfere passano per questi tre
Kangourou della Matematica 2012 finale nazionale italiana Mirabilandia, 7 maggio 2012 LIVELLO STUDENT S1. (5 punti ) Assegnati tre punti non allineati nello spazio, quante sfere passano per questi tre
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
1 LE PROPOSIZIONI. Gli esercizi di questo paragrafo sono a pag. 17
 La ogica riconoscere proposizioni e individuarne i vaore di veritaá operare con e proposizioni e riconoscere equivaenze ogiche stabiire a correttezza di un ragionamento ogico operare con i predicati usare
La ogica riconoscere proposizioni e individuarne i vaore di veritaá operare con e proposizioni e riconoscere equivaenze ogiche stabiire a correttezza di un ragionamento ogico operare con i predicati usare
LAVORO ESTIVO di MATEMATICA Classi Terze Scientifico Moderno N.B. DA CONSEGNARE ALLA PRIMA LEZIONE DI MATEMATICA DI SETTEMBRE
 LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
IL SISTEMA DI RIFERIMENTO
 IL SISTEMA DI RIFERIMENTO CARTESIANO E LA RETTA Per ricordare H Consideriamo una retta orientata r, fissiamo su di essa un punto O e prendiamo un segmento u come unitaá di misura; consideriamo un punto
IL SISTEMA DI RIFERIMENTO CARTESIANO E LA RETTA Per ricordare H Consideriamo una retta orientata r, fissiamo su di essa un punto O e prendiamo un segmento u come unitaá di misura; consideriamo un punto
Programma di Fisica Trigonometria essenziale
 Programma di Fisica Trigonometria essenziale (Per la scuola superiore) Autore: Enrico Campanelli Prima stesura: Giugno 013 Ultima revisione: Giugno 013 Per segnalare errori o per osservazioni e suggerimenti
Programma di Fisica Trigonometria essenziale (Per la scuola superiore) Autore: Enrico Campanelli Prima stesura: Giugno 013 Ultima revisione: Giugno 013 Per segnalare errori o per osservazioni e suggerimenti
I TRIANGOLI. Esistono vari tipi di triangoli che vengono classificati in base ai lati e agli angoli.
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli o vertici e da tre lati. Il triangolo è la forma geometrica con il minor numero di lati perché tre è il numero minimo di lati con cui si può
I TRIANGOLI Il triangolo è un poligono formato da tre angoli o vertici e da tre lati. Il triangolo è la forma geometrica con il minor numero di lati perché tre è il numero minimo di lati con cui si può
( ) ( ) ESEMPI. lim. Attribuendo ad x dei valori minori di x 0 (ad es. 0,999,...,0,5) si nota che la
 . Limiti di una funzione LIMITI DI UNA FUNZIONE Per ottenere un informazione competa su di una funzione occorrerebbe cacoare tutti i vaori dea funzione per ogni vaore di, ma ciò è impossibie perché tai
. Limiti di una funzione LIMITI DI UNA FUNZIONE Per ottenere un informazione competa su di una funzione occorrerebbe cacoare tutti i vaori dea funzione per ogni vaore di, ma ciò è impossibie perché tai
ROTAZIONI DEGLI ESTREMI DI UNA TRAVE PRISMATICA APPOGGIATA ALLE ESTREMITÁ E SOGGETTA AD UN CARICO VERTICALE
 M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
