PROBLEMI DI PROBABILITÀ
|
|
|
- Serafino Fusco
- 9 anni fa
- Visualizzazioni
Transcript
1 PROBLEMI DI PROBABILITÀ 1. Si dispongono a caso su uno scaffale sette libri, dei quali tre trattano di matematica. Qual è la probabilità che i tre libri di matematica si vengano a trovare l uno accanto all altro? ( ) 2. Un cubo con le facce colorate è diviso in 1000 cubetti congruenti. Si sceglie a caso uno dei 1000 cubetti cosí ottenuti. Si calcoli la probabilità che il cubetto estratto abbia: (a) esattamente due facce colorate; (b) almeno due facce colorate; (c) al piú due facce colorate. ( ) 3. Ad ogni istante si lanciano indipendentemente due monete; in una di esse la probabilità di ottenere testa è 1/2, nell altra è 1/3. Qual è la probabilità che di ottenere testa con entrambe le monete per la prima volta al quinto lancio? ( ) 4. Un giocatore inizia una serie di partite indipendenti nelle quali ad ogni istante vince con probabilità 1/3. Qual è la probabilità che la sua prima vincita avvenga in un istante multiplo di 3? ( ). 5. Ogni qual volta il giocatore A lancia una moneta equilibrata, tale cioè che la probabilità di ottenere testa sia 1/2, un secondo giocatore, B, lancia un dado equilibrato (ogni faccia ha probabilità 1/6). Qual è la probabilità che B ottenga come risultato 1 oppure 5 prima che A ottenga testa. ( ) 6. Siano date due urne. La prima, U 1, contiene 15 palline, delle quali 5 portano il numero 1 mentre 2 palline portano ognuna il numero k (k = 2, 3,..., 6). La seconda urna U 2 contiene in egual proporzione palline con i numeri da 1 a 6. (a) Si scelga a caso un urna e da questa si estragga a caso una pallina. Sia N il numero della pallina estratta; si calcolino P (N = k) per k = 1, 2,..., 6 e E(N). (b) Si sceglie a caso un urna, e, da questa, si estraggono con restituzione due palline; siano N 1 e N 2, rispettivamente i numeri delle due palline estratte. Qual è la probabilità P (N 1 = 3, N 2 = 4)? Sapendo che N 1 = 3 e N 2 = 4, qual è la probabilità che le palline siano state estratte dall urna U 1? (c) Sono indipendenti le v.a. del punto precedente? ( ) 7. Un urna contiene b palline bianche e c colorate. Le palline si intendono indistinguibili. (a) Si scriva uno spazio dei risultati atto a rappresentare l estrazione dall urna, senza restituzione, di due palline; (b) si calcoli la probabilità di estrarre in questo modo due palline di colori differenti; (c) come si modifica la risposta alla domanda precedente se l estrazione avviene con restituzione? ( ) Date: 5 febbraio
2 2 PROBLEMI DI PROBABILITÀ 8. Sia (X n ) una successione di v.a. indipendenti e tutte con legge di Bernoulli di parametro p e sia N una v.a., indipendente da quelle, con legge di Poisson di parametro θ > 0. Siano S 1 e S 2 le v.a. che contano rispettivamente il numero di successi, {X n = 1}, e quello dei fallimenti, {X n = 0}, in N prove. Allora (a) si scrivano S 1 e S 2 in funzione delle X n e di N; (b) si trovino le leggi di S 1 e di S 2 ; (c) si dica se S 1 e S 2 siano o no indipendenti. 9. Un urna contiene inizialmente b palline bianche e c palline colorate. Ad ogni istante, si estrae dall urna una pallina, se ne registra il colore e la si rimette quindi nell urna insieme a d palline dello stesso colore di quella estratta. Si calcoli la probabilità (a) che sia bianca la seconda pallina estratta; (b) che sia bianca la prima pallina estratta, sapendo che la seconda è bianca. ( ) 10. Siano X 1, X 2, X 3 tre v.a. indipendenti, tutte di legge geometrica con parametri rispettivamente eguali a p 1, p 2, p 3. (a) Si calcoli la probabilità P (X 1 X 2 X 3 ); (b) tre giocatori A, B e C lanciano a turno un dado nell ordine ABCABC... ; si calcoli la probabilità che A sia il primo a lanciare un 6, B il secondo e C il terzo. 11. Si considerino i termini della legge binomiale b(n, p : k); assegnati k in Z + e p in ]0, 1[, per quale valore di n è massimo b(n, p; k)? ( ) 12. (a) Si controlli se p n := 1 n (n + 1) definisca una legge di probabilità. (b) Sia X una v.a. tale che P (X = n) = (n N := {1, 2,..., n,... }) 1 n (n + 1) (n N). Esiste la speranza di X? Per quali valori di α > 0 esiste la speranza di X α? 13. Tre giocatori, A, B e C lanciano ciascuno una moneta equilibrata; A la lancia m volte, B n volte, C m + n volte. Si mostri che sono eguali le probabilità (a) che il numero di teste ottenuto da A sia eguale a quello ottenuto da B; (b) che il numero di teste ottenuto da C sia eguale al numero m di lanci eseguiti da A. 14. Una compagnia di assicurazioni assicura un egual numero di guidatori e di guidatrici. Ogni anno, indipendentemente dagli altri anni, è α la probabilità che un guidatore abbia un incidente che dia origine ad una richiesta di risarcimento; per una guidatrice l analoga probabilità è eguale a β. La compagnia sceglie a caso un assicurato. (a) Si individui uno schema d urna, vale a dire un estrazione di palline da una o piú urne che contengono palline nere e palline colorate, atto a rappresentare la situazione descritta sopra; (b) si calcoli la probabilità che l assicurato scelto causi un incidente con una richiesta di risarcimento nell anno in corso;
3 PROBLEMI DI PROBABILITÀ 3 (c) si calcoli la probabilità che l assicurato scelto causi un incidente con una richiesta di risarcimento in due anni consecutivi. (d) qual è la probabilità che l assicurato di (b) sia una guidatrice? ( ) 15. In un processo di Bernoulli (cioè in una serie di estrazioni con restituzione, in ognuna delle quali è p la probabilità di estrarre una pallina bianca) (a) qual è la probabilità di avere tutti successi nelle prime n prove? (b) qual è la probabilità che il primo fallimento avvenga all n esima prova? (c) qual è il numero medio di prove necessarie per avere il primo fallimento? 16. Un urna contiene b palline bianche, n palline nere e v palline verdi. In un estrazione con restituzione qual è la probabilità di estrarre una pallina bianca prima di estrarre una pallina nera? ( ) 17. Di una variabile aleatoria discreta X si sa che assume quattro valori, x 1, x 2, x 3 e x 4. Se è noto che (a) E(X) = 4; (b) x 1 = 2.5, x 2 = 3 e x 4 = 5; (c) p 1 = P (X = 2.5) = 0.1, p 2 = P (X = 3) = 0.25 e p 4 = P (X = 5) = 0.4, si calcolino x 3 e p 3 = P (X = x 3 ). Qual è la speranza della v.a. Y := 3 X + 5? 18. In un processo di Bernoulli (X n ) è p la probabilità di successo in ogni prova. Si calcoli la probabilità che sia eguale a k (k N) la differenza tra il tempo del secondo successo e quello del primo. 19. Si estraggono senza restituzione palline (distinguibili) da un urna che inizialmente ne contiene b bianche e n nere. (a) Si scriva uno spazio dei risultati atto a rappresentare l estrazione di k + 1 palline con k + 1 < b + n; (b) si mostri che la probabilità che la prima pallina estratta bianca sia la (k +1) esima è ( ) n + b k 1 b 1 ( ) ; b + n b (c) qual è la probabilità che, proseguendo le estrazioni sino a quando l urna contiene palline, l ultima pallina estratta sia bianca. ( ) 20. Sono date due urne U 1 e U 2 che contengono entrambe palline bianche e palline colorate; le proporzioni di palline bianche contenute nelle due urne sono rispettivamente p 1 e p 2. Si scelga a caso un urna e da questa si estraggano con restituzione due palline. (a) Si calcoli la probabilità P (B 1 ) che la prima pallina estratta sia bianca; (b) si calcoli la probabilità P (B 2 ) che la seconda pallina estratta sia bianca; (c) sono indipendenti gli eventi B 1 e B 2? 21. In un processo di Bernoulli (X n ) nel quale la probabilità di successo ad ogni prova è p, P (X n = 1) = p per ogni n N, siano T 1 e T 2, rispettivamente, le variabili aleatorie tempo del primo successo e tempo del secondo successo. (a) Si trovi la legge di T 2, P (T 2 = n), per n 2;
4 4 PROBLEMI DI PROBABILITÀ (b) Si determini, per n 2, la legge di T 1 condizionata dal sapere che T 2 = n, vale a dire la probabilità condizionata P (T 1 = k T 2 = n). 22. Un urna contiene inizialmente b palle bianche e c palle colorate. Ad ogni istante si estrae a caso dall urna una pallina, se ne nota il colore e la si rimette nell urna insieme ad altre d palline dello stesso colore di quella estratta. Si calcolino le probabilità: (a) che la seconda pallina estratta sia bianca; (b) che la prima pallina estratta sia bianca, sapendo che la seconda pallina estratta è bianca. 23. In un processo di Bernoulli (X n ) nel quale è p ]0, 1[ la probabilità di un successo, P (X n = 1) = p (n N), sia N la variabile aleatoria definita come il massimo numero naturale tale che sia X 1 = X 2 = = X N, N := max{k N : X 1 = X 2 = = X k }. Di N si trovino (a) la legge, e si mostri che {P (N = n) : n N} è effettivamente una legge di probabilità; (b) la sua speranza, se esiste. 24. Sia X una variabile aleatoria a valori in Z + : {0, 1, 2,... }. Posto p n := P (X = n) (n Z + ), si mostri che sono equivalenti le proprietà (a) X ha legge di Poisson di parametro θ > 0, X P(θ); (b) per ogni n N vale p n p n 1 = θ n. 25. In un processo di Bernoulli (X n ) nel quale la probabilità di successo ad ogni prova è p, P (X n = 1) = p per ogni n N, si calcolino (a) la probabilità che sia n j=1 X j = k per k = 0, 1,..., n; (b) la probabilità condizionata che sia X n = 1 sapendo che n j=1 X j = k. 26. Due giocatori A e B lanciano ciascuno una moneta equilibrata (per la quale, cioè, P (T ) = P (C) = 1/2). A effettua n lanci, mentre B ne effettua n + 1. Vince la partita chi ottiene il maggior numero di teste; si conviene che, in caso di parità, la partita sia vinta da A. Per quali valori di n il gioco è equo, vale a dire, P A = P B? Qui P A e P B sono, rispettivamente, le probabiltà di vittoria di A e di B. 27. Un urna contiene palline di tre colori diversi in egual proporzione. Si estraggono, con restituzione, n palline. Si calcoli la probabilità di estrarre: (a) palline di un solo colore; (b) palline di due colori; (c) palline di tre colori. 28. Un dado ha le facce numerate da 1 a 6 ed è costruito in modo tale che la probabilità di ogni faccia è proporzionale al numero scritto sulla faccia, p j = k j con k > 0 per j = 1, 2,..., 6.
5 PROBLEMI DI PROBABILITÀ 5 (a) Si calcoli la costante k; (b) qual è la probabilità che lanciando il dado si ottenga come risultato un numero dispari? (c) qual è la speranza della v.a. X che rappresenta il risultato di un lancio? 29. In un processo di Bernoulli (X n ), nel quale è p la probabilità di successo, P (X n = 1) = p per ogni n N, si calcolino (a) la probabilità che il terzo successo avvenga al tempo t = n; (b) la probabilità che il terzo successo avvenga al tempo t = n ed il primo successo al tempo t = k con k < n Un urna contiene n palline numerate da 1 a n. Si estraggono, senza restituzione tutte le palline. Qual è la probabilità che i tre numeri 1, 2 e 3 appaiano uno accanto all altro in quell ordine? 31. Si consideri la probabilità P definita nella famiglia delle parti dell insieme dei numeri naturali N := {1, 2,..., } mediante p n := 1 2 n. Per k 2 si definisca la variabile aleatoria X k tale che X k (n) sia il resto della divisione di n per k. (a) Si trovi la legge di X k ; (b) si mostri che quella trovata in (a) è effettivamente una legge di probabilità. (Suggerimento: si presti attenzione al caso del resto nullo). 32. Un urna contiene n palline numerate da 1 a n. Si estrae a caso una pallina. (a) Si calcoli la probabilità che la pallina estratta porti un numero divisibile per 3 o per 4; (b) si calcoli esplicitamente la probabilità di (a) nei due casi n = 50 e n = Si mostri che per ogni coppia A e B di eventi in uno spazio di probabilità (Ω, F, P ), vale la relazione P (A B) P (A) P (B) = P (A c ) P (B) P (A c B). 34. Un urna contiene 100 dadi dei quali la metà sono equilibrati, vale a dire che la probabilità di ogni faccia è egaule a 1/6; i dadi della rimanente metà sono stati truccati in maniera che la probabilità di ottenere 1 sia 1/2 mentre la probabilità di ogni altra faccia è 1/10. (a) Si estrae a caso un dado; se X rappresenta il risultato del lancio, si calcolino per k = 1, 2,..., 6, le probabilità P (X = k) e la speranza E(X); (b) si estrae a caso un dado e lo si lancia due volte; indicati con X 1 e X 2, rispettivamente, i risultati del primo e del secondo lancio, qual è la probabilità P (X 1 = 2, X 2 = 3)? Viceversa, se è noto che X 1 = 2 e X 2 = 3, qual è la probabilità che si tratti di uno dei dadi truccati? (c) sono indipendenti le v.a. X 1 e X 2?
6 6 PROBLEMI DI PROBABILITÀ ( ) 35. Un urna contiene 5 palline bianche e 5 palline colorate. Si estraggano senza restituzione dall urna 5 palline. Si calcolino le probabilità (a) che tutte le palline estratte siano dello stesso colore; (b) che si estraggano quattro palline di un colore e l altra di colore differente. ( ) 36. Si lancia per due volte una moneta equilibrata (per la quale, cioè, la probabiloità di ottenere testa è 1/2). Sia N il numero di teste ottenuto in questi due lanci e si lanci la moneta ancora N volte; se è X il numero complessivo di teste ottenute. (a) Si scrivano le probabilità P (X = k) per k = 0, 1, 2, 3, 4; (b) si controlli che si è cosí ottenuta una legge di probabilità. ( ) 37. Una famiglia ha tre figli; (a) qual è la probabilità che tutti e tre siano maschi, sapendo che almeno due sono maschi? (b) qual è la probabilità che tutti e tre siano maschi, sapendo che i primi due sono maschi? Si supponga che la probabilità che nasca un maschio o una femmina sia eguale a 1/2 e che ogni figlio sia indipendentemente maschio o femmina. ( ) 38. In un processo di Bernoulli nel quale è p la probabilità di successo si calcoli la probabilità di ottenere un numero pari di successi in n prove. Si considera 0 come un n umero pari. (Suggerimento: si ragioni per induzione). ( ) 39. Sia data una v.a. X che ha legge uniforme sui tre punti { 1, 0, 1}. Si trovi la legge della v.a. X 2 e la legge congiunta delle v.a. X e X 2. Si controlli che le leggi marginali del vettore aleatorio ( X, X 2) coincidono con quelle già note. ( ) 40. Sia dato un mazzo di 52 carte. Si considerino i seguenti due giochi: (a) si estrae a caso una carta dal mazzo; se questa è un asso, si lancia una moneta equilibrata, tale cioè che sia P (T ) = P (C) = 1/2; si vince se esce testa T. Se la carta estratta non è un asso si lancia un dado equilibrato, p({k}) = 1/6 per k = 1, 2,..., 6; in questo caso si vince se esce 1. (b) Si lancia una moneta equilibrata; se esce testa si estrae a caso una carta dal mazzo; si vince se questa è una asso. Se invece il lancio della moneta dà come risultato croce, si lancia un dado equilibrato; in questo caso si vince se il risultato è un 1 o un 2. In quale dei due giochi è piú probabilie vincere? ( ) 41. Si lanci due volte una moneta equilibrata, tale, cioè, che sia P (T ) = P (C) = 1/2; siano A, B e C, rispettivamente, gli eventi, A = il primo lancio dà come risultato testa, B = il secondo lancio dà come risultato testa e C = i due lanci danno lo stesso risultato. (a) Si mostri che gli eventi A, B e C sono a due a due indipendenti; (b) i tre eventi sono indipendenti?
7 PROBLEMI DI PROBABILITÀ 7 ( ) 42. Un urna contiene inizialmente una pallina bianca ed una colorata. Ad ogni istante si estrae a caso una pallina e la si sostituisce con un altra che è di colore bianco con probabilità p ]0, 1[ e colorata con probabilità q = 1 p. (a) Al tempo t = 1, vale a dire dopo la prima estrazione e la prima sostituzione, quante palline bianche può contenere l urna? (b) si calcoli la legge del numero di palline bianche presenti nell urna al tempo t = 1, cioè la probabilità che all istante t = 1 l urna contenga k palline bianche per tutti i valori possibili di k. ( ) 43. Si lanciano contemporaneamente due dadi equilibrati, uno bianco ed uno colorato; Qual è la probabilità che il punto segnato dal dado bianco sia maggiore di quello segnato dal dado colorato? ( ) 44. In un processo di Bernoulli nel quale è eguale a p la probabilità di un successo, P (X n = 1) = p (a) si rappresentino gli insiemi {T 4 = n} e {T 2 = k} {T 4 = n}, ove, al solito T j rappresenta il tempo del j esimo successo; (b) Si calcoli la probabilità condizionata P (T 2 = k T 4 = n). ( ) 45. Quattro coppie, ciascuna compota da marito e moglie si siedeno attorno ad un tavolo rotondo per cena. Qual è la probabilità che, sedendosi a caso, non si trovino sedute accanto due persone dello stesso sesso? ( ) 46. Sia X una variabile aleatoria tale che P (X = n) = k n! n = 0, 1, 2,.... (a) Si calcoli la costante k; (b) qual è la probabilità che X assuma un valore pari? (c) Si calcoli la speranza di X. ( ) 47. Si lanciano 5 dadi equilibrati, per ciascuno dei quali, cioè, vale P ({k}) = 1/6 (k = 1, 2,..., 6). Qual è la probabilità che almeno tre dadi diano lo stesso risultato? ( ) 48. In un processo di Bernoulli con probabilità di successo p ]0, 1[, si calcoli la probabilità condizionata P (T 3 = n T 2 = k), ove n > k e T 2 e T 3 sono i tempi del secondo e del terzo successo rispettivamente. ( ) 49. Sono date tre urne con la seguente composizione U 1 : U 2 : U 3 : 3 palline bianche e 2 palline colorate, 4 palline bianche e 4 palline colorate, 1 pallina bianca e 3 palline colorate.
8 8 PROBLEMI DI PROBABILITÀ Scelta, a caso, un urna se ne estrae una pallina, che risulta essere bianca. probabilità che essa sia stata estratta dall urna U 3? ( ) Qual è la 50. Un urna contiene b palline bianche e c palline colorate. Si estraggono, senza restituzione, due palline. Si calcoli la speranza del numero di palline bianche che si estraggono. Si paragoni il risultato con quello, ben noto, dell estrazione con restituzione. ( ) 51. Si lancia due volte un dado equilibrato. Siano A e B, rispettivamente, gli eventi la somma dei punti realizzati è dispari e almeno un lancio dà come risultato 1. Si calcolino le probabilità degli eventi A, B, A B e A B. ( ) 52. Per quale valore della costante C la successione p n := C 2n n! definisce la legge di probabilità di una variabile aleatoria X sui numeri naturali N := {1, 2,..., n,... }? Si trovino (a) P (X > 1); (b) il valore piú probabile di X. ( ) 53. In un processo di Bernoulli (X n ) nel quale è p la probabilità di successo ad ogni prova, P (X n = 1) = p ]0, 1[ (n N), si calcoli la probabilità condizionata che il tempo T 2 del secondo successo sia al piú eguale a n, T 2 n, sapendo che il primo successo è avvenuto al tempo k < n. ( ) 54. Data un urna che contiene 40 palline numerate da 1 a 40, si considerino i seguenti giochi. (a) Si estrae a caso una pallina. Se questa è un multiplo di 10 si lancia una moneta equlibrata e si vince se esce testa; se, invece, la pallina estratta non è un multiplo di 10, si lancia un dado equilibrato, per il quale, cioè, vale P ({k}) = 1/6 (k = 1, 2,..., 6); in questo caso si vince se esce 1; (b) si lancia una moneta equilibrata. Se esce testa si estrae una pallina dall urna e si vince se la pallina estratta è un multiplo di 10; se invece il lancio della moneta dà come risultato croce, si lancia un dado equilibrato; in questo caso si vince se il risultato è 1 o 2. Quale dei due giochi è piú favorevole? ( ) 55. In un processo di Bernoulli (X n ) nel quale è p la probabilità di successo ad ogni prova, P (X n = 1) = p ]0, 1[ (n N), siano T 1 e T 2 i tempi, rispettivamente, del primo e del secondo successo. Si indichi con Y 2 := T 2 T 1 il tempo che intercorre tra i due primi successi. (a) Si trovi la legge congiunta di T 1 e di Y 2, vale a dire, si determini, per j e k numeri naturali, la probabilità P (T 1 = j, Y 2 = k); (b) si trovi la legge di Y 2, P (Y 2 = k) per k naturale; (c) sono indipendenti le variabili aleatorie T 1 e Y 2? ( ) 56. Un urna contiene inizialmente b palline bianche e c palline colorate. Prima di estrarre una pallina, due palline sono sottratte dall urna.
9 PROBLEMI DI PROBABILITÀ 9 (a) Si calcoli la probabilità che la pallina estratta, dopo la sottrazione delle due palline, sia bianca; (b) se la pallina estratta è bianca, qual è la probabilità che siano state sottratte due palline colorate? ( ) 57. Un giocatore di roulette continua a puntare sul 19 rosso. Si calcoli la probabilità che prima di vincere siano usciti solo numeri rossi. Si ricordi che nella roulette vi sono 37 numeri, da 1 a 36, colorati metà in nero e metà in rosso e che vi è in piú lo 0, che non è colorato. 58. In un processo di Bernoulli (X n ) nel quale è p la probabilità di successo, P (X n = 1) = p (n N), si indichino con T 2 e T 3, rispettivamente, i tempi del secondo e del terzo successo. (a) Si rappresentino gli eventi {T 3 = n} e {T 2 = k} {T 3 = n} e se ne calcolino le probabilità; (b) si calcoli la probabilità condizionata che il secondo successo avvenga al tempo k sapendo che il terzo è avvenuto al tempo n; (c) quali sono i possibili valori di k? Si controlli che, fissato n, le probabilità calcolate in (b) definiscono una legge di probabilità. 59. Sono date tre urne identiche e n palline; queste sono distribuite a caso tra le urne, senza alcuna restrizione sul numero di palline che possono essere collocate in ciascuna urna. (a) Si scriva lo spazio dei risultati; (b) si calcoli la probabilità che almeno una delle urne rimanga vuota; (c) si calcoli esplicitamente la probabilità del punto precedente se n = In un processo di Bernoulli (X n ) nel quale è p la probabilità di successo, P (X n = 1) = p (n N), si calcoli la probabilità che il tempo intercorso tra il primo e il secondo successo sia eguale a quello del primo successo. Si calcoli, poi, esplicitamente tale probabilità quando p = 1/ Sono date n variabili aleatorie (=v.a.) indipendenti X 1, X 2,..., X n ; per ogni indice i {1, 2,..., n}, X i è una v.a. geometrica di parametro p i ]0, 1[. Si trovi la legge della v.a. X (1) := min{x 1, X 2,..., X n } e la si riconosca. 62. Si lancia 5 volte una moneta equilibrata (p = q = 1/2). Sapendo che si è avuta almeno una volta testa, si calcoli la probabilità che si sia ottenuto testa al primo lancio. 63. Un urna contiene palline bianche e colorate. La proporzione di palline bianche è p ]0, 1[. Dall urna si estraggono con restituzione n palline. Una seconda urna contiene n palline; di queste quelle bianche sono tante quante quelle estratte dalla prima urna. Qual è la probabilità di estrarre una pallina bianca dalla seconda urna? Se la pallina estratta dalla seconda urna è bianca, qual è la probabilità che essa contenesse k palline bianche? 64. Dati due eventi A e B, si trovi (A B) (A B c ).
10 10 PROBLEMI DI PROBABILITÀ 65. Per seguire una lezione quattro studentesse e tre studenti si siedono a caso in un banco. Qual è la probabilità che si siedano alternando uno studente a una studentessa? 66. Dato un processo di Bernoulli nel quale è p la probabilità di successo ad ogni prova, si calcoli la probabilità condizionata che il terzo successo avvenga al tempo n sapendo che il primo successo è avvenuto al tempo k. Si mostri anche che tale probabilità è eguale a quella che il secondo successo avvenga al tempo n k. 67. In una classe sono presenti 15 alunni; qual è la probabilità che nessuno di essi sia nato nell ultimo quadrimestre dell anno? 68. Un urna contiene 4 palline bianche e 3 palline colorate. In un estrazione senza restituzione di due palline si calcolino le probabilità (a) che le palline estratte siano dello stesso colore; (b) che almeno una delle palline estratte sia bianca. 69. Si lancia 3 volte un dado equilibrato ottenendo due volte come risultato 5. Sapendo questo, qual è la probabilità che il secondo lancio abbia dato come risultato 5? 70. In processo di Bernoulli nel quale è p ]0, 1[ la probabilità di successo ad ogni prova, qual è la probabilità che sia eguale a k {2, 3,... } la differenza tra l istante del terzo e quello del primo successo?
ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE
 ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE Docente titolare: Irene Crimaldi 26 novembre 2009 Es.1 Supponendo che la probabilità di nascita maschile e femminile sia la stessa, calcolare la probabilità
ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE Docente titolare: Irene Crimaldi 26 novembre 2009 Es.1 Supponendo che la probabilità di nascita maschile e femminile sia la stessa, calcolare la probabilità
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
IL CALCOLO DELLA PROBABILITÀ
 IL LOLO LL PROILITÀ 1 Una scatola contiene quattro dischetti rossi numerati da 1 a 4, sei dischetti verdi numerati da 1 a e cinque dischetti bianchi numerati da 1 a 5. Si estrae un dischetto. Scrivi gli
IL LOLO LL PROILITÀ 1 Una scatola contiene quattro dischetti rossi numerati da 1 a 4, sei dischetti verdi numerati da 1 a e cinque dischetti bianchi numerati da 1 a 5. Si estrae un dischetto. Scrivi gli
ESERCIZI SULLA PROBABILITA
 PROBABILITA CLASSICA ESERCIZI SULLA PROBABILITA 1) Si estrae una carta da un mazzo di 40 carte ; calcolare la probabilità che la carta sia: a. una figura; b. una carta di danari; c. un asso. 2) Un urna
PROBABILITA CLASSICA ESERCIZI SULLA PROBABILITA 1) Si estrae una carta da un mazzo di 40 carte ; calcolare la probabilità che la carta sia: a. una figura; b. una carta di danari; c. un asso. 2) Un urna
Matematica con elementi di statistica ESERCIZI: probabilità
 Matematica con elementi di statistica ESERCIZI: probabilità Esercizi sulla Probabilità Esercizio 1. In un corso di laurea uno studente deve scegliere un esame fra 8 di matematica e un esame fra 5 di fisica.
Matematica con elementi di statistica ESERCIZI: probabilità Esercizi sulla Probabilità Esercizio 1. In un corso di laurea uno studente deve scegliere un esame fra 8 di matematica e un esame fra 5 di fisica.
Test di autovalutazione
 Test Test di autovalutazione 0 0 0 0 0 0 0 70 80 90 00 n Il mio punteggio, in centesimi, è n Rispondi a ogni quesito segnando una sola delle alternative. n Confronta le tue risposte con le soluzioni. n
Test Test di autovalutazione 0 0 0 0 0 0 0 70 80 90 00 n Il mio punteggio, in centesimi, è n Rispondi a ogni quesito segnando una sola delle alternative. n Confronta le tue risposte con le soluzioni. n
Nelle ipotesi del precedente esercizio, in quanti modi potrebbe essere formata la classifica finale di tutti i 20 concorrenti? [2,4.
 CALCOLO COMBINATORIO Ad una gara partecipano 20 concorrenti; quanti terne di primi tre classificati si possono formare? (nell'ipotesi che non vi siano degli ex aequo) [6.840] Nelle ipotesi del precedente
CALCOLO COMBINATORIO Ad una gara partecipano 20 concorrenti; quanti terne di primi tre classificati si possono formare? (nell'ipotesi che non vi siano degli ex aequo) [6.840] Nelle ipotesi del precedente
prima urna seconda urna
 Un po di fortuna Considera il seguente gioco: ci sono due urne contenenti delle palline perfettamente uguali tra loro, ma colorate diversamente, alcune bianche, altre nere. Nella prima urna ci sono una
Un po di fortuna Considera il seguente gioco: ci sono due urne contenenti delle palline perfettamente uguali tra loro, ma colorate diversamente, alcune bianche, altre nere. Nella prima urna ci sono una
Esercitazione del 31/01/2012 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 1/01/2012 Istituzioni di Calcolo delle Probabilità Esercizio 1 Vengono lanciati due dadi regolari a 6 facce. (a) Calcolare la probabilità che la somma dei valori ottenuti sia 9? (b) Calcolare
Esercitazione del 1/01/2012 Istituzioni di Calcolo delle Probabilità Esercizio 1 Vengono lanciati due dadi regolari a 6 facce. (a) Calcolare la probabilità che la somma dei valori ottenuti sia 9? (b) Calcolare
È l insieme di tutti i possibili esiti di un esperimento aleatorio; si indica generalmente con il simbolo.
 A Ripasso Terminologia DOMADE Spazio campionario Evento Evento certo Evento elementare Evento impossibile Evento unione Evento intersezione Eventi incompatibili Evento contrario RISPOSTE È l insieme di
A Ripasso Terminologia DOMADE Spazio campionario Evento Evento certo Evento elementare Evento impossibile Evento unione Evento intersezione Eventi incompatibili Evento contrario RISPOSTE È l insieme di
Probabilità 1, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
Probabilità esempi. Aiutiamoci con una rappresentazione grafica:
 Probabilità esempi Paolo e Francesca giocano a dadi. Paolo scommette che, lanciando due dadi, si otterrà come somma 8 oppure 9. Francesca scommette che si otterrà come somma un numero minore o uguale a
Probabilità esempi Paolo e Francesca giocano a dadi. Paolo scommette che, lanciando due dadi, si otterrà come somma 8 oppure 9. Francesca scommette che si otterrà come somma un numero minore o uguale a
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore) Marco Riani [email protected] http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
STATISTICA A K (63 ore) Marco Riani [email protected] http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
Test di Matematica di base
 Test di Matematica di base Calcolo combinatorio e delle probabilitá Quanti oggetti possiamo differenziare con delle targhe di due simboli di cui il primo é una lettera dell alfabeto italiano e il secondo
Test di Matematica di base Calcolo combinatorio e delle probabilitá Quanti oggetti possiamo differenziare con delle targhe di due simboli di cui il primo é una lettera dell alfabeto italiano e il secondo
IL CALCOLO DELLE PROBABILITA
 IL CALCOLO DELLE PROBABILITA INTRODUZIONE Già 3000 anni fa gli Egizi praticavano un antenato del gioco dei dadi, che si svolgeva lanciando una pietra. Il gioco dei dadi era diffuso anche nell antica Roma,
IL CALCOLO DELLE PROBABILITA INTRODUZIONE Già 3000 anni fa gli Egizi praticavano un antenato del gioco dei dadi, che si svolgeva lanciando una pietra. Il gioco dei dadi era diffuso anche nell antica Roma,
258 Capitolo 9. La probabilità
 258 Capitolo 9 La probabilità 96 Esercizi 96 Esercizi dei singoli paragrafi 9 - Gli eventi 9 Quali dei seguenti eventi sono certi, probabili, impossibili a ) Il giorno di Pasquetta pioverà; b ) il giorno
258 Capitolo 9 La probabilità 96 Esercizi 96 Esercizi dei singoli paragrafi 9 - Gli eventi 9 Quali dei seguenti eventi sono certi, probabili, impossibili a ) Il giorno di Pasquetta pioverà; b ) il giorno
Variabili casuali ad una dimensione Testi degli esercizi. Variabili casuali ad una dimensione a.a. 2012/2013 1
 Variabili casuali ad una dimensione Testi degli esercizi 1 Costruzione di variabile casuale discreta Esercizio 1. Sia data un urna contenente 3 biglie rosse, 2 biglie bianche ed una biglia nera. Ad ogni
Variabili casuali ad una dimensione Testi degli esercizi 1 Costruzione di variabile casuale discreta Esercizio 1. Sia data un urna contenente 3 biglie rosse, 2 biglie bianche ed una biglia nera. Ad ogni
CONOSCENZE 1. il significato di evento casuale. 2. il significato di eventi impossibili, complementari;
 ARITMETICA ELEMENTIDICALCOLO DELLE PROBABILITAÁ PREREQUISITI l l l conoscere e costruire tabelle a doppia entrata conoscere il significato di frequenza statistica calcolare rapporti e percentuali CONOSCENZE.
ARITMETICA ELEMENTIDICALCOLO DELLE PROBABILITAÁ PREREQUISITI l l l conoscere e costruire tabelle a doppia entrata conoscere il significato di frequenza statistica calcolare rapporti e percentuali CONOSCENZE.
CP110 Probabilità: Esonero 1. Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
Corso di probabilità e statistica
 Università degli Studi di Verona Facoltà di Scienze MM.FF.NN. Corso di Laurea in Informatica Corso di probabilità e statistica (Prof.ssa L.Morato) Esercizi Parte I: probabilità classica e probabilità combinatoria,
Università degli Studi di Verona Facoltà di Scienze MM.FF.NN. Corso di Laurea in Informatica Corso di probabilità e statistica (Prof.ssa L.Morato) Esercizi Parte I: probabilità classica e probabilità combinatoria,
STATISTICA: esercizi svolti sulle VARIABILI CASUALI
 STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
Alcuni esercizi di probabilità (aggiornato al )
 COMPL. DI ANALISI MATEMATICA ED ELEMENTI DI PROBABILITA (L-Z) C.d.L. Ing. Civile - Università di Bologna A.A.2009-200 - Prof. G.Cupini Alcuni esercizi di probabilità (aggiornato al 2-7-200) (Grazie agli
COMPL. DI ANALISI MATEMATICA ED ELEMENTI DI PROBABILITA (L-Z) C.d.L. Ing. Civile - Università di Bologna A.A.2009-200 - Prof. G.Cupini Alcuni esercizi di probabilità (aggiornato al 2-7-200) (Grazie agli
Calcolo delle Probabilità 2013/14 Foglio di esercizi 3
 Calcolo delle Probabilità 203/4 Foglio di esercizi 3 Probabilità condizionale e indipendenza. Esercizio. Per rilevare la presenza di una certa malattia, si effettua un test. Se la persona sottoposta al
Calcolo delle Probabilità 203/4 Foglio di esercizi 3 Probabilità condizionale e indipendenza. Esercizio. Per rilevare la presenza di una certa malattia, si effettua un test. Se la persona sottoposta al
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
Probabilità e Statistica Esercitazioni. a.a. 2009/2010. C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica.
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Probabilità Ines Campa Probabilità e Statistica - Esercitazioni -
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Probabilità Ines Campa Probabilità e Statistica - Esercitazioni -
Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U 1. 2. 3. U 4. 5. 6
 EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
CALCOLO DELLE PROBABILITA - 24 Giugno 2015 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5,6.
 Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 4 Giugno 5 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5, Motivare dettagliatamente le risposte su fogli allegati e
Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 4 Giugno 5 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5, Motivare dettagliatamente le risposte su fogli allegati e
Lezione 12. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 12. A. Iodice.
 discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di Mercoledì giugno 4 (tempo a disposizione: ore. Scrivere su ogni foglio NOME e COGNOME. Le
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di Mercoledì giugno 4 (tempo a disposizione: ore. Scrivere su ogni foglio NOME e COGNOME. Le
Ψ PSICOMETRIA. Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE
 Ψ PSICOMETRIA Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE STATISTICA INFERENZIALE CAMPIONE caratteristiche conosciute POPOLAZIONE caratteristiche sconosciute STATISTICA INFERENZIALE STIMA
Ψ PSICOMETRIA Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE STATISTICA INFERENZIALE CAMPIONE caratteristiche conosciute POPOLAZIONE caratteristiche sconosciute STATISTICA INFERENZIALE STIMA
ESERCIZI SCHEDA N. 1: EVENTI E VARIABILI ALEATORIE
 ESERCIZI SCHEDA N. 1: EVENTI E VARIABILI ALEATORIE 1) Dato lo spazio campionario Ω = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); (2,2); (2,3); ; (6,6)} riferito al lancio di due dadi non truccati,
ESERCIZI SCHEDA N. 1: EVENTI E VARIABILI ALEATORIE 1) Dato lo spazio campionario Ω = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); (2,2); (2,3); ; (6,6)} riferito al lancio di due dadi non truccati,
Un elenco di esercizi per il corso Matematica docente: Alberto Dolcetti
 Un elenco di esercizi per il corso Matematica docente: Alberto Dolcetti Ricevo molti messaggi di posta elettronica che suggeriscono varie soluzioni per gli esercizi proposti. Questo non mi dispiace perchè
Un elenco di esercizi per il corso Matematica docente: Alberto Dolcetti Ricevo molti messaggi di posta elettronica che suggeriscono varie soluzioni per gli esercizi proposti. Questo non mi dispiace perchè
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV -VE
 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV -VE Scheda : Funzioni circolari, Equazioni e disequazioni goniometriche Risolvi la seguente equazione: sin + 4 sin cos + 5 = 0
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV -VE Scheda : Funzioni circolari, Equazioni e disequazioni goniometriche Risolvi la seguente equazione: sin + 4 sin cos + 5 = 0
LA PROBABILITAÁ ALGEBRA IL CALCOLO DELLE PROBABILITAÁ. richiami della teoria
 ALGEBRA IL CALCOLO DELLE PROBABILITAÁ richiami della teoria n un evento E si dice casuale o aleatorio, quando il suo verificarsi dipende unicamente dal caso; n un evento si dice certo quando eá possibile
ALGEBRA IL CALCOLO DELLE PROBABILITAÁ richiami della teoria n un evento E si dice casuale o aleatorio, quando il suo verificarsi dipende unicamente dal caso; n un evento si dice certo quando eá possibile
ELABORAZIONI STATISTICHE Conoscenze (tutti)
 Scegli il completamento corretto. ELABORAZIONI STATISTICHE Conoscenze (tutti) 1. Una variabile statistica è di tipo qualitativo se: a. fa riferimento ad una qualità b. viene espressa mediante un dato numerico
Scegli il completamento corretto. ELABORAZIONI STATISTICHE Conoscenze (tutti) 1. Una variabile statistica è di tipo qualitativo se: a. fa riferimento ad una qualità b. viene espressa mediante un dato numerico
COMPITO n. 1. c(4s + 6t) se 0 s t 1 f(s, t) = 0 altrimenti
 COMPITO n. 1 a) Si lancia due volte un dado non truccato. Quant è la probabilità dell evento al primo lancio esce un numero strettamente minore di 3 oppure al secondo lancio esce un numero strettamente
COMPITO n. 1 a) Si lancia due volte un dado non truccato. Quant è la probabilità dell evento al primo lancio esce un numero strettamente minore di 3 oppure al secondo lancio esce un numero strettamente
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
 SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
La probabilità composta
 La probabilità composta DEFINIZIONE. Un evento E si dice composto se il suo verificarsi è legato al verificarsi contemporaneo (o in successione) degli eventi E 1, E 2 che lo compongono. Consideriamo il
La probabilità composta DEFINIZIONE. Un evento E si dice composto se il suo verificarsi è legato al verificarsi contemporaneo (o in successione) degli eventi E 1, E 2 che lo compongono. Consideriamo il
STATISTICA ESERCITAZIONE 9
 STATISTICA ESERCITAZIONE 9 Dott. Giuseppe Pandolfo 19 Gennaio 2015 REGOLE DI CONTEGGIO Sequenze ordinate Sequenze non ordinate Estrazioni con ripetizione Estrazioni senza ripetizione Estrazioni con ripetizione
STATISTICA ESERCITAZIONE 9 Dott. Giuseppe Pandolfo 19 Gennaio 2015 REGOLE DI CONTEGGIO Sequenze ordinate Sequenze non ordinate Estrazioni con ripetizione Estrazioni senza ripetizione Estrazioni con ripetizione
Esercizi su variabili discrete: binomiali e ipergeometriche
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
CENTRO SALESIANO DON BOSCO TREVIGLIO Corso di Informatica
 ) Un urna contiene 0 palline numerate da a 0. Si calcoli la probabilità che: a) estraendo successivamente palline, rimettendo ogni volta la pallina estratta nell urna, si abbiano due numeri primi; b) estraendo
) Un urna contiene 0 palline numerate da a 0. Si calcoli la probabilità che: a) estraendo successivamente palline, rimettendo ogni volta la pallina estratta nell urna, si abbiano due numeri primi; b) estraendo
PROBABILITÀ. P ( E ) = f n
 PROBABILITÀ GLI EVENTI E LA PROBABILITÀ EVENTI CERTI, IMPOSSIBILI E ALEATORI Ci sono avvenimenti che accadono con certezza, mentre altri sicuramente non possono mai verificarsi. Per esempio, se una scatola
PROBABILITÀ GLI EVENTI E LA PROBABILITÀ EVENTI CERTI, IMPOSSIBILI E ALEATORI Ci sono avvenimenti che accadono con certezza, mentre altri sicuramente non possono mai verificarsi. Per esempio, se una scatola
Calcolo della probabilità
 Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
Statistica Matematica Prova scritta del 06/07/05 1. Risposte Domande x se 0 x 2, f(x) = 0 altrove;
 Statistica Matematica Prova scritta del 06/07/05 1 COGNOME: NOME: TEST Scrivere il numero della risposta sopra alla corrispondente domanda. Risposte Domande 1 2 3 4 5 6 7 8 9 10 1 Sia data una variabile
Statistica Matematica Prova scritta del 06/07/05 1 COGNOME: NOME: TEST Scrivere il numero della risposta sopra alla corrispondente domanda. Risposte Domande 1 2 3 4 5 6 7 8 9 10 1 Sia data una variabile
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Scheda 1: funzioni circolari, equazioni e disequazioni goniometriche
 Scheda : funzioni circolari, equazioni e disequazioni goniometriche Risolvi la seguente equazione: sin + sin cos + 5 = 0 5 = 5 cos + sin Suggerimento dell insegnante: ricorda che ( ) Risolvi la seguente
Scheda : funzioni circolari, equazioni e disequazioni goniometriche Risolvi la seguente equazione: sin + sin cos + 5 = 0 5 = 5 cos + sin Suggerimento dell insegnante: ricorda che ( ) Risolvi la seguente
Esercizi svolti di statistica. Gianpaolo Gabutti
 Esercizi svolti di statistica Gianpaolo Gabutti ([email protected]) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
Esercizi svolti di statistica Gianpaolo Gabutti ([email protected]) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE
 ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
Esempi di prove di verifica su calcolo combinatorio e delle probabilità Esempio 1 Esempio 2
 Esempi di prove di verifica su calcolo combinatorio e delle probabilità Esempio 1 Il compito verte sui seguenti contenuti irrinunciabili: probabilità totale e composta Competenze essenziali interessate:
Esempi di prove di verifica su calcolo combinatorio e delle probabilità Esempio 1 Il compito verte sui seguenti contenuti irrinunciabili: probabilità totale e composta Competenze essenziali interessate:
Il Calcolo delle Probabilità
 Il Calcolo delle Probabilità Introduzione storica I primi studi che portarono successivamente a concetti legati alla probabilità possono essere trovati a metà del XVI secolo in Liber de ludo aleæ di Girolamo
Il Calcolo delle Probabilità Introduzione storica I primi studi che portarono successivamente a concetti legati alla probabilità possono essere trovati a metà del XVI secolo in Liber de ludo aleæ di Girolamo
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
Alcuni esercizi di probabilità e statistica
 Alcuni esercizi di probabilità e statistica 1. Vi sono 2 urne, ciascuna contenente 10 palle. Nella prima urna ci sono 8 palle bianche e 2 nere. Nella seconda ve ne sono 7 bianche e 3 rosse. Qual è la probabilità
Alcuni esercizi di probabilità e statistica 1. Vi sono 2 urne, ciascuna contenente 10 palle. Nella prima urna ci sono 8 palle bianche e 2 nere. Nella seconda ve ne sono 7 bianche e 3 rosse. Qual è la probabilità
Probabilità e Statistica Esercitazioni. a.a. 2009/2010. C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica.
 Probabilità e Statistica Esercitazioni a.a. 2009/200 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Estrazioni I Ines Campa Probabilità e Statistica - Esercitazioni -
Probabilità e Statistica Esercitazioni a.a. 2009/200 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Estrazioni I Ines Campa Probabilità e Statistica - Esercitazioni -
1. Calcolo combinatorio, problemi di conteggio.
 1 1. Calcolo combinatorio, problemi di conteggio. 1. In quanti modi diversi 4 persone possono occupare 8 posti a sedere numerati? (D 8,4. Un allenatore dispone di 18 giocatori per scegliere la formazione
1 1. Calcolo combinatorio, problemi di conteggio. 1. In quanti modi diversi 4 persone possono occupare 8 posti a sedere numerati? (D 8,4. Un allenatore dispone di 18 giocatori per scegliere la formazione
P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =
![P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) = P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =](/thumbs/60/44901085.jpg) Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Kangourou Italia Gara del 28 marzo 2008 Categoria Student Per studenti di quarta o quinta della secondaria di secondo grado
 Testi_08.qxp 9-0-008 :6 Pagina 8 Kangourou Italia Gara del 8 marzo 008 ategoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. al N. 0 valgono punti ciascuno. Nelle
Testi_08.qxp 9-0-008 :6 Pagina 8 Kangourou Italia Gara del 8 marzo 008 ategoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. al N. 0 valgono punti ciascuno. Nelle
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATICA Scuola secondaria di II grado Classe... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
3 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 7 febbraio 2012
 3 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 7 febbraio 2012 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
3 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 7 febbraio 2012 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
Sia f la frequenza di un evento A e n sia la dimensione del campione. La probabilità dell'evento A è
 Cenni di probabilità di Carlo Elce Definizioni Lo spazio campionario per un esperimento è l'insieme di tutti i suoi possibili esiti. Per esempio, se l'esperimento è il lancio di due di dadi e si rappresentano
Cenni di probabilità di Carlo Elce Definizioni Lo spazio campionario per un esperimento è l'insieme di tutti i suoi possibili esiti. Per esempio, se l'esperimento è il lancio di due di dadi e si rappresentano
Note di probabilità. Mauro Saita Versione provvisoria, maggio 2014.
 Note di probabilità Mauro Saita Versione provvisoria, maggio 2014. Indice 1 Note di probabilità. 2 1.1 Eventi elementari. Spazio degli eventi.............................. 2 1.2 Definizione assiomatica
Note di probabilità Mauro Saita Versione provvisoria, maggio 2014. Indice 1 Note di probabilità. 2 1.1 Eventi elementari. Spazio degli eventi.............................. 2 1.2 Definizione assiomatica
Olimpiadi di Statistica Classe V - Fase Eliminatoria
 Olimpiadi di Statistica 2016 - Classe V - Fase Eliminatoria Domanda 1 Alla fine del torneo di calcetto organizzato dalla scuola, è stata analizzata la classifica dei marcatori dalla quale risulta la seguente
Olimpiadi di Statistica 2016 - Classe V - Fase Eliminatoria Domanda 1 Alla fine del torneo di calcetto organizzato dalla scuola, è stata analizzata la classifica dei marcatori dalla quale risulta la seguente
Catene di Markov - Foglio 1
 Catene di Markov - Foglio 1 1. Una pedina si muove su un circuito circolare a 4 vertici, numerati da 1 a 4. La pedina si trova inizialmente nel vertice 1. Ad ogni passo un giocatore lancia un dado equilibrato:
Catene di Markov - Foglio 1 1. Una pedina si muove su un circuito circolare a 4 vertici, numerati da 1 a 4. La pedina si trova inizialmente nel vertice 1. Ad ogni passo un giocatore lancia un dado equilibrato:
ESERCIZI DI CALCOLO COMBINATORIO
 ESERCIZI DI CALCOLO COMBINATORIO (G.T.Bagni) Sintesi delle nozioni teoriche da utilizzare a) Dati n elementi e k n, si dicono disposizioni semplici di n elementi di classe k tutti i raggruppamenti ottenuti
ESERCIZI DI CALCOLO COMBINATORIO (G.T.Bagni) Sintesi delle nozioni teoriche da utilizzare a) Dati n elementi e k n, si dicono disposizioni semplici di n elementi di classe k tutti i raggruppamenti ottenuti
Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata
 Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata Stefano Patti 1 19 ottobre 2005 Definizione 1 Sia (Ω, F) uno spazio probabilizzabile.
Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata Stefano Patti 1 19 ottobre 2005 Definizione 1 Sia (Ω, F) uno spazio probabilizzabile.
9 = Soluzione. Soluzione
 Esercizio 1 Un'urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare la probabilità di avere a) una pallina bianca; b) una pallina nera; e) una pallina non bianca; d) una pallina
Esercizio 1 Un'urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare la probabilità di avere a) una pallina bianca; b) una pallina nera; e) una pallina non bianca; d) una pallina
Calcolo delle Probabilità e Statistica
 Calcolo delle Probabilità e Statistica Alcuni esercizi Laura Poggiolini Dipartimento di Matematica Applicata Giovanni Sansone Università di Firenze 2 Indice 1 Probabilità: esercizi vari 1 1.1 Combinatorica
Calcolo delle Probabilità e Statistica Alcuni esercizi Laura Poggiolini Dipartimento di Matematica Applicata Giovanni Sansone Università di Firenze 2 Indice 1 Probabilità: esercizi vari 1 1.1 Combinatorica
PROBLEMI DI PROBABILITÀ 2
 PROBLEMI DI PROBABILITÀ 2. Si sceglie a caso un numero X nell intervallo (0, ). (a) Qual è la probabilità che la usa prima cifra decimale sia? (b) Qual è la probabilità che la seconda cifra decimale sia
PROBLEMI DI PROBABILITÀ 2. Si sceglie a caso un numero X nell intervallo (0, ). (a) Qual è la probabilità che la usa prima cifra decimale sia? (b) Qual è la probabilità che la seconda cifra decimale sia
b = 1 2σ 3. La lunghezza di una barra è un numero aleatorio X con densità della forma 0, x 0, 0 < x 1 a = 1 F (x) = 2 2x 1 x2
 CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
Corso di Fondamenti di TLC Esercizi di Probabilitá
 Corso di Fondamenti di TLC Esercizi di Probabilitá Exercise 0.1 Unurna contiene 2 biglie bianche e 5 nere. Estraiamo una prima biglia: se nera la rimettiamo dentro con altre due dello stesso colore, se
Corso di Fondamenti di TLC Esercizi di Probabilitá Exercise 0.1 Unurna contiene 2 biglie bianche e 5 nere. Estraiamo una prima biglia: se nera la rimettiamo dentro con altre due dello stesso colore, se
ESERCIZI DI CALCOLO PROBABILITÀ DISTRIBUZIONI DOPPIE E NOTEVOLI
 Variabili bidimensionali ESERCIZI DI CALCOLO PROBABILITÀ DISTRIBUZIONI DOPPIE E NOTEVOLI 1) Siano X 1 e X 2 due variabili casuali indipendenti che possono assumere valori 0, 1 e 3 rispettivamente con probabilità
Variabili bidimensionali ESERCIZI DI CALCOLO PROBABILITÀ DISTRIBUZIONI DOPPIE E NOTEVOLI 1) Siano X 1 e X 2 due variabili casuali indipendenti che possono assumere valori 0, 1 e 3 rispettivamente con probabilità
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 51 Introduzione Il Calcolo delle
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 51 Introduzione Il Calcolo delle
Probabilità: valutazione della possibilità che accada (o sia accaduto) r = 1 (c è un asso di cuori nel mazzo)
 Probabilità: valutazione della possibilità che accada (o sia accaduto) un evento. Probabilità di un evento P = r/n dove r = frequenza dell evento N = Numero di possibili eventi Esempio: Evento = estrazione
Probabilità: valutazione della possibilità che accada (o sia accaduto) un evento. Probabilità di un evento P = r/n dove r = frequenza dell evento N = Numero di possibili eventi Esempio: Evento = estrazione
(5 sin x + 4 cos x)dx [9]
![(5 sin x + 4 cos x)dx [9] (5 sin x + 4 cos x)dx [9]](/thumbs/53/32581225.jpg) FACOLTÀ DI SCIENZE MM. FF. NN. CORSO DI LAUREA IN SCIENZE NATURALI II Modulo di Matematica con elementi di statistica. Esercitazioni A.A. 009.00. Tutor: Mauro Soro, [email protected] Integrali definiti Risolvere
FACOLTÀ DI SCIENZE MM. FF. NN. CORSO DI LAUREA IN SCIENZE NATURALI II Modulo di Matematica con elementi di statistica. Esercitazioni A.A. 009.00. Tutor: Mauro Soro, [email protected] Integrali definiti Risolvere
Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco
 Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco Alfonso Iodice D Enza May 23, 2007 1 Esercizio Si consideri un mazzo di carte francesi di 2 carte e si supponga di stare giocando a poker.
Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco Alfonso Iodice D Enza May 23, 2007 1 Esercizio Si consideri un mazzo di carte francesi di 2 carte e si supponga di stare giocando a poker.
Distribuzione di Probabilità
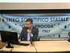 Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Lezione 3 Calcolo delle probabilità
 Lezione 3 Calcolo delle probabilità Definizione di probabilità La probabilità è lo studio degli esperimenti casuali e non deterministici Se lanciamo un dado sappiamo che cadrà ma non è certo che esca il
Lezione 3 Calcolo delle probabilità Definizione di probabilità La probabilità è lo studio degli esperimenti casuali e non deterministici Se lanciamo un dado sappiamo che cadrà ma non è certo che esca il
Capitolo 1: Probabilità
 Calcolo combinatorio Matematica e Informatica+Fisica ESERCIZI Modulo di Matematica e Informatica Corso di Laurea Magistrale in CTF - A.A. 2014/2015 Docente: Filippo Bighi, [email protected] Capitolo 1: Probabilità
Calcolo combinatorio Matematica e Informatica+Fisica ESERCIZI Modulo di Matematica e Informatica Corso di Laurea Magistrale in CTF - A.A. 2014/2015 Docente: Filippo Bighi, [email protected] Capitolo 1: Probabilità
Valore atteso, mazzi di carte e Monte Carlo. Anna Torre-Fulvio Bisi
 Valore atteso, mazzi di carte e Monte Carlo Anna Torre-Fulvio Bisi Eventi Indipendenti Due eventi A, B sono indipendenti se la probabilità che accadano entrambi è il prodotto della probabilità che accada
Valore atteso, mazzi di carte e Monte Carlo Anna Torre-Fulvio Bisi Eventi Indipendenti Due eventi A, B sono indipendenti se la probabilità che accadano entrambi è il prodotto della probabilità che accada
Probabilità discreta
 CAPITOLO 2 Probabilità discreta Esercizio 2.1 Eventi Un opportuno spazio degli eventi è dato da: Ω{(M,M), (M,F), (F, M), (F, F)}. L evento unione di primo figlio femmina e secondo figlio maschio è dato
CAPITOLO 2 Probabilità discreta Esercizio 2.1 Eventi Un opportuno spazio degli eventi è dato da: Ω{(M,M), (M,F), (F, M), (F, F)}. L evento unione di primo figlio femmina e secondo figlio maschio è dato
ESERCIZI SUL CALCOLO COMBINATORIO
 ESERCIZI SUL CALCOLO COMBINATORIO A) SVILUPPARE E CALCOLARE LE SEGUENTI ESPRESSIONI : numero esercizio risoluzione 1) D 3, ) P 4 3) P 6 3 4) 3,3 P 6 5) D ' 3, 6) C 4, 7) C n, n 8) D + D' C 4, 3, 3 3, 9)
ESERCIZI SUL CALCOLO COMBINATORIO A) SVILUPPARE E CALCOLARE LE SEGUENTI ESPRESSIONI : numero esercizio risoluzione 1) D 3, ) P 4 3) P 6 3 4) 3,3 P 6 5) D ' 3, 6) C 4, 7) C n, n 8) D + D' C 4, 3, 3 3, 9)
PROVA DI MATEMATICA VERSO LA RILEVAZIONE INVALSI SCUOLA SECONDARIA DI SECONDO GRADO. 30 quesiti. Scuola... Classe... Alunno...
 VERSO LA RILEVAZIONE INVALSI SCUOLA SECONDARIA DI SECONDO GRADO PROVA DI MATEMATICA 0 quesiti Scuola..................................................................................................................................................................................................
VERSO LA RILEVAZIONE INVALSI SCUOLA SECONDARIA DI SECONDO GRADO PROVA DI MATEMATICA 0 quesiti Scuola..................................................................................................................................................................................................
Corso di preparazione ai Giochi di Archimede Calcolo combinatorio & Probabilità
 Corso di preparazione ai Giochi di Archimede Calcolo combinatorio & Probabilità ) Quante quaterne (x, x2, x3, x4) di numeri interi non negativi soddisfano l equazione x+x2+x3+x4=7? a) 25 b) 289 c) 40 d)
Corso di preparazione ai Giochi di Archimede Calcolo combinatorio & Probabilità ) Quante quaterne (x, x2, x3, x4) di numeri interi non negativi soddisfano l equazione x+x2+x3+x4=7? a) 25 b) 289 c) 40 d)
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2006/07
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
Statistica. Esercitazione 10. Alfonso Iodice D Enza [email protected]. Università degli studi di Cassino. Statistica. A. Iodice. V.C.
 uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
La probabilità matematica
 1 La probabilità matematica In generale parliamo di eventi probabili o improbabili quando non siamo sicuri se si verificheranno. DEFINIZIONE. Un evento (E) si dice casuale, o aleatorio, quando il suo verificarsi
1 La probabilità matematica In generale parliamo di eventi probabili o improbabili quando non siamo sicuri se si verificheranno. DEFINIZIONE. Un evento (E) si dice casuale, o aleatorio, quando il suo verificarsi
Calcolo delle Probabilità 2013/14 Foglio di esercizi 2
 Calcolo delle Probabilità 2013/1 Foglio di esercizi 2 Calcolo combinatorio. Esercizio 1. In un mazzo di 52 carte da Poker ogni carta è identificata da un seme (cuori, quadri, fiori, picche e da un tipo
Calcolo delle Probabilità 2013/1 Foglio di esercizi 2 Calcolo combinatorio. Esercizio 1. In un mazzo di 52 carte da Poker ogni carta è identificata da un seme (cuori, quadri, fiori, picche e da un tipo
EVENTI FUTURI EQUIPROBABILI Lezione n. 3
 EVENTI FUTURI EQUIPROBABILI Lezione n. 3 Finalità: Enunciare le definizioni maturate attraverso l esercitazione pratica. Verificare la corrispondenza tra ipotesi formulate e risultati sperimentali. Metodo:
EVENTI FUTURI EQUIPROBABILI Lezione n. 3 Finalità: Enunciare le definizioni maturate attraverso l esercitazione pratica. Verificare la corrispondenza tra ipotesi formulate e risultati sperimentali. Metodo:
Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4. uscirà il numero 9
 Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4 o ancora: uscirà il numero 9 Possiamo dire che le previsione del tuo compagno sono la prima certa, la seconda
Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4 o ancora: uscirà il numero 9 Possiamo dire che le previsione del tuo compagno sono la prima certa, la seconda
Calcolo delle probabilità
 Capitolo 1 Calcolo delle probabilità Esercizio I. 1 Luca prende il treno per andare a scuola e cerca il suo amico Giovanni. Luca sa che è ugualmente probabile che Giovanni abbia preso il bus o il treno
Capitolo 1 Calcolo delle probabilità Esercizio I. 1 Luca prende il treno per andare a scuola e cerca il suo amico Giovanni. Luca sa che è ugualmente probabile che Giovanni abbia preso il bus o il treno
I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito.
 TEST DI AUTOVALUTAZIONE - SETTIMANA I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
TEST DI AUTOVALUTAZIONE - SETTIMANA I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
Il caso, probabilmente: la partita a dadi di Riccardo Mini
 Elementi di Probabilità presenti nell opera teatrale Il caso, probabilmente: la partita a dadi di Riccardo Mini con Fausto Bernardinello, Maria Eugenia D Equino, Annig Raimondi con la collaborazione dei
Elementi di Probabilità presenti nell opera teatrale Il caso, probabilmente: la partita a dadi di Riccardo Mini con Fausto Bernardinello, Maria Eugenia D Equino, Annig Raimondi con la collaborazione dei
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV A PT
 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV A PT Scheda : equazioni e disequazioni goniometriche. Risolvi la seguente equazione: sin + sin cos + 5 = 0. Suggerimento dell insegnante:
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA IV A PT Scheda : equazioni e disequazioni goniometriche. Risolvi la seguente equazione: sin + sin cos + 5 = 0. Suggerimento dell insegnante:
Preparazione all esame in italiano del ALGEBRA -
 TEST PSICOMETRICO Preparazione all esame in italiano del 2014 - - Febbraio Marzo 2014 Docente: Giacomo Sassun E-mail: [email protected] [email protected] Realizzato grazie al contributo dell UNIONE DELLE
TEST PSICOMETRICO Preparazione all esame in italiano del 2014 - - Febbraio Marzo 2014 Docente: Giacomo Sassun E-mail: [email protected] [email protected] Realizzato grazie al contributo dell UNIONE DELLE
TEST DI AUTOVALUTAZIONE PROBABILITÀ
 TEST DI AUTOVALUTAZIONE PROBABILITÀ Statistica 1 Parte A 1.1 Si considerino gli eventi A = nessuno studente ha superato l esame e B = nessuno studente maschio ha superato l esame. Allora A c B è uguale
TEST DI AUTOVALUTAZIONE PROBABILITÀ Statistica 1 Parte A 1.1 Si considerino gli eventi A = nessuno studente ha superato l esame e B = nessuno studente maschio ha superato l esame. Allora A c B è uguale
2. Se il rapporto tra le aree di due figure simili è 4, qual è il rapporto tra i corrispondenti perimetri?
 . 000 99,02 = 0,98,98 900,98 D. 90,98 2. Se il rapporto tra le aree di due figure simili è 4, qual è il rapporto tra i corrispondenti perimetri? 4 2 2 D. 4 3. Un cuoco prepara un piatto di tagliatelle
. 000 99,02 = 0,98,98 900,98 D. 90,98 2. Se il rapporto tra le aree di due figure simili è 4, qual è il rapporto tra i corrispondenti perimetri? 4 2 2 D. 4 3. Un cuoco prepara un piatto di tagliatelle
La probabilità del gioco o il gioco della probabilità? Dispensa probabilità e calcolo combinatorio
 La probabilità del gioco o il gioco della probabilità? Dispensa probabilità e calcolo combinatorio Massimo Buzzi, Lucio Alberto Monti 1 Mappe Riassuntive 1.1 Calcolo combinatorio 1.2 Probabilità 1 2 Glossario
La probabilità del gioco o il gioco della probabilità? Dispensa probabilità e calcolo combinatorio Massimo Buzzi, Lucio Alberto Monti 1 Mappe Riassuntive 1.1 Calcolo combinatorio 1.2 Probabilità 1 2 Glossario
