R. BARBONI COSTRUZIONI AEROSPAZIALI L elemento finito
|
|
|
- Fabiola Marini
- 7 anni fa
- Visualizzazioni
Transcript
1 R. BARBONI COSRUZIONI AEROSPAZIALI L elemento finito Nella realtà, aste, travi, piastre, gusci,... non sono sollecitati solo con carichi applicati ai loro estremi ed il loro comportamento non può essere rappresentato in modo esatto solo da due o quattro parametri come visto precedentemente. Così nel caso di trave inflessa con carichi distribuiti lungo l asse la (2.25) non rappresenta la soluzione esatta del problema dell intera trave. Se però immaginiamo di dividere idealmente la trave di lunghezza L in elementi di trave lunghi l n ed immaginiamo di concentrare il carico solo ai nodi, la (2.25) rappresenta una soluzione valida nell ambito di ogni elemento l n. Per ciascuno di essi il comportamento elastico è descritto dalla matrice di rigidezza (2.29). Il modello ad E.F. dell intera trave sarà dato assemblando le [K (e) ] dei vari elementi. q x z i z L M i,θ i M j,θ j l F i,w i F j,w j j x x Nel caso di figura, considerando 7 nodi, in ognuno dei quali sono possibili due G.L., il modello matematico del continuo trave è dato da un sistema discreto a 14 G.L., salvo i vincoli. In tale modo di procedere notiamo: a) che abbiamo assunto che la struttura è una trave a comportamento flessionale; b) che, nell ambito della teoria della trave, le variabili cinematiche sono lo spostamento fuori del piano w(x) e la rotazione θ(x); c) che lo spostamento w(x), in ogni elemento piccolo ma continuo, viene approssimato con un numero finito di parametri utilizzando la (2.24). Ne consegue, nell ipotesi di Kirchoff, la rotazione θ(x) = w/ x ; d) che i parametri con cui esprimere lo spostamento w(x) sono gli spostamenti e le rotazioni ai nodi dell elemento; e) che il carico distribuito q(x) è ad un sistema di forze e momenti concentrati ed applicati solo ai nodi. I passi c),d),e) fanno sì che un elemento continuo sia modellizzato in termini discreti. Il modello discreto dell elemento è detto elemento finito.
2 18 R. BARBONI ELEMENI FINII Con questa serie di ipotesi si realizza un modello approssimato del comportamento della struttura. L importante è fissare i criteri con cui si effettua la discretizzazione e capire il tipo e l ordine di approssimazione introdotto. Questo consente di poter raffinare il modello fino a tendere alla soluzione esatta del problema. ediamo i vari passi da fare in generale per arrivare al modello discreto. 1) Innanzi tutto la struttura reale, continua, viene idealmente tagliata da superfici e linee in modo da pensarla costituita da elementi. I punti estremi o di spigolo dell elemento sono i nodi. 2) Si identifica il comportamento di ogni elemento (o classe di elementi) della struttura con il comportamento di un elemento tipico nell ambito di una certa teoria dell elasticità. Si avranno così elementi tipo asta, trave,... In funzione del tipo di elemento si individuano le variabili cinematiche, che indicheremo genericamente come vettore spostamento {S(x,y,z)}, le variabili di deformazione {ε(x,y,z)} e di sforzo {σ(x,y,z)} 1. 3) Si discretizza il comportamento dell elemento rappresentando le variabili cinematiche {S} attraverso un numero discreto di parametri, definiti solo ed unicamente ai nodi. ali parametri { } sono indicati come spostamenti nodali. Il numero g delle componenti il vettore { }, indica il numero di variabili con cui è discretizzato l elemento e diremo che l elemento finito (E.F.) possiede g gradi di libertà (G.L.). Quindi: (4.1) {S(x,y,z)} = [N(x,y,z)] { } Ovviamente la (4.1) può risultare esatta solo nel caso di analisi statica e per elementi che siano connessi ad altri in un numero discreto di punti. Nel caso generale di elemento unito con continuità a quelli circostanti e di analisi dinamica la (4.1) rappresenta solo una espressione approssimata degli spostamenti. La matrice [N] è l insieme delle funzioni che consente di esprimere, punto per punto, lo spostamento all interno dell elemento in funzione di { }. Possiamo quindi pensare ed indicare le componenti di [N(x,y,z)] come funzioni di interpolazione degli spostamenti nodali. 4) Esprimere le deformazioni in termini degli spostamenti nodali. Ricordando le relazioni cinematiche, che legano le deformazioni agli spostamenti ed utilizzando le (4.1): (4.2) { ε } = [ Bxyz (,, )]{ } 1 Si noti: 1)-{S},{ε},{σ} sono funzioni di x,y,z, cioè l elemento è ancora un continuo; 2)-i nomi di tali vettori sono posti tra ad indicare che non sempre le dimensioni fisiche corrispondono al nome.
3 R. BARBONI COSRUZIONI AEROSPAZIALI 19 5) Attraverso i legami costitutivi del materiale possiamo esprimere gli sforzi in termini di { }: (4.3) { σ} = [ C]{ ε} = [ C][ B( x, y, z) ]{ } 6) Si esprimono le forze elastiche in termini degli spostamenti nodali { }. A tale scopo si possono impiegare varie tecniche: minimizzazione dell energia elastica, principio dei lavori virtuali, equazioni di Lagrange... Per la sua completa generalità e possibilità di utilizzo indipendentemente dalla natura delle forze in esame utilizziamo il principio dei lavori virtuali, per cui il lavoro virtuale delle forze elastiche risulta: (4.4) δl = { δε} { σ} d che, ricordando le (4.2,3), si scrive: (4.5) δl= { δ } [ B] [ C][ B] d { } = { δ } [ K]{ } avendo indicato con [K] la matrice di rigidezza: (4.6) [ K] = [ B] [ C][ B] d Pertanto le forze elastiche sono espresse come: (4.7) [ F ] [ K]{ } E = Si noti come per ottenere la (4.6) si siano utilizzate sia le relazioni cinematiche che quelle costitutive. Inoltre, integrando su tutto il volume, nella [K] compaiono anche le dimensioni geometriche oltre ai moduli elastici del materiale con cui è realizzato l elemento. 7) Si concentrano ai nodi le eventuali forze distribuite. Le forze (generalizzate), sia esterne che quelle dovute alle reazioni vincolari, che risultano concentrate in alcuni punti, non meritano una particolare analisi. Infatti possiamo sempre assumere i punti dove le forze sono applicate come nodi della struttura; in caso di forze distribuite, queste vanno opportunamente riportate come carichi concentrati applicati ai nodi. Invece nel caso di forze (generalizzate) distribuite, si deve provvedere a sostituirle con un sistema di forze (generalizzate) staticamente equivalente
4 20 R. BARBONI ELEMENI FINII applicato ai nodi. Chiaramente maggiore è il numero di nodi scelti, più accurata è l analisi ma maggiore il lavoro da eseguire. Una tale discretizzazione può prescindere dalla (4.1) ma in una ottica più rigorosa nell ambito della teoria degli E.F. è opportuno che anche la discretizzazione dei carichi segua la stessa logica seguita per valutare la (4.6). In quest ultimo caso si parla di matrice dei carichi consistente. Un modo semplice ma efficace per trovare il sistema di forze nodali consistente è quello di imporre che il lavoro virtuale delle forze ai nodi sia uguale al lavoro virtuale delle forze realmente applicate. Nel caso generale di forze per unità di volume {f }, forze per unità di superficie {f S }, e forze concentrate ai nodi {f N }, si scrive: (4.8) { δs} { f } d + { δs} { f } da + { δ } { f } = { δ } { F} A S N 8) Si scrive l equazione di equilibrio dell elemento. A tal fine è sufficiente uguagliare il lavoro virtuale delle forze interne espresso dalla (4.5) a quello delle forze esterne espresso dalla (4.8): (4.9) { δ } [ K]{ } = { δ } { F} che, dovendo valere per qualsiasi {δ } 0 porta alla classica relazione: (4.10) [ K]{ } = { F}
5 R. BARBONI COSRUZIONI AEROSPAZIALI Requisiti dell Elemento Finito Nei vari passi precedentemente esposti abbiamo sicuramente soddisfatto, avendole impiegate, alcune delle relazioni fondamentali alla base della teoria dell elasticità, quali: Le relazioni cinematiche (4.2). I legami costitutivi (4.3). Le condizioni (4.9) che garantiscono l equilibrio. Inoltre abbiamo tenuto conto della geometria dell elemento integrando su tutto il volume dello stesso. Il tutto partendo con l assumere il campo degli spostamenti nella forma (4.1), dove niente si è detto circa la scelta delle funzioni interpolanti [N]. Sempre nell ambito della teoria dell elasticità, gli spostamenti devono risultare continui e derivabili. Pertanto la [N(x,y,z)] deve essere scelta in modo da garantire spostamenti {S(x,y,z)} continui in ogni punto dell elemento, contorno compreso. Altri requisiti imposti alle funzioni interpolanti derivano dal garantire che nel processo di discretizzazione non vengano perse alcune caratteristiche proprie del continuo. Solo in tale caso si è garantiti che aumentando il numero di G.L. la struttura tende nuovamente al continuo e la soluzione tende alla soluzione esatta. Per avere convergenza monotona, l elemento finito deve risultare completo e compatibile. Proprietà che possono essere garantite solo attraverso una idonea scelta delle funzioni interpolanti [N]. A Un elemento gode della proprietà di completezza se soddisfa ai due seguenti requisiti: A1. Capacità di compiere spostamenti rigidi. La necessità di una tale proprietà è evidente dalla figura che riporta una trave prima e dopo la deformazione conseguente all applicazione del carico P. utti gli elementi, indipendentemente dal P fatto che subiscano deformazioni a seguito della sollecitazione, devono poter seguire il moto derivante da chi li precede e/o segue. A tali moti rigidi negli elementi 1,2,3,4 si vanno a sommare quelli conseguenti allo stato di sollecitazione. Gli elementi 5,6,7, pur non sollecitati, traslano e ruotano rigidamente. 5
6 22 R. BARBONI ELEMENI FINII Il numero dei modi rigidi possibili per un elemento può essere analizzato attraverso l analisi degli autovalori della relativa matrice di rigidezza: (5.1) [ K]{ X} = λ { X} da cui, indicando con [W], la matrice degli autovettori e [Λ] la corrispondente matrice diagonale degli autovalori: (5.2) [ W] [ K][ W] = [ Λ ] pertanto possiamo interpretare l autovalore come la rigidezza generalizzata relativa al corrispondente autovettore. In altri termini λ 1, λ 2,..., indica quanto è rigido l elemento nel modo corrispondente. Qualora si abbia λ=0, la rigidezza corrispondente è nulla e quindi la struttura si muove rigidamente. La trasformazione (5.2) consente pertanto di individuare i modi rigidi rispetto a quelli di deformazione elastica. A2. Capacità di garantire uno stato di deformazione costante al tendere a zero delle dimensioni dell E.F. Infatti lo stato di deformazione di un elemento che tende a zero tende a diventare costante e poichè un elemento finito può essere piccolo quanto si desidera, nella sua rappresentazione discreta deve essere implicita tale capacità. B Un elemento gode della proprietà di compatibilità se gli spostamenti sono continui non solo al suo interno ma anche al suo contorno, ovvero lungo i bordi di elementi contigui. Fisicamente la condizione di compatibilità garantisce che non vi siano lacerazioni e/o compenetrazioni tra elementi contigui una volta assemblati. La compatibilità è automaticamente soddisfatta tra elementi aste e travi, dal momento che sono uniti solo ai nodi dove si impone l uguaglianza degli spostamenti tra elementi che convergono sullo stesso nodo. Nel caso di elementi nello stato di sollecitazione o deformazione piana, elementi di lastra piana, elementi tridimensionali in cui le componenti di {S} sono u,v,w, la continuità è assicurata assumendo [N] lineare in x,y,z. Più difficile è garantire la compatibilità per elementi non monodimensionali soggetti a flessione, dove in [N] compaiono termini nelle potenze di x,y,z. Un modo di procedere per ottenere delle [N] che garantiscono i requisiti indicati in A,B è di scegliere le [S(x,y,z)] come combinazione lineare di funzioni [Φ(x,y,z)] continue e derivabili.
7 R. BARBONI COSRUZIONI AEROSPAZIALI 23 Una classe di funzioni Φ(x,y,z) molto utilizzate sono i polinomi, che sono funzioni continue e facilmente differenziabili. Indichiamo con {A} il vettore dei coefficienti della combinazione lineare: (5.3) {S(x,y,z)} = [Φ(x,y,z)]{A} ali coefficienti incogniti sono scelti in numero pari ai gradi di libertà g dell elemento, per cui il vettore {A} ha le stesse dimensioni del vettore { }. I coefficienti {A} possono essere espressi in termini degli spostamenti nodali ricordando che ai nodi deve risultare {S} n ={ }, quindi: (5.4) [Φ(x n,y n,z n )]{A}={ } da cui: (5.5) {A} = [Φ(x n,y n,z n )] 1 { } pertanto i coefficienti del polinomio non rappresentano uno spostamento fisico ma una combinazione lineare dei reali spostamenti nodali e per questo sono indicati come coordinate generalizzate. Elementi finiti la cui formulazione è basata assumendo per gli spostamenti espressioni che sono funzioni di coefficienti incogniti considerati come coordinate generalizzate sono detti modelli finiti in coordinate generalizzate. Sostituendo la (5.5) nella (5.3): (5.6) {S} = [Φ(x,y,z)] [Φ(x n,y n,z n )] 1 { }=[(N(x,y,z)]{ } ovvero la (4.1). Ovviamente, oltre ai polinomi possono essere usate altre funzioni, impiegando la stessa tecnica.
Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto
 Il Metodo degli Elementi Finiti Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto Dalle dispense del prof. Dario Amodio e dalle lezioni del prof. Giovanni Santucci Per ottenere la
Il Metodo degli Elementi Finiti Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto Dalle dispense del prof. Dario Amodio e dalle lezioni del prof. Giovanni Santucci Per ottenere la
Costruzioni in zona sismica
 Costruzioni in zona sismica Lezione 7 Sistemi a più gradi di libertà Il problema dinamico viene formulato con riferimento a strutture con un numero finito di gradi di libertà. Consideriamo le masse concentrate
Costruzioni in zona sismica Lezione 7 Sistemi a più gradi di libertà Il problema dinamico viene formulato con riferimento a strutture con un numero finito di gradi di libertà. Consideriamo le masse concentrate
CAPITOLO I TEORIA DELLA PIASTRA
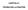 CAPITOLO I TEORIA DELLA PIASTRA R. BARBONI TEORIA DELLA PIASTRA 3 1. La piastra Si consideri la struttura di figura con riferimento ad un sistema di coordinato con, nel piano medio e z ortogonale ad esso,
CAPITOLO I TEORIA DELLA PIASTRA R. BARBONI TEORIA DELLA PIASTRA 3 1. La piastra Si consideri la struttura di figura con riferimento ad un sistema di coordinato con, nel piano medio e z ortogonale ad esso,
Statica delle murature
 Statica delle murature Corso di Laurea Specialistica in Ingegneria Edile - A.A. 2006-2007 Università degli Studi di Cagliari Prof. ing. Antonio Cazzani antonio.cazzani@ing.unitn.it http://www.ing.unitn.it/~cazzani/didattica/sdm
Statica delle murature Corso di Laurea Specialistica in Ingegneria Edile - A.A. 2006-2007 Università degli Studi di Cagliari Prof. ing. Antonio Cazzani antonio.cazzani@ing.unitn.it http://www.ing.unitn.it/~cazzani/didattica/sdm
1 Equilibrio statico nei corpi deformabili
 Equilibrio statico nei corpi deformabili Poiché i materiali reali non possono considerarsi rigidi, dobbiamo immaginare che le forze esterne creino altre forze interne che tendono ad allungare (comprimere)
Equilibrio statico nei corpi deformabili Poiché i materiali reali non possono considerarsi rigidi, dobbiamo immaginare che le forze esterne creino altre forze interne che tendono ad allungare (comprimere)
ELEMENTI MONODIMENSIONALI : TRAVE
 ELEMENTI MONODIMENSIONALI : TRAVE La trave è un elemento strutturale con una dimensione predominante sulle altre due. baricentro G sezione trasversale linea d asse rappresentazione schematica 1 ELEMENTI
ELEMENTI MONODIMENSIONALI : TRAVE La trave è un elemento strutturale con una dimensione predominante sulle altre due. baricentro G sezione trasversale linea d asse rappresentazione schematica 1 ELEMENTI
Università degli Studi di Cagliari - Facoltà di Ingegneria e Architettura. Fondamenti di Costruzioni Meccaniche Tensione e deformazione Carico assiale
 Esercizio N.1 Un asta di acciaio è lunga 2.2 m e non può allungarsi più di 1.2 mm quando le si applica un carico di 8.5 kn. Sapendo che E = 200 GPa, determinare: (a) il più piccolo diametro dell asta che
Esercizio N.1 Un asta di acciaio è lunga 2.2 m e non può allungarsi più di 1.2 mm quando le si applica un carico di 8.5 kn. Sapendo che E = 200 GPa, determinare: (a) il più piccolo diametro dell asta che
Verifiche di deformabilità e di stabilità degli elementi inflessi
 modulo D L acciaio Unità Il metodo alle tensioni ammissibili 1 Verifiche di deformabilità e di stabilità degli elementi inflessi Verifica nei confronti dello svergolamento (instabilità laterale) Esaminiamo
modulo D L acciaio Unità Il metodo alle tensioni ammissibili 1 Verifiche di deformabilità e di stabilità degli elementi inflessi Verifica nei confronti dello svergolamento (instabilità laterale) Esaminiamo
Dinamica delle Strutture
 Corso di Laurea magistrale in Ingegneria Civile e per l Ambiente e il Territorio Dinamica delle Strutture Prof. Adolfo SANTINI Ing. Francesco NUCERA Prof. Adolfo Santini - Dinamica delle Strutture 1 Dinamica
Corso di Laurea magistrale in Ingegneria Civile e per l Ambiente e il Territorio Dinamica delle Strutture Prof. Adolfo SANTINI Ing. Francesco NUCERA Prof. Adolfo Santini - Dinamica delle Strutture 1 Dinamica
PROGETTAZIONE DI STRUTTURE MECCANICHE
 PROGETTAZIONE DI STRUTTURE MECCANICHE Andrew Ruggiero A.A. 2011/12 Analisi matriciale delle strutture: caratterizzazione degli elementi A. Gugliotta, Elementi finiti Parte I Elementi e strutture Una qualsiasi
PROGETTAZIONE DI STRUTTURE MECCANICHE Andrew Ruggiero A.A. 2011/12 Analisi matriciale delle strutture: caratterizzazione degli elementi A. Gugliotta, Elementi finiti Parte I Elementi e strutture Una qualsiasi
Le deformazioni nelle travi rettilinee inflesse
 2 Le deformazioni nelle travi rettilinee inflesse Tema 2.1 Per la struttura riportata in figura 2.1 determinare l espressione analitica delle funzioni di rotazione ed abbassamento, integrando le equazioni
2 Le deformazioni nelle travi rettilinee inflesse Tema 2.1 Per la struttura riportata in figura 2.1 determinare l espressione analitica delle funzioni di rotazione ed abbassamento, integrando le equazioni
(P x) (P y) = x P t (P y) = x (P t P )y = x y.
 Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
Analisi di un telaio a due livelli e maglie di forma generica secondo il Metodo degli Spostamenti (MdS)
 Pagina 1 di 18 Analisi di un telaio a due livelli e maglie di forma generica secondo il Metodo degli Spostamenti (MdS) Schema Strutturale Valori numerici Si riportano nel seguito i valori numerici delle
Pagina 1 di 18 Analisi di un telaio a due livelli e maglie di forma generica secondo il Metodo degli Spostamenti (MdS) Schema Strutturale Valori numerici Si riportano nel seguito i valori numerici delle
IL SAP 2000 E IL CALCOLO DELLE SOLLECITAZIONI PER LA TRAVE CONTINUA
 prof. Renato Giannini IL SAP 2000 E IL CALCOLO DELLE SOLLECITAZIONI PER LA TRAVE CONTINUA (arch. Lorena Sguerri) Combinazioni di carico Solaio a due campate con mensola (balcone): combinazioni di carico
prof. Renato Giannini IL SAP 2000 E IL CALCOLO DELLE SOLLECITAZIONI PER LA TRAVE CONTINUA (arch. Lorena Sguerri) Combinazioni di carico Solaio a due campate con mensola (balcone): combinazioni di carico
Sommario 1 VOLUME CAPITOLO 1 - Matrici 1 VOLUME CAPITOLO 3 - Geometria delle masse 1 VOLUME CAPITOLO 2 - Notazione indiciale
 Sommario CAPITOLO 1 - Matrici...! Definizione! Matrici di tipo particolare Definizioni relative-! Definizioni ed operazioni fondamentali! Somma di matrici (o differenza)! Prodotto di due matrici! Prodotti
Sommario CAPITOLO 1 - Matrici...! Definizione! Matrici di tipo particolare Definizioni relative-! Definizioni ed operazioni fondamentali! Somma di matrici (o differenza)! Prodotto di due matrici! Prodotti
Capitolo 2. Statica del corpo rigido. 2.1 Azioni su un corpo rigido
 Capitolo 2 Statica del corpo rigido La statica è la parte della meccanica che si occupa dello studio dell equilibrio di corpi in quiete, ossia fermi, o mobili di moto rettilineo uniforme. In effetti applichiamo
Capitolo 2 Statica del corpo rigido La statica è la parte della meccanica che si occupa dello studio dell equilibrio di corpi in quiete, ossia fermi, o mobili di moto rettilineo uniforme. In effetti applichiamo
Introduzione al Calcolo Scientifico - A.A
 Introduzione al Calcolo Scientifico - A.A. 2009-2010 Discretizzazione di un problema ai limiti Si consideri il seguente problema ai limiti del secondo ordine (problema dell elasticità 1D in regime di piccole
Introduzione al Calcolo Scientifico - A.A. 2009-2010 Discretizzazione di un problema ai limiti Si consideri il seguente problema ai limiti del secondo ordine (problema dell elasticità 1D in regime di piccole
ESERCITAZIONE SUL CRITERIO
 TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
METODO DEGLI ELEMENTI FINITI
 Barlow Points In teoria potremmo valutare tensioni e deformazioni, o i gradienti per altri tipi di analisi, in qualsiasi punto interno all elemento. Tuttavia le tensioni e le deformazioni previste dal
Barlow Points In teoria potremmo valutare tensioni e deformazioni, o i gradienti per altri tipi di analisi, in qualsiasi punto interno all elemento. Tuttavia le tensioni e le deformazioni previste dal
TRAVI ALTE E ZONE DI DISCONTINUTA Lezione 1
 TRAVI ALTE E ZONE DI DISCONTINUTA Lezione 1 DEFINIZIONI PRINCIPI E METODI DI CALCOLO Definizione di D-Regions Metodi di calcolo che fanno uso di codici agli E.F. I modelli Strut-and-tie Principi del metodo
TRAVI ALTE E ZONE DI DISCONTINUTA Lezione 1 DEFINIZIONI PRINCIPI E METODI DI CALCOLO Definizione di D-Regions Metodi di calcolo che fanno uso di codici agli E.F. I modelli Strut-and-tie Principi del metodo
Giacomo Sacco Appunti di Costruzioni Edili
 Giacomo Sacco Appunti di Costruzioni Edili Le tensioni dovute a sforzo normale, momento, taglio e a pressoflessione. 1 Le tensioni. Il momento, il taglio e lo sforzo normale sono le azioni che agiscono
Giacomo Sacco Appunti di Costruzioni Edili Le tensioni dovute a sforzo normale, momento, taglio e a pressoflessione. 1 Le tensioni. Il momento, il taglio e lo sforzo normale sono le azioni che agiscono
Sollecitazioni semplici Il Taglio
 Sollecitazioni semplici Il Taglio Considerazioni introduttive La trattazione relativa al calcolo delle sollecitazioni flessionali, è stata asata sull ipotesi ce la struttura fosse soggetta unicamente a
Sollecitazioni semplici Il Taglio Considerazioni introduttive La trattazione relativa al calcolo delle sollecitazioni flessionali, è stata asata sull ipotesi ce la struttura fosse soggetta unicamente a
Tesina UNIVERSITÀ DEGLI STUDI G. D ANNUNZIO DI CHIETI-PESCARA FACOLTÀ DI ARCHITETTURA F 1. π/4
 UNIVERSITÀ DEGLI STUDI G. D ANNUNZIO DI CHIETI-ESCARA FACOLTÀ DI ARCHITETTURA CORSO DI LAUREA SECIALISTICA, CORSI DI LAUREA TRIENNALI SCIENZA DELLE COSTRUZIONI E TEORIA DELLE STRUTTURE (Canali B,C) a.a.
UNIVERSITÀ DEGLI STUDI G. D ANNUNZIO DI CHIETI-ESCARA FACOLTÀ DI ARCHITETTURA CORSO DI LAUREA SECIALISTICA, CORSI DI LAUREA TRIENNALI SCIENZA DELLE COSTRUZIONI E TEORIA DELLE STRUTTURE (Canali B,C) a.a.
L EQUILIBRIO DEL PUNTO MATERIALE
 1 L EQUILIBRIO DEL PUNTO MATERIALE La statica studia l equilibrio dei corpi. Un corpo è in equilibrio se è fermo e persevera nel suo stato di quiete al trascorrere del tempo. Un modello è la semplificazione
1 L EQUILIBRIO DEL PUNTO MATERIALE La statica studia l equilibrio dei corpi. Un corpo è in equilibrio se è fermo e persevera nel suo stato di quiete al trascorrere del tempo. Un modello è la semplificazione
Uno di questi casi è rappresentato dal cedimento in elementi di strutture soggetti a carichi di compressione che danno luogo ad instabilità elastica
 In alcuni casi una struttura soggetta a carichi statici può collassare con un meccanismo diverso da quello del superamento dei limiti di resistenza del materiale. Uno di questi casi è rappresentato dal
In alcuni casi una struttura soggetta a carichi statici può collassare con un meccanismo diverso da quello del superamento dei limiti di resistenza del materiale. Uno di questi casi è rappresentato dal
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica I parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Meccanica analitica I parte Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
RELAZIONE ESERCITAZIONI AUTODESK INVENTOR
 20 Ottobre 2015 RELAZIONE ESERCITAZIONI AUTODESK INVENTOR Corso di Costruzione di Macchine e Affidabilità C.d.L.M. in Ingegneria Meccanica Docente: Prof.ssa Cosmi Francesca Assistente: Dott.ssa Ravalico
20 Ottobre 2015 RELAZIONE ESERCITAZIONI AUTODESK INVENTOR Corso di Costruzione di Macchine e Affidabilità C.d.L.M. in Ingegneria Meccanica Docente: Prof.ssa Cosmi Francesca Assistente: Dott.ssa Ravalico
Cinematica ed equilibrio del corpo rigido
 omportamento meccanico dei materiali inematica piana omportamento meccanico dei materiali inematica ed equilibrio del corpo rigido inematica piana Equilibrio esterno aratteristiche di sollecitazione 2
omportamento meccanico dei materiali inematica piana omportamento meccanico dei materiali inematica ed equilibrio del corpo rigido inematica piana Equilibrio esterno aratteristiche di sollecitazione 2
Trave isostatica Studio della deformata con il metodo della LINEA ELASTICA
 Trave isostatica Studio della deformata con il metodo della LINEA ELASTICA Trave a mensola, di rigidezza flessionale costante pari a EI, soggetta a forza verticale agente all estremo liero. Determinare
Trave isostatica Studio della deformata con il metodo della LINEA ELASTICA Trave a mensola, di rigidezza flessionale costante pari a EI, soggetta a forza verticale agente all estremo liero. Determinare
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione numerica. Introduzione al calcolo numerico. Derivazione numerica (II) Derivazione numerica (III)
 Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
1. Impostazione di un semplice modello FEM
 Progettazione Assistita di Strutture Meccaniche 24/06/2011, pagina 1/5 Cognome: Anno accademico in cui si è seguito il corso Nome: [2010/2011] [2009/2010] [2008/2009] [........ ] Matricola: Componenti
Progettazione Assistita di Strutture Meccaniche 24/06/2011, pagina 1/5 Cognome: Anno accademico in cui si è seguito il corso Nome: [2010/2011] [2009/2010] [2008/2009] [........ ] Matricola: Componenti
Moto vario nelle correnti a superficie libera Nozione elementare di onda In termini generali un'onda consiste nella propagazione di un segnale
 1 Moto vario nelle correnti a superficie libera Nozione elementare di onda In termini generali un'onda consiste nella propagazione di un segnale attraverso un mezzo (nella fattispecie un liquido) con una
1 Moto vario nelle correnti a superficie libera Nozione elementare di onda In termini generali un'onda consiste nella propagazione di un segnale attraverso un mezzo (nella fattispecie un liquido) con una
2. Si Discretizzano i carichi in CARICHI CONCENTRATI in modo da riprodurre gli andamenti delle azioni interne. Si opera in pi passi: 2a.
 1 Prove Statiche Permettono la verifica del comportamento elastico struttura allo scopo di validare il modello numerico Le prove prevedono: 1. Struttura completa (full-scale) Sottostruttura (Es. solo centina,
1 Prove Statiche Permettono la verifica del comportamento elastico struttura allo scopo di validare il modello numerico Le prove prevedono: 1. Struttura completa (full-scale) Sottostruttura (Es. solo centina,
Corso di Riabilitazione Strutturale
 Corso di Riabilitazione Strutturale POTENZA, a.a. 2011 2012 VALUTAZIONE DIEDIFICI ESISTENTI IN C.A. I PARTE ANALISI E STRATEGIE DI INTERVENTO Dott. Marco VONA DiSGG, Università di Basilicata marco.vona@unibas.it
Corso di Riabilitazione Strutturale POTENZA, a.a. 2011 2012 VALUTAZIONE DIEDIFICI ESISTENTI IN C.A. I PARTE ANALISI E STRATEGIE DI INTERVENTO Dott. Marco VONA DiSGG, Università di Basilicata marco.vona@unibas.it
Anna Pandolfi Analisi Strutturale e Termica 4.1
 Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
La modellazione delle strutture
 La modellazione delle strutture 1 Programma 31-1-2012 Introduzione e brevi richiami al metodo degli elementi finiti 7-2-2012 La modellazione della geometria 14-2-2012 21-2-2012 28-2-2012 6-3-2012 13-32012
La modellazione delle strutture 1 Programma 31-1-2012 Introduzione e brevi richiami al metodo degli elementi finiti 7-2-2012 La modellazione della geometria 14-2-2012 21-2-2012 28-2-2012 6-3-2012 13-32012
Piastre sottili: soluzioni esatte. Piastra ellittica incastrata al bordo soggetta a carico distribuito costante
 Piastre sottili: soluzioni esatte Piastra ellittica incastrata al bordo soggetta a carico distribuito costante Piastre sottili: soluzioni esatte Piastra triangolare appoggiata al bordo soggetta a carico
Piastre sottili: soluzioni esatte Piastra ellittica incastrata al bordo soggetta a carico distribuito costante Piastre sottili: soluzioni esatte Piastra triangolare appoggiata al bordo soggetta a carico
Robotica industriale. Richiami di statica del corpo rigido. Prof. Paolo Rocco
 Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico
 5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
1 Cinematica del punto Componenti intrinseche di velocità e accelerazione Moto piano in coordinate polari... 5
 Indice 1 Cinematica del punto... 1 1.1 Componenti intrinseche di velocità e accelerazione... 3 1.2 Moto piano in coordinate polari... 5 2 Cinematica del corpo rigido... 9 2.1 Configurazioni rigide......
Indice 1 Cinematica del punto... 1 1.1 Componenti intrinseche di velocità e accelerazione... 3 1.2 Moto piano in coordinate polari... 5 2 Cinematica del corpo rigido... 9 2.1 Configurazioni rigide......
Lezione 4 - I vincoli interni
 Lezione 4 - I vincoli interni [Ultimarevisione: revisione:2agosto agosto2008] Proseguendo nello studio dei corpi rigidi, adotteremo d'ora in poi la seguente classificazione geometrica, necessariamente
Lezione 4 - I vincoli interni [Ultimarevisione: revisione:2agosto agosto2008] Proseguendo nello studio dei corpi rigidi, adotteremo d'ora in poi la seguente classificazione geometrica, necessariamente
DINAMICA DI SISTEMI AEROSPAZIALI Tema d esame 03 settembre 2012
 DINAMICA DI SISTEMI AEROSPAZIAI Tema d esame 3 settembre 1 / Esercizio 1. Il meccanismo in figura presenta due aste / B identiche AB e CD di lunghezza e massa trascurabile. e F due aste sono incernierate
DINAMICA DI SISTEMI AEROSPAZIAI Tema d esame 3 settembre 1 / Esercizio 1. Il meccanismo in figura presenta due aste / B identiche AB e CD di lunghezza e massa trascurabile. e F due aste sono incernierate
Consideriamo come piena solo l innalzamento del livello causato da un aumento delle portate nel corso d acqua considerato.
 Propagazione delle piene: generalità Consideriamo come piena solo l innalzamento del livello causato da un aumento delle portate nel corso d acqua considerato. La propagazione dell onda di piena dipende
Propagazione delle piene: generalità Consideriamo come piena solo l innalzamento del livello causato da un aumento delle portate nel corso d acqua considerato. La propagazione dell onda di piena dipende
Massa, temperatura, volume, densità sono grandezze scalari. La forza è una grandezza vettoriale
 Le forze (2 a parte) Massa, temperatura, volume, densità sono grandezze scalari La forza è una grandezza vettoriale Scalari e vettori Si definiscono SCALARI le grandezze fisiche che sono del tutto caratterizzate
Le forze (2 a parte) Massa, temperatura, volume, densità sono grandezze scalari La forza è una grandezza vettoriale Scalari e vettori Si definiscono SCALARI le grandezze fisiche che sono del tutto caratterizzate
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
La situazione è rappresentabile così:
 Forze Equivalenti Quando viene applicata una forza ad un corpo rigido è importante definire il punto di applicazione La stessa forza applicata a punti diversi del corpo può produrre effetti diversi! Con
Forze Equivalenti Quando viene applicata una forza ad un corpo rigido è importante definire il punto di applicazione La stessa forza applicata a punti diversi del corpo può produrre effetti diversi! Con
STUDIO DELLE RADICI DI UNA EQUAZIONE ALGEBRICA DI TERZO GRADO A COEFFICIENTI REALI
 M. G. BUSATO STUDIO DELLE RADICI DI UNA EQUAZIONE ALGEBRICA DI TERZO GRADO A COEFFICIENTI REALI mgbstudio.net PAGINA INTENZIONALMENTE VUOTA SOMMARIO In questo scritto viene compiuto lo studio dettagliato
M. G. BUSATO STUDIO DELLE RADICI DI UNA EQUAZIONE ALGEBRICA DI TERZO GRADO A COEFFICIENTI REALI mgbstudio.net PAGINA INTENZIONALMENTE VUOTA SOMMARIO In questo scritto viene compiuto lo studio dettagliato
Definizione di Lavoro
 Definizione Lavoro Caso Forza intensità costante che agisce lungo una retta: L = F s = Fs Caso Forza intensità e rezione variabile: s L = F ds = F ( s) ds 0 0 F(s) componente della forza lungo s. s Nel
Definizione Lavoro Caso Forza intensità costante che agisce lungo una retta: L = F s = Fs Caso Forza intensità e rezione variabile: s L = F ds = F ( s) ds 0 0 F(s) componente della forza lungo s. s Nel
ESERCIZI SVOLTI O CON TRACCIA DI SOLUZIONE SU STRUTTURE IPERSTATICHE
 ESERCIZI SVOLTI O CON TRACCIA DI SOLUZIONE SU STRUTTURE IPERSTATICHE 1 PROVA SCRITTA 11 gennaio 2013 - Esercizio 2 Data la struttura di figura, ricavare le equazioni delle azioni interne (M, N, T) e tracciarne
ESERCIZI SVOLTI O CON TRACCIA DI SOLUZIONE SU STRUTTURE IPERSTATICHE 1 PROVA SCRITTA 11 gennaio 2013 - Esercizio 2 Data la struttura di figura, ricavare le equazioni delle azioni interne (M, N, T) e tracciarne
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di 4 - DERIVAZIONE NUMERICA Lucio Demeio Dipartimento di Scienze Matematiche 1 Calcolo numerico delle derivate 2 3 Introduzione Idea di base L idea di base
Corso di Laurea in Ingegneria Informatica Corso di 4 - DERIVAZIONE NUMERICA Lucio Demeio Dipartimento di Scienze Matematiche 1 Calcolo numerico delle derivate 2 3 Introduzione Idea di base L idea di base
parte i a - la teoria 13
 3 parte i a - la teoria 13 CAPITOLO 1 - LE TENSOSTRUTTURE 13 1.1 - introduzione 13 1.2 - caratteristiche delle tensostrutture 17 1.3 - obiettivi della tesi 21 capitolo 2 - il sistema strutturale 22 2.1
3 parte i a - la teoria 13 CAPITOLO 1 - LE TENSOSTRUTTURE 13 1.1 - introduzione 13 1.2 - caratteristiche delle tensostrutture 17 1.3 - obiettivi della tesi 21 capitolo 2 - il sistema strutturale 22 2.1
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Metodo delle Forze nelle strutture a nodi spostabili
 Metodo delle Forze nelle strutture a nodi spostabili L inserimento delle cerniere nelle strutture a nodi spostabili rende queste labili ma quest operazione si rende necessaria se vogliamo utilizzare i
Metodo delle Forze nelle strutture a nodi spostabili L inserimento delle cerniere nelle strutture a nodi spostabili rende queste labili ma quest operazione si rende necessaria se vogliamo utilizzare i
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
LEZIONE 1. IL PROGETTO STRUTTURALE Parte 2. La modellazione. Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A
 Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà di Architettura Università degli Studi di Genova LEZIONE 1 IL PROGETTO STRUTTURALE Parte 2. La modellazione LA MODELLAZIONE INPUT
Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà di Architettura Università degli Studi di Genova LEZIONE 1 IL PROGETTO STRUTTURALE Parte 2. La modellazione LA MODELLAZIONE INPUT
Lezione 6 - Analisi statica
 ezione 6 - nalisi statica ü [.a. 211-212 : ultima revisione 7 ottobre 212] Si consideri la stessa struttura bidimensionale della lezione precedente, ossia un insieme di travi collegate tra loro ed al suolo
ezione 6 - nalisi statica ü [.a. 211-212 : ultima revisione 7 ottobre 212] Si consideri la stessa struttura bidimensionale della lezione precedente, ossia un insieme di travi collegate tra loro ed al suolo
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
TELAIO A NODI SPOSTABILI Esempio
 L = 6 m TELAIO A ODI SPOSTABILI Esempio La struttura di un edificio per uffici è costituita da una serie di telai come in figura, posti ad interasse di 5 m. Verificare le colonne in acciaio S235 (Fe360).
L = 6 m TELAIO A ODI SPOSTABILI Esempio La struttura di un edificio per uffici è costituita da una serie di telai come in figura, posti ad interasse di 5 m. Verificare le colonne in acciaio S235 (Fe360).
ACCIAIO Calcolo Strutturale
 ISTITUTO TECNICO COSTRUZIONI AMBIENTE TERRITORIO Appunti per il corso di PROGETTAZIONE COSTRUZIONI IMPIANTI ACCIAIO Calcolo Strutturale Aggiornamento: Aprile 2016 Prof. Ing. Del Giudice Tony GENERALITA
ISTITUTO TECNICO COSTRUZIONI AMBIENTE TERRITORIO Appunti per il corso di PROGETTAZIONE COSTRUZIONI IMPIANTI ACCIAIO Calcolo Strutturale Aggiornamento: Aprile 2016 Prof. Ing. Del Giudice Tony GENERALITA
Esercitazione 3 - Calcolo delle azioni interne
 Università degli Studi di ergamo orso di Laurea in Ingegneria Tessile orso di Elementi di Meccanica Esercitazione - alcolo delle azioni interne Esercizio n. La struttura di figura.a è composta da due aste
Università degli Studi di ergamo orso di Laurea in Ingegneria Tessile orso di Elementi di Meccanica Esercitazione - alcolo delle azioni interne Esercizio n. La struttura di figura.a è composta da due aste
Calcolo delle sollecitazioni di una struttura
 alcolo delle sollecitazioni di una struttura o scopo di questa esercitazione è il calcolo delle sollecitazioni agenti su una struttura ed il tracciamento dei relativi grafici; in pratica bisogna tracciare
alcolo delle sollecitazioni di una struttura o scopo di questa esercitazione è il calcolo delle sollecitazioni agenti su una struttura ed il tracciamento dei relativi grafici; in pratica bisogna tracciare
Esercitazione di Statica
 Appunti di Elementi di Meccanica Esercitazione di Statica v 1.0 7 ottobre 2008 Figura 1: Scaffale a mensole 1 Problema Lo scaffale è un oggetto di uso quotidiano, presente nella maggior parte delle abitazioni.
Appunti di Elementi di Meccanica Esercitazione di Statica v 1.0 7 ottobre 2008 Figura 1: Scaffale a mensole 1 Problema Lo scaffale è un oggetto di uso quotidiano, presente nella maggior parte delle abitazioni.
Lezione 39 - Le equazioni di congruenza
 Lezione 9 - Le equazioni di congruenza ü [.a. 0-0 : ultima revisione 7 agosto 0] Per definizione, in una trave iperstatica non e' possibile calcolare le reazioni vincolari con sole equazioni di equilibrio.
Lezione 9 - Le equazioni di congruenza ü [.a. 0-0 : ultima revisione 7 agosto 0] Per definizione, in una trave iperstatica non e' possibile calcolare le reazioni vincolari con sole equazioni di equilibrio.
Il Principio dei lavori virtuali
 Il Principio dei lavori virtuali Il P..V. rientra nella classe di quei principi energetici che indicano che i sistemi evolvono nel senso di minimizzare l energia associata ad ogni stato di possibile configurazione.
Il Principio dei lavori virtuali Il P..V. rientra nella classe di quei principi energetici che indicano che i sistemi evolvono nel senso di minimizzare l energia associata ad ogni stato di possibile configurazione.
Le lettere x, y, z rappresentano i segnali nei vari rami.
 Regole per l elaborazione di schemi a blocchi Oltre alle tre fondamentali precedenti regole (cascata, parallelo, retroazione), ne esiste una serie ulteriore che consente di semplificare i sistemi complessi,
Regole per l elaborazione di schemi a blocchi Oltre alle tre fondamentali precedenti regole (cascata, parallelo, retroazione), ne esiste una serie ulteriore che consente di semplificare i sistemi complessi,
Indice I vettori Geometria delle masse
 Indice 1 I vettori 1 1.1 Vettori: definizioni................................ 1 1.2 Componenti scalare e vettoriale di un vettore secondo una retta orientata. 2 1.3 Operazioni di somma, differenza tra
Indice 1 I vettori 1 1.1 Vettori: definizioni................................ 1 1.2 Componenti scalare e vettoriale di un vettore secondo una retta orientata. 2 1.3 Operazioni di somma, differenza tra
Valutazione della curvatura media di un elemento strutturale in c.a.
 16.4 Stato limite di deformazione 16.4.1 Generalità Lo stato limite di deformazione può essere definito come la perdita di funzionalità della struttura a causa di una sua eccessiva deformazione. Segnali
16.4 Stato limite di deformazione 16.4.1 Generalità Lo stato limite di deformazione può essere definito come la perdita di funzionalità della struttura a causa di una sua eccessiva deformazione. Segnali
modulo D L acciaio Gruppo III
 1 Calcolo dei pilastri composti Pilastri (o aste) composti Calcolo della snellezza equivalente La snellezza equivalente viene calcolata con le seguenti relazioni: aste calastrellate: λ eq = λ y2 + λ 1
1 Calcolo dei pilastri composti Pilastri (o aste) composti Calcolo della snellezza equivalente La snellezza equivalente viene calcolata con le seguenti relazioni: aste calastrellate: λ eq = λ y2 + λ 1
Analisi limite di sistemi di travi
 Analisi limite di sistemi di travi L analisi limite o calcolo a rottura consente di valutare direttamente la capacità portante ultima di una struttura, ovvero di valutare direttamente lo stato limite ultimo
Analisi limite di sistemi di travi L analisi limite o calcolo a rottura consente di valutare direttamente la capacità portante ultima di una struttura, ovvero di valutare direttamente lo stato limite ultimo
ANALISI STATICA RELATIVA ALLA CADUTA LIBERA DI UN OPERATORE IN FASE DI MONTAGGIO DELLA STRUTTURA METALLICA
 OGGETTO: ANALISI STATICA RELATIVA ALLA CADUTA LIBERA DI UN OPERATORE IN FASE DI MONTAGGIO DELLA STRUTTURA METALLICA PREMESSA L analisi strutturale è stata effettuata con lo scopo di valutare il valore
OGGETTO: ANALISI STATICA RELATIVA ALLA CADUTA LIBERA DI UN OPERATORE IN FASE DI MONTAGGIO DELLA STRUTTURA METALLICA PREMESSA L analisi strutturale è stata effettuata con lo scopo di valutare il valore
Capitolo 11. TORSIONE (prof. Elio Sacco) 11.1 Sollecitazione di torsione Torsione nella sezione circolare
 Capitolo TORSIONE (prof. Elio Sacco). Sollecitazione di torsione Si esamina il caso in cui la trave è soggetta ad una coppia torcente e 3 agente sulla base L della trave. Si utilizza il metodo seminverso
Capitolo TORSIONE (prof. Elio Sacco). Sollecitazione di torsione Si esamina il caso in cui la trave è soggetta ad una coppia torcente e 3 agente sulla base L della trave. Si utilizza il metodo seminverso
Calcolo strutturale dell albero a gomito di un motore motociclistico
 UNIVERSITÀ DEGLI STUDI DI BOLOGNA FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA MECCANICA DISEGNO TECNICO INDUSTRIALE Calcolo strutturale dell albero a gomito di un motore motociclistico Tesi di
UNIVERSITÀ DEGLI STUDI DI BOLOGNA FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA MECCANICA DISEGNO TECNICO INDUSTRIALE Calcolo strutturale dell albero a gomito di un motore motociclistico Tesi di
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta
 Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
La Struttura. Schema di scarico di un viadotto con travate semplicemente appoggiate. Schema di scarico di un ponte strallato
 La Struttura Obiettivo del Corso è quello di fornire un approccio metodologico per la trattazione analitica dei modelli meccanici della parte resistente della Costruzione. La trattazione è fondata su un
La Struttura Obiettivo del Corso è quello di fornire un approccio metodologico per la trattazione analitica dei modelli meccanici della parte resistente della Costruzione. La trattazione è fondata su un
Introduzione. Michelangelo Laterza Principi di Statica e di Dinamica delle Strutture
 Introduzione La meccanica è quella parte delle scienze applicate che studia le forze ed il moto. In questo campo è fondamentale la nozione di equilibrio, ovvero la condizione che si instaura quando le
Introduzione La meccanica è quella parte delle scienze applicate che studia le forze ed il moto. In questo campo è fondamentale la nozione di equilibrio, ovvero la condizione che si instaura quando le
Progetto di un Telaio Piano in C.A.
 Seconda Esercitazione Progettuale Progetto di un Telaio Piano in C.A. Analisi delle Sollecitazioni secondo il Metodo di Cross con vincoli ausiliari Seconda Esercitazione Progettuale (EP2) ~ 1 ~ a cura
Seconda Esercitazione Progettuale Progetto di un Telaio Piano in C.A. Analisi delle Sollecitazioni secondo il Metodo di Cross con vincoli ausiliari Seconda Esercitazione Progettuale (EP2) ~ 1 ~ a cura
Architettura Laboratorio di Costruzione I (A-L)
 Università degli Studi di Parma Architettura Laboratorio di Costruzione I (A-L) Anno accademico 2012/2013 Docenti: Prof. Roberto Brighenti e-mail: roberto.brighenti@unipr.it Tel.: 0521/905910 Ricevimento:
Università degli Studi di Parma Architettura Laboratorio di Costruzione I (A-L) Anno accademico 2012/2013 Docenti: Prof. Roberto Brighenti e-mail: roberto.brighenti@unipr.it Tel.: 0521/905910 Ricevimento:
Elementi di Teoria dei Sistemi. Definizione di sistema dinamico. Cosa significa Dinamico? Sistema dinamico a tempo continuo
 Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
POTENZE DI MATRICI QUADRATE
 POTENZE DI MATRICI QUADRATE In alcune applicazioni pratiche, quali lo studio di sistemi dinamici discreti, può essere necessario calcolare le potenze A k, per k N\{0}, di una matrice quadrata A M n n (R)
POTENZE DI MATRICI QUADRATE In alcune applicazioni pratiche, quali lo studio di sistemi dinamici discreti, può essere necessario calcolare le potenze A k, per k N\{0}, di una matrice quadrata A M n n (R)
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica
 CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI DEI SISTEMI LTI Ing. Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI DEI SISTEMI LTI Ing. Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
SISTEMI DI CONTROLLO CINEMATICA E DINAMICA DEI ROBOT
 SISTEMI DI CONTROLLO Laurea Specialistica in Ingegneria Meccanica e del Veicolo SISTEMI DI CONTROLLO CINEMATICA E DINAMICA DEI ROBOT Ing. Cristian Secchi Tel. 0522 522235 e-mail: secchi.cristian@unimore.it
SISTEMI DI CONTROLLO Laurea Specialistica in Ingegneria Meccanica e del Veicolo SISTEMI DI CONTROLLO CINEMATICA E DINAMICA DEI ROBOT Ing. Cristian Secchi Tel. 0522 522235 e-mail: secchi.cristian@unimore.it
Università degli Studi della Basilicata Facoltà di Ingegneria
 Università degli Studi della Basilicata Facoltà di Ingegneria Corso di TECNICA DELLE COSTRUZIONI Docente: Collaboratori: Prof. Ing. Angelo MASI Dr. Ing. Giuseppe Santarsiero Ing. Vincenzo Manfredi RICHIAMI
Università degli Studi della Basilicata Facoltà di Ingegneria Corso di TECNICA DELLE COSTRUZIONI Docente: Collaboratori: Prof. Ing. Angelo MASI Dr. Ing. Giuseppe Santarsiero Ing. Vincenzo Manfredi RICHIAMI
LABILITA DI STRUTTURE
 ESERCIZI SVOLTI O CON TRACCIA DI SOLUZIONE SU LAILITA DI STRUTTURE v 0.9 1 1 2 2n-1= 1 A C D 2n = 2 2(n-1) = 2 2n-1= 1 Numero totale di aste N = 2 GdL (gradi di libertà aste libere) = N 3 = 6 GdV (gradi
ESERCIZI SVOLTI O CON TRACCIA DI SOLUZIONE SU LAILITA DI STRUTTURE v 0.9 1 1 2 2n-1= 1 A C D 2n = 2 2(n-1) = 2 2n-1= 1 Numero totale di aste N = 2 GdL (gradi di libertà aste libere) = N 3 = 6 GdV (gradi
1 - Matrice delle masse e delle rigidezze
 Cilc per tutti gli appunti (AUOMAZIONE RAAMENI ERMICI ACCIAIO SCIENZA delle COSRUZIONI ) e-mail per suggerimenti SEMPLICE ESEMPIO NUMERICO DEL MEODO DI ANALISI DINAMICA Si vuole qui chiarire con un semplice
Cilc per tutti gli appunti (AUOMAZIONE RAAMENI ERMICI ACCIAIO SCIENZA delle COSRUZIONI ) e-mail per suggerimenti SEMPLICE ESEMPIO NUMERICO DEL MEODO DI ANALISI DINAMICA Si vuole qui chiarire con un semplice
CORSO DI MODELLAZIONE STRUTTURALE
 CORSO DI MODELLAZIONE STRUTTURALE Prof. Ing. Mario Pasquino a.a. 2012-2013 Esercitazioni mediante SAP2000 Tutor: dott. ing. Donato Cancellara Es. 1 (influenza della deformabilità tagliante: calcolo manuale
CORSO DI MODELLAZIONE STRUTTURALE Prof. Ing. Mario Pasquino a.a. 2012-2013 Esercitazioni mediante SAP2000 Tutor: dott. ing. Donato Cancellara Es. 1 (influenza della deformabilità tagliante: calcolo manuale
26. Corda elastica SPETTRO DELLA CORDA DISCRETA
 6. Corda elastica I modelli microscopici di un mezzo continuo consistono in sistemi di N particelle, atomi o molecole, che interagiscono tra loro con forze elettromagnetiche. Nei solidi cristallini le
6. Corda elastica I modelli microscopici di un mezzo continuo consistono in sistemi di N particelle, atomi o molecole, che interagiscono tra loro con forze elettromagnetiche. Nei solidi cristallini le
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
VERIFICA DI PORTANZA DELLE FONDAZIONI
 VERIFICA DI PORTANZA DELLE FONDAZIONI Capitolo 6.4 - OPERE DI FONDAZIONE Nelle verifiche di sicurezza devono essere presi in considerazione tutti i meccanismi di stato limite ultimo, sia a breve sia a
VERIFICA DI PORTANZA DELLE FONDAZIONI Capitolo 6.4 - OPERE DI FONDAZIONE Nelle verifiche di sicurezza devono essere presi in considerazione tutti i meccanismi di stato limite ultimo, sia a breve sia a
EQUAZIONI DIFFERENZIALI
 Indice 1 EQUAZIONI DIFFERENZIALI 3 1.1 Equazioni fisicamente significative...................... 3 1.1.1 A cosa servono?............................. 3 1.1.2 Legge di Newton............................
Indice 1 EQUAZIONI DIFFERENZIALI 3 1.1 Equazioni fisicamente significative...................... 3 1.1.1 A cosa servono?............................. 3 1.1.2 Legge di Newton............................
Appendice A: un esempio di scelta del mix ottimo di produzione in presenza di vincoli 19
 14 18-12-07 19:04 Pagina 411 Le decisioni di breve termine fra alternative diverse 411 i minori costi differenziali, almeno nella misura in cui la dimensione di costo è la più importante. Sebbene i costi
14 18-12-07 19:04 Pagina 411 Le decisioni di breve termine fra alternative diverse 411 i minori costi differenziali, almeno nella misura in cui la dimensione di costo è la più importante. Sebbene i costi
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente
 Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA
 INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA Sommario MOTO E TRAIETTORIA... 3 PUNTO MATERIALE... 3 TRAIETTORIA... 3 VELOCITÀ... 4 VELOCITÀ MEDIA... 4 VELOCITÀ ISTANTANEA...
INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA Sommario MOTO E TRAIETTORIA... 3 PUNTO MATERIALE... 3 TRAIETTORIA... 3 VELOCITÀ... 4 VELOCITÀ MEDIA... 4 VELOCITÀ ISTANTANEA...
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri:
 DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
iv Indice c
 Indice Prefazione ix 1 Numeri 1 1 Insiemi e logica 1 1.1 Concetti di base sugli insiemi 1 1.2 Un po di logica elementare 9 2 Sommatorie e coefficienti binomiali 13 2.1 Il simbolo di sommatoria 13 2.2 Fattoriale
Indice Prefazione ix 1 Numeri 1 1 Insiemi e logica 1 1.1 Concetti di base sugli insiemi 1 1.2 Un po di logica elementare 9 2 Sommatorie e coefficienti binomiali 13 2.1 Il simbolo di sommatoria 13 2.2 Fattoriale
Disequazioni di secondo grado
 Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
