x 1 x 2 x 3 y y y
|
|
|
- Sabrina Berardino
- 6 anni fa
- Visualizzazioni
Transcript
1 .8. ALTRI ESERCIZI Soluzioni Soluzione.4. x 1 x x 3 y y y Soluzione.6. Indichiamo con X a la variabile aleatoria guadagno in una partita seguendo la strategia a ; analogamente per le v.a. X b e X c. Lo spazio degli eventi è Ω = {CCC, CCT, CT C, CT T, T CC, T CT, T T C, T T T }; per l ipotesi di regolarità della moneta, si assume che gli eventi siano tutti equiprobabili con p = 1/8. In corrispondenza di ciascun evento ω = (ω 1, ω, ω 3 ) Ω, i valori di X a, X b, X c sono riportati nella seguente tabella: (ω 1, ω, ω 3 ) X a (ω) X b (ω) X b (ω) CCC CCT CTC CTT TCC TCT TTC TTT Calcolando i valori attesi di X a, X b, X c, si ottiene: E(X a ) = E(X b ) = E(X c ) = 0. Pertanto le tre strategie di gioco sono mediamente equivalenti. Per quanto riguarda la variabilità, tenendo conto del risultato precedente, si ha: Var(X a ) = E(X a) = 1 8 [( 7) ] = 56 8 = 7 Var(X b ) = E(X b ) = 1 8 [( 3) + ( 1) + ( 1) ] = 16 8 = Var(X c ) = E(X c ) = 1 8 [( 3) + ( 1) + ( 1) ( 1) ] = 4 8 = 3 e quindi la strategia a è quella che presenta la maggiore variabilità.
2 80 CAPITOLO. VARIABILI ALEATORIE DISCRETE Soluzione.7. Bisogna calcolare dapprima la probabilità p che una prova venga annullata; successivamente il numero atteso N di prove annullate sarà dato da N = 40p. La prova di uno studente viene annullata se, in almeno uno dei tre tentativi, lo studente viene scoperto dal docente, dove in ciascuna delle tre prove lo studente viene scoperto con probabilità 0.1 e non viene scoperto con probabilità 0.9. In questo caso per calcolare la probabilità p richiesta, è conveniente calcolare la probabilità 1 p dell evento complementare che lo studente non venga scoperto, che è data da: 1 p = = da cui p = e N = Soluzione.8. Innanzitutto è bene osservare che le due opzioni A e B hanno la stessa speranza matematica. Infatti, denotato con X la v.a. ricavo finale per ciascun euro investito, in base ai dati del problema risulta E[X] = 1.1 e Var(X) = 0.5. Denotate poi con A e B i guadagni ottenuti rispettivamente in base alle due strategie A e B, si ha: A := 1000X s X t + 500X u B := 5000X v dove X s, X t, X u e X v sono le quantità aleatorie ricavo per ciascun euro investito nel titolo azionario considerato (s, t, u, v) aventi tutte la stessa speranza matematica e la stessa varianza. da cui E[A] = 1000E[X s ] E[X t ] + 500E[X u ] = = 5500 E[B] = 5000 E[X v ] = = Sono invece diverse invece le varianze. Poichè la varianza della somma di v.a. indipendenti è uguale alla somma delle varianze delle rispettive v.a., tenento conto che Var(X) = 0.5 = 0.5: Var(A) = Var(1000X s X t + 500X u ) = 1000 Var(X s ) Var(X t ) Var(X u ) = = = Var(B) = Var(5000X v ) = 5000 Var(X v ) = = Quindi, sebbene mediamente le due opzioni siano equivalenti, la seconda è maggiormente rischiosa: statisticamente può consentire perdite o ricavi maggiori della prima. Soluzione.9. Lo spazio degli eventi Ω è il seguente: Ω = {T T, CT, T C, CC}. ciascuno con probabilità 1 in quanto assumiamo l indipendenza degli eventi elementari {C, T } 4 associati a ciascun lancio, cioè ad esempio P (T T ) = P (T ) P (T ) = 1 1 = 1. 4
3 .8. ALTRI ESERCIZI 81 Considerata la v.a. X= numero di teste ottenute in due lanci consecutivi di una moneta equilibrata, ne segue che la funzione di densità assume valori strettamente positivi nell insieme X = {0, 1, }: f(0) = P (X = 0) = P (CC) = 1 4 = 0.5 f(1) = P (X = 1) = P (CT ) + P (T C) = 1 = 0.5 f() = P (X = ) = P (T T ) = 1 4 = 0.5. Si ha pertanto: f(x) = 0.5 per x = 0 0, 50 per x = 1 0, 5 per x = 0 altrove. f(x) 1/ 1/4 1/4 0 1 La funzione di ripartizione F (x) viene costruita a partire dalla funzione di densità in base alla sua definizione: F (t) = P (X t). x
4 8 CAPITOLO. VARIABILI ALEATORIE DISCRETE Si ha pertanto: 0 per x < per 0 x < 1 F (x) = 0.75 per 1 x < 1.00 per x e tale funzione ha la seguente rappresentazione grafica: f(x) x Infine il calcolo della costante c tale che E(cX) = 5 si ottiene facilmente tenendo conto che E(cX) = ce(x) e che la speranza matematica di X è data da: E(X) = = 1. Pertanto c = 1. Soluzione.30. E sufficiente considerare lo spazio dei possibili risultati: Ω = {(CCC), (CCT ), (CT C), (CT T ), (T CC), (T CT ), (T T C), (T T T )} e quindi l evento richiesto A in funzione dei singoli eventi elementari: A = {(CCC), (T CC), (T T C), (T T T )}. Da cui segue: P (A) = #A #Ω = 4 8 = 1.
5 .8. ALTRI ESERCIZI 83 In maniera analoga, nel secondo punto, si considera l evento certo: Ω = {(CCCC), (CCCT ), (CCT C), (CCT T ), (CT CC), (CT CT ), (CT T C), (CT T T ), (T CCC), (T CCT ), (T CT C), (T CT T ), (T T CC), (T T CT ), (T T T C), (T T T T )}. e quindi l evento A richiesto: Da cui segue: A = {(CCCC), (T T T C), (T T T T )} P (A) = #A #Ω = 3 16 = Soluzione.33. I valori richiesti si ottengono da un sistema di due equazioni in due incognite. La prima equazione si ottiene tenendo conto che la somma delle probabilità deve essere uguale a 1, da cui segue a + b = 0.3; la secondoa si ottiene direttamente dalla condizione imposta: E[Y ] =.3 + b + 3a = 3. Soluzione.34. Dalla condizione E(Y ) = 0.95 segue: E(Y ) = 1 (0.5 + α) = α = α = 0.95 da cui α = 0.. Successivamente, per la condizione di coerenza, si ha: ( β) + ( α) = ( β) + ( ) = β = 1 da cui β = 1. la tabella si scrive quindi X Y Per il calcolo della covarianza richiesto si osservi preliminarmente che Cov(3X +, 5Y 1) = 3 5 Cov(X, Y ). Essendo Cov(X, Y ) = E(XY ) E(X)E(Y ), calcoliamo quindi: E(XY ) = = = 1.3 E(X) = = 1.95 E(Y ) = 0.95 da cui Cov(X, Y ) = = e quindi Cov(3X+, 5Y 1) = 15Cov(X, Y ) =
6 84 CAPITOLO. VARIABILI ALEATORIE DISCRETE Soluzione.36. Per definizione si ha: ρ xy = Cov(X, Y ) σ x σ y da cui in base alle ipotesi ρ xy = 0.5 e σ x = σ y = σ segue: 0.5 = Cov(X, Y ) σ Cov(X, Y ) = σ. Con lo stesso ragionamento si ottiene Cov(X, Z) = Cov(Y, Z) = σ /. In base alle proprietà del coefficiente di correlazione si ha pertanto: Per il punto successivo si ha: Cov(X, Y ) = ( 1) Cov(X, Y ) = σ. Infine: Var(X Y ) = Var(X) + Var(Y ) + Cov(X, Y ) = σ + σ σ = σ. Var(X/σ + Y/σ Z/σ) = 1 Var(X + Y Z) σ = 1 [Var(X) + Var(Y ) + Var(Z)+ σ +Cov(X, Y ) Cov(X, Z) Cov(Y, Z)] = 1 [ ] σ + σ + σ + σ σ σ σ =
7 Capitolo 3 Principali distribuzioni di probabilità discrete Vogliamo ora presentare alcune distribuzioni di probabilità notevoli che costituiscono lo schema teorico di fenomeni naturali di vario tipo. In questo capitolo consideriamo alcune distribuzioni di probabilità di tipo discreto; in seguito affronteremo le distribuzioni di probabilità di tipo continuo. 3.1 La distribuzione uniforme La distribuzione uniforme è la distribuzione di eventi equiprobabili. Diremo che una variabile aleatoria X segue una distribuzione uniforme su {1,,..., n} se ha funzione di probabilità: p(x) := 1 n per 1,..., n 0 altrimenti. In tal caso diremo che X segue una distribuzione uniforme e scriveremo X U(n). Speranza matematica e Varianza. Tenendo conto che: n = n = n(n + 1) n(n + 1)(n + 1) 6 possiamo calcolare speranza matematica e varianza: E(X) = 1 n ( n) = 1 n(n + 1) n 85 = n + 1
8 86 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE x Figura 3.1: Funzione di probabilità di distribuzione uniforme discreta su {1,,..., 10}. e quindi la varianza di X: Var(X) = E(X ) µ = 1 ( ) n + 1 n ( n ) = 1 ( ) n(n + 1)(n + 1) n + 1 = n + 1 [(n + 1) 3(n + 1)] n 6 1 = n La distribuzione binomiale La distribuzione binomiale è la distribuzione di probabilità del numero di successi in una successione di n prove ripetute ed indipendenti in ciascuna delle quali vi è probabilità costante di successo. Data una successione di n eventi A 1, A,..., A n indipendenti ed equiprobabili, con P (A 1 ) = = P (A n ) = p, la variabile aleatoria: X := A 1 + A + + A n (3.1) fornisce il numero di successi ottenuto nelle n prove. Ovviamente il numero di successi che può essere ottenuto nelle n prove è un numero intero compreso fra 0 e n; pertanto X assume valori nell insieme Ω X = {0, 1,..., n}. Vogliamo calcolare la distribuzione su Ω X originata dalla v.a. X. Consideriamo dapprima il caso in cui nelle prime x prove A 1,..., A x si ottenga un successo e nei successive n x prove A x+1,..., A n si ottenga un insuccesso, per x {0, 1,..., n}; cioè l evento A 1... A x A c x+1... A c n. Poichè per ipotesi gli eventi A 1,..., A n sono stocasticamente indipendenti ed equiprobabili, si ha: P (A 1,..., A x, A c x+1,..., A c n) = P (A 1 ) P (A x )P (A c x+1) P (A c n) n x volte x volte {}}{{}}{ = p p (1 p) (1 p) = p x (n p) n x.
9 3.. LA DISTRIBUZIONE BINOMIALE 87 L evento {X = x}, cioè l evento si sono ottenuti x successi nelle n prove, è dato dall unione di tutti gli eventi contenenti esattamente x successi e n x insuccessi (ovviamente l ordine non ha alcuna importanza); tali eventi sono disgiunti ed equiprobabili in quanto ciascuno di essi ha probabilità p x (n p) n x. Il numero di tali eventi è uguale al numero di combinazioni di classe x da un insieme di n elementi. Si ha pertanto: P {X = x} = ( ) n p x (1 p) n x x x = 0, 1,..., n Possiamo scrivere pertanto: ( ) n p x (1 p) n x se x = 0, 1,..., n p(x) := x 0 altrimenti. (3.) In tal caso diremo che X segue una distribuzione binomiale e scriveremo X B(n, p). Vogliamo dimostrare che la (3.) gode della proprietà x Ω X p(x) = 1. In base alla formula del binomio di Newton, si ha che per a, b R e per ogni n: (a + b) n = In particolare, per a = p e b = 1 p, si ottiene cioè la nostra tesi. 1 = n k=0 n k=0 ( ) n a k b n k. x ( ) n p k (1 p) n k, x Esempio 3.1 Sia X B(10, 0.3). Si ha allora: P (X = ) = ( ) = 10!!8! = = = P (X ) = P (X = 0) + P (X = 1) + P (X = ) ( ) ( ) ( ) = = = P (X > 3) = 1 P (X ) = 1 (P (X = 0) + P (X = 1) + P (X = )) = =
10 88 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE x Figura 3.: Funzione di probabilità distribuzione binomiale di parametri n = 10 e p = 0.3. Speranza matematica e Varianza. Per il calcolo della speranza matematica e della varianza di X, premettiamo il calcolo della speranza e della varianza di A i : E( A i ) = 1 p + 0 (1 p) = p (3.3) Var( A i ) = E( A i ) {E( A i )} = p p = p(1 p). (3.4) Pertanto dalla proprietà (.) della speranza e dalla (.40) della varianza, la speranza matematica e la varianza di una variabile aleatoria X B(n, p) sono date rispettivamente da: E(X) = E( A 1 ) + E( A ) + + E( A n ) = p + p + + p = np (3.5) Var(X) = Var( A 1 ) + Var( A ) + + Var( A n ) = p(1 p) + p(1 p) + p(1 p) = np(1 p). (3.6) Proposizione 3. Siano X 1,..., X k v.a. indipendenti, con X i B(n i, p) per i = 1,..., k. Allora la variabile aleatoria S k = X X k ha distribuzione B(n n k, p). Dimostrazione. Poichè X 1 segue una distribuzione binomiale di parametri n 1 e p, allora vuol dire che si può scrivere come: X 1 = A A n1, dove A 1,..., A n1 sono eventi indipendenti ed equiprobabili con P (A i ) = p, (i = 1,..., n 1 ). Analogamente per le altre variabili X,..., X k esisteranno eventi rispettivamente
11 3.. LA DISTRIBUZIONE BINOMIALE 89 (A n1 +1,..., A N 1+n ),..., (A nk 1 +1,..., A nk ) eventi indipendenti ed equiprobabili con probabilità p. Si ha pertanto: X 1 = A A n1 X = A n A n1 +n = e quindi considerara la variabile aleatoria: X k = A n1 + +n k A nk X = X X k = A A n1 +n + +n k segue una distribuzione binomiale di parametri n = n n k e p. Il successivo corollario è segue immediatamente dal caso precedente per n 1 = = n k = n: Corollario 3.3 Siano X 1,..., X k v.a. indipendenti aventi distribuzione B(n, p) per i = 1,..., k. Allora la variabile aleatoria S k = X X k ha distribuzione B(nk, p). Esempio 3.4 Ad esempio, se X, Y sono v.a. indipendenti con X B(10, 0.) e Y B(7, 0.), allora X + Y (17, 0.) Esempio 3.5 Sapendo che il 30 % dei passeggeri che hanno prenotato non si presenta alla partenza, una compagnia aerea accetta fino a 8 prenotazioni su un volo con capienza 4 posti. Qual è la probabilità che almeno un passeggero, che ha regolarmente prenotato, resti a terra? Sia X = numero di passeggeri che, avendo prenotato un posto sull aereo, si presentano per l imbarco. Evidentemente si ha X B(8, 0.7). Poichè l aereo dispone di 4 posti, fra coloro che hanno prenotato qualcuno non potrà partire se si presentano almeno 5 passeggeri al check-in; la probabilità di tale evento è: P (X 5) = P (X = 5) + P (X = 6) + P (X = 7) + P (X = 8). Poichè X B(8, 0.7) allora si ha: ( ) 8 P (X = 5) = (1 0.7) 8 5 = ( ) 8 P (X = 6) = (1 0.7) 8 6 = ( ) 8 P (X = 7) = (1 0.7) 8 7 = ( ) 8 P (X = 8) = (1 0.7) 8 8 = E quindi, la probabilità che al più 4 passeggeri si presentino per l imbarco è data da P (X 5) = = 1.57%.
12 90 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE Esempio 3.6 Analizzando le acque di scarico di un industria fortemente inquinata, si è osservato che una frazione θ = 0.7 di campioni di tali acque contiene una sostanza fortemente nociva e che tale sostanza di campioni inquinati si riduce a θ D = 0.4 se l industria mette in funzione l impianto di depurazione di cui è dotata (ma che ha un costo di esercizio molto elevato). Le autorità sanitarie effettuano senza preavviso un controllo delle acque di scarico, analizzando n = 1 campioni e trovando la sostanza nociva in h = 7 di essi. Assumendo che, prima di effettuare il prelievo, la probabilità che l impianto di depurazione sia attivo o meno sia la stessa (cioè P (D) = P (D c ) = 0.5), qual è la probabilità che l impianto sia attivo dopo aver preso visione dei risultati? Sia X = numero di campioni inquinati da un insieme di 1 prelievi. L insieme di tutti i possibili campioni che si possono prelevare dalla acque di scarico, rispettivamente nei due casi D e D c (depuratore in funzione o fermo al momento del prelievo), si può identificare con un urna contenente palline bianche (corrispondente ai campioni contenenti la sostanza nociva) nelle proporzioni θ D = 0.4 oppure θ = 0.7. Allora ricorrendo all approssimazione binomiale, si può scrivere: ( ) 1 P (X = 7 D) = = ( ) 1 P (X = 7 D c ) = = E quindi per il teorema di Bayes, supponendo equiprobabili le due ipotesi in esame, cioè P (D) = P (D c ) = 1/ (ma se si hanno altre informazioni questa scalta non è obbligatoria), si ha: P (X = 7 D)P (D) P (D X = 7) = P (X = 7 D)P (D) + P (X = 7 D c )P (D c ) = = P (D c P (X = 7 D c )P (D c ) X = 7) = P (X = 7 D)P (D) + P (X = 7 D c )P (D c ) = 0, = 1 P (D X = 7) = Esercizio 3.7 Una moneta è stata truccata in maniera tale che su 0 lanci l evento testa su presenti 6 volte con probabilità e 7 volte con probabilità Qual è la probabilità che su 10 lanci l evento testa non si verifichi mai? 3.3 La distribuzione ipergeometrica La distribuzione ipergeometrica segue lo stesso schema della legge binomiale ma, a differenza di quest ultima, si considerano esperimenti senza reimmissione. Considerata una
13 3.3. LA DISTRIBUZIONE IPERGEOMETRICA 91 successione (finita) di n estrazioni senza ripetizione da un urna contenente N palline, di cui una frazione pn bianche (con 0 < p < 1) e la restante parte qn = (1 p)n non bianche, sia X il numero di palline bianche X ottenute in una successione di n estrazioni con reimmissione. In questo caso Ω X è costituito dall insieme dei valori interi tali che: max{0, n qn} x min{n, pn}. Infatti in questo caso si tratta di estrazioni senza reimmissione ed indicano che il numero minimo e massimo di successi ottenibili in n estrazioni dipendono dal numero N di palline e dalla proporzione p di palline bianche contenute nell urna. Pertanto se il numero di palline estratte n è superiore al numero di palline nere presenti nell urna, il numero minimo di palline bianche non può essere 0 ma pari a n qn; al contrario non si può estrarre un numero di palline bianche superiore a quello presente nell urna. La funzione di probabilità data da: ( pn x )( (1 p)n n x ) se max{0, n qn} x min{n, pn} p(x) := ( N n) 0 altrimenti. In questo caso diremo che la variabile aleatoria X segue una distribuzione ipergeometrica di parametri interi positivi N, p e n, e scriveremo X H(N, p, n). La verifica della condizione x p(x) = 1 è abbastanza laboriosa e verrà qui omessa. Si noti che anche in questo caso la v.a. X è data da: X = A 1 + A + + A n (3.7) dove gli eventi A 1,..., A n sono equiprobabili, con P (A i ) = p per i = 1,..., n, ma non indipendenti. Si ha infatti: P (A 1 ) = p P (A ) = P (A A 1 )P (A 1 ) + P (A A c 1)P (A c 1) = pn 1 N 1 p + pn (1 p) = p. N 1 Iterando il ragionamento per i = 3,..., N si vede che P (A i ) = p per ogni i. Si può dimostrare che per N, mantenendo costante la proporzione p di palline bianche, si ha: lim N ( pn x )( ) (1 p)n n x ( ) = N n ( ) n p x (1 p) n x (3.8) x e pertanto la distribuzione binomiale costituisce il limite della distribuzione ipergeometrica per N.
14 9 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE Speranza matematica e Varianza. In base alla (3.7), la speranza matematica è da: E(X) = E( A 1 ) + E( A ) + + E( A n ) = np, (3.9) Per quanto riguarda la varianza, dalla (3.7) segue: Var(X) = n i=1 Var( A i ) + i j Cov( A i, A j ). (3.10) In base a quanto visto in precedenza nella (3.4) si ha Var( A i ) = pq. Per il calcolo della covarianza Cov( A i, A j ), consideriamo la relazione (.35) che nel caso qui in esame si scrive: Cov( A i, A j ) = E( A i A j ) E( A i )E( A j ). Si noti che risulta A i A j = A i A j = 1 se e solo l evento A i A j è vero; e quindi si ha: Segue pertanto E( A i A j ) = E( A i A j ) = P (A i A j ) = P (A i )P (A j A i ) = p pn 1 N 1. Cov( A i, A j ) = E( A i A j ) E( A i )E( A j ) = p pn 1 N 1 p e quindi sostituendo nella (3.10) si ottiene: n Var(X) = Var( A i ) + ( ) pn 1 Cov( A i, A j ) = npq + n(n 1)p N 1 p i=1 i j = npq + n(n 1)p p 1 ( N 1 = npq 1 n 1 ). (3.11) N 1 In particolare, per n = 1 la varianza della distribuzione ipergeometrica coincide con quella della distribuzione binomiale in quanto se si effettua un unica estrazione lo schema è lo stesso nei due casi. Inoltre per valori grandi di N la varianza della distribuzione ipergeometrica tende a quella della distribuzione binomiale, come del resto prevedibile in base alla (3.8). Esercizio 3.8 Gli archivi di un ufficio sono stati memorizzati in 30 dischi da 100 Mbyte, contenenti ognuno 100 file. Un programma dovrà accedere a 8 di questi file (tutti diversi). Qual è la probabilità che esso non debba usare il primo disco? La situazione in esame si modellizza con uno schema successo-insuccesso senza rimpiazzo: sono 0 prove ripetute in ognuna delle quali viene scelto un file fra i 3000 possibili. Consiedereremo successo la scelta di un file appartenente al primo disco (sono 100) e insuccesso la
15 3.4. LA DISTRIBUZIONE DI POISSON n T n T n 1 n T T x scelta di uno degli altri dischi (900 files). Non c è restituzione perchè un file, una volta letto, non verrà più richiamato in seguito, quindi X H(3000, 1, 8). La probabilità richiesta è 30 dunque ( )( ) P (X = 0) = 0 8 ( ) = Se invece le 8 voci fossero state scelte a caso con possibilità di ripetizione, il numero di volte in cui il programma avrebbe dovuto accedere al disco n.1 sarebbe stata una B(8, 1 ). La 30 probabilità che il disco non venga consultato è ( ) ( ) 0 ( 8 1 P (X = 0) = = ) Si noti che i due risultati sono molto vicini. Ciò è dovuto al fatto che le varianze delle due distribuzioni binomiale e ipergeometrica sono praticamente uguali, infatti nella (3.11) il rapporto: è molto prossimo allo zero. 8 n 1 N 1 = = La distribuzione di Poisson La distribuzione di Poisson è certamente una delle leggi di probabilità che trova maggiori applicazioni per descrivere fenomeni del mondo reale. Tale distribuzione è anche detta distribuzione degli eventi rari per sottolineare il fatto che in ciascuno dei casi in cui si applica, la probabilità che il singolo evento si verifichi è estremamente bassa. La distribuzione di probabilità di Poisson può quindi servire da modello matematico per fenomeni del tipo: il numero di automobili che si fermano ad una stazione di servizio in un certo intervallo di tempo, numero di utenti che prelevano del denaro da uno sportello bancomat in un certo intervallo di tempo, etc. La distribuzione di Poisson può essere costruita a partire da una successione di prove indipendenti, secondo lo schema che ha condotto alla legge binomiale. Si consideri un intervallo di lunghezza T > 0 ( e per semplicità si pensi a (0, T )) suddiviso in n sottointervalli di lunghezza T/n. Si supponga che un certo evento A (successo) possa
16 94 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE manifestarsi con la stessa probabilità p = α(t/n) proporzionale, secondo un coefficiente α > 0, all ampiezza T/n del singolo sottointervallo ed in modo indipendente in ognuno dei sottontervalli, e sia 1 p = 1 α(t/n) la probabilità che nel generico sottointervallo non si manifesti l evento A. Vogliamo ricavare la probabilità che l evento A si presenti in x degli n sottointervalli consederati. Indicato con X il numero dei sottointervalli in cui si manifesta l evento A, cioè il numero di successi, le ipotesi adottate consentono di applicare la distribuzione binomiale, e si ha: p(x) = ( n x ) ( αt n ) x ( 1 αt n ) n x x = 0, 1,,..., n. All aumentare del numero n dei sottointervalli di (0, T ), si ha: ( ) ( ) x ( n αt lim 1 αt ) n x (αt )x = e αt = λx n x n n x! x! e λ dove si è posto λ = αt > 0. L espressione precedente si ottiene considerando che: ( ) ( ) x ( n αt 1 αt ) n x n(n 1) (n x + 1)(n x)! = x n n x!(n x)! ( 1 αt ) n ( 1 αt ) x n n e che per n si ha: = 1 x! n(n 1) (n x + 1) n x ( αt n ) x ( n(n 1) (n x + 1) (αt ) x 1 αt n x n = n n(1 1 x 1 ) n(1 ) n n n n n ( 1 αt n ( 1 αt n 1 ) n e αt ) x 1. ) n ( 1 αt n La legge di Poisson appare, in questo modo, come una distribuzione che approssima la distribuzione binomiale nel caso in cui in questa si abbia un numero di prove n molto grande ed una probabilità di successo p in ciascuna prova molto piccola (essendo np = λ = costante). Più in generale, i campi di applicazione della distribuzione di Poisson si evincono meglio dallo schema seguente. Si supponga di essere interessati ad un certo evento (ad esempio, incidenti automobilistico su un tratto di strada). Si indichi con η(s, s + t) il numero di volte in cui l evento in questione si verifica nell intervallo temporale (s, s + t) e supponiamo che: 1. La probabilità che l evento si verifichi in un intervallo di tempo di ampiezza t > 0 sia uguale a αt, con α > 0, indipendentemente dall origine dell intervallo e per valori di t sufficientemente piccolo: P (η(s, s + t) = 1) = αt + o(t) s 0 ) x
17 3.4. LA DISTRIBUZIONE DI POISSON 95. la probabilità che in un intervallo di ampiezza h l evento si verifichi più di una volta sia trascurabile: P (η(s, s + t) > 1) = o(t) 3. Il numero degli eventi che si verificano in due intervalli disgiunti siano stocasticamente indipendenti, cioè dati s 1 < s < s 3 < s 4, allora le v.a. η(s 1, s ) e η(s 3, s 4 ) sono stocasticamente indipendenti. Sotto le precedenti ipotesi si può dimostrare che: αt (αt)x P (η(0, t) = x) = e x = 0, 1,,... x! Diremo che una variabile aleatoria X segue una distribuzione di Poisson di parametro λ > 0, e scriveremo X P(λ), se ha la seguente funzione di probabilità: λ λx e se x = 0, 1,,... p(x) := x! (3.1) 0 altrimenti. Per quanto riguarda la verifica della (.6) x=0 p(x) = 1, consideriamo lo sviluppo in serie della funzione esponenziale e λ : e λ λ k = k! k=0 da cui, moltiplicando ambo i membri per e λ si ottiene λ λk 1 = e k! cioè la nostra tesi. Speranza matematica e Varianza. La speranza matematica è data da: λ λx E(X) := x e x! = λ λ x 1 e λ (x 1)! = λ z λe λ z! = λ. x=0 Per il calcolo della varianza premettiamo il calcolo del momento secondo: E(X ) = x λ λx e x! = e λ λ x λx 1 (x 1)! Posto z = x 1, segue E(X ) = e λ λ Segue pertanto: z=0 x=0 (z + 1) λz z! = e λ λ k=0 x=1 z=0 x=1 (z + 1) λz z! z=0 Var(X) = E(X ) µ = λ(λ + 1) λ = λ. = λe(x + 1) = λ(λ + 1) Pertanto, nel caso della distribuzione di Poisson, speranza matematica e varianza coincidono.
18 96 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE x Figura 3.3: Funzione di probabilità distribuzione di Poisson con parametro λ = 4. Approssimazione della distribuzione binomiale con quella di Poisson. Per n > 50 e p < 0.1, si può approssimare una distribuzione Binomiale B(n, p) con una di Poisson P(λ) di parametro λ = np Proposizione 3.9 Siano X 1,..., X k v.a. indipendenti, con X i P (λ i ) per i = 1,..., k. Allora la variabile aleatoria S k = X X k ha distribuzione P (λ λ k ). Esercizio 3.10 All inizio di ogni mese, un negoziante ordina un certo prodotto per le vendite di tutto il mese. Egli può plausibilmente assumere che la variabile delle unità di prodotto venduto durante il mese segua una legge di Poisson con parametro λ = 4. Quante unità di prodotto deve avere in magazzino affinchè abbia una probabilità dell 88% di non restare senza prodotto? In base ai dati del problema, il numero X di unità vendute in un mese segue una distribuzione di Poisson di parametro λ = 4, cioè X P(4). Ogni mese possono essere vendute 0 unità di prodotto oppure un unità di prodotto, etc. Indicato con k il numero di unità di prodotto da ordinare, si richiede di determinare il più piccolo valore di k per cui risulti: P (X k) = k P (X = x) = x=1 k x=1 4 4x e x!. Dalla funzione di probabilità della distribuzione di Poisson P(4) si ricavano i valori: x P (X = x) P (X x)
19 3.4. LA DISTRIBUZIONE DI POISSON 97 e quindi segue che è necessario ordinare almeno k = 6 unità di prodotto. Esercizio 3.11 In una data succursale bancaria è stata valutata una probabilità p = che una persona effettui un prelievo superiore a 3000 euro. Calcolare la probabilità che, durante una normale mattina di lavoro in cui si presentano 00 persone, vi siano più di due persone che effettuino un prelievo superiore a 3000 euro. Il problema richiede il calcolo della probabilità che in una successione di n = 00 prove ripetute ed indipendenti, ciascuna delle quali presenta probabilità p = di successo e q = 1 p = di insuccesso, si verifichi un variabile di successi maggiore di due. Il modello del problema è pertanto costituito da una distribuzione binomiale di parametri n = 00 e p = Tuttavia, essendo la probabilità di successo in ciascuna prova molto piccola, lo stesso problema può essere formalizzato mediante una distribuzione di Poisson di parametro λ = np = 0.. Indichiamo con X il numero di persone che effettuano un prelievo superiore a 6 milioni in un normale giorno di lavoro, il problema pertanto richiede il calcolo di 00 P {X > } = P {X = k}. Ovviamente il calcolo può essere semplificato tenendo presente che k=3 P {X > } = 1 P {X } = 1 [P {X = 0} + P {X = 1} + P {X = }]. Utilizziamo dapprima una distribuzione binomiale, in tal caso X B(00, 0.001), e pertanto si ha: ( ) 00 P {X = 0} = p 0 (1 p) 00 = = ( ) 00 P (X = 1) = p (1 p) 199 = = ( ) 00 P (X = ) = p (1 p) 198 = = da cui P {X > } = 1 [P {X = 0} + P {X = 1} + P {X = }] = Utilizzando una distribuzione di Poisson di parametro λ = np = 0,, cioè X P(0.), si ha: P {X = 0} = e λ λ 0 = e 0. = ! P {X = 1} = e λ λ 1 = e 0, 0, = ! P {X = } = e λ λ = e 0. 0, = !
20 98 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE e quindi si perviene allo stesso risultato P {X > } = La distribuzione multinomiale Una generalizzazione della distribuzione binomiale può condurre alla cosidetta distribuzione multinomiale nel modo seguente. Consideriamo una successione di n prove ripetute ed indipendenti ciascuna delle quali ammetta k possibili risultati A 1,..., A k mutuamente esclusivi. Sia p i la probabilità che l esperimento fornisca il risultato A i, per i = 1,..., k. Siano x 1,..., x k 1 interi non negativi tali che x x k 1 n. La probabilità che esattamente x i prove abbiano risultato A i, per i = 1,... k 1, e quindi che le restanti x k = n (x x k 1 ) prove abbiano risultato A k, è chiaramente: ( ) n p x 1 1 p x k k x 1 x x, k dove la quantità: ( ) n := x 1 x x k n! x 1! x k! costituisce il coefficiente multinomiale ed è uguale al numero di modi in cui scegliere, fra le n prove, quelle in cui si verifica A 1, quelle in cui si verifica A, etc. Se (X 1,..., X k ) è un vettore aleatorio dove X j è il numero (aleatorio) di volte in cui l evento A j si è verificato, per x j = 0, 1,..., n, allora la funzione di probabilità di (X 1,..., X k ) è data da: P (X 1 = x 1,..., X k = x k ) = n! x 1! x k! px 1 1 p x k k se k i=1 x i = n 0 altrimenti (3.13) La distribuzione del vettore aleatorio (X 1,..., X k ) si chiama distribuzione multinomiale e scriveremo X M(n, p 1,..., p k ). Per la distribuzione multinomiale si ha: E(X j ) = np j, Var(X j ) = np j (1 p j ), Cov(X i, X j ) = E[(X i np i )(X j np j )] = np i p j. In particolare, ne segue che il coefficiente di correlazione fra X i e X j è dato da: ( ) 1/ p i p j ρ ij = i, j = 1,..., k 1, (i j). (1 p i )(1 p j )
21 3.6. LA DISTRIBUZIONE GEOMETRICA La distribuzione geometrica La distribuzione geometrica deriva dallo stesso schema della distribuzione binomiale ma nel caso ora in esame, invece di analizzare il numero complessivo di eventi favorevoli conseguiti in n prove, ci si interessa al numero di prove necessario per ottenere il primo successo, cioè il tempo di attesa del primo successo. Data una successione di eventi equiprobabili ed indipendenti A 1, A,... con P (A i ) = p per ogni i = 1,,..., con 0 < p < 1, denotiamo con X la quantità aleatoria indice del primo successo nella sequenza assegnata. Allora la v.a. X assume valori nell insieme dei numeri naturali ed ha funzione di probabilità p(1 p) x 1 se x = 1,,... p(x) := 0 altrimenti Diremo in tal caso che X segue una distribuzione geometrica di parametro p e scriveremo X G(p). Per quanto riguarda la verifica della relazione x=1 p(x) = 1, posto q = 1 p, si può immediatamente verificare che risulta: da cui cioè: k r=0 q r = 1 + q + + q k = 1 qk+1 1 q r=0 (1 p) r = 1 p r=0 q r = lim k k r=0 Da tale relazione segue immediatamente: q r o, equivalentemente, = = lim k 1 (1 p) k+1 p 1 (1 p)k+1 p = 1 p. (1 p) r 1 = 1 p. r=1 (1 p)p r 1 = 1, (3.14) r=1 e quindi la verifica della proprietà x p(x) = 1. Nel caso di leggi geometriche, particolare interesse riveste la seguente relazione: P {X x} = p(1 p) r 1 = r=x p(1 p) r 1+(x 1) = (1 p) x 1 p(1 p) r 1 r=1 = (1 p) x 1, (3.15) essendo r=1 p(1 p)r 1 = 1 per la (3.14). r=1.
22 100 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE x Figura 3.4: Funzione di probabilità distribuzione geometrica con parametro p = 0, 4. Speranza matematica e Varianza. Per quanto riguarda la speranza matematica si ha: E(X) = xp(1 p) x 1 = p x(1 p) x 1 d = p (1 p)x dp x=1 x=1 x=1 = p d (1 p) x = p d 1 p dp dp 1 (1 p) = p d 1 p = 1 dp p p. x=1 Per il calcolo della varianza, premettiamo il calcolo di E(X ): E(X ) = x p(1 p) x 1 = (x x + x)p(1 p) x 1 Segue pertanto: = x=1 x=1 x(x 1)p(1 p) x 1 + x=1 = p(1 p) = p(1 p) xp(1 p) x 1 x=1 x(x 1)(1 p) x + 1 p x=1 x=1 = p(1 p) p p d dp (1 p)x + 1 d 1 p 0p(1 p) + 1 p dp p p = (1 p) p Var(X) = E(X ) µ = p p + 1 p 0 p p. 1 p = 1 p p. Proprietà di assenza di memoria. La distribuzione geometrica è caratterizzata dalla seguente proprietà di assenza di memoria. Proposizione 3.1 X G(p) se e solo se P {X = r + n X > n} = P {X = r}, per qualunque coppia r, n di numeri interi.
23 P {X 14} = = LA DISTRIBUZIONE GEOMETRICA 101 Dimostrazione. La proprietà in esame segue da un applicazione della formula della probabilità condizionale. Si ha infatti: Poichè, in base alla (3.15), risulta: allora dalla (3.16) segue per r 1: P {X = r + n, X > n} P {X = r + n X > n} = P {X > n} P {X = r + n} =. (3.16) P {X > n} P {X > n} = (1 p) n P {X = r + n X > n} = p(1 p)n+r 1 (1 p) n = p(1 p) r 1 = P {X = r}. Più in generale, la proprietà di assenza di memoria implica che P {X r + n X > n} = P {X r}. Tale risultato afferma che, se un evento E non si è verificato nelle prime n prove, allora la probabilità che esso non si verifichi nelle successive r prove è la stessa di quella di non manifestarsi nelle prime r prove. Esempio 3.13 In una certa località balneare la probabilità che piova in un qualunque giorno del mese di agosto è p = 0, 05. Assumendo l indipendenza qual è la probabilità che la prima pioggia del mese avvenga il 15 agosto? E prima del 15 agosto? Si tratta di un applicazione della distribuzione geometrica. Se X indica la quantità aleatoria numero di giorni (a partire dal primo agosto) fino alla prima pioggia, allora X G(0, 04), pertanto si avrà: P {X = 15} = = 0.04, Esempio 3.14 Si consideri un macchinario la cui durata di funzionamento, in un opportuna unità di misura (mese, anno o altro), sia retta dalla legge geometrica di densità: p(x) = 0. (0, 8) x 1 x = 1,,... Sapendo che il macchinario non ha ancora cessato di funzionare dopo 5 periodi (unità di misura), qual è la probabilità che si guasti all ottavo periodo? P {X = 8 X > 5} = P {X = 8} P {X > 5} = P {X = 3} = 0. (0.8) = 0.18.
24 10 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE 3.7 La distribuzione binomiale negativa o di Pascal La distribuzione binomiale negativa è una generalizzazione della distribuzione geometrica. Sia data una successione di prove indipendenti ognuna delle quali produce un successo con probabilità 0 < p < 1 oppure un insuccesso con probabilità 1 p. La distribuzione binomiale negativa è la distribuzione di probabilità del numero di prove per ottenere esattamente r successi. Diremo che una v.a. X segue una distribuzione binomiale negativa di parametri interi positivi r 1 e 0 < p < 1, e scriveremo X BN(r, p), se ha la seguente distribuzione di probabilità: p(x) = ( ) x 1 p r (1 p) x r se x = r, r + 1,..., r 1 0 altrimenti. In particolare per r = 1 si ottiene la distribuzione geometrica. (3.17) Speranza matematica e Varianza. La speranza matematica e la varianza di una v.a. X BN(r, p) sono date rispettivamente da: E(X) = r p Var(X) = r(1 p) p Si noti che, dati X G(p) e Y BN(r, p), risulta E(Y ) = r E(X) Var(Y ) = r Var(X). Proposizione 3.15 Siano X 1,..., X k v.a. indipendenti, con X i BN(r i, p) per i = 1,..., k. Allora la variabile aleatoria S k = X X k ha distribuzione NB(r r k, p). Corollario 3.16 Siano X 1,..., X k v.a. indipendenti aventi distribuzione geometrica di parametro p. Allora la variabile aleatoria S k = X X k ha distribuzione BN(k, p). 3.8 Altri esercizi Esercizio 3.17 n commensali si ripartiscono a caso intorno ad una tavola rotonda. Sia X il più piccolo numero (aleatorio) di commensali che separa Pietro e Paolo. Calcolare la legge di X e la speranza matematica di X. Esercizio 3.18 Si supponga che in una grande azienda si effettuino mediamente quattro interventi di manutenzione del settore informatico in una giornata lavorativa di 8 ore. Si assuma che il numero di interventi di manutenzione nei periodi indicati segua una distribuzione di Poisson.
25 3.8. ALTRI ESERCIZI Valutare la probabilità che in due ore non vi sia nessun intervento di manutenzione;. Valutare la probabilità che in un ora vengano effettuati almeno due interventi di manutenzione. Esercizio 3.19 Data una successione di eventi indipendenti ed equiprobabili con probabilità uguale a 1/100, determinare 1. la probabilità che, osservandone 100, non se ne verifichi alcuno;. La probabilità che su 00, se ne verifichino almeno 3; 3. la probabilità che su 50 se ne verifichino più di due; 4. il numero minimo n di prove necessarie affinchè la probabilità di avere almeno un successo sia maggiore di Esercizio 3.0 Un urna contiene N palline di cui 30 bianche e le restanti nere. Calcolare N sapendo che la probabilità di ottenere palline bianche in 4 estrazioni con restituzione è pari a 3 3 / 7 e che le palline nere sono più numerose delle palline bianche. Esercizio 3.1 Da un urna U, contenente palline bianche e nere, e da un urna V, contenente palline bianche e tre nere, si estraggono rispettivamente palline e 3 palline senza restituzione. Indicando con X e Y rispettivamente i numeri aleatori di palline bianche estratte rispettivamente da U e da V, calcolare P (X + Y > ), P (X = 1 X + Y > ) e E(X + Y ) Esercizio 3. Date tre variabili aleatorie, indipendenti e con distribuzione geometrica di parametro p, calcolare: 1. la speranza matematica m della variabile X + Y Z;. la probabilità dell evento {.5 X + Y + Z 4.}; 3. la covarianza delle v.a. U = X + Y e V = X Y. Esercizio 3.3 Un canale di trasmissione dati può ricevere messaggi binari da due sorgenti diverse A e B con probabilità 1 ciascuna. Ognuna delle due sorgenti produce messaggi in cui i bit successivi sono tra loro indipendenti. Per la sorgente A i bit possono essere 1 oppure 0 con probabilità 1, mentre per la sorgente B, il valore 1 si verifica con probabilità 1 e lo 0 con 4 probabilità 3. Un messaggio di lunghezza n viene ricevuto in cui si osserva una proporzione di 4 1 pari a 0.4 (cioè in cui si trovano 0.4 n bit uguali a 1). 1. Supponiamo n = 10. Qual è la probabilità che si tratti della sorgente A? Quale delle due sorgenti è la più probabile? E se invece fosse n = 100?. Rispondere alle stesse domande del punto precedente supponendo che a priori i messaggi provengano con probabilità 30% dalla sorgente A e 70% dalla sorgente B.
26 104 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE Esercizio 3.4 Un urna U 1 contiene una pallina bianca e nere, mentre un urna U contiene palline bianche ed una nera. Da U 1 si estraggono due palline che vengono inserite in U. Successivamente da U si estrae una pallina che viene inserita in U 1. Considerati gli eventi: calcolare P (B), P (A B) e P (A B). A : le due palline inserite in U sono nere B : la pallina inserita in U 1 è bianca Esercizio 3.5 Due squadre di atletica A e B partecipano alla fase finale di un torneo che consiste in una serie di 7 incontri diretti. La squadra vincitrice è quella che si aggiudica per prima 4 vittorie. Assumendo che le due squadre abbiano la stessa probabilità di vincere una qualunque partita e che i risultati siano indipendenti, calcolare: 1. La probabilità che il torneo si concluda in al più 6 partite.. La probabilità che il torneo si concluda esattamente dopo 6 incontri dato che la squadra A ha vinto le prime due partite. Esercizio 3.6 Un azienda alimentare propone un nuovo tipo di merenda al cioccolato e crema di zabaione, rivolta particolarmente ai ragazzi aventi un età compresa fra 10 e 1 anni. L area marketing ha successivamente rilevato che, a livello nazionale, il 30% degli interessati ha visto almeno uno degli spot televisivi predisposti per la campagna pubblicitaria che ha lanciato il prodotto. Considerato un gruppo di 150 potenziali consumatori, ci si chiede: 1. qual è il numero atteso che ha visto almeno uno spot televisivo?. qual è la probabilità che ve siano stati almeno 50 che ha visto almeno uno spot? Esercizio 3.7 Siano X 1 e X due v.a. indipendenti aventi distribuzione di Poisson di parametri rispettivamente λ 1 = 3 e λ = 1, cioè X 1 P(3) e X P(1). i) Calcolare la funzione di ripartizione di X e rappresentarla graficamente; ii) considerata la v.a. Y = 3X 1 calcolare E[Y ] e P (Y 6). Considerata successivamente la v.a. W = X 1 X, calcolare: E[W ] e Var(W ). Esercizio 3.8 Siano X e Y due v.a. aventi distribuzione di Poisson di parametro λ = 9. i) Calcolare P (X ) e P (3X ) ii) Calcolare la covarianza di X e Y sapendo che il coefficiente di correlazione fra X e Y è uguale a /9. Esercizio 3.9 Una moneta viene tarata in maniera tale che, in una successione di 10 prove ripetute e indipendenti, la probabilità che l evento T ( testa ) si verifichi 4 volte sia uguale e che si verifichi 5 volte sia uguale a Calcolare la probabilità che nelle 10 prove l evento T si verifichi una sola volta. Esercizio 3.30 Uno studente, per ottenere informazioni relative ad assegnazioni di borse di studio, si rivolge all ufficio competente il quale dà al 60% informazioni esatte. Sapendo ciò, lo studente va 3 volte a chiedere sempre la stessa informazione ed ottiene volte la risposta A ed una volta la risposta contraria B. Calcolare la probabilità p che la risposta esatta sia la A. (Si supponga che A e B siano inizialmente equiprobabili e costituiscano una partizione dell evento certo).
27 3.8. ALTRI ESERCIZI Soluzioni Soluzione Sia n il numero totale di commensali, distinguiamo i due casi: n dispari e n pari. Se n è dispari, allora possiamo scrivere n = p + 1 dove p è un numero dispari, con p 1. In questo caso X è una v.a. con legge uniforme su {0, 1,..., p 1} e pertanto: E[X] = p Var(X) = p(p ) 1 Se n è pari, allora possiamo scrivere n = p, dove p è un numero dispari; in questo caso si ha: da cui, tenendo conto che segue: P (X = p 1) = 1 n 1 = 1 p 1 P (X = k) = p 1 = p (p ) = E[X] = p 1 p 1 + (p 1)(p ) per 1 k p (p 1)(p ) p 1. = (p 1) p 1. Soluzione Per quanto riguarda il primo esercizio, sia X la v.a. numero di interventi di manutenzione in un periodo di due ore ; il testo richiede il calcolo di P (X = 0). In base alle ipotesi, se mediamente nell azienda si richiedono 4 interventi ogni otto ore, allora si può assumere in base ad un semplice criterio di proporzionalità che mediamente verrà richiesto un intervento ogni due ore. Inoltre, poichè si assume che X segua una distribuzione di Poisson, allora si ha X P(1), cioè una distribuzione di Poisson di parametro λ = 1. Si ha pertanto: λ λ0 P (X = 0) = e 0! = e 1 = Con riferimento al secondo punto, sia Y la v.a. numero di interventi di manutenzione in un periodo di un ora. In base a considerazioni a quelle svolte in precedenza, Y segue una distribuzione di Poisson di parametro λ = 0.5, cioè Y P(0.5). Segue pertanto: P (Y ) = 1 P (Y 1) = 1 P (Y = 0) P (Y = 1) = 1 e 0! = 1 e 0.5 ( ) = e 1!
28 106 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE Soluzione Risolviamo il problema in due modi: con la distribuzione binomiale (soluzione esatta ) e con quella di Poisson (distribuzione approssimata ). Per quanto riguarda la soluzione con la distribuzione binomiale, sia X B(100, 0.01); quindi per il primo punto si ha: P (X = 0) = (0.99) 100 = Per quanto riguarda il secondo punto, sia X B(00, 0.01) e quindi: P (X 3) = 1 P (X ) = 1 [(0.99) (0.99) (0.01) (0.99) 198 ] = Ed infine, per il terzo punto, considerato X B(50, 0.01), si ha: P (X > ) = 1 P (X ) = 1 [P (X = 0) + P (X = 1) + P (X = )] = 1 [(0.99) (0.99) (0.99) 48 (0.01) ] = Utilizzando la distribuzione di Poisson, nel primo caso essendo λ = np = 1 si ha X P(1) e quindi P (X = 0) = e 1 = ; nel secondo caso essendo λ = np = si ha X P() e quindi P (X 3) = 1 P (X ) = 1 e (1 + + ) = 0.33 ; nel terzo caso essendo λ = np = 0.5 si ha X P(0.5) e quindi: P (X > ) = 1 P (X ) = 1 [P (X = 0) + P (X = 1) + P (X = )] = e 0.5 ( ) = Si nota che l approssimazione della distribuzione di Poisson a quella binomiale migliora al crescere di n. Infine, la probabilità di non avere successi in una successione di n prove ripetute e indipendenti è (0.99) n. Posto X B(n, 0.01), possiamo considerare pertanto la disequazione: e risolvendo rispetto a n si ottiene: P (X 1) = 1 P (X = 0) = (0.99) n > 0.98 n > log(0.0) log(0.99) = 389. da cui n = 390.
29 3.8. ALTRI ESERCIZI 107 Soluzione 3.0. Indicata con p la proporzione di palline bianche nell urna, in base ad i dati del problema risulta p < 1/. Trattandosi di estrazioni con restituzione, la probabilità di estrarre palline bianche in 4 prove è data da: ( ) 4 p (1 p) = 6p (1 p). In base ad i dati del problema, si tratta di risolvere l equazione: 6p (1 p) = 33 7 sotto il vincolo p < 1/. Tenendo conto che 6 = 3, dall equazione precedente si ottiene: p (1 p) = = 3 8 p(1 p) = 3 16 p p = 0 che ammette soluzioni: p 1 = 1/4 e p = 3/4. Solo la prima soddisfa il vincolo p < 1/ e pertanto l unica soluzione ammissibile è p = 1/4. Soluzione 3.1. P {X + Y > } = P {X + Y = 3} + P {X + Y = 4} = P {X =, Y = 1} + P {X = 1, Y = } + P {X =, Y = } = P {X = }P {Y = 1} + P {X = 1}P {Y = } + P {X = }P {Y = } dove ( ) ( ) P {X = 1} = 1 1 ( ) = = 3 ; ( ) ( ) P {X = } = 0 ( ) = ; ( ) ( ) 3 P {Y = 1} = P {Y = } = 1 ( ) = ; 3 ( ) ( ) 3 1 ( ) =
30 108 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE e quindi P {X + Y > } = = = 7 0. Passando al punto successivo: P {X = 1 X + Y > } = = P {X = 1, X + Y > } P {X + Y > } P {X = 1}P {Y = } P {X + Y > } = = P {X = 1, Y = } P {X + Y > } = 4 7. Infine essendo E[X + Y ] = E[X] + E[Y ] e E[X] = 0 P {X = 0} + 1 P {X = 1} + P {X = } = = 1 E[Y ] = 0 P {Y = 0} + 1 P {Y = 1} + P {Y = } = = 6 5 segue E[X + Y ] = E[X] + E[Y ] = = Soluzione 3.. m = 1 p + 1 p 1 p = 1 p P {.5 X + Y + Z 4.} = P {X + Y + Z = 3} + P {X + Y + Z = 4} = P (X = 1, Y = 1, Z = 1) + P (X =, Y = 1, Z = 1) + P (X = 1, Y =, Z = 1) + P (X = 1, Y = 1, Z = ) = P (X = 1)P (Y = 1)P (Z = 1) + P (X = )P (Y = 1)P (Z = 1) + P (X = 1)P (Y = )P (Z = 1) + P (X = 1)P (Y = 1)P (Z = ) = p 3 + 3p p p(1 p) Cov(X + Y, X Y ) = Cov(X, X) + Cov(Y, X) Cov(Y, X) Cov(Y, Y ) = Var(X) Var(Y ) = 0., essendo le variabili X, Y, Z identicamente distribuite.
31 3.8. ALTRI ESERCIZI 109 Soluzione 3.3. Indichiamo con A = il messaggio proviene dalla sorgente A B = il messaggio proviene dalla sorgente B C = viene ricevuto un messaggio in cui ci sono 0.4n bit uguali a 1 p A = probabilità che la sorgente A emetta un 1 = 1 p B = probabilità che la sorgente B emetta un 1 = 1 4. Dobbiamo calcolare P (A C). Essendo: Poniamo: da cui: e quindi poichè risulta: P (A C) = P (C A)P (A) P (C) X = E E n X A B(n, p A ) X B B(n, p B ) ( ) (1 ) P (C A) = P (X A = 4) = 4 ( ) (1 ) 10 4 ( ) 6 3 P (C B) = P (X B = 4) segue,poichè P (C) = P (C A)P (A) + P (C B)P (B) ( ) 10 ( ) P (C A)P (A) P (A C) = P (C A)P (A) + P (C B)P (B) = 4 ( ) ( ) 10 ( 1 ) ( ( ) 4) 4 4 P (A C) = = ( 3 4 ) Nel caso successivo, basta considerare la relazione precedente con P (A) = 0.3 e P (B) = 0.7: ( ) 10 ( ) 0.3 P (C A)P (A) P (C A)P (A) + P (C B)P (B) = 1 4 = ( ) ( 10 4 ) ( 1 ) ( 10 4 ) ( 1 4 ( 3 6 4) 4) 0.7
32 110 CAPITOLO 3. PRINCIPALI DISTRIBUZIONI DI PROBABILITÀ DISCRETE Da cui P (B C) = 1 P (A C) = 0.64 e quindi in questo caso è la sorgente B la più probabile. Soluzione 3.4. Per quanto riguarda il calcolo di P (B), considerata la partizione dell evento certo Ω in Ω = A A c, possiamo scrivere: P (B) = P (B Ω) = P (B (A A c )) = P (B A) + P (B A c ) = P (A)P (B A) + P (A c )P (B A C ). Osserviamo che se si verifica l evento A, nell urna U avremo palline bianche e 3 nere; pertanto risulta: P (B A) = P (A B c ) = = 3 5. Inoltre, tenendo conto che in base alla composizione iniziale dell urna U 1, segue: ( ) ( ) 1 P (A) = 0 ( ) = da cui si ottiene: P (B) = = Per il teorema delle probabilità composte segue: P (A B) = P (A B) P (B) = P (A)P (B A) P (B) = = 1 4. Infine per il teorema delle probabilità totali si ha: P (A B) = P (A) + P (B) P (A B) = = = Soluzione 3.6. Indichiamo con P (A i ) e P (B i ) rispettivamente la probabilità che la squadra A o B vinca la i-esima partita, con i = 1,..., 7. In base alle ipotesi del problema risulta P (A i ) = P (B i ) = 1. Non è pertanto ammesso il risultato di pareggio. In base alle regole fissate, il torneo si conclude quando una delle due squadre collezione 4 vittorie. La probabilità che il torneo si concluda entro sei partite è quindi data dalla somma della probabilità che la squadra A vinca quattro partite fra le prime sei e della probabilità che la squadra B vinca quattro partite fra le prime sei. Poichè le due squadre hanno la stessa probabilità di vincere ciascuna partita, allora le due squadre hanno la stessa probabilità di vincere il torneo entro sei
33 3.8. ALTRI ESERCIZI 111 partite; pertanto la probabilità che il torneo si concluda entro sei partite è pari al doppio della probabilità che una delle due squadre (ad esempio la squadra A) vinca il torneo entro sei partite. Indicato con X A il numero (aleatorio) necessario affinchè la squadra A vinca il torneo, si ha che X A segue una distribuzione binomiale negativa NB(4, 1 ). Essendo segue: e quindi P (il torneo si conclude entro 6 partite) = P (X A 6) P (X A 6) = P (X A = 4) + P (X A = 5) + P (X A = 6) ( ) ( ) 4 ( ) 0 ( ) ( ) 4 ( ) = = = ( 5 3 ) ( 1 P (il torneo si conclude entro 6 partite) = 11 3 = ) 4 ( ) 1 Per quanto concerne il secondo punto, poichè le prime due partite sono state vinte dalla squadra A, il torneo si conclude in sei partite se la squadra A consegue una vittoria nella terza o quarta o quinta partita e una vittoria nella sesta partita, oppure se la squadra B consegue quattro vittorie consecutive. Nel primo caso la probabilità è data da: ( 3 1 ) ( 1 ) ( 1 ) = , mentre nel secondo caso la probabilità che la squadra B vinca quattro partite cosecutive è: ( ) 4 1 = In definitiva la probabilità richiesta è: = 4 16 = 1 4. Soluzione 3.5. Sia X la v.a. numero di potenziali consumatori che ha visto almeno uno spot della campagna pubblicitaria. In base alle ipotesi, si ha X B(150, 0.3). Ne segue che il numero atteso è dato da: E[X] = np = = 45. Per affrontare il secondo punto, consideriamo l approssimazione normale alla distribuzione binomiale B(n, p) N(np, npq) B(150, 0.3) N(45, 31.5)
Esercizi svolti di statistica. Gianpaolo Gabutti
 Esercizi svolti di statistica Gianpaolo Gabutti (gabuttig@hotmail.com) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
Esercizi svolti di statistica Gianpaolo Gabutti (gabuttig@hotmail.com) 1 Introduzione Questo breve documento contiene lo svolgimento di alcuni esercizi di statistica da me svolti durante la preparazione
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha. P {X = a, Y = b} = P {X = a}p {Y = b}
 Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Esame di AM2 & EAP (270/04) a.a. 2009/10
 Quarto appello del 16 Luglio 2010 1. Un urna contiene delle palline numerate e distribuite in seguente maniera: Vengono estratte due palline senza rimpiazzo e siano X e Y rispettivamente il numero della
Quarto appello del 16 Luglio 2010 1. Un urna contiene delle palline numerate e distribuite in seguente maniera: Vengono estratte due palline senza rimpiazzo e siano X e Y rispettivamente il numero della
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
 SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
SOLUZIONI DEL 1 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA 1 Esercizio 0.1 Dato P (A) = 0.5 e P (A B) = 0.6, determinare P (B) nei casi in cui: a] A e B sono incompatibili; b] A e B sono indipendenti;
Probabilità 1, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
Probabilità, laurea triennale in Matematica I prova scritta sessione estiva a.a. 2008/09. Due roulette regolari vengono azionate più volte; sia T il numero di volte che occorre azionare la prima roulette
CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati
 CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 1. Dati gli eventi A,B,C, ognuno dei quali implica il successivo, e tali che P (A) è metà della probabilità di B, che a sua volta ha probabilità metà di quella
CALCOLO DELLE PROBABILITÀ - 9 giugno 1998 1. Dati gli eventi A,B,C, ognuno dei quali implica il successivo, e tali che P (A) è metà della probabilità di B, che a sua volta ha probabilità metà di quella
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
) la sua densità discreta sarà della forma. p X (0) = 1 2, p X(1) = 1 2,
 Esercizi settimana 6 Esercizi applicati Esercizio. Siano X e Y due v.a. discrete indipendenti tali che X B(, ) e Y B(, ), n 0. (i) Si calcoli la legge di X + Y ; (ii) Si calcoli la legge di X Y ; (iii)
Esercizi settimana 6 Esercizi applicati Esercizio. Siano X e Y due v.a. discrete indipendenti tali che X B(, ) e Y B(, ), n 0. (i) Si calcoli la legge di X + Y ; (ii) Si calcoli la legge di X Y ; (iii)
Lezione 12. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 12. A. Iodice.
 discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
STATISTICA: esercizi svolti sulle VARIABILI CASUALI
 STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
0 z < z < 2. 0 z < z 3
 CALCOLO DELLE PROBABILITÀ o - 7 gennaio 004. Elettronica : 4; Nettuno: 3.. Data un urna di composizione incognita con palline bianche e nere, sia K = il numero di palline bianche nell urna è il doppio
CALCOLO DELLE PROBABILITÀ o - 7 gennaio 004. Elettronica : 4; Nettuno: 3.. Data un urna di composizione incognita con palline bianche e nere, sia K = il numero di palline bianche nell urna è il doppio
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2006/07
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
Esercitazioni di Statistica
 Esercitazioni di Statistica Variabili casuali Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio Determinare se le funzioni seguenti: 0.0 se x < 0. se x = g(x) = 0.5 se x = 0.7 se x = 3 se x =
Esercitazioni di Statistica Variabili casuali Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio Determinare se le funzioni seguenti: 0.0 se x < 0. se x = g(x) = 0.5 se x = 0.7 se x = 3 se x =
Variabili aleatorie discrete. Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia
 Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Esercizi settimana 5. Esercizi applicati. Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 2 3
 1 Esercizi settimana 5 Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
1 Esercizi settimana 5 Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
1 Eventi. Operazioni tra eventi. Insiemi ed eventi. Insieme dei casi elementari. Definizione di probabilità.
 Quella che segue e la versione compatta delle slides usate a lezioni. NON sono appunti. Come testo di riferimento si può leggere Elementi di calcolo delle probabilità e statistica Rita Giuliano. Ed ETS
Quella che segue e la versione compatta delle slides usate a lezioni. NON sono appunti. Come testo di riferimento si può leggere Elementi di calcolo delle probabilità e statistica Rita Giuliano. Ed ETS
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale a.a. 2016/17
 Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Esercizi su variabili aleatorie discrete
 Esercizi su variabili aleatorie discrete Esercizio 1. Data la variabile aleatoria discreta X, caratterizzata dalla seguente rappresentazione nello spazio degli stati: 1 0,25 X = { 0 0,50 1 0,25 calcolare
Esercizi su variabili aleatorie discrete Esercizio 1. Data la variabile aleatoria discreta X, caratterizzata dalla seguente rappresentazione nello spazio degli stati: 1 0,25 X = { 0 0,50 1 0,25 calcolare
STATISTICA 1 ESERCITAZIONE 8
 STATISTICA 1 ESERCITAZIONE 8 Dott. Giuseppe Pandolfo 18 Novembre 2013 CALCOLO DELLE PROBABILITA Elementi del calcolo delle probabilità: 1) Esperimento: fenomeno caratterizzato da incertezza 2) Evento:
STATISTICA 1 ESERCITAZIONE 8 Dott. Giuseppe Pandolfo 18 Novembre 2013 CALCOLO DELLE PROBABILITA Elementi del calcolo delle probabilità: 1) Esperimento: fenomeno caratterizzato da incertezza 2) Evento:
X Vincita (in euro) Tabella 1: Vincite
 Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 9 Giugno 1 CdS in STAD, SIGAD - docente: G. Sanfilippo Motivare dettagliatamente
Cognome e Nome:....................................... Matricola............. CdS............. CALCOLO DELLE PROBABILITA - 9 Giugno 1 CdS in STAD, SIGAD - docente: G. Sanfilippo Motivare dettagliatamente
5. Distribuzioni. Corso di Simulazione. Anno accademico 2009/10
 Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2009/10 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
TEST n La funzione di ripartizione di una variabile aleatoria:
 TEST n. 1 1. Un esperimento consiste nell estrarre successivamente, con reimmissione nel mazzo, due carte da un mazzo di 52 carte. Individuare la probabilità di estrarre due assi. A 0.0059 B 0.0044 C 0.0045
TEST n. 1 1. Un esperimento consiste nell estrarre successivamente, con reimmissione nel mazzo, due carte da un mazzo di 52 carte. Individuare la probabilità di estrarre due assi. A 0.0059 B 0.0044 C 0.0045
P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
3. Distribuzioni. Corso di Simulazione. Anno accademico 2006/07
 Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Anno accademico 2006/07 Spazio di probabilità Ω spazio campione F 2 Ω spazio degli eventi: (i) Ω F (ii) A F = Ω \ A F (iii) A, B F = A B F P: F [0, 1] funzione di probabilità: (i) P(A) 0 (ii) P(Ω) = 1
Soluzione esercizi (quarta settimana)
 Soluzione esercizi (quarta settimana) Marco Riani Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? 1 Esempio Gioco la schedina mettendo a caso i segni (1 X
Soluzione esercizi (quarta settimana) Marco Riani Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? 1 Esempio Gioco la schedina mettendo a caso i segni (1 X
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità A. A. /5 prova scritta (//5(docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento dei punti non facoltativi
Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità A. A. /5 prova scritta (//5(docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento dei punti non facoltativi
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 2010-11 P.Baldi Lista di esercizi 3. Corso di Laurea in Biotecnologie Esercizio 1 Una v.a. X segue una legge N(2, ). Calcolare a1) P(X 1) a2) P(2
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 2010-11 P.Baldi Lista di esercizi 3. Corso di Laurea in Biotecnologie Esercizio 1 Una v.a. X segue una legge N(2, ). Calcolare a1) P(X 1) a2) P(2
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE
 ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE Docente titolare: Irene Crimaldi 26 novembre 2009 Es.1 Supponendo che la probabilità di nascita maschile e femminile sia la stessa, calcolare la probabilità
ESERCIZI SU EVENTI E VARIABILI ALEATORIE DISCRETE Docente titolare: Irene Crimaldi 26 novembre 2009 Es.1 Supponendo che la probabilità di nascita maschile e femminile sia la stessa, calcolare la probabilità
Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 16/06/2016 NOME: COGNOME: MATRICOLA: Esercizio 1 Cinque lettere
Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 16/06/2016 NOME: COGNOME: MATRICOLA: Esercizio 1 Cinque lettere
Variabili casuali ad una dimensione Testi degli esercizi. Variabili casuali ad una dimensione a.a. 2012/2013 1
 Variabili casuali ad una dimensione Testi degli esercizi 1 Costruzione di variabile casuale discreta Esercizio 1. Sia data un urna contenente 3 biglie rosse, 2 biglie bianche ed una biglia nera. Ad ogni
Variabili casuali ad una dimensione Testi degli esercizi 1 Costruzione di variabile casuale discreta Esercizio 1. Sia data un urna contenente 3 biglie rosse, 2 biglie bianche ed una biglia nera. Ad ogni
1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3.
 Corso di Laurea INTERFACOLTÀ - Esercitazione di Statistica n 6 ESERCIZIO 1: 1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3. lancio di
Corso di Laurea INTERFACOLTÀ - Esercitazione di Statistica n 6 ESERCIZIO 1: 1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3. lancio di
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 3 Abbiamo visto: Definizione di partizione di Teorema di Bayes Definizione di variabile aleatoria
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 3 Abbiamo visto: Definizione di partizione di Teorema di Bayes Definizione di variabile aleatoria
Corso di Statistica. Distribuzioni di probabilità per variabili casuali discrete. Prof.ssa T. Laureti a.a
 Corso di Statistica Distribuzioni di probabilità per variabili casuali discrete Prof.ssa T. Laureti a.a. 2013-2014 1 Variabili casuale di Bernoulli La v.c. di Bernoulli trae origine da una prova nella
Corso di Statistica Distribuzioni di probabilità per variabili casuali discrete Prof.ssa T. Laureti a.a. 2013-2014 1 Variabili casuale di Bernoulli La v.c. di Bernoulli trae origine da una prova nella
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Il modello binomiale Da studi interni è noto che il 35% dei clienti del Supermercato GD paga
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Il modello binomiale Da studi interni è noto che il 35% dei clienti del Supermercato GD paga
Metodi Matematici Probabilità e Statistica. Correzione Compitino del
 Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
Esercizi di Probabilità
 Esercizi di Probabilità Annalisa Cerquetti - Sandra Fortini Vai all indice Istituto di Metodi Quantitativi, Viale Isonzo, 25, 2033 Milano, Italy. E-mail: annalisa.cerquetti@unibocconi.it,sandra.fortini@unibocconi.it
Esercizi di Probabilità Annalisa Cerquetti - Sandra Fortini Vai all indice Istituto di Metodi Quantitativi, Viale Isonzo, 25, 2033 Milano, Italy. E-mail: annalisa.cerquetti@unibocconi.it,sandra.fortini@unibocconi.it
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Esercitazione 4 del corso di Statistica (parte 2)
 Esercitazione 4 del corso di Statistica (parte ) Dott.ssa Paola Costantini Febbraio Esercizio n. Il tempo di percorrenza del treno che collega la stazione di Roma Termini con l aeroporto di Fiumicino è
Esercitazione 4 del corso di Statistica (parte ) Dott.ssa Paola Costantini Febbraio Esercizio n. Il tempo di percorrenza del treno che collega la stazione di Roma Termini con l aeroporto di Fiumicino è
STATISTICA ESERCITAZIONE 9
 STATISTICA ESERCITAZIONE 9 Dott. Giuseppe Pandolfo 19 Gennaio 2015 REGOLE DI CONTEGGIO Sequenze ordinate Sequenze non ordinate Estrazioni con ripetizione Estrazioni senza ripetizione Estrazioni con ripetizione
STATISTICA ESERCITAZIONE 9 Dott. Giuseppe Pandolfo 19 Gennaio 2015 REGOLE DI CONTEGGIO Sequenze ordinate Sequenze non ordinate Estrazioni con ripetizione Estrazioni senza ripetizione Estrazioni con ripetizione
II Appello di Calcolo delle Probabilità Laurea Triennale in Matematica 2016/17
 II Appello di Calcolo delle Probabilità Laurea Triennale in Matematica 6/7 Martedì 4 febbraio 7 Cognome: Nome: Email: Se non è espressamente indicato il contrario, per la soluzione degli esercizi è possibile
II Appello di Calcolo delle Probabilità Laurea Triennale in Matematica 6/7 Martedì 4 febbraio 7 Cognome: Nome: Email: Se non è espressamente indicato il contrario, per la soluzione degli esercizi è possibile
Calcolo della probabilità
 Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA) A.A. 2016/17 - Prima prova in itinere
 Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica 69AA) A.A. 06/7 - Prima prova in itinere 07-0-03 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica 69AA) A.A. 06/7 - Prima prova in itinere 07-0-03 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
Statistica Applicata all edilizia: alcune distribuzioni di probabilità
 Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
b = 1 2σ 3. La lunghezza di una barra è un numero aleatorio X con densità della forma 0, x 0, 0 < x 1 a = 1 F (x) = 2 2x 1 x2
 CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
CALCOLO DELLE PROBABILITÀ E STATISTICA - 0 gennaio 2002 Informatica (N.O.) (Canali 4) esercizi -4 Vecchio Ordinamento esercizi -6. Da un lotto contenente 4 pezzi buoni e 2 difettosi si estraggono senza
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
CP110 Probabilità: Esonero 1. Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
Dipartimento di Matematica, Roma Tre Pietro Caputo 2009-2010, II semestre 1 aprile, 2010 CP110 Probabilità: Esonero 1 Testo e soluzione 1. (7 pt Una scatola contiene 15 palle numerate da 1 a 15. Le palle
PROBABILITA. DEFINIZIONE: Ogni singolo risultato di un esperimento casuale si chiama evento elementare
 PROBABILITA La teoria della probabilità si applica ad esperimenti aleatori o casuali: ossia, esperimenti il cui risultato non è prevedibile a priori. Ad esempio, lancio di un dado, lancio di una moneta,
PROBABILITA La teoria della probabilità si applica ad esperimenti aleatori o casuali: ossia, esperimenti il cui risultato non è prevedibile a priori. Ad esempio, lancio di un dado, lancio di una moneta,
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:
![Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza: Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:](/thumbs/72/66437341.jpg) Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
Probabilità e Statistica per l Informatica Esercitazione 4
 Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
LEZIONE 2.5. corso di statistica. Francesco Lagona Università Roma Tre. LEZIONE 2.5 p. 1/12
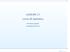 LEZIONE 2.5 p. 1/12 LEZIONE 2.5 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.5 p. 2/12 distribuzione doppia di due variabili aleatorie consideriamo la distribuzione doppia di due
LEZIONE 2.5 p. 1/12 LEZIONE 2.5 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.5 p. 2/12 distribuzione doppia di due variabili aleatorie consideriamo la distribuzione doppia di due
VARIABILI CASUALI CONTINUE
 p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
L assegnazione è coerente? SÌ NO. A e B sono stocasticamente indipendenti? SÌ NO
 CALCOLO DELLE PROBABILITÀ - gennaio 00 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati Nuovo Ordinamento esercizi -4. Vecchio Ordinamento esercizi -6..
CALCOLO DELLE PROBABILITÀ - gennaio 00 Scrivere le risposte negli appositi spazi Motivare dettagliatamente le risposte su fogli allegati Nuovo Ordinamento esercizi -4. Vecchio Ordinamento esercizi -6..
3.1 La probabilità: eventi e variabili casuali
 Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
Esercizi su variabili discrete: binomiali e ipergeometriche
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su variabili discrete: binomiali e ipergeometriche Es1 Due squadre di rugby si sfidano giocando fra loro varie partite La squadra che vince 4 partite
STATISTICA ESERCITAZIONE. 1) Specificare la distribuzione di probabilità della variabile e rappresentarla graficamente;
 0.00 0.05 0.10 0.15 0.20 STATISTICA ESERCITAZIONE Dott. Giuseppe Pandolfo 4 Maggio 2015 Esercizio 1 (Uniforme discreta) Si consideri l esperimento lancio di un dado non truccato. Sia X la variabile casuale
0.00 0.05 0.10 0.15 0.20 STATISTICA ESERCITAZIONE Dott. Giuseppe Pandolfo 4 Maggio 2015 Esercizio 1 (Uniforme discreta) Si consideri l esperimento lancio di un dado non truccato. Sia X la variabile casuale
CALCOLO DELLE PROBABILITA - 24 Giugno 2015 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5,6.
 Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 4 Giugno 5 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5, Motivare dettagliatamente le risposte su fogli allegati e
Cognome e Nome: Matricola CdS CALCOLO DELLE PROBABILITA - 4 Giugno 5 CdL in STAD, SIGAD Compito intero Seconda prova in itinere: esercizi 4,5, Motivare dettagliatamente le risposte su fogli allegati e
Facoltà di ECONOMIA Università di Pavia 20 Aprile 2004 Prova scritta di Analisi dei dati MODALITÀ A
 MODALITÀ A Riportare sul foglio nome, cognome, numero di matricola e modalità del testo d esame. Problema 1 (8 PUNTI) Su un collettivo di 10 clienti iscritti al programma frequent flyer di una nota compagnia
MODALITÀ A Riportare sul foglio nome, cognome, numero di matricola e modalità del testo d esame. Problema 1 (8 PUNTI) Su un collettivo di 10 clienti iscritti al programma frequent flyer di una nota compagnia
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità 1 A. A. 4/5 a prova in itinere 8/6/5docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento degli Esercizi
Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità 1 A. A. 4/5 a prova in itinere 8/6/5docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento degli Esercizi
Compiti tematici capp. 5,6
 Compiti tematici capp. 5,6 a cura di Giovanni M. Marchetti 2016 ver. 0.6 Indice Esercizi dai compiti a casa (HW..................................... 8 1. Se X e Y sono due variabili casuali independenti,
Compiti tematici capp. 5,6 a cura di Giovanni M. Marchetti 2016 ver. 0.6 Indice Esercizi dai compiti a casa (HW..................................... 8 1. Se X e Y sono due variabili casuali independenti,
Estrazioni senza restituzione da un urna di composizione incognita. P(E i)=
 Estrazioni senza restituzione da un urna di composizione incognita. Consideriamo n estrazioni senza restituzione da un urna contenente N palline, di cui r sono bianche, con r incognito. Introdotta la partizione
Estrazioni senza restituzione da un urna di composizione incognita. Consideriamo n estrazioni senza restituzione da un urna contenente N palline, di cui r sono bianche, con r incognito. Introdotta la partizione
Esercitazione N. 1 (11 ottobre 2016)
 Esercitazione N. 1 (11 ottobre 2016) Un'urna contiene elementi. Vengono estratti di seguito elementi, ogni elemento una volta estratto è riposto nell'urna. Calcolare la probabilità dell evento: Problema
Esercitazione N. 1 (11 ottobre 2016) Un'urna contiene elementi. Vengono estratti di seguito elementi, ogni elemento una volta estratto è riposto nell'urna. Calcolare la probabilità dell evento: Problema
Statistica. Esercitazione 10. Alfonso Iodice D Enza iodicede@unicas.it. Università degli studi di Cassino. Statistica. A. Iodice. V.C.
 uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Esercitazione 1 del corso di Statistica (parte 2)
 Esercitazione del corso di Statistica (parte Dott.ssa Paola Costantini 8 Gennaio 0 Esercizio n Compro due cassette contenenti 0 piante di rosa che ancora devono sbocciare. Nella prima cassetta ci sono
Esercitazione del corso di Statistica (parte Dott.ssa Paola Costantini 8 Gennaio 0 Esercizio n Compro due cassette contenenti 0 piante di rosa che ancora devono sbocciare. Nella prima cassetta ci sono
PROBABILITA. Distribuzione di probabilità
 DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
Matematica Applicata L-A Definizioni e teoremi
 Definizioni e teoremi Settembre - Dicembre 2008 Definizioni e teoremi di statistica tratte dalle lezioni del corso di Matematica Applicata L- A alla facoltà di Ingegneria Elettronica e delle Telecomunicazioni
Definizioni e teoremi Settembre - Dicembre 2008 Definizioni e teoremi di statistica tratte dalle lezioni del corso di Matematica Applicata L- A alla facoltà di Ingegneria Elettronica e delle Telecomunicazioni
Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 120 minuti
 Compito in classe 4D/17 Gennaio 006 1 Oggetto: compito in Classe 4D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 10 minuti Argomenti: Calcolo combinatorio e calcolo delle probabilità.
Compito in classe 4D/17 Gennaio 006 1 Oggetto: compito in Classe 4D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 10 minuti Argomenti: Calcolo combinatorio e calcolo delle probabilità.
STATISTICA (2) ESERCITAZIONE 1. Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 1 29.01.2014 Dott.ssa Antonella Costanzo Esercizio 1. Modelli discreti di probabilità: le v.c. binomiale e geometrica (come caso particolare della v.c. binomiale negativa)
STATISTICA (2) ESERCITAZIONE 1 29.01.2014 Dott.ssa Antonella Costanzo Esercizio 1. Modelli discreti di probabilità: le v.c. binomiale e geometrica (come caso particolare della v.c. binomiale negativa)
DISTRIBUZIONI DI PROBABILITA
 DISTRIBUZIONI DI PROBABILITA Nell associare ai risultati di un esperimento un valore numerico si costruisce una variabile casuale (o aleatoria, o stocastica). Ogni variabile casuale ha una corrispondente
DISTRIBUZIONI DI PROBABILITA Nell associare ai risultati di un esperimento un valore numerico si costruisce una variabile casuale (o aleatoria, o stocastica). Ogni variabile casuale ha una corrispondente
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
Statistica Metodologica
 Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
PROBLEMI DI PROBABILITÀ
 PROBLEMI DI PROBABILITÀ 1. Si dispongono a caso su uno scaffale sette libri, dei quali tre trattano di matematica. Qual è la probabilità che i tre libri di matematica si vengano a trovare l uno accanto
PROBLEMI DI PROBABILITÀ 1. Si dispongono a caso su uno scaffale sette libri, dei quali tre trattano di matematica. Qual è la probabilità che i tre libri di matematica si vengano a trovare l uno accanto
TEST DI AUTOVALUTAZIONE APPROSSIMAZIONE NORMALE
 TEST DI AUTOVALUTAZIONE APPROSSIMAZIONE NORMALE I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia Parte A. Sia X, X,...
TEST DI AUTOVALUTAZIONE APPROSSIMAZIONE NORMALE I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia Parte A. Sia X, X,...
( ) le colonne della matrice dei coefficienti, con. , risulta A 3 = A 1 + 4A 2 + 4A 5, A 4 = A 1 + A 2,
 1 Elementi di Analisi Matematica e Ricerca Operativa prova del 6 luglio 2016 1) Discutere il seguente problema di Programmazione Lineare: Trovare il massimo di p x 1, x 2, x 3, x 4 # x 2 + 4 x 3 + x 4
1 Elementi di Analisi Matematica e Ricerca Operativa prova del 6 luglio 2016 1) Discutere il seguente problema di Programmazione Lineare: Trovare il massimo di p x 1, x 2, x 3, x 4 # x 2 + 4 x 3 + x 4
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 8/04/2016
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 8/4/26 NOME: COGNOME: MATRICOLA: Esercizio Si supponga di avere
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 8/4/26 NOME: COGNOME: MATRICOLA: Esercizio Si supponga di avere
1 4 Esempio 2. Si determini la distribuzione di probabilità della variabile casuale X = punteggio ottenuto lanciando un dado. Si ha immediatamente:
 CAPITOLO TERZO VARIABILI CASUALI. Le variabili casuali e la loro distribuzione di probabilità In molte situazioni, dato uno spazio di probabilità S, si è interessati non tanto agli eventi elementari (o
CAPITOLO TERZO VARIABILI CASUALI. Le variabili casuali e la loro distribuzione di probabilità In molte situazioni, dato uno spazio di probabilità S, si è interessati non tanto agli eventi elementari (o
Prova di recupero di Probabilità e Statistica - A * 21/04/2006
 Prova di recupero di Probabilità e Statistica - A * /04/006 (NB: saranno prese in considerazione solo le risposte adeguatamente motivate) tempo di lavoro: Due ore. Per conseguire la patente di guida, un
Prova di recupero di Probabilità e Statistica - A * /04/006 (NB: saranno prese in considerazione solo le risposte adeguatamente motivate) tempo di lavoro: Due ore. Per conseguire la patente di guida, un
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore) Marco Riani mriani@unipr.it http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
STATISTICA A K (63 ore) Marco Riani mriani@unipr.it http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
X (o equivalentemente rispetto a X n ) è la
 Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
e n n xn ( 1) n ( 1) n n + 1 2e n x n 3n [ln x]n 1 n + 1 2e n 1
![e n n xn ( 1) n ( 1) n n + 1 2e n x n 3n [ln x]n 1 n + 1 2e n 1 e n n xn ( 1) n ( 1) n n + 1 2e n x n 3n [ln x]n 1 n + 1 2e n 1](/thumbs/70/62009507.jpg) 1) Studiare la seguente serie di funzioni en ( 1) n n x n 2) Studiare la seguente serie di funzioni ( 1) n n + 1 2e n xn 3) Studiare la seguente serie di funzioni 3n [ln x]n 1 2n 4) Studiare la seguente
1) Studiare la seguente serie di funzioni en ( 1) n n x n 2) Studiare la seguente serie di funzioni ( 1) n n + 1 2e n xn 3) Studiare la seguente serie di funzioni 3n [ln x]n 1 2n 4) Studiare la seguente
Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana /16
 Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana - 015/16 Esercizio 1 Per quali valori n Z \ {0} l espressione è un numero intero positivo? (n + 5)(n + 6) 6n Soluzione. Il problema
Esercizi di Matematica per la prova di ammissione alla Scuola Galileiana - 015/16 Esercizio 1 Per quali valori n Z \ {0} l espressione è un numero intero positivo? (n + 5)(n + 6) 6n Soluzione. Il problema
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino) Prova di giovedi febbraio 2005 (tempo a disposizione: 3 ore). consegna compiti e inizio orale Lunedì
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino) Prova di giovedi febbraio 2005 (tempo a disposizione: 3 ore). consegna compiti e inizio orale Lunedì
I appello di calcolo delle probabilità e statistica
 I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
un elemento scelto a caso dello spazio degli esiti di un fenomeno aleatorio;
 TEST DI AUTOVALUTAZIONE - SETTIMANA 3 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Una variabile casuale
TEST DI AUTOVALUTAZIONE - SETTIMANA 3 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Una variabile casuale
Esercizi di Calcolo combinatorio: disposizioni
 Calcolo combinatorio: disposizioni La Big Triple all ippodromo del luogo consiste nell indicare il corretto ordine di arrivo dei cavalli classificati tra i primi tre nella nona corsa. Se ci sono 12 cavalli
Calcolo combinatorio: disposizioni La Big Triple all ippodromo del luogo consiste nell indicare il corretto ordine di arrivo dei cavalli classificati tra i primi tre nella nona corsa. Se ci sono 12 cavalli
Lezione 3 Calcolo delle probabilità
 Lezione 3 Calcolo delle probabilità Definizione di probabilità La probabilità è lo studio degli esperimenti casuali e non deterministici Se lanciamo un dado sappiamo che cadrà ma non è certo che esca il
Lezione 3 Calcolo delle probabilità Definizione di probabilità La probabilità è lo studio degli esperimenti casuali e non deterministici Se lanciamo un dado sappiamo che cadrà ma non è certo che esca il
05. Errore campionario e numerosità campionaria
 Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
ESERCIZI HLAFO ALFIE MIMUN
 ESERCIZI HLAFO ALFIE MIMUN December, 27. Testo degli esercizi Risolvere i seguenti problemi: () Siano X, X 2, X 3 variabili aleatorie i.i.d. bernulliane di media.5 e siano Y, Y 2, Y 3, Y 4 variabili aleatorie
ESERCIZI HLAFO ALFIE MIMUN December, 27. Testo degli esercizi Risolvere i seguenti problemi: () Siano X, X 2, X 3 variabili aleatorie i.i.d. bernulliane di media.5 e siano Y, Y 2, Y 3, Y 4 variabili aleatorie
Il campionamento e l inferenza. Il campionamento e l inferenza
 Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2016/2017. Giovanni Lafratta
 Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2016/2017 Giovanni Lafratta ii Indice 1 Spazi, Disegni e Strategie Campionarie 1 2 Campionamento casuale
Concetti di teoria dei campioni ad uso degli studenti di Statistica Economica e Finanziaria, A.A. 2016/2017 Giovanni Lafratta ii Indice 1 Spazi, Disegni e Strategie Campionarie 1 2 Campionamento casuale
