ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
|
|
|
- Giorgiana Pappalardo
- 5 anni fa
- Visualizzazioni
Transcript
1 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3 t + t dt = 4 = [ ] log e4 4 e 4 = (settanh + e 3 t ln t + e 3 3 settanh e t 4 dt ). Esercizio Risolvere la disequazione z z < 3 e disegnare le soluzioni sul piano di Gauss. Svolgimento. Si ha z z = 4( z z)( z + z) = (ponendo z = x + iy) 8ixy, da cui z z = 8 xy. La soluzione è quindi {z = x + iy C : xy < 3 8 }, rappresentata in figura. Esercizio 3 Studiare la convergenza della serie al variare del parametro α >. + n= n ( cos(/n) + sin(/n α ) ) Svolgimento. Dagli sviluppi di MacLaurin di cos x e di sin x risulta, per n +, cos(/n) + sin(/n) = n + ( 4! n 4 + o n 4 ) + n α 3!8n 3α +!3n α + o ( ) n α,
2 Figura : Le soluzioni dell esercizio (Tema ). per cui il termine generale della serie, per n +, è asintotico a n (se α < ) n α (se α = ) /4n (se α > ) / e quindi ha segno definitivamente costante per n +. Se α il termine generale della serie non è infinitesimo e quindi la serie diverge (a ). Per α = la serie converge. Esercizio 4 Si consideri la funzione f(x) := arcsin x 4 + x. i) Determinare il dominio D di f, le sue eventuali simmetrie e studiarne il segno; determinare i limiti di f agli estremi di D; ii) studiare la derivabilità, calcolare la derivata e studiare la monotonia di f; determinarne gli eventuali punti di estremo relativo ed assoluto e calcolare i limiti significativi di f ; iii) disegnare un grafico qualitativo di f. Svolgimento. (i) La funzione è pari. D = {x R : x 4 }. La disequazione x 4 equivale a +x +x x 6 x, che è sempre verificata, mentre x 4 equivale a x + x, che è verificata per +x x. Pertanto D = [, + [ ( ], ]). D ora in poi assumeremo sempr. La funzione è continua in D, f() = arcsin( ) = π/ e lim x + f(x) = arcsin =, asintoto orizzontale. Il segno di f è dato dal segno dell argomento dell arcoseno, per cui f(x) se e solo s 4 e quindi x 4. (ii) In D si possono applicare le regole di derivazione se l argomento dell arcoseno è diverso da ±, cioè per x >. Per tali x si ha f (x) = x + x(x 4) ( + x ) ( ) = x 4 +x x + 8x + ( + x ) x + x 3, da cui si ricava che f (x) se e solo se x + 8x +, per x >, cioè per < x < 4 + 3, che pertanto è il punto di massimo assoluto, mentr = è il punto di minimo assoluto. Si ha lim f (x) = +, x +
3 Figura : Il grafico di f (Tema ). per cui il grafico di f, rappresentato nella figura, ha tangente verticale in (, π/). Esercizio Studiare la convergenza dell integrale generalizzato al variare di α, β R. + arctan(x ) arctan x x α (sinh x) β dx Svolgimento. L integranda f(x) è continua in ], [ ], + [, per cui bisogna studiare la convergenza dell integrale separatamente per x +, per x e per x +. Per x, f(x) x arctan x β/ = arctan, x β e quindi l integrale converge in se e solo se β < 4. Per x, f(x) arctan x x α x + α (sinh ) = arctan β α (sinh ) β x α, e quindi l integrale converge in se e solo se α <. Per x +, se β > π f(x) 4 (sinh x) β π ( β) e. (β x) Quest ultima espressione è o(/x ) per x + e quindi converge. Se β =, f(x) π /4x α, quindi converge se α > /. Se β <, f(x) π e β/ / β > /x per x + e quindi l integrale diverge. In sintesi, l integrale converge se α < e < β < 4 o se β = e / < α <. 3
4 Esercizio facoltativo. Sia I un intervallo chiuso e limitato e sia f : I R una funzione continua e tale che f(x) I per ogni x I. Dimostrare che esiste almeno un x I tale che f(x) = x. Svolgimento. Consideriamo la funzione g(x) = f(x) x, che vogliamo dimostrare che si annulla in almeno un punto di I := [a, b]. Se g(a), g(b) allora necessariamente g(a) > e g(b) <, per cui per il teorema degli zeri esiste x ]a, b[ tale che g( x) =. TEMA Esercizio Calcolare l integrale dx Svolgimento. Si ha dx = (ponendo t ex = t, per cui dx = dt/t) t(t + 4t + ) dt e = (t + ) + dt = arctan(t + ) e = arctan(e + ) arctan 3. e Esercizio Risolvere la disequazione 4 z 4z < e disegnare le soluzioni sul piano di Gauss. Svolgimento. Si ha 4 z 4z = 4( z z)( z + z) = (ponendo z = x + iy) 6ixy, da cui La soluzione è quindi 4 z 4z = 6 xy. {z = x + iy C : xy < 6 }, rappresentata in figura 3. Esercizio 3 Studiare la convergenza della serie al variare del parametro α >. + n= n ( e /nα cos(/n) ) Svolgimento. Dagli sviluppi di MacLaurin di e di cos x risulta, per n +, e /nα + cos n = + ( n α + 4n α + o n α ) + n + 4n 4 + o ( ) n 4, 4
5 Figura 3: Le soluzioni dell esercizio (Tema ). per cui il termine generale della serie, per n +, è asintotico a n (se α < ) n α n (se α = ) 6n 4 n (se α > ) n e quindi ha segno definitivamente costante per n +. Se α, il termine generale della serie non è infinitesimo e quindi la serie diverge (a ). Se α = la serie converge assolutamente e quindi converge. Esercizio 4 Si consideri la funzione f(x) := arcsin 4 x + x. i) Determinare il dominio D di f, le sue eventuali simmetrie e studiarne il segno; determinare i limiti di f agli estremi di D; ii) studiare la derivabilità, calcolare la derivata e studiare la monotonia di f; determinarne gli eventuali punti di estremo relativo ed assoluto e calcolare i limiti significativi di f ; iii) disegnare un grafico qualitativo di f. Svolgimento. (i) La funzione è pari, per cui la studiamo per x. Per tali x, D = {x > : 4 x +x }. La disequazione 4 x + x per x 4 equivale a x x +, che è sempre verificata, mentre per x < 4 equivale a x + x 3, che è verificata per x. Pertanto D = [, + [ ( ], ]). La funzione è continua in D, f() = arcsin() = π/ e lim x + f(x) = arcsin =, asintoto orizzontale. Il segno di f è dato dal segno dell argomento dell arcoseno, per cui f(x) se e solo s 4. (ii) In D si possono applicare le regole di derivazione se l argomento dell arcoseno è diverso da ±, cioè per x >. Per tali x si ha f (x) = ( + x ) (4 x)4x ( + x ) ( ) = 4 x +x x 6x ( + x ) x + x 3, da cui si ricava che f (x) se e solo s 6x, per x >, cioè per < x < /, che pertanto è il punto di minimo assoluto, mentr = è il punto di massimo assoluto. Si ha lim f (x) =, x +
6 Figura 4: Il grafico di f (Tema ). per cui il grafico di f, rappresentato in figura 4, ha tangente verticale in (, π/). Esercizio Studiare la convergenza dell integrale generalizzato al variare di α, β R. + arctan(x ) arctan x x 4 α (sinh 3 x) β dx Svolgimento. L integranda f(x) è continua in ], [ ], + [, per cui bisogna studiare la convergenza dell integrale separatamente per x +, per x e per x +. Per x, f(x) x arctan 4 α x β/3 = arctan 4 α, x β 3 e quindi l integrale converge in se e solo se β < 6. Per x, f(x) arctan x x α x + α (sinh 3 ) = arctan β 4 α (sinh 3 ) β x α, e quindi l integrale converge in se e solo se α <. Per x +, se β > π f(x) 4 (sinh 3 x) β π ( β) e (β 3. x) Quest ultima espressione è o(/x ) per x +, per cui l integrale converge. Se β =, f(x) π /4x α, quindi converge se α > /. Se β <, f è illimitata per x + e quindi l integrale diverge. In sintesi, l integrale converge se α < e < β < 6 o se β = e / < α <. TEMA 3 6
7 Esercizio [6 punti] Calcolare l integrale 3 log 4 9 dx Svolgimento. Si ha 3 log 4 9 dx = (ponendo ex = t, per cui dx = dt/t) 4 t 9 dt e 3 ( = 6 t 3 ), dt = t log t 3 e 3 t + 3 = ( ) 6 log 7 e3 3 e e 3 4 Esercizio Risolvere la disequazione 3z 3 z < e disegnare le soluzioni sul piano di Gauss. Svolgimento. Si ha 3z 3 z = 3(z z)(z + z) = (ponendo z = x + iy) ixy, da cui 3 z z = xy. La soluzione è quindi {z = x + iy C : xy < 6 }, rappresentata in figura. z Figura : Le soluzioni dell esercizio (Tema 3). Esercizio 3 Studiare la convergenza della serie al variare del parametro α >. + n= n ( cosh(/n α ) + cos(/n) ) 7
8 Svolgimento. Dagli sviluppi di MacLaurin di cosh x e di cos x risulta, per n +, cosh /n α + cos n = + n α + ( ) 4n 4α + o n 4α + n + ( ) 4n 4 + o n 4, per cui il termine generale della serie, per n +, è asintotico a n (se α < ) n α n (se α = ) n 4 n (se α > ) n e quindi ha segno definitivamente costante per n +. Se α, il termine generale della serie non è infinitesimo e quindi la serie diverge (a ± rispettivamente). Se α = la serie converge assolutamente e quindi converge (essendo asintotica alla serie n ). Esercizio 4 Si consideri la funzione f(x) := arcsin x 4 x + 3. i) Determinare il dominio D di f, le sue eventuali simmetrie e studiarne il segno; determinare i limiti di f agli estremi di D; ii) studiare la derivabilità, calcolare la derivata e studiare la monotonia di f; determinarne gli eventuali punti di estremo relativo ed assoluto e calcolare i limiti significativi di f ; iii) disegnare un grafico qualitativo di f. Svolgimento. (i) La funzione è pari, per cui la studiamo per x. Per tali x, D = {x > : x 4 x +3}. La disequazione x 4 x + 3 equivale al sistema { x 4 x + 3 x 4 x 3 la prima equazione è sempre verificata, mentre la seconda ammette come soluzione (in R + o ) x. Pertanto D = ( (, ] [, + ) ). La funzione è continua in D, f(/) = arcsin( ) = π/ e lim x + f(x) = arcsin =, e quindi y = é un asintoto orizzontale = / punto di minimo assoluto. Il segno di f è dato dal segno dell argomento dell arcoseno, per cui f(x) se e solo s 4. (ii) In D si possono applicare le regole di derivazione se l argomento dell arcoseno è diverso da ±, cioè per x >. Per tali x si ha f (x) = (x + 3) (x 4)4x (x + 3) ( ) = x 4 x +3 x + 6x + 3 (x + 3) (x + 3) (x 4), da cui si ricava che f (x) se e solo s 6x 3, per x > /, cioè per / < x < (8 + 7)/, che pertanto è il punto di massimo assoluto, mentr = / è il punto di minimo assoluto. Si ha lim f (x) =, x + per cui il grafico di f, rappresentato in figura 6, ha tangente verticale in (/, π/). Esercizio Studiare la convergenza dell integrale generalizzato + arctan(3 x) arctan x 9 x α (cosh x ) β dx 8
9 ... Figura 6: Il grafico di f (Tema 3). al variare di α, β R. Svolgimento. L integranda f(x) è continua in (, 3) (3, + ), per cui bisogna studiare la convergenza dell integrale separatamente per x +, per x 3 e per x +. Per x +, f(x) x arctan 3 9 ( ) α x β = β arctan 3 9 α x β, e quindi l integrale converge in se e solo se β <. Per x 3, 3 x arctan 3 f(x) 3 x α 6 α (cosh 3 ) = arctan 3 β 6 α (cosh 3 ) β 3 x α, e quindi l integrale converge in 3 se e solo se α <. Per x +, se β >, ( ) f(x) β π x α e. β x Quest ultima espressione è o(/x ) per x +, per cui l integrale converge per x + (per ogni valore di α). Se β =, f(x) π /4x α, quindi converge se α > /. Se β <, f è illimitata per x + e quindi l integrale diverge. In sintesi, l integrale converge se α < e < β < 4 o se β = e / < α <. TEMA 4 Esercizio. Calcolare l integrale 4 + dx Svolgimento. Operando la sostituzione t =, si ottiene 4 + dx = e t 4t + dt = 9 e (t ) + dt.
10 Sostituendo t = s, si ottiene e 4 + dx = s ds = [arctan s]e + = arctan(e ) + π 4. Esercizio. Risolvere la disequazione 9 z 9z < e disegnare le soluzioni sul piano di Gauss. Svolgimento. Si deve risolvere Per z = x + iy, si ottiene z z z + z < 9. xy < 8, rappresentato in figura Figura 7: Le soluzioni dell esercizio (Tema 4). Esercizio 3. Studiare la convergenza della serie + n= al variare del parametro α >. Svolgimento. Usando gli sviluppi di Mc Laurin n ( e /n tan /n α ) otteniamo e y = + y + y + o(y ) per y tan y = y + y3 3 + o(y4 ) per y, e /n tan n α = n + n 4 + o( n 4 ) n α + o( 3 n3α n 4α ).
11 Osserviamo che per ogni valore di α la serie è a termini di segno definitivamente costante. Inoltre si ha n ( e /nα tan /n ) n α se α (, ) se α = n se α (, + ). Per il teorema del confronto asintotico, concludiamo che la serie è convergente per α = e divergente per tutti gli altri valori di α >. Esercizio 4. Si consideri la funzione f(x) := arcsin 4 4 x x + 3. i) Determinare il dominio D di f, le sue eventuali simmetrie e studiarne il segno; determinare i limiti di f agli estremi di D; ii) studiare la derivabilità, calcolare la derivata e studiare la monotonia di f; determinarne gli eventuali punti di estremo relativo ed assoluto e calcolare i limiti significativi di f ; iii) disegnare un grafico qualitativo di f. Svolgimento. Osserviamo innanzitutto che f è una funzione continua sul suo dominio naturale (per i teoremi sulla continuità della funzione composta, del modulo e delle funzioni elementari) ed è pari; infatti si ha f( x) = arcsin 4 4 x 4 4 x ( x) = arcsin + 3 x + 3 = f(x). Possiamo pertanto studiare la funzione su [, + ) e poi ottenere il suo comportamento su (, ) per simmetria. Dominio. Per x [, + ), il suo dominio è dato da cioè (visto che x + 3 > sempre) cioè 4 4x x + 3 x 3 4 4x x + 3 x 4x + 7 e x + 4x. La prima disuguaglianza è sempre verificata mentre la seconda è vera per x (, ] [/, + ). Quindi sull intervallo [, + ), il dominio è [/, ). (Per simmetria: dom(f) = (, /] [/, ).) Segno. Per x [, + ), f quando 4 4x x + 3 cioè 4 4x, cioè x. Quindi f su [, /] [/, ] e f su (, ] [ + ). Limiti agli estremi del dominio. Con un cambio di variabile, abbiamo lim f(x) = lim arcsin y = x + y Inoltre, in x = /, per continuità di f, si ha lim x / + f(x) = f(/) = π/. Quindi, f ha y = come asintoto orizzontale sia per x + che per x. Derivabilità. Per i teoremi sulla derivabilità della funzione composta e poiché g(y) = arcsin y è derivabile su (, ), abbiamo che f C ((, /) (/, + )). Rimane da studiare la derivabilità di f nei punti / e /.
12 Calcolo f. Su [/, + ) abbiamo f (x) = (x + 3) [ x 4x ] (x + 3) (4 4x) Segno di f, monotonia e punti di estremo relativo ed assoluto. Per x [, + ), f quando x 4x che è vera solo per x + 4. Possiamo quindi dedurre che f è decrescente su (, + 4 ] e su [, + 4 ], f è crescente su [ + 4, ] e su [ + 4, + ), f presenta punti di minimo assoluto in x = ± + 4 (sono ovviamente punti di minimo relativo, hanno uguale valore per simmetria di f, e sono di minimo assoluto per il teorema di Lagrange), f presenta punti di massimo assoluto in x = ± (perché l immagine di arcsin è inclusa in [ π/, π/]). limiti di f e derivabilita in x = ±/. Osserviamo che si ha lim f (x) = ; x / + quindi la funzione non è derivabile nei punti x = / = /. grafico di f in figura Figura 8: Il grafico di f (Tema 4). Esercizio. Studiare la convergenza dell integrale generalizzato al variare di α, β R. + arctan x arctan( x) 4x α (cosh x ) β dx
13 Svolgimento. Innanzitutto osserviamo che la funzione integranda f può essere scritta come f(x) = arctan x arctan( x) x α + x α (cosh x ) β dx da cui si vede facilmente che f appartiene a C ((, /) (/, + )). I punti di integrazione impropria sono tre: x =, x = / e +. L integrale va risolto come + f(x) dx = lim a + /4 a f(x) dx + lim b / b /4 f(x) dx + lim c / + Studiamo separatamente il comportamento asintotico della f nei vari punti. Per x +. Abbiamo f(x) π x ( 4 (x /) β = π β ) x β ; c f(x) dx + lim d + per il teorema del confronto, abbiamo che il primo integrale è convergente se e solo se β <. Per x. Abbiamo arctan( x) ( x) e quindi otteniamo f(x) arctan(/) +α (cosh(/) ) β x α ; d f(x) dx. per il teorema del confronto, abbiamo che il secondo ed il terzo integrale sono convergenti se e solo se α <. Per x +. Abbiamo f(x) π 4 x α cosh β x π 4 x α e βx ; per il teorema del confronto, abbiamo che il quarto integrale diverge se β < e α o se β = ed α / mentre converge per β = ed α > / e per β > e α. In conclusione, l integrale iniziale converge se e solo se β (, ) e α < o β = e / < α <. 3
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del TEMA log x. f(x) = e
 Esercizio 1 [6 punti] Sia ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione Appello del 8.07.019 TEMA 1 f) = e +log. a) Determinare il dominio D di f; determinare i limiti di f agli estremi di
Esercizio 1 [6 punti] Sia ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione Appello del 8.07.019 TEMA 1 f) = e +log. a) Determinare il dominio D di f; determinare i limiti di f agli estremi di
APPELLO C AM1C 19 Gennaio f(x) = log( x + 2) x
 Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9.7.8 Esercizio Si consideri la funzione TEMA f log e. i Si determini il dominio D e si studi il segno di f; ii si determininio i iti
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9.7.8 Esercizio Si consideri la funzione TEMA f log e. i Si determini il dominio D e si studi il segno di f; ii si determininio i iti
ANALISI MATEMATICA 1 Commissione F. Albertini, V. Casarino e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 TEMA f = 2 arctan 2) log e 2 αx α sin x + 2x + x 6 + x + n n 2 log n xe x dx al variare di a R x a e x dx Tempo: due ore e mezza Viene corretto solo ciò che è scritto sul foglio intestato È vietato tenere
TEMA f = 2 arctan 2) log e 2 αx α sin x + 2x + x 6 + x + n n 2 log n xe x dx al variare di a R x a e x dx Tempo: due ore e mezza Viene corretto solo ciò che è scritto sul foglio intestato È vietato tenere
Temi d esame di Analisi Matematica 1
 Temi d esame di Analisi Matematica 1 Area di Ingegneria dell Informazione - a cura di M. Bardi 31.1.95 f(x) = xe arctan 1 x (insieme di definizione, segno, iti ed asintoti, continuità e derivabilità, crescenza
Temi d esame di Analisi Matematica 1 Area di Ingegneria dell Informazione - a cura di M. Bardi 31.1.95 f(x) = xe arctan 1 x (insieme di definizione, segno, iti ed asintoti, continuità e derivabilità, crescenza
Esercizi proposti. x b) f(x) = 2. Determinare i punti di non derivabilità delle funzioni
 Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Secondo appello 2005/ Tema 1
 Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del TEMA 1
 Esercizio Data la funzione ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3 TEMA fx = x 3 + logx, a determinarne il dominio, calcolarne i iti agli estremi e determinare eventuali
Esercizio Data la funzione ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3 TEMA fx = x 3 + logx, a determinarne il dominio, calcolarne i iti agli estremi e determinare eventuali
Analisi Matematica 1 - a.a. 2017/ Quarto appello
 Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
ANALISI MATEMATICA 1-11/02/2019 Corso di Laurea in Ingegneria Meccanica. Primo Appello - Test 1
 ANALISI MATEMATICA - /2/29 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
ANALISI MATEMATICA - /2/29 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
SCRITTO 02/07/18 - ANALISI MATEMATICA I
 SCRITTO 02/07/18 - ANALISI MATEMATICA I Esercizio 1. Determinare tutte le coppie z, w) C C tali che { zw = z 3 w 2 zw = 1 Soluzione: Dalla seconda equazione otteniamo che sia z che w non sono zero. Quindi
SCRITTO 02/07/18 - ANALISI MATEMATICA I Esercizio 1. Determinare tutte le coppie z, w) C C tali che { zw = z 3 w 2 zw = 1 Soluzione: Dalla seconda equazione otteniamo che sia z che w non sono zero. Quindi
Vicenza, 12 settembre 2016 Si consideri la funzione. sinh 2x sinh 2x 1 3x. f(x) =
 ANALISI MATEMATICA - Traccia di soluzioni Commissione F. Albertini, L. Caravenna e V. Casarino Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Esercizio, Tema [9 punti] Vicenza, settembre 06 Si
ANALISI MATEMATICA - Traccia di soluzioni Commissione F. Albertini, L. Caravenna e V. Casarino Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Esercizio, Tema [9 punti] Vicenza, settembre 06 Si
ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a Corsi di laurea in Scienze Statistiche
 ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a. 4- Corsi di laurea in Scienze Statistiche 4 febbraio TEMA Esercizio 8 punti) Si consideri la funzione ) e f) = arctan e a)
ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a. 4- Corsi di laurea in Scienze Statistiche 4 febbraio TEMA Esercizio 8 punti) Si consideri la funzione ) e f) = arctan e a)
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica 1 per IM - 11/02/2019. Tema 1 (parte di esercizi)
 Analisi Matematica per IM - /2/29 Cognome e Nome:....................................... Matricola:.................. Docente:.................. Tempo a disposizione: due ore. Il candidato, a meno che
Analisi Matematica per IM - /2/29 Cognome e Nome:....................................... Matricola:.................. Docente:.................. Tempo a disposizione: due ore. Il candidato, a meno che
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
APPELLO B AM1C 14 LUGLIO f(x) = xe 1
 Cognome e nome APPELLO B AM1C 14 LUGLIO 2009 Esercizio 1. Sia data la funzione f(x) = xe 1 log x. (a) Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali massimi,
Cognome e nome APPELLO B AM1C 14 LUGLIO 2009 Esercizio 1. Sia data la funzione f(x) = xe 1 log x. (a) Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali massimi,
Scritto d esame di Analisi Matematica I
 Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
Analisi Matematica 1 - a.a. 2017/ Secondo appello
 Analisi Matematica - a.a. 27/28 - Secondo appello Soluzione del test Test A 2 3 4 5 6 7 8 9 D D A B C B A E D D Test B 2 3 4 5 6 7 8 9 B A C C B E D E A A Test C 2 3 4 5 6 7 8 9 A C B E E D C B B C Test
Analisi Matematica - a.a. 27/28 - Secondo appello Soluzione del test Test A 2 3 4 5 6 7 8 9 D D A B C B A E D D Test B 2 3 4 5 6 7 8 9 B A C C B E D E A A Test C 2 3 4 5 6 7 8 9 A C B E E D C B B C Test
ANALISI MATEMATICA 1-23/01/2019 Corso di Laurea in Ingegneria Meccanica. Primo Appello - Test 1
 ANALISI MATEMATICA 1-23/1/219 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
ANALISI MATEMATICA 1-23/1/219 Corso di Laurea in Ingegneria Meccanica Il candidato deve riportare nella griglia le risposte che ritiene corrette. Al termine della prova il candidato deve riconsegnare questo
Analisi Matematica 1 - a.a. 2017/ Primo appello
 Analisi Matematica - a.a. 7/8 - Primo appello Soluzione del test Test A 3 4 5 6 7 8 9 C E E C D E A B B D Test B 3 4 5 6 7 8 9 A A B E B B C D E A Test C 3 4 5 6 7 8 9 B D C A E D E C D C Test D 3 4 5
Analisi Matematica - a.a. 7/8 - Primo appello Soluzione del test Test A 3 4 5 6 7 8 9 C E E C D E A B B D Test B 3 4 5 6 7 8 9 A A B E B B C D E A Test C 3 4 5 6 7 8 9 B D C A E D E C D C Test D 3 4 5
ANALISI MATEMATICA 1 - Parte B Commissione F. Albertini, L. Caravenna e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 ANALISI MATEMATICA - Parte B Commissione F Albertini, L Caravenna e M Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, febbraio 07 TEMA Esercizio [ punti] Si consideri la funzione
ANALISI MATEMATICA - Parte B Commissione F Albertini, L Caravenna e M Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, febbraio 07 TEMA Esercizio [ punti] Si consideri la funzione
Nozioni di base - Quiz - 2
 Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Secondo appello 2004/ Tema 1
 Secondo appello 2/25 - Tema Esercizio Risolvere l equazione di variabile complessa z 2 (z z)2 + (Re z) [ Im (z 2 ) ] =, () e disegnare le soluzioni sul piano di Gauss. Poniamo z = + i. Si ottiene che deve
Secondo appello 2/25 - Tema Esercizio Risolvere l equazione di variabile complessa z 2 (z z)2 + (Re z) [ Im (z 2 ) ] =, () e disegnare le soluzioni sul piano di Gauss. Poniamo z = + i. Si ottiene che deve
PER LA COMMISSIONE D ESAME 1E 2E 3E 4E 5E Totale
 Esame di Analisi Matematica Uno 31 Gennaio 2014 Fila: A 1 Università di Padova - Scuola di Ingegneria - Esame di Analisi Matematica Uno Lauree: Chimica e Materiali 31 Gennaio 2014 (Primo appello, a.a.
Esame di Analisi Matematica Uno 31 Gennaio 2014 Fila: A 1 Università di Padova - Scuola di Ingegneria - Esame di Analisi Matematica Uno Lauree: Chimica e Materiali 31 Gennaio 2014 (Primo appello, a.a.
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
B Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
APPELLO X AM1C 17 SETTEMBRE 2009
 Cognome e nome APPELLO X AMC 7 SETTEMBRE 29 Esercizio. Sia f(x) = x arctan x + log( + x 2 ) (a) Determinarne: insieme di esistenza e di derivabilità, iti ed eventuali asintoti, eventuali massimi, minimi
Cognome e nome APPELLO X AMC 7 SETTEMBRE 29 Esercizio. Sia f(x) = x arctan x + log( + x 2 ) (a) Determinarne: insieme di esistenza e di derivabilità, iti ed eventuali asintoti, eventuali massimi, minimi
ISTITUZIONI DI ANALISI MATEMATICA Commissione A. Cesaroni, P. Mannucci, A. Sommariva, a.a Corsi di laurea in Scienze Statistiche
 TEMA f(x = arccos( x (a ˆ Determiniamo il dominio Poichè arccos : [, ] [, π], poniamo x ovvero x Di conseguenza il dominio risulta D = [ 4, 4] ˆ Eventuali simmetrie: la funzione è pari ˆ Periodicità: la
TEMA f(x = arccos( x (a ˆ Determiniamo il dominio Poichè arccos : [, ] [, π], poniamo x ovvero x Di conseguenza il dominio risulta D = [ 4, 4] ˆ Eventuali simmetrie: la funzione è pari ˆ Periodicità: la
Provetta scritta di Calcolo I Corsi di laurea in Fisica - Scienza e Tecnologia dei Materiali Prova scritta del 7/12/2005 Fila A
 Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Es. 1 Es. 2 Es. 3 Es. 4 Totale. Punteggi degli esercizi: Es.1: 6 punti; Es.2: 6 punti; Es.3: 6 punti; Es.4: 12 punti.
 Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 1 Secondo appello 11 luglio 211 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.1:
Es. 1 Es. 2 Es. 3 Es. 4 Totale Analisi e Geometria 1 Secondo appello 11 luglio 211 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.1:
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2011 2012 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2011 2012 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2019 Soluzioni Scritto. a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità;
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 209 Soluzioni Scritto Data la funzione fx = x 2 x 6 x /3 a Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 209 Soluzioni Scritto Data la funzione fx = x 2 x 6 x /3 a Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b Calcolare, se esistono,
ANALISI MATEMATICA 1 - Parte B Commissione F. Albertini, L. Caravenna e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 ANALISI MATEMATICA - Parte B Commissione F. Albertini, L. Caravenna e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, 4 settembre 7 TEMA Esercizio [ punti] Si consideri la funzione
ANALISI MATEMATICA - Parte B Commissione F. Albertini, L. Caravenna e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, 4 settembre 7 TEMA Esercizio [ punti] Si consideri la funzione
Es. 1: 6 punti Es. 2: 12 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti Totale. sin x arctan x lim. 4 x 2. f(x) = x 2
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo appello, 1 Luglio 010 Cognome: Nome: Matricola: Compito A Es. 1: 6 punti Es. : 1 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo appello, 1 Luglio 010 Cognome: Nome: Matricola: Compito A Es. 1: 6 punti Es. : 1 punti Es. 3: 6 punti Es. 4: 6 punti Es. 5: 3 punti
Seconda prova in itinere di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano. A.A. 2015/2016. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
ANALISI MATEMATICA 1 Commissione F. Albertini, P. Mannucci e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 Vicenza, 27 gennaio 214 TEMA Esercizio 1 (9 punti Si consideri la funzione f(x =xe x 2 x+2 (a Determinare il dominio, eventuali simmetrie ed il segno di f; (b determinare i iti agli estremi del dominio,
Vicenza, 27 gennaio 214 TEMA Esercizio 1 (9 punti Si consideri la funzione f(x =xe x 2 x+2 (a Determinare il dominio, eventuali simmetrie ed il segno di f; (b determinare i iti agli estremi del dominio,
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria Analisi Matematica I - Prova scritta del 10 Luglio 2019
 Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Quarto Appello 4 Settembre 2018
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Quarto Appello 4 Settembre 8 Cognome: Nome: Matricola: T.: 4 punti T.: 4 punti Es.: 5 punti Es.: 9 punti Es.: 5 punti Es.4: 5 punti Totale.
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Quarto Appello 4 Settembre 8 Cognome: Nome: Matricola: T.: 4 punti T.: 4 punti Es.: 5 punti Es.: 9 punti Es.: 5 punti Es.4: 5 punti Totale.
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
INTEGRALI IMPROPRI. Esercizi svolti
 INTEGRALI IMPROPRI Esercizi svolti. Usando la definizione, calcolare i seguenti integrali impropri: a c d e f / + 5 d arctan + d 8 + 4 5/ + e + d 9 + 8 + + d 4 d. d. Usando la definizione di integrale
INTEGRALI IMPROPRI Esercizi svolti. Usando la definizione, calcolare i seguenti integrali impropri: a c d e f / + 5 d arctan + d 8 + 4 5/ + e + d 9 + 8 + + d 4 d. d. Usando la definizione di integrale
I appello - 11 Gennaio 2016
 Analisi Matematica - A.A. 5-6 Prove scritte di Analisi Matematica - A.A. 5/6 Corso di Laurea in Ingegneria Civile Corso di Laura in Ingegneria Informatica ed Elettronica I appello - Gennaio 6 Svolgere
Analisi Matematica - A.A. 5-6 Prove scritte di Analisi Matematica - A.A. 5/6 Corso di Laurea in Ingegneria Civile Corso di Laura in Ingegneria Informatica ed Elettronica I appello - Gennaio 6 Svolgere
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione, Canali 1 e 4 Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione, Canali e 4 Appello del 7.. NB: in fondo allo svolgimento del tema 4 si trovano alcuni brevi commenti agli errori più comuni trovati nella correzione.
ANALISI MATEMATICA Area dell Ingegneria dell Informazione, Canali e 4 Appello del 7.. NB: in fondo allo svolgimento del tema 4 si trovano alcuni brevi commenti agli errori più comuni trovati nella correzione.
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2018 Soluzioni Scritto. f(x) = ( ln 1 + x + 1 ) =
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA 1. Prova scritta del 24 luglio 2018
 Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA Prova scritta del 4 luglio 08 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 5)
Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA Prova scritta del 4 luglio 08 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 5)
Politecnico di Milano Ingegneria Industriale Analisi Matematica 1 e Geometria
 Politecnico di Milano Ingegneria Industriale Analisi Matematica e Geometria Preparazione al primo compito in itinere Cognome: Nome: Matricola: Prima Parte. Determinare, se esistono, il minimo, il massimo,
Politecnico di Milano Ingegneria Industriale Analisi Matematica e Geometria Preparazione al primo compito in itinere Cognome: Nome: Matricola: Prima Parte. Determinare, se esistono, il minimo, il massimo,
SOLUZIONI COMPITO del 1/02/2013 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A
 SOLUZIONI COMPITO del /0/0 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A Esercizio Osserviamo che la serie proposta è a termini di segno
SOLUZIONI COMPITO del /0/0 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A Esercizio Osserviamo che la serie proposta è a termini di segno
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2015/2016. Prof. M. Bramanti.
 Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 01/01. Prof. M. Bramanti 1 Tema n 1 4 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 01/01. Prof. M. Bramanti 1 Tema n 1 4 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Analisi Matematica 1 Foglio 1 Lunedì 3 ottobre. f(x) = log x 2 6x + 5.
 Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Compito n. 1 (Gennaio 2013)
 Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO 2002/03
 PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO / Prova scritta del 6// Denotato con a il numero delle lettere del nome, si consideri la serie nx + cos nx a nx, per x IR, e si determini per quali valori
PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO / Prova scritta del 6// Denotato con a il numero delle lettere del nome, si consideri la serie nx + cos nx a nx, per x IR, e si determini per quali valori
Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA 1. Prova scritta del 12 giugno 2018
 Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA Prova scritta del giugno 08 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 5) Determinare
Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA Prova scritta del giugno 08 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 5) Determinare
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO. f 1 (x) = arctan(x2 7x + 12) x 2,
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GIUGNO 007: SOLUZIONI ESERCIZIO - Data la funzione f 1 (x) = arctan(x 7x + 1) x, 7x + 1 si chiede
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GIUGNO 007: SOLUZIONI ESERCIZIO - Data la funzione f 1 (x) = arctan(x 7x + 1) x, 7x + 1 si chiede
ANALISI MATEMATICA I A.A. 02/03 PROVE SCRITTE E RISOLUZIONI
 ANALISI MATEMATICA I A.A. /3 PROVE SCRITTE E RISOLUZIONI L. GIACOMELLI, P. LORETI Contents I prova intermedia 5.. compito A 3 Risoluzioni 3 I prova intermedia 5.. compito B 5 Risoluzioni 6 I prova intermedia
ANALISI MATEMATICA I A.A. /3 PROVE SCRITTE E RISOLUZIONI L. GIACOMELLI, P. LORETI Contents I prova intermedia 5.. compito A 3 Risoluzioni 3 I prova intermedia 5.. compito B 5 Risoluzioni 6 I prova intermedia
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
1 Analisi mat. I - Esercizi del 13/10/99
 Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi e Geometria 1 Politecnico di Milano Ingegneria Industriale
 Analisi e Geometria Politecnico di Milano Ingegneria Industriale Docenti: P Antonietti, F Cipriani, F Colombo, F Lastaria G Mola, E Munarini, P Terenzi, C Visigalli Terzo appello, Settembre 9 Compito A
Analisi e Geometria Politecnico di Milano Ingegneria Industriale Docenti: P Antonietti, F Cipriani, F Colombo, F Lastaria G Mola, E Munarini, P Terenzi, C Visigalli Terzo appello, Settembre 9 Compito A
Analisi - 10 settembre 2008 Corso di Laurea in Fisica - Fisica ed Astrofisica
 Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
Analisi - 1 settembre 28 Corso di Laurea in Fisica - Fisica ed Astrofisica Chi deve fare lo scritto di Derivate e Integrali (vecchio ordinamento) deve svolgere gli esercizi: 1, 2, 3, 4, 5 Esercizio 1 Data
Docente: LANZARONE. Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4).
 Analisi e Geometria 1 Quarto Appello 4 Settembre 2018 Compito A Docente: LANZARONE Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4). T.(a) Enunciare e dimostrare la formula di integrazione per
Analisi e Geometria 1 Quarto Appello 4 Settembre 2018 Compito A Docente: LANZARONE Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4). T.(a) Enunciare e dimostrare la formula di integrazione per
Analisi Matematica A e B Soluzioni Prova scritta n. 3
 Analisi Matematica A e B Soluzioni Prova scritta n. Corso di laurea in Fisica, 207-208 9 luglio 208. Si consideri per α =, 2, 5, 8 la seguente funzione funzione F α : R\{0} R F α () = sin t dt. t α 6 Dire
Analisi Matematica A e B Soluzioni Prova scritta n. Corso di laurea in Fisica, 207-208 9 luglio 208. Si consideri per α =, 2, 5, 8 la seguente funzione funzione F α : R\{0} R F α () = sin t dt. t α 6 Dire
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA 1. Prova scritta del 25 febbraio 2017 Fila 1.
 Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del 5 febbraio 07 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 7) Posto
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del 5 febbraio 07 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 7) Posto
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
INTEGRALI Test di autovalutazione
 INTEGRALI Test di autovalutazione. L integrale ln 6 è uguale a (a) vale 5 2 (b) (c) (d) 4 5 vale ln 256 2 è negativo 2 5 + 4 5 2 5 + 4 5 d d 2. È data la funzione = e 2. Allora: (a) se F() è una primitiva
INTEGRALI Test di autovalutazione. L integrale ln 6 è uguale a (a) vale 5 2 (b) (c) (d) 4 5 vale ln 256 2 è negativo 2 5 + 4 5 2 5 + 4 5 d d 2. È data la funzione = e 2. Allora: (a) se F() è una primitiva
Calcolo 1 (L. Fanelli - F. Pacella)
 Matricola Corso di laurea in Matematica, aa 7/8 Calcolo (L Fanelli - F Pacella) Seconda prova in itinere 9 gennaio 8 I Cognome NORRIS Nome CHUCK Risolvere TRE E NON PIÙ DI TRE esercizi, motivando le risposte
Matricola Corso di laurea in Matematica, aa 7/8 Calcolo (L Fanelli - F Pacella) Seconda prova in itinere 9 gennaio 8 I Cognome NORRIS Nome CHUCK Risolvere TRE E NON PIÙ DI TRE esercizi, motivando le risposte
PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 2015/16
 PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 5/6 Prova scritta del //6 Si studi, al variare di x, il comportamento della serie n= n Ax n Ax, dove A denota il numero delle lettere del nome. Si studi la funzione
PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 5/6 Prova scritta del //6 Si studi, al variare di x, il comportamento della serie n= n Ax n Ax, dove A denota il numero delle lettere del nome. Si studi la funzione
Analisi I Ingegneria Chimica e Aerospaziale 1 o compitino
 1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
2. determinare i limiti agli estremi del dominio, eventuali asintoti, eventuali punti in cui è possibile prolungare la funzione per continuità;
 ANALISI MATEMATICA Commissione L. Caravenna, V. Casarino, S. occante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 27 Gennaio 25 TEMA - arte B Esercizio ( unti). Si consideri la funzione
ANALISI MATEMATICA Commissione L. Caravenna, V. Casarino, S. occante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 27 Gennaio 25 TEMA - arte B Esercizio ( unti). Si consideri la funzione
ANALISI MATEMATICA 1 - Parte B Commissione F. Albertini, L. Caravenna e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 ANALISI MATEMATICA 1 - Parte B Commissione F Albertini, L Caravenna e M Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, 4 luglio 017 TEMA1 Esercizio 1 [1 unti] Si consideri la funzione
ANALISI MATEMATICA 1 - Parte B Commissione F Albertini, L Caravenna e M Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Vicenza, 4 luglio 017 TEMA1 Esercizio 1 [1 unti] Si consideri la funzione
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA I - 28 Febbraio 2011, ore x e2x e 2x 1. f(x) = e 2x log(e 2x + 1) dx.
 Esame di ANALISI MATEMATICA I - 28 Febbraio 211, ore 8.3 A ESERCIZIO 1. (1 punti) Sia data la funzione f(x) = x e2x e 2x 1. (a) Determinarne il dominio e dimostrare che f si prolunga ad una funzione continua
Esame di ANALISI MATEMATICA I - 28 Febbraio 211, ore 8.3 A ESERCIZIO 1. (1 punti) Sia data la funzione f(x) = x e2x e 2x 1. (a) Determinarne il dominio e dimostrare che f si prolunga ad una funzione continua
UNIVERSITÁ DEGLI STUDI DI PERUGIA Facoltá di Ingegneria Edile-Architettura Prova scritta di ANALISI MATEMATICA I Soluzione della prova del
 UNIVERSITÁ DEGLI STUDI DI PERUGIA Facoltá di Ingegneria Edile-Architettura Prova scritta di ANALISI MATEMATICA I Soluzione della prova del 05.0.008. Stabilire, al variare di x IR, il comportamento della
UNIVERSITÁ DEGLI STUDI DI PERUGIA Facoltá di Ingegneria Edile-Architettura Prova scritta di ANALISI MATEMATICA I Soluzione della prova del 05.0.008. Stabilire, al variare di x IR, il comportamento della
Scrivere lo sviluppo di Mac Laurin di ordine 3 di una generica funzione f(x), e dire quali ipotesi si devono fare su f(x) per poterlo scrivere.
 Correzione dell esame di (Analisi) Matematica I - marzo 9 A ESERCIZIO (A) Scrivere lo sviluppo di Mac Laurin di ordine di una generica funzione f(x), e dire quali ipotesi si devono fare su f(x) per poterlo
Correzione dell esame di (Analisi) Matematica I - marzo 9 A ESERCIZIO (A) Scrivere lo sviluppo di Mac Laurin di ordine di una generica funzione f(x), e dire quali ipotesi si devono fare su f(x) per poterlo
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
Esercizio 1 Calcolare i limiti delle seguenti successioni per n + :
 Esercizio 1 Calcolare i limiti delle seguenti successioni per n + : 1. n = (n 2 + sin n) sin 2 n 2. n = n cos( π ) sin( 2π ) n 3n 2 3. n = n e sin 1 n n 4. n = log a (n n 2 1) + log a n 5. n = n + 5 n
Esercizio 1 Calcolare i limiti delle seguenti successioni per n + : 1. n = (n 2 + sin n) sin 2 n 2. n = n cos( π ) sin( 2π ) n 3n 2 3. n = n e sin 1 n n 4. n = log a (n n 2 1) + log a n 5. n = n + 5 n
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
Risoluzione del compito n. 7 (Settembre 2014/2)
 Risoluzione del compito n. 7 (Settembre 204/2) PROBLEMA Determinate tutte le soluzioni (z, w), con z, w C,del sistema { 2z 2 3iz = w 2 w 4 = z 4. Dalla seconda equazione si ricava subito che w 4 = z 4,
Risoluzione del compito n. 7 (Settembre 204/2) PROBLEMA Determinate tutte le soluzioni (z, w), con z, w C,del sistema { 2z 2 3iz = w 2 w 4 = z 4. Dalla seconda equazione si ricava subito che w 4 = z 4,
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica 1 e Geometria Secondo Appello 19 Giugno 2018
 Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica 1 e Geometria Secondo Appello 19 Giugno 218 Cognome: Nome: Matricola: 1. Disegnare il grafico della funzione
Politecnico di Milano Ingegneria Chimica, dei Materiali e delle Nanotecnologie Analisi Matematica 1 e Geometria Secondo Appello 19 Giugno 218 Cognome: Nome: Matricola: 1. Disegnare il grafico della funzione
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
Attenzione: i programmi sono cambiati negli anni. Non tutti gli esercizi nella presente raccolta riguardano argomenti trattati ora.
 Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-5 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-5 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Derivabilità, invertibilità e studi di funzione
 Derivabilità, invertibilità e studi di funzione. Studiare la continuità e la derivabilità delle funzioni elencate in tutto il loro dominio di definizione e calcolare la derivata nei punti in cui la funzione
Derivabilità, invertibilità e studi di funzione. Studiare la continuità e la derivabilità delle funzioni elencate in tutto il loro dominio di definizione e calcolare la derivata nei punti in cui la funzione
Esame del 15 Gennaio 2004 Vecchio Ordinamento. Per lo svolgimento di questa prova è concesso un tempo massimo di tre ore.
 Esame del Gennaio 4 Vecchio Ordinamento Per lo svolgimento di questa prova è concesso un tempo massimo di tre ore. Esercizio n. Calcolare il massimo e minimo assoluti della seguente funzione nell intervallo,
Esame del Gennaio 4 Vecchio Ordinamento Per lo svolgimento di questa prova è concesso un tempo massimo di tre ore. Esercizio n. Calcolare il massimo e minimo assoluti della seguente funzione nell intervallo,
Analisi e Geometria 1 Politecnico di Milano Ingegneria
 Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Primo Appello 13 Febbraio 2018
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Primo Appello 1 Febbraio 18 Cognome: Nome: Matricola: T.1: 4 punti T.: 4 punti Es.1: 4 punti Es.: 8 punti Es.: 5 punti Es.4: 7 punti Totale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Primo Appello 1 Febbraio 18 Cognome: Nome: Matricola: T.1: 4 punti T.: 4 punti Es.1: 4 punti Es.: 8 punti Es.: 5 punti Es.4: 7 punti Totale
Attenzione: i programmi sono cambiati negli anni. Non tutti gli esercizi nella presente raccolta riguardano argomenti trattati ora.
 Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-5 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-5 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2007 2008 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2007 2008 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Analisi e Geometria 1, Secondo appello 06 luglio 2016 (Compito A)
 Analisi e Geometria, Secondo appello 06 luglio 206 Compito A) Terza parte. Calcolare, al variare di α R, il valore del seguente limite di funzione sin x lim x 0 + x α x x ). sin x Soluzione: Utilizzando
Analisi e Geometria, Secondo appello 06 luglio 206 Compito A) Terza parte. Calcolare, al variare di α R, il valore del seguente limite di funzione sin x lim x 0 + x α x x ). sin x Soluzione: Utilizzando
COGNOME... NOME... Matricola... II corso Prof. Camporesi. Esame di ANALISI MATEMATICA - 9 Settembre 2004
 COGNOME... NOME... Matricola... II corso Prof. Camporesi Esame di ANALISI MATEMATICA - 9 Settembre 2004 A ESERCIZIO 1. (5 punti) 1. Risolvere in campo complesso l equazione z 5 + (1 + i)z = 0. 2. Dimostrare
COGNOME... NOME... Matricola... II corso Prof. Camporesi Esame di ANALISI MATEMATICA - 9 Settembre 2004 A ESERCIZIO 1. (5 punti) 1. Risolvere in campo complesso l equazione z 5 + (1 + i)z = 0. 2. Dimostrare
Correzione del compito di Analisi 1 e 2 del giorno 09/06/2017
 Correzione del compito di Analisi e 2 del giorno 9/6/27 Stra Federico 5 giugno 27 Esercizio Studiare, al variare di α R e R, la convergenza assoluta e la convergenza semplice della serie n n sin/n cos/n
Correzione del compito di Analisi e 2 del giorno 9/6/27 Stra Federico 5 giugno 27 Esercizio Studiare, al variare di α R e R, la convergenza assoluta e la convergenza semplice della serie n n sin/n cos/n
UNIVERSITÀ DEGLI STUDI DI PERUGIA Facoltà di Scienze MM. FF. e NN.
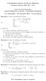 A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
SOLUZIONI COMPITO del 13/02/2019 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A
 SOLUZIONI COMPITO del /0/09 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Ponendo z = a + ib, da cui z = a + b, ed osservando che e iπ/ = i, l equazione proposta si riscrive nella forma a b
SOLUZIONI COMPITO del /0/09 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Ponendo z = a + ib, da cui z = a + b, ed osservando che e iπ/ = i, l equazione proposta si riscrive nella forma a b
Calcolo I - Corso di Laurea in Fisica - 19 Febbraio 2019 Soluzioni Scritto. a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità;
 Calcolo I - Corso di Laurea in Fisica - 9 Febbraio 209 Soluzioni Scritto ) Data la funzione fx) = arctanx + 4x 2 2 x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare,
Calcolo I - Corso di Laurea in Fisica - 9 Febbraio 209 Soluzioni Scritto ) Data la funzione fx) = arctanx + 4x 2 2 x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare,
