Sapienza, Università di Roma a.a. 2008/09. Note per il corso di. Analisi. Parte seconda. versione 1.0 (January 27, 2009) L.Lamberti e C.
|
|
|
- Vito Zanella
- 5 anni fa
- Visualizzazioni
Transcript
1 Spienz, Università di Rom /09 Note per il corso di Anlisi Prte second versione 1.0 (Jnury 27, 2009) L.Lmberti e C.Msci Corsi di lure in Fisic & Fisic ed Astrofisic
2
3 i Licenz c 2008 Lmberto Lmberti & Corrdo Msci Distribuzione Cretive Commons Tu sei libero di riprodurre, stmpre, inoltrre vi mil, fotocopire, distribuire quest oper lle seguenti condizioni: * Attribuzione: devi ttribuire l pternità dell oper nei modi indicti dll utore o d chi ti h dto l oper in licenz, * Non commercile: non puoi usre quest oper per fini commercili, * Non opere derivte: Non puoi lterre o trsformre quest oper, né usrl per crerne un ltr. (Licenz Cretive Commons Attribuzione - Non commercile - Non opere derivte 3.0 Testo completo:
4
5 Indice Cpitolo 1. L integrle 1 1. L re di un sottogrfico e l definizione di integrle 1 2. Istruzioni per l uso Il Teorem dell medi integrle Il Teorem fondmentle del clcolo integrle 20 Cpitolo 2. Zoologi dell integrzione Metodo di sostituzione Integrzione per prti Integrzione di funzioni rzionli 35 Cpitolo 3. I numeri complessi Nscit dei numeri complessi e loro infnzi Successioni, serie e continuità nei complessi L esponenzile complesso 52 Cpitolo 4. Equzioni differenzili Equzioni lineri del I ordine coefficiente costnte Equzioni lineri del II ordine coefficienti costnti omogenee Equzioni lineri del II ordine coefficienti costnti non omogenee 66 Cpitolo 5. Lo spzio rele multidimensionle Serve un struttur metric Quttro slti in R d : successioni di punti Informzioni di bse sull topologi di R d Ntur non fcit sltus: le curve 85 Cpitolo 6. Funzioni di più vribili Questioni elementri Le derivte przili Integrli curvilinei 110 iii
6 CAPITOLO 1 L integrle Il problem dell misurzione delle lunghezze di segmenti ci h condotti per un sentiero prticolrmente interessnte: di numeri nturli, i reltivi, i rzionli ed infine i numeri reli. E se ci viene l vogli di misurre ree di regioni del pino? Nel cso di un rettngolo, l re è not: è il prodotto delle lunghezze dei lti. Nel cso di un regione che si unione finit di rettngoli che si toccno l più lungo il perimetro, bst sommre le ree dei singoli rettngoli. M per regioni più generli? 1. L re di un sottogrfico e l definizione di integrle Dt un funzione f : [, b] [0, + ), l insieme S f = {(x, y) x b, 0 y f(x)} si dice sottogrfico di f nell intervllo [, b]. Come definire e/o clcolre l re di un sottogrfico di funzione? L re del sottogrfico delle funzioni costnti è elementre: se f(x) = C 0, il sottogrfico S f di f in [, b] è un rettngolo, l cui re è, d sempre, A(S f ) = (b ) C. Con poco impegno, possimo definire un clsse di funzioni il cui sottogrfico h un re fcile d clcolre. Definizione 1.1. Dto l intervllo [, b], un insieme P = {x 0, x 1,..., x n } tle che = x 0 < x 1 < < x n = b è un prtizione di [, b]. L mpiezz dell prtizione P è il numero P := mx{x i x i 1 : i = 1,..., n}. Un funzione f : [, b] R è un funzione costnte trtti (o funzione scl) se esiste un prtizione P = {x 0, x 1,..., x n } di [, b] tle che f è costnte su ogni intervllo [x i 1, x i ) per i = 1,..., n 1 e su [x n 1, x n ], ossi { αi x [x f(x) = i 1, x i ) i = 1,..., n 1 α n x [x n 1, x n ] dove α 1,..., α n sono numeri reli. Dto che per un funzione f costnte trtti e non negtiv il sottogrfico è un unione finit di rettngoli, l re di S f è dt dll somm delle ree di questi 1
7 2 1. L INTEGRALE rettngoli: A(S f ) = n f(ξ i )(x i x i 1 ) = i=1 n α i (x i x i 1 ) dove ξ i è un qulsisi punto di [x i 1, x i ). Dt un funzione f : [, b] R, non negtiv, possimo considerre pprossimzioni del sottogrfico S f dte d sottogrfici di funzioni costnti trtti g ed h, con g f h in [, b] (vedi Figur 1()) e utilizzre le ree dei sottogrfici pprossimnti come pprossimzioni dell re di S f. Per poter stimre per eccesso l funzione f con un funzione costnte trtti non negtiv occorre che l funzione f si superiormente limitt (vedi Figur 1(b)). Per l stim dl bsso con funzioni costnti trtti, serve nche che f si inferiormente limitt, ipotesi che nel nostro presente cso è utomticmente soddisftt dto che f è non negtiv. L ipotesi di limittezz dell funzione f è fondmentle qui, così come in tutto il Cpitolo e in tutt l definizione dell integrle definito. () y (b) y i=1 NO! x x Figur 1. () Un funzione pprossimt per eccesso e per difetto con due funzioni costnti trtti. (b) Un tenttivo (fllito) di pprossimzione per eccesso di un funzione non limitt superiormente. Dt un prtizione P = {x 0, x 1,..., x n } ci sono due funzioni f e f, costnti trtti negli intervlli definiti d P e tli che f f f, che dnno l migliore stim per difetto e l migliore per eccesso. Tli funzioni sono definite d f(x) = α i := inf [x i 1,x i ] f(x) x [x i 1, x i ), f(x) = β i := sup f(x) x [x i 1, x i ). [x i 1,x i ] In definitiv, dt un prtizione P dell intervllo [, b], (tutte le volte che A(S f ) h senso) si h A(S f ; P ) A(S f ) A(S f ; P ). dove A(S f ; P ) := A(S f ) = n α i (x i x i 1 ) A(S f ; P ) := A(S f ) = i=1 n β i (x i x i 1 ). i=1
8 1. L AREA DI UN SOTTOGRAFICO E LA DEFINIZIONE DI INTEGRALE 3 Figur 2. Due pprossimzioni per S f trmite le funzioni f e f. Dopo, si procede migliorre l pprossimzione trmite l scelt di un prtizione con un mpiezz più piccol. Un possibilità è scegliere un successione di prtizioni P n con mpiezz P n che tend zero per n. In questo modo, pssndo l limite nelle due successioni numeriche A(S f ; P n ) e A(S f ; P n ) si dovrebbe (incrocindo le dit) ottenere proprio l re richiest. Esempio 1.2. Si f(x) = x per x [, b] con 0 < b. Il sottogrfico dell funzione f nell intervllo [, b] h un form fmilire: nel cso in cui = 0, si trtt di un tringolo, e nel cso di > 0 si trtt di un trpezio. In entrmbi csi, l geometri elementre fornisce un formul per il clcolo dell re, che è dt d: (b )(b + ) 2 = b Cos succede se si clcol l re ttrverso il procedimento di pprossimzione per eccesso e per difetto proposto in precedenz? Dividimo l intervllo [, b] in n prti di ugule lunghezz trmite l prtizione P n = {x k = + kh : k = 0,..., n} dove h = (b )/n. Dto che f(x) = x è crescente, y y=x y y=x b x b x Figur 3. L funzione f(x) = x e le pprossimzioni determinte di punti + k(b ) n con k = 0,..., n. α k = inf x = x k 1 = + (k 1)h, β k = sup x = x k = + kh, [x k 1,x k ] [x k 1,x k ]
9 4 1. L INTEGRALE e x k x k 1 = h, vlgono n 1 n 1 A(S f ; P n ) = h + + ( + (n 1)h)h = h ( + kh) = hn + h 2 k, A(S f ; P n ) = ( + h)h + + ( + nh)h = h Tenendo conto dell formul n k=1 k = n(n + 1) 2 2 n(n 1) A(S f ; P n ) = hn + h 2 2 n(n + 1) A(S f ; P n ) = hn + h 2 k=0 k=0 n n ( + kh) = hn + h 2 k k=1 k=1 (dimostrtel!) e di h = b n 2 n(n 1) = (b ) + (b ) 2n 2 2 n(n + 1) = (b ) + (b ). 2n 2 Per n +, le due quntità tendono llo stesso limite: lim A(S f; P n ) = lim A(S (b )2 f; P n ) = (b ) + n + n + 2 che concord con le formule note dll geometri elementre. = b , Esempio 1.3. Pssimo considerre f(x) = x 2 in [, b] con 0 < b. Qul è l espressione dell re per il sottogrfico di x 2? Con l stess prtizione P n di prim. Dto che x 2 è crescente su [, b] per 0, d cui segue α i = inf x 2 = ( + (k 1)h ) 2, βi = sup x 2 = ( + kh ) 2, [x k 1,x k ] [x k 1,x k ] A(S f ; P n ) = 2 h + ( + h) 2 h + ( + 2h) 2 h + + ( + (n 1)h) 2 h A(S f ; P n ) = ( + h) 2 h + ( + 2h) 2 h + + ( + nh) 2 h Svolti i qudrti e tenuto presente che h = b, si ottiene n { } n 1 n 1 A(S f ; P n ) = h n 2 + 2h k + h 2 k 2 A(S f ; P n ) = h = (b ) { = (b ) { 2 + n 2 + 2h { 2 + k=0 2(b ) n 2 n k + h 2 k=1 2(b ) n 2 k=0 n 1 k + k=0 } n k 2 k=1 n k + k=1 (b )2 n 3 (b )2 n 3 } n 1 k 2 k=0 } n k 2 k=1
10 1. L AREA DI UN SOTTOGRAFICO E LA DEFINIZIONE DI INTEGRALE 5 Utilizzndo le formule n k = 1 2 n(n + 1) e n k=1 k=1 k 2 = 1 n(n + 1)(2n + 1) (dimostrtele!), 6 si ottiene { A(S f ; P n ) = (b ) 2 + (b ) n 1 } 2 (n 1)(2n 1) + (b ) n 6n { 2 A(S f ; P n ) = (b ) 2 + (b ) n + 1 } 2 (n + 1)(2n + 1) + (b ) n 6n 2 Quindi, pssndo l limite per n, lim A(S f; P n ) = lim A(S f; P n ) = b3 n + n =: A(S f). che è il vlore dell re cercto. Esempio 1.4. Sperimentimo l tecnic per un funzione più bizzrr: { 0 x [0, 1] \ Q, funzione di Dirichlet : D(x) := 1 x [0, 1] Q, Dt un qulsisi prtizione P = { = x 0 < x 1 < < x n = b}, in ognuno dei sottointervlli [x k 1, x k ] cdono si numeri rzionli che numeri irrzionli, quindi α i = inf D(x) = 0, β i = sup D(x) = 1. [x k 1,x k ] [x k 1,x k ] Pertnto, per ogni prtizione P, A(S D ; P ) = 0 e A(S D ; P ) = 1 e quindi sup A(S D ; P ) = 0 < 1 = inf A(S D; P ). P P Anche scegliendo prtizioni P con mpiezz sempre più piccol, le stime per difetto e quelle per eccesso restno sempre ben lontne le une dlle ltre. L interpretzione che dimo di quest situzione è che esistono sotto insiemi del pino cui non è possibile ssocire un re, ossi, per lcuni insiemi S, l espressione A(S) non h senso! Esempio 1.5. Ancor un esempio: f(x) = e x in [, b] con < b. Sceglimo ncor un volt l prtizione P n = {x k = + kh : k = 0,..., n} dove h = (b )/n. L funzione e x è crescente su [, b] quindi Perciò α i = inf [x k 1,x k ] ex = e x k 1 = e e (k 1)h, β i = sup e x = e x k = e e kh. [x k 1,x k ] A(S f ; P n ) = e h [ 1 + e h + e 2h + + e (n 1)h] = e h [ 1 + e h + (e h ) (e h ) n 1] A(S f ; P n ) = e h [ e h + e 2h + e 3h + + e nh] = e +h h [ 1 + e h + (e h ) (e h ) n 1]
11 6 1. L INTEGRALE Dto che 1 + e h + (e h ) (e h ) n 1 = (e nh 1)/(e h 1) e nh = b, A(S f ; P n ) = e h (e b 1) e h 1 A(S f ; P n ) = e+h h (e b 1) e h 1 Quindi, pssndo l limite per n, che è il vlore cercto. = h e h 1 (eb e ) = h e h 1 eh (e b e ) lim A(S f; P n ) = lim A(S f; P n ) = e b e, n + n + Tirimo le fil di quello che bbimo ftto fin qui. Considerndo l re di un regione del pino un concetto intuitivo, bbimo considerto il cso di sottogrfici di funzioni non negtive, proponendo un lgoritmo per il clcolo dell re: pprossimre per difetto e per eccesso l re richiest trmite ree di sottogrfici di funzioni costnti trtti e, fcendo tendere l mpiezz dell prtizione 0, ottenere il vlore dell re cerct. Trmite un certo numero di esempi, ci simo resi conto che il procedimento è rgionevole, m che in lcune situzioni non port nessun conclusione (come per l funzione di Dirichlet). Mettendo d prte, per il momento, il problem dell re e bttezzimo le funzioni per cui il procedimento di sopr descritto converge funzioni integrbili e il vlore limite delle pprossimzioni integrle (definito) dell funzione. Rispetto qunto ftto in precedenz, c è un differenz essenzile: le funzioni che considerimo possono vere segno qulsisi. Si f : [, b] R limitt e P = {x 0, x 1,..., x n } un prtizione di [, b]. Ponimo α i := inf f(x) e β i := sup f(x). [x i 1,x i ] [x i 1,x i ] Definizione 1.6. Somme integrli. Si chimno somm integrle per difetto/per eccesso di f reltivmente ll prtizione P, i vlori delle somme n n S(f; P ) := α i (x i x i 1 ) e S(f; P ) := β i (x i x i 1 ). i=1 L condizione di limittezz dell funzione f grntisce che, per ogni prtizione P, le somme integrli per difetto e per eccesso sono sempre ben definite. Definizione 1.7. Integrle definito. Un funzione f : [, b] R limitt si dice integrbile (secondo Riemnn) se vle l uguglinz (1) sup S(f; P ) = inf S(f; P ), P P i=1
12 1. L AREA DI UN SOTTOGRAFICO E LA DEFINIZIONE DI INTEGRALE 7 dove l estremo superiore e l estremo inferiore sono presi nell insieme di tutte le prtizioni P dell intervllo [, b]. Il vlore comune è l integrle definito di f in [, b] e si indic 1 con f(x) dx. L letter ust per indicre l vribile di integrzione è indifferente: l posto di f(x) dx, si può scrivere dto ll indice è ininfluente). f(t) dt o f(u) du (come per le sommtorie, in cui il nome Osservzione 1.8. Nell definizione di integrle, non viene ftt nessun richiest di positività dell funzione. Se l funzione integrnd f è positiv in [, b] ed è integrbile, l integrle d l definizione di re del sottogrfico di f in [, b] f 0 A({(x, y) : x b, 0 y f(x)}) := f(x) dx. Se f è negtiv in tutto o in prte dell intervllo, il significto dell integrle non è più quello di un re: l integrle è somm di termini positivi e negtivi, gli uni e gli ltri in corrispondenz delle zone in cui il grfico è sopr o sotto l sse x (vedi Figur 4) b Figur 4. L integrle non è l re: () un funzione costnte trtti, (b) un funzione qulsisi. L condizione di integrbilità dt dll definizione è chir e limpid d un punto di vist di rigore mtemtico. Meno chiro è come rispondere concretmente ll domnd: quli clssi di funzioni sono integrbili? Proposizione 1.9. Un funzione f : [, b] R è integrbile in [, b] se e solo se (2) ε > 0 P ε t.c. S(f; P ε ) S(f; P ε ) < ε. 1 Il simbolo dell integrle è un vrinte del simbolo di somm indicto d un lung S come si usv l tempo di Leibnitz. Il simbolo dx è l erede dell lunghezz dell intervllo x i x i 1. L uso dell d minuscol ricord che le pprossimzioni migliori si ottengono considerndo prtizioni con mpiezz piccol: x := x i x i 1 dx.
13 8 1. L INTEGRALE L condizione espress in (2) può essere riscritt come n S(f; P ε ) S(f; P ε ) = (β i α i ) (x i x i 1 ) < ε i=1 con α i e β i definiti in precedenz. Dto che tle condizione è sufficiente, per dimostrre l integrbilità di un funzione occorre stimre l differenz β i α i, cioè l vrizione f(y) f(x) per x, y [x i 1, x i ] per prtizioni con mpiezz piccol. Dimostrzione dell Proposizione 1.9. L definizione di integrbilità e le proprietà dell estremo superiore e dell estremo inferiore indicno che per ogni ε > 0, esistono prtizioni P ε e P ε tli che S(f; P ε) S(f; P ε ) < ε. Occorre or dimostrre che l stess stim vle per un scelt opportun di un stess prtizione P ε. Psso 1. Dimostrimo prim di tutto che (3) S(f; P 1 ) S(f; P 2 ) e S(f; P 2 ) S(f; P 1 ) P 2 P 1. Dto che P 2 P 1, si può costruire P 2 prtire d P 1 ggiungendo un numero finito di punti, bst studire il cso in cui P 2 = P 1 {ξ} (il cso generle si ottiene iterndo il procedimento). Inoltre considerimo solo le somme per difetto, l ltr prte è nlog. Supponimo P 1 = {x 0, x 1,..., x n } e ξ (x k 1, x k ) per un opportuno k {1,..., n}. Le espressioni di S(f; P 1 ) e di S(f; P 2 ) coincidono in tutti i termini trnne in quelli reltivi ll intervllo [x k 1, x k ] e quindi, indicndo con α = inf f(x), α = inf f(x), [x k 1,x k ] [x k 1,ξ] α = inf f(x), [ξ,x i ] vle, dto che α α e α α, [ ] S(f; P 2 ) S(f; P 1 ) = α (x k ξ) + α (ξ x k 1 ) α(x k x k 1 ) [ ] [ ] = α (x k ξ) + α (ξ x k 1 ) α(x k ξ) + α(ξ x k 1 ) Psso 2. Or dimostrimo che = (α α)(x k ξ) + (α α)(ξ x k 1 ) 0, S(f; P ) S(f; P ) P, P prtizioni. Inftti, per costruzione, S(f; P ) S(f; P ) per ogni prtizione P. Quindi, se considerimo l prtizione P = P P e utilizzimo (3): S(f; P ) S(f; P ) S(f; P ) S(f; P ). Psso 3. Infine, dimostrimo l Proposizione. Per ogni prtizione P, vle 0 inf P S(f; P ) sup S(f; P ) S(f; P ) S(f; P ) P
14 1. L AREA DI UN SOTTOGRAFICO E LA DEFINIZIONE DI INTEGRALE 9 Se per ogni ε > 0 esiste un prtizione P ε che verific (2), llor 0 inf P S(f; P ) sup S(f; P ) < ε ε > 0, P cioè inf P S(f; P ) = sup P S(f; P ), e f è integrbile. Se invece supponimo che l funzione f si integrbile, per ogni ε > 0 esistono due prtizioni P ε e P ε per cui vle S(f; P ε) S(f; P ε ) < ε. Scegliendo P ε = P ε P ε, grzie S(f; P ε ) S(f; P ε ) e S(f; P ε ) S(f; P ε), S(f; P ε ) S(f; P ε ) S(f; P ε) S(f; P ε ) < ε, cioè l condizione (2). Se si costruisce un successione di prtizioni P n per cui lim S(f; P n) = lim S(f; P n) = l, n + n + mggior rgione si vrà che: per ogni ε > 0 esiste un prtizione P n per cui vle 0 S(f; P n ) S(f; P n ) = [ S(f; P n ) l ] + [ l S(f; P n ) ] < 2ε cioè l funzione f è integrbile e l integrle è il vlore l. In prticolre, gli Esempi 1.2, 1.3, 1.5 indicno che le funzioni x, x 2 e e x sono integrbili in [, b] e che vlgono x dx = b , x 2 dx = b , L Esempio 1.4 mostr che esistono nche funzioni non integrbili! e x dx = e b e. Il volume di solidi di rotzione. L integrle è utile per il clcolo delle ree, m nche, in lcune situzioni specili, per il clcolo di volumi di solidi. Considerimo un funzione f : [, b] [0, + ) continu e disegnimone il grfico Γ f. Se si f ruotre il grfico Γ f ttorno ll sse x, si ottiene l superficie lterle di un solido Σ. Qul è il suo volume? Come per il clcolo delle ree, nche nel clcolo dei volumi bisogn prtire d un formul not. Qui, dimo per buon l regol che ci è stt insegnt d bmbini: il volume di un cilindro di rggio di bse r e ltezz h è πr 2 h. Rgionndo in mnier simile qunto ftto per l determinzione dell re di un sottogrfico, pprossimimo il solido con l unione di oggetti di cui conoscimo il volume. L scelt più rgionevole è l unione di cilindri ottenuti trmite un rotzione di rettngoli con lti prlleli gli ssi x e y come in Figur 5(b) Un pprossimzione di questo genere di Σ, si ottiene trmite l scelt di un prtizione P = { x 0 <
15 10 1. L INTEGRALE y y b x b x Figur 5. () Un solido di rotzione; (b) Un su pprossimzione con cilindri. x 1 < < x n = b} dell intervllo [, b] e di n punti ξ 1,..., ξ n tli che ξ i [x i 1, x i ]. Quindi l pprossimzione del volume V(Σ) di Σ è dt d n V(Σ) πf 2 (ξ i )(x i x i 1 ). i=1 Qundo l mpiezz dell prtizione tende zero, l errore di pprossimzione tende zero e si ottiene l formul desidert V(Σ) = π Colludimo l formul con un pio di esempi. f 2 (x) dx. Esempio Il volume del cono. Un cono di ltezz h e rggio di bse r, si può ottenere trmite un rotzione del grfico dell funzione f(x) = rx h x [0, h]. Quindi h ( rx ) 2 π r 2 h V(Σ) = π dx = x 2 dx = π r2 h 3 0 h h 2 0 h 2 3 = 1 3 π r2 h, che è l trdizionle formul del volume del cono. Esempio Il volume dell sfer. Un sfer di rggio r si ottiene con l rotzione del grfico di f(x) = r 2 x 2 Applicndo l formul del volume r ( ) 2 r V(Σ) = π r2 x 2 dx = π r Anche quest volt, giustmente, i conti tornno! r x [ r, r]. ( r 2 x 2) { dx = π 2r 3 2 } 3 r3 dx = 4 3 πr3. Esercizio Qul è il volume del solido ottenuto fcendo ruotre il grfico di e x per x [0, 1] ttorno ll sse x?
16 2. ISTRUZIONI PER L USO Istruzioni per l uso L integrle di un funzione limitt è l estremo superiore/inferiore di opportune sommtorie. Per le sommtorie vlgono tre proprietà fondmentli: dti 1,..., n, b 1,..., b n, α, β R, si hnno n n n linerità: (α k + βb k ) = α k + β dditività: k=1 n k = k=1 m k + k=1 monotonì: k b k k=1 n k=m+1 k n k k=1 n b k. Di conseguenz, nloghe proprietà vengono ereditte dgli integrli definiti. Linerità. Un combinzione linere di funzioni integrbile è integrbile: dti c 1, c 2 R e f, g integrbili in [, b], l funzione c 1 f + c 2 g è integrbile e vle (4) k=1 k=1 [c 1 f(x) + c 2 g(x)] dx = c 1 f(x) dx + c 2 g(x) dx Additività. Si f integrbile in [, b] e si c (, b). Allor f è integrbile in [, c] e in [c, b] e vle (5) f(x) dx = c f(x) dx + c f(x) dx < c < b. In prticolre, llor f è integrbile in ogni sottointervllo di [, b]. Monotonì. Per ogni coppi di funzioni f, g integrbili in [, b], (6) f(x) g(x) x [, b] = f(x) dx b k g(x) dx. Per or bbimo definito f(x) dx solo nel cso < b. E usnz diffus definire l integrle nel cso di = b o > b, in modo che si preservt l regol dell dditività. Scrivendo (5) con c =, si ottiene d cui segue f(x) dx = f(x) dx + f(x) dx := 0, f(x) dx, coerente con l eventule interpretzione in termini di ree.
17 12 1. L INTEGRALE Scrivimo (5) per b =, llor 0 = d cui segue l definizione c f(x) dx = f(x) dx := c c f(x) dx + c f(x) dx f(x) dx < c, dove il membro destro h il significto definito nel prgrfo precedente. Dll proprietà di monotonì dell integrle discende un proprietà che è, sostnzilmente, un disuguglinz tringolre per integrli : Proposizione 2.1. Se l funzione limitt f : [, b] R è integrbile in [, b], llor nche f è integrbile in [, b] e vle (7) f(x) dx b f(x) dx. Dedichimoci or dimostrre le proprietà dell integrle. Le proprietà di linerità e di dditività contengono due prti. Un prim prte concerne il ftto che dll integrbilità di lcune funzioni se ne deduce l integrbilità di certe ltre. L second prte mette in relzione tr loro gli integrli definiti delle vrie funzioni. Linerità. Sino f e g integrbili in [, b] e c 1, c 2 R. Dt P = {x 0, x 1,..., x n }, prtizione di [, b], bttezzimo α i = e, nlogmente, α f i = inf [c 1 f(x) + c 2 g(x)] e β i = sup [c 1 f(x) + c 2 g(x)], [x i 1,x i ] [x i 1,x i ] inf f(x), [x i 1,x i ] βf i = sup f(x), α g i = inf g(x), [x i 1,x i ] [x i 1,x i ] βg i = sup g(x). [x i 1,x i ] Per ogni x, y (x i 1, x i ), si h [c 1 f(x) + c 2 g(x)] [c 1 f(y) + c 2 g(y)] = c 1 [f(x) f(y)] + c 2 [g(x) g(y)] c 1 ( β f i α f i ) + c2 ( β g i αg i ), quindi, pssndo ll estremo superiore in x e ll estremo inferiore in y, si deduce che β i α i c 1 ( [β f i α f i ) + c2 ( β g i αg i ).
18 Perciò, per ogni prtizione P di [, b], S(c 1 f + c 2 g; P ) S(c 1 f + c 2 g; P ) = c 1 n i=1 2. ISTRUZIONI PER L USO 13 n [β i α i ] (x i x i 1 ) i=1 [ ] β f i α f i (x i x i 1 ) + c 2 n [α g i βg i ] (x i x i 1 ) i=1 = c 1 [ S(f; P ) S(f; P ) ] + c 2 [ S(g; P ) S(g; P ) ]. Dto che l funzione f è integrbile, grzie ll Proposizione 1.9, esiste un prtizione P 1 tle che S(f; P 1 ) S(f; P 1 ) < ε. Anlogmente, esiste un prtizione P 2 per cui S(g; P 1 ) S(g; P 1 ) < ε. Scegliendo l prtizione P = P 1 P 2, entrmbe le disequzioni sono soddisftte e quindi S(c 1 f + c 2 g; P ) S(c 1 f + c 2 g; P ) < ( c 1 + c 2 ) ε. Dll Proposizione 1.9, segue che l funzione c 1 f + c 2 g è integrbile in [, b]. Rest d dimostrre l formul (4). Dt l solit prtizione P = {x 0,..., x n }, sceglimo ξ 1, ξ 2,..., ξ n con ξ i (x i 1, x i ) per i = 1,..., n. Dto che n S(f; P ) f(ξ i )(x i x i 1 ) S(f; P ), S(f; P ) f(x) dx S(f; P ), si h (8) i=1 f(x) dx n f(ξ i )(x i x i 1 ) S(f; P ) S(f; P ) i=1 Aggiungendo e sottrendo i termini opportuni, si ricv [c 1 f + c 2 g] dx c 1 f dx c 2 g dx n [c 1 f + c 2 g] dx [c 1 f(ξ i ) + c 2 g(ξ i )] (x i x i 1 ) i=1 n + c 1 f dx f(ξ i )(x i x i 1 ) + c 2 g dx i=1 Utilizzndo (8), si deduce l disuguglinz [c 1 f + c 2 g] dx c 1 f dx c 2 g dx S(c 1 f + c 2 g; P ) S(c 1 f + c 2 g; P ) n g(ξ i )(x i x i 1 ). i=1 + c 1 [ S(f; P ) S(f; P ) ] + c 2 [ S(g; P ) S(g; P ) ].
19 14 1. L INTEGRALE Scegliendo un prtizione P per cui si ottiene S(f; P ) S(f; P ) < ε, S(g; P ) S(g; P ) < ε, S(c 1 f + c 2 g; P ) S(c 1 f + c 2 g; P ) < ε, [c 1 f + c 2 g] dx c 1 f dx c 2 g dx (1 + c 1 + c 2 ) ε. Dto che ε è rbitrrimente piccolo, non c è scmpo: (4) è dimostrt. L linerità grntisce, in prticolre, che l somm di funzioni integrbili è integrbile. Lo stesso vle per il prodotto, come enuncito nell esercizio che segue (m non è vero che l integrle del prodotto è il prodotto degli integrli!). Esercizio 2.2. Se f e g sono integrbili in [, b], nche il prodotto fg lo è. Soluzione. Le funzioni f e g sono limitte, quindi esistono M f, M g > 0 tli che f(x) M f e g(x) M g per ogni x. Dt l prtizione P = {x 0, x 1,..., x n } indichimo con α fg i = inf f(x)g(x) e βfg i = sup f(x)g(x), [x i 1,x i ] [x i 1,x i ] con significti nloghi per α f i, αg i, βf i e β g i. Dti x, y (x i 1, x i ), si h [ ] [ ] f(x)g(x) f(y)g(y) = f(x) f(y) g(x) + f(y) g(x) g(y) M g (β f i αf i ) + M f (β g i αg i ). Prendendo l estremo superiore in x e l estremo superiore in y, si ottiene Perciò β fg i α fg i M g (β f i αf i ) + M f (β g i αg i ). ] [ ] S(fg; P ) S(fg; P ) M g [S(f; P ) S(f; P ) + M f S(g; P ) S(g; P ). Dto che il termine secondo membro può essere reso rbitrrimente piccolo per P opportuno, l conclusione segue dll solit Proposizione 1.9. Additività. Se si pens ll ide geometric di prtenz, l proprietà di dditività sembr bbstnz nturle: per clcolre l re possimo dividere l regione in due prti e sommre i vlori delle ree delle due sottoregioni. M qui l cos è divers: prim di tutto bbimo un definizione nlitic d rispettre e ogni ffermzione deve discendere rigorosmente d quell definizione. In più c è un prticolre non bnle: chi grntisce che se un funzione è integrbile in [, b], llor è nche integrbile in [, c] e [c, b] per c (, b)? Seppur rgionevole, quest ffermzione è tutt d verificre. Per comodità, introducimo l funzione χ E : R R { 1 x E, funzione crtteristic di E: χ E (x) := 0 x / E.
20 2. ISTRUZIONI PER L USO 15 Se l insieme E è un intervllo, l funzione χ E è integrbile. Quindi, se f : [, b] R è integrbile in [, b] e c [, b], llor sono integrbili nche le funzioni prodotto fχ [,c] (x) e fχ [c,b] (x) e vle l uguglinz f(x) = f(x)χ [,c] (x) + f(x)χ [c,b] (x), Inoltre, dto che moltiplicre per un funzione crtteristic si trduce nel troncre zero l funzione f fuori dll insieme corrispondente, si hnno f(x)χ [,c] (x) dx = c Quindi, grzie ll linerità, f(x) dx = f(x) dx f(x)χ [,c] (x) dx + e f(x)χ [c,b] (x) dx = f(x)χ [c,b] (x) dx = c c f(x) dx + f(x) dx. c f(x) dx. Monotonì. Dimostrre l monotonì dell integrle è prticolrmente fcile. Se f(x) g(x) per ogni x [, b], llor inf f(x) inf g(x) x [x i 1,x i ] x [x i 1,x i ] [x i 1, x i ] [, b]. Quindi, per ogni prtizione P di [, b], vle S(f; P ) S(g; P ), e pssndo ll estremo superiore si ottiene l conclusione. Dimostrzione dell Proposizione 2.1. L prte più complict dell dimostrzione st nel verificre che effettivmente l funzione f si integrbile. Il problem è sempre lo stesso: dt P = {x 0,..., x n } prtizione di [, b] e posti A k = inf [x k 1,x k ] Sino α k = f(x), B k = inf [x k 1,x k ] sup [x k 1,x k ] f(x), β k = f(x), qule stim possimo recuperre per B k A k? sup f(x), dti x, y in (x k 1, x k ), si h [x k 1,x k ] f(x) f(y) f(x) f(y) βk α k, e prendendo l estremo superiore in x e l inferiore in y si ottiene B k A k β k α k. Con quest stim ll mno, si deduce che n S( f ; P ) S( f ; P ) (β k α k )(x k x k 1 ) = S(f; P ) S(f; P ). k=1 e grzie ll Proposizione 1.9 si rriv ll conclusione. L stim finle segue d ±f f, che, grzie ll monotonì dell integrle, implic ± f(x) dx f(x) dx,
21 16 1. L INTEGRALE d cui segue l conclusione. Esercizio 2.3. Dte f e g integrbili, dimostrre che nche f + (x) := mx{f(x), 0}, f (x) := min{f(x), 0}, mx{f(x), g(x)} e min{f(x), g(x)} sono integrbili. Un volt dto senso l concetto di integrle e determinte le proprietà principli, bisogn dedicrsi determinre un certo numero di funzioni che sino effettivmente integrbili, ltrimenti l oggetto ppen definito risulterebbe sostnzilmente inutile. Come si è detto, per dimostrre l integrbilità di f, bst mostrre ε > 0 P ε prtizione tle che S(f; P ε ) S(f; P ε ) ε. Dunque seguiremo quest strtegi: fisst un prtizione P, mostreremo che l differenz S(f; P ) S(f; P ) può essere res rbitrrimente piccol, ptto di scegliere un prtizione P l cui mpiezz P si sufficientemente piccol. L prim clsse che considerimo è quell delle funzioni monotòne in un intervllo chiuso e limitto. Tli funzioni sono sempre limitte (perché?). Teorem 2.4. Si f : [, b] R monotòn, llor è integrbile in [, b]. Dimostrzione. Supponimo che f si un funzione crescente. Dt un prtizione P = {x 0,..., x n }, gli estremi inferiori e superiori di f in [x i 1, x i ] sono α i = inf f(x) = f(x i 1 ) e β i = sup f(x) = f(x i ). [x i 1,x i ] [x i 1,x i ] Le somme integrli per difetto e per eccesso sono dte d n S(f; P ) = f(x i 1 )(x i 1 x i ) e S(f; P ) = i=1 e l loro differenz è stimt d S(f; P ) S(f; P ) = n f(x i )(x i 1 x i ). i=1 n [f(x i ) f(x i 1 )] (x i 1 x i ) i=1 Indicndo con P l mpiezz di P, cioè il mssimo delle lunghezze x i 1 x i, n S(f; P ) S(f; P ) P [f(x i ) f(x i 1 )] = P [f(b) f()]. i=1 Per ogni ε > 0, è possibile scegliere P sufficientemente piccol, in modo che l differenz S(f; P ) S(f; P ) si minore di ε, pertnto, grzie (ncor un volt!) ll Proposizione 1.9, l funzione è integrbile.
22 2. ISTRUZIONI PER L USO 17 A prtire dlle funzioni monotone e grzie l ftto che combinzioni lineri di funzioni integrbili sono integrbili, è possibile costruire un clsse ncor più mpi di funzioni. Ad esempio, si f un funzione definit in [, b] tle che, per qulche c [, b], l funzione f è crescente in [, c] e decrescente in [c, b]. Allor l funzione f si può riscrivere come differenz di due funzioni crescenti (vedi Figur 6): dove f 1 (x) = { f(x) x [, c] f(c) x [c, b] f = f 1 f 2 e f 2 (x) = { 0 x [, c] f(c) f(x) x [c, b] f = Quindi, nche funzioni con un cmbio di monotoni sono integrbili. Con un cof 1 f 2 - c b c b c b Figur 6. Un funzione f con un cmbio di monotoni, decompost come differenz delle funzioni crescenti f 1 e f 2. struzione nlog, si mostr che tutte le funzioni con un numero finito di cmbi di monotoni sono integrbili. Ad esempio, tutti i polinomi e, più in generle, tutte le funzioni rzionli sono integrbili. Esercizio 2.5. Conoscete un funzione definit in un intervllo limitto che bbi un numero infinito di cmbi di monotonì? L second clsse che considerimo è quell delle funzioni lipschitzine, cioè delle funzioni f : [, b] R tli che esist L > 0 per cui L > 0 t.c. f(x) f(y) L x y x, y [, b]. Teorem 2.6. Si f : [, b] R lipschitzin, llor è integrbile in [, b]. Dimostrzione. Fisst l benemt prtizione P = {x 0, x 1..., x n }, n S(f; P ) S(f; P ) = (β i α i )(x i x i 1 ), i=1 con il solito significto per α i e β i. Dto che f è lipschitzin, ess è nche continu in [, b], quindi mmette mssimo e minimo in ogni intervllo [x i 1, x i ] e vle α i = inf f = min f(x) = f(η i) e α i = sup f = mx f(x) = f(ξ i) (x i 1,x i ) [x i 1,x i ] (x i 1,x i ) [x i 1,x i ]
23 18 1. L INTEGRALE con η i e ξ i, rispettivmente, un punto di mssimo ed uno di minimo dell funzione f in [x i 1, x i ]. Sostituendo nell relzione precedente, si ottiene n n S(f; P ) S(f; P ) = (f(ξ i ) f(η i ))(x i x i 1 ) L ξ i η i (x i x i 1 ). i=1 Dto che ξ i, η i [x i 1, x i ], l differenz ξ i η i è minore o ugule dell mpiezz P dell prtizione. Quindi n S(f; P ) S(f; P ) L P (x i x i 1 ) L(b ) P. i=1 Scegliendo P tle che P < ε/l(b ), l differenz S(f; P ) S(f; P ) è strettmente minore di ε e, grzie ll Proposizione 1.9, segue l conclusione. Più in generle si può dimostrre il fondmentle Teorem 2.7. Si f : [, b] R continu, llor f è integrbile in [, b]. L dimostrzione pss per il concetto di uniforme continuità. Non dremo qui ulteriori dettgli sull questione. Esercizio 2.8. Dimostrre che l composizione di un funzione lipschitzin con un funzione integrbile dà luogo d un funzione integrbile. i=1 3. Il Teorem dell medi integrle Tutte le funzioni f : [, b] R integrbili sono, per definizione, funzioni limitte. In prticolre questo signific che dt un funzione integrbile, il suo integrle definito può sempre essere stimto in mnier rude : per le proprietà di monotonì dell integrle, se m f(x) M per ogni x [, b], m(b ) = m dx f(x) dx M dx = M(b ), Quest formul è intuitivmente ovvi: se pensimo d un funzione non negtiv e ll integrle come re, le quntità M(b ) e m(b ) rppresentno le ree di un rettngolo circoscritto ed inscritto nel sottogrfico di f (vedi Figur 7). L formul precedente si può riscrivere come m f M dove f, detto medi integrle 2 di f in [, b], è definito d (9) f := 1 b f(x) dx. 2 L medi ritmetic dei numeri f 1, f 2,..., f n è, per definizione (f 1 + f f n )/n. L medi integrle di un funzione in un intervllo è, in un certo senso, limite di medie ritmetiche di vlori ssunti dll funzione. Inftti, dt l prtizione di [, b] in sottointervlli di lunghezz x i = (b )/n
24 3. IL TEOREMA DELLA MEDIA INTEGRALE 19 y y=f(x) M b x m Figur 7. Significto geometrico dell stim m(b ) f(x) dx M(b ). Quindi, espresso prole, l medi integrle di un funzione f è sempre compres tr un qulsisi minornte ed un qulsisi mggiornte di f. Se f è continu in un intervllo [, b], si può dire qulcos di più. Per il teorem di Weierstrss, esistono due punti ξ, η [, b] tli che min [,b] f(x) = f(ξ) f(x) f(η) = mx f(x) [,b] x [, b]. Quindi f, definit in (9) è compres tr il mssimo ed il minimo dell funzione f in [, b]. Grzie l Teorem del vlore intermedio, si può concludere che per un funzione f continu in [, b], l medi integrle f sempre prte dell insieme immgine f([, b]). Teorem 3.1. Teorem dell Medi Integrle. Si f : [, b] R continu. Allor esiste ξ [, b] tle che f(ξ) = f con f definito in (9). Nel cso di un funzione non negtiv f, il teorem equivle d ffermre che esiste un rettngolo di bse [, b] ed un ltezz f(ξ) opportun con l stess re del sottogrfico di f in [, b]. Non è prticolrmente sconvolgente (m più vnti servirà) osservre che l formul (9) vle nche nel cso b <, inftti 1 b f(x) dx = 1 b b f(x) dx, e quest ultimo termine si può pplicre il Teorem dell Medi Integrle. per ogni i e scelti ξ i (x i 1, x i ), l medi ritmetic di f(ξ 1 ),..., f(ξ n ) è pri f(ξ 1 ) + + f(ξ n ) n = 1 b n f(ξ i )(x i x i 1 ). Per n, il termine destr converge proprio ll medi integrle di f in [, b]. i=1
25 20 1. L INTEGRALE Controesempio 3.2. Se l funzione f non è continu in tutto [, b], non è detto che vlg l conclusione del Teorem 3.1 Ad esempio, si consideri l funzione 1 x < 0, f(x) = sgn x = 0 x = 0, +1 x > 0, nell intervllo [ 1, 2]. Allor f è integrbile (per lmeno due motivi... quli?) µ = 1 2 ( 1) 2 che non f prte dell immgine dell funzione sgn x. 1 sgn x dx = 1 3 ( 1 + 2) = 1 3, Esercizio 3.3. Sino f C([, b]) e p C([, b]) tle che p(x) > 0 per ogni x. Dimostrre che esiste ξ [, b] tle che f(ξ) = f(x)p(x) dx. p(x) dx Soluzione. Se m e M indicno il minimo ed il mssimo di f in [, b], grzie l ftto che p(x) > 0, si h mp(x) f(x)p(x) Mp(x) per ogni x. Integrte in [, b], mescolte e concludete Il Teorem fondmentle del clcolo integrle Un volt fisst l funzione f, l integrle definito è un funzione degli estremi di integrzione e b. Per studire quest dipendenz, supponimo l estremo inferiore fissto l vlore e indichimo l estremo superiore (vribile) con x: considerimo, quindi, l funzione integrle (10) φ(x) = x f(t) dt. L formul (10) può essere utilizzt per generre nuove funzioni prtire d un funzione integrbile f. Ad esempio, si può definire 3 φ(x) := x 1 1 dt x > 0, t che h perfettmente senso, dto che l funzione 1 t intervllo [, b] con 0 < b. è un funzione continu in ogni Proposizione 4.1. Se f è integrbile in [, b], l funzione φ, definit in (10), è lipschitzin. 3 Tle funzione, come vedremo, si dimostr essere ugule l logritmo nturle e l formul precedente può quindi essere scelt come definizione nlitic di ln x.
26 4. IL TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE 21 Dimostrzione. Dto che f è integrbile, ess è nche limitt. Si M > 0 tle che f(t) M per ogni t [, b], llor, y y se x < y, φ(x) φ(y) = f(t) dt f(t) dt M(y x); x x x se x > y, φ(x) φ(y) = x f(t) dt f(t) dt M(x y). Quindi y f(t) M = φ(x) φ(y) M x y. In prticolre, se f è integrbile, l funzione φ è un funzione continu. Esercizio 4.2. Considerimo l funzione f(x) = sgn x. Spete riconoscere l funzione φ dt in (10) in questo cso? Esercizio 4.3. Si f : R R integrbile in ogni intervllo [, b] di R e si φ(x) := x 0 f(t) dt (i) Dimostrre che, se f(x) 0 per ogni x R, llor φ è non decrescente. (ii) Disegnre qulittivmente il grfico di φ nel cso in cui xf(x) > 0 per ogni x 0. Un volt stbilito che l funzione integrle φ è sempre lipschitzin, è nturle domndrsi se ess si nche derivbile. Considerimone il rpporto incrementle φ(x + h) φ(x) = 1 x+h x f(t) dt f(t) dt = 1 x+h f(t) dt h h h α (l ultim uguglinz è conseguenz delle proprietà di dditività dell integrle). Supponendo che l funzione integrnd f si continu, è possibile pplicre il Teorem dell Medi Integrle, Teorem 3.1, e riscrivere il rpporto incrementle come φ(x + h) φ(x) = f(ξ) h con ξ compreso tr x e x + h. Pssndo l limite h 0, dto che ξ x, si h φ φ(x + h) φ(x) (x) = lim h 0 h Abbimo quindi dimostrto il seguente risultto. Teorem 4.4. Si f C([, b]), α [, b] e φ(x) = α y = lim h 0 f(ξ) = f(x). x x f(t) dt per x [, b]. Allor φ è derivbile in [, b] e φ (x) = f(x). α
27 22 1. L INTEGRALE Un prim conseguenz (prtic) notevole è che, dto che simo in grdo di clcolrne l derivt, possimo dedurre molte proprietà qulittive importnti nche per un funzione che non si espress direttmente trmite funzioni elementri, m come integrle di un funzione elementre. Esempio 4.5. Considerimo l funzione funzione degli errori: Erf(x) = 2 x π Dl Teorem 4.4 deducimo che D (Erf(x)) = 2 π e x2 0 e t2 dt, > 0, quindi Erf(x) è strettmente crescente. Con un tecnologi più vnzt di quell che ci è disponibile questo livello, è possibile dimostrre che Erf(± ) = ±1. Il Teorem 4.4 risolve nche un problem interessnte: dt f, trovre un funzione F che risolv l equzione F = f. L equzione F = f è un equzione differenzile in cui il dto è l funzione f e l incognit è l funzione F. Un soluzione F di quest equzione si dice primitiv di f. Il Teorem 4.4 fferm che se f C([, b]) il problem F = f mmette lmeno un soluzione (dt dll funzione integrle φ), cioè esiste sempre lmeno un primitiv. D questo punto di vist si può intepretre l operzione di integrzione come l operzione invers dell derivzione. Tle operzione di inversione è univocmente definit? In ltri termini, dt un funzione f, qunte primitive esistono? Teorem 4.6. Si f : [, b] R e sino F e G due sue primitive. Allor esiste c R tle che F (x) G(x) = c per ogni x [, b]. Dimostrzione. L derivt dell funzione differenz F G è null: (F (x) G(x)) = F (x) G (x) = f(x) f(x) = 0. Per qunto già visto, l differenz F G deve essere costnte. Quindi, se f C([, b]), l equzione F soluzioni sono dell form x α f(t) dt + c c R. L clsse delle primitive dell funzione f si indic con f(x) dx, = f è completmente risolt: tutte le e si chim integrle indefinito di f. Si noti bene che l integrle indefinito di un funzione indic un clsse di funzioni, e non un singol funzione.
28 4. IL TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE 23 Ad etern memori, sintetizzimo i due risultti enunciti in un unico Teorem. Teorem 4.7. Teorem Fondmentle del Clcolo Integrle. Dt f C([, b]), le soluzioni dell equzione differenzile F = f sono tutte e sole dell form F (x) = x α f(t) dt + c, con α [, b] e c R. Se si cerc un primitiv F di un funzione f con l richiest ggiuntiv che l funzione F vlg in un punto ssegnto x 0 un vlore dto y 0, cioè se si vuole risolvere { F (11) dti f C([, b]), x 0 [, b], y 0 R, trovre F tle che (x) = f(x), F (x 0 ) = y 0, l soluzione F esiste, è unic ed è dt d (12) F (x) = y 0 + x x 0 f(t) dt. Il problem (11) rientr nell clsse dei problemi di Cuchy per equzioni differenzili. Osservzione 4.8. Il problem di Cuchy può essere interpretto in termini di moto di un prticell. Se f(x) è l velocità dell prticell ll istnte x e y 0 l su posizione ll istnte inizile x 0, l soluzione F = F (x), definit in (12), del problem di Cuchy (11), rppresent l posizione dell prticell ll istnte x. Primitive e clcolo degli integrli definiti. Il Teorem fondmentle del clcolo h un conseguenz interessnte che rigurd il clcolo esplicito di integrli definiti. Supponimo di voler clcolre (13) f(t) dt. e supponimo di conoscere già (per ltre vie) un primitiv dell funzione f, cioè un funzione F tle che F = f. Sppimo che nche l funzione integrle definit in (10) è un primitiv di f e, quindi, per il Teorem Fondmentle del Clcolo, differisce d F per un costnte, cioè φ(x) = F (x) + c per qulche c R. L costnte c può essere determint, clcolndo in x = : 0 = φ() = F () + c = c = F (). Si deduce quindi che φ(x) = F (x) F () e quindi f(t) dt = φ(b) = F (b) F ().
29 24 1. L INTEGRALE Quindi, se si conosce un primitiv F dell funzione f, l integrle definito di f in [, b] è ugule ll differenz dei vlori dell primitiv in b e in, cioè F = f = f(t) dt = F (b) F (). L differenz F (b) F () si indic nche con F (x) b o, [ F (x) Esempio 4.9. Considerimo l funzione f(x) = x 2. Dto che D(x 3 ) = 3x 2, si h ( ) 1 D 3 x3 = x 2, quindi un primitiv di x 2 è x 3 /3. Ottenimo perciò x 2 dx = 1 b 3 x3 = b , che è proprio l formul clcolt d inizio Cpitolo. Più in generle, dto che ( ) 1 D n + 1 xn+1 = x n, vle l formul x n dx = 1 b n + 1 xn+1 ] b = 1 n + 1 (bn+1 n+1 )..
30 CAPITOLO 2 Zoologi dell integrzione Per inizire, ricordimo i ftti principli che bbimo visto sugli integrli indefiniti. Dt un funzione f, si dice che F è un primitiv di f se F = f; l fmigli di primitive di un funzione f si indic con il simbolo f(x) dx. Se l funzione f è considert in un intervllo, tutte le primitive di f sono uguli meno di un costnte dditiv, cioè, dt F primitiv di f, f(x) dx = F (x) + C C R. Se l funzione F è un primitiv dell funzione f, llor vle F = f = f(x) dx = F (b) F (). In questo Cpitolo ci ponimo il problem di determinre esplicitmente primitive F di un funzione dt f, per opportune clssi di funzioni. Cos si intende qui con primitive esplicite? A prtire dlle operzioni elementri (ddizione, sottrzione, moltipliczione, divisione) e dlle funzioni trigonometriche ed esponenzili, formndo inverse e composte di queste funzioni, è possibile costruire un clsse molto mpi di funzioni che possimo descrivere come funzioni esplicite. Per qunto rigurd l operzione di derivzione, l derivt di un funzione esplicit è ess stess un funzione esplicit. Al contrrio, per l integrzione l situzione è differente: non è vero che tutti gli integrli delle funzioni esplicite si possno scrivere in termini di funzioni esplicite (d esempio, non è possibile esprimere in form esplicit, le primitive di e x2 ). Questo risultto può suonre sorprendente, m è un ftto dell vit. Prendere o lscire. Un prim clsse di funzioni che sono esplicitmente integrbili si determin prtire dl teorem fondmentle del clcolo, che, come noto, fferm F (x) = f(x) f(x) dx = F (x) + costnte. 25
31 26 2. ZOOLOGIA DELL INTEGRAZIONE In prticolre, quest proprietà indic che d ogni regol di derivzione corrisponde un regol di integrzione. Ad esempio D(x α+1 ) = (α + 1)x α x α dx = xα+1 + costnte α 1. α + 1 Allo stesso modo si ottengono ltre formule elementri: sin x dx = cos x + C, cos x dx = sin x + C, dx e x dx = e x + C, = ln x + C, x dx = rctn x + C, x dx = x 1 + x2 ln + C, dx dx = tn x + C, = cot x + C, cos 2 x dx 1 x 2 = rcsin x + C, sinh x dx = cosh x + C sin 2 x dx = rccos x + C, 1 x 2 cosh x dx = sinh x + C. Inoltre, grzie ll linerità dell integrle, nche combinzioni lineri di funzioni di cui si conosce l primitiv, possono essere integrte esplicitmente. Ad esempio, (1 + 2x + 3e x ) dx = 1 dx + 2 x dx + 3 e x dx = x + x 2 + 3e x + C. Trmite queste formule è possibile clcolre il vlore di certi integrli definiti, senz bisogno di pssre per le pprossimzioni con somme integrli per eccesso e per difetto. Pssimo or sviluppre i due metodi principli d ffincre lle formule di integrzione elementri: l integrzione per sostituzione e l integrzione per prti. Entrmbi, in sostnz, discendono d formule di derivzione: il primo discende dll derivzione di funzione compost, il secondo dll derivzione dell funzione prodotto. 1. Metodo di sostituzione Il metodo di sostituzione consiste nell introduzione di un nuov vribile, cioè, morlmente, nel cmbire punto di vist e osservre lo stesso oggetto d un ltr posizione. L formul di derivzione di funzione compost ssicur che ( (14) F (φ(u))) = F (φ(u))φ (u). Tle formul, lett in termini di integrzione, diviene (15) F (φ(x))φ (x) dx = F (φ(x)) + costnte
32 Ad esempio, 1. METODO DI SOSTITUZIONE 27 2x cos(x 2 ) dx = sin(x 2 ) + costnte, dove F (s) = sin s e φ(x) = x 2. Vedimo un ltro esempio. Clcolimo ln x x dx. Dto che D(ln x) = 1/x, qui F (s) = s e φ(x) = ln x. Quindi ln x x dx = ln x(ln x) dx = 1 2 (ln x)2 + costnte. M come individure un decomposizione dell funzione integrnd come in (15)? Occorre esercizio ed esperienz (nche un cert dose di intuizione non gust!). Vedimo l formul di sostituzione per integrli definiti: integrimo l formul (14) nell intervllo [α, β], F (φ(β)) F (φ(α)) = Ponendo = φ(α) e b = φ(β), Quindi ottenimo l formul β β α (F (φ(u)) du = F (φ(β)) F (φ(α)) = F (b) F () = α F (φ(u))φ (u) du = che, chimndo f = F, può essere riscritt come (16) β α f(φ(u))φ (u) du = f(x) dx β α F (φ(u))φ (u) du. F (x) dx, con F (x) dx. { = φ(α) b = φ(β) Quest formul esprime come si trsform l espressione dell integrle cmbindo l vribile di integrzione. Se, per clcolre f(x) dx, decidimo di porre x = φ(u), dobbimo sostituire formlmente dx con φ (u) du e cmbire gli estremi comptibilmente con l formul che colleg x con u, cioè x = φ(u). Ad esempio, per clcolre 1 0 e x dx, 1 + e2x ponimo x = ln u. Dto che φ(u) = ln u, dobbimo sostituire dx con 1 u du: 1 0 e x dx = 1 + e2x β α u 1 + u 2 1 u du.
33 28 2. ZOOLOGIA DELL INTEGRAZIONE Rimngono d clcolre α e β che sono soluzione di 0 = φ(α) = ln α e 1 = φ(β) = ln β. Invertendo l funzione φ ottenimo α = φ 1 (0) = e 0 = 1, β = φ 1 (1) = e 1 = e. In definitiv 1 e x e u 1 e dx = e2x u 2 u du = du u = rctn e π 2 4. Nel cso degli integrli indefiniti l formul di sostituzione prende l form (qui F è un primitiv di f, F = f) (17) f(φ(u))φ (u) du = f(x) dx = F (x) + C = F (φ(u)) + C Anche in questo cso si può usre, come regol mnemonic, l relzione x = φ(u) φ (u) du = dx. L uso delle virgolette st ricordre che non è stto dto senso i simboli du e dx e che l regol suscritt è solo formle 1. Nell uso di quest formul bison ricordrsi di tornre ll fine ll vribile u, sostituendo x con φ(u). Esempio 1.1. Si φ un funzione derivbile. Clcolimo φ (u) φ(u) du. Ponendo x = φ(u), si h dx = φ (u) du, quindi φ (u) dx φ(u) du = = ln x + C = ln φ(u) + C. x Ad esempio, dx x ln x = ln ln x + C, sin x tn x dx = dx = ln cos x + C. cos x Esempio 1.2. Allo stesso modo, ponendo x = φ(u) (e quindi dx = φ (u) du), [φ(u)] α φ (u) du = x α dx = xα+1 α C = 1 α + 1 [φ(u)]α+1 + C α 1. Ad esempio, sin k x cos x dx = 1 k + 1 sink+1 x + C. 1 Se si pens ll origine del simbolo dx negli integrli come limite dell lunghezz x di un dt prtizione, l sostituzione d dx du, con il reltivo termine moltiplictivo φ (u), indic che, nel cmbio di vribile, bisogn cmbire opportunmente nche l lunghezz dell intervllo dell prtizione, coerentemente con l trsformzione utilizzt.
34 1. METODO DI SOSTITUZIONE 29 L formul di sostituzione è sempre conveniente nel cso di funzioni composte di cui l ultim si linere: ponendo x = u + b f(u + b) du = 1 f(x) dx. Anche se l integrle di destr non fosse risolvibile, l espressione secondo membro è comunque più semplice. Spesso ci si trov lvorre con espressioni dell form h(φ(u)) du, dove l integrndo è un funzione compost h(φ(u)), senz il fttore moltiplictivo φ (u). E possibile pplicre l sostituzione x = φ(u)? Se l funzione φ è invertibile, con invers u = ψ(x), è possibile sostituire du l oggetto ψ (x) dx, ottenendo h(φ(u)) du = h(x) ψ (x) dx. Per giustificre in modo rigoroso quest formul, chimimo f(u) := h(φ(u)) h(φ(u)) du = f(u) du = f(ψ(x))ψ (x) dx = h(x)ψ (x) dx. Nel cso di integrli definiti occorre cmbire gli estremi di integrzione coerentemente con l nuov vribile introdott: h(φ(u)) du = φ(b) φ() Esempio 1.3. Clcolimo l integrle indefinito (1 + e x ) 2 dx. h(x) ψ (x) dx. Ponendo t = 1 + e x, si h x = ln(t 1) e dx = 1 dt e, di conseguenz, t 1 (1 + e x ) 2 t 2 dx = t 1 dt. Dto che t2 = t , t 1 t 1 ( (1 + e x ) 2 dx = t ) dt = 1 t 1 2 t2 + t + ln t 1 + C = 1 2 (1 + ex ) e x + x + C = 1 2 e2x + 2e x + x + C. Si srebbe nche potuto procedere utilizzndo l decomposzione (1+e x ) 2 = 1+2e x +e 2x e integrndo prtire dlle formule elementri.
35 30 2. ZOOLOGIA DELL INTEGRAZIONE Esempio 1.4. Clcolimo l integrle definito Dto che cos(2x) = 2 cos 2 x 1 π/2 cos 2 x dx = Ponimo nell integrle t = 2x: π/2 0 π/2 0 π/2 0 cos(2x) dx = 1 2 Quindi il vlore dell integrle è π/4. cos 2 x dx. ( ) cos(2x) + 1 dx = 1 2 π 0 π/2 cos t dt = 1 2 sin t π = 0. 0 cos(2x) dx + π 4. Esercizio 1.5. Fissto > 0, clcolre gli integrli (indefinito e definito) x 2 x 2 dx e x 2 x 2 dx. Esempio 1.6. Dti A, B, C R tli che := B 2 4AC < 0, come risolvere dx (18)? Ax 2 + Bx + C L condizione < 0, implic che il polinomio è irriducibile (non h rdici reli). In quest clsse di integrli rientr un integrle che conoscimo: dx (19) = rctn x + C. x L integrle (18) può essere risolto con un sostituzione opportun che lo riconduce (19). Invece di dre direttmente l soluzione, provimo ricostruire psso psso come poss essere ottenut. 1 Il grfico dell funzione è qulittivmente simile quello dell funzione 1 x 2 +1 Ax 2 +Bx+C (Fig.1). È possibile con trslzioni e diltzioni trsformre il grfico dell prim y 0 0 4A/! 1 0 -B/2A x Figur 1. Il grfico dell funzione 1 Ax 2 +Bx+C (e, trtteggito, quello di 1 x 2 +1 ). funzione in quello dell second? Bisogn prim di tutto correggere due difetti
36 2. INTEGRAZIONE PER PARTI 31 1 evidenti di f(x) = : il vlore mssimo è f( B/2A) = 4A/ e non 1, l sse Ax 2 +Bx+C di simmetri è x = B/2A e non x = 0. Per il primo problem, bst utilizzre l linerità dell integrle: l funzione f può essere riscritt come quindi f(x) = 4A g(x) dove g(x) := 1 4A 2 dx Ax 2 + Bx + C = 4A x2 + 4AB dx x + 4AC 4A 2 x2 + 4AB x + 4AC dove l funzione ll interno dell ultimo integrle vle 1 in x = B/2A. Per fre in modo che l sse di simmetri si in x = 0, bisogn trslre il grfico. Questo corrisponde d introdurre un nuov vribile u, legt d x dll relzione Con quest scelt, si h 4A2 x2 + 4AB dx Ax 2 + Bx + C = 4A u = x + B 2A. x + 4AC = 4A2 du 4A 2 u2 + 1 = 4A u2 + 1, quindi du ( ) , 2A u 1/2 Rest d modificre ncor un volt l vribile u, ttrverso l posizione v := 2A u, 1/2 2A che consiste nel diltre/comprimere (dipende dll grndezz di ) l vribile u 1/2 per un fttore opportuno. Così fcendo si rriv ll conclusione: dx Ax 2 + Bx + C = 4A du ( ) 2 = 2 dv + 1 1/2 v = 2 rctn v+costnte. 1/2 2A u 1/2 Per vere l espressione dell primitiv in x (e non in v), bst seguire ritroso le definizioni di v e di u. In definitiv: (qui = 4AC B 2 ) ( ) dx Ax 2 + Bx + C = 2 2Ax + B rctn + costnte. 2. Integrzione per prti Il metodo di integrzione per prti emerge dll formul di derivzione del prodotto: (fg) = f g + fg. Integrndo tle formul, si ottiene f(x)g(x) = g(x) f (x) dx + g (x) f(x) dx,
37 32 2. ZOOLOGIA DELL INTEGRAZIONE d cui l formul di integrzione per prti (20) g (x) f(x) dx = f(x)g(x) g(x) f (x) dx. Quest formul è not come integrzione per prti. Il metodo è vntggioso se per il termine g f si conosce un metodo di integrzione. Per gli integrli definiti, l formul (20) diviene (21) g (x) f(x) dx = f(b)g(b) f()g() g(x) f (x) dx. Esempio 2.1. Ecco un primo esempio di ppliczione dell formul (20) xe x dx = x(e x ) dx = xe x (x) e x dx = xe x e x dx = (x 1)e x + C. Anche nel cso dell funzione x 2 e x si può procedere in modo nlogo, pplicndo due volte l integrzione per prti, [ ] x 2 e x dx = x 2 (e x ) dx = x 2 e x 2 x e x dx = x 2 e x 2 xe x e x dx = x 2 e x 2 [(x 1)e x + C] = (x 2 2x + 2)e x + C. È possibile risolvere llo stesso modo un qulsisi integrle del tipo p(x)e x dx p polinomio di grdo n, inftti bst iterre n volte l uso dell formul di integrzione per prti p(x)e x dx = p(x)e x p (x)e x dx = [ p(x) p (x) ] e x + p (x)e x dx = = [ p(x) p (x) + + ( 1) n p (n) (x) ] e x + C Osservndo che e αx = α( ) 1 e αx, si possono determinre le primitive nche di funzioni del tipo p(x)e αx con p polinomio. Ad esempio, x 2 e 3x dx = 1 3 x2 e 3x 2 xe 3x dx 3 = 1 3 x2 e 3x 2 ( ) ( 1 xe 3x e 3x dx = 9 3 x2 2 9 x + 2 ) e 3x + C. 27 Esempio 2.2. Anche funzioni del tipo prodotto di polinomio e di sin x o cos x possono essere risolte integrndo per prti. I csi più semplici sono x sin x dx = x( cos x) dx = x cos x + cos x dx = sin x x cos x + C; x cos x dx = x(sin x) dx = x sin x sin x dx = cos x + x sin x + C.
38 2. INTEGRAZIONE PER PARTI 33 Iterndo il procedimento un certo numero di volte, si clcolno gli integrli p(x) sin(x) dx, p(x) cos(x) dx ( R). Esempio 2.3. Proponimoci di determinre tutte le primitive di x 2 sin(2x). Applichimo l integrzione per prti: x 2 sin(2x) dx = x ( 2 1 ) 2 cos(2x) dx = 1 2 x2 cos(2x) + x cos(2x) dx = 1 2 x2 cos(2x) + 1 x (sin(2x)) dx = x2 cos(2x) x sin(2x) 1 sin(2x) dx 2 = 1 2 x2 cos(2x) x sin(2x) + 1 cos(2x) + C. 4 Esempio 2.4. Sempre trmite l integrzione per prti, si risolvono nche p(x) ln x dx p polinomio. Clcolimo l integrle di ln x: ln x dx = 1 ln x dx = (x) ln x dx = x ln x = x ln x x 1 dx = x ln x x + C. x Anlogmente, ( ) 1 x ln x dx = 2 x2 ln x dx = 1 2 x2 ln x 1 2 In generle, dto k N, x k ln x dx = xk+1 k + 1 ln x 1 k + 1 Esercizio 2.5. Clcolre gli integrle indefiniti rctn x dx, x rctn x dx. x(ln x) dx x dx = 1 2 x2 ln x 1 4 x2 + C. ( x k dx = xk+1 ln x 1 ) + C. k + 1 k + 1 Esempio 2.6. Qui usimo l integrzione per prti in un modo leggermente diverso: iterndo l ppliczione di (20) tornimo ll integrle originle, ottenendo in questo modo un equzione per l primitiv. In questo modo risolvimo integrli dell form e x sin(bx) dx, e x cos(bx) dx.
39 34 2. ZOOLOGIA DELL INTEGRAZIONE Ad esempio, e 2x sin(3x) dx = 1 e 2x ( cos(3x)) dx = cos(3x)e2x + 2 e 2x cos(3x) dx 3 = 1 3 cos(3x)e2x + 2 e 2x (sin(3x)) dx 9 = 1 9 (2 sin(3x) 3 cos(3x)) e2x 4 e 2x sin(3x) dx. 9 Gurdndo il primo e l ultimo termine, si h e 2x sin(3x) dx = 1 ( ) 2 sin(3x) 3 cos(3x) e 2x e 2x sin(3x) dx, d cui, esplicitndo rispetto ll integrle richiesto, e 2x sin(3x) dx = 1 13( 2 sin(3x) 3 cos(3x) ) e 2x + C. In generle si ottengono le formule (verificre!) e x 1 sin(bx) dx = 2 + b ( sin(bx) b cos(bx)) 2 ex + C, e x 1 cos(bx) dx = 2 + b ( cos(bx) b sin(bx)) 2 ex + C. Formule ricorsive. Alcune fmiglie di integrli (dipendenti d un prmetro discreto n N), possono essere risolte in modo itertivo, cioè si risolve l integrle per n = 1, e poi si mostr come l integrle l psso n esimo si poss ricondurre l clcolo dell integrle (n 1) esimo. Vedimo un pio di esempi. Clcolimo I n = sin 2n x dx, n N. Allo stesso modo si può clcolre cos 2n x dx. Clcolimo I 1 : sin 2 x dx = sin x sin x dx = sin x ( cos x) dx = sin x cos x + cos 2 x dx = sin x cos x + (1 sin 2 x) dx = x sin x cos x sin 2 x dx. Abbimo ottenuto un relzione del tipo I 1 = x sin x cos x I 1, quindi I 1 = sin 2 x dx = 1 (x sin x cos x) + C. 2
40 3. INTEGRAZIONE DI FUNZIONI RAZIONALI 35 Per n N, I n+1 = sin 2n+1 x sin x dx = sin 2n+1 x ( cos x) dx = sin 2n+1 x cos x + (2n + 1) sin 2n x cos 2 x dx = sin 2n+1 x cos x + (2n + 1) sin 2n x(1 sin 2 x) dx = sin 2n+1 x cos x + (2n + 1)I n (2n + 1)I n+1. Quindi I n+1 = sin 2n+1 x cos x + (2n + 1)I n (2n + 1)I n+1, d cui si deduce I n+1 = 1 { (2n + 1)In sin 2n+1 x cos x } + C. 2n Integrzione di funzioni rzionli Affrontimo or il problem di integrre funzioni rzionli: P (x) Q(x) dx P, Q polinomi. Le primitive di un qulsisi funzione rzionle in termini di funzioni esplicite sono note, m non è in queste Note che troverete i dettgli dell questione. In concreto è possibile completre il clcolo ptto di sper fttorizzre il polinomio denomintore Q nel prodotto di termini irrudicibili, cioè polinomi di primo grdo (con molteplicità opportun) e polinomi di secondo grdo irriducibili (con molteplicità opportun). In questo Prgrfo vedremo come si integrino funzioni rzionli nel cso in cui il polinomio Q si di grdo l più due, o si fttorizzbile in termini di polinomi di grdo 1, cioè si riscrivibile nell form Q(x) = (x x 1 ) k1 (x x n ) kn, x 1,..., x n R, 0, k 1,..., k n N. Denomintore Q di grdo 1. Si Q(x) = (x x 0 ) con, x 0 R e 0. Se P è un polinomio di grdo p 1, trmite l lgoritmo di divisione dei polinomi, si determinno un polinomio P 1 di grdo p 1 e un costnte r R tli che P (x) Q(x) = P r 1(x) + (x x 0 ). Quindi l integrle si può decomporre nell somm di due integrli P (x) Q(x) dx = P 1 (x) dx + r dx. x x 0 Il polinomio P 1 è integrbile esplicitmente, grzie ll formul x k dx = xk+1 k C.
41 36 2. ZOOLOGIA DELL INTEGRAZIONE Anche l ltro integrle è risolubile esplicitmente: r dx = r (x x0 ) dx = r x x 0 x x 0 ln x x 0 + C. Vedimo un esempio. Clcolimo Dto che si h x x 2 dx = x x 2 dx. x x 2 = x4 + 2x 3 + 4x 2 + 8x x 2, ( x 4 + 2x 3 + 4x 2 + 8x x 2 ) dx = 1 5 x x x3 + 4x x + 33 ln x 2 + C. Denomintore Q di grdo 2. Supponimo che Q si un polinomio di grdo 2. In questo cso Q è scrivibile nell form Q(x) = (x 2 + 2bx + c), b, c R, 0. Se il polinomio numertore P h grdo p 2, llor è possibile pplicre l lgoritmo di divisione di polinomi e riscrivere l funzione rzionle come somm (22) P (x) Q(x) = P 1(x) + R(x) Q(x), dove P 1 è un polinomio di grdo p 2 e R è un polinomio di grdo minore o ugule 1. L integrle dell funzione rzionle è l somm di due integrli P (x) R(x) Q(x) dx = P 1 (x) dx + Q(x) dx. Il primo dei due integrli è risolubile esplicitmente per vi elementre. Considerimo il secondo. Supponimo che il resto R si di grdo 1 e scrivimolo nell form R(x) = α(x + β) con α 0 e β R. Si trtt di clcolre α(x + β) (x 2 + 2bx + c) dx = α x + β x 2 + 2bx + c dx. Come primo psso, costruimo numertore l derivt del denomintore. Moltiplichimo e dividimo per due e, successivmente, sommimo e sottrimo 2b α(x + β) (x 2 + 2bx + c) dx = α 2x + 2β 2 x 2 + 2bx + c dx = α (2x + 2b) + 2(β b) dx =. 2 x 2 + 2bx + c
42 3. INTEGRAZIONE DI FUNZIONI RAZIONALI 37 L integrle finle può essere riscritto come somm dei due integrli di cui il primo è dell form φ dx; quindi φ = α (x 2 + 2bx + c) 2α(β b) dx dx + 2 x 2 + 2bx + c 2 x 2 + 2bx + c = α 2 ln 2α(β b) dx x2 + 2bx + c + 2 x 2 + 2bx + c. Rimne quindi d risolvere l integrle (23) dx x 2 + 2bx + c. Nel cso in cui R in (22) si di grdo 0 ci si riconduce direttmente quest situzione. L risoluzione dell integrle (23) vri second di qunte rdici reli bbi il denomintore, cioè second che si b 2 > c, b 2 = c o b 2 < c. Trttimo i tre csi seprtemente. Ci ricondurremo (sostnzilmente) i seguenti integrli elementri dx Cso I : b 2 > c = ln x + C, x dx Cso II : b 2 = c x = 1 2 x + C, Cso I: b 2 > c. Cso III : b 2 < c dx = rctn x + C. 1 + x2 In questo cso il denomintore h due rdici reli x 2 + 2bx + c = 0 x = b ± b 2 c. Indicndo le rdici con x 1 e x 2, il polinomio si fttorizz: x 2 + 2bx + c = (x x 1 )(x x 2 ). Decomponimo l funzione integrnd nell form 1 x 2 + 2bx + c = A 1 + A 2, x x 1 x x 2 dove A 1, A 2 R sono due costnti d determinre. L somm delle due frzioni secondo membro è ugule (A 1 + A 2 )x (A 1 x 2 + A 2 x 1 ), x 2 + 2bx + c e quindi A 1 e A 2 devono essere tli che (A 1 + A 2 )x (A 1 x 2 + A 2 x 1 ) = 1. Dto che due polinomi coincidono se e solo se coincidono i loro coefficienti, le costnti A 1, A 2 sono le soluzioni del sistem linere (il cui determinnte è x 1 x 2 che, nel cso b 2 > c, è diverso d zero) A 1 + A 2 = 0, A 1 x 2 + A 2 x 1 = 1.
43 38 2. ZOOLOGIA DELL INTEGRAZIONE Individuti i vlori di A 1 e A 2, l integrle è risolto: dx x 2 + 2bx + c = A dx dx 1 + A 2 x x 1 x x 2 = A 1 ln x x 1 + A 2 ln x x 2 + C. Esercizio 3.1. Clcolre Cso II: b 2 = c. x 3 x 2 x 2 dx. In quest situzione, si trtt di risolvere dx x 2 + 2bx + b 2. Questo integrle è immedito, inftti dx x 2 + 2bx + b = 2 Esercizio 3.2. Clcolre x(x + 3) (x 1) 2 dx. dx (x + b) = 1 2 x + b + C. Cso III: b 2 < c. Questo cso è già stto considerto nell Esempio 1.6. Ritrovimo qui l stess soluzione senz fre ricorso l grfico dell funzione integrnd. Dto che il polinomio x 2 + 2bx + c è irriducibile, l obiettivo è di ricondursi, con un opportuno cmbimento di vribili, ll integrle elementre dx = rctn x + C. 1 + x2 Chimimo ν := 1 c b 2 > 0 e riscrivimo in mnier opportun il denomintore x 2 + 2bx + c = x 2 + 2bx + b 2 + (c b 2 ) = (x + b) ν 2 = 1 ν 2 { [ν(x + b)] }. Ponendo t = ν(x + b), dx x 2 + 2bx + c = ν dt 1 + t 2 = ν rctn t + C = ν rctn( ν(x + b) ) + C. Dll definizione di ν si deduce che ( ) dx x 2 + 2bx + c = 1 x + b rctn + C. c b 2 c b 2 Esercizio 3.3. Clcolre 3x 2 x 2 2x + 2 dx.
44 3. INTEGRAZIONE DI FUNZIONI RAZIONALI 39 Denomintore Q con sole rdici reli. Considerimo prim di tutto un cso semplice: il polinomio Q h rdici reli distinte, cioè Q(x) = (x x 1 ) (x x n ) x 1,..., x n R con x i x j se i j. Se p n, il primo pssggio è sempre lo stesso: si us l lgoritmo dell divisione di polinomi per riscrivere l funzione rzionle nell form P (x) Q(x) = P 1(x) + R(x) Q(x). dove P 1 è un polinomio di grdo p n, e R è un polinomio di grdo minore di n. L integrle si decompone in P (x) R(x) Q(x) dx = P 1 (x) dx + Q(x) dx. A questo punto sfruttimo l fttorizzzione di Q per riscrivere l funzione rzionle R/Q come somm di funzioni rzionli più semplici. Cerchimo n costnti A 1,..., A n tli che R(x) (x x 1 ) (x x n ) = 1 ( A1 + + x x 1 x x n Per determinre le costnti A 1,..., A n si può imporre l uguglinz dei due membri ottenendo un sistem linere. Equivlentemente si può moltiplicre per x x 1 entrmbi i membri R(x) (x x 2 ) (x x n ) = 1 A n ). { A 1 + A 2(x x 1 ) + + A } n(x x 1 ). x x 2 x x n e successivmente porre x = x 1, ottenendo il vlore di A 1 A 1 = R(x 1 ) (x 1 x 2 ) (x 1 x n ) Anlogmente per A 2,..., A n. Determinte le costnti A i, si clcol l integrle: R(x) Q(x) dx = 1 ( A1 + + A ) n dx x x 1 x x n = 1 (A 1 ln x x A n ln x x n ) + C. Per digerire l tecnic, clcolimo dx (x + 1)(x + 2)(x + 3). Dto che il grdo del numertore è minore del grdo del denomintore, non occorre pplicre l lgoritmo di divisione di polinomi. Pssimo subito ll decomposizione:
45 40 2. ZOOLOGIA DELL INTEGRAZIONE cerchimo A 1, A 2, A 3 R tli che 1 (x + 1)(x + 2)(x + 3) = A 1 x A 2 x A 3 x + 3. Moltiplichimo per x + 1 e clcolimo in x = 1 Anlogmente Quindi 1 (x + 2)(x + 3) = A 1 + A 2(x + 1) + A 3(x + 1) x + 2 x (x + 1)(x + 3) = A 1(x + 2) + A 2 + A 3(x + 2) x + 1 x + 3 = A 1 = 1 2. = A 2 = 1. 1 (x + 1)(x + 2) = A 1(x + 3) + A 2(x + 3) + A 3 = A 3 = 1 x + 1 x dx (x + 1)(x + 2)(x + 3) = 1 ( 1 2 x x ) dx x + 3 = 1 2 ln (x + 1)(x + 3) (x + 2) 2 + C. Pssimo l cso generle: il denomintore Q si decompone come Q(x) = (x x 1 ) k1 (x x n ) kn, x 1,..., x n R, k 1,..., k n N. Anche in questo cso, dopo ver pplicto (se necessrio) l lgoritmo di divisione di polinomi, si deve risolvere un integrle dell form R(x) Q(x) dx, dove R è un polinomio di grdo strettmente minore di quello di Q. In questo cso si cerc, nlogmente qunto ftto nel cso di Q di secondo grdo con due rdici coincidenti, un decomposizione dell form R(x) (x x 1 ) k 1 (x xn ) = 1 { A 1 1 A kn x x 1 (x x 1 ) + + A k1 1 2 (x x 1 ) + k 1 A dx (x x) k = + A1 n x x n + A 2 n (x x n ) + + A kn n 2 (x x n ) kn dove le costnti A j i R con i = 1,..., n e j = 1,..., k i sono d determinre. Un volt determinte queste costnti, l integrle è risolto dto che A ln x x + C k = 1, A k C k > 1. (x x) k 1 },
46 3. INTEGRAZIONE DI FUNZIONI RAZIONALI 41 Esempio 3.4. Ad esempio, considerimo l integrle dx x 2 (x + 1) 2. In questo cso cerchimo le costnti A, B, C, D R tli che 1 x 2 (x + 1) 2 = A x + B x 2 + Imponendo l uguglinz, si ottengono Perciò C x D (x + 1) 2. A = 2, B = 1, C = 2, D = 1. dx x 2 (x + 1) = 2 ln x x 1 x 1 x C. Altre clssi di funzioni. Vedimo qulche ltr clsse di funzioni che si possono ricondurre, trmite un cmbio di vribile, ll integrle di funzioni rzionli. Esempio 3.5. Supponimo di voler clcolre R(sin x, cos x) dx dove R è un funzione rzionle dei suoi rgomenti. Dlle relzioni (24) sin x = 2t e cos x = 1 ( t2 x ) dove t = tn, 1 + t t 2 2 ponendo t = tn(x/2) o, equivlentemente, x = 2 rctn t, dto che dx = 2/(1 + t 2 )dt, l integrle si trsform nell integrle di un funzione rzionle ( 2t R 1 + t, 1 ) t t t dt, 2 Ad esempio, dx 1 + t 2 sin x = 2 dt 2t 1 + t dt = = ln t + C = ln tn(x/2) + C. 2 t ( dx cos x = 2 dt 1 1 t = t + 1 ) dt = ln 1 + tn(x/2) 1 t 1 tn(x/2) + C. Non sempre l sostituzione (24) è conveniente. Ad esempio, considerimo sin x cos 100 x dx. Trmite (24), l integrle si trsform in sin x 4t(1 + t 2 cos 100 x dx = ) 98 dt, (1 t 2 ) 100
47 42 2. ZOOLOGIA DELL INTEGRAZIONE con un polinomio di grdo duecento denomintore! Che fre? Srebbe invece stto molto più semplice porre s = cos x, d cui sin x ds cos 100 x dx = s = s + C = cos 99 x + C. Esempio 3.6. Abbimo un problem: clcolre l re dell regione di pino { } x 2 Ω = (x, y) R : + y2 2 b 1, b > 0. 2 L re Ω di Ω è pri l vlore dell integrle definito Ω = 4b 1 (x2 / 2 ) dx. Introducimo l vribile t definit d x = cos t, d cui dx = sin t dt: π/2 Ω = 4b 1 cos2 t sin t dt = 4b 0 0 π/2 0 sin 2 t dt = 2b [t sin t cos t] π/2 0 = πb. Quindi l re dell regione delimitt dll ellissi di semissi e b è πb. Allo stesso modo è possibile integrre funzioni del tipo R(x, 1 (x 2 / 2 )) con R funzione rzionle dei suoi rgomenti. Inftti R(x, 1 (x 2 / 2 )) dx = R( cos t, sin t) sin t dt. dove x = cos t, e il secondo membro è un funzione rzionle in sin t e cos t.
48 CAPITOLO 3 I numeri complessi Fino d desso bbimo studito funzioni reli di vribile rele. Vri problemi mtemtici suggeriscono un estensione dell insieme dei numeri reli, prticolrmente utile nche per molte ppliczioni. Quest estensione dei numeri reli port d un nuovo concetto di numero: il numero complesso. 1. Nscit dei numeri complessi e loro infnzi Il problem di prtenz è il seguente: in R esistono polinomi di grdo mggiore di 1 che non hnno rdici (reli), d esempio, x Si potrebbe rimnere lì gurdre, rispondersi che è un ftto dell vit, e pssre d un ltro problem. Per chi invece desider cercre di ndre oltre, l ide plusibile è di costruire un nuovo insieme che estend l insieme dei numeri reli e che conteng nche il numero i, unità immginri, soluzione dell equzione x = 0. Dedichimoci ll costruzione di questo nuovo insieme, che indichimo con il simbolo C. Definizione 1.1. Si definisce insieme dei numeri complessi C l insieme C := {z = + ib :, b R} con l regol di clcolo seguente: i numeri complessi si sommno, sottrggono, moltiplicno, dividono tenendo conto dell proprietà i 2 = 1. L regol di clcolo di somm e moltipliczione per numeri complessi v lett, in concreto, come segue: dti z 1 = + ib e z 2 = c + id, llor z 1 + z 2 = ( + ib) + (c + id) = ( + c) + i(b + d), z 1 z 2 = ( + ib)(c + id) = c + i(d + bc) + i 2 bd = (c bd) + i(d + bc). Tutte le proprietà di somm e moltipliczione (commuttiv, ssocitiv, distributiv) vlgono nche in C. Piccolo glossrio per i numeri complessi z = + ib: numero complesso R = {z C : b = 0}: numeri reli i R = {z C : = 0}: immginri puri 43
49 44 3. I NUMERI COMPLESSI i: unità immginri Re z = : prte rele di z Im z = b: prte immginri di z L insieme C può essere rppresentto geometricmente come un pino C = {(, b) :, b R} = R 2. L struttur di C è comunque più ricc di quell del pino dto che in C è definit l operzione di prodotto. I numeri complessi si devono poter rppresentre sempre nell form +ib. Nel cso del rpporto di due numeri, può non essere evidente che questo si possibile. Vedimo un esempio prticolre. Supponimo di voler scrivere nell form + ib con, b R il numero complesso z = 1+i. Moltiplicndo e dividendo per 1 + i, e rgionndo con le 1 i stesse regole lgebriche note su R insieme ll relzione i 2 = 1, si ottiene 1 + i 1 i = 1 + i 1 i 1 + i 1 + i = (1 + i) 2 (1 i)(1 + i) = 1 + 2i + i2 1 i 2 = i. In generle, per scrivere un rpporto di numeri complessi nell form +ib, procedimo ll stess mnier. Sino, b, c, d R con (c, d) (0, 0), llor + ib c + id = + ib c + id c id c id = (c + bd) + i(bc d) c 2 + d 2. In prticolre l inverso del numero complesso c + id si scrive come 1 c + id = 1 c + id c id c id = c id c 2 + d = c 2 c 2 + d i d 2 c 2 + d, 2 che mostr che ogni numero complesso z diverso d 0 è invertibile, cioè esiste un numero z 1 tle che z z 1 = z 1 z = 1. Dto c + id C, il numero complesso c id C, che si ottiene cmbindo di segno l prte immginri h un ruolo determinnte in quest costruzione ed è detto complesso coniugto. Il complesso coniugto di z si indic con z. Esercizio 1.2. Verificre l vlidità di: z 1 + z 2 = z 1 + z 2 z 1 z 2 = z 1 z 2 z 1 z 2 = z 1 z 2 z 1 z 2 = z 1 z 2. Rppresentzione polre. Un numero complesso z = x+iy si può rppresentre come un punto P di coordinte (x, y) nel pino crtesino e, in qunto tle, può essere inviduto nche dlle coordinte polri (r, θ): x = r cos θ, y = r sin θ. In questo cso r = x 2 + y 2 è l distnz del punto P = (x, y) dll origine O e θ
50 1. NASCITA DEI NUMERI COMPLESSI E LORO INFANZIA 45 r z O! Figur 1. Rppresentzione polre di un numero complesso. misur l ngolo tr il semisse positivo x e il segmento di estremi 0 e z. Il numero complesso z = x + iy si può, quindi, scrivere come (25) z = r(cos θ + i sin θ). L quntità r è il modulo di z; l ngolo θ si dice rgomento di z e si indic con rg z. Per vi dell periodicità delle funzioni sin e cos, l rgomento non è individuto univocmente. Si prl di rgomento principle se θ [0, 2π) e si indic con Arg z (Attenzione! c è chi prl di rgomento principle se θ ( π, π]). Il complesso coniugto z di z corrisponde l numero complesso di stesso modulo di z e rgomento θ. Trmite l rppresentzione polre è fcile clcolre il prodotto di numeri complessi: zz = r(cos θ + i sin θ) r (cos θ + i sin θ ) = rr [ (cos θ cos θ sin θ sin θ ) + i(cos θ sin θ + sin θ cos θ ) ] = rr [ cos(θ + θ ) + i sin(θ + θ ) ]. Quest formul permette di dre un interpretzione geometric del prodotto di due numeri complessi: il risultto è un numero complesso il cui modulo è pri l prodotto dei moduli e l rgomento è l somm degli rgomenti. Ad esempio, che succede moltiplicndo un generico numero complesso z per l unità immginri i? Dto che il modulo di i è 1 e il suo rgomento è π, il numero iz si trov ll stess distnz dll origine di 2 z e h rgomento umentto di π rispetto quello di z. In definitiv, il numero iz si 2 ottiene ruotndo il punto z in senso ntiorrio di un ngolo retto. Dll formul per il prodotto, segue l formul per l potenz n esim di z z n = [ r(cos θ + i sin θ) ] n = r n [ cos(nθ) + i sin(nθ) ]. Il modulo nei complessi. Il modulo del numero complesso + i b è il modulo del punto (, b) R 2, cioè modulo di z = + ib : z := 2 + b 2 Il modulo di un numero complesso è sempre un numero rele non negtivo e gode delle stesse proprietà di cui gode il modulo rele
51 46 3. I NUMERI COMPLESSI Proposizione 1.3. Il modulo complesso gode delle seguenti proprietà: (i) z 0 per ogni z C e z = 0 se e solo se z = 0; (ii) z 1 z 2 = z 1 z 2 per ogni z 1, z 2 C; (iii) diseguglinz tringolre: z 1 + z 2 z 1 + z 2 per ogni z 1, z 2 C. Dimostrzione. L prim proprietà è evidente (bst osservre che un somm di qudrti è null se e solo se sono nulli entrmbi gli ddendi). L second si verific direttmente, se z 1 = x 1 + iy 1 e z 2 = x 2 + iy 2, llor z 1 z 2 = (x 1 x 2 y 1 y 2 ) + i(x 1 y 2 + x 2 y 1 ) = (x 1 x 2 y 1 y 2 ) 2 + (x 1 y 2 x 2 y 1 ) 2 = x 2 1x y1y x 2 1y2 2 + x 2 2y1 2 z 1 z 2 = x y1 2 x y2 2 = (x y1)(x y2) 2 = x 2 1x x 2 1y2 2 + y1x y1y Rest d dimostrre l diseguglinz tringolre. Per l definizione di modulo, l diseguglinz tringolre si riscrive come (26) (x1 + x 2 ) 2 + (y 1 + y 2 ) 2 x y x y 2 2 Elevndo l qudrto (x 1 + x 2 ) 2 + (y 1 + y 2 ) 2 x y (x y1)(x y2) 2 + x y2 2 Sviluppndo i qudrti dei due binomi sinistr e semplificndo, x 1 x 2 + y 1 y 2 (x y1)(x y2) 2 Se il termine sinistr è negtivo, l disuguglinz è verifict; ltrimenti, elevndo di nuovo l qudrto, x 2 1x x 1 x 2 y 1 y 2 + y 2 1y 2 2 (x y 2 1)(x y 2 2) = x 2 1x x 2 1y y 2 1x y 2 1y 2 2. Semplificndo si ottiene 2x 1 x 2 y 1 y 2 x 2 1y y 2 1x 2 2, che si può riscrivere come che è sempre ver. (x 1 y 2 x 2 y 1 ) 2 = x 2 1y 2 2 2x 1 x 2 y 1 y 2 + y 2 1x 2 2 0, Esercizio 1.4. Verificre che, per ogni z C, vlgono (nell second z 0) z z = z 2 e z 1 = z z 2 Il ftto che in C si definito il modulo (con le stesse proprietà note in R) è di fondmentle importnz: con quest oggetto è possibile estendere i complessi tutto quello che si è visto nei reli prtire dll nozione di distnz. Nel pino complesso C, l distnz tr due numeri complessi z e z é dt d z z, dove rppresent il modulo complesso.
52 2. SUCCESSIONI, SERIE E CONTINUITÀ NEI COMPLESSI 47 Grzie ll presenz dell distnz, è possibile introdurre in C il concetto di intorno. Definizione 1.5. Dto z 0 C e r > 0, l intorno di z 0 di rggio r (indicto con I(z 0 ; r)) è l insieme dei punti z C che distno d z 0 meno di r: D qui limiti e tutto il resto... I(z 0 ; r) := {z C : z z 0 < r}. Il Teorem fondmentle dell lgebr. Fin qui bbimo scoperto che l insieme C gode delle stesse proprietà di R per qunto rigurd le operzioni di somm e prodotto e nche per qunto rigurd l struttur metric. M in C, c è qulcos di più... Teorem 1.6 (Teorem fondmentle dell lgebr). Ogni polinomio p(z) = z + + n z n coefficienti complessi i C di grdo n 1 mmette lmeno uno zero z C, cioè esiste z C tle che p(z ) = 0. Conseguenz di questo Teorem è che un polinomio di grdo n in C h esttmente n zeri (contti con l loro molteplicità). Ad esempio, il polinomio coefficienti reli p(z) = z 2 + 2bz + c b, c R, mmette in C sempre due zeri: se b 2 > c, gli zeri sono reli e sono b ± b 2 c, se b 2 = c c è un unico zero, z = b, con molteplicità due, nel cso b 2 < c, gli zeri sono due numeri complessi coniugti, b ± i c b Successioni, serie e continuità nei complessi Un volt definito l insieme dei numeri complessi C e introdott l nozione di modulo, si può ripetere buon prte dell teori sviluppt in R: successioni, serie, limiti, continuità, derivbilità... Ripercorrimo or, rpidmente, quello che bbimo visto nel cso rele, vedendo come si possibile definire gli stessi oggetti nel cso complesso. Successioni complesse. Un funzione che ssoci d ogni numero nturle n N un vlore z n C è un successione compless. Un successione compless z n può essere penst come un fmigli di vlori ordinti in bse l loro indice n: z 0, z 1, z 2,.... Definizione 2.1. Un successione compless z n è convergente l C se (27) ε > 0 N N tle che z n l < ε n > N. Con un cert dose di fntsi, si scrive lim z n = l. n + Un successione z n è infinitesim se converge 0 per n +.
53 48 3. I NUMERI COMPLESSI Il modulo che compre in (27) è il modulo del numero complesso z n l, e l essere infinitesim signific semplicemente che comunque si fissi un intorno dell origine 0 (misurto dl vlore di ε), tutti gli elementi dell successione trnne l più un numero finito (controllto dll indice N) si trovno nell intorno fissto. Dto che il modulo complesso di un numero rele coincide con l usule definizione di modulo di un numero rele, l Definizione 2.1 è, tutti gli effetti, un estensione di quell già vist per le successioni reli. Osservzione 2.2. A gurdr bene, l (27) dice che l successione di numeri reli non negtivi d n := z n l tende zero per n +. Quindi un successione compless z n converge d l se e solo se l distnz di z n d l è infinitesim per n +. Esempio 2.3. Un esempio interessnte di successione compless è z n = q n (q C). Dto che z n = q n = q n, il comportmento dell successione nel cso q < 1 è determinto d quello dell successione rele n = q n q < 1 lim n + qn = 0. Cos succede nel cso q 1? Ad esempio, come si comportno le successioni complesse z n = (2i) n e w n = i n per n? Ad un successione compless z n = x n + iy n sono ssocite in modo nturle le due successioni reli x n e y n dell su prte rele e immginri, rispettivmente. E possibile dimostrre che (28) z n = x n + iy n è convergente in C x n, y n sono convergenti in R. Quindi trttre successioni complesse può essere visto come trttre contempornemente un coppi di successioni reli. Esercizio 2.4. (i) Dimostrre che, per ogni z C, vle mx{ Re z, Im z } z Re z + Im z. (ii) Utilizzre (i) per dimostrre l equivlenz (28). L differenz sostnzile tr C e R st nel ftto che in C non è definito un ordinmento. Questo vuol dire che, per successioni complesse, non h senso prlre di monotoni, né di divergenz + e. Rest ben definito il concetto di divergenz in modulo: l successione z n diverge d (o diverge in modulo), se l successione di numeri reli positivi z n diverge +.
54 2. SUCCESSIONI, SERIE E CONTINUITÀ NEI COMPLESSI 49 Serie complesse. Allo stesso modo, si possono considerre serie termini complessi. Un serie compless n=0 è convergente se, in C, esiste il limite dell successione compless s n := n z k (successione delle somme przili). Tle limite è detto somm dell serie. Esempio 2.5. Come nel cso rele, è possibile considerre l serie geometric, definit dll successione z n = q n con q C. L successione delle somme przili è s n = 1 + q + q q n 1 + q n = 1 qn+1 1 q. Quindi se q < 1, l serie converge e l su somm è (29) q n = 1 q C tle che q < 1. 1 q n=0 Ottenimo quindi l stess formul già vist nel cso rele. Anche l nozione di convergenz ssolut si estende l cso complesso. z n Definizione 2.6. L serie compless z n è ssolutmente convergente se l serie rele z n è convergente. n=0 n=0 Dto che l serie z n è un serie termini reli, è possibile, lmeno in lcuni csi, n=0 ricondurre l convergenz di un serie compless quell di un serie rele, tornndo quindi in un mbito più fmilire. Inoltre, vle sempre l impliczione convergenz ssolut convergenz (semplice). Inftti, se l serie z n è convergente, llor lo sono nche le serie Re z n e n=0 n=0 Im z n. Dto che per serie reli l convergenz ssolut implic l convergenz n=0 semplice, l precedente ffermzione implic che le serie reli di termini generici Re z n e Im z n sono semplicemente convergenti. Per concludere, bst osservre che n n n n Re s n = Re z k = Re z k e Im s n = Im z k = Im z k, e ricordre (28)... k=0 k=0 k=0 k=0 k=0
55 50 3. I NUMERI COMPLESSI Per serie convergenti, vle l seguente versione dell disuguglinz tringolre z n z n. n=0 Esempio 2.7. Utilizzimo l convergenz ssolut per dimostrre l convergenz di un serie compless fondmentle: z n (30) z C. n! n=0 Vi ricord qulcos? L convergenz di quest serie discende direttmente dll convergenz dell corrispondente serie nei reli. Inftti, studimo l convergenz ssolut e considerimo l serie z n n! = z n n!. n=0 Quest serie è convergente (l su somm è e z ), quindi l serie (30) è convergente ssolutmente e, di conseguenz, semplicemente. Funzioni complesse. Un funzione compless di vribile compless è: n=0 n=0 f : I C C dove I è il sottoinsieme di C in cui è definit l funzione f. Se, per ζ C, esiste r > 0 tle che l intorno di ζ di rggio r, escluso il punto ζ stesso, è contenuto in I, llor si può dre senso ll nozione di limite di f per z ζ utilizzndo l stess definizione già dt nel cso rele. lim z ζ Definizione 2.8. L funzione f tende d l C per z ζ I, e si scrive f(z) = ζ, se ε > 0, δ > 0 tle che f(z) l < ε z I, 0 < z ζ < δ. Se (come fremo sempre nel seguito) si suppone che per ogni ζ I esist r > 0 tle che l intorno di ζ di rggio r si intermente contenuto in I, in ltre prole, se si suppone che ogni punto ζ I si interno d I, llor è possibile estendere l definizione di continuità l cso di funzioni complesse di vribile compless. Definizione 2.9. L funzione f è continu in ζ I se lim z ζ f(z) = f(ζ), cioè se ε > 0, δ > 0 tle che f(z) f(ζ) < ε z I, z ζ < δ. Né più né meno dell definizione di continuità già vist nel cso rele, con l unic ccortezz che i moduli che compiono qui sono moduli di numeri complessi.
56 2. SUCCESSIONI, SERIE E CONTINUITÀ NEI COMPLESSI 51 Ad esempio, l funzione f(z) = 2iz 1 è continu in ζ per ogni ζ C. Inftti f(z) f(ζ) = (2iz 1) (2iζ 1) = 2i z ζ = 2 z ζ, quindi f(z) f(ζ) < ε per tutti vlori z per cui z ζ < δ = ε/2. Esempio Considerimo un ltro esempio: f(z) = z, cioè l funzione che ssoci d un numero complesso z = x + iy, il suo complesso coniugto x iy. Fissto ζ = ξ + iη, se z ζ (x ξ) 2 + (y η) 2 < δ, f(z) f(ζ) = (x iy) (ξ iη) = (x ξ) i(y η) = (x ξ) 2 + (y η) 2 < δ. L condizione f(z) f(ζ) < ε è soddisftt per δ = ε. Quli funzioni complesse sono continue? Rgionimo come già ftto in R. Somm, prodotto di funzioni continue sono funzioni continue. Quindi, dl ftto che le costnti e l funzione z sono funzioni continue, possimo dedurre che tutti i polinomi in C sono funzioni continue. Anlogmente per le funzioni rzionli. Infine è possibile definire l derivt di funzioni complesse (qui è fondmentle l possibilità di dividere per un numero complesso). Definizione Un funzione f è derivbile in ζ I (o olomorf in ζ I) se esiste finito il limite (31) f f(z) f(ζ) (ζ) = lim. z ζ z ζ Ad esempio, per clcolre l derivt dell funzione f(z) = z n (n N), bst riscrivere il rpporto incrementle nell form f(z) f(ζ) z ζ = zn ζ n z ζ e pssre l limite per z ζ, ottenendo ( z n ) = nz n 1 Anche in quest mbito è ver l impliczione: Perché? Bst rgionre come in R: = z n 1 + z n 2 ζ + + ζ n 1, n N. derivbilità continuità. f(z) f(ζ) lim [f(z) f(ζ)] = lim (z ζ) = f (ζ) 0 = 0 z ζ z ζ z ζ Nel cso rele, prtire dll operzione di derivzione bbimo dedotto informzioni reltive ll monotonì delle funzioni. E possibile fre lo stesso nel cso delle funzioni
57 52 3. I NUMERI COMPLESSI complesse? Assolutmente no! Dto che in C non è definito l ordinmento, non h senso prlre di funzioni crescenti/decrescenti. Anlogmente concetti come mssimo, minimo, convessità e concvità sono privi di senso per funzioni f : I C C. 3. L esponenzile complesso Un funzione prticolrmente importnte è l funzione esponenzile. Dto che l serie considert nell Esempio 2.7 è convergente per ogni z C, è più che rgionevole utilizzrl per definire l funzione esponenzile nche nei complessi: (32) e z := n=0 z n n! z C. Come si può immginre/sperre, nche per (32), vle l proprietà (33) e w+z = e w e z w, z C. L dimostrzione si bs sull uso dei prodotti di serie. Niente dettgli in quest sede. L funzione esponenzile è continu? È derivbile? L uno e l ltro. Dimostrimo prim di tutto l continuità in 0. Dto che e 0 = 1, bisogn stimre e z 1 : e z z n+1 1 = (n + 1)! = z z n (n + 1)! z z n (n + 1)! z z n = z e z, n! n=0 n=0 quindi, dto che e z e per z 1, n=0 e z 1 e z z 1, d cui si deduce l continuità in ζ = 0. Se ζ C, llor lim z ζ ez = lim e ζ+(z ζ) = e ζ lim e z ζ = e ζ lim e h = e ζ, z ζ z ζ h 0 quindi l funzione è continu in ζ. Anche per l derivbilità, considerimo prim ζ = 0: si h e z 1 z n 1 = z (n + 1)! = z z n (n + 2)!, quindi, per z 1, e z 1 1 z z n=0 n=1 che mostr che l derivt di e z in 0 è 1. Per ζ qulsisi, e z e ζ lim z ζ z ζ = lim e ζ+(z ζ) e ζ z ζ z ζ z n (n + 2)! z n=0 n=0 z n n! = e ζ lim z ζ e z ζ 1 z ζ n=0 = z e z e z, = e ζ lim h 0 e h 1 h = e ζ.
58 3. L ESPONENZIALE COMPLESSO 53 Quindi ( e z ) = e z z C. Fissto λ C, per l funzione f(z) = e λz, vle d(e λz ) dz λz d(λz) = e dz = λe λz. Per derivre l funzione f, bst moltiplicre per λ l funzione stess: in ltri termini, f(z) = e λz verific l equzione (differenzile) f = λf. Lo stesso è vero per le funzioni A e λz con A C. Qule equzione è soddisftt dll derivt second di f(z) = Ae λz? Fcile: f (z) = d(a λ eλz ) dz = A λ d(eλz ) dz = A λ 2 e λz = λ 2 f, quindi f λ 2 f = 0. Il ftto che le funzioni del tipo Ae λz soddisfino le semplicissime equzioni f λf = 0 e f λ 2 f = 0 f di quest clsse il mttone fondmentle per l costruzione delle soluzioni di equzioni differenzili lineri coefficienti costnti, come vedremo tr un pio di fogli. Formul di Eulero. Prim di concludere, deducimo un formul estremmente interessnte. Se clcolimo l esponenzile e z in z = ix i R, ottenimo e ix i n x n =. n! Dto che n=0 i 0 = i 4 = = 1, i 1 = i 5 = = i, i 2 = i 6 = = 1, i 3 = i 7 = = i, possimo scrivere e ix = ( 1) n x2n (2n)! + i ( 1) n x 2n+1 (2n + 1)!. n=0 Dlle formule di Tylor per le funzioni cos x e sin x, segue l formul di Eulero: n=0 (34) e ix = cos x + i sin x x R. Chi è dunque l esponenzile del numero complesso z = x + iy? Un sintesi opportun di esponenzile rele e funzioni trigonometriche: pplicndo (34), e z = e x+iy = e x e iy = e x (cos y + i sin y) = e x cos y + i e x sin y. In prticolre Re e z = e x cos y e Im e z = e x sin y.
59 54 3. I NUMERI COMPLESSI L formul di Eulero, interessnte di per sé, è estremmente comod per rppresentre i numeri complessi qundo si usino le coordinte polri (ρ, θ): z = ρ (cos θ + i sin θ) = ρ e iθ Le formule per il prodotto e le potenze diventno, fcendo uso dell rppresentzione esponenzile, conseguenze immedite di (33). Ad esempio, z 1 z 2 = (ρ 1 e iθ 1 ) (ρ 2 e iθ 2 ) = ρ 1 ρ 2 e i(θ 1+θ 2 ). D (34) si deduce, in prticolre, che l esponenzile complesso non è un funzione iniettiv e quindi nemmeno invertibile. L definizione dell funzione logritmo nei numeri complessi richiede quindi un prticolre ttenzione. Qui non pprofondiremo l questione. Anzi, non l toccheremo proprio.
60 CAPITOLO 4 Equzioni differenzili Il problem più semplice che bbimo ffrontto e che rientr nell ctegori delle equzioni differenzili è l determinzione di primitive dt f(x) trovre tutte le funzioni F (x) tli che F (x) = f(x). In generle, un equzione differenzile è un oggetto del tipo: F(x, y, y, y,... ) = 0, cioè è un relzione che colleg un funzione incognit y con l vribile indipendente x e con le derivte y, y,... Il cso dell ricerc delle primitive corrisponde ll scelt F = y F (x). Un funzione y, sufficientemente regolre, che verific F(x, y(x), y (x), y (x),... ) = 0, per ogni scelt dell vribile x, è dett soluzione (o integrle) dell equzione. In quel che segue, ci limitimo considerre lcuni tipi specifici di equzioni differenzili: le equzioni lineri. Il significto, in quest mbito, del vocbolo linere srà più chiro tr qulche pgin. 1. Equzioni lineri del I ordine coefficiente costnte Equzioni omogenee. Per inizire, considerimo un equzione differenzile prticolrmente semplice (35) y + y = 0 R. L equzione (35) è del primo ordine, linere, coefficiente costnti, omogene: del primo ordine perché nell equzione compre solo l derivt prim; linere perché l dipendenz d y, y è linere; coefficiente costnte perché il coefficienti di è indipendente d t; omogene, perché l funzione y = 0 è un soluzione dell equzione. Osservzione 1.1. Il termine linere. Supponimo che y 1 e y 2 sino due soluzioni dell equzione (35). Dti α, β R, considerimo w(t) := αy 1 (t) + βy 2 (t), combinzione linere di y 1 e y 2. Allor: w + w = αy 1 + βy 2 + αy 1 + βy 2 = α(y 1 + y 1 ) + β(y 2 + y 2 ) = 0. 55
61 56 4. EQUAZIONI DIFFERENZIALI Quindi, dl ftto che l equzione è linere e omogene discende l proprietà seguente: ogni combinzione linere di soluzioni di (35) è ess stess un soluzione di (35). Pssimo l problem di trovre tutte le soluzioni dell equzione (35). Dto che tle equzione è risolt d tutte le funzioni dell form Ae t con A R, ponimo y(t) = A(t) e t e cerchimo tutte le funzioni A per cui y è soluzioni. Dto che y = (A A)e t, l equzione (35) equivle (A A)e t + A e t = 0 A = 0. Dto che l derivt di A è identicmente null, A è costnte. Ricpitolndo: y (t) + y(t) = 0 t R y = Ae t per qulche A R. Se l soluzione cerct deve soddisfre, oltre ll equzione differenzile (35), l condizione inizile y(t 0 ) = y 0 per t 0, y 0 ssegnti, si prl di problem di Cuchy per (35): { y (36) trovre y = y(t) tle che + y = 0, y(t 0 ) = y 0 Determinre l soluzione è più che fcile: dto che conoscimo tutte le soluzioni dell equzione differenzile, bst determinre quli di queste verificno il vincolo imposto dll condizione inizile y(t 0 ) = y 0. Se y(t) = Ae t, sostituendo y 0 = y(t 0 ) = Ae t 0 A = y(t 0 )e t 0 = y 0 e t 0, quindi c è un unic soluzione per il problem di Cuchy (36) ed è y(t) = y 0 e (t t 0). Equzioni non omogenee. Dt un funzione f integrbile, considerimo (37) y + y = f(t) R, f : R R. L equzione (37) è del primo ordine, linere, coefficienti costnti, non omogene. L presenz del termine noto f = f(t) f in modo che y = 0 non si soluzione (trnne nel cso f 0). Per cercre le soluzioni di quest equzione utilizzimo il metodo di vrizione delle costnti: cerchimo soluzioni dell form y(t) = A(t)e t dove A = A(t) è un funzione d determinre. Dto che y = (A A)e t, sostituendo nell equzione differenzile: f = y + y = (A A)e t + Ae t = A e t A (t) = f(t)e t. Se l funzione f è integrbile in ogni intervllo di R, l funzione A è: A(t) = t 0 f(s)e s ds + C C R
62 1. EQUAZIONI LINEARI DEL I ORDINE A COEFFICIENTE COSTANTE 57 e quindi nche l funzione y è determint: y(t) = A(t)e t = Ce t + t 0 f(s)e (s t) ds C R. L soluzione dell equzione non omogene è quindi dell form y 0 (t) = Ce t soluzione generle di (35) y(t) = y 0 (t)+ȳ(t) dove t ȳ(t) = f(s)e (s t) ds soluzione prticolre di (37). 0 L ver scelto in ȳ come primo estremo di integrzione s = 0 è del tutto rbitrrio, un qulsisi ltro numero fissto srebbe ndto ltrettnto bene. Ad esempio, per trovre l soluzione del problem di Cuchy { y (38) trovre y = y(t) tle che + y = f(t), y(t 0 ) = y 0 è più comodo scegliere come primo estremo di integrzione t 0 di modo che y(t) = Ce t + y 0 = y(t 0 ) = Ce t 0 + e l soluzione richiest è t0 t t 0 f(s)e (s t) ds C R, t 0 f(s)e (s t) ds = Ce t 0 C = y 0 e t 0, y(t) = y 0 e (t t 0) + t t 0 f(s)e (s t) ds. Sistemi disccoppiti di equzioni lineri. Il cso di un unic funzione incognit è evidentemente il cso più semplice. In generle, è utile considerre situzioni in cui sono presenti più funzioni incognite: y 1, y 2,... Risolvere sistemi nel cso generle è complicto e non è quest l sede in cui ffrontre l questioni. Esiste però un situzione fcile in cui possibile ricondursi l cso studito in precedenz: ssegnte le costnti, b, c, cerchimo le soluzioni y 1, y 2 del sistem { y 1 + y 1 = 0, y 2 + by 1 + cy 2 = 0. L peculirità di questo sistem è che l prim equzione y 1 + y 1 = 0 è disccoppit dll second, cioè è un equzione per l sol incognit y 1 (y 2 non compre). Qui si può risolvere l prim equzione e, successivmente, risolvere l second dopo ver inserito l espressione esplicit per y 1. Procedimo y 1 + y 1 = 0 y 1 = Ae t A R,
63 58 4. EQUAZIONI DIFFERENZIALI quindi l equzione per y 2 diviene y 2 +cy 2 = Abe t, cioè un equzione non omogene. Perciò, se c, y 2 (t) = Be ct Ab Invece, se c =, t y 2 (t) = Be t Ab 0 e s+c(s t) ds = Be t + t 0 Ab c (e t e ct ) A, B R. e t ds = (B Abt) e t A, B R. Si fcci ttenzione lle costnti in gioco:, b, c sono dti del problem, mentre A, B sono costnti rbitrrie (ogni scelt di A, B corrisponde d un soluzione). Equzioni lineri del I ordine coefficiente vribile. Tornimo, or, l cso di un singol equzione differenzile, e considerimo il cso (39) y + (t)y = b(t) t R, dove e b sono funzioni reli continue e l funzione incognit y = y(x) è nch ess un funzione rele. L equzione differenzile (39) si dice equzione differenzile linere del primo ordine coefficiente vribile. Come sempre, il problem di Cuchy consiste nel trovre l soluzione di (40) y + (t)y = b(t) y(t 0 ) = y 0, dove t 0 e y 0 sono ssegnti. Ecco come procedere per determinre l integrle generle di (39). Indict con A un primitiv dell funzione, moltiplichimo l equzione per l funzione e A(t), ottenendo e A(t) y (t) + e A(t) (t)y(t) = e A(t) b(t). Il termine primo membro è l derivt dell funzione e A(t) y(t), inftti ( e A(t) y(t) ) = e A(t) y (t) + (e A(t) ) y(t) = e A(t) y (t) + e A(t) (t)y(t). Quindi l equzione prende l form ( e A(t) y(t) ) = e A(t) b(t). Clcolimo l integrle indefinito del secondo membro e A(t) b(t) dt = F (t) + C. Dto che l derivt di e A(t) y(t) è l funzione e A(t) b(t), deve vlere e A(t) y(t) = F (t) + C.
64 2. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI OMOGENEE 59 Esplicitndo rispetto y, ottenimo l soluzione generle di (39): A(t) = (t) dt, (41) y(t) = ( F (t) + C ) e A(t) dove F (t) = e A(t) b(t) dt, C R. Esercizio 1.2. Risolvere l equzione differenzile y + y cos t = 1 2 sin(2t). Nel cso in cui si debb risolvere un problem di Cuchy, quindi se è ssegnt nche l condizione inizile y(t 0 ) = y 0, bst imporre che l generic soluzione dt d (41) soddisfi l condizione dt. Un strd lterntiv, che utilizz l uso di integrli definiti (nziché indefiniti), segue lo stesso schem visto in precedenz: si clcol A, primitiv di, e si moltiplic l equzione per e A(t) in modo d ottenere ( y e A(t) ) = b(t) e A(t). si integr in (t 0, t) e, per il teorem fondmentle del clcolo integrle, y(t) e A(t) y(t 0 ) e A(t0) = b(t) e A(t) dt, t 0 si us l condizione y(t 0 ) = y 0 e si esplicit y(t), t y(t) = y 0 e A(t 0) A(t) + e A(t) t t 0 b(t) e A(t) dt, Se A(t) è scelt come t t 0 (s), ds, l formul può essere riscritt come ( t ) t ( t ) y(t) = y 0 exp (s) ds + b(t) exp (s) ds dt. t 0 t 0 t Esercizio 1.3. Risolvere il problem di Cuchy ty y + t ln t = 0 y(1) = Equzioni lineri del II ordine coefficienti costnti omogenee Considerimo un prticell, cioè un punto in cui supponimo concentrt l mss m, e supponimo che si muov lungo un rett. L posizione dell prticell l tempo t è individut d un funzione y = y(t), che ne rppresent l coordint rispetto d un sistem di riferimento fissto. L funzione y (t) è l velocità dell prticell, mentre y (t) ne è l ccelerzione. In meccnic, il moto dell prticell è custo dll presenz di forze, descritte qui d un funzione F, che giscono sull prticell stess. L legge di Newton fferm
65 60 4. EQUAZIONI DIFFERENZIALI che: l mss m moltiplict per l ccelerzione è ugule ll forz risultnte che gisce sull prticell: (42) my = F. Modellizzre l zione di un cert forz F sull prticell corrisponde d esprimere F in termini dell posizione y, dell velocità y, dell istnte t. Di conseguenz, l legge di Newton prende l form di un equzione differenzile (43) my = F (t, y, y ). Ad esempio, considerimo un prticell che si sposti lungo l sse y, su cui gisc un forz elstic F e, dirett verso l origine e proporzionle ll distnz dll origine. In ltre prole, supponimo F e = ky con k > 0 (k è il coefficiente di proporzionlità e misur l grndezz delle forz elstic). L legge di Newton dice che il moto dell prticell è descritto dll equzione (44) my = ky (equzione dell oscilltore rmonico) Se sull prticell gisce nche l forz d ttrito F, che supponimo proporzionle ll velocità y, m dirett in senso contrrio, cioè F = ry con r 0, ottenimo l equzione (45) my = ky ry (equzione dell oscilltore con ttrito). Questo è l esempio tipo di equzione di cui voglimo determinre le soluzioni. Studimo, perciò, l equzione differenzile del secondo ordine, linere, coefficienti costnti, omogene: (46) y + 2by + cy = 0 b, c R. L equzione è: del secondo ordine perché compiono derivte fino l secondo ordine; linere perché l dipendenz d y, y e y è linere; coefficienti costnti perché i coefficienti di b e c non dipendono dll vribile t; omogene, perché l funzione y = 0 è un soluzione dell equzione. Un esempio di equzione di questo genere è y + y = 0. Per ogni A, B R, l funzione y = A cos t + B sin t ne è soluzione (verifictelo!). Questo ftto è generle: dte y 1 e y 2 soluzioni di (46), tutte le combinzioni lineri di y 1 e y 2 sono soluzioni dell stess equzione. Definizione 2.1. Due funzioni y 1 e y 2 sono linermente dipendenti se un è proporzionle ll ltr, cioè se esistono due costnti α, β, non entrmbe nulle, tli che
66 2. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI OMOGENEE 61 αy 1 (t) + βy 2 (t) = 0 per ogni t. Si dicono linermente indipendenti se non sono linermente dipendenti. Esempio 2.2. Ad esempio, y 1 = sin t e y 2 = cos t sono soluzioni linermente indipendenti di y + y = 0. Inftti, se, per qulche α, β R, si h α sin t + β cos t = 0 per ogni t, llor t = 0 α sin 0 + β cos 0 = β = 0, Quindi α = β = 0. t = π 2 α sin π 2 + β cos π 2 = α = 0. Il risultto che segue (di cui omettimo l dimostrzione) descrive l struttur dell insieme delle soluzioni di (46). Teorem 2.3. Se y 1 e y 2 sono soluzioni linermente indipendenti di (46), tutte le soluzioni di (46) sono dell form y(t) = c 1 y 1 (t) + c 2 y 2 (t) c 1, c 2 R. Quindi, per conoscere tutte le soluzioni dell equzione differenzile linere (46) bst individure un coppi di soluzioni linermente indipendenti. Tutte le ltre soluzioni si ottengono per combinzione linere. Ad esempio, dto che sin t e cos t sono linermente indipendenti, tutte le soluzioni di y + y = 0 sono del tipo A sin t + B cos t con A, B R. Costruzione delle soluzioni linermente indipendenti. L obiettivo or è determinre un coppi di soluzioni linermente indipendenti dell equzione (46). A questo scopo procedimo in un mnier che può sembrre strn, m molto efficce: considerimo l stess equzione differenzile per funzioni vlori complessi, cioè cerchimo z = z(t) C tli che z + 2bz + cz = 0; determinimo due soluzioni complesse z 1 e z 2 opportune; sceglimo y 1 = Re z 1 e y 2 = Re z 2. Considerimo quindi l equzione (47) z + 2bz + cz = 0 b, c R, dove z : R C e cerchimo un soluzione dell form z = e λt dove λ C è d determinre. Dto che z = λe λt e z = λ 2 e λt, λ deve essere tle che λ 2 e λt + 2bλe λt + ce λt = 0 t R. Dto che e λt 0, λ deve essere soluzione dell equzione di secondo grdo compless (48) polinomio crtteristico: λ 2 + 2bλ + c = 0.
67 62 4. EQUAZIONI DIFFERENZIALI Studimo tre csi second del tipo di rdici del polinomio crtteristico. Cso I. b 2 > c. Il polinomio crtteristico (48) h due rdici reli λ 1 = b + b 2 c, λ 2 = b b 2 c. Ottenimo in corrispondenz due soluzioni z 1 (t) = e λ 1t z 2 (t) = e λ 2t. Prendendo l prte rele ottenimo le soluzioni y 1 e y 2 cercte, m... z 1 e z 2 sono funzioni vlori reli! Quindi in reltà y 1 e y 2 coincidono con z 1 e z 2, rispettivmente: y 1 (t) = Re z 1 (t) = e λ 1t y 2 (t) = Re z 2 (t) = e λ 2t. Per verificre che y 1, y 2 sono indipendenti, supponimo che esistno α, β R tli che αe λ 1t + βe λ 2t = 0. Derivndo e clcolndo entrmbe le relzioni per t = 0, si ottiene un sistem linere omogeneo per le incognite α, β α + β = 0, αλ 1 + βλ 2 = 0. Dto che il determinnte di questo sistem è λ 2 λ 1 = 2 b c 2 > 0, l unic soluzione è α = β = 0. In conclusione, nel cso b 2 > c, tutte le soluzioni di (46) sono dell form y(t) = c 1 e λ 1t + c 2 e λ 2t. Esercizio 2.4. Determinre le soluzioni dell equzione y 3y + 2y = 0. Cso II. b 2 = c. In questo cso il polinomio crtteristico è il qudrto di un binomio λ 2 + 2bλ + b 2 = (λ + b) 2, ed h un unic soluzione λ = b. In corrispondenz trovimo un unic soluzione z 1 (t) = e bt dell equzione differenzile. Per determinre un second soluzione (indipendente d z 1 ), considerimo z 2 (t) = te bt. Dto che si h z 2(t) = (1 bt)e bt z 2(t) = ( 2b + b 2 t)e bt, z 2(t) + 2bz 2(t) + b 2 z 2 (t) = [ ( 2b + b 2 t) + 2b(1 bt) + b 2 t ] e bt = 0. Quindi nche z 2 è soluzione dell equzione.
68 2. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI OMOGENEE 63 Osservzione 2.5. L scelt di z 2 è suggerit d un procedimento di limite, immginndo il cso di due rdici coincidenti come limite di un cso con due rdici distinte. Se λ 1 λ 2, l espressione eλ 2 t e λ 1 t λ 2 λ 1, è soluzione di (47). Per λ 2 λ 1 ottenimo e λ2t e λ1t lim λ 2 λ 1 λ 2 λ 1 che è l soluzione determint in precedenz. = lim λ 2 λ 1 e λ2t e λ1t λ 2 t λ 1 t t = teλ 1t, Come nel cso precedente, le due soluzioni complesse z 1 (t) = e bt e z 2 (t) = te bt sono vlori reli. Inoltre si trtt di soluzioni indipendenti. Inftti, sino α, β R tli che αe bt + βte bt = 0, per ogni t. Dividendo per e bt, si deduce α + βt = 0, cioè α = β = 0. In conclusione, tutte le soluzioni di (46) nel cso b 2 = c, sono del tipo y(t) = c 1 e bt + c 2 te bt = (c 1 + c 2 t)e bt c 1, c 2 R. Esercizio 2.6. Determinre tutte le soluzioni dell equzione y + 4y + 4y = 0. Cso III. b 2 < c. Qui, finlmente!, è necessrio l uso dei complessi. Se b 2 < c, il polinomio crtteristico λ 2 + 2bλ + c h due rdici complesse coniugte λ 2 + 2bλ + c = 0 λ {λ 1, λ 2 } dove { λ1 = b + i c b 2 λ 2 = b i c b 2 Nel seguito, indichimo con ν = c b 2 > 0. L equzione differenzile compless (47) h due soluzioni indipendenti dte d } z 1 (t) = e λ1t = e {cos(νt) bt + i sin(νt), } z 2 (t) = e λ2t = e {cos(νt) bt i sin(νt) L prte rele di queste due (distinte) soluzioni è però l stess: e bt cos(νt). Occorre quindi sostituire l soluzione z 2 con un ltr soluzione z 2 divers. Dto che e λ 1t è soluzione di (47), nche tutte le funzioni dell form Ae λ1t sono soluzioni dell stess equzione per ogni scelt di A C. Sceglimo A = i, ossi ponimo z 2 (t) = i e λ1t = i z 1 (t), e sceglimo come soluzioni dell equzione (47) le funzioni { } z 1 (t) = e {cos(νt) bt + i sin(νt) }, z 2 (t) = e bt sin(νt) i cos(νt). Le soluzioni linermente indipendenti di (46) sono dte dlle prti reli di z 1 e z 2 : y 1 (t) = Re z 1 (t) = e bt cos(νt), y 2 (t) = Re z 2 (t) = e bt sin(νt).
69 64 4. EQUAZIONI DIFFERENZIALI Quindi, nel cso b 2 < c, tutte le soluzioni di (46) sono dell form ) y(t) = e (c bt 1 cos(νt) + c 2 sin(νt) ν := c b 2. Dto che b = Re λ 1 e ν = Im λ 1, se preferite l le soluzioni si possono scrivere così: ) y(t) = e (c (Re λ) t 1 cos[(im λ) t] + c 2 sin[(im λ) t] con λ tle che λ 2 + 2bλ + c = 0 Esercizio 2.7. Dimostrre che, se ν 0, le funzioni e bt cos(νt) e e bt sin(νt) sono linermente indipendenti. Esercizio 2.8. Determinre tutte le soluzioni di y + y + y = 0. Anlizzimo le soluzioni nel cso b, c 0. Nel modello di oscilltore con ttrito, b e c sono postivi dto che rppresentno b = r c = k 2m m, dove m è l mss, r misur l ttrito e k misur l forz elstic. Nei Csi I e II, in cui b 2 c, ossi r 2 4km l soluzione è dt o dll sovrpposizione di due funzioni esponenzili { λ1 = b + b 2 c < 0, y(t) = c 1 e λ1t + c 2 e λ 2t con λ 2 = b b 2 c < 0. oppure dl prodotto di un funzione linere con un esponenzile y(t) = (c 1 + c 2 t)e bt. In entrmbi i csi, l soluzione tende sintoticmente zero per t + : lim y(t) = 0. t + Fisicmente questo corrisponde l ftto che l effetto di ttrito è tlmente forte d impedire ll forz elstic di generre un moto oscilltorio. Al contrrio, nel Cso III, b 2 < c, cioè per r 2 < 4km, le soluzioni sono y(t) = e bt (c 1 cos(νt) + c 2 sin(νt)) ν = c b 2. Se b > 0 (presenz di ttrito), le soluzioni sono il prodotto di un termine oscilltorio e di un termine esponenzile che regol l mpiezz delle oscillzioni e che tende 0 per t +. In questo cso si prl di oscillzioni rmoniche smorzte. Il vlore ν = c b 2 è l frequenz delle oscillzioni. Nel cso in cui b = 0 (ssenz di ttrito), le soluzioni sono dte d un combinzione linere di sin( c t) e cos( c t), e quindi dnno luogo oscillzioni periodiche non smorzte.
70 llor { y1 (0) c 1 + y 2 (0) c 2 = y 0 2. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI OMOGENEE 65 Problem di Cuchy. Per individure un unic soluzione occorre fissre le costnti di integrzione c 1 e c 2. Questo ftto è sensto rispetto l problem fisico: l evoluzione del moto dipende dlle condizioni inizili, cioè d posizione e velocità d un istnte t 0. Il problem di Cuchy per l equzione (46) è il problem di determinre l soluzione di { y + 2by + cy = 0, (49) y(t 0 ) = y 0, y (t 0 ) = y 1. dove t 0, y 0, y 1 R sono costnti ssegnte. Il problem è quindi di trovre, tr tutte le soluzioni dell equzione y + 2by + cy = 0, l unic che soddisfi le condizioni inizili y(t 0 ) = y 0 e y (t 0 ) = y 1. Esempio 2.9. Cerchimo l soluzione del problem di Cuchy y + y = 0 y(0) = 1, y (0) = 1. Dto che le soluzioni di y + y = 0 sono tutte e sole combinzioni lineri di sin t e cos t, considerimo un generic soluzione e imponimo che soddisfi le condizioni inizili. In questo modo ottenimo un sistem linere per le costnti c 1, c 2 : y(x) = c 1 cos t + c 2 sin t, y(0) = 1, y (0) = 1, implic { 1 c1 + 0 c 2 = 1 0 c c 2 = 1. Quindi c 1 = c 2 = 1 e l unic soluzione del problem è y(t) = cos t + sin t. In generle, se si sono determinte due soluzioni linermente indipendenti y 1 e y 2 di (46), è sempre possibile risolvere il problem di Cuchy imponendo le condizioni inizili dte in (49): si y(x) = c 1 y 1 (t) + c 2 y 2 (t), y(t 0 ) = y 0, y (t 0 ) = y 1, y 1(0) c 1 + y 2(0) c 2 = y 1. Il ftto che le soluzioni sino linermente indipendenti grntisce che il determinnte del sistem si sempre non nullo e che il sistem mmett un unic soluzione. Esercizio Determinre le soluzioni dei seguenti problemi di Cuchy { { y y 2y = 0 y + y 6y = 0 y(0) = 1, y (0) = 2, y(0) = 1, y (0) = 3,
71 66 4. EQUAZIONI DIFFERENZIALI 3. Equzioni lineri del II ordine coefficienti costnti non omogenee Tornimo ll esempio dell oscilltore con ttrito. Se supponimo che sull prticell gisc nche un forz estern f che si funzione solo del tempo, cioè f = f(t), l equzione del moto diviene my + ry + ky = f(t). Nel cso in cui l funzione f si null, si prl di moto libero, se invece f 0, si prl di moto forzto. Prendimo il toro per le corn e considerimo l equzione (50) y + 2by + cy = f(t) b, c R, dove f è un funzione ssegnt. L equzione differenzile (50) è del secondo ordine, linere, coefficienti costnti, non omogene. Se w e v sono due soluzioni, llor l funzione differenz u := w v soddisf l equzione omogene (46), come si può verificre con un semplice sostituzione. Vicevers, se u è un soluzione dell equzione omogene (46) e v dell equzione nonomogene (50), l somm w := u + v è soluzione dell equzione (50). Quindi l soluzione generle dell equzione non omogene (50) è y(t) = y 0 (t) + ȳ(t) dove { y0 soluzione generle di (46) ȳ soluzione prticolre di (50). Dto che bbimo già un strtegi generle per trovre tutte le soluzioni dell equzione omogene (46), per risolvere il problem nel cso non omogeneo, bst trovre un singol soluzione di (50). Principio di sovrpposizione. Supponimo di decomporre l funzione f come somm di due funzioni f 1 e f 2, cioè supponimo che si f(t) = f 1 (t) + f 2 (t). Se y 1 è un soluzione di y +2by +cy = f 1 (t) e y 2 è un soluzione di y +2by +cy = f 2 (t), llor l funzione somm y(t) := y 1 (t) + y 2 (t) è soluzione di (50). Questo ftto è noto come principio di sovrpposizione. Sostnzilmente signific che se bbimo un forz complict che, però, può essere decompost come somm di singole prti elementri, possimo ottenere l evoluzione del fenomeno completo sommndo le evoluzioni reltive d ogni singol prte. In termini mtemtici possimo dire che l soluzione generle di è dt d y + 2by + cy = f 1 (t) + + f n (t) y(t) = y 0 (t) + ȳ 1 (t) + + ȳ n (t)
72 dove 3. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI NON OMOGENEE 67 y 0 soluzione generle di y + 2by + cy = 0 ȳ i soluzione prticolre di y + 2by + cy = f i (t). L obiettivo è quindi quello di determinre un soluzione prticolre di (50) nel cso di f prticolrmente semplici e poi determinre l soluzione prticolre per funzioni più complicte che si decompongno come somm di funzioni semplici. Forznti periodiche. f(t) = Ce iωt Il cso più importnte è quello di forznte periodic, cioè del tipo C cos(ωt) o C sin(ωt) (C, ω R). Invece di lvorre con queste funzioni trigonometriche, è estremmente più semplice ed elegnte lvorre nell mbito complesso. Ponimo f(t) = Ce iωt e studimo (51) z + 2bz + cz = Ce iωt C, ω R, in cui l incognit è l funzione z = z(t) vlori in C. Prim di risolvere quest equzione, ponimoci il problem del ritorno : un volt trovt un soluzione z vlori complessi, come determinimo l soluzione rele y che cerchimo? Indichimo l funzione z, soluzione di (51), nell form z(t) = y 1 (t) + iy 2 (t), dove y 1 = Re z e y 2 = Im z. Inserendo in (51), bbimo y 1 + 2by 1 + cy 1 + i(y 2 + 2by 2 + cy 2 ) = C cos(ωt) + ic sin(ωt). Quindi, uguglindo l prte rele e l prte immginri, y 1 + 2by 1 + cy 1 = C cos(ωt) y 2 + 2by 2 + cy 2 = C sin(ωt), cioè y 1, prte rele di z, verific l equzione con temine forznte C cos(ωt) e y 2, prte immginri di z, con temine forznte C sin(ωt). A second dell funzione f che stimo considerndo, sceglieremo l prte rele o l prte immginri dell soluzione compless. Con l trnquillità di poter tornre nell mbito rele, riprendimo lo studio dell equzione (51) con l obiettivo di trovrne un soluzione prticolre. È sensto immginre che esist un soluzione con l stess frequenz di oscillzione di f: z(t) = σe iωt σ C. Il numero complesso σ è d determinre imponendo l condizione che z si soluzione dell equzione cerct.
73 68 4. EQUAZIONI DIFFERENZIALI Esempio 3.1. Prtimo d un problem specifico: trovre un soluzione di y y = cos t. Dto che cos t = Re e it, cerchimo σ C tle che z(t) = σe it si soluzione di z z = e it. Dto che z = σe it, sostituendo, ottenimo ( σ σ)e it = e it d cui σ = 1 2. Quindi l soluzione compless z è 1 2 eit. L soluzione prticolre ȳ dell equzione richiest è dt dll prte rele di z, cioè ȳ(t) = Re z(t) = 1 cos t. 2 Nel cso generle, dto che z (t) = iωσe iωt e z (t) = ω 2 σe iωt, sostituendo ed eliminndo il termine e iωt, ottenimo ω 2 σ + 2biωσ + cσ = C ( ω 2 + 2biω + c ) σ = C. Quindi, se c ω 2 + 2biω 0, σ = C c ω 2 + 2biω = C c ω2 2biω (c ω 2 ) 2 + 4b 2 ω 2. Questo vlore di σ può essere riscritto nell form esponenzile 1 α = σ = σ = Cαe iωδ dove (c ω2 ) 2 + 4b 2 ω 2 cos(ωδ) = (c ω 2 )α, sin(ωδ) = 2bωα L soluzione compless z è quindi z(t) = Cαe iω(t δ). di cui scegliere l prte rele o l prte immginri second dell funzione f dt. Esercizio 3.2. Determinre un soluzione prticolre di y + 2y + 2y = 2 sin(2t). Soluzione. Sostituendo z(t) = σe 2it in z + 2z + 2z = 2e 2it, segue 4σ + 4iσ + 2σ = 2 d cui σ = 1 2i 1 = 1+2i 5. Quindi z(t) = 1 + 2i [ ] cos(2t) + i sin(2t) 5 L soluzione prticolre è dt dll prte immginri di z y(t) = Im z(t) = 1 5[ 2 cos(2t) + sin(2t) ]. Attenzione! Il metodo ppen esposto funzion se c ω 2 +2biω 0. Rimne quindi d cpire il cso in cui c = ω 2, b ω = 0.
74 3. EQUAZIONI LINEARI DEL II ORDINE A COEFFICIENTI COSTANTI NON OMOGENEE 69 Per comincire, supponimo ω 0. L second condizione implic b = 0 e quindi z + cz = Ce iωt C, ω R. Cercndo soluzioni z(t) = σe iωt con σ C, ottenimo l equzione ( c ω 2) σ = C. Se ω 2 = c l relzione precedente dice che non esiste nessun soluzione dell form z(t) = σe iωt! Non ci perdimo d nimo e, in nlogi con qunto visto per le equzioni omogenee, cerchimo un soluzione dell form z(t) = σte iωt σ C. Dto che z (t) = σ ( 1 + iωt ) e iωt e z (t) = σ ( 2iω ω 2 t ) e iωt, sostituendo e semplificndo il termine e iωt, 2σiω = C = σ = C 2iω = C i 2ω vendo tenuto conto di ω 2 = c. Esercizio 3.3. Determinre un soluzione prticolre di y + y = sin t. Soluzione. Studimo l equzione compless z + z = e it e cerchimone soluzioni dell form z(t) = σte it. Sostituendo nell equzione z (t) = σ(1 + it)e it e z (t) = σ(2i t)e it, Quindi l soluzione compless è σ(2i t)e it + σte it = e it 2σ i = 1. z(t) = it 2 eit = it 2 (cos t + i sin t) = t 2 sin t i t cos t. 2 L soluzione desidert è l prte immginri di z: y(t) = Im z(t) = 1 2 t cos t. Rest escluso un solo cso: quello in cui c ω 2 + 2biω = 0 e ω = 0. Allor c = 0 e l equzione divent y + 2by = C. Ecco le soluzioni cercte in questi csi Verificte! b 0 : ȳ = Ct 2b e b = 0 : ȳ = Ct2 2. Risonnz. Se c ω 2 + 2biω 0, un soluzione prticolre dell equzione compless è 1 α = σ = z(t) = Cαe iω(t δ) dove (c ω 2 ) 2 + 4b 2 ω 2 cos(ωδ) = (c ω 2 )α, sin(ωδ) = 2bωα Il fttore α corrisponde d un fttore di distorsione e il fttore ωδ d un fttore di spostmento di fse rispetto l segnle esterno originle Ce iωt. Il fttore α descrive qunto il segnle esterno Ce iωt viene mplificto dl sistem. Immginimo b, c fissti, e supponimo di fr vrire l frequenz ω del segnle. Il grfico di 1 (52) φ(ω) = (c ω 2 ) 2 + 4b 2 ω 2 è detto curv di risonnz.
75 70 4. EQUAZIONI DIFFERENZIALI Nel cso b, c 0, φ è definit dppertutto, pri e tende zero per ω ± con ordine 2: 1/ (c ω lim 2 ) 2 + 4b 2 ω 2 [ ( ω ± 1/ω 2 = lim 1 c ) 2 4b 2 ] 1/2 + ω ± ω 2 ω 2 = 1. L derivt prim di φ è φ (ω) = 4ω[ω2 (c 2b 2 )] [ (c ω 2 ) 2 + 4b 2 ω 2] 3/2. Se 2b 2 c, l funzione h un ndmento prticolrmente semplice: decresce per ω > 0 e cresce per ω < 0, il suo vlore mssimo è ssunto in ω = 0 1 mx φ(ω) = φ(0) = ω R c. Se 2b 2 < c, l funzione h due punti di mssimo simmetrici nei vlori il mssimo dell funzione è dto d ω = ± c 2b 2, mx ω R φ(ω) = φ(± c 2b 2 ) = 1 2 b c b 2. Il ftto significtivo è che questo vlore mssimo tende + per b 0, cioè se l effetto dell ttrito è piccolo, per un scelt di ω prticolre (vicino c b 2 ), il sistem determinto dll equzione differenzile risponde l segnle esterno e iωt con un distorsione estremmente grnde. Questo fenomeno è detto fenomeno dell risonnz e ppre in ntur in moltissime situzioni differenti.
76 CAPITOLO 5 Lo spzio rele multidimensionle Lo spzio rele d dimensionle, indicto con R d (dove d N), è l insieme costituito d d ple ordinte, dette punti (o vettori), e indicte, nel seguito, con l notzione P = (x 1,..., x d ) dove x 1,..., x d indicno le coordinte del punto P. Per indicre un secondo punto verrà spesso utilizzt l letter Q (con corrispondenti coordinte dte d (y 1,..., y d )). Nei csi, prticolrmnte significtivi, plnre, i.e. d = 2, e spzile, i.e. d = 3., le corrispondenti coordinte srnno indicte con P = (x, y), P = (x, y, z), second dell situzione considert. L insieme R d è uno spzio vettorile su R grzie ll presenz delle operzioni di somm e prodotto per uno sclre: dti P = (x 1,..., x d ), Q = (y 1,..., y d ) R d e λ R, P + Q = (x 1 + y 1,..., x d + y d ), λ P = (λx 1,..., λx d ) Il vettore nullo (0,..., 0) viene indicto con l letter O. L differenz fondmentle tr il cso uni-dimensionle, d = 1, e il cso multidimensionle, d > 1, st nel ftto che. mentre differenz di R, nello spzio R d, d > 1, non è definit un nozione di ordine e simboli del tipo <, non hnno senso in relzione vettori di dimensione superiore d uno Serve un struttur metric Il modulo è l distnz di un punto dll origine del sistem di riferimento. Un volt definit tle distnz, grzie ll struttur di spzio vettorile, è possibile definire l distnz tr due punti qulsisi dello spzio. In ltri termini, dto il modulo, lo spzio considerto viene dotto di un struttur metric. D tle struttur discende, cten, il concetto di limite con nnessi e connessi. Come definire il modulo? Supponimo di vere scelto come misur delle distnze nel cso unidimensionle, quell definit ttrvero il vlore ssoluto: i punti di R di 1 In lcuni contesti specifici vengono introdotte relzioni di ordine (przile) nel cso di R d, d > 1, m nessun di queste srà considert in queste Note. 71
77 72 5. LO SPAZIO REALE MULTIDIMENSIONALE coordinte x e y distno, per definizione, x y. Pssimo l cso plnre: d = 2. Il Teorem di Pitgor fferm che, dto un tringolo rettngolo in R 2 di vertici O = (0, 0), P = (x, y) e Q = (x, 0) con x, y > 0 fissti, vle l relzione l(op ) 2 = l(oq) 2 + l(qp ) 2 dove l(ab) indic l lunghezz del segmento AB. L lunghezz di segmenti unidimensionli è not ed è dt dl modulo unidimensionle dell differenz delle coordinte: nel cso in considerzione l(oq) = x 0 e l(qp ) = y 0. Quindi l(op ) 2 = x 2 +y 2, cioè l(op ) = x 2 + y 2. Cos cmbi nel cso tridimensionle? Fissimo il punto P = (x, y, z) e considerimo il tringolo rettngolo di vertici O = (0, 0, 0), P = (x, y, z) e Q = (x, y, 0). Il clcolo del cso bidimensionle, mostr che l(oq) 2 = x 2 + y 2, quindi, sempre dndo fiduci l Teorem di Pitgor, l espressione dell distnz di P d O è dt d l(op ) = l(oq) 2 + l(qp ) 2 = x 2 + y 2 + z 2. A questo punto, non sorprende l definizione seguente. Definizione 1.1. Dto P = (x 1,..., x d ) R d si chim norm (o modulo, o vlore ssoluto) di P il numero rele (53) P d := x x 2 d = ( d k=1 x 2 k) 1/2. Nel cso unidimensionle d = 1, l relzione (53) diviene x 1 con l usule definizione di modulo di un numero rele. = x 2 che coincide Osservzione 1.2. Nello spzio R d è possibile definire nche il prodotto sclre: dti P = (x 1,..., x d ) e Q = (y 1,..., y d ), si pone P Q := x 1 y x d y d. L norm di P R d può essere, llor, riscritt nell form (54) P d = (P P ) 1/2. Il prodotto sclre permette di dre senso l concetto di ortogonlità e, per questo motivo, si dice che lo spzio R d, considerto con il prodotto sclre, è dotto di un struttur euclide. Dto che l norm d definit in (53) discende, ttrverso (54), dll introduzione del prodotto sclre, ess viene nche dett norm euclide. Per fini prtici, occorre prim di tutto convincersi del ftto che l norm d gode di proprietà nloghe quell utilizzte in lungo e in lrgo nel cso unidimensionle.
78 1. SERVE UNA STRUTTURA METRICA 73 Proposizione 1.3. (Proprietà dell norm) Per l norm d vlgono: i. (positività) P d 0 per ogni P R d e P d = 0 se e solo se P = O; ii. (omogeneità) λ P d = λ P d per ogni λ R e P R d ; iii. (disuguglinz tringolre) per ogni P, Q R d, (55) P + Q d P d + Q d. Premettimo ll dimostrzione di queste proprietà il risultto seguente. Lemm 1.4 (Disuguglinz di Cuchy Schwrz). Per ogni P, Q R d, vle (56) P Q P d Q d P, Q R d. Dimostrzione del Lemm 1.4. Dto t R, si h P + tq 2 d 0. Inoltre P + tq 2 d = (P + tq) (P + tq) = P 2 d + 2 P Q t + Q 2 t 2. Dto che il polinomio di secondo grdo P P Q t + Q 2 t2 è sempre non negtivo, d d il suo discriminnte (P Q) 2 P 2 Q 2 d d deve essere minore od ugule zero; ne segue l disuguglinz (56). Dimostrzione dell Proposizione 1.3. Le dimostrzioni di i. e ii. non riservno prticolri sorprese e sono lscite per esercizio l lettore. L proprietà iii. segue dll disuguglinz di Cuchy Schwrz. Inftti, utilizzndo (56), si ottiene P + Q 2 d = P 2 d + 2 P Q + Q 2 d P 2 d + 2 P Q + Q 2 d ( P d + Q d )2. Applicndo l rdice qudrt l primo e ll ultimo membro, si ottiene (55). L norm euclide d unidimensionle. gode di un ltr proprietà nlog quell già vist nel cso Corollrio 1.5. Per ogni P, Q R d, vle l disuguglinz (57) P d Q d P Q d. Dimostrzione. L disequzione (57) equivle P d P Q d Q d P d + P Q d. Entrmbe le disuguglinze sono conseguenz delle proprietà dell norm. Inftti: P d P Q d = Q + (P Q) d P Q d Q d + P Q d P Q d = Q d Q d = P + (Q P ) d P d + Q P d = P d + P Q d. L dimostrzione è complet.
79 74 5. LO SPAZIO REALE MULTIDIMENSIONALE In prim bttut, lo spzio vettorile R d può essere pensto come uno spzio isotropo, cioè uno spzio in cui tutti i punti sino uguli tr di loro. In prticolre, non c è nessun motivo per preferire il punto origine O d ltri punti del pino. Si potrebbe decidere, d esempio, di cmbire sistem di riferimento pplicndo un trslzione llo spzio R d, cioè si può pensre di scegliere un nuovo punto origine P 0 e di individure tutti i punti di R d ttrverso il vettore P P 0 nzichè trmite il vettore P = P O. Quest ide suggerisce di utilizzre l trslzione e l norm per introdurre un nozione di distnz tr punti qulsisi di R d. Definizione 1.6. Dti P, Q R d si chim distnz di P d Q il numero rele (58) d(p, Q) := P Q d. Dll definizione (58) e dll Proposizione 1.3, discendono lcune proprietà per l distnz (l cui dimostrzione è lscit per indispensbile esercizio). Proposizione 1.7. (Proprietà dell distnz) Per l distnz definit in (58) vlgono le seguenti proprietà: i. (positività) d(p, Q) 0 per ogni P, Q e d(p, Q) = 0 se e solo se P = Q; ii. (simmetri) d(p, Q) = d(q, P ) per ogni P, Q R d ; iii. (disuguglinz tringolre) per ogni P, Q, R R d, (59) d(p, Q) d(p, R) + d(r, Q). Osservzione 1.8. Conseguenz immedit dell definizione (58), è che l distnz d è invrinte per trslzioni, cioè per ogni P, Q R d e per ogni h R d vle d(p + h, Q + h) = d(p, Q). L distnz in R d gode nche di ltre proprietà di invrinz. Si A un trsformzione linere di R n in sè che si unitri 2, cioè tle che A 1 = A t. D (54) segue d(ap, AQ) = AP AQ = P A t AQ = P Q = d(p, Q). Si noti che mentre l invrinz per trslzioni segue solmente dll relzione che intercorre tr distnz e norm (si ved l formul (58)), l invrinz per rotzioni discende dll specific scelt opert nell definizione di norm. Con norme diverse, tle invrinz potrebbe non vlere. 2 Un esempio prticolrmente interessnte di trsformzione unitri, nel cso d = 2, e dto d ( ) cos θ sin θ A θ := θ R sin θ cos θ L mtrice A θ descrive l trsformzione del pino R 2 in sè dt d un rotzione in senso ntiorrio di ngolo θ ttorno l punto O.
80 1. SERVE UNA STRUTTURA METRICA 75 Un volt introdotte le nozioni di norm e distnz, si possono definire, senz difficoltà, i concetti di insiemi limitti 3 e di intorni di un punto. Definizione 1.9. Un insieme A R d è limitto se esiste M > 0 tle che P d M P A. Dto P 0 R d e r > 0, si chim intorno perto di centro P 0 e rggio r l insieme I r (P 0 ) := { P R d : P P 0 d < r } ; si chim intorno chiuso di centro P 0 e rggio r l insieme Ī r (P 0 ) := { P R d : P P 0 d r }. L condizione di limittezz può essere formult nche come segue: un insieme A R d è limitto se e solo se è contenuto in un intorno di centro O (e rggio M sufficientemente grnde). Altre norme. Oltre ll norm euclide, definit in (53), si possono considerre ltre espressioni che continuno soddisfre le stesse proprietà e che pertnto meritno nchesse il nome di norme. Considerimo, d esempio, il cso di R 2 (nloghe definizioni si possono dre nel cso generle). Dto p 1, considerimo oppure (x, y) 2,p := ( x p + y p ) 1/p. (x, y) 2, := mx{ x, y }. E possibile dimostrre che si ogni norm del tipo 2,p, p [1, ], verific le stesse proprietà esposte nell Proposizione 1.3. Le definizioni di intorno di un punto descrivono insiemi di tipo diverso. Sussiste, l rigurdo di tli vrie norme diverse, il seguente risultto. Proposizione Dto p [1, + ], esistono due costnti m p e M p tli che (60) m p (x, y) 2,2 (x, y) 2,p M p (x, y) 2,2 (x, y) R 2. Dimostrzione. L disuguglinz di destr è vlid con M p = 2 1/p, inftti (x, y) 2,p = ( x p + y p ) 1/p 2 1/p mx{ x, y } 2 1/p ( x 2 + y 2 ) 1/2. Per l ltr, si può procedere in mnier nlog: (x, y) 2,2 = ( x 2 + y 2 ) 1/2 2 1/2 mx{ x, y } 2 1/2 ( x p + y p ) 1/p, ottenendo l disuguglinz di sinistr con m p := 2 1/2. 3 Dto che in R d, d > 1, non sono definite nozioni di ordinmento, non h senso prlre di insiemi superiormente/inferiormente limitti.
81 76 5. LO SPAZIO REALE MULTIDIMENSIONALE Dlle disuguglinze (60) segue che: gli insiemi limitti rispetto ll norm euclide e quelli rispetto ll norm 2,p coincidono; nche se gli intorni reltivi norme diverse sono diversi, ll interno di ogni intorno reltivo d un norm, è sempre contenuto un intorno (se necessrio di rggio più piccolo) reltivo ll ltr norm. Quest proprietà è prticolrmente rilevnte nell mbito delle proprietà di convergenz (che vedremo tr poche righe). Versioni nloghe dell Proposizione 1.10 vlgono per qulsisi norm in R d che verifichi le proprietà elencte nell Proposizione Quttro slti in R d : successioni di punti Un successione di punti in R d è un ppliczione d N R d che ssoci d ogni numero nturle n un punto P n di R d. Trmite l definizione di distnz è possibile definire il concetto di limite di un successione P n R d utilizzndo l stess definizione del cso unidimensionle. Definizione 2.1. Sino P n, P R d per ogni n N. L successione P n converge P per n + e si scrive lim P n = P se n + (61) ε > 0, n ε N, n n ε, vle P n P d < ε. Che cos vuol dire, in concreto, che l successione P n converge P per n +? L definizione (61) v lett prtire dll fine: lcuni punti dell successione P n distno meno di ε dl punto limite P. Quindi, l convergenz di P n P indic un proprietà di vicinnz di (lcuni) punti dell successione l corrispondente punto limite. Occorre precisre, però, qunto sino vicini tli punti l punto limite e quli sino i punti godere di tle proprietà. è questo fine che vengono introdotti i (misteriosi) vlori ε e n ε. L vicinnz è quntifict dl prmetro ε, che è qulsisi. L rbitrrietà di ε f in modo che l definizione si interessnte qulsisi si l scl significtiv considert, indipendentemente dl gusto e dll preferenz dell utente di turno. Più il vlore di ε è piccolo e più l condizione P n P d < ε diviene restrittiv e, di conseguenz, soddisftt d un minor numero di punti dell successione. Il vlore n ε permette di individure punti dell successione per cui l relzione è soddisftt. L richiest, nell definizione di limite, è che l distnz di P n d P si minore di ε tutte le volte che si scelgno indici n sufficientemente grndi. In definitiv, fisst un qulsisi sogli di errore ε > 0, i termini dell successione P n sono ben pprossimti d P per tutte le scelte di n mggiori di n ε.
82 2. QUATTRO SALTI IN R d : SUCCESSIONI DI PUNTI 77 Osservzione 2.2. L nozione di convergenz si bs sull definizione di distnz. Disponendo di metriche diverse potrebbe quindi ccdere che un stess successione {P n } si convergente rispetto certe metriche e non convergente rispetto d ltre. Il risultto dell Proposizione 1.10 consente di riconoscere che se un successione {P n } è convergente rispetto ll metric euclide lo è nche rispetto lle metriche 2,p. Per questo motivo, metriche che verifichino stime del tipo (60) si dicono essere equivlenti ll metric euiclide. Come nel cso del limite di successioni reli, nche il limite di successioni di punti di R d è linere: se P n e Q n sono due successioni convergenti, rispettivmente, P e Q, lim α P n + β Q n = α P + β Q per ogni α, β R. n + L dimostrzione è conseguenz immedit dell disuguglinz (α P n + β Q n ) (α P + β Q) d α P n P d + β Q n Q d. Inoltre, come nel cso rele, il limite di un successione, qundo esiste, è unico. Un successione di punti P n è individut univocmente dlle successioni reli delle sue coordinte. Che relzione intercorre tr l convergenz dell successione P n e quell delle successioni delle coordinte? Proposizione 2.3. Si P n = (x n 1,..., x n d ) e P = ( x 1,..., x d ). Allor l successione P n converge P se e solo se lim n + xn j = x j per ogni j = 1,..., d. Dimostrzione. Dll definizione di distnz in R d, segue ( d ) 1/2 x n j x j P n P d = (x n k x k ) 2 per ogni j {1,..., d}. Di conseguenz, se x n k x k tende 0 per ogni k, llor nche P n P d tende zero. Vicevers, se P n P d tende zero, nche l successione rele x n j x j tende zero per n + per ogni j. L Proposizione 2.3 indic che determinre il limite di un successione di punti in R d equivle determinre i limiti di d successioni reli. Ad esempio, per le successioni P n := ( 1/n 2, e 1/n) e Q n := (n sin (1/n), sin n/n) vlgono i limiti lim P n = (0, 1) e n + lim Q n = (1, 0). n Come nel cso uni-dimensionle, ogni successione convergente è nche limitt e, di conseguenz, un successione non limitt non può essere convergente. k=1
83 78 5. LO SPAZIO REALE MULTIDIMENSIONALE Proposizione 2.4. Si {P n } un successione convergente. Allor l successione {P n } è limitt. Dimostrzione. Si P il limite dell successione P n. Per definizione, esiste n 1 tle che P n P d < 1 per ogni n n 1. Vle quindi l stim P n d P d + P n P d < P d + 1 n n 1. Per dimostrre l limittezz dell successione, bst controllre l norm dei termini P 0,..., P n 1 1. Quindi, scegliendo si h che P n M per ogni n N. M := mx{ P 0 d,..., P n 1 1 d, P d + 1}, Esercizio 2.5. Sino P n e Q n due successioni in R d che convergono, rispettivmente, P e Q. Dimostrre che l successione n := P n Q n converge P Q. L limittezz non è un condizione sufficiente per l convergenz: si pensi ll esempio fcile fcile dell successione n = ( 1) n. Occorre, quindi, qulche ipotesi ggiuntiv oltre ll limittezz per essere certi dell convergenz dell successione in questione. Nel cso uni-dimensionle, d esempio, vle il criterio di monotoni: un successione di numeri reli limitt e monoton è convergente. Nel cso di successioni vettorili, dto che in R n non è possibile introdurre un ordinmento totle se n 2, non esiste un nlogo di questo criterio. L ipotesi di limittezz, dunque, non implic l convergenz dell successione ssegnt. E vero però un proprietà più debole che necessit l definizione seguente. Definizione 2.6. Dt l successione di punti {P n } e un successione {n k } di numeri nturli, strettmente crescente, l successione {P n k } si dice essere un sottosuccessione dell successione {P n }. Il termine sottosuccessione puo essere chirito trmite lcuni esempi. Dt l successione {n} = {0, 1, 2, 3,...} dei numeri nturli: le successioni {1, 3, 5, 7,..., 2k + 1,... }, {1, 10, 100, 1000,..., 10 k,... } sono sottosuccessioni dell successione ssegnt; le successioni {1, 2, 3, π, 4,...}, {1, 3, 2, 4,...}, {1, 2, 2, 3, 4,...} non sono sottosuccessioni dell successione dei nturli {n}. Dll definizione di convergenz, segue immeditmente che se un successione di punti {P n } converge P llor tutte le sottosuccessioni di {P n } convergono llo stesso punto limite P.
84 2. QUATTRO SALTI IN R d : SUCCESSIONI DI PUNTI 79 Teorem 2.7 (Teorem di Bolzno Weierstrss). D ogni successione limitt {P n } è possibile estrrre lmeno un sottosuccessione {P n k } convergente. Dimostrzione. L dimostrzione è divis in due pssi: prim si consider il cso di R e poi il cso generle. 1. Cso uni-dimensionle. Dimostrimo prim di tutto il Teorem nel cso unidimensionle. Si {x n } un successione rele limitt, cioè intermente contenut nell intervllo I 0 := [, b] per qulche, b R, < b. Considerimo i sotto-intervlli I 0 ± definiti d I0 := [, + b ], I := [ + b 2, b]. Dto che x n è compost d un numero infinito di elementi, lmeno uno dei due sottointervlli I 0 ± contiene infiniti elementi dell successione x n. Indichimo con I 1, quello dei due sotto-intervlli per cui è verifict tle proprietà e con 1, b 1 i suoi estremi, I = [ 1, b 1 ] e ripetimo il rgionmento precedente. Considerimo i sotto-intervli I 1 ± definiti d I1 := [ 1, 1 + b 1 ], I := [ 1 + b 1 ], b 1. 2 Dto che un numero infinito di elementi {x n } si trovno in I 1, lmeno uno dei due sotto-intervlli I 1 ± contiene infiniti elementi dell successione x n. Indichimo con I 2 tle sotto-intervllo. Iterndo il procedimento, si costruisce un successione di intervlli chiusi e limitti I n, ciscuno contenente un numero infinito di elementi dell successione {x n }. Per l ssiom degli intervlli incpsulti, esiste l R contenuto in I n per ogni n. Costruimo or un sottosuccessione {x n k } di {x n } come segue: sceglimo n 1 in modo che x n 1 I 1 ; sceglimo n 2 > n 1 in modo che x n 2 I 2 ; in generle, sceglimo n k+1 > n k in modo che x n k+1 Ik+1. Per costruzione, x n k l < (b )/2 k, e, di conseguenz, l sottosuccessione x n k converge d l. 2. Cso multi-dimensionle. Considerimo il cso di successioni in R 2 (il cso generle è nlogo). Si {P n } = {(x n, y n )} un successione limitt in R 2. Ne segue che nche le due successioni di numeri reli delle coordinte {x n } e {y n } sono limitte, Applicndo ll successione {x n } il teorem di Bolzno Weierstrss uni-dimensionle, si deduce che esiste un sotto-successione {x n k } convergente. L sottosuccessione {y n k }, estrtt dll successione {y n } con gli stessi indici dell sotto-successione {x n k }, è limitt. Applicndo nuovmente il teorem di Bolzno Weierstrss unidimensionle, si deduce l esistenz di un sotto-sotto-successione {y nkj }
85 80 5. LO SPAZIO REALE MULTIDIMENSIONALE convergente. L successione P n k j := (xnkj, y nkj ), vendo entrmbe le successioni delle coordinte convergenti, è un successione convergente. Il criterio di Cuchy. Trmite il Teorem di Bolzno Weierstrss si dimostr un condizione necessri e sufficiente per l convergenz di successioni di punti: il criterio di Cuchy. Teorem 2.8 (Criterio di Cuchy). Un successione P n in R d è convergente se e solo se vle l condizione seguente (62) ε > 0, n ε N, m, n n ε, vle P m P n d < ε. Dimostrzione. Se l successione P n converge P, vle l stim P m P n d P m P d + P n P d, d cui segue che l condizione (62). Vicevers, se l successione {P n } è di Cuchy, llor è nche limitt. scegliendo ε = 1, si deduce, d (62), che, per un opportuno n 1 N vle P n d P n 1 d + P n P n 1 d < P n 1 d + 1 per ogni n n 1. Posto M := mx{ P 0 d, P 1 d,..., P n 1 1 d, P n 1 d + 1}, si h P n d M n N. Inftti, Grzie l Teorem di Bolzno Weierstrss, si deduce che esiste un sottosuccessione {P n k } convergente d un opportuno punto limite P. Per dimostrre che tutt l successione P n converge P, bst utilizzre l stim P n P d P n P n k d + P n k P d e lvorre con ccortezz con ε e n ε. I dettgli sono lsciti l volenteroso lettore. Esercizio 2.9. Si {P n } tle che, per qulche θ [0, 1) vlg l condizione P n+1 P n d θ P n P n 1 d n N \ {0}. Dimostrre che l successione P n converge d un P R d. L condizione (62) non necessit l conoscenz esplicit del limite P. Tle ftto permette di utilizzre il criterio di Cuchy come mttone fondmentle per un costruzione rigoros dell insieme dei numeri reli prtire di numeri rzionli (o, più in generle, per un costruzione dell insieme R d prtire d Q d ). L ide di bse st nel ftto che un numero rele è individuto d un successione (rzionle) che lo pprossimi con un errore piccolo qunto si vuole. Ad esempio, per pprossimre/definire il numero (irrzionle) π si può considerre l successione di numeri (rzionli) 0 = 3 1 = 3, 1 2 = 3, 14 3 = 3, = 3, = 3, ,
86 3. INFORMAZIONI DI BASE SULLA TOPOLOGIA DI R d 81 cioè l elemento n è quello che si ottiene considerndo i primi n decimli del numero π. D questo punto di vist, un numero è individuto d un successione di Cuchy in Q, cioè d un successione n tle che ε Q, ε > 0, n ε N, tle che m n < ε m, n n ε. L insieme delle successioni di Cuchy S = { {x n } : successione di Cuchy in Q }. const, però, di troppi elementi: esistono successioni diverse che rppresentno lo stesso numero (bst pensre due diverse successioni di rzionli che tendno zero). Occorre quindi rggruppre gli elementi di S in clssi di equivlenz, in modo che ogni singol clsse rppresenti un singolo numero rele. L relzione d equivlenz si definisce così: dte {x n } e {y n } in S {x n } {y n } se lim n + (x n y n ) = 0. E fcile verificre che si trtt di un relzione di equivlenz (riflessività e simmetri sono bnli, l trnsitività discende dll disuguglinz tringolre). A questo punto il gioco è ftto: l insieme dei numeri reli è il quoziente R := S/. 3. Informzioni di bse sull topologi di R d Prtimo d un problem prototipo: dt un funzione f : A R d R, determinre un soluzione dell equzione (63) f(p ) = 0. Supponimo di essere in grdo di dimostrre l esistenz di P n tli che f(p n ) non si nullo, m verifichi l stim f(p n ) 1 n. Il limite P dell successione P n è un buon cndidto d essere soluzione di (63), m......l successione P n è convergente d un limite P?...il limite P pprtiene ll insieme A?...è vero che f(p ) = 0? Ciscun di queste domnde port ll introduzione di un concetto importnte: l compttezz, l chiusur, l continuità. A seguire, vedimo i primi due, mentre il terzo srà esplorto in lungo e in lrgo più vnti. Definizione 3.1. Un insieme C R d è chiuso (rispetto ll operzione di limite) se per ogni successione P n A convergente il punto limite P pprtiene ll insieme A.
87 82 5. LO SPAZIO REALE MULTIDIMENSIONALE Esempio 3.2. Il prodotto crtesino [, b] [c, d] è un insieme chiuso di R 2, per ogni scelt di, b, c, d R. Inftti, si P n = (x n, y n ) [, b] [c, d] un successione convergente l limite P = ( x, ȳ). Dto che x n b, c y n d, n N, pssndo l limite per n +, si deduce che ( x, ȳ) [, b] [c, d]. Esempio 3.3. L insieme dei numeri nturli N in R è un insieme chiuso. Inftti, se x n è un successione di numeri nturli convergente d x, si h che, per qulche n, vle l stim x n x < 1/2 per ogni n n. Se m, n n, si h x n x m x n x + x m x < = 1, e, di conseguenz, x n = x m. Quindi l successione è costnte per n n e, pertnto, convergente. Esercizio 3.4. Si C un insieme finito di punti. Dimostrre che C è chiuso. In generle, un successione contenut in un insieme chiuso potrebbe non essere convergente. Occorre, quindi, un condizione che grntisc, qunto meno, l convergenz di un qulche sottosuccessione dell successione dt. Eccol. Definizione 3.5. Un insieme K R d è comptto (per successioni) 4 se d ogni successione P n K è sempre possibile estrrre un sottosuccessione P n k convergente qulche P C. Esempio 3.6. Il prodotto crtesino [, b] [c, d] è un insieme comptto di R 2, per ogni scelt di, b, c, d R. Inftti, si P n = (x n, y n ) [, b] [c, d]. Dto che l successione P n è limitt, ess mmette, per il Teorem di Bolzno Weierstrss un sottosuccessione P n k convergente d un qulche punto P e, dto che [, b] [c, d] è chiuso, il punto P pprtiene d [, b] [c, d]. Tutti gli insiemi comptti sono nche chiusi. Inftti, se P n K è un successione convergente P, ogni sottosuccessione P n k converge llo stesso limite P. Per definizione, quindi, P pprtiene d K. Il vicevers non è vero: esistono insiemi chiusi che non sono comptti. Esempio 3.7. L insieme dei numeri nturli N in R non è comptto. Inftti, tutte le sottosuccessioni di n = n sono illimitte e quindi non convergenti. L limittezz impedisce lle successioni di scppre ll infinito e, insieme ll chiusur, grntisce l esistenz di sottosuccessioni convergenti. 4 Esistono nche ltre definizioni di compttezz, utilizzte in mbiti più generli, che comunque, nel cso di R d coincidono con l compttezz per successioni.
88 3. INFORMAZIONI DI BASE SULLA TOPOLOGIA DI R d 83 Teorem 3.8 (Insiemi comptti di R d ). Un sottoinsieme K di R d è comptto (per successioni) se e solo se è chiuso e limitto. Dimostrzione. Si K comptto e, di conseguenz, chiuso. Supponimo, per ssurdo, che K non si limitto. Allor, per ogni k N esiste P n k tle che P n k d n e, di conseguenz, (64) lim k + P n k d = +. Dto che K è comptto, esiste un sottosuccessione di P n k, che indichimo per semplicità (e con buso di notzione...) sempre con P n k convergente qulche P K. In prticolre, dto che P n k d P d P n k P d, l successione rele P n k d converge P d, in contrddizione con (64). Vicevers, si A chiuso e limitto e si P n un successione in K. Per il Teorem di Bolzno Weierstrss, Teorem 2.7, è possibile estrrre un sottosuccessione P n k convergente d un punto P. Dto che l insieme K è chiuso, il punto limite pprtiene d K ed è quindi verifict l proprietà di compttezz. Prllelmente ll nozione di insieme chiuso, si introduce nche l nozione di insieme perto. Definizione 3.9. Si S R d. Un punto P R d è interno d S se esiste r > 0 tle che I r (P 0 ) = { P R d : P P 0 d < r } S. Un punto P R d è esterno d S se è interno ll insieme complementre R d \ S, cioè se esiste r > 0 tle che S I r (P 0 ) =. Un insieme A R d si dice perto se i suoi punti sono tutti interni. Esempio Dti, b, c R l insieme A := {x + by + c > 0} R 2 è perto. Inftti, dto P 0 = (x 0, y 0 ) A, si h I r (P 0 ) A per ogni scelt di r strettmente minore dell distnz P 0 dll rett di equzione x + by + c = 0. Esempio Dti, b, c R l insiemi C := {(x, y) R 2 : x + by + c 0} non è perto. Inftti, tutti i punti dell form P 0 = (x 0, y 0 ) con x 0 +by 0 +c = 0 pprtengono C 1, m ogni intorno di tli punti contiene sempre punti non pprtenenti C 1. Anlogo discorso vle per l insieme C 2 := {(x, y) R 2 : x + by + c = 0}. Che relzione intercorre tr insiemi perti e insiemi chiusi? Proposizione Un insieme A è perto se e solo se il suo complementre C := R d \ A è chiuso.
89 84 5. LO SPAZIO REALE MULTIDIMENSIONALE Dimostrzione. Supponimo A perto e dimostrimo che C := R d \ A è chiuso. Si {P n } un successione di punti in C convergente P. Se, per ssurdo, P pprtenesse d A, esisterebbe r > 0 tle che I r ( P ) A. In prticolre, per ogni n si vrebbe P n P r > 0 in contrddizione con il ftto che l successione P n converge P. Supponimo C = R d \A chiuso e dimostrimo che A è perto. Se, per ssurdo, A non fosse perto, esisterebbe P A non interno d A. Quindi, per ogni n N, esisterebbe P n C tle che P n I 1/n ( P ). L successione P n srebbe llor convergente l punto P, in contrddizione con l ipotesi. Gli insiemi perti e gli insiemi chiusi sono chiusi rispetto ll operzione di unione e di intersezione: cioè vlgono le ffermzioni seguenti se A 1, A 2 sono perti, llor nche A 1 A 2, A 1 A 2 sono perti; se C 1, C 2 sono chiusi, llor nche C 1 C 2, C 1 C 2 sono chiusi. Osservzione Nel cso di unione o intersezione di un numero infinito di perti/chiusi, l situzione è un po più delict. Vlgono le impliczioni seguenti: se A n, n N, è un successione di perti, llor l unione A n è un perto; n N se C n, n N, è un successione di chiusi, llor l intersezione C n è un chiuso. Non è difficile costruire esempi di successioni di perti l cui intersezione si un chiuso e successioni di chiusi l cui unione si un perto. Provteci. Per ogni insieme S R d è possibile distinguere tre ctegorie di punti: i punti interni, i punti esterni e... gli ltri, cioè i punti che non sono né interni né esterni d S. Definizione Un punto P R d è un punto di frontier dell insieme S se ogni intorno di P contiene punti di S e punti non pprtenenti d S: per ogni r > 0, S I r (P 0 ), (R d \ S) I r (P 0 ). L insieme dei punti di frontier di S si chim frontier di S e si denot con S. Si chim chiusur dell insieme S l insieme S := S S. L chiusur S di un insieme S è il più piccolo insieme chiuso contenente S. Esempio Per gli insiemi A := {(x, y) : x + by + c < 0}, C := {(x, y) : x + by + c 0}. con, b, c R, si h A = C = {(x, y) : x + by + c = 0}. A voi l verific. Esempio Per gli insiemi n N A := {(x, y) : x 2 + y 2 < r 2 }, C := {(x, y) : x 2 + y 2 r 2 }, con r > 0, si h A = C = {(x, y) : x 2 + y 2 = r 2 }.
90 4. NATURA NON FACIT SALTUS: LE CURVE 85 Esercizio Determinre l frontier e l chiusur dei seguenti insiemi S 1 = {(x, y) : 0 < x 2 + y 2 1}, S 2 = {(x, y) : x + y + 1 < 0, x + 1 < 0}, S 3 = {(0, 0), (1, 0), (0, 1)}, S 4 = {(x, y) : x, y 0, x + y 0} Esercizio Dimostrre che l frontier di un insieme S e del suo complementre T := R d \S coincidono, cioè S = T. Come espresso dl seguente risultto (l cui dimostrzione è lscit come esercizio), gli insiemi perti e gli insiemi chiusi hnno un relzione prticolre con l loro frontier. Proposizione Un insieme A è perto se e solo se A A = ; un insieme C è chiuso se e solo se C C. 4. Ntur non fcit sltus: le curve Un successione di punti P n R d può essere interprett come un sequenz di posizioni nello spzio d dimensionle di un prticell in movimento che viene osservt d istnti successivi t 0 < t 1 < < t n <... : il punto P n è l posizione ll istnte t n. Un mnier ltrettnto (o più?) interessnte per descrivere il moto di un punto è quell di considerre che l vribile temporle non vri in un insieme discreto, m in un insieme continuo 5. Questo corrisponde, in concreto considerre funzioni del tipo φ : I R R d dove I è un intervllo di R, che ssocino d uno sclre t I il vettore φ(t) = (φ 1 (t),..., φ d (t)). L funzione φ i che ssoci t l i esim componente di φ(t) si chim i esim componente di φ. Tenendo conto dell definizione di modulo in R d, è possibile, senz ftic, introdurre il concetto di continuità nche in questo contesto. Definizione 4.1. Si I un intervllo di R. Un funzione φ : I R R d è continu in t 0 I se (65) ε > 0, δ > 0 tle che φ(t) φ(t 0 ) d < ε t I, t t 0 < ε. Un funzione φ : I R R d è continu in I se è continu in tutti i punti di I. L insieme delle curve φ : I R R d continue in I si indic con il simbolo C(I; R d ). 5 L locuzione ltin Ntur non fcit sltus, formult per l prim volt d Crl von Linné, nell Philosophi Botnic, è stt utilizzt d Leibniz come ssiom per negre l esistenz di quntità discrete indivisibili ed esprimere che i processi nturli vrino in mnier continu.
91 86 5. LO SPAZIO REALE MULTIDIMENSIONALE Dll definizione di modulo e seguendo un strtegi nlog quell utilizzt nell Proposizione 2.3, si dimostr che l continuità dell funzione φ equivle ll continuità di tutte le sue componenti φ i. Un sottoclsse delle funzioni continue è dt dlle cosiddette funzioni lipschitzine: un funzione φ C(I; R d ) si dice lipschitzin se esiste L > 0 tle che (66) φ(t) φ(τ) d L t τ t, τ I. In questo cso, l condizione di continuità (65) è verifict scegliendo δ = ε/l. Come si vede, il vlore di δ è indipendente dl punto t 0 di continuità. Sempre rgionndo come nell Proposizione 2.3, si può mostrre che un funzione φ è lipschitzin se e solo se tutte le sue componenti φ i sono lipschitzine. Nell logic dell descrizione di un moto nello spzio, è rgionevole restringere l ttenzione funzioni φ le cui componenti φ 1,..., φ d sono derivbili. In questo modo, per ogni vlore t I è ben definito il vettore velocità φ (t) = ( φ 1(t),..., φ d (t)). L insieme delle curve φ : I R R d con derivt φ continu, si indic con il simbolo C 1 (I; R d ). Definizione 4.2. Si I R un intervllo di estremi e b. Un curv prmetrizzt regolre è un ppliczione φ C 1 (I; R d ) tle che (67) φ (t) 0 t I. Un curv prmetrizzt regolre trtti è un ppliczione φ C(I; R d ) tle che esiste un insieme S = { < t 0 < t 1 < < t N < b} I per cui vle φ è regolre trtti in [, t 0 ] I, [t 1, t 2 ],..., [t N 1, t N ], [t N, b] I In entrmbi i csi, l insieme immgine φ(i) è detto supporto dell curv. D un punto di vist cinemtico, l funzione φ che definisce l curv è l legge orri del moto in questione, mentre l insieme immgine φ(i) ne è l triettori. Si noti che l stess triettori può essere percors con leggi orrie diverse e che, prllelmente, curve prmetrizzte diverse possono vere lo stesso supporto. L condizione φ (t 0 ) 0 equivle richiedere che il moto del punto descritto dll legge orri φ non bbi mi velocità null; dl punto di vist geometrico, ess grntisce l esistenz in ogni punto dell curv di un rett tngente, l cui equzione prmetric è P = φ(t 0 ) + φ (t 0 )h con h R. Segmenti e poligonli. Considerimo due punti distinti P 0, P 1 R d. Come descrivere un moto d P 0 P 1 lungo un line rett (cioè per l vi più rpid)? In
92 4. NATURA NON FACIT SALTUS: LE CURVE 87 ltre prole, come prmetrizzre il segmento P 0 P 1? E immedito riconoscere che l definizione seguente φ(t) = P 0 + t(p 1 P 0 ) t [0, 1], risolve l questione. Come si not fcilmente, si h φ (t) = P 1 P 0 0 per ogni t e, di conseguenz, l curv φ è effettivmente regolre. Ovvimente, esistono (infinite) ltre mniere di prmetrizzre un segmento. Esempio 4.3. Il segmento nel pino di estremi (0, 1) e (1, 0) è prmetrizzto d { x = x(t) = t, t [0, 1]. y = y(t) = 1 t Lo stesso segmento può essere prmetrizzto in tnte mniere diverse, d esempio d { x = x(τ) = 1 cos(τ), τ [0, π/2]. y = y(τ) = cos(τ) Le due rppresentzioni prmetriche offerte differiscono dl punto di vist cinemtico. Clcolndo i corrispondenti vettori velocità si h (x, y )(t) = (1, 1) x (t) 2 + y (t) 2 = 2, (x, y )(τ) = sin(τ)(1, 1) x (τ) 2 + y (τ) 2 = 2 sin(τ). Quindi, nel primo cso, il moto è rettilineo uniforme (i.e. l velocità è costnte), nel secondo, il moto è ncor rettilineo, m l velocità cresce l crescere di τ [0, π/2]. Considerimo tre punti distinti P 0, P 1, P 2 R d. Come prmetrizzre il percorso d P 0 P 2 pssndo per P 1, ottenuto percorrendo i segmenti P 0 P 1 e P 1 P 2? Bst operre piccole modifiche ll prmetrizzzione vist per il cso di un singolo segmento: { P0 + t(p 1 P 0 ) t [0, 1], In questo cso, φ(t) = P 1 + (t 1)(P 2 P 1 ) t (1, 2] φ (t) = { P1 P 0 t [0, 1), P 2 P 1 t (1, 2] quindi, in generle, l prmetrizzzione è solo regolre trtti. In questo cso l insieme S dell Definizione 4.2 è composto d un singolo elemento: S = {1}. Pssimo l cso generle di n + 1 punti. Definizione 4.4. Assegnti n + 1 punti P 0, P 1, P 2,..., P n si dice poligonle S d essi determint l insieme unione degli n segmenti P 0 P 1,..., P n 1 P n. I punti P 0, P 1, P 2,..., P n sono detti vertici dell poligonle e i due punti P 0 e P n si dicono estremi dell poligonle S.
93 88 5. LO SPAZIO REALE MULTIDIMENSIONALE Prmetrizzre un poligonle Π non è così proibitivo: bst porre φ(t) = P k + (t k)(p k+1 P k ) t [k, k + 1], k [0, n 1]. Anche, in questo cso, in generle, l prmetrizzzione è solo regolre trtti con S = {1, 2..., n}. Altri esempi di curve. Il cso più noto è quello dei grfici di funzioni. Dt f : I R R di clsse C 1, il grfico dell funzione f si prmetrizz bnlmente ponendo φ(t) = (t, f(t)) t I. Dto che φ (t) = (1, f (t)), l curv è regolre. Non serve un grnde sforzo per trovre qulche esempio di curv che non si un grfico di funzione. Dti P 0 = (x 0, y 0 ) R 2 ed r > 0, l circonferenz di centro P 0 e rggio r si rppresent con { x = x(t) = x0 + r cos(t), t [0, 2 π). y = y(t) = x 0 + r sin(t) In mnier simile, dti P 0 = (x 0, y 0 ) R 2 ed, b > 0, l ellissi di semissi e b, centrt in P 0 e simmetric rispetto gli ssi coordinti, si rppresent prmetricmente con { x = x(t) = x0 + cos(t), t [0, 2 π). y = y(t) = x 0 + b sin(t) Un curv più originle è quell dt d φ(t) = (t 2, t 3 ) con t [ 1, 1]. Il grfico present un cuspide nel punto (0, 0). Si noti che, dto che φ (t) = (2 t, 3 t 2 ), l condizione (67) non è soddisftt in t = 0. L curv in esme, quindi, non è regolre. Si trtt, comunque, di un curv regolre trtti, con S = {0}. Tnto per grdire, vedimo nche un esempio di curv nello spzio tridimensionle. Dti > 0 e r > 0, l curv prmetrizzt dt d x = x(t) = r cos(t), y = y(t) = r sin(t), t R. z = z(t) = t h come supporto un elic circolre che si vvolge ttorno ll sse z. A second dell scelt di, l elic è più o meno ripid. Dto che φ (t) = ( r sin t, r cos t, ) 0 per ogni t, l curv è regolre.
94 4. NATURA NON FACIT SALTUS: LE CURVE 89 Lunghezz di curve. Il concetto di lunghezz è intuitivo: immginndo un curv come un oggetto deformbile, bst rddrizzre tle oggetto e confrontrlo con l unità di misur prescelt. M, come nel cso degli integrli definiti, occorre dre un definizione rigoros di lunghezz di un curv che, uspicbilmente, ne permett nche il clcolo esplicito, lmeno in un certo numero di situzioni semplici. Come procedere? Nell costruzione dell integrle, bbimo ricondotto il clcolo di un re con un bordo curvilineo quello di insiemi dti d unioni di rettngoli, pssndo poi l limite in mnier opportun. Nel cso di curve, l ide nturle è di utilizzre come pprossimnti le poligonli. In effetti, scegliendo un numero finito di punti dell curv e considerndo l poligonle determint d tli punti, si ottiene un nuov curv l cui lunghezz è minore o ugule dell lunghezz dell curv originle in esme. L lunghezz dell curv è dt dll estremo superiore delle lunghezze di tli poligonli pprossimnti. Vedimo di formlizzre precismente qunto descritto. Considerimo, un curv prmetrizzt regolre φ definit in I = [, b] R. Dt l prtizione π = { = t 0 < t 1 < < t n 1 < t n = b}, in corrispondenz dei quli srnno ssegnti sull curv i punti P i = φ(t i ). I punti P 0, P 1,..., P n definiscono l poligonle S(π) l cui lunghezz l(φ, π) è dt d n 1 n 1 l(φ, π) = P k+1 P k d = φ(t k+1 ) φ(t k ) d. k=0 Definizione 4.5. L lunghezz l di un curv prmetrizzt regolre trtti φ : [, b] R R d è dt d k=0 l(φ) := sup{l(φ, π) : π prtizione di [, b]}. Le curve regolri hnno tutte lunghezz finit. Inftti, dto che l funzione φ pprtiene C 1 ([, b]; R d ), le componenti φ i sono di clsse C 1 ed hnno quindi derivt limitt. Si M > 0 tle che φ i(t) M per ogni t [, b] e per ogni i {1,..., d}. Dti t, τ [, b], pplicndo il Teorem di Lgrnge, si deduce ( d ) 1/2 φ(t) φ(τ) d = (φ k (t) φ k (τ)) 2 M d t τ. k=1 Dt l prtizione π = { = t 0 < t 1 < < t n 1 < t n = b}, si h n 1 l(φ, π) = φ(t k+1 ) φ(t k ) d M n 1 d (t k+1 t k ) = M d (b ). k=0 L insieme {l(π) : π prtizione di [, b]} è quindi superiormente limitto e, di conseguenz, mmette estremo superiore finito. Un curv regolre trtti può essere k=0
95 90 5. LO SPAZIO REALE MULTIDIMENSIONALE penst come unione finit di curve regolri e, pertnto, mmette nch ess lunghezz finit. L definizione di lunghezz come estremo superiore è pienmente soddisfcente dl punto di vist teorico, m lsci qulche perplessità dl punto di vist opertivo: come clcolre in concreto l lunghezz di un curv? Teorem 4.6. Si φ : [, b] R R d un curv prmetrizzt regolre trtti. Vle l uguglinz (68) l(φ) = φ (t) d dt. Osservzione 4.7. Dto che l funzione φ è regolre trtti e si h φ (t) d φ (t 0 ) d φ (t) φ (t 0 ) d, è possibile decomporre l intervllo di integrzione [, b] in unione finit di sotto-intervlli chiusi in cui l funzione φ ( ) d è continu. Quindi, l funzione φ ( ) d è integrbile (secondo Riemnn) in [, b] e l integrle in (68) è ben definito. L dimostrzione dell relzione (68) si bs sull pprossimzione φ(τ) φ(t) φ (t) (τ t) τ t, che consiste nel sostituire il segmento di estremi φ(t) e φ(t + h) con un segmento tngente l supporto dell curv in φ(t) e di lunghezz opportun. Il seguente Lemm si propone di stimre con precisione l errore commesso in tle pprossimzione, in un cso leggermente più semplice. Lemm 4.8. Si I R un intervllo e si φ C 1 (I; R d ) tle che φ è lipschitzin in I. Allor, esiste C > 0 tle che (69) φ(τ) φ(t) φ (t) (τ t) d C τ t 2 per ogni t, τ I. Dimostrzione. Per ogni i {1,..., d}, dl Teorem di Lgrnge segue φ i (τ) φ i (t) φ i(t) (τ t) = ( φ i (σ i ) φ i(t) ) (τ t) per qulche σ i compreso tr τ e t. Utilizzndo l ipotesi di lipschitzinità di φ, si deduce che, per qulche L > 0, vle (70) φ i (τ) φ i (t) φ i(t) (τ t) L σ i t τ t L τ t 2. Utilizzndo (70), si ottiene L dimostrzione è complet. φ(τ) φ(t) φ (t) (τ t) d L d τ t 2.
96 4. NATURA NON FACIT SALTUS: LE CURVE 91 Grzie l Lemm 4.8, è possibile dimostrre il Teorem 4.6 supponendo, in ggiunt, φ lipschitzin. Dimostrzione (semplifict) del Teorem 4.6. Dt un prtizione π dell intervllo I, si h, utilizzndo (57) e (69), n 1 l(φ, π) φ n 1 (t k ) d (t k+1 t k ) φ(t k+1 ) φ(t k ) d φ (t k ) d (t k+1 t k ) (71) k=0 k=0 n 1 φ(tk+1 ) φ(t k ) φ (t k )(t k+1 t k ) d C k=0 n 1 (t k+1 t k ) 2 C (b ) π, dove π := mx k {0,n 1} (t k+1 t k ). Qundo l mpiezz π dell prtizione tende zero, l lunghezz l(φ, π) converge ll lunghezz l(π), mentre l sommtori n 1 φ (t k ) d (t k+1 t k ) tende ll integrle dell funzione φ (t) d rispetto t nell intervllo [, b]. Grzie ll stim (71), ne segue l formul (68). Esempio 4.9. Come prim verific/ppliczione dell formul (68), considerimo l circonferenz prmetrizzt d φ(t) = (cos t, sin t) con t [0, 2π]. In questo cso, si h φ (t) = ( sin t, cos t) e, di conseguenz, φ (t) d = 1 per ogni t. Perciò, l lunghezz richiest è l = 2π 0 k=0 1 dt = 2π, coerentemente con qunto noto dll geometri elementre. Esempio Clcolimo l lunghezz dell curv φ(t) = (t 2, t 3 ) con t [ 1, 1]. Dto che φ (t) = (2t, 3t 2 ), l lunghezz dell curv è 1 L = 4t2 + 9t 4 dt = 1 13 τ 1/2 dτ = 2 ( 13 ) vendo posto τ = 4 + 9t 2. Esempio Dti > 0 e r > 0, considerimo l rco di elic descritto dll prmetrizzzione φ(t) = (r cos t, r sin t, t) con t [t 0, t 1 ], t 0 < t 1. Dto che φ (t) = ( r sin t, r cos t, ) 0 per ogni t, l lunghezz dell curv è dt d l = t1 t 0 φ (t) d dt = dto che φ (t) d = r t1 k=0 t 0 r2 + 2 dt = r (t 1 t 0 ).
97 92 5. LO SPAZIO REALE MULTIDIMENSIONALE Nel cso di prmetrizzzione dell form φ(t) = (t, f(t)) con t [, b], dto che φ(t) = (1, f (t)), l espressione per l lunghezz dell curv prende l form l = 1 + (f (t)) 2 dt, che, quindi, esprime l formul per l lunghezz di un grfico di funzione. Esempio 4.12 (Lunghezz di un rco di prbol). Si f(t) = t 2 con t [0, ] con > 0. L lunghezz del grfico dell funzione f è pri l = (f (t)) 2 dt = 1 + 4t2 dt = 1 settsinh(2) cosh 2 τ dt 2 = 1 (settsinh(2) + 2 ) , vendo posto τ = settsinh(2t). 0 Esempio 4.13 (Lunghezz di un rco di curv esponenzile). Si f(t) = e t con t [0, ] con > 0. In questo cso, l lunghezz del grfico dell funzione f è dt d 1+e ( 2 l = 1 + (f (t)) 2 dt = 1 + e 2t dt = ) dt τ 2 1 = τ + 1 ( ) τ 1 1+e 2 2 ln = 1 + e τ ( ) ln e vendo posto τ = 1 + e 2t ed vendo pplicto qulche trttmento cosmetico... Cmbimenti di prmetro. L lunghezz dell curv è un concetto intrinseco, cioè non dipende dll prticolre scelt dell prmetrizzzione: uno stesso trgitto, nche se percorso con velocità diverse, indic sul contchilometri l stess lunghezz di strd. Formlizzimo precismente l questione. Definizione Due curve regolri φ C 1 ([, b]; R d ) e ψ C 1 ([α, β]; R d ) si dicono equivlenti se esiste un funzione rele di vribile rele g C 1 ([α, β]; [, b]) biunivoc tle che g (τ) 0 per ogni τ e (72) ψ(τ) = φ(g(τ)) τ [α, β]. In concreto, l funzione g consiste in un riprmetrizzzione dell curv: lo stesso supporto viene descritto si dl prmetro t che dl prmetro τ e l funzione g definisce l corrispondenz tr i due prmetri. In termini cinemtici, le due funzioni φ e ψ corrispondono due leggi orrie distinte e l funzione g mette in corrispondenz istnti reltivi ll stess posizione. 0
98 4. NATURA NON FACIT SALTUS: LE CURVE 93 Derivndo rispetto τ l relzione (72), si deduce dψ dτ = dφ dg dt dτ, che descrive l relzione che intercorre tr i vettori velocità delle due curve. Utilizzndo l formul 68 per l curv ψ ed introducendo l vribile t = g(τ), si ottiene β l(ψ) = dψ g(β) dτ = dφ g dτ dt dt g α d Dto che g 0 per ogni τ, l funzione g o è sempre strettmente positiv o è sempre strettmente negtiv. Nel primo cso, si h g(α) = e g(β) = b, quindi l(ψ) = dφ dt = l(φ). dt Se g < 0, si h g(α) = b e g(β) =, quindi l(ψ) = dφ g dt = dt g b d b d dφ dt g(α) d dt = d dφ dt d dt = l(φ). Quindi, le formule precedenti mostrno che curve equivlenti hnno l stess lunghezz. Oltre dre ulteriore conforto e coerenz ll definizione di lunghezz espress in (68), l precedente ffermzione permette di scegliere l prmetrizzzione che si preferisce nel clcolo dell lunghezz di un curv. Gli insiemi connessi. Un proprietà significtiv degli insiemi di R d è quell di essere connessi, cioè composti d un singolo pezzo. Sinonimi del vocbolo connesso sono i termini congiunto, llccito, perciò un mnier per formlizzre tle concetto è di richiedere che ogni coppi di punti dell insieme poss essere collegt d un percorso intermente contenuto nell insieme stesso. A second del tipo di percorsi mmissibili per relizzre tle collegmento tr punti, si utilizzno terminologie diverse. L versione più semplice di tutte è quell che consider come unici percorsi mmissibili i segmenti. Definizione Un insieme S R d è convesso se, per ogni P, Q S, si h t P + (1 t) Q S t [0, 1], cioè se il segmento di estremi P e Q è intermente contenuto in S. Esempio Ecco un piccolo elenco di insiemi convessi fcili : gli intervlli in R; i soprgrfici di funzioni convesse, cioè gli insiemi dell form S = {(x, y) : y f(x)} R 2, per f : I R R convess; i rettngoli nel pino, cioé insiemi dell form [, b] [c, d] R 2 ;
99 94 5. LO SPAZIO REALE MULTIDIMENSIONALE i prllelepipedi nello spzio, cioé insiemi dell form [, b] [c, d] [e, f] R 3 ; gli intorni di un punto, cioè insiemi dell form {P R d : P P 0 d < r} con P 0 R d e r > 0. Osservzione Se S 1 R d 1 e S 2 R d 2 sono due insiemi convessi, nche l insieme S := S 1 S 2 R d 1+d2 è convesso. Inftti, sino P = (x P, y P ), Q = (x Q, y Q ) R d 1 R d 2 due punti dell insieme S := S 1 S 2. Dto che i punti x P, x Q pprtengono d S 1, il punto t x P + (1 t) x Q pprtiene d S 1 per ogni t [0, 1]. Anlogmente, dto che i punti y P, y Q pprtengono d S 2, nche il punto t y P + (1 t) y Q è in S 2. Di conseguenz, il punto t P + (1 t) Q = (t x P + (1 t) x Q, t y P + (1 t) y Q ) pprtiene S 1 S 2 per ogni t [0, 1]. Esercizio Sino A e B due insiemi convessi di R n. L insieme A B è convesso? L insieme A B è convesso? L convessità è un richiest molto forte. Tnto forte che bst pportre piccole modifiche d un insieme convesso per ottenere un insieme non convesso. Ad esempio, se S R d è un insieme convesso e P 0 è interno d S, l insieme S \ {P 0 } non è convesso. Inftti, se r > 0 è tle che I r (P 0 ) S e v R d è un qulsisi vettore tle che v d < r, i due punti P ± := P 0 ± v pprtengono d S \ {P 0 }, m, dto che tp + (1 t)p = P 0 +(1 2t) v coincide con P 0 per t = 1/2, il segmento che li congiunge non è intermente contenuto nello stesso insieme. In generle, tutto le volte che si cre un buco in un insieme convesso eliminndo un sottoinsieme interno si ottiene un insieme non convesso. Un condizione più flessibile dell convessità è espress dll prossim definizione. Definizione Un insieme S si dice connesso per poligonli se per ogni coppi P, Q S esiste un poligonle di estremi P e Q intermente contenut in S. Tutti gli insiemi convessi sono nche connessi per poligonli. In questo cso, inftti, bst scegliere come poligonle il segmento che congiunge i due punti P e Q dell insieme. Esistono nche tntissimi insiemi che sono connessi per poligonli, m che non sono convessi. Ad esempio, le corone circolri nel pino, i ferri di cvllo, e tutti gli insiemi ottenibili prtire d un insieme connesso con modificzioni elsto plstiche, m senz frtture... Esempio Si I un intervllo di R e si f : I R un funzione continu. Il soprgrfico S := {(x, y) R 2 : y f(x)} è un insieme connesso per poligonli. Inftti, dti (x 1, y 1 ), (x 2, y 2 ) S con x 1 x 2, si M := mx f(x), che esiste finito per x [x 1,x 2 ] il Teorem di Weierstrss. Allor, l poligonle di vertici P 0 = (x 1, y 1 ), P 1 = (x 1, M), P 2 = (x 2, M) e P 3 = (x 2, y 2 ) è intermente contenut in S. Allo stesso modo, si mostr che il soprgrfico di un funzione superiormente limitt è connesso per poligonli.
100 4. NATURA NON FACIT SALTUS: LE CURVE 95 Esempio Un insieme convesso cui sino stti sottrtti un punto interno non è più convesso, m è connesso per poligonli. Inftti, si S l insieme convesso di prtenz, si P 0 interno d S. Se P, Q sono elementi di S, ci sono due eventulità: o il segmento di estremi P e Q non contiene il punto P 0, o P 0 pprtiene tle segmento. Nel primo cso non c è null d ggiungere. Nel secondo, occorre costruire un poligonle che connett P e Q, ggirndo il punto P 0. Volete provvedere voi? In generle, un insieme convesso cui sino stti sottrtti un numero finito di punti interni è un insieme connesso per poligonli. Esercizio Trovre un insieme S R d convesso tle che esist P 0 S (non interno d S) per cui S \ {P 0 } non si connesso per poligonli. Esercizio Sino A, B R d due insiemi connessi per poligonli. L insieme A B è convesso? L insieme A B è convesso? Esistono numerosi insiemi ftti di un solo pezzo che non sono connessi per poligonli: bst pensre d un rco S di circonferenz. E evidente che comunque si prendno due punti P, Q S non esiste lcun poligonle di estremi P e Q contenut in S, per il semplice motivo che non esistono poligonli contenute in S. Per inserire nche questo tipo di situzione, si introduce un ulteriore nuov definizione di connesso. Definizione Un insieme S si dice connesso per rchi se per ogni coppi P, Q S esiste un curv φ : [, b] R R d regolre trtti tle che φ() = P, φ(b) = Q, φ(t) S t [, b]. Dto che le poligonli sono prticolri scelte di curve regolri trtti, ogni insieme connesso per poligonli è nche connesso per rchi. Tutti gli rchi di curv (che non sino poligonli) sono insiemi connessi per rchi (ovvimente), m non connessi per poligonli.
101
102 CAPITOLO 6 Funzioni di più vribili 1. Questioni elementri Le funzioni sono lgoritmi che fnno corrispondere d ogni punto di un insieme (l insieme di definizione) un ltro punto di un ltro insieme (il codominio). In quel che segue, ci interesseremo l cso in cui l insieme di definizione I si un sottoinsieme del dominio R d e il codominio si l insieme R p dove d, p sono numeri interi positivi opportuni. In notzione, considerimo funzioni dell form seguente f : I R d R p. Si trtt di un regol che ssoci ll vribile indipendente (o input) P I l vribile dipendente (o output) Q R p. Pssimo in rssegn i tipi fondmentli di funzioni di questo genere. Funzioni reli di un vribile rele: d = p = 1. Sono funzioni f : I R R, già stto considerte in lungo e in lrgo nei Cpitoli precedenti. Le curve: d = 1, p > 1. Si trtt di funzioni del tipo φ : I R R p, di cui si è discusso nel Cpitolo precedente. Funzioni reli di più vribili reli: d > 1, p = 1. Si trtt di funzioni f : I R d R. Nel cso d = 2, si trtt di funzioni che fnno corrispondere i punti (x, y) R 2 un numero rele z = f(x, y) R; nel cso d = 3, sono funzioni che ssocino i punti (x, y, z) R 3 un numero rele w R. In generle, un funzione f d R d in R p equivle ll ssegnzione di p funzioni, indicte con f 1,..., f p, d R d in R che ssocino l punto P R d l i esim coordint del punto immgine f(p ) = (f(p ) 1,..., f(p ) p ) con i {1,..., p}: f i (P ) := f(p ) i P I R d. Per questo motivo, le funzioni reli di più vribili rele sono prticolrmente interessnti d nlizzre e, in quel che segue, ci dedicheremo con prticolre ttenzione proprio quest clsse. 97
103 98 6. FUNZIONI DI PIÙ VARIABILI Le trsformzioni di R d in sé: d = p 1. Nel cso d = 2, si trtt di trsformzioni del pino, cioè di funzioni che fnno corrispondere ll coppi (x, y) R 2 un nuov coppi (u, v) R 2. Un trsformzione del pino in sé può essere vist come un coppi di funzioni d I R 2 in R: (x, y) I u = u(x, y) R, (x, y) I v = v(x, y) R. In generle, si trtt di trsformzione che ssocino d un punto P = (x 1,..., x d ) un nuovo punto Q = (y 1,..., y d ). Un mpi clsse di trsformzioni di R d è quell delle trsformzioni lineri, cioè funzioni dell form f(p ) := A P, dove A è un mtrice di dimensione d d. Assegnt un funzione specific, come procedere per riconoscerne le proprietà più significtive? Nel cso di funzioni reli di un vribile rele, un strtegi bbstnz generle consiste nel rppresentre l ndmento qulittivo dell funzione disegnndone il grfico. Cos cmbi qundo l dimensione ument? Per or, ccontentimoci del cso di funzioni reli di più vribile rele. Il primo psso è quello di determinre l insieme di definizione dell funzione, qulor non si specificto esplicitmente. Un funzione è generlmente ssegnt indicndo un procedimento di clcolo che può essere pplicbile d lcuni punti di R d e non d ltri. Qulor non si specificto diversmente, l insieme dei punti P per cui il procedimento reltivo ll funzione è ben definito si consider essere l insieme di definizione dell funzione. Ad esempio, considerimo le funzioni f(x, y) = 1 x + y, g(x, y) = ln(1 x2 y 2 ), h(x, y) = 3x 2 + 2y 2 5. L funzione f è definit in R 2 privto dell rett di equzione x+y = 0; l funzione g h per insieme di definizione I il disco perto di centro lorigine e rggio 1: I := {(x, y) : x 2 + y 2 < 1}; l funzione h è definit in tutto R 2 privto dell interno dell ellisse di equzione 3x 2 + 2y 2 = 5. Un volt noti i punti per cui l funzione h senso, si potrebbe essere interessti d nlizzre, in mnier qulittiv, l ndmento dell funzione. Generlizzndo l definizione già vist nel cso di funzioni di un vribile rele, si chim grfico dell funzione f l insieme Γ f := {(P, Q) R d R : P I, Q = f(p )}. Nel cso d = 2, il grfico di un funzione z = f(x, y) h, qusi sempre l spetto di un superficie dello spzio. Se d 3, il grfico è un sottoinsieme di uno spzio con dimensione mggiore o ugule 4 e, di conseguenz, l su visulizzzione grfic risult sensibilmente più complict... In quel che segue, ci concentrimo principlmente sul cso di funzioni d R 2 in R.
104 1. QUESTIONI ELEMENTARI 99 Profili ltimetrici. Il grfico Γ f di un funzione f d R 2 in R può essere immginto come un superficie (di montgn o di pinur, second dell funzione) su cui si può libermente psseggire, trovndosi d ltezz z = f(x, y) non ppen le coordinte (crtesine) dell posizione sino dte dll coppi (x, y). Uno specifico cmmino sul grfico Γ f è quindi individuto d un legge orri che ssoci ll vribile tempo t un corrispondente coppi di coordinte (x(t), y(t)). In corrispondenz, ll istnte t, ci si trovre d ltezz h(t) := f(x(t), y(t)). Qulcos suon fmilire... l coppi (x(t), y(t)) è un curv vlori nell insieme di definzione dell funzione f e l ltezz h non è ltro che l composizione tr l funzione t φ(t) := (x(t), y(t)) e l funzione (x, y) z = f(x, y). Per coerenz con il punto di vist escursionistico, chimimo nel seguito l funzione compost h = f φ il profilo ltimetrico di f reltivo ll curv φ. Un profilo ltimetrico fornisce sempre un informzione przile reltiv ll struttur di un grfico di funzione, dto che si riferisce d uno specifico cmmino tr gli infiniti cmmini possibili. Comunque, utilizzndo l informzione reltiv d un certo numero di profili ltimetrici, si può sperre di ottenere un ide qulittiv dell struttur globle del grfico di un funzione. Esempio 1.1. Considerimo l funzione f(x, y) = x y, definit in tutto R 2. Provimo d esplorre il grfico di tle funzione considerndo un curv dell form φ(t) = (t, 0) con t R. Si trtt quindi di un esplorzione che consiste nel tenere costnte l vribile y e spostrsi nell direzione determint dll sse x. Il corrispondente profilo ltimetrico è h(t) = f(x(t), y(t)) = x(t) y(t) = t. Al crescere del tempo (e quindi l crescere dell vribile x), l ltezz corrispondente cresce in mnier linere (l funzione h è un polinomio di grdo 1). In ltre prole, l intersezione tr il grfico dell funzione f e il pino (x, z) nello spzio R 3 è dto d un rett. Se considerimo l curv ψ(τ) = (0, τ) con τ R, il profilo ltimetrico è h(τ) = f(x(τ), y(τ)) = x(τ) y(τ) = τ. Anche in questo cso il profilo ltimetrico è dto d un polinomio di grdo 1. A differenz del cso precedente, l crescere di τ l ltezz diminuisce. In generle, considerndo un curv dell form dell form φ(t) = t v con t R, dove v = (v 1, v 2 ) R 2 è un vettore fissto, si ottiene un profilo ltimetrico dto d un polinomio di primo grdo h(t) = f(x(t), y(t)) = v 1 t v 2 t + 1 = (v 1 v 2 ) t.
105 FUNZIONI DI PIÙ VARIABILI Tutte le sezioni del grfico dell funzione con pini verticli, dnno luogo rette e, quindi, il grfico dell funzione è un pino nello spzio. Esempio 1.2. Considerimo l funzione f(x, y) = x 2 + y 2, definit in tutto R 2. Dto un vettore v = (v 1, v 2 ) R 2 di norm unitri, considerimo l curv φ(t) = t v con t R. Il corrispondente profilo ltimetrico è h(t) = f(x(t), y(t)) = v 2 1 t 2 + v 2 2 t 2 = (v v 2 2) t 2 = t 2 Si trtt cioè di un prbol con concvità rivolt verso l lto e minimo nel punto t = 0. Come si vede, il profilo ltimetrico non vri l vrire dell scelt del vettore unitrio v, indice del ftto che il grfico dell funzione considert è invrinte per rotzioni ttorno ll sse z. Il grfico completo si ottiene quindi fcendo ruotre il grfico dell prbol z = t 2 ttorno ll sse z ed h quindi l form di un scodell ( sezione prbolic) rivolt verso l lto. Esempio 1.3. Piccol (m non tnto...) vrinte dell esempio precedente: studimo l funzione f(x, y) = x 2 y 2, definit in tutto R 2. Di nuovo, sceglimo come legge orri dell esplorzione l curv φ(t) = t v con t R, dove v = (v 1, v 2 ) R 2, v d = 1. Si h h(t) = f(x(t), y(t)) = v 2 1 t 2 v 2 2 t 2 = (v 2 1 v 2 2) t 2. In questo cso, second dell scelt di v il comportmento del profilo ltimetrico vri. Precismente: se v 1 > v 2, il profilo è quello di un prbol con concvità verso l lto e minimo in t = 0; se v 1 = v 2, il profilo è identicmente nullo; se v 1 < v 2, il profilo è quello di un prbol con concvità verso il bsso e mssimo in t = 0. Inoltre, l convessità è mssim per v = (±1, 0) e minim per v = (0, ±1). Il grfico dell funzione f h l form di un sell. Esempio 1.4. Studimo l funzione f(x, y) = xy (x, y) (0, 0). x 2 + y 2 Considerimo come curve di percorrenz dell superficie, le rette per l origine, espresse dlle funzioni φ(t) = t v con t R, dove v = (v 1, v 2 ) R 2, v d = 1. Il profilo ltimetrico è h(t) = f(v 1 t, v 2 t) = v 1 v 2 = v v1 2 + v2 2 1 v 2. L ltezz di ogni singolo profilo è costnte, con ltezz dipendente dll rett scelt. Il grfico è rppresentto in Figur 1.
106 1. QUESTIONI ELEMENTARI 101 Figur 1. Il grfico dell funzione f(x, y) = xy x 2 + y 2. I profili ltimetrici possono essere considerti nche per funzioni di d vribili con d 2. Dte un funzione f : I R d R e un curv φ : J R R d tle che φ(j) I, l funzione compost f φ : J R si chim profilo ltimetrico dell funzione f lungo l curv φ. Curve di livello. Tr i profili ltimetrici di un funzione dt, ne esistono lcuni prticolrmente interessnti: sono quelli costnti. Un mnier lterntiv per rppresentre un funzione f = f(x, y) è quello di disegnre nel pino (x, y) gli insiemi di livello γ 1 := {(x, y) : f(x, y) = 1}, γ 2 := {(x, y) : f(x, y) = 2}, γ 3 := {(x, y) : f(x, y) = 3},... e, in generle, γ c := {(x, y) : f(x, y) = c} con c R. Tle metodo, detto metodo delle linee di livello, è quello utilizzto nelle crte geogrfiche 1. Determinre insiemi di livello di un funzione è, in qulche modo, un procedimento inverso quello dei profili ltimetrici: dt l costnte c, si cercno tutti i percorsi possibili che dino come profilo ltimetrico il vlore costnte c. Esempio 1.5. Considerimo, di nuovo, l funzione f(x, y) = x y. Dto il livello c R, l insieme γ c := {(x, y) : f(x, y) = c} è determinto d x y = c y = x c. Si trtt quindi di rette prllele ll bisettrice del primo e terzo qudrnte. Il ftto che vrizioni di livello c uguli corrispondno trslzioni uguli, si trduce nel ftto che l pendenz dell superficie è sempre l stess. Esempio 1.6. Gli insiemi di livello dell funzione f(x, y) = x 2 + y 2 sono prticolrmente semplici: dt c 0, si h γ c := {(x, y) : x 2 + y 2 = c}, si trtt cioè di 1 Per rricchire l rppresentzione delle linee di livello, in topogrfi, si utilizzno nche scle cromtiche che rppresentno i rilievi: toni di mrrone vi vi più deciso per le ctene montuose, toni di blu sempre più intenso per le profondità degli oceni e così vi...
107 FUNZIONI DI PIÙ VARIABILI circonferenze centrte nell origine e di rggio c. Per c < 0, l insieme γ c è vuoto. Dll struttur delle curve di livello si riconosce l invrinz del grfico rispetto rotzioni ttorno ll sse z. A differenz del cso precedente, vrizioni uguli del livello c non corrispondono vrizioni uguli degli insiemi di livello: il rggio dell circonferenz γ c è c, quindi il rggio cresce più rpidmente in prossimità del punto (0, 0) e sempre più lentmente per vlori di c grndi. Nell rppresentzione per curve di livello (che in concreto viene effettut disegnndo un numero finito di curve reltive livelli distnz costnte), si vedrà un minore concentrzione di curve vicino l punto (0, 0). In corrispondenz, il grfico risult essere meno pendente vicino ll origine e più pendente mn mno che ci si llontn dl punto (0, 0). Esempio 1.7. Considerimo l funzione f(x, y) = x 2 y 2. reltiv l livello c = 0 è prticolrmente semplice: dto che f(x, y) = x 2 y 2 = (x y)(x + y), L insieme di livello si h γ 0 = {y = x} {y = x}, cioè l insieme di livello è dto dlle due bisettrici del pino (x, y). Scegliendo c 0, si h γ c = {x 2 y 2 = c}, il cui grfico nel pino rppresent un iperbole equilter con sintoti dti dlle bisettrici y = ±x. Se c > 0, l insieme γ c è contenuto nell regione { y < x }, mentre se c < 0, l insieme γ c è contenuto nell regione { x < y }. Nel cso di funzioni di più vribili, l definizione di insieme di livello è del tutto nlog. In genere, dto un livello c, l insieme di livello γ c = {P R d : f(p ) = c} è un unione di superfici di dimensione d 1. Funzioni con simmetrie. Disegnre il grfico di un funzione che possiede qulche form di simmetri è, come l solito, più fcile. Prtimo d un cso semplice semplice. Dt l funzione rele di un vribile rele F : I R R, considerimo l funzione di due vribili reli: f(x, y) = F (x). L funzione f è definit in I R, inftti, dto che non c è dipendenz esplicit dll vribile y, il vlore dell second coordint può essere qulsisi. Inoltre, sempre per l indipendenz dell funzione f dll vribile y, il grfico Γ f risult essere invrinte rispetto trslzioni nell direzione dell sse y: (73) Γ f + λ j = Γ f λ R. dove j = (0, 1). L proprietà (73) indic che per disegnre il grfico dell funzione f bst disegnre il grfico dell funzione F nel pino (x, z) e, poi, trslre prllelmente tle grfico nell direzione dell sse y (vedi Figur 2). Il cso di funzioni dell
108 1. QUESTIONI ELEMENTARI 103 Figur 2. Il grfico dell funzione F (x) = cos x e quell dell funzione f(x, y) = cos x. form f(x, y) = F (y) è del tutto nlogo, con l unic differenz che l invrinz è nell direzione dell sse x. Leggermente più in generle, dt un funzione F : I R R e dte due costnti, b R, non entrmbe nulle, si può considerre l funzione di due vribili reli: f(x, y) = F (x + by). Le curve di livello di un funzione di questo genere sono (unioni di) rette dell form x + by =costnte. Di conseguenz, il grfico dell funzione gode dell invrinz seguente (74) Γ f + λ v = Γ f λ R. dove v = ( b, ). Per disegnre il grfico dell funzione f, bst disegnre il grfico dell funzione F in uno qulsisi dei pini verticli ortogonli ll direzione di invrinz e poi trslre prllelmente nell direzione di v. Sperimentte vostro grdimento. Considerimo un secondo tipo di simmetri. Dt F : I R R, studimo l funzione di due vribili reli definit nel modo seguente f(x, y) = F ( x 2 + y 2 ). Gli insiemi di livello di un funzione di questo genere sono (unioni di) circonferenze centrte in (0, 0). Pertnto il grfico dell funzione f risult essere invrinte rispetto rotzioni ttorno ll sse z. Formlmente, definendo ( ) cos θ sin θ A θ := sin θ cos θ l mtrice che descrive l rotzione di ngolo θ in senso ntiorrio del pino (x, y), il grfico dell funzione f gode dell proprietà (75) A θ Γ f = Γ f θ [0, 2π).
109 FUNZIONI DI PIÙ VARIABILI Concretmente, l proprietà (75) indic che per disegnre il grfico dell funzione f, bst disegnre il grfico dell funzione F nel semipino (x, z) con x 0 e, successivmente, fr ruotre tle grfico ttorno ll sse z (vedi Figur 3). Figur 3. Il grfico delle funzioni F (x) = cos x e f(x, y) = cos( x 2 + y 2 ). Operzioni elementri su grfici. A prtire d grfici noti, è possibile dedurre l form di ltri grfici che si ottengno di primi ttrverso un certo numero di operzioni elementri. Qui, considerimo il cso di diltzioni/compressioni (o omotetie) e trslzioni. Supponimo di conoscere il grfico dell funzione f = f(x, y). Dto λ > 0, il grfico dell funzione g(x, y) = f(λ x, y) si ottiene prtire dl grfico dell funzione f pplicndo un compressione, nel cso λ > 1, o un diltzione, nel cso 0 < λ < 1, nell direzione dell sse x. Esempio 1.8. A mo d esempio, si considerino i grfici delle funzioni g(x, y) = 4 x 2 + y 2, h(x, y) = x2 4 + y2, che corrispondono, rispettivmente, d un compressione e un diltzionedel grfico dell funzione f(x, y) = x 2 + y 2, con fttori λ = 2 e λ = 1/2. Gli insiemi di livello delle funzioni g ed h reltivi l livello c = 1, d esempio, sono dti d ellissi di equzioni x 2 (1/2) 2 + y2 = 1, x y2 = 1, quindi ellissi con ssi di simmetri gli ssi coordinti x e y, e semissi di lunghezz 1/2 e 1, nel cso dell funzione g, e di lunghezz 2 e 1, nel cso dell funzione f. Considerzioni nloghe possono essere ftte per funzioni dell form g(x, y) = f(λ 1 x, λ 2 y)
Integrale di Riemann
 Integrle di Riemnn Hynek Kovrik Università di Bresci Anlisi Mtemtic Hynek Kovrik (Università di Bresci) Integrle di Riemnn Anlisi Mtemtic / 50 Motivzione: clcolo di re Hynek Kovrik (Università di Bresci)
Integrle di Riemnn Hynek Kovrik Università di Bresci Anlisi Mtemtic Hynek Kovrik (Università di Bresci) Integrle di Riemnn Anlisi Mtemtic / 50 Motivzione: clcolo di re Hynek Kovrik (Università di Bresci)
Capitolo 6. Integrali di funzioni di una variabile
 Cpitolo 6 Integrli di funzioni di un vribile Ci si pone il problem del riuscire misurre l re di figure il cui contorno non è costituit d segmenti. 6. L integrle definito Si f : [, b] R R un funzione limitt
Cpitolo 6 Integrli di funzioni di un vribile Ci si pone il problem del riuscire misurre l re di figure il cui contorno non è costituit d segmenti. 6. L integrle definito Si f : [, b] R R un funzione limitt
1 Integrale delle funzioni a scala
 INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
Teorema fondamentale del calcolo integrale
 Clcolo integrle Proprietà dell integrle deinito Teorem dell medi integrle Corollri del Teorem ond. clc. int. Regole di integrzione deinit Clcolo di ree 2 26 Politecnico di Torino 1 Estensione dell integrle
Clcolo integrle Proprietà dell integrle deinito Teorem dell medi integrle Corollri del Teorem ond. clc. int. Regole di integrzione deinit Clcolo di ree 2 26 Politecnico di Torino 1 Estensione dell integrle
5.4 Il teorema fondamentale del calcolo integrale
 Esercizi 5.3. Si f : R R un funzione continu, e supponimo che f bbi sintoti obliqui per ±. Provre che f è uniformemente continu in R.. Esibire un funzione f : R R limitt e di clsse C, m non uniformemente
Esercizi 5.3. Si f : R R un funzione continu, e supponimo che f bbi sintoti obliqui per ±. Provre che f è uniformemente continu in R.. Esibire un funzione f : R R limitt e di clsse C, m non uniformemente
CALCOLARE L AREA DI UNA REGIONE PIANA
 INTEGRALI Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione CALCOLARE
INTEGRALI Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione CALCOLARE
Capitolo 5. Integrali. 5.1 Integrali di funzioni a gradinata
 Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
Integrali definiti (nel senso di Riemann)
 Integrli definiti (nel senso di Riemnn) Problem: cos è l re di un figur pin? come clcolrl? Grficmente concetto intuitivo ed evidente. Tecnicmente ci sono definizioni e formule d hoc per le figure elementri.
Integrli definiti (nel senso di Riemnn) Problem: cos è l re di un figur pin? come clcolrl? Grficmente concetto intuitivo ed evidente. Tecnicmente ci sono definizioni e formule d hoc per le figure elementri.
Integrali impropri di funzioni di una variabile
 Integrli impropri di funzioni di un vribile. Le funzioni continue Considerimo nel seguito un delle piú importnti ppliczioni del teorem di uniforme continuitá delle funzioni continue su intervlli chiusi
Integrli impropri di funzioni di un vribile. Le funzioni continue Considerimo nel seguito un delle piú importnti ppliczioni del teorem di uniforme continuitá delle funzioni continue su intervlli chiusi
L integrale di Riemann
 L integrle di Riemnn Riccrd Rossi Università di Bresci Anlisi B Riccrd Rossi (Università di Bresci) L integrle di Riemnn Anlisi B 1 / 64 Motivzioni: clcolo di un re Si f : [, b] R continu e positiv. Problem
L integrle di Riemnn Riccrd Rossi Università di Bresci Anlisi B Riccrd Rossi (Università di Bresci) L integrle di Riemnn Anlisi B 1 / 64 Motivzioni: clcolo di un re Si f : [, b] R continu e positiv. Problem
ANALISI 1 1 DICIOTTESIMA - DICIANNOVESIMA LEZIONE Integrale secondo Riemann
 ANALISI 1 1 DICIOTTESIMA - DICIANNOVESIMA LEZIONE Integrle secondo Riemnn 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/
ANALISI 1 1 DICIOTTESIMA - DICIANNOVESIMA LEZIONE Integrle secondo Riemnn 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/
1 Il problema del calcolo dell area di una regione piana limitata
 Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Introduzione al calcolo integrale
 Introduzione l clcolo integrle Indice: Integrle di Riemnn. Proprietà delle funzioni integrbili. Continuità dell funzione integrle. Teorem dell Medi. Teorem Fondmentle del Clcolo Integrle. Metodi di integrzione.
Introduzione l clcolo integrle Indice: Integrle di Riemnn. Proprietà delle funzioni integrbili. Continuità dell funzione integrle. Teorem dell Medi. Teorem Fondmentle del Clcolo Integrle. Metodi di integrzione.
Integrali. Il concetto di integrale nasce per risolvere due classi di problemi:
 Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Corso di Analisi Matematica. Calcolo integrale
 .. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
.. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
S D f = M k (f)(x k x k 1 ). k=1. Dalla definizione discende immediatamente che SD f S D f per ogni
 Integrle di Riemnn 1 Funzioni integrbili Dto un intervllo non degenere [, b], indichimo con T[, b] l collezione dei sottoinsiemi finiti di [, b] che contengono {, b}. Ogni D T[, b] si chimerà suddivisione
Integrle di Riemnn 1 Funzioni integrbili Dto un intervllo non degenere [, b], indichimo con T[, b] l collezione dei sottoinsiemi finiti di [, b] che contengono {, b}. Ogni D T[, b] si chimerà suddivisione
Osserviamo che per trovare le costanti A e B possiamo anche ragionare così: se moltiplichiamo l equazione x + 1 (x + 2)(x + 3) = A.
 88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
Integrali. Il concetto di integrale nasce per risolvere due classi di problemi:
 Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrali impropri in R
 Integrli impropri in Flvino Bttelli Diprtimento di Scienze Mtemtiche Università Politecnic delle Mrche Ancon Integrli impropri Indichimo con = {1, 2, 3,...} l insieme dei numeri nturli, con 0 = {0, 1,
Integrli impropri in Flvino Bttelli Diprtimento di Scienze Mtemtiche Università Politecnic delle Mrche Ancon Integrli impropri Indichimo con = {1, 2, 3,...} l insieme dei numeri nturli, con 0 = {0, 1,
COMPLEMENTI SUGLI INTEGRALI DEFINITI. A. Figà Talamanca
 COMPLEMENTI SUGLI INTEGRALI DEFINITI A. Figà Tlmnc 27 ottobre 2010 2 0.1 Introduzione C è un modo pprentemente semplice ed intuitivo per introdurre l integrle (definito) di un funzione f definit su un
COMPLEMENTI SUGLI INTEGRALI DEFINITI A. Figà Tlmnc 27 ottobre 2010 2 0.1 Introduzione C è un modo pprentemente semplice ed intuitivo per introdurre l integrle (definito) di un funzione f definit su un
Sua maestà l Integrale
 CAPITOLO 7 Su mestà l Integrle Con fierezz e sicumer, ecco incedere regle il Signor dell Misur: su Mestde l Integrle. N. Brbecue 1. L re di un sottogrfico: strtegi d ttcco È opinione comune che conoscere
CAPITOLO 7 Su mestà l Integrle Con fierezz e sicumer, ecco incedere regle il Signor dell Misur: su Mestde l Integrle. N. Brbecue 1. L re di un sottogrfico: strtegi d ttcco È opinione comune che conoscere
Capitolo IV Cenni di calcolo integrale
 Liceo Lugno, - 4B (Luc Rovelli) Cpitolo IV Cenni di clcolo integrle. Introduzione: ree e funzioni primitive Il clcolo integrle si occup principlmente di questioni, pprentemente senz relzione tr loro: dti,
Liceo Lugno, - 4B (Luc Rovelli) Cpitolo IV Cenni di clcolo integrle. Introduzione: ree e funzioni primitive Il clcolo integrle si occup principlmente di questioni, pprentemente senz relzione tr loro: dti,
Laurea triennale in Scienze della Natura a.a. 2009/2010. Regole di Calcolo
 Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
Integrazione definita
 Integrzione definit Si [,b] R un intervllo chiuso e limitto. Si f : [,b] R limitt. Def. Trpezoide di f sull intervllo [,b] è l regione di pino delimitt dll sse =, dlle rette = e = b e dl grfico di f. Viene
Integrzione definit Si [,b] R un intervllo chiuso e limitto. Si f : [,b] R limitt. Def. Trpezoide di f sull intervllo [,b] è l regione di pino delimitt dll sse =, dlle rette = e = b e dl grfico di f. Viene
Corso di Analisi Matematica Calcolo integrale per funzioni di una variabile
 Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =
![1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) = 1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =](/thumbs/19/319521.jpg) Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Integrali dipendenti da un parametro e derivazione sotto il segno di integrale.
 1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
f(x) f(x 0 ) lim (x) := f(x) f(x 0)
 Cpitolo 3 Derivte 31 Definizione **Definizione 31 (Punto di derivilità) Si f :[, ]! R un funzione e si 2 [, ] Allor f si dice derivile in se esiste finito il In questo cso si dice punto di derivilità per
Cpitolo 3 Derivte 31 Definizione **Definizione 31 (Punto di derivilità) Si f :[, ]! R un funzione e si 2 [, ] Allor f si dice derivile in se esiste finito il In questo cso si dice punto di derivilità per
Appunti di calcolo integrale
 prte II Integrle definito Liceo Scientifico A. Volt - Milno 23 mrzo 2017 Integrle definito Si y = f (x) un funzione continu in I = [, b]. Si chim trpezoide l figur curviline pin delimitt: dl grfico dell
prte II Integrle definito Liceo Scientifico A. Volt - Milno 23 mrzo 2017 Integrle definito Si y = f (x) un funzione continu in I = [, b]. Si chim trpezoide l figur curviline pin delimitt: dl grfico dell
Anno 5. Applicazione del calcolo degli integrali definiti
 Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
7. Derivate Definizione 1
 7. Derivte Il concetto di derivt è importntissimo e molto nturle. Per vere un esempio concreto, penste l moto di un mcchin: se f(t) è l funzione che esprime qunt strd vete percorso fino d un certo istnte
7. Derivte Il concetto di derivt è importntissimo e molto nturle. Per vere un esempio concreto, penste l moto di un mcchin: se f(t) è l funzione che esprime qunt strd vete percorso fino d un certo istnte
Integrale definito (p.204)
 Integrle definito (p.4) Trttimo dei cenni sull teori dell integrzione nel cso di funzioni continue (integrle di Cuchy). Gli integrli si estendono l cso di funzioni limitte (integrle di Riemnn). Nel clcolo
Integrle definito (p.4) Trttimo dei cenni sull teori dell integrzione nel cso di funzioni continue (integrle di Cuchy). Gli integrli si estendono l cso di funzioni limitte (integrle di Riemnn). Nel clcolo
Il problema delle aree. Metodo di esaustione.
 INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
Integrale definito (p.204)
 Integrle definito (p.04) Trttimo dei cenni sull teori dell integrzione nel cso di funzioni continue (integrle di Cuchy). Gli integrli si estendono l cso di funzioni limitte (integrle di Riemnn). Nel clcolo
Integrle definito (p.04) Trttimo dei cenni sull teori dell integrzione nel cso di funzioni continue (integrle di Cuchy). Gli integrli si estendono l cso di funzioni limitte (integrle di Riemnn). Nel clcolo
Foglio N.3. PRIMITIVE. Pn (x) Q m (x) dx
 Integrli di Funzioni Rzionli: Foglio N3 PRIMITIVE Pn (x) Q m (x) dx dove P n (x) e Q m (x) sonopolinomidigrdon ed m rispettivmente Un funzione rzionle il cui denomintore P n (x) è un polinomio di grdo
Integrli di Funzioni Rzionli: Foglio N3 PRIMITIVE Pn (x) Q m (x) dx dove P n (x) e Q m (x) sonopolinomidigrdon ed m rispettivmente Un funzione rzionle il cui denomintore P n (x) è un polinomio di grdo
FUNZIONI IPERBOLICHE
 FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI
 FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
Integrali in senso generalizzato
 Integrli in senso generlizzto Pol Rubbioni Anlisi Mtemtic II - CdL in Ingegneri Informtic ed Elettronic.. 6/7 Integrzione su domini non itti Definizione. Un funzione continu f : [, + [ R si dice integrbile
Integrli in senso generlizzto Pol Rubbioni Anlisi Mtemtic II - CdL in Ingegneri Informtic ed Elettronic.. 6/7 Integrzione su domini non itti Definizione. Un funzione continu f : [, + [ R si dice integrbile
26/03/2012. Integrale Definito. Calcolo delle Aree. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi:
 ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 11 - Integrli Anno Accdemico 2015/2016 M. Tumminello, V. Lcgnin,
Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 11 - Integrli Anno Accdemico 2015/2016 M. Tumminello, V. Lcgnin,
Definizione (primitiva, integrale indefinito). Data una funzione f diremo che una funzione F è una primitiva di f se
 Cpitolo 6 Integrli L opertore derivt D ssoci d un funzione f l su derivt: Df f 0 Ci ciedimo se è possiile invertire quest operzione, vle dire trovre un funzione l cui derivt si un funzione ssegnt Definizione
Cpitolo 6 Integrli L opertore derivt D ssoci d un funzione f l su derivt: Df f 0 Ci ciedimo se è possiile invertire quest operzione, vle dire trovre un funzione l cui derivt si un funzione ssegnt Definizione
Tutorato di analisi 1
 Tutorto di nlisi 1 Alen Kushov Collegio Volt 1 / 8 Introduzione Integrzione ll Riemnn Integrle orientto Linerità dell integrle Teorem fondmentle del clcolo Regole di clcolo Integrli impropri 2 / 8 Integrzione
Tutorto di nlisi 1 Alen Kushov Collegio Volt 1 / 8 Introduzione Integrzione ll Riemnn Integrle orientto Linerità dell integrle Teorem fondmentle del clcolo Regole di clcolo Integrli impropri 2 / 8 Integrzione
CAPITOLO 5. Integrazione
 CAPITOLO 5 Integrzione 1. L re di un sottogrfico: strtegi d ttcco È opinione comune che conoscere l re di un regione del pino si proprietà utile. Tringoli, rettngoli, cerchi e qulche ltr mncit di oggetti
CAPITOLO 5 Integrzione 1. L re di un sottogrfico: strtegi d ttcco È opinione comune che conoscere l re di un regione del pino si proprietà utile. Tringoli, rettngoli, cerchi e qulche ltr mncit di oggetti
7 Simulazione di prova d Esame di Stato
 7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
UNITA 13. GLI ESPONENZIALI
 UNITA. GLI ESPONENZIALI. Le potenze con esponente intero, rzionle e rele.. Le proprietà delle potenze.. Equzioni esponenzili che si riconducono ll stess bse. 4. L funzione esponenzile. 5. Il grfico dell
UNITA. GLI ESPONENZIALI. Le potenze con esponente intero, rzionle e rele.. Le proprietà delle potenze.. Equzioni esponenzili che si riconducono ll stess bse. 4. L funzione esponenzile. 5. Il grfico dell
Capitolo 2. Il problema del calcolo delle aree
 Cpitolo 2 Il prolem del clcolo delle ree Introduzione Il prolem del clcolo delle ree nsce più di 2000 nni f qundo i greci tentrono di clcolre le ree con un metodo detto di esustione. Tle metodo può essere
Cpitolo 2 Il prolem del clcolo delle ree Introduzione Il prolem del clcolo delle ree nsce più di 2000 nni f qundo i greci tentrono di clcolre le ree con un metodo detto di esustione. Tle metodo può essere
Integrali in senso generalizzato
 Integrli in senso generlizzto Pol Rubbioni Integrzione su domini non itti Definizione.. Un funzione continu f : [, + [ R si dice integrbile in senso generlizzto (brevemente, G-integrbile) se esiste finito
Integrli in senso generlizzto Pol Rubbioni Integrzione su domini non itti Definizione.. Un funzione continu f : [, + [ R si dice integrbile in senso generlizzto (brevemente, G-integrbile) se esiste finito
Verica di Matematica su Integrale Denito, Integrazione Numerica e calcolo di aree [1]
![Verica di Matematica su Integrale Denito, Integrazione Numerica e calcolo di aree [1] Verica di Matematica su Integrale Denito, Integrazione Numerica e calcolo di aree [1]](/thumbs/87/96430750.jpg) Veric di Mtemtic su Integrle Denito, Integrzione Numeric e clcolo di ree []. Si consideri il seguente integrle denito: Determinre il vlore estto di I; I = 2 ( e x )dx. il vlore estto dell're A T del trpezoide
Veric di Mtemtic su Integrle Denito, Integrzione Numeric e clcolo di ree []. Si consideri il seguente integrle denito: Determinre il vlore estto di I; I = 2 ( e x )dx. il vlore estto dell're A T del trpezoide
Analisi Corso di Laurea in Fisica e Astrofisica. Registro didattico A.A
 Anlisi Corso di Lure in Fisic e Astrofisic Registro didttico A.A. 2011 2012 2 febbrio 2012 Lezione 1-2 (4 ottobre 2011). Numeri nturli, interi, irrzionli, rzionli. Dimostrzione dell irrzionlità di 2. Numeri
Anlisi Corso di Lure in Fisic e Astrofisic Registro didttico A.A. 2011 2012 2 febbrio 2012 Lezione 1-2 (4 ottobre 2011). Numeri nturli, interi, irrzionli, rzionli. Dimostrzione dell irrzionlità di 2. Numeri
CORSO DI CALCOLO E BIOSTATISTICA. A.A APPUNTI SUGLI INTEGRALI
 CORSO DI CALCOLO E BIOSTATISTICA. A.A. 212-213. APPUNTI SUGLI INTEGRALI Il testo che segue contiene brevi ppunti reltivi lle lezioni svolte sull teori elementre dell integrzione di funzioni reli di un
CORSO DI CALCOLO E BIOSTATISTICA. A.A. 212-213. APPUNTI SUGLI INTEGRALI Il testo che segue contiene brevi ppunti reltivi lle lezioni svolte sull teori elementre dell integrzione di funzioni reli di un
CALCOLO NUMERICO. Francesca Mazzia. a.a. 2008/2009. Integrazione. Dipartimento Interuniversitario di Matematica. Università di Bari
 CALCOLO NUMERICO Frncesc Mzzi Diprtimento Interuniversitrio di Mtemtic Università di Bri.. 2008/2009 Integrzione () 29 mggio 2009 1 / 18 Integrzione Problem: pprossimre integrli definiti del tipo: f (x)dx,
CALCOLO NUMERICO Frncesc Mzzi Diprtimento Interuniversitrio di Mtemtic Università di Bri.. 2008/2009 Integrzione () 29 mggio 2009 1 / 18 Integrzione Problem: pprossimre integrli definiti del tipo: f (x)dx,
Esercizi svolti Limiti. Prof. Chirizzi Marco.
 Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
14 - Integrazione numerica
 Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 4 - Integrzione numeric Anno Accdemico 205/206 M. Tumminello, V.
Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 4 - Integrzione numeric Anno Accdemico 205/206 M. Tumminello, V.
Serie di Potenze. Introduciamo il concetto di convergenza puntuale ed uniforme per successioni. { 0 se 1 < x < 1
 Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
DISPENSE DI ANALISI MATEMATICA. Indice
 DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
IL CONTRIBUTO DEI GRECI. A = b. h. Parallelogramma h. h b
 Mtemtic per Scienze Nturli, Aree ed integrli 1 IL CONTRIBUTO DEI GRECI h Rettngolo: A =. h h Prllelogrmm A =. h h Tringolo A =!h 2 Poligono come somm di tringoli Cerchio O r A = ". r 2 Mtemtic per Scienze
Mtemtic per Scienze Nturli, Aree ed integrli 1 IL CONTRIBUTO DEI GRECI h Rettngolo: A =. h h Prllelogrmm A =. h h Tringolo A =!h 2 Poligono come somm di tringoli Cerchio O r A = ". r 2 Mtemtic per Scienze
1 Equazioni e disequazioni di secondo grado
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
Analisi Matematica 1 Venticinquesima lezione[1cm]integrale di Riemann 5 marzo (cont.) / 20
![Analisi Matematica 1 Venticinquesima lezione[1cm]integrale di Riemann 5 marzo (cont.) / 20 Analisi Matematica 1 Venticinquesima lezione[1cm]integrale di Riemann 5 marzo (cont.) / 20](/thumbs/97/134401325.jpg) Anlisi Mtemtic 1 Venticinquesim lezione Integrle di Riemnn (cont.) prof. Cludio Sccon Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Anlisi Mtemtic 1 Venticinquesim lezione Integrle di Riemnn (cont.) prof. Cludio Sccon Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Formulario di Analisi Matematica 1
 Formulrio di Anlisi Mtemtic Indice degli rgomenti Punti interni, isolti, di ccumulzione e di frontier Alcune costnti Proprietà delle potenze Proprietà degli esponenzili Proprietà dei logritmi Proprietà
Formulrio di Anlisi Mtemtic Indice degli rgomenti Punti interni, isolti, di ccumulzione e di frontier Alcune costnti Proprietà delle potenze Proprietà degli esponenzili Proprietà dei logritmi Proprietà
b a 2. Il candidato spieghi, avvalendosi di un esempio, il teorema del valor medio.
 Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
CALCOLO NUMERICO. Francesca Mazzia. Integrazione. Dipartimento Interuniversitario di Matematica. Università di Bari
 CALCOLO NUMERICO Frncesc Mzzi Diprtimento Interuniversitrio di Mtemtic Università di Bri Integrzione 1 Integrzione Problem: pprossimre integrli definiti del tipo: f(x)dx, Sceglimo n + 1 punti nell intervllo
CALCOLO NUMERICO Frncesc Mzzi Diprtimento Interuniversitrio di Mtemtic Università di Bri Integrzione 1 Integrzione Problem: pprossimre integrli definiti del tipo: f(x)dx, Sceglimo n + 1 punti nell intervllo
Appunti sull integrale di Riemann. Roberto Monti. 11 Gennaio Versione riveduta
 Appunti sull integrle di Riemnn Roberto Monti Gennio - Versione rivedut Indice Cpitolo. Integrle di Riemnn 5. Definizione dell integrle di Riemnn 5. Teorem Fondmentle del Clcolo Integrle 8. Integrzione
Appunti sull integrle di Riemnn Roberto Monti Gennio - Versione rivedut Indice Cpitolo. Integrle di Riemnn 5. Definizione dell integrle di Riemnn 5. Teorem Fondmentle del Clcolo Integrle 8. Integrzione
B8. Equazioni di secondo grado
 B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
Appunti ad uso degli studenti del Corso di Matematica per CTF
 Appunti d uso degli studenti del Corso di Mtemtic per CTF Prof. Sergio Steffè, AA2016/17 Sommrio Questi ppunti sono scritti su misur per gli studenti del corso di Mtemtic per CTF dell Anno Accdemico 2016/17,
Appunti d uso degli studenti del Corso di Mtemtic per CTF Prof. Sergio Steffè, AA2016/17 Sommrio Questi ppunti sono scritti su misur per gli studenti del corso di Mtemtic per CTF dell Anno Accdemico 2016/17,
corrispondenza dal piano in sé, che ad ogni punto P del piano fa corrispondere il punto P' in
 Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Matematica I, Funzione integrale
 Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
" Osservazione. 6.1 Integrale indefinito. R Definizione (Primitiva) E Esempio 6.1 CAPITOLO 6
 CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
Differenziale. Consideriamo la variazione finita, x della variabile indipendente a cui corrisponde una variazione finita della funzione f x, f x y
 Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
11. I teoremi del calcolo differenziale, I
 11. I teoremi del clcolo differenzile, I 11. Funzioni di clsse C 1 Abbimo visto, cfr Cpitolo 9, che l esistenz delle sole derivte przili non è sufficiente grntire l differenzibilit in un punto dto. Pero
11. I teoremi del clcolo differenzile, I 11. Funzioni di clsse C 1 Abbimo visto, cfr Cpitolo 9, che l esistenz delle sole derivte przili non è sufficiente grntire l differenzibilit in un punto dto. Pero
ANALISI REALE E COMPLESSA a.a. 2007-2008
 ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
Calcolo integrale. Capitolo Primitive ed integrale inde nito
 Cpitolo 9 Clcolo integrle 9.1 Primitive ed integrle inde nito De nizione 9.1 Assegnt un funzione f : A! R, si de nisce primitiv di f un qulunque funzione F : A! R derivbile, tle che F 0 (x) = f(x), per
Cpitolo 9 Clcolo integrle 9.1 Primitive ed integrle inde nito De nizione 9.1 Assegnt un funzione f : A! R, si de nisce primitiv di f un qulunque funzione F : A! R derivbile, tle che F 0 (x) = f(x), per
1 Espressioni polinomiali
 1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
Esponenziali e logaritmi
 Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Chapter 1. Integrali doppi
 Chpter 1 Integrli doppi Nelle presenti note esporremo un pproccio semplificto ll teori degli integrli doppi. efiniremo tli integrli direttmente su domini normli, come limiti di opportune somme integrli.
Chpter 1 Integrli doppi Nelle presenti note esporremo un pproccio semplificto ll teori degli integrli doppi. efiniremo tli integrli direttmente su domini normli, come limiti di opportune somme integrli.
Integrali curvilinei (integrali di densità) Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli curvilinei di prim specie (integrli di densità) 15 Dicembre 215 Indice 1 Integrli di line di prim specie
Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli curvilinei di prim specie (integrli di densità) 15 Dicembre 215 Indice 1 Integrli di line di prim specie
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli di line di prim specie (Integrli di densità lungo cmmini non orientti) Gennio 213 Indice 1 Integrli di
Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli di line di prim specie (Integrli di densità lungo cmmini non orientti) Gennio 213 Indice 1 Integrli di
Metodi di integrazione
 CAPITOLO 6 Metodi di integrzione. Introduzione Tnto per comincire, ricordimo i ftti principli che bbimo visto sugli integrli indefiniti: dt un funzione f, un funzione F è un primitiv di f o un integrle
CAPITOLO 6 Metodi di integrzione. Introduzione Tnto per comincire, ricordimo i ftti principli che bbimo visto sugli integrli indefiniti: dt un funzione f, un funzione F è un primitiv di f o un integrle
Erasmo Modica. : K K K
 L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
Analisi e Geometria 1
 Anlisi e Geometri Esercizi sugli integrli Integrli propri. Clcolre i seguenti integrli immediti: I = I = I 5 = ln e e d I = e + e + 6e + e d I = rtg ln ( + ln ) d I 6 = e e + d d rtg + ( + ) ( + ( + )
Anlisi e Geometri Esercizi sugli integrli Integrli propri. Clcolre i seguenti integrli immediti: I = I = I 5 = ln e e d I = e + e + 6e + e d I = rtg ln ( + ln ) d I 6 = e e + d d rtg + ( + ) ( + ( + )
Appunti di Matematica 1 - I polinomi - Polinomi. I vari monomi che compongono il polinomio si chiamano termini del polinomio.
 ppunti di Mtemtic Polinomi Un polinomio è un somm lgebric di monomi. Esempio: b ; y y ; b c sono polinomi. I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche
ppunti di Mtemtic Polinomi Un polinomio è un somm lgebric di monomi. Esempio: b ; y y ; b c sono polinomi. I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche
Matematica generale CTF
 L integrle di Riemn 2 dicembre 2015 Somme di Drboux Considerimo con un funzione sempre positiv, limitt (non necessrimente continu) e definit su un intervllo: f : [, b] R e cerchimo di clcolre l re dell
L integrle di Riemn 2 dicembre 2015 Somme di Drboux Considerimo con un funzione sempre positiv, limitt (non necessrimente continu) e definit su un intervllo: f : [, b] R e cerchimo di clcolre l re dell
Note di Derivate ed Integrali
 1 Note di Derivte ed Integrli Versione 1.0 Lmberto Lmberti & Corrdo Msci prte II Integrle, derivte, teoremi sulle derivte, nlisi locle, nlisi globle 16 Ottobre 2002 2 Indice 1 L integrle 5 1.1 Aree ed
1 Note di Derivte ed Integrli Versione 1.0 Lmberto Lmberti & Corrdo Msci prte II Integrle, derivte, teoremi sulle derivte, nlisi locle, nlisi globle 16 Ottobre 2002 2 Indice 1 L integrle 5 1.1 Aree ed
11. Rango di una matrice.
 Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
ANALISI 1 1 VENTIDUESIMA LEZIONE Integrali impropri
 ANALISI 1 1 VENTIDUESIMA LEZIONE Integrli impropri 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 VENTIDUESIMA LEZIONE Integrli impropri 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
TEST DI MATEMATICA. Funzioni in una, Funzioni in due variabili Integrali Equazioni differenziali. 1) Il valore del limite seguente. e e. e 1.
 TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
PNI SESSIONE SUPPLETIVA QUESITO 1
 www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
Area del Trapezoide. f(x) A f(a) f(b) f(x)
 Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
Dimostrazione del teorema di Gauss Green nel piano
 imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
ORDINAMENTO 2002 SESSIONE STRAORDINARIA - QUESITI QUESITO 1
 www.mtefili.it ORDINAMENTO 2002 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Si D il dominio di un funzione rele di vribile rele f (x) e si x 0 un elemento di D: definire l continuità e l discontinuità di
www.mtefili.it ORDINAMENTO 2002 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Si D il dominio di un funzione rele di vribile rele f (x) e si x 0 un elemento di D: definire l continuità e l discontinuità di
L integrale di Mengoli Cauchy e il teorema fondamentale del calcolo integrale
 SCIENTIA http://www.scientijournl.org/ Interntionl Review of Scientific Synthesis ISSN 2282-2119 Quderni di Mtemtic 215 Mtemtic Open Source http://www.etrbyte.info L integrle di Mengoli Cuchy e il teorem
SCIENTIA http://www.scientijournl.org/ Interntionl Review of Scientific Synthesis ISSN 2282-2119 Quderni di Mtemtic 215 Mtemtic Open Source http://www.etrbyte.info L integrle di Mengoli Cuchy e il teorem
Trasformate di Laplace nel campo reale
 Trsformte di Lplce nel cmpo rele Funzioni generlmente continue Definizione. Un funzione f si dice generlmente continu in (, b) se esistono un numero finito di punti x = < x < < x n = b tli che f è definit
Trsformte di Lplce nel cmpo rele Funzioni generlmente continue Definizione. Un funzione f si dice generlmente continu in (, b) se esistono un numero finito di punti x = < x < < x n = b tli che f è definit
Integrali. all integrale definito all integrale indefinito. Integrali: riepilogo
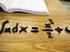 Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx.
![Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx. Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx.](/thumbs/74/71411974.jpg) Cpitolo 6 Serie di Fourier 6.1. Introduzione Un polinomio trigonometrico di grdo N nell intervllo [, π] è un funzione g(x), periodic di periodo, dell form g(x) = N n= N c n e inx per un qulche scelt delle
Cpitolo 6 Serie di Fourier 6.1. Introduzione Un polinomio trigonometrico di grdo N nell intervllo [, π] è un funzione g(x), periodic di periodo, dell form g(x) = N n= N c n e inx per un qulche scelt delle
