1 Probabilità. 1.1 Primi esercizi di probabilità con l uso del calcolo combinatorio
|
|
|
- Teodora Perini
- 8 anni fa
- Visualizzazioni
Transcript
1 Indice 1 Probabilità Primi esercizi di probabilità con l uso del calcolo combinatorio Probabilità condizionata, indipendenza e teorema di Bayes....
2 2
3 1 Probabilità 1.1 Primi esercizi di probabilità con l uso del calcolo combinatorio Esercizio 1 Tre carte vengono estatte in blocco da un mazzo da 52 (4 semi, 1 ranghi. Calcolare la probabilità che a siano tutte di cuori; b siano tutte dello stesso seme; c siano dello stesso rango; d siano due di cuori e una di quadri; e siano due di quadri e una di cuori; I modi di estrarre carte da un mazzo da da 52 sono dati dal coefficiente binomiale di 52 su, ( 52 = 22100, perciò a la probabilità di estartte tre carte di cuori è (1 ( 52 = b la probabilità di estrarre tra carte dello stesso seme, significa che si possono estrarre tre carte di cuori oppure tre carte di fiori, oppure tre carte di picche oppure tre carte di quadri quindi i casi favorevoli sono ( 1 ( 1 ( 1 ( 1 = 4 ( 1 = Quindi, la probabilità di estarre tre carte dello steso seme è = c la probabilità di estrarre tre carte dello stesso rango è data i casi possibili che sono dati da, i casi di avere tre assi, oppure tre due, oppure... tre di un qualsiasi rango. In tal modo, la probabilità è pari a 1 (4 ( 52 = d la probabilità che ci siano due carte di cuori e una di quadri si calcola nel seguente modo ( 1 1 ( 1 2 ( 52 =
4 2 Capitolo 1 e per simmetria, la probabilità di avere di avere due carte di quadri e una di cuori è esattamente uguale alla probabilità di avere due caret di cuori ed una di quadri e quindi il valore calcolato al passo precedente. Esercizio 2 Un progammatore vuole implementare un codice su una calcolatore parallelo costituito da 10 processori: {A, B, C,..., L}. Il codice elaborato richiede l utilizzo di 8 processori. a Quante sono le possibili 8-uple di processori che la macchina può scegliere per svolgere il compito assegnato? b Quale è la probabilità che venga usato il processore A? a È chiaro che il numero di k-tuple che si possono formare da un insieme di n oggetti si calcola utilizzando il coefficiente binomiale di ( n k, quindi nel caso particolare del nostro esercizio, il numero di 8-tiple che si possono formare è dato dal coefficiente binomiale ( 10 8 = 10! 8!2! = = 45. b Per contare quante 8-tuple contengono il processore A si può procedere nel seguente modo: un processore è fissato (è A quindi posso scegliere 7 tra i 9 processori rimanenti e lo posso fare in ( 9 7 modi diversi. La probabilità che venga usato il processore A è data quindi dal rapporto tra i casi favorevoli e i ( casi possibili: 9 7 ( 10 8 = 4 5. Esercizio Il mondiale di Lippi. Per le partite di qualificazione al prossimo mondiale, possiamo ipotizzare che il commissario tecnico della Nazionale Lippi convocherà i seguenti giocatori, divisi per ruolo: Portieri : Abbiati, Amelia, Buffon. Difensori : Barzagli, Pasqual, Cannavaro, Grosso, Zambrotta, Bonera, Santon, Chiellini. Centrocampisti : Aquilani, Camoranesi, De Rossi, Gattuso, Maggio, Montolivo, Perrotta, Pirlo. Attaccanti : Del Piero, Di Natale, Gilardino, Inzaghi, Rossi, Toni. Ipotizziamo, inoltre, che Lippi voglia giocare con un 4--. a Quante possibili squadre potrebbe mettere in campo? b Nell ipotesi in cui i giocatori di uno stesso ruolo abbiano la stessa probabilità di giocare, qual è la probabilità che Toni giochi? E che Toni e De Rossi giochino insieme? a Ragionando in un modo irragionevole, cioè non distinguendo i ruoli dei giocatori, i modi possibili di scegliere 11 atleti tra i 25 possibili sono dati da ( = Ragionando in maniera più reale, invece, i modi possibili di
5 Probabilità disporre i giocatori in campo, oltre al 4-- prescelto da Lippi, possono essere 4-4-2, 4-5-1, -4- e -5-2, così che, il numero di modi possibili diventa pari a ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( = Considerando unicamente il 4-- Lippi può metter in campo solo ( ( ( ( = squadre. b Ragionando come nell esercizio precedente, possiamo dire che, avendo deciso di far giocare Toni, Lippi può sceglire due attaccanti sui 5 che gli rimangono, per cui i casi favorevoli sono ( ( 4( ( 2, mentre i casi possibili sono ( ( 8 ( 8 ( 6 1 4, per cui la probabilità che giochi Toni, avendo fissato lo schema 4-- è data da ( 1( 8 4( 8 ( 5 2 ( 1( 8 4( 8 ( 6 = 0.5. Per calcolatre la probabilità che giochino insieme Toni e De Rossi bisogna calcolare i casi favorevoli a questo evento (i casi possibili sono ( ( 4( (. Se Lippi volesse schierare in campo Toni, avrebbe ancora due attaccanti da scegliere sui 5 rimanenti e, se volesse far giocare De Rossi, avrebbe da scegliere ancora due centrocampisti dei 7 rimanenti, per cui il numero delle formazioni 4-- con Toni e De Rossi sicuramente presenti in campo è ( ( 4( 2( 2 e la probabilità che giochino Toni e De Rossi è data da ( 1( 8 4( 7 2( 5 2 ( 1( 8 4( 8 ( 6 = Probabilità condizionata, indipendenza e teorema di Bayes Esercizio 4 Un fruttivendolo al mercato è decisamente furbo: nasconde i difetti delle mele che vende rivolgendo al cliente la parte migliore della buccia. Così a guardare le cassette di mele che espone, tutte sembrano perfette. Ma sappiamo che nella prima il 70% delle mele è intatto, nella seconda il 20%, nella terza il 50%. Le cassette contengono, ognuna, 0 mele. Decido di comprare una sola mela, e per decidere da quale cassetta estrarla, tiro un dado: se esce un numero minore di scelgo dalla prima, tra e 5 (escluso dalla seconda, altrimenti dalla terza. a Qual é la probabilità che la mela scelta sia buona? b Qual è la probabilitá che il dado abbia restituito 4 se ho trovato invece una mela marcia? Definiamo i seguenti eventi: B = {la mela scelta è buona}; M = {la mela scelta è marcia}; I = {si estrae la mela dalla prima cassetta}; II =
6 4 Capitolo 1 {si estrae la mela dalla seconda cassetta}; III = {si estrae la mela dalla terza cassetta}; per rispondere alla prima domanda occorre calcolare, con la legge delle probabilità totali P (B = P (B IP (I P (B IIP (II P (B IIIP (III = = = ; Osserviamo ora che la probabilità di ottenere 4 lanciando un dado è chiaramente 1/6, pertanto si ha P (4 M = P (M 4P (4 P (M = 0.8 1/6 1 7/15 = 1 4. Esercizio 5 Supponiamo di avere due urne, ognuna con 50 palline. Nella prima 20 sono rosse e le restanti bianche, nella seconda 10 sono bianche e le restanti rosse. Estraggo una pallina dalla prima urna: se è bianca la reinserisco ed estraggo una pallina dalla seconda, altrimenti la reinserisco e riestraggo una pallina dalla prima. a Qual è la probabilità di ottenere una rossa alla seconda estrazione. b Se si ottiene una pallina bianca alla seconda estrazione, qual è la probabilità che anche la prima fosse bianca? c Qual è la probabilità che si siano ottenute due palline dello stesso colore? a La probabilità di avere una pallina rossa alla seconda estrazione si ottiene applicando la legge delle probabilità totali; pertanto, denotando con ir ed ib, i = 1, 2, rispettivamente gli eventi la i-esima pallina estratta è rossa e la i-esima pallina estratta è bianca, Inoltre, poiché P (2R = P (2R 1RP (1R P (2R 1BP (1B = = = P (2B = P (2B 1RP (1R P (2B 1BP (1B = = = 9 25 = 1 P (2R, per il teorema di Bayes si ha
7 Probabilità 5 b P (1B 2B = = P (2B 1BP (1B P (2B 1/5 /5 = 1 9/25 ; = c dal momento che le estrazioni avvengono in ogni caso con reinserimento, la probabilità richiesta vale P (1R 2R = = Esercizio 6 Supponiamo di avere due urne, ognuna con 40 palline. Nella prima, il 20% sono rosse e le restanti bianche, nella seconda 5% sono bianche e le restanti rosse. Estraggo una pallina dalla prima urna: se è bianca tiro una moneta truccata con trucco p = 1/ (cioè la probabilità di ottenere testa è 1/. Se esce testa, reinserisco la pallina estratta ed estraggo una pallina dalla seconda urna, se esce croce, reinserisco ed estraggo una seconda pallina dalla prima urna. Se la pallina estratta è invece rossa, non la reinserisco e ne estraggo una seconda dalla prima urna. a Qual è la probabilità di ottenere una rossa alla seconda estrazione. b Se si ottiene una pallina bianca alla seconda estrazione, qual è la probabilità che anche la prima fosse bianca? c Qual è la probabilità che sia abbia ottenuto due palline dello stesso colore? d Per avere due palline dello stesso colore, mi conviene usare la moneta truccata o una moneta equa? a Con la medesima notazione dell esercizio precedente, calcolando le seguenti probabilità P (2R 1R = 7/9, P (1R = 8/40, P (1B = 2/40, per la legge delle probabilità totali vale che P (2R = P (2R 1RP (1R P (2R 1BP (1B. Rimane da valutare la P (2R 1B, sempre con la legge delle probabilità totali, ma con un dfferente evento condizionante: P (2R 1B = P ({2R 1B} T P (T P ({2R 1B} CP (C = = = 9 20.
8 6 Capitolo 1 Pertanto la P (2R richiesta, vale P (2R = P (2R 1RP (1R P (2R 1BP (1B = = = = b Con il teorema di Bayes si calcola P (1B 2B = P (2B 1BP (1B ; P (2B ma occorre valutare anche e P (2B 1B = P ({2B 1B} T P (T P ({2B 1B} CP (C = = = 11 20, Quindi P (2B = P (2B 1BP (1B P (2B 1RP (1R = = = P (1B 2B = P (2B 1BP (1B P (2B = c Vale che: P (1R 2R = P (1RP (2R = ; P (1B 2B = P (1BP (2B = d Ripetendo gli stessi calcoli utilizzando una moneta equa, si ottiene che P (1R 2R ; P (1B 2B , e quindi, rimanendo invariata la seconda probabilità (perché non dipende dal lancio della moneta, la prima migliora con l utilizzo della moneta equa.
9 Probabilità 7 Esercizio 7 Il test ELISA è una tecnica biochimica utilizzata in immunologia per svelare la presenza di un anticorpo o un antigene in un campione, ed generalmente utilizzato come strumento diagnostico per l AIDS. Uno dei suoi maggiori problemi, è la sua specificità (probabilità che un campione sano risulti negativo al test non perfetta. Si sa che questo test da esito negativo se è effettivamente presente il virus (falso negativo con probabilità , mentre da esito positivo anche se il virus non è presente (falso positivo con probabiltià È anche stimata in 2 casi su 1000 individui la presenza di portatori del virus HIV. a Calcolare la probabiltà che un paziente con un test positivo sia malato; b Calcolare la probabiltà che un paziente con un test positivo sia sano; c Calcolare la probabiltà che un paziente con un test negativo sia malato; d Calcolare la probabiltà che un paziente con un test negativo sia sano; Siano gli eventi - = {il test è negativo}, = {il test è positivo}, V = {il paziente è malato}, V c = {il paziente è sano}; vale quindi che a P ( V = , P ( V c = 0.014, P (V = P (V = = P ( V P (V P ( V P (V P ( V c P (V c = / / / , dove evidentemente P ( V = 1 P ( V = b Vale banalmente che c P (V = = d Di conseguenza P (V c = 1 P (V 0.876, P ( V P (V P ( V P (V P ( V c P (V c = / /1000 ( / P (V c = 1 P (V = Esercizio 8 Gioco alla roulette americana (8 numeri: {00, 0, 1,..., 6} e decido di puntare sul rosso o sul nero a seconda che il lancio di una moneta di trucco 1/4 (che eseguo di nascosto mi dia testa o croce.
10 8 Capitolo 1 a Qual è la probabilità di vincere ad ogni giocata? b Se ho perso alla prima giocata, posso ritenere che la mia moneta sia ingannevole nell indirizzarmi la seconda puntata? c E se invece ho vinto, posso continuare tranquillamente a credere nel potere divinatorio della mia moneta? a La roulette è costituita da 18 numeri neri, 18 rossi, lo 0 ed il 00, dunque la probabilità di vincere ad ogni giocata è p = ; osserviamo che la probabilità di perdere ad ogni lancio è 1 p = 20 8 ; ad ogni giocata, se si suppone che la vincita consista soltanto nel recuperare il valore della giocata, il gioco non è equo, perché il valore atteso della vincita è minore di zero. Supponendo infatti di giocare g, e che l evento V rappresenti la vincita, con una simbologia che risulterà chiara nel seguito possiamo scrivere, per ogni giocata E(V = g 18 8 g = 20 8 g. La roulette dovrebbe garantire una vincita ad ogni giocata di 8/ volte la posta, per rendere il gioco equo ad ogni scommessa. b La probabilità di perdere la seconda giocata dato che si è già persa la prima, risulta uguale sempre a 1 p, indipendentemente dal colore che gioco, e quindi dal trucco della moneta. Per convincercene utilizziamo la definizione di probabilità condizionata: P (perdere II lancio perso al I lancio = P (perdere II lancio perso al I lancio. P (perdere I lancio Il valore del denominatore, in dipendenza dalla giocata, dovrebbe essere per la legge delle probabilità totali P (perdere I lancio = P (perdere I lancio giocato rossop (rosso P (perdere I lancio giocato nerop (nero = = = 20 8, che, come si vede, in realtà è indipendente dalla giocata che si compie. Per quanto riguarda il numeratore, la probabilità può essere visualizzata utilizzando il seguente albero:
11 Probabilità 9 Esercizio 9 Un dado equilibrato viene lanciato due volte. a Qual è la probabilità che il punteggio ottenuto sia maggiore di 9, ammesso che uno dei due dadi mostri la faccia 5? b Qual è la probabilità di ottenere un punteggio maggiore di 9 se con il primo lancio il punteggio ottenuto è 5? c Qual è la probabilità di ottenere un punteggio maggiore di 9 se con il secondo lancio il punteggio ottenuto è 5? Esercizio 10 Decido di lanciare 10 monete finchè non ottengo 8 teste (cioè: annullo il lancio e lo ripeto se non sono uscite almeno 8 teste. Che probabilità ho di ottenere testa su tutte le 10 monete? L esperimento consiste nel lancio di 10 monete a priori indipendenti; ognuna ha probabilità 1/2 di presentare testa dopo il lancio. Pertanto P (10 teste = ( 1 10 = Esercizio 11 In un paese lontano la popolazione è costituita solo da donne. Il 50% ha i capelli neri, il 0% i capelli biondi, il 20% rossi. Le nere sono sempre in ritardo agli appuntamenti, il 60% delle bionde arriva in ritardo, mentre le rosse ritardatarie sono il 90%. Diamo un appuntamento ad una ragazza del paese, senza sapere nulla di lei. a Con quale probabilità arriverà in ritardo? b È in ritardo: con quale probabilità è bionda? a Per la legge delle probabilità totali si ha P (ritardo = P (ritardo morap (mora P (ritardo biondap (bionda P (ritardo rossap (rossa = = = b Direttamente dal teorema di Bayes si ottiene P (ritardo biondap (bionda P (bionda ritardo = = P (ritardo = Esercizio 12 Un urna contiene 10 palline bianche e 10 rosse. Estraggo una pallina: se è bianca la reinserisco nell urna con una dello stesso colore, se è rossa lancio una moneta equilibrata e reinserisco la pallina estratta con 2 dello stesso colore se esce testa, con se esce croce.
12 10 Capitolo 1 a Qual è la composizione dell urna dopo un estrazione? E dopo due? b.1 Dopo la procedura descritta, decido di estrarre due palline in sequenza. Qual è la probabilità di estrarre una rossa come seconda? b.2 Se ho estratto una pallina rossa come seconda, qual è la probabilità che la prima fosse bianca? E che fosse rossa? Esercizio 1 Abbiamo due urne: una composta da palline bianche e 2 nere, la seconda composta da 4 palline bianche e nere. Lancio una moneta equa (la probabilità di avere testa è uguale alla probabilità di avere croce ed è pari ad un mezzo: se esce testa estraggo dalla prima urna, se esce croce estraggo dalla seconda urna. a Calcolare la probabilità che la pallina estratta sia nera; b Calcolare la probabilità che la moneta abbia dato croce sapendo che è uscita una pallina bianca. Definiamo i seguenti eventi T= esce testa nel lancio della moneta ; C= esce croce nel lancio della moneta ; N= viene estratta una pallina nera; B= viene estratta una pallina bianca. a La probabilità di avere una pallina nera si calcola usando il teorema della probabilità totali, cioè la probabilità di avere una nera e testa nel lancio della moneta più la la probabilità di avere una nera e croce nel lancio della moneta P (N = P (N T P (N C. Per il teorema della probabilità condizionata si ha P (N = P (N T P (T P (N C P (C = =... = La situazione è ben descritta in Figura 1.1. b Viene richiesto di calcolare P (C B. Si usa il teorema di Bayes come segue P (C B = P (B C P (B = P (B C P (C P (B C P (C P (B T P (T = = = Esercizio 14 (Urne di Polya Un urna contiene palline bianche 5 rosse. Si estrae una pallina a caso: se è bianca la si rimette nell urna insieme ad altre due bianche; se esce una rossa la si rimette nell urna insieme ad un altra bianca. Si procede quindi in altre due estrazioni seguendo sempre la stessa legge.
13 Probabilità 11 P (T = 1 2 P (C = P (B = 5 P (N = 2 5 P (B = 4 P (N = Figura 1.1 Figura ad albero relativa all Esercizio 1 a Qual è la probabilità che le tre palline estratte siano tutte rosse? b Qual è la probabilità che le tre palline estratte siano tutte dello stesso colore? In Figura 1.2 son schematizzate le tre estrazioni successive. Indichiamo con R i l evento all i-esima estrazione la pallina è rossa B, 5R... B 1 R 1 5B, 5R.. 4B, 5R B 2 R 2 R 2 B 2 6B, 5R. 6B, 5R 6B, 5R 5B, 5R R B R B R B R B Figura 1.2 Figura ad albero relativa all Esercizio 14
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
ESERCIZI. x + 3 x 2 1. a) y = 4x2 + 3x 2x + 2 ; b) y = 6x2 x 1. (x + 2) 2 c) y =
 ESERCIZI Testi (1) Un urna contiene 20 palline di cui 8 rosse 3 bianche e 9 nere; calcolare la probabilità che: (a) tutte e tre siano rosse; (b) tutte e tre bianche; (c) 2 rosse e una nera; (d) almeno
ESERCIZI Testi (1) Un urna contiene 20 palline di cui 8 rosse 3 bianche e 9 nere; calcolare la probabilità che: (a) tutte e tre siano rosse; (b) tutte e tre bianche; (c) 2 rosse e una nera; (d) almeno
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Si considerino gli eventi A = nessuno studente ha superato l esame e B = nessuno studente maschio ha superato l esame. Allora A c B è uguale a:
 TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Ancora sull indipendenza. Se A e B sono indipendenti allora lo sono anche
 Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Esercizi di calcolo combinatorio
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
A = { escono 2 teste e due croci (indipendentemente dall ordine) } B = { al primo tiro esce testa }.
 ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
Probabilità e Statistica Esercitazioni. a.a. 2006/2007
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Esercizi sul calcolo delle probabilità
 Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni
 Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes
 Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Esercizi di Calcolo delle Probabilità (calcolo combinatorio)
 Esercizi di Calcolo delle Probabilità (calcolo combinatorio 1. Lanciamo due dadi regolari. Qual è la probabilità che la somma delle facce rivolte verso l alto sia pari a 7? 1/6 2. Due palline vengono estratte
Esercizi di Calcolo delle Probabilità (calcolo combinatorio 1. Lanciamo due dadi regolari. Qual è la probabilità che la somma delle facce rivolte verso l alto sia pari a 7? 1/6 2. Due palline vengono estratte
Statistica 1. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Capitolo 4 Probabilità
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Somma logica di eventi
 Somma logica di eventi Da un urna contenente 24 palline numerate si estrae una pallina. Calcolare la probabilità dei seguenti eventi: a) esce un numero divisibile per 5 o superiore a 20, b) esce un numero
Somma logica di eventi Da un urna contenente 24 palline numerate si estrae una pallina. Calcolare la probabilità dei seguenti eventi: a) esce un numero divisibile per 5 o superiore a 20, b) esce un numero
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Probabilità e Statistica Esercitazioni. a.a. 2009/2010. C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico.
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Probabilità Ines Campa e Marco Longhi Probabilità e Statistica - Esercitazioni
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Probabilità Ines Campa e Marco Longhi Probabilità e Statistica - Esercitazioni
Corso di Matematica. Corso di Laurea in Farmacia, Facoltà di Farmacia. Università degli Studi di Pisa. Maria Luisa Chiofalo.
 Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
1 Probabilità condizionata
 1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
1 Probabilità condizionata Accade spesso di voler calcolare delle probabilità quando si è in possesso di informazioni parziali sull esito di un esperimento, o di voler calcolare la probabilità di un evento
COMPITO n. 1. 3. Siano X, Y due variabili aleatorie tali che il vettore (X, Y ) sia distribuito uniformemente
 COMPITO n. 1 a) Nel gioco del poker ad ogni giocatore vengono distribuite cinque carte da un normale mazzo di 52. Quant è la probabilità che un giocatore riceva una scala di re (ovvero 9, 10, J, Q, K anche
COMPITO n. 1 a) Nel gioco del poker ad ogni giocatore vengono distribuite cinque carte da un normale mazzo di 52. Quant è la probabilità che un giocatore riceva una scala di re (ovvero 9, 10, J, Q, K anche
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Esercitazioni del corso di Statistica Proff. Mortera/Vicard a.a. 2011/2012
 Esercitazioni del corso di Statistica Proff. Mortera/Vicard a.a. 2011/2012 Esercizi di calcolo delle probabilità 1. Nel 1980 la popolazione USA era così composta: 10% della California, 6% di origine ispanica,
Esercitazioni del corso di Statistica Proff. Mortera/Vicard a.a. 2011/2012 Esercizi di calcolo delle probabilità 1. Nel 1980 la popolazione USA era così composta: 10% della California, 6% di origine ispanica,
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Corso di Calcolo delle Probabilità e Statistica. Esercizi su variabili aleatorie discrete
 Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
COEFFICIENTI BINOMIALI
 COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 9 giugno 006 Spazi di probabilità finiti e uniformi Esercizio Un urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare
Esercizi di Probabilità e Statistica Samuel Rota Bulò 9 giugno 006 Spazi di probabilità finiti e uniformi Esercizio Un urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
Calcolare la probabilità dei seguenti eventi: P(fare ambo con i numeri 7 ed 17 con le prime due estrazioni):
 ESERCIZIO 1 Il signor Felice sta giocando a tombola nel circolo PASSATEMPO e ha deciso di giocare usando la sola cartella di seguito riportata: 7 17 26 40 74 1 14 50 69 87 13 43 57 62 73 Serie 1, n. 1
ESERCIZIO 1 Il signor Felice sta giocando a tombola nel circolo PASSATEMPO e ha deciso di giocare usando la sola cartella di seguito riportata: 7 17 26 40 74 1 14 50 69 87 13 43 57 62 73 Serie 1, n. 1
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
La variabile casuale Binomiale
 La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
Esericizi di calcolo combinatorio
 Esericizi di calcolo combinatorio Alessandro De Gregorio Sapienza Università di Roma alessandrodegregorio@uniroma1it Problema (riepilogativo) La segretaria di un ufficio deve depositare 3 lettere in 5
Esericizi di calcolo combinatorio Alessandro De Gregorio Sapienza Università di Roma alessandrodegregorio@uniroma1it Problema (riepilogativo) La segretaria di un ufficio deve depositare 3 lettere in 5
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Esercizio 1. Svolgimento
 Esercizio 1 Vengono lanciate contemporaneamente 6 monete. Si calcoli: a) la probabilità che si presentino esattamente 2 testa ; b) la probabilità di ottenere almeno 4 testa ; c) la probabilità che l evento
Esercizio 1 Vengono lanciate contemporaneamente 6 monete. Si calcoli: a) la probabilità che si presentino esattamente 2 testa ; b) la probabilità di ottenere almeno 4 testa ; c) la probabilità che l evento
1 di 6. Usando un modello di probabilità
 Corso di Statistica, II parte ESERCIZIO 1 Gastone in occasione di una festa a PAPEROPOLI compra 3 biglietti per partecipare all'estrazione a sorte di 3 premi. Sapendo che sono stati venduti 30 biglietti
Corso di Statistica, II parte ESERCIZIO 1 Gastone in occasione di una festa a PAPEROPOLI compra 3 biglietti per partecipare all'estrazione a sorte di 3 premi. Sapendo che sono stati venduti 30 biglietti
Test statistici di verifica di ipotesi
 Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Calcolo combinatorio
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Problema del condannato*
 Problema del condannato* Esempio 35 In un paese orientale un prigioniero è stato condannato a morte da uno sceicco. Prima dell esecuzione, lo sceicco o re una possibilità di salvezza al condannato, mettendogli
Problema del condannato* Esempio 35 In un paese orientale un prigioniero è stato condannato a morte da uno sceicco. Prima dell esecuzione, lo sceicco o re una possibilità di salvezza al condannato, mettendogli
Elementi di calcolo delle probabilità
 Elementi di calcolo delle probabilità Definizione di probabilità A) Qui davanti a me ho un urna contenente 2 palline bianche e 998 nere. Mi metto una benda sugli occhi, scuoto ripetutamente l urna ed estraggo
Elementi di calcolo delle probabilità Definizione di probabilità A) Qui davanti a me ho un urna contenente 2 palline bianche e 998 nere. Mi metto una benda sugli occhi, scuoto ripetutamente l urna ed estraggo
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Anteprima Finale Categoria Corsi di Statistica
 1 di 8 08/04/2011 9.01 SiS-Scuola-28-SEZIONE STATISTICA fad TC128STAT Quiz Finale Categoria Corsi di Statistica Tentativo 1 Sei collegato come piero zulli. (Esci) Info Risultati Anteprima Modifica Anteprima
1 di 8 08/04/2011 9.01 SiS-Scuola-28-SEZIONE STATISTICA fad TC128STAT Quiz Finale Categoria Corsi di Statistica Tentativo 1 Sei collegato come piero zulli. (Esci) Info Risultati Anteprima Modifica Anteprima
Tutorato di Probabilità e Statistica
 Università Ca Foscari di Venezia Dipartimento di informatica 20 aprile 2006 Variabili aleatorie... Example Giochiamo alla roulette per tre volte 1 milione sull uscita del numero 29. Qual è la probabilità
Università Ca Foscari di Venezia Dipartimento di informatica 20 aprile 2006 Variabili aleatorie... Example Giochiamo alla roulette per tre volte 1 milione sull uscita del numero 29. Qual è la probabilità
Il prodotto di tre numeri in progressione aritmetica è 16640, il più piccolo è 20. Calcolare i tre numeri.
 Scrivi i primi termini delle seguenti successioni: =1; =; = + Individua la legge che genera ognuna delle seguenti successioni: -1,, -, 4, -5, In una progressione aritmetica la somma del primo, quarto,
Scrivi i primi termini delle seguenti successioni: =1; =; = + Individua la legge che genera ognuna delle seguenti successioni: -1,, -, 4, -5, In una progressione aritmetica la somma del primo, quarto,
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Esercitazioni 2013/14
 Esercitazioni 2013/14 Esercizio 1 Due ditte V e W partecipano ad una gara di appalto per la costruzione di un tratto di autostrada che viene assegnato a seconda del prezzo. L offerta fatta dalla ditta
Esercitazioni 2013/14 Esercizio 1 Due ditte V e W partecipano ad una gara di appalto per la costruzione di un tratto di autostrada che viene assegnato a seconda del prezzo. L offerta fatta dalla ditta
PROBABILITA' E VARIABILI CASUALI
 PROBABILITA' E VARIABILI CASUALI ESERCIZIO 1 Due giocatori estraggono due carte a caso da un mazzo di carte napoletane. Calcolare: 1) la probabilità che la prima carta sia una figura oppure una carta di
PROBABILITA' E VARIABILI CASUALI ESERCIZIO 1 Due giocatori estraggono due carte a caso da un mazzo di carte napoletane. Calcolare: 1) la probabilità che la prima carta sia una figura oppure una carta di
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Esercizi di Ricerca Operativa II
 Esercizi di Ricerca Operativa II Raffaele Pesenti January 12, 06 Domande su utilità 1. Determinare quale è l utilità che un giocatore di roulette assegna a 100,00 Euro, nel momento che gioca tale cifra
Esercizi di Ricerca Operativa II Raffaele Pesenti January 12, 06 Domande su utilità 1. Determinare quale è l utilità che un giocatore di roulette assegna a 100,00 Euro, nel momento che gioca tale cifra
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
ESERCIZI EVENTI E VARIABILI ALEATORIE
 ESERCIZI EVENTI E VARIABILI ALEATORIE 1) Considera la tabella seguente, che descrive la situazione occupazionale di 63 persone in relazione al titolo di studio. Occupazione SI NO Titolo Licenza media 5%
ESERCIZI EVENTI E VARIABILI ALEATORIE 1) Considera la tabella seguente, che descrive la situazione occupazionale di 63 persone in relazione al titolo di studio. Occupazione SI NO Titolo Licenza media 5%
CARTE. Regolamento Belote. Regole del gioco: Determinazione del seme di briscola (Belote classico):
 CARTE aggiornato al 25/06/2014 Entrambe le gare di carte si svolgeranno presso il salone Polivalente di Pinasca. Entrambe le gare saranno giocate da giocatori in coppia, la coppia può essere diversa nelle
CARTE aggiornato al 25/06/2014 Entrambe le gare di carte si svolgeranno presso il salone Polivalente di Pinasca. Entrambe le gare saranno giocate da giocatori in coppia, la coppia può essere diversa nelle
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 9 marzo 2010 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2010.html TEOREMI DI ESISTENZA TEOREMI DI ESISTENZA Teorema
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 9 marzo 2010 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2010.html TEOREMI DI ESISTENZA TEOREMI DI ESISTENZA Teorema
Teoria della probabilità Assiomi e teoremi
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Assiomi e teoremi A.A. 2008-09 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Assiomi e teoremi A.A. 2008-09 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento
Regolamento In italiano
 Exploding Kittens Regolamento In italiano Giocatori: 2-5 (fino a 9 se si uniscono due mazzi) Contenuto: 56 carte Ehi! Non leggete questo regolamento! Leggere è il modo peggiore per imparare a giocare a
Exploding Kittens Regolamento In italiano Giocatori: 2-5 (fino a 9 se si uniscono due mazzi) Contenuto: 56 carte Ehi! Non leggete questo regolamento! Leggere è il modo peggiore per imparare a giocare a
Appunti ed esercizi di combinatoria. Alberto Carraro
 Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
Pinella Singolo ASC-CAAM 2013/14
 Pinella Singolo ASC-CAAM 2013/14 Vedi Calendario Premi del campionato ( si svolge in 4/5 tappe di qualificazione ) : > Trofei per i primi nr 4 ( quattro ) > Ai prmi due omaggio pernottamento in residence
Pinella Singolo ASC-CAAM 2013/14 Vedi Calendario Premi del campionato ( si svolge in 4/5 tappe di qualificazione ) : > Trofei per i primi nr 4 ( quattro ) > Ai prmi due omaggio pernottamento in residence
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
VINCERE AL BLACKJACK
 VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9
 Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9 19 Carte di colore Blu che vanno dallo 0 al 9 19 Carte di colore Giallo che
Regole del gioco UNO CONTENUTO DELLA CONFEZIONE: 108 Carte così distribuite: 19 Carte di colore Rosso che vanno dallo 0 al 9 19 Carte di colore Blu che vanno dallo 0 al 9 19 Carte di colore Giallo che
Equilibrio bayesiano perfetto. Giochi di segnalazione
 Equilibrio bayesiano perfetto. Giochi di segnalazione Appunti a cura di Stefano Moretti, Silvia VILLA e Fioravante PATRONE versione del 26 maggio 2006 Indice 1 Equilibrio bayesiano perfetto 2 2 Giochi
Equilibrio bayesiano perfetto. Giochi di segnalazione Appunti a cura di Stefano Moretti, Silvia VILLA e Fioravante PATRONE versione del 26 maggio 2006 Indice 1 Equilibrio bayesiano perfetto 2 2 Giochi
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Cenni sul calcolo combinatorio
 Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
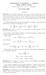 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Microeconomia per la Finanza - Esercitazione 3 Bayesian updating
 Microeconomia per la Finanza - Esercitazione 3 Bayesian updating pcrosetto@luiss.it 6 Maggio 2010 1. Che faremo? Dove trovare i materiali: http://docenti.luiss.it/crosetto/ 1 Ripasso di probabilità 2 Regola
Microeconomia per la Finanza - Esercitazione 3 Bayesian updating pcrosetto@luiss.it 6 Maggio 2010 1. Che faremo? Dove trovare i materiali: http://docenti.luiss.it/crosetto/ 1 Ripasso di probabilità 2 Regola
Calcolo delle probabilitá: esercizi svolti fino all 8 febbraio
 Calcolo delle probabilitá: esercizi svolti fino all 8 febbraio Alessandro Sicco sicco@dm.unito.it Lezione 1. Calcolo combinatorio, formula delle probabilitá totali, formula di Bayes Esercizio 1.1. 7 bambini
Calcolo delle probabilitá: esercizi svolti fino all 8 febbraio Alessandro Sicco sicco@dm.unito.it Lezione 1. Calcolo combinatorio, formula delle probabilitá totali, formula di Bayes Esercizio 1.1. 7 bambini
Traduzione e adattamento a cura di Gylas per Giochi Rari
 Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
LEZIONE 3. Ing. Andrea Ghedi AA 2009/2010. Ing. Andrea Ghedi AA 2009/2010
 LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
Un gioco con tre dadi
 Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011
 2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
Esercizi di Probabilità e statistica. Francesco Caravenna Paolo Dai Pra
 Esercizi di Probabilità e statistica Francesco Caravenna Paolo Dai Pra Capitolo 1 Spazi di probabilità discreti 1.1 Proprietà fondamentali Esercizio 1 Esprimere ciascuno dei seguenti eventi in termini
Esercizi di Probabilità e statistica Francesco Caravenna Paolo Dai Pra Capitolo 1 Spazi di probabilità discreti 1.1 Proprietà fondamentali Esercizio 1 Esprimere ciascuno dei seguenti eventi in termini
Paperone e Rockerduck: a cosa serve l antitrust?
 Paperone e Rockerduck: a cosa serve l antitrust? Paperone Anna Torre, Rockerduck Ludovico Pernazza 1-14 giugno 01 Università di Pavia, Dipartimento di Matematica Concorrenza Due imprese Pap e Rock operano
Paperone e Rockerduck: a cosa serve l antitrust? Paperone Anna Torre, Rockerduck Ludovico Pernazza 1-14 giugno 01 Università di Pavia, Dipartimento di Matematica Concorrenza Due imprese Pap e Rock operano
Calcolo delle probabilità
 Calcolo delle probabilità Il problema di Monty Hill nel film 21 Elementare!! Statistiche, cambio di variabili. 1 Il coefficiente di correlazione tra Indicee Stipendio vale 0,94. E possibile asserire che
Calcolo delle probabilità Il problema di Monty Hill nel film 21 Elementare!! Statistiche, cambio di variabili. 1 Il coefficiente di correlazione tra Indicee Stipendio vale 0,94. E possibile asserire che
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 16 luglio 2006 V.a. discrete e distribuzioni discrete Esercizio 1 Dimostrare la proprietà della mancanza di memoria della legge geometrica, ovvero
Esercizi di Probabilità e Statistica Samuel Rota Bulò 16 luglio 2006 V.a. discrete e distribuzioni discrete Esercizio 1 Dimostrare la proprietà della mancanza di memoria della legge geometrica, ovvero
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
