2 n p n (x y) 1 + p n (x y) ;
|
|
|
- Modesto Pisano
- 5 anni fa
- Visualizzazioni
Transcript
1 1. Spazi di Fréchet Riportiamo brevemente nozioni e risultati principali sugli spazi di Fréchet. Per le dimostrazioni ed eventuali approfondimenti si può consultare il libro di W. Rudin Functional Analysis. Su uno spazio vettoriale V (che supporremo complesso, salvo avviso contrario) si consideri una famiglia numerabile P = {p n } n N di seminorme. Indichiamo con τ P la meno fine tra tutte le topologie τ su V che rendano continua l applicazione identica i : (V, τ) (V, p n ) per ogni n. Si dice che P è una famiglia separante di seminorme se per ogni x V esiste n tale che p n (x) > 0. Supporremo sempre che P sia separante. Proposizione 1.1. La topologia τ P gode delle seguenti proprietà: (1) (V, τ P ) è separato e localmente convesso; (2) le intersezioni finite degli insiemi B n,m = { x : p n (x) < 1 } m formano un sistema findamentale di intorni di 0; (3) τ P è una topologia metrica, nel senso che è la topologia indotta dalla distanza (1.1) d P (x, y) = n 2 n p n (x y) 1 + p n (x y) ; (4) una successione {x j } di punti di V converge a x nella topologia τ P se e solo se converge a x rispetto a ciascuna delle seminorme p n, ossia se lim p n(x x j ) = 0 n ; j (5) una successione {x j } di punti di V è di Cauchy nella topologia τ P se e solo se è di Cauchy rispetto a ciascuna delle seminorme p n. La distanza d P nella (1.1) è invariante, nel senso che per ogni x, y, z V. d P (x + z, y + z) = d P (x, y) Proposizione 1.2. Sia V uno spazio vettoriale topologico. Le seguenti proprietà sono equivalenti: (1) la topologia di V è definita da una famiglia numerabile e separante di seminorme; (2) V è localmente convesso e la sua topologia è indotta da una distanza invariante. Uno spazio vettoriale topologico si dice di Fréchet se la sua topologia soddisfa le proprietà della Proposizione 1.2 ed è completo. 1
2 2 Esempio. Dato un compatto K in R n, sia D(K) lo spazio delle funzioni di classe C su R n con supporto contenuto in K. Si ponga p k (f) = α f. α k Chiaramente la famiglia P = {p k } è separante, per il semplice fatto che ciascuna di esse è una norma. Verifichiamo che D(K) è completo per la distanza d P. Sia {f j } una successione di Cauchy in D(K). Segue dalla Proposizione 1.1(5) che lim i,j p k(f i f j ) = 0 per ogni k. Di conseguenza per ogni α la successione { α f j } è di Cauchy rispetto alla norma uniforme. In particolare le f j convergono uniformemente a una funzione f, ed è un risultato ben noto che allora le derivare α f j convergono a α f uniformemente per ogni α. Dunque f è C e ha supporto in K, ossia è in D(K). Le f j convergono a f rispetto a ognuna delle norme p k. Per la Proposizione 1.1(4), esse convergono a f nella topologia τ P. Applicazioni lineari. Sia T : V W un applicazione lineare tra due spazi di Fréchet. Siano P = {p n } e Q = {q n } due famiglie di seminorme che definiscono le topologie di V e W rispettivamente. Proposizione 1.3. T è continua se e solo se per ogni intero n esistono un intero m e una costante C n tali che m (1.2) q n (T x) C n p k (x) per ogni x V. Da questo enunciato discendono le seguenti conseguenze: Corollario 1.4. (1) Sia T un applicazione lineare di uno spazio di Fréchet V (dotato di seminorme P = {p n }) in uno spazio di Banach W. Allora T è continua se e solo se esistono un intero m e una costante C tali che m T (x) W C p k (x). (2) Due famiglie separanti di seminorme P = {p n } e P = {p n} su V definiscono la stessa topologia se e solo se per ogni intero n esistono un intero m e una costante C n tali che per ogni x V. p n (x) C n p n(x) C n m m p k(x), p k (x)
3 3 Data una famiglia di seminorme P = {p n }, si ponga p n(x) = n p k (x). Poiché p n (x) p n(x) n p k(x), le due famiglie di seminorme sono equivalenti, nel senso che definiscono la stessa topologia. La famiglia {p n} ha il vantaggio di essere crescente. Si noti che se una famiglia di seminorme {p n } su uno spazio V è crescente, la (1.2) si può scrivere più semplicemente nella forma e analogamente nel Corollario 1.4(1). q n (T x) C n p m (x), Teoremi su operatori lineari e forme bilineari. Teorema di Hahn-Banach. Sia W un sottospazio vettoriale di uno spazio di Fréchet V, dotato di una famiglia crescente di seminorme {p n }. Sia T un funzionale lineare su W, tale che T (x) Cp n (x) per ogni x W. Esiste allora un prolungamento lineare T di T a tutto V tale che T (x) Cp n (x) per ogni x V. Un sottoinsieme E di uno spazio di Fréchet V si dice limitato se per ogni seminorma p n si ha sup { p n (x) : x E } <. Una famiglia T di operatori lineari tra due spazi vettoriali topologici V e W si dice equicontinua se per ogni intorno U di 0 in W esiste un intorno U di 0 in V tale che T (U ) U per ogni T T. Quando V e W sono spazi di Fréchet, dotati di famiglie crescenti di seminorme {p n } e {q n } rispettivamente, una famiglia T di operatori lineari è equicontinua se e solo se per ogni intero n esistono un intero m e una costante C n tali che q n (T x) C n p m (x) per ogni x V e T T. Teorema di limitatezza uniforme, o di Banach-Steinhaus. Sia T una famiglia di operatori lineari continui tra due spazi di Fréchet V e W. Se per ogni x V l insieme E x = {T x : T T } è limitato in W, allora T è equicontinua. Teorema dell applicazione aperta. Sia T un operatore lineare continuo tra due spazi di Fréchet V e W. Se T è suriettivo, allora T è aperto. In particolare, se T è iniettivo, allora anche T 1 è continuo. Teorema del grafico chiuso. Sia T un operatore lineare tra due spazi di Fréchet V e W. Si supponga che il suo grafico Γ T = {(x, T x) : x V } sia chiuso in V W, ossia che le ipotesi: (1) lim j x j = x in V, (2) lim j T (x j ) = y in V implichino che y = T x. Allora T è continuo. Una forma bilineare B : V W C, dove V e W sono spazi vettoriali topologici, si dice separatamente continua se (1) B(x 0, ) è continua su W per ogni x 0 V ; (2) B(, y 0 ) è continua su V per ogni y 0 W.
4 4 Teorema di Bourbaki. Sia B una forma bilineare separatamente continua sul prodotto di due spazi di Fréchet V e W. Allora B è continua. 2. Lo spazio delle funzioni test Cominciamo con alcuni preliminari sulla duttilità delle funzioni C. Si consideri su R la funzione f(t) = { e 1 t 2 se t > 0 0 se t 0. È noto che f è C. Quindi g(t) = f(t)f(1 t) è pure C e ha supporto in [0, 1]. Sia c > 0 tale che 1 0 g(t) dt = c 1 e si ponga t G(t) = c g(u) du. Allora G è C, crescente, G(t) = 0 per t 0 e G(t) = 1 per t 1. Se si pone, per δ > 0, ( ) t G δ (t) = G, δ allora G δ (t) = 1 per t δ, e per il resto gode delle stesse proprietà di G. Se b > 2δ, la funzione H b,δ (t) = G δ (t)g δ (b t) è C, ha supporto in [0, b], è uguale a 1 su [δ, b δ], è crescente su [0, δ] e decrescente su [b δ, b]. È importante a questo punto valutare la grandezza delle derivate delle funzioni che abbiamo costruito. Si osservi che ( ) G (n) t δ (t) = δ n G (n) δ, per cui G (n) δ (t) C n δ n. Di conseguenza, applicando la regola di Leibniz, (2.1) H (n) b,δ (t) C nδ n. Per mezzo di una opportuna traslazione, la funzione H b,δ può essere riportata su un generico intervallo [a, b], in modo da avere il seguente enunciato.
5 Proposizione 2.1. Dati un intervallo [a, b] e un sottointervallo [a, b ] (a, b), esiste una funzione f di classe C su R con supporto in [a, b], tale che 0 f(t) 1, identicamente uguale a 1 su [a, b ] e tale che, posto δ = min{a a, b b }, f (n) (t) C n δ n, dove le C n sono costanti assolute. Passiamo ora a più dimensioni. Si prenda una funzione g di classe C su R, pari, tale che 0 g(t) 1, con supporto in [ 1, 1] e uguale a 1 su [ 1/2, 1/2]. Su R n si ponga ϕ ( x) = g( x ). Poiché x è una funzione C fuori dall origine, ϕ è pure C fuori dall origine. D altra parte ϕ è anche C sulla palla di centro 0 e raggio 1/2, essendo ivi costante. Dato δ > 0, la funzione ( x ) ϕ δ (x) = ϕ δ ha supporto nella palla chiusa di centro 0 e raggio δ, ed è identicamente uguale a 1 sulla palla di raggio δ/2. Inoltre, se b α = α ϕ, si ha (2.2) α ϕ δ (x) b α δ α. Teorema 2.2. Dati un aperto A R n e un compatto K A, sia d (0, + ] la distanza di K dal complementare di A. Dato δ < d, esiste una funzione ψ 0, di classe C su R n, con supporto compatto in A, identicamente uguale a 1 su un intorno di K, e tale che α ψ(x) C α,n δ α, dove le costanti C α,n dipendono solo da α e dalla dimensione n. Dimostrazione. Siano K = {x : d(x, K) δ/4}, K = {x : d(x, K) δ/2}, K = {x : d(x, K) 3δ/4}. Allora K, K e K sono compatti e K K K K A. Si definisca Derivando sotto integrale, si ha u(x) = χ K ϕ δ/4 (x) = χ K (y)ϕ δ/4 (x y) dy R n = ϕ δ/4 (x y) dy. K α u(x) = α ϕ δ/4 (x y) dy. K Poiché la funzione integranda è diversa da 0 solo quando x y < δ/4, l integrale è esteso a K B(x, δ/4), che ha misura minore o uguale a ω n δ n /4 n (dove ω n è la misura della palla unitaria). Di conseguenza, per la (2.2), α u(x) C α,n δ n α. Se x K, allora K B(x, δ/4) =, per cui u(x) = 0. Quindi supp u K. 5
6 6 Se x K, B(x, δ/4) K, per cui u(x) = ϕ δ/4 (x y) dy R n = ϕ δ/4 (y) dy R n = 4 n δ n R n ϕ(x) dx = c n δ n. Si verifica allora facilmente che ψ(x) = c 1 n δ n u(x) ha le proprietà richieste. Topologia di D(A). Sia A R n un aperto non vuoto. Ricordiamo che, dato un compatto K A, si indica con D(K) lo spazio de Fréchet delle funzioni C su A con supporto in K, dotato delle norme p k (f) = α f. α k La convergenza di una successione {f k } nella topologia di D(K) è la convergenza uniforme di tutte le successioni { α f k }, per ogni multiindice α. Poniamo D(A) = D(K), K compatto,k A e indichiamo con i K : D(K) D(A) l inclusione. Su D(A) introduciamo la topologia più fine che renda continue le varie inclusioni i K. Proposizione 2.3. Valgono le seguenti proprietà: (1) un sottoinsieme U D(A) è aperto se e solo se per ogni K U D(K) è aperto nella topologia di D(K); (2) la topologia indotta da D(A) su D(K) coincide con la topologia propria di D(K); (3) un applicazione lineare T da D(A) in uno spazio vettoriale topologico V è continua se e solo se per ogni K A compatto, l applicazione T i K : D(K) V è continua. Dimostrazione. La (1) è una riformulazione della condizione che definisce la topologia di D(A). La (2) e la (3) sono conseguenze immediate della (1). Dobbiamo ora premettere un lemma di carattere topologico, di facile verifica. Lemma 2.4. Sia A un aperto di R n. Posto K j = { x A : x j, d(x, c A) 1 } j se A R n, e K j = {x : x j} se A = R n, allora j=1 K j = A e ogni compatto K A è contenuto in uno dei K j.
7 Teorema 2.5. Una successione {f n } converge a f in D(A) se e solo se i supporti delle f n e di f sono contenuti in un unico compatto K A, e tutte le derivate α f n convergono a α f uniformemente. Dimostrazione. Se i supporti delle f n sono contenuti in un unico compatto K ed esse convergono a f in D(K), allora esse convergono a f anche in D(A) per la Proposizione 2.3(2). Supponiamo viceversa che le f n convergano a f in D(A). Sostituendo f n con f n f, possiamo supporre che f = 0. Per assurdo, ammettiamo che i supporti delle f n non siano contenuti in un unico compatto. Esisterebbe allora una sottosuccessione f nj con la seguente proprietà: considerati i compatti K j del Lemma 2.4, per ogni j esiste un punto x j K j tale che f nj (x j ) 0. Posto ε j = f nj (x j ), si consideri l insieme U = {g D(A) : g(x j ) < ε j j}. Verifichiamo che U è aperto in D(A). Dato un compatto K A, sia j tale che K K j. Allora solo i punti x 1,..., x j 1 possono essere contenuti in K. Pertanto U D(K) = {g D(K) : g(x j ) < ε j j = 1,..., j 1}. Per j = 1,..., j si consideri il funzionale lineare Φ j (g) = g(x j ) su D(K). Esso è continuo perché Φ(g) p 0 (g). Dunque l insieme U j = {g : g(x j ) < ε j } è aperto in D(K). Ma U D(K) = j j=1 U j, da cui l asserto. Quindi U è un intorno di 0 in D(A). Tuttavia nessuna delle f nj è in U, da cui l assurdo. Una volta stabilito che i supporti delle f n sono contenuti in un unico compatto, il resto segue dalla Proposizione 2.3(2). Corollario 2.6. Sia T un applicazione lineare di D(A) in D(A ). Allora T è continua se e solo se per ogni compatto K A esiste un compatto K A tale che T ( D(K) ) D(K ) e T i K : D(K) D(K ) è continua. Dimostrazione. Supponiamo che la condizione nell enunciato sia soddisfatta. Allora T i K è continua per ogni K come funzione da D(K) in D(A ), per la continuità dell inclusione i K. Per la Proposizione 2.3(3), T è continua. Viceversa, si supponga T continua e sia K A compatto. Allora T i K è continua. Presa una successione {K j } di compatti di A come nel Lemma 2.4, ammettiamo per assurdo che T ( D(K) ) non sia contenuto in D(K j ) per nessun j. Per ogni j esisterebbe allora f j D(K) tale che supp T f j K j. Possiamo supporre che lim j f j = 0. Infatti, se d è la distanza (1.1) su D(K), si può sostituire f j con un opportuno multiplo scalare λ j f j in modo che d(λ j f j, 0) < 1/j. Ma essendo T continua, dovremmo allora avere lim j T f j = 0, in particolare i supporti delle T f j dovrebbero essere contenuti in un unico compatto K. Ma ciò è assurdo perché ogni compatto di A è contenuto in uno dei K j. Corollario 2.7. Le seguenti applicazioni lineari di D(A) in sé sono continue: (1) T α f = α f per ogni multi-indice α; (2) T Φ f = fφ per ogni Φ C (A). 7
8 8 Inoltre, se A = R n, l applicazione T g f = f g(x) = f(x y)g(y) dy R n è continua per ogni g L 1 (R n ) con supporto compatto. Dimostrazione. Osserviamo che se f D(K), con K A, allora anche T α f D(K). Inoltre p k (T α f) p k+ α (f). Dunque T α i K è continua da D(K) in sé. Per il Corollario 2.6, T α è continua. Per f D(K) si ha poi, per la regola di Leibniz, p k (fφ) = α (fφ) α k α k β α c α,β β f α β Φ) α k, β k C K β k = C K p k (f). c α,β β f α β Φ),K β f Dunque anche T Φ è continua. Infine sia f D(K), e si consideri la convoluzione f g. Derivando sotto integrale, si vede che f g è C. Inoltre, sia K 0 il supporto compatto di g. Allora la somma K = K + K 0 = {y + z : y K, z K 0 } è pure compatta. Ma f g(x) = 0 se x K. Infatti l integrale di convoluzione è esteso agli y che soddisfano entrambe le condizioni y K 0 e x y K. Se esistesse almeno un y con queste proprietà, si avrebbe x K + K 0, contro l ipotesi. Dunque T g applica D(K) in D(K ). A questo punto si ha f g(x) f(x y) g(y) dy K 0 g 1 f, per cui p 0 (f g) g 1 p 0 (f). 3. Distribuzioni Si chiama distribuzione su A un funzionale lineare continuo T : D(A) C. Useremo la notazione T, f in luogo di T (f). In base alla Proposizione 2.3(3), un funzionale lineare T su D(A) è continuo (cioè definisce una distribuzione) se e solo se per ogni compatto K A esistono un intero n = n(k) e una costante C = C(K) tali che per ogni f D(K) T, f Cpn (f),
9 9 dove p n (f) = α n D α f. Esempi. Sia ϕ(x) una funzione localmente integrabile su A. Il funzionale T ϕ, f = f(x)ϕ(x) dx definisce una distribuzione su A. Se infatti f D(K) con K A, si ha T ϕ, f f(x) ϕ(x) dx f ϕ(x) dx. K A Si ha quindi in questo caso n(k) = 0 per ogni K e C(K) = ϕ(x) dx. K Scriveremo nel seguito ϕ, f in luogo di T ϕ, f quando la distribuzione e definita dall integrazione con la funzione ϕ localmente integrabile. Diremo anche che la distribuzione coincide con la funzione ϕ. Più in generale, si ponga T, f = A α f(x)ϕ(x) dx, sempre con ϕ localmente integrabile su A. Si ha allora T, f ϕ(x) dx p n (f) con n = α. La delta di Dirac nel punto x 0 A è definita da K δ x0, f = f(x 0 ). Si verifica facilmente che n(k) = 0 e C(K) = 1 per ogni K. Operazioni su distribuzioni. Ovviamente le distribuzioni su A si possono sommare e moltiplicare per scalari. Esse formano dunque uno spazio vettoriale, che si indica con D (A). Vediamo ora come si definiscono le derivate di una distribuzione. Per motivare la definizione, supponiamo inizialmente di avere una distribuzione coincidente con una funzione ϕ di classe C 1. In questo caso vogliamo che la derivata j ϕ di ϕ come distribuzione nella variabile x j coincida con la derivata di ϕ come funzione nella variabile x j. Si osservi allora che integrando per parti j ϕ, f = f(x) j ϕ(x) dx A = j f(x)ϕ(x) dx A = ϕ, j f (l integrazione per parti non produce termini al bordo in quanto f si annulla sulla frontiera di A). Per estensione definiamo allora per una generica T D (A) (3.1) j T, f = T, j f. K
10 10 Proposizione 3.1. La (3.1) definisce una distribuzione j T. Dimostrazione. In base al Corollario 2.7(1), l applicazione j : D(A) D(A) è continua. Di conseguenza la composizione T j : D(A) C è continua. Per definizione, j T = T j, da cui la tesi. Iterando l operazione di derivazione, si pone (3.2) α T, f = ( 1) α T, α f. Siano T D (A) e Φ C (A). Si definisce T Φ D (A) ponendo (3.3) T Φ, f = T, Φf. La continuità di T Φ segue dal Corollario 2.7(2). Vogliamo ora definire la convoluzione T g di T D (R n ) con g D(R n ). Per motivare la definizione, supponiamo che T coincida con la funzione ϕ localmente integrabile su R n. In tal caso vogliamo ottenere la normale convoluzione ϕ g(x) = ϕ(y)g(x y) dy. R n Si ha allora ϕ g, f = ϕ(y)g(x y) dy f(x) dx ( ) = ϕ(y) g(x y)f(x) dx dy = ϕ, ǧ f, dove si è posto ǧ(x) = g( x). Per estensione, sostituendo ϕ con una generica distribuzione T D (R n ), si pone (3.4) T g, f = T, ǧ f. Esempi. Abbiamo detto che se T coincide con una funzione ϕ di classe C 1 le sua derivate prime distribuzionali coincidono con le derivate ordinarie. Se ϕ non è C 1, ma solo localmente integrabile, le sue derivate possono differire notevolmente dalla nozione ordinaria di derivata puntuale. Si prenda ad esempio su R una funzione a gradino { a se x < x0 ϕ(x) = b se x > x 0,
11 con a b. La derivata puntuale esiste per x x 0 ed è nulla. La derivata distribuzionale di ϕ, che indichiamo qui con Dϕ, si ottiene invece come segue (considerando una funzione test f D(R)): Dϕ, f = ϕ, f = x0 = af(x) af (x) dx x 0 = (b a)f(x 0 ). bf(x) x 0 x 0 bf (x) dx 11 Si ha quindi Dϕ = (b a)δ x0. Un altro esempio interessante è il seguente. Si consideri la funzione localmente integrabile ϕ(x) = log x su R. Per calcolarne la derivata distribuzionale Dϕ procediamo come prima, ponendo, per f D(R), Dϕ, f = ϕ, f = f (x) log x dx. L integrazione per parti non può essere fatta direttamente, per la singolarità del logaritmo in 0. Conviene invece eliminare dal dominio di integrazione un intorno simmetrico ( ε, ε) di 0, osservando che Si ha allora Dϕ, f = lim ε 0 ( = lim ε 0 f (x) log x dx = lim f ε 0 x >ε (x) log x dx. + = lim ε 0 ( ε f (x) log x dx + f(x) log x ε ε ε f(x) log x ) f (x) log x dx ε f(x) 1 ) x dx + f(x) 1 x dx ( (f(ε) f( ε) ) log ε + ε x >ε Poiché f è derivabile in 0, f(ε) f( ε) Cε, per cui ( ) lim f(ε) f( ε) log ε = 0. ε 0 f(x) 1 x dx ). Si ha quindi Dϕ, f = lim f(x) ε 0 x >ε 1 x dx.
12 12 L espressione a secondo membro prende il nome di integrale con valore principale e si indica con il simbolo p.v. f(x) 1 x dx. Occorre tener presente che non si tratta di un normale integrale. Per esempio, non è assolutamente convergente; inoltre la sua convergenza presuppone che f sia derivabile in 0. Si verifica facilmente che le derivate della delta di Dirac in x 0 sono date da α δ x0, f = ( 1) α α f(x 0 ). Vediamo ora un esempio di convoluzione. Se g D(R n ), calcoliamo δ x0 g. Per la (3.4) si ha δ x0 g, f = δ x0, ǧ f = ǧ f(x 0 ) = ǧ(x 0 x)f(x) dx = g(x x 0 )f(x) dx. da cui si deduce che δ x0 g coincide con una funzione, precisamente δ x0 g(x) = g(x x 0 ). L effetto su g della convoluzione con δ x0 di un incremento x 0. è dunque la traslazione del suo grafico Supporto di una distribuzione. Si dice che una distribuzione T è nulla su un aperto A A se T, f = 0 per ogni funzione test f con supporto contenuto in A. Lemma 3.2. Se una distribuzione T è nulla su due aperti A 1 e A 2, allora è nulla anche su A 1 A 2. Dimostrazione. Sia f D(A) con supporto K contenuto in A 1 A 2. L insieme K 1 = K \ A 2 è compatto e contenuto in A 1. Sia ϕ una funzione C con supporto compatto in A 1 e uguale a 1 in un intorno V di K 1. Si decomponga f come f = fϕ + (f fϕ). Allora T, f = T, fϕ + T, f fϕ. Poiché T è nulla su A 1, T, fϕ = 0. Inoltre il supporto di f fϕ è contenuto in K \ V, che è un compatto contenuto in A 2. Di conseguenza anche T, f fϕ = 0. Si conclude allora che T, f = 0.
13 Corollario 3.3. Data T D (A), esiste un massimo aperto A A su cui T è nulla. Dimostrazione. Si consideri la famiglia A degli aperti A A su cui T è nulla, parzialmente ordinata per inclusione. A questa famiglia si può applicare il Lemma di Zorn. Sia infatti {A j } j J una sottofamiglia di A totalmente ordinata e si prenda A = j J A j. Se f ha supporto compatto K A, per la proprietà di ricoprimento finito esiste j J tale che K A j. Ma allora T, f = 0 perché T è nulla su A j. In conclusione T è nulla su A. Esistono dunque, per il Lemma di Zorn, elementi massimali in A. Se A 1 e A 2 sono due di tali aperti massimali, T è nulla su entrambi. Per il Lemma 3.2, T è nulla anche sull unione, e dunque A 1 = A 2 per la loro massimalità. Si chiama supporto di T il complementare del massimo aperto su cui T è nulla. Esso viene indicato con supp T. Per definizione, il supporto di una distribuzione è un chiuso. Esso è vuoto se e solo se T si annulla su tutto A, ossia se e solo se T = 0. Proposizione 3.4. Valgono le seguenti proprietà: (1) se f D(A) e supp f supp T =, allora T, f = 0; (2) se Φ C (A) e supp Φ supp T =, allora T Φ = 0; (3) se Ψ C (A) e Ψ(x) = 1 su un intorno di supp T, allora T Ψ = T. Dimostrazione. La (1) è ovvia, in quanto T è nulla sul complementare del suo supporto. Per la (2), si prenda f D(A). Allora T Φ, f = T, Φf, dove fφ D(A) e supp (fφ) supp Φ. Per la (1), T, Φf = 0, da cui la conclusione. Per la (3), si osservi che il supporto di Ψ 1 è disgiunto dal supporto di T. Per la (2), T (Ψ 1) = T Ψ T = 0, da cui la tesi. Si osservi che, nella (2), l ipotesi che supp Φ supp T = è più forte che richiedere semplicemente che Φ si annulli sul supporto di T : si richiede infatti che Φ si annulli in un intorno di supp T. La conclusione della (2) non è vera nella sola ipotesi che Φ sia nulla su supp T. Si prenda ad esempio T = δ 0, Φ(x) = x su R. Osserviamo innanzitutto che suppδ 0 = {0}. Infatti se f D(R) ha supporto in R \ {0}, allora δ 0, f = f (0) = 0. Quindi Φ si annulla sul supporto di T. Ma, se ora f D(R), xδ 0, f = δ 0, xf = δ 0, f + xf = f(0). Quindi xδ 0 = δ 0. Considerazioni analoghe valgono per la (1) e la (3). Si dice che due distribuzioni T e U coincidono su un aperto A A se T U è nulla su A. Segue facilmente dalla Proposizione 3.4 che date T D (A) e Φ C (A) con Φ(x) = 1 su A, allora T Φ coincide con T su A. Sia T una distribuzione su A con supporto compatto. In tal caso il funzionale lineare T : D(A) C si può estendere a C (A). Per fare ciò si prenda una 13
14 14 funzione F D(A) che sia identicamente uguale a 1 in un intorno si supp T. Si ponga allora T, Φ def = T, F Φ. Questa è una buona definizione in quanto (1) F Φ D(A), in quanto F ha supporto compatto; (2) la definizione non dipende dalla scelta di F ; infatti se G è un altra funzione in D(A) uguale a 1 in un intorno di supp T, allora T, F Φ T, GΦ = T, (F G)Φ = 0, in quanto (F G)Φ si annulla in intorno di supp T. Ordine di una distribuzione. Nella definizione di distribuzione data all inizio di questo paragrafo compare un intero n(k), dipendente dal compatto K A, che indica quale norma p n (f) su D(K) controlla il valore di T, f. Si dice che T D (A) ha ordine finito n se questi interi n(k) si possono prendere tutti uguali a n (o minori), ossia se per ogni compatto K esiste una costante C = C(K) tale che T, f Cpn (f). Le distribuzioni che abbiamo incontrato finora hanno tutte ordine finito. In particolare quelle definite da integrali con funzioni localmente integrabili hanno ordine 0. Inoltre è abbastanza evidente che se T ha ordine finito n, allora α T ha ordine n + α. Si verifichi che la distribuzione p.v.1/x ha ordine 1 (in quanto derivata di log x che ha ordine 0), ma non ha ordine zero! Esistono distribuzioni che non hanno ordine finito. Per costruirne una, si prenda una successione di punti {x k } che tendano verso un punto in A { }, e si ponga Se f D(A), T, f = T = δ (k) x k. ( 1) k f (k) (x k ). Poiché f ha supporto compatto, solo un numero finito dei termini della serie è diverso da 0, per cui T, f è ben definito. Dato un compatto K A, esso contiene solo un numero finito di punti, compresi nell insieme {x 1,..., x m }, con m dipendente da K. Se f D(K), m T, f f (k) (x k ) m f (k) = p m (f). Poiché al variare di K intervengono tutte le derivate di f, è ovvio che non si può controllare il valore di T, f con una stessa norma p m (f).
15 Proposizione 3.5. Una distribuzione con supporto compatto ha ordine finito. Dimostrazione. Sia K = supp T il supporto compatto della distribuzione T. Si prenda ϕ D(A) uguale a 1 su un intorno di K e sia K il supporto di ϕ. Esiste allora un intero n tale che per ogni g D(K ) T, g Cp n (g). Sia ora f D(A). Per la Proposizone 3.4(3), T, f = T ϕ, f = T, fϕ. 15 Poiché fϕ D(K ), T, f Cpn (fϕ) C p n (f), come si verifica facilmente applicando la regola di Leibniz. Se K è un comptto contenuto in A, indichiamo con D m (K) lo spazio di Banach delle funzioni di classe C m in R n e con supporto in K, dotato della norma p m. In dichiamo poi con D m (A) lo spazio delle funzioni di classe C m con supporto compatto in A, dotato della topologia più fine che rende continue le inclusioni i K : D m (K) D m (A) per ogni K compatto. Si verifica facilmente che l inclusione i m : D(A) D m (A) è continua e ha immagine densa per ogni m. Proposizione 3.6. Una distribuzione T ha ordine finito m se e solo se si estende con continuità a D m (A). Dimostrazione. Un funzionale lineare T su D m (A) è continuo se e solo se per ogni K esiste una costante C(K) tale che per ogni f D m (K) (3.5) T, f C(K)pm (f). Se T è una distribuzione di ordine m, vale la (3.5) per ogni f D(K). Essendo D(K) denso in D m (K), T si estende in modo unico a D m (K) e si conserva la disuguaglianza (3.5). Poiché ciò vale per ogni K, T si estende a tutto D m (A) rimanendo continuo. Viceversa se T ha un estensione continua a D m (A), allora vale la (3.5) per ogni K compatto e per ogni f D m (K). A maggior ragione la (3.5) vale per f D(K), per cui T è una distribuzione di ordine m.
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Geometria Superiore Esercizi 1 (da consegnare entro... )
 Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Appunti di Analisi convessa. Paolo Acquistapace
 Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni
 Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
C. Borelli - C. Invernizzi
 Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 3 (999) C. Borelli - C. Invernizzi SULLA STABILITÀ DELL EQUAZIONE FUNZIONALE DEI POLINOMI Sommario. In this paper we obtain some stability results generalizing
Rend. Sem. Mat. Univ. Pol. Torino Vol. 57, 3 (999) C. Borelli - C. Invernizzi SULLA STABILITÀ DELL EQUAZIONE FUNZIONALE DEI POLINOMI Sommario. In this paper we obtain some stability results generalizing
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Introduzione alla programmazione lineare. Mauro Pagliacci
 Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
ELEMENTI DI ANALISI SPETTRALE 1 I DUE DOMINI
 Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
5 DERIVATA. 5.1 Continuità
 5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
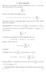 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Misure e funzioni a variazione limitata
 Capitolo 2 Misure e funzioni a variazione limitata 2.1 Richiami di teoria della misura e integrazione Sia un insieme non vuoto e sia F una σ-algebra su, cioè una famiglia di sottoinsiemi di che gode delle
Capitolo 2 Misure e funzioni a variazione limitata 2.1 Richiami di teoria della misura e integrazione Sia un insieme non vuoto e sia F una σ-algebra su, cioè una famiglia di sottoinsiemi di che gode delle
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Soluzioni classiche dell'equazione di Laplace e di Poisson
 Soluzioni classiche dell'equazione di Laplace e di Poisson Antonio Paradies Dipartimento di Matematica e Applicazioni Renato Caccioppoli Università degli studi di Napoli Federico II Napoli, 25 Febbraio
Soluzioni classiche dell'equazione di Laplace e di Poisson Antonio Paradies Dipartimento di Matematica e Applicazioni Renato Caccioppoli Università degli studi di Napoli Federico II Napoli, 25 Febbraio
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
Equazioni non lineari
 Equazioni non lineari Data una funzione f : [a, b] R si cerca α [a, b] tale che f (α) = 0. I metodi numerici per la risoluzione di questo problema sono metodi iterativi. Teorema Data una funzione continua
Equazioni non lineari Data una funzione f : [a, b] R si cerca α [a, b] tale che f (α) = 0. I metodi numerici per la risoluzione di questo problema sono metodi iterativi. Teorema Data una funzione continua
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
7. SINGOLARITA E RESIDUI. 7.1 Punti Singolari Isolati.
 7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 1 INTRODUZIONE
 2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
EQUAZIONI non LINEARI
 EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Parte 2. Metodi Matematici per la Meccanica Quantistica. Spazi di pre-hilbert e spazi di Hilbert. Gianpiero CATTANEO
 Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
Appunti di Complementi di Matematica. Jacobo Pejsachowicz (a cura di Nathan Quadrio)
 Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Appunti del corso di Probabilità e Processi Stocastici
 Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Note del corso di SISTEMI DINAMICI. Massimiliano Berti
 Note del corso di SISTEMI DINAMICI Massimiliano Berti 16 Dicembre 2011 Versione preliminare Introduzione Va sotto il nome Sistemi Dinamici la teoria delle equazioni differenziali ordinarie, cioè di equazioni
Note del corso di SISTEMI DINAMICI Massimiliano Berti 16 Dicembre 2011 Versione preliminare Introduzione Va sotto il nome Sistemi Dinamici la teoria delle equazioni differenziali ordinarie, cioè di equazioni
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI
 Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Anno 5 4. Funzioni reali: il dominio
 Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Analisi Matematica II (Fisica e Astronomia) Esercizi di ricapitolazione n. 1
 Analisi Matematica II (Fisica e Astronomia) Esercizi di ricapitolazione n. Università di Padova - Lauree in Fisica ed Astronomia - A.A. 8/9 venerdì 8 maggio 9 Questi esercizi sono proposti come preparazione
Analisi Matematica II (Fisica e Astronomia) Esercizi di ricapitolazione n. Università di Padova - Lauree in Fisica ed Astronomia - A.A. 8/9 venerdì 8 maggio 9 Questi esercizi sono proposti come preparazione
Numeri Complessi. 4. Ricordando che, se z è un numero complesso, zz è un numero reale, mettere sotto la forma. z 2 + 2z + 2 = 0. z 2 + 2z + 6 = 0.
 Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Problemi di approssimazione per operatori positivi in spazi adattati
 UNIVERSITÀ DEGLI STUDI DI BARI Dottorato di Ricerca in Matematica XV Ciclo A.A. 2002 2003 Tesi di Dottorato Problemi di approssimazione per operatori positivi in spazi adattati Presentata da Mirella CAPPELLETTI
UNIVERSITÀ DEGLI STUDI DI BARI Dottorato di Ricerca in Matematica XV Ciclo A.A. 2002 2003 Tesi di Dottorato Problemi di approssimazione per operatori positivi in spazi adattati Presentata da Mirella CAPPELLETTI
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
POLITECNICO di BARI - A.A. 2012/2013 Corso di Laurea in INGEGNERIA Informatica e dell Automazione
 POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Stabilità di Lyapunov
 Stabilità di Lyapunov Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona Introduzione. In queste note presentiamo i primi elementi della teoria della stabilità
Stabilità di Lyapunov Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona Introduzione. In queste note presentiamo i primi elementi della teoria della stabilità
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
L. Pandolfi. Lezioni di Analisi Matematica 2
 L. Pandolfi Lezioni di Analisi Matematica 2 i Il testo presenta tre blocchi principali di argomenti: A Successioni e serie numeriche e di funzioni: Cap., e 2. B Questa parte consta di due, da studiarsi
L. Pandolfi Lezioni di Analisi Matematica 2 i Il testo presenta tre blocchi principali di argomenti: A Successioni e serie numeriche e di funzioni: Cap., e 2. B Questa parte consta di due, da studiarsi
Analisi Mat. 1 - Ing. Inform. - Soluzioni del compito del 23-3-06
 Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
SOLUZIONE DEL PROBLEMA 2 CORSO DI ORDINAMENTO 2013. 8 4 + x 2, con dominio R (infatti x2 + 4 0 per ogni. 8 4 + ( x) = 8. 4 + x 2
 SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
Moto per curvatura nel piano
 Università degli Studi di Ferrara Facoltà di scienze matematiche, fisiche e naturali Corso di Laurea Triennale in Matematica Moto per curvatura nel piano Relatore: Dott. Michele Miranda Candidato: Luca
Università degli Studi di Ferrara Facoltà di scienze matematiche, fisiche e naturali Corso di Laurea Triennale in Matematica Moto per curvatura nel piano Relatore: Dott. Michele Miranda Candidato: Luca
Grafico qualitativo di una funzione reale di variabile reale
 Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Analisi Matematica 3 appunti
 Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
ESERCITAZIONI DI ANALISI 1 FOGLIO 1 FOGLIO 2 FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI. Marco Pezzulla
 ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
NOTAZIONI DIFFERENZIALI IN FISICA
 NOTAZIONI IFFERENZIALI IN FISICA Elio Proietti Abstract (Versione agosto 2012) Il tumultuoso sviluppo ed i successi del calcolo differenziale nel Settecento indussero il matematico Jean-Baptiste d Alambert
NOTAZIONI IFFERENZIALI IN FISICA Elio Proietti Abstract (Versione agosto 2012) Il tumultuoso sviluppo ed i successi del calcolo differenziale nel Settecento indussero il matematico Jean-Baptiste d Alambert
Alcune note sulle serie di potenze 1
 Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Durata della prova: 3h. 2 +y 4. tan y sin y lim = 1. (x 4 +y 2 )y 3
 Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Integrali di superficie: esercizi svolti
 Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
Integrali doppi - Esercizi svolti
 Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
VALORE PIÙ CONVENIENTE DEL RENDIMENTO
 VALORE PIÙ CONVENIENTE DEL RENDIENTO In una macchina elettrica ad un rendimento più elevato corrisponde un minor valore delle perdite e quindi un risparmio nelle spese di esercizio (in quanto minori risultano
VALORE PIÙ CONVENIENTE DEL RENDIENTO In una macchina elettrica ad un rendimento più elevato corrisponde un minor valore delle perdite e quindi un risparmio nelle spese di esercizio (in quanto minori risultano
MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO
 Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
