CRITERI DI RESISTENZA DEI MATERIALI
|
|
|
- Lia Agnese Vanni
- 8 anni fa
- Visualizzazioni
Transcript
1 CRITERI DI RESISTENZA DEI MATERIALI Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi, si entra in fase plastica per i materiali duttili, o si raggiunge la crisi per i materiali fragili. Materiali Duttili σ Materiali Fragili σ σ 0 ε σ T ε σ 0 σ C La finalità dei criteri di resistenza è quella di mettere in relazione i parametri critici del materiale ottenuti da prove sperimentali per i materiali duttili la tensione di snervamento σ 0 per i materiali fragili la tensioni di rottura a compressione e trazione σ C e σ T con la resistenza dell elemento soggetto in genere ad uno stato di tensione biassiale o triassiale.
2 La teoria dei criteri di resistenza introduce gli stati tensionali ugualmente pericolosi o monoassiali equivalenti, che sono caratterizzati da una tensione monoassiale equivalente detta tensione eale σ definita in funzione dello stato di sforzo effettivamente agente (espresso nel riferimento principale o in un qualunque riferimento cartesiano) σ = f ( σ, σ, σ ) σ = f ( σ, σ, σ, τ, τ, τ ) I II III x y z xy yz zx Per ciascun criterio di resistenza la crisi si verifica quando la tensione eale raggiunge il valore limite, di snervamento o rottura rispettivamente se il materiale è duttile o fragile. La differenza tra i vari criteri di resistenza è data da come in ognuno di essi viene definita la tensione eale.
3 CRITERIO DI GALILEO - RANKINE Questo criterio, valo per i materiali fragili, è detto anche criterio della massima tensione normale. Esso assume che la crisi ha luogo quando una delle tre tensioni principali raggiunge il valore limite. Secondo il criterio di Galileo-Rankine la tensione eale a trazione e a compressione viene assunta rispettivamente pari a: + { I II III } { } σ = max σ, σ, σ σ = min σ, σ, σ I II III Introducendo le tensioni di rottura a trazione σ T e a compressione σ C si può esprimere il criterio attraverso le doppie diseguaglianze : σ σ σ {,, } C i T i = I II III Che definiscono nello spazio delle tensioni un dominio di resistenza (insieme di stati tensionali ammissibili) avente forma di cubo.
4 Nel caso di stati di tensione piani (II =0) il criterio può essere espresso attraverso le 4 disequazioni : σ σ σ σ σ σ C I T C II T Che definiscono nel piano O I un dominio di resistenza di forma quadrata. I punti al suo interno corrispondono a stati di sforzo sicuri secondo il criterio di Galileo-Rankine. I σc O σ T σ T σ C
5 Il criterio di Galileo-Rankine presenta il limite di non tenere conto dell interazione tra le tensioni principali. Facendo riferimento sempre al caso di stato tensione piano, conseriamo ad esempio un elemento soggetto, in due casi differenti, a tensioni principali aventi lo stesso segno e segno opposto : I I I I ( a ) ( b) E evente che nel caso (a) la tensione principale I contrasta la dilatazione trasversale causata dalla (e viceversa) per cui la resistenza del blocco aumenta rispetto al caso (b) I Vi sono invece coppie di valori (,I ) per le quali il criterio di Galileo-Rankine non tiene conto di questo fatto, associando alle configurazioni di tensione dei due casi lo stesso grado di pericolo. ( σ, σ ) ( σ, σ ) I I II II O
6 CRITERI DI RESISTENZA PER MATERIALI DUTTILI Nei materiali duttili come i metalli la tensione al limite di snervamento σ 0 è teoricamente uguale in valore assoluto a trazione e compressione. L aggiunta di una pressione rostatica, anche di valore estremamente elevato, non altera tale limite. Entrambe le proprietà hanno avuto ampie conferme sperimentali In particolare per quanto riguarda la seconda negli anni 50 Brgman eseguì una serie di prove di trazione su provini immersi in una camera a pressione capace di sovrapporre fino a atmosfere (z2500 MPa) costatando che il limite di snervamento rimaneva inalterato. Un criterio di resistenza per materiali duttili deve tenere conto di queste proprietà Due sono i criteri più adottati, perché maggiormente valati dalla sperimentazione : Il criterio di TRESCA Il criterio di HUBER-MISES -HENKY
7 IL CRITERIO DI TRESCA Secondo Tresca (1868) nell intorno di un punto l indice del pericolo è dato dalla massima tensione tangenziale. 1 τ = τmax = max σ σ, σ σ, σ σ 2 { } I II II III I III Poiché in regime monoassiale si ha τ max = 1 σ 2 I Lo stato tensionale monoassiale equivalente è caratterizzato dalla tensione eale σ = 2τ
8 L espressione analitica del criterio di Tresca assume pertanto la forma : { I II II III I III } 0 σ = max σ σ, σ σ, σ σ σ Il criterio rispetta le condizioni di simmetria e indipendenza dalla componente rostatica della tensione. Ad esso corrisponde, nello spazio delle tensioni principali, un dominio di resistenza avente la forma di un prisma a base esagonale regolare e l asse coincente con la trisettrice del primo ottante. La sua intersezione con il piano O I, di forma esagonale irregolare, è il dominio di resistenza per stati di tensione piani. II I σ 0 I σ 0 σ 0 σ 0
9 IL CRITERIO DI HUBER-MISES MISES-HENKY Questo criterio proposto da Huber (1904) è stato esaminato e sviluppato nei vari aspetti da Von Mises (1913) e Henky (1923). E anche noto come criterio della massima tensione tangenziale media o della massima tensione tangenziale ottaedrale o della massima energia specifica di distorsione I diversi nomi derivano dalle differenti procedure adottate dagli autori per pervenire alla stessa espressione della tensione eale. Si richiama che per la trave elastica è stata definita energia specifica di deformazione o potenziale elastico la sequente quantità: Ψ Ψ * 1 T 1 T 1 T Ψ tot = q Q = q Kq = Q DQ Essendo q e Q i vettori delle caratteristiche della deformazione e della sollecitazione, K e D le matrici di rigezza e deformabilità Ψ e Ψ* definiscono il potenziale elastico rispettivamente nello spazio delle caratteristiche di deformazione e di sollecitazione. Ψ* è detto potenziale complementare.
10 Nello scrivere le quantità precedenti si è fatto riferimento al legame costitutivo : Nel caso del solo trimensionale, essendo il legame costitutivo esprimibile nella forma: -1 e = Ds ; s = Ee ; ( D = E ) Con e e s vettori di ordine 6 contenenti le componenti speciali della deformazione e della tensione, il potenziale elastico si può esprimere nella forma: Ψ Ψ * 1 T 1 T 1 T Ψ tot = e s = e Ee = s Ds Nella precedente relazione Ψ e Ψ* definiscono il potenziale elastico rispettivamente nello spazio delle deformazioni e in quello delle tensioni. Nel secondo caso il potenziale è detto complementare. Ad esempio, per solo omogeneo ed isotropo, nello spazio delle tensioni e delle deformazioni principali, si può scrivere 1 1 Ψ tot = εσ i i = ( εi σi + εii σii + εiii σiii ) i = 1 q = DQ ; Q = K q
11 1 Il potenziale complementare ( essendo ε1 = [ σi ν ( σii + σiii )] essere scritto come segue : E etc ) può e che ν Ψ tot = Ψ * = ( σ ) ( ) 2 I + σ E II + II σ E I I + I II + II Tenendo presente che σiσii + σiiσiii + σiiiσi = I σ = I + II + III = I + II + III + I II + II III + III I I σ 1 ( σ σ σ ) ( σ σ σ ) 2( σ σ σ σ σ σ ) ovvero = σ1 2 σ2 σi σii σiii I I Si ottiene l espressione del potenziale elastico complementare in funzione degli invarianti primo e secondo della tensione : 1 1 * 2 I +ν Ψ = E E I 2 σ1 σ2
12 Sottraendo al potenziale elastico l aliquota dovuta alla sola dilatazione della materia 1 2ν 2 Ψ * dil = Iσ 1 6E Si ottiene il potenziale elastico distorsivo 1 +ν 2 Ψ * dist = Ψ * Ψ * dil = ( Iσ1 3 Iσ2) 3E Che può essere scritto in forma alternativa come segue: 1 + ν Ψ * dist = ( σi σii ) ( σii σiii ) ( σi σiii ) 6E + + Nel caso di tensione monoassiale (I =II =0) si ha Ψ * = dist 1 +ν σ 3E 2 I Da cui 1 σ = ( σ σ ) + ( σ σ ) + ( σ σ ) = I 3I I II II III I III σ1 σ2
13 A differenza del criterio di Tresca attraverso il criterio di Huber-Mises- Henky è possibile esprimere la tensione eale in funzione delle componenti speciali della tensione espresse in un qualunque riferimento cartesiano. A tale espressione si perviene ricordando che gli invarianti primo e secondo della tensione possono essere scritti come: I σ 1 = σx + σy + σz x y z x y y z z x xy yz zx σ = σ + σ + σ ( σ σ + σ σ + σ σ ) + 3( τ + τ + τ ) x y y z z x xy yz zx I σ 2 = σ σ + σ σ + σ σ ( τ + τ + τ ) Per cui I Il dominio di resistenza nello spazio delle tensioni principali è un cilindro a base circolare avente asse coincente con la trisettrice del primo ottante. Nel caso di stato piano di tensione il dominio di resistenza è un ellisse circoscritto all esagono di Tresca. σ 0 σ 0 σ 0 σ 0
14 PARTICOLARIZZAZIONE PER IL SOLIDO DI DE SAINT-VENANT Nel caso del solo di De Saint-Venant composto da materiale duttile omogeneo e isotropo le tensioni principali si determinano risolvendo l equazione λ 0 τxz 3 2 Det ( σ λi ) = Det 0 λ τyz = λ Iσ1λ + Iσ2λ Iσ3 = 0 τxz τyz σz λ con 2 2 σ1 σz σ2 τxz τyz σ3 I = ; I = ; I = 0 Si ottiene: z ± z + 4( xz + yz ) I σ σ τ τ σ λ = = 2 σ II Per il criterio di Tresca la tensione eale è Per il criterio di H.M.H si ha invece I II z xz yz σ = σ σ = σ + 4( τ + τ ) z xz yz σ == σ + 3( τ + τ )
Verifiche di sicurezza di una costruzione 1/2
 Verifiche di sicurezza di una costruzione 1/2 Le costruzioni devono soddisfare opportuni requisiti di sicurezza nei confronti della loro capacità portante Capacità portante Attitudine di una struttura
Verifiche di sicurezza di una costruzione 1/2 Le costruzioni devono soddisfare opportuni requisiti di sicurezza nei confronti della loro capacità portante Capacità portante Attitudine di una struttura
CRITERI DI RESISTENZA DEI MATERIALI
 CRTER D RESSTENZA DE MATERAL Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
CRTER D RESSTENZA DE MATERAL Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
RESISTENZA DEI MATERIALI TEST
 RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
LEZIONI N 24 E 25 UNIONI SALDATE
 LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
Lezione. Tecnica delle Costruzioni
 Lezione Tecnica delle Costruzioni 1 Flessione composta tensoflessione Risposta della sezione Campo elastico σ + A I Risposta della sezione Al limite elastico el, Per calcolare el, : σ A + el, I f f + el,
Lezione Tecnica delle Costruzioni 1 Flessione composta tensoflessione Risposta della sezione Campo elastico σ + A I Risposta della sezione Al limite elastico el, Per calcolare el, : σ A + el, I f f + el,
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Horae. Horae Software per la Progettazione Architettonica e Strutturale
 1 IL MATERIALE X-LAM Nel programma CDSWin il materiale X-LAM pu ò essere utilizzato solo come elemento parete verticale. Quindi, dal punto di vista strutturale, il suo comportamento è prevalentemente a
1 IL MATERIALE X-LAM Nel programma CDSWin il materiale X-LAM pu ò essere utilizzato solo come elemento parete verticale. Quindi, dal punto di vista strutturale, il suo comportamento è prevalentemente a
--- durezza --- trazione -- resilienza
 Proprietà meccaniche Necessità di conoscere il comportamento meccanico di un certo componente di una certa forma in una certa applicazione prove di laboratorio analisi del comportamento del componente
Proprietà meccaniche Necessità di conoscere il comportamento meccanico di un certo componente di una certa forma in una certa applicazione prove di laboratorio analisi del comportamento del componente
TEST DI VALIDAZIONE DEL SOFTWARE VEM NL
 1 2 TEST DI VALIDAZIONE DEL SOFTWARE VEM NL Confronto dei risultati tra il software VEM NL el il metodo SAM proposto dall Unità di Ricerca dell Università di Pavia. Stacec s.r.l. Software e servizi per
1 2 TEST DI VALIDAZIONE DEL SOFTWARE VEM NL Confronto dei risultati tra il software VEM NL el il metodo SAM proposto dall Unità di Ricerca dell Università di Pavia. Stacec s.r.l. Software e servizi per
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
LEZIONE 7. PROGETTO DI STRUTTURE IN LEGNO Parte II. Criteri di verifica. Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A.
 Corso i TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà i Architettura Università egli Stui i Genova LEZIONE 7 PROGETTO DI STRUTTURE IN LEGNO Parte II. Criteri i verifica NORMATIVA DI
Corso i TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà i Architettura Università egli Stui i Genova LEZIONE 7 PROGETTO DI STRUTTURE IN LEGNO Parte II. Criteri i verifica NORMATIVA DI
23 CAPITOLO 2: RELAZIONI TRA LE DIVERSE FASI DI UN CAMPIONE DI TERRENO
 v 23 CAPITOLO 2: RELAZIONI TRA LE DIERSE FASI DI UN CAMPIONE DI TERRENO CAPITOLO 2: RELAZIONI TRA LE DIERSE FASI DI UN CAMPIONE DI TERRENO Un campione di terreno viene considerato come un sistema multifase,
v 23 CAPITOLO 2: RELAZIONI TRA LE DIERSE FASI DI UN CAMPIONE DI TERRENO CAPITOLO 2: RELAZIONI TRA LE DIERSE FASI DI UN CAMPIONE DI TERRENO Un campione di terreno viene considerato come un sistema multifase,
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CALCOLO TEORICO DELLE CONNESSIONI
 CALCOLO TEORICO DELLE CONNESSIONI Relatore: INDICE: Connettori metallici a gambo cilindrico alle tensioni ammissibili Approccio di calcolo agli stati limite - Teoria di Johansen - Formule proposte dalle
CALCOLO TEORICO DELLE CONNESSIONI Relatore: INDICE: Connettori metallici a gambo cilindrico alle tensioni ammissibili Approccio di calcolo agli stati limite - Teoria di Johansen - Formule proposte dalle
STRUTTURE MISTE ACCIAIO-CLS Lezione 2
 STRUTTURE MISTE ACCIAIO-CLS Lezione 2 I SISTEMI DI CONNESSIONE Tipologie di connettori Calcolo della sollecitazione nei connettori Connettori a totale ripristino di resistenza Connettori a parziale ripristino
STRUTTURE MISTE ACCIAIO-CLS Lezione 2 I SISTEMI DI CONNESSIONE Tipologie di connettori Calcolo della sollecitazione nei connettori Connettori a totale ripristino di resistenza Connettori a parziale ripristino
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Il valore assoluto. F. Battelli Università Politecnica delle Marche, Ancona. Pesaro, Precorso di Analisi 1, 22-28 Settembre 2005 p.
 Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
VERIFICA OPERE IN C.A. CORPO "A"
 VERIFICA OPERE IN C.A. CORPO "A" 1 VERIFICA PIASTRA FONDALE...3 VERIFICA RESTANTI OPERE IN C.A...9 VERIFICHE SLE...11 2 VERIFICA PIASTRA FONDALE Verifica a flessione Stati limiti La piastra fondale presenta
VERIFICA OPERE IN C.A. CORPO "A" 1 VERIFICA PIASTRA FONDALE...3 VERIFICA RESTANTI OPERE IN C.A...9 VERIFICHE SLE...11 2 VERIFICA PIASTRA FONDALE Verifica a flessione Stati limiti La piastra fondale presenta
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Generalità e note di teoria
 Capitolo 1 Generalità e note di teoria In questo capitolo sono riportate alcune note delle teorie utilizzate, riguardanti: Verifiche di resistenza. Dati del problema e convenzioni. Ipotesi fondamentali.
Capitolo 1 Generalità e note di teoria In questo capitolo sono riportate alcune note delle teorie utilizzate, riguardanti: Verifiche di resistenza. Dati del problema e convenzioni. Ipotesi fondamentali.
Per prima cosa si determinano le caratteristiche geometriche e meccaniche della sezione del profilo, nel nostro caso sono le seguenti;
 !""##"!$%&'((""!" )**&)+,)-./0)*$1110,)-./0)*!""##"!$%&'((""!" *&)23+-0-$4--56%--0.),0-,-%323 -&3%/ La presente relazione ha lo scopo di illustrare il meccanismo di calcolo che sta alla base del dimensionamento
!""##"!$%&'((""!" )**&)+,)-./0)*$1110,)-./0)*!""##"!$%&'((""!" *&)23+-0-$4--56%--0.),0-,-%323 -&3%/ La presente relazione ha lo scopo di illustrare il meccanismo di calcolo che sta alla base del dimensionamento
6. Modalità di rottura e criteri di resistenza
 6. Modalità di rottura e criteri di resistenza 6.. Generalità Per definire un criterio di resistenza è necessario tener conto dei particolari processi che portano al cedimento inteso come il verificarsi
6. Modalità di rottura e criteri di resistenza 6.. Generalità Per definire un criterio di resistenza è necessario tener conto dei particolari processi che portano al cedimento inteso come il verificarsi
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo
 I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo diverse metodologie. 1 La tempra termica (o fisica) si basa
I processi di tempra sono condotti sul manufatto finito per generare sforzi residui di compressione in superficie. Vengono sfruttate allo scopo diverse metodologie. 1 La tempra termica (o fisica) si basa
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Il c.a.p. nelle nuove Norme Tecniche
 Il c.a.p. nelle nuove Norme Tecniche plizzari@ing.unibs.it Università di Brescia Corso di Tecnica delle Costruzioni Verifica di una struttura esistente Corso Tecnica delle Costruzioni 2/71 Comportamento
Il c.a.p. nelle nuove Norme Tecniche plizzari@ing.unibs.it Università di Brescia Corso di Tecnica delle Costruzioni Verifica di una struttura esistente Corso Tecnica delle Costruzioni 2/71 Comportamento
tecnologia PROPRIETÀ DEI METALLI Scuola secondaria primo grado. classi prime Autore: Giuseppe FRANZÈ
 tecnologia PROPRIETÀ DEI METALLI Scuola secondaria primo grado. classi prime Autore: Giuseppe FRANZÈ LE PROPRIETÀ DEI MATERIALI DA COSTRUZIONE Si possono considerare come l'insieme delle caratteristiche
tecnologia PROPRIETÀ DEI METALLI Scuola secondaria primo grado. classi prime Autore: Giuseppe FRANZÈ LE PROPRIETÀ DEI MATERIALI DA COSTRUZIONE Si possono considerare come l'insieme delle caratteristiche
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Aerospaziali PER MATERIALI ISOTROPI PARTE 1. Prof. Claudio Scarponi Ing. Carlo Andreotti
 Aerospaziali CRITERI DI ROTTURA STATICI PER MATERIALI ISOTROPI PARTE 1 Prof. Claudio Scarponi TIPOLOGIE DI SOLLECITAZIONE Un provino può essere sottoposto a 2 tipi di sollecitazione: 1. Semplice Statica
Aerospaziali CRITERI DI ROTTURA STATICI PER MATERIALI ISOTROPI PARTE 1 Prof. Claudio Scarponi TIPOLOGIE DI SOLLECITAZIONE Un provino può essere sottoposto a 2 tipi di sollecitazione: 1. Semplice Statica
ESERCIZI SVOLTI. 2 Il calcestruzzo armato 2.4 La flessione composta
 ESERCIZI SVOLTI Costruire la frontiera del dominio di resistenza della sezione rettangolare di mm con armatura simmetrica A s,tot + 6, copriferro mm, impiegando calcestruzzo classe C /. Resistenza di calcolo
ESERCIZI SVOLTI Costruire la frontiera del dominio di resistenza della sezione rettangolare di mm con armatura simmetrica A s,tot + 6, copriferro mm, impiegando calcestruzzo classe C /. Resistenza di calcolo
Proprietà meccaniche. Prove meccaniche. prova di trazione prova di compressione prova di piegamento prova di durezza prova di fatica prova di creep
 Proprietà meccaniche Prove meccaniche prova di trazione prova di compressione prova di piegamento prova di durezza prova di fatica prova di creep Prova di trazione provini di dimensione standard deformazione
Proprietà meccaniche Prove meccaniche prova di trazione prova di compressione prova di piegamento prova di durezza prova di fatica prova di creep Prova di trazione provini di dimensione standard deformazione
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Istituto Tecnico per Geometri Corso di Costruzioni Edili
 Istituto Tecnico per Geometri Corso di Costruzioni Edili Prof. Giacomo Sacco LEZIONI SUL CEMENTO ARMATO Sforzo normale, Flessione e taglio CONCETTI FONDAMENTALI Il calcestruzzo ha una bassa resistenza
Istituto Tecnico per Geometri Corso di Costruzioni Edili Prof. Giacomo Sacco LEZIONI SUL CEMENTO ARMATO Sforzo normale, Flessione e taglio CONCETTI FONDAMENTALI Il calcestruzzo ha una bassa resistenza
Certificazione di produzione di codice di calcolo Programma CAP3
 1 Certificazione di produzione di codice di calcolo Programma CAP3 1) CARATTERISTICHE DEL CODICE Titolo programma : CAP3 - Travi precompresse ad armatura pretesa, Metodo agli stati limite. Autore : ing.
1 Certificazione di produzione di codice di calcolo Programma CAP3 1) CARATTERISTICHE DEL CODICE Titolo programma : CAP3 - Travi precompresse ad armatura pretesa, Metodo agli stati limite. Autore : ing.
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
PROGETTAZIONE MECCANICA CON COSMOS/Works. Informazioni di base
 PROGETTAZIONE MECCANICA CON COSMOS/Works Informazioni di base Che cos è COSMOS/Works? COSMOS/Works è un software per sviluppare progettazioni essenzialmente meccaniche completamente integrato col modellatore
PROGETTAZIONE MECCANICA CON COSMOS/Works Informazioni di base Che cos è COSMOS/Works? COSMOS/Works è un software per sviluppare progettazioni essenzialmente meccaniche completamente integrato col modellatore
STRUTTURE IN CEMENTO ARMATO - V
 Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì STRUTTURE IN CEMENTO ARMATO - V AGGIORNAMENTO 22/09/2012 DOMINIO DI RESISTENZA Prendiamo in considerazione la trave rettangolare
Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì STRUTTURE IN CEMENTO ARMATO - V AGGIORNAMENTO 22/09/2012 DOMINIO DI RESISTENZA Prendiamo in considerazione la trave rettangolare
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Bassa massa volumica (peso)= basse forze inerziali sismiche (peso del legno= 450 Kg/m³ 30-40 kg/m² ;
 BUON COMPORTAMENTO IN ZONA SISMICA Il legno come materiale e le strutture in legno in generale sono naturalmente dotate di alcune caratteristiche intrinseche che ne rendono non solo adatto ma consigliabile
BUON COMPORTAMENTO IN ZONA SISMICA Il legno come materiale e le strutture in legno in generale sono naturalmente dotate di alcune caratteristiche intrinseche che ne rendono non solo adatto ma consigliabile
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
LA CORRENTE ELETTRICA CONTINUA
 LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
Appunti sulle funi. Le Funi Carmine Napoli
 Appunti sulle funi DEFINIZIONE Fune: è un organo flessibile formato da un insieme di fili di acciaio, di forma e dimensioni appropriate, avvolti elicoidalmente in uno o più gruppi concentrici attorno ad
Appunti sulle funi DEFINIZIONE Fune: è un organo flessibile formato da un insieme di fili di acciaio, di forma e dimensioni appropriate, avvolti elicoidalmente in uno o più gruppi concentrici attorno ad
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE
 Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Elementi Costruttivi delle Macchine. Esercizi Resistenza statica -Effetto di intaglio. Politecnico di Torino CeTeM
 E. E. E.3 E.4 E.5 E.6 Un punto di un componente in acciaio 4Cr4 bonificato (R p0, 800 Ma, R m 000-00 Ma) è soggetto allo stato di tensione: xx xy xz 0 0 0 yx yy yz 0 0 0 Ma 0 0 360 zx zy zz Calcolare il
E. E. E.3 E.4 E.5 E.6 Un punto di un componente in acciaio 4Cr4 bonificato (R p0, 800 Ma, R m 000-00 Ma) è soggetto allo stato di tensione: xx xy xz 0 0 0 yx yy yz 0 0 0 Ma 0 0 360 zx zy zz Calcolare il
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Soluzione del tema d esame di matematica, A.S. 2005/2006
 Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto
 Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto Claudio Tamagnini Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di
Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto Claudio Tamagnini Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Forme bilineari e prodotti scalari. Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione. b :
 Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Analisi e consolidamento di colonne e pilastri in muratura
 CORSO DI RECUPERO E CONSERVAZIONE DEGLI EDIFICI A.A. 2010-2011 Analisi e consolidamento di colonne e pilastri in muratura Resistenza a compressione (1) I materiali lapidei naturali ed artificiali raggiungono
CORSO DI RECUPERO E CONSERVAZIONE DEGLI EDIFICI A.A. 2010-2011 Analisi e consolidamento di colonne e pilastri in muratura Resistenza a compressione (1) I materiali lapidei naturali ed artificiali raggiungono
Capacità di assorbire una deformazione plastica senza rompersi: alta=duttile (es. oro) bassa=fragile (es. vetro)
 Capacità di assorbire una deformazione plastica senza rompersi: alta=duttile (es. oro) bassa=fragile (es. vetro) E dipendente dalla temperatura:capacità di riposizionamento di difetti ed atomi (diffusione
Capacità di assorbire una deformazione plastica senza rompersi: alta=duttile (es. oro) bassa=fragile (es. vetro) E dipendente dalla temperatura:capacità di riposizionamento di difetti ed atomi (diffusione
LEGAME COSTITUTIVO ELASTICO LINEARE
 LGAM COSIUIVO LASICO LINAR L equilibrio di forze e tensioni e la congruenza di spostamenti e deformazioni prescindono dalla natura del materiale che costituisce la struttura, e le equazioni che ne governano
LGAM COSIUIVO LASICO LINAR L equilibrio di forze e tensioni e la congruenza di spostamenti e deformazioni prescindono dalla natura del materiale che costituisce la struttura, e le equazioni che ne governano
Le funzioni di due variabili
 Le funzioni di due variabili 1)DEFINIZIONE Se consideriamo una coppia di numeri reali X,Y e ad essi facciamo corrispondere un altro numero reale Z, allora abbiamo determinato una funzione reale di due
Le funzioni di due variabili 1)DEFINIZIONE Se consideriamo una coppia di numeri reali X,Y e ad essi facciamo corrispondere un altro numero reale Z, allora abbiamo determinato una funzione reale di due
GRANDEZZE SINUSOIDALI
 GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
BOZZA. Materiale muratura e verifiche per carichi verticali. Luca Salvatori. Dipartimento di Ingegneria Civile e Ambientale. Università di Firenze
 BOZZA Materiale muratura e verifiche per carichi verticali Luca Salvatori Dipartimento di Ingegneria Civile e Ambientale Università di Firenze Materiale Muratura 1 Il materiale muratura Materiale complesso
BOZZA Materiale muratura e verifiche per carichi verticali Luca Salvatori Dipartimento di Ingegneria Civile e Ambientale Università di Firenze Materiale Muratura 1 Il materiale muratura Materiale complesso
CONDUTTORI, CAPACITA' E DIELETTRICI
 CONDUTTORI, CAPACITA' E DIELETTRICI Capacità di un conduttore isolato Se trasferiamo una carica elettrica su di un conduttore isolato questa si distribuisce sulla superficie in modo che il conduttore sia
CONDUTTORI, CAPACITA' E DIELETTRICI Capacità di un conduttore isolato Se trasferiamo una carica elettrica su di un conduttore isolato questa si distribuisce sulla superficie in modo che il conduttore sia
CORRENTE ELETTRICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V 2 isolati tra loro V 2 > V 1 V 2
 COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
LA TRAVE DI FONDAZIONE SU SUOLO ELASTICO STRATIFICATO DI SPESSORE LIMITATO CON MODULO ELASTICO VARIABILE CON LA PROFONDITÀ
 LA TRAVE DI FONDAZIONE SU SUOLO ELASTICO STRATIFICATO DI SPESSORE LIMITATO CON MODULO ELASTICO VARIABILE CON LA PROFONDITÀ Giovanni Dalerci, Rossella Bovolenta Università degli Studi di Genova Dipartimento
LA TRAVE DI FONDAZIONE SU SUOLO ELASTICO STRATIFICATO DI SPESSORE LIMITATO CON MODULO ELASTICO VARIABILE CON LA PROFONDITÀ Giovanni Dalerci, Rossella Bovolenta Università degli Studi di Genova Dipartimento
ELETTROSTATICA + Carica Elettrica + Campi Elettrici + Legge di Gauss + Potenziale Elettrico + Capacita Elettrica
 ELETTROSTATICA + Carica Elettrica + Campi Elettrici + Legge di Gauss + Potenziale Elettrico + Capacita Elettrica ELETTRODINAMICA + Correnti + Campi Magnetici + Induzione e Induttanza + Equazioni di Maxwell
ELETTROSTATICA + Carica Elettrica + Campi Elettrici + Legge di Gauss + Potenziale Elettrico + Capacita Elettrica ELETTRODINAMICA + Correnti + Campi Magnetici + Induzione e Induttanza + Equazioni di Maxwell
6. Calcolare le derivate parziali prime e seconde, verificando la validità del teorema di Schwarz:
 FUNZIONI DI PIU VARIABILI Esercizi svolti. Determinare il dominio delle seguenti funzioni e rappresentarlo graficamente : (a) f log( x y ) (b) f log(x + y ) (c) f y x 4 (d) f sin(x + y ) (e) f log(xy +
FUNZIONI DI PIU VARIABILI Esercizi svolti. Determinare il dominio delle seguenti funzioni e rappresentarlo graficamente : (a) f log( x y ) (b) f log(x + y ) (c) f y x 4 (d) f sin(x + y ) (e) f log(xy +
Problema. caso uniassiale prova di trazione. caso multiassiale (carico generico)
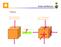 Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
PALI Si distinguono: Nel caso 1 il palo non modifica il moto ondoso, mentre nel caso 2 il moto ondoso è modificato dal palo.
 PALI Si distinguono: 1. pali di piccolo diametro se D/L0,05 Nel caso 1 il palo non modifica il moto ondoso, mentre nel caso 2 il moto ondoso è modificato dal palo.
PALI Si distinguono: 1. pali di piccolo diametro se D/L0,05 Nel caso 1 il palo non modifica il moto ondoso, mentre nel caso 2 il moto ondoso è modificato dal palo.
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
RAPPRESENTAZIONE BINARIA DEI NUMERI. Andrea Bobbio Anno Accademico 1996-1997
 1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
Termodinamica: legge zero e temperatura
 Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
Integrali doppi - Esercizi svolti
 Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
LEZIONI N 9, 10, 11 E 12 COSTRUZIONI DI ACCIAIO: IPOTESI DI BASE E METODI DI VERIFICA
 LEZIONI N 9, 10, 11 E 12 COSTRUZIONI DI ACCIAIO: IPOTESI DI BASE E METODI DI VERIFICA L acciaio da carpenteria è una lega Fe-C a basso tenore di carbonio, dall 1 al 3 per mille circa. Gli acciai da costruzione
LEZIONI N 9, 10, 11 E 12 COSTRUZIONI DI ACCIAIO: IPOTESI DI BASE E METODI DI VERIFICA L acciaio da carpenteria è una lega Fe-C a basso tenore di carbonio, dall 1 al 3 per mille circa. Gli acciai da costruzione
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
PORTANZA DELLE FONDAZIONI
 1 N.T.C. 2008, Capitolo 6.4 - OPERE DI FONDAZIONE Nelle verifiche di sicurezza devono essere presi in considerazione tutti i meccanismi di stato limite ultimo, sia a breve sia a lungo termine. Gli stati
1 N.T.C. 2008, Capitolo 6.4 - OPERE DI FONDAZIONE Nelle verifiche di sicurezza devono essere presi in considerazione tutti i meccanismi di stato limite ultimo, sia a breve sia a lungo termine. Gli stati
