Risultati Esercizi volume Ottica Visuale
|
|
|
- Ugo Rocca
- 8 anni fa
- Visualizzazioni
Transcript
1 Risultati Esercizi volume Ottica Visuale Zeri F, Rossetti A, Fossetti A, Calossi A. Capitolo 2 Es.2.1: Effettuare il calcolo del potere della cornea, attraverso la formula per lenti sottili usando i dati di Dunne et al (1992) per maschi e femmine riportati in Tab.2.1. E possibile calcolare il potere della cornea con la formula per lenti sottili (Eq.2.1) calcolando prima il potere dei singoli diottri con la Eq.2.2. Per la superficie anteriore n=1,0 e n =1,376 Per la superficie posteriore n=1,376 e n =1,336 Secondo i dati medi di Dunn et al (1992), nei maschi r 1 =8,08 r 2 =6,65 F 1 =1,376-1,00/8, =46,53D F2=1,336-1,376/6, =-6,01D F=46,53-6,02=40,52D Secondo i dati medi di Dunn et al (1992), nelle femmine r 1 =7,93 r 2 =6,53 F1=1,376-1,00/7, =47,41D F2=1,336-1,376/6, =-6,12D F=47,41-6,12=41,29D Es.2.2: Ripetere il calcolo con i dati dell Es.2.1, ma usando in questo caso la formula per lenti spesse (considerare uno spessore corneale di 0,5 mm). In questo caso per calcolare il potere della cornea viene usata la Eq.2.3. Il potere dei singoli diottri è stato già calcolato per l Es.2.1 Quindi nei maschi: F=46,53 +(-6,01) [46,53 (-6,01) (0,0005/1,376)]=40,62D e nelle femmine: F=47,41+(-6,12) [47,41 (-6,12) (0,0005/1,376)]=41,39D Es.2.3: Calcolare il potere totale della cornea nel caso in cui ci si trovi ad aprire gli occhi sott acqua (n acqua =1,33), applicando la formula per lenti sottili ai dati medi di curvatura di Patel e collaboratori (1993), riportati in tabella 2.1. Per calcolare il potere della cornea con la formula per lenti sottili (Eq.2.1) è necessario calcolare prima il potere dei singoli diottri con la Eq.2.2. Per la superficie anteriore n=1,33 e n =1,376 Per la superficie posteriore n=1,376 e n =1,336 Secondo i dati di Patel e collaboratori (1993) r 1 = 7,68 mm e r 2 = 5,81 mm Quindi: F 1 =1,376-1,33/7, =5,56D F2=1,336-1,376/5, =-6,88D F=5,56-6,88=-1.32D Es.2.4: Effettuare il calcolo del potere del cristallino, attraverso la formula per lenti
2 spesse considerando: - un raggio della prima superficie di 13 mm - un raggio della seconda superficie di -7,8 mm - uno spessore del cristallino di 4 mm - un indice di rifrazione del cristallino di 1,42 e un indice di rifrazione di acqueo e vitreo di 1,336. Viene prima calcolato il potere dei singoli diottri con la Eq.2.2. Per la superficie anteriore n=1,336 e n =1,42 Per la superficie posteriore n=1,42 e n =1,336 F 1 =1,42-1,336/ =6,46D F2=1,336-1,42/-7, =10,77D Il calcolo del potere totale del cristallino si effettua applicando la Eq.2.3. F=6,46 +(10,77) [6,46 (10,77) (0,004/1,42)]=17,03D Es.2.5: Il cristallino non accomodato dell occhio schematico di Rabbetts-Bennetts possiede le seguenti caratteristiche: r 1 =11,0 mm r 2 =-6,47 n=1,422 t=3,70 mm Sapendo che l indice di rifrazione dell umor acqueo e del vitreo è uguale ed equivale a 1,336, calcola la differenza nel potere equivalente del cristallino quando, durante l accomodazione, il raggio anteriore diventa di +7,00 mm, quello posteriore di -5,50 e lo spessore 3,93 mm. Viene prima calcolato il potere dei singoli diottri nella condizione non accomodata con la Eq.2.2. Per la superficie anteriore n=1,336 e n =1,422 Per la superficie posteriore n=1,422 e n =1,336 F 1 =1,422-1,336/ =7,82D F2=1,336-1,422/-6, =13,29D Il calcolo del potere totale del cristallino si effettua applicando la Eq.2.3. F=7,82 +(13,29) [7,82 (13,29) (0,0037/1,422)]=21,08D Viene poi calcolato il potere dei singoli diottri nella condizione accomodata con la Eq.2.2. Ancora una volta per la superficie anteriore n=1,336 e n =1,422 e per la superficie posteriore n=1,422 e n =1,336 F 1 =1,422-1,336/7, =12,29D F2=1,336-1,422/-5, =15,64D Si calcola il potere totale del cristallino in condizione accomodata applicando la Eq.2.3. F=12,29 +(15,64) [12,29 (15,64) (0,00393/1,422)]=27,40D La differenza di potere del cristallino tra le due condizioni, accomodata e non accomodata, è quindi: Diff=27,40-21,08= 6,32 D Es.2.6: Verifica che l angolo sotteso nel campo visivo dalla fovea sia quello indicato nel testo, sapendo che le dimensioni lineari della fovea sono per l appunto 0,3 per 0,2 mm e la distanza tra fovea (che coincide con il secondo fuoco principale; F ) e il secondo punto nodale (N ) sia uguale a 16,67 mm (è la distanza tra F e N nell occhio
3 schematico di Bennett e Rabbetts). La verifica può essere effettuata sapendo che l angolo sotteso da un oggetto al primo punto nodale (ω) equivale a quello sotteso dall immagine al secondo punto nodale (ω ). Quindi l angolo sotteso dalla fovea al secondo punto nodale (ω ) sarà uguale alla proiezione della fovea nello spazio sottesa al primo punto nodale (ω). Si può calcolare ω per il diametro maggiore (Ø max ) e minore(ø min ) della fovea sapendo che tgω =Ø/ F N effettuando il calcolo per i due diametri si trova che: ω (Ø max )=tg -1 (0,0003/0,01667)=1,03 ω (Ø max )= tg -1 (0,0002/0,01667)=0,69 Es.2.7: Calcolare la grandezza della proiezione della fovea nello spazio ad una distanza (d) di 40 cm dal primo punto nodale, sapendo che le dimensioni lineari della fovea sono 0,3 per 0,2 mm e la distanza tra fovea, coincidente con il secondo fuoco principale (F ), e secondo punto nodale (N ) è uguale a 16,67 mm (la distanza tra F e N nell occhio schematico di Bennett e Rabbetts). Anche in questo caso si può procedere al calcolo sapendo che l angolo sotteso da un oggetto al primo punto nodale (ω) equivale a quello sotteso dall immagine al secondo punto nodale (ω ). Viene calcolato inizialmente l angolo sotteso dalla fovea al secondo punto nodale (ω ) per i due diametri secondo quanto visto al precedente esercizio ω (Ø max )=tg -1 (0,0003/0,01667)=1,03 ω (Ø max )= tg -1 (0,0002/0,01667)=0,69 La proiezione della fovea (h) a 40 cm (d) dal primo punto nodale sarà calcolabile sapendo che l angolo di proiezione al primo punto nodale è uguale a ω. Quindi: h= tgω d h max = tg1,03 0,40=0,0072m h min = tg 0,69 0,40=0,0048m Capitolo 5 Es.5.1: Calcolare f e, f e e k e di un occhio ridotto non standard emmetrope con F e =66,0D. Per risolvere l esercizio si usano le equazioni Eq.5.1 e Eq.5.2 f e =-n/f e =-1/66=-15,15mm f e =n /F e =(4/3)/66=20,20mm Essendo un occhio ridotto emmetrope f e k e quindi: k e =20,20mm Es.5.2: Un oggetto sottende 1 ( w) ad un occhio ridotto standard emmetrope. Calcolare la grandezza dell immagine retinica h.
4 Per risolvere l esercizio si usa l equazione Eq.5.7 h =-0,02222 ¾ tan 1= h =-0,000291m=291µm Es.5.3: Un oggetto sottende 1 (w) ad un occhio ridotto emm etrope con Fe=+57,0D. Calcolare la grandezza dell immagine retinica h Per risolvere l esercizio si usa l equazione Eq.5.8 h =-k ¾ tan w= Visto che l occhio è emmetrope, k f e quindi: f e =n /F= (4/3)/57=0,0233 h =-0,0233 ¾ tan 1 = m=-306µm Es.5.4: Un oggetto sottende 1 ( w) ad un occhio ridotto emmetrope con Fe=+63,0D. Calcolare la grandezza dell immagine retinica (h ) Anche in questo caso per risolvere l esercizio si usa l equazione Eq.5.8 h =-k ¾ tan w= Visto che l occhio è emmetrope, k f e f e =n /F= 4/3 /63=0,0211m h =-0,0211 ¾ tan 1 = m=-277µm Es.5.5: Un oggetto sottende 20 (w) ad un occhio ridotto emmetrope con lunghezza assiale di 20 mm (k ). Calcolare la grandezza dell immagine retinica h. Anche in questo caso per risolvere l esercizio si usa l equazione Eq.5.8 h =-k ¾ tan w= L angolo w sotteso dall oggetto deve però essere trasformato in gradi. 20 =0,333 h =-0,020 ¾ tan 0,333 = m=-87µm Es.5.6: In un occhio ridotto emmetrope con lunghezza assiale di 23 mm (k ) si forma un immagine retinica (h ) di -500µm. Calcolare l angolo sotteso dall oggetto. Partendo dall Eq.5.8 si risolve l equazione per w: w=tan -1 (h (4/3) / -k ) w=tan -1 (-0,0005 (4/3) / -0,023)=1,66 Es.5.7: Il punto remoto di un occhio ridotto e a 20 cm davanti alla superficie ridotta. Se il potere dell occhio e di 65.00D, quanto sarà la sua lunghezza assiale? Si trova innanzi tutto l ametropia attraverso la Eq.5.12 K=1/k= 1/-0,20= -5,00D Viene poi calcolata la lunghezza diottrica dalla Eq.5.10 K =K+F e K =-5+65=60D e da questa la lunghezza assiale con Eq.5.13 k =n /K =4/3/60= 22,22mm
5 Es.5.8: La prima lunghezza focale di un occhio ridotto e di 17 mm e la sua lunghezza assiale di 23,00 mm. A che distanza si trova il punto remoto? Si trova innanzi tutto il potere dell occhio con la Eq.5.1 F=-n/f= F=-1/-0,017=+58,82D Viene poi calcolata la lunghezza diottrica dalla Eq.5.13 K =n /k = (4/3)/0,023=+57,97D Viene poi calcolata l ametropia attraverso la formula per l ametropia (Eq.5.10): K=K -Fe=+57,97-58,82=-0,85D E dall ametropia la distanza dal punto remoto (k) attraverso la Eq.5.12: k=n/k=1/-0,85=-1.17m Es.5.9: L ametropia di un occhio ridotto standard con ipermetropia assiale e di +5,00D. Qual è la sua lunghezza assiale? In un occhio ridotto standard con ipermetropia assiale F e F 0 Sapendo che (Eq.5.10) K =K+F e : K =+5,0+60,0=+65,0D E dalla Eq.5.13: k =(4/3) /65= 20,51mm Es.5.10: L ametropia di un occhio ridotto standard con ipermetropia refrattiva e di +5,00D. Qual e la lunghezza della seconda focale? La lunghezza della seconda focale può essere ricavata dalla Eq.5.2: f e =n /F e A sua volta il potere effettivo dell occhio viene ricavato dalla formula per l ametropia (Eq.5.10): F e =K -K Sapendo che l ipermetropia è refrattiva K K 0 Quindi: F e =60,0-5,0=+55,0D f e =4/3 /55= 24,24mm Es.5.11: Calcolare la distanza del punto remoto e la lunghezza assiale di un occhio ridotto con miopia assiale di 2.00 D. k=n/k k=1/-2,0=-0,50m K =K+F 0 K =-2,00+60,0=+58,0D k =n /K =4/3/58= 22,98mm Es.5.12: Calcolare la distanza del punto remoto e la lunghezza assiale di un occhio ridotto con ipermetropia assiale di 2.00 D. la distanza del punto remoto si calcola con l Eq.5.12 k=n/k k=1/2,0=0,50m
6 La lunghezza diottrica si calcola dalla Eq.5.10, dove il potere dell occhio coincide con quello standard essendo l ipermetropia assiale. K =K+F 0 K =2,00+60,0=+62,0D Quindi: k =n /K =4/3/62= 21,50mm Es.5.13: Calcolare la distanza del punto remoto e la lunghezza assiale di un occhio ridotto con miopia refrattiva di 2.00 D Come nel precedente esercizio, k=n/k k=1/-2,0=-0,50m Nella miopia refrattiva k =k 0 k 0 = 22,22mm Es.5.14: Calcolare la distanza del punto remoto e la lunghezza assiale di un occhio ridotto con ipermetropia refrattiva di 5.00 D. Come nel precedente esercizio, k=n/k k=1/5,0=0,20m Nella iperemtropia refrattiva k =k 0 k 0 = 22,22mm Es.5.15: Calcolare la distanza del punto remoto di un occhio con ipermetropia refrattiva di potere effettivo (F e ) pari a 56,50D. Si userà la formula per l ametropia (Eq.5.10) sapendo che la lunghezza diottrica è standard perché l ipermetropia è refrattiva: K 0 =K+F e = K=K 0 -F e = 60-56,5=+3,5 Quindi: k=n/k k=1/3,5=28,57cm Es.5.16: Calcolare il potere di un occhio con miopia refrattiva di 4,00D. Se un oggetto di 10mm e posto sul punto remoto, quale sarà la grandezza dell immagine retinica? Come nell esercizio precedente si userà la formula per l ipermetropia (Eq.5.10) sapendo che la lunghezza diottrica è standard perché la miopia è refrattiva: F e =K 0 -K= 60+4=64,0D Viene poi calcolato l ingrandimento attraverso l Eq.5.17: I T =K/K 0 =-4/60=-0,066 E con la Eq.5.15 viene calcolata la grandezza dell immagine retinica h = I T h=10-0,066=-0,666mm Es.5.17: Calcolare la grandezza dell immagine retinica di un oggetto alto 1 cm, posto sul punto remoto di un occhio miope, situato a 20 cm dalla superficie ridotta. Eseguire il calcolo per una miopia assiale e una refrattiva. Si calcola per prima cosa l ametropia: K=1/-0,20=-5,00D Nel caso della miopia refrattiva la Eq.5.17 sarà:
7 I T =K/K 0 =-5/60=-0,083 Quindi: h = I T h=1-0,083=-0,0833 cm Nel caso della miopia assiale la Eq.5.17 sarà: I T =K/K = K =K+F 0 =-5,0+60=+55,0D I T =-5/55=-0,090 h = I T h=1-0,090=-0,0909 cm Es.5.18: Costruire un diagramma cartesiano con in ascissa l ametropia K e in ordinata la lunghezza assiale k. Indicare nel grafico la lunghezza assiale corrispondente alle ametropie assiali comprese tra +5,00 e -10,00 (in passi di 1 D). Es.5.19: Calcolare la grandezza dell immagine retinica di base che si forma quando un oggetto sottende un angolo di 30 alla superficie ridotta di un occhio con ametropia assiale di K=+5,00D. Ripetere il calcolo per un ametropia refrattiva dello stesso valore. Si utilizza l Eq.5.8: h =-k ¾ tan w Nel caso dell ametropia assiale (iperemetropia) K =K+F o =5+60=65,0D k =n /K =4/3 / 65= 20,51mm h =-0,02051 ¾ tan 0,5 =-134 µm Nel caso dell ametropia refrattiva (iperemetropia) k o =22,22mm h =-0,0222 ¾ tan 0,5 =-145 µm Es.5.20: Calcolare la grandezza dell immagine retinica di base che si forma quando un oggetto sottende un angolo di 30 alla superficie ridotta di un occhio con ametropia assiale di K=-5,00D. Ripetere il calcolo per un ametropia refrattiva dello stesso valore. Come nell esercizio precedente si utilizza l Eq.5.8: h =-k ¾ tan w Nel caso dell ametropia assiale (miopia) K =K+F o =-5+60=55,0D k =n /K = 4/3 /55= 24,24mm h =-0,02424 ¾ tan 0,5 =-158 µm Nel caso dell ametropia refrattiva (miopia) k o =22,22mm h =-0,0222 ¾ tan 0,5 =-145 µm
8 Es.5.21: Calcolare la grandezza dell immagine retinica di base che si forma quando un oggetto sottende un angolo di 40 alla superficie ridotta di un occhio con un ametropia assiale il cui punto remoto si trova a 10 cm davanti alla superficie ridotta. Come nell esercizio precedente si utilizza l Eq.5.8: h =-k ¾ tan w La lunghezza oculare si calcolerà a partire dalla lunghezza diottrica calcolata con l Eq.5.10: K =K+F o = Dove: K=n/k= 1/-0,10=-10,00D K =K+F o =-10,0+60,0=+50,0D k =n /K = (4/3) /50= 26,66mm w=40 =0,011 h =-0,02666 ¾ tan 0,011 =-3,8 µm Es.5.22: Inserire su un diagramma cartesiano la grandezza dell immagine retinica di base (ordinata) in funzione delle ametropie (ascissa) assiali e refrattive comprese tra +5,00 e -10,00 (in step di 1 D) per un oggetto che sottende un angolo di 1 alla superficie ridotta. Es.5.23: Calcolare la grandezza del cerchio di confusione che si forma sulla retina di un occhio con ipermetropia assiale con k =21 mm e diametro pupillare di 2 mm relativa ad un punto oggetto che si trova all infinito. Attraverso la formula dei punti coniugati (Eq.5.11): L =L+F 0 L=0 e F 0 =60D; quindi: L =60; l =(4/3)/60=22,22mm Attraverso la Eq.5.19: j= Ø P (l -k ) / l j=2 (22,22-21)/22,22=0,11mm Es.5.24: Calcolare la grandezza del cerchio di confusione che si forma sulla retina di un occhio con ipermetropia assiale con k =21 mm e diametro pupillare di 6 mm relativa ad un punto oggetto che si trova all infinito. Come nell esercizio precedente L =L+F 0 L =60; l =(4/3)/60=22,22mm j= Ø P (l -k ) / l j=6 (22,22-21)/22,22=0,32 mm
9 Es.5.25: Un occhio ridotto miope di 6,00D guarda un punto oggetto a 2 metri di fronte ad esso. Calcolare la grandezza del cerchio di confusione retinico quando il diametro pupillare e di 6 mm e l ametropia e assiale. Attraverso la formula dei punti coniugati (Eq.5.11) deve essere ricavata la vergenza immagine: L =L+Fe; La vergenza oggetto sarà: L=n/l= 1/-2=-0,50D Essendo l ametropia assiale F 0 =60D; quindi: L =60+(-0,50)= 59,50D; Si ricava la distanza immagine: l =(4/3)/59,50=22,4mm Si ricava a questo punto la lunghezza assiale: K =K+F 0 =-6+60=+54D; k =4/3/54=24,7 Attraverso la Eq.5.19: j= Ø P (k l ) / l j=6 (24,7-22,4)/22,4=0,61mm Es.5.26: Un punto oggetto e posto a 25 cm di fronte ad un occhio ridotto con ametropia assiale e k =21mm. Calcolare la grandezza del cerchio di confusione retinico quando il diametro pupillare e di 6 mm. Analogamente all esercizio precedente: L =L+F 0 ; L=n/l= 1/-0,25=-4,0D L =60+(-4)= 56; l =(4/3)/56=22,4mm j= Ø P (l -k ) / l J=6 (23,8-21)/23,8=0,71mm Es.5.27: L ametropia oculare di un occhio ridotto con miopia assiale e di 10,D. Calcolare la correzione necessaria per una distanza al vertice di 14mm. Viene per prima cosa trovata la distanza k. k=n/k=1/-10=-0,1d E poi possibile la focale della lente correttrice posta alla distanza d attraverso la Eq.5.23: f lo = k + d v f lo =-0,10+0,014=-0,086m Il potere della lente correttrice sarà: F lo =1/f lo =1/-0,086=-11,62D Es.5.28: Un paziente usa una lente a contatto di -34,0D che lo emmetropizza. Quale potere dovrebbe avere un occhiale usato a 14mm per avere lo stesso effetto correttivo? Usare per il calcolo il metodo step along.
10 Es.5.29: L ametropia oculare di un occhio ridotto con ipermetropia assiale e di 10,D. Calcolare la correzione necessaria per una distanza al vertice di 14mm. Viene per prima cosa trovata la distanza k. k=n/k=1/10=0,1d E poi possibile la focale della lente correttrice posta alla distanza d attraverso la Eq.5.23: f lo = k + d v f lo =0,10+0,014=0,114m Il potere della lente correttrice sarà: F lo =1/f lo =1/0,114=+8,77D Capitolo 13 Es.13.1: Trasforma un acuità visiva di 20/40 in decimale, in decimi, MAR e in log MAR. ND=20/40=0,5; Decimi=0,5*10/10= 5/10; MAR=1/ND=1/0,5=2 ; logmar=0,3 Es.13.2: Trasforma un acuità visiva di -0,2 logmar in MAR, notazione decimale, decimi e frazione di Snellen sapendo che l esame è stato eseguito a 6 metri. MAR=antilog(-0,2)=0,63; ND=1/MAR=1/0,63=1,58; Decimi=1,58*10/10=15,8/10; frazione di Snellen=6/(6*0,63)=6/3,78 Es.13.3: Trasforma un acuità visiva di 1/10 in notazione decimale, frazione di Snellen (sia per una distanza di 20 feet che 6 m), MAR, e logmar. ND=1/10=0,1; MAR=1/0,1=10 ; logmar=log10=1; frazione di Snellen(6 m)=6/(6*10)=6/60; frazione di Snellen (20 ft)=20/(20*10)=20/200. Es.13.4: Calcola l altezza di una lettera di 10/10 inserita in un ottotipo utilizzato ad una distanza di 4 m. Si calcola per prima cosa il MAR, sapendo che il MAR è il reciproco della notazione decimale. 10/10 in ND=1 MAR=1/1=1 α=1 ; l angolo va trasformato in gradi α=1/60=0,0167 h d =tg 0,016 4=0,00116m h L =h d *5= 0,0058m
11 Es.13.5: Calcola l altezza di una lettera di 6/60. Anche in questo caso si calcola il MAR, sapendo che il MAR è il reciproco della notazione decimale. Si riduce la frazione di Snellen alla notazione decimale: 6/60 in ND=0,1 MAR=1/0,1=10 α=10 ; l angolo va trasformato in gradi α=10/60=0,167 La distanza d esame è specificata dal numeratore della frazione di Snellen (6 m). h d =tg 0,167 6=0,017m h L =h d 5= 0,087 m Es.13.6: Calcola il valore in notazione M. di un testo per lettura scritto in corpo 10. L altezza-x può essere trovata moltiplicano 0,175 per i punti del carattere. Quindi Altezza-x=0,175x10: 1,75mm Il punto M equivale alla distanza a cui la lettera sottende 5. Quindi d=altezza-x/tg5 = 0,00175/tg0,08 = 1,2 M Appendice II Es. A.II.1: Calcolare l angolo di convergenza per due persone che hanno una distanza interpupillare rispettivamente di 56 mm e 62 mm mentre fissano un oggetto posto, sulla linea mediana tra i due occhi, a 50 cm dal piano tangente alle superfici corneali. (si consideri una distanza tra piano corneale e centro di rotazione di 13 mm). In entrambi i casi si applicherà la Eq. A.II.4: Dove d sarà uguale alla somma tra la distanza dell oggetto al piano tangente alle superfici corneali e la distanza tra piano corneale e centro di rotazione (d c ): d=0,50+0,013=0,513 m Per la prima persona con dp di 56 mm il calcolo è il seguente: φ= 2 tg -1 [(0,056/2)0,513]=6,25 Per la seconda persona con dp di 62 mm analogamente: φ= 2 tg -1 [(0,062/2)0,513]=6,92 Es. A.II.2: Ripetere l esercizio A.II.1 portando la distanza di fissazione a 25 cm. In questo caso d sarà uguale a: d=0,25+0,013=0,263 m Analogamente a quanto effettuato nell Es.A.II.1 per la prima persona con dp di 56 mm il calcolo è il seguente: φ= 2 tg -1 [(0,056/2)0,263]=12,15 Per la seconda persona con dp di 62 mm analogamente: φ= 2 tg -1 [(0,062/2)0,263]=13,44
12 Es.A.II.3: Confrontando i risultati degli esercizi A.II.1 e A.II.2 verifica che le modifiche all angolo di convergenza in funzione della diversa distanza interpupillare e distanza di fissazione siano concordi a quanto illustrato in Fig.A.II.12 I risultati sono coerenti infatti l angolo di convergenza aumenta all aumentare della distanza interpupillare e al diminuire della distanza di fissazione. Es.A.II.4: Calcola l angolo di convergenza in angoli metrici nel caso di due persone, la prima con una distanza interpupillare di 56 mm la seconda di 62 mm, che fissano un oggetto posto sulla linea mediana tra i due occhi, a 50 cm dal piano tangente alle superfici corneali. (si consideri una distanza tra piano corneale e centro di rotazione di 13 mm). L angolo di convergenza in angoli metrici si calcola con l Eq. A.II.5 e quindi non dipende dalla distanza interpupillare. Se calcolato al centro di rotazione sarà semplicemente uguale al reciproco della distanza d calcolata così: d=0,50+0,013=0,263 m φ(am)=1/0,263=3,802 Es.A.II.5: Calcola l angolo di convergenza in diottrie prismatiche nel caso delle due persone dell Es.A.II.4. L angolo di convergenza in diottrie prismatiche si calcola con l Eq.A.II.6. Quindi : Per la prima persona φ ( )= 3,8 56=21,29 Per la seconda persona φ ( )= 3,8 62= 23,57 Es.A.II.6: Il punto prossimo di convergenza di un bambino con distanza interpupillare di 54 mm è a 7 cm dal piano passante per i centri di rotazione oculari. Calcolare l angolo di convergenza al punto prossimo di convergenza in gradi, angoli metrici e diottrie prismatiche. Come per l Es.A.II.1 si applica l Eq. A.II.4 per calcolare l angolo di convergenza in gradi: Se anche in questo caso si considera una d c di 13mm: d=0,07+0,013=0,083 m e quindi: φ= 2 tg -1 [(0,054/2)0,083]=37,28 L angolo di convergenza in angoli metrici si calcola con l Eq. A.II.5: φ(am)=1/0,083=12,05 L angolo di convergenza in diottrie prismatiche si calcola con l Eq.A.II.6. Quindi : φ ( )= 12,048 5,4=65,06
1.Visione_01 Ottica geometrica. Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona
 1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
I VIZI DI REFRAZIONE EMMETROPIA ACCOMODAZIONE. Occhio: sistema diottrico con potere refrattivo 60 D
 I VIZI DI REFRAZIONE Dr. Umberto Benelli U.O. Oculistica Universitaria EMMETROPIA Occhio: sistema diottrico con potere refrattivo 60 D Emmetropia: quando ad accomodazione rilasciata i raggi luminosi vanno
I VIZI DI REFRAZIONE Dr. Umberto Benelli U.O. Oculistica Universitaria EMMETROPIA Occhio: sistema diottrico con potere refrattivo 60 D Emmetropia: quando ad accomodazione rilasciata i raggi luminosi vanno
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo
 PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
OTTICA DELLA VISIONE Mauro Zuppardo 2015
 OTTICA DELLA VISIONE OTTICA DELLA VISIONE STIGMATICO ASTIGMATICO OTTICA DELLA VISIONE 90 SUPERFICIE TOROIDALE Disco di Minima Confusione Intervallo di Sturm Asso O=co OTTICA DELLA VISIONE Disco di Minima
OTTICA DELLA VISIONE OTTICA DELLA VISIONE STIGMATICO ASTIGMATICO OTTICA DELLA VISIONE 90 SUPERFICIE TOROIDALE Disco di Minima Confusione Intervallo di Sturm Asso O=co OTTICA DELLA VISIONE Disco di Minima
4. LA CORREZIONE OFTALMICA
 Capitolo 4 4. A COEZIOE OFTAMICA DEE AMETOPIE 1. GEEAITÀ a correzione ottica delle ametropie avviene ponendo davanti all occhio ametrope una lente correttiva di grado adeguato e nella posizione adeguata,
Capitolo 4 4. A COEZIOE OFTAMICA DEE AMETOPIE 1. GEEAITÀ a correzione ottica delle ametropie avviene ponendo davanti all occhio ametrope una lente correttiva di grado adeguato e nella posizione adeguata,
Lenti sottili: Definizione
 Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza assiale)
 Ovvero le ametropie che possiamo riscontrare nell occhio Ametropia Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza
Ovvero le ametropie che possiamo riscontrare nell occhio Ametropia Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza
1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti
 L occhio MPZ 1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti retina muscolo cornea iride pupilla cristallino nervo
L occhio MPZ 1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti retina muscolo cornea iride pupilla cristallino nervo
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
- Formazione delle immagini per riflessione: specchio sferico
 Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Ottica geometrica. L ottica geometrica tratta i. propagazione in linea retta e dei. rifrazione della luce.
 Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Il microscopio ottico. La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei
 Il microscopio ottico La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei Ingrandimento Un oggetto può essere visto a fuoco se posizionato
Il microscopio ottico La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei Ingrandimento Un oggetto può essere visto a fuoco se posizionato
La Cheratocoagulazione Radiale
 La Cheratocoagulazione Radiale Author: Marco Abbondanza La Stampa Medica Europea, vol. 8, no. 2. 1988 RIASSUNTO L autore illustra una nuova metodica di chirurgia refrattiva, la cheratocoagulazione capace
La Cheratocoagulazione Radiale Author: Marco Abbondanza La Stampa Medica Europea, vol. 8, no. 2. 1988 RIASSUNTO L autore illustra una nuova metodica di chirurgia refrattiva, la cheratocoagulazione capace
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
2. OTTICA FISIOLOGICA
 2. OTTICA FISIOLOGICA 1. MODELLI DELL OCCHIO L occhio è costituito da una serie di diottri con curvature non propriamente sferiche. Gli indici di rifrazione sono diversi tra individuo e individuo e molto
2. OTTICA FISIOLOGICA 1. MODELLI DELL OCCHIO L occhio è costituito da una serie di diottri con curvature non propriamente sferiche. Gli indici di rifrazione sono diversi tra individuo e individuo e molto
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Codice Fiscale dell'utente in esame: Cognome: Nome: Codice Fiscale: Telefono fisso e/o cellulare: Email:
 Analisi della funzione visiva secondo il Data: Professionista rilevatore: Raccolta dati Utente Dati Aagnrafici dell'utente in esame Cognome: Nome: Codice Fiscale: Telefono fisso e/o cellulare: Email: Dichiarazioni
Analisi della funzione visiva secondo il Data: Professionista rilevatore: Raccolta dati Utente Dati Aagnrafici dell'utente in esame Cognome: Nome: Codice Fiscale: Telefono fisso e/o cellulare: Email: Dichiarazioni
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
OTTICA DELLA VISIONE. Disegno schematico dell occhio umano
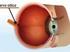 OTTICA DELLA VISIONE Disegno schematico dell occhio umano OTTICA DELLA VISIONE Parametri fisici Raggio di curvatura (cm) Cornea 0.8 Anteriore del cristallino Posteriore del cristallino.0 0.6 Indice di
OTTICA DELLA VISIONE Disegno schematico dell occhio umano OTTICA DELLA VISIONE Parametri fisici Raggio di curvatura (cm) Cornea 0.8 Anteriore del cristallino Posteriore del cristallino.0 0.6 Indice di
Ottica della Contattologia I. Ottica delle lac. Differenze ottiche nella clinica della visione
 Ottica della Cotattologia I Ottica delle LAC Ottica delle lac 1.Le differeze ottiche tra lac e occhiali ell ambito della cliica della visioe 2.Le lac dal puto di vista ottico Dr. Fabrizio Zeri zeri@fis.uiroma3.it
Ottica della Cotattologia I Ottica delle LAC Ottica delle lac 1.Le differeze ottiche tra lac e occhiali ell ambito della cliica della visioe 2.Le lac dal puto di vista ottico Dr. Fabrizio Zeri zeri@fis.uiroma3.it
ESERCIZI CINEMATICA IN UNA DIMENSIONE
 ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
Metodologia del rilevamento delle misure di un soggetto
 Cap. II LE MISURE La realizzazione di un capo confezionato si basa sulla conoscenza delle misure del soggetto a cui è destinato e, in funzione del sistema produttivo, potranno essere rilevate direttamente
Cap. II LE MISURE La realizzazione di un capo confezionato si basa sulla conoscenza delle misure del soggetto a cui è destinato e, in funzione del sistema produttivo, potranno essere rilevate direttamente
La misura degli angoli
 La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
Argomenti di diottrica oculare
 0303_Oftalmologia_cap03:Layout 1 23-01-2013 11:49 Pagina 51 CAPITOLO 3 Argomenti di diottrica oculare Giampaolo Lucarini 3.1 INTRODUZIONE ALLʼOTTICA PARASSIALE Il compito dell ottica geometrica è sostanzialmente
0303_Oftalmologia_cap03:Layout 1 23-01-2013 11:49 Pagina 51 CAPITOLO 3 Argomenti di diottrica oculare Giampaolo Lucarini 3.1 INTRODUZIONE ALLʼOTTICA PARASSIALE Il compito dell ottica geometrica è sostanzialmente
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
4.6 Lenti Capitolo 4 Ottica
 4.6 Lenti Esercizio 04 Due lenti biconvesse sono posizionate lungo il cammino ottico di un fascio di luce, separate da una distanza d. Il fascio di luce è parallelo e esce parallelo dopo le due lenti.
4.6 Lenti Esercizio 04 Due lenti biconvesse sono posizionate lungo il cammino ottico di un fascio di luce, separate da una distanza d. Il fascio di luce è parallelo e esce parallelo dopo le due lenti.
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Laboratorio per il corso Scienza dei Materiali II
 UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
LA FASE MONOCULARE DELL ESAME VISIVO. Relatore: Silvio Maffioletti
 LA FASE MONOCULARE DELL ESAME VISIVO Relatore: Silvio Maffioletti La fase monoculare Sistemare il forottero davanti al soggetto Metterlo in bolla Regolare la distanza interpupillare Controllare la distanza
LA FASE MONOCULARE DELL ESAME VISIVO Relatore: Silvio Maffioletti La fase monoculare Sistemare il forottero davanti al soggetto Metterlo in bolla Regolare la distanza interpupillare Controllare la distanza
Istituto di formazione professionale Don Bosco
 Istituto di formazione professionale Don Bosco Settore elettrico ELETTROTECNICA Eserciziario A.S. 204 205 CIRCUITI ELETTRICI, CAMPI ELETTRICI E MAGNETICI e MACCHINE ELETTRICHE Fabio PANOZZO 4 Capitolo
Istituto di formazione professionale Don Bosco Settore elettrico ELETTROTECNICA Eserciziario A.S. 204 205 CIRCUITI ELETTRICI, CAMPI ELETTRICI E MAGNETICI e MACCHINE ELETTRICHE Fabio PANOZZO 4 Capitolo
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
IL MICROSCOPIO OTTICO. DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011
 IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
illuminazione artificiale
 illuminazione artificiale Illuminazione artificiale degli interni Il progetto di illuminazione degli interni deve essere studiato e calcolato in funzione della destinazione d uso e dei compiti visivi del
illuminazione artificiale Illuminazione artificiale degli interni Il progetto di illuminazione degli interni deve essere studiato e calcolato in funzione della destinazione d uso e dei compiti visivi del
OTTICA, OTTICA APPLICATA
 OTTICA, OTTICA APPLICATA PROGRAMMAZIONE INIZIALE ANNO SCOLASTICO: 2014-2015 INSEGNANTE: DACCA ADRIANA BENEDUCE LUCIA CLASSE: IIIB Ott SETTORE: Servizi INDIRIZZO: Servizi Socio Sanitari articolazione Ottici
OTTICA, OTTICA APPLICATA PROGRAMMAZIONE INIZIALE ANNO SCOLASTICO: 2014-2015 INSEGNANTE: DACCA ADRIANA BENEDUCE LUCIA CLASSE: IIIB Ott SETTORE: Servizi INDIRIZZO: Servizi Socio Sanitari articolazione Ottici
LENTE A CONTATTO VS CORREZIONE OFTALMICA:
 PLATFORM optic REVIEW PROFESSIONAL IN COLLABORAZIONE CON SOPTI - SOCIETÀ OPTOMETRICA ITALIANA LENTE A CONTATTO VS CORREZIONE OFTALMICA: implicazioni refrattive, accomodative e binoculari PARTE 1: IMPLICAZIONI
PLATFORM optic REVIEW PROFESSIONAL IN COLLABORAZIONE CON SOPTI - SOCIETÀ OPTOMETRICA ITALIANA LENTE A CONTATTO VS CORREZIONE OFTALMICA: implicazioni refrattive, accomodative e binoculari PARTE 1: IMPLICAZIONI
Classificazione Semplificata dei gradi di ipovisione, vista fragile e relativi ausili più idonei per lontano
 Lenti prismatiche ingrandenti ed altri ausili ottici innovativi per lontano Dr. Biagio Jurilli Ottico optometrista Centro Ipovisione Optics International FIRENZE, 19 gennaio 2014 Stazione di Santa Maria
Lenti prismatiche ingrandenti ed altri ausili ottici innovativi per lontano Dr. Biagio Jurilli Ottico optometrista Centro Ipovisione Optics International FIRENZE, 19 gennaio 2014 Stazione di Santa Maria
Soluzione di equazioni quadratiche
 Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Interesse, sconto, ratei e risconti
 129 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 129 129.1.1 Esercizio per il calcolo dell interesse semplice........................
129 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 129 129.1.1 Esercizio per il calcolo dell interesse semplice........................
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
I teoremi di Euclide e di Pitagora
 I teoremi di Euclide e di Pitagora In questa dispensa vengono presentati i due teoremi di Euclide ed il teorema di Pitagora, fondamentali per affrontare diverse questioni sui triangoli rettangoli. I teoremi
I teoremi di Euclide e di Pitagora In questa dispensa vengono presentati i due teoremi di Euclide ed il teorema di Pitagora, fondamentali per affrontare diverse questioni sui triangoli rettangoli. I teoremi
VISIONE_01 OTTICA GEOMETRICA. FGE aa
 VISIONE_01 OTTICA GEOMETRICA FGE aa.2015-16 OBIETTIVI Principi di refrazione delle lenti, indice di refrazione Lenti biconcave e lenti biconvesse, fuoco principale e distanza focale Potere refrattivo di
VISIONE_01 OTTICA GEOMETRICA FGE aa.2015-16 OBIETTIVI Principi di refrazione delle lenti, indice di refrazione Lenti biconcave e lenti biconvesse, fuoco principale e distanza focale Potere refrattivo di
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei
 La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei La microscopia ottica è una tecnica di osservazione capace di produrre immagini ingrandite
La parola microscopio è stata coniata dai membri dell Accademia dei Lincei di cui faceva parte anche Galileo Galilei La microscopia ottica è una tecnica di osservazione capace di produrre immagini ingrandite
Specchio parabolico: MIRASCOPE. a cura di Pietro Pozzoli
 Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
IL LASER PER I DIFETTI DELLA VISTA
 IL LASER PER I DIFETTI DELLA VISTA LA MIOPIA Si parla di miopia quando la vista da lontano è ridotta. Il miope vede bene a distanza ravvicinata, mentre le immagini lontane appaiono sfuocate. La ragione
IL LASER PER I DIFETTI DELLA VISTA LA MIOPIA Si parla di miopia quando la vista da lontano è ridotta. Il miope vede bene a distanza ravvicinata, mentre le immagini lontane appaiono sfuocate. La ragione
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Interazione & Multimedia 1
 Il nostro viaggio nell image processing deve iniziare con lo studio di come l occhio umano percepisce una immagine e come la elabora. Ci interessa capire quali sono i limiti della visione umana al fine
Il nostro viaggio nell image processing deve iniziare con lo studio di come l occhio umano percepisce una immagine e come la elabora. Ci interessa capire quali sono i limiti della visione umana al fine
Si definisce astigmatico l occhio che con l accomodazione completamente
 ASTIGMATISMO Si definisce astigmatico l occhio che con l accomodazione completamente rilassata focalizzerà l immagine di un punto posto ipoteticamente all infinito in due focali rappresentate da due linee
ASTIGMATISMO Si definisce astigmatico l occhio che con l accomodazione completamente rilassata focalizzerà l immagine di un punto posto ipoteticamente all infinito in due focali rappresentate da due linee
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
MATEMATICA 5 PERIODI
 BAC EUROPEO 2008 MATEMATICA 5 PERIODI DATA 5 giugno 2008 DURATA DELL ESAME : 4 ore (240 minuti) MATERIALE AUTORIZZATO Formulario delle scuole europee Calcolatrice non grafica e non programmabile AVVERTENZE
BAC EUROPEO 2008 MATEMATICA 5 PERIODI DATA 5 giugno 2008 DURATA DELL ESAME : 4 ore (240 minuti) MATERIALE AUTORIZZATO Formulario delle scuole europee Calcolatrice non grafica e non programmabile AVVERTENZE
CHIRURGIA REFRATTIVA
 CHIRURGIA REFRATTIVA Responsabile: Dott. Marco Tavolato Perché un immagine possa essere vista, una complessa catena di eventi deve avvenire nell occhio. La luce entra nell occhio attraversando cornea,
CHIRURGIA REFRATTIVA Responsabile: Dott. Marco Tavolato Perché un immagine possa essere vista, una complessa catena di eventi deve avvenire nell occhio. La luce entra nell occhio attraversando cornea,
Massimi e minimi vincolati
 Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
Ottica fotografica. Lezioni per il corso di Fisica per gli studenti del diploma di Ottica
 Ottica fotografica Lezioni per il corso di Fisica per gli studenti del diploma di Ottica Alessandro Farini alessandro.farini@inoa.it Istituto Nazionale di Ottica Applicata-CNR 2 luglio 2009 Alessandro
Ottica fotografica Lezioni per il corso di Fisica per gli studenti del diploma di Ottica Alessandro Farini alessandro.farini@inoa.it Istituto Nazionale di Ottica Applicata-CNR 2 luglio 2009 Alessandro
Lenti, Cannocchiali e Telescopi
 tradizione e rivoluzione nell insegnamento delle scienze Istruzioni dettagliate per gli esperimenti mostrati nel video Lenti, Cannocchiali e Telescopi prodotto da Reinventore con il contributo del MIUR
tradizione e rivoluzione nell insegnamento delle scienze Istruzioni dettagliate per gli esperimenti mostrati nel video Lenti, Cannocchiali e Telescopi prodotto da Reinventore con il contributo del MIUR
Matematica - Sessione 1 / Produzione Esame di Qualifica (III Livello Europeo) Terzo Anno
 Id orso ata.. Nome e ognome Tipo prova Matematica - Sessione 1 / Produzione Esame di Qualifica (III Livello Europeo) Terzo Anno a.f. 2014/2015 omanda 1 M9063-00 Un aeroplano ha p posti di prima classe
Id orso ata.. Nome e ognome Tipo prova Matematica - Sessione 1 / Produzione Esame di Qualifica (III Livello Europeo) Terzo Anno a.f. 2014/2015 omanda 1 M9063-00 Un aeroplano ha p posti di prima classe
Ottica geometrica. Superfici rifrangenti e lenti
 Nome ile d:\scuola\corsi\corso isica\ottica\lenti.doc Creato il 09/05/003 0.33 Dimensione ile: 48640 byte Andrea Zucchini Elaborato il 8/05/003 alle ore.54, salvato il 8/05/03 0.54 stampato il 8/05/003.54
Nome ile d:\scuola\corsi\corso isica\ottica\lenti.doc Creato il 09/05/003 0.33 Dimensione ile: 48640 byte Andrea Zucchini Elaborato il 8/05/003 alle ore.54, salvato il 8/05/03 0.54 stampato il 8/05/003.54
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Lenti progressive opto in. Informazioni e trattamenti specifici sulla presbiopia.
 Lenti progressive opto in. Informazioni e trattamenti specifici sulla presbiopia. LA PRESBIOPIA La presbiopia è una modificazione fisiologica, di tipo funzionale, di una struttura oculare: il cristallino.
Lenti progressive opto in. Informazioni e trattamenti specifici sulla presbiopia. LA PRESBIOPIA La presbiopia è una modificazione fisiologica, di tipo funzionale, di una struttura oculare: il cristallino.
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
LA MISURAZIONE DEL CARATTERE
 TPO PROGETTAZIONE UD 03 GESTIONE DEL CARATTERE IL TIPOMETRO LA MISURAZIONE DEL CARATTERE A.F. 2011/2012 MASSIMO FRANCESCHINI - SILVIA CAVARZERE 1 IL TIPOMETRO: PARTI FONDAMENTALI Il tipometro è uno strumento
TPO PROGETTAZIONE UD 03 GESTIONE DEL CARATTERE IL TIPOMETRO LA MISURAZIONE DEL CARATTERE A.F. 2011/2012 MASSIMO FRANCESCHINI - SILVIA CAVARZERE 1 IL TIPOMETRO: PARTI FONDAMENTALI Il tipometro è uno strumento
Interesse, sconto, ratei e risconti
 TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Ripasso pre-requisiti di scienze per gli studenti che si iscrivono alle classi prime
 Ripasso pre-requisiti di scienze per gli studenti che si iscrivono alle classi prime Per seguire proficuamente i corsi di scienze della scuola superiore devi conoscere alcune definizioni e concetti di
Ripasso pre-requisiti di scienze per gli studenti che si iscrivono alle classi prime Per seguire proficuamente i corsi di scienze della scuola superiore devi conoscere alcune definizioni e concetti di
MULTIFOCALI LENTI A CONTATTO INTRODUZIONE
 Mario Giovanzana Milano 15dicembre 00 LENTI A CONTATTO MULTIFOCALI INTRODUZIONE Nell ambito della mia professione nel corso degli anni ho sviluppato la progettazione delle lenti a contatto, che gestisco
Mario Giovanzana Milano 15dicembre 00 LENTI A CONTATTO MULTIFOCALI INTRODUZIONE Nell ambito della mia professione nel corso degli anni ho sviluppato la progettazione delle lenti a contatto, che gestisco
Lunghezza ocale. Donato Di Bello
 F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
PROGRAMMAZIONE LATTARI
 PROGRAMMAZIONE LATTARI 1T ESERCITAZIONE DI LENTI OFTALMICHE Modulo 1: cenni di anatomia oculare: Unità didattica 1: le tre tonache che rivestono il bulbo oculare Unità didattica 2: gli organi accessori
PROGRAMMAZIONE LATTARI 1T ESERCITAZIONE DI LENTI OFTALMICHE Modulo 1: cenni di anatomia oculare: Unità didattica 1: le tre tonache che rivestono il bulbo oculare Unità didattica 2: gli organi accessori
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
G6. Studio di funzione
 G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
Il Microscopio. Il microscopio, dal greco micron (piccolo) e. skopein (guardare), è uno strumento che. permette di ottenere un immagine ingrandita
 Il Microscopio Il Microscopio Il microscopio, dal greco micron (piccolo) e skopein (guardare), è uno strumento che permette di ottenere un immagine ingrandita degli oggetti osservati. Unità di misura Unità
Il Microscopio Il Microscopio Il microscopio, dal greco micron (piccolo) e skopein (guardare), è uno strumento che permette di ottenere un immagine ingrandita degli oggetti osservati. Unità di misura Unità
Gli strumenti ottici. Capitolo. Concetti da rivedere 22.1 I SISTEMI DI LENTI
 22txtI:GIAMBATTISTA 4-2-2007 2:03 Pagina 865 Capitolo 22 Gli strumenti ottici La distinzione tra immagini reali e virtuali (Paragrafo 2.6) L ingrandimento (Paragrafo 2.8) La rifrazione (Paragrafo 2.3)
22txtI:GIAMBATTISTA 4-2-2007 2:03 Pagina 865 Capitolo 22 Gli strumenti ottici La distinzione tra immagini reali e virtuali (Paragrafo 2.6) L ingrandimento (Paragrafo 2.8) La rifrazione (Paragrafo 2.3)
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Ottica visuale. Corso di laurea in Ottica ed Optometria. Facoltà di Scienze M.F.N. Università del Salento Vincenzo Martella optometrista
 Ottica visuale Parte 4 Le ametropie e la loro correzione Corso di laurea in Ottica ed Optometria Facoltà di Scienze M.F.N. Università del Salento Vincenzo Martella optometrista Contatti: 0833/541063 392
Ottica visuale Parte 4 Le ametropie e la loro correzione Corso di laurea in Ottica ed Optometria Facoltà di Scienze M.F.N. Università del Salento Vincenzo Martella optometrista Contatti: 0833/541063 392
ESEMPI DI TEST DI INGRESSO FISICA 2010 G. Selvaggi, R. Stella Dipartimento Interateneo di fisica di Fisica 3 marzo 2010
 ESEMPI DI TEST DI INGRESSO FISICA 2010 G. Selvaggi, R. Stella Dipartimento Interateneo di fisica di Fisica 3 marzo 2010 1 Fisica 1. Un ciclista percorre 14.4km in mezz ora. La sua velocità media è a. 3.6
ESEMPI DI TEST DI INGRESSO FISICA 2010 G. Selvaggi, R. Stella Dipartimento Interateneo di fisica di Fisica 3 marzo 2010 1 Fisica 1. Un ciclista percorre 14.4km in mezz ora. La sua velocità media è a. 3.6
A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA D ISTITUTO COMPETENZA CHIAVE EUROPEA DISCIPLINA
 ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
Moltiplicazione TUTORIAL SUL REGOLO CALCOLATORE - 1. Introduzione
 TUTORIAL SUL REGOLO CALCOLATORE - 1 Introduzione Questo non è realmente un tutorial, è più una demo auto-guidata. Questa pagina fornisce esempi numerici dei calcoli di base che un regolo calcolatore può
TUTORIAL SUL REGOLO CALCOLATORE - 1 Introduzione Questo non è realmente un tutorial, è più una demo auto-guidata. Questa pagina fornisce esempi numerici dei calcoli di base che un regolo calcolatore può
ISTITUTO COMPRENSIVO MONTEGROTTO TERME SCUOLA PRIMARIA DISCIPLINA: MATEMATICA - CLASSE PRIMA OBIETTIVI DI APPRENDIMENTO
 PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATIA Scuola secondaria di II grado lasse... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATIA Scuola secondaria di II grado lasse... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE
 DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
Ministero dell Istruzione, dell Università e della Ricerca
 Ministero dell Istruzione, dell Università e della Ricerca Ufficio Scolastico Regionale per il Lazio Istiituto Comprensiivo Don Lorenzo Miillanii Scuola dell Infanzia Primaria Secondaria di I grado anche
Ministero dell Istruzione, dell Università e della Ricerca Ufficio Scolastico Regionale per il Lazio Istiituto Comprensiivo Don Lorenzo Miillanii Scuola dell Infanzia Primaria Secondaria di I grado anche
Ottica fisiopatologica
 Ottica fisiopatologica Introduzione La visione è una funzione complessa che dipende da FATTORI AMBIENTALI interazione luce-materia FATTORI ANATOMO-FISIOLOGICI oculari sistema nervoso centrale L occhio
Ottica fisiopatologica Introduzione La visione è una funzione complessa che dipende da FATTORI AMBIENTALI interazione luce-materia FATTORI ANATOMO-FISIOLOGICI oculari sistema nervoso centrale L occhio
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
PERCORSO DIDATTICO DI OTTICA GEOMETRICA
 PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE. Operare con i numeri
 COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Ottica fisiologica (2)
 Ottica fisiologica (2) Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it http://homes.dsi.unimi.it/~boccignone/giuseppeboccignone_webpage/modelli_percezione.html
Ottica fisiologica (2) Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it http://homes.dsi.unimi.it/~boccignone/giuseppeboccignone_webpage/modelli_percezione.html
