STRUMENTAZIONE ELETTRONICA DI MISURA II
|
|
|
- Ernesto Manfredi
- 8 anni fa
- Visualizzazioni
Transcript
1 Dispense per il corso di: STRUMENTAZIONE ELETTRONICA DI MISURA II Prof. D'ANTONA GABRIELE A cura di Ugo Ambrosetti e Massmiliano Galli
2 Dispensa del corso di Strumentazione Elettronica di Misura II a cura di Ugo Ambrosetti e Massimiliano Galli Indice : Sezione 1 Introduzione al Corso Trasmissione dell informazione Trasmissioni numerico Segnali analogici, certi ed aleatori Rappresentazione di segnali analogici Rappresentazione di processi aleatori Segnali numerici Teoria delle probabilità Segnali e sistemi Caratteristiche dei sistemi Caratteristiche dei segnali Aspetti fisici delle grandezze energetiche Serie di Fourier Segnali reali Simmetria coniugata Interpretazione degli Xn come fasori Serie Trigonometrica Serie di Fourier a banda limitata Teorema di Parseval Spettro di Potenza per segnali periodici Esempi di Sviluppi in Serie di Fourier Definizione T.d.F Densità di energia Appendici Sintesi delle proprietà della trasformata di Fourier Trasformate di segnali Teorema del Campionamento Aliasing Energia di un segnale campionato Uso pratico Trasformata discreta di Fourier Relazione tra DFT e trasformata Z Filtraggio numerico via DFT Teoria delle probabilità Assiomi delle probabilità Teoremi di base Probabilità condizionali Teorema di Bayes Indipendenza statistica
3 Dispensa del corso di Strumentazione Elettronica di Misura II a cura di Ugo Ambrosetti e Massimiliano Galli Variabili aleatorie Funzioni di densità e di distribuzione di probabilità Medie, momenti e momenti centrati Variabile aleatoria a distribuzione uniforme Processi Stazionari ed Ergodici Media di insieme Medie temporali Medie temporali calcolate come medie di insieme Processi stazionari Processi stazionari ed erodici Riassumendo Processo ad aleatorietà parametrica Correlazione e Covarianza Correlazione Covarianza e Indipendenza Statistica Statistiche dei Processi Autocorrelazione Proprietà dell autocorrelazione Densità Spettrale Teorema di Wiener Esempi Stima spettrale Sezione 2 Meccanismi di Rumore Introduzione Rumore termico Rumore shot (equazione di Schottky) Rumore 1/f (excess noise) Proprietà statistiche del rumore 1/f Stazionarietà Gaussianità I processi di rumore 1/f sono presenti all equilibrio termico? Rumore nei bipoli passivi Rapporto segnale rumore dei generatori Rumore nelle reti due porte Reti passive Rapporto SNR in uscita Fattore di rumore Reti attive Fattore di rumore per reti in cascata Gli amplificatori operazionali Il componente ideale Configurazioni lineari Amplificatore in configurazione invertente Circuito integratore e derivatore
4 Dispensa del corso di Strumentazione Elettronica di Misura II a cura di Ugo Ambrosetti e Massimiliano Galli Configurazioni a scatto Il comparatore Comparatore con isteresi Multivibratore astabile L amplificatore differenziale La reiezione del modo comune L amplificatore per strumentazione Schema circuitale Il bilanciamento degli ingressi Il rumore negli amplificatori operazionali Circuito equivalente (modo differenziale) Il rumore nell amplificatore operazionale Circuito equivalente per Offset e Derive Bias e Offset all uscita di una generica configurazione Progetto a basso rumore Sezione 3 Rivelazione dei segnali Filtraggio Filtro del primo ordine Filtro a finestra mobile Filtraggio lineare ottimo Filtro di Wiener Filtro adattato Tecniche di correlazione Rivelazione del segnale (Riassunto) BoxCar sampling gate Lock-in Sezione 4 PLL (Phase Locked Loop) Principio di funzionamento Introduzione ai blocchi fondamentali Phase Detector Phase-Frequency Detector e Charge Pump Voltage-Controlled Oscillator Low-Pass Filter Dinamica del Phase-Locked Loop Sezione 5 Collegamenti e mezzi trasmissivi Dimensionamento di un collegamento Collegamenti in cavo Costanti distribuite, grandezze derivate, e condizioni generali Trasmissione in cavo Casi limite Tipologie di cavi
5 Dispensa del corso di Strumentazione Elettronica di Misura II a cura di Ugo Ambrosetti e Massimiliano Galli Coppie simmetriche Cavo coassiale Collegamenti in fibra ottica Generalità Propagazione luminosa Multiplazione a divisione di lunghezza d onda WDM Ridondanza e pericoli naturali Sonet
6 Sezione 1: Introduzione al corso CAPITOLO 1 INTRODUZIONE: 1.1 Trasmissione dell informazione: L origine del segnale da trasmettere è indicata come sorgente, di tipo analogico o numerico per i due tipi di segnale. Ciò che giace tra sorgente e destinatario viene descritto da una entità astratta denominata canale di comunicazione, le cui caratteristiche condizionano i messaggi trasmessi. Il canale può ad esempio imporre una limitazione alla banda di frequenze del segnale in transito; cause fisiche ineliminabili producono inoltre, al lato ricevente, l insorgere di un segnale di disturbo additivo, comunemente indicato con il termine di rumore, che causa la ricezione di un segnale diverso da quello stesso presente all uscita del canale. Pertanto, ci si preoccupa di caratterizzare il canale in modo da scegliere i metodi di trasmissione più idonei a rendere minima l alterazione sul messaggio trasmesso. L entità delle alterazioni subite dal messaggio viene spesso quantificata in termini di rapporto segnale rumore (SNR o SIGNAL-TO-NOISE RATIO), che rappresenta un indice di qualità del collegamento stesso, e che per ora definiamo genericamente come il rapporto tra l entità del segnale utile ricevuto e quello del rumore ad esso sovrapposto (n = segnale utile ricevuto / rumore). La linea di trasmissione è costituita da un mezzo trasmissivo su cui si propaga un segnale di natura elettrica, occorrono perciò un sistema di traduzione e dei dispositivi di adattamento (es. equalizzatori, amplificatori, codificatori di linea..) per rendere le caratteristiche del segnale adatte a quelle della linea. 1.2 Trasmissioni numerico: Qualora si desideri trasmettere un segnale numerico, questo deve in generale essere convertito in un segnale analogico mediante l utilizzo di dispositivi chiamati Modem, come rappresentato dalla figura seguente. Il progetto del canale numerico è caratterizzato da un fattore di qualità individuato dalla probabilità di errore che è definita come la frequenza con cui i simboli ricevuti differiscono da quelli trasmessi. Nelle trasmissioni numeriche, si può introdurre una ridondanza nella sequenza trasmessa, inviando più simboli di quanti non ne produca la sorgente; i simboli in più sono scelti con criteri che li rendono dipendenti tra loro, per rendere possibile la riduzione della probabilità d errore: il ricevitore è in grado di accorgesi che si è verificato un errore (se non c è la dipendenza) e può attuare delle contromisure (es. correzione dell errore isolato FEC, oppure può chiedere la ritrasmissione). Queste trasformazioni di codifica devono poi essere rimosse all uscita con un decodificatore. Poniamoci ora il problema di utilizzare un canale numerico per effettuare una trasmissione analogica. Il vantaggio di tale contorsione è da ricercarsi nel migliore comportamento delle trasmissioni numeriche rispetto ai disturbi, nonché alla loro generalità. Per ottenere il risultato desiderato, occorre applicare alla sorgente analogica un procedimento di campionamento, prelevandone i valori ad istanti discreti, e quindi di quantizzazione, rappresentando tali valori mediante un insieme finito di simboli. Il risultato è una sequenza numerica che può essere di nuovo convertita nel segnale originario, utilizzando un dispositivo di conversione digitale-analogica (DAC) dal lato del ricevitore. 1
7 Sezione 1: Introduzione al corso La riduzione dei valori campionati ad un numero finito di elementi introduce un ulteriore distorsione. L entità del rumore di quantizzazione è inversamente legata alla risoluzione. CLAUDE SHANNON, enunciò negli anni 50 una serie di teoremi, che sono la base dell analisi dei sistemi di comunicazione: Un qualsiasi canale pone un limite al massimo flusso informativo che transita in esso. Il limite deriva dai vincoli che il canale impone sulla massima banda B del segnale in transito, sulla massima potenza di segnale S ricevuta, e sulla potenza di rumore N presente al ricevitore. Il massimo flusso di informazione in transito prende il nome di capacità di canale C, e può essere espresso come: C = B log2 (1 + S/N) [bit/sec] Una qualsiasi sorgente produce un flusso informativo in bit/secondo tanto più elevato quanto minore è la distorsione introdotta dal processo di quantizzazione. Considerando una coppia sorgente + canale, dato che il canale limita il massimo flusso informativo prodotto dalla sorgente, quest ultima verrà necessariamente riprodotta con una distorsione tanto maggiore quanto minore è la capacità di canale. 1.3 Segnali analogici, certi ed aleatori: I segnali analogici, indicati con s (t) rappresentano l andamento nel tempo di una grandezza elettrica (es. segnale vocale: in cui un onda trasversale di pressione-velocità è convertita in una tensione da un microfono, oppure segnale di immagine, che è bidimensionale, e definito su di un piano anziché nel tempo, rappresentato da una grandezza S (x, y) che ne individua la luminanza, e scandito per linee generando un segnale temporale. Un segnale può anche assumere valori complessi, in questo caso il segnale assume contemporaneamente due diversi valori: parte reale e parte immaginaria, oppure modulo e fase). E importante distinguere tra i segnali cosiddetti certi e quelli aleatori. Un esempio di segnale certo può essere una cosinusoide di cui sia nota sia l ampiezza che la fase, mentre un segnale aleatorio non è noto con esattezza prima che questo venga prodotto (ad esempio il rumore di un ruscello, o le notizie presenti in un telegiornale). L insieme di tutti i segnali aleatori appartenenti ad una medesima classe viene indicato nel suo complesso come processo aleatorio, ed un segnale particolare di questo insieme come una sua realizzazione Rappresentazione di segnali analogici: Lo studio delle proprietà dei segnali si articola prendendo in considerazione per gli stessi rappresentazioni alternative, scelte in modo da poter valutare più agevolmente le alterazioni subite dai segnali nel passaggio attraverso sistemi fisici. In particolare, sarà definito lo sviluppo in serie di Fourier per la rappresentazione dei segnali periodici, e quindi la trasformata di Fourier che descrive una classe più ampia di segnali. L analisi di Fourier consente di definire il concetto di banda occupata da un segnale, nonché di come la sua potenza e/o energia si distribuisce in frequenza; quest ultimo andamento viene indicato con il termine di Spettro di Densità di Potenza (o di Energia) Rappresentazione di processi aleatori: Anche nel caso in cui il segnale non è noto a priori, e dunque è impossibile calcolarne la trasformata di Fourier in forma chiusa, si può ugualmente giungere ad una rappresentazione che caratterizzi le realizzazioni del processo nei termini della distribuzione (statistica) in frequenza della potenza di segnale. Ciò è possibile considerando la funzione di autocorrelazione, che esprime il grado di interdipendenza statistica tra i valori assunti in istanti diversi dalle realizzazioni del processo, e che costituisce un elemento unificante ai fini della stima spettrale dei segnali (processi molto correlati 2
8 Sezione 1: Introduzione al corso siano caratterizzati da una densità di potenza di tipo colorato che indica la prevalenza di alcune frequenze su altre, mentre processi scarsamente correlati saranno identificati da una densità di potenza di tipo bianco ovvero la presenza di tutte le lunghezze d onda in ugual misura). 1.4 Segnali numerici Sono indicati con la notazione s [k], per evidenziare che il loro dominio è l insieme dei numeri interi. Sono valide le stesse definizioni fornite a riguardo dei segnali analogici, relativamente ai concetti di potenza, energia e periodicità, utilizzando qui delle sommatorie in luogo degli integrali. Un segnale viene chiamato numerico quando assume valori appartenenti ad un insieme finito di simboli; per questo motivo, la sua essenza è indicata anche come sequenza simbolica. Segnali tempo-discreti: si può alternativamente rappresentare ogni carattere con un diverso valore di tensione, ottenendo un segnale analogico che è una rappresentazione a più livelli di tensione della sequenza originaria. Il concetto di occupazione di banda, applicabile ai segnali analogici, è qui sostituito da quello di velocità di emissione, espressa in simboli/secondo, ed indicata come frequenza di simbolo. Una sequenza prodotta da una sorgente numerica si presta facilmente ad essere trasformata in un altra, con un diverso alfabeto ed una differente frequenza di simbolo. 1.5 Teoria delle probabilità: Molti dei concetti utilizzati per trattare i processi aleatori, per definire la quantità di informazione di un messaggio, le prestazioni di un canale, il dimensionamento di reti di comunicazione, sono fondati sulla conoscenza della teoria delle probabilità, che verrà pertanto illustrata, almeno nei suoi concetti fondamentali nel proseguo della dispensa. 1.6 Segnali e sistemi: Un sistema è un gruppo di oggetti che interagiscono armoniosamente, e che sono combinati in modo da conseguire un obbiettivo desiderato. Un segnale è un evento che veicola un contenuto informativo. Nel nostro caso, possiamo interessarci alla risposta di un sistema ad un dato segnale. A volte, un sistema è descritto unicamente in termini della sua risposta a determinati segnali Caratteristiche dei sistemi: Idealizziamo ora un sistema come una trasformazione T [.], tale che ad ogni segnale di ingresso x (t) corrisponda una uscita y (t): T [x (t)] = y (t) In base a tale formalismo, riportiamo alcune caratteristiche dei sistemi, che ne descrivono il comportamento in termini più generali: Linearità: un sistema è lineare quando l uscita associata ad una combinazione lineare di ingressi, è la combinazione lineare delle uscite previste per ogni singolo ingresso: Al contrario, un legame ingresso-uscita senza memoria14 del tipo y (t) = g (x (t)), in cui g (.) è una generica funzione non lineare, non è lineare! Stazionarietà o Permanenza: un sistema è permanente (o stazionario) se l uscita associata ad un ingresso traslato nel tempo, è la traslazione temporale dell uscita che si avrebbe per lo stesso ingresso non traslato, ovvero se: 3
9 Sezione 1: Introduzione al corso T [x (t)] = y (t), allora T [x (t ζ )] = y (t ζ) Nel caso contrario, il sistema è detto tempo-variante. Casualità o Realizzabilità fisica: determina l impossibilità di osservare un uscita, prima di aver applicato un qualunque ingresso. Una definizione alternativa asserisce che i valori di uscita y (t) ad un istante t = t0, non possono dipendere da valori di ingresso x (t) per t > t0. Stabilità: è definita come la proprietà di fornire uscite limitate (in ampiezza) per ingressi limitati Caratteristiche dei segnali: Da un punto di vista analitico, un segnale è una funzione del tempo per il quale si possono operare le classificazioni: Segnale di potenza: un segnale analogico può avere una estensione temporale limitata, oppure si può immaginare che si estenda da meno infinito a infinito. Nel secondo caso il segnale si dice di potenza se ne esiste (ed è diversa da zero) la media quadratica: Un segnale di potenza è inoltre detto Segnale periodico di periodo T, nel caso in cui si verifichi che s (t) = s (t + T) per qualsiasi valore di t. Segnale di energia: un segnale di durata limitata o illimitata, se esiste il valore: In particolare, se un segnale ha durata limitata, ovvero è nullo per t al di fuori di un intervallo [t1, t2], allora è anche di energia. Segnale impulsivo: un segnale di energia, che tende a zero come (o più velocemente di 1/t) Riassumendo: Un segnale impulsivo è di energia; Un segnale a durata limitata è impulsivo, e di energia; Un segnale periodico non è di energia, ma di potenza; 4
10 Sezione 1: Introduzione al corso Aspetti fisici delle grandezze energetiche: Potenza istantanea: se consideriamo una resistenza R, ed applichiamo ai suoi capi una tensione v (t), in essa scorre una corrente i (t) = v(t) / R, e la potenza ceduta alla resistenza ad ogni istante t è pari a: p (t) = v (t) i (t) che si misura in Watt (equivalente a Joule/secondo), e che rappresenta la potenza istantanea assorbita. Energia: se integriamo p (t) su di un intervallo temporale T, si ottiene l energia complessiva assorbita da R nell intervallo T: nello stesso intervallo T, la resistenza assorbe una potenza: [Watt] che costituisce una media a breve termine dell energia assorbita nell intervallo T. Se un segnale x (t) è periodico con periodo T, i valori di et (t) = pt (t) coincidono con quelli calcolabili con T comunque grande. Se R = 1, tali valori coincidono inoltre con le definizioni di potenza ed energia del segnale: Potenza dissipata: se la resistenza è diversa da 1 le due quantità non coincidono più. Nelle misure fisiche in genere si ottiene la potenza dissipata sullo strumento di misura (o irradiata dall antenna, o dagli altoparlanti) espressa in Watt. Per risalire alla potenza/energia di segnale delle grandezze elettriche presenti ai suoi capi (tensione o corrente) occorre dividere (o moltiplicare) la potenza in Watt per R. Valore efficace: si indica allora come valore efficace quel livello di segnale continuo che produrrebbe lo stesso effetto energetico. 5
11 Sezione 1: Introduzione al corso CAPITOLO 2 SERIE DI FOURIER: 2.1 Serie di Fourier: Come anticipato, un segnale periodico x (t) è un segnale di potenza, che assume ripetutamente gli stessi valori a distanza multipla di un intervallo temporale T denominato periodo, ovvero tale che: x (t) = x (t + T) L inverso di T è detto frequenza fondamentale F = 1 / T o prima armonica di x (t), espressa in Hertz, dimensionalmente pari all inverso di un tempo [sec 1]. Per i segnali periodici esiste una forma di rappresentazione basata sulla conoscenza di una serie infinita di coefficienti complessi {Xn} denominati coefficienti di Fourier, calcolabili a partire da un periodo del segnale come: e che permettono la ricostruzione di x (t), sotto forma di una combinazione lineare di infinite funzioni esponenziali complesse, mediante l espressione nota come serie di Fourier: Osserviamo che: La conoscenza di {Xn} equivale a quella di x (t) e viceversa, esistendo il modo di passare dall una all altra rappresentazione; Le funzioni della base di rappresentazione sono funzioni trigonometriche a frequenza multipla (n-esima) della fondamentale, detta anche n-esima armonica. I termini sono chiamati componenti armoniche di x (t) a frequenza f = nf; Il coefficiente rappresenta la componente continua (o valor medio) di x (t); La serie di Fourier dà valori esatti in tutti i punti in cui x (t) è continuo, mentre in corrispondenza di discontinuità di prima specie fornisce un valore pari alla media dei valori agli estremi, cosicché il valore dell energia di un periodo è preservato; I coefficienti di Fourier Xn possono essere calcolati anche per un segnale di estensione finita T. Antitrasformando, il segnale diventa periodico! Se poniamo nf = f (con f variabile continua), possiamo interpretare le componenti armoniche come i valori campionati di una funzione (complessa) delle frequenza: Xn = X (nf). Ad X (f) si dà il nome di 6
12 Sezione 1: Introduzione al corso inviluppo dello spettro di ampiezza di x (t), che si ottiene estendendo la definizione dei coefficienti di Fourier: I coefficienti Xn sono valori complessi. Al loro posto si possono usare, in alternativa: essendo: segnali reali: Simmetria coniugata: I coefficienti della serie di Fourier possono essere calcolati anche per segnali complessi; nel caso particolare di x (t) reale i coefficienti di Fourier risultano godere della proprietà di simmetria coniugata, espressa come e che significa che i coefficienti con indice n negativo possiedono una parte reale uguale a quella dei coefficienti con (uguale) indice positivo, e parte immaginaria cambiata di segno. Ciò comporta una proprietà analoga per il modulo e la fase di {Xn}, e dunque possiamo scrivere: Tali relazioni evidenziano che: Se x (t) è reale, i coefficienti Xn risultano avere modulo pari e fase dispari, ovvero parte reale pari e parte immaginaria dispari. Un corollario di questo risultato è che: Se x (t) è reale pari, i coefficienti Xn sono reali (pari), mentre se x (t) è reale dispari, gli Xn sono immaginari (dispari) Interpretazione degli Xn come fasori: Confrontando la formula di ricostruzione: e quella: 7
13 Sezione 1: Introduzione al corso ricavata per il caso di un coseno, e tenendo conto della proprietà di simmetria coniugata, si nota come un segnale reale possa essere pensato composto a partire da un insieme infinito di fasori (pari al doppio dei coefficienti Xn), rotante ognuno con una velocità angolare multipla della frequenza fondamentale Serie Trigonometrica: Nel caso in cui gli Xn abbiano simmetria coniugata, la formula di ricostruzione può scriversi: ovvero in forma di serie di coseni; si noti che X0 è necessariamente reale, in quanto la fase deve risultare una funzione dispari della frequenza. In modo simile, le proprietà relative alle parti reale ed immaginaria permettono di scrivere: in cui: Pertanto, nel caso in cui x (t) sia un segnale reale, la serie di Fourier si riduce ad uno sviluppo in termini di funzioni trigonometriche, ed in particolare ad una serie di soli coseni nel caso in cui x (t) sia pari, oppure una serie di soli seni, nel caso in cui sia dispari Serie di Fourier a banda limitata: Consideriamo un onda quadra con duty-cycle del 50%: rappresentata mediante una serie troncata di Fourier in cui si considerano solo i coefficienti Xn con indice Sappiamo che e per =T/2 si ottiene, che risulta diversa da zero solo con n dispari e quindi: 8
14 Sezione 1: Introduzione al corso Essendo inoltre x (t) reale pari, sappiamo che può essere espresso come serie di coseni: 2.2 Teorema di Parseval: Stabilisce l equivalenza di due rappresentazioni del segnale dal punto di vista energetico. La potenza, infatti, è calcolabile in modo simile in entrambi i domini del tempo e della frequenza, risultando: Sviluppiamo i calcoli che danno luogo al risultato mostrato: Ortogonalità degli esponenziali complessi: nei precedenti calcoli si è fatto uso del risultato: che deriva dalla circostanza che la funzione integranda (per n m) è periodica con periodo uguale o sotto-multiplo di T, e quindi a valor medio nullo; per n = m invece essa vale = 1, e dunque il risultato. Questo prende il nome di Proprietà di Ortogonalità degli esponenziali complessi Spettro di Potenza per segnali periodici: L integrale seguente, oltre a misurare la potenza del segnale periodico x (t), ne misura la norma quadratica da un punto di vista algebrico. 9
15 Sezione 1: Introduzione al corso Tornando ad esaminare il risultato è la potenza di una singola componente armonica di x (t): espresso dal teorema di Parseval, notiamo che e quindi osserviamo che: La potenza totale di un segnale periodico x (t) è pari alla somma delle potenze delle sue componenti armoniche Si presti attenzione che il risultato è una diretta conseguenza dell ortogonalità della base di rappresentazione. In generale, la potenza di una somma non è pari alla somma delle potenze; l uguaglianza ha luogo solo nel caso di in cui gli addendi siano ortogonali. La successione rappresenta come la potenza totale si ripartisce tra le diverse armoniche a frequenza f = nf, e prende il nome di Spettro di Potenza del segnale x (t). Osserviamo che necessariamente i termini risultano reali e positivi. Inoltre, se x (t) è reale, risulta, e quindi si ottiene ; pertanto un segnale reale è caratterizzato da uno spettro di potenza pari. 2.3 Esempi di Sviluppi in Serie di Fourier: 10
16 Sezione 1: Introduzione al corso 11
17 Sezione 1: Introduzione al corso CAPITOLO 3 TRASFORMATA DI FOURIER: Abbiamo già osservato che lo sviluppo in serie di Fourier può essere applicato ad un segnale limitato nel tempo, e che l uso della formula di ricostruzione rende periodico il segnale originario. Se però facciamo tendere ad infinito il periodo fittizio T su cui sono calcolati i coefficienti Xn, le armoniche della serie di Fourier tendono ad infittirsi, fino ad arrivare ad una distanza infinitesima; allo stesso tempo, la periodicizzazione del segnale ricostruito tende via via a scomparire. 3.1 Definizione: La trasformata di Fourier serve a rappresentare quei segnali per i quali non sussiste una struttura periodica, ed è un operatore funzionale che, applicato ad un segnale definito nel dominio del tempo, ne individua un altro nel dominio della variabile continua frequenza (a differenza della serie discreta di Fourier, idonea al caso in cui siano presenti solo armoniche della fondamentale). L operazione di trasformazione è spesso indicata con la simbologia X (f) = F {x (t)}, ed il segnale trasformato si indica con la stessa variabile di quello nel tempo, resa maiuscola. La sua definizione formale dal punto di vista analitico è: la cui esistenza è garantita per segnali x (t) impulsivi (ovvero per i quali cioè assolutamente sommabili). Un segnale impulsivo è anche di energia, mentre non è sempre vero il viceversa. Spesso però, X (f) esiste anche per segnali di energia; vedremo inoltre che può essere definita (grazie ad operazioni di passaggio al limite) anche per segnali di potenza periodici. L antitrasformata di Fourier è l operatore analitico che svolge l associazione inversa a,e che consente di ottenere, a partire da un segnale definito nel dominio della frequenza, quel segnale nel dominio del tempo la cui trasformata è il primo segnale. L operazione di antitrasformazione è definita come: e vale ovunque x (t) sia continuo, mentre nelle discontinuità di prima specie fornisce il valor medio di x (t). Il risultato della trasformata è anche detto spettro di ampiezza complessa, mentre M (f) ed sono detti spettri di modulo e fase. La formula di ricostruzione, se messa a confronto con la serie di Fourier, può essere pensata come una somma integrale di infinite componenti di ampiezza (complessa) infinitesima, evidenziando come ora siano presenti tutte le frequenze e non solo le armoniche. Una seconda analogia con la serie di Fourier deriva dal considerare un segnale x (t) di durata limitata T, e calcolare per. In tal caso, è facile verificare che risulta con Xn pari all n-esimo coefficiente di Fourier calcolato per x (t) su quello stesso periodo. 12
18 Sezione 1: Introduzione al corso 3.2 Densità di energia: Similmente al caso dei segnali periodici, viene ora stabilita una relazione tra l energia di un segnale, e la distribuzione della stessa nel dominio della frequenza. Definiamo come prodotto scalare tra i segnali di energia x (t) e y (t) (detto anche energia incrociata) il valore: che, nel caso in cui x (t) = y (t), coincide con l energia trasformata di Fourier possiamo scrivere: di x (t). Se entrambi x (t) e y (t) possiedono Il risultato: esprime il teorema di Parseval per segnali di energia, ed implica che le trasformate di segnali ortogonali, sono anch esse ortogonali. Ponendo ora x (t) = y (t), si ottiene: Esaminando quest ultima espressione, possiamo indicare: come lo spettro di densità di energia di x (t). Infatti, l integrale rappresenta il contributo all energia totale di x (t), limitatamente alla banda di frequenze comprese tra f1 ed f Appendici: Sintesi delle proprietà della trasformata di Fourier: 13
19 Sezione 1: Introduzione al corso Trasformate di segnali: 14
20 Sezione 1: Introduzione al corso CAPITOLO 4 CENNI SUL CAMPIONAMENTO E L ELABORAZIONE NUMERICA DEI SEGNALI 4.1 Teorema del Campionamento: Un segnale con spettro nullo a frequenze maggiori di W, è univocamente definito a partire dai valori che assume agli istanti t = n / 2W, con n intero. La frequenza 2W è chiamata frequenza di Nyquist. In virtù del teorema, l andamento di un segnale x (t) limitato in banda tra W e W può essere ricostruito in base ai suoi campioni, presi a frequenza doppia della sua banda a frequenze positive, per mezzo della formula: in cui la funzione sinc (2Wt) è mostrata in figura, assieme ad una sua replica traslata. Per dimostrare il risultato, studiamo il circuito riportato in figura che mostra uno schema simbolico che (come vedremo) realizza le stesse operazioni della formula di ricostruzione, operando un campionamento con periodo Tc = 1/ 2W. Calcoliamo innanzitutto lo spettro di ampiezza X (f) del segnale che esce dal moltiplicatore, che ha subito un alterazione notevole rispetto a quello di X (f) in ingresso. Infatti, il segnale: ha uno spettro di ampiezza: 15
21 Sezione 1: Introduzione al corso dove il penultimo passaggio scambia l integrale di una somma con una somma di integrali, e l ultimo passaggio tiene conto della proprietà di convoluzione con un impulso. In definitiva si è mostrato che X (f) è costituito dalle repliche di X (f) centrate a multipli della frequenza di campionamento. Pertanto, il filtro passa-basso H (f) (chiamato anche con il nome di filtro di restituzione) lascia passare solo una delle repliche spettrali, e dunque è evidente come: Per quanto riguarda la formula di ricostruzione che fa uso dei campioni x(n/2w) e delle funzioni sinc(2wt), deriva anch essa dallo schema illustrato, e può essere interpretata con l aiuto della figura sotto. Infatti, y (t) è il risultato della convoluzione tra x (t) e h (t), e dunque ogni impulso di cui è composto x (t), quando convoluto con h (t), trasla la forma d onda h (t) all istante nt c a cui è centrato l impulso. In formule: con: Questo risultato mostra come il teorema del campionamento definisca essenzialmente una formula di interpolazione: i valori del segnale ricostruito hanno l esatto valore dei campioni di segnale negli istanti di campionamento, mentre negli istanti intermedi il valore si forma dalla somma di tutte le code dei sinc adiacenti. Il processo di costruzione grafica ora descritto è riportato nella figura precedente Aliasing: Questo termine ha origine dalla parola inglese alias (copia, clone) e sta ad indicare il fenomeno che si produce nell applicare il teorema del campionamento quando i requisiti non sono soddisfatti, e cioè 16
Il Campionameto dei segnali e la loro rappresentazione. 1 e prende il nome frequenza di
 Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08. Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
La trasformata Zeta. Marco Marcon
 La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
Introduzione al Campionamento e
 Introduzione al Campionamento e all analisi analisi in frequenza Presentazione basata sul Cap.V di Introduction of Engineering Experimentation, A.J.Wheeler, A.R.Ganj, Prentice Hall Campionamento L'utilizzo
Introduzione al Campionamento e all analisi analisi in frequenza Presentazione basata sul Cap.V di Introduction of Engineering Experimentation, A.J.Wheeler, A.R.Ganj, Prentice Hall Campionamento L'utilizzo
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Controlli Automatici T. Trasformata di Laplace e Funzione di trasferimento. Parte 3 Aggiornamento: Settembre 2010. Prof. L.
 Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
GRANDEZZE ALTERNATE SINUSOIDALI
 GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
Elementi di teoria dei segnali /b
 Elementi di teoria dei segnali /b VERSIONE 29.4.01 Filtri e larghezza di banda dei canali Digitalizzazione e teorema del campionamento Capacità di canale e larghezza di banda Multiplexing e modulazioni
Elementi di teoria dei segnali /b VERSIONE 29.4.01 Filtri e larghezza di banda dei canali Digitalizzazione e teorema del campionamento Capacità di canale e larghezza di banda Multiplexing e modulazioni
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Corso di Fondamenti di Telecomunicazioni
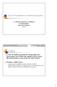 Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Circuiti amplificatori
 Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Forma d onda rettangolare non alternativa.
 Forma d onda rettangolare non alternativa. Lo studio della forma d onda rettangolare è utile, perché consente di conoscere il contenuto armonico di un segnale digitale. FIGURA 33 Forma d onda rettangolare.
Forma d onda rettangolare non alternativa. Lo studio della forma d onda rettangolare è utile, perché consente di conoscere il contenuto armonico di un segnale digitale. FIGURA 33 Forma d onda rettangolare.
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici. a Corrente Alternata. Sergio Benenti 7 settembre 2013
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Lezione 28 Maggio I Parte
 Lezione 28 Maggio I Parte La volta scorsa abbiamo fatto un analisi dei fenomeni di diafonia e avevamo trovato che per la diafonia vicina il valore medio del quadrato del segnale indotto dalla diafonia
Lezione 28 Maggio I Parte La volta scorsa abbiamo fatto un analisi dei fenomeni di diafonia e avevamo trovato che per la diafonia vicina il valore medio del quadrato del segnale indotto dalla diafonia
Segnali e Sistemi. Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici. Gianni Borghesan e Giovanni Marro
 Segnali e Sistemi Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici Gianni Borghesan e Giovanni Marro Indice Introduzione 2. Notazione............................. 2 2 Classificazione
Segnali e Sistemi Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici Gianni Borghesan e Giovanni Marro Indice Introduzione 2. Notazione............................. 2 2 Classificazione
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Università di Napoli Parthenope Facoltà di Ingegneria
 Università di Napoli Parthenope Facoltà di Ingegneria Corso di rasmissione Numerica docente: Prof. Vito Pascazio 18 a Lezione: 13/1/4 19 a Lezione: 14/1/4 Sommario rasmissione di segnali PM numerici su
Università di Napoli Parthenope Facoltà di Ingegneria Corso di rasmissione Numerica docente: Prof. Vito Pascazio 18 a Lezione: 13/1/4 19 a Lezione: 14/1/4 Sommario rasmissione di segnali PM numerici su
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Segnali in formato numerico Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Segnali in formato numerico Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Corso di. Dott.ssa Donatella Cocca
 Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Analisi dei segnali nel dominio della frequenza
 Laboratorio di Telecomunicazioni - a.a. 2010/2011 Lezione n. 7 Analisi dei segnali nel dominio della frequenza docente L.Verdoliva In questa lezione affrontiamo il problema dell analisi dei segnali tempo
Laboratorio di Telecomunicazioni - a.a. 2010/2011 Lezione n. 7 Analisi dei segnali nel dominio della frequenza docente L.Verdoliva In questa lezione affrontiamo il problema dell analisi dei segnali tempo
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Appendice Circuiti con amplificatori operazionali
 Appendice Circuiti con amplificatori operazionali - Appendice Circuiti con amplificatori operazionali - L amplificatore operazionale Il componente ideale L amplificatore operazionale è un dispositivo che
Appendice Circuiti con amplificatori operazionali - Appendice Circuiti con amplificatori operazionali - L amplificatore operazionale Il componente ideale L amplificatore operazionale è un dispositivo che
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Trasformate di Laplace
 TdL 1 TdL 2 Trasformate di Laplace La trasformata di Laplace e un OPERATORE funzionale Importanza dei modelli dinamici Risolvere equazioni differenziali (lineari a coefficienti costanti) Tempo t Dominio
TdL 1 TdL 2 Trasformate di Laplace La trasformata di Laplace e un OPERATORE funzionale Importanza dei modelli dinamici Risolvere equazioni differenziali (lineari a coefficienti costanti) Tempo t Dominio
Suono: aspetti fisici. Tutorial a cura di Aldo Torrebruno
 Suono: aspetti fisici Tutorial a cura di Aldo Torrebruno 1. Cos è il suono Il suono è generalmente prodotto dalla vibrazione di corpi elastici sottoposti ad urti o sollecitazioni (corde vocali, corde di
Suono: aspetti fisici Tutorial a cura di Aldo Torrebruno 1. Cos è il suono Il suono è generalmente prodotto dalla vibrazione di corpi elastici sottoposti ad urti o sollecitazioni (corde vocali, corde di
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/2005
 COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/005 1. Gli esercizi devono essere risolti su fogli separati: uno per la prima parte del compito (esercizi 1/4), uno per la seconda parte (esercizi
COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/005 1. Gli esercizi devono essere risolti su fogli separati: uno per la prima parte del compito (esercizi 1/4), uno per la seconda parte (esercizi
Caratterizzazione dei segnali aleatori nel dominio della frequenza
 Capitolo 5 Caratterizzazione dei segnali aleatori nel dominio della frequenza 5. Introduzione In questo capitolo affrontiamo lo studio dei segnali aleatori nel dominio della frequenza. Prendiamo come esempio
Capitolo 5 Caratterizzazione dei segnali aleatori nel dominio della frequenza 5. Introduzione In questo capitolo affrontiamo lo studio dei segnali aleatori nel dominio della frequenza. Prendiamo come esempio
IL FILTRAGGIO DEL SEGNALE
 CAPITOLO 4 IL FILTRAGGIO DEL SEGNALE 4.1 - SISTEMA LINEARE NON DISTORCENTE E un sistema lineare che restituisce in uscita una replica indistorta del segnale di entrata, intendendo x(t) y(t) = Ax(t-t 0
CAPITOLO 4 IL FILTRAGGIO DEL SEGNALE 4.1 - SISTEMA LINEARE NON DISTORCENTE E un sistema lineare che restituisce in uscita una replica indistorta del segnale di entrata, intendendo x(t) y(t) = Ax(t-t 0
 Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
DISCRETIZZAZIONE DI UN SEGNALE ANALOGICO:
 DISCRETIZZAZIONE DI UN SEGNALE ANALOGICO: nel processo di digitalizzazione che permette di convertire un segnale analogico in modo da poterlo elaborare con dispositivi numerici di calcolo, si operano due
DISCRETIZZAZIONE DI UN SEGNALE ANALOGICO: nel processo di digitalizzazione che permette di convertire un segnale analogico in modo da poterlo elaborare con dispositivi numerici di calcolo, si operano due
Descrizione del funzionamento di un Lock-in Amplifier
 Descrizione del funzionamento di un Lock-in Amplifier S.C. 0 luglio 004 1 Propositi di un amplificatore Lock-in Il Lock-in Amplifier é uno strumento che permette di misurare l ampiezza V 0 di una tensione
Descrizione del funzionamento di un Lock-in Amplifier S.C. 0 luglio 004 1 Propositi di un amplificatore Lock-in Il Lock-in Amplifier é uno strumento che permette di misurare l ampiezza V 0 di una tensione
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
ARCHITETTURA DI RETE FOLEGNANI ANDREA
 ARCHITETTURA DI RETE FOLEGNANI ANDREA INTRODUZIONE È denominata Architettura di rete un insieme di livelli e protocolli. Le reti sono organizzate gerarchicamente in livelli, ciascuno dei quali interagisce
ARCHITETTURA DI RETE FOLEGNANI ANDREA INTRODUZIONE È denominata Architettura di rete un insieme di livelli e protocolli. Le reti sono organizzate gerarchicamente in livelli, ciascuno dei quali interagisce
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005
 Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Rappresentazione dei numeri in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Facciamo qualche precisazione
 Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Funzioni. Funzioni /2
 Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Parte II Indice. Operazioni aritmetiche tra valori rappresentati in binario puro. Rappresentazione di numeri con segno
 Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Università degli Studi di Cassino e del Lazio Meridionale. Area Didattica di Ingegneria. Corso di Laurea in Ingegneria Industriale
 Università degli Studi di Cassino e del Lazio Meridionale Area Didattica di Ingegneria Corso di Laurea in Ingegneria Industriale Lezioni del Corso di Misure Industriali 1 Università degli Studi di Cassino
Università degli Studi di Cassino e del Lazio Meridionale Area Didattica di Ingegneria Corso di Laurea in Ingegneria Industriale Lezioni del Corso di Misure Industriali 1 Università degli Studi di Cassino
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
2) Codici univocamente decifrabili e codici a prefisso.
 Argomenti della Lezione ) Codici di sorgente 2) Codici univocamente decifrabili e codici a prefisso. 3) Disuguaglianza di Kraft 4) Primo Teorema di Shannon 5) Codifica di Huffman Codifica di sorgente Il
Argomenti della Lezione ) Codici di sorgente 2) Codici univocamente decifrabili e codici a prefisso. 3) Disuguaglianza di Kraft 4) Primo Teorema di Shannon 5) Codifica di Huffman Codifica di sorgente Il
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Un po di statistica. Christian Ferrari. Laboratorio di Matematica
 Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Informatica. Rappresentazione binaria Per esempio +101010000 diventa +0.10101 10 18/10/2007. Introduzione ai sistemi informatici 1
 Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
v in v out x c1 (t) Molt. di N.L. H(f) n
 Comunicazioni elettriche A - Prof. Giulio Colavolpe Compito n. 3 3.1 Lo schema di Fig. 1 è un modulatore FM (a banda larga). L oscillatore che genera la portante per il modulatore FM e per la conversione
Comunicazioni elettriche A - Prof. Giulio Colavolpe Compito n. 3 3.1 Lo schema di Fig. 1 è un modulatore FM (a banda larga). L oscillatore che genera la portante per il modulatore FM e per la conversione
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
