Osservazioni sul differenziale
|
|
|
- Enrico Tarantino
- 7 anni fa
- Visualizzazioni
Transcript
1 Osservazioni sul differenziale ( ) 11 ottobre 2010 Scopo di questo articolo è di presentare il concetto di differenziale per le funzioni reali di una o più variabili reali. L intento non è quello di proporre una trattazione sistematica ed esaustiva, quanto piuttosto quello di evidenziare il significato e l importanza del concetto di funzione differenziabile, in particolare per le funzioni di almeno due variabili. Indice Introduzione Funzioni lineari Funzioni di R in R Funzioni di R 2 in R Funzioni di R n in R La scrittura tradizionale Funzioni di R n in R m Algebra dei differenziali Introduzione Il concetto di differenziale è un concetto di straordinaria importanza sia teorica che pratica, in quanto solo le funzioni differenziabili sono dotate di tangente (o di piano tangente, o di iperpiano tangente), cioè solo le funzioni differenziabili sono ben approssimabili, in un intorno del punto dove si calcola il differenziale, con una funzione particolarmente semplice, come sono le funzioni polinomiali di primo grado. L importanza del differenziale emerge tuttavia solo con le funzioni (reali) di almeno due variabili, in quanto nel caso delle funzioni di una sola variabile reale una funzione è differenziabile se e solo se è derivabile, e siccome il concetto di derivata appare più semplice, di solito è l unico ad essere trattato. Inoltre, a mio modo di vedere, le strategie usate per introdurre il concetto di differenziale sono spesso poco chiare e fuorvianti; se si usa la dovuta precisione terminologica e si chiariscono accuratamente tutti gli aspetti, il concetto di differenziale cesserà di essere quell oggetto misterioso che è per la maggior parte degli studenti. Per chiarire quanto sopra affermato riporto la definizione di differenziale (per funzioni reali di una variabile reale) presa da un testo molto in voga (si tratta comunque della definizione più diffusa): Il 1
2 Osservazioni sul differenziale 2 differenziale di una funzione è il prodotto della derivata della funzione per l incremento arbitrario della variabile indipendente. Dopo aver letto questa definizione (e magari aver anche esaminato alcuni esempi) credo sia abbastanza difficile rispondere a una domanda del tipo: ma il differenziale è un numero, oppure è una funzione? Se è una funzione, di quante variabili? E qual è il suo grafico cartesiano? 1 Funzioni lineari Le funzioni lineari sono le funzioni fondamentali nello studio degli spazi vettoriali. Ne richiamiamo brevemente la definizione che ci servirà in quanto il differenziale di una funzione è una funzione lineare, limitandoci al caso di spazi vettoriali su R. Definizione 1. Dati due spazi vettoriali V e W, entrambi sul corpo dei numeri reali, una funzione f : V W si dice lineare se (1) f(λ u + µ v) = λf( u) + µf( v), λ, µ R e u, v V. La definizione data significa che se una funzione è lineare è indifferente scegliere di eseguire prima alcune operazioni (lineari!) su due vettori di V e poi applicare la funzione, oppure applicare prima la funzione e poi eseguire le corrispondenti operazioni sulle immagini dei due vettori di V. Nel caso di funzioni di R n in R le funzioni lineari sono sempre di uno dei tipi seguenti: (2) f : R n R, f (x 1 ) = a 1 x 1 (n = 1) f (x 1, x 2 ) = a 1 x 1 + a 2 x 2 (n = 2) f (x 1, x 2, x 3 ) = a 1 x 1 + a 2 x 2 + a 3 x 3 (n = 3) Le funzioni di R n in R m possono essere sempre pensate come una m-upla di funzioni di R n in R, e quindi le funzioni lineari saranno m-uple di funzioni di uno dei tipi sopra considerati: f 1 (x 1,..., x n ) = a 11 x a 1n x n f (3) f : R n R m 2 (x 1,..., x n ) = a 21 x a 2n x n,... f m (x 1,..., x n ) = a m1 x a mn x n Posto x 1 x 2 a a 1n (4) x =. e A =....., a x m1... a mn n è ben noto che la funzione si può scrivere, in forma matriciale, come (5) f : R n R m, x A x. Per comodità di scrittura, comunque, scriveremo il vettore x sempre come vettore riga anzichè come vettore colonna, x = (x 1,..., x n ). Gli spazi vettoriali R n, per le applicazioni che ci interessano, sono pensati anche dotati del prodotto scalare canonico e della norma dedotta dal prodotto scalare. Nel caso delle funzioni di R 2 o di R 3 in R è tradizione indicare le variabili con (x, y) e (x, y, z) rispettivamente, anziché con (x 1, x 2 ) oppure (x 1, x 2, x 3 ). Poiché però in questo articolo vogliamo.
3 Osservazioni sul differenziale 3 proporre una trattazione unificata dei vari casi, manterremo la notazione con gli indici, riservando la y (ed eventualmente y = (y 1,..., y m )) per la variabile dipendente. Per le funzioni a valori in R, se si usa una rappresentazione cartesiana, le funzioni lineari hanno un grafico particolarmente semplice e significativo, come di seguito indicato. Una retta per l origine del piano Ox 1 y, nel caso n = 1, e il numero a 1 rappresenta il coefficiente angolare della retta; se poi si scrive l equazione della retta in forma implicita (o normale), a 1 x 1 y = 0, si deduce che il vettore (a 1, 1) è un vettore perpendicolare alla retta. Un piano per l origine dello spazio Ox 1 x 2 y nel caso di n = 2; se si scrive l equazione del piano in forma implicita (o normale), a 1 x 1 + a 2 x 2 y = 0, si vede che il vettore (a 1, a 2, 1) è un vettore perpendicolare al piano. Un iperpiano per l origine dello spazio quadridimensionale Ox 1 x 2 x 3 y nel caso di n = 3; se si scrive l equazione dell iperpiano in forma implicita (o normale), a 1 x 1 + a 2 x 2 + a 3 x 3 y = 0, si vede che il vettore (a 1, a 2, a 3 1) è un vettore perpendicolare all iperpiano. 2 Funzioni di R in R Come già accennato, nel caso di funzioni reali di una sola variabile reale, il concetto di differenziabilità non introduce sostanziali novità rispetto a quello di derivabilità. Tuttavia è opportuno trattare ugualmente in dettaglio il problema, in quanto in questa situazione l interpretazione grafico-geometrica è particolarmente semplice e significativa. Sia f : I R R una funzione reale di una variabile reale; per semplicità supporremo che il dominio I sia un intervallo aperto, di modo che i punti che considereremo saranno sempre interni all intervallo. Supporremo inoltre che la funzione f sia continua in I. Sia x 0 un punto di I, e f(x 0 ) il corrispondente valore della funzione. Siamo interessati a valutare la variazione della funzione al passaggio da x 0 a un punto generico x situato nei pressi di x 0 ; se poniamo (6) h = x x 0, questa variazione sarà data da (7) f x0 (h) = f(x 0 + h) f(x 0 ), che è una funzione di h, una volta fissato x 0. Questa variazione prende il nome di incremento della funzione f relativo all incremento h della variabile e al punto x 0. y y f(x 0 + h) f(x0) f f(x 0 + h) x0 (h) f x0 (h) h fx0(h) h fx0(h) x x 0 + h x 0 x 0 + h x Figura 1 Incremento f x0 (h) di una funzione Figura 2 Incremento f x0 (h) in funzione di h
4 Osservazioni sul differenziale 4 Nella figura 1 è evidenziato l incremento a partire da un dato punto x 0 (questo incremento è positivo se f(x 0 + h) > f(x 0 ), altrimenti è negativo, e il tutto dipende sia dal segno di h, cioè dal fatto che x 0 + h sia a destra o a sinistra di x 0 sia dal tipo di funzione considerata); nella figura 2 è rappresentato lo stesso incremento in funzione di h: si tratta semplicemente della traslazione rigida del grafico della figura 1 ottenuta spostando il punto (x 0, f(x 0 )) sull origine. La domanda che dà origine al concetto di differenziale è la seguente: è possibile approssimare l incremento, cioè la funzione il cui grafico è rappresentato nella figura 2, con una funzione lineare, ovvero una funzione avente per grafico una retta passante per l origine? Per rispondere alla domanda consideriamo una generica funzione lineare, x L x0 (x) e valutiamo l errore che si commette calcolando L x0 (h) al posto di f x0 (h), errore che è dato da (8) ω(h) = f x0 (h) L x0 (h). Nella figura 3 che segue è visualizzata la situazione corrispondente a una particolare scelta della funzione L x0. Naturalmente ω(h) sarà positivo o negativo a seconda che f x0 (h) sia maggiore o minore di L x0 (h). y h fx0(h) Lx0(h) ω(h) ω(h) h L x0 (h) fx0(h) x Figura 3 Una possibile funzione lineare, L x0, approssimante f x0 (h) Nelle ipotesi di continuità (1) in cui ci siamo posti, è chiaro che (9) lim ω(h) = lim f x0 (h) L x0 (h) = lim ( f(x0 + h) f(x 0 ) ) L x0 (h) = 0, ovvero che ω è una funzione infinitesima, al tendere di h a 0. Ci possiamo ora chiedere se è possibile scegliere la funzione lineare L x0 in modo che ω sia addirittura un infinitesimo di ordine superiore rispetto ad h, ovvero in modo tale che ω(h) (10) lim = lim f(x 0 + h) f(x 0 ) L x0 (h) f x0 (h) L x0 (h) = lim = 0. h L esempio seguente prova che, in genere, la risposta è negativa. Consideriamo la funzione x sin 1 (11) f : R R, f(x) = x, se x 0, 0, se x = 0 1 La continuità serve per concludere che lim f(x0 + h) = f(x0).
5 Osservazioni sul differenziale 5 e una generica funzione lineare, L x0 (h) = mh. Sia inoltre x 0 = 0. Si ha allora { h sin 1 mh, se h 0 (12) ω(h) = h, 0, se h = 0 da cui ω(h) h sin 1 (13) lim = lim h mh = lim (sin 1h ) m, ed è ben noto che questo limite non esiste, qualunque sia m. Se invece consideriamo la funzione data da f(x) = x 2, il punto x 0 = 1, e ancora una generica funzione lineare L x0 (h) = mh, otteniamo (14) ω(h) = ( (1 + h) 2 1 ) mh = h 2 + 2h mh, da cui ω(h) (15) lim = lim h 2 + 2h mh = lim(h + 2 m), e si conclude facilmente che questo limite è zero se, e solo se, m = 2. Poiché 2 è esattamente la derivata della funzione f in esame, in corrispondenza al punto x 0 = 1, ne concludiamo che (16) ω(h) = f 1 (h) L x0 (h) = f(1 + h) f(1) f (1)h f(1 + h) = f(1) + f (1)h + ω(h). Se teniamo conto, vedi la formula (6) nella pagina 3, che h = x 1, otteniamo (17) f(x) = f(1) + f (1)(x 1) + ω(x 1), ovvero: la funzione, nei pressi del punto 1, può essere approssimata dalla retta tangente al grafico, a meno di un infinitesimo di ordine superiore rispetto a x 1. La situazione che si verifica per la funzione f(x) = x 2 è di grande importanza e porta alla introduzione del concetto di differenziale. Definizione 2. Sia f : I R una funzione definita in un (intervallo) aperto I di R. La funzione f si dice differenziabile in un punto x 0 I se esiste una funzione lineare L x0 : R R tale che f(x 0 + h) f(x 0 ) L x0 (h) f x0 (h) L x0 (h) (18) lim = lim = 0. In tale ipotesi la funzione L x0 si chiama differenziale della funzione f nel punto x 0, e si indica con il simbolo (19) df x0. Si noti che il differenziale di una funzione in un punto è una funzione (lineare), non un numero. Inoltre, posto ω(h) = f x0 (h) df x0 (h), si ha (20) f x0 (h) = df x0 (h) + ω(h), e si deduce dalla definizione precedente che il differenziale di una funzione in un punto x 0, relativamente all incremento h della variabile, approssima l incremento della funzione nelle stesse condizioni a meno di un infinitesimo di ordine superiore ad h. Se teniamo di nuovo conto della (6), possiamo dire che se f è differenziabile in un punto x 0, si ha (21) f(x) = f(x 0 ) + df x0 (x x 0 ) + ω(x x 0 ), dove ω è una funzione infinitesima, al tendere di x a x 0, di ordine superiore rispetto a x x 0. La situazione che abbiamo riscontrato per la funzione f(x) = x 2 non è eccezionale: in effetti, per le funzioni di una variabile reale, si dimostra il seguente teorema.
6 Osservazioni sul differenziale 6 Teorema 3. Una funzione f : I R è differenziabile in un punto x 0 I se e solo se è derivabile in x 0 e, in questo caso caso, si ha (2) (22) L x0 (x x 0 ) = df x0 (x x 0 ) = f (x 0 )(x x 0 ). Ne segue che la formula (21) si può riscrivere nella forma (23) f(x) = f(x 0 ) + f (x 0 )(x x 0 ) + ω(x x 0 ). È proprio in conseguenza della formula (23) che la retta r di equazione y = f(x 0 ) + f (x 0 )(x x 0 ) prende il nome di retta tangente al grafico della funzione f, in corrispondenza al punto x 0 : la formula infatti afferma che la funzione f può essere approssimata con la retta r a meno di un infinitesimo di ordine superiore rispetto a x x 0, ovvero che, almeno in un intorno di x 0, i grafici della funzione f e della retta r sono quasi coincidenti. Naturalmente bisogna sempre tenere conto del significato di infinitesimo o di infinitesimo di ordine superiore: l approssimazione è buona in un opportuno intorno del punto x 0, ma nulla si può affermare circa l ampiezza di questo intorno. Può benissimo darsi che, su tutto un intervallo prefissato circondante il punto x 0, ci siano altre approssimazioni lineari molto migliori globalmente di quella fornita localmente dalla retta tangente. Si tenga ben presente che il differenziale di una funzione non ha come grafico la retta tangente: il differenziale è una funzione lineare dell incremento h (e dunque ha come grafico una retta per l origine); la retta tangente si ottiene, vedi la formula (21), calcolando il differenziale in x x 0 e aggiungendo f(x 0 ), ovvero traslando il grafico del differenziale in modo che il punto (0, 0) vada a coincidere con il punto (x 0, f(x 0 )). È opportuno dare alla formula (23) una forma adatta ad essere generalizzata a funzioni di R n in R (e poi anche a casi ancora più complessi). Per questo: indichiamo con x il generico punto del dominio di f: per funzioni di una variabile il vettore x avrà solo una componente, per due variabili ne avrà invece due: x = (x 1, x 2 ), ecc; detto i il versore dell asse x, chiamiamo gradiente della funzione f nel punto x 0 il vettore (sempre a una componente!) (24) f( x 0 ) = f ( x 0 ) i. Se indichiamo il prodotto scalare (canonico) con, il differenziale della funzione si potrà scrivere come (25) df x0 ( x x 0 ) = f( x 0 ) ( x x 0 ) e la formula (23) si riscriverà nella forma seguente: (26) f( x) = f( x 0 ) + f( x 0 ) ( x x 0 ) + ω( x x 0 ), forma che ritroveremo intatta trattando il caso di più dimensioni. Osserviamo che, con queste notazioni, l equazione della retta tangente al grafico della funzione f nel punto (x 0, f(x 0 )) si può scrivere in una delle forme (27) y = f(x 0 ) + df x0 (x x 0 ), y = f( x 0 ) + f x0 ( x x 0 ). La figura 4 seguente, dove ci siamo limitati al caso h > 0 per semplicità, illustra il significato geometrico del differenziale. 2 Si noti, nella formula (22), una certa difficoltà di lettura dovuta alle notazioni: mentre in df x0 (x x 0) le parentesi tonde racchiudono l argomento della funzione df x0, in f (x 0)(x x 0) la seconda coppia di parentesi serve a racchiudere il termine (x x 0) nel prodotto di due fattori.
7 Osservazioni sul differenziale 7 y f(x 0 + h) ω(h) y = f(x 0 ) + d f x0 (x x 0 ) d f x0 (h) f x0 (h) f(x 0 ) x 0 x 0 + h x Figura 4 Differenziale e significato geometrico 3 Funzioni di R 2 in R Sia ora f : D R 2 R una funzione definita in un sottoinsieme (che supporremo aperto per semplicità) di R 2 e a valori in R. Sia x 0 = (x 1,0, x 2,0 ) un punto di D e f( x 0 ) il corrispondente valore della funzione. Come nel caso di una variabile siamo interessati a valutare la variazione della funzione al passaggio da x 0 a un punto generico x situato nei pressi di x 0 ; se poniamo (28) h = x x0 = (h 1, h 2 ), questa variazione sarà data da (29) f x0 ( h) = f( x 0 + h) f( x 0 ), che è una funzione di h, una volta fissato x 0. Anche in questo caso vogliamo verificare se è possibile approssimare l incremento con una funzione lineare, ovvero una funzione avente come grafico una piano passante per l origine. In perfetta analogia con la definizione 2, possiamo dare la definizione seguente di funzione differenziabile. Definizione 4. Sia f : D R una funzione definita in un aperto D di R 2. La funzione si dice differenziabile nel punto x 0 D se esiste una funzione lineare L x0 : R 2 R tale che f( x 0 + (30) lim h) f( x 0 ) L x0 ( h) f (h 1,h 2 ) (0,0) = lim x0 ( h) L x0 ( h) h (h 1,h 2 ) (0,0) = 0 h In tale ipotesi la funzione L x0 il simbolo si chiama differenziale della funzione f nel punto x 0, e si indica con (31) df x0. Anche in questo caso si può notare che il differenziale di una funzione in un punto è una funzione (lineare), non un numero, e precisamente, trattandosi di una funzione lineare di R 2 in R, una funzione del tipo (32) L x0 ( h) = L x0 (h 1, h 2 ) = df x0 (h 1, h 2 ) = a 1 h 1 + a 2 h 2,
8 Osservazioni sul differenziale 8 dove i due coefficienti a 1, a 2 dipendono da x 0 = (x 1,0, x 2,0 ). Naturalmente anche in questo caso la definizione data implicherà che (33) f x0 ( h) = df x0 ( h) + ω( h), ovvero, tenendo conto che h = x x 0, (34) f( x) = f( x 0 ) + df x0 ( x x 0 ) + ω( x x 0 ). La funzione ω è infinitesima, per x x 0, di ordine superiore rispetto a x x 0, cioè rispetto alla distanza tra x e x 0. Questa volta la situazione analitica è più complessa che non nel caso delle funzioni di una variabile e può tranquillamente succedere che la funzione f abbia, in x 0, entrambe le derivate parziali, o addirittura tutte le derivate direzionali, senza essere differenziabile. Del resto, come è ben noto, l esistenza delle derivate parziali e, purtroppo, anche di tutte le derivate direzionali in un punto non è nemmeno condizione sufficiente per la continuità della funzione. Vale però il seguente teorema, che esprime in sostanza una condizione necessaria per la differenziabilità. Teorema 5. Se una funzione f : D R 2 R è differenziabile in un punto x 0, allora è continua e parzialmente derivabile in x 0 e inoltre si ha (35) df x0 ( x x 0 ) = f ( x 0 )(x 1 x 1,0 ) + f ( x 0 )(x 2 x 2,0 ). Ridefinendo il gradiente della funzione f come estensione della definizione data nel caso di una variabile, si ottiene: (36) f( x 0 ) = f ( x 0 ) i + f ( x 0 ) j. Dunque il differenziale si potrà scrivere come (37) df x0 ( x x 0 ) = f( x 0 ) ( x x 0 ) e la formula (34) si riscriverà nella forma (38) f( x) = f( x 0 ) + f ( x 0 )(x 1 x 1,0 ) + f ( x 0 )(x 2 x 2,0 ) + ω( x x 0 ), oppure (39) f( x) = f( x 0 ) + f( x 0 ) ( x x 0 ) + ω( x x 0 ). Per gli stessi motivi già segnalati nel caso delle funzioni di una variabile, il piano di equazione (40) y = f( x 0 ) + f ( x 0 )(x 1 x 1,0 ) + f ( x 0 )(x 2 x 2,0 ) è il piano tangente al grafico della funzione f, nel punto x 0. È importante il fatto che se una funzione è differenziabile in un punto x 0 allora è ivi derivabile secondo una qualunque direzione orientata e, detto u = (l, m) il versore della direzione, si ha (41) f u ( x 0) = f( x 0 ) u = f ( x 0 ) l + f ( x 0 ) m. A scanso di equivoci è opportuno ricordare (ancora una volta!) che non vale il viceversa: una funzione può essere derivabile lungo ogni direzione senza essere differenziabile, e in questo caso la derivata direzionale non si potrà esprimere con la formula (41). La figura 5 seguente illustra il significato geometrico del differenziale per una funzione di due variabili. Nella figura sono rappresentati:
9 Osservazioni sul differenziale 9 una parte del dominio D della funzione nel piano Ox 1 x 2, precisamente il rettangolo R di vertici opposti x 0 e x = x 0 + h; la parte di piano y = f( x 0 ) sovrastante il rettangolo R; la parte di piano tangente sovrastante il rettangolo R: y = f( x 0 ) + f( x 0 ) ( x x 0 ); il lembo della superficie-grafico della funzione f, sovrastante il rettangolo R. y ω( x x 0 ) f x0 ( x x 0 ) d f x0 ( x x 0 ) x 1 O x 0 x x 2 Figura 5 Differenziale in due variabili e significato geometrico Si può verificare la sostanziale identità tra le immagini riportate nelle figure 4 e 5, e in particolare il fatto che il piano tangente costituisce una approssimazione del grafico della funzione, nei pressi del punto x 0. 4 Funzioni di R n in R Mentre il passaggio dalle funzioni di una variabile a quelle di due variabili è abbastanza delicato, in quanto l esistenza delle derivate parziali non garantisce, da sola, la differenziabilità di una funzione, il passaggio a un numero di variabili maggiore di 2 ormai è solo questione formale: nulla cambia nella sostanza. Si tratterà solo di tenere conto del fatto che x, x 0, h avranno n componenti, anziché solo due. Naturalmente non si avrà più a disposizione una rappresentazione cartesiana significativa come quella proposta nella figura 5, e il concetto di piano tangente sarà sostituito da quello di iperpiano tangente, sempre senza alcuna possibilità di interpretazione geometrica elementare. Rimane il fatto essenziale (ed è questo che serve nelle applicazioni, al di là della visualizzazione grafica!), che l incremento di una funzione si può approssimare, in un intorno di un punto dove la funzione è differenziabile, con una funzione lineare, il differenziale df x0. Approssimazioni di ordine più elevato (polinomiali di grado due, tre, ecc.) sono oggetto della formula di Taylor. Riscriviamo, a titolo d esempio, le formule che si riferiscono al caso di una funzione di R 3 in R, in un punto x 0. Gradiente di una funzione: f( x 0 ) = f ( x 0 ) i + f ( x 0 ) j + f ( x 0 ) x k. 3
10 Osservazioni sul differenziale 10 Differenziale di una funzione: df x0 ( x x 0 ) = f( x 0 ) ( x x 0 ) = f ( x 0 )(x 1 x 1,0 )+ f ( x 0 )(x 2 x 2,0 )+ f x 3 ( x 0 )(x 3 x 3,0 ). Iperpiano tangente: y = f( x 0 ) + f( x 0 ) ( x x 0 ). Derivata secondo la direzione del versore u = (l, m, n): f u ( x 0) = f( x 0 ) u = f ( x 0 ) l + f ( x 0 ) m + f ( x 0 ) n. x 3 Ricordiamo, per completezza, una condizione sufficiente per la differenziabilità di una funzione di R n in R, (n 2). Teorema 6 (del differenziale totale). Sia f : D R n R, una funzione definita in un (aperto) D di R n. Se f è parzialmente derivabile in un intorno I di un punto x 0 e le derivate parziali sono continue in x 0, allora la funzione è differenziabile in x 0. Si noti come questo teorema richieda la continuità delle funzioni derivate parziali in x 0, e non la semplice esistenza delle derivate parziali: mentre l esistenza della derivate parziali concerne solo la restrizione della funzione a una direzione, passante per x 0, parallela agli assi, la continuità delle derivate stesse concerne tutto un intorno n-dimensionale del punto x 0, e questo è in accordo con il fatto che la differenziabilità è proprio una questione che coinvolge tutto un intorno n-dimensionale del punto x 0. 5 La scrittura tradizionale Tradizionalmente le formule relative al differenziale vengono scritte in una forma molto significativa per le applicazioni, ma che va presa con molta cautela. Ne facciamo solo un breve cenno. Il caso delle funzioni di una variabile Cominciamo con il caso delle funzioni di una variabile e consideriamo la funzione (42) g : R R, g(x) = x, cioè la funzione identica di R in R. Poiché g (x 0 ) = 1, x 0 R, il differenziale della funzione g sarà lo stesso (cioè la stessa funzione) in ogni punto, e precisamente la funzione L(h) = h, ovvero (43) dg x0 (h) = h dg x0 (x x 0 ) = x x 0. È abitudine indicare la funzione g semplicemente con x (3). Tenendo anche conto che il differenziale non dipende da x 0, si omette di esplicitare questa dipendenza, e anziché dg x0 (x x 0 ) si scrive semplicemente dx(x x 0 ) ( dx calcolato in x x 0 ). Anzi, siccome il differenziale si calcola naturalmente sempre in x x 0, cioè nell incremento, si evita anche di esplicitare il fatto che il dx è calcolato in x x 0 e la (43) si scrive semplicemente (44) dx = x x 0. 3 Si tratta di una scrittura che può dar luogo ad equivoci, ma che può essere precisata con rigore. Come sempre nella lettura di una formula matematica occorre avere presente le convenzioni adottate (e tenere presente che non si può sempre scrivere tutto con la più assoluta precisione, altrimenti certe formule diventerebbero chilometriche!).
11 Osservazioni sul differenziale 11 A questo punto anche nel differenziale di una generica funzione f di una variabile si omette di esplicitare il fatto che il differenziale va calcolato in x x 0, e si scrive semplicemente (45) df x0 = f (x 0 ) dx. È (anche) la formula (45) che dà origine al tradizionale simbolo per la derivata di una funzione: (46) f (x 0 ) = df dx (x 0). Il caso delle funzioni di più variabili Considerazioni simili si possono fare per funzioni reali di più variabili reali. Occorrerà sempre tenere ben presente che la differenziabilità è, ora, una condizione più restrittiva che non la semplice esistenza delle derivate parziali. Trattiamo esplicitamente il caso di due variabili, il caso generale è assolutamente identico. Consideriamo le due funzioni (47) π 1 ( x) = x 1, π 2 ( x) = x 2, dove i nomi π 1 e π 2 sono stati scelti perché le due funzioni sostanzialmente proiettano il generico punto x del piano Ox 1 x 2 sull asse x 1 e x 2 rispettivamente, fornendo la prima e la seconda componente di x. È immediato constatare che, per ogni x 0, (48) Dunque π 1 ( x 0 ) = 1, π 1 ( x 0 ) = 0, mentre π 2 ( x 0 ) = 0, π 2 ( x 0 ) = 1. (49) dπ 1, x0 ( x x 0 ) = x 1 x 1,0, dπ 2, x0 ( x x 0 ) = x 2 x 2,0, da cui, con le stesse convenzioni utilizzate nel caso di una variabile, (50) dx 1 = x 1 x 1,0, dx 2 = x 2 x 2,0, e, infine, (51) df x0 = f ( x 0 ) dx 1 + f ( x 0 ) dx 2. 6 Funzioni di R n in R m Le funzioni di R n in R m non presentano sostanziali novità rispetto ai casi precedenti, in quanto si possono pensare come m-uple di funzioni di R n in R, dette funzioni componenti: tutte le considerazioni fatte si applicheranno alle singole funzioni componenti. La cosa significativa da segnalare è che, avendo m funzioni di R n in R, avremo m gradienti, ciascuno con n componenti: è ovvio che essi potranno essere scritti in una matrice, J, a m righe e n colonne, come segue. f 1 f 1 f 1... x n f 2 f 2 f 2... (52) J( x 0 ) = x n,. f m. f m f m x n
12 Osservazioni sul differenziale 12 dove tutte le derivate vanno calcolate in x 0. La matrice così costruita si chiama matrice jacobiana e le formule che legano il differenziale al gradiente saranno sostituite dalla formula (53) df x0 ( x x 0 ) = J( x 0 )( x x 0 ). Continueranno a valere tutte le considerazioni che abbiamo già fatto in precedenza, compreso il Teorema del differenziale totale che, per maggiore chiarezza, riformuliamo qui di seguito. Teorema 7 (del differenziale totale). Sia f : D R n R m, una funzione definita in un (aperto) D di R n. Se tutte le componenti (f 1, f 2,..., f m ) di f sono parzialmente derivabili in un intorno I di un punto x 0 e le derivate parziali sono continue in x 0, allora la funzione è differenziabile in x 0, cioè esiste una funzione lineare L x0 : R n R m, tale che f( x 0 + (54) lim h) f( x 0 ) L x0 ( h) f h 0 = lim x0 ( h) L x0 ( h) h h 0 = 0. h È opportuno segnalare che nel caso di funzioni R R m, poiché le singole componenti sono funzioni di una sola variabile, varranno tutte le proprietà specifiche di questo caso, in particolare la differenziabilità coinciderà con la derivabilità (ordinaria perché si tratta di funzioni di una sola variabile) delle m componenti della funzione. Si tratta di un caso particolarmente importante: le curve di R m (in particolare di R 2 e R 3 ) sono proprio funzioni di questo tipo: dunque la differenziabilità è essenzialmente diversa dalla derivabilità quando il dominio è multidimensionale. 7 Algebra dei differenziali Concludiamo questa serie di osservazioni sul concetto di differenziale ricordando i seguenti risultati. 1. Siano f e g due funzioni di R n in R m, entrambi differenziabili in x 0. Allora f +g è differenziabile in x 0 e si ha (55) d(f + g) x0 ( x x 0 ) = df x0 ( x x 0 ) + dg x0 ( x x 0 ). 2. Siano f : A R n R p una funzione differenziabile in x 0 A e g : B R p R m, una funzione differenziabile in y 0 = f( x 0 ) B; sia inoltre h = g f : A R n R m la funzione composta di f e g. Allora h è differenziabile in x 0 e si ha (56) dh x0 ( x x 0 ) = dg y0 ( y y 0 ) df x0 ( x x 0 ). In termini di matrici jacobiane la formula (56) si scrive (57) J h ( x 0 ) = J g ( y 0 )J f ( x 0 ), con ovvio significato dei simboli. È in particolare la seconda delle due proprietà elencate che giustifica l importanza del concetto di differenziale, come estensione naturale a più dimensioni del concetto di derivata: mentre la composta di due funzioni (di più variabili!) derivabili (magari lungo ogni direzione), può non essere affatto derivabile (anzi addirittura nemmeno continua), la composta di due funzioni differenziabili è differenziabile, esattamente come succedeva per la derivabilità nel caso di funzioni di una variabile.
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Osservazioni sulle funzioni composte
 Osservazioni sulle funzioni composte ) 30 dicembre 2009 Scopo di questo articolo è di trattare alcuni problemi legati alla derivabilità delle funzioni composte nel caso di funzioni di R n in R m Non si
Osservazioni sulle funzioni composte ) 30 dicembre 2009 Scopo di questo articolo è di trattare alcuni problemi legati alla derivabilità delle funzioni composte nel caso di funzioni di R n in R m Non si
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Esempio di grafico di una funzione reale di due variabili reali
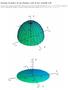 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
DIFFERENZIAZIONE. Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim
 DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
R. Capone Analisi Matematica Calcolo Differenziale Funzioni di due variabili
 Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
1 Prodotto cartesiano di due insiemi 1. 5 Soluzioni degli esercizi 6
 1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Mauro Sassetti. Calcolo differenziale ed integrale. per funzioni di due variabili reali.
 Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Da una a più variabili: derivate
 Da una a più variabili: derivate ( ) 5 gennaio 2011 Scopo di questo articolo è di evidenziare le analogie e le differenze, relativamente al calcolo differenziale, fra le funzioni di una variabile reale
Da una a più variabili: derivate ( ) 5 gennaio 2011 Scopo di questo articolo è di evidenziare le analogie e le differenze, relativamente al calcolo differenziale, fra le funzioni di una variabile reale
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Derivate parziali, derivate direzionali, differenziabilità. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) =
 Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Breve formulario di matematica
 Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
21 IL RAPPORTO INCREMENTALE - DERIVATE
 21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Derivazione numerica. Introduzione al calcolo numerico. Derivazione numerica (II) Derivazione numerica (III)
 Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3.4, 3.9. Esercizi 3.4, 3.9.
 Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
LEZIONE 11. s V : V V V (v 1, v 2 ) v 1 + v 2 = s V (v 1, v 2 ), p V : k V V. per cui valgono:
 LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
La formula di Taylor per funzioni di più variabili
 La formula di Taylor per funzioni di più variabili Il polinomio di Taylor Due variabili. Sia A R 2 un aperto, f : A R una funzione sufficientemente regolare, (x, y) un punto di A. Sia (h, k) un vettore
La formula di Taylor per funzioni di più variabili Il polinomio di Taylor Due variabili. Sia A R 2 un aperto, f : A R una funzione sufficientemente regolare, (x, y) un punto di A. Sia (h, k) un vettore
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Equazione della retta tangente al grafico di una funzione
 Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Funzioni di R n a R m e la matrice Jacobiana
 0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
0.1 Funzioni di R n a R m. Politecnico di Torino. Funzioni di R n a R m e la matrice Jacobiana Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto 0.1 Funzioni di R n
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Esercitazione sugli sviluppi in serie di Taylor
 Esercitazione sugli sviluppi in serie di Taylor Davide Boscaini Queste sono le note da cui ho tratto le lezioni frontali del 1 e 13 Gennaio 011. Come tali sono ben lungi dall essere esenti da errori, invito
Esercitazione sugli sviluppi in serie di Taylor Davide Boscaini Queste sono le note da cui ho tratto le lezioni frontali del 1 e 13 Gennaio 011. Come tali sono ben lungi dall essere esenti da errori, invito
Estremi liberi. (H x, x) x 2 (1) F (x) =
 Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
Analisi Matematica 1
 Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
(x x 0 ) 2. Lezione del 24 ottobre
 Lezione del 4 ottobre 1. Premessa I fatti descritti nei punti seguenti si possono vedere come molto lontani sviluppi di alcuni fatti elementari riguardanti le funzioni polinomiali di II grado. Diamo per
Lezione del 4 ottobre 1. Premessa I fatti descritti nei punti seguenti si possono vedere come molto lontani sviluppi di alcuni fatti elementari riguardanti le funzioni polinomiali di II grado. Diamo per
ESAME DI MATEMATICA I parte Vicenza, 05/06/2017. x log 2 x?
 A. Peretti Svolgimento dei temi d esame di Matematica A.A. 6/7 ESAME DI MATEMATICA I parte Vicenza, 5/6/7 log? Domanda. Per quali valori di è definita l espressione L espressione è definita se l argomento
A. Peretti Svolgimento dei temi d esame di Matematica A.A. 6/7 ESAME DI MATEMATICA I parte Vicenza, 5/6/7 log? Domanda. Per quali valori di è definita l espressione L espressione è definita se l argomento
Sistemi lineari e spazi vettoriali 1 / 14
 Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini.
 Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Analisi Matematica II (Prof. Paolo Marcellini)
 Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Dato un intervallo limitato A di estremi a e b con a b, si definisce misura dell intervallo il numero b a e si indica con :
 E-school di Arrigo Amadori Analisi I Integrali di Riemann 01 Introduzione. L integrale è, oltre alla derivata, l altro oggetto fondamentale che sta alla base del calcolo differenziale. Con gli integrali
E-school di Arrigo Amadori Analisi I Integrali di Riemann 01 Introduzione. L integrale è, oltre alla derivata, l altro oggetto fondamentale che sta alla base del calcolo differenziale. Con gli integrali
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
Coniche - risposte 1.9
 Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
LEZIONE 12. Y = f(x) = f( x j,1 f(e j ) = x j,1 A j = AX = µ A (X),
 LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
OPERAZIONI SU SPAZI DI HILBERT. Nel seguito introdurremo i concetti di prodotto diretto e somma diretta di due spazi di Hilbert.
 2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
LA RETTA NEL PIANO CARTESIANO
 LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04/11/ 13
 Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Funzioni di più variabili a valori vettoriali n t m
 Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Soluzione Problema 1
 Soluzione Problema 1 1. Ricordiamo che una funzione h(x) è derivabile in un punto c se esiste finita la sua derivata nel punto c. Per il significato geometrico della derivata ciò significa che esiste ed
Soluzione Problema 1 1. Ricordiamo che una funzione h(x) è derivabile in un punto c se esiste finita la sua derivata nel punto c. Per il significato geometrico della derivata ciò significa che esiste ed
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Prodotto scalare e norma
 Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Derivate delle funzioni di una variabile.
 Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Curve e lunghezza di una curva
 Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
7.5 Il caso vincolato: preliminari
 7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
1 Equazioni parametriche e cartesiane di sottospazi affini di R n
 2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
2 Trapani Dispensa di Geometria, Equazioni parametriche e cartesiane di sottospazi affini di R n Un sottospazio affine Σ di R n e il traslato di un sottospazio vettoriale. Cioe esiste un sottospazio vettoriale
Richiami sullo studio di funzione
 Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3
![Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3](/thumbs/69/60553365.jpg) 1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
Esercizi sulle funzioni di due variabili: parte II
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
2. I numeri reali e le funzioni di variabile reale
 . I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
. I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
GEOMETRIA ANALITICA
 GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LE EQUAZIONI DIFFERENZIALI. che, insieme alle loro derivate, soddisfano un equazione differenziale.
 LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
LEZIONE 13. Figura 13.1
 LEZIONE 3 Ritorniamo al nostro rettangolo R di vertici A = (, ), B = (, ), C = (, 3), D = (, 3) a partire dal segmento OU unitario di estremi l origine O ed il punto U = (, ). y D C R A B O Figura 3. Tra
LEZIONE 3 Ritorniamo al nostro rettangolo R di vertici A = (, ), B = (, ), C = (, 3), D = (, 3) a partire dal segmento OU unitario di estremi l origine O ed il punto U = (, ). y D C R A B O Figura 3. Tra
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
