Matematica finanziaria: svolgimento prova di esonero del 15 maggio 2007
|
|
|
- Martino Gasparini
- 8 anni fa
- Visualizzazioni
Transcript
1 Matematica finanziaria: svolgimento prova di esonero del 5 maggio 2 a. Assumendo che il colore dei capelli negli esseri umani sia determinato da una coppia di alleli, diciamo (B, S), presi a caso con probabilità 2, 2 } uno dalla madre e uno dal padre, in maniera tale che si è biondi se e soltanto se entrambi gli alleli sono B, e sapendo che: sia Bobo che Bubi hanno i capelli scuri; le coppie di alleli sono equiprobabili; la scelta di un allele da un genitore non influenza la scelta del secondo allele dell altro genitore; determinare la probabilità che il figlio di Bobo e Bubi sia biondo. Svolgimento. Denotiamo con S e B rispettivamente l allele relativo al capello scuro e l allele relativo al capello biondo, e con la coppia ordinata (, ) gli alleli presenti in un individuo (per convenzione, decidiamo che il primo rappresenti l allele paterno e il secondo l allele materno). Le possibili combinazioni di alleli in Bobo e Bubi sono allora (S, S), (S, B), (B, S)} (punto ) e ciascuna di esse ha probabilità (punto 2). Abbiamo allora: Probfiglio biondo} dal testo = Proballele preso da Bobo = B e allele preso da Bubi = B} punto = Proballele preso da Bobo = B}Proballele preso da Bubi = B}. Calcoliamo allora Proballele preso da Bobo = B}. Se sapessimo quali sono gli alleli di Bobo, sarebbe fatta! Ad esempio, se gli alleli di Bobo fossero (S, B), la probabilità che il figlio di Bobo (Bebe) abbia preso dal padre l allele B sarebbe 2 (come specificato nel testo). Ma questo è proprio un lavoro da probabilità condizionata: io conosco le probabilità che mi servono condizionate alla conoscenza degli alleli di Bobo! Usando la relazione ProbX} = ProbX Y }ProbY } + + ProbX Y n }ProbY n } valida se Y,..., Y n sono eventi disgiunti ed esaustivi ottengo Proballele preso da Bobo = B} = Proballele preso da Bobo = B alleli Bobo = (S, S)}Proballeli Bobo = (S, S)} + Proballele preso da Bobo = B alleli Bobo = (S, B)}Proballeli Bobo = (S, B)} + Proballele preso da Bobo = B alleli Bobo = (B, S)}Proballeli Bobo = (B, S)} = = Quindi la probilità che Bebe abbia preso da Bobo proprio l allele B è, e lo stesso vale per la probilità che Bebe abbia preso da Bubi proprio l allele B (abbiamo infatti esattamente le stesse informazioni su Bobo e Bubi). Quindi la probabilità cercata è ProbBebe biondo} = Proballele preso da Bobo = B}Proballele preso da Bubi = B} = = 9 b. Frugando in soffitta tra ricordi di famiglia, Bobo trova una foto dei suoi genitori, nella quale si vede chiaramente che il suo babbo è biondo! Con questa nuova informazione, determinare la probabilità che il figlio di Bobo e Bubi sia biondo. Svolgimento. Come nell esercizio precedente, ma questa volta l informazione è asimmetrica: il babbo di di Bobo è biondo, quindi le possibili combinazioni di alleli in Bobo sono (B, S)} (il primo allele -quello preso dal babbo- deve essere per forza B!). Abbiamo quindi: ProbBebe biondo} = Proballele preso da Bobo = B}Proballele preso da Bubi = B} = 2 = 6 2. Vicino alla foto dei suoi genitori, Bobo trova un obbligazione acquistata anni prima dal babbo, di valore facciale e, remunerata con cedole annuali del 2%, con vita residua anni e 2 mesi. Un amico di Bubi -un giapponese biondo di nome BoBan- propone a Bobo l acquisto dell obbligazione per 2e. Bobo usa un tasso di valutazione del %, pertanto pensa:... il titolo dura ancora anni e rotti, quindi incasserò cedole e il valore facciale, cioè 6e, che scontati al % su 8 mesi diventano 8.6e... e accetta l offerta di BoBan. Sapendo che: O meglio, le scelte degli alleli sono indipendenti.
2 queste obbligazioni vengono rimborsate progressivamente in maniera uniforme; l obbligazione trovata da Bobo non è stata ancora rimborsata; determinare: (a) la probabilità che il rimborso avvenga esattamente tra 2 mesi; (b) il valore al tempo del titolo con il criterio del valor medio, usando un tasso di valutazione del % annuo; (c) i 2 errori nel ragionamento di Bobo. Svolgimento. L obbligazione trovata da Bobo fornisce cedole di 2 l una (il 2% di è 2), e verrà rimborsata tra 2 mesi, anno e 2 mesi, 2 anni e 2 mesi o anni e 2 mesi con probabilità 4 (questo è il significato di rimborso progressivo uniforme ). La variabile aleatoria rimborso tra due mesi è quindi (2, 4 ), (2, 4 )}, mentre quella rimborso tra un anno e due mesi è (2, 4 ), (, 4 ), (2, 2 4 )} e così via. Il grafico di evoluzione temporale dell obbligazione è allora: (2, 4 ),(2, 4 )} /6 (2, 4 ),(, 4 ),(2, 2 4 )} /6 (2, 4 ),(, 2 4 ),(2, 4 )} /6 (2, 4 ),(, 4 )} 9/6 dove abbiamo scelto di rappresentare il tempo in anni (e dunque due mesi sono /6 di anno) in quanto tutte le quantità sono annuali! Fatto questo, le prime due risposte sono immediate: (a) è 4, mentre per (b) calcoliamo i valori medi delle variabili aleatorie e otteniamo: 45 /6 4 /6 5 /6 Usando come detto nel testo il fattore di sconto ν =., il valore al tempo viene: 45ν /6 + 4ν /6 + 5ν /6 + ν 9/6 =.5 Per quanto riguarda gli errori di Bobo, bisogna per prima cosa capire che ragionamento ha fatto! Il suo pensiero è:... il titolo dura ancora anni e rotti, quindi incasserò cedole [... ] -primo errore, le cedole sono 4, non! Poi pensa: [... ] e il valore facciale, cioè 6e[... ] -secondo errore, se anche ci fossero cedole da 2 l una (notare che Bobo sta diventando bravo, ha saputo calcolare bene il 2% di ) non si possono sommare quantità presenti a tempi differenti senza prima scontare opportunamente! È un errore gravissimo! Infine Bobo dice: [... ] che scontati al % su 8 mesi diventano 8.6e..., e questo conto è giusto. Bobo ha fatto anche un terzo errore: invece di applicare il criterio del valor medio, ha risolto l incertezza assumendo che l obbligazione venga rimborsata per ultima!. Sempre nei ricordi di famiglia, Bobo trova uno scambio di lettere tra i suoi genitori nel quale entrambi appaiono desiderare per Bobo una carriera da astronauta! Bobo decide pertanto di iscriversi a un master in astronautologia, che gli costerà subito 5e, e altri 5e tra 2 anni. Questo master, se frequentato con successo, gli garantirà, a partire dal prossimo anno, 4 rimborsi spese annuali di e ciascuno per la partecipazione a un tirocinio. (a) Dire se esiste, e nel caso calcolare al meglio di 2 cifre decimali, il tir di questa operazione finanziaria. (b) Assumendo che Bobo possieda al tempo solo 2e, e che sia possibile investire e prendere denaro in prestito al 5%, calcolare il rea al 5%. (c) Si poteva capire il segno del rea del punto precedente senza fare calcoli? Svolgimento. Solita evoluzione temporale dell operazione finanziaria che Bobo sta per affrontare: Per rispondere ad (a), usiamo Norström: le somme parziali 5, 2, 4,, 2} hanno primo termine negativo, ultimo termine positivo, e cambiano segno una volta sola! Quindi il tir esiste (e Norström ci dice anche che è positivo). Per calcolarlo dobbiamo risolvere l equazione nell incognita ν rea(ν) =, che scritta esplicitamente è: 5 + ν 2ν 2 + ν + ν 4 =. 9/6 4
3 rea(ν) f().88 ν.885 ν f() Figura : Grafico approssimativo della funzione rea(ν). Dopo opportuna semplificazione l equazione diventa 5 + ν 2ν 2 + ν + ν 4 =, ed è chiaro che tale equazione non è risolvibile in maniera esatta, almeno a prima vista. Usiamo quindi il metodo della bisezione, che fornisce una soluzione ν con l approssimazione che meglio crediamo. Detto f(ν) il polinomio 5 + ν 2ν 2 + ν + ν 4, abbiamo f() < e f() >. Il calcolo di f(ν) per ν =.88 e ν =.89 fornisce ν [.88,.89], e volendo decidere se approssimare per eccesso o per difetto calcoliamo anche f(.885) >, da cui ν =.88 (vedi figura ) e finalmente i = ν =.4. Il punto (b) è ingannevole: apparentemente richiede di calcolare il rea al 5% con una normalizzazione finanziaria dovuta al fatto che Bobo non possiede il capitale necessario per iscriversi al master, e quindi dovrà prendere in prestito quel che gli manca. Inoltre, il fatto che venga dato un tasso di investimento porta a pensare di dover investire le entrate dell operazione finanziaria man mano che queste si presentano. Facciamo quello che abbiamo appena detto, aggiungendo al grafico di prima anche il prestito al tempo di 8 (Bobo aveva di suo solo 2, e il master costa 5), l investimento al tempo di, il ritiro al tempo 2 di parte del montante di quanto investito al tempo per pagare gli altri 5 richiesti, e così via. Indicando con i f e i r i tassi rispettivamente di finanziamento e reinvestimento, abbiamo: (( + i r ) 2) ( + i r ) 2 ( + i r ) (( + i r ) 2)( + i r ) ( + i f ) Più facile dirlo che scriverlo: a ogni scadenza non voglio avere soldi inutilizzati, quindi investo al tasso i r tutto quel che entra, e se devo pagare qualcosa lo prelevo dai soldi che ho investito alla scadenza precedente. Alla fine pago i debiti che ho dovuto contrarre nel corso dell operazione finanziaria al tasso i f (in questo caso solo i 8 che abbiamo preso in prestito all inizio). Quindi a ogni scadenza avremo, e l operazione finanziaria diventa: 2 K 2 4 dove ho indicato con K la somma di tutte le entrate e uscite al tempo 4: Il valore attuale al tasso i v è allora: K = 8( + i f ) 4 + ( + i r ) 2( + i r ) 2 + ( + i r ) +. rea(i v ) = 8( + i f ) 4 + ( + i r ) 2( + i r ) 2 + ( + i r ) + ( + i v ) 4 2
4 È chiaro allora che se i f, i r e i v sono gli stessi tutto quel che abbiamo fatto è stato inutile: capitalizzare al tasso i r o i f per poi scontare al tasso i v significa non fare nulla, quando tutti i tassi sono uguali! Formalmente, denotando il tasso comune del 5% con i: rea(i) = 8( + i)4 + ( + i) 2( + i) 2 + ( + i) + ( + i) 4 2 = i 2 ( + i) 2 + ( + i) + ( + i) 4 2 = i 2 ( + i) 2 + ( + i) + ( + i) 4 = 25.8 e quest ultimo è proprio il rea che avrei ottenuto direttamente se non avessi fatto alcuna normalizzazione! Questo esercizio insegna dunque che se i tassi di finanziamento, reinvestimento e valutazione coincidono, non serve alcuna normalizzazione! Per concludere, il punto (c): certo che potevamo capire il segno del rea! Calcolare il rea al 5% significa confrontare l operazione finanziaria con l ipotesi alternativa di investire i propri capitali al 5%. Ma abbiamo calcolato che l operazione finanziaria rende il 4%, quindi non è conveniente rispetto a un investimento al 5%: il rea deve pertanto rifiutarla, cioè deve venire negativo! Solo corso da 6 crediti 4. Bobo non supera neanche gli esami del primo anno del master. Dovendo quindi far fronte a vari debiti 2, decide di fare quello che in fondo è il suo mestiere: investire in borsa su titoli rischiosi, e in quanto tali altamente redditizi! Constatato che il tasso privo di rischio è del 5% mensile, Bobo trova una call europea con prezzo d esercizio 95 e scadenza tra mese, e viene a sapere da fonti certe che il prezzo del sottostante, che ora è e, nel prossimo mese potrà solo salire del % con probabilità.9, o scendere del % con probabilità.. Bobo (che evidentemente non ha mai sentito parlare di modello binomiale) pensa:... questa call mi darà tra mese 5e con probabilità.9, quindi tra mese varrà.5e, e pertanto adesso vale 2.86e.... Accetta quindi l offerta di BoBan, che gentilmente gliele vende al prezzo di 2e l una. (a) Calcolare il valore della call con l ipotesi di non-arbitraggio. (b) Determinare la composizione in azioni e soldi di un portafoglio capace di replicare la call a scadenza. (c) Determinare una strategia d arbitraggio per BoBan. (d) Determinare quante call BoBan deve vendere a Bobo per guadagnare esattamente 9 e. (e) Spiegare il ragionamento di Bobo e trovare l errore. Svolgimento. Le domande (a), (b) e (c) sono tutte collegate tra loro: il valore della call è univocamente determinato dall esigenza di avere un mercato coerente (cioè privo di possibilità di arbitraggio), e nel caso questo non accada (ovvero, se per caso il prezzo proposto da BoBan non è quello giusto!) è possibile comprare e vendere lo stesso prodotto sotto forme diverse -la call e il portafoglio replicante-, ovviamente comprando quello che costa meno e vendendo quello che costa di più. Fatta questa premessa, osserviamo che visto che BoBan vende la call al prezzo di 2, e visto il testo della domanda (c), possiamo inferire che il prezzo della call calcolato affiché non ci sia arbitraggio verrà minore di 2, e BoBan potrà diventare ricco comprando il portafoglio replicante che poi a scadenza userà come se fosse una call! Dalla teoria conosciamo due metodi per il calcolo del valore di una call europea con sottostante che non fornisce dividendi: valor medio neutrale al rischio attualizzato e valore al tempo del portafoglio replicante. A scopo didattico, usiamo entrambi i metodi. Metodo : mondo neutrale al rischio. Sappiamo che il criterio del valor medio (quello che usa Bobo) non si può usare nella valutazione dei titoli derivati, perché fornisce un prezzo sbagliato (dove sbagliato significa che genera possibilità di arbitraggio). C è però un eccezione: se usiamo delle probabilità particolari, dette neutrali al rischio, questo metodo funziona! Detti u e d i fattori moltiplicativi di evoluzione del prezzo del sottostante, ed r il fattore di rendimento privo di rischio, le probabilità neutrali al rischio π e ρ sono date da π = r d u d ρ = u r u d Particolarizzando al nostro esercizio, otteniamo u =. (aumentare un prezzo del % vuol dire moltiplicare quel prezzo per.), d =.9 (diminuire un prezzo del % vuol dire moltiplicare quel prezzo per.9), e r = +.5 =.5. Controlliamo che le unità di misura dei tempi siano tutte coerenti tra loro -lo sono: il 2 Il finanziamento di 8e chiesto per iscriversi al master, gli oltre e che deve pagare per le fragole comprate nell esonero scorso, le spese per il figlio Bebe...
5 Valore sottostante = Valore call = 5 Valore sottostante = Valore sottostante = 9 Valore call = Figura 2: Valori call/sottostante su un albero ad uno stadio. Valore sottostante = Valore call = 5 Valore sottostante = Valore portafoglio = +.5L Valore portafoglio = + L Valore sottostante = 9 Valore call = Valore portafoglio = 9 +.5L Figura : Valori call/sottostante su un albero ad uno stadio. tasso privo di rischio è mensile, e l evoluzione binomiale del sottostante è data mensilmente- e andiamo avanti. Otteniamo le probabilità neutrali al rischio π = r d u d = 4 ρ = u r u d = 4 che dobbiamo usare per calcolare il valor medio del payoff della call. Quant è il payoff della call? Se il prezzo del sottostante sale del %, diventerà, e il possessore della call potrà avere ciò che vale al prezzo di 95, guadagnandoci 5. Se il prezzo del sottostante scende del %, diventerà 9, e il possessore della call non comprerà a 95 ciò che potrebbe avere a 9: pertanto il valore della call sarà! Tutto questo si sintetizza in genere nel grafico ad albero in figura 2. Il criterio del valor medio valido solo se usiamo le probabilità neutrali al rischio dice che possiamo calcolare il valore dell opzione semplicemente come valor medio dei suoi payoff (5 con probabilità 4 e con probabilità 4 ), dunque: valor medio call tra mese = = 45 4 Poiché noi vogliamo il valore della call ora, e non tra un mese, dobbiamo attualizzare al tasso privo di rischio: valore call al tempo = = = 45 5 = 5 2 Prima di andare avanti, osserviamo che la domanda (d) chiede di calcolare quante call deve vendere BoBan per guadagnare 9 : quindi siamo ben felici di avere trovato un prezzo per la call con al denominatore, e ci guardiamo bene dall eseguire la divisione! Dunque il prezzo giusto per la call è 5 84, chiaramente minore del prezzo offerto da BoBan = 2. Ogni call venduta da BoBan a Bobo frutterà a BoBan 84 5 = 9, e quindi la risposta alla domanda (d) è. Il metodo 2 per calcolare il valore della call è la costruzione di un portafoglio replicante, cioè di un portafoglio di azioni e contante che al tempo finale sia equivalente alla call. Diciamo il numero di azioni contenute in questo portafoglio, e L il contante. Il portafoglio al tempo vale + L, mentre il suo valore al tempo dipende da cosa succede al sottostante: se l azione sarà salita, il portafoglio varrà +.5L, mentre nel caso in cui l azione sarà scesa, il portafoglio varrà 9 +.5L. Analogamente, la call varrà 5 o. Questo si sintetizza ancora con un grafico ad albero (figura ). Richiedere che il portafoglio replichi la call a scadenza significa richiedere che il valore del portafoglio a scadenza sia 5 o se l azione è salita o scesa, e questo significa richiedere che il seguente sistema sia soddisfatto: +.5L = L = Il determinante del sistema è.5( 9), quindi abbiamo un unica soluzione (, L), corrispondente ad un unica composizione di portafoglio. Risolviamo il sistema con il metodo che più ci aggrada (qui uso Cramer): = = L = = = 45
6 da cui il valore in del portafoglio (che deve essere il valore in della call, visto che a scadenza sono equivalenti!): valore portafoglio in = = 5 = che è proprio il valore della call trovato con le probabilità neutrali al rischio! Ricapitoliamo cosa abbiamo fatto. Abbiamo trovato il valore della call in con due metodi (domanda (a)) e il secondo metodo ha comportato la costruzione di un portafoglio replicante (domanda (b)). Nel frattempo abbiamo osservato che ciascuna call del valore di 5 venduta a 2 comporta per il venditore un guadagno di 2 5, e con questa informazione abbiamo dato la risposta alla domanda (d). Rimane la domanda (c), alla quale abbiamo risposto parzialmente: l arbitraggio richiesto è vendita call-acquisto portafoglio, che si sintetizza in genere con il seguente grafico di evoluzione temporale (indichiamo con C( ) e P ( ) il valore della call e del portafoglio rispettivamente): C() = 2 P () = ( + L) = = 5 C() P () = 2 5 = 9 C() = ( 5,.9), (,.)} P () = (5,.9), (,.)} P () C() = = 5 vendita call acquisto portafoglio totale Infine, la domanda (e): cosa ha pensato Bobo? Ha usato il criterio del valor medio con le probabilità soggettive che gli erano state date (.9 e.), e questo metodo non funziona mai a meno che le probabilità scelte non siano proprio quelle neutrali al rischio! Solo corso da crediti 5. Bobo non supera neanche gli esami del primo anno del master. Dovendo quindi far fronte a vari debiti, decide di fare quello che in fondo è il suo mestiere: investire in borsa su titoli rischiosi, e in quanto tali altamente redditizi! Constatato che il tasso privo di rischio è del 5% mensile, Bobo trova una call europea con prezzo d esercizio e scadenza tra mesi, e viene a sapere da fonti certe che il prezzo del sottostante, che ora è e, nei prossimi mesi potrà ogni mese solo salire del % con probabilità.9, o scendere del % con probabilità.. Bobo (che evidentemente non ha mai sentito parlare di modello binomiale) pensa:... questa call tra mesi mi darà mediamente 6.84e, e pertanto adesso vale 4.55e.... Accetta quindi l offerta di BoBan, che gentilmente gliele vende al prezzo di 4e l una. (a) Calcolare il valore della call con l ipotesi di non-arbitraggio (formula di Cox-Ross-Rubinstein). (b) Descrivere nel modo più chiaro possibile un portafoglio dinamico composto da azioni e soldi capace di replicare la call a scadenza. (c) Dire quanto guadagna BoBan per ogni call venduta a Bobo. (d) Spiegare il ragionamento di Bobo, trovare l errore, e dire in quale caso il suo ragionamento avrebbe prodotto il risultato corretto per C(). Svolgimento. Questo esercizio è una versione più elaborata del precedente: si usano le stesse tecniche sui singoli periodi, che in questo caso sono. Per capire questo svolgimento, è necessario prima aver capito lo svolgimento dell esercizio precedente! Come prima cosa, disegniamo il grafo (vedi figura 4) contenente sottostante e call, e denotiamo per maggiore chiarezza il valore del sottostante e della call rispettivamente con A( ) e C( ). L esercizio chiede essenzialmente di trovare tutti i punti interrogativi. Una prima osservazione che facciamo è che alcuni di questi punti interrogativi sono, visto che comunque vada a partire da li si otterrà come valore finale della call: otteniamo perciò la figura 5. La domanda (a) richiede l utilizzo della formula di Cox-Ross-Rubinstein: C() = n ( ) n r n C u n j d j π n j ρ j j j= = ( ) ( ).5 (C u π + C u2 d π 2 ρ + C ud 2 = = 8.42 ( ) πρ 2 + C d 2 ( ) ρ ) Il finanziamento di 8e chiesto per iscriversi al master, gli oltre e che deve pagare per le fragole comprate nell esonero scorso, le spese per il figlio Bebe...
7 A() =. C() = C u = 2. A(2) = 2 C(2) =? A() = A() = 8.9 C() =? C() = C u 2 d = A() = A(2) = 99 C() =? C(2) =? A() = 9 A() = 89. C() =? C() = C ud 2 = A(2) = 8 C(2) =? A() = 2.9 C() = C d = Figura 4: Valori call/sottostante su periodi. A() =. C() = C u = 2. A(2) = 2 C(2) =? A() = A() = 8.9 C() =? C() = C u 2 d = A() = A(2) = 99 C() =? C(2) = A() = 9 A() = 89. C() = C() = C ud 2 = A(2) = 8 C(2) = A() = 2.9 C() = C d = Figura 5: Valori call/sottostante su periodi, riempita con i valori evidenti.
8 A() =. C() = C u = 2. A(2) = 2 P () =. +.5L C(2) =? P (2) = 2 + L A() = 8.9 C() = C u 2 d = P () = L Figura 6: Sottografo della figura 5. A() = C() =? P () = + L Figura : Sottografo 2 della figura 5. A(2) = 2 C(2) = C u 2 = 6.5 P (2) = 2 +.5L A(2) = 99 C(2) = C ud = P (2) = L La domanda (b) richiede il calcolo delle coppie (, L) alle scadenze, e 2, ovvero richiede di applicare quanto fatto nell esercizio precedente al sottografo dato in figura 6: Per trovare C u 2 dobbiamo quindi risolvere il seguente sistema:. +.5L = L = = L = 99 e corrispondentemente C u 2 = = 6.5. Il sistema successivo sarà allora associato al sottografo dato in figura da cui 2 +.5L = 6.5 = L = L =.4 C() = C u =.5.4 =.85 Infine, abbiamo la figura 8 da cui +.5L = L = = L = 5.5 C() = = 8.42 che è lo stesso valore dato dalla formula di Cox-Ross-Rubinstein! La descrizione del portafoglio dinamico replicante della call è dunque la seguente: al tempo acquisto azioni e prendo in prestito 5.5. Al tempo, se l azione è salita compro altre =.65 azioni, e per questo devo prendere in prestito altri.65 =.68, portando così l ammontare del debito a =.4 (che guarda caso è proprio il valore di L al periodo!). Se l azione al tempo è scesa, liquido il portafoglio: ovvero, vendo le azioni a 9 l una, ottenendo = 5.5, e pago il debito di = 5.5, rimanendo in pari (infatti in questo caso la call vale ). Al tempo 2, se l azione è ancora salita, compro ancora = azioni, spendendo = 24.5 portando così l ammontare del debito a = Se al tempo l azione è ancora salita, liquido il portafoglio e ottengo = 2.5 dalla vendita delle azioni, e devo restituire =.95, ottenendo infine = 2., che è esattamente il payoff della call nel caso u. A() = C() =? P () = + L Figura 8: Sottografo della figura 5. A() = C() = C u =.85 P () = +.5L A() = 9 C() = C d = P () = 9 +.5L
9 Per quanto riguarda (c), BoBan vende a 4 qualcosa che vale 8.42, quindi guadagna per ciascuna di queste transazioni = Per ultimo, il ragionamento di Bobo: evidentemente ha applicato il criterio del valor medio con le probabilità assegnate nel testo. L unico caso in cui avrebbe avuto il risultato corretto sarebbe stato nel caso in cui le probabilità assegnate avessero coinciso con le probabilità neutrali al rischio.
Matematica finanziaria: svolgimento della prova di esame del 4 settembre 2007 1
 Matematica finanziaria: svolgimento della prova di esame del 4 settembre. Calcolare il montante che si ottiene dopo anni con un investimento di e in regime nominale al tasso annuale del % pagabile due
Matematica finanziaria: svolgimento della prova di esame del 4 settembre. Calcolare il montante che si ottiene dopo anni con un investimento di e in regime nominale al tasso annuale del % pagabile due
Matematica finanziaria: svolgimento prova di esame del 21 giugno 2005 (con esercizio 1 corretto)
 Matematica finanziaria: svolgimento prova di esame del giugno 5 (con esercizio corretto). [6 punti cleai, 6 punti altri] Si possiede un capitale di e e lo si vuole impiegare per anni. Supponendo che eventuali
Matematica finanziaria: svolgimento prova di esame del giugno 5 (con esercizio corretto). [6 punti cleai, 6 punti altri] Si possiede un capitale di e e lo si vuole impiegare per anni. Supponendo che eventuali
Pertanto la formula per una prima approssimazione del tasso di rendimento a scadenza fornisce
 A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
Matematica finanziaria: svolgimento della prova di esonero del 28 marzo 2007
 Matematica finanziaria: svolgimento della prova di esonero del 28 marzo 27. Bobo e Bubi affrontano la loro prima crisi familiare a causa della mancanza di una lavastoviglie. Decidono pertanto di acquistarne
Matematica finanziaria: svolgimento della prova di esonero del 28 marzo 27. Bobo e Bubi affrontano la loro prima crisi familiare a causa della mancanza di una lavastoviglie. Decidono pertanto di acquistarne
Matematica finanziaria: svolgimento prova di esame del 5 luglio 2005
 Matematica finanziaria: svolgimento prova di esame del 5 luglio 5. [5 punti cleai, 5 punti altri] Prestiamo e a un amico. Ci si accorda per un tasso di remunerazione del 6% annuale (posticipato), per un
Matematica finanziaria: svolgimento prova di esame del 5 luglio 5. [5 punti cleai, 5 punti altri] Prestiamo e a un amico. Ci si accorda per un tasso di remunerazione del 6% annuale (posticipato), per un
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Una percentuale di una certa importanza nel mondo economico è il tasso di interesse. Il tasso di
 Capitalizzazione e attualizzazione finanziaria Una percentuale di una certa importanza nel mondo economico è il tasso di interesse. Il tasso di interesse rappresenta quella quota di una certa somma presa
Capitalizzazione e attualizzazione finanziaria Una percentuale di una certa importanza nel mondo economico è il tasso di interesse. Il tasso di interesse rappresenta quella quota di una certa somma presa
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
ESERCITAZIONE MATEMATICA FINANZIARIA OPZIONI. Matematica finanziaria Dott. Andrea Erdas Anno Accademico 2011/2012
 ESERCITAZIONE MATEMATICA FINANZIARIA 1 OPZIONI 2 LE OPZIONI Le opzioni sono contratti che forniscono al detentore il diritto di acquistare o vendere una certa quantità del bene sottostante a una certa
ESERCITAZIONE MATEMATICA FINANZIARIA 1 OPZIONI 2 LE OPZIONI Le opzioni sono contratti che forniscono al detentore il diritto di acquistare o vendere una certa quantità del bene sottostante a una certa
COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013. - Come cambia il REA atteso se l'obbligazione sarà ancora in vita dopo le prime tre estrazioni?
 UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
COMPLEMENTI SULLE LEGGI FINANZIARIE
 COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
Macroeconomia, Esercitazione 2. 1 Esercizi. 1.1 Moneta/1. 1.2 Moneta/2. 1.3 Moneta/3. A cura di Giuseppe Gori (giuseppe.gori@unibo.
 acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016. 1. Esercizi 4
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi 4 Piani di ammortamento Esercizio 1. Un debito di 1000e viene rimborsato a tasso annuo i = 10%
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi 4 Piani di ammortamento Esercizio 1. Un debito di 1000e viene rimborsato a tasso annuo i = 10%
Matematica Finanziaria A - corso part time prova d esame del 21 Aprile 2010 modalità A
 prova d esame del 21 Aprile 2010 modalità A 1. Un tizio ha bisogno di 600 euro che può chiedere, in alternativa, a due banche: A e B. La banca A propone un rimborso a quote capitale costanti mediante tre
prova d esame del 21 Aprile 2010 modalità A 1. Un tizio ha bisogno di 600 euro che può chiedere, in alternativa, a due banche: A e B. La banca A propone un rimborso a quote capitale costanti mediante tre
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
TRACCE DI MATEMATICA FINANZIARIA
 TRACCE DI MATEMATICA FINANZIARIA 1. Determinare il capitale da investire tra tre mesi per ottenere, nel regime dello sconto commerciale, un montante di 2800 tra tre anni e tre mesi sapendo che il tasso
TRACCE DI MATEMATICA FINANZIARIA 1. Determinare il capitale da investire tra tre mesi per ottenere, nel regime dello sconto commerciale, un montante di 2800 tra tre anni e tre mesi sapendo che il tasso
studi e analisi finanziarie LA PUT-CALL PARITY
 LA PUT-CALL PARITY Questa relazione chiarisce se sia possibile effettuare degli arbitraggi e, quindi, guadagnare senza rischi. La put call parity è una relazione che lega tra loro: il prezzo del call,
LA PUT-CALL PARITY Questa relazione chiarisce se sia possibile effettuare degli arbitraggi e, quindi, guadagnare senza rischi. La put call parity è una relazione che lega tra loro: il prezzo del call,
Il sistema monetario
 Il sistema monetario Premessa: in un sistema economico senza moneta il commercio richiede la doppia coincidenza dei desideri. L esistenza del denaro rende più facili gli scambi. Moneta: insieme di tutti
Il sistema monetario Premessa: in un sistema economico senza moneta il commercio richiede la doppia coincidenza dei desideri. L esistenza del denaro rende più facili gli scambi. Moneta: insieme di tutti
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL
 LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
Matematica Finanziaria Soluzione della prova scritta del 15/05/09
 Matematica Finanziaria Soluzione della prova scritta del 15/05/09 ESERCIZIO 1 Il valore in t = 60 semestri dei versamenti effettuati dall individuo è W (m) = R(1 + i 2 ) m + R(1 + i 2 ) m 1 +... R(1 +
Matematica Finanziaria Soluzione della prova scritta del 15/05/09 ESERCIZIO 1 Il valore in t = 60 semestri dei versamenti effettuati dall individuo è W (m) = R(1 + i 2 ) m + R(1 + i 2 ) m 1 +... R(1 +
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti. Enrico Saltari Università di Roma La Sapienza
 MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
Capitolo Terzo Valore attuale e costo opportunità del capitale
 Capitolo Terzo Valore attuale e costo opportunità del capitale 1. IL VALORE ATTUALE La logica di investimento aziendale è assolutamente identica a quella adottata per gli strumenti finanziari. Per poter
Capitolo Terzo Valore attuale e costo opportunità del capitale 1. IL VALORE ATTUALE La logica di investimento aziendale è assolutamente identica a quella adottata per gli strumenti finanziari. Per poter
Le basi della Partita Doppia in 1.000 parole Facile e comprensibile. Ovviamente gratis.
 Le basi della Partita Doppia in 1.000 parole Facile e comprensibile. Ovviamente gratis. Qual è la differenza tra Dare e Avere? E tra Stato Patrimoniale e Conto Economico? In 1.000 parole riuscirete a comprendere
Le basi della Partita Doppia in 1.000 parole Facile e comprensibile. Ovviamente gratis. Qual è la differenza tra Dare e Avere? E tra Stato Patrimoniale e Conto Economico? In 1.000 parole riuscirete a comprendere
Il concetto di Dare/Avere
 NISABA SOLUTION Il concetto di Dare/Avere Comprendere i fondamenti delle registrazioni in Partita Doppia Sara Mazza Edizione 2012 Sommario Introduzione... 3 Il Bilancio d Esercizio... 4 Stato Patrimoniale...
NISABA SOLUTION Il concetto di Dare/Avere Comprendere i fondamenti delle registrazioni in Partita Doppia Sara Mazza Edizione 2012 Sommario Introduzione... 3 Il Bilancio d Esercizio... 4 Stato Patrimoniale...
IL CAPITALE. 1) Domanda di capitale 2) Offerta di capitale
 IL CAPITALE 1) Domanda di capitale 2) Offerta di capitale CAPITALE FINANZIARIO E CAPITALE REALE Col termine capitale i si può riferire a due concetti differenti Il capitale finanziario è costituito dalla
IL CAPITALE 1) Domanda di capitale 2) Offerta di capitale CAPITALE FINANZIARIO E CAPITALE REALE Col termine capitale i si può riferire a due concetti differenti Il capitale finanziario è costituito dalla
INTRODUZIONE I CICLI DI BORSA
 www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Esercizio 1 Calcolare il montante F di 10.000 con un interesse semplice del 15% annuo, dopo 4 anni. [16.000 ]
![Esercizio 1 Calcolare il montante F di 10.000 con un interesse semplice del 15% annuo, dopo 4 anni. [16.000 ] Esercizio 1 Calcolare il montante F di 10.000 con un interesse semplice del 15% annuo, dopo 4 anni. [16.000 ]](/thumbs/25/5413969.jpg) Esercizio 1 Calcolare il montante F di 10.000 con un interesse semplice del 15% annuo, dopo 4 anni. [16.000 ] Esercizio 2 Del precedente esercizio calcolare il montante in regime di capitalizzazione composta.
Esercizio 1 Calcolare il montante F di 10.000 con un interesse semplice del 15% annuo, dopo 4 anni. [16.000 ] Esercizio 2 Del precedente esercizio calcolare il montante in regime di capitalizzazione composta.
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti
 Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti 1. Un capitale d ammontare 100 viene investito, in regime di interesse semplice, al tasso annuo
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti 1. Un capitale d ammontare 100 viene investito, in regime di interesse semplice, al tasso annuo
Le Scelte Finanziarie. S. Corsaro Matematica Finanziaria a.a. 2007/08
 Le Scelte Finanziarie 1 Tasso Interno di Rendimento Consideriamo un operazione finanziaria (t 0 =0): 0 x 0 t 1 t 2 t m...... x 1 x 2 x m Posto: x = x0, x1,, xm { } si definisce tasso interno di rendimento
Le Scelte Finanziarie 1 Tasso Interno di Rendimento Consideriamo un operazione finanziaria (t 0 =0): 0 x 0 t 1 t 2 t m...... x 1 x 2 x m Posto: x = x0, x1,, xm { } si definisce tasso interno di rendimento
Calcolare i Rendimenti di Titoli Obbligazionari a tasso fisso con flusso cedolare costante (tipo BTP)
 Calcolare i Rendimenti di Titoli Obbligazionari a tasso fisso con flusso cedolare costante (tipo BTP) Nel caso dei btp (o di altri titoli analoghi) bisogna inserire i seguenti valori: Data di acquisto:
Calcolare i Rendimenti di Titoli Obbligazionari a tasso fisso con flusso cedolare costante (tipo BTP) Nel caso dei btp (o di altri titoli analoghi) bisogna inserire i seguenti valori: Data di acquisto:
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016. 1. Esercizi 3
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi 3 Piani di ammortamento Esercizio 1. Un prestito di 12000e viene rimborsato in 10 anni con rate
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi 3 Piani di ammortamento Esercizio 1. Un prestito di 12000e viene rimborsato in 10 anni con rate
Equivalenza economica
 Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
Valore attuale, obiettivi dell impresa e corporate governance. dott. Matteo Rossi
 Valore attuale, obiettivi dell impresa e corporate governance dott. Matteo Rossi Prospetto F/I Happy Finance Conto Economico 2008 2009 Reddito Netto 350-500 Ammortamenti 800 800 Accantonamenti 2000 300
Valore attuale, obiettivi dell impresa e corporate governance dott. Matteo Rossi Prospetto F/I Happy Finance Conto Economico 2008 2009 Reddito Netto 350-500 Ammortamenti 800 800 Accantonamenti 2000 300
Come si individua il cheapest to delivery per il future obbligazionario nel basket di bonds sottostanti
 Come si individua il cheapest to delivery per il future obbligazionario nel basket di bonds sottostanti Come calcolare il rendimento del future di un bond (btp bund oat tnote, ecc) in funzione del prezzo
Come si individua il cheapest to delivery per il future obbligazionario nel basket di bonds sottostanti Come calcolare il rendimento del future di un bond (btp bund oat tnote, ecc) in funzione del prezzo
Il modello binomiale ad un periodo
 Opzioni Un opzione dà al suo possessore il diritto (ma non l obbligo) di fare qualcosa. Un opzione call (put) europea su un azione che non paga dividendi dà al possessore il diritto di comprare (vendere)
Opzioni Un opzione dà al suo possessore il diritto (ma non l obbligo) di fare qualcosa. Un opzione call (put) europea su un azione che non paga dividendi dà al possessore il diritto di comprare (vendere)
studi e analisi finanziarie La Duration
 La Duration Cerchiamo di capire perchè le obbligazioni a tasso fisso possono oscillare di prezzo e, quindi, anche il valore di un fondo di investimento obbligazionario possa diminuire. Spesso si crede
La Duration Cerchiamo di capire perchè le obbligazioni a tasso fisso possono oscillare di prezzo e, quindi, anche il valore di un fondo di investimento obbligazionario possa diminuire. Spesso si crede
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016. 1. Esercizi: lezione 03/11/2015
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi: lezione 03/11/2015 Piani di ammortamento Esercizio 1. Un finanziamento pari a 100000e viene rimborsato
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi: lezione 03/11/2015 Piani di ammortamento Esercizio 1. Un finanziamento pari a 100000e viene rimborsato
FORWARD RATE AGREEMENT
 FORWARD RATE AGREEMENT FLAVIO ANGELINI. Definizioni In generale, un contratto a termine o forward permette una compravendita di una certa quantità di un bene differita a una data futura a un prezzo fissato
FORWARD RATE AGREEMENT FLAVIO ANGELINI. Definizioni In generale, un contratto a termine o forward permette una compravendita di una certa quantità di un bene differita a una data futura a un prezzo fissato
Un modello matematico di investimento ottimale
 Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
INTRODUZIONE AI CICLI
 www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
OPERAZIONI DI PRESTITO
 APPUNTI DI ESTIMO La matematica finanziaria si occupa delle operazioni finanziarie, delle loro valutazioni, nonché del loro confronto. Si definisce operazione finanziaria, qualsiasi operazione che prevede
APPUNTI DI ESTIMO La matematica finanziaria si occupa delle operazioni finanziarie, delle loro valutazioni, nonché del loro confronto. Si definisce operazione finanziaria, qualsiasi operazione che prevede
b. Che cosa succede alla frazione di reddito nazionale che viene risparmiata?
 Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
Esercizi svolti in aula
 Esercizi svolti in aula 23 maggio 2012 Esercizio 1 (Esercizio 1 del compito di matematica finanziaria 1 (CdL EA) del 16-02-10) Un individuo vuole accumulare su un conto corrente la somma di 10.000 Euro
Esercizi svolti in aula 23 maggio 2012 Esercizio 1 (Esercizio 1 del compito di matematica finanziaria 1 (CdL EA) del 16-02-10) Un individuo vuole accumulare su un conto corrente la somma di 10.000 Euro
Il paracadute delle opzioni
 Pubblicazioni PlayOptions Il paracadute delle opzioni Strategist Cagalli Tiziano Disclaimer I pensieri e le analisi qui esposte non sono un servizio di consulenza o sollecitazione al pubblico risparmio.
Pubblicazioni PlayOptions Il paracadute delle opzioni Strategist Cagalli Tiziano Disclaimer I pensieri e le analisi qui esposte non sono un servizio di consulenza o sollecitazione al pubblico risparmio.
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
IL VALORE FINANZIARIO DEL TEMPO. Docente: Prof. Massimo Mariani
 IL VALORE FINANZIARIO DEL TEMPO Docente: Prof. Massimo Mariani 1 SOMMARIO Il concetto di tempo Il valore finanziario del tempo Le determinanti del tasso di interesse La formula di Fisher I flussi di cassa
IL VALORE FINANZIARIO DEL TEMPO Docente: Prof. Massimo Mariani 1 SOMMARIO Il concetto di tempo Il valore finanziario del tempo Le determinanti del tasso di interesse La formula di Fisher I flussi di cassa
Il SENTIMENT E LA PSICOLOGIA
 CAPITOLO 2 Il SENTIMENT E LA PSICOLOGIA 2.1.Cosa muove i mercati? Il primo passo operativo da fare nel trading è l analisi del sentiment dei mercati. Con questa espressione faccio riferimento al livello
CAPITOLO 2 Il SENTIMENT E LA PSICOLOGIA 2.1.Cosa muove i mercati? Il primo passo operativo da fare nel trading è l analisi del sentiment dei mercati. Con questa espressione faccio riferimento al livello
Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie
 Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie Economia degli Intermediari Finanziari 29 aprile 2009 A.A. 2008-2009 Agenda 1. Il calcolo
Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie Economia degli Intermediari Finanziari 29 aprile 2009 A.A. 2008-2009 Agenda 1. Il calcolo
Valore equo di un derivato. Contingent claim
 Contingent claim Ci occuperemo ora di determinare il prezzo equo di un prodotto derivato, come le opzioni, e di come coprire il rischio associato a questi contratti. Assumeremo come dinamica dei prezzi
Contingent claim Ci occuperemo ora di determinare il prezzo equo di un prodotto derivato, come le opzioni, e di come coprire il rischio associato a questi contratti. Assumeremo come dinamica dei prezzi
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016. 1. Esercizi: lezione 24/11/2015
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi: lezione 24/11/2015 Valutazioni di operazioni finanziarie Esercizio 1. Un operazione finanziaria
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2015/2016 1. Esercizi: lezione 24/11/2015 Valutazioni di operazioni finanziarie Esercizio 1. Un operazione finanziaria
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Blanchard, Macroeconomia Una prospettiva europea, Il Mulino 2011 Capitolo IV. I mercati finanziari. Capitolo IV. I mercati finanziari
 Capitolo IV. I mercati finanziari 1. La domanda di moneta La moneta può essere usata per transazioni, ma non paga interessi. In realtà ci sono due tipi di moneta: il circolante, la moneta metallica e cartacea,
Capitolo IV. I mercati finanziari 1. La domanda di moneta La moneta può essere usata per transazioni, ma non paga interessi. In realtà ci sono due tipi di moneta: il circolante, la moneta metallica e cartacea,
Leasing secondo lo IAS 17
 Leasing secondo lo IAS 17 Leasing: Ias 17 Lo Ias 17 prevede modalità diverse di rappresentazione contabile a seconda si tratti di leasing finanziario o di leasing operativo. Il leasing è un contratto per
Leasing secondo lo IAS 17 Leasing: Ias 17 Lo Ias 17 prevede modalità diverse di rappresentazione contabile a seconda si tratti di leasing finanziario o di leasing operativo. Il leasing è un contratto per
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
Risparmio e Investimento
 Risparmio e Investimento Risparmiando un paese ha a disposizione più risorse da utilizzare per investire in beni capitali I beni capitali a loro volta fanno aumentare la produttività La produttività incide
Risparmio e Investimento Risparmiando un paese ha a disposizione più risorse da utilizzare per investire in beni capitali I beni capitali a loro volta fanno aumentare la produttività La produttività incide
IL MODELLO CICLICO BATTLEPLAN
 www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
OPZIONI, DURATION E INTEREST RATE SWAP (IRS)
 ESERCITAZIONE MATEMATICA FINANZIARIA 1 OPZIONI, DURATION E INTEREST RATE SWAP (IRS) Valutazione delle opzioni Esercizio 1 2 ESERCIZIO 1 Il portafoglio di un investitore è composto di 520 azioni della società
ESERCITAZIONE MATEMATICA FINANZIARIA 1 OPZIONI, DURATION E INTEREST RATE SWAP (IRS) Valutazione delle opzioni Esercizio 1 2 ESERCIZIO 1 Il portafoglio di un investitore è composto di 520 azioni della società
GIANLUIGI BALLARANI. I 10 Errori di Chi Non Riesce a Rendere Negli Esami Come Vorrebbe
 GIANLUIGI BALLARANI I 10 Errori di Chi Non Riesce a Rendere Negli Esami Come Vorrebbe Individuarli e correggerli 1 di 6 Autore di Esami No Problem 1 Titolo I 10 Errori di Chi Non Riesce a Rendere Negli
GIANLUIGI BALLARANI I 10 Errori di Chi Non Riesce a Rendere Negli Esami Come Vorrebbe Individuarli e correggerli 1 di 6 Autore di Esami No Problem 1 Titolo I 10 Errori di Chi Non Riesce a Rendere Negli
IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE.
 IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE. Lezione 5 Castellanza, 17 Ottobre 2007 2 Summary Il costo del capitale La relazione rischio/rendimento
IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE. Lezione 5 Castellanza, 17 Ottobre 2007 2 Summary Il costo del capitale La relazione rischio/rendimento
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Richiami di teoria della domanda di moneta
 Richiami di teoria della domanda di moneta Parte seconda La teoria della preferenza della liquidità di Keynes Keynes distingue tre moventi principali per cui si detiene moneta. Transattivo Precauzionale
Richiami di teoria della domanda di moneta Parte seconda La teoria della preferenza della liquidità di Keynes Keynes distingue tre moventi principali per cui si detiene moneta. Transattivo Precauzionale
Soluzione dell esercizio del 2 Febbraio 2004
 Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI
 VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
IL RISCHIO DI INVESTIRE IN AZIONI DIMINUISCE CON IL PASSARE DEL TEMPO?
 IL RISCHIO DI INVESTIRE IN AZIONI DIMINUISCE CON IL PASSARE DEL TEMPO? Versione preliminare: 1 Agosto 28 Nicola Zanella E-mail: n.zanella@yahoo.it ABSTRACT I seguenti grafici riguardano il rischio di investire
IL RISCHIO DI INVESTIRE IN AZIONI DIMINUISCE CON IL PASSARE DEL TEMPO? Versione preliminare: 1 Agosto 28 Nicola Zanella E-mail: n.zanella@yahoo.it ABSTRACT I seguenti grafici riguardano il rischio di investire
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
Acquisizione delle immobilizzazioni materiali: acquisto
 Acquisizione delle immobilizzazioni materiali: acquisto Premessa Le immobilizzazioni, sia esse materiali che immateriali, possono entrare a far parte del patrimonio aziendale in tre modi diversi: in seguito
Acquisizione delle immobilizzazioni materiali: acquisto Premessa Le immobilizzazioni, sia esse materiali che immateriali, possono entrare a far parte del patrimonio aziendale in tre modi diversi: in seguito
DERIVATI REGOLAMENTATI OPZIONI E FUTURES ORARIO DI NEGOZIAZIONE : 9,00 17,40
 DERIVATI REGOLAMENTATI OPZIONI E FUTURES ORARIO DI NEGOZIAZIONE : 9,00 17,40 LE OPZIONI - Definizione Le opzioni sono contratti finanziari che danno al compratore il diritto, ma non il dovere, di comprare,
DERIVATI REGOLAMENTATI OPZIONI E FUTURES ORARIO DI NEGOZIAZIONE : 9,00 17,40 LE OPZIONI - Definizione Le opzioni sono contratti finanziari che danno al compratore il diritto, ma non il dovere, di comprare,
Capitalizzazione semplice e composta (sul libro a pag. 386 e seguenti)
 Capitalizzazione semplice e composta (sul libro a pag. 386 e seguenti) Operazione finanziaria = un operazione in cui avviene uno scambio di denaro in tempi diversi. Mutuante o creditore = chi concede il
Capitalizzazione semplice e composta (sul libro a pag. 386 e seguenti) Operazione finanziaria = un operazione in cui avviene uno scambio di denaro in tempi diversi. Mutuante o creditore = chi concede il
Dato il Mercato, è possibile individuare il valore e la duration del portafoglio:
 TEORIA DELL IMMUNIZZAZIONE FINANZIARIA Con il termine immunizzazione finanziaria si intende una metodologia matematica finalizzata a neutralizzare gli effetti della variazione del tasso di valutazione
TEORIA DELL IMMUNIZZAZIONE FINANZIARIA Con il termine immunizzazione finanziaria si intende una metodologia matematica finalizzata a neutralizzare gli effetti della variazione del tasso di valutazione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Misure finanziarie del rendimento: il Van
 Misure finanziarie del rendimento: il Van 6.XI.2013 Il valore attuale netto Il valore attuale netto di un progetto si calcola per mezzo di un modello finanziario basato su stime circa i ricavi i costi
Misure finanziarie del rendimento: il Van 6.XI.2013 Il valore attuale netto Il valore attuale netto di un progetto si calcola per mezzo di un modello finanziario basato su stime circa i ricavi i costi
Che Cosa È GlobalAdShare (GAS)
 Versione 1.0 Che Cosa È GlobalAdShare (GAS) GAS è una piattaforma che fornisce una serie di servizi pubblicitari ai propri membri. Il 100% dei profitti che vengono generati dagli acquisti dei pacchetti
Versione 1.0 Che Cosa È GlobalAdShare (GAS) GAS è una piattaforma che fornisce una serie di servizi pubblicitari ai propri membri. Il 100% dei profitti che vengono generati dagli acquisti dei pacchetti
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Risparmio, investimenti e sistema finanziario
 Risparmio, investimenti e sistema finanziario Una relazione fondamentale per la crescita economica è quella tra risparmio e investimenti. In un economia di mercato occorre individuare meccanismi capaci
Risparmio, investimenti e sistema finanziario Una relazione fondamentale per la crescita economica è quella tra risparmio e investimenti. In un economia di mercato occorre individuare meccanismi capaci
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005. Lezione 11
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 11 In questa lezione vedremo alcune applicazioni della tecnica greedy al progetto di algoritmi on-line. Vediamo
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 11 In questa lezione vedremo alcune applicazioni della tecnica greedy al progetto di algoritmi on-line. Vediamo
Funzioni. Funzioni /2
 Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Determinare l ammontare x da versare per centrare l obiettivo di costituzione.
 Esercizi di matematica finanziaria 1 VAN - DCF - TIR Esercizio 1.1. Un investitore desidera disporre tra 3 anni d un capitale M = 10000 euro. Investe subito la somma c 0 pari a 1/4 di M. Farà poi un ulteriore
Esercizi di matematica finanziaria 1 VAN - DCF - TIR Esercizio 1.1. Un investitore desidera disporre tra 3 anni d un capitale M = 10000 euro. Investe subito la somma c 0 pari a 1/4 di M. Farà poi un ulteriore
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
5 Risparmio e investimento nel lungo periodo
 5 Risparmio e investimento nel lungo periodo 5.1 Il ruolo del mercato finanziario Il ruolo macroeconomico del sistema finanziario è quello di far affluire i fondi risparmiati ai soggetti che li spendono.
5 Risparmio e investimento nel lungo periodo 5.1 Il ruolo del mercato finanziario Il ruolo macroeconomico del sistema finanziario è quello di far affluire i fondi risparmiati ai soggetti che li spendono.
Misure finanziarie del rendimento: il Van
 Misure finanziarie del rendimento: il Van 12.XI.2014 Il valore attuale netto Il valore attuale netto di un progetto si calcola l per mezzo di un modello finanziario basato su stime circa i ricavi i costi
Misure finanziarie del rendimento: il Van 12.XI.2014 Il valore attuale netto Il valore attuale netto di un progetto si calcola l per mezzo di un modello finanziario basato su stime circa i ricavi i costi
Analisi Costi-Benefici
 Politica economica (A-D) Sapienza Università di Rome Analisi Costi-Benefici Giovanni Di Bartolomeo Sapienza Università di Roma Scelta pubblica Intervento pubblico realizzazione di progetti esempi: infrastrutture,
Politica economica (A-D) Sapienza Università di Rome Analisi Costi-Benefici Giovanni Di Bartolomeo Sapienza Università di Roma Scelta pubblica Intervento pubblico realizzazione di progetti esempi: infrastrutture,
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
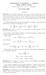 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea
 Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
Indice. 1 Il settore reale --------------------------------------------------------------------------------------------- 3
 INSEGNAMENTO DI ECONOMIA POLITICA LEZIONE VI IL MERCATO REALE PROF. ALDO VASTOLA Indice 1 Il settore reale ---------------------------------------------------------------------------------------------
INSEGNAMENTO DI ECONOMIA POLITICA LEZIONE VI IL MERCATO REALE PROF. ALDO VASTOLA Indice 1 Il settore reale ---------------------------------------------------------------------------------------------
Interesse, sconto, ratei e risconti
 TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Mercati finanziari e valore degli investimenti
 7 Mercati finanziari e valore degli investimenti Problemi teorici. Nei mercati finanziari vengono vendute e acquistate attività. Attraverso tali mercati i cambiamenti nella politica del governo e le altre
7 Mercati finanziari e valore degli investimenti Problemi teorici. Nei mercati finanziari vengono vendute e acquistate attività. Attraverso tali mercati i cambiamenti nella politica del governo e le altre
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
1 MATEMATICA FINANZIARIA
 1 MATEMATICA FINANZIARIA 1.1 26.6.2000 Data la seguente operazione finanziaria: k = 0 1 2 3 4 F k = -800 200 300 300 400 a. determinare il TIR b. detreminare il VAN corrispondente ad un interesse periodale
1 MATEMATICA FINANZIARIA 1.1 26.6.2000 Data la seguente operazione finanziaria: k = 0 1 2 3 4 F k = -800 200 300 300 400 a. determinare il TIR b. detreminare il VAN corrispondente ad un interesse periodale
Cosa e' la percentuale e come si calcola
 Cosa e' la percentuale e come si calcola La percentuale e' un calcolo molto semplice che permette di valutare la forza di un evento questo simbolo % si legge percento. il 20% di 90 si calcola cosi 20/100*90
Cosa e' la percentuale e come si calcola La percentuale e' un calcolo molto semplice che permette di valutare la forza di un evento questo simbolo % si legge percento. il 20% di 90 si calcola cosi 20/100*90
