LA DIAGONALIZZAZIONE DI UN ENDOMORFISMO. goosesteps. Queste note sono un complemento alla lezione del 5 febbraio.
|
|
|
- Gennaro Conte
- 5 anni fa
- Visualizzazioni
Transcript
1 L DIGONLIZZZIONE DI UN ENDOMORFISMO goosestes Queste note sono un comlemento alla lezione del 5 feraio.. utovalori e autovettori di un endomorfismo lineare Sia T : V! V un endomorfismo lineare dello sazio vettoriale V sul camo K. Definizione.. Un vettore v V {O} si dice un autovettore di T se T (v) = v er un certo K. In altre arole un autovettore di T è un vettore diverso da O dello sazio V che ha la seguente rorietà: la T lo manda in un multilo di sé stesso. Definizione.. Se v V {O} è un autovettore di T tale che T (v) = allora lo scalare K si dice autovalore di T relativo a v (e viceversa si dirà che v è un autovettore relativo all autovalore ). Si noti che l autovalore uò essere K: seeresemiot non è iniettiva, ossia Ker T ) {O}, tutti gli elementi w (Ker T) {O} soddisfano v T (w) =O =w ossia sono autovettori relativi all autovalore. Definizione.. Dato autosazio relativo a. K chiamiamo l insieme V = {v V T (v) = v} nche se aiamo definito l autosazio V er qualunque K, inrealtàv è semre uguale a {O} amenoche non sia un autovalore di T.Questoèdunqueil caso interessante: se è un autovalore di T allora V è costituito da O edatutti gli autovettori relativi a. Esercizio.4. Verificare che un autosazio V è un sottosazio vettoriale di V. Osservazione.5. In articolare aiamo notato che V = Ker T. Perché er noi sono imortanti autovettori e autovalori? Suoniamo che V aia dimensione n e ensiamo a cosa succederee se riuscissimo a trovare una ase di V, {v,v,...,v n }, comosta solo da autovettori di T. vremmo, er ogni i =,,...,n, T (v i )= i v i
2 er certi autovalori i (sui quali non aiamo informazioni, er esemio otreero anche essere tutti uguali = = n ). ome saree fatta la matrice [T ] v,v,...,v n v,v,...,v n associata a T risetto a questa ase? Ricordandosi come si costruiscono le matrici osserviamo che la rima colonna conterree il vettore T (v ) scritto in termini della ase {v,v,...,v n }, ossia T (v )= la seconda il vettore T (v )=v + matrice saree diagonale: [T ] v,v,...,v = n v,v,...,v n v +v +v +v 4 + +v n v +v + +v n e così via. Quindi la n... n Ora, una matrice diagonale è er noi leggiilissima ; a colo d occhio ossiamo saere tutto di T : il suo rango (dunque anche la dimensione del nucleo), quali sono esattamente i vettori di Ker T, quali sono (se esistono) i sottosazi in cui T si comorta come l identità, ossia i sottosazi costituiti dai vettori di V che T lascia fissi, eccetera. Dunque studiamo gli autovalori e gli autovettori di T nella seranza di trovare asi uone che ci ermettano di conoscere ene il comortamento di T. Ma esistono semre queste asi uone, ossia asi costituite solo da autovettori di T? NO, non semre. Se er un certo endomorfismo T esiste una ase uona si dice che T è diagonalizzaile, altrimenti T è non diagonalizzaile. Esemio.6. onsideriamo l endomorfismo R : R! R dato da una rotazione di angolo con centro l origine. Si verifica immediatamente che, risetto alla ase standard di R, questo endomorfismo è raresentato dalla matrice cos sin [R sin cos Per esemio, nel caso di una rotazione di 6 (ovvero ), aiamo: [R ]= Nel caso in cui < <, non ci sono vettori v 6= O che vengono mandati in un multilo di se stessi, visto che tutti i vettori vengono ruotati di un angolo che non è nullo e non è di 8. Dunque non ci sono autovettori e autovalori. Nel caso = la rotazione è l identità, dunque tutti i vettori v 6= O sono autovettori relativi all autovalore, e V = R.
3 Nel caso = la rotazione è uguale a I, dunque tutti i vettori v 6= O sono autovettori relativi all autovalore -, e V = R. Esemio.7. onsideriamo l endomorfismo T :! che, risetto alla ase standard di, è raresentato dalla matrice [T ]= Si tratta della stessa matrice che nell esemio recedente era associata alla rotazione di nel iano reale ma stavolta, visto che stiamo considerando uno sazio vettoriale comlesso, riusciamo a trovare autovettori e autovalori er T. Si verifica infatti ı (esercizio!) che il vettore è un autovettore relativo all autovalore +ı e ı che il vettore è un autovettore relativo all autovalore ı. Poiché i due vettori sono linearmente indiendenti sul camo, costituiscono una ase. Dunque T è diagonalizzaile e ossiamo facilmente verificare che ı V +ı =< > ı V ı =< > = V ı V +ı.. Il olinomio caratteristico di un endomorfismo Vogliamo trovare dei criteri semlici che ci ermettano di decidere se un endomorfismo è diagonalizzaile o no. Un uon rimo asso è quello di avere un metodo che, dato un endomorfismo T : V! V e osto n = dim V,ciermettadidecidere se uno scalare K è o no un autovalore di T. Entrano qui in gioco i olinomi e le loro radici. Innanzitutto osserviamo che, a nché K sia un autovalore, secondo la definizione isogna che esista un v V {O} tale che T (v) = v. Questa equazione si uò riscrivere anche come T (v) I(v) =O dove I : V! V è l identità (qui e nel seguito indicheremo con I sia l alicazione identità sia la matrice identità). Riscriviamo ancora: (T I)(v) =O iamo scoerto che, se T ossiede un autovalore, allora l endomorfismo T I non è iniettivo: infatti manda il vettore non nullo v in O. Dunque, se scegliamo una ase qualunque er V e costruiamo la matrice [T ] associata a T, la matrice [T I] =[T ] I dovrà avere determinante uguale a : det([t ] I) =.
4 Osserviamo che il nucleo di [T ] I equellodi I [T ] coincidono e allora vale anche det( I [T ]) =. Questa osservazione è la remessa er la seguente definizione: Definizione.. Dato un endomorfismo lineare T : V! V con n = dim V, scegliamo una ase er V e costruiamo la matrice [T ] associata a T risetto a tale ase. Il olinomio caratteristico P T (t) K[t] dell endomorfismo T è definito da: P T (t) =det(t[i] [T ]). Osservazione.. ) Perché la definizione data aia senso innanzitutto isogna verificare che det(t[i] [T ]) sia veramente un olinomio. Utilizzando la definizione di determinante P n... si mostra facilmente che P T (t) è un olinomio di grado n con coe ciente direttore : P T (t) =t n +... ) È fondamentale inoltre che la definizione aena data non dienda dalla ase scelta di V : non saree una definizione uona se con la scelta di due asi diverse ottenessimo due olinomi caratteristici diversi. Questo rolema in e etti non si verifica. Infatti, se scegliamo due asi e di V, come saiamo le due matrici [T ] e[t ] sono legate dalla seguente relazione: esiste una matrice [B] invertiile tale che [T ] =[B] [T ] [B] Usando il teorema di Binet a questo unto verifichiamo che B [T ] B = [B] [T ] B [B] = = det [B] B B [T ] det ([B]) = [T ] iamo dunque mostrato che P T (t) =det (ti della ase. [T ] [B] = [T ]) non diende dalla scelta lcuni di voi avranno notato che aiamo usato il teorema di Binet, che avevamo dimostrato er matrici con coe cienti in un camo. In questo caso alcuni dei coe cienti sono olinomi di grado, dunque non aartengono a K. Inrealtàossiamoensarecheicoe cientiaartengano al camo K(t) dellefunzionirazionali(ossiailcamoicuielementisonofrazioniconunolinomio al numeratore e un olinomio non nullo al denominatore) e dunque ossiamo alicare il teorema di Binet senza rolemi. Un modo alternativo di aggirare l oiezione sull uso del teorema di Binet è i l s e g u e n t e : i a s s a g g i c h e a i a m o f a t t o v a l g o n o q u a n d o a l o s t o d i t oniamo un qualunque elemento a K. SeilcamoK ha almeno n elementi (er esemio se è infinito), questo significa che iolinomidet ti [T ] e det ti [T ] danno lo stesso valore su n diversi elementi di K. Dunque devono coincidere (erché? Imostate un sistema, e troverete una matrice di Vandermonde!). 4
5 Esercizio.. Grazie all osservazione recedente, saiamo in articolare che i coe cienti di T (t) non diendono dalla ase scelta. hiamiamo dunque r : End(V )! K la funzione che, ad ogni endomorfismo T associa il coe ciente di t r in P T (t). Dimostrare che n è uguale a meno la traccia ossia n (T ) = T (T )(dove T indica la traccia) e che è uguale, a meno del segno, al determinante ossia (T )=±Det(T ). Il olinomio caratteristico ci fornisce dunque l esemio di altre funzioni che, come il determinante e la traccia, coinvolgono i coe cienti di una matrice [T ] ma in realtà non diendono dalla ase scelta. Possiamo a questo unto enunciare il teorema rinciale che siega l utilità del olinomio caratteristico ai fini del rolema della diagonalizzazione. Teorema.4. onsiderato T come sora, vale che uno scalare K è u n autovalore di T se e solo se è u n a r a d i c e d i P T (t), ossiaseesolosep T ( )= Dimostrazione. iamo già visto (l osservazione rima della definizione del olinomio caratteristico) che se è un autovalore di T allora det( I [T ]) = P T ( ) =. Resta dunque da dimostrare il viceversa. Suoniamo che det( I [T ]) = P T ( )= : allora l alicazione lineare I T non è iniettiva. Dunque esiste v V {O} tale che ( I T )(v) =. Questo si uò riscrivere anche come T (v) = iamo trovato un autovettore che ha autovalore e quindi aiamo mostrato, come volevamo, che è un autovalore di T. Esemio.5. onsideriamo l endomorfismo T dell Esemio.7. Il suo olinomio caratteristico risulta P T (t) =t t+ (verificare!). Questo olinomio ha due radici in, ovvero ı e +ı, che in e etti, come saiamo, sono gli autovalori di T. Notiamo che t t+ non ha invece radici in R, coerentemente col fatto, osservato nell Esemio.6, che la rotazione R del iano reale non ammette autovettori. Esercizio.6. Sia F : R! R l alicazione lineare definita, nella ase standard di R, dalla matrice: [F ]= alcolare P F (t). Esercizio.7. Sia F :! l alicazione lineare definita, nella ase standard di, dalla matrice: [F ]=@ i i alcolare P F (t). Esercizio.8. Sia F : 4! 4 l alicazione lineare definita, nella ase standard di 4, dalla matrice: [F ]= B alcolare P F (t). 5 v
6 . Una strategia er scorire se un endomorfismo è diagonalizzaile In questo aragrafo descriviamo una strategia in quattro assi che ci ermette di scorire se un endomorfismo T : V! V,doveV è uno sazio vettoriale sul camo K di dimensione n, è diagonalizzaile, e, in caso sia diagonalizzaile, di trovare una ase che lo diagonalizza (ossia una ase di V fatta tutta da autovettori di T )e di scrivere la matrice diagonale che raresenta T risetto a tale ase. La nostra strategia sarà la seguente: PSSO. Data T, troviamo gli autovalori di T utilizzando il olinomio caratteristico. PSSO. Suoniamo di aver trovato gli autovalori,,..., k: a questo unto scoriamo chi sono i relativi autosazi V,V,...,V k. PSSO. Un teorema (vedi Teorema.) ci assicurerà che gli autosazi V,V,...,V k sono in somma diretta. Quindi se V V V k = V allora è ossiile trovare una ase uona, fatta da autovettori di T e T è diagonalizzaile. Per scrivere una ase uona asta scegliere una ase er ogni V i e oi fare l unione. ltrimenti, se T non è diagonalizzaile. V V V k ( V PSSO 4. Se T è risultata diagonalizzaile, usando la ase trovata si scrive la matrice diagonale [T ]. Vediamo i dettagli asso er asso... Passo. Di questo ci siamo già occuati nel aragrafo recedente: er saere quali sono gli autovalori di un endomorfismo T ossiamo calcolare il olinomio caratteristico P T (t) e trovare le sue radici in K... Passo. Suoniamo dunque di aver scoerto che T ha i seguenti autovalori:,,..., k, tutti distinti fra loro. Vogliamo individuare gli autosazi V,V,...V k. Per questo asterà risolvere dei sistemi lineari: er ogni i =,,...,k, l autosazio V i è costituito er definizione dai vettori v V tali che T (v) = i v, ossia, scelta una ase di V e dunque trovata la matrice [T ], dalle soluzioni del sistema 6
7 lineare ([T ] ii) x x x n x n = Passo. ominciamo col dimostrare il seguente teorema. Teorema.. Dato un endomorfismo lineare T : V! V,siano,,..., k degli autovalori di T distinti fra loro. onsideriamo ora degli autovettori v V,v V,...,v k V k. llora {v,v,...,v k } è un insieme di vettori linearmente indiendenti. Osservazione.. Sesso ci si riferisce a questo teorema con la frase: autovettori relativi ad autovalori distinti sono linearmente indiendenti. Dimostrazione. Procediamo er induzione su k. Per k = l enunciato è anale erché {v } è un insieme di vettori linearmente indiendenti (c è un vettore solo... ed è diverso da O erché è un autovettore). Suoniamo di aver dimostrato che l enunciato è vero fino al caso di k vettori e cerchiamo di dimostrarlo er k. Suoniamo allora di avere un insieme di vettori {v,v,...,v k } come nelle iotesi e che valga: (.) a v + a v + + a k v k = O Per mostrare che {v,v,...,v k } è un insieme di vettori linearmente indiendenti doiamo mostrare che questo uò accadere solo quando a = a = = a k =. Dalla equazione scritta ne ricaviamo due in due modi diversi. Prima alichiamo T ad entrami i memri e er linearità otteniamo che svolgendo il calcolo diventa a T (v )+a T (v )+ + a k T (v k )=O a v + a v + + a k k v k = O Poi invece moltilichiamo l equazione er k ottenendo: a k v + a k v + + a k k v k = O Per sottrazione da queste due equazioni ricaviamo: a ( k )v + a ( k )v + + a k ( k k )v k = O Ma questa è una cominazione lineare dei k vettori {v,v,...,v k } uguale a O: er iotesi induttiva tutti i coe cienti devono essere uguali a. Visto che gli scalari k i sono tutti diversi da zero (gli autovalori in questione sono distinti fra loro er iotesi) questo imlica che a = a = = a k =. Sostituendo nella equazione iniziale (.), notiamo che deve essere anche a k =. Il seguente teorema è un ra orzamento del recedente. Teorema.. Dato un endomorfismo lineare T : V! V,siano,,..., k degli autovalori di T distinti fra loro. llora gli autosazi V,V,...,V k sono in somma diretta. 7
8 Dimostrazione. Ricordiamo che dire che gli autosazi V,V,...,V k sono in somma diretta vuol dire che se ne rendiamo uno qualunque, diciamo V tanto er fissare la notazione, la sua intersezione con la somma di tutti gli altri è anale, ossia V \ (V + + V k )={O}. Suoniamo er assurdo che non sia così, e che ci sia un vettore w 6= O tale che llora ossiamo scrivere w in due modi: erché w V,e w V \ (V + + V k ) w = v V {O} w = v + v + + v k (dove i v j V j er ogni j) vistochew V + + V k. lcuni dei vettori v j otreero essere uguali a O, ma non tutti (se fossero tutti uguali a O allora anche w saree uguale a O). Diciamo che, a meno di riordinamenti, i vettori diversi da zero siano v,...,v s, con s ale k. Dunque vale: v = w = v + v + + v s Da questa uguaglianza ricaviamo la relazione v v v v s = O che rivela che gli autovettori {v,...v s } sono linearmente diendenti, assurdo erché contraddice il Teorema. (si tratta di autovettori relativi ad autovalori distinti). Osservazione.4. Il teorema che aiamo aena dimostrato è un caso articolare del seguente fatto iù generale. Suoniamo che in uno sazio vettoriale V ci siano dei sottosazi,,..., k con la seguente rorietà: ogni insieme {v,...,v k } di vettori non nulli scelti in modo che, er ogni i, v i i, è un insieme di vettori linearmente indiendenti. llora i sottosazi,,..., k sono in somma diretta. Provate a dimostrarlo (la dimostrazione è del tutto analoga a quella del teorema sora). Nelle iotesi del teorema recedente saiamo allora (riguardate il Paragrafo 4 delle disense L FORMUL DI GRSSMNN PER SOTTOSPZI E IL ONET- TO DI SOMM DIRETT ), che la dimensione della somma degli autosazi è la massima ossiile, ossia dim (V V V k )=dim V + dim V + + dim V k Osserviamo che aiamo dunque già ottenuto un criterio er dire se T è diagonalizzaile o no. Infatti, se allora dim V + dim V + + dim V k = n = dim V V V V k = V e quindi è ossiile trovare una ase uona, fatta da autovettori di T, insomma T è diagonalizzaile. Per scrivere una simile ase uona, come saiamo dal Paragrafo 4 delle disense citate sora, asta scegliere una ase er ogni V i e oi fare l unione. 8
9 ltrimenti, se (.) dim V + dim V + + dim V k <n= dim V T non è diagonalizzaile. Infatti non è ossiile trovare una ase di autovettori: se la trovassimo contraddiremmo la (.)..4. Passo 4. Se l endomorfismo T è diagonalizzaile, scegliamo dunque una ase di autovettori nel modo descritto al Passo, e avremo una matrice associata [T ] che risulterà diagonale. Manteniamo le notazioni introdotte al Passo : allora sulla diagonale troveremo dim V coe cienti uguali a, dim V coe cienti uguali a,...,dim V k coe cienti uguali a k. Il rango di T sarà uguale al numero dei coe cienti non zero che troviamo sulla diagonale di [T ], la dimensione del nucleo sarà uguale al numero dei coe cienti uguali a zero che troviamo sulla diagonale di [T ]. 4. Il criterio della moltelicità algerica e della moltelicità geometrica Nel aragrafo recedente aiamo descritto un algoritmo che ci ermette di decidere se un endomorfismo è diagonalizzaile o no. In questo aragrafo faremo una osservazione che ci ermetterà di riformulare questo algoritmo e di individuare alcune scorciatoie. onsideriamo come al solito un endomorfismo T : V! V,doveV è uno sazio vettoriale sul camo K con n = dim V. alcoliamo il suo olinomio caratteristico e fattorizziamolo in K[t]. Otterremo una esressione del tio: P T (t) =(t ) a (t ) a (t k) a k f(t) dove,,..., k sono gli autovalori di T in K e sono tutti distinti fra loro, e f(t) o è oure è un olinomio di grado > che non ha radici in K. Se la T è diagonalizzaile, allora esiste una ase di V in cui la matrice associata [T ] ha forma diagonale e sulla diagonale comaiono,,..., k. Più esattamente, er ogni i =,,...,k, i comare dim V i volte. Dunque in questo caso ossiamo ricalcolare il olinomio caratteristico P T usando [T ] : P T (t) =Det (ti [T ] ) Si tratta di calcolare il determinante di una matrice diagonale e si osserva allora che P T si fattorizza come rodotto di fattori lineari (cioè olinomi di grado ): P T (t) =(t ) dim V (t ) dim V (t k) dim V k il che dimostra che il fattore f(t) è. In sintesi: Proosizione 4.. Se l endomorfismo T è diagonalizzaile sul camo K, allora il suo olinomio caratteristico P T (t) si fattorizza come rodotto di fattori lineari in K[t]: P T (t) =(t ) dim V (t ) dim V (t k) dim V k 9
10 Dunque se P T non si fattorizza come rodotto di olinomi di grado in K[t] ossiamo concludere che T non è diagonalizzaile. Ma cosa ossiamo dire del viceversa? Se P T si fattorizza come rodotto di fattori lineari in K[t] allora T è diagonalizzaile? NO, in generale non è vero. Basta considerare er esemio l alicazione lineare L : R! R che nelle asi standard è raresentata dalla matrice Il olinomio caratteristico è P L (t) = (t ) ma l alicazione non è diagonalizzaile: ossiamo verificarlo alicando il criterio del aragrafo recedente, infatti L ha il solo autosazio V e se ne calcoliamo la dimensione scoriamo che dim V =< =dim R. Prima di enunciare il nuovo criterio diamo qualche definizione: Definizione 4.. Data T come sora con olinomio caratteristico P T (t) =(t ) a (t ) a (t k) a k f(t) dove f(t) o è oure è un olinomio di grado > che non ha radici in K, diremo che, er ogni i =,,...,k, a i è l a moltelicità algerica dell autovalore i. hiameremo invece moltelicità geometrica dell autovalore i il numero intero ositivo dim V i. Proosizione 4.. Dati T : V! V e P T (t) =(t ) a (t ) a (t k) a k f(t) come sora, er ogni autovalore i vale che la sua moltelicità geometrica è minore o uguale alla sua moltelicità algerica: dim V i ale a i Dimostrazione. Nella roosizione recedente aiamo già visto che se l alicazione T è diagonalizzaile, allora vale dim V i = a i 8i =,,...,k Se invece T non è diagonalizzaile, ricordando che gli autosazi sono in somma diretta V V V k ossiamo cominciare a costruire una ase di V rendendo una ase er ogni V i facendo l unione, che chiameremo. Poiché in questo caso e dim V V V k <dimv l insieme non è ancora una ase di V, ma è solo un insieme di vettori linearmente indiendenti; ossiamo allora, er il teorema di comletamento, scegliere degli elementi s,...,s r tali che = [{s,...,s r } sia una ase. Risetto a questa ase
11 la matrice di T ha la seguente forma: [T ] = k k ossia ha una arte diagonale, dove troviamo rietuto dim V volte, rietuto dim V volte... k rietuto dim V k volte, e oi sulle ultime r colonne, che corrisondono a T (s ),T(s ),...,T(s r ) non saiamo dire nulla. Osserviamo erò che, sviluando il determinante di ti [T ] a artire dalla rima colonna, oi dalla seconda, oi dalla terza, e così via otteniamo: P T (t) =Det (ti [T ] )=(t ) dim V (t ) dim V (t k) dim V k Det M dove M è il minore r r che sta nell angolo in asso a destra di ti [T ]. Ricordiamo ora la fattorizzazione er P T P T (t) =(t ) a (t ) a (t k) a k f(t) dove f(t) è un olinomio di grado > che non ha radici in K. Da questa fattorizzazione si ricava suito che la otenza massima di (t ) chedividep T (t) èa. Dunque, qualunque olinomio sia Det M, ossiamo dire che, er ogni i =,,...,k, dim V i ale a i. Le disuguaglianze aena dimostrate imlicano suito il risultato rinciale di questa sezione: Teorema 4.4 (riterio delle moltelicità algerica e geometrica.). Dato un endomorfismo lineare T : V! V di uno sazio vettoriale V (di dimensione finita n) sul camo K, siano,,..., k gli autovalori (distinti fra loro) di T in K. llorat è diagonalizzaile se e solo se P T si fattorizza come rodotto di fattori lineari e, er ogni autovalore i, la sua moltelicità algerica e quella geometrica sono uguali. Dimostrazione. iamo già visto, nelle dimostrazioni delle roosizioni recedenti, che se T è diagonalizzaile allora P T si fattorizza come rodotto di fattori lineari e, er ogni i vale moltelicità algerica di i = dim V i.
12 Viceversa, se P T si fattorizza come rodotto di fattori lineari P T (t) =(t ) a (t ) a (t k) a k e, er ogni autovalore i, la sua moltelicità algerica a i e quella geometrica sono uguali, allora calcoliamo dim V V V k Tale dimensione è uguale a kx ma er la nostra iotesi i= dim V i kx dim V i = i= che è uguale al grado del olinomio caratteristico P T,edunquean = dim V. llora dim V V V k = V kx i= e T è diagonalizzaile come volevamo dimostrare. Esercizio 4.5. Dato un endomorfismo lineare T : V! V di uno sazio vettoriale V sul camo K, dimostrare che se un autovalore di T ha moltelicità algerica uguale a allora anche la sua moltelicità geometrica è uguale a. 5. Esemi Esemio 5.. Sia T : R! R un endomorfismo lineare la cui matrice risetto alla ase standard è: [T ]=@ Vogliamo caire se è diagonalizzaile o no, e, se lo è, vogliamo trovare una ase comosta da autovettori. Innanzitutto calcoliamo il olinomio caratteristico: t P T = t + =(t ) (t+) t Gli autovalori sono dunque e. La moltelicità algerica di è uguale a e coincide con la sua moltelicità geometrica. Rietiamo infatti in questo caso articolare il ragionamento che alcuni lettori avranno già utilizzato er risolvere l Esercizio 4.5: infatti la moltelicità geometrica di è (visto che è autovalore ), e er la Proosizione 4. deve essere minore o uguale alla moltelicità algerica, quindi è esattamente e coincide con la moltelicità algerica. Dunque, volendo alicare il criterio del Teorema 4.4, doiamo studiare l autovalore, che ha moltelicità algerica, e controllare se la sua moltelicità a i La moltelicità geometrica di una autovalore è semre, visto che, er definizione, l autosazio relativo a tale autovalore non è anale.
13 geometrica è uguale a o no. La moltelicità geometrica di è la dimensione dell autosazio V = Ker (I T ), dunque doiamo calcolare la dimensione = Si osserva suito che la matrice ha rango uguale a, di conseguenza la dimensione del Ker è uguale a. nche er quel che riguarda l autovalore la moltelicità geometrica risulta uguale alla moltelicità algerica, dunque l alicazione T è diagonalizzaile. Per trovare una ase formata da autovettori, doiamo scegliere una ase di V e una ase di V e fare l unione. ominciamo col trovare una ase di V, ossia una ase di Ker (I T Risolvendo ilsistema a occhio, si vede suito che una ossiile ase è data Per trovare una ase di V che, come saiamo, ha dimensione, asta individuare un vettore non nullo in V = = 4 nche in questo caso il sistema associato si risolve immediatamente: è facile osservare che il costituisce una ase di V. Dunque una ase che diagonalizza l endomorfismo T è data dai vettori v La matrice di T risetto a tale ase è data da [T ] v,v,v = Esemio 5.. Si consideri l alicazione lineare F a ase standard, ha matrice: a [F a ]=@ a : R! R che, risetto alla
14 Vogliamo studiare, al variare del arametro a R, la diagonalizzailità di F a.per rima cosa calcoliamo il olinomio caratteristico P Fa (t): a t a P Fa a = t a = t Ora osserviamo che il olinomio t =(t a)(t (a + )t +a + ) (a + )t +a + ha radici a +± a Tali radici sono reali se e solo se a 4a ovvero se e solo se a 4 oure a ale. Visto che il camo in cui stiamo cercando gli autovalori è R, er il Teorema 4.4 ossiamo intanto concludere che: se < a < 4 l endomorfismo F a non è diagonalizzaile. Se invece a 4 oure a ale, aiamo tre autovalori reali: a + a 4a a ++ a, 4a, a e la rima cosa che ci conviene fare è calcolare le loro moltelicità algeriche, ossia caire se er qualche valore di a questi autovalori coincidono. Infatti, er i valori di a er cui questi tre autovalori sono a due a due distinti ossiamo suito dire, in ase al Teorema 4.4, che F a è diagonalizzaile: gli autovalori hanno moltelicità algerica uguale a, e dunque (vedi Esercizio 4.5), anche moltelicità geometrica uguale a. rontiamo il rolema della coincidenza studiando searatamente le tre ossiili uguaglianze: a + a 4a = a ++ a 4a a + a 4a = a a ++ a 4a = a La rima di queste uguaglianze è vera se e solo se a 4a = a 4a ovvero se e solo se a 4a = ovvero se e solo se a = oure a = 4. Invece si verifica suito che le uguaglianze a + a 4a = a a ++ a 4a = a non sono mai vere, qualunque sia il valore di a. Dunque i casi che richiedono attenzione sono solo a =ea = 4; ossiamo trarre una seconda conclusione: se a > 4 oure a < l endomorfismo F a è diagonalizzaile. 4 4a
15 Studiamo infine i due casi rimasti: er quel che riguarda a =, gli autovalori di F sono e e il olinomio caratteristico P F (t) èt(t ). Per caire se F è diagonalizzaile isogna calcolare la moltelicità geometrica di, ossia calcolare dim V = = dim La matrice ha rango, dunque il Ker ha dimensione. La moltelicità geometrica dell autovalore è uguale a, mentre la moltelicità algerica è uguale a : l endomorfismo F non è diagonalizzaile. Per quel che riguarda a = 4, gli autovalori di F 4 sono 4 e e il olinomio caratteristico P F4 (t) è(t 4)(t ). Per caire se F 4 è diagonalizzaile isogna calcolare la moltelicità geometrica di, ossia calcolare dim V = 4 4 = come nel caso recedente, il Ker ha dimensione e risulta che l endomorfismo F 4 non è diagonalizzaile. 6. ltri esercizi Esercizio 6.. Sia : R 4! R 4 l alicazione lineare che nella ase standard è raresentatata dalla matrice [] = Dire se è diagonalizzaile. Descrivere gli autovalori e gli autosazi di. Esercizio 6.. Sia F :! l alicazione lineare definita, nella ase standard di, dalla matrice: [F ]=@ i Dire se F è diagonalizzaile e, se lo è, trovare un ase di autovettori [nota: ricordate che stiamo lavorando sul camo ]. Esercizio 6.. onsideriamo l endomorfismo lineare L a di R diendente dal arametro reale a e definito da: L a (x, y, z) =(ax + y + z,x + ay + z, x + y + az) () Discutere la diagonalizzailità di L a al variare del arametro reale a. () Determinare, se esiste, una ase di R di autovettori er L. Esercizio 6.4. Sia T : R! R l endomorfismo la cui matrice risetto alla ase standard Dire se T è diagonalizzaile e, se lo è, trovare una ase fatta da autovettori. 5
16 Esercizio 6.5. a) Si consideri l endomorfismo :! a cui nella ase standard è associata la matrice Trovare gli autovettori di edirese è diagonalizzaile. ) Si consideri l endomorfismo B : R! R a cui nella ase standard è associata la matrice i) Per quali valori di R è diagonalizzaile? ii) Sia k un intero ositivo. Si trovino, in funzione di k e del arametro, gli autovalori dell endomorfismo B k. Esercizio 6.6. onsideriamo l alicazione lineare a : R 4! R 4 definita risetto alla ase standard dalla seguente matrice: [ a ]= a Dire se esistono, e in caso a ermativo trovare quali, valori del arametro a R er cui a è diagonalizzaile. Determinare inoltre gli autovettori di. Esercizio 6.7. Sia F a : R! R l alicazione lineare la cui matrice associata risetto alla ase canonica è la seguente: [F a ]=@ a + () Determinare er quali valori del arametro a la matrice [F a ]èinvertiile. () Trovare i valori di a er i quali F a è diagonalizzaile. () Trovare, se esiste, una ase di autovettori di F a quando a =/. Esercizio 6.8. Sia T a : R! R l endomorfismo lineare che, risetto alla ase standard di R, è raresentato dalla seguente matrice: a 7a a Per quali valori di a R l endomorfismo T a è diagonalizzaile? Esercizio 6.9. Sia T a : R! R l endomorfismo lineare che, risetto alla ase standard di R, è raresentato dalla seguente a a) Per quali valori di a R l endomorfismo T a è diagonalizzaile? ) Trovare, er ogni a er cui T a è diagonalizzaile, una ase di R costituita da autovettori di T a. 6
17 Esercizio 6.. Sia T a : R! R l endomorfismo lineare che, risetto alla ase standard di R, è raresentato dalla seguente matrice: a 4a a + Per quali valori di a R l endomorfismo T a è diagonalizzaile? Esercizio 6.. Sia T k : R! R l alicazione lineare che, risetto alla ase standard di R, è raresentata dalla seguente k a) Per quali valori di k R T k è diagonalizzaile? ) Nei casi in cui T k è diagonalizzaile, trovare una ase fatta da autovettori. Esercizio 6.. Sia T a : R 4! R 4 l endomorfismo lineare che, risetto alla ase standard di R 4, è raresentato dalla seguente matrice: a B a a a) Per quali valori di a R l endomorfismo T a è diagonalizzaile? ) Trovare, er ogni a er cui T a è diagonalizzaile, una ase di R 4 costituita da autovettori di T a. Esercizio 6.. Sia V uno sazio vettoriale di dimensione finita n sul camo K e sia T : V! V un endomorfismo lineare. Dimostrare che esiste in K[t] un olinomio di grado minore o uguale a n tale che è l endomorfismo nullo. f(t) =a n t n + + a t + a f(t )=a n T n + + a T + a I Esercizio 6.4. Un endomorfismo lineare T : V! V si dice nilotente se er un certo intero ositivo n vale che T n = T T T T è l endomorfismo nullo. Dimostrare che se T è nilotente allora ha un unico autovalore: =. Esercizio 6.5. Nel caso in cui V sia uno sazio vettoriale sul camo dimostrare il viceversa dell enunciato dell esercizio recedente, ossia che se T ha un unico autovalore, uguale a, allora T è nilotente. Se il camo è R esisachet ha un unico autovalore reale, uguale a, allora si uò concludere che T è nilotente? nalogamente, una matrice quadrata si dice nilotente se er un certo intero ositivo n vale che n è l a m a t r i c e n u l l a. 7
18 Esercizio 6.6. Sia V uno sazio vettoriale di dimensione 4 sul camo K esia T : V! V un endomorfismo lineare che, risetto ad una certa ase, è raresentato dalla matrice: [T ]= L endomorfismo T è nilotente? È diagonalizzaile? Esercizio 6.7. Sia T : V! V un endomorfismo lineare e sia un autovalore. Dimostrare che, er un ogni intero ositivo n, n è un autovalore di T n. Esercizio 6.8. Sia V uno sazio vettoriale di dimensione finita sul camo K esia T : V! V un endomorfismo lineare diverso da I eda I. Suoniamo che valga T = I. Individuare gli autovalori di T e dimostrare che T è diagonalizzaile. Esercizio 6.9 (Proiezione lineare su un sottosazio). Sia V uno sazio vettoriale di dimensione finita sul camo K esiat : V! V un endomorfismo lineare diverso da I e dall endomorfismo nullo. Suoniamo che valga T = T. Dimostrare che T è diagonalizzaile e ha due autovalori, e. Osservare che questo equivale a dire che T è u n a roiezione lineare di V su V : T manda V surgettivamente su V e lascia fissi tutti i vettori di V.Siav,v,...,v n una ase che diagonalizza T, con V =<v,v,...,v i > e V =<v i+,...,v n >: scrivendo i vettori risetto a questa ase, la T è l alicazione tale che [T ] a.. a i a i+.. a n = Esercizio 6. (Diagonalizzazione simultanea di endomorfismi che commutano). Sia V uno sazio vettoriale di dimensione finita n sul camo K e siano T ed S due endomorfismi lineari diagonalizzaili. Dimostrare che, se vale T S = S T allora esiste una ase di V che diagonalizza S e T simultaneamente. Dimostrare che è vero anche il viceversa, ossia che se esiste una ase di V che diagonalizza S e T simultaneamente allora T ed S commutano. Suggerimento. ominciare con l osservare che, se è un autovalore er S e V è i l s u o a u t o s a z i o, a l l o r a T (V ) V. Esercizio 6.. Trovare, se ossiile, una ase di R che diagonalizza simultaneamante gli endomorfismi T ed S che, nella ase standard, sono raresentati risettivamente dalle matrici: [T ]= [S] = a.. a i
Corso di Matematica Discreta. Anno accademico Appunti sulla diagonalizzazione.
 Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Traccia dello svolgimento di alcuni esercizi del compito del 15/04/08
 Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Isometrie. (f (g h))(x) = f(g(h(x))) = ((f g) h)(x).
 Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
Esercizi con martingale Pietro Caputo 23 novembre 2006
 Esercizi con martingale Pietro Cauto 23 novembre 2006 Esercizio 1. Sia {X n } la asseggiata aleatoria simmetrica su Z con X 0 = 0, vale a dire che Z k = X k X k 1, k = 1, 2,... sono indiendenti e valgono
Esercizi con martingale Pietro Cauto 23 novembre 2006 Esercizio 1. Sia {X n } la asseggiata aleatoria simmetrica su Z con X 0 = 0, vale a dire che Z k = X k X k 1, k = 1, 2,... sono indiendenti e valgono
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento della prova scritta - fuori corso - di Matematica II 11 Novembre 2010
 UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento Prova scritta di Matematica II 09 Febbraio 2011
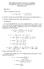 UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
Problemi sulle equazioni parametriche
 A Problemi sulle equazioni arametriche Le soluzioni di un equazione letterale sono funzioni dei arametri che in essa comaiono e ci si uò chiedere er quali valori di tali arametri un equazione ha delle
A Problemi sulle equazioni arametriche Le soluzioni di un equazione letterale sono funzioni dei arametri che in essa comaiono e ci si uò chiedere er quali valori di tali arametri un equazione ha delle
Capitolo 2. Funzioni
 Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Soluzione: La matrice M cercata è quella formata dagli autovettori di A. Il polinomio caratteristico di A è: p t (A) = (t 1)(t 3) 0 4 V 1 = Ker
 Compito di Algebra Lineare - Ingegneria Biomedica 4 luglio 7 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può
Compito di Algebra Lineare - Ingegneria Biomedica 4 luglio 7 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può
Comportamento asintotico delle Catene di Markov
 Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
Soluzioni delle Esercitazioni VIII 21-25/11/2016. = lnx ln1 = lnx. f(t)dt.
 Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Problema Determina l equazione omogenea del completamento proiettivo della conica a ne di equazione: 2x 2 3y 2 +5x 2y +3=0.
 8 Esercizi svolti Coniche a ni Nel iano a ne (reale o comlesso) sia fissato un sitema di riferimento con coordinate (, ). Si consideri il comletamento roiettivo con coordinate omogenee [X,X,X ] tali che
8 Esercizi svolti Coniche a ni Nel iano a ne (reale o comlesso) sia fissato un sitema di riferimento con coordinate (, ). Si consideri il comletamento roiettivo con coordinate omogenee [X,X,X ] tali che
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
Alcuni esercizi sulla diagonalizzazione di matrici. campo dei reali. Se lo è calcolare una base spettrale e la relativa forma diagonale di A.
 Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
Corso di Laurea in Fisica. Geometria 1. a.a Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 17/11/06 B =
 Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Esercizio 1. Sono dati i vettori. 1 A v2 3 ;1A v3 k 0. (e) Calcolare la proiezione ortogonale su W? del vettore v ;1 SOLUZIONE
 CORSI DI LURE IN INGEGNERI ELETTROTECNIC E INGEGNERI MECCNIC {.. 9- PROV SCRITT DI GEOMETRI DEL -- Corsi dei Pro. M. BORDONI, M. MRIETTI Esercizio. Sono dati i vettori v = @ ; v = @ ; v = @ k con k arametro
CORSI DI LURE IN INGEGNERI ELETTROTECNIC E INGEGNERI MECCNIC {.. 9- PROV SCRITT DI GEOMETRI DEL -- Corsi dei Pro. M. BORDONI, M. MRIETTI Esercizio. Sono dati i vettori v = @ ; v = @ ; v = @ k con k arametro
Applicazioni lineari e diagonalizzazione
 Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Probabilità e tempi medi di assorbimento
 Probabilità e temi medi di assorbimento 6.1 Probabilità di assorbimento Consideriamo una catena con un numero finito di stati che indichiamo con S = {1, 2,... r}. Sia C una classe chiusa di S. Se la catena
Probabilità e temi medi di assorbimento 6.1 Probabilità di assorbimento Consideriamo una catena con un numero finito di stati che indichiamo con S = {1, 2,... r}. Sia C una classe chiusa di S. Se la catena
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
SOLUZIONE = p 4 x = 1 4 x2 +
 SOLUIONE (a) Per rovare che F () = + arcsin è una rimitiva di f() = sull intervallo (, ) è su ciente rovare che F () =f(), er ogni (, ) F () = + + / / = + + = = + + = + = f() (b) Sicuramente G() è una
SOLUIONE (a) Per rovare che F () = + arcsin è una rimitiva di f() = sull intervallo (, ) è su ciente rovare che F () =f(), er ogni (, ) F () = + + / / = + + = = + + = + = f() (b) Sicuramente G() è una
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI
 M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Prodotto scalare e matrici < PX,PY >=< X,Y >
 Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Esercizi proposti - Gruppo 7
 Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8
![Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8 Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8](/thumbs/103/157085746.jpg) Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Cubiche e affinità nelpiano
 Cubiche e affinità neliano Francesco Daddi Marzo 2009 Vogliamo dimostrare che, assegnata una qualsiasi coia di funzioni cubiche, esiste un affinità che trasforma l una nell altra. E ossibile collegare
Cubiche e affinità neliano Francesco Daddi Marzo 2009 Vogliamo dimostrare che, assegnata una qualsiasi coia di funzioni cubiche, esiste un affinità che trasforma l una nell altra. E ossibile collegare
Parte 7. Autovettori e autovalori
 Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Criteri di diagonalizzabilità Maurizio Cornalba 18/12/2013
 Criteri di diagonalizzabilità Maurizio Cornalba 8/2/203 Sia K un campo e sia P (t) un polinomio a coefficienti in K. Se a K, la molteplicità di a come radice di P (t), che indicheremo con m a, è il massimo
Criteri di diagonalizzabilità Maurizio Cornalba 8/2/203 Sia K un campo e sia P (t) un polinomio a coefficienti in K. Se a K, la molteplicità di a come radice di P (t), che indicheremo con m a, è il massimo
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
LA DIAGONALIZZAZIONE. asdf. Polinomi di matrici. 30 January 2012
 asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
11 settembre Soluzione esame di geometria - Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura 3 ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Esercizi Di Geometria 1 (BAER) Canale 1
 Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Corso Matematica Discreta Anno accademico Lista domande per l orale breve.
 Corso Matematica Discreta Anno accademico 2014-2015 Lista domande per l orale breve. 1. Dimostrare una delle leggi che coinvolgono l intersezione, l unione, il complementare (associativa, distributiva
Corso Matematica Discreta Anno accademico 2014-2015 Lista domande per l orale breve. 1. Dimostrare una delle leggi che coinvolgono l intersezione, l unione, il complementare (associativa, distributiva
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
DEFINIZIONE PROVVISORIA DI LOGARITMO ED ESPONENZIALE
 DEFINIZIONE PROVVISORIA DI LOGARITMO ED ESPONENZIALE 0 novemre 20 Come dice il titolo, in questi appunti vogliamo dare una definizione rigorosa, ma provvisoria, dei logaritmi e degli esponenziali. Si tratta
DEFINIZIONE PROVVISORIA DI LOGARITMO ED ESPONENZIALE 0 novemre 20 Come dice il titolo, in questi appunti vogliamo dare una definizione rigorosa, ma provvisoria, dei logaritmi e degli esponenziali. Si tratta
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Cambiamento di coordinate e matrice di passaggio
 Camiamento di coordinate e matrice di passaggio In queste note spieghiamo come usare le matrici di passaggio da una ase B ad una ase B per calcolare come camiano le coordinate di un vettore passando da
Camiamento di coordinate e matrice di passaggio In queste note spieghiamo come usare le matrici di passaggio da una ase B ad una ase B per calcolare come camiano le coordinate di un vettore passando da
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Corso Matematica Discreta Anno accademico Lista domande per l orale breve.
 Corso Matematica Discreta Anno accademico 2015-2016 Lista domande per l orale breve. 1. Dimostrare una delle leggi che coinvolgono l intersezione, l unione, il complementare di insiemi contenute nel Teorema
Corso Matematica Discreta Anno accademico 2015-2016 Lista domande per l orale breve. 1. Dimostrare una delle leggi che coinvolgono l intersezione, l unione, il complementare di insiemi contenute nel Teorema
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2011-2012 Prova scritta del 28-1-2013 TESTO E SOLUZIONI 1. Per k R considerare il sistema lineare X 1 X 2 + kx 3 =
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2011-2012 Prova scritta del 28-1-2013 TESTO E SOLUZIONI 1. Per k R considerare il sistema lineare X 1 X 2 + kx 3 =
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
Compito di MD 4 Giugno 2014
 Compito di MD 4 Giugno 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive di motivazioni,
Compito di MD 4 Giugno 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive di motivazioni,
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Autovettori e autovalori
 Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del
 Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del 66 Problema Si consideri la trasformazione lineare L: R 4 R 3 la cui matrice
Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del 66 Problema Si consideri la trasformazione lineare L: R 4 R 3 la cui matrice
