Secondo semestre. Successioni numeriche
|
|
|
- Fabriciano Corona
- 5 anni fa
- Visualizzazioni
Transcript
1 Registro delle lezioni del corso di Analisi Matematica Università di Firenze - Scuola di Ingegneria Corso di Laurea in Ingegneria Meccanica Meccanica e Gestionale E N a.a. 2016/17 - Prof. M.Patrizia Pera 1 a settimana - dal Successioni numeriche Secondo semestre Definizione. Una successione in un insieme X è un applicazione (o funzione) f: N X. Se il codominio X è un sottoinsieme di R, la successione si dice reale (o di numeri reali). Data una successione f: N X, per motivi di tradizione e di semplicità, l immagine di un generico n N si denota col simbolo a n, invece che con f(n). Il valore a n associato ad n si chiama termine n-esimo della successione o elemento di indice n. I numeri naturali sono detti gli indici della successione. Vari modi di indicare una successione f: N X sono: - f: N X (è quello più corretto ma il meno usato); - a 1, a 2,..., a n,... (elencando i termini); - {a n } n N (specificando che il dominio è N ) o anche {a n } (usato quando risulta chiaro dal contesto che rappresenta una successione). Da ora in avanti, a meno che non sia diversamente specificato, ci occuperemo di successioni di numeri reali. In questo caso vale la convenzione che abbiamo adottato per le funzioni reali: per semplicità, a meno che non sia detto esplicitamente, si assume che il codominio coincida con R. Esempi di successioni reali: 1, 1 2, 1 3,, 1 n,... 1, 1, 1,..., ( 1) n,... 2, 4, 6,..., 2n, , 2 3, 3 4,..., n n+1,... Alcune successioni sono definite in modo ricorsivo, cioè: 1) assegnando il primo termine (o i primi k-termini); 2) dando una legge per ricavare il termine (n + 1)-esimo dai termini precedenti. Versione del 30 maggio
2 Un esempio di successione definita in modo ricorsivo è rappresentato dalla successione di Fibonacci (matematico pisano della prima metà del XIII secolo), dove sono assegnati i primi due termini, a 1 = 1 e a 2 = 1, ed ogni altro termine è somma dei due precedenti, cioè a n+1 = a n + a n 1. Tale successione governa alcuni fenomeni naturali come, ad esempio, il numero dei discendenti dei conigli e il numero degli antenati delle api (nelle varie generazioni). Un altro esempio di successione ricorsiva si ottiene ponendo b n = a n+1 /a n, dove {a n } è la successione di Fibonacci. Si ha b 1 = 1 e b n+1 = 1+1/b n. Si può provare che tale successione ha come limite (vedere sotto per la definizione di limite) il numero (1 + 5)/2 che è detto sezione aurea e ha importanti applicazioni nell architettura e nella pittura. Osservazione. Attenzione a non fare confusione tra i termini della successione (che sono sempre infiniti: il primo, il secondo, il terzo, ecc.) e i valori assunti dalla successione che possono essere anche un numero finito. Ad esempio, la successione {a n } n N = {( 1) n } n N assume solo i valori 1 e 1 ma, ciascuno, infinite volte (il primo termine è 1, il secondo è 1, il terzo è 1,..., l n-esimo è ( 1) n,... ). Definizione. Si dice che una successione {a n } tende (o converge) a l R, e si scrive a n l (per n + ), se per ogni ɛ > 0 esiste un indice N (dipendente da ɛ) tale che per n > N si ha a n l < ɛ. Il numero l è detto il limite di {a n } e si scrive anche lim n + a n = l oppure lim a n = l. La seconda notazione, particolarmente sintetica, è giustificata dal fatto che + è l unico punto di accumulazione per N e quindi l unica nozione di limite che ha senso per le successioni è per n +. Osserviamo anche che nella definizione di limite affermare che per ogni ɛ > 0 esiste N N tale che per n > N si abbia a n l < ɛ è equivalente a verificare che per ogni ɛ > 0 esiste N R tale che per n > N si abbia a n l < ɛ. In altre parole è sufficiente che la disuguaglianza a n l < ɛ sia soddisfatta per tutti gli indici n maggiori di un certo numero reale N che può anche non essere un intero positivo. Definizione. Si dice che {a n } tende (o diverge) a + [ ] (si scrive a n + [a n ]) se per ogni M R esiste un indice N (dipendente da M) tale che per n > N si ha a n > M [a n < M]. Definizione. Una successione {a n } si dice convergente se ammette limite finito, divergente se il limite è + o e non regolare quando non ammette limite. Versione del 30 maggio
3 Esempio. Verifichiamo che 1 lim n + n = 0. Dato ɛ > 0, dobbiamo determinare N N tale che se n > N si abbia 1 n < ɛ o, equivalentemente, ɛ < 1 n < ɛ. Ovviamente risulta 1/n > ɛ per ogni n N ed è sufficiente prendere N = [1/ɛ] perché se n > N si abbia 1 n < ɛ (ricordiamo che [1/ɛ] denota la parte intera di 1/ɛ). Per quanto osservato sopra, se cerchiamo N R e non necessariamente N N, sarà sufficiente prendere N = 1/ɛ, senza ricorrere alla parte intera di tale numero. Esercizio. Verificare, mediante la definizione di limite, che n n Svolgimento. Fissiamo ɛ > 0. Occorre provare che esiste un N N tale che n > N n n < ɛ. La disequazione è equivalente alla coppia di disequazioni ɛ < n n < ɛ. La disuguaglianza n n+1 1 < ɛ è vera per ogni n N in quanto il primo membro è negativo, mentre ɛ < 1 n+1 è vera per ogni n N che sia maggiore di 1 ɛ 1. Esercizio. Verificare, usando la definizione di limite, che 3n + 1 lim n + n + 2 = 3; n 3 + 2n + 1 lim n + 2n 3 = 1 4 2, lim n + n2 + n = +, lim n + n2 + n =. Versione del 30 maggio
4 Esercizio. Provare che la successione {( 1) n } è non regolare. Teorema. (Unicità del limite). Il limite di una successione, se esiste (finito o infinito), è unico. I concetti di funzione limitata superiormente, limitata inferiormente, limitata sono già stati definiti per arbitrarie funzioni a valori reali. Essi rimangono pertanto validi anche per le successioni reali, essendo queste delle particolari funzioni a valori reali (l unica distinzione riguarda il dominio, non il codominio). Ad esempio, diremo che la successione {a n } è limitata se esiste M > 0 tale che a n M per ogni n N. Teorema. Ogni successione convergente è limitata. Osservazione. Esistono successioni limitate ma non convergenti. Ad esempio, la successione {a n } = {( 1) n }. Definizione. Diremo che una successione {a n } soddisfa una certa proprietà P definitivamente se esiste N N tale che i termini a n soddisfano P per ogni n > N. In altre parole, se {a n } soddisfa P definitivamente significa che i termini della successione per i quali P può non essere soddisfatta sono in numero finito. Esempio. La successione di termine n-esimo a n = n 7 n + 3 è definitivamente positiva essendo a n > 0 per ogni n > 7. Esempio. Una successione {a n } converge ad l se per ogni ɛ > 0 si ha a n l < ɛ definitivamente. I risultati che seguono sono stati già enunciati nel contesto delle proprietà dei limiti di funzioni reali di variabile reale. Per completezza li riportiamo interpretandoli nell ambito delle successioni. Teorema. (Permanenza del segno per le successioni). Sia {a n } una successione reale. Se a n tende ad un limite maggiore di 0 (anche + ), allora a n > 0 definitivamente (cioè esiste N N tale che a n > 0 per ogni n > N). Dimostrazione. Supponiamo che il limite l della successione {a n } sia finito e positivo. Fissato ɛ = l/2, dalla definizione di limite si deduce che l ɛ < a n < l + ɛ definitivamente. Quindi, essendo l ɛ = l l/2 = l/2 > 0, si ottiene 0 < a n definitivamente. Analizziamo ora il caso in cui il limite sia +. Fissato un qualunque M > 0, si ha (sempre per la definizione di limite) a n > M definitivamente e quindi, a maggior ragione, a n > 0 definitivamente. Versione del 30 maggio
5 Teorema. (Operazioni sui limiti per le successioni). Siano {a n } e {b n } due successioni tali che a n λ e b n µ, dove λ, µ R. Allora, quando ha senso nei reali estesi (cioè tranne i casi, 0/0, 0 e / ), si ha: 1) a n + b n λ + µ ; 2) a n b n λµ ; 3) a n /b n λ/µ. Riportiamo alcuni esempi per mostrare come non sia conveniente dare un senso, nei reali estesi, alle espressioni, 0/0, 0 e / (dette forme indeterminate): ( ) (n + 1) n 1 ( ) n 2 n + (0 ) (1/n)n 1 (0 ) (1/n)n 2 + (0/0) (1/n)/(1/n) 1 (0/0) (1/n 2 )/(1/n) 0 ( / ) n/n 1 ( / ) n 2 /n + Esercizio. Usando il teorema precedente, calcolare n 2 + n + 1 lim n 6n 2 + 3n ; lim n n n Il risultato che segue è una facile conseguenza del teorema della permanenza del segno. Teorema (del confronto dei limiti per le successioni). Se a n l R, b n m R e a n b n definitivamente, allora l m. Dimostrazione. Se, per assurdo, l fosse maggiore di m, la successione {a n b n } tenderebbe al numero positivo l m. Di conseguenza, per il teorema della permanenza del segno, risulterebbe a n b n > 0 definitivamente, in contrasto con l ipotesi a n b n, n N. Un caso particolare del Teorema del confronto dei limiti per le successioni è il seguente corollario. Versione del 30 maggio
6 Corollario. Se {a n } è una successione reale a termini non negativi (rispettivamente non positivi) convergente ad l, allora risulta l 0 (risp. l 0). Teorema (dei carabinieri per le successioni). successioni tali che a n b n c n. Se a n l R e c n l R, allora anche b n l. Siano {a n }, {b n } e {c n } tre Dimostrazione. Fissiamo un ɛ > 0. Poiché a n l, esiste un n 1 tale che l ɛ < a n < l + ɛ per tutti gli n > n 1. Per lo stesso ɛ è possibile determinare un n 2 tale che l ɛ < c n < l + ɛ per n > n 2. Quindi, se n > N := max{n 1, n 2 }, allora l ɛ < a n b n c n < l + ɛ, da cui si ottiene l ɛ < b n < l + ɛ per tutti gli n > N. Osservazione. Osserviamo che il teorema dei carabinieri è ancora valido se si suppone che la condizione a n b n c n (ferme restando le altre ipotesi) valga definitivamente (non occorre sia vera per ogni n N). L importante è che i carabinieri {a n } e {c n } prima o poi catturino {b n } e si dirigano entrambi dalla stessa parte. Esempio. La successione { sen n } n è rapporto di due successioni: {sen n} e {n}. Il suo limite non si può determinare applicando il Teorema sulle operazioni dei limiti perché la successione {sen n} non ha limite per n (cosa che noi non dimostreremo). D altra parte si ha 1 n sen n n e quindi dal Teorema dei carabinieri si deduce sen n n 0. 1 n, Definizione. Una successione si dice infinitesima se è convergente a zero. E immediato verificare che Teorema. La successione {a n } è infinitesima se e solo se la successione { a n } è infinitesima. Osservazione. Nella proposizione precedente non si può sostituire 0 con un valore l 0. Infatti, ad esempio, la successione a n = ( 1) n non ammette limite, Versione del 30 maggio
7 ma a n = 1 e quindi converge a 1. In generale, vale però la seguente implicazione: a n l a n l. Il seguente teorema è utile in molte occasioni: Teorema. La successione prodotto di una successione limitata per una infinitesima è infinitesima. Dimostrazione. Sia {a n } una successione limitata. Perciò esiste M > 0 tale che a n M per ogni n N. Sia b n tale che lim n + b n = 0. Si ha 0 a n b n M b n, da cui, per il Teorema dei carabinieri e per il teorema precedente, si deduce che {a n b n } è infinitesima. Esempio. Dal teorema precedente si deduce immediatamente che le successioni { } { } ( 1) n sen n e n n 2 n sono infinitesime. Teorema (del carabiniere per le successioni). Siano {a n }, {b n } due successioni tali che a n b n definitivamente. Se a n + (b n ), allora anche b n + (a n ). Analogamente a ciò che si è visto per le funzioni, gli estremi inferiore e superiore di {a n } sono gli estremi inferiore e superiore dell insieme dei valori assunti dalla successione e si denotano, rispettivamente, con inf a n e sup a n, n N o più semplicemente con inf a n e sup a n. Se una successione {a n } non è limitata superiormente [inferiormente] si pone n N sup a n = + [inf a n = ]. Osservazione. La seguente caratterizzazione per l estremo superiore [estremo inferiore] di una successione è analoga a quella data per una funzione reale: sup a n = l R [ inf a n = l R] se e solo se Versione del 30 maggio
8 1) a n l, [a n l] n N; 2) ɛ > 0 esiste un indice n ɛ tale che a nɛ > l ɛ [a nɛ < l + ɛ]. Esercizio. Provare che ( ) n 2 sup( 1) n n N n + 3 = 1 e inf n N ( 1)n ( ) n 2 = 1. n + 3 Suggerimento. Per provare la prima delle due uguaglianze usiamo la caratterizzazione richiamata sopra. La 1) è verificata essendo ovviamente ( ) n 2 ( 1) n 1 n + 3 per ogni n N. Per quanto riguarda la 2) si tratta di verificare che per ogni ɛ > 0 è possibile determinare un indice n ɛ tale che ( ) nɛ 2 ( 1) nɛ > 1 ɛ. n ɛ + 3 È sufficiente prendere come n ɛ un n pari e tale che n > (3(1 ɛ) + 2)/ɛ. Definizione. Una successione {a n } si dice crescente [decrescente] se per ogni m, n N con m < n si ha a m a n [a m a n ]. Una successione {a n } si dice strettamente crescente [strettamente decrescente] se per ogni m, n N con m < n si ha a m < a n [a m > a n ]. Le successioni (strettamente) crescenti o (strettamente) decrescenti sono dette successioni (strettamente) monotòne. Osservazione. È facile verificare che la definizione di successione monotona è equivalente alla seguente: {a n } si dice crescente [decrescente] se, per ogni n N risulta a n a n+1 [a n a n+1 ]. Teorema. (Limite per successioni monotone). Se {a n } è una successione monotona, allora ammette limite. Precisamente si ha lim a n = sup a n se {a n } è crescente e lim a n = inf a n se è decrescente. In particolare se {a n }, oltre ad essere monotona, è anche limitata, allora è convergente, se invece non è limitata, è divergente. Dimostrazione. (Facoltativa) Assumiamo, per fissare le idee, che la successione {a n } sia crescente (il caso {a n } decrescente è analogo). Supponiamo prima che l estremo superiore di {a n } sia finito e denotiamolo, per brevità, con la lettera l. Fissiamo un arbitrario ɛ > 0. Poiché (per definizione di Versione del 30 maggio
9 estremo superiore) l è il minimo maggiorante per {a n }, il numero l ɛ non può essere un maggiorante per {a n }. Non è vero quindi che tutti gli a n verificano la condizione a n l ɛ. Ne esiste quindi (almeno) uno, denotiamolo a n, che non verifica tale condizione. Esiste cioè un indice n per il quale risulta a n > l ɛ (proprietà (2) della caratterizzazione dell estremo superiore). Dato che abbiamo supposto {a n } crescente, se n è un qualunque indice maggiore di n, si ha a n a n e quindi, a maggior ragione, l ɛ < a n. D altra parte l è un maggiorante per gli a n e, di conseguenza, per ogni n (e non solo per quelli maggiori di n) risulta a n l (proprietà (1) della caratterizzazione dell estremo superiore). In conclusione, possiamo affermare che per gli n > n si ha l ɛ < a n < l + ɛ, e quindi, per la definizione di limite, a n l = sup a n. Supponiamo ora sup a n = + e fissiamo un M > 0. Poiché (in base al significato della notazione sup a n = + ) la successione non è limitata superiormente, il numero M non può essere un maggiorante per tutti gli a n. Esiste quindi un indice n per il quale risulta a n > M. Dato che la successione è crescente, quando n > n si ha a n > M. Dunque, per la definizione di limite, a n + = sup a n. Osservazione. La condizione espressa dal teorema precedente è ovviamente solo sufficiente. Ad esempio la successione {a n } = { ( 1)n n } è convergente (infatti tende a 0), ma non è monotona. Si ha sup a n = max a n = 1/2 e inf a n = min a n = 1. Un esempio importante di successione monotona è il seguente: Esempio. Il numero e. Consideriamo la successione il cui termine n-esimo è ( a n = ) n n Si può provare che essa è: strettamente crescente; limitata superiormente (3 è un maggiorante). Perciò, per il teorema del limite per le successioni monotone, è convergente. Il suo limite si denota con e ed è detto numero di Nepero. Tale numero è irrazionale e un suo valore approssimato (a meno di 10 9 ) è dato da 2, Notiamo che questa è una delle possibili definizioni del numero e (un altra, che vedremo in seguito, è quella basata sulla nozione di serie). Il logaritmo naturale (o in base e) di un numero x si denota ln x o log x. Versione del 30 maggio
10 Esempio. Proviamo che ( lim 1 1 ) n = 1 n + n e. Si ha ( 1 1 n) n = D altra parte ( ) n = n 1 ( ) n n 1+1 = n 1 ( n n 1 1 ) n. [ ( ) n 1 ( ) ] e. n 1 n 1 Esempio. Proviamo che ( lim x = e. x ± x) Per x > 0, si ha ( ) [x] ( x ( 1 + [x] + 1 x) 1 ) [x]+1. [x] D altra parte, dal limite della successione {(1 + 1/n) n } considerato sopra, si deduce che il primo e l ultimo membro della precedente disequazione tendono a e. Di conseguenza, per il Teorema dei carabinieri, si ottiene che il limite per x + è uguale a e. Applicando il Teorema di cambiamento di variabile per i limiti e tenendo conto del fatto che (1 1/n) n 1/e, si verifica che anche il limite per x è uguale a e. Inoltre, ponendo x = 1/y e applicando nuovamente il Teorema di cambiamento di variabile, si deduce che lim x 0 (1 + x)1/x = e. Infine, tenendo conto della continuità della funzione logaritmo, si ottiene Infatti, si ha log(1 + x) lim = 1. x 0 x log(1 + x) lim = lim log (1 + x) 1/x = log e = 1. x 0 x x 0 Versione del 30 maggio
11 2 a settimana - dal Il seguente risultato mette in relazione il limite di successione e quello di funzione. Teorema ( di collegamento ). Sia f: X R R e sia α R un punto di accumulazione per X. Allora lim x α f(x) = λ R se e solo se per ogni successione {a n } n N, a n X, a n α, a n α si ha lim n f(a n ) = λ. Usando il teorema di collegamento e i limiti di funzione provati in precedenza si ottiene immediatamente che: se {a n } è una qualunque successione infinitesima, allora e sen a n 1 cos a n lim = 1, lim n a n n a 2 n log(1 + a n ) lim = 1. n a n = 1 2 In maniera analoga: se {a n } è una qualunque successione divergente (a + oppure a ), allora ( lim ) an = e. n a n Da quest ultimo risultato si deduce facilmente che ( ) n + k + 1 n lim = e, lim n n + k n ( n + k n + k + 1 ) n = 1 e. Esempio. Usando il teorema di collegamento si può provare che non esiste il limite per x + di sen x. Basta infatti considerare le successioni di termine n-esimo a n = π 2 + 2nπ, a n = 3 2 π + 2nπ e osservare che lim n sen a n = 1 mentre lim n sen a n = 1. Nel calcolo dei limiti di successione sono utili i seguenti teoremi. Teorema. Sia data una successione {a n } a termini positivi. Allora si ha lim n + n an = purché esista il limite al secondo membro. a n+1 lim, n + a n Versione del 30 maggio
12 Esempio. Usando il teorema precedente si deduce immediatamente che n h 1, (h > 1); n n n 1 ; n! + ; n n n n! e. Ad esempio, si ha lim n + n n n lim n + n! = lim n + n n = (n + 1) n+1 (n + 1)! n + 1 lim = 1. n + n n! n n = lim n + ( ) n + 1 n = e. Teorema (criterio del rapporto per le successioni). Sia {a n } una successione a termini positivi. Supponiamo che la successione {b n } = {a n+1 /a n } ottenuta da {a n } facendo il rapporto tra un termine e il precedente ammetta limite β (finito o infinito). Allora, se β < 1 la successione {a n } è infinitesima, se β > 1 la successione è infinita. Esempio. Facendo uso del criterio del rapporto si deduce che n Ad esempio, si ha n α rn 0 (α > 0, r > 1), rn n! 0, n! n n 0. lim n + (n + 1)! n n (n + 1) n+1 n! = da cui, per il criterio del rapporto, n!/n n 0. Esempio. Proviamo che lim n + rn = ( n ) n lim 1 = n + n + 1 e < 1, 0 se r < 1 1 se r = 1 + se r > 1 se r 1 Dimostrazione. Consideriamo ad esempio il caso r < 1. Per il criterio del rapporto, essendo r n+1 lim n + r n = r < 1, si ottiene r n 0. Di conseguenza, poiché come visto in precedenza una successione è infinitesima se e solo se lo è il suo valore assoluto, allora anche r n 0. Gli altri casi sono lasciati per esercizio. Versione del 30 maggio
13 Esempio. Si ha la seguente scala di infiniti: log n, n α (α > 0), r n (r > 1), n!, n n. La scala va intesa nel senso che il limite tra un infinito e il successivo è 0. Serie numeriche Prendiamo ora in esame un esempio particolarmente importante di successione reale. Data una successione reale {a n } n N associamo ad essa la successione {s n } n N di termine n-esimo Ci interessa studiare il limite Tale limite si indica con il simbolo s n = a 1 + a a n = lim s n. n + a k, k=1 n a k. detto serie (numerica), e si legge somma per k che va da 1 a infinito di a k. Ovviamente al posto di k si può usare un qualunque altro indice (si pensi al significato di sommatoria). In altre parole, col simbolo si intende a n, n=1 lim n + n a k. La successione {s n } si dice successione delle somme parziali (o delle ridotte) della serie, mentre a n è detto il termine generale. Il carattere della serie è, per definizione, il carattere della successione {s n }. In altre parole, si dice che la serie converge [diverge] se {s n } converge [diverge]; se il limite di {s n } non esiste, la serie è indeterminata (o irregolare). Il limite s (finito o infinito) di {s n }, quando esiste, si dice somma della serie e si scrive s = k=1 a n. n=1 k=1 Versione del 30 maggio
14 Talvolta, invece di sommare a partire da n = 1, si parte da un indice n 0 N (può essere utile anche n 0 = 0). Scriveremo allora n=n 0 a n. Si vede facilmente che il carattere di una serie non cambia se si modifica un numero finito di termini. La serie geometrica (Esempio importante.) La serie n=0 è detta geometrica. Osserviamo che in una serie geometrica il rapporto tra un termine e il precedente è costante (ossia, non dipende da n) e vale r. Tale rapporto si chiama ragione della serie. Una serie geometrica converge se e solo se la sua ragione è in valore assoluto minore di uno. Inoltre, la somma è 1/(1 r). E noto infatti che r n s n = 1 rn+1 1 r. Perciò, {s n } è convergente se e solo se r < 1 (infatti, in tal caso, r n+1 0). Di conseguenza, se r < 1, si ha o, anche, r n 1 r n+1 = lim n + 1 r n=0 r n = r r n = n=1 Ad esempio, per r = 1/2, si ottiene n=1 n=0 1 2 n = 1. = 1 1 r, r 1 r. A titolo di esempio, consideriamo il numero decimale periodico 3, 1 7 = 3, Si può scrivere 3, 1 7 = 3, 1 + 0, , , = 3, Versione del 30 maggio
15 Ovvero Si ha n=2 3, 1 7 = n n = n=0 n= n = 7/ /10, essendo n=0 1/10n una serie geometrica di ragione 1/10. Si ha pertanto 3, 1 7 = / /10 = In modo analogo si prova che ogni numero decimale periodico è razionale e se ne determina la frazione generatrice. Esempio. La serie n=1 ( 1)n è indeterminata. Infatti si ha s n = 0 se n è pari e s n = 1 se n è dispari. Perciò lim n + s n non esiste. Teorema. Condizione necessaria affinché una serie sia convergente è che il termine generale tenda a zero. Dimostrazione. Sia n=n 0 a n una serie convergente. Ciò significa, per definizione, che la successione {s n } delle somme parziali converge ad un numero (finito) s. Osserviamo che a n = s n s n 1 e che (oltre ad {s n }) anche {s n 1 } converge ad s (infatti, se s n s < ɛ per n > N, allora s n 1 s < ɛ per n > N + 1). Si ha allora lim a n = lim (s n s n 1 ) = s s = 0. n n Osservazione. La precedente condizione non è sufficiente. Proveremo infatti, facendo uso del criterio dell integrale che enunceremo successivamente, che la serie n=1 1/n (detta armonica) non è convergente, sebbene il suo termine generale sia infinitesimo. Esercizio. Sia n=n 0 a n una serie convergente e sia c R. Provare che ca n = c a n. n=n 0 n=n 0 Esercizio. Siano n=n 0 a n e n=n 0 b n due serie convergenti. Provare che (a n + b n ) = a n + b n. n=n 0 n=n 0 n=n 0 Versione del 30 maggio
16 Osservazione (importante). Se una serie n=n 0 a n è a termini non negativi (ossia a n 0 per ogni n), allora la successione {s n } delle sue somme parziali è crescente. Infatti, essendo a n 0, risulta s n = s n 1 + a n s n 1. Perciò, per il teorema sul limite delle successioni monotone, il limite di {s n } esiste sempre (finito o infinito) dal momento che coincide con l estremo superiore di {s n }. In tal caso, la somma della serie è ben definita e rappresenta un numero reale esteso (ovviamente positivo). In altre parole, una serie a termini non negativi o è convergente o è divergente. Analoghe considerazioni valgono, ovviamente, anche per le serie a termini non positivi. Esempio. Consideriamo la serie n=1 1 n α, α > 0, detta serie armonica generalizzata. Si può provare (ad esempio mediante il criterio dell integrale che enunceremo dopo) che la serie converge se e solo se α > 1. Di conseguenza, essendo a termini positivi, essa diverge per 0 < α 1. Talvolta non ha interesse o non si riesce a calcolare esplicitamente la somma di una serie; di solito si cerca di stabilirne il carattere. Successivamente, dopo aver provato che una serie converge, la sua somma (se interessa) potrà essere stimata con metodi numerici mediante l ausilio di un computer. Diamo ora un criterio utile per stabilire il carattere di una serie a termini positivi. Criterio del confronto per le serie a termini positivi. Siano n=n 0 a n e n=n 0 b n due serie a termini non negativi. Supponiamo a n b n per n n 0. Allora, se converge la serie n=n 0 b n (detta maggiorante), converge anche (la minorante) n=n 0 a n e si ha a n b n ; n=n 0 n=n 0 se diverge la minorante, diverge anche la maggiorante. Dimostrazione. Poiché le due serie sono a termini non negativi, le successioni delle somme parziali n n s n = a k e σ n = b k k=n 0 k=n 0 Versione del 30 maggio
17 risultano crescenti e, conseguentemente, per il teorema del limite di successioni monotone, per entrambe esiste (finito o infinito) il limite per n +. Poiché a n b n per n n 0, si deduce s n σ n per ogni n n 0. Perciò, se n=n 0 b n è convergente (cioè se la successione {σ n } è convergente), dal teorema del confronto dei limiti, si ottiene che la successione {s n } e, quindi, la serie n=n 0 a n sono convergenti. Di conseguenza, se n=n 0 a n diverge, la serie n=n 0 b n non può convergere e quindi necessariamente diverge (ricordarsi che esiste il limite di σ n ). Esercizio. Proviamo che la serie è convergente. Si ha n sen 2 n n 3 + n sen 2 n n 3 + n 1 n 3 + n 1 n 3. La conclusione segue dal criterio del confronto, ricordando che n 1 n 3 è convergente. Esercizio. Proviamo che la serie è convergente. Infatti si ha n 2 + ( 1) n 2 n 2 + ( 1) n 2 n 3 2 n e n ( 1 2 )n, essendo una serie geometrica di ragione 1 2, è convergente. Un utile corollario del criterio del confronto è il seguente: Criterio del confronto asintotico per le serie a termini positivi. Sia n=n 0 a n una serie a termini non negativi. Supponiamo che per qualche α > 0 si abbia Allora, lim n + nα a n = λ R. 1. se 0 < λ < + la serie ha lo stesso carattere di n 1 solo se α > 1); n α (cioè converge se e 2. se λ = 0 e α > 1 la serie converge; 3. se λ = + e α 1 la serie diverge. Versione del 30 maggio
18 Esempio. Consideriamo Poiché n 1 n + 2 arctang 1 n. 1 lim n + n2 n + 2 arctang 1 ( n = lim 1 1 n + n2 n + 2 n + o( 1 ) n ) = 1, per il punto 1) del criterio del confronto asintotico, la serie data ha lo stesso carattere di n 1 n 2 e quindi è convergente. Esempio. Consideriamo Usando la formula di Taylor si ha n 1 n sen 1 n tang 1 n 2. 1 n ( 1 n 1 + o( 1 )) 6n 3 n o( 1 = ) n 2 n o( 1 ) 6n 3 n o( 1 ). n 2 n 2 Perciò, il termine generale della serie data è un infinitesimo di ordine 1. Di conseguenza, per il punto 1) del criterio del confronto asintotico, la serie diverge avendo lo stesso carattere della serie armonica. Esempio. Consideriamo ne n. n Poiché lim n + n α+1 /e n = 0 per ogni α > 0 e quindi, in particolare, anche per ogni α > 1, per il punto 2) del criterio del confronto asintotico, la serie data converge. Esempio. Consideriamo n 1 log n. Poiché lim n + n α / log n = + per ogni α > 0 e quindi, in particolare, anche per ogni α 1, per il punto 3) del criterio del confronto asintotico, la serie data diverge. Un utile criterio per stabilire il carattere di una serie numerica a termini positivi è il seguente: Versione del 30 maggio
19 Criterio dell integrale. Sia n 0 N e sia f: [n 0, + ) R una funzione continua positiva e decrescente. Allora + f(n) e f(x) dx n=n 0 n 0 hanno lo stesso carattere. Più precisamente si ha + + f(x) dx f(n) f(x) dx. n 0 +1 n 0 Esempio. armonica n=n 0 +1 Dal criterio dell integrale si deduce immediatamente che la serie n=1 è divergente. Più precisamente, sempre usando il criterio dell integrale, è facile verificare che la serie armonica generalizzata converge se e solo se α > 1. è convergente se e solo se α > 1. n=1 1 n 1 n α, È sufficiente infatti ricordare che l integrale improprio n= x α dx Esercizio. Usando il criterio dell integrale, provare che 1 n log n e log 2 n n sono divergenti. n=1 Se la serie n=n 0 a n non è di segno costante, in alcuni casi è utile considerare la serie dei valori assoluti, cioè n=n 0 a n. Vale il seguente risultato Criterio della convergenza assoluta. Se converge n=n 0 a n, converge anche n=n 0 a n e vale la disuguaglianza n=n 0 a n a n. n=n 0 Versione del 30 maggio
20 Osservazione. Si osservi che la disuguaglianza nel precedente teorema ha senso in virtù dell affermazione che la serie n=n 0 a n è convergente. In questo caso, infatti, tale serie rappresenta un numero reale, e quindi ha senso il suo valore assoluto. Definizione. La serie n=n 0 a n si dice assolutamente convergente se è convergente la serie n=n 0 a n. Osservazione. Tenendo conto della definizione precedente, il criterio della convergenza assoluta si può enunciare affermando che se una serie è assolutamente convergente, allora è convergente. Esistono anche serie convergenti ma non assolutamente convergenti. Ad esempio, la serie n=1 ( 1)n 1 n è convergente (ciò si può dimostrare facendo uso del criterio di Leibniz che vedremo dopo). D altra parte, la serie dei valori assoluti n=1 ( 1)n 1 n, che è la serie armonica, come sappiamo non converge. Un altro esempio di serie convergente ma non assolutamente convergente è n=1 sen n n. Il criterio del confronto per le serie a termini positivi è ovviamente un criterio di convergenza assoluta. Infatti, data la serie n=n 0 a n esso si può applicare (come mostrato nell esempio che segue) alla serie n=n 0 a n per studiarne il carattere. Esempio. 1) La serie n=1 cos n n 3. è convergente, come si verifica subito applicando il criterio del confronto a cos n n 3 n=1 e applicando successivamente alla serie data il criterio della convergenza assoluta. 2) Consideriamo la serie n=0 ( ) 2 n sen π 3 2 n. Si ha ( ) 2 n sen π 3 2 n ( ) 2 n 3 e quest ultimo è il termine n-esimo di una serie geometrica di ragione 2/3 (quindi convergente). Di conseguenza, ( ) 2 n sen π 3 2 n n=0 Versione del 30 maggio
21 è convergente e, quindi, per il criterio della convergenza assoluta, è convergente. n=0 ( ) 2 n sen π 3 2 n Una serie del tipo n=n 0 ( 1) n a n, a n 0, si dice a segni alterni. Per le serie a segni alterni si può dimostrare il seguente criterio di convergenza: Criterio di Leibniz. Sia n=n 0 ( 1) n a n una serie a segni alterni. Se la successione {a n } è decrescente ed è infinitesima, allora la serie è convergente. Inoltre, denotata con s la sua somma e con s n la sua somma parziale n-esima, risulta s s n < a n+1, n N, ossia l errore che si commette nella valutazione di s arrestandosi alla somma parziale n-esima è inferiore, in valore assoluto, al valore assoluto del primo termine trascurato. A titolo di esempio osserviamo che la serie ( 1) n n=1 soddisfa le due ipotesi del criterio di Leibniz e pertanto è convergente. D altra parte, come già osservato in precedenza, essa non è assolutamente convergente. Inoltre, detta s la sua somma, risulta s n n ( 1) k < 1 k n + 1. k=1 Versione del 30 maggio
22 3 a settimana - dal Serie di funzioni Una serie del tipo n=n 0 f n (x), dove le f n sono funzioni reali di variabile reale, è detta serie di funzioni (reali di variabile reale). Si dice che la serie è definita in un insieme X R se il dominio di tutte le funzioni contiene X (ossia, se sono tutte definite per ogni x X). Ovviamente, ogni volta che si fissa x X, si ottiene una serie numerica che può essere convergente oppure no, a seconda che la successione di funzioni {s n (x)} delle somme parziali n-esime (dove s n (x) = n k=n 0 f k (x)) sia convergente o meno. L insieme dei numeri x X per cui la serie converge si chiama insieme di convergenza (puntuale). Ad esempio, l insieme di convergenza della serie n=0 è l intervallo ( 1, 1), visto che si tratta di una serie geometrica di ragione x R. In analogia con le serie numeriche, se n=n 0 f n (x) converge in un punto x, diremo che la serie di funzioni n=n 0 f n (x) converge assolutamente in x. Dal criterio di convergenza assoluta per le serie numeriche si ottiene subito che la convergenza assoluta di una serie di funzioni implica la sua convergenza (puntuale). Se una serie di funzioni n=n 0 f n (x) converge puntualmente in un insieme A X, allora per ogni x A la somma della serie è un numero reale che possiamo denotare con f(x). Possiamo scrivere perciò f(x) = x n n=n 0 f n (x), x A. Risulta così definita una funzione reale di variabile reale f: A R. È naturale porsi la domanda se una tale funzione sia continua quando sono continue tutte le f n. In altre parole: è ancora vero che la somma di funzioni continue è una funzione continua nel caso di infiniti addendi? La risposta è negativa. L esempio seguente illustra questo fatto. Versione del 30 maggio
23 Esempio. Consideriamo, nell intervallo [0, 1], la serie di funzioni (x n x n+1 ) n=1 che si può anche riscrivere nella forma (1 x)x n. n=1 Per x [0, 1) la serie è geometrica di ragione x e primo termine (1 x)x; pertanto converge e la sua somma è data da (1 x)x 1 x = x. Per x = 1 tutte le funzioni f n (x) = (1 x)x n sono nulle e, di conseguenza, la serie converge anche in tale punto ed ha somma zero. Si può concludere che la serie converge in tutto l intervallo chiuso [0, 1] e la sua somma è { x se x [0, 1) f(x) = 0 se x = 1 che è una funzione discontinua, sebbene tutte le f n addirittura C ). siano continue (sono È utile perciò introdurre un altro tipo di convergenza, la convergenza totale, che implica la convergenza assoluta e garantisce, tra l altro, la continuità della funzione somma. Definizione. Si dice che la serie di funzioni n=n 0 f n (x) converge totalmente in un insieme A R se esiste una serie numerica convergente n=n 0 c n tale che f n (x) c n, n n 0 e x A. Notiamo che se una serie di funzioni n=n 0 f n (x) converge totalmente in un insieme A, allora (come conseguenza dei criteri di convergenza assoluta e del confronto) converge (assolutamente) per ogni x A. Risulta quindi ben definita la funzione somma f(x) = f n (x). n=n 0 Osserviamo inoltre che, supponendo ogni f n limitata, la più piccola serie numerica che domina n=n 0 f n (x) è quella il cui termine generale λ n è dato da λ n = sup{ f n (x) : x A}. Versione del 30 maggio
24 Pertanto, se tale serie numerica converge, allora la serie di funzioni converge totalmente. In caso contrario, ossia se n=n 0 λ n = +, per il criterio del confronto nessuna serie numerica che domina la serie di funzioni può convergere. Possiamo quindi enunciare il seguente Teorema. (facoltativo) Condizione necessaria e sufficiente affinché una serie di funzioni n=n 0 f n (x) converga totalmente in un insieme A è che sia convergente la serie numerica dove λ n = sup{ f n (x) : x A}. n=n 0 λ n, Esempio. Consideriamo la serie di funzioni n=2 ( x n ) n log 1 + n(n 1) 2. Osserviamo che il termine generale f n (x) = n log (1 + x n n(n 1) 2 ) tende a zero se e solo se x 1; perciò la serie può convergere in x se e solo se x [ 1, 1]. Fissato x [ 1, 1], si ha ( x n ) ( ) 1 1 f n (x) = n log 1 + n(n 1) 2 n log 1 + n(n 1) 2 (n 1) 2, da cui, essendo la serie 1 n=2 convergente, dal criterio del confronto si (n 1) 2 deduce che la serie data è assolutamente convergente in x. D altra parte, posto 1 c n =, dal fatto che (n 1) 2 n=2 c n è una serie numerica maggiorante e convergente, si deduce anche che la serie data converge totalmente nell intervallo [ 1, 1]. Consideriamo invece la serie n=2 ) n log (1 + x n. n(n 1) Anche in questo caso il termine generale tende a zero se e solo se x 1. Però la serie converge puntualmente solo per x ( 1, 1), in quanto per x = 1 e x = 1 Versione del 30 maggio
25 si ha ( n=2 n log armonica n=1 1 n n(n 1). Inoltre, essendo sup n log x ( 1,1) ) che diverge avendo lo stesso carattere della serie ) ( (1 + x n = n log 1 + n(n 1) ) 1, n(n 1) la serie non converge totalmente in ( 1, 1) in quanto, come visto sopra, ) n=2 (1 n log + 1 n(n 1) è divergente. Considerando invece un intervallo della forma [ r, r] con 0 < r < 1, si ha ) ( sup n log (1 + x n r n ) = n log 1 + = λ n, x [ r,r] n(n 1) n(n 1) ed essendo n λ n convergente si può concludere che la serie data converge totalmente in [ r, r]. Esercizio. Provare che la serie n=1 1 n x log(1 + 1 n ) converge puntualmente se x > 2 e converge totalmente in [r, + ), con r > 2. Teorema. Sia n=n 0 f n (x) una serie di funzioni continue convergente totalmente in un insieme A e sia la somma della serie. Allora f(x) := f n (x) n=n 0 i) (continuità) la funzione f risulta continua in A; ii) (passaggio al limite sotto l integrale) per ogni intervallo [a, b] A si ha n=n 0 b a f n(x) dx = b a n=n 0 f n (x) dx; iii) (derivabilità) se inoltre le funzioni f n sono di classe C 1 in A e se la serie n=n 0 f n(x) delle derivate converge totalmente in A, allora f risulta di classe C 1 in A e si ha f (x) = n=n 0 f n(x). Versione del 30 maggio
26 Serie di potenze Un esempio importante di serie di funzioni è costituito dalle serie di potenze. Una serie di funzioni del tipo a n (x x 0 ) n, n=0 dove x 0 e gli a n sono numeri reali assegnati, si dice una serie di potenze in campo reale. Il punto x 0 si chiama centro della serie. Una serie di potenze converge ovviamente in x = x 0 (e la sua somma in tal caso vale a 0 ). Dal teorema che segue si deduce che l insieme di convergenza di una serie di potenze è un intervallo (eventualmente ridotto al punto x = x 0 ). Teorema. Supponiamo che la serie di potenze n=0 a n(x x 0 ) n converga in un punto x x 0. Allora la serie converge assolutamente in ogni x tale che x x 0 < x x 0. Inoltre converge totalmente in ogni intervallo del tipo [x 0 r, x 0 + r] con 0 < r < x x 0. Dimostrazione. Poiché la serie converge puntualmente in x, il termine n-esimo tende a 0 per n. Di conseguenza, essendo le successioni convergenti necessariamente limitate, esiste M > 0 tale che a n ( x x 0 ) n M. Pertanto, preso x tale che x x 0 < x x 0 risulta a n (x x 0 ) n = a n ( x x 0 ) n ( ) x x0 n M x x 0 ( ) x x0 n. x x 0 Per come è stato scelto x, la serie geometrica ( n x x0 n=0 x x 0 ) ha ragione minore di 1 e quindi converge. Perciò, per il criterio del confronto, n=0 a n(x x 0 ) n converge, cioè n=0 a n(x x 0 ) n converge assolutamente in x. Sia ora r tale che 0 < r < x x 0. Con la stessa dimostrazione fatta sopra si ottiene ( ) a n (x x 0 ) n r n M. x x 0 Perciò n=0 a n(x x 0 ) n, essendo dominata dalla serie numerica convergente ( n=0 M r n, x x 0 ) risulta totalmente convergente in [x0 r, x 0 + r]. Dal teorema precedente si ottiene il seguente Teorema. Sia data la serie di potenze a n (x x 0 ) n. n=0 Versione del 30 maggio
27 Allora, o la serie converge solo in x = x 0, oppure esiste R > 0 (eventualmente anche infinito) tale che la serie converge assolutamente se x x 0 < R e non converge se x x 0 > R. Inoltre la serie converge totalmente in ogni intervallo [x 0 r, x 0 + r], con 0 < r < R. Dal risultato precedente si deduce perciò che l insieme di convergenza di una serie di potenze centrata in x 0 è un intervallo (aperto, chiuso o semiaperto) e che x 0 è equidistante dagli estremi (finiti o infiniti che siano). Osserviamo che non si può dire nulla a priori del comportamento della serie nei punti x 0 R e x 0 + R. Ad esempio: la serie n xn n ha raggio di convergenza 1 e converge (non assolutamente) in x = 1 mentre non converge in x = 1; la serie n xn ha raggio n 2 di convergenza 1 e converge assolutamente sia in x = 1 che in x = 1; la serie n nxn ha raggio di convergenza 1 e non converge negli estremi dell intervallo ( 1, 1) (il termine generale non tende a zero). Definizione. La semiampiezza R dell intervallo di convergenza di una serie di potenze si chiama raggio di convergenza della serie. Per calcolare il raggio di convergenza, fissato x R, si può ricorrere agli usuali criteri per le serie a termini positivi applicandoli alla serie n=0 a n x x 0 n, pensata come una serie numerica dipendente dal parametro x. Altrimenti, si può usare ad esempio il seguente Teorema. Sia data una serie di potenze n=0 a n(x x 0 ) n e supponiamo che esista lim n n a n. Allora si ha R = 1 lim n n a n con la convenzione che R = 0 se lim n n a n = + e R = + se lim n n a n = 0 Osservazione. Un altro criterio per il calcolo del raggio di convergenza di una serie di potenze si ottiene ricordando che se esiste lim n + a n+1 a n, allora si ha Esempio. lim n + n an = a n+1 lim. n + a n 1. La serie ha raggio di convergenza R = 1. n=0 x n n Versione del 30 maggio
28 2. La serie n=0 ha raggio di convergenza R = 1/e. 3. La serie ha raggio di convergenza R = +. n=0 n n n! xn x n n! 4. La serie ha raggio di convergenza R = 0. n!x n n=0 Serie di Taylor Sia data una serie di potenze n=0 a n(x x 0 ) n e supponiamo che abbia raggio di convergenza R > 0. Allora è ben definita, nell intervallo (x 0 R, x 0 + R), la somma della serie, cioè una funzione f tale che f(x) := a n (x x 0 ) n, x (x 0 R, x 0 + R). n=0 Teorema. La funzione f definita dalla serie di potenze n=0 a n(x x 0 ) n è continua in ogni punto dell intervallo (x 0 R, x 0 + R). Dimostrazione. Sia x un qualunque punto dell intervallo (x 0 R, x 0 + R). Esiste un numero r, con 0 < r < R, tale che l intervallo (x 0 r, x 0 + r) contiene x. Di conseguenza, poiché la serie è totalmente convergente in [x 0 r, x 0 + r], la funzione somma f è ivi continua. Questo implica, in particolare, che f è continua anche nel punto x. Vediamo altre proprietà delle serie di potenze. Lemma (di invarianza del dominio di convergenza). Supponiamo che la serie di potenze a n (x x 0 ) n n=0 Versione del 30 maggio
29 abbia raggio di convergenza R > 0. Allora le due serie e na n (x x 0 ) n 1 n=1 n=0 hanno raggio di convergenza R. a n n + 1 (x x 0) n+1 Il lemma precedente serve per provare che le serie di potenze sono derivabili termine a termine e integrabili termine a termine ; si ha cioè il seguente Teorema (di derivazione e integrazione delle serie di potenze). Sia f(x) := a n (x x 0 ) n, x (x 0 R, x 0 + R) n=0 una funzione definita da una serie di potenze. Allora f è derivabile in (x 0 R, x 0 + R) e si ha f (x) = na n (x x 0 ) n 1. n=1 Inoltre, per ogni x (x 0 R, x 0 + R) si ha x x 0 f(t)dt = n=0 a n n + 1 (x x 0) n+1. Dimostrazione. (facoltativa) Fissato un qualunque punto x appartenente all intervallo di convergenza (x 0 R, x 0 + R) della prima serie, esiste un intervallo (x 0 r, x 0 + r), con 0 < r < R, contenente x. Per il lemma precedente, R è anche il raggio di convergenza della serie delle derivate, e quindi, in base al teorema della convergenza totale per le serie di potenze, entrambe le serie convergono totalmente in [x 0 r, x 0 + r]. Dal teorema di derivabilità delle serie di funzioni segue che f è derivabile in x e risulta f (x) = na n (x x 0 ) n 1. n=1 Inoltre, dal teorema di passaggio al limite sotto il segno di integrale, si ha x x 0 f(t)dt = x a n (t x 0 ) n dt = x 0 n=0 Versione del 30 maggio
30 = n=0 x x 0 a n (t x 0 ) n dt = n=0 a n n + 1 (x x 0) n+1. Osservazione. Poiché la derivata di una serie di potenze è ancora una serie di potenze, dal teorema precedente segue che le funzioni definite tramite serie di potenze sono di classe C. Sia dunque f(x) := a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) a n (x x 0 ) n + una funzione definita mediante una serie di potenze nell intervallo (x 0 R, x 0 +R). Ponendo x = x 0, si ottiene a 0 = f(x 0 ). Derivando e ponendo di nuovo x = x 0, si ha a 1 = f (x 0 ). Analogamente, mediante derivate successive (vedi l osservazione precedente), si ottiene a n = f (n) (x 0 ). n! Pertanto, risulta necessariamente dove f (0) (x 0 ) denota f(x 0 ). f(x) = n=0 f (n) (x 0 ) n! (x x 0 ) n, In altre parole, la serie di potenze n=0 a n(x x 0 ) n coincide in (x 0 R, x 0 + R) con la serie di potenze f (n) (x 0 ) (x x 0 ) n, n! n=0 che è detta serie di Taylor di f di centro x 0 (o di MacLaurin, quando x 0 = 0). Il ragionamento precedente prova cioè che se una funzione è definita mediante una serie di potenze, essa risulta di classe C in x 0 e la sua serie di Taylor ha per somma la funzione stessa. D altra parte, data una funzione di classe C in x 0, si può considerare la serie di Taylor di f di centro x 0, cioè Ci chiediamo: n=0 f (n) (x 0 ) n! (x x 0 ) n. Versione del 30 maggio
31 1) se esista un intorno di x 0 nel quale questa serie sia convergente; 2) supposto che esista un tale intorno, se in esso la somma della serie sia proprio f(x). Definizione. Una funzione f si dice sviluppabile in serie di Taylor in un intorno di un punto x 0 (o analitica in x 0 ) se esiste un intorno di x 0 in cui vale l uguaglianza f(x) = n=0 f (n) (x 0 ) n! (x x 0 ) n. Si dice che f è analitica se ogni punto del suo dominio ammette un intorno in cui f è sviluppabile in serie di Taylor (ossia, se è analitica in ogni punto del suo dominio). Osservazione. Esistono funzioni di classe C ma non analitiche. Una di queste è { e 1/x 2 se x 0 f(x) = 0 se x = 0, le cui derivate successive (come si potrebbe provare usando un corollario del teorema di Lagrange) risultano tutte continue e nulle nel punto x 0 = 0. Quindi, se f fosse analitica, in un intorno del punto x 0 = 0 dovrebbe valere l uguaglianza f(x) = n=0 f (n) (0) x n, n! e ciò è impossibile perché f(x) 0 per x 0, mentre la sua serie di Taylor f (n) (0) n=0 n! x n ha per somma zero (essendo nulli tutti i suoi termini). Si ha la seguente condizione necessaria e sufficiente affinché una funzione sia sviluppabile in serie di Taylor. Teorema. Una funzione f di classe C in x 0 è sviluppabile in serie di Taylor in un intorno (x 0 R, x 0 + R) di x 0 se e solo se, per ogni x (x 0 R, x 0 + R), risulta lim n R n (x x 0 ) = 0, dove R n (x x 0 ) = f(x) n k=0 denota il resto n-esimo della formula di Taylor. f (k) (x 0 ) k! (x x 0 ) k Esempio. La funzione f(x) = e x è sviluppabile in serie di MacLaurin e tale serie ha raggio di convergenza R = +. Fissiamo un punto x R. Sappiamo che se e x Versione del 30 maggio
32 è effettivamente sviluppabile in serie di MacLaurin, allora si deve necessariamente avere e x f (n) (0) = x n x n = n! n!. n=0 n=0 Per il teorema precedente, ciò equivale ad affermare che dove la somma parziale n-esima lim R n(x) = lim n n (ex P n (x)) = 0, P n (x) = non è altro che il polinomio di MacLaurin di e x di ordine n. Scrivendo il resto R n (x) nella forma di Lagrange, si potrebbe facilmente far vedere che in effetti esso tende a 0 per n +. Per l arbitrarietà del punto x, possiamo concludere che lo sviluppo è valido in tutto R. Ponendo x = 1 nello sviluppo in serie di MacLaurin di e x si ottiene il numero e espresso mediante una serie numerica: 1 e = n!. n=0 Mostriamo ora che la funzione e x è analitica, cioè che è sviluppabile in serie di Taylor in ogni punto di R (facoltativo). A tale scopo fissiamo x 0 R e poniamo, per comodità, x = x 0 + h. Si ha Quindi n k=0 e x = e x 0+h = e x 0 e h = e x 0 (1 + h + h2 2! + + hn n! + ) = x k k! e x 0 + e x 0 h + e x 0 h2 2! + + ex 0 hn n! + e x = e x 0 + e x 0 (x x 0 ) + e x (x x 0 0) e x (x x 0 0) n + 2! n! Esercizio. In maniera analoga a quanto fatto per la funzione esponenziale, si può provare che le funzioni cos x e sen x sono sviluppabili in serie di MacLaurin. Determinarne lo sviluppo e l intorno di validità. Il metodo usato per sviluppare in serie di MacLaurin le funzioni e x, sen x e cos x (basato su una stima del resto della formula di Taylor) non è adatto per la funzione f(x) = log(1 + x). In questo caso conviene procedere diversamente: Versione del 30 maggio
33 1. si determina prima lo sviluppo della derivata f (x) di f(x); 2. successivamente, mediante il teorema di integrazione termine a termine delle serie di potenze, si trova una primitiva dello sviluppo di f (x); 3. infine, tra tutte le primitive di f (x) espresse in serie di potenze, si sceglie quella che coincide con f(x). Tale metodo è adatto anche per determinare lo sviluppo di arctang x e, in generale, di tutte le funzioni di cui è facile sviluppare la derivata. A tale proposito ricordiamo che due primitive di una stessa funzione (definita in un intervallo) differiscono per una costante e, di conseguenza, se coincidono in un punto, coincidono in tutto l intervallo di definizione. Cominciamo col determinare, col metodo appena esposto, lo sviluppo di MacLaurin di log(1 + x). La derivata (1 + x) 1 di log(1 + x) rappresenta, per x ( 1, 1), la somma di una serie geometrica di ragione x e primo termine 1. Quindi, per x ( 1, 1), si ha (1 + x) 1 = 1 x + x 2 x ( 1) n x n + Dal teorema di derivazione delle serie di potenze si deduce che g(x) = x x2 2 + x3 3 x4 xn ( 1)n 4 n è una primitiva di (1 + x) 1 ; ma, è bene precisare, soltanto per x appartenente al comune dominio di convergenza ( 1, 1) delle due serie. Dunque, log(1 + x) e g(x) hanno la stessa derivata per x ( 1, 1). Poiché coincidono per x = 0, si può concludere che log(1 + x) = x x2 2 + x3 3 x4 xn ( 1)n + x ( 1, 1). 4 n + 1 Esercizio. Provare che la funzione arctang x è sviluppabile in serie di MacLaurin, determinarne lo sviluppo e l intervallo di validità. Suggerimento. Sviluppare prima la derivata di arctang x. Esercizio. Provare che la funzione e x2 è sviluppabile in serie di MacLaurin, determinarne lo sviluppo e l intervallo di validità. Suggerimento. Si ricorda che l uguaglianza e x = 1 + x + x2 2! + + xn n! + Versione del 30 maggio
34 è valida per ogni numero reale x, e quindi, in particolare, è valida per ogni numero reale x 2. Esercizio. Provare che la funzione degli errori, erf x = 2 x e t2 dt, π è sviluppabile in serie di MacLaurin, determinarne lo sviluppo e l intervallo di validità. Suggerimento. Sviluppare prima la derivata di erf x. Esercizio. Provare che la funzione { sen x f(x) = x se x 0 1 se x = 0 è sviluppabile in serie di MacLaurin, determinarne lo sviluppo e l intervallo di validità. Suggerimento. Sviluppare prima sen x. Dato α R, consideriamo la funzione f(x) = (1 + x) α che è senz altro definita e C nell intervallo ( 1, + ). Si ha f (n) (0) = α(α 1) (α n + 1), per cui la serie di MacLaurin di f è ( ) α x n, n n=0 ove ricordiamo che ( α n) è il coefficiente binomiale ( ) α α(α 1) (α n + 1) =, n n! Si può provare che per x < 1 e qualunque sia α si ha ( ) α (1 + x) α = x n. n 0 n=0 ( ) α = 1. 0 Questa serie di potenze è detta serie binomiale. Se α è un numero naturale la serie è una somma finita. Infatti si riduce alla somma dei primi α + 1 termini essendo i coefficienti binomiali tutti nulli per n > α. In questo caso prende il nome di binomio di Newton. Esercizio. Scrivere i primi quattro termini della serie di MacLaurin di f(x) = 1 + x (α = 1/2) e di f(x) = 1 1+x (α = (1/2)). Versione del 30 maggio
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Geometria Superiore Esercizi 1 (da consegnare entro... )
 Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Corso di Laurea in Ingegneria Informatica Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
INDICAZIONI PER LA RICERCA DEGLI ASINTOTI VERTICALI
 2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni
 Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Esame di Analisi Matematica prova scritta del 23 settembre 2013
 Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Riconoscere e formalizzare le dipendenze funzionali
 Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Analisi Matematica 3 appunti
 Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
Anno 5 4. Funzioni reali: il dominio
 Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Diario del corso di Analisi Matematica 1 (a.a. 2015/16)
 Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
5 DERIVATA. 5.1 Continuità
 5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique.
 Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO
 Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Esercizi sulla conversione tra unità di misura
 Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
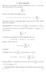 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Appunti di Analisi Matematica 1. Docente: Klaus Engel. Università degli Studi dell Aquila Facoltà di Ingegneria A.A. 2011/12
 Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica
 Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica Nome... N. Matricola... Ancona, 29 marzo 2014 1. (7 punti) Studiare la funzione determinandone: f(x) = e x x il dominio;
Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica Nome... N. Matricola... Ancona, 29 marzo 2014 1. (7 punti) Studiare la funzione determinandone: f(x) = e x x il dominio;
LA FUNZIONE ESPONENZIALE E IL LOGARITMO
 LA FUNZIONE ESPONENZIALE E IL LOGARITMO APPUNTI PER IL CORSO DI ANALISI MATEMATICA I G. MAUCERI Indice 1. Introduzione 1 2. La funzione esponenziale 2 3. Il numero e di Nepero 9 4. L irrazionalità di e
LA FUNZIONE ESPONENZIALE E IL LOGARITMO APPUNTI PER IL CORSO DI ANALISI MATEMATICA I G. MAUCERI Indice 1. Introduzione 1 2. La funzione esponenziale 2 3. Il numero e di Nepero 9 4. L irrazionalità di e
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A
 MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando i
MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando i
Alcune note sulle serie di potenze 1
 Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
7. SINGOLARITA E RESIDUI. 7.1 Punti Singolari Isolati.
 7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
Piano di lavoro di Matematica
 ISTITUTO DI ISTRUZIONE SUPERIORE Liceo Scientifico ALDO MORO Istituto to Tecnico Via Gallo Pecca n. 4/6-10086 Rivarolo Canavese Tel 0124 454511 - Fax 0124 454545 - Cod. Fiscale 85502120018 E-mail: segreteria@istitutomoro.it
ISTITUTO DI ISTRUZIONE SUPERIORE Liceo Scientifico ALDO MORO Istituto to Tecnico Via Gallo Pecca n. 4/6-10086 Rivarolo Canavese Tel 0124 454511 - Fax 0124 454545 - Cod. Fiscale 85502120018 E-mail: segreteria@istitutomoro.it
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
EQUAZIONI CON VALORE ASSOLUTO DISEQUAZIONI CON VALORE ASSOLUTO
 EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Numeri Complessi. 4. Ricordando che, se z è un numero complesso, zz è un numero reale, mettere sotto la forma. z 2 + 2z + 2 = 0. z 2 + 2z + 6 = 0.
 Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Capitolo 2. Serie Numeriche
 Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Capitolo 4. Funzioni continue e limiti. 4.1 Intorni
 Capitolo 4 Funzioni continue e iti In questo capitolo definiremo la nozione di funzione continua e ne studieremo le proprietà fondamentali. Introdurremo inoltre l operazione fondamentale dell analisi infinitesimale,
Capitolo 4 Funzioni continue e iti In questo capitolo definiremo la nozione di funzione continua e ne studieremo le proprietà fondamentali. Introdurremo inoltre l operazione fondamentale dell analisi infinitesimale,
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Syllabus: argomenti di Matematica delle prove di valutazione
 Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
ELEMENTI DI ANALISI SPETTRALE 1 I DUE DOMINI
 Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Definizione Dati due insiemi A e B, contenuti nel campo reale R, si definisce funzione reale di variabile reale una legge f : A
 Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
NUMERI COMPLESSI. Test di autovalutazione
 NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
ESERCITAZIONI DI ANALISI 1 FOGLIO 1 FOGLIO 2 FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI. Marco Pezzulla
 ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
2. Variabilità mediante il confronto di valori caratteristici della
 2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI)
 1 Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI) Approssimazioni di Taylor BPS, Capitolo 5, pagine 256 268 Approssimazione lineare, il simbolo
1 Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI) Approssimazioni di Taylor BPS, Capitolo 5, pagine 256 268 Approssimazione lineare, il simbolo
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
7 Esercizi e complementi di Elettrotecnica per allievi non elettrici. Circuiti elementari
 7 Esercizi e complementi di Elettrotecnica per allievi non elettrici Circuiti elementari Gli esercizi proposti in questa sezione hanno lo scopo di introdurre l allievo ad alcune tecniche, semplici e fondamentali,
7 Esercizi e complementi di Elettrotecnica per allievi non elettrici Circuiti elementari Gli esercizi proposti in questa sezione hanno lo scopo di introdurre l allievo ad alcune tecniche, semplici e fondamentali,
Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio
 Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio. Funzioni e insiemi numerici.4 Verificare che (A B) (A B) = (A A ) B. ) Sia (a, b) (A B) (A B). Allora a (A A ) e b B, da cui (a,
Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio. Funzioni e insiemi numerici.4 Verificare che (A B) (A B) = (A A ) B. ) Sia (a, b) (A B) (A B). Allora a (A A ) e b B, da cui (a,
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
1. Intorni di un punto. Punti di accumulazione.
 1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
L. Pandolfi. Lezioni di Analisi Matematica 2
 L. Pandolfi Lezioni di Analisi Matematica 2 i Il testo presenta tre blocchi principali di argomenti: A Successioni e serie numeriche e di funzioni: Cap., e 2. B Questa parte consta di due, da studiarsi
L. Pandolfi Lezioni di Analisi Matematica 2 i Il testo presenta tre blocchi principali di argomenti: A Successioni e serie numeriche e di funzioni: Cap., e 2. B Questa parte consta di due, da studiarsi
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Esercitazioni di Reti Logiche. Lezione 1 Rappresentazione dell'informazione. Zeynep KIZILTAN zkiziltan@deis.unibo.it
 Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN zkiziltan@deis.unibo.it Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN zkiziltan@deis.unibo.it Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di LIMITI NOTEVOLI Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Numero e ( lim 1 + 1 n ( = e lim 1 + n + n) 1 = e + ) Dimostrazione
Corso di Laurea in Ingegneria Edile Corso di LIMITI NOTEVOLI Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Numero e ( lim 1 + 1 n ( = e lim 1 + n + n) 1 = e + ) Dimostrazione
REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE)
 REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE) 30/09/2013 ore 3 I numeri naturali, relativi, razionali e loro proprieta'. Incompletezza del campo dei numeri razionali. I numeri reali come allineamenti
REGISTRO LEZIONI A.A. 2013/2014 (INGEGNERIA GESTIONALE) 30/09/2013 ore 3 I numeri naturali, relativi, razionali e loro proprieta'. Incompletezza del campo dei numeri razionali. I numeri reali come allineamenti
MATEMATICA e COMPLEMENTI di MATEMATICA
 ALLEGATO N.8_b MATEMATICA e COMPLEMENTI di MATEMATICA DESTINATARI gli studenti delle classi: terze e quarte nuovo ordinamento RISULTATI DI APPRENDIMENTO DELL OBBLIGO D ISTRUZIONE, CHIAVE EUROPEA Padroneggiare
ALLEGATO N.8_b MATEMATICA e COMPLEMENTI di MATEMATICA DESTINATARI gli studenti delle classi: terze e quarte nuovo ordinamento RISULTATI DI APPRENDIMENTO DELL OBBLIGO D ISTRUZIONE, CHIAVE EUROPEA Padroneggiare
Appunti di Analisi Matematica 1. Docente:Fabio Camilli. SAPIENZA, Università di Roma A.A. 2014/15. http://www.dmmm.uniroma1.it/~fabio.
 Appunti di Analisi Matematica Docente:Fabio Camilli SAPIENZA, Università di Roma A.A. 4/5 http://www.dmmm.uniroma.it/~fabio.camilli/ (Versione del 9 luglio 5) Note scritte in collaborazione con il prof.
Appunti di Analisi Matematica Docente:Fabio Camilli SAPIENZA, Università di Roma A.A. 4/5 http://www.dmmm.uniroma.it/~fabio.camilli/ (Versione del 9 luglio 5) Note scritte in collaborazione con il prof.
Esercizi sui Circuiti RC
 Esercizi sui Circuiti RC Problema 1 Due condensatori di capacità C = 6 µf, due resistenze R = 2.2 kω ed una batteria da 12 V sono collegati in serie come in Figura 1a. I condensatori sono inizialmente
Esercizi sui Circuiti RC Problema 1 Due condensatori di capacità C = 6 µf, due resistenze R = 2.2 kω ed una batteria da 12 V sono collegati in serie come in Figura 1a. I condensatori sono inizialmente
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
