A) Intorni in R. Chiamiamo intorno di x R ogni intervallo aperto contenente x. Ciascuno di essi contiene un intorno sferico di x, ]x-r, x+r[, r >0.
|
|
|
- Annabella Beretta
- 5 anni fa
- Visualizzazioni
Transcript
1 L. Verardi Alcuni lucidi su limiti, continuità e derivate 1 CTOPOLOGIA DI R C Poniamo R = R {+, - } A) Intorni in R Chiamiamo intorno di x R ogni intervallo aperto contenente x. Ciascuno di essi contiene un intorno sferico di x, ]x-r, x+r[, r >0. Chiamiamo intorni di + le semirette aperte ]a, + [, a R {- }. Ciascuno di essi contiene un intervallo ]M, + [, con M reale positivo. Chiamiamo intorni di - le semirette aperte ], a[, a R {+ }. Ciascuno di essi contiene un intervallo ]-, -M[, con M reale positivo. Proprietà dell'intersezione. Sia x R e siano I ed I' due suoi intorni. Allora anche I I' è un intorno di x. Proprietà T2 o di Hausdorff. Siano x ed x' appartenenti ad R, x x'. Allora esistono un intorno I di x ed un intorno I' di x' tali che I I' = ø.
2 L. Verardi Alcuni lucidi su limiti, continuità e derivate 2 B) Punti d'accumulazione in R Siano E R ed x 0 R. a) x 0 è detto punto di accumulazione di E se in ogni intorno di x 0 esistono (infiniti) elementi di E diversi da x 0. Ossia, per ogni intorno I di x 0 si ha I E\{x 0 } ø. Il derivato D(E) di E è l'insieme dei punti di accumulazione di E in R. b) x 0 si dice punto non isolato di E se x 0 E D(E); si dice isolato se x 0 E\D(E) c) x 0 si dice interno ad E se esiste un intorno di x 0 interamente contenuto in E. In tal caso, x 0 è anche punto non isolato di E. In R per un intervallo tutti i punti diversi dagli estremi sono interni; il derivato è la sua chiusura, comprendente anche gli estremi. Invece, tutti i punti di N sono isolati; il derivato è {+ }.
3 L. Verardi Alcuni lucidi su limiti, continuità e derivate 3 DEFINIZIONE DI LIMITE Siano dati: - un sottoinsieme non vuoto E di R, - una funzione f:e R, - un x0 R, che sia punto di accumulazione per E (ossia x0 D(E)) - un elemento l R. Dati E R, E, x0 D(E), l R, diremo che f ha limite l per x tendente ad x0 su E se per ogni intorno I di l esiste un intorno J di x0 tale che per ogni x E J, x x0 si ha f(x) I. NOTE: a) La condizione x 0 D(E) assicura che l'insieme E J\{x 0 } è sempre non vuoto qualunque sia l'intorno J di x 0. b) I valori di x che determinano il limite di f sono quelli di un intorno U di x 0, ossia si può calcolare il limite su E U anziché su tutto E.
4 L. Verardi Alcuni lucidi su limiti, continuità e derivate 4 Teorema di unicità del limite. Siano E R, f:e R, x 0 D(E). Se f ha due limiti l ed l' per x tendente ad x 0 su E, allora l = l'. Dimostrazione. Supponiamo per assurdo l l'. (Nelle figure seguenti si suppone l < l'). Per la proprietà di Hausdorff esistono un intorno I di l ed un intorno I' di l' tali che I I' = ø.
5 L. Verardi Alcuni lucidi su limiti, continuità e derivate 5 Poiché l è un limite per x tendente ad x 0 su E ed I è un intorno di l, per la definizione di limite esiste un intorno J di x 0 tale che per ogni x E J\{x 0 } si ha f(x) I.
6 L. Verardi Alcuni lucidi su limiti, continuità e derivate 6 Ma anche l' è un limite per x tendente ad x 0 su E ed I' è un suo intorno, quindi per la definizione di limite esiste un intorno J' di x 0 tale che per ogni x E J'\{x 0 } si ha f(x) I'.
7 L. Verardi Alcuni lucidi su limiti, continuità e derivate 7 Per la proprietà dell'intersezione, anche J J' è un intorno di x 0, e poiché x 0 D(E), l'insieme E (J J') ha infiniti elementi. Possiamo allora prendere un elemento x E (J J'), x x 0. Ma allora si ha contemporaneamente f(x) I e f(x) I. In definitiva, f(x) I I'=ø, assurdo. Allora non può essere l l'. Dunque, l = l'.
8 L. Verardi Alcuni lucidi su limiti, continuità e derivate 8 Come calcolare un limite? 1. - Nei punti non isolati di E, il candidato come limite l di f per x x 0 è f(x 0 ), ossia il valore della funzione in x 0. Se ciò accade, ossia se l = f(x 0 ), la funzione si dice continua in x Per una successione s:n R, l'unico limite si fa per n +. Si può cercarlo attribuendo ad n valori sempre più grandi Sia B E, che abbia ancora x 0 come punto di accumulazione e calcoliamo il limite della restrizione di f a B. Se esiste, è il candidato ad essere il limite di f su E. Se cambiando sottoinsieme si trova un limite diverso, allora la funzione non ha limite su E. Solitamente questi sottoinsiemi sono: B = {x E x > x0} oppure B = {x E x < x0}. I due limiti in tal caso di chiamano rispettivamente limiti destro e sinistro di f in x0: ( ) ( ) lim + x"x 0 f x lim # x"x 0 f x Se esistono e sono uguali, il limite esiste.
9 L. Verardi Alcuni lucidi su limiti, continuità e derivate 9 ESERCIZIO: Calcoliamo tutti i limiti della funzione logaritmo. Siano E = R + = ]0, + [ ed f:e R, tale che f(x) = ln(x) (in base e). Distinguiamo tre casi: 1) x 0 = 0. Assegnando ad x valori sempre più prossimi a zero, vedremo che log(x) decresce sempre più verso il -, per cui ipotizziamo lim ln ( x ) = #$. x"0 Verifica: sia I = ]-, -M[ un intorno di -, M > 0. La condizione f(x) I diventa ln(x)<-m. Per la crescenza di ex si deduce: x = e ln x ( ) <e "M = 1 e M Poniamo J = ]-, e-m[, che M>0 è un intorno di zero e per ogni x J E=]0, e M[ si ha f(x) I.Dunque, lim ln x x"0 ( ) = #$
10 L. Verardi Alcuni lucidi su limiti, continuità e derivate 10 2) x 0 = +. Sostituiamo ad x valori sempre più grandi: anche ln(x) cresce e sembra tendere a +. Ipotizziamo lim ln x x"+# ( ) = +#. Verifica: sia I = ]M, + [ un intorno di +, M > 0. La condizione f(x) I diventa ln(x) > M, da cui segue x > em. Poniamo allora J = ]em, + [, che è sempre un intorno di + e allora, per ogni x J E (= J), si ha f(x) I. Dunque, lim ln x x"+# ( ) = +#. 3) Sia infine x 0 E: ipotizziamo che sia # lim ln( x) = ln% & x ( x"x $ 0. ' 0 Verifica. Sia I = ]log(x 0 )-ε, log(x 0 )+ε[ un intorno di log(x 0 ), con ε > 0. La condizione f(x) I diviene: log(x 0 )- ε < log(x) < log(x 0 )+ ε -ε < log(x)-log(x 0 ) < ε. -ε < log(x/x 0 ) < ε e "# < x x 0 <e # x 0 "e #$ < x < x 0 "e $ ( essendo x 0 > 0) % Poniamo quindi J = x 0 "e #$, x 0 "e $ & ' Per ogni x J (= J E) si ha f(x) I, dato che i passaggi eseguiti sono tutti reversibili. Ma J è un intorno di x 0? Occorrono alcuni passaggi: "# < 0 < # $ e "# < e 0 < e # ( ) *
11 L. Verardi Alcuni lucidi su limiti, continuità e derivate 11 Ricordiamo che e0 = 1. Di qui otteniamo: x 0 "e #$ < x < x 0 "e $. Questa condizione è proprio quella che serve per affermare che x 0 J in ogni caso. Dunque, J è l'intorno di x 0 cercato e il risultato è "vero". Conseguenza: la funzione logaritmo è continua in ogni x 0 ]0, + [. Altre funzioni continue su R: - le costanti f(x) = c - l identità f(x) = x - il seno: f(x) = sin(x) La verifica delle prime due è immediata, mentre più difficile è dimostrare l ultima. Dalla continuità di queste funzioni dedurremo con teoremi generali la continuità delle altre funzioni elementari: polinomi, funzioni razionali fratte funzioni esponenziali e logaritmiche coseno, tangente, arcotangente radicali e funzioni potenza valore assoluto
12 L. Verardi Alcuni lucidi su limiti, continuità e derivate 12 Teorema della permanenza del segno. Siano E R, f:e R, x 0 D(E), lim x"x0 f(x)=l#r. a) Se l > 0 esiste un intorno J di x0 tale che per ogni x E J\{x 0 } si ha f(x) > 0. b) Se l < 0 esiste un intorno J di x0 tale che per ogni x E J\{x 0 } si ha f(x) < 0. Dimostrazione. a) Sia I = ]0, + [. Allora I è un intorno di l, quindi, per la definizione di limite, esiste un intorno J di x0 tale che per ogni x E J\{x0} si ha f(x) I, ossia f(x) > 0. In modo analogo si dimostra anche b). Inverso parziale del teorema della permanenza del segno. Siano E R, f:e R, x 0 D(E), lim x"x0 f(x)=l#r. a) Se esiste un intorno J' di x0 tale che per ogni x E J'\{x 0 } si ha f(x) > 0, allora l 0. b) Se esiste un intorno J' di x0 tale che per ogni x E J'\{x 0 } si ha f(x) < 0, allora l 0. Dimostrazione. a) Se fosse l < 0 si andrebbe contro quanto affermato nel teorema precedente. b) Idem.
13 L. Verardi Alcuni lucidi su limiti, continuità e derivate 13 Primo teorema del confronto (o dei carabinieri). Siano E R, x 0 D(E), siano f,g,h:e R, ed esista un intorno J di x0 tale che per ogni x E J\{x0} si abbia f(x) g(x) h(x) Se lim f(x) = lim h(x) = l R, anche x"x0 x"x0 lim g(x) esiste ed è uguale ad l. x"x 0 ESEMPIO: "x > 0, #1 $ sin x Poiché lim x"+# $1 x = 0= lim ( ) $ 1 % #1 x $ sin ( x ) x"+# sin(x) del confronto, lim = 0 x"+# x x $ 1 x 1, allora per il teorema x
14 L. Verardi Alcuni lucidi su limiti, continuità e derivate 14 Secondo teorema del confronto. Siano E R, x 0 D(E), f, g:e R, ed esista un intorno J di x0 tale che per ogni x E J\{x0} sia f(x) g(x). a) Se lim x"x0 f(x) = +, anche lim x"x0 g(x) = +. b) Se lim x"x0 g(x) = -, anche lim x"x0 f(x) = -. NOTA. Le funzioni periodiche non hanno limite per x ±. Per esempio, sia f(x) = sin(x). Se consideriamo la sua restrizione al { }, allora sottoinsieme B = x = k " # k $ Z sen(x) su B vale costantemente 0 ed anche il limite per x ± di sin(x) su B vale 0. Dunque 0 è il solo candidato ad essere il limite del seno per x ± su R. Tuttavia, non è così. Se si prende l intorno I = # 0 " 1 2, & % $ 2' ( di 0, in ogni intorno J di + o di ci sono degli x per cui sin(x) = 1, (x = π/2 + 2kπ, k Z) e quindi sin(x) I. Perciò il limite non c è.
15 L. Verardi Alcuni lucidi su limiti, continuità e derivate 15 Il teorema degli zeri E' data la funzione f:r + R, f(x )=x!ln (x )-1, il cui grafico è in figura e che taglia l'asse x in un punto c. Come trovarlo? Restringiamo la funzione all'intervallo [1, 2], in cui f(1) = -1 < 0, f(2) 0.38 > 0. Il suo punto medio è = 1.5, ed è una prima approssimazione della radice. Si ha f(1.5) < 0.
16 L. Verardi Alcuni lucidi su limiti, continuità e derivate 16 Se l'approssimazione non è sufficiente, scegliamo il nuovo intervallo [1.5, 2], in cui f(1.5)<0, f(2)>0, ed è lungo metà del precedente, ossia 1/2. Il suo punto medio è = 1.75, ed è una 2 nuova approssimazione della radice; si ha f(1.75) -0,02<0. Se non ci basta, consideriamo il nuovo intervallo [1.75, 2], in cui f(1.75)<0, f(2)>0, lungo metà del precedente, ossia 1/4. Il punto medio dell'intervallo [1.75, 2] è = e si ha f(1.875) 0,179>0. 2 Si noti che l'approssimazione è peggiorata.
17 L. Verardi Alcuni lucidi su limiti, continuità e derivate 17 Consideriamo allora il nuovo intervallo [1.75, 1,875], in cui f(1.75)<0, f(1,875)>0, lungo metà del precedente, ossia 1/8. Ad ogni passo, l'intervallo si dimezza e l'approssimazione tende a migliorare. a b m=(a+b)/2 f(m) ,5-0, ,5 2 1,75-0, ,75 2 1,875 0, ,75 1,875 1,8125 0, ,75 1,8125 1, , ,75 1, , , ,75 1, , , , , , , , , , , , , , , , , , ,0001
18 L. Verardi Alcuni lucidi su limiti, continuità e derivate 18 Il teorema degli zeri (B. Bolzano). Siano a, b R, a < b, f:[a, b] R, continua, tale che f(a) ed f(b) hanno segni opposti. Allora esiste c ]a, b[, tale che f(c) = 0 Si prenda il punto medio m 1 = a+b 2 di [a, b]. Se f(m 1 )=0, la radice è trovata, c=m 1 ed abbiamo finito. Altrimenti, si avrà f(m 1 ) > 0 o f(m 1 ) < 0. " Nel primo caso poniamo a 1 = a $ #. $ b 1 =m % 1 Nel secondo poniamo a 1 =m $ 1 # $ b 1 =b " %. In entrambi i casi otteniamo un nuovo intervallo, [a 1, b 1 ], sul quale f è continua e tale che f(a 1 )<0 ed f(b 1 )>0. Il vantaggio è che il nuovo intervallo è la metà del primo: b 1 -a 1 = (b-a)/2. Possiamo ripetere il procedimento a partire dal nuovo intervallo: prendere il suo punto medio m 2, ecc.
19 L. Verardi Alcuni lucidi su limiti, continuità e derivate 19 Se non siamo fortunati, il procedimento proseguirà indefinitamente, producendo due successioni: a a 1 a 2... a n b n... b 2 b 1 b. tali che per ogni n 1 si ha f(a n )<0, f(b n )>0 e b n "a n = b"a 2 n n #$ %%%%%%# 0 Per la continuità di R, le due successioni racchiudono un unico numero, c, tale che a n <c<b n per ogni n 1. Si ha allora lim a n = c = lim b n. n"# n"# Questo punto c è la radice cercata. Infatti, poiché f(an)<0 ed f(bn)>0 per ogni n 1, per il teorema della permanenza del segno e la continuità di f si ha: f(c)= lim f(a n )#0 n!" f(c)= lim f(b n!" n )$0 % ' & ' (' ) f(c)= 0 NOTA. Ogni strumento di calcolo termina il suo procedimento quando la differenza tra a n e b n è tanto piccola che non riesce più a distinguerli e quindi per lui sono uguali. A questo punto esso pone c = a n
20 L. Verardi Alcuni lucidi su limiti, continuità e derivate 20 Le derivate Un viaggio Bologna Centrale - Rimini. Partenza ore 7, arrivo ore 8, durata 1 ora Distanza: 100 Km. La velocità media è 100 Km/ora. La distanza da Bologna di una località è una funzione s = s(t) del tempo. Fissati due "istanti" t 1 e t 2, la velocità media fra le corrispondenti località s(t 1 ) ed s(t 2 ) è: v m = spazio percorso tempo impiegato = s(t 2)" s(t 1 ) t 2 "t 1
21 L. Verardi Alcuni lucidi su limiti, continuità e derivate 21 Il tachimetro della locomotiva fornisce un altro tipo di velocità, che varia continuamente. Essa si può pensare misurata "istante per istante" e viene detta velocità istantanea. Per definirla al tempo t 0, calcoliamo la velocità media nell'intervallo fra t 0 ed un istante t via via più prossimo a t 0. Più precisamente, la velocità istantanea v(t 0 ) al tempo t 0 si definisce così: ( ) # s( t 0 ) s t lim t"t 0 t # t 0 Se si ripete per ogni istante t 0, nasce una funzione del tempo detta velocità di quel treno.
22 L. Verardi Alcuni lucidi su limiti, continuità e derivate 22 In un allevamento, si pesa ogni giorno un capo di bestiame. Il peso è una funzione del tempo, p = p(t). Nel periodo fra due date t 1 e t 2, l'accrescimento medio è dato dal rapporto p(t 2 ) " p(t 1 ) t 2 " t 1 fra aumento di peso e tempo trascorso. L accrescimento istantaneo del capo di bestiame al tempo t 0 è: p(t) # p(t lim 0 ) t"t 0 t # t 0 Se si ripete per ogni istante t 0, si ottiene la funzione accrescimento di quel capo.
23 L. Verardi Alcuni lucidi su limiti, continuità e derivate 23 Siano E un intervallo ed f:e R una funzione continua. Il suo grafico y = f(x) è una curva del piano cartesiano. Siano P 0 = (x 0, f(x 0 )) e P = (x, f(x)) distinti. La retta PP 0 si chiama secante. Il suo coefficiente angolare è f(x) " f(x 0 ) x " x 0. La tangente in P 0 al grafico y = f(x) di f è per definizione la retta per P 0 il cui coefficiente angolare è lim x"x 0 f(x) # f(x 0 ) x # x 0. Se ha senso ripetere ciò per ogni x 0 si ottiene la funzione pendenza di f.
24 L. Verardi Alcuni lucidi su limiti, continuità e derivate 24 Siano E R, E ø, f:e R, x 0 un punto non isolato di E. La funzione x " f(x) # f(x 0 ) x # x 0 definita su E\{x 0 } è detta rapporto incrementale relativo ad f e ad x 0. Chiamiamo derivata f'(x 0 ) di f in x 0 il f(x) # f(x lim 0 ) x"x 0 x # x, se esiste. 0 Diremo che f è derivabile in x 0 se f(x) # f(x lim 0 ) x"x 0 x # x 0 esiste ed è finito. Se tutti i punti di E sono non isolati e in essi la funzione f è derivabile, nasce una nuova funzione f':e R, detta derivata di f su E, che ad ogni x E associa la derivata f'(x) di f in x.
25 L. Verardi Alcuni lucidi su limiti, continuità e derivate 25 TIPI DI PUNTI DI MINIMO RELATIVO estremo punto angoloso cuspide p. di discontinuità punto critico punto critico
26 L. Verardi Alcuni lucidi su limiti, continuità e derivate 26 f:e R, x 0 E, Teorema di Fermat Siano E R, per f. Se x 0 è ad E ed f è in x 0 allora f '(x 0 ) = 0.. Sia x 0 un punto interno ad E e di minimo relativo per f: esiste un intorno J di x 0 tale che per ogni x J E si ha f(x) f(x 0 ). Allora il segno del rapporto incrementale x " f(x)# f(x 0) x#x è 0 per ogni x J E perché il numeratore è 0. Per l'inverso del teorema di permanenza del segno si ha quindi: f "(x 0 )= lim f(x)$ f(x 0 ) x#x + x$x % f(x)$ f(x 0 ) f "(x 0 )= lim x#x 0 $ x$x 0 & 0 ' ) ) ) ( ) ) ) * + f "(x 0 )= 0. Se il punto x 0 non è interno ad E, oppure se f non è derivabile in x 0, non possiamo applicare questo teorema.
27 L. Verardi Alcuni lucidi su limiti, continuità e derivate 27 I TEOREMI DI ROLLE E LAGRANGE. Sia f:[a, b] R, continua su [a, b], derivabile almeno su ]a, b[. Se f(a) = f(b) allora esiste c ]a, b[ tale che f'(c) = 0. Sia f:[a, b] R, continua su [a, b] e derivabile almeno su ]a, b[. Allora esiste c ]a, b[ tale che f "(c)= f(b)# f(a) b#a.. Ossia, c'è un punto in cui la pendenza della curva è uguale alla pendenza media della curva fra i punti A e B.
28 L. Verardi Alcuni lucidi su limiti, continuità e derivate 28 Tabella di derivate e primitive di alcune funzioni funzione derivata primitiva 1 0 x x n, n 1 n.x n-1 x n+1 /(n+1) 1/x, x 0-1/x 2 log x 1/x n, x 0, n 2 n/x n+1 x -n+1 /(-n+1) sin(x) cos(x) - cos(x) cos(x) - sen(x) sin(x) tan(x) 1+(tan(x)) 2 - ln cos(x) ex ex ex ln(x), x > 0 1/x x.ln(x) - x tan "1 ( x ) 1/(1+x 2 ) -ln(1+x 2 )/2 sign(x), x 0 0 x x sign(x), x 0 (x. x )/2 x 1/(2 x), x > 0 2 x 3 /3
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
Derivazione. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivate di funzioni 1 / 40
 Derivate di funzioni 1 / 40 Variazione assoluta Sia data una funzione f (x) e due suoi valori in corrispondenza dei punti x 0 e x 0 + h, con h > 0. Supponiamo di voler determinare di quanto varia il valore
Derivate di funzioni 1 / 40 Variazione assoluta Sia data una funzione f (x) e due suoi valori in corrispondenza dei punti x 0 e x 0 + h, con h > 0. Supponiamo di voler determinare di quanto varia il valore
2. SIGNIFICATO FISICO DELLA DERIVATA
 . SIGNIFICATO FISICO DELLA DERIVATA Esempi 1. Un auto viaggia lungo un percorso rettilineo, con velocità costante uguale a 70 km/h. Scrivere la legge oraria s= s(t) e rappresentarla graficamente. 1. Scriviamo
. SIGNIFICATO FISICO DELLA DERIVATA Esempi 1. Un auto viaggia lungo un percorso rettilineo, con velocità costante uguale a 70 km/h. Scrivere la legge oraria s= s(t) e rappresentarla graficamente. 1. Scriviamo
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Insiemi numerici. Definizioni
 1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
1 Insiemi numerici Gli insiemi numerici sono insiemi i cui elementi sono numeri, cioè appartengono all'insieme N dei naturali, degli interi Z, dei razionali Q, dei reali R o dei complessi C ( es.: A =
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R una funzione derivabile in 0 tale che f(0) = f (0) = 0. Si consideri la funzione g(x) = f(x). Allora, necessariamente sin x (a) lim g(x) = 0 (b) lim g(x) = 1 (c)
Test di autovalutazione 1. Sia f : R R una funzione derivabile in 0 tale che f(0) = f (0) = 0. Si consideri la funzione g(x) = f(x). Allora, necessariamente sin x (a) lim g(x) = 0 (b) lim g(x) = 1 (c)
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
DERIVATE. Rispondere ai seguenti quesiti. Una sola risposta è corretta. 1. Data la funzione f(x) =2+ x 7, quale delle seguente affermazioni èvera?
 DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
Sia y = f(x) definita in un intervallo I. x 0 è punto di massimo assoluto. x 0 è punto di minimo assoluto. x 0 è punto di massimo relativo o locale se
 PUNTI ESTREMANTI E PUNTI STAZIONARI. MASSIMI E MINIMI ASSOLUTI E RELATIVI. TEOREMI DI FERMAT, ROLLE E LAGRANGE. CONDIZIONI NECESSARIE E SUFFICIENTI PER MASSIMI E MINIMI RELATIVI. PROBLEMI DI MASSIMO E
PUNTI ESTREMANTI E PUNTI STAZIONARI. MASSIMI E MINIMI ASSOLUTI E RELATIVI. TEOREMI DI FERMAT, ROLLE E LAGRANGE. CONDIZIONI NECESSARIE E SUFFICIENTI PER MASSIMI E MINIMI RELATIVI. PROBLEMI DI MASSIMO E
DERIVATE. Equazione della retta tangente al grafico di f nel suo punto P(x 0 ;y 0 ):
 DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
10 - Massimi, minimi e flessi
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 10 - Massimi, minimi e flessi Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 10 - Massimi, minimi e flessi Anno Accademico 2015/2016
Derivate. 24 settembre 2007
 Derivate 24 settembre 2007 Rapporto incrementale di una funzione Siano f : X R e x 0 X. La funzione g x0 (x) = f(x) f(x 0) x x 0 si chiama rapporto incrementale di f relativo al punto x 0. E[g x0 ] = X
Derivate 24 settembre 2007 Rapporto incrementale di una funzione Siano f : X R e x 0 X. La funzione g x0 (x) = f(x) f(x 0) x x 0 si chiama rapporto incrementale di f relativo al punto x 0. E[g x0 ] = X
Esercitazione 9 - Funzioni
 Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio.
 FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua Non è una funzione continua diciamo che
FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua Non è una funzione continua diciamo che
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
Analisi matematica I. Sviluppi di Taylor e applicazioni. Sviluppi di Taylor. Operazioni sugli sviluppi di Taylor e applicazioni
 Analisi matematica I e applicazioni Operazioni sugli sviluppi di Taylor e applicazioni 2 2006 Politecnico di Torino 1 e applicazioni Formule di Taylor con resto di Peano: caso e n =0 n =1 Formule di Taylor
Analisi matematica I e applicazioni Operazioni sugli sviluppi di Taylor e applicazioni 2 2006 Politecnico di Torino 1 e applicazioni Formule di Taylor con resto di Peano: caso e n =0 n =1 Formule di Taylor
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Matematica generale CTF
 Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Proprietà globali delle funzioni continue
 Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Analisi Matematica. Alcune funzioni elementari
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria Formule di Taylor Ottobre 2012
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Derivate. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33
 Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Le derivate: introduzione storica
 Le derivate: introduzione storica I due fondamentali capitoli dell analisi matematica sono il calcolo differenziale e il calcolo integrale. Mentre il calcolo integrale trova le sue origini nella matematica
Le derivate: introduzione storica I due fondamentali capitoli dell analisi matematica sono il calcolo differenziale e il calcolo integrale. Mentre il calcolo integrale trova le sue origini nella matematica
Giovanni Rapisarda. Derivata di una funzione. df dx. Sia. una funzione definita in un intervallo. Fissato un punto
 Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
Corso di Laurea in Ingegneria Edile Corso di TEOREMI DEL CALCOLO DIFFERENZIALE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Teorema di Estremi locali Richiamiamo la
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
y x y x A (x 1,y 1 ) = (c, f(c)) B(x 2,y 2 ) = (c+h, f(c+h)) m =
 DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
Matematica Lezione 19
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
DERIVATE. 1.Definizione di derivata.
 DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Lo studio di funzione. 18 febbraio 2013
 Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE. Le FUNZIONI RAZIONALI INTERE (i polinomi) hanno come insieme di definizione R.
 ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
Punti di discontinuità
 Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Lezione 18 (8 gennaio) Limiti
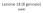 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
4.3 Teoremi sulle funzioni derivabili
 4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
ORDINAMENTO SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
Esercizi con soluzioni dell esercitazione del 31/10/17
 Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
Corso di Laurea in Ingegneria Civile Analisi Matematica I
 Corso di Laurea in Ingegneria Civile Analisi Matematica I Lezioni A.A. 2006/2007, prof. G. Stefani Primo periodo 18/09/06-15/12/06 Testi consigliati: M.Bertsch, R.Dal Passo - Elementi di Analisi Matematica
Corso di Laurea in Ingegneria Civile Analisi Matematica I Lezioni A.A. 2006/2007, prof. G. Stefani Primo periodo 18/09/06-15/12/06 Testi consigliati: M.Bertsch, R.Dal Passo - Elementi di Analisi Matematica
ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE
 ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE Determinare l incremento della funzione f (x) = x 2 relativo al punto x 0 e all incremento x x 0, nei seguenti casi:. x 0 =, x = 2 2. x 0 =, x =. 3. x 0 =,
ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE Determinare l incremento della funzione f (x) = x 2 relativo al punto x 0 e all incremento x x 0, nei seguenti casi:. x 0 =, x = 2 2. x 0 =, x =. 3. x 0 =,
Anno 5 Regole di derivazione
 Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO COGNOME: NOME: MATR.: (x 1); C: y = ; D: y = 2 x; E: N.A.
 Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO 10 marzo 017 COGNOME: NOME: MATR.: 1) La retta tangente al grafico di f(x) = e x 1 x+ nel punto (1, ) è A: y = x + 4; B: y = (4x+) (x 1); C:
Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO 10 marzo 017 COGNOME: NOME: MATR.: 1) La retta tangente al grafico di f(x) = e x 1 x+ nel punto (1, ) è A: y = x + 4; B: y = (4x+) (x 1); C:
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
13 LIMITI DI FUNZIONI
 3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
FUNZIONI CONTINUE E FUNZIONI LIMITATE
 FUNZIONI CONTINUE E FUNZIONI LIMITATE FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua
FUNZIONI CONTINUE E FUNZIONI LIMITATE FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
12/10/05 (2 ore): Esercizi vari sull ellisse, iperbole, parabola. Disequazioni in due variabili. Equazione dell iperbole equilatera. Esempi.
 Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
1 Successioni di funzioni
 Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Analisi Matematica 1
 Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Corso di Matematica per la Chimica. Dott.ssa Maria Carmela De Bonis a.a
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni non lineari Sia F C 0 ([a, b]), cioé F è una funzione continua in un intervallo [a, b] R, tale che F(a)F(b) < 0 1.5 1 F(b) 0.5 0 a
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni non lineari Sia F C 0 ([a, b]), cioé F è una funzione continua in un intervallo [a, b] R, tale che F(a)F(b) < 0 1.5 1 F(b) 0.5 0 a
Matematica. Tutorato Attivo: Derivate. Alessio Bianchi. Matematica 20 maggio 2017
 Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital
 Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Dispense di Matematica Analisi Matematica. Riccarda Rossi
 Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Calcolo differenziale
 Calcolo differenziale L operazione di derivata Sia f: AR. Si vuole conoscere l equazione della retta tangente al grafico della funzione in un punto. Retta secante y f(+h) Q Rapporto incrementale y=f()
Calcolo differenziale L operazione di derivata Sia f: AR. Si vuole conoscere l equazione della retta tangente al grafico della funzione in un punto. Retta secante y f(+h) Q Rapporto incrementale y=f()
Calcolo differenziale I
 Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
23 INVERTIBILITÀ E CONTINUITÀ
 23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
FUNZIONI ELEMENTARI Funzione retta
 1 FUNZIONI ELEMENTARI Funzione retta L equazione generale della funzione retta è y = a x + b dove a, b sono numeri reali fissati. Il termine b si chiama termine noto e dà l ordinata dell intersezione tra
1 FUNZIONI ELEMENTARI Funzione retta L equazione generale della funzione retta è y = a x + b dove a, b sono numeri reali fissati. Il termine b si chiama termine noto e dà l ordinata dell intersezione tra
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
