Algoritmi e Strutture di Dati
|
|
|
- Adolfo Verde
- 4 anni fa
- Visualizzazioni
Transcript
1 Algotm e Stuttue d Dat Quck-sot m.patgnan Nota d copyght queste sldes sono potette dalle legg sul copyght l ttolo ed l copyght elatv alle sldes (nclus, ma non lmtatamente, mmagn, foto, anmazon, vdeo, audo, musca e testo) sono d popetà degl auto ndcat sulla pma pagna le sldes possono essee podotte ed utlzzate lbeamente, non a fn d luco, da unvestà e scuole pubblche e da sttut pubblc d ceca ogn alto uso o poduzone è vetata, se non esplctamente autozzata pe sctto, a po, da pate degl auto gl auto non s assumono nessuna esponsabltà pe l contenuto delle sldes, che sono comunque soggette a cambamento questa nota d copyght non deve essee ma mossa e deve essee potata anche n cas d uso pazale
2 Quck-sot Algotmo d odnamento n loco ma non stable Tempo d esecuzone nel caso peggoe Θ(n 2 ) nel caso mgloe e medo Θ(n lg n) fatto costant nascost nella notazone Θ sono abbastanza pccol Intodotto da Hoae nel 962 la vesone che vedemo è una vaante dovuta a Lomuto Basato sul paadgma dvde et mpea Dvde et mpea nel quck-sot Pe odnae un sottoaay A[p...] Dvde A[p...] vene patto (e sstemato) n due sottoaay non vuot A[p...q ] e A[q+...], n modo che ogn elemento del pmo sa mnoe o uguale ad A[q] e ogn elemento del secondo sa maggoe ad A[q] l ndce q vene calcolato dalla pocedua d patzonamento Impea due sottoaay A[p...q ] e A[q+...] sono odnat, cosvamente Combna non c è nente da fae: A[p...] è odnato 2
3 QUICK_SORT(A,p,). f p < Pocedua QUICK_SORT 2. q = PARTITION(A,p,) 3. QUICK_SORT(A,p,q-). QUICK_SORT(A,q+,) La pocedua QUICK_SORT odna n loco l ntevallo A[p..] se p =, alloa l ntevallo contene una sola casella ed è gà odnato: l nvocazone d QUICK-SORT non ha effetto se p >, alloa l ntevallo è un ntevallo degenee e l nvocazone d QUICK-SORT non ha effetto Il valoe q tonato da PARTITION è tale che p q Pe odnae l nteo aay vene nvocata la pocedua: QUICK_SORT(A,0,A.length-) Esecuzone d QUICK_SORT su PARTITION p 2 p 3 2 p PARTITION p p p p p p 6 7 PARTITION PARTITION 3
4 Pocedua PARTITION PARTITION(A,p,) /* s assume p < */. = A[] /* A[] è scelto come pvot */ 2. = p /* saà l ultmo elemento */ 3. fo = p to /* scoo l aay */. f A[] 5. = + 6. SCAMBIA(A,,) 7. SCAMBIA(A,+,) 8. etun + /* la poszone coente del pvot */ La pocedua PARTITION vene nvocata su un ntevallo d almeno due element (p < ) due cas base due element sono odnat due element non sono odnat Esecuzone d PARTITION su
5 Esecuzone d PARTITION su 6 Caso base : PARTITION su una coppa odnata PARTITION(A,p,) /* s assume p < */. = A[] /* A[] è scelto come pvot */ 2. = p /* saà l ultmo elemento */ 3. fo = p to /* scoo l aay */. f A[] 5. = + 6. SCAMBIA(A,,) 7. SCAMBIA(A,+,) 8. etun + /* la poszone coente del pvot */ Esecuzone d PARTITION su 8 7 Caso base 2: PARTITION su una coppa non odnata PARTITION(A,p,) /* s assume p < */. = A[] /* A[] è scelto come pvot */ 2. = p /* saà l ultmo elemento */ 3. fo = p to /* scoo l aay */. f A[] 5. = + 6. SCAMBIA(A,,) 7. SCAMBIA(A,+,) 8. etun + /* la poszone coente del pvot */
6 Tempo d esecuzone d PARTITION PARTITION(A,p,) /* s assume p < */. = A[] /* A[] è scelto come pvot */ 2. = p /* saà l ultmo elemento */ 3. fo = p to /* scoo l aay */. f A[] 5. = + 6. SCAMBIA(A,,) 7. SCAMBIA(A,+,) 8. etun + /* la poszone coente del pvot */ Le assegnazon nzal e fnal chedono tempo costante Nel caso peggoe, come nel caso mgloe, l sottoaay A[p...] vene scoso pe nteo da snsta veso desta Il tempo d esecuzone T PARTITION (n) Θ(n) Esecz. Che cosa succedeebbe nel QUICK_SORT se PARTITION(A,p,) esttusse un valoe q uguale a? 2. Illustae le opeazon d PARTITION sull aay A = <3, 9, 9, 5, 2, 8, 7,,, 2, 6, 2> 3. Illustae le opeazon d PARTITION su un aay gà odnato n senso decescente gà odnato n senso cescente. Quale valoe esttusce PARTITION se tutt gl element dell aay A[p...] hanno lo stesso valoe? 6
7 Esecuzone d PARTITION su Esecuzone d PARTITION su
8 Caso peggoe e mgloe pe QUICK_SORT Il caso peggoe pe QUICK_SORT è quando PARTITION elegge a pvot (assegna alla vaable ) l valoe massmo o mnmo dell aay n questo caso QUICK_SORT non coe su due sottoaay blancat, ma coe su un sottoaay pù coto d una casella ed un sottoaay degenee Il caso mgloe pe QUICK_SORT è nvece quando PARTITION elegge a pvot l valoe medano dell aay n questo caso QUICK_SORT coe su due sottoaay blancat Anals del caso mgloe pe QUICK_SORT Nel caso mgloe l tempo d calcolo d QUICK_SORT su un aay con n poszon è T(n) = 2 T(n/2) + Θ(n) Questa equazone d coenza può essee solta con l teoema dell espeto T(n) = a T(n/b) + p(n k ) Nello specale caso n cu a=2 b=2 k= Che pe a = b k s solve n T(n) = Θ(n k log n) = Θ(n log n) 8
9 Anals del caso peggoe pe QUICK_SORT S ha T(0) T(n) = a = T(n-) + Θ(n) Sappamo che la soluzone d questa equazone d ccoenza è T(n) = a + n g(k) k= E dunque Θ(k) = Θ( n T(n) = n k= k= k) = Θ(n 2 ) Anals del caso medo pe QUICK_SORT S può dmostae fomalmente che nel caso medo QUICK_SORT ha una complesstà Θ(n log n) l anals, peò, è molto pù complessa del caso mgloe e del caso peggoe Nel seguto vedemo solamente due consdeazon ntutve che c autano a gustfcae l sultato. qual è la complesstà nel caso n cu lo sblancamento della cosone non supea ma una detemnata sogla 2. qual è la complesstà nel caso n cu coson sblancate s altenano a coson pù blancate 9
10 Caso blancato 9-a- Supponamo che PARTITION dvda l sottoaay n due pat che hanno una popozone fssa supponamo che la popozone sa 9-a- Abbamo T(n) T(9n/0) + T(n/0) + cn dove cn esplcta Θ(n) Rcosone con popozone 9-a- n cn log 0/9 n log 0 n 00 n 0 n 9 00 n 9 00 n 9 0 n n 8 00 n n cn cn cn cn cn Cò fa pesumee che l costo nel caso medo sa molto vcno al caso mgloe O(n lg n) 0
11 Altenanza d coson blancate e sblancate Supponamo che nel 20% de cas PARTITION poduca una patzone meno blancata d 9-a- Supponamo che nell albeo delle chamate cosve una patzone sblancata sa sempe seguta da una blancata Il costo d una patzone sblancata può essee assobto dal costo della patzone blancata n 0 n- Θ(n) n Θ(n) n-2 2 n-2 2 Θ(n) n-2 2 n-2 2 Θ(n) Vesone andomzzata d QUICK_SORT E possble modfcae QUICK_SORT n manea che cas peggo non concdano con dsposzon notevol degl element RANDOMIZED_PARTITION(A,p,). = RANDOM(p,) 2. SCAMBIA(A,,) 3. etun PARTITION(A,p,) RANDOMIZED_QUICK_SORT(A,p,). f p < then 2. q = RANDOMIZED_PARTITION(A,p,) 3. RANDOMIZED_QUICK_SORT(A,p,q-). RANDOMIZED_QUICK_SORT(A,q+,)
12 Stabltà d QUICK_SORT QUICK_SORT non è stable: Algotm d odnamento pe confonto stable n loco caso peggoe caso medo caso mgloe SELECTION-SORT INSERTION-SORT MERGE-SORT HEAP-SORT QUICK-SORT Θ(n) Θ(n log n) Θ(n 2 ) Θ(n 2 ) Θ(n log n) Θ(n log n) Θ(n log n) Θ(n 2 ) Θ(n 2 ) s s no s s s s s no no 2
Algoritmi basati sulla tecnica Divide et Impera
 Qucksort Algortm basat sulla tecnca Dvde et Impera In questo corso: Rcerca bnara Mergesort (ordnamento) Qucksort (ordnamento) Moltplcazone d nter Moltplcazone d matrc (non n programma) NOTA: nonostante
Qucksort Algortm basat sulla tecnca Dvde et Impera In questo corso: Rcerca bnara Mergesort (ordnamento) Qucksort (ordnamento) Moltplcazone d nter Moltplcazone d matrc (non n programma) NOTA: nonostante
Quick Sort. PARTITION(A,p,r) risistema il sottoarray A[p...r] e riporta l indice q:
![Quick Sort. PARTITION(A,p,r) risistema il sottoarray A[p...r] e riporta l indice q: Quick Sort. PARTITION(A,p,r) risistema il sottoarray A[p...r] e riporta l indice q:](/thumbs/93/111654321.jpg) Quick Sort - Ordinamento in loco - Tempo di esecuzione nel caso peggiore: Θ(n 2 ) - Tempo di esecuzione nel caso medio: Θ(n lg n) - I fattori costanti nascosti nella notazione Θ sono abbastanza piccoli
Quick Sort - Ordinamento in loco - Tempo di esecuzione nel caso peggiore: Θ(n 2 ) - Tempo di esecuzione nel caso medio: Θ(n lg n) - I fattori costanti nascosti nella notazione Θ sono abbastanza piccoli
ESPERIMENTO CASUALE. P(X) è la funzione di probabilità secondo la quale ad ogni numero reale di X si assegna una misura di probabilità.
 ESPERIMENTO CASUALE S Spazo camponao : è l nseme d event necessa e ncompatbl che s pesentano come sultat dell ESPERIMENTO CASUALE. X è l nseme de nume eal assocato ad S, n modo che ad ogn elemento (evento)
ESPERIMENTO CASUALE S Spazo camponao : è l nseme d event necessa e ncompatbl che s pesentano come sultat dell ESPERIMENTO CASUALE. X è l nseme de nume eal assocato ad S, n modo che ad ogn elemento (evento)
Sessione live #1 Settimana #2 dal 10 al 16 marzo. Statistica descrittiva: Indici di posizione, dispersione e forma Istogramma frequenze, box plot
 Sessone lve #1 Settmana # dal 10 al 16 mazo Statstca descttva: Indc d poszone, dspesone e foma Istogamma fequenze, box plot Lezon CD: 1 - - 3 Eseczo 1 S consde la seguente dstbuzone delle nduste tessl
Sessone lve #1 Settmana # dal 10 al 16 mazo Statstca descttva: Indc d poszone, dspesone e foma Istogamma fequenze, box plot Lezon CD: 1 - - 3 Eseczo 1 S consde la seguente dstbuzone delle nduste tessl
MACCHINA ELEMENTARE CON UN SOLO AVVOLGIMENTO
 MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente
 Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente Divide et impera - Schema generale Divide-et-impera (P, n) if n k then risolvi direttamente
Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente Divide et impera - Schema generale Divide-et-impera (P, n) if n k then risolvi direttamente
Risultati esame scritto Fisica 2-29/09/2014 orali: alle ore presso aula O
 sultat esame sctto Fsca - 9/9/ oal: -- alle oe. pesso aula O gl student nteessat a vsonae lo sctto sono pegat d pesentas l gono dell'oale Nuovo odnamento matcola voto 66 9 6 ammesso 9 nc 5 9 5 56 nc 5
sultat esame sctto Fsca - 9/9/ oal: -- alle oe. pesso aula O gl student nteessat a vsonae lo sctto sono pegat d pesentas l gono dell'oale Nuovo odnamento matcola voto 66 9 6 ammesso 9 nc 5 9 5 56 nc 5
ESERCITAZIONE DEL 10 MARZO 2005
 ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
QUICKSORT. Basato sul paradigma divide-et-impera (come MERGE-SORT)
 QUICKSORT Basato sul paradigma divide-et-impera (come MERGE-SORT) Divide: stabilisce un valore di q tale da dividere l array A[p.. r] in due sottoarray non vuoti A[p.. q] e A[q+1.. r], dove ogni elemento
QUICKSORT Basato sul paradigma divide-et-impera (come MERGE-SORT) Divide: stabilisce un valore di q tale da dividere l array A[p.. r] in due sottoarray non vuoti A[p.. q] e A[q+1.. r], dove ogni elemento
Calcolo del lavoro compiuto dalle forze elementari
 Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Gli algoritmi ricorsivi di ordinamento. Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 ordinamento Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Merge Sort Ricorsivo, divide et impera Stabile Divisione: due sottovettori SX e DX rispetto al centro del vettore. p r A.A.
ordinamento Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Merge Sort Ricorsivo, divide et impera Stabile Divisione: due sottovettori SX e DX rispetto al centro del vettore. p r A.A.
I vettori. A cura di dott. Francesca Fattori Speranza dott. Francesca Paolucci
 I vetto cua d dott. Fancesca Fatto Speana (speana@fs.unoma3.t) dott. Fancesca Paolucc GRNDEZZE SLRI E VETTORILI S defnscono gandee SLRI quelle gandee caatteate solo da un valoe numeco o modulo come: tempo,
I vetto cua d dott. Fancesca Fatto Speana (speana@fs.unoma3.t) dott. Fancesca Paolucc GRNDEZZE SLRI E VETTORILI S defnscono gandee SLRI quelle gandee caatteate solo da un valoe numeco o modulo come: tempo,
IL Potenziale elettrostatico
 Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A 2
 RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A La rappresentazone n Complemento a Due d un numero ntero relatvo (.-3,-,-1,0,+1,+,.) una volta stablta la precsone che s vuole ottenere (coè l numero d
RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A La rappresentazone n Complemento a Due d un numero ntero relatvo (.-3,-,-1,0,+1,+,.) una volta stablta la precsone che s vuole ottenere (coè l numero d
Approfondimento 7.4 - Altri tipi di test di significatività del coefficiente di correlazione di Pearson
 Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
Algebra vettoriale: un breve formulario. E r
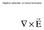 slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
CAPITOLO 6. Dunque, se il volume è costante, la variazione di temperatura si può calcolare nel seguente modo:
 Intoduzone alla Temodnamca Esecz svolt CAITOO 6 Eseczo n 6 Calcolae la vaazone d tempeatua d mol d un gas ( C R ) che assobe caloe (q J): a) Se la pessone è costante; b) Se l volume è costante In quale
Intoduzone alla Temodnamca Esecz svolt CAITOO 6 Eseczo n 6 Calcolae la vaazone d tempeatua d mol d un gas ( C R ) che assobe caloe (q J): a) Se la pessone è costante; b) Se l volume è costante In quale
Definizione di mutua induzione
 Mutua nduzone Defnzone d mutua nduzone Una nduttanza poduce un campo magnetco popozonale alla coente che v scoe. Se le lnee d foza d questo campo magnetco ntesecano una seconda nduttanza, n questo d poduce
Mutua nduzone Defnzone d mutua nduzone Una nduttanza poduce un campo magnetco popozonale alla coente che v scoe. Se le lnee d foza d questo campo magnetco ntesecano una seconda nduttanza, n questo d poduce
Sviluppo dell algoritmo per l allineamento dello spettrometro magnetico di PAMELA
 Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Corrente elettrica. Conduttore in equilibrio. Condutture in cui è mantenuta una differenza di potenziale (ddp) E=0 V=cost
 Coente elettca Conduttoe n equlbo B E 0 E0 cost B Conduttue n cu è mantenuta una dffeenza d potenzale (ddp) > B E 0 _ B Un campo elettco all nteno d un conduttoe appesenta una stuazone d non equlbo. Un
Coente elettca Conduttoe n equlbo B E 0 E0 cost B Conduttue n cu è mantenuta una dffeenza d potenzale (ddp) > B E 0 _ B Un campo elettco all nteno d un conduttoe appesenta una stuazone d non equlbo. Un
Lezione 12. Funzioni polinomiali. Radici di un polinomio. Teorema di Ruffini.
 Lezone Peequs: Lezone. Funzon polnomal. Radc d un polnomo. Teoema d Ruffn. Sa K un campo e sa L un campo d cu K è soocampo (n al caso s dce anche che L è un'esensone d K). Sa f ( X ) K[ X ] e sa α L. Alloa,
Lezone Peequs: Lezone. Funzon polnomal. Radc d un polnomo. Teoema d Ruffn. Sa K un campo e sa L un campo d cu K è soocampo (n al caso s dce anche che L è un'esensone d K). Sa f ( X ) K[ X ] e sa α L. Alloa,
Architetture aritmetiche. Corso di Organizzazione dei Calcolatori Mariagiovanna Sami
 Archtetture artmetche Corso d Organzzazone de Calcolator Maragovanna Sam 27-8 8 Sommator: : Full Adder s = x y c + x y c + x y c + x y c Full Adder x y c s x y c = x y + x c + + y c c + Full Adder c x
Archtetture artmetche Corso d Organzzazone de Calcolator Maragovanna Sam 27-8 8 Sommator: : Full Adder s = x y c + x y c + x y c + x y c Full Adder x y c s x y c = x y + x c + + y c c + Full Adder c x
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
EX 1 Calcolare la velocità di rinculo di un fucile di 4 kg che spara un proiettile di 0.05kg alla velocità di 280m/s.
 SITEMI ISOLATI EX 1 Calcolae la veloctà d nculo d un ucle d 4 kg che spaa un poettle d 0.05kg alla veloctà d 80m/s. EX Un one che vagga alla veloctà d = 6*10 5 m/s colpsce un alto one emo. S osseva che
SITEMI ISOLATI EX 1 Calcolae la veloctà d nculo d un ucle d 4 kg che spaa un poettle d 0.05kg alla veloctà d 80m/s. EX Un one che vagga alla veloctà d = 6*10 5 m/s colpsce un alto one emo. S osseva che
Condizioni di equilibrio TD nelle reazioni chimiche
 Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
CONDUZIONE NON STAZIONARIA
 CONDUZIONE NON AZIONARIA Caso geneale de sstem a tempeatua unfome ebbene l pocesso d conduzone non stazonaa n un soldo sa comunemente dovuto allo sco temco convettvo dal fludo ccostante, alt pocess d sco
CONDUZIONE NON AZIONARIA Caso geneale de sstem a tempeatua unfome ebbene l pocesso d conduzone non stazonaa n un soldo sa comunemente dovuto allo sco temco convettvo dal fludo ccostante, alt pocess d sco
Esercizio. Alcuni esercizi su algoritmi e programmazione. Schema a blocchi. Calcolo massimo, minimo e media
 Alcun esercz su algortm e programmazone Fondament d Informatca A Ingegnera Gestonale Unverstà degl Stud d Bresca Docente: Prof. Alfonso Gerevn Scrvere l algortmo e l dagramma d flusso per l seguente problema:
Alcun esercz su algortm e programmazone Fondament d Informatca A Ingegnera Gestonale Unverstà degl Stud d Bresca Docente: Prof. Alfonso Gerevn Scrvere l algortmo e l dagramma d flusso per l seguente problema:
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Economia del turismo
 Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Calcolo della derivata nel punto iniziale. Estrapolazione al primo ordine in t/2 e calcolo della derivata. Estrapolazione al secondo ordine in t
 Il meodo d Runge-Kua Rassumendo possamo de che l meodo d Runge- Kua d odne due consse nell esegue una esapolazone del pmo odne da a x(/ nel aluae la deaa x (/ e nell ulzzala pe oenee una sma d x( esaa
Il meodo d Runge-Kua Rassumendo possamo de che l meodo d Runge- Kua d odne due consse nell esegue una esapolazone del pmo odne da a x(/ nel aluae la deaa x (/ e nell ulzzala pe oenee una sma d x( esaa
Per regnare occorre tenere divisi i nemici e trarne vantaggio. fai ad ogni passo la scelta più conveniente
 Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Approcci algoritmici. Capitolo Approccio sequenziale. y = y (che collegano il modello di trasporto a quello di
 Captolo 3 Appocc algotmc In questo captolo descveemo alcun appocc algotmc mat alla soluone del poblema pesentato nel pmo captolo. C sono dves mod d pos spetto ad un poblema con un numeo così elevato d
Captolo 3 Appocc algotmc In questo captolo descveemo alcun appocc algotmc mat alla soluone del poblema pesentato nel pmo captolo. C sono dves mod d pos spetto ad un poblema con un numeo così elevato d
Esercizio. Alcuni esercizi su algoritmi e programmazione. Schema a blocchi. Calcolo massimo, minimo e media
 Alcun esercz su algortm e programmazone Fondament d Informatca A Ingegnera Gestonale Unverstà degl Stud d Bresca Docente: Prof. Alfonso Gerevn Scrvere l algortmo e l dagramma d flusso per l seguente problema:
Alcun esercz su algortm e programmazone Fondament d Informatca A Ingegnera Gestonale Unverstà degl Stud d Bresca Docente: Prof. Alfonso Gerevn Scrvere l algortmo e l dagramma d flusso per l seguente problema:
Sommario. Facoltà di Economia E E2 E 5 E 4. S x1. Le Variabili Casuali o Variabili Aleatorie. francesco mola. Lezione n 13.
 Coso d Statstca Facoltà d conoma a.a. - fancesco mola Sommao Le Vaabl Casual o Vaabl Aleatoe Lezone n Lez._a.a. 9- statstca-fancesco mola Vaabl Casual Vaabl Casual (cont. Una Vaable Casuale è una egola
Coso d Statstca Facoltà d conoma a.a. - fancesco mola Sommao Le Vaabl Casual o Vaabl Aleatoe Lezone n Lez._a.a. 9- statstca-fancesco mola Vaabl Casual Vaabl Casual (cont. Una Vaable Casuale è una egola
PROBLEMA DI SCELTA FRA DUE REGIMI DI
 PROBLEMA DI SCELTA FRA DUE REGIMI DI CAPITALIZZAZIONE Prerequst: legge d captalzzazone semplce legge d captalzzazone composta logartm e loro propretà dervate d una funzone pendenza d una curva n un punto
PROBLEMA DI SCELTA FRA DUE REGIMI DI CAPITALIZZAZIONE Prerequst: legge d captalzzazone semplce legge d captalzzazone composta logartm e loro propretà dervate d una funzone pendenza d una curva n un punto
 Dstbuzo Bvaate d due Vaabl Cosdeamo ua dstbuzoe bvaata costtuta da due vaabl statstche. Possamo defe, spetto al solto schema, le seguet mede pazal (essedo e vaabl statstche, tutte le modaltà ad esse elatve
Dstbuzo Bvaate d due Vaabl Cosdeamo ua dstbuzoe bvaata costtuta da due vaabl statstche. Possamo defe, spetto al solto schema, le seguet mede pazal (essedo e vaabl statstche, tutte le modaltà ad esse elatve
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2013/2014 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2013/2014 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
PROPRIETÀ DEL CAMPO ELETTROSTATICO (PARTE 2) G. Pugliese 1
 PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2015/2016 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2015/2016 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Dpatmento d Economa, Statstca e Fnanza Unvestà
Algoritmi di Ordinamento. Fondamenti di Informatica Prof. Ing. Salvatore Cavalieri
 Algortm d Ordnamento Fondament d Informatca Prof. Ing. Salvatore Cavaler 1 Introduzone Ordnare una sequenza d nformazon sgnfca effettuare una permutazone n modo da rspettare una relazone d ordne tra gl
Algortm d Ordnamento Fondament d Informatca Prof. Ing. Salvatore Cavaler 1 Introduzone Ordnare una sequenza d nformazon sgnfca effettuare una permutazone n modo da rspettare una relazone d ordne tra gl
Code a priorità (Heap) Definizione Heapify (mantenimento coda a priorità) Costruire un Heap Insert, Maximum e Extract-Max
 Code a prortà (Heap) Defnzone Heapfy (mantenmento coda a prortà) Costrure un Heap Insert, Maxmum e Extract-Max Coda a prortà (Heap) Una coda a prortà può essere rappresentato da un albero bnaro completo.
Code a prortà (Heap) Defnzone Heapfy (mantenmento coda a prortà) Costrure un Heap Insert, Maxmum e Extract-Max Coda a prortà (Heap) Una coda a prortà può essere rappresentato da un albero bnaro completo.
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
3 Il teorema di Gauss
 3 Il teoema d Gauss 3. Il flusso d un vettoe attaveso una supefce Pe una pozone d supefce che sa pana, dsposta nello spazo, c è una dezone che sulta ndvduata n modo unvoco ed è quella della pependcolae
3 Il teoema d Gauss 3. Il flusso d un vettoe attaveso una supefce Pe una pozone d supefce che sa pana, dsposta nello spazo, c è una dezone che sulta ndvduata n modo unvoco ed è quella della pependcolae
Statica del corpo rigido Sistemi equivalenti di forze
 Statca el copo go Sstem equvalent foze S efnsce Copo Rgo un copo che è nefomable: Tutt punt el copo go mantengono nalteata la ecpoca stanza qualunque foza estena agsca su ess E ovvamente un astazone Con
Statca el copo go Sstem equvalent foze S efnsce Copo Rgo un copo che è nefomable: Tutt punt el copo go mantengono nalteata la ecpoca stanza qualunque foza estena agsca su ess E ovvamente un astazone Con
Università di Cassino Corso di Statistica 1 Esercitazione del 17/10/2006 Dott. Alfonso Piscitelli. Esercizio 1
 Unverstà d Cassno Corso d Statstca Eserctazone del 7/0/006 Dott. Alfonso Psctell Eserczo Il seguente data set rporta la rlevazone d alcun caratter su un collettvo d 0 soggett. Soggetto Sesso Età Reddto
Unverstà d Cassno Corso d Statstca Eserctazone del 7/0/006 Dott. Alfonso Psctell Eserczo Il seguente data set rporta la rlevazone d alcun caratter su un collettvo d 0 soggett. Soggetto Sesso Età Reddto
Elementi di Calcolo delle Probabilità
 Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2011/2012 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Facoltà d Economa UnCal Calendao - Lezon: dal
Element d Calcolo delle obabltà Coso d Calcolo delle obabltà ed Infeenza a.a. 2011/2012 - mo Semeste of. Flppo DOMM Coso d Lauea Magstale n Economa pplcata Facoltà d Economa UnCal Calendao - Lezon: dal
Lezione 9. N-poli. N-poli passivi. Pilotato in tensione
 Lezone 9 N-pol 4 Fn oa c samo lmtat a bpol. Esstono peò anche dspostv che non sono conducbl a bpol, nel senso che non nteagscono con l esteno attaveso due sol pol. In fgua è appesentato un quadpolo, ma
Lezone 9 N-pol 4 Fn oa c samo lmtat a bpol. Esstono peò anche dspostv che non sono conducbl a bpol, nel senso che non nteagscono con l esteno attaveso due sol pol. In fgua è appesentato un quadpolo, ma
Sistemi Intelligenti Reinforcement Learning: Evaluative Feedback
 Sstem Intellgent Renfocement Leanng: Evaluatve Feedbac Albeto Boghese Unvestà degl Stud d Mlano Laboatoo d Sstem Intellgent Applcat (AIS-Lab Dpatmento d Scenze dell Infomazone boghese@ds.unm.t /9 http:\\homes.ds.unm.t\
Sstem Intellgent Renfocement Leanng: Evaluatve Feedbac Albeto Boghese Unvestà degl Stud d Mlano Laboatoo d Sstem Intellgent Applcat (AIS-Lab Dpatmento d Scenze dell Infomazone boghese@ds.unm.t /9 http:\\homes.ds.unm.t\
Sommario. Corso di Statistica Facoltà di Economia. Le Variabili Casuali o Variabili Aleatorie. Lezione n 16. Francesco Mola. Variabili Casuali (cont
 Coso d Statstca Facoltà d conoma Lezone n 6 z Sommao Le Vaabl Casual o Vaabl Aleatoe a.a. - Fancesco Mola a.a. - statstca-fancesco mola Vaabl Casual Vaabl Casual (cont cont.) Una Vaable Casuale è una egola
Coso d Statstca Facoltà d conoma Lezone n 6 z Sommao Le Vaabl Casual o Vaabl Aleatoe a.a. - Fancesco Mola a.a. - statstca-fancesco mola Vaabl Casual Vaabl Casual (cont cont.) Una Vaable Casuale è una egola
Sorgenti Numeriche - Soluzioni
 Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
I vettori. Grandezze scalari: Grandezze vettoriali
 I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
ESERCITAZIONE DEL 3 MARZO 2005
 ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
Lezione 2 a - Statistica descrittiva per variabili quantitative
 Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 x 1 =103 2 x 2 =97 3 x 3 =90
Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 x 1 =103 2 x 2 =97 3 x 3 =90
Prima prova di gruppo
 Prma prova d gruppo Es. Una metodologa d anals produce fals postv nel 3% de cas e fals negatv nell % de cas. Calcolate quale è l esto pù probable (postvo o negatvo se due anals consecutve esegute sullo
Prma prova d gruppo Es. Una metodologa d anals produce fals postv nel 3% de cas e fals negatv nell % de cas. Calcolate quale è l esto pù probable (postvo o negatvo se due anals consecutve esegute sullo
Tecniche Algoritmiche: divide et impera
 Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Università degli Studi di Roma Tor Vergata Facoltà di Ingegneria Corso di Laurea in Ingegneria Medica. Algoritmi
 Unverstà degl Stud d Roma Tor Vergata Facoltà d Ingegnera Corso d Laurea n Ingegnera Medca Algortm Rev.2.2 of 2016-04-20 Elaborazone dat Problem che s presentano spesso sono 1. rcorsvo (es. successone
Unverstà degl Stud d Roma Tor Vergata Facoltà d Ingegnera Corso d Laurea n Ingegnera Medca Algortm Rev.2.2 of 2016-04-20 Elaborazone dat Problem che s presentano spesso sono 1. rcorsvo (es. successone
2 Θ. d hkl. sen 2 / hkl. sen 2
 La legge d Bagg e le equazo d Laue osce eslusvamete le codzo pe avee u asco datto. No dce se l asco datto saà pù o meo teso o tee coto della stuttua ma solo del etcolo Da valo agola a cu s ossevao less
La legge d Bagg e le equazo d Laue osce eslusvamete le codzo pe avee u asco datto. No dce se l asco datto saà pù o meo teso o tee coto della stuttua ma solo del etcolo Da valo agola a cu s ossevao less
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Una semplice applicazione del metodo delle caratteristiche: la propagazione di un onda di marea all interno di un canale a sezione rettangolare.
 Una semplce applcazone del metodo delle caratterstche: la propagazone d un onda d marea all nterno d un canale a sezone rettangolare. In generale la propagazone d un onda monodmensonale n una corrente
Una semplce applcazone del metodo delle caratterstche: la propagazone d un onda d marea all nterno d un canale a sezone rettangolare. In generale la propagazone d un onda monodmensonale n una corrente
Il procedimento può essere pensato come una ricerca in un insieme ordinato, il peso incognito può essere cercato con il metodo della ricerca binaria.
 SCELTA OTTIMALE DEL PROCEDIMENTO PER PESARE Il procedmento può essere pensato come una rcerca n un nseme ordnato, l peso ncognto può essere cercato con l metodo della rcerca bnara. PESI CAMPIONE IN BASE
SCELTA OTTIMALE DEL PROCEDIMENTO PER PESARE Il procedmento può essere pensato come una rcerca n un nseme ordnato, l peso ncognto può essere cercato con l metodo della rcerca bnara. PESI CAMPIONE IN BASE
Fluidodinamica Applicata Esempi (1-5) di Flusso Irrotazionale
 Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Fisica Generale A. Terzo principio della dinamica. Scuola di Ingegneria e Architettura UNIBO Cesena Anno Accademico Maurizio Piccinini
 Fsca eeale A Tezo pcpo della damca Scuola d Igegea e Achtettua UNIBO Cesea Ao Accademco 205 206 Tezo pcpo Og volta che u copo (A) esecta ua foza su u alto copo (B), l secodo esecta sul pmo ua foza vettoalmete
Fsca eeale A Tezo pcpo della damca Scuola d Igegea e Achtettua UNIBO Cesea Ao Accademco 205 206 Tezo pcpo Og volta che u copo (A) esecta ua foza su u alto copo (B), l secodo esecta sul pmo ua foza vettoalmete
Verifiche di congruità tecnica delle offerte rispetto ai margini
 Dsposzone tecnca d funzonaento Pagna 1 d 7 Dsposzone tecnca d funzonaento n. 10 rev.1 MPE (a sens dell artcolo 4 del Testo ntegrato della Dscplna del ercato elettrco, approvato con decreto del Mnstro delle
Dsposzone tecnca d funzonaento Pagna 1 d 7 Dsposzone tecnca d funzonaento n. 10 rev.1 MPE (a sens dell artcolo 4 del Testo ntegrato della Dscplna del ercato elettrco, approvato con decreto del Mnstro delle
4. ALGORITMI GREEDY. cambia-monete scheduling a minimo il ritardo. Il problema del cambia-monete. Proprietà di una soluzione ottima
 Il problema del camba-monete. ALGORITMI GREEDY camba-monete schedulng a mnmo l rtardo Scopo. Dat tagl dsponbl: c, c, 5c, 0c, 0c, 50c,, progettare un algortmo che data una certa somma la camb usando l mnmo
Il problema del camba-monete. ALGORITMI GREEDY camba-monete schedulng a mnmo l rtardo Scopo. Dat tagl dsponbl: c, c, 5c, 0c, 0c, 50c,, progettare un algortmo che data una certa somma la camb usando l mnmo
posizione, velocità, quantità di moto, energia cinetica, momento angolare, ecc.
 Unvestà a Sapena FONDAMENTI DEA MECCANICA QUANTISTICA Pma delle legg ( Postulat vedamo concett Vaabl dnamce Funone d onda o d stato 3 Opeato Vaable Dnamca S tatta d una qualsas vaable ce defnsce l moto
Unvestà a Sapena FONDAMENTI DEA MECCANICA QUANTISTICA Pma delle legg ( Postulat vedamo concett Vaabl dnamce Funone d onda o d stato 3 Opeato Vaable Dnamca S tatta d una qualsas vaable ce defnsce l moto
Allenamenti di matematica: Teoria dei numeri e algebra modulare Soluzioni esercizi
 Allenament d matematca: Teora de numer e algebra modulare Soluzon esercz 29 novembre 2013 1. Canguro salterno. Un canguro salterno s trova a ped d una scala nfnta che ntende salre nel seguente modo: Salta
Allenament d matematca: Teora de numer e algebra modulare Soluzon esercz 29 novembre 2013 1. Canguro salterno. Un canguro salterno s trova a ped d una scala nfnta che ntende salre nel seguente modo: Salta
Lezione 2 le misure di sintesi: le medie
 Lezone le msure d sntes: le mede Cattedra d Bostatstca Dpartmento d Scenze spermental e clnche, Unverstà degl Stud G. d Annunzo d Chet-Pescara Prof. Enzo Ballone Lezone a- Statstca descrttva per varabl
Lezone le msure d sntes: le mede Cattedra d Bostatstca Dpartmento d Scenze spermental e clnche, Unverstà degl Stud G. d Annunzo d Chet-Pescara Prof. Enzo Ballone Lezone a- Statstca descrttva per varabl
Specifica calcolo soddisfazione discenti
 INDICE 1 SCOPO CAMPO DI APPLICAZIONE 3 DEFINIZIONI E CALCOLO PER LE DOMANDE INFORMATIVE 4 DEFINIZIONI E CALCOLO PER LE DOMANDE CON GIUDIZI 5 DEVIAZIONE STANDARD PER LE DOMANDE CON GIUDIZI 6 RACCOLTA ED
INDICE 1 SCOPO CAMPO DI APPLICAZIONE 3 DEFINIZIONI E CALCOLO PER LE DOMANDE INFORMATIVE 4 DEFINIZIONI E CALCOLO PER LE DOMANDE CON GIUDIZI 5 DEVIAZIONE STANDARD PER LE DOMANDE CON GIUDIZI 6 RACCOLTA ED
Errata corrige del libro Fondamenti di Informatica in Java
 corrge del lbro Fondament d Informatca n Java Emlo D Gacomo, Walter Ddmo Captolo 1 R1 R2 R3 Rn PC IR PSW Untà d controllo Pag. 23, Fgura 1.2 Bus nterno ALU MAR MDR al bus dat al bus ndrzz al bus d controllo
corrge del lbro Fondament d Informatca n Java Emlo D Gacomo, Walter Ddmo Captolo 1 R1 R2 R3 Rn PC IR PSW Untà d controllo Pag. 23, Fgura 1.2 Bus nterno ALU MAR MDR al bus dat al bus ndrzz al bus d controllo
LAVORO ESTIVO 4CO1 / 4 CO2
 LVORO ESTIVO CO / CO LE EQUZIONI ESPONENZILI 7 7 7 LE DISEQUZIONI ESPONENZILI 7 LE EQUZIONI LOGRITMICHE [ ] [ ] log log log log log log log log log ln ln ln ln ln ln log log log LE DISEQUZIONI LOGRITMICHE
LVORO ESTIVO CO / CO LE EQUZIONI ESPONENZILI 7 7 7 LE DISEQUZIONI ESPONENZILI 7 LE EQUZIONI LOGRITMICHE [ ] [ ] log log log log log log log log log ln ln ln ln ln ln log log log LE DISEQUZIONI LOGRITMICHE
Il campo B è uscente. Fisica Generale per Architettura - G. Cantatore 1
 Lezone 18 - Foza magnetca su fl pecos da coent Abbamo vsto che un campo magnetco esecta una foza sulle cache n movmento: quando queste cache n moto sono confnate all nteno d un conduttoe flfome c aspettamo
Lezone 18 - Foza magnetca su fl pecos da coent Abbamo vsto che un campo magnetco esecta una foza sulle cache n movmento: quando queste cache n moto sono confnate all nteno d un conduttoe flfome c aspettamo
Analisi ammortizzata. Illustriamo il metodo con due esempi. operazioni su di una pila Sia P una pila di interi con le solite operazioni:
 Anals ammortzzata Anals ammortzzata S consdera l tempo rchesto per esegure, nel caso pessmo, una ntera sequenza d operazon. Se le operazon costose sono relatvamente meno frequent allora l costo rchesto
Anals ammortzzata Anals ammortzzata S consdera l tempo rchesto per esegure, nel caso pessmo, una ntera sequenza d operazon. Se le operazon costose sono relatvamente meno frequent allora l costo rchesto
Divide et impera. Divide et Impera
 Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Una rendita è una somma di capitali pagabili (o esigibili) a determinate scadenze, fissate secondo intervalli regolari di tempo.
 14. Le endte 14.1 Nozon geneal Una endta è una somma d captal pagabl (o esgbl) a detemnate scadenze, fssate secondo ntevall egola d tempo. Ognuno d quest captal è detto ata; gl ntevall sono dett peod e
14. Le endte 14.1 Nozon geneal Una endta è una somma d captal pagabl (o esgbl) a detemnate scadenze, fssate secondo ntevall egola d tempo. Ognuno d quest captal è detto ata; gl ntevall sono dett peod e
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
Divide et impera. Vittorio Maniezzo Università di Bologna
 Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
= = M r F. lungo la stessa direzione quindi. hanno sempre. risultante nulla. costituiscono sempre. ma una coppia di forze a braccio nullo
 Secoda equazoe cadale pe l tezo pcpo della damca le foze tee s mafestao sempe a coppe d foze d azoe e eazoe che s esectao lugo la stessa dezoe qud hao sempe sultate ulla costtuscoo sempe ua coppa d foze
Secoda equazoe cadale pe l tezo pcpo della damca le foze tee s mafestao sempe a coppe d foze d azoe e eazoe che s esectao lugo la stessa dezoe qud hao sempe sultate ulla costtuscoo sempe ua coppa d foze
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017. Esercizi 3
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Esercz 3 Pan d ammortamento Eserczo 1. Un prestto d 12000e vene rmborsato n 10 ann con rate mensl e pano all
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Esercz 3 Pan d ammortamento Eserczo 1. Un prestto d 12000e vene rmborsato n 10 ann con rate mensl e pano all
Ministero della Salute D.G. della programmazione sanitaria --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA
 Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
Definizione della tariffa per l accertamento di conformità degli strumenti di misura
 Provvedmento adottato dalla Gunta del 6/7/2007 Defnzone della tarffa per l accertamento d conformtà degl strument d msura. Per l accertamento d conformtà degl strument d msura sono defnte le seguent 6
Provvedmento adottato dalla Gunta del 6/7/2007 Defnzone della tarffa per l accertamento d conformtà degl strument d msura. Per l accertamento d conformtà degl strument d msura sono defnte le seguent 6
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione
 In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
Modello del Gruppo d Acquisto
 InVMall - Intellgent Vrtual Mall Modello del Gruppo d Acqusto Survey L attvtà svolta per la realzzazone dell attvtà B7 Defnzone del Gruppo d Acqusto e de Relatv Algortm d Inferenza, prevsta dal captolato
InVMall - Intellgent Vrtual Mall Modello del Gruppo d Acqusto Survey L attvtà svolta per la realzzazone dell attvtà B7 Defnzone del Gruppo d Acqusto e de Relatv Algortm d Inferenza, prevsta dal captolato
Il paradigma della programmazione dinamica
 Il paradgma della programmazone dnamca Paolo Camurat Dp. Automatca e Informatca Poltecnco d Torno Tpologe d problem Problem d rcerca: ete una oluzone valda? cclo Hamltonano: dato un grafo non orentato,
Il paradgma della programmazone dnamca Paolo Camurat Dp. Automatca e Informatca Poltecnco d Torno Tpologe d problem Problem d rcerca: ete una oluzone valda? cclo Hamltonano: dato un grafo non orentato,
Individuazione di linee e curve. Minimi quadrati. Visione e Percezione. Model fitting: algoritmi per trovare le linee. a = vettore dei parametri
 Segmentazone tramte modell ad hoc Indvduazone d lnee e curve Obbettvo: Data l mmagne d output d un algortmo d rlevamento d bord, trova tutte le stanze d una certa curva (lnea o ellss) o una sua parte.
Segmentazone tramte modell ad hoc Indvduazone d lnee e curve Obbettvo: Data l mmagne d output d un algortmo d rlevamento d bord, trova tutte le stanze d una certa curva (lnea o ellss) o una sua parte.
QuickSort (1962, The Computer Journal)
 QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
ANALISI STATISTICA DELLE INCERTEZZE CASUALI
 AALISI STATISTICA DELLE ICERTEZZE CASUALI Consderamo l caso della msura d una grandezza fsca che sa affetta da error casual. Per ottenere maggor nformazone sul valore vero della grandezza rpetamo pù volte
AALISI STATISTICA DELLE ICERTEZZE CASUALI Consderamo l caso della msura d una grandezza fsca che sa affetta da error casual. Per ottenere maggor nformazone sul valore vero della grandezza rpetamo pù volte
Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi
 Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi Algoritmi basati sulla tecnica Divide et Impera In questo corso: Ricerca binaria
Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi Algoritmi basati sulla tecnica Divide et Impera In questo corso: Ricerca binaria
Lezione 2 a - Statistica descrittiva per variabili quantitative
 Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 1 =103 2 2 =97 3 3 =90 4 4 =119
Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 1 =103 2 2 =97 3 3 =90 4 4 =119
Sostituire cf(n) a ciascun termine O(f(n)), dove c è una costante reale simbolica specifica per quel termine
 Esempio 1 Ricorrenza da risolvere BASE T(1) = O(1) INDUZIONE T(n) = O(1) + T(n 1) per n > 1 Procedimento Sostituire cf(n) a ciascun termine O(f(n)), dove c è una costante reale simbolica specifica per
Esempio 1 Ricorrenza da risolvere BASE T(1) = O(1) INDUZIONE T(n) = O(1) + T(n 1) per n > 1 Procedimento Sostituire cf(n) a ciascun termine O(f(n)), dove c è una costante reale simbolica specifica per
Il campo elettrico è conservativo. L A1B = F i l r
 F = qe α l 2 Il campo elettco è consevatvo n L = F l In un campo elettco stazonao l lavoo non dpende dalla taettoa ma solo dal punto nzale e dal punto fnale. L = L 2 La foza elettca è consevatva 2 Se calcolamo
F = qe α l 2 Il campo elettco è consevatvo n L = F l In un campo elettco stazonao l lavoo non dpende dalla taettoa ma solo dal punto nzale e dal punto fnale. L = L 2 La foza elettca è consevatva 2 Se calcolamo
ESERCITAZIONE 8. Esercitazioni del corso FONDAMENTI DI PROCESSI CHIMICI Prof. Gianpiero Groppi
 Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Ottimizzazione Combinatoria
 Ottmzzazone Combnatoa Clusteng de dat Lezone Lezon a cua d Sla Canale contatto e-mal: canale@ds.unoma.t Unestà d Roma La Sapenza Dpatmento d Infomatca e Sstemstca Coso d Lauea n Ingegnea Gestonale Defnzone
Ottmzzazone Combnatoa Clusteng de dat Lezone Lezon a cua d Sla Canale contatto e-mal: canale@ds.unoma.t Unestà d Roma La Sapenza Dpatmento d Infomatca e Sstemstca Coso d Lauea n Ingegnea Gestonale Defnzone
ALGORITMI Docente: Prof. Domenico Cantone
 CORSO SPECILE DI DURT NNULE PER IL CONSEGUIMENTO DELL BILITZIONE LL INSEGNMENTO NELL SCUOL SECONDRI DI I e II GRDO Indirizzo Fisico - Informatico - Matematico a.a. 00/07 - Classe - Informatica LGORITMI
CORSO SPECILE DI DURT NNULE PER IL CONSEGUIMENTO DELL BILITZIONE LL INSEGNMENTO NELL SCUOL SECONDRI DI I e II GRDO Indirizzo Fisico - Informatico - Matematico a.a. 00/07 - Classe - Informatica LGORITMI
Le operazioni che vogliamo realizzare sono. Supporremo che una tabella T abbia i seguenti attributi: 1. Table(T): costruisce una tabella vuota T.
 tabelle dnamche Tabelle dnamche Spesso non s conosce a pror quanta memora serve per memorzzare una struttura dat (tabella d dat ~ array, tabella hash, heap, stack, ecc.. Può captare qund d allocare una
tabelle dnamche Tabelle dnamche Spesso non s conosce a pror quanta memora serve per memorzzare una struttura dat (tabella d dat ~ array, tabella hash, heap, stack, ecc.. Può captare qund d allocare una
ESERCIZIO 4.1 Si consideri una popolazione consistente delle quattro misurazioni 0, 3, 12 e 20 descritta dalla seguente distribuzione di probabilità:
 ESERCIZIO. S consder una popolazone consstente delle quattro msurazon,, e descrtta dalla seguente dstrbuzone d probabltà: X P(X) ¼ ¼ ¼ ¼ S estrae casualmente usando uno schema d camponamento senza rpetzone
ESERCIZIO. S consder una popolazone consstente delle quattro msurazon,, e descrtta dalla seguente dstrbuzone d probabltà: X P(X) ¼ ¼ ¼ ¼ S estrae casualmente usando uno schema d camponamento senza rpetzone
= 4. L unita di misura della carica elettrica nel S.I. è il coulomb (C).
 LGG DI COULOMB (3) L unta d msua della caca elettca nel.i. è l coulomb (C). F π o La caca elettca d C è uella caca che posta nel vuoto ad m d dstanza da una caca elettca uguale la espnge con la foza d
LGG DI COULOMB (3) L unta d msua della caca elettca nel.i. è l coulomb (C). F π o La caca elettca d C è uella caca che posta nel vuoto ad m d dstanza da una caca elettca uguale la espnge con la foza d
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa 2012-2013 lezione 13: 24 aprile 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 13: 24 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? reammortamento uò accadere che, dopo l erogazone
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 13: 24 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? reammortamento uò accadere che, dopo l erogazone
Algoritmi e Strutture di Dati I 1. Algoritmi e Strutture di Dati I Massimo Franceschet francesc
 Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc m.franceschet@unich.it Algoritmi e Strutture di Dati I 2 Problema dell ordinamento
Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc m.franceschet@unich.it Algoritmi e Strutture di Dati I 2 Problema dell ordinamento
Il problema dell'ordinamento. Algoritmi e Laboratorio a.a Lezioni. prof. Elio Giovannetti
 Unverstà d Torno Facoltà d Scenze MFN Corso d Stud n Informatca Currculum SR (Sstem e Ret) Algortm e Laboratoro a.a. 25-6 Lezon prof. Elo Govannett Parte 7 Algortm d ordnamento elementar (quadratc). versone
Unverstà d Torno Facoltà d Scenze MFN Corso d Stud n Informatca Currculum SR (Sstem e Ret) Algortm e Laboratoro a.a. 25-6 Lezon prof. Elo Govannett Parte 7 Algortm d ordnamento elementar (quadratc). versone
