Collegio dei Geometri di Bergamo I.S.I.S. Quarenghi
|
|
|
- Oliviero Cavallaro
- 8 anni fa
- Visualizzazioni
Transcript
1 Collegio dei Geometri di Bergamo I.S.I.S. Quarenghi Corso di preparazione agli Esami di abilitazione alla libera professione di Geometra Sessione 009 TOPOGRAFIA Docente Ing. Aldo Piantoni
2 Come misuriamo gli angoli? Sistema sessagesimale gradi primi e secondi sistema sessadecimale gradi, decimi centesimi Radianti centesimali (gon C g) TRIANGOLO RETTANGOLO PRIMO MODULO Da ricordare il teorema di Pitagora la somma del quadrato dei cateti = al quadrato dell ipotenusa b =a +c c b a In tutti i triangoli la somma degli angoli interni è uguale ad un angolo piatto. Relazioni fondamentali senα = rapporto tra il cateto opposto all angolo ed ipotenusa =a/b cosα = rapporto tra cateto adiacente all angolo ed ipotenusa= c/b tanα = rapporto tra cateto opposto all angolo e cateto adiacente = a/c Attenzione! Prima di iniziare qualsiasi calcolo verificate che la calcolatrice operi nel sistema angolare corretto Fate attenzione alla precisione dei dati assegnati (n di decimali) per avere un risultato congruente
3 Triangoli qualsiasi Anche per essi la somma degli angoli interni è pari ad un angolo piatto sussistono due relazioni particolarmente importanti tra gli elementi di un triangolo qualsiasi per essere risolvibile debbono essere noti tre elementi di cui almeno un lato (area ) TEOREMA DEI SENI all interno di un triangolo qualsiasi rimane costante il rapporto tra il lato ed il seno dell angolo opposto a/sinα = b/sinβ = c/sinγ = R ( diametro circonferenza circoscritta) è utile per ricavare il lato noti un lato e gli angoli n.b. - da utilizzare con attenzione per calcolare gli angoli perché la funzione arcsin ammette due risultati (α ; 00-α) per lo stesso valore del seno TEOREMA DI CARNOT (del coseno) in un triangolo qualsiasi il quadrato di un lato è pari alla somma del quadrato degli altri due diminuita del doppio prodotto dei lati per il coseno dell angolo compreso. a =b + c -ab x cosα Utile nel caso si debbano calcolare gli angoli noti i lati perché la funzione arcos ammette un solo risultato per angoli minori di 00 Il calcolo dell area nel triangolo α = arcos [(b +c -a )/bc)] Vi sono diverse modalità per il calcolo dell area del triangolo (b x h)/ (b x a x sinγ)/ (b x sin ץ x sin α) /sin β (p x (p-a) x (p-b) x (p-c)) 3
4 1. MISURA DELLE DISTANZE SECONDO MODULO La distanza tra due punti può essere reale o inclinata (d r ), orizzontale (d or ), topografica o ridotta (d T ). Partendo dalla distanza reale, le altre due si ricavano dalle equazioni: d o r = d r x sen φ = d r x sen (CV) R d T = d or R + Q dove: φ ; (CV) : angolo verticale o zenitale Q: quota media s.l.m. Per distanze superiori a qualche chilometro conviene usare la seguente espressione che considera le correzioni dovute alla sfericità ed al fenomeno di rifrazione atmosferica: d o r = d r x sen(cv) (1- k/)x d r cos CV)/R in cui: k = coefficiente di rifrazione, in media pari a 0,14 R = raggio della sfera locale, mediamente Km Precisione media sulle distanze: distanziometri ad onde: 5 mm + 5 ppm = 5 mm + 5 mm/km stadia: 10 cm + 0,1 cm/m = 10 cm ppm. MISURA DEI DISLIVELLI LIVELLAZIONI GEOMETRICHE (a visuale orizzontale): Da un estremo: AB = altezza strumentale lettura alla stadia = (h A -L B ) Dal mezzo: AB = lettura alla stadia indietro (contro-battuta) lettura alla stadia avanti (battuta) =(L A -L B ) Composta: AB = somme delle contro-battute somma delle battute 4
5 LIVELLAZIONE TACHEOMETRICA (a visuale inclinata) AB = h A - l B +AB/tan(CV)+(1-k)AB /(R) AB: distanza orizzontale h A, l B : altezza strumentale e altezza del prisma( o lettura media) (CV): angolo zenitale o verticale k: coefficiente di rifrazione, assunto mediamente pari a 0,14 R: raggio della sfera locale, mediamente km METODOLOGIE DI RILIEVO Un rilievo è isodeterminato se le misure sono strettamente sufficienti a stabilire la posizione reciproca dei punti rilevati, mentre è iperdeterminato n volte se le misure sono sovrabbondanti. Se invece le misure effettuate non sono sufficienti il rilievo è labile. 1. Rilievo celerimetrico o di dettaglio Tipologia del rilievo: ISODETERMINATO, sia in planimetria che in quota Determinazione del punto A nel sistema di riferimento celerimetrico nel punto di stazione S: X Y Q A A A = X = Y S = Q + SA senϑ + SA cosϑ S S + h S h A SA + SA SA tanϕ SA SA + (1 k) R COLLEGAMENTO DIRETTO DI DUE STAZIONI Le due stazioni S e T sono reciprocamente visibili ed a distanza inferiore alla portata del distanziometro. In questo caso è possibile stazionare in S e collimare T misurando quindi distanza ed azimut θ ST ; da T si ricollima S imponendo al cerchio orizzontale una lettura θ TS = θ ST
6 Così facendo in S e T il CO ha il medesimo orientamento ed è possibile calcolare le coordinate di T nonché le coordinate dei punti battuti da T X T =X s +ST sen (θ ST ) ; Y T =Y s +ST cos (θ ST ) punto P battuto da T X P = X T +TP sen (θ TP ) ; Y P = Y T +TP cos (θ TP ) COLLEGAMENTO INDIRETTO DI DUE STAZIONI Serve a collegare due stazioni non reciprocamente visibili, in appoggio a due punti A e B, contemporaneamente visibili dalle due stazioni S e T. Tipologia del rilievo: IPERDETERMINATO sia in planimetria che in quota. In planimetria si fanno quattro misure dalla stazione S e dalla stazione T (due angoli di direzione e due distanze da ciascuna). Le incognite sono le coordinate dei tre punti A, B e T, e l angolo di disorientamento ε: quindi 8 misure e 7 incognite = 1 iperdeterminazione. In quota, il dislivello ST può essere calcolato lungo due percorsi diversi: SAT e SBT, quindi una iperdeterminazione. Per il calcolo planimetrico sì calcola prima il disorientamento ε nella stazione T mediante la differenza tra i due azimut θ AB e θ AB, quindi si calcolano le coordinate della stazione T prima con riferimento al punto A e poi con riferimento al punto B e si effettua la media aritmetica dei due valori determinati. COLLEGAMENTO MISTO DI DUE STAZIONI 6
7 Si adotta nei casi in cui le due stazioni se pur reciprocamente visibili sono a distanza maggiore della portata del distanziometro ma comunque inferiore al doppio della medesima. In questo caso si utilizza un punto intermedio A in modo tale che si possano misurare le distanze SA e TA e quindi calcolare la distanza ST risolvendo il triangolo AST. Si procede poi come per il collegamento diretto.. Rilievo per intersezioni.1 Intersezione in avanti Tipologia del rilievo: ISODETERMINATO in planimetria, IPERDE- TERMINATO in quota 7
8 Sono note le coordinate di due punti accessibili S e T, si devono determinare le coordinate di un punto inaccessibile A. Dalle due stazioni si determinano gli angoli orizzontali in S e in T, gli angoli zenitali e la distanza reciproca tra esse (base). Per determinare le distanze incognite dalle stazioni al punto inaccessibile si applica il teorema dei seni. SA= ST senγ/senα ; ΤΑ=ST senβ/senα Quindi si calcolano le coordinate con le formule di conversione Polari Rettangolari. X A = X S + (X A ) S = X S + SA sen(sa) Y A = Y S + (Y A ) S = Y S + SA cos(sa) X A = X T + (X A ) T = X T + TA sen(ta) Y A = Y T + (Y A ) T = Y T + TA cos(ta) Per la quota si applica la formula della livellazione tacheometrica prima da S e poi da T, e si esegue la media aritmetica dei due valori (1 iperdeterminazione in quota).. Intersezione inversa con tre punti (SNELLIUS-POTHENOT) Tipologia del rilievo: ISODETERMINATO in planimetria, IPERDE- TERMINATO in quota. Sono note le coordinate di tre punti inaccessibili A, B e C, si devono determinare le coordinate di un punto accessibile P, in cui si effettua la stazione. Dalla stazione P si determinano gli angoli orizzontali α e β formati con le congiungenti i tre vertici noti, e gli angoli zenitali. Si disegna la circonferenza passante per due punti noti e quello incognito, ad 8
9 es. A, B e P: si congiunge P con il terzo vertice noto C e si risolve il triangolo ABH applicando il teorema dei seni, constatando che due degli angoli interni di detto triangolo sono pari ad α e β. Si ricava quindi l azimut ϑ HC = ϑ PC che permette di determinare l angolo BAP e quindi di risolvere il triangolo BAP, ancora col teorema dei seni. Si possono quindi calcolare le coordinate di P con le formule di conversione Polari Rettangolari. Per la quota si applica la formula della livellazione tacheometrica relativa alle tre collimazioni in A, B e C, e si esegue la media aritmetica dei tre valori ( iperdeterminazioni in quota)..3 Intersezione inversa con due punti o problema della distanza i- naccessibile (HANSEN) Tipologia del rilievo: ISODETERMINATO in planimetria, IPERDE- TERMINATO in quota. Sono note le coordinate di due punti inaccessibili A e B, si devono determinare le coordinate di un punto accessibile P, in cui si effettua la stazione. Dalla stazione P si determinano gli angoli orizzontali e verticali formati con le congiungenti i due vertici noti, e un punto di appoggio Q; da quest ultimo si effettuano le stesse misurazioni. Si considera quindi un quadrilatero fittizio, simile a quello effettivo, in cui si pone arbitrariamente la distanza PQ (base) uguale ad un certo valore. Si potrebbe eventualmente anche misurare tale base, in tal caso il problema planimetrico diventerebbe iperdeterminato. Si considerano quindi i due triangoli 9
10 che i lati congiungenti la stazione P con i due vertici noti formano con la base fittizia, e si determinano tali lati mediante il teorema dei seni. Si considera quindi il triangolo formato da questi ultimi lati e si applica il teorema di Carnot diretto ed inverso per determinare la distanza tra i punti di coordinate note e l angolo adiacente. Dal confronto tra la distanza così determinata e quella effettiva, ricavabile dalle coordinate, si determina il rapporto di similitudine tra il quadrilatero fittizio e quello effettivo, risalendo così alla distanza effettiva PA. Mediante le formule di conversione Polari Rettangolari si determinano le coordinate di P. Per la quota si applica la formula della livellazione tacheometrica relativa alle due collimazioni in A e B, e si esegue la media aritmetica dei due valori (1 iperdeterminazione in quota). Se i dislivelli sono stati misurati anche dalla stazione ausiliaria Q si hanno altre due ulteriori determinazioni di quota. 3. Rilievo per poligonazioni Angolo al vertice: è l angolo ottenuto dalla rotazione del lato precedente verso quello seguente in senso orario. FORMULA DI TRASPORTO DEGLI AZIMUT θ succ.= θ prec. + angolo al vertice + 00 gon se θ prec.+angolo al vert. < 00 gon - 00 gon se θ prec.+angolo al vert. > 00 gon gon se θ prec.+angolo al vert. > 600 gon 3.1 Poligonali aperte non orientate Tipologia del rilievo: ISODETERMINATO in planimetria a) Calcolo degli azimut, partendo dal primo azimut fissato a priori, in base alla scelta del sistema di coordinate b) Calcolo delle coordinate parziali di ogni vertice rispetto al precedente 10
11 c) Calcolo delle coordinate assolute dei vertici 3. Poligonali chiuse non orientate Tipologia del rilievo: IPERDETERMINATO in planimetria (3 volte) a) Compensazione angolare, con ripartizione in parti uguali dell errore di chiusura angolare b) Calcolo degli azimut, partendo dal primo azimut fissato a priori, ed utilizzando gli angoli al vertice compensati c) Calcolo delle coordinate parziali di ogni vertice rispetto al precedente d) Compensazione lineare delle coordinate parziali, con ripartizione degli errori di chiusura lineare in parti proporzionali al loro valore assoluto e) Calcolo delle coordinate assolute dei vertici 3.3 Poligonali chiuse solo angolarmente Tipologia del rilievo: IPERDETERMINATO in planimetria ( volte) a) Compensazione angolare, con ripartizione in parti uguali dell errore di chiusura angolare b) Calcolo degli azimut, partendo dal primo azimut fissato a priori, ed utilizzando gli angoli al vertice compensati. Nella scelta degli assi, uno di questi deve passare per il lato incognito c) Calcolo delle coordinate parziali perpendicolari al lato incognito di ogni vertice rispetto al precedente d) Compensazione lineare delle coordinate parziali, come sopra e) Calcolo delle coordinate parziali parallele al lato incognito dei vertici, la cui somma dà la lunghezza del lato incognito f) Eventuale calcolo delle coordinate assolute dei vertici 11
12 3.4 Poligonali chiuse orientate Tipologia del rilievo: IPERDETERMINATO in planimetria (3 volte) a) Compensazione angolare, con ripartizione in parti uguali dell errore di chiusura angolare b) Calcolo degli azimut, partendo dal primo azimut determinato dalla conoscenza delle coordinate di due punti o assegnato, ed utilizzando gli angoli al vertice compensati c) Calcolo delle coordinate parziali di ogni vertice rispetto al precedente d) Compensazione lineare delle coordinate parziali, con ripartizione degli errori di chiusura lineare in parti proporzionali alloro valore assoluto, ad eccezione dei punti di coordinate note e) Calcolo delle coordinate assolute dei vertici 3.5 Poligonali aperte ad estremi vincolati Tipologia del rilievo: IPERDETERMINATO in planimetria (3 volte) a) Calcolo degli azimut provvisori, partendo dal primo azimut utilizzando le coordinate dei primi due punti b) Determinazione dell errore di chiusura angolare, confrontando l ultimo azimut calcolato con la formula di trasporto degli azimut, e mediante le coordinate degli ultimi due punti c) Compensazione angolare degli azimut, con ripartizione in parti u- guali dell errore di chiusura angolare d) Calcolo delle coordinate parziali provvisorie di ogni vertice rispetto al precedente 1
13 e) Determinazione degli errori di chiusura lineare, confrontando la somma delle coordinate parziali provvisoria, con quella ottenibile dai punti di coordinate note f) Ripartizione degli errori in parti proporzionali ai valori assoluti delle coordinate g) Calcolo delle coordinate assolute dei vertici 4. Rilievo per trilaterazioni Tipologia del rilievo: ISODETERMINATO in planimetria Si uniscono i vertici da determinare in modo da formare triangoli dei quali si misurano le lunghezze dei lati. Gli angoli si possono ricavare in ciascun triangolo applicando il teorema di Carnot inverso. E possibile rendere iperdeterminato il rilievo creando altri triangoli congiungenti i vertici assegnati. ERRORI NELLE MISURE INDIRETTE 1. Formula di trasmissione degli errori Data la grandezza F (x, y,...) determinata misurando direttamente le grandezze X ± σ X ; Y ± σ Y ;, il suo scarto quadratico medio può essere ricavato dalla formula: σ f =± F σ X X F + σ Y + Y cioè la radice quadrata della somma delle derivate parziali di tutte le variabili al quadrato, moltiplicate per i quadrati dei rispettivi scarti quadratici medi.. Compensazione empirica delle livellazioni Livellazioni tacheometriche e trigonometriche: l errore medio può essere assunto proporzionale alla distanza misurata. Il peso delle varie determinazioni da utilizzare nella media ponderata può quindi essere assunto pari al reciproco del quadrato della distanza misurata. Livellazioni geometriche: l errore medio può essere assunto proporzionale alla radice quadrata della distanza misurata. Il peso delle varie determinazioni da utilizzare nella media ponderata può quindi essere assunto pari al reciproco della distanza misurata. 13
14 1. Deformazioni cartografiche Modulo di deformazione lineare m: rapporto tra la lunghezza di un segmento misurato sulla carta e il corrispondente misurato sulla superficie di riferimento (ellissoide). Se in un punto della carta si ha m = 1, in tal punto la carta è equidistante. Deformazione angolare δ: differenza tra un angolo misurato sulla carta e il corrispondente misurato sulla superficie di riferimento (ellissoide). Se δ = 0, la carta è conforme. Modulo di deformazione superficiale µ: rapporto tra l area di una superficie misurata sulla carta e la corrispondente misurata. Se in punto della carta si ha µ = 1, in tal punto la carta è equivalente. Se la carta è conforme µ = m. Se sono presenti tutte le tre deformazioni sopra elencate, ma con valori piccoli, la carta è afillattica.. Proiezioni Proiezioni prospettiche: gli elementi da rappresentare sono proiettati su un piano. Proiezioni per sviluppo: gli elementi da rappresentare sono proiettati su una superficie sviluppabile in piano (cilindro o cono). Le proiezioni per sviluppo più utilizzate sono: proiezione diretta di Mercatore: proiezione su cilindro tangente all equatore, conforme, equidistante all equatore. La deformazione lineare può essere calcolata in prima approssimazione con la formula ottenuta considerando la superficie di riferimento sferica: m = 1 cosϕ (ϕ :latitudine) proiezione di Gauss: la Terra è suddivisa in 60 fusi, di ampiezza in longitudine pari a 6 ciascuno, rappresentati con una proiezione su cilindro tangente al meridiano centrale. E una rappresentazione conforme. Per ridurre la deformazione lineare media, che altrimenti sarebbe sempre una dilatazione compresa tra 1 e 1,0008, si riducono le distanze da rappresentare del fattore 0,9996. In tal modo la deformazione lineare è contenuta nell intervallo da 0,9996 a 1,0004. La deformazione lineare può essere calcolata in prima approssimazione con la seguente formula: 14
15 m = 0,9996 ( λ λ cos ϕ ) (φ: latitudine; λ: longitudine; λ 0 longitudine del meridiano centrale) In campo internazionale la proiezione di Gauss o inversa di Mercatore è utilizzata per la rappresentazione UTM (Universal Tranverse Mercator), con numerazione dei fusi da 1 a 60, partendo dall antimeridiano di Greenwich. In Italia tale proiezione è utilizzata per la rappresentazione Gauss-Boaga, utilizzando due soli fusi denominati Est ed Ovest, ampliati ciascuno verso Est di circa 30. Alle coordinate Est è aggiunto un valore convenzionale, chiamato falsa origine, allo scopo di non avere valori negativi. Sistema UTM: Sistema Gauss-Boaga: km per tutti i fusi km per il fuso Ovest +.50 km per il fuso Est Convergenza dei meridiani: è l angolo formato tra le trasformate dei meridiani (Nord geografico) e la parallela all asse X (Nord). In prima approssimazione vale: ץ = (λ λ 0 ) sen φ 1. Area di poligoni 1.1 Metodi analitici TERZO MODULO Formula di camminamento: n 1 n 1 1 A= di 1 di senαi 1 di di sen αi + αi i= i= 3 Formula di Gauss: 1 A = n i= 1 Y i ( ) ( X X )( positiva con vertici orientati in senso antiorario) i 1 i+ 1 15
16 Mediante coordinate polari: n 1 A = di di 1 sen ϑ i+ 1 i= 1 ( ϑ ) +. Divisione delle superfici agrarie i.1 Divisione di un triangolo con dividenti uscenti da un vertice Il triangolo di partenza (avente area A T e base b T ) e quelli derivati hanno la stessa altezza, per le basi b i relative a tale altezza sono proporzionali alle rispettive aree: b i = b T A i /A T. Divisione di un triangolo con dividenti parallele ad un lato Il triangolo di partenza è simile a quelli derivati, per cui le loro aree stanno tra loro come i quadrati dei lati corrispondenti: Ai bi = bt A.3 Divisione di un triangolo con dividenti perpendicolari ad un lato Si può considerare la similitudine tra i triangoli derivati e quello di raffronto, ottenuto mandando l altezza relativa al lato cui devono risultare perpendicolari le nuove dividenti, ed applicare la formula precedente..4 Problema del trapezio Per staccare un area assegnata A dall appezzamento delimitato da tre lati, in cui quello intermedio a forma angoli α e β con gli altri due, con una nuova dividente b parallela al lato intermedio, si applica la seguente e- quazione, ottenuta moltiplicando membro a membro l espressione della somma e della differenza delle basi: b = a A(cotα + cot β ) La distanza della nuova dividente dal lato intermedio (altezza del trapezio) e la lunghezza dei due lati obliqui si determinano con le seguenti espressioni. T 16
17 A h h h = d1 = d = a + b senα senβ 3. Spostamento e rettifica di confini 3.1 Spostamento di un confine con nuova dividente uscente da un punto assegnato Detto AB il confine di partenza, formante angoli α e β con confini laterali, da spostare in A B, con distanza AA nota, si impone che l area del triangolo AA B sia uguale a quella del triangolo A B B. Si ricavano gli elementi incogniti del triangolo AA B, di cui sono noti due lati e l angolo compreso, applicando il teorema di Carnot. La posizione dell estremo B si ricava quindi imponendo l uguaglianza delle aree. A BB ' = A' B sen ( ABA' +β ) 3. Spostamento di un confine con nuova dividente parallela a una direzione assegnata 17
18 Sia AB il confine di partenza, formante angoli α (ottuso) e β coi confini laterali, da spostare nella nuova dividente A B, formante un angolo assegnato ץ con il confine laterale passante per A. Da A si manda la parallela alla direzione assegnata, fino ad incontrare in C l altro confine. Si impone che l area A del triangolo ABC sia uguale a quella del trapezio AA B C. A' B' = AC A A h = AC + A' B' h BB' = BC senacb [ cot( 180 γ ) + cot ACB] AA' = h senγ 3.3 Rettifica di un confine bilatero con dividente uscente da un punto assegnato 1) Si rettifica il confine bilatero con un unico confine rettilineo AB uscente dal primo vertice, imponendo che l area del triangolo ABC sua uguale a quella del nuovo triangolo ACB ; ) si sostituisce il confine così determinato con quello uscente dal punto assegnato, come visto al punto Rettifica di un confine bilatero con dividente parallela ad una direzione assegnata 18
19 Dato il confine bilatero ABC, con lati ed angoli noti, la rettifica si effettua mandando da A la parallela alla direzione assegnata fino ad incontrare in C l altro confine laterale. Se tale congiungente non interseca il confine bilatero, si impone che l area del quadrilatero ABCC sia uguale a quella del trapezio AMNC. Se invece la congiungente AC interseca la spezzata si dovranno calcolare separatamente le aree dei due triangoli ABP e PCC, ed imporre che l area del trapezio sia pari alla differenza tra le aree dei due triangoli. 3.5 Rettifica di confini poligonali In linea di principio si applicano i procedimenti precedenti; conviene però calcolare le aree mediante la formula di Gauss, che vale anche nei casi di poligoni intrecciati. Si deve ricordare che il segno delle aree ottenute con la formula di Gauss è positivo per le aree i cui vertici sono orientati in senso antiorario. SPIANAMENTI 1. Tronco di prisma generico È il solido con spigoli verticali e basi qualunque. Il suo volume è dato dal prodotto dell area della sezione retta per la distanza tra i due piani orizzontali passanti per i baricentri delle basi. V = A h G Per il solido a base triangolare l altezza tra i baricentri h G è data dalla media aritmetica delle tre altezze dei tre spigoli. Se il poligono di base non è triangolare, conviene suddividere il prisma in prismi triangolari elementari, e determinare il volume di ciascuno di essi.. Spianamenti orizzontali a quota assegnata Dopo aver calcolato le quote rosse (dislivello tra la quota di progetto e quella del terreno): r i = q p Q i (i = 1,,3,, n) si stabilisce in quale situazione ci si trova. 1) Quote rosse tutte positive o tutte negative (o nulle) spianamento di tutto riporto o di tutto sterro. Si suddivide l appezzamento in falde triangolari, e si calcola il volume del solido delimitato dal piano di 19
20 progetto e da ciascuna falda. Indicando con Ai l area della generica falda: ri, 1 + ri, + ri,3 V = Ai 3 ) Quote rosse in parte positive e in parte negative spianamento di sterro e riporto. Si individuano le zone di sterro e di riporto mediante i punti di passaggio, nei tratti dove le quote rosse hanno segno alterno. Indicati con 1 e gli estremi di quota rossa di segno opposto, le distanze si determinano con le formule: d r I d 1 P = d1 d P = 1 r1 + r r1 + r r Si suddividono quindi le zone di sterro e di riporto in falde triangolari, e si calcola il volume del solido delimitato dal piano di progetto e da ciascuna falda. Indicando con A i,rip e A j,st, l area della generica falda rispettivamente di riporto e di sterro: V rip = ri A i + r 3 + r r Aj + r 3 + r, 1 i, i,3 j,1 j, j,3 Vst = 3. Spianamenti orizzontali di compenso Si calcola dapprima il volume fittizio di terreno compreso tra la superficie attuale e una superficie di riferimento orizzontale a quota arbitraria q rif, ma comunque inferiore a tutte quelle del terreno, rientrando così nel caso 1 precedente (spianamento di solo sterro). Si impone poi che tale volume sia pari a quello del parallelepipedo avente per base la superficie di riferimento precedentemente adottata, e se ne ricava quindi l altezza: V h = A fittizio La quota di progetto risulta quindi pari alla somma della quota di riferimento con tale altezza: q p = q rif + h Si calcolano quindi le quote rosse: totale 0
21 r i = q p Q i (i = 1,,3, n) che risulteranno sicuramente in parte positive e in parte negative. Si procede quindi come indicato al punto ) del paragrafo precedente, verificando che i volumi di sterro e riporto siano uguali. 4. Spianamenti inclinati a giacitura assegnata di compenso Per assegnare la giacitura del piano di progetto si utilizza la retta di massima pendenza. Deve essere nota la pendenza del piano o la quota di un punto, altrimenti esisterebbero infinite soluzioni al problema. Inizialmente, si determinano le quote dei vertici sottostanti a quelli assegnati, appartenenti ad un piano di riferimento parallelo a quello di progetto: pertanto la retta di massima pendenza di tale piano di riferimento coincide con quella del piano di progetto, ma è traslata verso il basso per a- vere quote sempre inferiori a quelle del terreno. Si determina quindi il volume fittizio di terreno compreso tra la superficie attuale e la superficie di riferimento inclinata precedentemente determinata. Si determinano quindi le quote rosse (tutte negative o nulle), rientrando così al caso 1 (solo sterro). Si impone poi che tale volume sia pari a quello del parallelepipedo avente per base la superficie di riferimento inclinata precedentemente adottata, e se ne ricava quindi l altezza: V fittizio h = A La retta di massima pendenza di progetto risulta quindi uguale a quella del piano di riferimento, ma traslata verso l alto dell altezza h. Si calcolano quindi le quote rosse effettive: totale r i = q p,i Q i (i = 1,,3, n) che risulteranno sicuramente in parte positive e in parte negative. Si individuano le zone di sterro e di riporto mediante i punti di passaggio, nei tratti dove le quote rosse hanno segno alterno, e si procede come visto per gli spianamenti orizzontali. 1
22 STRADE 1. Curve circolari Il raggio minimo è dato dall equazione: R min = g v ( + ) f t p t con g accelerazione di gravità (9,81 m/s ); v velocità di progetto; f t, p t coefficiente di aderenza (0,43-0,9) e pendenza trasversale (min,5%, max 7%). Relazione tra angolo al centro della curva ω e angolo al vertice v: ω + v = 00 gon. Sviluppo della curva: prodotto del raggio r per l angolo al centro espresso in radianti. l = r x ω rad Relazione tra raggio r e tangente t: r v ω = tan = cot t Espressioni per il calcolo della corda c e della saetta s c ω ω = rsen, s = r 1 cos Allargamento della carreggiata in curva: e =K/r (K = 30-45). Curve circolari condizionate Curva passante per tre punti: è un arco della circonferenza circoscritta. Il centro è sull intersezione degli assi dei lati ottenuti congiungendo i tre punti: r = lato sen ( angolo opposto)
23 Curva tangente a tre rettifili: è un arco della circonferenza ex-inscritta al triangolo ottenuto prolungando i due rettifili estremi. Il centro è sulla bisettrice dei tre angoli formati dai rettifili: r = area semiperimetro lato tangente Curva passante per un punto P: si ricava il rapporto tra il raggio e la congiungente il centro con il vertice, considerando il triangolo rettangolo formato tra il raggio e la tangente e quello ottenuto congiungendo il punto P con il centro e il vertice. Uguagliando i due rapporti si ottiene l angolo in P, scegliendo la soluzione corretta OPV, da cui si ricava il raggio: r = SEN VP ( α + OPV ) senα 3. Livellette Le livellette sono tratti stradali a pendenza costante. Esse devono essere tracciate tenendo conto dei seguenti criteri: - gli sterri devono approssimativamente compensare i riporti; - le livellette non devono essere troppo corte; - si devono evitare variazioni di livelletta all interno di un rettifilo o di una curva; - si deve ridurre la pendenza in corrispondenza di ponti e di tornanti; - si devono evitare brusche variazioni di pendenza tra una livelletta e l altra. 4. Calcolo dei volumi del solido stradale Si calcola l area di sterro e di riporto di tutte le sezioni trasversali, scomponendo tali superfici in triangoli e trapezi. Si approssima il solido stradale a un prismoide, avente per basi due sezioni consecutive di area A 1 e A e per altezza la distanza d tra tali sezioni. Se si considera l area della sezione intermedia pari alla media delle due basi, la formula di Torricelli V= (A 1 + 4A m + A )*d/6 si semplifica nella formula delle sezioni ragguagliate: 3
24 V = A A 1 + d Tale formula suggerisce anche un calcolo grafico dei volumi, essendo la stessa espressione dell area del trapezio, assumendo per basi le aree e per altezza la distanza tra le sezioni (profilo delle aree). Il calcolo si esegue considerando una coppia di sezioni successive per volta. Nel caso in cui una sezione sia di sterro e l altra di riporto si deve determinare prima la linea di passaggio d s = d*a S /(A R +A S ) ; d r = d*a R /(A R +A S ) e quindi V S = A S *d s / ; V R =A R *dr/ Nel caso in cui le sezioni siano miste (mezza costa) si deve suddividere in senso longitudinale il solido stradale in modo tale da avere strisce di solido che ricadono nei casi visti. I volumi di sterro e di riporto devono essere suddivisi in due categorie, cui andranno applicati prezzi unitari diversi. Paleggi: sono quei movimenti di terra che possono essere eseguiti senza movimenti longitudinali di materiale. Movimenti longitudinali: quelli che necessitano di trasporto di materiale in senso longitudinale. 5. Tracciamento delle curve circolari Può essere effettuato in diversi modi, secondo le condizioni in cui si presenta la curva. Nei vari casi si individua un certo numero n di picchetti equidistanziati, che suddividono la curva in n + 1 archi uguali cui corrisponde un angolo al centro pari a: ω β = n +1 I metodi maggiormente utilizzati sono: - per normali alla tangente, quando la curva è accessibile al suo esterno: si utilizza un sistema di assi cartesiani avente origine in un punto di tangenza, e assi X e Y diretti rispettivamente lungo il raggio e la tangente: xi = r r cos yi = r sen ( i β ) ( i β ) i = 1,,..., n 4
25 - per normali alla corda, quando la curva è accessibile al suo interno: si utilizza un sistema di assi cartesiani avente origine nel punto medio della corda, e assi X e Y diretti rispettivamente lungo la corda e la bisettrice. Se il numero di parti in cui la curva viene suddivisa è dispari, si ottiene anche il punto medio della curva, cui si attribuisce l indice 0: xi = ± r sen yi = r cos ( i β ) ( i β ) ω r cos i = 0,1,,...,( n 1) / - con stazione totale. Si deve disporre nella zona di tracciamento di almeno due punti di coordinate note. Con il metodo di Porro di collegamento tra due stazioni si ottengono le coordinate del punto di stazione e l angolo di disorientamento (il rilievo è iperdeterminato una volta, per cui si fa la media aritmetica di due determinazioni). Si determinano quindi le coordinate polari di ogni punto da picchettare. 5
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
IL SISTEMA CARTOGRAFICO NAZIONALE
 IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
a. 10 4 b. 10-15 c. 10 25 d. 10-4 a. 4,375 10-7 b. 3,625 10-6 c. 4,375 10 2 d. nessuno dei precedenti valori a. 10-5 b. 10 +5 c. 10 +15 d.
 1) Il valore di 5 10 20 è: a. 10 4 b. 10-15 c. 10 25 d. 10-4 2) Il valore del rapporto (2,8 10-4 ) / (6,4 10 2 ) è: a. 4,375 10-7 b. 3,625 10-6 c. 4,375 10 2 d. nessuno dei precedenti valori 3) La quantità
1) Il valore di 5 10 20 è: a. 10 4 b. 10-15 c. 10 25 d. 10-4 2) Il valore del rapporto (2,8 10-4 ) / (6,4 10 2 ) è: a. 4,375 10-7 b. 3,625 10-6 c. 4,375 10 2 d. nessuno dei precedenti valori 3) La quantità
TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA. 04-09-2014 XXIV Corso di Alpinismo A1
 Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
PROGRAMMI PER GLI ESAMI I PATENTE DE MAESTRI E DELLE MAESTRE DELLE SCUOLE PRIMARIE
 Programmi per le Scuole normali e magistrali, e per gli esami di Patente de Maestri e delle Maestre delle Scuole primarie approvati con regio decreto 9 novembre 1861 n. 315 (Raccolta ufficiale delle leggi
Programmi per le Scuole normali e magistrali, e per gli esami di Patente de Maestri e delle Maestre delle Scuole primarie approvati con regio decreto 9 novembre 1861 n. 315 (Raccolta ufficiale delle leggi
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Sistema di riferimento
 Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
LEZIONI DI TOPOGRAFIA
 Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
3. Sia g(x) = 4. Si calcoli l area del triangolo mistilineo ROS, ove l arco RS appartiene al grafico di f(x) o, indifferentemente, di g(x).
 Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
Ma cosa si pensava della forma della terra prima delle fotografie?
 Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
SISTEMI DI RIFERIMENTO E PROIEZIONI
 SISTEMI DI RIFERIMENTO E PROIEZIONI Esistono 3 tipi di dati: 1- Dati tabellari (informativi) 2- Dati geometrici (territoriali) 3- Dati geometrici e tabellari (informativi territoriali) La localizzazione
SISTEMI DI RIFERIMENTO E PROIEZIONI Esistono 3 tipi di dati: 1- Dati tabellari (informativi) 2- Dati geometrici (territoriali) 3- Dati geometrici e tabellari (informativi territoriali) La localizzazione
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
Liceo G.B. Vico Corsico
 Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
LE FUNZIONI MATEMATICHE
 ALGEBRA LE FUNZIONI MATEMATICHE E IL PIANO CARTESIANO PREREQUISITI l l l l l conoscere il concetto di insieme conoscere il concetto di relazione disporre i dati in una tabella rappresentare i dati mediante
ALGEBRA LE FUNZIONI MATEMATICHE E IL PIANO CARTESIANO PREREQUISITI l l l l l conoscere il concetto di insieme conoscere il concetto di relazione disporre i dati in una tabella rappresentare i dati mediante
α r = l / R l = lunghezza dell'arco sotteso R = raggio circonferenza sottomultipli: mrad = 10-3 rad µrad = 10-6 rad
 Ing. Andrea Lingua Fondamenti di Geodesia e Cartografia 1.1 Unità di misura angolari e conversioni Con angolo si intende una porzione di piano delimitata da due semirette: l'ampiezza dell'angolo è rappresentata
Ing. Andrea Lingua Fondamenti di Geodesia e Cartografia 1.1 Unità di misura angolari e conversioni Con angolo si intende una porzione di piano delimitata da due semirette: l'ampiezza dell'angolo è rappresentata
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri. rel. 0.1. Esercizi di Topografia distribuzione gratuita 1/6
 ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
Corso di ordinamento Sessione straordinaria - a.s. 2009-2010 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA
 Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
SIMULAZIONE DI PROVA D ESAME CORSO DI ORDINAMENTO
 SIMULAZINE DI PRVA D ESAME CRS DI RDINAMENT Risolvi uno dei due problemi e 5 dei quesiti del questionario. PRBLEMA Considera la famiglia di funzioni k ln f k () se k se e la funzione g() ln se. se. Determina
SIMULAZINE DI PRVA D ESAME CRS DI RDINAMENT Risolvi uno dei due problemi e 5 dei quesiti del questionario. PRBLEMA Considera la famiglia di funzioni k ln f k () se k se e la funzione g() ln se. se. Determina
Elenco Ordinato per Materia Chimica
 ( [B,25404] Perché le ossa degli uccelli sono pneumatiche, cioè ripiene di aria? C (A) per consentire i movimenti angolari (B) per immagazzinare come riserva di ossigeno X(C) per essere più leggere onde
( [B,25404] Perché le ossa degli uccelli sono pneumatiche, cioè ripiene di aria? C (A) per consentire i movimenti angolari (B) per immagazzinare come riserva di ossigeno X(C) per essere più leggere onde
Maturità Scientifica PNI, sessione ordinaria 2000-2001
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
ESAME DI STATO 2002 SECONDA PROVA SCRITTA PER IL LICEO SCIENTIFICO DI ORDINAMENTO
 ARCHIMEDE 4/ 97 ESAME DI STATO SECONDA PROVA SCRITTA PER IL LICEO SCIENTIFICO DI ORDINAMENTO Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PROBLEMA In un
ARCHIMEDE 4/ 97 ESAME DI STATO SECONDA PROVA SCRITTA PER IL LICEO SCIENTIFICO DI ORDINAMENTO Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PROBLEMA In un
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
SOLUZIONE DEL PROBLEMA 2 CORSO DI ORDINAMENTO 2013. 8 4 + x 2, con dominio R (infatti x2 + 4 0 per ogni. 8 4 + ( x) = 8. 4 + x 2
 SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
DALLE CARTE ALLE SEZIONI GEOLOGICHE
 DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
DERIVATE DELLE FUNZIONI. esercizi proposti dal Prof. Gianluigi Trivia
 DERIVATE DELLE FUNZIONI esercizi proposti dal Prof. Gianluigi Trivia Incremento della variabile indipendente e della funzione. Se, sono due valori della variabile indipendente, y f ) e y f ) le corrispondenti
DERIVATE DELLE FUNZIONI esercizi proposti dal Prof. Gianluigi Trivia Incremento della variabile indipendente e della funzione. Se, sono due valori della variabile indipendente, y f ) e y f ) le corrispondenti
PLANIMETRIA E PROFILO INSIEME
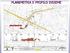 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta
 Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
ESERCIZI CINEMATICA IN UNA DIMENSIONE
 ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2008
 PRVA SPERIMENTALE P.N.I. 8 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 8 Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Nel piano riferito
PRVA SPERIMENTALE P.N.I. 8 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 8 Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Nel piano riferito
Punti notevoli di un triangolo
 Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Geometria analitica di base (prima parte)
 SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Programmazione per competenze del corso Matematica, Secondo biennio
 Programmazione per del corso Matematica, Secondo biennio Competenze di area Traguardi per lo sviluppo delle degli elementi del calcolo algebrico algebriche di primo e secondo grado di grado superiore al
Programmazione per del corso Matematica, Secondo biennio Competenze di area Traguardi per lo sviluppo delle degli elementi del calcolo algebrico algebriche di primo e secondo grado di grado superiore al
Trigonometria: breve riepilogo.
 Corso di laurea in Matematica Corso di Analisi Matematica - Dott.ssa Sandra Lucente Trigonometria: breve riepilogo. Definizioni iniziali Saper misurare un angolo in gradi sessagesimali, saper svolgere
Corso di laurea in Matematica Corso di Analisi Matematica - Dott.ssa Sandra Lucente Trigonometria: breve riepilogo. Definizioni iniziali Saper misurare un angolo in gradi sessagesimali, saper svolgere
ISTITUTO DI ISTRUZIONE SUPERIORE Michele BUNIVA
 DIPARTIMENTO DI DISCIPLINE TECNICHE AREA CAT Programma di TOPOGRAFIA E FOTOGRAMMETRIA Classe 3 C.A.T. COSTRUZIONI AMBIENTE E TERRITORIO Anno scolastico 0 / 03 Docente TINELLI PASQUALE VENTURA ANGELO CRISAFI
DIPARTIMENTO DI DISCIPLINE TECNICHE AREA CAT Programma di TOPOGRAFIA E FOTOGRAMMETRIA Classe 3 C.A.T. COSTRUZIONI AMBIENTE E TERRITORIO Anno scolastico 0 / 03 Docente TINELLI PASQUALE VENTURA ANGELO CRISAFI
SOLUZIONI D = (-1,+ ).
 SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Anno 4 I Triangoli qualsiasi
 Anno 4 I Triangoli qualsiasi 1 Introduzione In questa lezione descriveremo i triangoli qualunque. Enunceremo i teoremi su questi triangoli e illustreremo le loro applicazioni. Al termine della lezione
Anno 4 I Triangoli qualsiasi 1 Introduzione In questa lezione descriveremo i triangoli qualunque. Enunceremo i teoremi su questi triangoli e illustreremo le loro applicazioni. Al termine della lezione
La trigonometria prima della trigonometria. Maurizio Berni
 La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
Docente: DI LISCIA F. CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI
 Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2001 Sessione suppletiva
 ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 1 Sessione suppletiva Il candidato risolva uno dei due problemi e dei 1 quesiti in cui si articola il questionario. PRBLEM 1 Si consideri la funzione reale
ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 1 Sessione suppletiva Il candidato risolva uno dei due problemi e dei 1 quesiti in cui si articola il questionario. PRBLEM 1 Si consideri la funzione reale
0. Piano cartesiano 1
 0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI
 DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI. PROBLEMA 1: Tra i rettangoli di perimetro 20 cm, determina quello di area massima.
 PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI Introduzione Vengono qui presentati alcuni semplici problemi di massimo e minimo. Leggi con attenzione e completa i passaggi mancanti. Prova
PROBLEMI DI MASSIMO E MINIMO ESEMPI INTRODUTTIVI ELEMENTARI Introduzione Vengono qui presentati alcuni semplici problemi di massimo e minimo. Leggi con attenzione e completa i passaggi mancanti. Prova
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
Rilevazione degli apprendimenti
 Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATIA Scuola secondaria di II grado lasse... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Rilevazione degli apprendimenti Anno Scolastico 00-0 PROVA DI MATEMATIA Scuola secondaria di II grado lasse... Studente... Simulazioni di prove costruite secondo il Quadro di riferimento Invalsi pubblicato
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta.
 CLASSE III C RECUPERO GEOMETRIA AREA PERIMETRO POLIGONI Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta. ES: se ho fatto questo disegno e so che 1 quadretto vale
CLASSE III C RECUPERO GEOMETRIA AREA PERIMETRO POLIGONI Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta. ES: se ho fatto questo disegno e so che 1 quadretto vale
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
TAVOLE E FORMULARI DI MATEMATICA PER LE SCUOLE MEDIE E SUPERIORI DI OGNI ORDINE E GRADO
 TAVOLE E FORMULARI DI MATEMATICA PER LE SCUOLE MEDIE E SUPERIORI DI OGNI ORDINE E GRADO Carlo Sintini www.matematicamente.it INDICE TAVOLE NUMERICHE Potenze e radici quadre e cube dei numeri fino a 200
TAVOLE E FORMULARI DI MATEMATICA PER LE SCUOLE MEDIE E SUPERIORI DI OGNI ORDINE E GRADO Carlo Sintini www.matematicamente.it INDICE TAVOLE NUMERICHE Potenze e radici quadre e cube dei numeri fino a 200
Laboratorio di Rappresentazione e Modellazione dell Architettura
 Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Trasformazioni geometriche nel piano cartesiano
 Trasformazioni geometriche nel piano cartesiano Francesco Biccari 18 marzo 2013 Una trasformazione geometrica del piano è una legge (corrispondenza biunivoca) che consente di associare a un determinato
Trasformazioni geometriche nel piano cartesiano Francesco Biccari 18 marzo 2013 Una trasformazione geometrica del piano è una legge (corrispondenza biunivoca) che consente di associare a un determinato
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
