Massimo Bucca matr Aerodinamica. martedì 2 ottobre 2001
|
|
|
- Leonardo Lorenzi
- 5 anni fa
- Visualizzazioni
Transcript
1 Massmo Bcca matr Arodnamca martdì ottobr S n ala agsc la fora arodnamca, qsta pò ssr scomposta lngo d dron prfrnal, c sono la dron normal parallla alla dron c l fldo c ncontra la nostra ala a a mont dll ala stssa. L F V D L componnt dlla fora arodnamca ngono camat portana rsstna, s ndcano con l lttr L D. Dfnamo com portana la componnt normal alla dron dl ttor loctà dlla fora arodnamca, rsstna la componnt parallla alla dron dl ttor loctà asntotca. Abbamo sto dal corso d fldodnamca c l mo pù sofstcato pr stdar n fldo qnd anc n corpo mmrso n sso, sono l qaon d Nar- Stoks. Qst c prmttono d conoscr ttt l arabl fldodnamc c ntrano n goco nl fnomno, ma sbbn sono n mo molto potnt, sono nllo stsso tmpo n mo poco pratco pr l norm costo comptaonal c n sg pr rsolrl n modo soddsfacnt. Allora s è costrtt a scndr a d compromss, n pratca ntrodrr dntro l nostro modllo dll smplfcaon c c prmttono comnq d arrar a d rsltat soddsfacnt. L smplfcaon pù mportant c andrmo a far pr stdar l nostro sstma fldomccanco sono d: Andrmo a trascrar la comprmbltà dl fldo, E/o andrmo a trascrar la scostà dl fldo. Sappamo c l grppo admnsonal c rgola la comprmbltà n n fnomno fldodnamco è l nmro d Mac, coè V Ma a
2 Massmo Bcca matr do con V s ndca la loctà asntotca con a s è ndcata la clrtà dl sono. Possamo affrmar c pù alto è l nmro d Mac pù alta sarà la dpndna dl fnomno fsco dalla comprmbltà. An possamo dr c l nostro fnomno pò ssr camato sbsonco s l Ma, sarà sprsonco s l Ma 4, sarà nfn prsonco s l nmro d Mac è maggor d 4. Ttt fnomn con nmro d Mac comprs fra.3 ngono anc camat transonc. Comnq possamo dr c l fftto dlla comprmbltà comnca a fars sntr propro da Ma.3. No nl nostro stdo partrmo dallo stato pù smplc possbl coè da Ma. Abbamo sto c l altra smplfcaon c andamo ad apportar al nostro modllo è qlla d fldo non scoso. Sappamo c qsta nlla raltà è na non rtà, nfatt non sstono d fld n c la scostà non facca sntr so fftt, ma possamo dr c n alcn qsto fftto è trascrabl. Il grppo admnsonal c tn conto dgl fftt dlla scostà è l nmro d Rnolds, dfnto com V L R. ν Dal nmro d Rnolds capsco c gl fftt dlla scostà s annllano, o pr lo mno dntano nfntsm, qando l nmro d Rnolds tnd a alor molto grand. Qsto prò non ol dr c n ttta la corrnt qst fftt sano trascrabl. Infatt nll mmdat cnan d n contorno soldo, sopratttto dntro lo strato lmt l nmro d Rnolds non spra ma l ntà, qnd localmnt gl fftt dlla scostà sono ttt altro c trascrabl. Da n pnto d sta analtco sccd c qando R tnd ad nfnto, trmn all drat scond dll N-S scompaono, qnd l nostr qaon s abbassano d satta. Qsta d ssr racqstata con l nsrmnto dl modllo dllo strato lmt, n c sono dscrtt n modo sffcnt gl fftt local dlla scostà. S bad bn c rnncar alla scostà c porta a non potr pù tlar la condon d prftta adson alla part solda, coè V(c). Un altra smplfcaon c farmo è c l campo d moto sa rrotaonal. Qsta smplfcaon c porta ad lmnar n altro problma c pò sorgr consdrando d corp c lascano na sca notol. Infatt n qsta ttt l condon ttt gl strmnt analtc c andrmo ad tlar non algono pù, qnd spporrmo c la sca sa sottl. Fortnatamnt profl d c c dobbamo occpar anno n bordo d scta molto ago s tlat con angol d ncdna ragonol, qsto c prmtt d ssr abbastana cornt con l fatto c la sca dbba ssr molto sottl. Essndo molto sottl possamo pnsar c ssa sa, nlla trattaon analtca, comparabl ad na rtta, coè na spc d dscontntà dl campo d moto c pr l rsto è rrotaonal.
3 Massmo Bcca matr Prma d ntrar nl complsso campo dll arodnamca, conn far na pccola loc trattaon sl calcolo tnsoral. Dfnamo ttor na granda fsca carattrata da tr nmr c cambano al arar dl sstma d rfrmnto com cambrbbro l componnt dl ttor n snso gomtrco. Consdramo n ttor d componnt, s potamo n cambamnto d sstma d rfrmnto, non faccamo altro c tlar na matrc d rotaon, coè 3 j j j R, la sommatora dgl R j sono 9 nmr c rgolano la rotaon, non sono ttt ndpndnt, ma ssndo la matrc d rotaon smmtrca, solo 6 sono ndpndnt. Proamo adsso c sa c sono gal, pr far cò basta rfcar c anno la stssa lnga, 3 3,, k j k j k j k k k j j j R R R R l dfnto prò jk k j j R k R δ 3,, s ottn k k k l 3. Il nostro scopo prncpal è qllo d ntrodrr dll grand c non dpndono dal nostro sstma d rfrmnto. Il prodotto ttoral è psdo-narant. Possamo dmostrarlo faclmnt, nfatt 3 3, 3 3,, k k k k j k j jk k j k j k j k k k j j j R R R R δ s d c non dpnd dal sstma d rfrmnto.
4 4 Massmo Bcca matr mrcoldì 3 ottobr Consdramo na fnon scalar f n ttor, possamo troar na rlaon lnar c mtt n rlaon l ttor la fnon scalar, tramt 3 coffcnt c : f 3 c c s nc no oglamo andar a troar na rlaon c c lga n ttor f ad n altro ttor, notamo c coffcnt c ntrano n goco nlla rlaon sono dntat 9, f 3 k Dobbamo capr com arano qst 9 coffcnt n modo da stablr con satta s qsta rlaon sa o mno narant. Portata n n altro sstma d rfrmnto abbamo: 3 3 R f c k k k j R R f 3 c 3 R kj l l k,, k j 3 R c 3 j R kj j sapndo c ottn, 3 3 f l δ l f Rl R f dfnndo, 3,k R lck Rkj clj (*) s f l 3 j c I coffcnt non sono arbtrar ma dono sgr la rgola data dalla rlaon (*), scramnt posso affrmar c s posso farlo allora posso cambar l sstma d rfrmnto sna problm. Adsso andamo ad lncar alcn opraon fra grand tnsoral c sono narant: a b c a b c coè a j b c j lj j
5 Massmo Bcca matr c contraon d n tnsor, o tracca d c Tr ( c ) s doppo prodotto tnsoral s b c 3, j b j c j Gl approcc allo stdo d n fldo possono ssr portat da n pnto d sta macroscopco o da n pnto d sta mcroscopco. Qllo c no srmo sarà macroscopco, ma malgrado sa macroscopco sso s basrà s fondrà con na son mcroscopca. S andamo a consdrar l nostro sstma fldo com na massa costtta da sngol partcll possamo ncorrr n d problm, l pù grosso d qal è qllo d scoprr c nostr rsltat non srono a nnt, coè abbamo ottnto d rsltat ntl. Allora dobbamo crcar n altro pnto d sta, n altro potrbb ssr qllo statstco o probablstco c c prmtt d costrr d lgam fra l arabl macroscopc crt loro dstrbon d grand a c no samo ntrssat. Il nostro scopo ltmo è qllo d rscr a scrr dll qaon c rgardano l nostro sstma fldo, ma c sano ndpndnt dal sstma d rfrmnto. Partamo con l consdrar na poron d fldo c contn n crto nmro d partcll N. Qsta poron d fldo la potamo solata con l mondo strno, la -sma partclla arà na massa m, l for ntrmolcolar c sstono fra l N partcll ngono raccolt n n'nca nrga potnal pot. La -sma partclla arà na loctà propra c camamo loctà mcroscopca, ottnta drando la poson dlla partclla rsptto al tmpo, d dt possamo scrr l blanco dlla consraon dlla massa dlla qanttà d moto, d dt S camamo N m, N d m dt N d pot, m. dt N m M N, m Q N pot, m E
6 6 Massmo Bcca matr possamo dfnr qnd anc passar all grand spcfc, coè pr ntà d olm, M ρ, V Q Q, V E E. V Adsso oglamo troar l qaon d blanco, coè collgar la araon dllo tmpo con l flsso dlla nostra granda fsca attrarso l nostro olm d controllo. Prma d fra cò dobbamo dr c cosa ottnamo dal flsso d na granda scalar. Infatt no ancora non sappamo c granda ottnamo, s no scalar o n ttor. Sappamo c, f dv J f ds t V oppr f dv J f nds. t Notamo c s foss no scalar l ntro ntgral dorbb dpndr dalla sprfc, cò c non oglo c sccda. M accorgo c nl scondo caso sstndo lo scalar tra l ttor flsso la normal alla sprfc, qsto problma non sssst prcé andr a prndr la sa proon. Qnd concldo dcndo c l flsso d na granda scalar d ssr n ttor. Con n ragonamnto analogo s pò arrar alla conclson c l flsso d no scalar è n tnsor, f dv J nds. f t Tramt l torma d Stoks, c c da l gaglana tra l ntgral dl flsso stso alla sprfc con l ntgral dlla drgna stsa a ttto l olm d ntgraon, possamo ancora scrr, f dv J f nds t V V V V f t J f dv s l ntgral al pr qalnq olm s la fnon scalar f è contna drabl, allora possamo andar ad annllar drttamnt la fnon ntgranda,
7 Massmo Bcca matr f t J f, rscrtta pr l nostr qanttà, coè pr la massa, la qanttà d moto l nrga, dnta, ρ J ρ t Q t E t J Q J E Comncamo a consdrar n fldo n qt, sappamo c qsto è dscrtto appno qando è noto l so stato trmodnamco. La qanttà d moto total, s l nostro sstma s troa dntro n contntor cso, pò ssr consdrata nlla qnd l so stato trmodnamco n compltamnt dscrtto da sol d grand, la massa l nrga dll partcll c lo compongono. Ma a no non ntrssano d sstm c sono n qt, spponamo d ar n sstma mccanco c non sa n qt c non sa nanc n qlbro trmodnamco. Spponamo ancora prò, c qsto qlbro trmodnamco non sa tanto lontano dal raggngmnto. S pò affrmar c possano sstr dll rgon dl sstma c sono gà n qlbro, nll rgon c ancora non lo sono tmp carattrstc c occorrono al raggngmnto dll qlbro, sono bass n confronto con tmp carattrstc dll ntro sstma. l << L l t << T L
8 8 Massmo Bcca matr I flss d massa, d qanttà d moto d nrga sono fnon dll grand trmodnamc, coè ρ J ρ ( ρ, Q E), J J ( ρ, Q E), J E J E ( ρ, Q, E) J,, Q Q. Andamo a troar la forma d qst flss. Comncamo con l flsso dlla massa, c è J Q ρ qsto c prmtt d dfnr la loctà macroscopca com, ma anc, N df N df N m m m Q J N ρ Q ρ m ρ l qaon d blanco pr la massa dnta, ρ t ( ρ). A qsto pnto dobbamo cdrc, l qaon troata sarà ndpndnt dal sstma d rfrmnto? Vrfcamolo ntrodcndo na trasformaon qalnq da a, t t t l lgam fra l drat sarà, t t ( )
9 Massmo Bcca matr andamo a scrr con qst opportn trasformaon l qaon d blanco c aamo calcolato pr la massa. Nl noo sstma d rfrmnto t l blanco d massa dnta, ρ ρ ρ t t la massa s mantn costant ndpndntmnt dal sstma d rfrmnt, qnd ρ ρ, po noto c s a, N N N ( ) Q m Q Q m m ρ ρ Q t ρ ( Q ρ ) ρ ( ρ ) ρ Q ρ ma dato c ( ) ρ s ottn, ρ t Q abbamo ottnto la stssa qaon, qnd l qaon d blanco dlla massa è narant. Adsso passamo a troarc qlla dlla qanttà d moto, l problma prò non è facl com pr la massa, n qanto con la massa aamo troato faclmnt l flsso d massa, q non è altrttanto facl. Qnd oprrmo al contraro, coè andrmo a troarc l flsso mponndo c l qaon d blanco sa narant. L qaon d blanco pr la qanttà d moto è, Q t J Q costrndo la drata con l cambo d rfrmnto ottnamo, t ( Q ρ ) ( ) ( Q ρ ) J Q Q t ρ t ( ) Q ( ) ρ J Q
10 Massmo Bcca matr Q t Q ( ) Q ( ) ρ J Q Q t ( J Q Q ) Q ρ affncé l qaon sa narant dobbamo mporr c, ( J Q Q ) J ρ Q Q ssndo narant con qsta opportna sclta dl flsso, possamo scglr qalnq loctà, pr comodtà scglamo, n modo c anc Q, ottnamo allora, J ( J ρ ) Q Q troamo c l flsso d qanttà d moto J è proporonal al tnsor ntaro I, na fnon proporonal è data dalla fnon scalar p(ρ,e), la fnon scalar prnd l nom d prsson, possamo scrr ( ρ, E) p( ρ E)I J J, Q Q l qaon d blanco dlla qanttà d moto dnta, Q t ( ρ pi) s rcord c pi p. Andamo adsso a rcaarc l flsso d nrga d consgna l so blanco. Partamo dalla E J E t E N N pot m m passamo al sstma tramt l solt trasformaon, pot ( ) E ρ Q
11 Massmo Bcca matr ( ) J E Q E t t Q t E ρ ρ tlando l qaon d blanco consdrando la loctà costant ottnamo, ( ) Q E Q J J t E Q E ρ com fatto pr la qanttà d moto andamo a scglr n sstma d rfrmnto comodo, coè pr pr Q, s ottn c l flsso d nrga d ar la forma, E J J J Q E E ρ tramt l dnttà ttoral I p J Q E E ρ s a E pi J J E E ma dondo alr l sotropa d ssndo l flsso J dll nrga n tnsor d ordn dspar, qnd non narant rsptto al sstma d rfrmnto, qsto flsso non pò sstr, dnq l flsso d nrga s rdc a E pi J E l qaon d blanco sarà, p t ρ ρ Abbamo dnq troato l qaon d blanco pr la massa, pr la qanttà d moto pr l nrga. Qst tr qaon anno sotto l nom d qaon d Elro.
12 Massmo Bcca matr Il sstma d qaon d Elro è, ρ t Q t ( ρ) ( ρ pi) ρ t ρ p possamo notar c l qaon scrtt n qsta forma, coè con la drata rsptto al tmpo po con la drgna d n crto ttor, anno dtt n forma consrata. Non smpr la forma consrata è la forma pù smplc pr laorar con qst forml, crto s no abbamo gà pronto n algortmo al c c consnt d ntrodrr soltanto l qanttà all ntrno dlla drata tmporal qlla dntro la drgna, qsta forma è prfrbl n qanto abbamo sbto sott occo l d grand, ma s oglamo far cont no stss allora possamo andar a smplfcar n po qst forml. Comncamo con qlla d contntà, splctando la drgna dl prodotto tra la dnstà la loctà, ρ ρ ρ t prm d trmn possono ssr prs assm anno sotto l nom d drata sostanal, Dρ ρ Dt Passamo ora alla qanttà d moto, com prmo trmn o la drata tmporal dl prodotto tra la dnstà la loctà, lo slppo d o: ( ρ ) t ρ ρ t t ( ρ) ρ t
13 Massmo Bcca matr adsso andamo a splctarc d trmn con la drgna, ( ρ pi ) ( ρ) ( pi ) ( ρ) ρ( ) p com s d faclmnt d trmn s ldono a cnda qnd l qaon dnta, ρ ρ t ( ) p Qsta forma dll qaon dlla qanttà d moto è camata forma contta. Ora tocca all qaon dll nrga slppamo la drata tmporal la drgna, ρ t ρ t ( ρ) ρ ( p) ** pr l qaon d contntà l prmo l tro trmn s ldono, co rstant trmn facco na combnaon lnar con l qaon dlla qanttà d moto moltplcata scalarmnt pr, ottngo ρ t ρ sottrando mmbro a mmbro con la ** s ottn p ρ ρ t p c pò ssr scrtta n forma d drata sostanal, D ρ p Dt Qando andamo ad assmr c l nostro fldo è ncomprmbl sgnfca assmr c dρ dp
14 4 Massmo Bcca matr n qsto caso l qaon d stato dnta ρ cost. Qsto c porta a capr c dll tr qaon d blanco c abbamo rcaato, qlla dll nrga dnta dsaccoppata rsptto all altr d. Dnta dl ttto scondara s oglamo calcolar l nostro campo do moto, a mno c non olgamo calcolar la tmpratra n tal caso è fondamntal. Allora nl caso d dnstà costant l nostr qaon dntano t p ρ ( ) Ttto qllo c è stato troato, ttt ragonamnt c c anno portato alla formlaon dll qaon d blanco s basano slla condon pots dll qlbro local. Adsso faccamo n passo aant crcamo d toglrc da qsto ncolo, no sappamo c l flsso dll nostr grand dpnd dallo stato trmodnamco dl sstma, dpnd qnd dallo stato pntal c anno l grand d stato n n dtrmnato pnto n n dtrmnato tmpo. Spponamo adsso d spostarc dall qlbro, ma non d tantssmo, samo n prossmtà dll qlbro. Possamo pnsar c l gnrco flsso sa la somma dl flsso c no abbamo all qlbro pù n flsso c è doto al gradnt dll arabl d stato, coè J f ( d ( ) ) ρ, E, Q J f ( ρ, E Q) q J, f Qnd andamo a corrggr l flsso con n trmn rcaato dallo slppo n sr d Talor d l/l, sotto l pots d lnartà. Qsta granda è dsspata consdrando l pots d lnartà possamo dr c l flsso dlla qanttà d moto d ssr, ( ) J d Q a ρ b Q c E Adsso no oglamo c l nostro flsso sa ndpndnt dal sstma d rfrmnto, qnd d ssr anc ndpndnt l flsso dsspato, abbamo gà affrmato c non sstono tnsor d ordn dspar c sano ndpndnt dal sstma d rfrmnto. Qnd posso concldr c tnsor a c dono ncssaramnt nll affncé J Q (d) possa sstr. A dr l ro anc l scondo trmn prsnta dll dffcoltà, nfatt s consdramo la qanttà d moto, abbamo Q Q ρ
15 Massmo Bcca matr c accorgamo c anc la qanttà d moto non è narant, qnd andamo a sosttr la dpndna dl flsso, nc dlla qanttà d moto mttamo la loctà c ssndo n ttor è scramnt narant, s a ( ) J d Q b b non potrà non ssr c la combnaon lnar d solo tr tnsor d ordn 4 c sono crtamnt narant, coè ottnamo,, k b ( ρ, E) δ ( ) ( ) jδ k β ρ, E δ δ jk γ ρ E δ kδ j α,, j,, k δ δ j k k δ j, k δ k k δ j k k k δ j ( ) I, k δ δ jk k j, k δ k δ j k j ( ) T possamo concldr dcndo c la part dsspata dl flsso dnta, J ( d ) Q ( ) I β ( ) T α γ A olt pò rtornar tl scrr l flsso dsspato con la part smmtrca antsmmtrca dl gradnt dlla loctà. ( ) ( ) ( ) T SIM ( ) ( ANT ( ) ) tlando qst d rlaon l flsso dsspato dnta, T J ( d ) Q ( SIM ) ( ) I ( β γ )( ( β )( ) ( ANT ) α ) γ Qsto laoro è stato fatto prcé s samo d front al caso partcolar d moto rgdo, sappamo gà c la rotaon rgda a n tnsor c è antsmmtrco con tracca nlla, qnd prm d trmn scompaono, s oglamo c l flsso dsspato sa nllo, dobbamo mporr c β γ. In qsto caso l flsso dnta, J ( d ) Q T ( ) I ( ( ) ) α β
16 6 Massmo Bcca matr c pò ssr ancora rscrtto com, J ( d ) Q µ λ 3 ( ) ( SIM ) ( ) I ( )I S pò far dscorso analogo sl flsso dll nrga l qal prò a qsta forma, ( ) J d E d ρ f E nfatt s pò notar faclmnt c qsta olta andrà a solo l scondo trmn lgato al tnsor d ordn dspar, con na trattaon analtca s arra alla conclson c l flsso dsspato dll nrga a na forma dl tpo, ( ) J d E k T. martdì 9 ottobr L obtto dlla arodnamca è l calcolo dll for d momnt c agscono slla nostra ala. S andamo a prndr l qaon d blanco dlla qanttà d moto, andamo a consdrar la qanttà d moto total, somma dll qanttà d moto dll sngol partcll c formano l nostro sstma, d ssr gal al flsso dl ttor J Q. Q dv J nds Q t Qsta rlaon l so qalnt dffrnal al ndpndntmnt s c troamo d front ad n fldo o ad n soldo, o ad n sstma c s compon d ntramb. Qsto prcé non abbamo fatto nssna pots slla sotropa dl sstma. S c troamo d front n sstma dl tpo, V
17 Massmo Bcca matr Ossramo c s facssmo tndr l olm, n c s troa l fldo, al contorno dl proflo, Capamo c l proprtà d olm, tndndo l olm stsso al olm dl proflo, dntano l proprtà dl corpo. Qnd nll qaon d blanco dlla qanttà d moto l I trmn c da la fora a c è sottoposto l corpo sotto l aon dl fldo. Abbamo dtto c l II trmn è qllo dll proprtà d sprfc, c sono dpndnt dal flsso dl fldo. S prndamo n consdraon n fldo non scoso sappamo c l flsso dlla qanttà d moto a na forma partcolar, c c prmtt d scrr c la fora arodnamca sarà, F ρ pi nds ( ) V ma ssndo l fldo non scoso, slla part dl proflo la loctà non s annllrà qnd arrà la condon n, allora s a F V p nds Rcordamoc smpr c l flsso J Q al dmnsonalmnt no sforo. Samo n n caso sml a sold soggtt a sfor, solo c lì lo sforo ra doto a dll dformaon, q lo sforo è doto a dll loctà. Possamo far n altra ossraon slla fora arodnamca, nfatt s andamo a prndr l nostro proflo con l nostro olm d controllo, ma qsta olta nc d rdrlo sl proflo, lo allargamo all nfnto possamo concldr c l for fldodnamc sono smpr gal all for agnt sl copro s l fldo s mo s moto nform. Qsto capta prcé l ntgral drant dalla qanttà d moto dlla part d olm dl fldo è nllo, dato c l moto dl fldo è staonaro, l ntgral s sprfc dorbb ssr nllo n qanto non c è flsso ntto, ssndo l moto staonaro, qnd c rsta solo l trmn concrnnt la fora agnt sl corpo. Qsto rsltato è molto tl, prcé sotto l pots d staonartà c consnt d trascrar la gomtra dl nostro proflo.
18 8 Massmo Bcca matr Il problma dffrnal non è bn dfnto s non rscamo a cdrlo, coè s non rscamo a troar l condon al contorno. L nostr ncognt sono 5 drant dall ncognt dll qaon d blanco, ma tramt l qaon d stato rscamo a dmnr l ncognt ndpndnt qnd anc l nmro dll condon al contorno ncssar pr la rsolon nmrca dll qaon d blanco. S ancora no rscamo a costrr l nostro sstma d rfrmnto n modo tal c sso sa soldal al proflo stsso, possamo mporr c la loctà sl corpo sa nlla, c, qsto c prmtt d ar gà tr condon al contorno. La qarta condon c n da na granda dl campo trmco, c non c ntrssa a tanto pr qanto rgarda l campo d moto ma s oglamo conoscr l campo d tmpratra samo costrtt a rsolrlo. Ma s samo n prsna d n fldo ncomprmbl non scoso allora l qaon d blanco dll nrga è prfttamnt dsaccoppata dall altr d, qsto c prmtt d scndr a sol tr condon al contorno. Solo c nasc l problma c non portò sar pù la condon d prftta adson, sarò costrtto a porr com condon al contorno c la drata dlla loctà lngo la normal dl proflo sa nlla, coè la condon d non pntrabltà dl corpo. L altr condon sono c l loctà tangnt al proflo non sono affatto nll, n gnral la gstfcaon d qsta trattaon c rcdrà d rcaar lo strato lmt. Rprndamo l qaon d Elro nl caso d fldo ncomprmbl non scoso, t p ρ ( ) rcordamo anc c l qaon d blanco, dsaccoppata rsptto all altr d, ra così fatta, D ρ ρ Dt dall qaon sostanal d contntà ottngo, Dρ D p Dρ ρ Dt Dt ρ Dt rcordando c, ottnamo, p Tds d pd d pd d ρ ρ dρ
19 Massmo Bcca matr T Ds Dt Ds Dt abbamo ottnto c l sstma è anc sontropco. Ando l sstma araon d ntropa nlla, c prmtt d scrr la dnstà, c ra fnon dlla prsson dll ntropa, com fnon dlla sola prsson, coè ( p s) ρ( p) ρ ρ, c prmtt d dfnr na fnon P, com P dp ρ ( p) nl caso n c l sstma sa comprmbl sontropco l sstma d qaon sarà, ρ ( ρ) t ( ) P F t Possamo ntrodrr anc l qaon d blanco sotto la forma d Crocco, nfatt s prndamo n consdraon l scondo trmn dll qaon d blanco dlla qanttà d moto, rcordando la rlaon ttoral ( ) ( ) ( ) dfnndo ω s a, ( ) ω l qaon d blanco dnta consdrando la rsltant dll for nll, t P ω. Da qsta formla s possono rcaar l rlaon d torm d Brnoll:. Caso staonaro, P ω
20 Massmo Bcca matr moltplcando scalarmnt pr s ottn, P da c s d caramnt l bnomo è costant lngo ogn lna d corrnt.. Caso rrotaonal staonaro, P da c s d sbto c l bnomo s mantn costant n ttto l campo d moto. 3. Caso rrotaonal, P t s sst n potnal scalar pr c possa scrr, allora s a, ( ) P t P t P t s concld dcndo c qsto trnomo c abbamo troato s mantn costant n ttto l campo d moto, s not c qsta olta la costana è soltanto spaal ma non tmporal. S l nostro campo d moto è n campo d moto rrotaonal, allora possamo trasformar ltrormnt la nostra qaon d blanco dlla qanttà d moto, nfatt passamo a far l rotor d ttta l qaon, ottnamo t ω P qsta qaon è qas qalnt al sstma, ( ) t ω ω ω
21 Massmo Bcca matr Ho dtto c l qaon prcdnt è qas qalnt al sstma sopra scrtto, pocé non è dtto c ttt l solon dl sstma sano solon dll qaon, l crsa è smpr ro. S l domno è monoconnsso allora l solon dl sstma dll qaon andranno a concdr, altrmnt bsogna garantr c la solon sa tal c la qanttà ω sa n gradnt, c sa garantto anc t ω dc t Pr l nostro stdo c conn far l passaggo dall coordnat lran, coè fss nllo spao, ad n sstma d coordnat lagrangan, coè con n sstma mobl nllo spao c sga stant pr stant l nostro sstma fsco. Il sstma d rfrmnto lagrangano s mo con loctà par a qlla macroscopca dl fldo, andamo a dr com s trasformano l drat olt n drat lagrangan. La gnrca trasformaon n spao tmpo è, j ξ ξ j t ξ t j t t j t t t l passaggo da trna fssa a trna lagrangana è spcfcato da, scopramo c la drata sostanal sarà j t t j t t t j j Tornando slla nostra qaon n ortctà, ottnta facndo l rotor dll qaon d blanco dlla qanttà d moto, sapndo c ( ω ) ( ) ω ( ) ω ( ω ) ( ω ) l prmo trmn dll gaglana ttoral s annlla tramt l qaon d contntà, l tro pr dato c la drgna d n rotor è nlla pr dfnon. Allora l qaon n ortctà dnta,
22 Massmo Bcca matr ( ) ( ) t ω ω ω ( ) Dt D ω ω n coordnat lagrangan abbamo, l l ξ ξ l l l Dt D ξ ξ ω ω ω l scondo trmn sprm l componnt dlla drata sostanal dlla ortctà l tro sprm l coordnat lagrangan. Ma sappamo anc Dt D l l ξ ξ dato c la ξ l tmpo sono ndpndnt posso scrr, l l Dt D ξ ξ qnd s a l l l l Dt D Dt D ξ ξ ω ξ ξ ω ω ω prndndo n consdraon l prmo mmbro s a, ( ) l l Dt D Dt D ω δ ω ma l l l l ξ ξ δ qnd s a, l l l l Dt D Dt D Dt D Dt D ω ξ ξ ω ξ ξ ω ξ ξ ω s nota c, gaglando l d drat s anno d trmn gal, rsta solo l Dt D ω ξ ξ l drat d l rsptto all ξ ssndo lo jacobano dlla trasformaon non è ma nllo qnd lo possamo smplfcar ottnr,
23 Massmo Bcca matr ξ ω ω ( ) ω ω ( ) ξ do con ω () s è ndcat la costant d ntgraon. S pò notar c nlla nostra trattaon abbamo fatto scomparr l drat tmporal, ma qst n rtà non sono scompars prcé la dpndna dal tmpo rman smpr nll coordnat lagrangan dlla. Qsta rlaon c dc c s abbamo n campo d moto n c la ortctà nal è nlla nll s tr componnt, allora ssa s mantrrà nlla pr l rsto dl tmpo, qalnq sa l moto dl sstma lagrangano. Qsto è molto mportant nl nostro stdo d n proflo, nfatt s no assmamo c all nfnto la loctà s mantn costant c la ortctà è nlla, allora sa scr c l proflo starà n n campo d moto rrotaonal, oltr ad ssr n fldo non scoso ncomprmbl pr pots, scldndo caramnt la sca c è na rgon dl campo d dscontntà. Mrcoldì ottobr Abbamo rcaato l componnt dlla ortctà nl caso d fldo non scoso ncomprmbl, andamo adsso a dr com qll forml possono arar nl caso d fldo comprmbl. Nl caso comprmbl sappamo c l qaon d blanco dlla ortctà è, Dω ω Dt ( ) ω ( ) gra all qaon d contntà l prmo trmn pò ssr scrtto com, qnd s a, Dω Dρ Dω Dρ D ω ω ρ ω ρ Dt ρ Dt ρ Dt ρ Dt Dt ρ D Dt ω ω ρ ρ S not c l rsltato raggnto è sml a qllo nl caso prcdnt, con la sola dffrna c lì c ra solo la ortctà, al contraro qa compar l rapporto dlla ortctà rsptto alla dnstà. Scrndo la formla raggnta n coordnat lagrangan, facndoc atar da passagg fatt n prcdna, s a, ω ω ρ ρ ( ). ξ
24 4 Massmo Bcca matr Anc n qsto caso s la condon all nfnto è nform o è d qt, allora possamo concldr c n ttto l campo la ortctà sarà nlla. Passamo all qaon d blanco dlla massa, scramola n coordnat lagrangan, partamo dalla drata sostanal dlla massa, Dρ ρ Dt com abbamo fatto n prcdna, andamo a scomporr la drgna dlla loctà, scrndola prma n coordnat cartsan passando po n coordnat lagrangan, l qaon dnta, ξ j ξ j D Dt j ξ ξ j Dρ D ξ j ρ Dt Dt ξ j rcordamo c s abbamo na matrc A con dtrmnant A, possamo dr A : da A dc d dc A do c è n paramtro qalnq. Consdrando nl nostro caso l tmpo com paramtro rconoscndo con J l dtrmnant Jacobano dlla ξ trasformaon c lga l coordnat a qll ξ, s a s J non è sngolar, J Dρ DJ ρ Dt Dt Dρ ρ J Dt DJ Dt D ρ Dt ( J ) all stant nal la dnstà al ρ() ρ () lo jacobano al, n qanto all stant nal sstm d rfrmnto cartsano lagrangano anno a concdr. Lo jacobano c dc com ara l rapporto dgl lmnt d olm n drs sstm ξ, man mano c l sstma lagrangano s ol. Qnd la rlaon c fa capr c la dnstà ρ olrà n manra nrsa rsptto al olm.
25 Massmo Bcca matr Qllo c abbamo fno ad ora dtto a n grosso dftto, nfatt l solon c no rtroamo ngono for da qaon dffrnal. Sappamo c qando sst na dscontntà dl campo d stdo non possamo pù tlarl. Qnd samo costrtt a rpgar s dll qaon d tpo ntgral. Andamo a gardar alcn torm c c rranno tl sotto l pots cnmatca c ω. Il torma d Stoks c dc, ω nds dc S Il torma d Kln c dc c s no calcolamo l sgnt ntgral dc lngo n prcorso cso c s mo con loctà macroscopca, possamo pnsar a crc fatt col fmo, la drata dll ntgral s mantrrà gal a ro, D Dt S ( dc) Dmostraon: D Dt ( ) ( ) dc D d D dξ j Dt Dt ξ j l cammno dll ntgral dpnd dal tmpo, ma ssndo passato all coordnat lagrangan qsta dpndna scompar, qnd posso portar la drata all ntrno dll ntgral. Dopo passo a scomporr d ntgral c ottngo drando l prodotto dlla fnon ntgranda, D Dt dξ j ξ j D Dt dξ j ξ j D Dt dξ j ξ j dmostrar l torma sgnfca dmostrar c qst d ntgral sono ntramb nll, prndamo n consdraon prma l scondo D Dt D dξ dξ dξ j j j ξ j ξ j Dt ξ j ξ j dξ j c accorgamo c è l ntgral d n dffrnal satto, c calcolato n n prcorso cso è banalmnt ro. Da notar com fno a qsto pnto non abbamo fatto so dll qaon dl moto.
26 6 Massmo Bcca matr Passamo adsso all altro ntgral, D Dt dξ j ξ j D P tramt la drata sostanal Dt dnta, P dξ j ξ j P dξ j ξ j anc q abbamo raggnto n ntgral d n dffrnal satto, c è nllo prcé l prcorso è cso. Qnd anc la drata dll ntgral nal sarà nllo l torma d Kln è stato dmostrato, nll pots d fldo non scoso ncomprmbl o comprmbl sontropco. Dal torma d Kln possamo rcaar torm d Hlmot, c sono n msto d consdraon cnmatc dnamc, passamo comnq prma a dfnr alcn grand fsc. S dfnsc lna ortcosa l logo d pnt c anno stant pr stant paralllo l ttor ortctà, matmatcamnt dfnta localmnt com ω ds. Possamo dfnr com sprfc ortcosa na sprfc c a com drttrc dll ln ortcos. S na sprfc ortcosa a com gnratrc na lna csa allora s parlrà d tbo ortcoso, l ara dlla gnratrc rrà camata son dl tbo. S n tbo ortcoso a na son c tnd a ro, coè la cra altro non è c n pnto, allora parlrmo d flamnto ortcoso. Il prmo torma d Hlmot raccd n s qst d proprtà: ) l flsso d ortctà rslta costant n ogn son d n tbo ortcoso, ) s s prnd n tbo ortcoso o flamnto ortcoso la crcolaon è costant attrarso qalsas lna c crconda l tbo stsso. Il scondo torma d Hlmot c dc c na sprfc c è n n dato stant sprfc ortcosa lo sarà pr ttt gl stant sccss. Qsto torma dra da qllo d Kln. Sosttr al ttor loctà n potnal scalar è na cosa c m gratfca molto, prcé m fa capr c c troamo d front ad n campo rrotaonal. Ma qsto non smpr è possbl farlo, prcé do star attnto al tpo d domno o o. Infatt s oglo c l mo campo d moto sa onq rrotaonal do ar o far n modo c sa monoconnsso. Prtroppo n problma arodnamco non è qas ma monoconnsso, nfatt s consdro l pano do gac la son dl mo proflo, m accorgo faclmnt c l proflo stsso fa n modo c l domno non sa monoconnsso. Inc s trattamo l problma n tr dmnson allora è monoconnsso, prcé anc s costrsco n prcorso cso attorno all ala, posso smpr strarr for qsto prcorso rdrlo n n pnto nllo spao.
27 Massmo Bcca matr Concldamo dcndo c l problma arodnamco è smpr monoconnsso n tr dmnson, n d dmnson nc è bconnsso. Rcordando c stamo smpr trattando con fldo staonaro non scoso, abbamo troato c s l mo domno è bconnsso allora l potnal scalar non sarà monodromo, coè non arà n sol alor n n dtrmnato pnto dl domno. Allora no possamo spar l domno tramt na strsca d aprtra nfntsma, Così facndo l domno è monoconnsso, nfatt non posso crcar l proflo con na cra csa. Logcamnt qllo c abbamo fatto è soltanto n trcco, prcé l problma sssst comnq, nfatt l alor dl potnal attrarso la strsca è comnq drso, ma all ntrno dl domno prato dlla strsca l potnal sarà contno. La sclta d do porr la strsca non è obblgatora, anc s drmo c conn scglr n posto rsptto ad n altro. E c la strsca d ssr nfntsma d lnga nfnta. Nl caso d fldo ncomprmbl moto rrotaonal possamo scrr qsto sstma d qaon, scrndo la loctà tramt l so potnal scalar, s ottn l qaon d Laplac, Qsta qaon dffrnal dl scondo ordn è lnar, qsto c prmtt d applcar l prncpo d sorapposon dgl fftt. Andamo adsso a troar l possbl condon al contorno pr l qaon d Laplac,. S oglo c la loctà all nfnto sa allora posso dr c l potnal sarà, ( )
28 8 Massmo Bcca matr l altra condon possamo rcaarla consdrando l corpo, no sappamo c l fldo è non scoso, qnd non possamo dr nlla crca la loctà sl corpo, ma possamo dr c la componnt normal dlla loctà sl corpo è crtamnt nlla, coè la condon d non pntrabltà, ( n) ( ) c n. L condon al contorno c abbamo rcaato sono rfrt ad n sstma d rfrmnto fsso, s c mttamo soldal con l fldo, l condon cambano. Infatt la loctà all nfnto sarà nlla, la loctà sl corpo sarà la loctà, coè ( ) c ( ) n n c. Abbamo dtto n prcdna c l taglo c no ffttamo al nostro domno, pr rndrlo monoconnsso, non sarà fatto n n posto qalnq, ma sso arà n lgam con la sca dl nostro oggtto. Dorò rsolr l qaon d Laplac facndo n modo c l taglo m tolga la dscontntà rotaonal c la sca m dà nl mo domno d calcolo. Pr rsolr l mo problma, do ar anc dll condon al contorno dlla sca, c sono dopp prcé s bord dlla sca sappamo c l potnal è dscontno, allora posso andar ad applcar na qaon d blanco attrarso n contorno cso, c m raccd n po dlla sca, n modo da rcaar dll rlaon c m ntrodcono n lgam tra l qanttà a caallo dlla sca. Pr far cò non posso tlar dll rlaon dffrnal, pocé l campo prsnta na dscontntà, passo allora a dll qaon d tpo ntgral. c godì ottobr Data la loctà prs d pnt sl pano P P, l potnal sarà: ( P ) ( P ) s P P anno a concdr, allora c troamo d front ad n prcorso cso l ntgral pr l torma d Stoks sarà nllo. I alor d (P ) possono assmr nfnt alor, ma sappamo con crta c qst alor sono mltpl ntr dlla crcolaon dlla loctà, coè P P Γ dc dc
29 Massmo Bcca matr Abbamo dtto c l taglo non andrà fatto n n pnto arbtraro, ma no mponamo do farlo. E rsolndo l qaon d Laplac ado a dtrmnar lgam c sstono tra l grand attrarso l salto c s cra sl taglo. Immagnamo d ar n tratto dlla sca, d costrr ntorno ad ssa n prcorso cso, () A F B C E D Andamo a scrr la consraon dlla massa n forma ntgral, s a ndl () B C D E F A d d d d d d A B C D E F l dstan rtcal rsptto a qll orontal dl prcorso sono molto pù pccol, qnd contrbt dgl ntgral lgat a possono ssr pnsat nll, ma nllo stsso tmpo l dstan AB ED non sono ccss, pr far n modo c la sca possa ssr pnsata rttlna, qnd qll dstan possono consdrars gal, s a AB ED n n samo arrat alla conclson c l componnt normal dlla loctà sono gal, qnd anc contn, saranno gal anc l componnt normal dl potnal. Ma andando a consdrar la sca com na lna d corrnt, sappamo c na lna d corrnt non a componnt normal, qnd possamo ancora scrr, n n (solo slla sca). A qsta conclson samo arrat andando a stdar la consraon dlla massa, s andamo a consdrar la consraon dlla qanttà d moto s a, ( ρ pi ) n ( ) ρ pi n
30 3 Massmo Bcca matr ma ssndo nllo l prodotto scalar dlla loctà con l rsor normal, dalla rlaon c rsta soltanto, p p. Qlla c abbamo rcaato è na rlaon n c compar la prsson, ma o oglo tradrla n trmn d potnal, pr far cò mtto n goco l torma d Brnoll, d o ( ) ( ) p p t t t ( ) s dfnamo ottnamo, ( ) ( ) t ( ) ( ) ( ) s dfnsco la loctà d n pnto dlla sca com la mda dll loctà d pnt al d sopra al d sotto dlla sca, ottngo t t ( ) ( ) ( ) ( ) D Dt ( ) Notamo c l qaon d Laplac non è dpndnt dal tmpo, ma qsto è pra apparna nfatt la dpndna dl tmpo è stata spostata nll condon al contorno. Infn possamo dr c l qaon d Laplac c consnt d stdar l campo d moto, scldndo con n trcco l nca rgon d campo c è scramnt rotaonal, c prsnta na dffcoltà ntrnsca d stdo. L qaon d Laplac non c dc nlla s qanto rgarda la sca, ma no mponamo c l taglo d domno prnda n goco la sca c la lmn dal campo d moto. La dscontntà rman n qanto da ntramb l part dlla sca l potnal assm d alor compltamnt drs, ma qsta dscontntà n sprata rcaando, com abbamo fatto, altr condon al contorno c c prmttono d lgar grand com la loctà normal la prsson da c camo rsct a rcaar l potnal.
31 Massmo Bcca matr Passamo ora a dr alcn form rsolt dll qaon d Laplac, la sclta dl sstma d rfrmnto dpnd dal tpo d fnomno c sto stdando, comnq sappamo c l qaon d Laplac potrà ssr scrtta com, qsta forma è n coordnat cartsan. No non sappamo c forma arà la solon d qsta qaon, ma proo s possa ssr d qsto tpo, ( ) F( ) G( ), sosttndo dntro l qaon s a, ( ) G( ) F( ) G ( ) F F F ( ) ( ) G G ( ) ( ) affncé la somma d d fnon d arabl drsa sano gal a ro, d accadr c l d fnon sano costant, ( ) ( ) F G A F G ( ) ( ) F ( ) AF( ) G ( ) AG( ) l solon d qst qaon dffrnal aranno na forma dl tpo, F ( ) k k ± A ± a a C a R s s A < A G ( ) k k ± A ± a a C a R s s A > A qnd la solon dll qaon sarà, ± a ± a ( ), Ma arando l domno d calcolo l condon al contorno, la solon pù gnral possbl c possamo scrr a na forma dl tpo,
32 3 Massmo Bcca matr (, ) k( a) S prndo n consdraon na gomtra n c l mo domno sa solo la part posta dll, qnd la ma condon al contorno sa solo na fnon dlla sola,, g a ( ) ( ) do pr star attnto a non far andar ad nfnto l mo potnal, n qsto caso basta mttr n alor assolto la a all sponnt dlla, prcé sono scro c l contrbto drant dalla sa lmtato, pocé sono fnon gonomtrc, tramt la ma condon al contorno o a da a (, ) k( a) da g( ) sfrttando la trasformata d Forr s pò prndr l nrsa d ar, k a π ( ) a g d. mrcoldì 7 ottobr Abbamo rcaato l qaon d Laplac, abbamo anc sto la forma c pò assm na sa solon sprssa com l prodotto d d fnon dpndnt da arabl sparat. Ma ttto l procdmnto sgto è stato solto n coordnat cartsan, qsto a olt pò ssr n lmt molto alto sopratttto qando samo n prsna d domn crcolar. Infatt s samo n qsto caso l coordnat pù adatt sono qll clndrc, la topologa sfrca o clndrca a bn anc n cas d profl, cosa c a no ntrssa molto. Qando abbamo rcaato la solon dll qaon d Laplac mdant l procdmnto d sparaon d arabl, abbamo laorato n coordnat cartsan, ora non è assoltamnt dtto c n coordnat polar alga ancora qllo c abbamo fatto pr l caso cartsano, qnd samo costrtt a rfar cont. In coordnat polar l qaon d Laplac dnta, r θ r r r r anc q oglamo crcar dll fnon solon c abbamo la forma, ( r θ ) F( r) G( θ ),
33 Massmo Bcca matr sosttndo nll qaon d Laplac s a: r G FG F r r ( r ) G r G F ( rf ) abbamo sparato l arabl, l prmo addndo è fnon solo dlla θ, mntr l scondo è fnon solo dlla r, affncé dano somma nlla d accadr c ntramb sano gal a costant, coè G A G r F ( rf ) A La prma qaon dffrnal, qlla dpndnt da θ, è sml a qll st nl caso cartsano, qnd arà solon dl tpo, G ± aθ ( θ ) la sconda qaon è na qaon d Elro, coè a coffcnt non costant, ma c pò ssr rportata a coffcnt costant con la banal sostton d arabl d log r t dt dr r r dt d dr qnd la nostra qaon r ( rf ) AF n fnon d t dntrà, con solon F tt AF F ± at ( t) tornando nlla arabl r, s a F ± a ( r) r Qnd notamo c l d solon sparat anno facca drsa, cosa c non accada nl caso cartsano. In pù accad c l solon troat non comprndono ttt l solon possbl al arar dlla costant A, nfatt s spponamo c A sa nlla abbamo ( ) G( θ ) C C θ G θ
34 34 Massmo Bcca matr a r r ( rf ) ( rf ) rf a F F() r a logr b qst d solon non nano comprs nll solon gnral troat con A qalnq. Passamo adsso a laorar sll condon al contorno spponamo d conoscr la condon sl contorno crcolar d raggo r. Coè spponamo d conoscr la (r,θ)g(θ), la solon gnral sarà la combnaon lnar pù gnral possbl fra l solon r troat sparatamnt, rcordamo c no θ stamo crcando l potnal n n pnto r all strno dl crco d raggo r, qnd dobbamo star attnt c l nostro potnal r non ada all nfnto. La solon gnral sarà, ( r, θ ) a r b Cθ k( a) log abbamo dtto c l potnal non pò drgr allora l tro trmn non pò sstr prcé all nfnto l potnal d ssr nform. Dondo l fnon ssr contn mplca c l sponnt a dntro l ntgral non pò ssr ral ma ntro, d consgna al posto dll ntgral posso sosttr na sommatora così fatta, k a aθ n n ( a) r da ( A r B r ) n ma c accorgamo c anc qando r tnd all nfnto l potnal drg, qnd dobbamo lmnar dalla sommatora anc l potn d r con sponnt posto. La solon dntrà, n n r a aθ nθ da ( r, θ ) a r b log adsso na smplc trasformata d Forr la condon al contorno sl crco d raggo r c prmttono d rcaar coffcnt dlla sommatora k n, coè ( ) ( ) n nθ n π r, θ g θ a logr b knr k ( θ ) n r g n n k n r n nθ π nθ dθ
35 Massmo Bcca matr Fnora abbamo stdato com troar l potnal n n pnto all strno dl contorno sclto, ma oglamo anc trattar l caso n c l nostro pnto sta all ntrno dl contorno. Il dscorso da far è abbastana analogo, solo c mntr prma lmnao trmn dlla sommatora con sponnt posto, qsta olta dorò lmnar qll con sponnt ngato. E pr lo stsso moto do lmnar l trmn c compar con l logartmo prcé sso prsnta na dscontntà n ro. Dtto qsto la solon arà forma ( r, θ ) b Pr qanto rgarda la condon al contorno pr l problma ntrno non camba assoltamnt nnt, nfatt rsta qlla c abbamo troato prma con l dot araon d sgno, qnd possamo dr c c è na smmtra dlla condon d tpo Drclt pr l problma strno ntrno. Cosa c non accad s andamo a prndr na condon al contorno d tpo Nmann, nfatt s consdro la drata radal pr l problma ntrno, o o n k n r n nθ g ( θ ) ( ) r r, θ n k n n r n nθ nrtndo con la trasformata d Forr s a, k n n r n π π g ( θ ) nθ dθ andamo adsso a notar c, s n l prmo mmbro dnta dntcamnt nllo, qnd s anc l scondo mmbro, coè l ntgral, fa ro non o casn l mo problma è bn posto, s ro non è allora l mo problma è mal posto. Affncé sa bn posto do rspttar la condon d compatbltà l ndl. Qsta condon non a logo d sstr s consdramo l problma strno, nfatt n ql caso dato c la solon gnral camba la sa drata d consgna anc, s arà na condon al contorno dl tpo, g ( θ ) ( r θ ) n nθ r, kn n r n a r
36 36 Massmo Bcca matr ando n grado d lbrtà n pù, rsco comnq a soddsfar la condon d mda non nlla dlla condon al contorno. Qnd m accorgo c l problma polar con condon d tpo Nmann non è affatto smmtrco. Con l coordnat polar possono ssr rsolt non solo domn prttamnt crcolar, ma anc domn c rapprsntano coron crcolar, Oppr spcc d domn crcolar, θ θ n qsto caso l solon aranno sponnt non ntro ma ral, prcé ssndo l domno lmtato scondo l ampa non c è l problma dlla contntà. Prma d andar a dr qalc caso partcolar d solon dll qaon d Laplac, ntrodcamo l conctto d fnon d corrnt, s abbamo n campo d moto pano na lna c nsc d pnt A B la fnon, ψ l ( A, B) l ndl
37 Massmo Bcca matr s spponamo d porr l orgn dl sstma d rfrmnto nl pnto A, la fnon d corrnt ψ non dpndrà pù dal pnto A. s spponamo ancora d ar n moto rrotaonal ncomprmbl allora la fnon d corrnt ψ non dpnd dal prcorso sclto, sarà solon dll qaon d Laplac coè ψ. S prndamo n consdraon l solto problma arodnamco, possamo dr c l corpo è lna d corrnt, qnd anc la ψ è costant s ogn lna d corrnt, s l condon al contorno sono dl tpo Drclt sfrttando la ψ s anno l sgnt forml, ψ ψ Portamo alcn smp d corrnt, ncomncamo con l caso d corrnt parallla ad n pano oblqo, V Il potnal qllo ψ saranno, ψ (, ) (, ) Prndamo l caso dlla sorgnt d ntnstà q, caramnt è sprssa pr ntà d profondtà, s q > allora s tratta d na ra propra sorgnt, s q < allora s tratta d n poo. Consdrando n coordnat polar l nostro sstma pr dtrmnar la loctà radal, basta consdrar na corona crcolar da c s rcaa
38 38 Massmo Bcca matr ( r, θ ) ψ q logr π q π ( r, θ ) θ ψ cost cost l trmn log(r) prnd l nom d trmn d monopolo o sorgnt. In qsto partcolar caso sst n caso dal, coè qando s nrtono l cr dl potnal ψ qll dl potnal. Qando qsto accad fscamnt s a l caso dl ortc pano con crcolaon Γ, potnal dntano ψ ( r, θ ) Γ θ π Γ π ( r, θ ) log r ψ cost Γ cost S abbamo n sstma cnmatco c comprnd na sorgnt n poo post ad na crta dstana d qsto n camato dopptta, po ad n crto stant faccamo acnar qst d sorgnt n modo da far tndr a ro la loro dstana, facndo n modo c l prodotto q d s mantnga costant d gal a qd cst µ cost ψ cost
39 Massmo Bcca matr con µ ndcamo l ntnstà dlla dopptta d è carattrato da n sgno, anc n qsto caso possamo rcaar d potnal d ar, ( r, θ ) ψ ( r, θ ) µ cosθ π r µ snθ π r S mttamo assm na dopptta n moto nform, ottnamo sapndo c al l prncpo dlla sorapposon dgl fftt, Y ψ cost V µ snθ µ snθ ψ V rv snθ snθ rv π r π r µ πr notamo c θ pr θ π s a c l potnal ψ s annlla, ma qsto accad pr pr l alor r µ r πv Notamo c anc l domno crcolar d raggo r è lna d corrnt, qnd non abbamo fatto altro c dsgnar la lna d corrnt d moto nform c nst n clndro. Andamo ora a calcolarc l loctà, pr draon dal potnal ψ, facl rfcar c, ψ r r V cosθ r θ r ψ r V snθ r r θ ( ) snθ r V. θ
40 4 Massmo Bcca matr godì 8 ottobr Rgardando ancora l problma dl clndro nstto da na corrnt nform, possamo notar dall ln a potnal ψ costant c l nostro problma prsnta na smmtra sa pr qanto rgarda l ass dll, ma anc pr qanto rgarda l ass dll. S andamo a calcolarc dall loctà tangnal l coffcnt d prsson, lo dagrammamo pr la loctà, s a C p π sfra clndro Da qllo c abbamo troato sgono d mportant rflsson. Dalla smmtra rsptto all ass c n c non sst portana, qsto rsltato prò non contrasta con la raltà sprmntal, prcé sappamo c n clndro non n rotaon rlata rsptto al fldo, non gnra portana. Ma dalla smmtra rsptto all ass dll notamo c non s gnra nanc rsstna, qsto n raltà non sccd. Qsta contraddon c a sotto l nom d paradosso d D Almbrt, spnta dal fatto c s è trascrata la scostà dl fldo, c c è srta pr far dll smplfcaon matmatc pr rcaar l nostr forml. Infatt anc nlla raltà s non assmo scostà non s gnrrbb rsstna c comnq c è smpr. Contnamo a dr altr mtod rsolt dlla nostra qaon d Laplac. Abbamo sto fno ad ora l mtodo dll sparaon dll arabl, sa n coordnat cartsan c n coordnat polar. E samo rsct a rcaar na solon dl tpo (r,θ), allora m cdo, s sst la (r,θ) sstrà la solon (/r,θ), solon sì d n altro problma ma comnq solon c rfca l qaon d Laplac? Ebbn sst. Qllo c facco pr prma cosa troar la formla d Laplac n coordnat polar nlla noa arabl r, r
41 Massmo Bcca matr sappamo c la drata prma sarà, r r r allora l qaon d Laplac dnta, r 3 r r r r θ Spponamo d olr calcolar qando è l potnal d na sorgnt, c a la forma log r r n coordnat cartsan dnta la solon, n coordnat polar armo ( ) ( ) ) log ( r cosθ ) ( r θ ) ) log sn Qnd l altra solon, d non sappamo qal problma ma comnq solon d Laplac, s ottn sosttndo alla r la sa nrsa, coè log r r Notamo c mntr prma la sngolartà dlla solon staa nl pnto r, adsso no l abbamo spostata nl pnto r r r Qsto mtodo d rcrca dll solon è l mtodo dll mmagn. Ma c possamo cdr a c cosa c sr la. Spponamo d ar l crco ntaro, sappamo c la solon la solon anno lo stsso alor, s andamo a consdrar la fnon 3
42 4 Massmo Bcca matr c sarà crtamnt solon, prcé combnaon lnar d solon d Laplac, qsta solon sarà dntcamnt nlla sl crco ntaro, qnd non abbamo fatto altro c troar l campo d moto d na sorgnt c dffrsc con n clndro. Un problma così posto, ando prso com condon al contorno alor dll solon sl crco ntaro è d tpo Drclt, ma s no abbamo condon d tpo Nmann, allora nc dlla dffrna dll fnon dobbamo prndr la somma dll solon, coè 4 Vdamo l prcé. Pr drlo dobbamo farc la drata normal dlla solon 4 sl crco ntaro, r 4 r r r r r r r r r r Andamo a dr adsso na applcaon dl mtodo dll mmagn, pr na spccata dos d fantasa rprndamo l problma dl clndro nstto da na corrnt d fldo c s mo con loctà nform. Sappamo c l potnal d na corrnt nform è, (, ) V ( r,θ ) V r cosθ andamo a prndr l mmagn d qsta solon, coè V cosθ r adsso andamo a troar la somma dll fnon troat, prndo la somma prcé la condon al contorno è d tpo Nmann, coè la non pntrabltà dl clndro, V r cosθ cosθ V. r
43 Massmo Bcca matr Abbamo sto c sotto l mtodo dlla sparaon d arabl c sta la trasformata d Forr, c c consnt la scomposon dll coordnat al contorno n trmn d fnon snsodal, pr po applcar l prncpo dll sorapposon dgl fftt. Adsso andamo a dr l mtodo d Grn c al contraro d qanto sto n prcdna s basa slla somma nfnta da alor pntal pr la dtrmnaon dlla solon. Consdramo la fnon d Laplac non omogna, coè la fnon d Posson, g( r) qsta qaon è lnar qnd arrà l prncpo dlla sorapposon dgl fftt, qsto c consnt d dr c la fnon solon dll qaon sarà dl tpo, ( r ) c. c g( r) G( r, r) dv, V l prmo trmn dl scondo mmbro c dc c la fnon d dpndr dall condon al contorno, l scondo trmn c da l nformaon c la solon sarà data dall ntgral dl prodotto dlla fnon trmn noto calcolata n ttt pnt dl domno pr na fnon G, dtta fnon d Grn, calcolata n non solo n ttto l domno ma anc nl pnto r. Andamo adsso a smplfcar qsta sprsson, sopratttto andar ad lmnar l drat dl potnal pr sosttrl con l drat dlla fnon d Grn. G G G g( r) G dv V G V G g ( r) dv ( G ) G V G dv ( G ) nds ( G ) V dv com s nota faclmnt samo rsct ad lmnar ttt l drat scond d anc lmnato n ntgral d olm n no al contorno, ma sappamo ancora G ( G ) G ( G ) G V G dv n ( G ) ds n ( G ) ds V G dv
44 44 Massmo Bcca matr Ma no oglamo la solon, coè la (r ), qnd ado a scglr na partcolar forma dlla fnon d Grn, coè dfnsco G δ ( r r ) do la fnon δ è camata fnon d Drac, qsta fnon a la partcolartà c l so ntgral calcolato n n domno nfntsmo qando ssa tnd ad nfnto dnta ntaro. A qsto pnto l ntgral d olm dnta la solon sarà, G dv δ ( r r ) ( ) dv r V V ( r ) G g() r dv () r (, r ) G r n G r, V ( r ) ( r) n ds * Adsso s sono n grado d troar na fnon d Grn adatta al mo contorno c m prmtta d lmnar a pror alcn trmn o fatto bgnè, altrmnt sono costrtto ad ntgrar, l prmo trmn è n ntgral noto, qnd faclmnt ntgrabl. Andamo a dr alcn form c possamo troar al arar dl nostro domno dlla fnon d Grn. Comncamo col caso d n domno sna contorno, s spponamo d mttrc sll orgn s arà c G δ r l solon dono godr dlla smmtra rsptto all angolo, qnd non d ssrc la dpndna dlla solon rsptto a θ, noltr trann nll orgn è anc solon d Laplac, qst consdraon c prmttono d dr c l nca forma c possamo ar è dl tpo ( ) G a logr b dobbamo rfcar c l ntgral stso ad n domno nfntsmo dlla G sa ntaro, com contorno scglamo n crco nfntsmo, d abbamo S n a r π ( a logr b ) ds rdθ πa
45 Massmo Bcca matr qnd la condon affncé qsto ntgral sa ntaro è fnon d Grn arà na forma dl tpo, a π. Qnd la G logr b π posta non nll orgn sarà G log r r b. π In tr dmnson la solon contnrà ad ssr ndpndnt da θ, la fnon d Grn sarà, a G b r andamo a rfcar lo stsso ntgral, rcordandoc c qsta olta non armo n angolo pano ma n angolo soldo, qnd s arà S a n r a r 4π b ds r d 4 a Ω π a 4π G b 4π r non nll orgn G b 4π r r. Fno ad ora abbamo sto cas n c l contorno non ssta, n altro caso smplc da stdar è qllo con contorno crcolar, nfatt andamo a prndr n crco d raggo ntaro n c r sta all ntrno dl crco con condon al contorno (,θ) g(θ). S rsco a troar na fnon d Grn fatta n modo c sl contorno ssa s annll, allora crtamnt no d d addnd dll ntgral * s n andranno. Crcar na fnon c sa annll sl contorno è molto facl troarla con l mtodo dll mmagn, pr smpo G log ( ) ( ) log π π r r
46 Massmo Bcca matr la solon sarà, ( ) θ rd r G r G r così facndo samo scr c l scondo trmn dll ntgral d sprfc s annlla dato c la G sl contorno, così com l abbamo costrta è nlla. La la conoscamo prcé è na condon al contorno, abbamo trascrato l ntgral d olm prcé è n dato dl problma, dopo arlo ntgrato. Con la nostra sclta d G, la sa drata radal sarbb stata, ( ) ( ) ( ) ( ) sn cos sn sn cos cos sn cos sn sn cos cos 4 r r r r r r r r r r r G θ θ θ θ θ θ θ θ θ θ θ θ π la nostra solon d potnal dnta, ( ) ( ) π θ θ d r G g r r S nc dlla condon sl crco ntaro armmo ato na condon dl tpo Nmann, armmo costrto la G nc c con la dffrna, con la somma non sarbb cambato n bl nlla. martdì 3 ottobr Andamo a scrr la formla d Grn pr n crco d raggo ρ, con la G d spao lbro, s a ( ) ( ) ( ) π π π θ θ ρ π θ ρ ρ π θ ρ π θ ρ, log, d d n b d r n qanto l scondo addndo d ssr nllo, qsta rlaon c a sotto l nom d corollaro dlla mda, c dc c l ntgral dl potnal ntorno s n crco d raggo qalnq c da l potnal calcolato nll orgn. Ma s pò stndr l ragonamnto al potnal d qalnq pnto r, non dpndndo dal raggo dl crco l ntgral s pò calcolar s qalnq crco cntrato nl pnto olto. Qsto rsltato c prmtt d capr dmostrar c la solon ottnta da C.C. d tpo Drclt è nca. Dcamo anc c la solon d Laplac non pò ar massm mnm a mno c qst non s troano sl contorno.
47 Massmo Bcca matr Spponamo c c sano d solon dl potnal A B, ssndo solon dll qaon d Laplac, sono fnon lnar qnd anc la dffrna dll d sarà na fnon solon dll qaon d Laplac, 3 ma s n contorno d raggo qalnq ntramb l solon dono ar lo stsso alor pr l corollaro dlla mda, ottngo c la dffrna è nlla, qnd l potnal C è nllo sl contorno, ma ssndo nlla sl contorno d ssr nlla onq, da q l nctà d d potnal A B. L forml d Grn c prmttono d ar n nformaon qaltata d com sarà l nostro campo d moto all nfnto, sna spcfcar l nostro problma d Laplac, c cdamo cosa sccd qando r a ad nfnto. Cdr qsto qal a cdr c la dstana tra r r tnd ad nfnto, coè r >> r Qsta condon n assna d sca c a bn, n prsna d sca non tanto prcé ssndo c anc la sca a all nfnto, c sarà qalc pnto slla sca c s acna ad r. Prndamo smpr n consdraon la formla d Grn con la fnon G smpr qlla d spao lbro, n partcolar concntramo la nostra attnon sl scondo addndo dll ntgral, trascrando ntal costant, log r r dl n slppamo n sr d Talor la qanttà r r r rˆ r r r rˆ r rˆ r r r r rˆ rˆ r r r r Talor r r r rˆ r... r a a log r r a logr r r l prmo addndo tnndo dntro l ntgral la drata dlla G, coè r r () r n dl () r r r r r ˆ... ndl
48 48 Massmo Bcca matr ottnamo c è dllo stsso tpo dl scondo addndo con la dffrna dlla non prsna dl logartmo, qsto c consnt d dr c qando r a all nfnto l potnal pò anc sso andar all nfnto, ma la loctà ssndo la sa drata tnd a ro. Il logartmo non c è smpr, ma lo troamo solo qando abbamo flsso d massa, qando non c è l potnal dpnd dal ttor r com /r, mntr la loctà dpndrà com n fattor /r. Andamo a calcolarc la fora c agsc sl nostro proflo, F J S Q nds calcolata attrarso na sprfc molto prossma al proflo, sappamo anc c s l nostro fldo è non scoso la fora s rdc a, F pnds. S Ma s l moto è staonaro, possamo pnsar c la araon dlla qanttà d moto sa nlla n ttto l campo d moto, qnd possamo allargar la sprfc S portarla all nfnto, possamo anc applcar Brnoll, consdrar la loctà com la somma dlla loctà all nfnto pù na componnt nfntsma d araon, coè p p V V V V ρ ρ la fora dnta, F ρ ( VV pi ) S nds p p F ρ VV I nds ρ V V V V V S ρ S ρ I ds l prmo trmn dll ntgral ssndo costant s pò portar for, s ottn l ntgral n ds, qnd possamo trascrar l trmn, allo stsso modo posso S far pr l rapporto p /ρ. Il tro trmn dll ntgral, ssndo V costant, lo porto for m rman l ntgral nds, c pr la condon d non pntrabltà S è nllo, qnd andamo a trascrar l so trmn. S samo n D possamo trascrar l trmn, prcé sappamo c all nfnto la loctà dpnd da /r, qnd ql prodotto dpndrà da /r.
LA CARTA DI SMITH... 2 Introduzione... 2 Visualizzazione di z N, di y N e di ρ L... 6 Visualizzazione dei valori di tensione e corrente in assenza di
 Appnt d amp lttromagntc aptolo 8 part II n d trasmsson A ARTA DI SMITH... 2 Introdon... 2 Vsalaon d, d y d... 6 Vsalaon d valor d tnson corrnt n assna d prdt... 7 alcolo dl ROS... 9 ESERII UMERII SUA ARTA
Appnt d amp lttromagntc aptolo 8 part II n d trasmsson A ARTA DI SMITH... 2 Introdon... 2 Vsalaon d, d y d... 6 Vsalaon d valor d tnson corrnt n assna d prdt... 7 alcolo dl ROS... 9 ESERII UMERII SUA ARTA
Le onde elastiche monocromatiche
 L ond lastch monocromatch Ptagora Samo 570-495 a.c. Jan Baptst Josph Forr Franca, 1768 1830 Ptagora so allv ddro n mplso straordnaro alla tora d nmr alla tora dl sono. Ptagora è attrbto l prmo stdo sstmatco
L ond lastch monocromatch Ptagora Samo 570-495 a.c. Jan Baptst Josph Forr Franca, 1768 1830 Ptagora so allv ddro n mplso straordnaro alla tora d nmr alla tora dl sono. Ptagora è attrbto l prmo stdo sstmatco
Il problema della Trave Inflessa
 Il problma dlla Tra Inflssa q F EI m Problma dlla tra EI q L F m ϕ - c ϕ spostamnto trasrsal rotaon curatura flssonal y M EI c momnto flttnt T d q T M q -T taglo carco trasrsal M M T TdT MdM quaon d campo
Il problma dlla Tra Inflssa q F EI m Problma dlla tra EI q L F m ϕ - c ϕ spostamnto trasrsal rotaon curatura flssonal y M EI c momnto flttnt T d q T M q -T taglo carco trasrsal M M T TdT MdM quaon d campo
Esercitazioni di Elettrotecnica: circuiti in regime stazionario
 Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
Interferenza e diffrazione con gli esponenziali complessi. Nota
 Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Le soluzioni della prova scritta di Matematica del 24 Aprile 2014
 L soluzon dlla prova scrtta d Matmatca dl Aprl. Sa data la unzon 3 a. Trova l domno d b. Scrv, splctamnt pr stso non sono sucnt dsgnn, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l
L soluzon dlla prova scrtta d Matmatca dl Aprl. Sa data la unzon 3 a. Trova l domno d b. Scrv, splctamnt pr stso non sono sucnt dsgnn, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l
Problema 1D della barra inclinata
 roblma D dlla barra nclnata snθ cosθ cosθ - snθ f EA cosθ θ snθ θ - snθ θ cosθ EA f quaon d campo y y EA L condon al contorno EM: Asta nclnata Spostamnt nl rfrmnto local laon rfrmnto local-global snθ cosθ
roblma D dlla barra nclnata snθ cosθ cosθ - snθ f EA cosθ θ snθ θ - snθ θ cosθ EA f quaon d campo y y EA L condon al contorno EM: Asta nclnata Spostamnt nl rfrmnto local laon rfrmnto local-global snθ cosθ
Esercizio 1. Costruire un esempio di variabili casuali X ed Y tali che Cov(x,y) = 0, ma X ed Y siano dipendenti.
 srcz d conomtra: sr srczo Costrur un smpo d varabl casual d tal ch Cov(,), ma d sano dpndnt. Soluzon Dobbamo vrcar l sgunt condzon: σ [ ] [ ] [ ] covaranza nulla ) ( ) ( ) dpndnza non lnar Prma cosa da
srcz d conomtra: sr srczo Costrur un smpo d varabl casual d tal ch Cov(,), ma d sano dpndnt. Soluzon Dobbamo vrcar l sgunt condzon: σ [ ] [ ] [ ] covaranza nulla ) ( ) ( ) dpndnza non lnar Prma cosa da
METODO DEGLI ELEMENTI FINITI
 Introduon al METODO DEGLI ELEMENTI FINITI Ossrvaon su mtod varaonal approssmat classc L unon approssmant dvono: Soddsar rqust d contnutà Essr lnarmnt ndpndnt complt Soddsar l condon al contorno ssnal Dcoltà:
Introduon al METODO DEGLI ELEMENTI FINITI Ossrvaon su mtod varaonal approssmat classc L unon approssmant dvono: Soddsar rqust d contnutà Essr lnarmnt ndpndnt complt Soddsar l condon al contorno ssnal Dcoltà:
SOLUZIONI. risparmio totale = D altra parte la traccia di dice anche che: e 64 L = produzione. Pertanto si ha: Quindi si ha un risparmio del 9,902%.
 SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
Principi ed applicazioni del metodo degli elementi finiti. Formulazione base con approccio agli spostamenti
 Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Le soluzioni della prova scritta di Matematica per il corso di laurea in Chimica e Tecnologie Farmaceutiche (raggruppamento A-L)
 L soluzon dlla prova scrtta d Matmatca pr l corso d laura n Chmca Tcnolo Farmacutch raruppamnto A-L. Data la unzon a. trova l domno d b. scrv, splctamnt pr stso, qual sono l ntrvall n cu rsulta postva
L soluzon dlla prova scrtta d Matmatca pr l corso d laura n Chmca Tcnolo Farmacutch raruppamnto A-L. Data la unzon a. trova l domno d b. scrv, splctamnt pr stso, qual sono l ntrvall n cu rsulta postva
T 2. Figura 1: Conduzione monodimensionale in una lastra piana
 CONDUZIONE EMICA a condzon è l mccansmo d scambo trmco ch ha logo tra corp a contatto o tra d rgon dllo stsso mzzo soldo o fldo a dvrsa tmpratra. Il mccansmo d trasfrmnto dl calor avvn con modaltà dvrs
CONDUZIONE EMICA a condzon è l mccansmo d scambo trmco ch ha logo tra corp a contatto o tra d rgon dllo stsso mzzo soldo o fldo a dvrsa tmpratra. Il mccansmo d trasfrmnto dl calor avvn con modaltà dvrs
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa (3)
 Corso d Mtod Matmatc pr l Inggnra A.A. 206/207 Esrc svolt sull funon d varabl complssa 3 Marco Bramant Poltcnco d Mlano Novmbr 8, 206 Classfcaon dll sngolartà d una funon, calcolo d svlupp d Laurnt, calcolo
Corso d Mtod Matmatc pr l Inggnra A.A. 206/207 Esrc svolt sull funon d varabl complssa 3 Marco Bramant Poltcnco d Mlano Novmbr 8, 206 Classfcaon dll sngolartà d una funon, calcolo d svlupp d Laurnt, calcolo
di Enzo Zanghì 1
 M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
MATRICE DI TRASFERIMENTO
 MATRICE DI TRASFERIMETO In qusto captolo vn prsntato l mtodo d calcolo dtto mtodo dlla matrc d trasfrmnto. Esso rsulta molto utl pr dtrmnar n modo satto l comportamnto crtco d sstm ch possono ssr dscrtt
MATRICE DI TRASFERIMETO In qusto captolo vn prsntato l mtodo d calcolo dtto mtodo dlla matrc d trasfrmnto. Esso rsulta molto utl pr dtrmnar n modo satto l comportamnto crtco d sstm ch possono ssr dscrtt
Teoria. Tale retta limite non sempre esiste. Si veda il grafico sottostante. Matematica 1
 LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
Esercizi di Elettrotecnica. prof. Antonio Maffucci Università degli Studi di Cassino. Circuiti in regime stazionario
 srcz d lttrotcnca prof. ntono Maffucc Unrstà dgl Stud d assno rcut n rgm stazonaro rson. ottobr 7 . Maffucc srcz d lttrotcnca - rcut n rgm stazonaro rson. ottobr 7. Sr paralllo parttor. S.. alcolar la
srcz d lttrotcnca prof. ntono Maffucc Unrstà dgl Stud d assno rcut n rgm stazonaro rson. ottobr 7 . Maffucc srcz d lttrotcnca - rcut n rgm stazonaro rson. ottobr 7. Sr paralllo parttor. S.. alcolar la
ELETTROTECNICA Ingegneria Industriale
 LTTOTCNCA nggnra ndutral MTOD D ANALS TASFOMATO DAL MUTU NDUTTANZ Stfano Pator Dpartmnto d nggnra Archtttura Coro d lttrotcnca (04N) a.a. 0-4 Torma d Thnn Condramo un bpolo L collgato al rto dl crcuto
LTTOTCNCA nggnra ndutral MTOD D ANALS TASFOMATO DAL MUTU NDUTTANZ Stfano Pator Dpartmnto d nggnra Archtttura Coro d lttrotcnca (04N) a.a. 0-4 Torma d Thnn Condramo un bpolo L collgato al rto dl crcuto
Indice delle esercitazioni (Ing. Rossato)
 ndc dll srctazon (ng. ossato) Esrctazon numro Potnza 8 Marzo 999 Connzon Carattrstch Esrctazon numro Gnrator ral 5 Marzo 999 l dodo Parttor d tnson d corrnt Esrctazon numro Shft d gnrator Torma d Mllman
ndc dll srctazon (ng. ossato) Esrctazon numro Potnza 8 Marzo 999 Connzon Carattrstch Esrctazon numro Gnrator ral 5 Marzo 999 l dodo Parttor d tnson d corrnt Esrctazon numro Shft d gnrator Torma d Mllman
Indice delle lezioni (Prof. Storti-Gajani)
 Indc dll lzon (Prof. Stort-Gajan) Lzon numro cham d Elttromagntsmo Marzo 999 Lzon numro Approssmazon a paramtr Marzo 999 concntrat Lgg d Krchhoff d Ohm Bpol lttrc Collgamnt n sr n paralllo Lzon numro Potnza
Indc dll lzon (Prof. Stort-Gajan) Lzon numro cham d Elttromagntsmo Marzo 999 Lzon numro Approssmazon a paramtr Marzo 999 concntrat Lgg d Krchhoff d Ohm Bpol lttrc Collgamnt n sr n paralllo Lzon numro Potnza
Lezione 7. Numeri primi. Teorema Fondamentale dell'aritmetica.
 Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorema Fondamentale dell'artmetca Defnzone 7 Un nmero ntero p dverso da 0 e s dce prmo se per ogn a b Z Altrment p s dce composto p ab p a oppre
Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorema Fondamentale dell'artmetca Defnzone 7 Un nmero ntero p dverso da 0 e s dce prmo se per ogn a b Z Altrment p s dce composto p ab p a oppre
Apprendimento per Perceptron: esempio. Apprendimento di Reti di Perceptron. Discesa di Gradiente. gradiente
 / 3 ; J DA E F DA DA I DA $ N 45 2 dov "#$ &'#$, 9? K 9 O L M M K 9L 7 9 AC AC Sstm d Elaborazon dll Informazon 9 Sstm d Elaborazon dll Informazon Apprndmnto pr Prcptron smpo Apprndmnto d Rt d Prcptron
/ 3 ; J DA E F DA DA I DA $ N 45 2 dov "#$ &'#$, 9? K 9 O L M M K 9L 7 9 AC AC Sstm d Elaborazon dll Informazon 9 Sstm d Elaborazon dll Informazon Apprndmnto pr Prcptron smpo Apprndmnto d Rt d Prcptron
Lezione 14 I PRINCIPI DELLA MECCANICA DEI FLUIDI
 Appnt de cors d Idralca 1 e Idrodnamca 1 Lezone 14 I PRINCIPI DELLA ECCANICA DEI FLUIDI Il moto de fld è controllato da alcn prncp fondamental della fsca. Ennceremo nel segto: - l prncpo d conservazone
Appnt de cors d Idralca 1 e Idrodnamca 1 Lezone 14 I PRINCIPI DELLA ECCANICA DEI FLUIDI Il moto de fld è controllato da alcn prncp fondamental della fsca. Ennceremo nel segto: - l prncpo d conservazone
Autoinduzione. 4 L: coefficiente di autoinduzione o. 4 r. Un circuito percorso da corrente genera un B (legge di Ampere-Laplace):
 S ds u r Autonduzon Un crcuto prcorso da corrnt gnra un B (lgg d Ampr-aplac): ds ur B 4 r Produc un flusso attravrso l crcuto stsso (così com attravrso una ualunu S ch abba com contorno) nds r 4 : coffcnt
S ds u r Autonduzon Un crcuto prcorso da corrnt gnra un B (lgg d Ampr-aplac): ds ur B 4 r Produc un flusso attravrso l crcuto stsso (così com attravrso una ualunu S ch abba com contorno) nds r 4 : coffcnt
Page 1. Corso di ELETTRONICA INDUSTRIALE. Trasformatori ad alta frequenza. frequenza. frequenza. ad alta frequenza. ad alta.
 Corso EETTROCA DUTRAE Trasformator a alta frqnza Trasformator a alta frqnza Motvazon pr l so trasformator a AF Rcham sl trasformator al Rlazon tra l tnson Rlazon tra l corrnt Trasformator a pú avvolgmnt
Corso EETTROCA DUTRAE Trasformator a alta frqnza Trasformator a alta frqnza Motvazon pr l so trasformator a AF Rcham sl trasformator al Rlazon tra l tnson Rlazon tra l corrnt Trasformator a pú avvolgmnt
LEZIONE N 11 IL CEMENTO ARMATO PRECOMPRESSO
 Unvrstà dgl Stud d Roma Tr Facoltà d Inggnra Corso d Tcnca dll dll Costruon I Modulo / 007-0808 LEZIOE 11 IL CEMETO RMTO PRECOMPRESSO IL CO RISULTTE IL SISTEM EQUILETE LL PRECOMPRESSIOE Gnraltà Il sstma
Unvrstà dgl Stud d Roma Tr Facoltà d Inggnra Corso d Tcnca dll dll Costruon I Modulo / 007-0808 LEZIOE 11 IL CEMETO RMTO PRECOMPRESSO IL CO RISULTTE IL SISTEM EQUILETE LL PRECOMPRESSIOE Gnraltà Il sstma
Il Metodo degli Elementi Finiti
 Il Mtodo dgl Elmnt Fnt Il Mtodo dgl Elmnt Fnt Dall dspns dl prof. Daro Amodo dall lzon dl prof. Govann Santucc L.Corts Progttazon Mccanca agl Elmnt Fnt (a.a. 20-202) Il Mtodo dgl Elmnt Fnt Introduzon In
Il Mtodo dgl Elmnt Fnt Il Mtodo dgl Elmnt Fnt Dall dspns dl prof. Daro Amodo dall lzon dl prof. Govann Santucc L.Corts Progttazon Mccanca agl Elmnt Fnt (a.a. 20-202) Il Mtodo dgl Elmnt Fnt Introduzon In
RIFLETTOMETRIA NEL DOMINIO DEL TEMPO (TDR)
 RFLETTOMETRA NEL DOMNO DEL TEMPO (TDR) Scopo dll srctaon La rflttomtra nl domno dl tmpo è una tcnca frquntmnt utlata, mpgando prncp dll co, pr carattrar ln d comuncaon, localar guast sa nll ln d trasmsson
RFLETTOMETRA NEL DOMNO DEL TEMPO (TDR) Scopo dll srctaon La rflttomtra nl domno dl tmpo è una tcnca frquntmnt utlata, mpgando prncp dll co, pr carattrar ln d comuncaon, localar guast sa nll ln d trasmsson
Calori specifici (isolanti)
 Calor spcfc (solant) Modllo d Enstn pr l calor spcfco dgl solant Modllo Prndamo com modllo un nsm d (molt) oscllator armonc undmnsonal trattamo qusto modllo quantstcamnt. lvll nrgtc d ogn componnt sono
Calor spcfc (solant) Modllo d Enstn pr l calor spcfco dgl solant Modllo Prndamo com modllo un nsm d (molt) oscllator armonc undmnsonal trattamo qusto modllo quantstcamnt. lvll nrgtc d ogn componnt sono
Corso di ELETTRONICA INDUSTRIALE
 Corso ELETTOICA IDUSTIALE Trasformator a alta frqnza Trasformator a alta frqnza Motvazon pr l so trasformator a AF cham sl trasformator al lazon tra l tnson lazon tra l corrnt Trasformator a pú avvolgmnt
Corso ELETTOICA IDUSTIALE Trasformator a alta frqnza Trasformator a alta frqnza Motvazon pr l so trasformator a AF cham sl trasformator al lazon tra l tnson lazon tra l corrnt Trasformator a pú avvolgmnt
Problemi piani: L elemento triangolare a 3 nodi
 Prol pn: L lnto trngolr 3 nod Elnt dnsonl: stto d tnson pn In olt s, pr ssndo l oggtto d stdr n soldo ontno, l shtzzzon dl oportnto strttrl pò ssr ftt on n odllo ontno dnsonl, on n sffnt grdo d pprosszon.
Prol pn: L lnto trngolr 3 nod Elnt dnsonl: stto d tnson pn In olt s, pr ssndo l oggtto d stdr n soldo ontno, l shtzzzon dl oportnto strttrl pò ssr ftt on n odllo ontno dnsonl, on n sffnt grdo d pprosszon.
Modelli equivalenti del BJT
 Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
I sistemi aperti e i volumi di controllo
 I sisti aprti i voli di controllo 1 Sisti c volvono in rgi stazionario Si dfinisc rgi stazionario ql odo di volvr di n sista pr ci si vrificano i sgnti coportanti: nssna proprità all intrno dl sista varia
I sisti aprti i voli di controllo 1 Sisti c volvono in rgi stazionario Si dfinisc rgi stazionario ql odo di volvr di n sista pr ci si vrificano i sgnti coportanti: nssna proprità all intrno dl sista varia
VALUTAZIONI DI ERRORE
 CORSO DI PROGETTAZIONE ASSISTITA DELLE STRUTTURE MECCANICHE PARTE IIIA VALUTAZIONI DI ERRORE VALUTAZIONE DELL ERRORE Il mtodo EF fornsc soluzon approssmat. S l f.n d forma rspttano dtrmnat condzon, l mtodo
CORSO DI PROGETTAZIONE ASSISTITA DELLE STRUTTURE MECCANICHE PARTE IIIA VALUTAZIONI DI ERRORE VALUTAZIONE DELL ERRORE Il mtodo EF fornsc soluzon approssmat. S l f.n d forma rspttano dtrmnat condzon, l mtodo
Appendice 1. Approfondimento dei metodi statistici
 Appndc 1 Approfondmnto d mtod statstc APPROFONDIMENTO DEI METODI STATISTICI TASSO STANDARDIZZATO PER ETÀ DI MORTALITÀ (TSDM) E DI OSPEDALIZZAZIONE (TSDH). Il Tasso Standardzzato (TSD) è calcolato com
Appndc 1 Approfondmnto d mtod statstc APPROFONDIMENTO DEI METODI STATISTICI TASSO STANDARDIZZATO PER ETÀ DI MORTALITÀ (TSDM) E DI OSPEDALIZZAZIONE (TSDH). Il Tasso Standardzzato (TSD) è calcolato com
teoria dell Orbitale Molecolare - Molecular Orbital (MO)
 toa dll Obtal olcola - olcula Obtal (O) L ng l funzon d onda dgl stat stazona d un sstma quantstco sono dat dall soluzon dlla quazon d Schodng: P un sstma molcola, composto da nucl d ltton la Ψ è funzon
toa dll Obtal olcola - olcula Obtal (O) L ng l funzon d onda dgl stat stazona d un sstma quantstco sono dat dall soluzon dlla quazon d Schodng: P un sstma molcola, composto da nucl d ltton la Ψ è funzon
17. Le soluzioni dell equazione di Schrödinger approfondimento
 7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
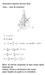 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
STUDIO DELL AMPLIFICAZIONE MEDIANTE I PARAMETRI IBRIDI h PARTE PRIMA: TEORIA
 N.d.C. - Amplfcazon STUDO DELL AMPLFCAZONE MEDANTE PAAMET BD PATE PMA: TEOA Prrqst: Conoscnza dl lmnt dll'lttrotcnca dll'lttronca d as. Ott: Essr n rado d accostars alla tora d qadrpol, con l ntrodzon
N.d.C. - Amplfcazon STUDO DELL AMPLFCAZONE MEDANTE PAAMET BD PATE PMA: TEOA Prrqst: Conoscnza dl lmnt dll'lttrotcnca dll'lttronca d as. Ott: Essr n rado d accostars alla tora d qadrpol, con l ntrodzon
Norma UNI EN ISO 13788
 UNI EN ISO 13788 (2003: PRESTAZIONE IGROTERMICA DEI COMPONENTI E DEGLI ELEMENTI PER EDILIZIA TEMPERATURA SUPERFICIALE INTERNA PER EVITARE L'UMIDITA' SUPERFICIALE CRITICA E CONDENSAZIONE INTERSTIZIALE METODO
UNI EN ISO 13788 (2003: PRESTAZIONE IGROTERMICA DEI COMPONENTI E DEGLI ELEMENTI PER EDILIZIA TEMPERATURA SUPERFICIALE INTERNA PER EVITARE L'UMIDITA' SUPERFICIALE CRITICA E CONDENSAZIONE INTERSTIZIALE METODO
RELAZIONI TRA ROTAZIONI E MOMENTI DI ESTREMITA PER LE ASTE A SEZIONE COSTANTE
 FACOLTÀ DI STUDI INGEGNERIA E ARCHITETTURA A. A. 2017-2018 - Corso d Laura agstra n Archtttura TECNICA DELLE COSTRUZIONI (9 CFU) DOCENTE: ING. GIUSEPPE ACALUSO RELAZIONI TRA ROTAZIONI E OENTI DI ESTREITA
FACOLTÀ DI STUDI INGEGNERIA E ARCHITETTURA A. A. 2017-2018 - Corso d Laura agstra n Archtttura TECNICA DELLE COSTRUZIONI (9 CFU) DOCENTE: ING. GIUSEPPE ACALUSO RELAZIONI TRA ROTAZIONI E OENTI DI ESTREITA
Facoltà di Ingegneria Corso di Problemi Strutturali dei Monumenti e dell edilizia Storica Esercizio svolto da Fabrizio Cortesini
 Faoltà d Inggnra orso d Problm Struttural d Monumnt dll dlza Stora Esrzo svolto da Fabrzo ortsn Ex. Aro alolo dl pù polo moltplator d ollasso d un aro soggtto a forz vrtal ostant d a forz orzzontal rsnt
Faoltà d Inggnra orso d Problm Struttural d Monumnt dll dlza Stora Esrzo svolto da Fabrzo ortsn Ex. Aro alolo dl pù polo moltplator d ollasso d un aro soggtto a forz vrtal ostant d a forz orzzontal rsnt
G(r,r ) è la funzione diadica di Green. L equazione differenziale soddisfatta da G(r,r ) è simile a quella soddisfatta dal campo elettrico Er ( ).
 1 La funion diadica di Grn prmtt di sprimr il campo lttrico in funion dll su sorgnti. Poiché sia il campo lttrico Er ( ) sia la sorgnt lttrica Jr ( ) sono quantità vttoriali, la funion di Grn risulta ssr
1 La funion diadica di Grn prmtt di sprimr il campo lttrico in funion dll su sorgnti. Poiché sia il campo lttrico Er ( ) sia la sorgnt lttrica Jr ( ) sono quantità vttoriali, la funion di Grn risulta ssr
Biennio CLEM - Prof. B. Quintieri. Anno Accademico 2012-2013, I Semestre. (Tratto da: Feenstra-Taylor: International Economics)
 CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE
 STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE Ni paragrafi prcdnti abbiamo dtrminato, pr l vari quazioni diffrnziali saminat, l soluzioni di quilibrio dl modllo. In qusto paragrafo,
STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE Ni paragrafi prcdnti abbiamo dtrminato, pr l vari quazioni diffrnziali saminat, l soluzioni di quilibrio dl modllo. In qusto paragrafo,
CEMENTO ARMATO PRECOMPRESSO Lezione 5
 Unvrstà dgl Stud d Roma Tr - Facoltà d Inggnra Laura magstral n Inggnra Cvl n roton Corso d Comlmnt d Tcnca dll Costruon / 28-9 9 CEETO RTO RECORESSO Lon 5 L DISOSIZIOE DEI CVI l cavo rsultant Il traccato
Unvrstà dgl Stud d Roma Tr - Facoltà d Inggnra Laura magstral n Inggnra Cvl n roton Corso d Comlmnt d Tcnca dll Costruon / 28-9 9 CEETO RTO RECORESSO Lon 5 L DISOSIZIOE DEI CVI l cavo rsultant Il traccato
Effetti di carico. Ai fini dei problemi di effetto di carico, i casi 3) e 4) sono equivalenti tra loro
 ppunt d Msur Elttrch Efftt d carco Introduzon... oltmtro ampromtro... Studo dgl fftt d carco pr una msura d tnson...2 Caso partcolar: msura d tnson con mpdnza ntrna dl crcuto rsstva 5 INTODUZIONE oglamo
ppunt d Msur Elttrch Efftt d carco Introduzon... oltmtro ampromtro... Studo dgl fftt d carco pr una msura d tnson...2 Caso partcolar: msura d tnson con mpdnza ntrna dl crcuto rsstva 5 INTODUZIONE oglamo
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
 Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Definizione della lossodromia Figura 6.1
 MRIO UTGGIO CPITOO NIGZIONE OSSODROMI E ORTODROMIC.0 a navgazon utlzza dffrnt trmn pr dscrvr dvrs mtod matmatc pr dfnr la drzon la dstanza tra du dffrnt punt sulla suprfc dlla trra. S possono dfnr l sgunt
MRIO UTGGIO CPITOO NIGZIONE OSSODROMI E ORTODROMIC.0 a navgazon utlzza dffrnt trmn pr dscrvr dvrs mtod matmatc pr dfnr la drzon la dstanza tra du dffrnt punt sulla suprfc dlla trra. S possono dfnr l sgunt
Lezione 3 Cenni di meccanica statistica classica e quantistica
 Lzon Cnn d mccanca statstca classca quantstca Fsca dllo Stato Soldo http://www.d.unf.t/fsca/bruzz/fss.html Elttronca a.a. 7-8 Sommaro. Partcll dstngubl ndstngubl. Idnttà ndstngubltà. Frmon - Il prncpo
Lzon Cnn d mccanca statstca classca quantstca Fsca dllo Stato Soldo http://www.d.unf.t/fsca/bruzz/fss.html Elttronca a.a. 7-8 Sommaro. Partcll dstngubl ndstngubl. Idnttà ndstngubltà. Frmon - Il prncpo
Compito di Fisica Generale I (Mod. A) Corsi di studio in Fisica ed Astronomia 4 aprile 2011
 Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Definizione e proprietà dei numeri complessi
 umr complss Dfo proprtà d umr complss Rapprstao gomtrca d umr complss Espoal d u umro complsso Cougao d u umro complsso Radc -sm dll utà Dfo proprtà d umr complss U umro complsso é ua coppa ordata d umr
umr complss Dfo proprtà d umr complss Rapprstao gomtrca d umr complss Espoal d u umro complsso Cougao d u umro complsso Radc -sm dll utà Dfo proprtà d umr complss U umro complsso é ua coppa ordata d umr
CAMPO LONTANO GENERATO DA UNA APERTURA
 Potnzal Vtto Magntco P l campo d sognt magntch (aptu) occo utlzza l dual dl potnzal vtto A (utlzzato p l cont lttch) ch vn ndcato con vn dtto potnzal vtto magntco o d tzgald. all quazon d Maxwll s ha,
Potnzal Vtto Magntco P l campo d sognt magntch (aptu) occo utlzza l dual dl potnzal vtto A (utlzzato p l cont lttch) ch vn ndcato con vn dtto potnzal vtto magntco o d tzgald. all quazon d Maxwll s ha,
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
i 12 i 3 v 7(25,$'(,&,5&8,7, '(),1,=,21,(/(**,',.,5&++2))
 7(5,$'(,&,5&8,7, '(),,,,(/(**,',.,5&)) Un FLUFXLWRHOHWWULFR è un tubo d flusso dl ttor dnstà d corrnt total (- t - '/ t); tal ttor è solnodal n tutto lo spazo (lgg dlla crcutazon magntca: - t ) qund è
7(5,$'(,&,5&8,7, '(),,,,(/(**,',.,5&)) Un FLUFXLWRHOHWWULFR è un tubo d flusso dl ttor dnstà d corrnt total (- t - '/ t); tal ttor è solnodal n tutto lo spazo (lgg dlla crcutazon magntca: - t ) qund è
Scattering in Meccanica Quantistica
 Scattrng n Mccanca Quantstca Sommaro Trattazon ndpndnt da tmpo do scattrng Svuppo n ond parza Torma ottco Rgoa d oro scattrng Esmpo: potnza d Yukawa Scattrng astco d anastco Fabrzo Banch Formu Ut x x =
Scattrng n Mccanca Quantstca Sommaro Trattazon ndpndnt da tmpo do scattrng Svuppo n ond parza Torma ottco Rgoa d oro scattrng Esmpo: potnza d Yukawa Scattrng astco d anastco Fabrzo Banch Formu Ut x x =
Tecniche per la ricerca delle primitive delle funzioni continue
 Capitolo 4 Tcnich pr la ricrca dll primitiv dll funzioni continu Nl paragrafo.7 abbiamo dato la dfinizion di primitiva di una funzion f avnt pr dominio un intrvallo I; abbiamo visto ch s F 0 è una primitiva
Capitolo 4 Tcnich pr la ricrca dll primitiv dll funzioni continu Nl paragrafo.7 abbiamo dato la dfinizion di primitiva di una funzion f avnt pr dominio un intrvallo I; abbiamo visto ch s F 0 è una primitiva
Processi di separazione
 6. Procss d sparazon 6.. Carattrstch d procss d sparazon La sparazon d soluzon mscl n loro sngol componnt costtusc un oprazon d grand mportanza pr l ndustra chmca, ptrolchmca ptrolfra. Quas tutt procss
6. Procss d sparazon 6.. Carattrstch d procss d sparazon La sparazon d soluzon mscl n loro sngol componnt costtusc un oprazon d grand mportanza pr l ndustra chmca, ptrolchmca ptrolfra. Quas tutt procss
Esercitazione 2. Francesca Apollonio Dipartimento Ingegneria Elettronica
 srcitaion Francsca pollonio Dipartimnto Inggnria lttronica -mail: () t cos( ω t ϕ) ampia pulsaion Vttori complssi Data una granda scalar (t) variabil cosinusoidalmnt nl tmpo fas i può sprimr (t) com sgu:
srcitaion Francsca pollonio Dipartimnto Inggnria lttronica -mail: () t cos( ω t ϕ) ampia pulsaion Vttori complssi Data una granda scalar (t) variabil cosinusoidalmnt nl tmpo fas i può sprimr (t) com sgu:
SOLUZIONE PROBLEMA 1 SOLUZIONE PROBLEMA 1 1
 SOLUZIONE PROBLEMA 1 1 SOLUZIONE PROBLEMA 1 1. Studiamo la funzion q ( = at, ssndo a b costanti rali con a >. Il dominio dlla funzion è tutto R la funzion è ovunqu continua. Il grafico dlla funzion non
SOLUZIONE PROBLEMA 1 1 SOLUZIONE PROBLEMA 1 1. Studiamo la funzion q ( = at, ssndo a b costanti rali con a >. Il dominio dlla funzion è tutto R la funzion è ovunqu continua. Il grafico dlla funzion non
Materiali ed Approcci Innovativi per il Progetto in Zona Sismica e la Mitigazione della Vulnerabilità delle Strutture
 Matral d Approcc Innovatv pr l Progtto n Zona Ssmca la Mtgazon dlla Vulnrabltà dll Struttur Salrno, 12 13 fbbrao 2006 Una pù smplc procdura pr la valutazon dlla rsposta ssmca dll struttur attravrso anals
Matral d Approcc Innovatv pr l Progtto n Zona Ssmca la Mtgazon dlla Vulnrabltà dll Struttur Salrno, 12 13 fbbrao 2006 Una pù smplc procdura pr la valutazon dlla rsposta ssmca dll struttur attravrso anals
Q & Tracce svolte di esercizi sulla Trasmissione del Calore Prof. Mistretta a.a. 2009/2010
 racc olt d rcz ulla raon dl alor Prof. trtta a.a. 009/00 Erczo n. S condr una part d atton alta 4 larga 6 pa 0 la cu ucbltà trca è λ λ 0 8 [/( )]. In un crto gorno alor urat dll tpratur dlla uprfc ntrna
racc olt d rcz ulla raon dl alor Prof. trtta a.a. 009/00 Erczo n. S condr una part d atton alta 4 larga 6 pa 0 la cu ucbltà trca è λ λ 0 8 [/( )]. In un crto gorno alor urat dll tpratur dlla uprfc ntrna
Ulteriori esercizi svolti
 Ultriori srcizi svolti Effttuar uno studio qualitativo dll sgunti funzioni ) 4 f ( ) ) ( + ) f ( ) + 3) f ( ) con particolar rifrimnto ai sgunti asptti: a) trova il dominio di f b) indica quali sono gli
Ultriori srcizi svolti Effttuar uno studio qualitativo dll sgunti funzioni ) 4 f ( ) ) ( + ) f ( ) + 3) f ( ) con particolar rifrimnto ai sgunti asptti: a) trova il dominio di f b) indica quali sono gli
La carta di Smith. Origine
 a carta d Smth uca nctt a.a. 08-09 Orgn Fu ntrodotta da P. Smth d Bll abs nl 1939 Error rtnrla suprata da mtod numrc Molt strumnt d msura CAD prsntano dat n output su carta d Smth Molt problm sull ln d
a carta d Smth uca nctt a.a. 08-09 Orgn Fu ntrodotta da P. Smth d Bll abs nl 1939 Error rtnrla suprata da mtod numrc Molt strumnt d msura CAD prsntano dat n output su carta d Smth Molt problm sull ln d
Capgemini Italia Spa. Ingegneria del Software. Roma, 11 Dicembre 2009
 Capgmn Ita Spa Inggnra dl Softwar Roma, 11 Dcmbr 2009 Soc Ntwork Gorfrnzato su Mobl Fzon Rzzar soc ntwork (tpo facbook o lnkn) n cu è possbl aggornar nl propro proflo propra poszon attu (tt longt) rndr
Capgmn Ita Spa Inggnra dl Softwar Roma, 11 Dcmbr 2009 Soc Ntwork Gorfrnzato su Mobl Fzon Rzzar soc ntwork (tpo facbook o lnkn) n cu è possbl aggornar nl propro proflo propra poszon attu (tt longt) rndr
METODO DEGLI ELEMENTI FINITI
 Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
INDICI DI POSIZIONE O DI TENDENZA CENTRALE
 IDICI DI POSIZIOE O DI TEDEZA CETRALE Gl ndc d poszon, o d tndnza cntral, sono numr ch sprmono la snts numrca d una dstrbuzon statstca (d ora n avant ndcata dal smbolo ) d una varabl X. I valor ossrvat
IDICI DI POSIZIOE O DI TEDEZA CETRALE Gl ndc d poszon, o d tndnza cntral, sono numr ch sprmono la snts numrca d una dstrbuzon statstca (d ora n avant ndcata dal smbolo ) d una varabl X. I valor ossrvat
Trasformatore. Parte 2 Trasformatori trifase www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 16-11-2012) Trasformatore trifase (1)
 Trasformator Part Trasformator trfas www.d.ng.unbo.t/prs/mastr/ddattca.htm (vrson dl 1-11-01) Trasformator trfas Pr trasfrr nrga lttrca tra du rt trfas s possono utlzzar tr trasformator monofas, ugual
Trasformator Part Trasformator trfas www.d.ng.unbo.t/prs/mastr/ddattca.htm (vrson dl 1-11-01) Trasformator trfas Pr trasfrr nrga lttrca tra du rt trfas s possono utlzzar tr trasformator monofas, ugual
Enrico Borghi LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN SISTEMA DI PARTICELLE
 Enrco Borgh LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN SISTEMA DI PARTICELLE La mccanca nwtonana sstm costtut a pú partcll puntform può ssr svluppata partno alla lgg fonamntal rfrta a una
Enrco Borgh LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN SISTEMA DI PARTICELLE La mccanca nwtonana sstm costtut a pú partcll puntform può ssr svluppata partno alla lgg fonamntal rfrta a una
ANALISI MATEMATICA PROVA SCRITTA. Libri, appunti e calcolatrici non ammessi
 Nom, Cognom... Matricola... ANALISI MATMATICA PROA SCRITTA CORSO DI LAURA IN INGGNRIA MCCANICA A.A. 7/8 Libri, appunti calcolatrici non ammssi Prima part - Lo studnt scriva solo la risposta, dirttamnt
Nom, Cognom... Matricola... ANALISI MATMATICA PROA SCRITTA CORSO DI LAURA IN INGGNRIA MCCANICA A.A. 7/8 Libri, appunti calcolatrici non ammssi Prima part - Lo studnt scriva solo la risposta, dirttamnt
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
ELEMENTI DI ELABORAZIONE DEI SEGNALI PER TELELOCALIZZAZIONE
 ELEMENTI DI ELABOAZIONE DEI SEGNALI PE TELELOCALIZZAZIONE nota pr l corso d Elaborazon d Sgnal pr Tlcomuncazon a cura d F. Bndtto G. Gunta. Introduzon al problma dlla dcson I componnt d bas d un problma
ELEMENTI DI ELABOAZIONE DEI SEGNALI PE TELELOCALIZZAZIONE nota pr l corso d Elaborazon d Sgnal pr Tlcomuncazon a cura d F. Bndtto G. Gunta. Introduzon al problma dlla dcson I componnt d bas d un problma
Istogrammi ad intervalli
 Istogrammi ad intrvalli Abbiamo visto com costruir un istogramma pr rapprsntar un insim di misur dlla stssa granda isica. S la snsibilità dllo strumnto di misura è alta, è probabil ch tra gli N valori
Istogrammi ad intrvalli Abbiamo visto com costruir un istogramma pr rapprsntar un insim di misur dlla stssa granda isica. S la snsibilità dllo strumnto di misura è alta, è probabil ch tra gli N valori
Teorema (seconda condizione sufficiente per i campi conservativi piani): Sia F ( x, y)
 Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
dove A è una costante caratteristica dello specifico metallo e k è la costante di Boltzmann.
 ) Il riscaldamnto dl filo comporta la cssion di nrgia al rticolo cristallino quindi agli lttroni dgli orbitali più strni; s l nrgia acquisita dagli lttroni risulta suprior all nrgia di lgam (Vi, do Vi
) Il riscaldamnto dl filo comporta la cssion di nrgia al rticolo cristallino quindi agli lttroni dgli orbitali più strni; s l nrgia acquisita dagli lttroni risulta suprior all nrgia di lgam (Vi, do Vi
FUNZIONI. Dominio: il dominio di una funzione è l insieme delle x in cui una funzione è definita.
 FUNZIONI Dominio: il dominio di una funzion è l insim dll in cui una funzion è dfinita. Funzioni Fratt: una funzion si dic fratta quando compar la al dnominator Pr calcolar il dominio di una funzion fratta
FUNZIONI Dominio: il dominio di una funzion è l insim dll in cui una funzion è dfinita. Funzioni Fratt: una funzion si dic fratta quando compar la al dnominator Pr calcolar il dominio di una funzion fratta
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI. (1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni:
 PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
Geotecnica e Laboratorio. Teoria della consolidazione monodimensionale
 Corso di Lara a ciclo Unico in Inggnria Edil-Architttra Gotcnica Laboratorio Toria dlla consolidaion monodimnsional Prof. Ing. Marco Favartti -mail: marco.favartti@nipd.it wbsit: www.marcofavartti.nt 1
Corso di Lara a ciclo Unico in Inggnria Edil-Architttra Gotcnica Laboratorio Toria dlla consolidaion monodimnsional Prof. Ing. Marco Favartti -mail: marco.favartti@nipd.it wbsit: www.marcofavartti.nt 1
Fisica Generale VI Scheda n. 1 esercizi di riepilogo dei contenuti di base necessari. 1.) Dimostrare le seguenti identità vettoriali:
 Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
θ 2 i r 2 r La multifunzione f (z) = z z i
 1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
Corpi rigidi (prima parte)
 Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
3 - Trasformata di Fourier discreta Discrete Fourier Transform ( DFT)
 3 - rasormata d orr dscrta Dscrt orr rasorm D - Dscrtzzazo dlla sr d orr - Dzo rortà dlla D - D d sgal traslat - U smo d D - ormla d vrso dlla D - Egaglaza d Parsval - D ral 3 - Dscrtzzazo dlla sr d orr
3 - rasormata d orr dscrta Dscrt orr rasorm D - Dscrtzzazo dlla sr d orr - Dzo rortà dlla D - D d sgal traslat - U smo d D - ormla d vrso dlla D - Egaglaza d Parsval - D ral 3 - Dscrtzzazo dlla sr d orr
Esercitazione 2: Risoluzione
 #a Tenson ltostatche vertcal e orontal Pnto d calcolo [m] O 0 [kn/m 3 ] K 0 v v' h' h 0 0 0 0 0 W 6 0.71 0 108.0 108.0 77.0 77.0 18.0 88.0 108.0 A 8 20 144.0 124.0 75.6 95.6 P1 15 Presson nterstal: Tenson
#a Tenson ltostatche vertcal e orontal Pnto d calcolo [m] O 0 [kn/m 3 ] K 0 v v' h' h 0 0 0 0 0 W 6 0.71 0 108.0 108.0 77.0 77.0 18.0 88.0 108.0 A 8 20 144.0 124.0 75.6 95.6 P1 15 Presson nterstal: Tenson
8. Circuiti non lineari
 8. Crc non lnar odo dal. odo ral. nal d crc con dod mdan l modllo dal. Modllo dl dodo con cada d non. Modo rafco. nal d n crco lmaor d non mdan modo rafco. odo dodo dal = = < Cararca rafca Un dodo dal
8. Crc non lnar odo dal. odo ral. nal d crc con dod mdan l modllo dal. Modllo dl dodo con cada d non. Modo rafco. nal d n crco lmaor d non mdan modo rafco. odo dodo dal = = < Cararca rafca Un dodo dal
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
 Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Definiamo Centro di Massa (CM) del sistema il punto individuato dalla coordinata: a) d
 Cntro d assa d un ssta Assuao un corpo coplsso qualsas costtuto da n punt lntar cascuno d assa lo charo ssta d punt atral. Partao da un ssta atto da du ass d. Consdrao co ass dl ssta d rrnto, la rtta passant
Cntro d assa d un ssta Assuao un corpo coplsso qualsas costtuto da n punt lntar cascuno d assa lo charo ssta d punt atral. Partao da un ssta atto da du ass d. Consdrao co ass dl ssta d rrnto, la rtta passant
lim β α e detto infinitesimo una qualsiasi quantita tendente a zero quando una dati due infinitesimi α e β non esiste
 Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
Dinamica del corpo rigido
 Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico Comunicazione Opzione Sportiva Tema di matematica
 wwwmatmaticamntit Nicola D Rosa maturità Esam di stato di istruzion scondaria suprior Indirizzi: Scintifico Comunicazion Opzion Sportiva Tma di matmatica Il candidato risolva uno di du problmi risponda
wwwmatmaticamntit Nicola D Rosa maturità Esam di stato di istruzion scondaria suprior Indirizzi: Scintifico Comunicazion Opzion Sportiva Tma di matmatica Il candidato risolva uno di du problmi risponda
POTENZE NECESSARIE E DISPONIBILI
 POTENZE NECESSARIE E DISPONIBILI In qusto capitolo ci proponiamo di dtrminar l curv dll potnz ncssari pr l vari condizioni di volo. Tali curv dipndranno da divrsi fattori com il pso dl vlivolo, la quota,
POTENZE NECESSARIE E DISPONIBILI In qusto capitolo ci proponiamo di dtrminar l curv dll potnz ncssari pr l vari condizioni di volo. Tali curv dipndranno da divrsi fattori com il pso dl vlivolo, la quota,
Alessandro Ottola matr. 208003 lezione del 11/3/2010 ora 10:30-13:30. Parete omogenea sottoposta a differenze termiche e diffusione
 Alssandro Ottola matr. 0800 lzon dl //00 ora 0:0-:0 Indc Dagramma d Glasr... Part omogna sottoosta a dffrnz trmch dffuson... Dagramma d Glasr r art omogna... 4 Dagramma d Glasr r art multstrato... 5 Esrczo
Alssandro Ottola matr. 0800 lzon dl //00 ora 0:0-:0 Indc Dagramma d Glasr... Part omogna sottoosta a dffrnz trmch dffuson... Dagramma d Glasr r art omogna... 4 Dagramma d Glasr r art multstrato... 5 Esrczo
CINEMATICA del corpo rigido
 SEZINE CINEMAICA del corpo rgdo Le segent note sono na sntes estrema de concett alla base della dnamca de corp rgd. Lo stdente pò consderare d aer appreso realmente tal concett solo se è n grado d rsolere
SEZINE CINEMAICA del corpo rgdo Le segent note sono na sntes estrema de concett alla base della dnamca de corp rgd. Lo stdente pò consderare d aer appreso realmente tal concett solo se è n grado d rsolere
BASI TEORICHE DEL METODO DEGLI ELEMENTI FINITI (MEF)
 BASI TEORICHE DE METODO DEGI EEMETI FIITI MEF DOCETE oardo BERTII Dp. d Iggra Mccaca clar dlla Prodzo Tl. : 5-8366 E.al : loardo.brt@g.p.t Urstà d Psa 6 Urstà d Psa 6 Sst d qazo dffrzal all drat parzal
BASI TEORICHE DE METODO DEGI EEMETI FIITI MEF DOCETE oardo BERTII Dp. d Iggra Mccaca clar dlla Prodzo Tl. : 5-8366 E.al : loardo.brt@g.p.t Urstà d Psa 6 Urstà d Psa 6 Sst d qazo dffrzal all drat parzal
Svolgimento di alcuni esercizi
 Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Sistemi trifase. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 30-10-2012) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Multivibratori. Si suddividono in: Bistabili Astabili (oscillatori a rilassamento) Monostabili
 Elttronica - anzoni Multiibratori Si dfiniscono multiibratori i circuiti in grado di gnrar transizioni di alcun grandzz tnsioni o corrnti con tmpi di commutazion di durata br risptto al priodo. Pr qusta
Elttronica - anzoni Multiibratori Si dfiniscono multiibratori i circuiti in grado di gnrar transizioni di alcun grandzz tnsioni o corrnti con tmpi di commutazion di durata br risptto al priodo. Pr qusta
( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA
![( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA ( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA](/thumbs/69/60720045.jpg) 8 9 DERIVATA DI UNA FUNZIONE COMPOSTA La drivata di una funion composta ( funion di funion si ottin (dim all pagin 0 : a drivando la funion principal ( qulla ch si applica pr ultima risptto al suo argomnto
8 9 DERIVATA DI UNA FUNZIONE COMPOSTA La drivata di una funion composta ( funion di funion si ottin (dim all pagin 0 : a drivando la funion principal ( qulla ch si applica pr ultima risptto al suo argomnto
