Segnali a tempo continuo
|
|
|
- Romina Mariana Pesce
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo IV CARAERIZZAZIOE EERGEICA DEI SEGALI IV. - Denità pettrale di potenza. Segnali a tempo continuo Analogamente al cao dei egnali determinati, è utile individuare una caratterizzazione energetica di un egnale aleatorio nel dominio della requenza. A tal ine è opportuno aociare, quando poibile, al egnale aleatorio la ua denità pettrale di potenza. Sia dato un egnale aleatorio tale che quai tutte le ue manietazioni abbiano potenza peciica inita, cioè tale che l'inieme delle manietazioni di potenza non limitata cotituica un evento di probabilità nulla. È naturale aociare ad un tale proceo una denità pettrale di potenza che ia la media tatitica di quelle delle ue manietazioni. Più preciamente, ia (t,ζ) una generica manietazione di un egnale aleatorio; com è noto dall'analii dei Segnali Determinati, la denità pettrale di potenza w (,ζ) della generica manietazione (t,ζ) è data da: S (, ζ) S (, ζ) S (, ζ) (IV..) w (, ζ ) = lim = lim t dove S (, ζ) è la traormata di Fourier del egnale troncato (, t ζ ) = (, t ζ)rect (IV..) S (, ζ ) = ( t, ζ ) e dt = ( t, ζ) e dt jπt jπt e cioè: La denità pettrale di potenza W ( ) di un egnale aleatorio i ottiene eettuando la media tatitica della quantità w (,ζ) cioè i pone: (IV..3) W ( ) = E{ w (, ζ ) Applicando il teorema di Wiener per egnali a potenza inita alla generica manietazione ( t, ζ ) i ha: (IV..4) w (, ζ ) = F { γ ( t, ζ) eendo: (IV..5) γ ( t, ζ ) = lim ( t + τ, ζ) ( t, ζ) dt la unzione di autocorrelazione. enendo conto delle (IV..4) e (IV..5), la (IV..3), commutando gli operatori F { e E {, diventa: (IV..6) W( ) = E{ F{ γ( t, ζ ) = F { E{ γ( t, ζ) od anche, ricordando l epreione della unzione di autocorrelazione data dalla (IV..5): (IV..7) W ( ) = F E lim t + τ ζ t ζ dt = E { t + τ ζ t ζ dt (, ) (, ) F lim (, ) (, ) In altri termini, la denità pettrale di un egnale aleatorio i può eprimere come egue:
2 -3- G. Mamola: Fondamenti di Comunicazioni Elettriche j (IV..8) { πτ W ( ) = F φ () τ = φ () τ e dτ eendo la unzione φ() τ deinita dalla: (IV..9) φ() τ = lim E { t t dt R t dt ( + τ, ζ) (, ζ ) = lim τ (, ) La denità pettrale di potenza di un egnale aleatorio è uguale alla traormata di Fou- R (, t τ ) = E ( t + τ, ζ) (, t ζ) ( ), rier della media temporale della unzione di autocorrelazione { deinita dalla (IV..9). La (IV..8) cotituice il teorema di Wiener per egnali aleatori. el cao di egnali tazionari (almeno in eno lato), la media tatitica dipende olo da τ, per cui i ha: (IV..0) φ () τ = R () τ e pertanto: j (IV..) { Con rierimento alla (IV..9) i deduce: W ( ) = F R ( τ ) = R ( τ) e dτ (IV..) φ ( 0) = lim { (, ζ) πτ E t dt { ( +τζ, ) ( t, ζ) E t che, ricordando la proprietà 4 della raormata di Fourier, equivale alla: (IV..3) { lim E t ζ dt = W dτ (, ) ( ) La media temporale del valore quadratico medio tatitico di un egnale aleatorio i ottiene dall integrale u tutto della denità pettrale. Se il egnale è tazionario in autocorrelazione, la precedente diventa: (IV..4) ( ) m = W ( ) dτ IV. - Funzione di autocorrelazione. La unzione di autocorrelazione: (IV..) R(, t τ ) = E{ ( t + τ, ζ) (, t ζ) di un egnale aleatorio gioca un ruolo ondamentale nella caratterizzazione energetica dei egnali. Ponendo nella (IV..) τ = 0 i ottiene: (IV..) R { (, t ) E (, t ) Dalla (IV..), operando la traormazione t 0 = ζ 0 τ t dicende: (IV..3) { { { R (, t τ ) = E ( t τ, ζ) (, t ζ ) = E ( t + τ, ζ) (, t ζ ) = E ( t, ζ) ( t τ, ζ ) = R (, t τ) Dall ovvia condizione: (IV..4) E{ ( t, ) ( t, ) 0 + τ ζ +λ ζ ( ) Oervando che il valore medio tatitico di una variabile aleatoria complea Z( ζ ) = X( ζ ) + jy( ζ ) vale E { Z( ζ ) = E{ X( ζ ) + je{ Y( ζ ), i riconoce acilmente che la unzione di autocorrelazione di un egnale aleatorio compleo dipende dalla matrice di correlazione del vettore aleatorio compoto dalla parte reale e dalla parte immaginaria del egnale.
3 Cap. IV Caratterizzazione energetica dei egnali -33- valida per qualiai valore della cotante complea λ, dicende: (IV..5) R ( t +τ, 0) +λ R ( t, τ ) +λr ( t, τ ) + λ R ( t, 0) 0 Poiché la orma quadratica è emideinita poitiva, il uo determinante deve riultare non R( t +τ, 0) R( t, τ) negativo. È dunque 0 da cui: R (, t τ) R (, t 0) (IV..6) R ( t, τ) R ( t, 0) R ( t + τ, 0) el cao di egnali tazionari la (IV..) diventa: (IV..7) R { ( ) E ( t ) e la (IV..3), i empliica nella: 0 = 0 (IV..8) R( τ ) = R( τ) e cioè la R (τ) gode della immetria hermitiana. Inine la diuguaglianza (IV..6) diventa: (IV..9) R () τ R () 0 Le proprietà della unzione di autocorrelazione per egnali tempo continui ono riaunte nella ab. IV. abella IV.I Proprietà dell autocorrelazione di egnali a tempo continuo Segnali tazionari Segnali non tazionari τ = { +τ ζ ζ R (, t τ ) = E{ ( t+τ, ζ) (, t ζ ) R () E ( t, ) (, t ) = { ζ R (,) { (, ) t t = E t ζ R (0) E ( t, ) R ( τ ) = R ( τ ) R (, t τ ) = R (, t τ ) R () τ R (0) R ( t, τ) R ( t, 0) R ( t + τ, 0) Al poto dell autocorrelazione è utile, in certi cai, introdurre la unzione di autocovarianza deinita dalla: (IV..0) { { { (, ) { (, ) { (, ) σ (, t τ ) = E (, t ζ) E (, t ζ ) ( t +τζ, ) E ( t + τ, ζ ) = = R t τ E t ζ E t + τ ζ Eempio E.IV. L autocorrelazione della derivata (t,ζ) di un egnale è data dalla: R () τ = E{ () t ( t + τ ) Se il egnale è tazionario i ha: t ( + h) t ( ) t ( + τ + h) t ( + τ) R ( τ ) = E{ lim lim = h 0 h h 0 h eendo () t ( + ht )( +τ+ h) tt ()( +τ+ h) t ( + ht )( +τ ) + tt ()( +τ) { = lim E = h 0 h R () τ R ( τ h) R ( τ+ h) R () τ d R () τ = lim = h 0 h h h dτ R τ la unzione di autocorrelazione del egnale ( t, ζ ).
4 -34- G. Mamola: Fondamenti di Comunicazioni Elettriche La denità pettrale di potenza di ( t, ζ ) può eere eprea in termini della denità pettrale del egnale di potenza di ( t, ζ ) ; i ha: d R () τ W ( ) = F = 4π W ( ) dτ È da notare che tale riultato poteva eere ottenuto emplicemente oervando che la xt () d dt yt () derivata di un egnale può eere coniderata come il egnale in ucita dal itema lineare rappreentato in Fig. E., quando al uo ingreo è applicato il egnale x() t. Poiché la ripota in Fig. E.IV. requenza del itema è H( ) = jπ, ne viene W ( ) H( ) W ( ). = IV.3 - Segnali ditinti. Funzioni di correlazione e denità pettrale incrociate. Le coniderazioni volte nei precedenti paragrai poono eere acilmente etee al cao di n egnali aleatori reali e tempo continui i (t,ζ). In quel che egue è conveniente introdurre il vettore (t,ζ) (t, ζ) (IV.3.) (t,ζ) = n (t, ζ) Si deinice matrice di correlazione la matrice: { { { { R(, t τ ) = E (, t ζ ) ( t + τ, ζ ) = E ( t, ζ ) ( t +τζ, ) E ( t, ζ ) ( t +τζ, ) E ( t, ζ ) n( t +τζ, ) (IV.3.) E{ ( t, ζ ) ( t +τζ, ) E{ ( t, ζ ) ( t +τζ, ) E{ ( t, ζ ) n( t +τζ, ) = E{ n( t, ζ ) ( t +τζ, ) E{ n( t, ζ ) ( t +τζ, ) E{ n( t, ζ ) n( t +τζ, ) Ea dipende dalle variabili t e τ a meno che i egnali non iano congiuntamente tazionari. In queto cao la matrice di correlazione dipende olo da (IV.3.3) R() τ = E{ (, t ζ ) ( t +τζ, ) τ e i ha: Con rierimento alla (IV.3.) gli elementi della diagonale principale della matrice di correlazione ono le autocorrelazioni dei egnali i (t,ζ), mentre gli altri elementi rappreentano le mutue correlazioni o correlazioni incrociate. Riulta ovviamente: (IV.3.4) Rij( t, τ ) = Rji( t, τ) Se i egnali i (t,ζ) ono tazionari la precedente diventa: (IV.3.5) Rij() τ = Rji( τ) Si prenda in eame il egnale: (IV.3.6) t (, ζ ) = ( t, ζ ) + k( t+ τ, ζ) k { dove è una cotante complea. Dall ovvia condizione E (, t ζ) 0 dicende che la orma quadratica: (IV.3.7) R (, t 0) + kr (, t τ ) + k R (, t τ ) + k R ( t + τ, 0) 0 è emideinita poitiva. Ciò comporta che i deve veriicare la condizione:
5 (IV.3.8) dalla quale i deduce: (IV.3.9) Cap. IV Caratterizzazione energetica dei egnali -35- R (, t 0) R (, t τ) 0 R (, t τ ) R 0 ( t + τ, ) R (, t τ) R (, t 0) R ( t + τ, 0) Sei egnali ( t, ζ ) e ( t, ζ ) ono congiuntamente tazionari, la precedente diviene: (IV.3.0) R ( τ) R ( 0) R ( 0) In certi cai, è preeribile caratterizzare n egnali aleatori mediante la matrice di covarianza coì deinita: { (IV.3.) σ [ ] [ ] dove m () t (IV.3.) ( t, τ ) = E ( t, ζ) m ( t) ( t + τ, ζ) m ( t + τ ) = R ( t, τ) m ( t) m ( t + τ) è il vettore dei valori medi dei egnali valutato nell'itante t deinito dalla: m { (, ) { (, ζ) E t ζ E t () t = E{ n( t, ζ) Due egnali aleatori (t, ζ) e (t, ζ) i dicono ortogonali e la loro unzione di mutua correlazione è nulla, incorrelati e è nulla la loro unzione di mutua covarianza. È da notare che e i egnali ono tatiticamente indipendenti ono anche incorrelati dal momento che riulta: (IV.3.3) R (, t t + τ ) = E{ (, t ζ) E{ ( t + τ, ζ) on è vero il contrario cioè e due egnali ono incorrelati non è detto che ei iano anche tatiticamente indipendenti. IV.4 Il rumore bianco. Un egnale aleatorio ntζ (, ) tazionario la cui denità pettrale è cotante è denominato rumore bianco. Per tale egnale riulta: 0 (IV.4.) Wn ( ) = = cot Poiché manietamente il valore quadratico medio del egnale dato dall integrale Wn ( ) d non è deinito, tale egnale non è iicamente realizzabile; tuttavia riulta un modello molto utile perché parecchi diturbi, quali ad e. il rumore termico, il rumore atmoerico ed altro, preentano una denità pettrale preoché cotante almeno entro la banda di interee. La unzione di autocorrelazione del rumore bianco vale: 0 (IV.4.) Rn () τ = δ() τ Un tipo di rumore bianco a valore quadratico medio inito è quello in cui la denità pettrale i mantiene cotante olo all interno di una banda inita e nulla al di uori. A econda della dilocazione della banda nel dominio della requenza il rumore bianco i claiica in rumore di tipo paa-bao e in tumore di tipo paa-banda.
6 -36- G. Mamola: Fondamenti di Comunicazioni Elettriche IV.4. Il rumore bianco di tipo paa-bao. Si ha: 0 (IV.4.3) Wn ( ) = rect m Riulta: (IV.4.4) Rn() τ = 0 minc( m τ ) La denità pettrale e la unzione di autocorrelazione del rumore di tipo paa-bao ono riportati in Fig. IV.. IV.4. Il rumore bianco di tipo paa-banda. Si ha: (IV.4.5) La unzione di autocorrelazione vale: 0 [, ] Wn ( ) = 0 [, ] (IV.4.6) Rn ( τ ) = 0B inc( Bτ) co( π0τ) dove 0 e B denotano ripettivamente la requenza centrale e l ampiezza di banda del egnale aleatorio dati dalle: (IV.4.7) ( ) W( ) n 0 = + B = 0 La denità pettrale e la unzione di autocorrelazione del rumore di tipo paa-bao ono riportati in Fig. IV.. a) W ( ) n 0 a) m Rn () τ 0 m m b) 0 Rn () τ B 0 0 B b) τ τ Fig. IV. - Denità ed autocorrelazione di un rumore di tipo paabao. Fig. IV. - Denità ed autocorrelazione di un rumore di tipo paabanda.
7 Cap. IV Caratterizzazione energetica dei egnali -37- Segnali a tempo dicreto IV.5 - Denità pettrale di potenza. La denità pettrale di potenza W ( ) per i egnali a tempo dicreto è deinita, analogamente a quanto vito per i egnali a tempo continuo, come la media tatitica delle denità pettrali di potenza delle manietazioni. Se n (, ζ ) denota la generica manietazione di un egnale aleatorio, la denità pettrale di potenza è: (IV.5.) w (, ) lim (, ) lim (, ) ζ = S ζ = S ζ S(, ζ) ( + ) ( + ) dove S (, ζ) denota la traormata di Fourier dicreta del egnale troncato (n,ζ) e cioè: (IV.5.) S (, ζ ) = ( n, ζ ) e = ( n, ζ) e jπn jπn n= n= Eettuando la media tatitica della quantità w (,ζ) i ottiene la denità pettrale di potenza del egnale aleatorio: (IV.5.3) W ( ) = E{ w (, ζ ) Applicando il teorema di Wiener per egnali a potenza inita alla generica manietazione n (, ζ ) i ha: (IV.5.4) w (, ζ ) = F { γ ( k, ζ) eendo: (IV.5.5) γ( k, ζ ) = lim ( n, ζ )( n + k, ζ) + n= la unzione di autocorrelazione. enendo conto delle (IV.5.5) e (IV.5.5), la (IV.5.3), commutando gli operatori { diventa: (IV.5.6) W( ) = E{ F{ γ( k, ζ ) = F { E{ γ( k, ζ) e cioè: (IV.5.7) W ( ) = F E lim ( n, ζ ) ( n + k, ζ ) = + n= = F lim E{ ( n, ζ) ( n + k, ζ) + n= F e E {, Analogamente al cao di egnali tempo continui, la denità pettrale di un egnale aleatorio tempo dicreto i può eprimere come egue: k = (IV.5.8) { W ( ) = F φ ( k) = φ ( k) e eendo la unzione φ() τ deinita dalla: (IV.5.9) φ ( k ) = lim E { ( n, ζ )( n + k, ζ ) = lim R ( n, n + k ) + + j πk n= n= La denità pettrale di potenza di un egnale aleatorio è uguale alla traormata di Fourier dicreta della media temporale della unzione di autocorrelazione
8 -38- G. Mamola: Fondamenti di Comunicazioni Elettriche { R ( n, k) = E ( n, ζ ) ( n + k, ζ), deinita dalla (IV..9). La (IV.5.8) cotituice il teorema di Wiener per egnali aleatori. el cao di egnali tazionari (almeno in eno lato), i ha: (IV.5.0) φ ( k ) = R ( k ) e pertanto: (IV.5.) { Ponendo nella (IV.5.9) k = 0 i deduce: W( ) = F R( k) = R( k) e k = j kπk (IV.5.) φ 0 { ( ) = lim E ( n, ζ) + n= che, ricordando la proprietà 4 della raormata di Fourier, equivale alla: (IV.5.3) { lim E ( n, ζ ) = W( ) dτ + n= La media temporale del valore quadratico medio tatitico di un egnale aleatorio i ottiene dall integrale u tutto della denità pettrale. La immetria hermitiana di cui gode l autocorrelazione, a ì che riulti φ (k) =φ ( k), la quale comporta che la denità pettrale di potenza è una unzione reale e pari del uo argomento. IV.6 - Funzione di autocorrelazione. Sia (n,ζ) un egnale aleatorio a tempo dicreto. La ua unzione di autocorrelazione è deinita dalla: (IV.6.) R( n, k) = E{ ( n, ζ ) ( n + k, ζ) la quale, in generale, dipende dagli indici n e k. Se il egnale è tazionario (almeno in eno lato) l autocorrelazione dipende olo dalla dierenza tra gli itanti di oervazione e quindi dipende da un olo indice: R ( k) = E ( n, ζ ) ( n + k, ζ) (IV.6.) { Ponendo nella (IV.6.), k = 0 i ottiene: (IV.6.3) R { ( n, ) E ( n, ) che, nel cao di egnali tazionari, i riduce alla: 0 = ζ 0 (IV.6.4) R { ( ) E ( n, ) 0 = ζ 0 Dalla (IV.6.), operando la traormazione n k n, i deduce acilmente: (IV.6.5) { { R ( n, k ) = E ( n, ζ) ( n k, ζ ) = E ( n, ζ ) ( n + k, ζ ) = R ( n, k ) che e il egnale è tazionario, diventa: (IV.6.6) R ( k) = R ( k) Pertanto l autocorrelazione di un egnale tazionario, almeno in eno lato, gode della immetria hermitiana. Le proprietà dell autocorrelazione ono riaunte nella ab. IV.4
9 Cap. IV Caratterizzazione energetica dei egnali -39- abella IV. Proprietà dell autocorrelazione di egnali a tempo dicreto Segnali tazionari Segnali non tazionari = { ζ + ζ R ( n, k) = E{ ( n, ζ ) ( n + k, ζ R ( k) E ( n, ) ( n k, = { ζ R (, ) { (, ) n n = E n ζ R (0) E ( n, ) R ( k) = R ( k) R ( n, m) = R ( m, n) R ( k) R (0) R ( m, n ) R ( m, m ) R ( n, n )
SEGNALI A TEMPO CONTINUO. Segnali a energia finita. t un segnale a energia finita e a tempo continuo. L energia specifica 2 *
 Capitolo IV CARAERIZZAZIOE EERGEICA DEI SEGALI SEGALI A EMO COIUO Segnali a energia finita IV. Densità spettrale di energia. Sia s() t un segnale a energia finita e a tempo continuo. L energia specifica
Capitolo IV CARAERIZZAZIOE EERGEICA DEI SEGALI SEGALI A EMO COIUO Segnali a energia finita IV. Densità spettrale di energia. Sia s() t un segnale a energia finita e a tempo continuo. L energia specifica
Corso di SEGNALI a.a
 Coro di SEGNALI anno accademico 008-009 Appunti u: Teorema del Campionamento Introduzione Il proceo di campionamento è di enorme importanza ai ini della realizzazione dei dipoitivi digitali per le telecomunicazioni.
Coro di SEGNALI anno accademico 008-009 Appunti u: Teorema del Campionamento Introduzione Il proceo di campionamento è di enorme importanza ai ini della realizzazione dei dipoitivi digitali per le telecomunicazioni.
SEGNALI E SISTEMI 31 agosto 2017
 SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
Uso della trasformata di Laplace per il calcolo della risposta
 Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Corso di Fondamenti di Telecomunicazioni
 Coro di Fondamenti di elecomunicazioni - SEGNALI E SPERI Pro. Mario Barbera [parte 3] Fondamenti di LC - Pro. M. Barbera - Segnali e pettri [parte 3] = 3 log Banda di un egnale Deinizione di banda di un
Coro di Fondamenti di elecomunicazioni - SEGNALI E SPERI Pro. Mario Barbera [parte 3] Fondamenti di LC - Pro. M. Barbera - Segnali e pettri [parte 3] = 3 log Banda di un egnale Deinizione di banda di un
Sistemi a segnali campionati
 Capitolo. INRODUZIONE 6. Sitemi a egnali campionati Si conideri il eguente itema lineare tempo continuo: G() : ẋ(t) Ax(t)+Bu(t) y(t) Cx(t) U() G() Y() Se i inerice un ricotruttore di ordine zero H () e
Capitolo. INRODUZIONE 6. Sitemi a egnali campionati Si conideri il eguente itema lineare tempo continuo: G() : ẋ(t) Ax(t)+Bu(t) y(t) Cx(t) U() G() Y() Se i inerice un ricotruttore di ordine zero H () e
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
1 = (parabola unitaria) si determini l errore di regolazione a regime:
 A - Tet d ingreo alla Prova Scritta di Controlli Automatici A del Ottobre 00 ( + ) ( ) + ) Dato un itema dinamico Σ con funzione di traferimento T() crivere i modi di Σ : ( + ) + 9 t { modi di Σ } {, tt,,
A - Tet d ingreo alla Prova Scritta di Controlli Automatici A del Ottobre 00 ( + ) ( ) + ) Dato un itema dinamico Σ con funzione di traferimento T() crivere i modi di Σ : ( + ) + 9 t { modi di Σ } {, tt,,
Rumore termico. Telecomunicazioni per l Aerospazio. P. Lombardo DIET, Univ. di Roma La Sapienza Rumore - 1
 Rumore termico elecomunicazioni per l Aeropazio. Lombardo DI, Univ. di Roma La Sapienza Rumore - Rumore ermico: tatitica Il rumore ha una denità di probabilità gauiana Itogramma Volt Volt Realizzazione
Rumore termico elecomunicazioni per l Aeropazio. Lombardo DI, Univ. di Roma La Sapienza Rumore - Rumore ermico: tatitica Il rumore ha una denità di probabilità gauiana Itogramma Volt Volt Realizzazione
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Bittanti, BIO A-K) Settembre Si conideri il eguente itema dinamico a tempo continuo decritto mediante chema a blocchi: ut () _ yt () 9 a Si calcoli la funione
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Bittanti, BIO A-K) Settembre Si conideri il eguente itema dinamico a tempo continuo decritto mediante chema a blocchi: ut () _ yt () 9 a Si calcoli la funione
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c ; P 1 1( ( + 4 ; P ( ( + ( + 3 ;
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c ; P 1 1( ( + 4 ; P ( ( + ( + 3 ;
dove x 0 R n è fissato.
 AMMISSIONE AL QUARTO ANNO: prova di ANALISI MATEMATICA (matematici e fiici) 26 Sia α (, ) (a) Provare che eite c α >, indipendente da t e, tale che (b) Calcolare c /2 (t σ) α (σ ) α dσ = c α, t, () (c)
AMMISSIONE AL QUARTO ANNO: prova di ANALISI MATEMATICA (matematici e fiici) 26 Sia α (, ) (a) Provare che eite c α >, indipendente da t e, tale che (b) Calcolare c /2 (t σ) α (σ ) α dσ = c α, t, () (c)
K c s h. P(s) 1/K d. U(s) + Y(s)
 Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A ) Corso di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno
 Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A. 5 6) Coro di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 6 GENNAIO 7 Ripondere
Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A. 5 6) Coro di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 6 GENNAIO 7 Ripondere
Modello monodimensionale per le correnti in moto turbolento vario. Fig. 1
 Modello monodimenionale per le correnti in moto turbolento vario 1. Decompoizione dei campi di moto turbolento vario Prima di affrontare la definizione del modello per le correnti in moto turbolento vario,
Modello monodimenionale per le correnti in moto turbolento vario 1. Decompoizione dei campi di moto turbolento vario Prima di affrontare la definizione del modello per le correnti in moto turbolento vario,
ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST
 ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST PROPRIETÀ DEI SISTEMI IN RETROAZIONE U E G () H () Si fa riferimento ad un generico itema in retroazione con funzione di traferimento a ciclo chiuo.
ANALISI DI SISTEMI IN RETROAZIONE TEOREMA DI NYQUIST PROPRIETÀ DEI SISTEMI IN RETROAZIONE U E G () H () Si fa riferimento ad un generico itema in retroazione con funzione di traferimento a ciclo chiuo.
Esercizi svolti di geometria delle aree Alibrandi U., Fuschi P., Pisano A., Sofi A. ESERCIZIO n.7
 ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
ESERCZO n.7 Data la ezione cava riportata in Figura, determinare: a) gli ai principali centrali di inerzia; b) l ellie principale centrale di inerzia; c) il nocciolo centrale di inerzia. cm cm A#7 . Determinazione
Daniela Tondini
 Daniela Tondini dtondini@unite.it Facoltà di Medicina veterinaria CdS in Tutela e beneere animale Univerità degli Studi di Teramo 1 Gli indici tatitici i uddividono in: indici tatitici di poizione indici
Daniela Tondini dtondini@unite.it Facoltà di Medicina veterinaria CdS in Tutela e beneere animale Univerità degli Studi di Teramo 1 Gli indici tatitici i uddividono in: indici tatitici di poizione indici
1. (solo nuovo ordinamento e diploma) Dato il sistema di controllo raffigurato, con
 Eame di Fondamenti di Automatica Coro di Laurea Nuovo e Vecchio Ord. in Ingegneria Elettronica Simulazione 9 Novembre 7 Cognome: Nome Matricola: E-mail: 1. (olo nuovo ordinamento e diploma) Dato il itema
Eame di Fondamenti di Automatica Coro di Laurea Nuovo e Vecchio Ord. in Ingegneria Elettronica Simulazione 9 Novembre 7 Cognome: Nome Matricola: E-mail: 1. (olo nuovo ordinamento e diploma) Dato il itema
Lezione 9. Schemi di controllo avanzati parte prima. F. Previdi - Controlli Automatici - Lez. 9 1
 Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
ẋ 2 = x 1 10x u y = x 1 + x 2 [
 Soluzione dell appello del 16 luglio 212 1. Si conideri il itema lineare decritto dalle eguenti equazioni: 1.1 Trovare le condizioni iniziali x() = ẋ 1 = x 1 ẋ 2 = x 1 1x 2 1u = x 1 x 2 [ x1, x 2, aociato
Soluzione dell appello del 16 luglio 212 1. Si conideri il itema lineare decritto dalle eguenti equazioni: 1.1 Trovare le condizioni iniziali x() = ẋ 1 = x 1 ẋ 2 = x 1 1x 2 1u = x 1 x 2 [ x1, x 2, aociato
COMUNICAZIONI ELETTRICHE
 COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
Corso di SEGNALI a.a Corso di SEGNALI. anno accademico Trasformata di Fourier: esercizi d esame
 Corso di SEGNLI a.a.008 009 Corso di SEGNLI anno accademico 008-009 rasormata di Fourier: esercizi d esame. Successivamente si calcoli il valore di () per 0, ±/ e ±/. Per calcolare la trasormata di questo
Corso di SEGNLI a.a.008 009 Corso di SEGNLI anno accademico 008-009 rasormata di Fourier: esercizi d esame. Successivamente si calcoli il valore di () per 0, ±/ e ±/. Per calcolare la trasormata di questo
Sistemi LTI a Tempo Continuo
 Capitolo 3 Sistemi LTI a Tempo Continuo 3.1 Proprietà di Linearità e Tempo Invarianza 3.1.1 Linearità Si indichi con T [.] la trasormazione ingresso-uscita, o unzione di traserimento, di un sistema S 1,
Capitolo 3 Sistemi LTI a Tempo Continuo 3.1 Proprietà di Linearità e Tempo Invarianza 3.1.1 Linearità Si indichi con T [.] la trasormazione ingresso-uscita, o unzione di traserimento, di un sistema S 1,
Teoria dei Segnali Proprietà della trasformata di Fourier; correlazione tra segnali; autocorrelazione
 Teoria dei Segnali Proprietà della trasformata di Fourier; correlazione tra segnali; autocorrelazione p. 1 Teoria dei Segnali Proprietà della trasformata di Fourier; correlazione tra segnali; autocorrelazione
Teoria dei Segnali Proprietà della trasformata di Fourier; correlazione tra segnali; autocorrelazione p. 1 Teoria dei Segnali Proprietà della trasformata di Fourier; correlazione tra segnali; autocorrelazione
Esempio di Processo Aleatorio La passeggiata casuale Per ogni kt si genera una v.a. Y Bernoulliana con ( A) ( A) 1 k = 1,2,... { }
 Esempio di Processo Aleatorio La passeggiata casuale Per ogni kt si genera una v.a. Y Bernoulliana con ( A) ( A) Se Y = A X{ kt} = X{ ( k 1) T} + 1 k = 1,2,... { } Y = A X{ kt} = X{ ( k 1) T} 1 k = 1,2,...
Esempio di Processo Aleatorio La passeggiata casuale Per ogni kt si genera una v.a. Y Bernoulliana con ( A) ( A) Se Y = A X{ kt} = X{ ( k 1) T} + 1 k = 1,2,... { } Y = A X{ kt} = X{ ( k 1) T} 1 k = 1,2,...
Esercizi di Controlli Automatici - 9 A.A. 2009/2010
 Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
Eercizi di Controlli Automatici - 9 A.A. 2009/200 Eercizio. Dato il eguente chema, in cui gli amplificatori operazionali ono uppoti ideali, i calcoli la funzione di traferimento G() tra v in (t) e v out
ESERCIZI SULLE SUPERFICI. 1) Calcolare le curvature principali, la curvatura media e la curvatura Gaussiana della sfera
 ESERCIZI SULLE SUPERFICI Calcolare le curvature principali, la curvatura media e la curvatura Gauiana della fera α u; v = r in u co v ; r in u in v ; r co u Dato il paraboloide ellittico α u; v = u; v;
ESERCIZI SULLE SUPERFICI Calcolare le curvature principali, la curvatura media e la curvatura Gauiana della fera α u; v = r in u co v ; r in u in v ; r co u Dato il paraboloide ellittico α u; v = u; v;
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI. corso: Teoria dei Circuiti. docente: Stefano PASTORE. 1 Esempio di tableau dinamico (tempo e Laplace)
 ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico
Corso Tecnologie dei Sistemi di Controllo. Controllo PID
 Coro Controllo PID Ing. Valerio Scordamaglia Univerità Mediterranea di Reggio Calabria, Loc. Feo di Vito, 896, RC, Italia D.I.M.E.T. : Dipartimento di Informatica, Matematica, Elettronica e Traporti Struttura
Coro Controllo PID Ing. Valerio Scordamaglia Univerità Mediterranea di Reggio Calabria, Loc. Feo di Vito, 896, RC, Italia D.I.M.E.T. : Dipartimento di Informatica, Matematica, Elettronica e Traporti Struttura
Esercitazione di Controlli Automatici 1 n 2. a.a. 2006/07
 6 marzo 007 Eercitazione di Controlli Automatici n a.a. 006/07 Riferendoi al itema di controllo della temperatura in un locale di piccole dimenioni dicuo nella eercitazione precedente, e di eguito riportato:.
6 marzo 007 Eercitazione di Controlli Automatici n a.a. 006/07 Riferendoi al itema di controllo della temperatura in un locale di piccole dimenioni dicuo nella eercitazione precedente, e di eguito riportato:.
DINAMICHE COMPLESSE NEL FERRO DI CAVALLO
 DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
Teoria dei segnali terza edizione
 Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Trasformazione di Laplace
 Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
Esercizi di Segnali e Sistemi. GLI ESERCIZI 1,2,3,4,11 COSTITUISCONO UN TEMA D ESAME TIPICO
 Eercizi di Segnali e Sitemi. GLI ESERCIZI,2,3,4, COSTITUISCONO UN TEMA D ESAME TIPICO Eempio Conideriamo la funzione di traferimento G() = + Si calcoli la forma di Smith Mc-Millan. Soluzione: G() = N(),
Eercizi di Segnali e Sitemi. GLI ESERCIZI,2,3,4, COSTITUISCONO UN TEMA D ESAME TIPICO Eempio Conideriamo la funzione di traferimento G() = + Si calcoli la forma di Smith Mc-Millan. Soluzione: G() = N(),
Tecnologie dei Sistemi di Automazione
 Facoltà di Ingegneria Tecnologie dei Sitemi di Automazione rof. Gianmaria De Tommai Lezione 4 Regolatori ID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno
Facoltà di Ingegneria Tecnologie dei Sitemi di Automazione rof. Gianmaria De Tommai Lezione 4 Regolatori ID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno
Introduzione. Esempio di costruzione one del contorno delle radici. Esempio... 4
 Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Errori e cifre significative. Incontro iniziale LAB2GO
 Errori e cifre ignificative Incontro iniziale LABGO La ditribuzione gauiana f tinyurl.com/labcalcquiz Propagazione degli errori Miure dirette: la grandezza fiica viene miurata direttamente (ad e. Speore
Errori e cifre ignificative Incontro iniziale LABGO La ditribuzione gauiana f tinyurl.com/labcalcquiz Propagazione degli errori Miure dirette: la grandezza fiica viene miurata direttamente (ad e. Speore
1 La trasformata di Laplace
 La traformata di Laplace Sia I un intervallo contenente il emiae reale poitivo: R + = [, + ) I e ia f : I C una funzione a valori reali o complei. Denizione.. La funzione f è L-traformabile (o traformabile
La traformata di Laplace Sia I un intervallo contenente il emiae reale poitivo: R + = [, + ) I e ia f : I C una funzione a valori reali o complei. Denizione.. La funzione f è L-traformabile (o traformabile
Esame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento) 16 Giugno 2008 (Bozza di soluzione)
 Eame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento 6 Giugno 28 (Bozza di oluzione NB. Si coniglia vivamente di ripaare anche argomenti non trettamente inerenti la materia oggetto della prova
Eame di FONDAMENTI di AUTOMATICA Compito B (Nuovo ordinamento 6 Giugno 28 (Bozza di oluzione NB. Si coniglia vivamente di ripaare anche argomenti non trettamente inerenti la materia oggetto della prova
Modellistica e controllo PID di un pendolo inverso
 Modellitica e controllo PID di un pendolo invero Note per le lezioni del coro di Controlli Automatici - A.A. 2009/0 Prof.a Maria Elena Valcher Modellitica Un ata di maa m è incernierata ad un carrello
Modellitica e controllo PID di un pendolo invero Note per le lezioni del coro di Controlli Automatici - A.A. 2009/0 Prof.a Maria Elena Valcher Modellitica Un ata di maa m è incernierata ad un carrello
1) Entropia di variabili aleatorie continue. 2) Esempi di variabili aleatorie continue. 3) Canali di comunicazione continui. 4) Canale Gaussiano
 Argomenti della Lezione 1) Entropia di variabili aleatorie continue ) Esempi di variabili aleatorie continue 3) Canali di comunicazione continui 4) Canale Gaussiano 5) Limite di Shannon 1 Entropia di una
Argomenti della Lezione 1) Entropia di variabili aleatorie continue ) Esempi di variabili aleatorie continue 3) Canali di comunicazione continui 4) Canale Gaussiano 5) Limite di Shannon 1 Entropia di una
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi e del Controllo Compito A del 23 Dicembre 200 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Indicare il numero e il tipo di parametri che caratterizzano la funzione
Teoria dei Sitemi e del Controllo Compito A del 23 Dicembre 200 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Indicare il numero e il tipo di parametri che caratterizzano la funzione
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 17 gennaio Soluzioni compito 1
 ANALISI MATEMATICA II Sapiena Univerità di Roma - Laurea in Ingegneria Informatica Eame del 7 gennaio 07 - Soluioni compito E Calcolare il eguente integrale di funione di variabile reale con i metodi della
ANALISI MATEMATICA II Sapiena Univerità di Roma - Laurea in Ingegneria Informatica Eame del 7 gennaio 07 - Soluioni compito E Calcolare il eguente integrale di funione di variabile reale con i metodi della
Trasformate al limite
 Bozza Data 6/0/007 Trasormate al limite La unzione generalizzata delta di Dirac Funzioni, unzionali e distribuzioni Prima di deinire la delta di Dirac conviene ricordare le seguenti deinizioni: unzione
Bozza Data 6/0/007 Trasormate al limite La unzione generalizzata delta di Dirac Funzioni, unzionali e distribuzioni Prima di deinire la delta di Dirac conviene ricordare le seguenti deinizioni: unzione
UNIVERSITA DI FIRENZE Facoltà di Ingegneria. Fisica Tecnica G. Grazzini. Superfici estese
 Superici etee Nella legge di Newton per la convezione compare la upericie di cambio inieme al coeiciente di convezione; perciò e non riuciamo ad aumentare quet'ultimo, tenteremo di accrecere la upericie
Superici etee Nella legge di Newton per la convezione compare la upericie di cambio inieme al coeiciente di convezione; perciò e non riuciamo ad aumentare quet'ultimo, tenteremo di accrecere la upericie
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI
 RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Introduzione Se il segnale d ingresso di un sistema Lineare Tempo-Invariante (LTI e un esponenziale
RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Introduzione Se il segnale d ingresso di un sistema Lineare Tempo-Invariante (LTI e un esponenziale
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A )
 Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A.-) Es. La variabile aleatoria ha densità di probabilità uniorme nell intervallo [,]. Trovare valor medio e varianza di. La densità di probabilità
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A.-) Es. La variabile aleatoria ha densità di probabilità uniorme nell intervallo [,]. Trovare valor medio e varianza di. La densità di probabilità
PROCESSI CASUALI 1 Fondamenti di segnf a o lin d e a t m ra e s n mtii s T si L o C ne
 PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
Fondamenti di Telecomunicazioni Allievi Ingegneria Fisica Prima Prova Recupero 20/02/2003
 Fondamenti di Telecomunicazioni Allievi Ingegneria Fiica Prima Prova Recupero //. Calcolare l'antitraformata di Fourier di (f) definito come + co( π ft); f < / T ( f) = altrove e tracciarne l'andamento
Fondamenti di Telecomunicazioni Allievi Ingegneria Fiica Prima Prova Recupero //. Calcolare l'antitraformata di Fourier di (f) definito come + co( π ft); f < / T ( f) = altrove e tracciarne l'andamento
LA TRASFORMATA DI LAPLACE
 LA RASFORMAA DI LAPLACE Per decrivere l evoluzione di un itema in regime tranitorio, oia durante il paaggio delle ucite da un regime tazionario ad un altro, è neceario ricorrere ad un modello più generale
LA RASFORMAA DI LAPLACE Per decrivere l evoluzione di un itema in regime tranitorio, oia durante il paaggio delle ucite da un regime tazionario ad un altro, è neceario ricorrere ad un modello più generale
Trasformata di Laplace
 Complementi di Analii per Informatica *** Capitolo 6 Traformata di Laplace Sergio Benenti Prima verione ettembre 23 Reviione ettembre 27 Pierre Simon marchee di Laplace (749 827) Indice 6 Definizione 62
Complementi di Analii per Informatica *** Capitolo 6 Traformata di Laplace Sergio Benenti Prima verione ettembre 23 Reviione ettembre 27 Pierre Simon marchee di Laplace (749 827) Indice 6 Definizione 62
Analizzatore di spettro numerico a FFT. La ricostruzione del segnale nel rispetto del teorema del campionamento!!! LPF: filtro anti aliasing
 Analizzatore di pettro numerico a FFT La ricotruzione del egnale nel ripetto del teorema del campionamento!!! LPF: filtro anti aliaing i Numero finito di campioni!!!!! Analizzatore di pettro numerico a
Analizzatore di pettro numerico a FFT La ricotruzione del egnale nel ripetto del teorema del campionamento!!! LPF: filtro anti aliaing i Numero finito di campioni!!!!! Analizzatore di pettro numerico a
DINAMICA DEI FLUIDI PERFETTI. L equazione di Bernoulli (Daniel Bernoulli, ) è una delle prime
 CAPITOLO 3. DINAMICA DEI FLUIDI PERFETTI 3.1 Equazione di Bernoulli L equazione di Bernoulli (Daniel Bernoulli, 1700 178) è una delle prime equazioni della Fluidodinamica. Se ea viene applicata ripettando
CAPITOLO 3. DINAMICA DEI FLUIDI PERFETTI 3.1 Equazione di Bernoulli L equazione di Bernoulli (Daniel Bernoulli, 1700 178) è una delle prime equazioni della Fluidodinamica. Se ea viene applicata ripettando
Richiami di teoria della probabilità
 Richiami di teoria della probabilità Lo spazio fondamentale S F rappresenta l insieme di tutti i risultati ξ i che si escludono mutuamente che si possono ottenere da un esperimento aleatorio. Esempio.
Richiami di teoria della probabilità Lo spazio fondamentale S F rappresenta l insieme di tutti i risultati ξ i che si escludono mutuamente che si possono ottenere da un esperimento aleatorio. Esempio.
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo
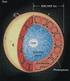 7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
Controlli Automatici (AUT) - 09AKSBL. Progetto dinamico. Funzioni compensatrici elementari. Struttura di controllo con compensazione in cascata d a
 Controlli Automatici (AUT) - 9AKSBL Funzioni compenatrici elementari Progetto di controllori in cacata Struttura di controllo con compenazione in cacata d a r + + e + C () + u + G() y - d y + dt + L obiettivo
Controlli Automatici (AUT) - 9AKSBL Funzioni compenatrici elementari Progetto di controllori in cacata Struttura di controllo con compenazione in cacata d a r + + e + C () + u + G() y - d y + dt + L obiettivo
Corso di Fondamenti di Automatica A.A. 2015/16. Diagrammi di Bode
 1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 200 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 200 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi e del Controllo Compito del Febbraio 206 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere l andamento temporale della funzione di ucita y(k), oluzione dell
Teoria dei Sitemi e del Controllo Compito del Febbraio 206 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere l andamento temporale della funzione di ucita y(k), oluzione dell
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi e del Controllo Compito del Gennaio 206 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione generale dell equazione alle differenze x(k +) = Ax(k)+Bu(k)
Teoria dei Sitemi e del Controllo Compito del Gennaio 206 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione generale dell equazione alle differenze x(k +) = Ax(k)+Bu(k)
Risonanza. Tracciare gli andamenti del modulo e della fase dell impedenza in funzione della frequenza f per il seguente bipolo: A R 1 R 2
 6 Eercitazioni aggiuntive Eercizio 6. Tracciare gli andamenti del modulo e della fae dell impedenza in funzione della frequenza f per il eguente bipolo: A B [W]; [W]; [mf] Si calcoli l impedenza del bipolo
6 Eercitazioni aggiuntive Eercizio 6. Tracciare gli andamenti del modulo e della fae dell impedenza in funzione della frequenza f per il eguente bipolo: A B [W]; [W]; [mf] Si calcoli l impedenza del bipolo
ESERCIZIO 1 L/2 C.R. D
 SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
Tecnologie Informatiche per l Automazione Industriale
 Tecnologie Informatiche per l Automazione Indutriale Prof. Gianmaria De Tommai Regolatori PID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno accademico N46
Tecnologie Informatiche per l Automazione Indutriale Prof. Gianmaria De Tommai Regolatori PID indutriali: Leggi di controllo e utilizzo Coro di Laurea Codice inegnamento Email docente Anno accademico N46
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi e del Controllo Compito A del 5 Febbraio 05 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ(t) =
Teoria dei Sitemi e del Controllo Compito A del 5 Febbraio 05 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ(t) =
Controllo di Azionamenti Elettrici. Lezione n 3. Caratteristiche e predisposizione dei regolatori PID
 Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
Il Luogo delle Radici
 Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
Trasformata di Fourier
 Trasformata di Fourier Ø Risposta impulsiva e integrale di convoluzione Ø Rappresentazione di segnali nel tempo e in frequenza Ø Filtri idealmente e fisicamente realizzabili, stabilità Ø Trasformazioni
Trasformata di Fourier Ø Risposta impulsiva e integrale di convoluzione Ø Rappresentazione di segnali nel tempo e in frequenza Ø Filtri idealmente e fisicamente realizzabili, stabilità Ø Trasformazioni
CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI ˆ = SULL INTERFACCIA TRA DUE MEZZI OMOGENEI
 CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI SULL INTERFACCIA TRA DUE MEZZI OMOGENEI Conideriamo le equazioni di Maxwell in una regione di pazio riempita da un mezzo omogeneo e iotropo caratterizzato
CONDIZIONI DI RACCORDO DEI CAMPI ELETTROMAGNETICI SULL INTERFACCIA TRA DUE MEZZI OMOGENEI Conideriamo le equazioni di Maxwell in una regione di pazio riempita da un mezzo omogeneo e iotropo caratterizzato
Punto 1 Il sistema proposto di tipo retroazionato può essere rappresentato con lo schema a blocchi riportato in Fig. 1.
 Pag. di SOLUZIONE dei primi 4 punti richieti dalla Prova. Leggo bene il teto e poi? La mia Maetra mi diceva empre: Prima la figura. Punto Il itema propoto di tipo retroazionato può eere rappreentato con
Pag. di SOLUZIONE dei primi 4 punti richieti dalla Prova. Leggo bene il teto e poi? La mia Maetra mi diceva empre: Prima la figura. Punto Il itema propoto di tipo retroazionato può eere rappreentato con
FUNZIONI DI TRASFERIMENTO
 FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
Sistemi di controllo
 Cognome: Nome: N. Matr.: Sitemi di controllo Ingegneria Meccanica e Ingegneria del Veicolo Compito del 11 ettembre 2014 - Quiz Per ciacuno dei eguenti queiti, egnare con una crocetta le ripote che i ritengono
Cognome: Nome: N. Matr.: Sitemi di controllo Ingegneria Meccanica e Ingegneria del Veicolo Compito del 11 ettembre 2014 - Quiz Per ciacuno dei eguenti queiti, egnare con una crocetta le ripote che i ritengono
UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE ATTENZIONE
 U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
Specifiche sulla banda passante negli amplificatori a microonde
 pecifiche ulla banda paante negli amplificatori a microonde Gli amplificatori a microonde trattano egnali modulati, il cui pettro ha in genere una etenione B molto minore della frequenza centrale f 0 (portante).
pecifiche ulla banda paante negli amplificatori a microonde Gli amplificatori a microonde trattano egnali modulati, il cui pettro ha in genere una etenione B molto minore della frequenza centrale f 0 (portante).
Lezione 19 ALCUNI PROBLEMI RELATIVI A CONDOTTE A SEZIONE CIRCOLARE
 Appunti dei cori di Idraulica e Idrodinamica ezione 9 ACNI PROBEMI REATIVI A CONOTTE A SEZIONE CIRCOARE Come accennato nella EZIONE 8, e conideriamo il moto tazionario di un fluido incomprimibile all interno
Appunti dei cori di Idraulica e Idrodinamica ezione 9 ACNI PROBEMI REATIVI A CONOTTE A SEZIONE CIRCOARE Come accennato nella EZIONE 8, e conideriamo il moto tazionario di un fluido incomprimibile all interno
corso di Terminali per i Trasporti e la Logistica Umberto Crisalli
 coro di Terminali per i Traporti e la Logitica ELEMENTI DI TEORIA DELLE CODE Umberto Crialli crialli@ing.uniroma.it INTRODUZIONE Simulazione dei terminali In generale, un terminale è cotituito da un inieme
coro di Terminali per i Traporti e la Logitica ELEMENTI DI TEORIA DELLE CODE Umberto Crialli crialli@ing.uniroma.it INTRODUZIONE Simulazione dei terminali In generale, un terminale è cotituito da un inieme
I Segnali nella comunicazione
 I Segnali nella comunicazione Nella lingua italiana il termine segnale indica una convenzione, la cui unzione è quella di comunicare qualcosa ( segnale di Partenza, segnale di aiuto, segnale stradale ecc.).
I Segnali nella comunicazione Nella lingua italiana il termine segnale indica una convenzione, la cui unzione è quella di comunicare qualcosa ( segnale di Partenza, segnale di aiuto, segnale stradale ecc.).
Esercizio. Il circuito di figura rappresenta un filtro passa-banda. Dopo aver ricavato la funzione di trasferimento, sapendo che
 Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
Eercizio Clae 5ª Elettronici Materia Sitemi Argomento Funzioni di traferimento Il circuito di figura rappreenta un filtro paa-banda. Dopo aver ricavato la funzione di traferimento, apendo che R = 2k Ω
I sistemi retroazionati. Per lo studio si può utilizzarne uno a reazione unitaria per rendere standard i risultati:
 I itemi retroazionati Facciamo riferimento allo chema a blocchi: Per lo tudio i può utilizzarne uno a reazione unitaria per rendere tandard i riultati: i due ono equivalenti: infatti il primo ha una f.d.t.
I itemi retroazionati Facciamo riferimento allo chema a blocchi: Per lo tudio i può utilizzarne uno a reazione unitaria per rendere tandard i riultati: i due ono equivalenti: infatti il primo ha una f.d.t.
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
SEGNALI E SISTEMI PASSA-BANDA
 SEGNALI E SISTEMI PASSA-ANDA Componnti a runz poitiv ngativ. Si conidri un gnal ) t ral la cui traormata di Fourir è rapprnta in Fig.. S ) S ) S ) Nll analii di gnali è talvolta util introdurr l grandzz
SEGNALI E SISTEMI PASSA-ANDA Componnti a runz poitiv ngativ. Si conidri un gnal ) t ral la cui traormata di Fourir è rapprnta in Fig.. S ) S ) S ) Nll analii di gnali è talvolta util introdurr l grandzz
Corso di Fondamenti di Telecomunicazioni
 Coro di Fondamenti di Teleomuniazioni 6 - SEGNALI IN ANDA PASSANTE E MODULAZIONI Pro. Mario arbera [parte Fondamenti di TLC - Pro. M. arbera Struttura della lezione Inviluppo ompleo e egnali modulati Spettro
Coro di Fondamenti di Teleomuniazioni 6 - SEGNALI IN ANDA PASSANTE E MODULAZIONI Pro. Mario arbera [parte Fondamenti di TLC - Pro. M. arbera Struttura della lezione Inviluppo ompleo e egnali modulati Spettro
Ripasso segnali e processi casuali. Trasmissione dell Informazione
 Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Trasformata di Laplace
 Traformata di Laplace In matematica e in particolare nell'analii funzionale la traformata di Laplace di una funzione f (t ) (definita per tutti i numeri reali e localmente integrabile) è la funzione F
Traformata di Laplace In matematica e in particolare nell'analii funzionale la traformata di Laplace di una funzione f (t ) (definita per tutti i numeri reali e localmente integrabile) è la funzione F
Segnali ad energia ed a potenza finita
 Bozza Data 07/03/008 Segnali ad energia ed a potenza finita Energia e potenza di un segnale Definizioni di energia e potenza Dato un segnale (t), in generale complesso, si definisce potenza istantanea
Bozza Data 07/03/008 Segnali ad energia ed a potenza finita Energia e potenza di un segnale Definizioni di energia e potenza Dato un segnale (t), in generale complesso, si definisce potenza istantanea
Fondamenti di Automatica Figura 1: Schema di centrifuga industriale: a) vista in assonometria b) vista frontale.
 Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
Fondamenti di Automatica 6-9-26 Figura : Schema di centrifuga indutriale: a) vita in aonometria b) vita frontale. A In Fig..a è riportato lo chema emplificato di una centrifuga orizzontale indutriale di
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 14 Gennaio 2010
 CORSO DI LURE IN SCIENZE BIOLOGICHE Prova critta di FISIC 4 Gennaio 00 ) Un bambino lancia una palla di maa m = 00 gr verticalmente vero l alto con velocità v 0 = m/, a partire da una roccia alta h 0 =
CORSO DI LURE IN SCIENZE BIOLOGICHE Prova critta di FISIC 4 Gennaio 00 ) Un bambino lancia una palla di maa m = 00 gr verticalmente vero l alto con velocità v 0 = m/, a partire da una roccia alta h 0 =
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Sorgenti Analogiche - Soluzioni
 Sorgenti Analogiche - Soluzioni Soluzione: l oggetto dell analisi ha semplicemente il seguente schema a blocchi: Ampliicatore: Funzione di traserimento o dinamica + K* saturazione Disegnamo quindi la sua
Sorgenti Analogiche - Soluzioni Soluzione: l oggetto dell analisi ha semplicemente il seguente schema a blocchi: Ampliicatore: Funzione di traserimento o dinamica + K* saturazione Disegnamo quindi la sua
Definizioni e relazioni fondamentali
 Capitolo 1 Definizioni e relazioni fondamentali 1.1 Definizioni di E e B Il campo elettrico E (m 1 ) e l induzione magnetica B (T) ono definiti in riferimento alla forza che agice u una carica in movimento
Capitolo 1 Definizioni e relazioni fondamentali 1.1 Definizioni di E e B Il campo elettrico E (m 1 ) e l induzione magnetica B (T) ono definiti in riferimento alla forza che agice u una carica in movimento
Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1
![Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1 Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1](/thumbs/98/134926211.jpg) I itemi termici La reitenza termica Se ue corpi aventi temperature ivere vengono mei a contatto, i ha un paaggio i quantità i calore al corpo a temperatura maggiore vero quello a temperatura minore, fino
I itemi termici La reitenza termica Se ue corpi aventi temperature ivere vengono mei a contatto, i ha un paaggio i quantità i calore al corpo a temperatura maggiore vero quello a temperatura minore, fino
Criterio di stabilità di Bode. tramite la risposta in frequenza viene indicata come condizione di innesco dell instabilità la
 Criterio di tabilità di Bode Sia dato un itema retroazionato con f.d.t. eprea F( H ( tramite la ripota in frequenza viene indicata come condizione di inneco dell intabilità la G ( j H ( j 0 cioè G ( j
Criterio di tabilità di Bode Sia dato un itema retroazionato con f.d.t. eprea F( H ( tramite la ripota in frequenza viene indicata come condizione di inneco dell intabilità la G ( j H ( j 0 cioè G ( j
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi e del Controllo Compito del Dicembre Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione generale della eguente equazione alle differenze tempo-variante
Teoria dei Sitemi e del Controllo Compito del Dicembre Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Scrivere la oluzione generale della eguente equazione alle differenze tempo-variante
Esercitazione 05: Collegamenti bullonati e saldature
 Meccanica e Tecnica delle Cotruzioni Meccaniche Eercitazioni del coro. Periodo II Prof. Leonardo BERTINI Ing. Ciro SNTUS Eercitazione 05: Collegamenti bullonati e aldature Indice 1 Collegamenti bullonati
Meccanica e Tecnica delle Cotruzioni Meccaniche Eercitazioni del coro. Periodo II Prof. Leonardo BERTINI Ing. Ciro SNTUS Eercitazione 05: Collegamenti bullonati e aldature Indice 1 Collegamenti bullonati
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
