SUI SISTEMI DI DISEQUAZIONI IN DUE INCOGNITE
|
|
|
- Maddalena Bertini
- 7 anni fa
- Visualizzazioni
Transcript
1 SUI SISTEMI DI DISEQUAZIONI IN DUE INCOGNITE.Sistema di disequazioni in due incognite di primo grado Una disequazione di primo grado in due incognite: a b c nel piano cartesiano, rappresenta uno dei due semipiani nei quali la retta a b c =, divide il piano stesso. Il metodo più semplice per individuare di quale dei due semipiani si tratta consiste nello scegliere, a piacere, un punto non appartenente alla retta detto punto spia e verificare se le sue coordinate soddisfano o meno la disequazione data: nel primo caso il semipiano sarà quello che contiene il punto spia, nel secondo caso sarà il semipiano opposto. Pertanto nel piano cartesiano un sistema di disequazioni di primo grado in due incognite rappresenta l insieme intersezione dei corrispondenti semipiani. Questa intersezione può essere un poligono convesso, un semipiano, una regione angolare, una striscia,, non è escluso che risulti vuota, o un unico punto, o un segmento, o una semiretta, o una retta. Esempio: Il sistema 6 6 rappresenta l insieme dei punti del piano intersezione dei semipiani: Ognuno di tali semipiani viene individuato prendendo come punto spia l origine delle coordinate. L intersezione è la regione colorata in blu: -6
2 .Sistema di disequazioni in due incognite di grado maggiore di uno Una disequazione di grado in due incognite, nel piano cartesiano, rappresenta una delle due parti nelle quali la conica associata alla disequazione considerata divide il piano stesso. Il metodo per individuare di quale delle due parti di piano si tratta è analogo a quello indicato per una disequazione di primo grado. Associando ad una disequazione di grado un altra disequazione (di primo o di secondo grado) si ottiene un sistema di disequazioni di grado maggiore di uno (esattamente di secondo grado o di quarto grado) che rappresenta nel piano cartesiano l insieme dei punti intersezione delle due parti di piano soluzioni di ciascuna delle due disequazioni. Esempio: Determinare l insieme dei punti P (,) per cui ha senso l espressione: L espressione ha senso se e solo se:. Ciò è equivalente all unione dei seguenti sistemi (*) e (**) > < Il sistema(*) risulta soddisfatto dall insieme dei punti intersezione della regione del piano per cui è (punti esterni e sul cerchio di centro l origine e raggio ) col semipiano >. Tale regione è quella colorata.
3 In modo analogo si trova che il sistema (**) risulta soddisfatto nella regione colorata. Pertanto la regione di piano annerita della seguente figura è quella per cui ha senso l espressione data.
4 . Un problema pratico I sistemi di disequazioni, al pari dei sistemi di equazioni, trovano notevoli applicazioni nella risoluzione di numerosi problemi vari. Diamo qui un esempio di un problema per la risoluzione del quale, il modello matematico di cui ci si serve è proprio un sistema di disequazioni lineari. Problema Utilizzando solo due dei tre alimenti A, B e C la cui composizione risulta dalla seguente tabella: Composizione Alimento A Alimento B Alimento C Proteine % % % Carboidrati % 5% 4% è possibile effettuare una dieta che prevede un consumo giornaliero di p proteine compreso tra 75g e 5g, di c carboidrati compreso tra 5g e g in modo che la quantita complessiva di proteine e carboidrati non superi i 75g? Soluzione: Le diete possibili sono tre. caso: la dieta viene effettuata con i soli alimenti A e B. caso: la dieta viene effettuata con i soli alimenti A e C. caso: la dieta viene effettuata con i soli alimenti B e C. LEGENDA p = quantità totale in grammi di proteine c = quantità totale in grammi di carboidrati = quantità totale in grammi dell alimento = quantità totale in grammi dell alimento ) A B ) A C ) B C Le condizioni poste dal problema conducono al seguente sistema di disequazioni lineari: (*) 75 p 5 5 c p c 75 Poiché le ultime due disequazioni portano ad esaminare solo regioni di punti che stanno nel primo quadrante, consideriamo solo le condizioni imposte dalle prime tre disequazioni.
5 Per ciascuno dei tre casi possibili rappresentiamo nel piano cartesiano la regione di punti le cui coordinate costituiscono coppie di quantità ammissibili dei due alimenti. Primo caso: La dieta viene effettuata con i soli alimenti A e B. Il sistema (*) diventa (*) ( )75,, 5 ( )5,, 5 ( ),,5 75 Considerato come punto spia l origine delle coordinate, l individuazione dei semipiani soluzioni delle disequazioni porta ai seguenti risultati: - la disequazione (a) e soddisfatta nel semipiano che non contiene O; la disequazione (b) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*)e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (a) e (b). - la disequzione (c) e soddisfatta nel semipiano che non contiene O; la disequazione (d) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*) e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (c) e (d). - la disequazione (e) e soddisfatta nel semipiano che contiene O. Le soluzioni del sistema sono date dall insieme intersezione delle due sopraddette strisce di piani e il semipiano individuato dalla disequazione (e) Tale intersezione e costituita solo dal punto R. Grafico Primo caso ( a) 75 ( b ) 5 ( c)4 5 ( d)4 6 ( e) Legenda: Rette: a // b Rette: c // d Retta: e R (5 ; ) R 5
6 La dieta deve consistere di,5 kg del solo alimento A Secondo caso: La dieta viene effettuata con i soli alimenti A e C. Il sistema (*) diventa (*) ( )75,, 5 ()5,,4 (),,5 75 ( a) 75 ( b) 5 ( c) 5. ( d ) 5 ( e) 5 75 Considerato come punto spia l origine delle coordinate, l individuazione dei semipiani soluzioni delle disequazioni porta ai seguenti risultati: - la disequazione (a) e soddisfatta nel semipiano che non contiene O; la disequazione (b) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*)e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (a) e (b). - la disequzione (c) e soddisfatta nel semipiano che non contiene O; la disequazione (d) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*) e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (c) e (d) - la disequazione (e) e soddisfatta nel semipiano che contiene O. Le soluzioni del sistema sono date dall insieme intersezione delle due sopraddette strisce di piani e il semipiano individuato dalla disequazione (e). Tale intersezione e la regione i cui punti sono contenuti nel triangolo di vertici R (; 75) S (5; 5) T (5;). Grafico Secondo caso Legenda: Rette: a // b Rette: c // d Retta: e R A S Triangolo dai vertici R(;75) S (5; 5) T (5; ) T
7 La dieta può essere realizzata in infiniti modi. Le quantità ammissibili degli alimenti A e C sono date da coppie di valori, che sono le coordinate dei punti contenuti nel sopraddetto triangolo RST. Terzo caso: La dieta viene effettuata con i soli alimenti B e C. Il sistema (*) diventa (*) ( )75,, 5 ()5,5,4 (),5,5 75 ( a) 75 ( b ) 5 ( c) 8 5. ( d) 8 6 ( e)7 75 Considerato come punto spia l origine delle coordinate, l individuazione dei semipiani soluzioni delle disequazioni porta ai seguenti risultati - la disequazione (a) e soddisfatta nel semipiano che non contiene O; la disequazione (b) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*)e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (a) e (b). - la disequzione (c) e soddisfatta nel semipiano che non contiene O; la disequazione (d) e soddisfatta nel semipiano che contiene O. Da queste due si deduce che la relazione () del sistema (*) e soddisfatta da tutti i punti del primo quadrante che sono compresi nella striscia di piano individuata dalle due rette (c) e (d). - la disequazione (e) e soddisfatta nel semipiano che contiene O. Le soluzioni del sistema sono date dall insieme intersezione delle due sopraddette strisce di piani e il semipiano individuato dalla disequazione (e). Tale intersezione e la regione i cui punti sono contenuti nel triangolo di vertici R (; 75) S (77; 596) T (85;48). Grafico terzo caso Legenda: Rette: a // b Rette: c // d S R T Retta: e Triangolo dai vertici R(;75) S (77; 596) T (48;85)
8 La dieta può essere realizzata in infiniti modi. Le quantità ammissibili degli alimenti B e C sono date dalle coppie di valori che sono le coordinate dei punti contenuti nel sopraddetto triangolo RST. 4.Esercizi Proposti Rappresentare geometricamente l insieme dei punti del piano cartesiano soddisfacenti alla disequazione ( ) ( 5) 6 <. Rappresentare geometricamente l insieme dei punti del piano per cui risulta: a) b) 6 6 c) Rappresentare geometricamente l insieme dei punti del piano per cui hanno senso le seguenti espressioni: a) b) c) ) )( ( d)log ( ) e) log 4 Trovare al variare di k R l insieme dei punti del piano per cui ha senso l espressione: k 8
Problemi di scelta ESEMPI
 ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
Soluzione grafica di problemi PM in 2 variabili
 Capitolo 4 Soluzione grafica di problemi PM in 2 variabili In questo paragrafo si vuole fornire una interpretazione geometrica di un problema di Programmazione matematica. In particolare, quando un problema
Capitolo 4 Soluzione grafica di problemi PM in 2 variabili In questo paragrafo si vuole fornire una interpretazione geometrica di un problema di Programmazione matematica. In particolare, quando un problema
ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 421 E SEGUENTI
 ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 421 E SEGUENTI ESERCIZIO N. 6 PAG. 418 z 100 + 200 100 vincoli 3 2 + 20 0 Si rappresenta la REGIONE AMMISSIBILE ottenendo Determino le coordinate dei
ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 421 E SEGUENTI ESERCIZIO N. 6 PAG. 418 z 100 + 200 100 vincoli 3 2 + 20 0 Si rappresenta la REGIONE AMMISSIBILE ottenendo Determino le coordinate dei
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Geometria analitica di base (seconda parte)
 SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
Esercizio L1 L2 L3 L4 L5 L6 L7 L8. Sia f (x) = 4 x. Allora f (x + 1) f (x) è uguale a. Risposta. Risulta immediatamente
 Sia f (x) = 4 x. Allora f (x + 1) f (x) è uguale a [1] 4 [2] f (x) [3] 2f (x) [4] 3f (x) [5] 4f (x) Risulta immediatamente f (x 1) f (x) = 4 x+1 4 x = 4 x 4 1 4 x = 4 x (4 1) = 3 4 x = 3f (x). E noto che
Sia f (x) = 4 x. Allora f (x + 1) f (x) è uguale a [1] 4 [2] f (x) [3] 2f (x) [4] 3f (x) [5] 4f (x) Risulta immediatamente f (x 1) f (x) = 4 x+1 4 x = 4 x 4 1 4 x = 4 x (4 1) = 3 4 x = 3f (x). E noto che
ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 417 E SEGUENTI. Esercizio n. 1 pag 417. vincoli
 ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 47 E SEGUENTI Esercizio n. pag 47 6 x x z vincoli 0 0 4 x x x x x x Si rappresenta la REGIONE AMMISSIBILE ottenendo La regione ammissibile, individuata
ESERCIZI SVOLTI DI PROGRAMMAZIONE LINEARE TOMO G PAG 47 E SEGUENTI Esercizio n. pag 47 6 x x z vincoli 0 0 4 x x x x x x Si rappresenta la REGIONE AMMISSIBILE ottenendo La regione ammissibile, individuata
Soluzione grafica di problemi PM in 2 variabili
 Capitolo 4 Soluzione grafica di problemi PM in 2 variabili In questo paragrafo si vuole fornire una interpretazione geometrica di un problema di Programmazione matematica. In particolare, quando un problema
Capitolo 4 Soluzione grafica di problemi PM in 2 variabili In questo paragrafo si vuole fornire una interpretazione geometrica di un problema di Programmazione matematica. In particolare, quando un problema
Precorso di Matematica
 Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Equazioni e disequazioni algebriche. Soluzione. Si tratta del quadrato di un binomio. Si ha pertanto. (x m y n ) 2 = x 2m 2x m y n + y 2n
 Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
La circonferenza nel piano cartesiano
 La circonferenza nel piano cartesiano 1. Definizione ed equazione. Si chiama circonferenza C, di centro C( α, β ) e raggio r, l insieme di tutti e soli i punti del piano che hanno distanza r da C. L equazione
La circonferenza nel piano cartesiano 1. Definizione ed equazione. Si chiama circonferenza C, di centro C( α, β ) e raggio r, l insieme di tutti e soli i punti del piano che hanno distanza r da C. L equazione
Protocollo dei saperi imprescindibili Ordine di scuola: tecnico della grafica
 DISCIPLINA: MATEMATICA Protocollo dei saperi imprescindibili Ordine di scuola: tecnico della grafica RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima tecnico della grafica calcolo numerico
DISCIPLINA: MATEMATICA Protocollo dei saperi imprescindibili Ordine di scuola: tecnico della grafica RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima tecnico della grafica calcolo numerico
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
PROBLEMI DI SCELTA dipendenti da due variabili d azione
 prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
1. conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio
 Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
Liceo Scientifico Statale A. Einstein
 . PROGRAMMA SVOLTO DAL DOCENTE DI MATEMATICA Prof.ssa Alessandra Desogus a.s. 2015/16 3^ F Libro di testo adottato : L.Sasso La matematica a colori (vol.3) (edizione blu) Ripasso Equazioni di vario tipo
. PROGRAMMA SVOLTO DAL DOCENTE DI MATEMATICA Prof.ssa Alessandra Desogus a.s. 2015/16 3^ F Libro di testo adottato : L.Sasso La matematica a colori (vol.3) (edizione blu) Ripasso Equazioni di vario tipo
LEZIONE 10. S(C,ρ) Figura 10.1
 LEZIONE 10 10.1. Sfere nello spazio. In questa lezione studieremo alcuni oggetti geometrici non lineari, circonferenze e sfere nello spazio A 3. Poiché le proprietà delle circonferenze nel piano sono del
LEZIONE 10 10.1. Sfere nello spazio. In questa lezione studieremo alcuni oggetti geometrici non lineari, circonferenze e sfere nello spazio A 3. Poiché le proprietà delle circonferenze nel piano sono del
Istituto di Istruzione Superiore L. da Vinci Civitanova Marche. Anno scolastico PROGRAMMA SVOLTO. Materia: Matematica
 Anno scolastico 2015-2016 PROGRAMMA SVOLTO Materia: Matematica Docente: Massimiliano Iori Classe : 2F Indirizzo: Linguistico Disequazioni lineari Le diseguaglianze: definizioni e proprietà. Disequazioni
Anno scolastico 2015-2016 PROGRAMMA SVOLTO Materia: Matematica Docente: Massimiliano Iori Classe : 2F Indirizzo: Linguistico Disequazioni lineari Le diseguaglianze: definizioni e proprietà. Disequazioni
PROGRAMMAZIONE LINEARE
 PROGRAMMAZIONE LINEARE La programmazione lineare ha un ruolo fondamentale tra i metodi risolutivi per i problemi di ottimizzazione. Storicamente questo settore della matematica, che è strettamente connesso
PROGRAMMAZIONE LINEARE La programmazione lineare ha un ruolo fondamentale tra i metodi risolutivi per i problemi di ottimizzazione. Storicamente questo settore della matematica, che è strettamente connesso
LICEO SCIENTIFICO STATALE FILIPPO LUSSANA - BERGAMO. PROGRAMMA EFFETTIVAMENTE SVOLTO a. s. 2014/15
 LICEO SCIENTIFICO STATALE FILIPPO LUSSANA - BERGAMO PROGRAMMA EFFETTIVAMENTE SVOLTO a. s. 2014/15 CLASSE : 3N indirizzo scienze applicate DOCENTE: CAPRI MATTEO MATERIA: MATEMATICA Libro di testo utilizzato:
LICEO SCIENTIFICO STATALE FILIPPO LUSSANA - BERGAMO PROGRAMMA EFFETTIVAMENTE SVOLTO a. s. 2014/15 CLASSE : 3N indirizzo scienze applicate DOCENTE: CAPRI MATTEO MATERIA: MATEMATICA Libro di testo utilizzato:
Programma di MATEMATICA svolto nella Classe Prima A
 LICEO ARTISTICO BOCCIONI A.S. 2014-2015 Programma di MATEMATICA svolto nella Classe Prima A Prof.ssa Albertina Costanzo I numeri naturali e i numeri interi L insieme dei numeri naturali N. Le quattro operazioni.
LICEO ARTISTICO BOCCIONI A.S. 2014-2015 Programma di MATEMATICA svolto nella Classe Prima A Prof.ssa Albertina Costanzo I numeri naturali e i numeri interi L insieme dei numeri naturali N. Le quattro operazioni.
Liceo G.B. Vico Corsico
 P a g. 1 Liceo G.B. Vico Corsico Classe: 2^H Materia: Matematica Insegnante: De Dominicis Sara Testo utilizzato: La matematica a colori EDIZIONE AZZURRA Volume 1, Volume 2 Leonardo Sasso - Petrini Programma
P a g. 1 Liceo G.B. Vico Corsico Classe: 2^H Materia: Matematica Insegnante: De Dominicis Sara Testo utilizzato: La matematica a colori EDIZIONE AZZURRA Volume 1, Volume 2 Leonardo Sasso - Petrini Programma
8 Valore assoluto. 8.1 Definizione e proprietà
 8 Valore assoluto 8. Definizione e proprietà Si dice valore assoluto o modulo di un numero reale, e si indica con, il numero stesso se questo è positivo o nullo, altrimenti il suo opposto -, in simboli:
8 Valore assoluto 8. Definizione e proprietà Si dice valore assoluto o modulo di un numero reale, e si indica con, il numero stesso se questo è positivo o nullo, altrimenti il suo opposto -, in simboli:
Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi.
 Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi. (1) Sia A l insieme dei numeri dispari minori di 56 e divisibili per 3. Quale delle seguenti affermazioni
Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi. (1) Sia A l insieme dei numeri dispari minori di 56 e divisibili per 3. Quale delle seguenti affermazioni
quindi, applicando la legge di annullamento del prodotto, si ottiene l insieme delle soluzioni: x x da cui:
 ) Risolvi le seguenti equazioni e scrivi le soluzioni reali in ordine crescente, indicando se sono multiple e quante sono le eventuali soluzioni non reali: ( ) ( ) per risolvere questa equazione si applica
) Risolvi le seguenti equazioni e scrivi le soluzioni reali in ordine crescente, indicando se sono multiple e quante sono le eventuali soluzioni non reali: ( ) ( ) per risolvere questa equazione si applica
Soluzione dei sistemi lineari con metodo grafico classe 2H
 Soluzione dei sistemi lineari con metodo grafico classe H (con esempi di utilizzo del software open source multipiattaforma Geogebra e calcolatrice grafica Texas Instruments TI-89) Metodo grafico Il metodo
Soluzione dei sistemi lineari con metodo grafico classe H (con esempi di utilizzo del software open source multipiattaforma Geogebra e calcolatrice grafica Texas Instruments TI-89) Metodo grafico Il metodo
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
In un triangolo un lato è maggiore della differenza degli altri due, pertanto dal triangolo si ha > dividendo per =1.
 L iperbole L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi. Come si evince del grafico, la differenza delle distanze
L iperbole L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi. Come si evince del grafico, la differenza delle distanze
Definizione: Dato un sottoinsieme non vuoti di. Si chiama funzione identica o identità di in sé la funzione tale che.
 Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Facoltà di Farmacia Corso di Matematica con elementi di Statistica Docente: Riccardo Rosso. Cenni sulla programmazione lineare
 Facoltà di Farmacia Corso di Matematica con elementi di Statistica Docente: Riccardo Rosso Cenni sulla programmazione lineare Illustriamo le idee di fondo della programmazione lineare, disciplina matematica
Facoltà di Farmacia Corso di Matematica con elementi di Statistica Docente: Riccardo Rosso Cenni sulla programmazione lineare Illustriamo le idee di fondo della programmazione lineare, disciplina matematica
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010
 PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
PROGRAMMA DI MATEMATICA
 Docente: Rosinella Cuomo Classe: IID Anno scolastico 2017/2018 ALGEBRA PROGRAMMA DI MATEMATICA 1. Le disequazioni di primo grado Insiemi di numeri sulla retta Disuguaglianze numeriche Disequazioni equivalenti
Docente: Rosinella Cuomo Classe: IID Anno scolastico 2017/2018 ALGEBRA PROGRAMMA DI MATEMATICA 1. Le disequazioni di primo grado Insiemi di numeri sulla retta Disuguaglianze numeriche Disequazioni equivalenti
LA RETTA
 EQUAZIONE DEL Ogni equazione di I grado in due variabili x e y rappresenta nel piano cartesiano una retta, per cui si dice che a x + b y + c = 0 è l equazione di una retta in forma implicita. OSSERVAZIONE:
EQUAZIONE DEL Ogni equazione di I grado in due variabili x e y rappresenta nel piano cartesiano una retta, per cui si dice che a x + b y + c = 0 è l equazione di una retta in forma implicita. OSSERVAZIONE:
12 gennaio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
MODULI DI MATEMATICA (SECONDO BIENNIO)
 DIPARTIMENTO SCIENTIFICO Asse* Matematico Scientifico - tecnologico Triennio MODULI DI MATEMATICA (SECONDO BIENNIO) SUPERVISORE DI AREA Prof. FRANCESCO SCANDURRA MODULO N. 1 MATEMATICA Matematico TERZA
DIPARTIMENTO SCIENTIFICO Asse* Matematico Scientifico - tecnologico Triennio MODULI DI MATEMATICA (SECONDO BIENNIO) SUPERVISORE DI AREA Prof. FRANCESCO SCANDURRA MODULO N. 1 MATEMATICA Matematico TERZA
QUESTIONARIO FINALE DI AUTOVALUTAZIONE. a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi
 QUESTIONARIO FINALE DI AUTOVALUTAZIONE a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 2006-2007 1 1) L espressione ( 2 log x)( 2 log 2 2 x) è definita
QUESTIONARIO FINALE DI AUTOVALUTAZIONE a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 2006-2007 1 1) L espressione ( 2 log x)( 2 log 2 2 x) è definita
ELEMENTI DI GEOMETRIA ANALITICA Conoscenze (tutti)
 ELEMENTI DI GEMETRIA ANALITICA Conoscenze (tutti) 1. Completa. a. La formula matematica che mette in relazione il valore della x con il corrispondente valore della y si chiama... b. Le equazioni di primo
ELEMENTI DI GEMETRIA ANALITICA Conoscenze (tutti) 1. Completa. a. La formula matematica che mette in relazione il valore della x con il corrispondente valore della y si chiama... b. Le equazioni di primo
La prima è la parte positiva (al di sopra dell asse y) della circonferenza di equazione. e raggio r = 2 ; la seconda è una retta (vedi figura).
 Macerata 3 febbraio 0 classe 3M COMPITO DI MATEMATICA SOLUZIONE QUESITO a) Rappresenta graficamente la curva descritta dalla seguente equazione: y y + + = 0 Per la presenza del valore assoluto dobbiamo
Macerata 3 febbraio 0 classe 3M COMPITO DI MATEMATICA SOLUZIONE QUESITO a) Rappresenta graficamente la curva descritta dalla seguente equazione: y y + + = 0 Per la presenza del valore assoluto dobbiamo
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
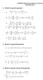 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
Geometria analitica di base. Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa
 Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa Equazioni di primo grado nel piano cartesiano Risoluzione grafica di un equazione
Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa Equazioni di primo grado nel piano cartesiano Risoluzione grafica di un equazione
Disequazioni goniometriche
 Disequazioni goniometriche Si definiscono disequazioni goniometriche le disequazioni nelle quali l angolo incognito è espresso mediante funzioni goniometriche (seno, coseno, tangente etc.). Per le disequazioni
Disequazioni goniometriche Si definiscono disequazioni goniometriche le disequazioni nelle quali l angolo incognito è espresso mediante funzioni goniometriche (seno, coseno, tangente etc.). Per le disequazioni
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE
 QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a ESPONENZIALI E LOGARITMI GEOMETRIA DELLO SPAZIO a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1 1)
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a ESPONENZIALI E LOGARITMI GEOMETRIA DELLO SPAZIO a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1 1)
PROGRAMMA di MATEMATICA
 Liceo Scientifico F. Lussana - Bergamo PROGRAMMA di MATEMATICA Classe 3^ F a.s. 2013/14 - Docente: Marcella Cotroneo Libro di testo : Leonardo Sasso "Nuova Matematica a colori 3" - Petrini Ore settimanali
Liceo Scientifico F. Lussana - Bergamo PROGRAMMA di MATEMATICA Classe 3^ F a.s. 2013/14 - Docente: Marcella Cotroneo Libro di testo : Leonardo Sasso "Nuova Matematica a colori 3" - Petrini Ore settimanali
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari)
 Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima servizi commerciali calcolo numerico (N,
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. - IMPERATORE D. CLASSE/INDIRIZZO: prima servizi commerciali calcolo numerico (N,
Macerata 19 dicembre 2014 classe 3M COMPITO DI MATEMATICA RECUPERO ASSENTI ( ) ( ) ( ) C 2; 1.
 Macerata 9 dicembre 04 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI SOLUZIONE QUESITO In un riferimento cartesiano ortogonale è dato il fascio di rette: k + x k y + k + = 0. Determina il centro C del
Macerata 9 dicembre 04 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI SOLUZIONE QUESITO In un riferimento cartesiano ortogonale è dato il fascio di rette: k + x k y + k + = 0. Determina il centro C del
MATEMATICA LA PARABOLA GSCATULLO
 MATEMATICA LA PARABOLA GSCATULLO La Parabola Introduzione e definizione Prima di affrontare la parabola e la sua analisi matematica, appare opportuno definirla nelle sue caratteristiche essenziali. Anzitutto
MATEMATICA LA PARABOLA GSCATULLO La Parabola Introduzione e definizione Prima di affrontare la parabola e la sua analisi matematica, appare opportuno definirla nelle sue caratteristiche essenziali. Anzitutto
Punti, linee e piani nello spazio
 Punti, linee e piani nello spazio DEFINIZIONE. La geometria dello spazio o geometria dei solidi o ancora geometria solida è il settore della geometria che si occupa dei corpi a tre dimensioni (lunghezza,
Punti, linee e piani nello spazio DEFINIZIONE. La geometria dello spazio o geometria dei solidi o ancora geometria solida è il settore della geometria che si occupa dei corpi a tre dimensioni (lunghezza,
3A ALGEBRA Numeri relativi Esercizi supplementari di verifica 1 Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione.
 Numeri relativi Esercizi supplementari di verifica Esercizio Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F L insieme dei numeri interi relativi è un sottoinsieme dell
Numeri relativi Esercizi supplementari di verifica Esercizio Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F L insieme dei numeri interi relativi è un sottoinsieme dell
SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO
 FACOLTÀ DI INGEGNERIA CORSO DI AZZERAMENTO - MATEMATICA ANNO ACCADEMICO 010-011 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
FACOLTÀ DI INGEGNERIA CORSO DI AZZERAMENTO - MATEMATICA ANNO ACCADEMICO 010-011 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
Esercitazione per la prova di recupero del debito formativo
 LEZIONI ED ESERCITAZIONI DI MATEMATICA Prof. Francesco Marchi 1 Esercitazione per la prova di recupero del debito formativo 24 febbraio 2010 1 Per altri materiali didattici o per contattarmi: Blog personale:
LEZIONI ED ESERCITAZIONI DI MATEMATICA Prof. Francesco Marchi 1 Esercitazione per la prova di recupero del debito formativo 24 febbraio 2010 1 Per altri materiali didattici o per contattarmi: Blog personale:
LA CIRCONFERENZA E LA SUA EQUAZIONE
 LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
Compito di matematica Classe III ASA 23 aprile 2015
 Compito di matematica Classe III ASA 3 aprile 015 A. Descrivere mediante un opportuno sistema di disequazioni nelle variabili x e y la parte di piano colorata: A1 A A1: y 1 x + x 1 4 x y 0 A: x 4 + y 9
Compito di matematica Classe III ASA 3 aprile 015 A. Descrivere mediante un opportuno sistema di disequazioni nelle variabili x e y la parte di piano colorata: A1 A A1: y 1 x + x 1 4 x y 0 A: x 4 + y 9
SCIENZE MATEMATICHE FISICHE e NATURALI
 UNIVERSITÀ di ROMA TOR VERGATA FACOLTÀ di SCIENZE MATEMATICHE FISICHE e NATURALI Argomenti di Matematica delle prove di valutazione Anno 03-04 A. Manipolazioni algebriche, semplificazioni; calcolo elementare
UNIVERSITÀ di ROMA TOR VERGATA FACOLTÀ di SCIENZE MATEMATICHE FISICHE e NATURALI Argomenti di Matematica delle prove di valutazione Anno 03-04 A. Manipolazioni algebriche, semplificazioni; calcolo elementare
Problemi sulla circonferenza verso l esame di stato
 Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
valore di a: verso l alto (ordinate crescenti) se a>0, verso il basso (ordinate decrescenti) se a<0;
 La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
SCHEDA DI LAVORO N.1 LABORATORIO PREMESSA
 SCHEDA DI LAVORO N.1 LABORATORIO Problemi di modellizzazione PREMESSA La soluzione di semplici problemi di programmazione lineare permette di affrontare e approfondire il concetto di ottimizzazione nell
SCHEDA DI LAVORO N.1 LABORATORIO Problemi di modellizzazione PREMESSA La soluzione di semplici problemi di programmazione lineare permette di affrontare e approfondire il concetto di ottimizzazione nell
I.I.S. Via Silvestri 301 Roma. Liceo Scientifico M. Malpighi. Anno scolastico
 I.I.S. Via Silvestri 301 Roma Liceo Scientifico M. Malpighi Anno scolastico 2018-19 Programma di MATEMATICA svolto nella classe I sezione A Docente prof.ssa Ornella Masci ALGEBRA NUMERI NATURALI: - Ripetizione
I.I.S. Via Silvestri 301 Roma Liceo Scientifico M. Malpighi Anno scolastico 2018-19 Programma di MATEMATICA svolto nella classe I sezione A Docente prof.ssa Ornella Masci ALGEBRA NUMERI NATURALI: - Ripetizione
PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2015-2016 INSEGNANTE: MASCI ORNELLA ALGEBRA - Equazioni letterali fratte
PROGRAMMA DI MATEMATICA PER LA CLASSE 2^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA I.I.S. VIA SILVESTRI ANNO SCOLASTICO 2015-2016 INSEGNANTE: MASCI ORNELLA ALGEBRA - Equazioni letterali fratte
SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO
 DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 013-014 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 013-014 ESERCIZI RELATIVI A SISTEMI DI RIFERIMENTO SU UNA RETTA E SU UN PIANO Esercizio 1: Fissato su una retta un sistema di riferimento
Classi: Seconde Disciplina: MATEMATICA Ore settimanali previste: 4
 Classi: Seconde Disciplina: MATEMATICA Ore settimanali previste: 4 Prerequisiti per l'accesso al modulo 0: CALCOLO LETTERALE, PRODOTTI NOTEVOLI modulo Titolo Modulo Titolo unità didattiche Ore previste
Classi: Seconde Disciplina: MATEMATICA Ore settimanali previste: 4 Prerequisiti per l'accesso al modulo 0: CALCOLO LETTERALE, PRODOTTI NOTEVOLI modulo Titolo Modulo Titolo unità didattiche Ore previste
Soluzione di Adriana Lanza
 La dieta Un medico prescrive a Silvia, per un breve periodo di tempo, una dieta ristretta a pochi alimenti (cereali, legumi e pesce) il cui complessivo apporto calorico giornaliero non deve superare le
La dieta Un medico prescrive a Silvia, per un breve periodo di tempo, una dieta ristretta a pochi alimenti (cereali, legumi e pesce) il cui complessivo apporto calorico giornaliero non deve superare le
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
ISTITUTO TECNICO INDUSTRIALE G. FERRARIS
 ISTITUTO TECNICO INDUSTRIALE G. FERRARIS EMPOLI PIANO DI LAVORO PROF. BICCI ANDREA CONSIGLIO DI CLASSE 3 SEZ. B Informatica INDIRIZZO INFORMATICO ANNO SCOLASTICO 2015-2016 MATERIE MATEMATICA (tre ore settimanali)
ISTITUTO TECNICO INDUSTRIALE G. FERRARIS EMPOLI PIANO DI LAVORO PROF. BICCI ANDREA CONSIGLIO DI CLASSE 3 SEZ. B Informatica INDIRIZZO INFORMATICO ANNO SCOLASTICO 2015-2016 MATERIE MATEMATICA (tre ore settimanali)
L equazione generica della funzione costante è y=k, il grafico è una retta parallela all asse x (asse delle ascisse). retta parallela all'asse x y
 La funzione costante L equazione generica della funzione costante è =k, il grafico è una retta parallela all asse (asse delle ascisse). Esempio di esercizio, dall equazione al grafico: =- retta parallela
La funzione costante L equazione generica della funzione costante è =k, il grafico è una retta parallela all asse (asse delle ascisse). Esempio di esercizio, dall equazione al grafico: =- retta parallela
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
a rappresenta l intercetta o termine noto della retta, ossia il valore della y quando x = 0.
 Esercitazioni sulla prima parte delle lezioni di Micro Richiamo di Analisi Matematica La forma funzionale più semplice è la retta, la quale può essere genericamente descritta dalla seguente relazione:
Esercitazioni sulla prima parte delle lezioni di Micro Richiamo di Analisi Matematica La forma funzionale più semplice è la retta, la quale può essere genericamente descritta dalla seguente relazione:
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Disequazioni - ulteriori esercizi proposti 1
 Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
quindi, applicando la legge di annullamento del prodotto, si ottiene l insieme delle soluzioni:
 ) Risolvi le seguenti equazioni e scrivi le soluzioni reali in ordine crescente, indicando se sono multiple e quante sono le eventuali soluzioni non reali: ( ) ( ) questa equazione equivale a ( ) ( ) quindi
) Risolvi le seguenti equazioni e scrivi le soluzioni reali in ordine crescente, indicando se sono multiple e quante sono le eventuali soluzioni non reali: ( ) ( ) questa equazione equivale a ( ) ( ) quindi
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico Prova di Matematica : Piano cartesiano e retta Alunno: Classe: 2 C
 Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 010-011 Prova di Matematica : Piano cartesiano e retta Alunno: Classe: C 10.03.011 prof. Mimmo Corrado Dato il triangolo di vertici: 6; 3, ; 1, 4;
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 010-011 Prova di Matematica : Piano cartesiano e retta Alunno: Classe: C 10.03.011 prof. Mimmo Corrado Dato il triangolo di vertici: 6; 3, ; 1, 4;
Appunti: il piano cartesiano. Distanza tra due punti
 ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ANNO SCOLASTICO 2017 /2018 A026 MATEMATICA
 ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
1 Test. 1. Il polinomio x 3 + 3x 2 4x é divisibile per. (a) x 3 (b) x + 2 (c) x + 4 (d) x + 1 (e) x L equazione x 2 x = 0 é verificata:
 1 Test 1. Il polinomio x 3 + 3x 4x é divisibile per (a) x 3 (b) x + (c) x + 4 (d) x + 1 (e) x 4. L equazione x x = 0 é verificata: (a) solo per x = 1 (b) per ogni valore reale di x (c) solo per x = 1 (d)
1 Test 1. Il polinomio x 3 + 3x 4x é divisibile per (a) x 3 (b) x + (c) x + 4 (d) x + 1 (e) x 4. L equazione x x = 0 é verificata: (a) solo per x = 1 (b) per ogni valore reale di x (c) solo per x = 1 (d)
LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI
 LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI SPAZIO: l insieme di tutti i punti. PUNTI ALLINEATI: punti che appartengono alla stessa retta PUNTI COMPLANARI: punti che appartengono allo stesso
LA GEOMETRIA DELLO SPAZIO: CENNI DI TEORIA ED ESERCIZI SPAZIO: l insieme di tutti i punti. PUNTI ALLINEATI: punti che appartengono alla stessa retta PUNTI COMPLANARI: punti che appartengono allo stesso
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
MODULI DI MATEMATICA (PRIMO BIENNIO)
 DIPARTIMENTO SCIENTIFICO Asse* Matematico Scientifico - tecnologico Biennio dell obbligo MODULI DI MATEMATICA (PRIMO BIENNIO) SUPERVISORE DI AREA Prof. FRANCESCO SCANDURRA MODULO N. 1 MATEMATICA Matematico
DIPARTIMENTO SCIENTIFICO Asse* Matematico Scientifico - tecnologico Biennio dell obbligo MODULI DI MATEMATICA (PRIMO BIENNIO) SUPERVISORE DI AREA Prof. FRANCESCO SCANDURRA MODULO N. 1 MATEMATICA Matematico
1 EQUAZIONI GONIOMETRICHE
 1 EQUAZIONI GONIOMETRICHE Esempio 1 Risolvere senx = Soluzione. La misura dei due angoli positivi, minori di un angolo giro, che soddisfano l equazione data sono: 4 Tutte le soluzioni sono quindi date
1 EQUAZIONI GONIOMETRICHE Esempio 1 Risolvere senx = Soluzione. La misura dei due angoli positivi, minori di un angolo giro, che soddisfano l equazione data sono: 4 Tutte le soluzioni sono quindi date
PROGRAMMA FINALE A.S. 2016/2017
 PROGRAMMA FINALE A.S. 2016/2017 MATERIA CLASSE INDIRIZZO DOCENTE LIBRO DI TESTO Matematica III SCIENTIFICO Ermanno Giuseppe FRABOTTA Leonardo Sasso - La Matematica a Colori - BLU - Vol 3 Blu - Petrini
PROGRAMMA FINALE A.S. 2016/2017 MATERIA CLASSE INDIRIZZO DOCENTE LIBRO DI TESTO Matematica III SCIENTIFICO Ermanno Giuseppe FRABOTTA Leonardo Sasso - La Matematica a Colori - BLU - Vol 3 Blu - Petrini
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
Mutue posizioni della parabola con gli assi cartesiani
 Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
RIPASSO ANNO PRECEDENTE
 RIPASSO ANNO PRECEDENTE OBIETTIVI Conoscenze - Il calcolo numerico - Le operazioni in Q - Le operazioni e le espressioni con i monomi - Le operazioni nell'insieme dei monomi e nell'insieme dei polinomi
RIPASSO ANNO PRECEDENTE OBIETTIVI Conoscenze - Il calcolo numerico - Le operazioni in Q - Le operazioni e le espressioni con i monomi - Le operazioni nell'insieme dei monomi e nell'insieme dei polinomi
Esercizi sulle equazioni logaritmiche
 Esercizi sulle equazioni logaritmiche Per definizione il logaritmo in base a di un numero positivo x, con a > 0 e a 1, è l esponente che occorre dare alla base a per ottenere il numero x. In simboli log
Esercizi sulle equazioni logaritmiche Per definizione il logaritmo in base a di un numero positivo x, con a > 0 e a 1, è l esponente che occorre dare alla base a per ottenere il numero x. In simboli log
Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016
 Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016 NUCLEI DISCIPLINARI OBIETTIVI SPECIFICI 1. RIPASSO Saper operare con: 0.1 scomposizioni 0.2 frazioni algebriche
Programma di matematica Classe: II BL Docente: Alessandra Mancini Anno scolastico: 2015/2016 NUCLEI DISCIPLINARI OBIETTIVI SPECIFICI 1. RIPASSO Saper operare con: 0.1 scomposizioni 0.2 frazioni algebriche
Distanza tra punti e punto medio di un segmento. x1 + x 2
 Distanza tra punti e punto medio di un segmento Siano P = (x 1, y 1 ) e Q = (x 2, y 2 ) due punti del piano cartesiano. La distanza di P da Q vale: P Q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 (si utilizza il Teorema
Distanza tra punti e punto medio di un segmento Siano P = (x 1, y 1 ) e Q = (x 2, y 2 ) due punti del piano cartesiano. La distanza di P da Q vale: P Q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 (si utilizza il Teorema
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO INSEGNANTE: MASCI ORNELLA
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO 2014-2015 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione dei numeri naturali e delle quattro operazioni
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI ANNO SCOLASTICO 2014-2015 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione dei numeri naturali e delle quattro operazioni
L iperbole. x 2 = 1. a 2 b 2. Si noti che tale equazione è stata ottenuta rispetto ad un riferimento privilegiato, detto RIFERIMENTO CANONICO.
 L iperbole Fisso nel piano due punti distinti, F ed F FUOCHI F ed F l insieme: Si dice IPERBOLE di {P R : dist(p ; F ) dist(p ; F ) = a} Se dist(f ; F ) = c, fisso un sistema di assi cartesiano tale che
L iperbole Fisso nel piano due punti distinti, F ed F FUOCHI F ed F l insieme: Si dice IPERBOLE di {P R : dist(p ; F ) dist(p ; F ) = a} Se dist(f ; F ) = c, fisso un sistema di assi cartesiano tale che
Università del Salento Facoltà di Scienze Matematiche Fisiche e Naturali. Matematica e Fisica
 Università del Salento Facoltà di Scienze Matematiche Fisiche e Naturali Test d INGRESSO Matematica e Fisica 2017-2018 A 1. In un parallelogramma due lati consecutivi sono lunghi a e b e l angolo tra essi
Università del Salento Facoltà di Scienze Matematiche Fisiche e Naturali Test d INGRESSO Matematica e Fisica 2017-2018 A 1. In un parallelogramma due lati consecutivi sono lunghi a e b e l angolo tra essi
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA DISEQUAZIONI E SISTEMI Dr. Erasmo Modica erasmo@galois.it SISTEMI DI EQUAZIONI DI PRIMO GRADO Definizione: Si definisce
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA DISEQUAZIONI E SISTEMI Dr. Erasmo Modica erasmo@galois.it SISTEMI DI EQUAZIONI DI PRIMO GRADO Definizione: Si definisce
a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
 Esercizi svolti Esercizio 1. Dati i punti: A(1, 1, 0), B( 1, 1, 4), C(1, 1, 3), D(2, 2, 8) dello spazio R 3 a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
Esercizi svolti Esercizio 1. Dati i punti: A(1, 1, 0), B( 1, 1, 4), C(1, 1, 3), D(2, 2, 8) dello spazio R 3 a) Perché posso affermare che sono complanari? b) Determina l equazione del piano che li contiene
Ore annue: 132 MODULO 1
 Liceo B. Russell VIA IV NOVEMBRE 35, 38023 CLES Indirizzo: Liceo Linguistico CLASSI 2 e Programmazione Didattica Disciplina: Ore annue: 132 Matematica Settembre ottobre MODULO 1 novembre Disequazioni numeriche
Liceo B. Russell VIA IV NOVEMBRE 35, 38023 CLES Indirizzo: Liceo Linguistico CLASSI 2 e Programmazione Didattica Disciplina: Ore annue: 132 Matematica Settembre ottobre MODULO 1 novembre Disequazioni numeriche
