Simmetria morfologica e gruppi puntuali
|
|
|
- Pio Brunetti
- 7 anni fa
- Visualizzazioni
Transcript
1 Simmetria morfologica e gruppi puntuali Il sistema cristallino di un campione può essere determinato dall osservazione morfologica o da una serie di misure di proprietà fisiche. P.es. cristalli che mostrano simmetria cubica (NaCl) ovviamente appartengono al sistema cubico. La forma della cella cristallina e quella del cristallo coincidono. Tuttavia, altre forme cristalline sono compatibili con la simmetria puntuale del reticolo cubico; in questi casi la forma della cella unitaria e l aspetto esterno (o abito) non coincidono. CaF 2 cristallizza spesso sotto forma di ottaedri. L abito è determinato da fattori complessi, chimici e fisici, per lo più di carattere cinetico. Come correlare diversi abiti alla simmetria reale del cristallo? Basta osservare il tipo e numero di elementi di simmetria del cristallo: Un cubo ed un ottaedro hanno la stessa simmetria Un tetraedro ha minor simmetria Tutte e tre le forme posseggono 4 assi ternari inclinati di , ovvero appartengono allo stesso sistema cristallino. NaCl e CaF 2 sono ambedue cubici (nonostante la diversa morfologia!)
2 Definizioni utili: Una trasformazione geometrica che porta un oggetto in autocoincidenza è detta operazione di simmetria. Elemento di simmetria: ente geometrico che permette l esistenza di operazioni di simmetria. Es.: un vettore di traslazione reticolare a (elemento di simmetria) permette l esistenza di operazioni di simmetria caratterizzate dalla traslazione secondo na (n intero, positivo, nullo o negativo). Se l operazione di simmetria lascia inalterato almeno un punto, si parla di simmetria puntuale. Il luogo geometrico (punto, linea o piano) che è inalterato dall operazione di simmetria coincide con l elemento di simmetria. Identità: operazione banale che lascia inalterato un oggetto Simbolo (E) In termini geometrici in termini matriciali E x, y, z in x, y, z x x y = y z z
3 Piano di Riflessione: lascia inalterato l oggetto per rilessione normale ad esso. Simbolo = m In termini geometrici in termini matriciali m y x, y, z in x, -y, z x x y = y z z Asse di rotazione: lascia indistinguibile un oggetto dopo rotazione intorno ad esso. L ordine dell asse è dato da X, ove X = 360 /ε ed ε è il minimo angolo diverso da 0 richiesto per avere autocoincidenza. Asse binario: X = 2; ε = 180 Simbolo (2) In termini geometrici in termini matriciali 2 y x, y, z in -x, y, -z x x y = y z z
4 Asse ternario: X = 3; ε = 120 ; Simbolo 3 Asse quaternario: X = 4; ε = 90 ; 4 4 z x, y, z in y, -x, z x x y = y z z Asse quinario: X = 5; ε = 72 ; 5 Asse senario: X = 6; ε = 60 ; 6 etc. N.B. una rotazione di 360 corrisponde con l identità: X = 1, ε = 360, Simbolo (1) Centro di inversione: correla coppie di punti opposti rispetto ad esso tramite l operazione di inversione. Simbolo (-1) In termini geometrici in termini matriciali -1 x, y, z in -x, -y, -z x x y = y z z
5 Combinazione di operazioni di simmetria (concettualmente, moltiplicazione) C = A*B significa applicare un operazione B, poi la A, per ottenere l operazione C P.es. Due rotazioni consecutive concordi di 90 generano una rotazione di 180 : 2 = 4 * = * P.es. Due rotazioni consecutive discordi di 90 generano una rotazione di 0 : E = inv(4)*4 oppure E = 4-1 * = inv * P.es. Una rotazione di 180 seguita da una riflessione attraverso un piano perpendicolare all asse binario equivale ad una inversione: -1 = m y * 2 y = * Esistono operazioni di simmetria che concettualmente derivano dalla combinazione di inversioni, riflessioni e rotazioni, ma le cui componenti non sono operazioni di simmetria dell oggetto: operazioni composte.
6 Asse di rotoinversione: operazione di simmetria composta generata dall applicazione successiva di una rotazione (X) ed una inversione (-1). Simbolo (-X) (-X) = (-1) * X Assi di rotoinversione 1: rotazione di inversione -1 = -1 * 1 2: rotazione di inversione -2 = -1 * 2 Quindi 2 = m 3: rotazione di inversione -3 = -1 * 3 4: rotazione di 90 + inversione -4 = -1 * 4-4 z x, y, z in -y, x, -z x x y = y z z 6: rotazione di 60 + inversione -1 = -1 * 6 1: rotazione di inversione -1 = -1 * 1
7 Solo assi di rotoinversione di ordine dispari (-1 e 3) implicano la presenza effettiva di un centro ( 1) di inversione. L applicazione successiva di due rotoinversioni 4 (attorno allo stesso asse) genera una rotazione di 180 (asse binario). 2 z = -4 z * -4 z = * Assi di rotoriflessione: operazioni di simmetria composta generate dall applicazione successiva di una rotazione intorno ad un asse (X) ed una riflessione nel piano normale ad esso (-2 = m). Simbolo (S x ) (S x ) = (-2) * X Le operazioni ad esso associate non sono nuove operazioni di simmetria: infatti si dimostra che: S 1 = m; S 2 = -1; S 3 = -6; S 4 = -4; S 6 = -3
8 Definizione di Gruppo matematico: Collezione di elementi caratterizzati da una operazione, detta di moltiplicazione tale che: 1. Esiste l elemento neutro; 2. Per ogni elemento esiste l elemento inverso; 3. Il prodotto tra due elementi appartiene alla collezione. Esempi: L insieme dei numeri interi, negativi, nulli e positivi. Esso costituisce gruppo rispetto all operazione di addizione (+), con elemento nullo lo 0 ed inverso inv(n) = (-n), dato che per ogni n: 1. n = n = n + (-n) 3. n+m appartiene all insieme L insieme dei numeri razionali (tranne lo zero!). Esso costituisce gruppo rispetto all operazione di moltiplicazione (*), con elemento nullo 1 ed inverso inv(n) = n -1, dato che per ogni n: 1. n = n * = n * inv(-n) 3. n*m appartiene all insieme Gruppo di simmetria: collezione di operazioni (non elementi!) di simmetria che soddisfano le definizioni di gruppo, e per cui il prodotto è l applicazione successiva ordinata delle operazioni di base. Non è detto che A*B = B*A, ovvero il prodotto non è necessariamente commutativo (vedi l algebra delle matrici ). Per i gruppi di simmetria, E (o 1) è l elemento neutro. inv(-1) = E; inv(m) = E; inv(x) = rotazione di 360/X ; inv(-x) = rotoinversione di 360/X
9 Simmetria molecolare (puntuale): Ogni molecola (rigida e statica ) ha una ben determinata simmetria, caratterizzata da elementi di simmetria ed operazioni di simmetria che costituiscono un gruppo. Il gruppo puntuale contiene tutte le operazioni di simmetria e può essere caratterizzato dalla notazione di Schönflies (tipica per i chimici) o quella di Hermann-Mauguin (tipica per i fisici, i cristallografi ed i mineralogisti). Esiste una corrispondenza biunivoca tra le due notazioni. E anche possibile caratterizzare la morfologia di un cristallo (o qualsiasi altro oggetto finito) con le stesse notazioni. Esempi: Molecola: H-M Sch. CH 3 -CHFCl 1 C 1 m-[ch(oh)cooh] 2, ac. Mesotartarico -1 C i 1-cloronaftalene, o NOCl m C s E-1,2-dicloroetilene 2/m C 2h Difenilacetilene, staggered 222 D 2 Z-1,2-dicloroetilene mm2 C 2v Etilene mmm D 2h Naftalene mmm D 2h C(SCH 3 ) 4-4 S 4 XeOF 4 4mm C 4v C 3 H 4 allene -42m D 2d [PtCl 4 ] 2-4/mmm D 4h IO 3 -, SeO 3 2-, AsO 3 3-3m C 3v Cicloesano a sedia -3m D 3d H 3 BO 3-6 C 3h Esaazacoronene 6/m C 6h Esafenilbenzene (propeller) 622 D 6 NO 3 -, CO 3 2-, PF 5-6m2 D 3h Benzene 6/mmm D 6h C(CH 3 ) 4 (sfalsato) 23 T
10 CH 4-43m T d SF 6, C 8 H 8 cubano m-3m O h Etano, φ = 0, 120, 240 eclissato -6m2 D 3h Etano, φ = 60, 180, 300 sfalsato -3m D 3d Etano, φ k*60 32 D 3 Gruppi puntuali non cristallografici: CO, HCN, CN - m C v H 2, CO 2, C 2 H 2 /mm D h Ferrocene eclissato 5/mm2 D 5h Ferrocene sfalsato -10m2 D 5d S 8-82m D 4d C 60 2/m 3 5 I h
11 Determinazione sistematica del gruppo puntuale Primi passi: 1. Determinare quanti più possibili elementi di simmetria sono presenti; 2. Determinare se ci sono uno o più assi di ordine superiore a 2 (tipo 3, 4, etc.) 3. Determinare se c è un centro di inversione. Usare un diagramma di flusso del tipo:
12
13 Regole di nomenclatura di Hermann-Mauguin: X2 = asse di rotazione X e assi binari ad esso Xm = asse di rotazione X e piani di rifl. ad esso // -X2 = asse di rotoinversione X e assi binario ad esso -Xm = asse di rotoinversione X e piani di rifl. ad esso // X/mm(m) = asse di rotazione X e piani di rifl. sia // I diversi gruppi puntuali cristallografici (32 classi cristalline) possono essere classificati nei 7 sistemi cristallini:
14 Nel sistema cubico: il primo simbolo si riferisce alla direzione x (o y, o z) il secondo agli assi ternari, il terzo agli assi paralleli alle diagonali di faccia (od ai piani normali ad esse) Quindi, per un cubo: 4/m 3 2/m, spesso abbreviato in m3m Per un tetraedro, il gruppo puntuale ha simbolo -43m Nel sistema ortorombico: i tre simboli riguardano gli assi x, y e z, nell ordine Un prisma retto ha simmetria 2/m 2/m 2/m (ovvero mmm) Una piramide rettangolare retta ha simmetria mm2 Nel sistema monoclino: l unico simbolo si riferisce all asse y: può essere 2, m o 2/m Nel sistema triclino: Esistono solo 1 e 1 Nei sistemi tetragonale, esagonale e trigonale: il primo simbolo si riferisce all asse unico (z) gli altri due a direzioni perendicolari ad esso, lungo gli assi x (o y) e le bisettrici di ciascun quadrante (o sestante) Il gruppo puntuale è 4 2 m Quanto sono comuni queste classi cristalline? Non esistono casi reali di cristalli delle classi 432 e 6 50% dei composti inorganici = m e 2/m 30-40% dei composti organici = classe 2/m composti biologici chirali = spesso classe 2
15 Questi tre cristalli hanno ovviamente forme diverse (ed anche simmetrie) diverse: appartengono a classi cristalline differenti (gruppi puntuali diversi). Una volta aggiunto il centro di inversione (che tutti i reticoli posseggono!), questi cristalli hanno simmetria puntuale mmm, e quindi appartengono tutti al sistema ortorombico. Così come erano stati individuati 10 gruppi planari cristallografici indipendenti, esistono solo 32 gruppi puntuali 3D cristallografici, compatibili cioè con la traslazione. (J.F.C.Hessel, 1830) Ma questi cristalli hanno simmetria diverse: avranno anche proprietà fisiche diverse? Le proprietà fisiche (ottiche, termiche, magnetiche, etc.) sono normalmente espresse in termini di coefficienti, ovvero come rapporto tra due quantità misurabili. Esempi: A = εcl (coefficiente di estinzione molare) m = αe (polarizzabilità)
16 Le quantità misurabili sono spesso vettori (dotati di modulo e direzione), o più raramente scalari (non dipendono dalla direzione) I cristalli sono oggetti anisotropi e comportano una descrizione delle proprietà fisiche in termini vettoriali. Solo in qualche caso (alte simmetrie, cristalli isotropi) o per certe proprietà (T, calore, ε, etc.) si incontrano grandezze scalari. Come caratterizzare dal punto di vista della simmetria e delle diverse proprietà fisiche le 32 classi cristalline? Enantiomorfismo (cristalli non sovrapponibili alla propria immagine speculare). Il gruppo puntuale (1) C 1 è detto asimmetrico; Gli altri gruppi puntuali che hanno solamente assi di rotazione propri sono detti chirali o dissimmetrici; I gruppi enantiomorfici sono: X: (1), 2, 3, 4, 6 gruppi C n ; X2: 222, 32, 422, 622 gruppi D n ; X3: 23, 432 gruppi T, O Molecole enantiomorfiche sono dette enantiomeri. Cristalli che contengono un enantiomero risolto possono solamente appartenere a una delle classi enantiomorfe. Attività ottica: abilità di molecole o cristalli a ruotare il piano della luce polarizzata. Può esistere solamente in gruppi puntuali enantiomorfici. Attività ottica cristallina: Il cristallo è otticamente attivo, ma la sua attività ottica è persa quando esso è sciolto o fuso. Sono enatiomorfiche sia la morfologia che la struttura. Esempi: MgSO 4.7H 2 O (222), SiO 2 (quarzo, 32), NaClO 3 (23).
17 Attività ottica molecolare: I cristalli di molecole enantiomere sono enantiomorfi, e l attività ottica viene conservata per dissoluzione o fusione. La proprietà ottica è assegnata non all impaccamento cristallino, ma alla dissimmetria molecolare. Esempi: acido D-tartarico (2), otticamente attivo acido DL-tartarico (-1), racemato, inattivo acido meso-tartatico (-1), inattivo Cristalli dei gruppi puntuali m, mm2, -4 e 42m possono mostrare altre proprietà ottiche, diverse dalla rotazione lella luce polarizzata (birifrangenza, pleocroismo, dispersione) Piezoelettricità: capacità di un cristallo di sviluppare separazione di cariche su facce opposte per pressione o tensione lungo certe direzioni. Esempio: cristalli di quarzo (32) tagliati normalmente ad a. La direzione di pressione o tensione è una direzione polare. Assi polari sono quelli la cui inversione porta a cambiamento di proprietà fisiche (direzioni parallele ed antiparallele). Pressione o tensione sviluppano cariche opposte.
18 Effetto reversibile: applicando un campo elettrico, i cristalli si espandono o si comprimono. L effetto piezoelettrico si osserva solamente in gruppi puntuali che hanno assi polari (che, ovviamente, sono noncentrosimmetrici). I gruppi in cui l effetto piezoelettrico è possibile sono 20 dei 21 gruppi che non posseggono centri di inversione (tranne il 432!). Applicazioni tecnologiche: amplificatori, microfoni, componenti elettronici. Radio a Galena (PbS, -43m), bilance e orologi al quarzo. Piroelettricità: capacità di un cristallo a sviluppare cariche opposte su facce opposte se scaldato. Se raffreddato, si sviluppano cariche di segno opposto. Esempio: Tormalina (3m). I cristalli piroelettrici hanno un dipolo permanente. Il cambio di temperatura modifica l entità (modulo) del dipolo. L effetto è temporaneo, per conduzione le cariche vengono più o meno rapidamente dissipate. L effetto piroelettrico è possibile solamente in quei gruppi puntuali le cui operazioni di simmetria non alterano la direzione del dipolo, ovvero i gruppi 2, 3, 4 e 6; mm2, 3m, 4mm e 6mm (il dipolo giace lungo l asse unico) e i gruppi 1 ed m. (10 gruppi puntuali). L effetto piroelettrico si osserva solamente in questi 10 gruppi puntuali (che, ovviamente, sono noncentrosimmetrici). I 10 gruppi polari sono quindi: m mm2 3m 4mm 6mm Tutti i gruppi piroelettrici sono anche piezolettrici (NON vale il contrario!)
19 Momento Dipolare Molecolare: Per molecole isolate, posseggono un momento dipolare (permanente) non-nullo quelle appartenenti alle classi di simmetria che premettono la piroelettricità. La misura del momento dipolare permette di ottenere informazioni stereochimiche di molecole normalmente gassose, non facilmente ottenibili come cristalli. Esempio: PF 3 ha un momento dipolare, BF 3 no. Infatti, PF 3 è piramidale (-6m2), mentre BF 3 è planare (3m). Ferroelettricità: capacità di un cristallo a sviluppare cariche opposte su facce opposte se sottoposto ad un campo elettrico. Valgono le stesse regole della piroelettricità. Esempio: BaTiO 3. Ad alta T (> T Curie), cubico m3m (struttura perovskite); A bassa T (<T Curie), si distorce (due assi si accorciano, uno si allunga): tetragonale 4mm; Ulteriore diminuzione di T porta successivamente a mm2 e poi a 3m (tutti gruppi polari).
20 Ricapitolando: I sistemi cristallini sono 7 Triclino, Monoclino, Ortorombico, Trigonale, Esagonale, Tetragonale, Cubico I reticoli di Bravais sono 14 Triclino P, Monoclino P,C; Ortorombico P,C,I,F; Romboedrico R, Esagonale P, Tetragonale P,I, Cubico P,I,F; I gruppi puntuali cristallografici sono 32 (classi) I gruppi puntuali centrosimmetrici sono 11 I gruppi puntuali non-centrosimmetrici sono 21 I gruppi puntuali enantiomorfi sono 11 I gruppi puntuali otticamente attivi sono 11 (+4 = 15) I gruppi puntuali piezoelettrici sono 20 I gruppi puntuali piroelettrici sono 10 (polari)
21 Elementi di simmetria traslazionale Traslazione: operazione che non riorienta un oggetto ma lo sposta di un multiplo di un vettore (reticolare). In termini geometrici T(n,m,p) x, y, z in x+na, y+mb, z+pc in termini matriciali (somma di vettori) x na x y = mb + y z pc z Asse di rotazione elicogiro o screw: genera operazioni composte da una rotazione propria ed una traslazione di una frazione di un vettore traslazionale. Angolo di rotazione ε = 360 /X (X = 1, 2, 3, 4, 6) Traslazione di un vettore s parallelo all asse t (di lunghezza τ), dove s è la componente elicogira. Si dimostra che s può valere solo 0, τ/x, 2τ/X, (X-1)τ/X; Le diverse operazioni indipendenti sono X 0, X 1, X 2, X X-1
22 Ovviamente X 0 = X; Per assi elicogiri binari esiste solo 2 1 ; Per assi elicogiri ternari esistono solo 3 1 e 3 2 ; 3 1 e 3 2 sono mutuamente enantiomorfi. Per assi elicogiri quaternari esistono solo 4 1, 4 2, 4 3 ; 4 1 e 4 3 sono mutuamente enantiomorfi. Per assi elicogiri senari esisono solo 6 1, 6 2, 6 3, 6 4, 6 5 ; 6 1 e 6 5 sono mutuamente enantiomorfi. 6 2 e 6 4 sono mutuamente enantiomorfi. In termini matriciali: x = Mx + s (rotazione + traslazione)
23
24 Piano di riflessione con scorrimento (glide plane): genera operazioni composte da una riflessione propria ed una traslazione di una frazione di un vettore traslazionale. Riflessione Traslazione di un vettore g parallelo al piano glide, dove g è la componente di scorrimento. Tipicamente, g è metà della traslazione di reticolo parallela al piano glide, ovvero g = ½ τ
25 Piano glide di tipo a: riflessione normale ad un piano con traslazione di ½ a. Piano glide di tipo b: riflessione normale ad un piano con traslazione di ½ b. Piano glide di tipo c: riflessione normale ad un piano con traslazione di ½ c. Esempio di Piano glide di tipo n: (diagonale) riflessione normale ad un piano con traslazione di ½ (a+b). Esempio di Piano glide di tipo d: (diamond, raro) riflessione normale ad un piano con traslazione di ¼ (t 1 +t 2 ). In termini matriciali: x = Mx + g (riflessione + traslazione)
26 Gruppi spaziali. Combinando i 32 gruppi puntuali con i 14 Reticoli di Bravais (ovvero associando alle operazioni puntuali le operazioni di traslazione) si possono ottenere 230 Gruppi Spaziali (e non 32 x 14 = 448!) I gruppi spaziali, determinati indipendentemente da Fedorov (Mosca,), Sohncke (Monaco), Schönflies (Gottinga) e Barlow (Londra) verso la fine del 1800, sono veri gruppi matematici che contengono simmetrie puntuali, traslazionali e composte (assi screw e piani glide). Qualsiasi sistema 3D ordinato DEVE appartenere ad uno delle 230 tipologie possibili, così come in 2D erano possibili solamente 17 gruppi planari. I diversi gruppi spaziali indicano la relazione reciproca di motivi nello spazio, senza definire la forma e l orientazione del motivo di base. P.es. AgClO 4 ed urea NH 2 CONH 2 mostrano lo stesso gruppo spaziale (I-4m2) ma strutture (motivi molecolari o ionici) completamente diverse! L intera catalogazione è distribuita dalle Tabelle Internazionali per le Cristallografia, che utilizza la simbologia di Herrmann-Mauguin. Il simbolo H-M contiene dapprima una lettera maiuscola, che individua il reticolo di Bravais: P, C, I, F, R (qualche volta, per diversa orientazione degli assi appaiono anche A e B). Seguono poi 1, 2 o 3 campi (numeri o lettere) che descrivono elementi di simmetria minimali (detti generatori), che per loro composizione, assieme al tipo di reticolo, permettono di generare l insieme completo delle operazioni di simmetria del gruppo.
27 Esempi: P 1 indica un gruppo spaziale triclino (ovviamente primitivo) che contiene un centro di simmetria. L unico altro gruppo spaziale triclino è P 1 (acentrico). P 2/m indica un gruppo spaziale monoclino primitivo, che possiede un asse binario perpendicolare ad un piano di riflessione (e quindi generano un centro). Suoi sottogruppi propri sono P 2 (acentrico), P m (acentrico) e P 1 (triclino, centrico!), a seconda che io rimuova, delle quattro operazioni iniziali [E, -1, 2, m] le coppie (-1,m), (-1,2) o (2,m). C 2/m è un gruppo spaziale che contiene [E, -1, 2, m] + altre quattro operazioni generate dalla traslazione di reticolo C +1/2(a+b). P 2 1 /c indica in gruppo spaziale monoclino primitivo, in cui sono presenti un asse elicogiro binario ed un piano di scorrimento perpendicolare ad esso, con traslazione di ½ c. La combinazione di questi due elementi genera un centro di simmetria (-1) che non sta né sul piano né sull asse. Sottogruppi propri sono P 2 1 (acentrico), P c (acentrico) e P 1 (triclino, centrico!), a seconda che io rimuova, delle quattro operazioni iniziali [E, -1, 2 1, c] le coppie (-1,c), (-1,2 1 ) o (2 1 /c). P b c n è un gruppo spaziale ortorombico primitivo, che possiede un piano di scorrimento di tipo b perpendicolare ad a, un piano di scorrimento di tipo c perpendicolare a b, ed un piano di scorrimento diagonale n perpendicolare a c. Questi generatori implicano anche la presenta di centri di inversione (-1) ed assi binari propri od elicogiri. L insieme delle otto operazioni di simmetria che fanno gruppo pertanto è: [E, 2 1 (a), 2(b), 2 1 (c), -1, b( a), c( b), n( c)] Il simbolo H-M esteso è P 2 1 /b 2/c 2 1 /n
28 P è un gruppo spaziale tetragonale primitivo che possiede un asse elicogiro 4 2 (lungo z) ed assi binari sia lungo gli assi coordinati (x e y) che lungo le bisettrici dei quadranti (rette y = x e y = -x). La combinazione di questi elementi NON genera centri di simmetria. Il gruppo è acentrico. P 6 3 m c è un gruppo esagonale (acentrico) che possiede un asse elicogiro 6 3 (lungo z), un piano di riflessione (verticale) coincidente con xz (ed anche yz!) ed un piano di riflessione (verticale) con traslazione di ½ c e contenente la bisettrice di un sestante del piano xy (a 30 dall asse x). F d 3 m è un gruppo cubico (centrico), che contiene ben 192 operazioni di simmetria. Il reticolo è Cubico a facce centrate (F), esistono piani di scorrimento di tipo diamond, assi ternari lungo le diagonali di corpo e piani di riflessione m che normali alle diagonali di faccia. Tutte le altre operazioni di simmetria sono generate dalle varie combinazioni di F, d, 3 ed m.
29 Proprietà dei gruppi spaziali: Il numero di punti equivalenti nella cella unitaria è chiamata molteplicità. Essa equivale al numero di operazioni di simmetria del gruppo. Una posizione generale è un gruppo di punti equivalenti con simmetria puntuale (simmetria di sito) 1. Ovvero nessuna! Una posizione speciale è un gruppo di punti equivalenti con simmetria puntuale (simmetria di sito) maggiore di 1. L unità asimmetrica di un gruppo spaziale è la più piccola parte della cella che, attraverso le operazioni di simmetria di gruppo, riempie completamente la cella stessa. I suo volume è dato da: V(unità asim.) = V(cella)/molteplicità della posizione generale All interno dell unità asimmetrica NON esiste alcuna coppia di punti correlata da un operazione di simmetria del gruppo. L unità asimmetrica contiene TUTTA l informazione necessaria per la descrizione della struttura cristallina, una volta noti il gruppo spaziale e la cella. Per descrivere una struttura cristallina bisogna quindi indicare le dimensioni della cella (6 parametri), il gruppo spaziale e il motivo (o contenuto) dell unità asimmetrica.
30 Come si leggono le Tabelle Internazionali? (1) Simbolo Gruppo Spaziale (H-M), Simbolo Schönflies, gruppo puntuale, sistema cristallino, numero d ordine, simbolo esteso; (2) Proiezione degli elementi di simmetria sul piano xy con a verticale e b orizzontale, origine in alto a sinistra; (3) Proiezione di una posizione generale sul piano xy, con indicazione della coordinata z e della chiralità (,); (4) Scelta dell origine della cella rispetto agli elementi di simmetria; (5) Indicazione dell unità asimmetrica; (6) Le operazioni di simmetria del gruppo spaziale; (7) Molteplicità della posizione, posizione di Wyckoff (ordine antialfabetico), la simmetria di sito (gruppo puntuale), coordinate dei punti equivalenti.
31
Reticoli di Bravais e sistemi cristallini
 Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Simmetrie Cristallografiche A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
Materiale didattico: dispense fornite durante il corso
 Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri:
 DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
Struttura e geometria cristallina
 Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Simmetria Molecolare
 Simmetria Molecolare Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca simmetria: artefatti e natura elemento di simmetria operazione di simmetria piano di riflessione riflessione elementi
Simmetria Molecolare Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca simmetria: artefatti e natura elemento di simmetria operazione di simmetria piano di riflessione riflessione elementi
La matematica del CAD. Vettori e Matrici
 La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) GRUPPO: insieme di elementi correlati dalle seguenti regole:
 APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
POLIEDRI IN CRISTALLOGRAFIA
 POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
INDICE CAPITOLO 1 CAPITOLO 1
 INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
LA PROIEZIONE STEREOGRAFICA (PARTE I)
 Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
VETTORI E SCALARI DEFINIZIONI. Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura.
 VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: Fax
 I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 marconi@provincia.padova.it www.itismarconipadova.it Settore tecnologico Indirizzo meccanica meccatronica ed energia
I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 marconi@provincia.padova.it www.itismarconipadova.it Settore tecnologico Indirizzo meccanica meccatronica ed energia
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
CORSO DI BIOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO
 CORSO DI BIOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO LE IMMAGINE CONTENUTE SONO STATE TRATTE DAL LIBRO FONDAMENTI DI FISICA DI D. HALLIDAY,
CORSO DI BIOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO LE IMMAGINE CONTENUTE SONO STATE TRATTE DAL LIBRO FONDAMENTI DI FISICA DI D. HALLIDAY,
proprietà: comportamento del materiale in determinate condizioni, quindi possibilità di prevedere e progettare
 La struttura dei materiali definizioni e classificazioni Chi è lo scienziato dei materiali? un conoscitore della natura dei materiali e quindi di: struttura: concetto vago perché molte definizioni sono
La struttura dei materiali definizioni e classificazioni Chi è lo scienziato dei materiali? un conoscitore della natura dei materiali e quindi di: struttura: concetto vago perché molte definizioni sono
Posizioni Atomiche nelle Celle Unitarie Cubiche
 Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
1. Le forze intermolecolari 2. Molecole polari e apolari 3. Le forze dipolo-dipolo e le forze di London 4. Il legame a idrogeno 5. Legami a confronto
 Unità n 12 Le forze intermolecolari e gli stati condensati della materia 1. Le forze intermolecolari 2. Molecole polari e apolari 3. Le forze dipolo-dipolo e le forze di London 4. Il legame a idrogeno
Unità n 12 Le forze intermolecolari e gli stati condensati della materia 1. Le forze intermolecolari 2. Molecole polari e apolari 3. Le forze dipolo-dipolo e le forze di London 4. Il legame a idrogeno
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
Capitolo 12 Le forze intermolecolari e gli stati condensati della materia
 Capitolo 12 Le forze intermolecolari e gli stati condensati della materia 1. Le forze intermolecolari 2. Molecole polari e apolari 3. Le forze dipolo-dipolo e le forze di London 4. Il legame a idrogeno
Capitolo 12 Le forze intermolecolari e gli stati condensati della materia 1. Le forze intermolecolari 2. Molecole polari e apolari 3. Le forze dipolo-dipolo e le forze di London 4. Il legame a idrogeno
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova
 Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
Nozioni introduttive e notazioni
 Nozioni introduttive e notazioni 1.1 Insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Definiamo un insieme come una collezione
Nozioni introduttive e notazioni 1.1 Insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Definiamo un insieme come una collezione
Corso di Fisica. Lezione 2 Scalari e vettori Parte 1
 Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Reticoli bidimensionali e simmetria
 Reticoli bidimensionali e simmetria La descrizione dei tutte le strutture cristalline può avvenire seguendo due processi logici: Elencando, caso per caso, ogni struttura, tentando poi di trovare delle
Reticoli bidimensionali e simmetria La descrizione dei tutte le strutture cristalline può avvenire seguendo due processi logici: Elencando, caso per caso, ogni struttura, tentando poi di trovare delle
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Le simmetrie dei poliedri regolari
 Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
2. I numeri reali e le funzioni di variabile reale
 . I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
. I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
V il segmento orientato. V con VETTORI. Costruzione di un vettore bidimensionale
 VETTORI Costruzione di un vettore bidimensionale Nel piano con un righello si traccia una retta r tratteggiata Su r si disegna un segmento di lunghezza l d una delle estremità si disegni la punta di una
VETTORI Costruzione di un vettore bidimensionale Nel piano con un righello si traccia una retta r tratteggiata Su r si disegna un segmento di lunghezza l d una delle estremità si disegni la punta di una
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
Descrittori quantitativi della geometria cristallina: assi, piani ed indici.
 Descrittori quantitativi della geometria cristallina: assi, piani ed indici. Assi di cella (con angoli interassiali) Reticolo di Bravais Simmetria puntuale (classi) Simmetria spaziale Come individuare
Descrittori quantitativi della geometria cristallina: assi, piani ed indici. Assi di cella (con angoli interassiali) Reticolo di Bravais Simmetria puntuale (classi) Simmetria spaziale Come individuare
Che cos è un insieme? Come si individua un insieme? 1. Scrivendone esplicitamente gli elementi: C = {2, 4, 6, 8, 10,...}.
 Teoria degli insiemi Che cos è un insieme? Come si individua un insieme? 1. Scrivendone esplicitamente gli elementi: A = {a, b, c} B = {1, 2} C = {2, 4, 6, 8, 10,...}. 2. Enunciando una proprietà che è
Teoria degli insiemi Che cos è un insieme? Come si individua un insieme? 1. Scrivendone esplicitamente gli elementi: A = {a, b, c} B = {1, 2} C = {2, 4, 6, 8, 10,...}. 2. Enunciando una proprietà che è
1 Nozioni utili sul piano cartesiano
 Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica
 Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}). 2) Nello spazio vettoriale
Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}). 2) Nello spazio vettoriale
a) Parallela a y = x + 2 b) Perpendicolare a y = x +2. Soluzioni
 Svolgimento Esercizi Esercizi: 1) Una particella arriva nel punto (-2,2) dopo che le sue coordinate hanno subito gli incrementi x=-5, y=1. Da dove è partita? 2) Disegnare il grafico di C = 5/9 (F -32)
Svolgimento Esercizi Esercizi: 1) Una particella arriva nel punto (-2,2) dopo che le sue coordinate hanno subito gli incrementi x=-5, y=1. Da dove è partita? 2) Disegnare il grafico di C = 5/9 (F -32)
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
1. LA GEOMETRIA ANALITICA
 LA GEOMETRIA ANALITICA IL PIANO CARTESIANO Coordinate cartesiane Due rette orientate nel piano perpendicolari tra loro, aventi come punto d intersezione il punto O, costituiscono un sistema di riferimento
LA GEOMETRIA ANALITICA IL PIANO CARTESIANO Coordinate cartesiane Due rette orientate nel piano perpendicolari tra loro, aventi come punto d intersezione il punto O, costituiscono un sistema di riferimento
Testi consigliati: Walter Borchardt-Ott, Crystallochemistry, Springer Christopher Hammond, Introduzione alla Cristallografia, Zanichelli
 Cristallografia Corso complementare per la laurea triennale in Chimica Numero di crediti: 3 Docente: Anna Corrias; Tel: 070 6754351; e-mail: corrias@unica.it Programma: Definizione di stato cristallino,
Cristallografia Corso complementare per la laurea triennale in Chimica Numero di crediti: 3 Docente: Anna Corrias; Tel: 070 6754351; e-mail: corrias@unica.it Programma: Definizione di stato cristallino,
Valitutti, Falasca, Tifi, Gentile. Chimica. concetti e modelli.blu
 Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 15 Le forze intermolecolari e gli stati condensati della materia 3 Sommario 1. Le forze intermolecolari 2. Molecole polari e
Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 15 Le forze intermolecolari e gli stati condensati della materia 3 Sommario 1. Le forze intermolecolari 2. Molecole polari e
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A
 MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
Le trasformazioni geometriche nel piano cartesiano. x = ϕ(x', y') τ 1 : G(x', y') = 0. la sua inversa.
 τ : P P' oppure P'=τ(P) P immagine di P trasformato di P secondo τ se α è una figura geometrica α =τ(α) è la figura geometrica trasformata x' = f (x, y) τ : y' = g(x, y) espressione analitica della trasformazione
τ : P P' oppure P'=τ(P) P immagine di P trasformato di P secondo τ se α è una figura geometrica α =τ(α) è la figura geometrica trasformata x' = f (x, y) τ : y' = g(x, y) espressione analitica della trasformazione
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
Prontuario degli argomenti di Algebra
 Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Si ottiene facendo precedere i numeri naturali dal segno + o dal segno -.
 I numeri naturali non sono adatti per risolvere tutti i problemi. Esempio. La temperatura atmosferica di un mattino estivo, sopra lo zero, viene indicata con un numero preceduto dal segno + (+19 C, +25
I numeri naturali non sono adatti per risolvere tutti i problemi. Esempio. La temperatura atmosferica di un mattino estivo, sopra lo zero, viene indicata con un numero preceduto dal segno + (+19 C, +25
2 HCl. H 2 + Cl 2 ATOMI E MOLECOLE. Ipotesi di Dalton
 Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
ALGEBRA VETTORIALE Corso di Fisica per la Facoltà di Farmacia, Università Gabriele D Annunzio, Chieti-Pescara, Cosimo Del Gratta 2008
 LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
Corso di Studi di Fisica Corso di Chimica
 Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Lezioni 17-18 2010 Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della
Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Lezioni 17-18 2010 Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della
Richiami sugli insiemi numerici
 Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
Gli stati di aggregazione della materia.
 Gli stati di aggregazione della materia. Stati di aggregazione della materia: Solido, liquido, gassoso Passaggi di stato: Solido Liquido (fusione) e liquido solido (solidificazione); Liquido aeriforme
Gli stati di aggregazione della materia. Stati di aggregazione della materia: Solido, liquido, gassoso Passaggi di stato: Solido Liquido (fusione) e liquido solido (solidificazione); Liquido aeriforme
Matematica per le scienze sociali Elementi di base. Francesco Lagona
 Matematica per le scienze sociali Elementi di base Francesco Lagona University of Roma Tre F. Lagona (francesco.lagona@uniroma3.it) 1 / 24 Outline 1 Struttura del corso 2 Algebra booleana 3 Algebra degli
Matematica per le scienze sociali Elementi di base Francesco Lagona University of Roma Tre F. Lagona (francesco.lagona@uniroma3.it) 1 / 24 Outline 1 Struttura del corso 2 Algebra booleana 3 Algebra degli
Informatica Grafica. Un introduzione
 Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
1. SIMMETRIA. 1.1 Operazioni ed elementi di simmetria puntuale
 1. SIMMETRIA Molte proprietà molecolari sono determinate dalla simmetria delle molecole stesse, come del resto molte proprietà dei solidi sono determinate dalla simmetria del loro reticolo cristallino.
1. SIMMETRIA Molte proprietà molecolari sono determinate dalla simmetria delle molecole stesse, come del resto molte proprietà dei solidi sono determinate dalla simmetria del loro reticolo cristallino.
1- Geometria dello spazio. Vettori
 1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
Scienza dei Materiali 1 Esercitazioni
 Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
SIMMETRIE NEL PIANO CARTESIANO
 Simmetrie nel piano cartesiano - Marzo 011 SIMMETRIE NEL PIANO CARTESIANO SIMMETRIE RISPETTO AGLI ASSI CARTESIANI ASSE X: P ( x,y ) a P1 ( x, y ) ; punto medio: M1 ( x,0) ASSE Y: P ( x,y ) a P ( x, y ),
Simmetrie nel piano cartesiano - Marzo 011 SIMMETRIE NEL PIANO CARTESIANO SIMMETRIE RISPETTO AGLI ASSI CARTESIANI ASSE X: P ( x,y ) a P1 ( x, y ) ; punto medio: M1 ( x,0) ASSE Y: P ( x,y ) a P ( x, y ),
Definizione: Dato un sottoinsieme non vuoti di. Si chiama funzione identica o identità di in sé la funzione tale che.
 Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
ARITMETICA. Gli insiemi UNITA 1. Programma svolto di aritmetica e geometria classe 1 ^ D A.S
 Programma svolto di aritmetica e geometria classe 1 ^ D A.S. 2014-2015 Scuola Secondaria di primo grado S. Quasimodo di Fornacette Istituto Comprensivo di Calcinaia DOCENTE: Monica Macchi UNITA ARITMETICA
Programma svolto di aritmetica e geometria classe 1 ^ D A.S. 2014-2015 Scuola Secondaria di primo grado S. Quasimodo di Fornacette Istituto Comprensivo di Calcinaia DOCENTE: Monica Macchi UNITA ARITMETICA
CHIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA.
 CIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA. non simmetrica rispetto al piano piano di simmetria La mano destra non è sovrapponibile alla mano sinistra: ne è invece l'immagine
CIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA. non simmetrica rispetto al piano piano di simmetria La mano destra non è sovrapponibile alla mano sinistra: ne è invece l'immagine
Esercizi di Algebra 2, C.S. in Matematica, a.a
 26 Esercizi di Algebra 2, C.S. in Matematica, a.a.2008-09. Parte V. Anelli Nota. Salvo contrario avviso il termine anello sta per anello commutativo con identità. Es. 154. Provare che per ogni intero n
26 Esercizi di Algebra 2, C.S. in Matematica, a.a.2008-09. Parte V. Anelli Nota. Salvo contrario avviso il termine anello sta per anello commutativo con identità. Es. 154. Provare che per ogni intero n
Programma di Algebra 1
 Programma di Algebra 1 A. A. 2015/2016 Docenti: Alberto Canonaco e Gian Pietro Pirola Richiami su relazioni di equivalenza: definizione, classe di equivalenza di un elemento, insieme quoziente e proiezione
Programma di Algebra 1 A. A. 2015/2016 Docenti: Alberto Canonaco e Gian Pietro Pirola Richiami su relazioni di equivalenza: definizione, classe di equivalenza di un elemento, insieme quoziente e proiezione
ELEMENTI di TEORIA degli INSIEMI
 ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
GEOMETRIA ANALITICA. Il Piano cartesiano
 GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
Cos è un trasformazione chimica?
 Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Definizione: Due monomi si dicono simili se hanno la stessa parte letterale.
 CALCOLO LETTERALE Definizione: Data una formula si dicono variabili le lettere alle quali può essere sostituito qualsiasi valore numerico; i numeri si dicono, invece, costanti. Nella formula per il calcolo
CALCOLO LETTERALE Definizione: Data una formula si dicono variabili le lettere alle quali può essere sostituito qualsiasi valore numerico; i numeri si dicono, invece, costanti. Nella formula per il calcolo
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Gruppi puntuali. Primo elemento
 Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Grandezze scalari e vettoriali
 VETTORI Grandezze scalari e vettoriali Tra le grandezze misurabili alcune sono completamente definite da un numero e da un unità di misura, altre invece sono completamente definite solo quando, oltre ad
VETTORI Grandezze scalari e vettoriali Tra le grandezze misurabili alcune sono completamente definite da un numero e da un unità di misura, altre invece sono completamente definite solo quando, oltre ad
Funzioni reali di variabile reale
 Funzioni reali di variabile reale Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni reali di variabile reale 1 / 50 Funzioni Definizione Sia A un sottoinsieme di R.
Funzioni reali di variabile reale Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni reali di variabile reale 1 / 50 Funzioni Definizione Sia A un sottoinsieme di R.
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
TRASFORMAZIONI GEOMETRICHE
 TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
Moltiplicazione. Divisione. Multipli e divisori
 Addizione Sottrazione Potenze Moltiplicazione Divisione Multipli e divisori LE QUATTRO OPERAZIONI Una operazione aritmetica è quel procedimento che fa corrispondere ad una coppia ordinata di numeri (termini
Addizione Sottrazione Potenze Moltiplicazione Divisione Multipli e divisori LE QUATTRO OPERAZIONI Una operazione aritmetica è quel procedimento che fa corrispondere ad una coppia ordinata di numeri (termini
Combinazione operatori di simmetria senza componenti traslazionali
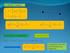 Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
La composizione di isometrie
 La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni + CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni + CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Elementi di Algebra Lineare. Spazio Vettoriale (lineare)
 Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
1.3. Logaritmi ed esponenziali
 1.3. Logaritmi ed esponenziali 1. Rappresentazione sugli assi cartesiani 2. Relazione 3. Definizione di funzione 4. La funzione esponenziale 5. Il logaritmo 6. La funzione logaritma 1-3 1 Rappresentazione
1.3. Logaritmi ed esponenziali 1. Rappresentazione sugli assi cartesiani 2. Relazione 3. Definizione di funzione 4. La funzione esponenziale 5. Il logaritmo 6. La funzione logaritma 1-3 1 Rappresentazione
C 4 H 10 C 4 H 10. Hanno la stessa formula molecolare C 4 H 10.
 Isomeria costituzionale negli alcani Isomeri costituzionali (strutturali): composti con uguale formula molecolare ma diversa formula di struttura (con un diverso ordine con cui sono legati i loro atomi).
Isomeria costituzionale negli alcani Isomeri costituzionali (strutturali): composti con uguale formula molecolare ma diversa formula di struttura (con un diverso ordine con cui sono legati i loro atomi).
Problemi sulla circonferenza verso l esame di stato
 Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria. PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13
 Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
IBRIDAZIONE e GEOMETRIA MOLECOLARE
 IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
R. Capone Analisi Matematica Integrali multipli
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Prodotto scalare e norma
 Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
APPUNTI DI MATEMATICA ALGEBRA \ CALCOLO LETTERALE \ MONOMI (1)
 LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2015/2016 M. Tumminello,
Distanza tra punti e punto medio di un segmento. x1 + x 2
 Distanza tra punti e punto medio di un segmento Siano P = (x 1, y 1 ) e Q = (x 2, y 2 ) due punti del piano cartesiano. La distanza di P da Q vale: P Q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 (si utilizza il Teorema
Distanza tra punti e punto medio di un segmento Siano P = (x 1, y 1 ) e Q = (x 2, y 2 ) due punti del piano cartesiano. La distanza di P da Q vale: P Q = (x 1 x 2 ) 2 + (y 1 y 2 ) 2 (si utilizza il Teorema
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
11 aprile Annalisa Tirella.
 Scienze dei Materiali A.A. 2010/2011 11 aprile 2011 Annalisa Tirella a.tirella@centropiaggio.unipi.it Metalli I metalli sono elementi chimici che possono essere utilizzati sia puri che in forma di leghe
Scienze dei Materiali A.A. 2010/2011 11 aprile 2011 Annalisa Tirella a.tirella@centropiaggio.unipi.it Metalli I metalli sono elementi chimici che possono essere utilizzati sia puri che in forma di leghe
