Sommario. Metodologie di progetto. Introduzione. Modello del Sistema. Diagramma a Blocchi. Progetto
|
|
|
- Leo Manzoni
- 8 anni fa
- Visualizzazioni
Transcript
1 Sommario Metodologie di progetto Massimo Violate troduzioe Progetto a Livello Porte Logiche Progetto a Livello Registri Progetto a Livello Sistema. troduzioe U sistema è ua collezioe di oggetti, compoeti, coessi a formare u etità omogeea co ua precisa fuzioalità La fuzioalità del sistema è data da: Fuzioi svolte dai compoeti Modo co cui soo coessi i compoeti. Modello del Sistema L attività di progetto è strettamete dipedete da quella di modellameto, attraverso la quale l idea di ciò che si vuole realizzare viee espressa formalmete utilizzado u appropriato modello della realtà Sul modello è possibile eseguire ua serie di verifiche (ad esempio tramite simulazioe) prima della realizzazioe fisica. Diagramma a Blocchi Progetto Vertici: compoeti Archi: liee per il trasferimeto dati x 1 AND NOT OR NOT x 1 EXOR x 2 Dati di parteza: Fuzioalità del sistema da realizzare Fuzioi svolte dai compoeti Progettare: coettere i compoeti i modo tale che il loro comportameto globale soddisfi la fuzioalità richiesta, ed il costo sia miimo. x 2 AND
2 Costo Espresso i termii ecoomici ($): Costo del progetto Costo di produzioe Costi di mautezioe Espresso i termii fisici : Velocità co cui è svolta la fuzioalità richiesta Cosumo di poteza Livello di Progetto E defiito dal tipo di compoeti utilizzati i fase di progetto U compoete ad u certo livello corrispode ad u isieme di compoeti a livello iferiore Livelli cosiderati: Livello Porte Logiche Livello Registri Livello Sistema. Caratteristiche Flusso di progetto Livello Porte Logiche Registri Sistema Compoeti Uità di Dato Porte Logiche, Bit Flip-Flop Registri, Reti Combiatorie, Parole Reti Sequeziali Blocchi CPU, Memorie di Parole Uità di Tempo ps-s s-µs ms-s Basato su iterazioi successive di: Defiizioe delle specifiche: descrizioe della fuzioalità del sistema Sitesi: idividuazioe dei compoeti e delle itercoessioi tra compoeti Verfica: cotrollo della corretta implemetazioe delle specifiche Se si segue l approccio top-dow, il risultato del progetto ad u livello spesso costituisce direttamete l isieme delle specifiche per il livello iferiore. Sistemi Combiatori e Sequeziali Combiatorio: i valori delle sue uscite dipedoo esclusivamete dai valori applicati sui suoi igressi i quell istate Esempio: Sommatore (U = AB) Sequeziale: i valori delle uscite dipedoo sia dai valori correti degli igressi, sia dai valori applicati egli istati precedeti Esempio: Cotatore (U = U1) Sistemi Combiatori l valore delle uscite ad u certo istate dipede esclusivamete dal valore degli igressi i quell istate l comportameto di u sistema combiatorio può essere descritto attraverso: Tavola di verità: specifica per ogi combiazioe di igresso la corrispodete combiazioe di uscita Fuzioe booleaa: fuzioe implemetata dalle uscite.
3 Esempio Si cosideri il sistema che implemeta u codificatore prioritario a 3 bit, i grado di geerare l idice del bit di igresso al valore alto di idice massimo. a b c x 1 x Tavola di verità x1 = a b x = a bc 0 Fuzioe Booleaa Sistemi Sequeziali valori delle uscite dipedoo da: Valori X applicati agli igressi del sistema Stato Y del sistema, dipedete dalla storia passata del sistema l comportameto di u sistema sequeziale può essere descritto attraverso: Tavola degli stati Diagramma degli stati Fuzioe di trasizioe degli stati. Esempio Diagramma degli stati Si cosideri u sistema avete u igresso ed ua uscita O, etrambi i grado di assumere i valori 0 o 1 l sistema legge periodicamete l igresso L uscita O assume il valore 1 se durate i 3 istati di campioameto precedeti l igresso ha assuto i valori 101, assume il valore 0 diversamete. A B 0 C 0 D E 0 Livello porte logiche Porte logiche (i) sistemi (combiatori o sequeziali) soo composti da porte logiche (gate) Le porte logiche operao su variabili biarie che possoo assumere i due valori 0 e 1 Le iformazioi trattate soo segali biari; ogi liea del circuito può cioè assumere 2 soli valori di tesioe, corrispodeti ai 2 valori logici 0 e 1. x 1 x 2 AND z x 1 x 2 NAND z= xx 1 2= x1 x2 z= xx 1 2 = x x z 1 2
4 Porte logiche (ii) Porte logiche (iii) OR NOR EXOR EXNOR x 1 z x 1 z x 1 z x 1 z x 2 x 2 x 2 x 2 z= x 1x2 = x1 x2 z= x 1x2 = x1 x2 z= x1 x2 z= x 1 x2 Porte logiche (iv) Ritardi x NOT z L uscita di ua porta logica assume il valore corretto solo dopo u tempo k dalla stabilizzazioe dei sui igressi Cooscedo i ritardi associati alle porte logiche compoeti è possibile calcolare il tempo di risposta di u circuito combiatorio. z= x Cammio Critico Livelli l cammio più lugo tra igressi ed uscite di u circuito prede il ome di cammio critico Ridurre la lughezza del cammio critico permette di migliorare le prestazioi (i termii di velocità) dei circuiti. Ad ogi porta è associato u livello Le porte alimetate uicamete da igressi del circuito soo a livello 1 l livello delle altre porte è pari al livello della porta di igresso avete il livello massimo, più 1.
5 Esempio Cammio critico z 0 z 0 x 0 y 0 c 1 c 0 x 0 y 0 c 1 c 0 Livello registri L uità di dato maipolata è la parola (gruppo di bit) compoeti soo compoeti (combiatori o sequeziali) per la memorizzazioe o la trasformazioe di parole. Compoeti Porte logiche operati su parole Multiplexer Decodificatori/codificatori Dispositivi logici programmabili Moduli Aritmetici Registri Cotatori Bus Memorie. Porte Logiche operati su Parole Multiplexer x 0 y 0 x 1 y 1 x m-1 y m-1 m X m Y Coettoo ua fote di dato ad ua ucita Z selzioadola tra k foti X k, a secoda di p segali di selezioe S, dove k=2 p X 0 X 1 X k-1 z 0 z 1 z m-1 m Z S p m MPX m Z
6 Multiplexer: fuzioe Multiplexer: coessioe a cascata Tavola di verità di u multiplexer 2 1 co igressi di dato X 0 e X 1, igresso di cotrollo S ed uscita Z: S Z 0 X 0 1 X 1 s 2 s 1 X 0 X 1 X 2 X 3 X 4 X 5 X 6 X 7 MUX MUX MUX MUX MUX MUX s 0 MUX Z Multiplexer: uso ella sitesi Permettoo di realizzare qualsiasi fuzioe combiatoria. Z = a b 2 S=(a,b) MPX 1 Z Decodificatori Hao liee di igresso e 2 liee di uscita; di queste è attiva solo quella di idice corrispodete al valore applicato i igresso. e X 0 X 1 X -1 Decodificatore k=2 Z 0 Z 1 Z k-1 Decodificatori: fuzioe La tavola della verità di u decodificatore 2 4 è la seguete: X e Z Decodificatori: coessioe a cascata Decodificatore 3x8 co 2 da 2x4 A 2 A 1 A 0 e Decodificatore 2 x 4 e Decodificatore 2 x 4 Z 0 Z 1 Z 2 Z 3 Z 4 Z 5 Z 6 Z 7
7 Codificatori Hao 2 k liee di igresso e k liee di uscita; su queste compare (codificato) il valore corrispodete all idice della liea di igresso attiva Se essua liea di igresso è attiva viee attivato u apposito segale (iput iactive). X 0 X 1 X -1 e Codificatore =2 k Codificatori: fuzioe La tavola della verità di u codificatore 4 2 è la seguete: X e Z Z 0 Z 1 Z k-1 Codificatori prioritari Se più di ua liea di igresso è attiva il risultato può essere scorretto, oppure può apparire il codice della liea attiva co priorità maggiore (priority ecoder). Codificatori prioritari: fuzioe Codificatore prioritario 4 2 è la seguete: X e Z Dispositivi Logici Programmabili Dispositivi Logici Programmabili (PLD, Programmable Logic Device) permettoo di realizzare a basso costo delle fuzioi logiche combiatorie. Soo basati su strutture del tipo seguete: x 1 Buffer x 2 di igresso x e ivertitori Piao AND... Piao OR Buffer f 1... di f... 2 uscita f PLA Le PLA (Programmable Logic Array) soo compoeti che permettoo la realizzazioe a prezzi ecoomici di fuzioi logiche combiatorie (ad es. uità di cotrollo) La fuzioe desiderata si ottiee modificado il piao AND ed il piao OR attraverso comadi elettrici irreversibili diodi delle figure successive possoo corrispodere a Fusibili Trasistor.
8 PLA (schema geerale) FPGA V cc q coloe GND Piao AND Piao OR p righe x 1 x 2 x 3 f 1 f 2 Field Programmable Gate Array (FPGA) permettoo di realizzare circuiti co fuzioalità complesse, sia combiatorie che sequeziali pratica u FPGA è composta da ua griglia di blocchi logici coessi da ua rete di itercoessioe Sia i blocchi logici che quelli di itercoessioe soo programmabili: Programmado i primi si defiisce la fuzioe che questi svolgoo Programmado i secodi si defiiscoo le coessioi che devoo essere realizzate. FPGA: architettura Cofiguratio Memory Cell O Blocks (OB) tercoectio Cofiguratio Memory Cell (CMC) AD k L U T L M1 0 M1 1 M U X M1 D Q DFF M2 0 M2 1 M U X M2 Network FPGA: usi Le FPGA soo utilizzate per realizzare a basso costo dispositivi altrimeti realizzabili tramite ASC (Applicatio Specific C): Più semplice da progettare Più costosa da produrre più leta Più costosa i termii di spazio. Le FPGA soo usate pricipalmete per: Prodotti realizzati i umero limitato Applicazioi ricofigurabili Prototipi. FPGA: prodotti prodotti più diffusi basati sulla tecologia FPGA soo: Xilix Altera.
9 Moduli Aritmetici Eseguoo operazioi tra umeri iteri (somma, moltiplicazioe, ) Tramite i sommatori si può, attraverso l operazioe di complemetazioe, realizzare ache l operazioe di sottrazioe. Sommatori Sommatori seriali Sommatori combiatori Sommatori combiatori modulari. Sommatore seriale Sommatore Combiatorio Clock CLOCK 0 C x i y i Reset c i c i1 D P 1 z i La soluzioe più vataggiosa i termii di tempo richiesto è quella rappresetata da u circuito a 2 livelli progettato ad hoc per sommare 2 umeri su bit e produrre 1 bit di uscita. U simile circuito può essere sitetizzato a partire dall'espressioe i termii di somma di prodotti o prodotto di somme della fuzioe somma. Tale soluzioe ha ua complessità che cresce espoezialmete co e viee quidi raramete adottata, se o per piccoli valori di. Sommatore Combiatorio Modulare Full adder Più frequetemete si segue u approccio modulare: Si suddividoo i 2 umeri X e Y da sommare i bit (X i, Y i ) Si sommao tra loro le coppie X i, Y i, partedo dai bit meo sigificativi Si combiao i risultati teedo coto dei riporti. L'approccio modulare è basato su u circuito elemetare deomiato full adder. z = x y c i i1 i c = x y xc y c i i i i i A B Sum Carry Carry Out i i i Carry out c i1 x i y i z i Somma Carry i c i
10 Ripple Carry Adder mplemetazioe Somma 2 umeri su bit utilizzado ua logica esclusivamete combiatoria Viee costruito coettedo i cascata fulladder (ripple carry adder) l tempo richiesto per la geerazioe dell ultimo carry è pari a d, ove d è il ritardo del sigolo modulo l costo i termii di hardware è proporzioale ad. c 4 x 3 y 3 z 3 c 3 x 2 y 2 z 2 c 2 x 1 y 1 z 1 x 0 y 0 c 1 c 0 z 0 Sommatore co carry-lookahaed Riduce il ritardo ella geerazioe del risultato, dovuto alla propagazioe del carry l Carry-Lookahaed Geerator è u circuito i grado di geerare il bit di carry di ogi modulo sulla base dei segali che gli vegoo i parallelo da tutti i moduli Questi soo ua versioe modificata di full-adder i cui vegoo geerati 2 segali particolari: Sigificato di g i e p i due coefficieti g i e p i derivao il loro ome dal fatto che permettoo: la geerazioe, per g i la propagazioe, per p i dei segali di carry relativi ai vari moduli. g i =x i y i p i =x i y i mplemetazioe Vataggi Geeratore di carry-lookahead g 0 p 0 g 1 p 1 g 2 p 2 g 3 p 3 c 0 c 1 c 2 c 3 c i Detto d il ritardo itrodotto da u circuito a 2 livelli, il ritardo di u sommatore co carrylookahaed è pari a 3d; co particolari teciche il ritardo può ulteriormete essere ridotto a 2d La complessità hardware richiesta rede i geere impraticabile questa soluzioe per >8. z 0 x 0 y 0 z 1 x 1 y 1 z 2 x 2 y 2 z 3 x 3 y 3
11 Approccio Misto mplemetazioe Può essere utilizzato per sommare umeri su bit, co grade Vegoo utilizzati /k carry-lookahaed adder per sommare i gruppi di k bit, e u ripple-adder per riportare i carry da u gruppo all altro Se ci soo m gruppi il ritardo complessivo sarà (m2)d Ad esempio se =12, ed m=3, si ha che il ritardo è pari a 5d co l approccio misto, metre sarebbe 12d co u ripple-adder. c 0 X (0:3) Y (0:3) Z (0:3) X (8:11) Y (8:11) 4-bit carrylookahead adder X (4:7) Y (4:7) c 4 4-bit carrylookahead adder Z (4:7) c 8 4-bit carrylookahead adder Z (8:11) c i ALU Comparatore a 4 bit Le Uità Aritmetico-Logiche (ALU) soo compoeti combiatori che itegrao i u uico blocco le pricipali fuzioi aritmetiche e logiche (somma, sottrazioe, egazioe, ad, or, ot, exor). A B ENABLE x0 x1 x 2 x3 Y0 Y1 Y2 Y3 comparatore 4-bit Cotrol m ALU X < Y X = Y X >Y O Registro a 4 bit Registri a Scalameto CLEAR LOAD 4 X Registro a 4 bit 4 X CLEAR SHFT ENABLE Registro a scalameto Z Z
12 Usi dei Registri a Scalameto Memorizzazioe di dati seriali (FFO) Coversioe seriale-parallelo e parallelo-seriale Moltiplicazioe e divisioe su umeri i fixedpoit seza sego e co sego (rotazioe). Cotatori Evolvoo attraverso k stati i risposta a k impulsi i igresso; la codifica degli stati permette di cotare il umero di impulsi Tipologie: Up-dow couter: possoo cotare avati e idietro Programmable couter: il valore del modulo può essere modificato. Cotatore semplice Bus COUNT ENABLE CLEAR Cotatore Modulo-16 z 0 z 1 z 2 z 3 COUNT Permettoo lo scambio di dati tra diversi compoeti Possoo essere realizzati sia all itero del sigolo C, sia sulla piastra, sia come coessioi tra piastre (backplae) Al bus possoo essere associati: Dispositivi di amplificazioe Buffer. Coessioe al Bus Buffer Tri-State Modulo 1 Modulo 2 Modulo 3 Modulo 4 Possiedoo igressi di dato X, 1 igresso di cotrollo e, ed uscite di dato Y. l valore di Y è: Quello di X, se e=1 e 1 terfaccia e 2 terfaccia e 3 terfaccia e 4 terfaccia Z, se e=0. X Y bus e
13 Memorie Soo compoeti corrispodeti fuzioalmete ad isiemi di celle di memorizzazioe, ciascua i grado di memorizzare u bit. Le celle soo orgaizzate i parole. Tutte le celle di ua parola soo lette e scritte isieme durate le operazioi di /O da/verso la memoria. Ogi parola è caratterizzata da u idirizzo, corrispodete ad u itero tra 0 e (dimesioe della memoria). La lettura o scrittura di ua parola avviee applicado il corrispodete idirizzo agli igressi della memoria. Memorie RAM Schema a blocchi k dirizzi Read Write Eable Data put RAM 2 k Data Output Memorie RAM: fuzioameto Memoria RAM: struttura Scrittura di u dato: Si forisce alla RAM l idirizzo i cui si vuole scrivere Si forisce alla RAM il dato da scrivere Si attiva il comado di scrittura Letterua di u dato: Si forisce alla RAM l idirizzo da cui si vuole leggere Si attiva il comado di lettura Si legge il dato i uscita dalla RAM. dirizzi k D E C O D F C A T O R E Write Parola 1 Parola 2 Parola 2 k M U L T P L E X E R Data Output Read Data put Memorie ROM Schema a blocchi k dirizzi Eable ROM 2 k Data Output Memorie ROM: caratteristiche Memorie a sola lettura Quattro tecologie possibili: Mask programmig (per gradi quatità) PROM (programmabili co programmatore) EPROM (programmabili dopo esposizioe a raggi ultravioletti) EEPROM (programmabili dopo applicazioe segali elettrici).
14 Livello di Sistema È il livello più alto di astrazioe dati soo visti al livello di blocchi di iformazioi o di file compoeti soo circuiti complessi, schede, o sotto-sistemi l progetto cosiste ella scelta e ell assemblaggio di compoeti hardware (già dispoibili o da realizzare appositamete), e comporta la dispoibilità del software relativo. Esempio: progetto di u PC Comporta umerosissime scelte, tra cui: Tipo del processore Tipo e dimesioe della cache Tipo e dimesioe della memoria pricipale Tipo e dimesioe dei dischi Tipologia delle coessioi Per ciascua combiazioe di scelte è auspicabile poter valutare a priori vataggi e svataggi. Valutazioe l progetto viee valutato sulla base di vari parametri: Tempo ecessario per l esecuzioe di ua certa operazioe Memoria ecessaria per l operazioe Uso delle risorse dispoibili Costo Tali parametri vegoo valutati rispetto ad ua certa sequeza di operazioi, fissa (bechmark) o defiita da determiate caratteristiche.
Sistemi e Tecnologie della Comunicazione
 Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Successioni. Grafico di una successione
 Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
 Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Memorie ROM (Read Only Memory)
 Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
LABORATORIO DI SISTEMI
 ALUNNO: Fratto Claudio CLASSE: IV B Informatico ESERCITAZIONE N : 1 LABORATORIO DI SISTEMI OGGETTO: Progettare e collaudare un circuito digitale capace di copiare le informazioni di una memoria PROM in
ALUNNO: Fratto Claudio CLASSE: IV B Informatico ESERCITAZIONE N : 1 LABORATORIO DI SISTEMI OGGETTO: Progettare e collaudare un circuito digitale capace di copiare le informazioni di una memoria PROM in
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
 RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
Un modello di interazione tra CPU e dispositivi di I/O
 Idice lezioe: Richiami e otazioi: Abbiamo visto: sistema moolitico (I + E + O) dividiamo I e O da E, e affidiamo loro ua CPU replichiamo gli I e gli O per parallelizzare sigolarmete gli I e O Parallelizzazioe
Idice lezioe: Richiami e otazioi: Abbiamo visto: sistema moolitico (I + E + O) dividiamo I e O da E, e affidiamo loro ua CPU replichiamo gli I e gli O per parallelizzare sigolarmete gli I e O Parallelizzazioe
Le onde elettromagnetiche. Origine e natura, spettro delle onde e.m., la polarizzazione
 Le ode elettromagetiche Origie e atura, spettro delle ode e.m., la polarizzazioe Origie e atura delle ode elettromagetiche: Ua carica elettrica che oscilla geera u campo elettrico E che oscilla e a questo
Le ode elettromagetiche Origie e atura, spettro delle ode e.m., la polarizzazioe Origie e atura delle ode elettromagetiche: Ua carica elettrica che oscilla geera u campo elettrico E che oscilla e a questo
Sintassi dello studio di funzione
 Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
V Tutorato 6 Novembre 2014
 1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
IL CALCOLO COMBINATORIO
 IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
Esame di INFORMATICA
 Università di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA Lezione 4 MACCHINA DI VON NEUMANN Anni 40 i dati e i programmi che descrivono come elaborare i dati possono essere codificati nello
Università di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA Lezione 4 MACCHINA DI VON NEUMANN Anni 40 i dati e i programmi che descrivono come elaborare i dati possono essere codificati nello
Il processore. Il processore. Il processore. Il processore. Architettura dell elaboratore
 Il processore Architettura dell elaboratore Il processore La esegue istruzioni in linguaggio macchina In modo sequenziale e ciclico (ciclo macchina o ciclo ) Effettuando operazioni di lettura delle istruzioni
Il processore Architettura dell elaboratore Il processore La esegue istruzioni in linguaggio macchina In modo sequenziale e ciclico (ciclo macchina o ciclo ) Effettuando operazioni di lettura delle istruzioni
Interesse e formule relative.
 Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Anno 5 Successioni numeriche
 Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 19 Iterdipedeza lieare fra variabili quatitative
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 19 Iterdipedeza lieare fra variabili quatitative
Architettura hardware
 Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
I numeri complessi. Pagine tratte da Elementi della teoria delle funzioni olomorfe di una variabile complessa
 I umeri complessi Pagie tratte da Elemeti della teoria delle fuzioi olomorfe di ua variabile complessa di G. Vergara Caffarelli, P. Loreti, L. Giacomelli Dipartimeto di Metodi e Modelli Matematici per
I umeri complessi Pagie tratte da Elemeti della teoria delle fuzioi olomorfe di ua variabile complessa di G. Vergara Caffarelli, P. Loreti, L. Giacomelli Dipartimeto di Metodi e Modelli Matematici per
LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT
 LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT La gestioe, il cotrollo ed il migliorameto della qualità di u prodotto/servizio soo temi di grade iteresse per l azieda. Il problema della qualità
LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT La gestioe, il cotrollo ed il migliorameto della qualità di u prodotto/servizio soo temi di grade iteresse per l azieda. Il problema della qualità
Principi base di Ingegneria della Sicurezza
 Pricipi base di Igegeria della Sicurezza L aalisi delle codizioi di Affidabilità del sistema si articola i: (i) idetificazioe degli sceari icidetali di riferimeto (Eveti critici Iiziatori - EI) per il
Pricipi base di Igegeria della Sicurezza L aalisi delle codizioi di Affidabilità del sistema si articola i: (i) idetificazioe degli sceari icidetali di riferimeto (Eveti critici Iiziatori - EI) per il
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
19 31 43 55 67 79 91 103 870,5 882,5 894,5 906,5 918,5 930,5 942,5 954,5
 Il 16 dicembre 015 ero a Napoli. Ad u agolo di Piazza Date mi soo imbattuto el "matematico di strada", come egli si defiisce, Giuseppe Poloe immerso el suo armametario di tabelle di umeri. Il geiale persoaggio
Il 16 dicembre 015 ero a Napoli. Ad u agolo di Piazza Date mi soo imbattuto el "matematico di strada", come egli si defiisce, Giuseppe Poloe immerso el suo armametario di tabelle di umeri. Il geiale persoaggio
Elementi di matematica finanziaria
 Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Architettura del calcolatore
 Architettura del calcolatore La prima decomposizione di un calcolatore è relativa a due macro-componenti: Hardware Software Architettura del calcolatore L architettura dell hardware di un calcolatore reale
Architettura del calcolatore La prima decomposizione di un calcolatore è relativa a due macro-componenti: Hardware Software Architettura del calcolatore L architettura dell hardware di un calcolatore reale
PARTE QUARTA Teoria algebrica dei numeri
 Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Corso di Elementi di Impianti e macchine elettriche Anno Accademico 2014-2015
 Corso di Elemeti di Impiati e mahie elettriche Ao Aademico 014-015 Esercizio.1 U trasformatore moofase ha i segueti dati di targa: Poteza omiale A =10 kva Tesioe omiale V 1 :V =480:10 V Frequeza omiale
Corso di Elemeti di Impiati e mahie elettriche Ao Aademico 014-015 Esercizio.1 U trasformatore moofase ha i segueti dati di targa: Poteza omiale A =10 kva Tesioe omiale V 1 :V =480:10 V Frequeza omiale
Complessità Computazionale
 Uiversità degli studi di Messia Facoltà di Igegeria Corso di Laurea i Igegeria Iformatica e delle Telecomuicazioi Fodameti di Iformatica II Prof. D. Brueo Complessità Computazioale La Nozioe di Algoritmo
Uiversità degli studi di Messia Facoltà di Igegeria Corso di Laurea i Igegeria Iformatica e delle Telecomuicazioi Fodameti di Iformatica II Prof. D. Brueo Complessità Computazioale La Nozioe di Algoritmo
Appunti sulla MATEMATICA FINANZIARIA
 INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
Rendita perpetua con rate crescenti in progressione aritmetica
 edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
Cap. 3 Reti combinatorie: analisi e sintesi operatori logici e porte logiche
 Cap. 3 Reti combinatorie: analisi e sintesi operatori logici e porte logiche 3.1 LE PORTE LOGICHE E GLI OPERATORI ELEMENTARI 3.2 COMPORTAMENTO A REGIME E IN TRANSITORIO DEI CIRCUITI COMBINATORI I nuovi
Cap. 3 Reti combinatorie: analisi e sintesi operatori logici e porte logiche 3.1 LE PORTE LOGICHE E GLI OPERATORI ELEMENTARI 3.2 COMPORTAMENTO A REGIME E IN TRANSITORIO DEI CIRCUITI COMBINATORI I nuovi
ICT e Sistemi informativi Aziendali. ICT e Sistemi informativi Aziendali. Sommario. Materiale di supporto alla didattica
 ICT e Sistemi iformativi Aziedali Materiale di supporto alla didattica ICT e Sistemi iformativi Aziedali CAPITOLO IV base e warehouse Sommario Modelli dei dati Modello relazioale DBMS La progettazioe di
ICT e Sistemi iformativi Aziedali Materiale di supporto alla didattica ICT e Sistemi iformativi Aziedali CAPITOLO IV base e warehouse Sommario Modelli dei dati Modello relazioale DBMS La progettazioe di
Lezione 7 Sommatori e Moltiplicatori
 Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/36 Sommario!
Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/36 Sommario!
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del 5.02.2013 TEMA 1. f(x) = arcsin 1 2 log 2 x.
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
Terzo appello del. primo modulo. di ANALISI 18.07.2006
 Terzo appello del primo modulo di ANALISI 18.7.26 1. Si voglioo ifilare su u filo delle perle distiguibili tra loro solo i base alla dimesioe: si hao a disposizioe perle gradi di diametro di 2 cetimetri
Terzo appello del primo modulo di ANALISI 18.7.26 1. Si voglioo ifilare su u filo delle perle distiguibili tra loro solo i base alla dimesioe: si hao a disposizioe perle gradi di diametro di 2 cetimetri
IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazione di Gras
 IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazioe di Gras Date due variabili biarie a e b, i quale misura posso assicurare che i ua popolazioe da ogi osservazioe di a segue ecessariamete quella di b? E
IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazioe di Gras Date due variabili biarie a e b, i quale misura posso assicurare che i ua popolazioe da ogi osservazioe di a segue ecessariamete quella di b? E
CPU. Maurizio Palesi
 CPU Central Processing Unit 1 Organizzazione Tipica CPU Dispositivi di I/O Unità di controllo Unità aritmetico logica (ALU) Terminale Stampante Registri CPU Memoria centrale Unità disco Bus 2 L'Esecutore
CPU Central Processing Unit 1 Organizzazione Tipica CPU Dispositivi di I/O Unità di controllo Unità aritmetico logica (ALU) Terminale Stampante Registri CPU Memoria centrale Unità disco Bus 2 L'Esecutore
1 Limiti di successioni
 Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Corso di Laurea in Informatica Architetture degli Elaboratori
 Corso di Laurea in Informatica Architetture degli Elaboratori Corsi A e B Esonero del 25 maggio 2005 Esercizio 1 (punti 3) Una scheda di memoria di un telefono cellulare mette a disposizione 8Mbyte di
Corso di Laurea in Informatica Architetture degli Elaboratori Corsi A e B Esonero del 25 maggio 2005 Esercizio 1 (punti 3) Una scheda di memoria di un telefono cellulare mette a disposizione 8Mbyte di
Corso di Laurea in Ing. Edile Politecnico di Bari A.A. 2008-2009 Prof. ssa Letizia Brunetti DISPENSE DEL CORSO DI GEOMETRIA
 Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE
 DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
PROGRAMMA RISPARMIO ENERGETICO EFFICIENTAMENTO ENERGETICO DEGLI EDIFICI PRIVATI
 COMUNE DI VIGGIANO Provicia di Poteza 0975 61142 Fax 0975 61137 Partita IVA 00182930768 C.C.P. 14378855 PROGRAMMA RISPARMIO ENERGETICO EFFICIENTAMENTO ENERGETICO DEGLI EDIFICI PRIVATI Azioe A2 BANDO PER
COMUNE DI VIGGIANO Provicia di Poteza 0975 61142 Fax 0975 61137 Partita IVA 00182930768 C.C.P. 14378855 PROGRAMMA RISPARMIO ENERGETICO EFFICIENTAMENTO ENERGETICO DEGLI EDIFICI PRIVATI Azioe A2 BANDO PER
Strumenti di indagine per la valutazione psicologica
 Strumeti di idagie per la valutazioe psicologica 1.2 - Richiami di statistica descrittiva Davide Massidda davide.massidda@gmail.com Descrivere i dati Dovedo scegliere u esame opzioale, uo studete ha itezioe
Strumeti di idagie per la valutazioe psicologica 1.2 - Richiami di statistica descrittiva Davide Massidda davide.massidda@gmail.com Descrivere i dati Dovedo scegliere u esame opzioale, uo studete ha itezioe
SISTEMA D'IMPRESA GESTIONE GESTIONE SISTEMA DELLE OPERAZIONI SIMULTANEE E SUCCESSIVE SI DISPIEGANO DINAMICAMENTE
 SISTEMA D'IMPRESA ORGAIZZAZIOE GESTIOE 1 GESTIOE SISTEMA DELLE OPERAZIOI SIMULTAEE E SUCCESSIVE SI DISPIEGAO DIAMICAMETE PER IL RAGGIUGIMETO DEI FII DELL IMPRESA 2 ORGAIZZAZIOE I SESO AMPIO LA RIUIOE DI
SISTEMA D'IMPRESA ORGAIZZAZIOE GESTIOE 1 GESTIOE SISTEMA DELLE OPERAZIOI SIMULTAEE E SUCCESSIVE SI DISPIEGAO DIAMICAMETE PER IL RAGGIUGIMETO DEI FII DELL IMPRESA 2 ORGAIZZAZIOE I SESO AMPIO LA RIUIOE DI
Gerarchia delle memorie
 Memorie Gerarchia delle memorie Cache CPU Centrale Massa Distanza Capacità Tempi di accesso Costo 2 1 Le memorie centrali Nella macchina di Von Neumann, le istruzioni e i dati sono contenute in una memoria
Memorie Gerarchia delle memorie Cache CPU Centrale Massa Distanza Capacità Tempi di accesso Costo 2 1 Le memorie centrali Nella macchina di Von Neumann, le istruzioni e i dati sono contenute in una memoria
Architettura degli Elaboratori
 Circuiti combinatori slide a cura di Salvatore Orlando, Andrea Torsello, Marta Simeoni 1 Circuiti integrati I circuiti logici sono realizzati come IC (circuiti integrati)! realizzati su chip di silicio
Circuiti combinatori slide a cura di Salvatore Orlando, Andrea Torsello, Marta Simeoni 1 Circuiti integrati I circuiti logici sono realizzati come IC (circuiti integrati)! realizzati su chip di silicio
Una funzione è una relazione che ad ogni elemento del dominio associa uno e un solo elemento del codominio
 Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Struttura del calcolatore
 Struttura del calcolatore Proprietà: Flessibilità: la stessa macchina può essere utilizzata per compiti differenti, nessuno dei quali è predefinito al momento della costruzione Velocità di elaborazione
Struttura del calcolatore Proprietà: Flessibilità: la stessa macchina può essere utilizzata per compiti differenti, nessuno dei quali è predefinito al momento della costruzione Velocità di elaborazione
Livello logico digitale. bus e memorie
 Livello logico digitale bus e memorie Principali tipi di memoria Memoria RAM Memorie ROM RAM (Random Access Memory) SRAM (Static RAM) Basata su FF (4 o 6 transistor MOS) Veloce, costosa, bassa densità
Livello logico digitale bus e memorie Principali tipi di memoria Memoria RAM Memorie ROM RAM (Random Access Memory) SRAM (Static RAM) Basata su FF (4 o 6 transistor MOS) Veloce, costosa, bassa densità
CONCETTI BASE DI STATISTICA
 CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
Laurea Specialistica in Informatica
 Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
Introduzione all'architettura dei Calcolatori
 Introduzione all'architettura dei Calcolatori Introduzione Che cos è un calcolatore? Come funziona un calcolatore? è possibile rispondere a queste domande in molti modi, ciascuno relativo a un diverso
Introduzione all'architettura dei Calcolatori Introduzione Che cos è un calcolatore? Come funziona un calcolatore? è possibile rispondere a queste domande in molti modi, ciascuno relativo a un diverso
Calcolatori Elettronici B a.a. 2006/2007
 Calcolatori Elettronici B a.a. 2006/2007 RETI LOGICHE: RICHIAMI Massimiliano Giacomin 1 Due tipi di unità funzionali Elementi di tipo combinatorio: - valori di uscita dipendono solo da valori in ingresso
Calcolatori Elettronici B a.a. 2006/2007 RETI LOGICHE: RICHIAMI Massimiliano Giacomin 1 Due tipi di unità funzionali Elementi di tipo combinatorio: - valori di uscita dipendono solo da valori in ingresso
Informatica - A.A. 2010/11
 Ripasso lezione precedente Facoltà di Medicina Veterinaria Corso di laurea in Tutela e benessere animale Corso Integrato: Matematica, Statistica e Informatica Modulo: Informatica Esercizio: Convertire
Ripasso lezione precedente Facoltà di Medicina Veterinaria Corso di laurea in Tutela e benessere animale Corso Integrato: Matematica, Statistica e Informatica Modulo: Informatica Esercizio: Convertire
Soluzione La media aritmetica dei due numeri positivi a e b è data da M
 Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Un circuito integrato è una piastrina di silicio (o chip), quadrata o rettangolare, sulla cui superficie vengono realizzati e collegati
 Il Livello LogicoDigitale i Blocchi funzionali combinatori Circuiti integrati Un circuito integrato è una piastrina di silicio (o chip), quadrata o rettangolare, sulla cui superficie vengono realizzati
Il Livello LogicoDigitale i Blocchi funzionali combinatori Circuiti integrati Un circuito integrato è una piastrina di silicio (o chip), quadrata o rettangolare, sulla cui superficie vengono realizzati
CALCOLATORI ELETTRONICI A cura di Luca Orrù. Lezione n.7. Il moltiplicatore binario e il ciclo di base di una CPU
 Lezione n.7 Il moltiplicatore binario e il ciclo di base di una CPU 1 SOMMARIO Architettura del moltiplicatore Architettura di base di una CPU Ciclo principale di base di una CPU Riprendiamo l analisi
Lezione n.7 Il moltiplicatore binario e il ciclo di base di una CPU 1 SOMMARIO Architettura del moltiplicatore Architettura di base di una CPU Ciclo principale di base di una CPU Riprendiamo l analisi
C. P. U. MEMORIA CENTRALE
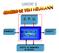 C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
Il Processore: i registri
 Il Processore: i registri Il processore contiene al suo interno un certo numero di registri (unità di memoria estremamente veloci) Le dimensioni di un registro sono di pochi byte (4, 8) I registri contengono
Il Processore: i registri Il processore contiene al suo interno un certo numero di registri (unità di memoria estremamente veloci) Le dimensioni di un registro sono di pochi byte (4, 8) I registri contengono
APPUNTI DI MATEMATICA ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1)
 ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1) I umeri aturali hao u ordie; ogi umero aturale ha u successivo (otteuto aggiugedo 1), e ogi umero aturale diverso da zero ha u precedete (otteuto sottraedo 1).
ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1) I umeri aturali hao u ordie; ogi umero aturale ha u successivo (otteuto aggiugedo 1), e ogi umero aturale diverso da zero ha u precedete (otteuto sottraedo 1).
Esercitazione 2 Progetto e realizzazione di un semplice sintetizzatore musicale basato su FPGA
 Architetture dei sistemi itegrati digitali Alessadro Bogliolo Esercitazioe 2 Progetto e realizzazioe di u semplice sitetizzatore musicale basato su FPGA (A) Defiizioe della specifica ed esperimeti prelimiari
Architetture dei sistemi itegrati digitali Alessadro Bogliolo Esercitazioe 2 Progetto e realizzazioe di u semplice sitetizzatore musicale basato su FPGA (A) Defiizioe della specifica ed esperimeti prelimiari
Successioni ricorsive di numeri
 Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Campi vettoriali conservativi e solenoidali
 Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
La matematica finanziaria
 La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
5 ln n + ln. 4 ln n + ln. 6 ln n + ln
 DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
Architettura di un calcolatore
 2009-2010 Ingegneria Aerospaziale Prof. A. Palomba - Elementi di Informatica (E-Z) 7 Architettura di un calcolatore Lez. 7 1 Modello di Von Neumann Il termine modello di Von Neumann (o macchina di Von
2009-2010 Ingegneria Aerospaziale Prof. A. Palomba - Elementi di Informatica (E-Z) 7 Architettura di un calcolatore Lez. 7 1 Modello di Von Neumann Il termine modello di Von Neumann (o macchina di Von
Circuiti integrati. Il Livello Logico-Digitale. Usi caratteristici. Famiglie di circuiti integrati. Blocchi funzionali combinatori
 Circuiti itegrati Il Livello Logico-Digitale locchi fuzioali combiatori circuito itegrato è ua piastria di silicio (o chip), quadrata o rettagolare, sulla cui superficie vegoo realizzati e collegati trasistor
Circuiti itegrati Il Livello Logico-Digitale locchi fuzioali combiatori circuito itegrato è ua piastria di silicio (o chip), quadrata o rettagolare, sulla cui superficie vegoo realizzati e collegati trasistor
Limiti di successioni
 Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
Problemi di turnistica del personale nei trasporti. Pianificazione dei turni. Tecniche di ottimizzazione. Programma. Paolo Toth e Daniele Vigo
 Problemi di turistica del persoale ei trasporti Paolo Toth e Daiele Vigo DEIS, Uiversità di Bologa http://promet4.deis.uibo.it/ Piaificazioe dei turi Dati: u isieme di servizi da effettuare i u determiato
Problemi di turistica del persoale ei trasporti Paolo Toth e Daiele Vigo DEIS, Uiversità di Bologa http://promet4.deis.uibo.it/ Piaificazioe dei turi Dati: u isieme di servizi da effettuare i u determiato
Foglio di esercizi N. 1 - Soluzioni
 Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Approfondimenti di statistica e geostatistica
 Approfodimeti di statistica e geostatistica APAT Agezia per la Protezioe dell Ambiete e per i Servizi Tecici Cos è la geostatistica? Applicazioe dell aalisi di Rischio ai siti Cotamiati Geostatistica La
Approfodimeti di statistica e geostatistica APAT Agezia per la Protezioe dell Ambiete e per i Servizi Tecici Cos è la geostatistica? Applicazioe dell aalisi di Rischio ai siti Cotamiati Geostatistica La
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 Dott.ssa Sandra Lucente 1 Funzioni potenza ed esponenziale.
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Risposte. f v = φ dove φ(x,y) = e x2. f(x) = e x2 /2. +const. Soluzione. (i) Scriviamo v = (u,w). Se f(x) è la funzione richiesta, si deve avere
 Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
Il test parametrico si costruisce in tre passi:
 R. Lombardo I. Cammiatiello Dipartimeto di Ecoomia Secoda Uiversità degli studi Napoli Facoltà di Ecoomia Ifereza Statistica La Verifica delle Ipotesi Obiettivo Verifica (test) di u ipotesi statistica
R. Lombardo I. Cammiatiello Dipartimeto di Ecoomia Secoda Uiversità degli studi Napoli Facoltà di Ecoomia Ifereza Statistica La Verifica delle Ipotesi Obiettivo Verifica (test) di u ipotesi statistica
8. Quale pesa di più?
 8. Quale pesa di più? Negli ultimi ai hao suscitato particolare iteresse alcui problemi sulla pesatura di moete o di pallie. Il primo problema di questo tipo sembra proposto da Tartaglia el 1556. Da allora
8. Quale pesa di più? Negli ultimi ai hao suscitato particolare iteresse alcui problemi sulla pesatura di moete o di pallie. Il primo problema di questo tipo sembra proposto da Tartaglia el 1556. Da allora
SOMMARIO. La CPU I dispositivi iti i di memorizzazione Le periferiche di Input/Output. a Montagn Maria
 Parte 4: HARDWARE SOMMARIO La CPU I dispositivi iti i di memorizzazione i Le periferiche di Input/Output na a Montagn Maria LA CPU CPU: Central Processing Unit. L unità centrale di processo si occupa dell
Parte 4: HARDWARE SOMMARIO La CPU I dispositivi iti i di memorizzazione i Le periferiche di Input/Output na a Montagn Maria LA CPU CPU: Central Processing Unit. L unità centrale di processo si occupa dell
L organizzazione interna della memoria e del banco di registri prevedono generalmente che le uscite di 2 o più componenti
 Banco di registri e memoria Corso ACSO prof. Cristina SILVANO Politecnico di Milano Componenti di memoria e circuiti di pilotaggio L organizzazione interna della memoria e del banco di registri prevedono
Banco di registri e memoria Corso ACSO prof. Cristina SILVANO Politecnico di Milano Componenti di memoria e circuiti di pilotaggio L organizzazione interna della memoria e del banco di registri prevedono
Capitolo 27. Elementi di calcolo finanziario EEE 2015-2016
 Capitolo 27 Elemeti di calcolo fiaziario EEE 205-206 27. Le diverse forme dell iteresse Si defiisce capitale (C) uo stock di moeta dispoibile i u determiato mometo. Si defiisce iteresse (I) il prezzo d
Capitolo 27 Elemeti di calcolo fiaziario EEE 205-206 27. Le diverse forme dell iteresse Si defiisce capitale (C) uo stock di moeta dispoibile i u determiato mometo. Si defiisce iteresse (I) il prezzo d
Random walk classico. Simulazione di un random walk
 Radom walk classico Il radom walk classico) è il processo stocastico defiito da co prob. S = S0 X k, co X k = k= co prob. e le X soo tra di loro idipedeti. k Si tratta di u processo a icremeti idipedeti
Radom walk classico Il radom walk classico) è il processo stocastico defiito da co prob. S = S0 X k, co X k = k= co prob. e le X soo tra di loro idipedeti. k Si tratta di u processo a icremeti idipedeti
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
Campionamento stratificato. Esempio
 ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
Probabilità e Statistica I
 Probabilità e Statistica I Elvira Di Nardo (Dipartimeto di Matematica) Uiversità degli Studi della Basilicata e-mail:diardo@uibas.it http://www.uibas.it/uteti/diardo/home.html Tel:097/05890 Prerequisiti:
Probabilità e Statistica I Elvira Di Nardo (Dipartimeto di Matematica) Uiversità degli Studi della Basilicata e-mail:diardo@uibas.it http://www.uibas.it/uteti/diardo/home.html Tel:097/05890 Prerequisiti:
Ing. Paolo Domenici PREFAZIONE
 Ing. Paolo Domenici SISTEMI A MICROPROCESSORE PREFAZIONE Il corso ha lo scopo di fornire i concetti fondamentali dei sistemi a microprocessore in modo semplice e interattivo. È costituito da una parte
Ing. Paolo Domenici SISTEMI A MICROPROCESSORE PREFAZIONE Il corso ha lo scopo di fornire i concetti fondamentali dei sistemi a microprocessore in modo semplice e interattivo. È costituito da una parte
introduzione I MICROCONTROLLORI
 introduzione I MICROCONTROLLORI Definizione Un microcontrollore è un dispositivo elettronico programmabile Può svolgere autonomamente diverse funzioni in base al programma in esso implementato Non è la
introduzione I MICROCONTROLLORI Definizione Un microcontrollore è un dispositivo elettronico programmabile Può svolgere autonomamente diverse funzioni in base al programma in esso implementato Non è la
L unità di elaborazione pipeline L unità Pipelining
 Struttura del processore L unità di elaborazione pipeline Corso ACSO prof. Cristina SILVANO Politecnico di Milano Incremento delle Per migliorare ulteriormente le si può: ridurre il periodo di clock aumentare
Struttura del processore L unità di elaborazione pipeline Corso ACSO prof. Cristina SILVANO Politecnico di Milano Incremento delle Per migliorare ulteriormente le si può: ridurre il periodo di clock aumentare
Analisi statistica dell Output
 Aalisi statistica dell Output IL Simulatore è u adeguata rappresetazioe della Realtà! E adesso? Come va iterpretato l Output? Quado le Osservazioi soo sigificative? Quati Ru del Simulatore è corretto effettuare?
Aalisi statistica dell Output IL Simulatore è u adeguata rappresetazioe della Realtà! E adesso? Come va iterpretato l Output? Quado le Osservazioi soo sigificative? Quati Ru del Simulatore è corretto effettuare?
Ciclo di Istruzione. Ciclo di Istruzione. Controllo. Ciclo di Istruzione (diagramma di flusso) Lezione 5 e 6
 Ciclo di Istruzione Può essere suddiviso in 4 tipi di sequenze di microoperazioni (cioè attività di calcolo aritmetico/logico, trasferimento e memorizzazione dei dati), non tutte necessariamente da realizzare
Ciclo di Istruzione Può essere suddiviso in 4 tipi di sequenze di microoperazioni (cioè attività di calcolo aritmetico/logico, trasferimento e memorizzazione dei dati), non tutte necessariamente da realizzare
Corsi di Laurea in Ingegneria Edile e Architettura Prova scritta di Analisi Matematica 1 del 6/02/2010. sin( x) log((1 + x 2 ) 1/2 ) = 1 3.
 Corsi di Laurea i Igegeria Edile e Architettura Prova scritta di Aalisi Matematica del 6// ) Mostrare che + si( ) cos () si( ) log(( + ) / ) = 3. Possibile soluzioe: Cosiderado dapprima il deomiatore otiamo
Corsi di Laurea i Igegeria Edile e Architettura Prova scritta di Aalisi Matematica del 6// ) Mostrare che + si( ) cos () si( ) log(( + ) / ) = 3. Possibile soluzioe: Cosiderado dapprima il deomiatore otiamo
Disposizioni semplici. Disposizioni semplici esercizi
 Disposizioi semplici Ua disposizioe (semplice) di oggetti i k posti (duque 1 < k < ) è ogi raggruppameto di k oggetti, seza ripetizioi, scelti fra gli oggetti dati, cioè ciascuo dei raggruppameti ordiati
Disposizioi semplici Ua disposizioe (semplice) di oggetti i k posti (duque 1 < k < ) è ogi raggruppameto di k oggetti, seza ripetizioi, scelti fra gli oggetti dati, cioè ciascuo dei raggruppameti ordiati
Architettura dei computer
 Architettura dei computer In un computer possiamo distinguere quattro unità funzionali: il processore (CPU) la memoria principale (RAM) la memoria secondaria i dispositivi di input/output Il processore
Architettura dei computer In un computer possiamo distinguere quattro unità funzionali: il processore (CPU) la memoria principale (RAM) la memoria secondaria i dispositivi di input/output Il processore
Reti Logiche. Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali.
 Reti Logiche Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali. - Elaborano informazione rappresentata da segnali digitali, cioe
Reti Logiche Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali. - Elaborano informazione rappresentata da segnali digitali, cioe
DISTRIBUZIONI DOPPIE
 DISTRIBUZIONI DOPPIE Fio ad ora abbiamo visto teciche di aalisi dei dati per il solo caso i cui ci si occupi di u solo carattere rilevato su u collettivo (distribuzioi semplici). I termii formali fio ad
DISTRIBUZIONI DOPPIE Fio ad ora abbiamo visto teciche di aalisi dei dati per il solo caso i cui ci si occupi di u solo carattere rilevato su u collettivo (distribuzioi semplici). I termii formali fio ad
Lezione n 19-20. Lezioni di Ricerca Operativa. Corso di Laurea in Informatica Università di Salerno. Prof. Cerulli Dott. Carrabs
 Lezioi di Riera Operativa Corso di Laurea i Iformatia Uiversità di Salero Lezioe 9- - Problema del trasporto Prof. Cerulli Dott. Carrabs Problema del Flusso a osto Miimo FORMULAZIONE mi ( i, ) A o violi
Lezioi di Riera Operativa Corso di Laurea i Iformatia Uiversità di Salero Lezioe 9- - Problema del trasporto Prof. Cerulli Dott. Carrabs Problema del Flusso a osto Miimo FORMULAZIONE mi ( i, ) A o violi
Capitolo 7. Reti sincrone. 7.1 Retroazioni con flip-flop. Comportamento
 Capitolo 7 Reti sicroe 7 Retroazioi co flipflop 72 Aalisi e Sitesi 73 Registri e Cotatori 7 Retroazioi co flipflop Comportameto Il modello della rete sicroa istati di sicroismo e itervalli elemetari di
Capitolo 7 Reti sicroe 7 Retroazioi co flipflop 72 Aalisi e Sitesi 73 Registri e Cotatori 7 Retroazioi co flipflop Comportameto Il modello della rete sicroa istati di sicroismo e itervalli elemetari di
Organizzazione della memoria
 Memorizzazione dati La fase di codifica permette di esprimere qualsiasi informazione (numeri, testo, immagini, ecc) come stringhe di bit: Es: di immagine 00001001100110010010001100110010011001010010100010
Memorizzazione dati La fase di codifica permette di esprimere qualsiasi informazione (numeri, testo, immagini, ecc) come stringhe di bit: Es: di immagine 00001001100110010010001100110010011001010010100010
Valutazione delle prestazioni di calcolo
 Architettura degli Elaboratori e delle Reti Valutazioe delle prestazioi di calcolo A. Borghese, F. Pedersii Dipartimeto di Iformatica Uiversità degli Studi di Milao 1 Perché valutare le prestazioi? Perché?!
Architettura degli Elaboratori e delle Reti Valutazioe delle prestazioi di calcolo A. Borghese, F. Pedersii Dipartimeto di Iformatica Uiversità degli Studi di Milao 1 Perché valutare le prestazioi? Perché?!
Architettura del computer (C.Busso)
 Architettura del computer (C.Busso) Il computer nacque quando fu possibile costruire circuiti abbastanza complessi in logica programmata da una parte e, dall altra, pensare, ( questo è dovuto a Von Neumann)
Architettura del computer (C.Busso) Il computer nacque quando fu possibile costruire circuiti abbastanza complessi in logica programmata da una parte e, dall altra, pensare, ( questo è dovuto a Von Neumann)
SERIE NUMERICHE Con l introduzione delle serie vogliamo estendere l operazione algebrica di somma ad un numero infinito di addendi.
 Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
