Capitolo II VETTORI GEOMETRICI E SISTEMI DI RIFERIMENTO
|
|
|
- Filippa Mauro
- 6 anni fa
- Visualizzazioni
Transcript
1 Capitolo II VETTRI GEMETRICI E SISTEMI DI RIFERIMENT 1. Vettori applicati Il lettore arà certamente familiarità col concetto di ettore, usato nei corsi di fisica per indiiduare alcune grandezze (elocità, accelerazione, forza, ecc.). Si ricordi che con il termine ettore o, più precisamente ettore applicato, si indica un oggetto che è completamente indiiduato da una direzione, un erso, una lunghezza (o modulo) e un punto di applicazione. Per fissare le notazioni, un ettore applicato errà denotato con B A, oe A e B sono due punti dello spazio (a olte anche con il simbolo AB); in tal caso la sua direzione è quella della retta per A e B, il suo erso è quello da A a B, il suo modulo, denotato usualmente con B A è la lunghezza del segmento AB (rispetto ad una fissata unità di misura), e A è il suo punto di applicazione. Indichiamo con W 3 (rispettiamente W 2 ) l insieme di tutti i ettori applicati nello spazio (rispettiamente nel piano), cioè, indicato con S lo spazio ordinario, si ha: W 3 = {B A A,B S}. Si può considerare il sottoinsieme V 3 A di W3 costituito da tutti i ettori aenti lo stesso punto di applicazione A: V 3 A = {B A B S}. Si osseri che W 3 = A S V 3 A sserazione. Fissato un punto dello spazio, è eidente che V 3 = {B B S} è naturalmente in corrispondenza biunioca con S, in quanto, ad ogni ettore B V 3 resta associato l estremo B, e iceersa. È noto che in V 3 è definita una somma di ettori, mediante la regola del parallelogramma. Più precisamente, (A )+(B ) = (C ), oe C è il quarto ertice del parallelogramma i cui altri tre ertici sono A,, B. B C Figura 2 Il ettore si dice ettore nullo e si denoterà con 0 (osseriamo che 0 ha direzione e erso indeterminati e modulo nullo). È eidente che V 3 A è chiuso rispetto alla somma di ettori; inoltre si ha la seguente: Brundu-Landi, Note di Algebra lineare e Geometria,
2 1.2. Proposizione. (V 3,+,0) è un gruppo abeliano. Dimostrazione. È chiaro che 0 è elemento neutro; per ogni ettore A, esiste il suo opposto A, doe A è il punto simmetrico di A rispetto ad. A' Figura 3 A La proprietà commutatia segue direttamente dalla definizione di somma di ettori. Resta da erificare la proprietà associatia di cui diamo una dimostrazione grafica Figura 4 Dalla fisica è ben noto che si possono considerare i multipli di ettori(ad esempio considerando un oggetto che si muoe a elocità doppia di un altro, ecc.). Questofattosi puòinterpretarenelgruppov 3 definendounasecondaoperazionechecoinolge gli elementi di V 3 e i numeri reali, che, in questo contesto, per differenziarli dai ettori, engono anche chiamati scalari (reali) Definizione. Si dice prodotto di uno scalare λ R per un ettore A il ettore tale che : i) B, A, sono allineati; B = λ(a ), ii) B e A hanno lo stesso erso (e si dicono concordi) se λ > 0, B e A hanno erso opposto (e si dicono discordi) se λ < 0; iii) B = λ A. Esaminiamo le proprietà di tale operazione. 12 Capitolo II - Vettori geometrici e sistemi di riferimento
3 1.4. Proposizione. Comunque scelti λ,µ R e A,B V 3, algono i seguenti fatti: 1) λ(µ(a )) = (λµ)(a ); 2) 1(A ) = A ; 3) (λ+µ)(a ) = λ(a )+µ(a ); 4) λ((a )+(B )) = λ(a )+λ(b ). Dimostrazione. 1) Poniamo C = λ(µ(a )) e D = (λµ)(a ). Dalla definizione, C e D appartengono entrambi alla retta per e A, dunque C e D hanno la stessa direzione. Inoltre dall esame dei segni di λ e µ, si erifica facilmente che C e D sono concordi: ad esempio, se λ > 0 e µ < 0, segue che C è concorde con µ(a ), quindi è discorde con A ; d altra parte λµ < 0, dunque D è anch esso discorde con A. Infine C = λ µ A = λµ A = D. La proprietà 2) segue direttamente dalla definizione. 4) Poniamo C = (A )+(B ) e C = (A )+(B ), oe A = λ(a ) e B = λ(b ). Vogliamo erificare che λ(c ) = C. B C B' C' A Figura 5 Poiché A è parallelo a A per definizione, anche BC è parallelo a B C ; inoltre B è parallelo a B, dunque gli angoli BC e B C sono uguali. Inoltre λ = B /B = A /A = B C /BC. Quindi i triangoli BC e B C sono simili. Da cui i ettori C e C sono paralleli e concordi e C = λ C. Quindi C = λ(c). 3) Si dimostra in modo analogo alla 4). Quanto precede mette in eidenza che V 3, rispetto alle operazioni di somma e di prodotto per uno scalare, ha una struttura più ricca di quella di gruppo abeliano. Tale struttura prende il nome naturale di spazio ettoriale, nozione che errà trattata in dettaglio nel Capitolo III. A' 2. Sistemi di riferimento È ben noto il concetto di sistema di riferimento; riprendiamo breemente i punti fondamentali, utilizzando il linguaggio ettoriale Definizione. Data una retta r, un sistema di riferimento Λ su r è il dato di un punto r e di un ettore i = A, con A r e A. Il punto si dice origine del sistema di riferimento, la lunghezza del segmento A è l unità di misura di Λ e il erso di i si dice orientamento di Λ. Attraerso Λ si stabilisce una corrispondenza biunioca tra i punti di r e i numeri reali; più precisamente, ad ogni punto P r si associa il numero reale x tale che P = xi. Viceersa, dato x R, rimane indiiduato il punto P di r che è estremo del ettore xi. Il numero x si dice ascissa del punto P e si scrie P = (x). Il sistema di riferimento Λ si denoterà anche con (;x) oppure con (;i). Brundu-Landi, Note di Algebra lineare e Geometria,
4 2.2. Definizione. Dato un piano α, un sistema di riferimento Π su α è il dato di un punto α e di due ettori non nulli i = A e j = B, con A, B α, A = B e tali che i si sorappone a j ruotando di un angolo φ in senso antiorario, con 0 < φ < π. Il punto si dice origine del sistema di riferimento, la lunghezza del segmenti A e B è l unità di misura di Π. La retta orientata passante per e aente stessa direzione e stesso erso di i si dice asse x o asse delle ascisse. Analogamente, si definisce l asse y o asse delle ordinate come la retta orientata indiiduata da j. Analogamente a quanto isto in precedenza, attraerso Π si stabilisce una corrispondenza biunioca tra i punti di α e le coppie di numeri reali; più precisamente, ad ogni punto P α si associa la coppia ordinata (x,y) tale che P = xi+yj (regola del parallelogramma). Viceersa, dato (x,y) R 2, rimane indiiduato il punto P di α che è estremo del ettore xi+yj. yj P(x,y) j i xi Figura 6 I numeri x e y si dicono coordinate di P e, più precisamente x si dice ascissa e y si dice ordinata del punto P; scrieremo P = (x,y). I ettori i,j si dicono ersori fondamentali, doe la parola ersore indica un ettore di modulo 1. Il sistema di riferimento Π si denoterà anche con (;x,y) oppure con (;i,j) Definizione. Un sistema di riferimento Π = (; i, j) su un piano α si dice sistema di riferimento cartesiano ortogonale se l angolo tra i e j (percorso i per sorapporsi a j ruotando in senso antiorario) è di π/2. Per definire un sistema di riferimento cartesiano nello spazio, introduciamo la seguente nozione Definizione. Una terna ordinata di ettori applicati non complanari u,, V 3 si dice destrorsa se, guardando il piano indiiduato da u e (risp. e, risp. e u) dalla parte di (risp. u, risp. ), u si sorappone a (risp. si sorappone a, risp. si sorappone a u) ruotando in senso antiorario di un angolo minore di π Definizione. Dato lo spazio S, un sistema di riferimento cartesiano Σ su S è il dato di un punto S e di tre ettori non nulli i = A, j = B e k = C con A,B,C S, A = B = C e tali che i,j,k formano una terna destrorsa. Il punto si dice origine del sistema di riferimento, la lunghezza del segmenti A, B e C è l unità di misura di Σ. La retta orientatapassanteper e aente stessa direzione e stesso erso di i si dice asse x o asse delle ascisse. Analogamente, si definiscono l asse y o asse delle ordinatee l asse z o asse delle quote. In particolare useremo la notazione P = (x, y, z), chiamando, rispettiamente, tali coordinate: ascissa, ordinata e quota del punto P. Porremo, infine, Σ = (;i,j,k) = (;x,y,z). I ettori i,j,k si dicono ersori fondamentali. Infine il sistema Σ si dice cartesiano ortogonale se i,j,k sono a due a due ortogonali. Come isto in precedenza, si stabilisce una corrispondenzabiunioca tra i punti di S e le terne di numeri reali, attraerso V 3 ; più precisamente: S V 3 R3, 14 Capitolo II - Vettori geometrici e sistemi di riferimento
5 e tali corrispondenze sono definite da P P (x,y,z) doe P = xi+yj+zk, come nella figura sottostante. zk k P(x,y,z) i j yj xi Figura Definizione. Con le notazioni precedenti, se P = (x,y,z), quindi P = xi +yj +zk, i numeri reali x,y,z si dicono componenti del ettore applicato P. Notazione. In generale, useremo anche la notazione per un ettore, = P, e aremo quindi = xi+yj+zk. Spesso è coneniente indicare le componenti di con x, y, z, quindi = x i+ y j+ z k. In seguito, per semplificare la notazione, scrieremo = ( x, y, z ), sottointendendo che tali componenti sono riferite al sistema di riferimento (; i, j, k) sserazione. Mentre un ettore è un oggetto geometrico inariante, le sue componenti dipendono dal particolare sistema di riferimento fissato Esempi. 1)Ilettorenullo0 = hacomponenti(0,0,0)intuttiisistemidiriferimento di origine ed è l unico ettore che gode di tale proprietà. 2) I ersori fondamentali hanno le seguenti componenti: i = (1,0,0), j = (0,1,0), k = (0,0,1) nel sistema di riferimento (;i,j,k). 3)Iettorideipiani coordinati(cioèipianiindiiduatidaunacoppiadiassi)sonodeltiposeguente: = (a,b,0), con a,b R, se appartiene al piano xy, = (0,b,c ), se appartiene al piano yz, = (a,0,c ), se appartiene al piano xz Proposizione. In un sistema di riferimento cartesiano ortogonale (; x, y, z) si consideri un generico ettore = ( x, y, z ). Allora = x 2 +y 2 +z. 2 Dimostrazione. Segue immediatamente usando il teorema di Pitagora. Vediamo ora come la rappresentazione dei ettori attraerso le loro componenti ci permetta di esprimere algebricamente le operazioni tra ettori. Brundu-Landi, Note di Algebra lineare e Geometria,
6 2.9. Proposizione. Dati lo scalare λ R e i ettori = x i+ y j+ z k e = x i+ y j+ z k, si ha: + = ( x + x )i+( y + y )j+( z + z )k e anche λ = λ x i+λ y j+λ z k. Dimostrazione. Poiché + = ( x i+ y j+ z k)+( x i+ y j+ z k), applicando opportunamente le proprietà commutatia e associatia della somma si ha: + = ( x i+ x i)+( y j+ y j)+( z k+ z k). Applicando infine la distributiità del prodotto rispetto alla somma si ha il risultato. In modo analogo si dimostra la seconda sserazione. Usando la notazione compatta = ( x, y, z ) e = ( x, y, z ), dalla proposizione precedente segue ( x, y, z )+( x, y, z ) = ( x + x, y + y, z + z ) λ( x, y, z ) = (λ x,λ y,λ z ). Dall osserazione precedente e dalla corrispondenza biunioca V 3 R3 si definiscono in modo naturale le seguenti operazioni in R 3 : Definizione. Siano (x 1,x 2,x 3 ) e (y 1,y 2,y 3 ) due elementi di R 3 e sia λ R; allora (x 1,x 2,x 3 )+(y 1,y 2,y 3 ) = (x 1 +y 1,x 2 +y 2,x 3 +y 3 ); λ(x 1,x 2,x 3 ) = (λx 1,λx 2,λx 3 ). Queste operazioni erranno studiate più in dettaglio nel Capitolo III, Ulteriori operazioni tra ettori Nello studio della fisica, il lettore arà già incontrato i concetti di prodotto scalare, prodotto ettoriale e prodotto misto di ettori. In questo paragrafo riprendiamo breemente tali operazioni Definizione. Siano, V 3 due ettori. Si dice prodotto scalare di e e si indica con il numero reale = cosα doe α =, 0 α π, è l angolo formato da e. (Si tenga conto che la trattazione del prodotto scalare in V 2 è del tutto analoga.) 3.2. sserazione. Dalladefinizionesiha chiaramenteche, seèil ettorenullo, allora = 0. Inoltre si hanno immediatamente le ulteriori proprietà: i) se e sono due ettori non nulli, allora = 0 cosα = Capitolo II - Vettori geometrici e sistemi di riferimento
7 ii) Per ogni V 3 si ha = 2. In particolare = 0 = 0. Infine, da i) e ii) segue se (;i,j,k) è un sistema di riferimento cartesiano ortogonale, allora: iii) i i = j j = k k = 1 e inoltre i j = j k = k i = Proposizione. Dati i ettori u,, V 3 e λ R, si hanno i seguenti fatti: i) = ; ii) (λ) = (λ) = λ( ); iii) u (+) = u +u. Dimostrazione. i) Segue dalla definizione e dalla proprietà commutatia del prodotto in R; infatti = cos = cosŵ =. ii) Posti: a = (λ), b = (λ), c = λ( ), dalla definizione di prodotto scalare e dalle proprietà del modulo di un ettore si hanno: a = (λ) = λ cosα = λ cosα b = (λ) = λ cosα = λ cosα c = λ( ) = λ( cosα) = λ cosα doe α = (λ), α = (λ) e α =. Si noti che, se λ = 0, a = b = c = 0. Mentre se λ > 0, allora λ = λ e α = α = α ; dunque, dalle proprietà commutatia e associatia del prodotto in R, si ottiene a = b = c. Infine, λ < 0, allora λ = λ e α = α = π α e quindi cosα = cosα = cosα. Pertanto, dalla commutatiità e associatiità del prodotto in R, si ottiene a = b = c. iii) Diamo un idea del caso generale supponendo che u,, siano paralleli. Si possono presentare ari casi, a seconda dei ersi dei tre ettori. Ad esempio, se sono tutti concordi, si ha: u (+) = u + = u ( + ) = = u + u = u +u. Se inece e sono concordi, ma discordi da u, si ha u (+) = u + = u ( + ) = = u u = u +u. Gli altri casi sono lasciati al lettore. Usando la rappresentazione di un ettore attraerso le sue componenti rispetto alla terna fondamentale i,j,k, si ha la seguente facile formulazione del prodotto scalare che si noti bene ale solo in un sistema di riferimento ortogonale. Brundu-Landi, Note di Algebra lineare e Geometria,
8 3.4. Proposizione. Nello spazio con sistema di riferimento cartesiano ortogonale (; i, j, k) si considerino due ettori = ( x, y, z ) e = ( x, y, z ). Allora = x x + y y + z z. Dimostrazione. Poiché = x i+ y j+ z k e = x i+ y j+ z k, per 3.3, ii) e iii), si ha = ( x i+ y j+ z k) ( x i+ y j+ z k) = = x x i i+ y x j i+ z x k i+ x y i j+ y y j j+ z y k j + x z i k+ y z j k+ z z k k Per 3.2, iii) si ha che i j = = j k = 0, mentre i i = j j = k k = 1. Sostituendonell espressione precedente, si ha la tesi Esempio. Vogliamo erificare che i ettori = (2,3,1) e = (1, 1,1) sono ortogonali. Per 3.2 i) basta proare che = 0. D altra parte, per 3.4 si ha: = ( 1)+1 1 = 0. La seguente nozione, legata a quella di prodotto scalare, tornerà utile negli spazi euclidei Definizione. Dati due ettori e non nulli, si dice proiezione ortogonale di su il ettore (parallelo a ) definito da = 2 e illustrato dalla seguente figura: Figura 8 Con le proprietà del prodotto scalare iste nella Proposizione 3.3. si ha direttamente il seguente risultato: 3.6. Lemma. Comunque scelti i ettori u,, V 3, algono i seguenti fatti: a) (u+) = u +. b) = =. La seguente figura illustra il punto (a) del precedente lemma: u A B u C A' u B' Figura 9 18 Capitolo II - Vettori geometrici e sistemi di riferimento
9 3.7. sserazione. Il prodotto scalare tra ettori dello spazio è sostanzialmente un applicazione σ : V 3 V3 R definita da σ(,) =. Analogamenteilprodottoscalaretraettoridelpianoindiiduaun applicazioneσ : V 2 V2 R Definizione. Siano, V 3 due ettori. Si dice prodotto ettoriale di e e si indica con il ettore il cui modulo ale = sinα doe α =, 0 α π, è l angolo formato da e ; la sua direzione è ortogonale sia a che a e il suo erso è tale che,, è una terna destrorsa sserazione. Dalladefinizionesihachiaramenteche,seèilettorenullo,allora = 0. Inoltre si hanno immediatamente le ulteriori proprietà: i) se e sono due ettori non nulli, allora = 0 sinα = 0. In particolare = 0. ii) Se i, j, k è la terna fondamentale di un sistema di riferimento cartesiano ortogonale allora: i j = k = j i, j k = i = k j, k i = j = i k. mettiamo la dimostrazione delle seguenti proprietà (le prime due sono facili erifiche) Proposizione. Dati i ettori u,, V 3 i) = ; ii) (λ) = (λ) = λ( ); iii) u (+) = u +u. e λ R, si hanno i seguenti fatti: Proposizione. Siano = ( x, y, z ) e = ( x, y, z ) due ettori di V 3. Allora = ( y z z y, z x x z, x y y x ). Dimostrazione. Del tutto analoga a quella di 3.4, tenendo conto di 3.10 e di 3.9 ii) Esempio. Vogliamo erificare che i ettori = (1,0, 1) e = ( 2,0,2) sono paralleli. Per 3.9 i) basta erificare che = 0. D altra parte, per l espressione 3.11 si ha: = (0,0,0) sserazione. Il prodotto ettoriale tra ettori dello spazio è un applicazione tra insiemi τ : V 3 V3 V3 definita da τ(,) =. Contrariamente al prodotto scalare, non ha senso definire il prodotto ettoriale tra ettori del piano in quanto il risultato non sarebbe nel piano Definizione. Dati i ettori u,, V 3, si definisce prodotto misto di u,, il numero reale u ( ) = u. Brundu-Landi, Note di Algebra lineare e Geometria,
10 3.14. Proposizione. Siano u = (u x,u y,u z ), = ( x, y, z ) e = ( x, y, z ) tre ettori di V 3 ; allora u = u x ( y z z y )+u y ( z x x z )+u z ( x y y x ). Dimostrazione. Segue immediatamente da 3.4 e C è una interpretazione del prodotto ettoriale e del prodotto misto, rispettiamente, come area di un parallelogramma e olume di un parallelepipedo Proposizione. Dati i ettori u,, V 3, 1) posto α = l angolo formato da e e posta A l area del parallelogramma che ha tali ettori come lati, si ha: A = sinα =. 2) Posto θ = u( ) l angolo formato dai ettori u e e posto V il olume del parallelepipedo che ha come spigoli u,,, si ha: V = A u cosθ = u. Dimostrazione. I due risultati sono eidenti dalle due figure seguenti. α θ α 20 Capitolo II - Vettori geometrici e sistemi di riferimento
LEZIONE 7. k definiamo prodotto scalare di v e w il numero. = v x w x + v y w y + v z w z. w z
 LEZINE 7 7.1. Prodotto scalare. Fissiamo un sistema di riferimento ı j k in S 3. Dati i ettori geometrici = ı + y j + k e w = w ı + j + k definiamo prodotto scalare di e w il numero, w = ( y ) w = + y
LEZINE 7 7.1. Prodotto scalare. Fissiamo un sistema di riferimento ı j k in S 3. Dati i ettori geometrici = ı + y j + k e w = w ı + j + k definiamo prodotto scalare di e w il numero, w = ( y ) w = + y
I VETTORI DELLO SPAZIO
 I VETTORI DELLO SPAZIO Riferimento cartesiano ortogonale nello spaio Bisogna assegnare nello spaio un punto O (detto origine e tre rette per esso a due a due perpendicolari e orientate in modo concorde
I VETTORI DELLO SPAZIO Riferimento cartesiano ortogonale nello spaio Bisogna assegnare nello spaio un punto O (detto origine e tre rette per esso a due a due perpendicolari e orientate in modo concorde
Elementi di calcolo vettoriale
 Mathit Elementi di calcolo ettoriale Nozione di ettore Grandezze ettoriali e grandezze scalari Segmenti orientati e ettori Definizioni Operazioni con i ettori Somma e differenza di ettori Moltiplicazione
Mathit Elementi di calcolo ettoriale Nozione di ettore Grandezze ettoriali e grandezze scalari Segmenti orientati e ettori Definizioni Operazioni con i ettori Somma e differenza di ettori Moltiplicazione
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Vettori. Capitolo Vettori applicati e vettori liberi
 apitolo 3 Vettori 3.1 Vettori applicati e vettori liberi In questo numero introduciamo il concetto di vettore geometrico su una retta, nel piano e nello spazio che ci consentirà di sviluppare un linguaggio
apitolo 3 Vettori 3.1 Vettori applicati e vettori liberi In questo numero introduciamo il concetto di vettore geometrico su una retta, nel piano e nello spazio che ci consentirà di sviluppare un linguaggio
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Operazioni coi vettori
 Operazioni coi ettori Opposto di un ettore I ersori Somma e differenza tra ettori Componenti di un ettore Prodotto scalare Prodotto ettoriale Rappresentazione matriciale di un ettore I ettori Per definire
Operazioni coi ettori Opposto di un ettore I ersori Somma e differenza tra ettori Componenti di un ettore Prodotto scalare Prodotto ettoriale Rappresentazione matriciale di un ettore I ettori Per definire
Prodotto scalare e norma
 Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
VETTORI GEOMETRICI / RICHIAMI
 M.GUIDA, S.ROLANDO, 2016 1 VETTORI GEOMETRICI / RICHIAMI Chiamiamo vettore un qualsiasi segmento orientato del piano o dello spazio. Orientare un segmento significa scegliere un verso per percorrerlo,
M.GUIDA, S.ROLANDO, 2016 1 VETTORI GEOMETRICI / RICHIAMI Chiamiamo vettore un qualsiasi segmento orientato del piano o dello spazio. Orientare un segmento significa scegliere un verso per percorrerlo,
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei.
 Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Note per il corso di Geometria e algebra lineare 2009-10 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
Vettori e Calcolo vettoriale
 Vettori e Calcolo vettoriale Ci poniamo nello spazio ordinario S, in cui valgono gli assiomi della geometria euclidea. I vettori vengono rappresentati mediante frecce, con un punto iniziale e un punto
Vettori e Calcolo vettoriale Ci poniamo nello spazio ordinario S, in cui valgono gli assiomi della geometria euclidea. I vettori vengono rappresentati mediante frecce, con un punto iniziale e un punto
Le prime sono dette grandezze scalari: esempi sono la massa, la temperatura, la pressione, il lavoro di una forza ecc... ecc.
 CP. - TEORI DEI VETTORI GEOMETRICI &. Introduione L'introduione dei ettori nasce dalla necessità che nelle sciene fisico - matematiche esistono grandee che sono definite solo da un numero, eentualmente
CP. - TEORI DEI VETTORI GEOMETRICI &. Introduione L'introduione dei ettori nasce dalla necessità che nelle sciene fisico - matematiche esistono grandee che sono definite solo da un numero, eentualmente
Prodotto scalare. Piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
ELEMENTI DI ALGEBRA VETTORIALE. Armando Bazzani Dipartimento di Fisica Università di Bologna, INFN sezione di Bologna
 ELEMENTI DI ALGEBRA VETTORIALE Armando Bazzani Dipartimento di Fisica Uniersità di Bologna, INFN sezione di Bologna Spazi Vettoriali Nella realtà si incontrano spesso grandezze che non si possono definire
ELEMENTI DI ALGEBRA VETTORIALE Armando Bazzani Dipartimento di Fisica Uniersità di Bologna, INFN sezione di Bologna Spazi Vettoriali Nella realtà si incontrano spesso grandezze che non si possono definire
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI.
 VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Elementi di calcolo vettoriale e matriciale per il corso di Matematica. per Architettura Ambientale (sede di Piacenza)
 Elementi di calcolo ettoriale e matriciale per il corso di Matematica per Architettura Ambientale (sede di Piacenza) Armando Bazzani Dipartimento di Fisica Uniersità di Bologna, INFN sezione di Bologna
Elementi di calcolo ettoriale e matriciale per il corso di Matematica per Architettura Ambientale (sede di Piacenza) Armando Bazzani Dipartimento di Fisica Uniersità di Bologna, INFN sezione di Bologna
, 3x y = a 2 = b 2 + c 2 2bc cos α.
 Esercizi. Soluzioni. (.A ) Siano x = e y =. 2 (i) Calcolare e disegnare i vettori x, 2x, x, 0x. (ii) Calcolare e disegnare i vettori x + y, x y, y e x y. (iii) Calcolare x, y, x + y e x y. Sol. 2 0 (i)
Esercizi. Soluzioni. (.A ) Siano x = e y =. 2 (i) Calcolare e disegnare i vettori x, 2x, x, 0x. (ii) Calcolare e disegnare i vettori x + y, x y, y e x y. (iii) Calcolare x, y, x + y e x y. Sol. 2 0 (i)
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
Capitolo XI GEOMETRIA LINEARE AFFINE EUCLIDEA
 Capitolo XI GEOMETRIA LINEARE AFFINE EUCLIDEA 1. Spazi affini euclidei Se, in luogo dello spazio affine costruito a partire dallo spazio vettoriale R n, si considera quello associato allo spazio euclideo
Capitolo XI GEOMETRIA LINEARE AFFINE EUCLIDEA 1. Spazi affini euclidei Se, in luogo dello spazio affine costruito a partire dallo spazio vettoriale R n, si considera quello associato allo spazio euclideo
Metodo delle coordinate. Rette nel piano. Mauro Saita. Versione provvisoria. Novembre 2015.
 . Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
. Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
APPUNTI DELLE LEZIONI
 APPUNTI DELLE LEZIONI Giorgio Follo (follogio@libero.it) I.T.I.S. A. Artom Asti Versione del 27/2/2011 Sommario. In qesti appnti engono riportate le nozioni elementeari s ettori e prodotto scalare, per
APPUNTI DELLE LEZIONI Giorgio Follo (follogio@libero.it) I.T.I.S. A. Artom Asti Versione del 27/2/2011 Sommario. In qesti appnti engono riportate le nozioni elementeari s ettori e prodotto scalare, per
Appunti sul corso di Complementi di Matematica (modulo Analisi)
 Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
LEZIONE 5. Typeset by AMS-TEX
 LEZINE 5 5.1. Vettori geometrici. In questo lezione inizieremo a studiare enti geometrici ben noti quali punti, segmenti (orientati), rette, piani nel piano A 2 e nello spazio A 3 affini (cioè in cui valgono
LEZINE 5 5.1. Vettori geometrici. In questo lezione inizieremo a studiare enti geometrici ben noti quali punti, segmenti (orientati), rette, piani nel piano A 2 e nello spazio A 3 affini (cioè in cui valgono
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Bivettori. Determinanti. Prodotto vettoriale.
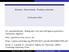 Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Geometria Analitica nello Spazio
 Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
21. (cenni di) Geometria analitica del piano.
 . (cenni di) Geometria analitica del piano... Definizione. Sia π un piano e sia O un suo punto. Siano i e j due versori ortogonali tra loro e paralleli al piano π. Diremo che la terna ordinata (O, i, j)
. (cenni di) Geometria analitica del piano... Definizione. Sia π un piano e sia O un suo punto. Siano i e j due versori ortogonali tra loro e paralleli al piano π. Diremo che la terna ordinata (O, i, j)
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri:
 DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
a.a MG.VETTORI E RETTE
 a.a. 2013-2014 MG.VETTORI E RETTE Definizione 0.1. Un vettore applicato o segmento orientato dello spazio ordinario è il dato di una coppia ordinata di punti dello spazio, il primo detto punto iniziale
a.a. 2013-2014 MG.VETTORI E RETTE Definizione 0.1. Un vettore applicato o segmento orientato dello spazio ordinario è il dato di una coppia ordinata di punti dello spazio, il primo detto punto iniziale
LEZIONE 6. Typeset by AMS-TEX
 LEZINE 6 6.1. Vettori geometrici. In questo lezione inizieremo a studiare enti geometrici ben noti quali punti, segmenti (orientati), rette, piani nel piano S 2 e nello spazio S 3 ordinari (cioè in cui
LEZINE 6 6.1. Vettori geometrici. In questo lezione inizieremo a studiare enti geometrici ben noti quali punti, segmenti (orientati), rette, piani nel piano S 2 e nello spazio S 3 ordinari (cioè in cui
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry)
 GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
Grandezze scalari e vettoriali-esempi
 Grandezze scalari e vettoriali-esempi Massa Tempo Temperatura Pressione Posizione lungo un asse (linea) Volume Lavoro Energia Posizione nel piano Posizione nello spazio Velocità Accelerazione Forza Quantità
Grandezze scalari e vettoriali-esempi Massa Tempo Temperatura Pressione Posizione lungo un asse (linea) Volume Lavoro Energia Posizione nel piano Posizione nello spazio Velocità Accelerazione Forza Quantità
Corso di Geometria Lezione II: Spazi vettoriali
 .. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
.. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
Prodotto scalare. Piani e rette nello spazio. Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in n. Piani e rette nello spazio. 17 Gennaio 2016 Indice 1 Prodotto scalare nello spazio
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in n. Piani e rette nello spazio. 17 Gennaio 2016 Indice 1 Prodotto scalare nello spazio
Mauro Saita Gennaio Equazioni cartesiane di rette e equazioni parametriche di piani Esempi...
 ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
Corso di Matematica B - Ingegneria Informatica Testi di Esercizi. A1. Siano u, v, w vettori. Quali tra le seguenti operazioni hanno senso?
 A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
Lezione 1
 Lezione 1 Ordini di grandezza Dimensioni fisiche Grandezze scalari e vettoriali Algebra dei vettori Coordinate Cartesiane e rappresentazioni grafiche Verifica Cenno sulle dimensioni delle grandezze fisiche
Lezione 1 Ordini di grandezza Dimensioni fisiche Grandezze scalari e vettoriali Algebra dei vettori Coordinate Cartesiane e rappresentazioni grafiche Verifica Cenno sulle dimensioni delle grandezze fisiche
Capitolo 1 Vettori applicati e geometria dello spazio
 Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Rappresentazioni del piano e dello spazio
 1 Rappresentazioni del piano e dello spazio 1.1 Coordinate polari, cilindriche, sferiche Un punto P del piano cartesiano, di coordinate (x, y), può anche essere indiiduato mediante le sue coordinate polari
1 Rappresentazioni del piano e dello spazio 1.1 Coordinate polari, cilindriche, sferiche Un punto P del piano cartesiano, di coordinate (x, y), può anche essere indiiduato mediante le sue coordinate polari
V il segmento orientato. V con VETTORI. Costruzione di un vettore bidimensionale
 VETTORI Costruzione di un vettore bidimensionale Nel piano con un righello si traccia una retta r tratteggiata Su r si disegna un segmento di lunghezza l d una delle estremità si disegni la punta di una
VETTORI Costruzione di un vettore bidimensionale Nel piano con un righello si traccia una retta r tratteggiata Su r si disegna un segmento di lunghezza l d una delle estremità si disegni la punta di una
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
Geometria analitica pagina 1 di 5
 Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
Prodotto interno (prodotto scalare definito positivo)
 Contenuto Prodotto scalare. Lunghezza, ortogonalità. Sistemi e basi ortonormali. Somma diretta: V = U U. Proiezioni. Teorema di Pitagora, disuguaglianza di Cauchy-Schwarz. Angoli. Federico Lastaria. Analisi
Contenuto Prodotto scalare. Lunghezza, ortogonalità. Sistemi e basi ortonormali. Somma diretta: V = U U. Proiezioni. Teorema di Pitagora, disuguaglianza di Cauchy-Schwarz. Angoli. Federico Lastaria. Analisi
Richiami sugli insiemi numerici
 Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
Analisi statistica e matematico-finanziaria II. Alfonso Iodice D Enza Università degli studi di Cassino e del Lazio Meridionale
 delle sui delle Analisi statistica e matematico-finanziaria II Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale sulle particolari ali dei dati Outline
delle sui delle Analisi statistica e matematico-finanziaria II Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale sulle particolari ali dei dati Outline
RELAZIONI e CORRISPONDENZE
 RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
2 Algebra lineare. 2.1 Lo spazio euclideo R n
 2 Algebra lineare 2.1 Lo spazio euclideo R n Dato un numero n N, il simbolo R n sta ad indicare il prodotto cartesiano R R di n copie di R; in altre parole, si tratta delle n-uple ( coppie per n = 2, terne
2 Algebra lineare 2.1 Lo spazio euclideo R n Dato un numero n N, il simbolo R n sta ad indicare il prodotto cartesiano R R di n copie di R; in altre parole, si tratta delle n-uple ( coppie per n = 2, terne
Capitolo I: Complementi di geometria vettoriale
 Liceo Lugano 1, 01-013 3E (Luca Rovelli) Capitolo I: Complementi di geometria vettoriale 1. Vettori geometrici in V 3 Dal momento che i concetti fondamentali sono già stati approfonditi nel piano, ci limitiamo
Liceo Lugano 1, 01-013 3E (Luca Rovelli) Capitolo I: Complementi di geometria vettoriale 1. Vettori geometrici in V 3 Dal momento che i concetti fondamentali sono già stati approfonditi nel piano, ci limitiamo
1- Geometria dello spazio. Vettori
 1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
I Vettori nello Spazio Euclideo
 I Vettori nello Spazio Euclideo Vettori geometrici In questa sezione ogliamo descriere un esempio di spazio ettoriale che potrebbe serire da modello su cui interpretare le definizioni più astratte che
I Vettori nello Spazio Euclideo Vettori geometrici In questa sezione ogliamo descriere un esempio di spazio ettoriale che potrebbe serire da modello su cui interpretare le definizioni più astratte che
Parte 9. Geometria del piano
 Parte 9. Geometria del piano A. Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Vettori geometrici del piano, 1 2 Lo spazio vettoriale VO 2, 3 3 Sistemi di riferimento, 8 4 Equazioni
Parte 9. Geometria del piano A. Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Vettori geometrici del piano, 1 2 Lo spazio vettoriale VO 2, 3 3 Sistemi di riferimento, 8 4 Equazioni
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Esercizi di Geometria e Algebra Lineare
 Esercizi di Geometria e Algebra Lineare 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}) 2) Nello spazio vettoriale R 3 sul campo R, sia
Esercizi di Geometria e Algebra Lineare 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}) 2) Nello spazio vettoriale R 3 sul campo R, sia
Spazi vettoriali. Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali.
 Spazi vettoriali Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali. Piano vettoriale geometrico G 2 Il contesto del discorso che svolgiamo in questa parte e il piano della geometria elementare,
Spazi vettoriali Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali. Piano vettoriale geometrico G 2 Il contesto del discorso che svolgiamo in questa parte e il piano della geometria elementare,
Capitolo 1. I vettori
 Capitolo 1 I ettori Prima di entrare nel cuore della meccanica e affrontarne i concetti di base, è importante acquisire padronanza con gli oggetti e gli strumenti che erranno utilizzati: i ettori e l algebra
Capitolo 1 I ettori Prima di entrare nel cuore della meccanica e affrontarne i concetti di base, è importante acquisire padronanza con gli oggetti e gli strumenti che erranno utilizzati: i ettori e l algebra
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Geometria analitica - Testo pagina 1 di 5 67
 Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Geometria analitica dello spazio
 Geometria analitica dello spazio Note per l insegnamento di Matematica per Scienze Naturali e Ambientali e Scienze Geologiche Marco Abate Dipartimento di Matematica, Università di Pisa Largo Pontecorvo
Geometria analitica dello spazio Note per l insegnamento di Matematica per Scienze Naturali e Ambientali e Scienze Geologiche Marco Abate Dipartimento di Matematica, Università di Pisa Largo Pontecorvo
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
La retta nel piano. Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione.
 La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
Esercizi di Geometria Affine
 Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
vettori V Sia inoltre l angolo che il primo vettore deve percorrere per sovrapporsi al secondo. * **
 Prodotto scalare di vettori. Consideriasmo due vettori u e v e siano O e O due rappresentanti applicati in O. Indichiamo come al solito con u = O la norma (cioè l intensità) del vettore u Sia inoltre l
Prodotto scalare di vettori. Consideriasmo due vettori u e v e siano O e O due rappresentanti applicati in O. Indichiamo come al solito con u = O la norma (cioè l intensità) del vettore u Sia inoltre l
Lezione 2: Spazi Vettoriali
 Lezione 2: Spazi Vettoriali In questa lezione vogliamo introdurre il vero protagonista dell algebra lineare: lo spazio vettoriale. Si tratta di una astrazione che comprende concetti che già ben conosciamo;
Lezione 2: Spazi Vettoriali In questa lezione vogliamo introdurre il vero protagonista dell algebra lineare: lo spazio vettoriale. Si tratta di una astrazione che comprende concetti che già ben conosciamo;
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Ferruccio Orecchia. esercizi di GEOMETRIA 1
 A01 102 Ferruccio Orecchia esercizi di GEOMETRIA 1 Copyright MCMXCIV ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 A/B 00173 Roma (06) 93781065 ISBN 978
A01 102 Ferruccio Orecchia esercizi di GEOMETRIA 1 Copyright MCMXCIV ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 A/B 00173 Roma (06) 93781065 ISBN 978
Alfonso Iodice D Enza
 Strumenti quantitativi per l economia e la finanza I Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale ali dei Il coefficiente () Statistica 1 / 50 Outline
Strumenti quantitativi per l economia e la finanza I Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino e del Lazio Meridionale ali dei Il coefficiente () Statistica 1 / 50 Outline
(f g)(x) = f(g(x)), (f (g h))(x) = f(g(h(x))) = ((f g) h)(x).
 Trasformazioni geometriche di R In questo paragrafo studiamo alcune trasformazioni geometriche del piano R Per trasformazioni si intendono sempre delle applicazioni bigettive f : R R Le trasformazioni
Trasformazioni geometriche di R In questo paragrafo studiamo alcune trasformazioni geometriche del piano R Per trasformazioni si intendono sempre delle applicazioni bigettive f : R R Le trasformazioni
Ferruccio Orecchia. esercizi di GEOMETRIA 1
 A01 102 Ferruccio Orecchia esercizi di GEOMETRIA 1 Copyright MCMXCIV ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 A/B 00173 Roma (06) 93781065 ISBN 978
A01 102 Ferruccio Orecchia esercizi di GEOMETRIA 1 Copyright MCMXCIV ARACNE editrice S.r.l. www.aracneeditrice.it info@aracneeditrice.it via Raffaele Garofalo, 133 A/B 00173 Roma (06) 93781065 ISBN 978
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
LEZIONE 36. si dice regolare se è. per ogni (u 0, v 0 ) D. Una superficie S R 3 is dice regolare se esiste una sua parametrizzazione regolare.
 LEZIONE 36 36.1. La definizione di superficie. In questo paragrafo iniziamo a dare alcuni esempi di superfici ed a definire alcuni oggetti ad esse naturalmente associati. Come già fatto per le curve, considereremo
LEZIONE 36 36.1. La definizione di superficie. In questo paragrafo iniziamo a dare alcuni esempi di superfici ed a definire alcuni oggetti ad esse naturalmente associati. Come già fatto per le curve, considereremo
VETTORI NELLO SPAZIO ORDINARIO ,
 VETTORI E GEOMETRIA ANALITICA 1 VETTORI NELLO SPAZIO ORDINARIO Vettori ordinari ed operazioni. Dipendenza ed indipendenza lineare, basi. Prodotto scalare, proiezioni, angoli. Prodotto vettoriale e prodotto
VETTORI E GEOMETRIA ANALITICA 1 VETTORI NELLO SPAZIO ORDINARIO Vettori ordinari ed operazioni. Dipendenza ed indipendenza lineare, basi. Prodotto scalare, proiezioni, angoli. Prodotto vettoriale e prodotto
GEOMETRIA 1 Corso di Geometria 1 (prima parte)
 GEOMETRIA 1 Corso di Geometria 1 (prima parte) Maria Dedò e Cristina Turrini 2011/2012 Maria Dedò e Cristina Turrini (2011/2012) GEOMETRIA 1 1 / 109 index Vettori 1 Vettori 2 Retta, piano e spazio affini
GEOMETRIA 1 Corso di Geometria 1 (prima parte) Maria Dedò e Cristina Turrini 2011/2012 Maria Dedò e Cristina Turrini (2011/2012) GEOMETRIA 1 1 / 109 index Vettori 1 Vettori 2 Retta, piano e spazio affini
Matematica Lezione 4
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 4 Sonia Cannas 18/10/2018 Proporzioni Esempio Da un rubinetto di una vasca fuoriescono 60 litri di acqua in 4 minuti. Quanti litri
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 4 Sonia Cannas 18/10/2018 Proporzioni Esempio Da un rubinetto di una vasca fuoriescono 60 litri di acqua in 4 minuti. Quanti litri
Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica
 Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}). 2) Nello spazio vettoriale
Esercizi di Geometria e Algebra Lineare C.d.L. Ingegneria Meccanica 1) Dati i vettori a = (2, 4), b = (1, 2), c = ( 1, 1), d = (3, 6), stabilire se c e d appartengono a Span(a, b}). 2) Nello spazio vettoriale
Geometria analitica: rette e piani
 Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
2.1 Numeri naturali, interi relativi, razionali
 2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
a) Parallela a y = x + 2 b) Perpendicolare a y = x +2. Soluzioni
 Svolgimento Esercizi Esercizi: 1) Una particella arriva nel punto (-2,2) dopo che le sue coordinate hanno subito gli incrementi x=-5, y=1. Da dove è partita? 2) Disegnare il grafico di C = 5/9 (F -32)
Svolgimento Esercizi Esercizi: 1) Una particella arriva nel punto (-2,2) dopo che le sue coordinate hanno subito gli incrementi x=-5, y=1. Da dove è partita? 2) Disegnare il grafico di C = 5/9 (F -32)
GEOMETRIA ANALITICA Prof. Erasmo Modica
 ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEZIONE DISTACCATA DI CEFALÙ CLASSE V C GEOMETRIA ANALITICA Prof. Erasmo Modica LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEZIONE DISTACCATA DI CEFALÙ CLASSE V C GEOMETRIA ANALITICA Prof. Erasmo Modica LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
Corso di Fisica I per Matematica
 Corso di Fisica I per Matematica DOCENTE: Marina COBAL: marina.cobal@cern.ch Tel. 339-2326287 TESTO di RIFERIMENTO: Mazzoldi, Nigro, Voci: Elementi d fisica,meccanica e Termodinamica Ed. EdiSES FONDAMENTI
Corso di Fisica I per Matematica DOCENTE: Marina COBAL: marina.cobal@cern.ch Tel. 339-2326287 TESTO di RIFERIMENTO: Mazzoldi, Nigro, Voci: Elementi d fisica,meccanica e Termodinamica Ed. EdiSES FONDAMENTI
(P x) (P y) = x P t (P y) = x (P t P )y = x y.
 Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
Matrici ortogonali Se P è una matrice reale n n, allora (P x) y x (P t y) per ogni x,y R n (colonne) Dim (P x) y (P x) t y (x t P t )y x t (P t y) x (P t y), CVD Ulteriori caratterizzazioni delle matrici
15 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
Copyright Esselibri S.p.A.
 Un isometria è perciò una trasformazione geometrica che conserva la distanza tra due punti. onsideriamo alcune particolari trasformazioni isometriche. 2.1.1. Traslazioni hiamiamo vettore un segmento sul
Un isometria è perciò una trasformazione geometrica che conserva la distanza tra due punti. onsideriamo alcune particolari trasformazioni isometriche. 2.1.1. Traslazioni hiamiamo vettore un segmento sul
Cenni di geometria differenziale delle superfici.
 Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
