ii) d(x, y) =d(y, x) per ogni x, y in X (simmetria); Uno spazio metrico è una coppia (X, d) con X insieme qualsiasi, e d distanza su X.
|
|
|
- Rita Scarpa
- 5 anni fa
- Visualizzazioni
Transcript
1 Caitolo 1 Sazi metrici 1.1 Definizioni ed esemi Definizione Sia X un insieme qualsiasi. Una distanza su X è un alicazione d : X X R tale che i) d(x, y) 0 er ogni x, y in X, e d(x, y) = 0 se e solo se x = y (ositività); ii) d(x, y) =d(y, x) er ogni x, y in X (simmetria); iii) d(x, y) d(x, z)+d(z,y) er ogni x, y e z in X (disuguaglianza triangolare). Uno sazio metrico è una coia (X, d) con X insieme qualsiasi, e d distanza su X. Esemio 1.1. Sia X un insieme qualsiasi e d(x, y) =1sex y, d(x, y) =0 se x = y. Si verifica facilmente che i) e ii) valgono; er la iii), se x = y non c è nulla da dimostrare; se x y, si deve rovare che d(x, z)+d(z,y) 1 er ogni x, y e z in X con x y, fatto questo che risulta essere vero, essendo almeno uno tra i valori d(x, z) ed(y, z) uguale a 1 (non ossono essere entrambi nulli, dato che se lo fossero, si avrebbe x = z e z = y er la i), da cui x = y, ilche non è). La distanza d rende il nome di distanza discreta. Esemio Sia X = R e d(x, y) = x y. Allora (R, )è uno sazio metrico (le tre rorietà sono ben note...).
2 CAPITOLO 1. SPAZI METRICI 3 Teorema (Disuguaglianza di Cauchy-Schwartz) Date due N-le di numeri reali (s 1,...,s N ) e (t 1,...,t N ),siha: s i t i 1 (s i + t i ). (1.1) ( N ) 1 ( s i t i s N i t i. (1.) Dimostrazione. La formula (1.1) si ottiene sommando (er i che va da 1 a N) le disuguaglianze s i t i s i + t i, evidentemente vere essendo equivalenti alla disuguaglianza ( s i t i ) 0. Per dimostrare la (1.), osserviamo che è evidentemente vera se (s 1,...,s N )= (0,...,0) o se (t 1,...,t N )=(0,...,0); altrimenti, alichiamo la (1.1) alle N-le (x 1,...,x N )e(y 1,...,y N ) definite da x i = s i ( N s i, y i = t i ( N t i. Si ottiene, essendo N x i =1= N y i, 1 ( N ) s 1 ( N i t i da cui la tesi. s i t i = s i t i ( N ) s 1 ( ) N i t 1 i 1, Esemio Sia X = R N e ( N ) 1 d((x 1,...,x N ), (y 1,...,y N )) = (x i y i ). Si ha che (R N,d)è uno sazio metrico. La i) e la ii) sono evidenti, mentre er la iii) rocediamo come segue, indicando con X =(x 1,...,x N ), Y =
3 CAPITOLO 1. SPAZI METRICI 4 (y 1,...,y N )ez =(z 1,...,z N ) tre vettori di R N : [d(x, Y )] = (x i y i ) = (x i z i + z i y i ) = [(x i z i ) +(x i z i )(z i y i )+(z i y i ) ] =[d(x, Z)] +[d(z, Y )] + (x i z i )(z i y i ). Alicando la (1.), si ha ( N ) (x i z i )(z i y i ) (x i z i ) ( N ) (z i y i ) Pertanto, = d(x, Y ) d(z, Y ). [d(x, Y )] [d(x, Z)] +[d(z, Y )] +d(x, Z) d(z, Y )=[d(x, Z)+d(Z, Y )], che è la iii). Teorema (Disuguaglianza di Young) Siano s, t due numeri reali e siano e q due numeri reali tali che Allora >1, q > 1, st s q =1. + t q q. (1.3) Dimostrazione. Se uno tra s e t è zero, non c è nulla da rovare. Se sono entrambi non nulli, dividiamo la (1.3) er t q, ottenendo s s t q 1 t + 1 q q. Definiamo ρ = s t q 1.
4 CAPITOLO 1. SPAZI METRICI 5 Essendo 1/ +1/q =1,siha(q 1) = q, e quindi ρ = s s = t (q 1) t. q Dimostrare la (1.3) è quindi equivalente a mostrare che er ogni ρ 0, ovvero che ρ ρ + 1 q, ϕ(ρ) = ρ ρ + 1 q è ositiva su [0, + ). Si ha ϕ(0) = 1/q, mentre ϕ diverge er ρ tendente a + (essendo >1). Si ha oi ϕ (ρ) =ρ 1 1, e quindi ϕ (ρ) = 0 se e solo se ρ = 1. Si vede facilmente che ρ =1èdi minimo (assoluto) er ϕ; essendo ϕ(1) = q =0, si ha la tesi. Semlice conseguenza del Teorema recedente (si ragiona come nella dimostrazione del Teorema 1.1.4) è il risultato che segue. Teorema (Disuguaglianza di Hölder) Siano date due N-le di numeri reali (s 1,...,s N ) e (t 1,...,t N ). Siano e q due numeri reali tali che Allora >1, q > 1, q =1. s i t i 1 s i + 1 t i q. (1.4) q ( N ) 1 ( N ) s i t i s i 1 q t i q. (1.5)
5 CAPITOLO 1. SPAZI METRICI 6 Si osservi che essendo 1/+1/ = 1 (!), le formule (1.1) e (1.) sono casi articolari di (1.4) e (1.5). Esemio Sia X = R N, >1e d ((x 1,...,x N ), (y 1,...,y N )) = ( N x i y i Allora (R N,d )è uno sazio metrico. Al solito, i) e ii) sono evidenti, mentre la disuguaglianza triangolare è di dimostrazione iù comlicata; si ha (suonendo d (X, Y ) 0, altrimenti la tesi è banale). [d (X, Y )] = x i y i = x i y i 1 x i y i = x i y i x i z i + z i y i x i y i 1 x i z i + x i y i 1 z i y i. (1.6) Alicando la (1.5), si ha e ( x i y i 1 N x i z i x i y i ( 1) q q ( N x i z i, ( x i y i 1 N z i y i Essendo ( 1)q =, si ha allora x i y i ( 1) q q ( N z i y i. e x i y i 1 x i z i [d (X, Y )] q d (X, Z), x i y i 1 z i y i [d (X, Y )] q d (Z, Y ).
6 CAPITOLO 1. SPAZI METRICI 7 Sostituendo in (1.6), si ha [d (X, Y )] [d (X, Y )] q [d (X, Z)+d (Z, Y )]. Dividendo er d (X, Y )(cheè diverso da zero er iotesi), si ottiene la disuguaglianza triangolare osservando che /q = 1. Semre in R N è ossibile definire d ((x 1,...,x N ), (y 1,...,y N )) = max{ x i y i,,...,n}. Lo sazio (R N,d )è uno sazio metrico (verifica molto semlice, in questo caso). Esercizio Dimostrare che lim + d ((x 1,...,x N ), (y 1,...,y N )) = d ((x 1,...,x N ), (y 1,...,y N )). Teorema (Cauchy-Schwartz e Hölder) Siano date {s n } e {t n } due successioni di numeri reali; a) se si ha + + s n < +, s n t n ( + s n + t n < +, ( + t n ; (1.7) b) dati e q due numeri reali tali che se si ha + >1, q > 1, s n < +, q =1, t n q < +, + ( + ( s n t n s n + t n q q. (1.8)
7 CAPITOLO 1. SPAZI METRICI 8 Dimostrazione. Dimostriamo solo la rima formula (l altra ha dimostrazione analoga). Sia N fissato; alicando (1.), si ha ( N ) 1 ( s n t n s N n t n ( + s n ( + t n ; la seconda disuguaglianza è dovuta al fatto che le serie sono a termini non negativi (e quindi la successione delle somme arziali è monotona crescente). Pertanto, essendo la disuguaglianza recedente vera er ogni N in N, si ha su { N s n t n,n N } ( + s n ( + t n Essendo la serie di termine generico s n t n una serie a termini non negativi, la successione delle somme arziali è monotona crescente, cosicché l estremo sueriore coincide con il limite er N tendente a +, cioè la somma della serie.. Esemio Sia 1, e siano { X = l = {x n } R : d ({x n }, {y n })= ( + + x n < + x n y n Allora (l,d )è uno sazio metrico. Come al solito, i) e ii) sono di verifica immediata, iù comlicato è il controllo della disuguaglianza triangolare. La verifica si effettua come nel caso di (R n,d ), usando (1.8). Se =1,la verifica discende semlicemente dalla disugaglianza triangolare in R. Si noti che gli sazi l soddisfano le seguenti inclusioni, se q> 1: l 1 l l q, e le inclusioni sono strette. Per verificare le inclusioni, è sufficiente osservare che se {x n } aartiene a l, allora x n tende a zero, e quindi x n tende a zero. Pertanto, x n è definitivamente minore di 1, il che imlica che x n q }.,
8 CAPITOLO 1. SPAZI METRICI 9 x n definitivamente (essendo q>). Quindi {x n } aartiene a l q (er il criterio del confronto). L inclusione è stretta in quanto (ad esemio) x n = 1/[n 1/q ln (n)] èinl q ma non in l se <q. Sia oi X = l = {{x n } R : {x n } è limitata}, d ({x n }, {y n }) = su{ x n y n,n N}. (1.9) Allora (l,d )è uno sazio metrico (la verifica questa volta è facile!) tale che l l er ogni 1, con inclusione stretta (ogni successione limitata ma non infinitesima non aartiene ad l dal momento che la condizione necessaria di convergenza della serie non è verificata). Esemio Siano e X = C 0 ([a, b], R) ={f :[a, b] R f continua}, d (f,g) = su{ f(x) g(x),x [a, b]} = max{ f(x) g(x),x [a, b]}. Allora (C 0 ([a, b], R),d )è uno sazio metrico, come si verifica facilmente (anche la disuguaglianza triangolare!). Esemio Siano e X = C 0 ([a, b], R) ={f :[a, b] R f continua}, d 1 (f,g) = b a f(x) g(x) dx. Allora (C 0 ([a, b], R),d 1 )è uno sazio metrico: la ii) e la iii) sono facilmente verificate (ricordando la monotonia dell integrale), mentre la i) segue dall osservazione che se l integrale del modulo di una funzione continua h è nullo, allora h è identicamente nulla. Infatti, se h non fosse nulla, esisterebbe x 0 in [a, b] tale che h(x 0 ) > 0; er il teorema della ermanenza del segno, esisterebbe un intorno (x 0 δ, x 0 + δ) sul quale si ha h(x) > h(x 0 ) /. Pertanto 0= da cui l assurdo. b a h(x) dx x0 +δ x 0 δ h(x) dx>δ h(x 0 ) > 0,
9 CAPITOLO 1. SPAZI METRICI 10 Teorema (Disuguaglianza di Hölder) Siano f e g due funzioni in C 0 ([a, b], R) e siano e q maggiori di 1 e tali che 1/ +1/q =1. Allora b a ( b f(x) g(x) dx f(x) dx a ( b g(x) q dx a q. (1.10) Dimostrazione. È sufficiente artire dalla disuguaglianza di Young, vera er ogni x in [a, b], f(x) g(x) f(x) + g(x) q q, integrare i due termini su [a, b] e oi alicare la disuguaglianza così trovata a f(x) g(x) f(x) = ( b a f(x) dx ), ḡ(x) = 1 ( b a g(x) q dx ), 1 q non rima di aver osservato che se l integrale di f(x) (o di g(x) q )è nullo, la f (ovvero la g) è nulla e la disuguaglianza (1.10) è banalmente vera. Esemio Siano >1, e X = C 0 ([a, b], R) ={f :[a, b] R f continua}, ( b d (f,g) = f(x) g(x) dx a. Ragionando come nell Esemio , ed usando la (1.10), si dimostra facilmente che (C 0 ([a, b], R),d )è uno sazio metrico. (!)Esercizio Dimostrare che lim + d (f,g) =d (f,g).
10 CAPITOLO 1. SPAZI METRICI 11 Esemio Siano X = C 1 ([a, b], R) ={f :[a, b] R f continua con derivata continua}, d,1 (f,g) = su{ f (x) g (x),x [a, b]} = d (f,g ), e d,1 (f,g) =d (f,g )+d (f,g). Allora (C 1 ([a, b], R), d,1 ) non è uno sazio metrico (dal momento che se f e g differiscono er una costante, d è nulla), mentre (C 1 ([a, b], R),d,1 )lo è. Dal momento che l aggiunta di d (f,g) è dovuta solo alla necessità di distinguere due funzioni la cui differenza è costante, si uò considerare su C 1 ([a, b], R) la distanza d,1 (f,g) =d (f,g )+ f(x 0 ) g(x 0 ), con x 0 unto qualsiasi di [a, b]. In questa maniera, er calcolare la distanza tra f e g è sufficiente conoscere le derivate di f e g, ed il valore delle due funzioni in un unico unto (e non su tutto l intervallo). 1. Prorietà degli sazi metrici Definizione 1..1 Sia (X, d) uno sazio metrico, sia x 0 in X e r>0. La sfera aerta di centro x 0 e raggio r è l insieme B d (x 0,r)={x X : d(x, x 0 ) <r}. Le sfere di (R,d )er =1, 3,,3e (rocedendo dall interno verso l esterno)
11 CAPITOLO 1. SPAZI METRICI 1 Un sottoinsieme A di (X, d) si dice aerto se er ogni x 0 in A esiste r>0 tale che B d (x 0,r) A. Un sottoinsieme C di (X, d) si dice chiuso se A = C c = X \C è aerto. Si verifica facilmente che in (X, discreta) ogni sottoinsieme è aerto (e quindi anche chiuso), mentre gli aerti di (R, )edi(r N,d ) (er ogni ) sono gli aerti soliti. Definizione 1.. Sia (X, d) uno sazio metrico. Una successione {x n } contenuta in X si dice convergente a x 0 in X se si ha lim n + d(x n,x 0 )=0. Quindi, come si vede, la definizione di convergenza in uno sazio metrico è ricondotta (in maniera naturale) alla convergenza a zero in R (meglio, nello sazio metrico (R, )) della successione {d(x n,x 0 )}. Ad esemio, nello sazio metrico dell Esemio 1.1., le successioni convergenti sono tutte e sole le successioni che sono definitivamente costanti. La convergenza in (R, )ein(r N,d ) (er ogni ) è la convergenza solita chesidà er successioni in R ed in R N (quest ultima è come è noto equivalente alla convergenza in (R, ) delle N comonenti). La convergenza in C 0 ([a, b]),d )è la convergenza uniforme. Teorema 1..3 Sia {x n } una successione convergente in (X, d). Allora il limite è unico. Dimostrazione. Se x n convergesse a x 0 eay 0, si avrebbe lim d(x n,x 0 ) = lim d(x n,y 0 )=0. n + n + Ma allora, er la disuguaglianza triangolare, d(x 0,y 0 ) d(x n,x 0 )+d(x n,y 0 ), da cui, ricordando che d(x 0,y 0 ) 0 e assando al limite, d(x 0,y 0 ) = 0. Pertanto, x 0 = y 0.
12 CAPITOLO 1. SPAZI METRICI 13 Definizione 1..4 Siano (X, d) e(y, d) due sazi metrici. Una funzione f : X Y si dice continua in x 0 X se, er ogni successione {x n } di X convergente a x 0, la successione {f(x n )} di Y converge a f(x 0 ). Analogamente, d(f(x n ),f(x 0 ))=0. lim d(x n,x 0 ) 0 Questa definizione negli sazi metrici è equivalente all altra (ben nota) data in termini di ε e δ: ε >0 δ ε > 0:d(x, x 0 ) <δ ε d(f(x),f(x 0 )) <ε. Esemio 1..5 Siano (X, discreta) e (Y, d) due sazi metrici. Allora ogni funzione f : X Y è continua. Infatti, se {x n } è una qualsiasi successione convergente in (X, discreta) a x 0, allora si deve avere x n = x 0 definitivamente. Pertanto, f(x n )=f(x 0 ) definitivamente, da cui d(f(x n ),f(x 0 )) 0. Esercizio 1..6 Sia (X, d) uno sazio metrico e sia x 0 in X. Dimostrare che la funzione d x0 : X R definita da d x0 (x) =d(x 0,x)è continua. Definizione 1..7 Sia (Y,d) uno sazio metrico. Una funzione f : X Y si dice limitata se esistono M>0edy 0 in Y tali che f(x) B d (y 0,M), x X. (.1) Definizione 1..8 Siano (X, d) e(y, d) due sazi metrici. Definiamo L(X, Y )={f : X Y,flimitata}, C(X, Y )={f : X Y,fcontinua e limitata}. L insieme L(X, Y ) (e quindi anche C(X, Y ) che ne è un sottoinsieme) uò essere reso uno sazio metrico introducendo la distanza d (f,g) = su x X d(f(x),g(x)). (.) È facile verificare che d è effettivamente una distanza; si noti che èben definita erché sia f che g sono funzioni limitate. Nel caso in cui (X, d) = ([a, b], )e(y, d) =(R, ), C(X, Y )è rorio C 0 ([a, b], R), dal momento che la limitatezza delle funzioni continue su [a, b]è data dal teorema di Weierstrass. Inoltre, d è esattamente la distanza definita nell Esemio
13 CAPITOLO 1. SPAZI METRICI 14 Esemio 1..9 Siano (X, d) = (N, discreta) e (Y, d) = (R, ). Si ha allora, dal momento che ogni funzione f da X a Y non è niente altro che una successione di numeri reali, L(X, Y )={successioni limitate di numeri reali} = l. Inoltre, essendo ogni funzione da X a Y continua (Esemio 1..5), si ha C(X, Y ) = L(X, Y ). La distanza d definita da (.) è esattamente la distanza definita su l da (1.9). 1.3 Sazi metrici comleti Il seguente teorema mostra come una successione convergente soddisfi una rorietà aggiuntiva. Teorema Sia (X, d) uno sazio metrico e sia {x n } una successione in X convergente a x 0 in X. Allora la successione {x n } soddisfa la condizione di Cauchy, ovvero ε >0, n ε N : d(x n,x m ) <ε n, m n ε. Dimostrazione. Se x n converge a x 0 in X, er ogni ε>0 esiste n ε tale che d(x n,x 0 ) <ε/ er ogni n n ε.senemsono entrambi maggiori di n ε si ha allora, er la disuguaglianza triangolare, da cui la tesi. d(x n,x m ) d(x n,x 0 )+d(x 0,x m ) <ε, Esemio 1.3. Il viceversa del teorema recedente non è vero: non tutte le successioni di Cauchy sono convergenti. Sia X =(0, ) e d(x, y) = x y. Allora (X, d)è uno sazio metrico, come si verifica facilmente, e la successione x n =1/n, ur essendo di Cauchy, non è convergente. La successione èdi Cauchy erché è convergente in (R,d), ma non è convergente in X erché il suo (unico!) limite è zero, che non aartiene ad X. Definizione Uno sazio metrico si dice comleto se ogni successione di Cauchy è convergente.
14 CAPITOLO 1. SPAZI METRICI 15 Nell Esemio 1.1. lo sazio è comleto erché le successioni di Cauchy sono tutte e sole le successioni definitivamente costanti (quindi convergenti). Tutti gli sazi metrici su R o R N considerati nei vari esemi sono comleti. Un rimo risultato generale sulla comletezza è il seguente. Teorema Sia (X, d) uno sazio metrico comleto, e sia C X un insieme chiuso. Allora (C, d) è comleto. Dimostrazione. Sia {x n } una successione di Cauchy in (C, d). Allora {x n } è una successione di Cauchy in (X, d), che è comleto er iotesi. Pertanto, esiste x 0 in X tale che x n converge a x 0. Essendo C chiuso, x 0 aartiene a C (se, infatti, x 0 non aartenesse a C, sarebbe nel comlementare di C, che è aerto; allora esisterebbe un numero reale r>0 tale che B d (x 0,r) C =, il che è assurdo erché la successione {x n } si trova definitivamente in tale intorno er definizione di limite), che quindi è comleto. Un secondo risultato, ben iù imortante, riguarda L(X, Y ) e C(X, Y ). Teorema Siano (X, d) e (Y, d) due sazi metrici. Se (Y, d) è comleto, lo sono sia L(X, Y ) e C(X, Y ), dotati della metrica definita da (.). Dimostrazione. Sia {f n } una successione di Cauchy in (L(X, Y ),d )). Allora ε >0 n ε N : su d(f n (x),f m (x)) <ε n, m n ε. x X Per definizione di su, questo imlica che ε >0 n ε N : d(f n (x),f m (x)) <ε n, m n ε, x X. Pertanto, er ogni x in X la successione {f n (x)} è di Cauchy in (Y, d), comleto, e quindi converge ad un elemento di Y che definiremo f(x). Passando al limite er m tendente ad infinito nella disuguaglianza d(f n (x),f m (x)) <ε, si trova (grazie all Esercizio 1..6) ε >0 n ε N : d(f n (x),f(x)) ε, n n ε, x X. (3.1) Sia ora y in Y. Si ha, er la disuguaglianza triangolare, ed essendo f nε limitata er iotesi, d(f(x),y) d(f(x),f nε (x)) + d(f nε (x),y) ε + M,
15 CAPITOLO 1. SPAZI METRICI 16 e quindi f aartiene a L(X, Y ). Inoltre, rendendo l estremo sueriore er x in X in (3.1), si ha ε >0 n ε N : d (f n (x),f(x)) ε n n ε, e quindi f n converge a f in (L(X, Y ),d ). Se {f n } è una successione di Cauchy in C(X, Y ), lo stesso ragionamento svolto recedentemente ermette di costruire una funzione in L(X, Y ) tale che f n converge a f in d. L unica cosa da dimostrare è ertanto la continuità di f. Sex 0 e x 1 aartengono a X, siha d(f(x 0 ),f(x 1 )) d(f(x 0 ),f nε (x 0 )) + d(f nε (x 0 ),f nε (x 1 )) + d(f nε (x 1 ),f(x 1 )). La rima e la terza quantità sono minori di ε, mentre la seconda uò essere scelta iccola rendendo x 0 ed x 1 vicini (dal momento che f nε è continua). Pertanto, f è continua. Corollario Sia (C 0 ([a, b], R),d ) che (l,d ) sono comleti. Teorema Sia >1. Lo sazio (l,d ) è comleto. Dimostrazione. allora Sia {x (n) } una successione di Cauchy in (l,d ). Si ha ( + ε >0 n ε N : Pertanto, er ogni k in N, k=1 x (n) k ε >0 n ε N : x (n) k x (m) k <ε n, m n ε. (3.) x (m) k <ε n, m n ε, e quindi la successione {n x (n) k } è di Cauchy in (R, ), che è comleto. Siano allora x k il limite er n tendente ad infinito di x (n) k,e x la successione {x k }. Dal momento che da (3.) segue che, er ogni N in N, ε >0 n ε N : ( N k=1 x (n) k x (m) k <ε n, m n ε,
16 CAPITOLO 1. SPAZI METRICI 17 assando al limite er m tendente ad infinito, si ha ε >0 n ε N : ( N k=1 x (n) k Prendendo l estremo sueriore su N in N, x k <ε n n ε. ε >0 n ε N : ( + k=1 x (n) k x k <ε n n ε, da cui segue che {x (n) } converge a x in (l,d ). Il fatto che x aartenga ad l segue oi dalla disuguaglianza triangolare er d : ( + k=1 x k essendo x (nε) in l. = d ( x, 0) d ( x, x (nε) )+d (x (nε), 0) < +, Esemio Lo sazio C 0 ([a, b]),d 1 ) non è comleto. Consideriamo infatti C 0 ([ 1, 1], R) e la successione f n (x) così definita: 1 se x [ 1, 1/n], f n (x) = nx se x ( 1/n, 1/n) 1 se x [1/n, 1]. La successione f n è di Cauchy; infatti f n e f m differiscono al iù (se m>n) sull insieme ( 1/n, 1/n) e su questo insieme si ha f n (x) f m (x). Allora d 1 (f n,f m )= 1 1 f n (x) f m (x) dx = 1/n 1/n f n (x) f m (x) dx 4 n, che uò essere reso minore di ε se n è sufficientemente grande. D altra arte non esiste nessuna funzione continua f tale che Sia infatti a>0; allora d 1 (f n,f)= 1 a 1 1 f n (x) f(x) dx 0. f n (x) f(x) dx 0,
17 CAPITOLO 1. SPAZI METRICI 18 essendo questa quantità ositiva e minore di d 1 (f n,f). Se n è tale che 1/n<a (fatto che accade definitivamente), dalla definizione di f n si ha 1 a 1 f(x) dx 0, da cui (essendo questa quantità indiendente da n), 1 a 1 f(x) dx =0, il che imlica che f 1su[a, 1] er ogni a>0. Con ragionamento analogo si rova che f 1su[ 1, a] con a>0. Ma allora lim f(x) = 1 1= lim f(x), x 0 x 0 + e quindi f non uò essere continua in x =0. Esemio Lo sazio (X, d) = ((0, 1), ) non è comleto. Può, erò, essere reso comleto, aggiungendo i due unti 0 ed 1, senza modificare la distanza; in altre arole, si uò rendere la chiusura di X in R (di (X, ) nello sazio metrico (R, )), ed ottenere così uno sazio metrico comleto. L aggiunta dei due unti 0 ed 1 è minimale nel senso che er rendere X comleto (senza cambiare metrica) non è necessario utilizzare altri unti. Si osservi che esistono successioni di Cauchy tutte contenute in X che convergono a0oad1(mentre non esistono successioni di Cauchy contenute in X che convergono ad un qualsiasi numero reale non aartenente a [0, 1]). Lo sazio (X, d) =(Q, ) non è comleto. Ad esemio, la successione ( x n = 1+ n n, è contenuta in Q,è di Cauchy (erché converge in R ad e ), ma il limite non è un numero razionale. Anche in questo caso, come nel recedente, si uò rendere (Q, ) comleto aggiungendo i limiti delle successioni di Cauchy di razionali. Ricordando che ogni numero reale è limite (in (R, )) di una successione di razionali (dunque di una successione di Cauchy di razionali), si ottiene tutto R. Lo sazio (X, d) =({f C 0 ([a, b], R) :d (f,0) < 1},d ) non è comleto. Ad esemio, la successione f n (x) =1 1 èinx, è di Cauchy (dal n
18 CAPITOLO 1. SPAZI METRICI 19 momento che converge uniformemente a f(x) = 1), ma il suo limite non èinx. Anche in questo caso, si uò rendere (X, d) comleto aggiungendo le funzioni continue su [a, b] tali che d (f,0) = 1. Il risultato, che è({f C 0 ([a, b], R) : d (f,0) 1},d ), è comleto essendo chiuso in (C 0 ([a, b], R),d ), come si verifica facilmente. Si noti che, essendo ossibile ottenere ogni funzione f tale che d (f,0) = 1 come limite uniforme della successione f n = n f (che è tutta contenuta in X), e dal momento che nessuna funzione tale che d (f,0) > 1 uò essere ottenuta come limite uniforme n+1 di funzioni in X, ancora una volta abbiamo reso X comleto aggiungendo i limiti delle successioni di Cauchy contenute in X. A questo unto ci si uò chiedere se questa oerazione si uò semre effettuare. La risosta è affermativa, ed è data dal seguente teorema. Teorema (Comletamento) Dato uno sazio metrico (X, d), esiste uno sazio metrico comleto (Y, d) ed un alicazione i : X Y tale che 1. i è un isometria, ovvero d(i(x 0 ),i(x 1 )) = d(x 0,x 1 ), er ogni x 0, x 1 in X;. i(x) è denso in Y, ovvero la chiusura di i(x) in Y è Y. Dimostrazione. Sia C = {{x n } di Cauchy in (X, d)}. Passo 1: Se {x n } e {y n } aartengono a C, allora la successione z n = d(x n,y n )è di Cauchy in (R, ). Infatti si ha z n = d(x n,y n ) d(x n,x m )+d(x m,y m )+d(y m,y n )=d(x n,x m )+z m +d(y m,y n ), da cui z n z m d(x n,x m )+d(y m,y n ). Scambiando il ruolo di n e m si trova la disuguaglianza z m z n d(x n,x m )+ d(y m,y n ), da cui segue z n z m d(x n,x m )+d(y m,y n ).
19 CAPITOLO 1. SPAZI METRICI 0 A questo unto, fissato ε>0, è sufficiente scegliere n ed m iù grandi di n ε = max(n ε ({x n }),n ε ({y n })) er avere che z n z m <ε. Passo : Essendo (R, ) comleto, er ogni coia di successioni {x n } e {y n } di C, esiste il limite di d(x n,y n ). Definiamo in C la relazione seguente {x n }ρ{y n } lim n + d(x n,y n )=0. Si vede facilmente che ρ è una relazione di equivalenza (la transitività è conseguenza della disuguaglianza triangolare) su C. Definiamo Y come lo sazio quoziente di C modulo la relazione ρ. Successivamente, rendiamo Y uno sazio metrico nel modo seguente: siano x eȳ in Y, e siano {x n } e {y n } due successioni in [ x] e[ȳ] risettivamente. Allora d( x, ȳ) = lim n + d(x n,y n ). Tale definizione è ben osta, dal momento che cambiando raresentanti in [ x] e[ȳ] il limite non cambia (semre er la disuguaglianza triangolare). La funzione d è non negativa (dal momento che d lo è), e si annulla se e solo se x =ȳ (er definizione, se il limite di d(x n,y n )è zero, {x n } e {y n } sono nella stessa classe di equivalenza). La simmetria è conseguenza della simmetria di d, mentre la disuguaglianza triangolare segue assando al limite er n tendente ad infinito nella disuguaglianza d(x n,y n ) d(x n,z n )+d(z n,y n ). Passo 3: Dato x in X, definiamo cost(x) la successione che ha tutte le comonenti uguali ad x. Tale successione è evidentemente in C. Definiamo i : X Y nel modo seguente: i(x) = [cost(x)]. Essendo la definizione di d indiendente dalla scelta del raresentante nella classe di equivalenza, si uò scegliere la successione cost(x) in [cost(x)] e si ha allora d(i(x),i(y)) = e quindi i è un isometria. lim d((cost(x)) n, (cost(y)) n ) = lim d(x, y) =d(x, y), n + n + Passo 4: i(x) è denso in (Y, d).
20 CAPITOLO 1. SPAZI METRICI 1 Sia ȳ in Y, e sia {x m } una successione qualsiasi in [ȳ]. Definiamo y m = i(x m ) = [cost(x m )] e calcoliamo d(y m,y). Si ha d(y m,y) = lim d((cost(x m)) n,x n ) = lim d(x m,x n ). n + n + Essendo la successione {x m } in C, la successione {x m } è di Cauchy in (X, d). Pertanto, er ogni ε>0, esiste n ε in N tale che d(x m,x n ) <ε, n, m n ε. Questo fatto imlica che, er ogni ε>0, esiste n ε in N tale che lim n + d(x m,x n ) ε, m n ε (ricordiamo che tale limite esiste erché la successione {n d(x m,x n )} è di Cauchy in (R, )). Pertanto, er ogni ε>0, esiste n ε in N tale che d(y m,y) ε er ogni m>n ε, ovvero si ha che {y m } converge a y in (Y, d). Passo 5: (Y, d) è comleto. Sia {x (n) } una successione di Cauchy in (Y, d). Dal momento che i(x) è denso in (Y, d), er ogni n in N esiste x n in X tale che d(x (n),i(x n )) 1 n. (3.3) Mostriamo che la successione {x n } èinc. Si ha infatti (ricordando che i è un isometria), d(x n,x m )= d(i(x n ),i(x m )) d(i(x n ),x (n) )+ d(x (n),x (m) )+ d(x (m),i(x m )). Usando (3.3), e scegliendo n e m sufficientemente grandi (in modo che 1 n e 1 siano minori di ε, e in modo che d(x (n),x (m) ) sia anch essa minore di m ε), si rova che d(x n,x m ) < 3ε e quindi {x n } èinc. Sia ora x =[{x n }]; mostriamo che {x (n) } converge a x in (Y, d). Si ha infatti, semre er (3.3), e er definizione di d, d( x, x (n) ) d( x, i(x n )) + d(i(x n ),x (n) ) lim d(x n,x m )+ 1 m + n. Ricordando che {x n } è di Cauchy, se n è sufficientemente grande si ha lim n + d(x n,x m ) ε e 1 n ε. Pertanto, er tali n, d( x, x (n) ) ε, da cui la tesi.
21 CAPITOLO 1. SPAZI METRICI Osservazione Si uò anche dimostrare che lo sazio metrico (Y, d)è unico a meno di isometrie, ovvero se esiste un altro sazio metrico (Z, d) che verifica 1. e. del teorema recedente, allora esiste un isometria biiettiva ī tra (Y, d) e(z, d). (!)Esercizio Nel caso di (C 0 ([a, b], R),d 1 ), chi sono Y e i? Ovvero, se {f n } è una successione di Cauchy in d 1, che rorietà ha il suo limite in Y? È chiaro che non è ossibile ragionare come nell Esemio 1.3.9, erché in tutti e tre i casi era sufficiente renderne la chiusura (e scegliere er i l identità) er comletarlo (dato che lo sazio non comleto era contenuto in un altro comleto). In questo caso C 0 ([a, b], R) è già tutto lo sazio, il che vuol dire che sarà necessario amliarlo con funzioni non continue er renderlo comleto. Ma non tutte le funzioni discontinue sono integrabili (secondo Riemann)...
CAPITOLO 1. Spazi metrici. 1. Definizioni ed esempi
 CAPITOLO 1 Sazi metrici 1. Definizioni ed esemi Definizione 1.1. Sia X un insieme qualsiasi. Una distanza su X è un alicazione d : X X R tale che i) d(x, y) 0 er ogni x, y in X, e d(x, y) = 0 se e solo
CAPITOLO 1 Sazi metrici 1. Definizioni ed esemi Definizione 1.1. Sia X un insieme qualsiasi. Una distanza su X è un alicazione d : X X R tale che i) d(x, y) 0 er ogni x, y in X, e d(x, y) = 0 se e solo
15. Gli spazi L p Funzioni di classe L p.
 5. Gli sazi L. In questo caitolo, dati lo sazio di misura (Ω, A, µ) e un esonente ]0, + [, soffermiamo la nostra attenzione sulle funzioni numeriche f, A-misurabili in Ω, er le quali l integrale f dµ assume
5. Gli sazi L. In questo caitolo, dati lo sazio di misura (Ω, A, µ) e un esonente ]0, + [, soffermiamo la nostra attenzione sulle funzioni numeriche f, A-misurabili in Ω, er le quali l integrale f dµ assume
2. determinare i limiti agli estremi del dominio, eventuali asintoti, eventuali punti in cui è possibile prolungare la funzione per continuità;
 ANALISI MATEMATICA Commissione L. Caravenna, V. Casarino, S. occante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 27 Gennaio 25 TEMA - arte B Esercizio ( unti). Si consideri la funzione
ANALISI MATEMATICA Commissione L. Caravenna, V. Casarino, S. occante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 27 Gennaio 25 TEMA - arte B Esercizio ( unti). Si consideri la funzione
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Successioni numeriche (II)
 Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
1 Successioni di funzioni
 Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
COMPLETAMENTO DI SPAZI METRICI
 COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
Esercizi 8 12 gennaio 2009
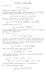 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Esercizi del Corso di Istituzioni di Analisi Superiore, I modulo
 sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
AM Sett. 11. IL TEOREMA DI COMPATTEZZA DI RELLICH. u n p. c(r) sup. u n (x + h) u n (x) dx
 AM30 0- Sett.. IL TEOREMA DI COMPATTEZZA DI RELLICH. Sia u n C 0 (B R ), con su n ( u n ) < +. Allora (i) se < < N, u n ha una sottosuccessione convergente in L r (B R ) r < N N. (ii) se = N, u n ha una
AM30 0- Sett.. IL TEOREMA DI COMPATTEZZA DI RELLICH. Sia u n C 0 (B R ), con su n ( u n ) < +. Allora (i) se < < N, u n ha una sottosuccessione convergente in L r (B R ) r < N N. (ii) se = N, u n ha una
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento della prova scritta - fuori corso - di Matematica II 11 Novembre 2010
 UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 15/04/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
SPAZI METRICI COMPLETI
 Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Analisi Matematica 1. Serie numeriche. (Parte 2) Dott. Ezio Di Costanzo.
 Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
LA TRASFORMATA DI FOURIER
 LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
Alcuni Teoremi sulle funzioni continue e uniforme continuità
 Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
CP110 Probabilità: Esame 2 settembre 2013 Testo e soluzione
 Diartimento di Matematica, Roma Tre Pietro Cauto 212-13, II semestre 2 settembre, 213 CP11 Probabilità: Esame 2 settembre 213 Testo e soluzione 1. (6 ts) Abbiamo due mazzi di carte francesi, il mazzo A
Diartimento di Matematica, Roma Tre Pietro Cauto 212-13, II semestre 2 settembre, 213 CP11 Probabilità: Esame 2 settembre 213 Testo e soluzione 1. (6 ts) Abbiamo due mazzi di carte francesi, il mazzo A
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93
 Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Successioni di funzioni: esercizi svolti
 Successioni di funzioni: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore Esercizio 1 Determinare il limite puntuale delle seguenti successioni di
Successioni di funzioni: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore Esercizio 1 Determinare il limite puntuale delle seguenti successioni di
h i (x) ϕ(x)dl N (x) q.o. inω.
 CAPITOLO 7 Introduzione agli azi di obolev 7.1 azi di obolev Definizione 7.1.1. iaaerto connesso non vuoto dir ( 2 20,1 + ; lo sazio di obolevw 1, ( è definito da W 1, ( := { u L (; g 1,g 2,...,g L ( :
CAPITOLO 7 Introduzione agli azi di obolev 7.1 azi di obolev Definizione 7.1.1. iaaerto connesso non vuoto dir ( 2 20,1 + ; lo sazio di obolevw 1, ( è definito da W 1, ( := { u L (; g 1,g 2,...,g L ( :
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
14 Spazi metrici completi
 54 2006-apr-26 Geometria e Topologia I 14 Spazi metrici completi (14.1) Definizione. Una successione {x n } n in uno spazio metrico si dice di Cauchy se per ogni ɛ > 0 esiste un intero N = N(ɛ) per cui
54 2006-apr-26 Geometria e Topologia I 14 Spazi metrici completi (14.1) Definizione. Una successione {x n } n in uno spazio metrico si dice di Cauchy se per ogni ɛ > 0 esiste un intero N = N(ɛ) per cui
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria Formule di Taylor Ottobre 2012
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Esercizi proposti - Gruppo 7
 Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
13 LIMITI DI FUNZIONI
 3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
Massimo limite e minimo limite di una funzione
 Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Un paio di esempi su serie e successioni di funzioni
 Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
R 2 e i numeri complessi
 L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Isometrie. (f (g h))(x) = f(g(h(x))) = ((f g) h)(x).
 Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
Spazi Metrici. Capitolo 1
 Capitolo 1 Spazi Metrici Uno spazio metrico è un insieme X dotato di una metrica. La metrica associa ad ogni coppia di elementi (punti) dix una distanza. La metrica è definita assiomaticamente, gli assiomi
Capitolo 1 Spazi Metrici Uno spazio metrico è un insieme X dotato di una metrica. La metrica associa ad ogni coppia di elementi (punti) dix una distanza. La metrica è definita assiomaticamente, gli assiomi
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche
 C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 18/03/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 8/03/03 D.BARTOLUCCI, D.GUIDO. La continuità uniforme I ESERCIZIO: Dimostrare che la funzione f(x) = x 3, x A = (, ] non è uniformemente continua
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 8/03/03 D.BARTOLUCCI, D.GUIDO. La continuità uniforme I ESERCIZIO: Dimostrare che la funzione f(x) = x 3, x A = (, ] non è uniformemente continua
Comportamento asintotico delle Catene di Markov
 Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Esercizi con martingale Pietro Caputo 23 novembre 2006
 Esercizi con martingale Pietro Cauto 23 novembre 2006 Esercizio 1. Sia {X n } la asseggiata aleatoria simmetrica su Z con X 0 = 0, vale a dire che Z k = X k X k 1, k = 1, 2,... sono indiendenti e valgono
Esercizi con martingale Pietro Cauto 23 novembre 2006 Esercizio 1. Sia {X n } la asseggiata aleatoria simmetrica su Z con X 0 = 0, vale a dire che Z k = X k X k 1, k = 1, 2,... sono indiendenti e valgono
Elementi di Analisi funzionale
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE CORSO DI LAUREA MAGISTRALE IN MATEMATICA (Classe LM-40 Matematica) Elementi di Analisi funzionale Disense er il corso di Analisi sueriore 1 A.A. 2017/2018
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE CORSO DI LAUREA MAGISTRALE IN MATEMATICA (Classe LM-40 Matematica) Elementi di Analisi funzionale Disense er il corso di Analisi sueriore 1 A.A. 2017/2018
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.2 Funzioni Complesse Una funzione complessa di variabile complessa f : E C, E C è un applicazione ce associa un numero complesso f(z) ad ogni z E, con E sottoinsieme del
Capitolo 1 ANALISI COMPLESSA 1 1.2 Funzioni Complesse Una funzione complessa di variabile complessa f : E C, E C è un applicazione ce associa un numero complesso f(z) ad ogni z E, con E sottoinsieme del
DISUGUAGLIANZE. Umberto Marconi Dipartimento di Matematica Pura e Applicata Padova
 1. PREMESSA 1 DISUGUAGLIANZE Umberto Marconi Diartimento di Matematica Pura e Alicata Padova 1 Premessa Riassumiamo alcune disuguaglianze standard riguardanti somme e integrali (le dimostrazioni seguiranno
1. PREMESSA 1 DISUGUAGLIANZE Umberto Marconi Diartimento di Matematica Pura e Alicata Padova 1 Premessa Riassumiamo alcune disuguaglianze standard riguardanti somme e integrali (le dimostrazioni seguiranno
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b
![Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b](/thumbs/73/69556821.jpg) sercizi ) Tutte le distanze introdotte a lezione (meno la metrica discreta) sono invarianti per traslazioni; ovvero, d(x, y) = d(x + z, y + z) per ogni x, y e z. Definire su X = una metrica non invariante
sercizi ) Tutte le distanze introdotte a lezione (meno la metrica discreta) sono invarianti per traslazioni; ovvero, d(x, y) = d(x + z, y + z) per ogni x, y e z. Definire su X = una metrica non invariante
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie
 ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Dispense sulla distanza di Hausdorff
 Dispense sulla distanza di Hausdorff Fabio Ferri Giada Franz Federico Glaudo 23 aprile 2014 Sommario In questo documento studieremo le proprietà della distanza di Hausdorff, la naturale distanza indotta
Dispense sulla distanza di Hausdorff Fabio Ferri Giada Franz Federico Glaudo 23 aprile 2014 Sommario In questo documento studieremo le proprietà della distanza di Hausdorff, la naturale distanza indotta
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
F. Fagnani, A. Tabacco e P. Tilli. Versione 21 marzo. Introduzione all Analisi Complessa e Teoria delle distribuzioni.
 F. Fagnani, A. Tabacco e P. Tilli Introduzione all Analisi Complessa e Teoria delle distribuzioni 2 marzo 2006 3 Serie di Taylor e di Laurent. Residui 3. Successioni e serie di numeri complessi Una successione
F. Fagnani, A. Tabacco e P. Tilli Introduzione all Analisi Complessa e Teoria delle distribuzioni 2 marzo 2006 3 Serie di Taylor e di Laurent. Residui 3. Successioni e serie di numeri complessi Una successione
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Spazi Metrici. Capitolo 1
 Capitolo 1 Spazi Metrici Uno spazio metrico è un insieme X dotato di una metrica. La metrica associa ad ogni coppia di elementi (punti) di X una distanza. La metrica è definita assiomaticamente, gli assiomi
Capitolo 1 Spazi Metrici Uno spazio metrico è un insieme X dotato di una metrica. La metrica associa ad ogni coppia di elementi (punti) di X una distanza. La metrica è definita assiomaticamente, gli assiomi
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
5.1 Definizione della misura in R 2
 Capitolo 5 Misure prodotto 5.1 Definizione della misura in 2 Nell introdurre la misura secondo Lebesgue in, abbiamo definito la misura esterna di un sottoinsieme qualsiasi E come m famiglia numerabile
Capitolo 5 Misure prodotto 5.1 Definizione della misura in 2 Nell introdurre la misura secondo Lebesgue in, abbiamo definito la misura esterna di un sottoinsieme qualsiasi E come m famiglia numerabile
Spazi di Funzioni. Docente:Alessandra Cutrì. A. Cutrì e Metodi Matematici per l ingegneria Ing. Gestionale
 Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Uno spazio Vettoriale V si dice NORMATO se è definita su V una norma, cioè una funzione che verifica: v 0 e v = 0 v = 0 λv = λ v λ R(o
Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Uno spazio Vettoriale V si dice NORMATO se è definita su V una norma, cioè una funzione che verifica: v 0 e v = 0 v = 0 λv = λ v λ R(o
Capitolo 4. Gli spazi L p 4.1 L 1 (E)
 Capitolo 4 Gli spazi L p 4.1 L 1 () Nel precedente capitolo abbiamo introdotto l integrale secondo Lebesgue per funzione misurabili su un insieme misurabile. In particolare, e per dimostrare il teorema
Capitolo 4 Gli spazi L p 4.1 L 1 () Nel precedente capitolo abbiamo introdotto l integrale secondo Lebesgue per funzione misurabili su un insieme misurabile. In particolare, e per dimostrare il teorema
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
k=0 a k k=0 a k, quando si voglia precisare qual è l indice iniziale: si possono infatti considerare anche serie del tipo k=1 a k, k=50 a k,
 2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R.
 COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
COMPLETEZZA DELL INSIEME DEI NUMERI REALI R. FABIO CIPRIANI 1. Completezza dell insieme dei numeri reali R. Nell insieme dei numeri reali R la condizione di Cauchy e necessaria e sufficiente per la convergenza
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Corso di Laurea Magistrale in Matematica Ferrara, Primo parziale (P) e Compito totale (T) di Analisi Funzionale
 Corso di Laurea Magistrale in Matematica Primo arziale P e Comito totale T di Analisi Funzionale 1 P: 24 unti, T: 16 unti Sia 1, sia a 1, 1 e er ogni x = x k k N l sia T a x := a k x k. a P: 4 unti, T:
Corso di Laurea Magistrale in Matematica Primo arziale P e Comito totale T di Analisi Funzionale 1 P: 24 unti, T: 16 unti Sia 1, sia a 1, 1 e er ogni x = x k k N l sia T a x := a k x k. a P: 4 unti, T:
Principali differenze tra la ristampa 2014 e l edizione 2008
 Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
Per determinare il dominio di f, occorre imporre x 6= 2,x>0elogx>0 di
 Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].
![4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1]. 4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].](/thumbs/96/128120172.jpg) Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
Completezza e compattezza
 1 Completezza e compattezza Spazi metrici completi Data una successione x : N X, j x j, una sua sottosuccessione è la composizione x ν, ove ν : N N è strettamente crescente. Data una successione (x j )
1 Completezza e compattezza Spazi metrici completi Data una successione x : N X, j x j, una sua sottosuccessione è la composizione x ν, ove ν : N N è strettamente crescente. Data una successione (x j )
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Vicenza, 12 settembre 2016 Si consideri la funzione. sinh 2x sinh 2x 1 3x. f(x) =
 ANALISI MATEMATICA - Traccia di soluzioni Commissione F. Albertini, L. Caravenna e V. Casarino Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Esercizio, Tema [9 punti] Vicenza, settembre 06 Si
ANALISI MATEMATICA - Traccia di soluzioni Commissione F. Albertini, L. Caravenna e V. Casarino Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza Esercizio, Tema [9 punti] Vicenza, settembre 06 Si
CAPITOLO 9. Le serie di potenze
 CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
CAPITOLO 9 Le serie di potenze Ahlfors, pag. 33,..,45 Bozza da rivedere Le funzioni analitiche sono piú o meno polinomi in z, o i loro limiti, somme di serie di potenze in z. Prerequisiti fondamentali
Svolgimento degli esercizi del Capitolo 1
 Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
E, la successione di numeri {f n (x 0. n f n(x) (15.1)
 Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Analisi Matematica B Soluzioni prova scritta parziale n. 2
 Analisi Matematica B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 017-018 9 febbraio 018 1. Determinare il numero di soluzioni reali dell equazione x 4 = ln(1 + x ). Svolgimento. Posto
Analisi Matematica B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 017-018 9 febbraio 018 1. Determinare il numero di soluzioni reali dell equazione x 4 = ln(1 + x ). Svolgimento. Posto
