168. Catene di cerchi all interno di lunule e lenti Giovanni Lucca
|
|
|
- Ruggero Lamberti
- 5 anni fa
- Visualizzazioni
Transcript
1 68. Ctene d cech ll nteno d lunule e lent Govnn Lucc vnn_lucc@nwnd.t Sunto Studmo le ctene nfnte d cech che possono foms ll nteno delle egon sultnt dll ntesezone d due cech. Astct We stud the nfnte chns of mutull tngent ccles tht cn e fomed nsde the egons esultng fom the ntesecton of two ccles.. Intoduzone S possono dsegne dffeent tp d ctene, fnte o nfnte, composte d cech mutumente tngent, n elzone ll ecpoc poszone d due cech pncpl e. Le pù note sono le ctene d Stene [] che possono essee tccte ll nteno dell egone nule t due cech e, uno ll nteno dell lto, non ntesects e non cossl; sono note nche le ctene d Pppo [] che possono foms ll nteno dell egone t due cech tngent ntenmente. Infne, può consdes l cso n cu e sono tngent estenmente oppue uno de due cech degene n un ett [3]. Qu voglmo stude l cso n cu e sono ntesecnt fomndo così le te egon mostte n Fg.: lunul lente lunul Fg.: Regon fomte dll ntesezone d due cech L egone comune d entm cech è chmt lente Le due egon estene, pptenent d un cecho soltnto, sono chmte lunule. Voglmo stude le ctene nfnte d cech, mutumente tngent, che possono foms ll nteno d un lente e d un lunul.(s vedno le Fg. e ).
2 Fg. : Cten d cech ll nteno d un lente Fg. : Cten d cech ll nteno d un lunul. In ptcole, detemneemo le fomule eltve lle coodnte del cento e del ggo del geneco cecho -esmo dell cten; nolte poveemo nche lcune popetà eltve lle ctene stesse.
3 3. Luogo ssocto cent de cech Consdemo un sstem d femento ctesno dove due punt A nd B, poszont sull sse delle e sept dll dstnz, hnno spettvmente coodnte (-/, ) e (/, ). Sno A nd B cent de due cech e vent spettvmente ggo e. Affnché esst l ntesezone t e deve vlee l seguente elzone: () Povmo o le seguent popetà: Il cento d ogn cecho ll nteno d un lente e tngente s d che gce su un peole vente fuoch n A e B ed equzone: () Il cento d ogn cecho ll nteno d un lunul e tngente s d che gce su un ellsse vente fuoch n A e B ed equzone: (3) Alfne d dmoste l pte ) dell popetà, fccmo femento Fg.3. Fg.3: Cecho tngente ll nteno d un lente.
4 Il vetce P del tngolo APB, vente coodnte (, ), è l cento d un geneco cecho tngente s d (n J) che (n S) mente PJ=PS=() ne è l ggo. Amo che: AP=-() BP=-() AB= Espmendo l e del tngolo APB n due dffeent mod, coè ttveso l sempodotto dell se con l ltezz PH= e pe mezzo del teoem d Eone, possmo scvee: d cu s cv: ll (5), ottenmo: () (6) Inolte, gudndo tngol APH e BPH n Fg.3, possmo scvee: Eguglndo le equzon sop, ottenmo: e, sosttuendo l (6) nell (7), mo: (7) (8) Infne elevndo l qudto entm mem dell (8) s ottene l equzone (). E mmedto vefce, dll equzone (), che le coodnte de fuoch sono concdent con quelle de punt A e B. Pe qunto gud l punto ), fccmo femento ll Fg.3. (5)
5 Fg.3: Cecho tngente ll nteno d un lunul. L dmostzone è completmente smle quell eltv l punto ) con l unc dffeenz che, n questo cso, AP=+(). Vlgono le seguent elzon: (9) () e qund, elevndo l qudto entm mem d (), s ottene l equzone (3). E mmedto vefce, dll equzone (3), che le coodnte de fuoch sono concdent con quelle de punt A e B. Infne, poché tl popetà sono vlde pe ogn geneco cecho tngente s d che ll nteno d un lente o d un lunul, ne concludmo che le popetà vlgono pe tutt cech d un cten. 5
6 6 3. Coodnte de cent e gg de cech dell cten Lo scopo d questo pgfo è detemne espesson nltche pe le coodnte del cento e ggo del geneco cecho -esmo d un cten s nel cso dell lente che nel cso dell lunul. Un metodo convenente è quello d use l tecnc dell nvesone ccole []. efnmo dppm punt C nd ndvdut dll ntesezone de cech e ; le loo coodnte sono dte d: C,, Se consdemo come cecho d nvesone γ quello vente cento n e ggo ugule ll lunghezz del segmento C coè: () mo che due cech e sono tsfomt spettvmente ette e. S ved l Fg α β γ ψ α' β' A B C Fg.: Invesone ccole de cech e. Convene o code un popetà genele d ogn nvesone ccole: l tngenz t cech e cech e t cech e ette, è mntenut nche seguto dell opezone d nvesone. Petnto, le ctene d cech mostte nelle Fg. sono tsfomte nelle ctene ll nteno dell egone compes t le ette nd. S ved l Fg.5 pe l lente e l Fg.5 pe l lunul.
7 Fg.5: Invesone (lnee ttteggte) d un cten d cech ll nteno d un lente. 6 Fg.5: Invesone (lnee ttteggte) d un cten d cech ll nteno d un lunul. 7
8 Così, pe mezzo dell nvesone ccole, mo d solvee un polem pù semplce che consste nello stude un cten d cech tngent lle ette e nvece che cech e. Petnto, detemneemo dppm le coodnte de cent (, ) ed gg de cech mmgne; ess venno qund tsfomt, n se lle fomule d nvesone ccole [], pe tove le elzon che stmo cecndo. Tuttv pe detemne (, ) ed, è convenente utlzze un lto sstem ctesno XY vente ogne nel punto C e sse X concdente con l ett. In questo sstem d femento, le mmgn, secondo opezone d nvesone, sono mostte n Fg.6. Fg.6: Cten d cech nel sstem ctesno XY. E fcle vedee che esstono semplc elzon t le coodnte de cent (X, Y ) e ggo del geneco cecho -esmo con quelle d un to cecho nzle ndvduto mednte l ndce coè: X Y sn sn X X,,, sn Y Y,,, sn () () sn sn,,, (3) 8
9 9 tn X Y () essendo l ngolo t le ette e. Pe l seguto è necesso conoscee le espesson delle ette e e del cecho γ; n ptcole, s può note che l ett è l sse dcle de cech e γ mente l ett è l sse dcle de cech e γ spettvmente. L equzone del cecho γ è: (5) mente le equzon d e sono spettvmente: 3 (6) 3 (7) O, detemneemo dppm le espesson delle coodnte de cent e de gg delle mmgn nvesve e qund le tsfomeemo, n ccodo con le fomule pe l nvesone ccole [], pe tove le elzon che stmo cecndo. Pe gon d evtà e d spzo, pesentmo solo pssgg ed sultt fondmentl. Come pecedentemente, suddvdmo sultt dstnguendo l cso dell lente d quello dell lunul. A. Fomule pe l lente Ptendo dlle fomule (6) e (7), è possle detemne tn() e qund possmo dedue: tn (8) sn sn (9) Sempe ptendo dlle fomule (6) e (7) è possle ottenee le espesson de cosen detto delle ette e ; nftt, pe mezzo d tl espesson, possmo scvee le fomule d oto-tslzone tte tsfome le coodnte de cent () e () dl sstem d femento uslo XY l sstem d femento pncple. Così, le coodnte de cent delle mmgn nvesve sono: () ()
10 Tenendo conto dell (3) e dell (9), l ggo è dto d: () Infne, nvetendo le (), () e (), s ottene: (3) () (5) B. Fomule pe l lunul In questo cso, c s deve code che le mmgn nvesve non sono contenute nell e pptenente ll ngolo m n quell pptenente ll ngolo supplemente. (S confontno le Fg.5 e 5); petnto, mo: tn (6) sn sn (7) (8) (9)
11 (3) Infne, nvetendo le (8), (9) e (3), s ottene: (3) (3) (33) Le fomule (3), (), (5) e (3), (3), (33) sono espesse n funzone del ggo dell mmgne nvesv del pmo cecho dell cten; n Appendce s può tove l fomul che mette n elzone ed.. Luogo de punt d tngenz In questo pgfo, mostmo un lt popetà eltv punt d tngenz t cech delle ctene. Tutt punt d tngenz t due cech consecutv d un cten, pptengono d un medesmo cecho vente ggo R t e coodnte del cento ( t, t ) le cu espesson, nel cso dell lente, sono dte d: R t (3),, t t (35) Nel cso dell lunul, esse sono dte d: R t (36),, t t (37) S vedno le Fg. 7 e 7.
12 Fg.7: Luogo de punt d tngenz; cten d cech ll nteno d un lente Fg.7: Luogo de punt d tngenz; cten d cech ll nteno d un lunul.
13 3 Al fne d pove l (3) e l (35), è convenente code che l nvesone ccole consev l tngenz t dffeent cuve dopo l tsfomzone. Gudndo Fg.6, vedmo che tutt punt d tngenz pptengono ll settce dell ngolo. Tle settce h equzone: (38) L nvesone ccole d tle settce (spetto l cecho γ) è l cecho che stmo cecndo vente equzone: (39) d cu s cvno l (3) e l (35). In mne nlog possono essee povte le fomule eltve ll lunul, coè l (36) e l (37). In questo cso, s deve consdee l ngolo supplemente d vente settce dt d: () L su mmgne secondo nvesone ccole (spetto l cecho γ) è l cecho vente equzone: () d cu s cvno l (36) e l (37). 5. Concluson Amo studto le ctene nfnte d cech che possono foms ll nteno delle dffeent e dul egon genete dll ntesezone d due cech; coè lent e lunule. Tle dultà s flette nelle fomule e nelle popetà geometche cttezznt le ctene. Appendce Il pmo cecho dell cten ndvduto mednte l ndce h odnt del cento che può essee scelt tmente puché s soddsftt l seguente condzone: (A) L cospondente scss del cento =( ) può essee clcolt pe mezzo dell fomul (8) o pe mezzo dell () spettvmente nel cso dell lente e dell lunul. Il ggo =( ) è clcolto pe mezzo dell (6) o dell (9) spettvmente nel cso dell lente o dell lunul. Un volt detemnto, l ggo dell mmgne nvesv del pmo cecho (che ppe nelle fomule (3), (),(5) e (3), (3), (33)) è dto d: (A)
14 Blogf Wessten, Ec W. "Stene Chn." Fom MthWold, A Wolfm We Resouce. vn Lmoen, Floo nd Wessten, Ec W. "Pppus Chn." Fom MthWold, A Wolfm We Resouce. H. Th. On the pont of contct n nfnte chns, Gzette of the Austln Mthemtcl Socet, vol. 33 n. 6, p Wessten, Ec W. "Inveson." Fom MthWold, A Wolfm We Resouce.
, m = = = è la risultante delle sole forze esterne, dal momento che quella delle forze interne è nulla
 Eseczo l cento d ss () d un sste d punt tel è un punto geoetco l cu poszone spetto d un sste d feento è ndvdut dl ggo vettoe:, dove ed ppesentno spettvente le sse e vetto poszone de sngol punt tel che
Eseczo l cento d ss () d un sste d punt tel è un punto geoetco l cu poszone spetto d un sste d feento è ndvdut dl ggo vettoe:, dove ed ppesentno spettvente le sse e vetto poszone de sngol punt tel che
= dt. ! r 2. r cm. d dt = = ! r 4. r 3. Dinamica dei sistemi di particelle e di corpi estesi
 Dnmc de sstem d ptcelle e d cop es Pe un sstem d punt mtel, s defnsc l cento d mss n tl modo che: m m Def.: m 1 m 1 ovveo Segue che: d Ovveo che Defnendo qund : P Segue che dp m ( ) m ( m ) d d m v mv
Dnmc de sstem d ptcelle e d cop es Pe un sstem d punt mtel, s defnsc l cento d mss n tl modo che: m m Def.: m 1 m 1 ovveo Segue che: d Ovveo che Defnendo qund : P Segue che dp m ( ) m ( m ) d d m v mv
Unità Didattica N 5 Il riferimento cartesiano
 01 Mtemtc Lceo \ Untà Ddttc N 5 : l femento ctesno 1 Untà Ddttc N 5 Il femento ctesno 01) Coodnt scss 0) Coodnte ctesne nel pno 03) Ve spece d sstem d femento 04) Rppesentzone ctesn d un vettoe 05) Le
01 Mtemtc Lceo \ Untà Ddttc N 5 : l femento ctesno 1 Untà Ddttc N 5 Il femento ctesno 01) Coodnt scss 0) Coodnte ctesne nel pno 03) Ve spece d sstem d femento 04) Rppesentzone ctesn d un vettoe 05) Le
Numero 17 Aprile 2012
 Numeo 17 Aple 1 Spl y Mc-Q http://www.flck.com/photos/mc-q/18857667/ TEOREMI INVERSI I PITAGORA E EUCLIE LUNULE E LENTI SEGMENTI PARALLELI LABORATORIO I PITAGORA SIMMETRIE ATTRAVERSAMENTO EL FIUME - LIBRI
Numeo 17 Aple 1 Spl y Mc-Q http://www.flck.com/photos/mc-q/18857667/ TEOREMI INVERSI I PITAGORA E EUCLIE LUNULE E LENTI SEGMENTI PARALLELI LABORATORIO I PITAGORA SIMMETRIE ATTRAVERSAMENTO EL FIUME - LIBRI
Fisica II - Ingegneria Biomedica - A.A. 2016/ Appello del 4/7/2017
 sc II - Ingegne omedc -.. 6/ - ppello del // ---------------------------------------------------------------------------------------------------------------------- Nome ognome N o Mtcol -----------------------------------------------------------------------------------------------------------------------
sc II - Ingegne omedc -.. 6/ - ppello del // ---------------------------------------------------------------------------------------------------------------------- Nome ognome N o Mtcol -----------------------------------------------------------------------------------------------------------------------
I vettori. Grandezze scalari: Grandezze vettoriali
 I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
Vettori. Le grandezze fisiche sono: scalari; vettoriali;
 Vetto 1 Le gndee fsche sono: scl; vettol; Def: Gnde scle defnt unvocmente d un numeo (postvo o negtvo) (con oppotun untà d msu) es.: tempo, mss, tempetu, cc elettc, Def: Gnde vettole (vd. pgn seguente)
Vetto 1 Le gndee fsche sono: scl; vettol; Def: Gnde scle defnt unvocmente d un numeo (postvo o negtvo) (con oppotun untà d msu) es.: tempo, mss, tempetu, cc elettc, Def: Gnde vettole (vd. pgn seguente)
POLITECNICO DI MILANO IV FACOLTÀ Ingegneria Aerospaziale II Verifica di Fisica Sperimentale A+B 4 Luglio 2006
 POITENIO DI MIANO IV FAOTÀ Ingegne Aeospzle II Vefc Fsc Spementle A+B 4 uglo 6 Gustfce le sposte e scvee n moo cho e leggble Sosttue vlo numec solo ll fne, opo ve cvto le espesson lettel Ince nome e cognome
POITENIO DI MIANO IV FAOTÀ Ingegne Aeospzle II Vefc Fsc Spementle A+B 4 uglo 6 Gustfce le sposte e scvee n moo cho e leggble Sosttue vlo numec solo ll fne, opo ve cvto le espesson lettel Ince nome e cognome
I vettori. Grandezze scalari e grandezze vettoriali
 I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
Meccanica Dinamica del corpo rigido
 eccnc 7-8 Dnmc del copo gdo 8 Equon del moto: ω L F m ( E ) TOT omento ngole: Eneg cnetc: Sstem d punt E K dp dt L L + L ω ( ) E otone d un copo gdo L ω omento d ne: dl dt dm V L L ω L dstn dll sse d otone
eccnc 7-8 Dnmc del copo gdo 8 Equon del moto: ω L F m ( E ) TOT omento ngole: Eneg cnetc: Sstem d punt E K dp dt L L + L ω ( ) E otone d un copo gdo L ω omento d ne: dl dt dm V L L ω L dstn dll sse d otone
Fisica II - Ingegneria Biomedica - A.A. 2016/ Appello del 13/9/2017
 sc II - Ingegne oedc -.. 6/ - ppello del /9/ ---------------------------------------------------------------------------------------------------------------------- oe: ognoe: o Mtcol: ----------------------------------------------------------------------------------------------------------------------
sc II - Ingegne oedc -.. 6/ - ppello del /9/ ---------------------------------------------------------------------------------------------------------------------- oe: ognoe: o Mtcol: ----------------------------------------------------------------------------------------------------------------------
SISTEMI DI CONDOTTE: La verifica idraulica
 SISTEMI DI CONDOTTE: L vefc dulc Clo Cpon Unvestà degl Stud d Pv Dptmento d Ingegne Idulc e Ambentle Poszone del del poblem Rete esstente d cu è not l geomet E pefsst l eogzone (ppocco DDA: Demnd Dven
SISTEMI DI CONDOTTE: L vefc dulc Clo Cpon Unvestà degl Stud d Pv Dptmento d Ingegne Idulc e Ambentle Poszone del del poblem Rete esstente d cu è not l geomet E pefsst l eogzone (ppocco DDA: Demnd Dven
A) Meccanica Soluzione
 A) Meccnc Un uot omogene d ggo R, mss M e momento d nez spetto l popo sse I, otol senz stsce su un pno ozzontle scbo sotto l zone d un momento motoe noto τ. S A l foz d ttto con l suolo, l ccelezone del
A) Meccnc Un uot omogene d ggo R, mss M e momento d nez spetto l popo sse I, otol senz stsce su un pno ozzontle scbo sotto l zone d un momento motoe noto τ. S A l foz d ttto con l suolo, l ccelezone del
Forze conservative e non conservative: definizione
 oze consevtve e non consevtve: denzone Un oz s dce consevtv se l lvoo d ess computo su un punto mtele che compe un qulss pecoso chuso l e sempe nullo coe se ➉ l Tutte le oze che non sodno l suddett elzone
oze consevtve e non consevtve: denzone Un oz s dce consevtv se l lvoo d ess computo su un punto mtele che compe un qulss pecoso chuso l e sempe nullo coe se ➉ l Tutte le oze che non sodno l suddett elzone
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
IL Potenziale elettrostatico
 Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
N 10 I NUMERI COMPLESSI
 Untà Ddttc N 0 I NUMERI COMPLESSI 0) Introduzone dell untà mmgnr 0) Introduzone elementre de numer compless 0) Alcune operzon su numer compless 0) Rppresentzone geometrc de numer compless 05) Rppresentzone
Untà Ddttc N 0 I NUMERI COMPLESSI 0) Introduzone dell untà mmgnr 0) Introduzone elementre de numer compless 0) Alcune operzon su numer compless 0) Rppresentzone geometrc de numer compless 05) Rppresentzone
Esercizio e ˆ. x d. 4 cos( sin(
 seczo.7 onsdemo le 4 cche n fgu con =-e, = +e, =+4e, 4 =+e; =5, d = cm, d =d = cm; (e=.6-9 ). lcole modulo, dezone e veso dell foz gente sull ptcell 4 pe effetto delle lte d e k F d e k F ˆ 8 ˆ; 4 4 4
seczo.7 onsdemo le 4 cche n fgu con =-e, = +e, =+4e, 4 =+e; =5, d = cm, d =d = cm; (e=.6-9 ). lcole modulo, dezone e veso dell foz gente sull ptcell 4 pe effetto delle lte d e k F d e k F ˆ 8 ˆ; 4 4 4
In generale i piani possono essere tra loro
 Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Unità Didattica N 32. Le trasformazioni geometriche
 1 Untà Ddttc N Le trsformzon geometrche 1) Le trsformzon del pno n sé ) L smmetr centrle ) L smmetr ssle 4) L trslzone 5) L trslzone degl ss crtesn 6) L ' ffntà 7) L smltudne 8) L omotet 09) Le sometre
1 Untà Ddttc N Le trsformzon geometrche 1) Le trsformzon del pno n sé ) L smmetr centrle ) L smmetr ssle 4) L trslzone 5) L trslzone degl ss crtesn 6) L ' ffntà 7) L smltudne 8) L omotet 09) Le sometre
Doppi bipoli. (versione del ) Doppi bipoli (o 2-porte)
 opp pol www.de.n.uno.t/pes/mst/ddttc.tm (esone del 3--4) opp pol (o -pote) opp pol: component con due cope d temnl (pote) tl ce, pe cscun copp, l coente entnte n uno de temnl è uule quell uscente dll lto
opp pol www.de.n.uno.t/pes/mst/ddttc.tm (esone del 3--4) opp pol (o -pote) opp pol: component con due cope d temnl (pote) tl ce, pe cscun copp, l coente entnte n uno de temnl è uule quell uscente dll lto
Il campo magnetico. H.C. Oersted 1819
 Il cmpo mgnetco Le popetà mgnetche d lcun mtel eno gà note gl ntch gec, omn e cnes: pesso quest popol nftt e conoscut l cpctà d un sostnz: l mgnette (Fe 3 O 4 ) d tte lmtu d feo. Inolte ossevono che un
Il cmpo mgnetco Le popetà mgnetche d lcun mtel eno gà note gl ntch gec, omn e cnes: pesso quest popol nftt e conoscut l cpctà d un sostnz: l mgnette (Fe 3 O 4 ) d tte lmtu d feo. Inolte ossevono che un
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettomgnetsmo Pof. Fncesco Rgus Unvestà degl Stud d Mlno Lezone n. 21 16..218 Sogent del cmpo mgnetco Dvegenz e otoe del cmpo mgnetco Applczon dell legge d Ampèe Anno Accdemco 217/218 Il cmpo mgnetco
Elettomgnetsmo Pof. Fncesco Rgus Unvestà degl Stud d Mlno Lezone n. 21 16..218 Sogent del cmpo mgnetco Dvegenz e otoe del cmpo mgnetco Applczon dell legge d Ampèe Anno Accdemco 217/218 Il cmpo mgnetco
I vettori. a b. 180 α B A. Un segmento orientato è un segmento su cui è stato fissato un verso. di percorrenza, da verso oppure da verso.
 I vettor B Un segmento orentto è un segmento su cu è stto fssto un verso B d percorrenz, d verso oppure d verso. A A Il segmento orentto d verso è ndcto con l smolo. Due segment orentt che hnno l stess
I vettor B Un segmento orentto è un segmento su cu è stto fssto un verso B d percorrenz, d verso oppure d verso. A A Il segmento orentto d verso è ndcto con l smolo. Due segment orentt che hnno l stess
Il lavoro è quindi una grandezza scalare le cui unita di misura sono: = Joule = J
 Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
1) Una carica puntiforme q si trova al centro di una sfera cava conduttrice di raggio
 1) Un cic puntifome si tov l cento di un sfe cv conduttice di ggio inteno e spessoe. Clcole nel cso di conduttoe isolto: il cmpo elettico, il potenzile e l enegi elettosttic in tutto lo spzio. Cso ()
1) Un cic puntifome si tov l cento di un sfe cv conduttice di ggio inteno e spessoe. Clcole nel cso di conduttoe isolto: il cmpo elettico, il potenzile e l enegi elettosttic in tutto lo spzio. Cso ()
Operatori differenziali (1)
 Opeato dffeenal Gadente opea s no scalae; a come sltato n vettoe gad Φ Φ Φ Φ Φ Dvegena opea s n vettoe; a come sltato no scalae dv Rotaonale o otoe opea s n vettoe; a come sltato n vettoe ot Esectaon d
Opeato dffeenal Gadente opea s no scalae; a come sltato n vettoe gad Φ Φ Φ Φ Φ Dvegena opea s n vettoe; a come sltato no scalae dv Rotaonale o otoe opea s n vettoe; a come sltato n vettoe ot Esectaon d
Lezione 7. Numeri primi. Teorema Fondamentale dell'aritmetica.
 Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorem Fondmentle dell'artmetc Defnzone 7 Un nmero ntero p dverso d 0 e s dce prmo se per ogn b Z Altrment p s dce composto p b p oppre p b Defnzone
Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorem Fondmentle dell'artmetc Defnzone 7 Un nmero ntero p dverso d 0 e s dce prmo se per ogn b Z Altrment p s dce composto p b p oppre p b Defnzone
Geometria Analitica. Parabola (asse verticale) Geometria Analitica La retta. ; y2. x = y = y = ax parabola passante per l origine e con asse l asse y
 Geometr Anlt Dstnz tr due punt nel pno rtesno P ( x x ) + ( y ) P y Punto medo d due punt nel pno rtesno M x + x y + ( x ; y ) ; M M y Are d un trngolo nel pno rtesno prtre dlle oordnte de suo x y punt
Geometr Anlt Dstnz tr due punt nel pno rtesno P ( x x ) + ( y ) P y Punto medo d due punt nel pno rtesno M x + x y + ( x ; y ) ; M M y Are d un trngolo nel pno rtesno prtre dlle oordnte de suo x y punt
LEGGE DI FARADAY, LEGGE DI LENZ, INDUTTANZA, ENERGIA MAGNETICA
 A. Chodon esecz d Fsc II LEGGE DI FARADAY, LEGGE DI LENZ, INDUTTANZA, ENERGIA MAGNETICA Eseczo 1 Un bobn costtut d N spe d e cm e esstenz complessv R 5Ω è post t le espnson d un elettomgnete e gce n un
A. Chodon esecz d Fsc II LEGGE DI FARADAY, LEGGE DI LENZ, INDUTTANZA, ENERGIA MAGNETICA Eseczo 1 Un bobn costtut d N spe d e cm e esstenz complessv R 5Ω è post t le espnson d un elettomgnete e gce n un
Calcoli di campo elettrico
 Clcl d cmp elettc Il pncp d svppszne pe l cmp elettc Il cmp elettc genet dlle sgent,, è p ll smm de cp elettc,,... genet dlle sngle sgent: + +... Inftt, mltplcnd mb memb dell euzne pe, s tv ( + +...) +...
Clcl d cmp elettc Il pncp d svppszne pe l cmp elettc Il cmp elettc genet dlle sgent,, è p ll smm de cp elettc,,... genet dlle sngle sgent: + +... Inftt, mltplcnd mb memb dell euzne pe, s tv ( + +...) +...
Evandro Cozzi Giuseppe Della Monica INTRODUZIONE ALLA MECCANICA DELLE TERRE E DELLE ROCCE
 Endo Cozz Guseppe Dell Mon INTRODUIONE ALLA MECCANICA DELLE TERRE E DELLE ROCCE Copyght MMI ARACNE edte S..l. www.needte.t nfo@needte.t Rffele Goflo, 133 A/B 00173 Rom (06) 93781065 ISBN 978 88 548 809
Endo Cozz Guseppe Dell Mon INTRODUIONE ALLA MECCANICA DELLE TERRE E DELLE ROCCE Copyght MMI ARACNE edte S..l. www.needte.t nfo@needte.t Rffele Goflo, 133 A/B 00173 Rom (06) 93781065 ISBN 978 88 548 809
1) Un filo rettilineo infinito percorso da corrente i genera un campo magnetico con le seguenti proprietà:
 Ogne el Cmpo Mgneto Rpotmo ue ftt spementl. 1) Un flo ettlneo nfnto peoso oente gene un mpo mgneto on le seguent popetà: l ntenstà ument lnemente on m eese lnemente on ovveo B, qun le lnee mpo sono onfeenze
Ogne el Cmpo Mgneto Rpotmo ue ftt spementl. 1) Un flo ettlneo nfnto peoso oente gene un mpo mgneto on le seguent popetà: l ntenstà ument lnemente on m eese lnemente on ovveo B, qun le lnee mpo sono onfeenze
Versione 20 dicembre. Integrali curvilinei. 2.1 Curve nel piano e nello spazio
 2 Integrl curvlne 2. Curve nel pno e nello spzo S I un qulunque ntervllo dell rett rele e s : I R 3 un funzone. Indchmo con (t) = ( x(t), y(t), z(t) ) R 3 l punto mmgne d t I ttrverso. Dcmo che è un funzone
2 Integrl curvlne 2. Curve nel pno e nello spzo S I un qulunque ntervllo dell rett rele e s : I R 3 un funzone. Indchmo con (t) = ( x(t), y(t), z(t) ) R 3 l punto mmgne d t I ttrverso. Dcmo che è un funzone
CINEMATICA DEL MOTO ROTATORIO DI UNA PARTICELLA
 CINEMAICA DEL MOO OAOIO DI UNA PAICELLA MOO CICOLAE: VELOCIA ANGOLAE ED ACCELEAZIONE ANGOLAE Si considei un pticell P in moto cicole che descive un co di ciconfeenz s. L ngolo di otzione ispetto d un sse
CINEMAICA DEL MOO OAOIO DI UNA PAICELLA MOO CICOLAE: VELOCIA ANGOLAE ED ACCELEAZIONE ANGOLAE Si considei un pticell P in moto cicole che descive un co di ciconfeenz s. L ngolo di otzione ispetto d un sse
3.1 Ridisegnando il circuito senza incroci e applicando la trasformazione triangolo-stella si ottengono gli schemi seguenti.
 . dsegnndo l crcuto senz ncroc e pplcndo l trsformzone trngolostell s ottengono gl schem seguent. Ω Ω eq Ω Ω Ω Ω Ω Ω eq Ω Ω Ω Ω eq Ω eq // Ω. S trsform l stell edenzt n rosso n un trngolo (le resstenze
. dsegnndo l crcuto senz ncroc e pplcndo l trsformzone trngolostell s ottengono gl schem seguent. Ω Ω eq Ω Ω Ω Ω Ω Ω eq Ω Ω Ω Ω eq Ω eq // Ω. S trsform l stell edenzt n rosso n un trngolo (le resstenze
ESERCITAZIONE 8. Esercitazioni del corso FONDAMENTI DI PROCESSI CHIMICI Prof. Gianpiero Groppi
 Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Facoltà di Ingegneria Fisica I Prova in itinere 10 feb 2005 Compito A
 Eeczo n. Un blocco, d denon tcubl e d d 4 Fcoltà d ngegne Fc Pov n tnee feb 5 Copto A kg, legto d un flo, vene ftto uote ozzontlente u un pno enz ttto, decvendo un cecho d ggo. 8 ll veloctà d odulo cotnte
Eeczo n. Un blocco, d denon tcubl e d d 4 Fcoltà d ngegne Fc Pov n tnee feb 5 Copto A kg, legto d un flo, vene ftto uote ozzontlente u un pno enz ttto, decvendo un cecho d ggo. 8 ll veloctà d odulo cotnte
ESERCITAZIONE DEL 3 MARZO 2005
 ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
ESERCITAZIONE DEL 10 MARZO 2005
 ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
Esempio. b) Nel punto P b ( 0,0,1.5 m) E ( P) Poiché sia E1 che E2 sono diretti lungo y
 sempo sempo: Due ptcelle e, con cc 6 nc e 8 nc, s tovno nelle poszon coonte (,y,z)(0,0,0) e (0,-.0m,0) spettvmente. Detemne l cmpo elettco ) Nel punto P (0,.0 m, 0) z b) Nel punto P b ( 0,0,.5 m) ( P)
sempo sempo: Due ptcelle e, con cc 6 nc e 8 nc, s tovno nelle poszon coonte (,y,z)(0,0,0) e (0,-.0m,0) spettvmente. Detemne l cmpo elettco ) Nel punto P (0,.0 m, 0) z b) Nel punto P b ( 0,0,.5 m) ( P)
Economia del turismo
 Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Fisica II. 1 Esercitazioni
 isic II Esecizi svolti Esecizio. Clcole l foz che gisce sull cic Q µc, dovut lle ciche Q - µc e Q 7 µc disposte come ipotto in figu Q Q α 5 cm 6 cm Q Soluzione: L foz che gisce sull cic Q è dt dll composizione
isic II Esecizi svolti Esecizio. Clcole l foz che gisce sull cic Q µc, dovut lle ciche Q - µc e Q 7 µc disposte come ipotto in figu Q Q α 5 cm 6 cm Q Soluzione: L foz che gisce sull cic Q è dt dll composizione
Interpolazione dei dati
 Unverstà degl Stud d Br Dprtmento d Chmc 9 gugno 0 F.Mvell Lortoro d Chmc Fsc I.. 0-0 Interpolzone Curve Interpolzone de dt Qundo s conosce l legge fsc che mette n relzone tr loro due vrl e, mednte prmetr,,
Unverstà degl Stud d Br Dprtmento d Chmc 9 gugno 0 F.Mvell Lortoro d Chmc Fsc I.. 0-0 Interpolzone Curve Interpolzone de dt Qundo s conosce l legge fsc che mette n relzone tr loro due vrl e, mednte prmetr,,
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Volume di un solido di rotazione
 Volume di un solido di rotione Si un rco di curv vente equione f. Se f() è un funione continu e non negtiv nell'intervllo limitto e chiuso,, si dimostr che il volume del solido generto dl trpeoide CD in
Volume di un solido di rotione Si un rco di curv vente equione f. Se f() è un funione continu e non negtiv nell'intervllo limitto e chiuso,, si dimostr che il volume del solido generto dl trpeoide CD in
Sistemi di coordinate curvilinee (1)
 Sstem d coodnate clnee ( Un sstema d coodnate clnee ( nello spao R è defnto con femento ad n sstema catesano da fnon del tpo: con femento ad n sstema catesano da fnon del tpo: ( ( : La fnone ettoale: (
Sstem d coodnate clnee ( Un sstema d coodnate clnee ( nello spao R è defnto con femento ad n sstema catesano da fnon del tpo: con femento ad n sstema catesano da fnon del tpo: ( ( : La fnone ettoale: (
[ m] [ V] Dinamica del corpo rigido #1
![[ m] [ V] Dinamica del corpo rigido #1 [ m] [ V] Dinamica del corpo rigido #1](/thumbs/95/124191097.jpg) Dnc del copo gdo # Nel seguto, sono beeente dscusse lcune gndee fsche de cop estes, e n ptcole de cop gd, che sultno fondentl pe l descone dell dnc. L denstà Pe defne l denstà d un copo, se ne consde un
Dnc del copo gdo # Nel seguto, sono beeente dscusse lcune gndee fsche de cop estes, e n ptcole de cop gd, che sultno fondentl pe l descone dell dnc. L denstà Pe defne l denstà d un copo, se ne consde un
Algebra vettoriale: un breve formulario. E r
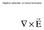 slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
Facoltà di Ingegneria 2 a prova in itinere di Fisica II Compito A
 Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Regressione Lineare Semplice
 reressone lnere Reressone nere Semplce Per ottenere l veloctà d un corpo s msur l su poszone vr temp. Spendo che l relzone tr l poszone del corpo s l tempo t è dt dll lee s = v t trovre con l reressone
reressone lnere Reressone nere Semplce Per ottenere l veloctà d un corpo s msur l su poszone vr temp. Spendo che l relzone tr l poszone del corpo s l tempo t è dt dll lee s = v t trovre con l reressone
r v E r = Quadrilatero articolato 3 β α ω 1 v r δ v r E v r E/B 1 = manovella 2 = bilanciere 3 = biella
 Qudilteo ticolto Si uole detemine l elocità ngole del bilnciee M V / / / / mnoell bilnciee biell N copi igidi Vincoli ceniee estene intene dl -() Si suppong di conoscee l elocità ngole dell mnoell e l
Qudilteo ticolto Si uole detemine l elocità ngole del bilnciee M V / / / / mnoell bilnciee biell N copi igidi Vincoli ceniee estene intene dl -() Si suppong di conoscee l elocità ngole dell mnoell e l
Teorema del momento angolare. Momento angolare totale rispetto al polo P che può essere mobile F31 F13 F32. r r r r r F23. r r P1 F21.
 Teoea del oento angolae F F3 3 Moento angolae totale spetto al polo che può essee oble F3 F3 F3 L ( v ) F O d v + dv + [( ) + ( )] (E) (I) v v v F F Teoea del oento angolae (E) v + + v v v F v v p M (
Teoea del oento angolae F F3 3 Moento angolae totale spetto al polo che può essee oble F3 F3 F3 L ( v ) F O d v + dv + [( ) + ( )] (E) (I) v v v F F Teoea del oento angolae (E) v + + v v v F v v p M (
Obiettivi Specifici di apprendimento GEOGRAFIA. CURRICOLO VERTICALE DI ISTITUTO (dalla Cl. I Sc.Primaria alla Cl. III Sc.Second. 1 gr.
 bettv pecfc d ppendmento GGAFA VA D ( cpm cecond 1 g) A NNZ ABÀ sse cpm gnzzto tempo e spz (pm, po, mente, sop, sotto, dvnt, deto, vcno, ontno,snst, dest, ecc) sse cpm ement costtutv deo spzo vssuto: funzon,
bettv pecfc d ppendmento GGAFA VA D ( cpm cecond 1 g) A NNZ ABÀ sse cpm gnzzto tempo e spz (pm, po, mente, sop, sotto, dvnt, deto, vcno, ontno,snst, dest, ecc) sse cpm ement costtutv deo spzo vssuto: funzon,
I vettori. Grandezze scalari: Grandezze vettoriali
 Grndee sclr: I ettor engono defnte dl loro lore numerco esemp: lunghe d un segmento, re d un fgur pn, tempertur d un corpo, ecc. Grndee ettorl engono defnte, oltre che dl loro lore numerco, d un dreone
Grndee sclr: I ettor engono defnte dl loro lore numerco esemp: lunghe d un segmento, re d un fgur pn, tempertur d un corpo, ecc. Grndee ettorl engono defnte, oltre che dl loro lore numerco, d un dreone
Esercitazioni di Elettrotecnica: doppi-bipoli
 . Mffucc: serctzon su dopp-pol er.-9 Unerstà degl tud d ssno serctzon d lettrotecnc: dopp-pol prof. ntono Mffucc er.. ottore 9 . Mffucc: serctzon su dopp-pol er.-9. opp-pol n rege stzonro.. on rferento
. Mffucc: serctzon su dopp-pol er.-9 Unerstà degl tud d ssno serctzon d lettrotecnc: dopp-pol prof. ntono Mffucc er.. ottore 9 . Mffucc: serctzon su dopp-pol er.-9. opp-pol n rege stzonro.. on rferento
UNA DISUGUAGLIANZA PER CORPI CONVESSI IN R 4
 Luc Ppes n. 7 See eto quntttv luglo UNA DISUGUAGLIANZA PER CORPI CONVESSI IN R Gogo Peezol Intouzone «The geomety of moe thn thee mensons s entely moen bnch of mthemthcs gong no fthe bc thn the fst pt
Luc Ppes n. 7 See eto quntttv luglo UNA DISUGUAGLIANZA PER CORPI CONVESSI IN R Gogo Peezol Intouzone «The geomety of moe thn thee mensons s entely moen bnch of mthemthcs gong no fthe bc thn the fst pt
1. In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione: y ax x b = + +
 . In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
. In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
ipotenusa cateto adiacente ad α cateto opposto ad α ipotenusa cateto adiacente ad α ipotenusa cateto adiacente ad α
 Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
Risultati esame scritto Fisica 2 del 03/10/2016 orali: 11/10/2016 alle ore presso aula H
 sultt esme scrtto Fsc del //6 orl: //6 lle ore. presso ul H gl student nteresst vsonre lo scrtto sono pregt d presentrs l gorno dell'orle mtrcol voto 98 7 mmesso 8 7 mmesso 7 7 mmesso 6 7 mmesso 9 7 mmesso
sultt esme scrtto Fsc del //6 orl: //6 lle ore. presso ul H gl student nteresst vsonre lo scrtto sono pregt d presentrs l gorno dell'orle mtrcol voto 98 7 mmesso 8 7 mmesso 7 7 mmesso 6 7 mmesso 9 7 mmesso
I equazione cardinale della dinamica
 I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
I vettori. Grandezze scalari: Grandezze ve9oriali
 I ettor Grndee sclr: engono defnte dl loro lore numerco esemp: lunghe d un segmento, re d un fgur pn, tempertur d un corpo, ecc. Grndee e9orl engono defnte, oltre che dl loro lore numerco, d un dreone
I ettor Grndee sclr: engono defnte dl loro lore numerco esemp: lunghe d un segmento, re d un fgur pn, tempertur d un corpo, ecc. Grndee e9orl engono defnte, oltre che dl loro lore numerco, d un dreone
Compito di matematica Classe III ASA 26 marzo 2015
 Compito di mtemtic Clsse III ASA 6 mrzo 05 Quesiti. Per quli vlori di l espressione può rppresentre l eccentricità di un ellisse? Dovrà risultre 0 < e
Compito di mtemtic Clsse III ASA 6 mrzo 05 Quesiti. Per quli vlori di l espressione può rppresentre l eccentricità di un ellisse? Dovrà risultre 0 < e
MACCHINE SEMPLICI e COMPOSTE
 OBIETTIVI: MCCHINE SEMLICI e COMOSTE (Distillzione veticle) conoscenz del pincipio di funzionmento delle mcchine spee svolgee ppliczioni sulle mcchine Mcchin (def.) Foz esistente (def.) Foz motice (def.)
OBIETTIVI: MCCHINE SEMLICI e COMOSTE (Distillzione veticle) conoscenz del pincipio di funzionmento delle mcchine spee svolgee ppliczioni sulle mcchine Mcchin (def.) Foz esistente (def.) Foz motice (def.)
Si noti che da questa definizione segue che il punto C è il punto medio del segmento PP'. Figura 1
 APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
Capitolo 4 : Problema 45
 Cptolo 4 : Proble 45 Scelgo per convenenz l sse X lungo superfce dell tvol lsc col verso postvo concorde con l forz pplct F=+ ˆ N. S ssue che durnte l oto le tre sse sno sepre ccostte e = = = qund 3 Y
Cptolo 4 : Proble 45 Scelgo per convenenz l sse X lungo superfce dell tvol lsc col verso postvo concorde con l forz pplct F=+ ˆ N. S ssue che durnte l oto le tre sse sno sepre ccostte e = = = qund 3 Y
U.D. N 15 Funzioni e loro rappresentazione grafica
 54 Unità Didttic N 5 Funzioni e loro rppresentzione grfic U.D. N 5 Funzioni e loro rppresentzione grfic ) Le coordinte crtesine ) L distnz tr due punti 3) Coordinte del punto medio di un segmento 4) Le
54 Unità Didttic N 5 Funzioni e loro rppresentzione grfic U.D. N 5 Funzioni e loro rppresentzione grfic ) Le coordinte crtesine ) L distnz tr due punti 3) Coordinte del punto medio di un segmento 4) Le
Fluidodinamica Applicata Esempi (1-5) di Flusso Irrotazionale
 Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Poltecnco d Tono Fldodnamca Applcata 3. Esemp -5 d Flsso Iotaonale Flsso bdmensonale La none d coente Nel caso bdmensonale c è n lteoe popetà: Fg.3 Integamo n A ed samo Gass. dd nds n n A A A ma se è desctta
Problemi Omogenei e Non Omogenei
 Le Condzon l Contorno Tpo: Tepertur Fsst T = f r, t sul contorno S T = sul contorno S Tpo: Flusso Fssto T n = f rt, sul contorno S T n = sul contorno S 3 Tpo: Sco Convettvo T k + ht = f ( r, t) sul contorno
Le Condzon l Contorno Tpo: Tepertur Fsst T = f r, t sul contorno S T = sul contorno S Tpo: Flusso Fssto T n = f rt, sul contorno S T n = sul contorno S 3 Tpo: Sco Convettvo T k + ht = f ( r, t) sul contorno
Soluzione a) Detta F la forza impulsiva dovuta al corpo, il momento dell impulso, calcolato rispetto al punto di sospensione, è dato da
 A) meccnc Un srr omogene d lunghezz l, lrghezz trscurle e mss M è ppes vertclmente d un estremtà mednte un perno ttorno cu puo` ruotre. Contro l estremt` ler dell srr vene scglto un corpo che nell urto
A) meccnc Un srr omogene d lunghezz l, lrghezz trscurle e mss M è ppes vertclmente d un estremtà mednte un perno ttorno cu puo` ruotre. Contro l estremt` ler dell srr vene scglto un corpo che nell urto
Spettroscopia rotazionale
 Spettrosop rotzonle n prm pprossmzone l desrzone dello spettro rotzonle d un moleol tom f rfermento ll trttzone QM del rottore rgdo due msse he ruotno ttorno d un sse perpendolre l legme e pssnte per l
Spettrosop rotzonle n prm pprossmzone l desrzone dello spettro rotzonle d un moleol tom f rfermento ll trttzone QM del rottore rgdo due msse he ruotno ttorno d un sse perpendolre l legme e pssnte per l
MAPPE DI GEOMETRIA PER LA PRIMA LICEO
 Enti geometici fondmentli (pgin ) Opezioni con gmenti e ngoli (pgin 3) Nomencltu dei tingoli (pgin 4 Popietà dei tingoli (pgin 5) Citei di conguenz dei tingoli (pgin 6) Le ette (pgin 7) Le ette pllele
Enti geometici fondmentli (pgin ) Opezioni con gmenti e ngoli (pgin 3) Nomencltu dei tingoli (pgin 4 Popietà dei tingoli (pgin 5) Citei di conguenz dei tingoli (pgin 6) Le ette (pgin 7) Le ette pllele
Economia del turismo. Prof.ssa Carla Massidda
 Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Tangenti a una conica: il metodo del Doppio sdoppiamento 1
 Tangent a una conca: l metodo del Doppo sdoppamento 1 Franco Goacchno Sunto Ecco un metodo alternatvo per determnare le tangent a una conca da un qualsas punto del pano. Esso consste nell applcare volte
Tangent a una conca: l metodo del Doppo sdoppamento 1 Franco Goacchno Sunto Ecco un metodo alternatvo per determnare le tangent a una conca da un qualsas punto del pano. Esso consste nell applcare volte
Area del Trapezoide. f(x) A f(a) f(b) f(x)
 Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Calcolo del lavoro compiuto dalle forze elementari
 Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE
 INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE (Delbezone del Consglo Comunle n. 5 del 12.02.2007 - Defnzone gevolt) L t. 1, comm 336 dell Legge Fnnz 2005, pevede che sno Comun,
INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE (Delbezone del Consglo Comunle n. 5 del 12.02.2007 - Defnzone gevolt) L t. 1, comm 336 dell Legge Fnnz 2005, pevede che sno Comun,
MECCANICA STATICA CINEMATICA DINAMICA
 MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
Facoltà di Ingegneria Prova scritta di Fisica II
 Fcoltà di ngegnei Pov scitt di Fisic..7 7 Tm Not: ε = 8.85, 4 = π Nm A Esecizio n. Dto il cmpo elettico E = î x y z ( V / m) si detemini l densità di cic ρ nel punto P=(,,) e l cic totle in un cuo vente
Fcoltà di ngegnei Pov scitt di Fisic..7 7 Tm Not: ε = 8.85, 4 = π Nm A Esecizio n. Dto il cmpo elettico E = î x y z ( V / m) si detemini l densità di cic ρ nel punto P=(,,) e l cic totle in un cuo vente
Unità Didattica N 27 Circonferenza e cerchio
 56 La ciconfeenza ed il cechio Ciconfeenza e cechio 01) Definizioni e popietà 02) Popietà delle code 03) Ciconfeenza passante pe te punti 04) Code e loo distanza dal cento 05) Angoli, achi e code 06) Mutua
56 La ciconfeenza ed il cechio Ciconfeenza e cechio 01) Definizioni e popietà 02) Popietà delle code 03) Ciconfeenza passante pe te punti 04) Code e loo distanza dal cento 05) Angoli, achi e code 06) Mutua
Esercitazioni Capitolo 8-9 Impianti di riscaldamento
 Eserctzon Cptolo 8-9 Impnt d rscldmento 1) In un locle rscldto (volume V 400 [m 3 ]) l rnnovo d r è n 0.5 (1/h). Nell potes d un tempertur estern t e - 5 [ C], qunto vle l flusso termco per ventlzone v.
Eserctzon Cptolo 8-9 Impnt d rscldmento 1) In un locle rscldto (volume V 400 [m 3 ]) l rnnovo d r è n 0.5 (1/h). Nell potes d un tempertur estern t e - 5 [ C], qunto vle l flusso termco per ventlzone v.
PROPRIETÀ DEL CAMPO ELETTROSTATICO (PARTE 2) G. Pugliese 1
 PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
Teoremi su correnti e tensioni
 Teorem su corrent e tenson 1) ombnzone lnere efnzone: n un crcuto, ogn corrente e tensone è dt un combnzone lnere d genertor: V = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... I = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... oe
Teorem su corrent e tenson 1) ombnzone lnere efnzone: n un crcuto, ogn corrente e tensone è dt un combnzone lnere d genertor: V = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... I = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... oe
Grandezze vettoriali. Descrizione matematica: l ente matematico vettore
 Gndezze vettoili. Descizione mtemtic: l ente mtemtico vettoe I concetti nuovi e fecondi di somm di vettoi, podotti di vettoi ecc. sono pplicti ll meccnic... Secondo [l utoe] il vntggio mggioe del [metodo]
Gndezze vettoili. Descizione mtemtic: l ente mtemtico vettoe I concetti nuovi e fecondi di somm di vettoi, podotti di vettoi ecc. sono pplicti ll meccnic... Secondo [l utoe] il vntggio mggioe del [metodo]
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esecz sulle et elettche n coente contnua (pate ) Eseczo 3: etemnae gl equalent d Theenn e d Noton del bpolo complementae al esstoe R 5 nel ccuto n fgua e calcolae la coente che ccola attaeso l esstoe R
Esecz sulle et elettche n coente contnua (pate ) Eseczo 3: etemnae gl equalent d Theenn e d Noton del bpolo complementae al esstoe R 5 nel ccuto n fgua e calcolae la coente che ccola attaeso l esstoe R
le proiezioni centrali 07corso tecniche di rappresentazione dello spazio docente Arch. Emilio Di Gristina
 le poiezioni cenli 07coso tecniche di ppesenzione dello spzio docente Ach. Emilio Di Gistin Il metodo delle poiezioni cenli Il metodo delle poiezioni cenli consente di ppesene su di un pino le figue dello
le poiezioni cenli 07coso tecniche di ppesenzione dello spzio docente Ach. Emilio Di Gistin Il metodo delle poiezioni cenli Il metodo delle poiezioni cenli consente di ppesene su di un pino le figue dello
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLASSI 3 S.M. DA CONSEGNARE IL PRIMO GIORNO DI ATTIVITA DI SPORTELLO
 LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
Scrivere 2.1 cm implica dire che la misura sia compresa nell intervallo mm
 Il lto d un ddo è pr. cm. Usndo le cfre sgnfctve per stmre l errore clcolre l volume del cuo. Supponendo che l devzone stndrd nell msur del lto s d mm clcolre l devzone stndrd che ssoct ll msur del volume.
Il lto d un ddo è pr. cm. Usndo le cfre sgnfctve per stmre l errore clcolre l volume del cuo. Supponendo che l devzone stndrd nell msur del lto s d mm clcolre l devzone stndrd che ssoct ll msur del volume.
APOTEMA AREA POLIGONO REGOLARE LUNGHEZZA CIRCONFERENZA LUNGHEZZA ARCO CIRCONFERENZA AREA CERCHIO AREA SETTORE CIRCOLARE AREA CORONA CIRCOLARE
 CERCHIO E CIRCONFERENZ CIRCONFERENZ CERCHIO POSIZIONE RETT RISPETTO CIRCONFERENZ POSIZIONE DI DUE CIRCONFERENZE NGOLI L CENTRO NGOLI LL CIRCONFERENZ SETTORE CIRCOLRE PROPRIET CORDE E RCHI POLIGONI INSCRITTI
CERCHIO E CIRCONFERENZ CIRCONFERENZ CERCHIO POSIZIONE RETT RISPETTO CIRCONFERENZ POSIZIONE DI DUE CIRCONFERENZE NGOLI L CENTRO NGOLI LL CIRCONFERENZ SETTORE CIRCOLRE PROPRIET CORDE E RCHI POLIGONI INSCRITTI
Cinematica del punto. 3D
 Cinemic del puno. 3D z O () () P() z() () in fom eoile OP( ) ( ) Veoe posizione oeo eoe sposmeno dll oigine L ppesenzione eoile pemee un descizione sineic del moo. z P() Nei clcoli pici in genee si usno
Cinemic del puno. 3D z O () () P() z() () in fom eoile OP( ) ( ) Veoe posizione oeo eoe sposmeno dll oigine L ppesenzione eoile pemee un descizione sineic del moo. z P() Nei clcoli pici in genee si usno
Area di una superficie piana o gobba 1. Area di una superficie piana. f x dx 0 e quindi :
 Are di un superficie pin o go Are di un superficie pin L're dell superficie del trpezoide si B ottiene pplicndo l seguente formul: f d [] A T e risult 0 [, ] è f f d 0 e quindi : [] f d f d f d f d c Nel
Are di un superficie pin o go Are di un superficie pin L're dell superficie del trpezoide si B ottiene pplicndo l seguente formul: f d [] A T e risult 0 [, ] è f f d 0 e quindi : [] f d f d f d f d c Nel
Fisica II. 6 Esercitazioni
 Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Dimostrazione del teorema di Gauss Green nel piano
 imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
Campo elettrico in un conduttore
 Cmpo elettico in un conduttoe In entmbi i csi se il conduttoe è isolto e possiede un cic totle, dett cic si dispone sull supeficie esten del conduttoe; se così non fosse inftti ci sebbe un foz sulle ciche
Cmpo elettico in un conduttoe In entmbi i csi se il conduttoe è isolto e possiede un cic totle, dett cic si dispone sull supeficie esten del conduttoe; se così non fosse inftti ci sebbe un foz sulle ciche
Sviluppo dell algoritmo per l allineamento dello spettrometro magnetico di PAMELA
 Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
