Obiettivi Specifici di apprendimento GEOGRAFIA. CURRICOLO VERTICALE DI ISTITUTO (dalla Cl. I Sc.Primaria alla Cl. III Sc.Second. 1 gr.
|
|
|
- Gennaro Castelli
- 8 anni fa
- Visualizzazioni
Transcript
1 bettv pecfc d ppendmento GGAFA VA D ( cpm cecond 1 g) A NNZ ABÀ sse cpm gnzzto tempo e spz (pm, po, mente, sop, sotto, dvnt, deto, vcno, ontno,snst, dest, ecc) sse cpm ement costtutv deo spzo vssuto: funzon, ezon e ppesentzon ppoto t età geogfc e su ppesentzone: pm ppocc con gobo e ct geogfc, poszone etv ed ssout, oczzzone ement fsc ed ntopc, fss e mob de pesggo: spz pet e chus ompotment degut tute deg spz vssut e de'mbente conoscee pop poszone e que deg oggett neo spzo vssuto, spetto dves punt d femento Anzze uno spzo ttveso ttvzone d tutt sstem senso, scopne g eement cttezznt ndvdue sempc ezon t g eement cttezznt un mbente ppesente gfcmente n pnt spz vssut e pecos, nche utzzndo un smboog non convenzone Descvee vebmente, utzzndo ndcto topoogc, g spostment pop e d t eement neo spzo vssuto Fomue poposte d ognzzzone d spz vssut ('u, pop stnz, pco, ecc) e d pnfczone d compotment d ssumee n t spz ents e muoves neo spzo fsco e ppesentto utzzndo dves punt d femento eggee e podue sempc ppesentzon conche e ctogfche (pnte, mppe, cte topogfche) d teto demtt, utzzndo codc non convenzon e e egende conoscee e ppesente gfcmente pncp tp d pesggo (ubno, ue, costeo, montno, ecc) Descvee un pesggo ne suo eement essenz, usndo un temnoog v v pù ppopt VA D (d cpm cecond 1 g) 17
2 A NNZ ABÀ popo tetoo comune e povnce conoscee g eement fsc e ntopc sse con dstbuzone de pù evdent e d un pesggo cogendo pncp cpm sgnfctv eement fsc e ntopc e e ppot d connessone e oo tsfomzon ne tempo ntedpendenz 'uomo e e sue ttvtà come pte conoscee e tsfomzon ne v de'mbente e de su fuzone mbent geogfc podotte d fenomen fsc, tmosfec e d'ntevento de'uomo, pe mego compendee ppoto uomo/mbente gnzze un pecoso pedone (ne gdno, ne cote), d pecoee secondo e egoe de codce stde e ppesento gfcmente cce schzz de popo tetoo comune con 'uso de smboog convenzone e non Descvee un mbente ne suo eement essenz, usndo un temnoog ppopt sse V cpm ppesentzone ctogfc: sc gfc e numec, ct temtc e ctogmm o spzo fsco: mofoog, dogf e cm o spzo ntopco: sevz, o spzo economco e e sose oncetto d confne: egon cmtche ed mmnsttve popo tetoo egone e dstbuzone de pù sgnfctv eement fsc ed ntopc ents e muoves n uno spzo demtto utzzndo stument, schzz, mppe ment, pnte e cte topogfche sseve e eggee gfc, cte geogfche dves sc, cte temtche, ctogmm, fotogfe eee (obque, zent) e mmgn d stete coe dstnze su cte, utzzndo sc gfc e/o numec cce schzz d pecos fnzzt e mppe ment d teto not de pop egone, utzzndo eventumente smboog convenzone conoscee e pù evdent modfczon ppotte ne tempo su tetoo egone, utzzndo nche fotogfe e cte ffettue confont t età vcne e ontne spoe con temnoog specfc qunto ppeso VA D (d cpm cecond 1 g) - GGAFA 18
3 A NNZ ABÀ sse V cpm ppesentzon tbe e gfche etve dt tbe te pncp pe ndvduzone dee egon tne (egon pesggstche, cmtche, mmnsttve, stoche) ement fsc ed ntopc d cscun pesggo geogfco tno t e dstbuzone de pù sgnfctv eement fsc ed ntopc t e su poszone n uop e ne mondo oncetto d svuppo sostenbe sseve e eggee gfc, cte geogfche dves sc, cte temtche, ctogmm, fotogfe eee (obque, zent) e mmgn d stete Dscmne e dvese egon tne, dto un cteo (mofoog, cm, demtzone mmnsttv) conoscee e pù evdent modfczon ppotte ne tempo d uomo su tetoo nzone, utzzndo nche fotogfe e cte Pogette tne d vggo, segnndo e coegndo e dvese tppe sue cte conoscee nesso t mbente e e sue sose d un to e e condzon d vt de uomo d to Popoe ed ssumee compotment vot tute deg spz vssut, de ptmono mbente e cutue Vebzze con un nguggo ppopto sutt de cec geogfc 19
4 sse cecond 1 g NB PN QAD D NNZ ABBAA A A A A - pncp fome d ppesentzone gfc (deogmm, stogmm, dgmm be), ctogf (cte fsche, potche, std, temtche, topogfche e topoogche) - concett d dstnz tne, dstnz economc n temn d tempo e cost, etcoo geogfco, coodnte geogfche (ttudne, ongtudne, ttudne), fuso oo - popozone: denstà, movmento ntue e fuss mgto - stem tetoe e sstem ntopofsco, - ttestche fsco-ntopche de uop e d cun tt che compongono: spett fsc, soco economc e cutu - e ogn de none uope e e sue dvese fome sttuzon - t ne none uope onoscenz de mbente fsco e umno, nche ttveso ossevzone - onoscee g eement ntu de tetoo - pe conoscee t eement ne popo tetoo vssuto o n un tetoo ppesentto - onoscee pù evdent ntevent d umnzzzone d un tetoo: nsedment, vbtà, stuttue ge - conoscee g eement che dstnguono un egone so deg stument pop de dscpn - se con suffcente utonom bo d testo - pes oente neo spzo e nee cte geogfche - eggee cte geogfche, tbee, gfc e mmgn fotogfche pe tne nfomzon - ostue gfc e/o ctogmm ompensone dee ezon t stuzon mbent, cutu, soco-potche ed economche - conoscee g eement pncp de ppoto uomo-mbente - onoscee età etnco-geogfche dvese ompensone de nguggo specfco - conoscee temn specfc, smbo geogfc, egende d vo tpo, gfc - pege sgnfcto de temnoog geogfc - spmes utzzndo temn degut 20 V A D ( d c P m
5 A NNZ ABÀ sse cecond 1 g NB PN QAD D NNZ ABBAA A A A A - pncp fome d ppesentzone gfc (deogmm, stogmm, dgmm be), ctogf (cte fsche, potche, std, temtche, topogfche e topoogche) - concett d dstnz tne, dstnz economc n temn d tempo e cost, etcoo geogfco, coodnte geogfche (ttudne, ongtudne, ttudne), fuso oo - popozone: denstà, movmento ntue e fuss mgto - stem tetoe e sstem ntopofsco, - ttestche fsco-ntopche de uop e d cun tt che compongono: spett fsc, soco economc e cutu - e ogn de none uope e e sue dvese fome sttuzon - t ne none uope onoscenz de mbente fsco e umno, nche ttveso ossevzone - onoscee e descvee g eement de mbente (fsco e umno) - Descvee n modo odnto e coetto e cttestche d un e geogfc - pe ccogee e ognzze mte e dt etv d un pobemtc o d un tetoo so deg stument pop de dscpn - tzze n modo funzone bo d testo e tnte - se cte geogfche, tbee, gfc e mmgn fotogfche pe descvee e cttestche d un tetoo ompensone dee ezon t stuzon mbent, cutu, soco-potche ed economche - conoscee e tsfomzon mbent - conoscee ntevento de uomo su mbente - ompendee e conseguenze deg ntevent ntopc su mbente ompensone de nguggo specfco - onoscee temnoog specfc - ompendee test n cu s contenut temnoog specfc - spmes utzzndo temn specfc 21
6 sse cecond 1 g - vuppo umno, svuppo sostenbe e pocess d gobzzzone: mode d ppcbtà e sstem teto - Mode etv ognzzzone de tetoo e pncp tem e pobem de mondo - Nuov stument e metod d ppesentzone deo spzo geogfco (teeevmento, ctogf computezzt) - t mente de mondo con dstbuzone dee tee emese, d cun stt e cttà, de pù sgnfctv eement fsc e dee gnd ee soco economche e cutu - ttestche deg mbent exteuope e oo ppoto con e popozon che e btno, nzzte pe gnd ee cutu e geopotche - dves dstbuzone de eddto ne mondo: stuzone economco soce, ndcto d povetà e cchezz - pù sgnfctv tem geontopc contempone ttveso utzzo d document e dt quntttv e quttv, desunt d dvese font (test specfc, stmp quotdn e peodc, teevsone, udovsv, ntenet) onoscenz de mbente fsco e umno, nche ttveso ossevzone - oczze su ct e nzze pncp eement e fenomen pesent ne teto exteuope - Descvee con un nguggo specfco ctte deg mbent e de pesgg ext-euope - onoscee e oczze e pncp pobemtche mbent e soco-economche mond - ccogee e ognzze mtee pe un cec su spett e pobem de mondo ttue so deg stument pop de dscpn - se n modo utonomo test - ntepete e confonte ppesentzon ctogfche, mmgn, tbee e gfc ompensone dee ezon t stuzon mbent, cutu, soco-potche ed economche ogee e ezon d ntedpendenz t g eement e fenomen d cttee fsco e ntopco pe coege fenomen demogfc, economc e soc de mondo onfonte età etncogeogfche dvese ompensone de nguggo specfco - onoscee e utzze coettmente temnoog specfc - pe espoe e gone su pobemtche d geogfc fsc e umn pesent ne teto ext-euope 22 V A D ( d c P m
7 23
Vettori. Le grandezze fisiche sono: scalari; vettoriali;
 Vetto 1 Le gndee fsche sono: scl; vettol; Def: Gnde scle defnt unvocmente d un numeo (postvo o negtvo) (con oppotun untà d msu) es.: tempo, mss, tempetu, cc elettc, Def: Gnde vettole (vd. pgn seguente)
Vetto 1 Le gndee fsche sono: scl; vettol; Def: Gnde scle defnt unvocmente d un numeo (postvo o negtvo) (con oppotun untà d msu) es.: tempo, mss, tempetu, cc elettc, Def: Gnde vettole (vd. pgn seguente)
SISTEMI DI CONDOTTE: La verifica idraulica
 SISTEMI DI CONDOTTE: L vefc dulc Clo Cpon Unvestà degl Stud d Pv Dptmento d Ingegne Idulc e Ambentle Poszone del del poblem Rete esstente d cu è not l geomet E pefsst l eogzone (ppocco DDA: Demnd Dven
SISTEMI DI CONDOTTE: L vefc dulc Clo Cpon Unvestà degl Stud d Pv Dptmento d Ingegne Idulc e Ambentle Poszone del del poblem Rete esstente d cu è not l geomet E pefsst l eogzone (ppocco DDA: Demnd Dven
Economia del turismo. Prof.ssa Carla Massidda
 Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
I vettori. Grandezze scalari: Grandezze vettoriali
 I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
dal12gennai. o chiama il numero dedicato alle Iscrizioni On Line: 06 5849 4025
 Annosco s co015/016 Denom nz onescuo www. s uz Cod cesc uo Con Adeco e ed ' nnosco s co01013, e sc z on ec ssp mede e s uz on sco s ches dogno d neeg do vvengonoesc us vmen e nmod à on ne. En n sc z onon
Annosco s co015/016 Denom nz onescuo www. s uz Cod cesc uo Con Adeco e ed ' nnosco s co01013, e sc z on ec ssp mede e s uz on sco s ches dogno d neeg do vvengonoesc us vmen e nmod à on ne. En n sc z onon
Economia del turismo
 Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Scrivere 2.1 cm implica dire che la misura sia compresa nell intervallo mm
 Il lto d un ddo è pr. cm. Usndo le cfre sgnfctve per stmre l errore clcolre l volume del cuo. Supponendo che l devzone stndrd nell msur del lto s d mm clcolre l devzone stndrd che ssoct ll msur del volume.
Il lto d un ddo è pr. cm. Usndo le cfre sgnfctve per stmre l errore clcolre l volume del cuo. Supponendo che l devzone stndrd nell msur del lto s d mm clcolre l devzone stndrd che ssoct ll msur del volume.
AZIONAMENTI ELETTRICI 2. Modello del motore asincrono trifase ed osservatori di flusso
 Poltecnco d ono CeeM ZIONMENI EERICI 4 Motoe ancono tfae Modello del motoe ancono tfae ed oeato d fluo S conde la macchna chematzzata con aolgment tatoc pot a π/ ta loo e f nello pazo e aolgment otoc,
Poltecnco d ono CeeM ZIONMENI EERICI 4 Motoe ancono tfae Modello del motoe ancono tfae ed oeato d fluo S conde la macchna chematzzata con aolgment tatoc pot a π/ ta loo e f nello pazo e aolgment otoc,
ADPF COSTONE NEWS. Newsletter dell adpf costone con risultati notizie e classifiche dalla serie A2 all U13 NEXT MATCH
 ADPF COSTONE NEWS Newette de dpf te utt te e fhe d ee A2 U13 NEXT MATCH SABATO 22 OTTOBRE 21.00 PALACOSTONE SIENA VS um.t e fee wm L egge dee ex Sftt u mp de quttm fme umb, tt p d M&C., ug ud e due ex
ADPF COSTONE NEWS Newette de dpf te utt te e fhe d ee A2 U13 NEXT MATCH SABATO 22 OTTOBRE 21.00 PALACOSTONE SIENA VS um.t e fee wm L egge dee ex Sftt u mp de quttm fme umb, tt p d M&C., ug ud e due ex
INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE
 INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE (Delbezone del Consglo Comunle n. 5 del 12.02.2007 - Defnzone gevolt) L t. 1, comm 336 dell Legge Fnnz 2005, pevede che sno Comun,
INFORMAZIONI UTILI PER VERIFICA/AGGIORNAMENTO DEL CLASSAMENTO CATASTALE (Delbezone del Consglo Comunle n. 5 del 12.02.2007 - Defnzone gevolt) L t. 1, comm 336 dell Legge Fnnz 2005, pevede che sno Comun,
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
58% 158% 41% PENETRAZIONE INTERNET PENETRAZIONE MOBILE PENETRAZIONE SMARTPHONE SUL TOTALE DELLA POPOLAZIONE SCENARIO DESKTOP VS MOBILE ITALIA
 SCENARIO DESKTOP VS MOBILE ITALIA PENETRAZIONE INTERNET 58% PENETRAZIONE MOBILE 158% 41% PENETRAZIONE SMARTPHONE SUL TOTALE DELLA POPOLAZIONE SOURCE: US CENSUS BUREU, INTERNETWORLDSTATS CNNIC GENNAIO 2014
SCENARIO DESKTOP VS MOBILE ITALIA PENETRAZIONE INTERNET 58% PENETRAZIONE MOBILE 158% 41% PENETRAZIONE SMARTPHONE SUL TOTALE DELLA POPOLAZIONE SOURCE: US CENSUS BUREU, INTERNETWORLDSTATS CNNIC GENNAIO 2014
Il lavoro è quindi una grandezza scalare le cui unita di misura sono: = Joule = J
 Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Il campo magnetico. sommario21.1. capitolo 21.2
 I campo magnetco captoo 21 I campo magnetco d un magnete Campo magnetco geneato da una coente eettca 21.2.1 Campo magnetco geneato da un fo nfnto ettneo pecoso da coente 21.2.2 Campo magnetco geneato da
I campo magnetco captoo 21 I campo magnetco d un magnete Campo magnetco geneato da una coente eettca 21.2.1 Campo magnetco geneato da un fo nfnto ettneo pecoso da coente 21.2.2 Campo magnetco geneato da
I PROBLEMI DI MASSIMO E DI MINIMO
 I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
Workshop MatFinTN 2012
 Wokshop MatFnTN 2012 Dalla Bnson Attbuton al Black&Ltteman model: anals matematche nell'asset management D.ssa Tzana Rgon Lauea n Matematca conseguta pesso l'unvestà d Tento con tes dal ttolo: Metod d
Wokshop MatFnTN 2012 Dalla Bnson Attbuton al Black&Ltteman model: anals matematche nell'asset management D.ssa Tzana Rgon Lauea n Matematca conseguta pesso l'unvestà d Tento con tes dal ttolo: Metod d
13. Richiami di analisi vettoriale
 13. Rchm d nls vettole Rchm d nls vettole 347 13.1. Scl, vetto, tenso Le gndee che entno n goco ne enomen sc possono essee ppesentte tmte unon del tempo, t e delle coodnte d un geneco punto (, ) vlutte
13. Rchm d nls vettole Rchm d nls vettole 347 13.1. Scl, vetto, tenso Le gndee che entno n goco ne enomen sc possono essee ppesentte tmte unon del tempo, t e delle coodnte d un geneco punto (, ) vlutte
I vettori. Grandezze scalari e grandezze vettoriali
 I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
GRANDEZZE MAGNETICHE Prof. Chirizzi Marco www.elettrone.altervista.org marco.chirizzi@libero.it
 Soenoide GRANDEZZE MAGNETICHE Pof. Chiizzi Maco www.eettone.atevista.og maco.chiizzi@ibeo.it PREMESSA La pesente dispensa ha come obiettivo queo di gaantie agi aievi de coso di Fisica de biennio, ad indiizzo
Soenoide GRANDEZZE MAGNETICHE Pof. Chiizzi Maco www.eettone.atevista.og maco.chiizzi@ibeo.it PREMESSA La pesente dispensa ha come obiettivo queo di gaantie agi aievi de coso di Fisica de biennio, ad indiizzo
ESTENSIONE ED EQUIVALENZA EQUIVALENZA DI POLIGONI
 ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
Meccanica Dinamica del corpo rigido
 eccanca 07-08 7 Denstà Defnamo denstà d un eemento nfntesmo d ρ d ρ d In geneae ρ ρ( ) ρ( x,, ) < ρ Tea > 5.5 g cm ρtea ρ( ) 3 Pofo d denstà dea Tea Costa:. -.9 g cm -3 anteo: 3.4-5.6 g cm -3 Se assa totae
eccanca 07-08 7 Denstà Defnamo denstà d un eemento nfntesmo d ρ d ρ d In geneae ρ ρ( ) ρ( x,, ) < ρ Tea > 5.5 g cm ρtea ρ( ) 3 Pofo d denstà dea Tea Costa:. -.9 g cm -3 anteo: 3.4-5.6 g cm -3 Se assa totae
Campo Magnetico. Magnetostatica
 Magnetso Capo Magnetco Magnetostatca Un capo agnetco può essee ceato da cache eettche n oto, coè da una coente, oppue da un agnete peanente. Speentaente s tova che un agnete pesenta due poatà: poo nod
Magnetso Capo Magnetco Magnetostatca Un capo agnetco può essee ceato da cache eettche n oto, coè da una coente, oppue da un agnete peanente. Speentaente s tova che un agnete pesenta due poatà: poo nod
Regressione Lineare Semplice
 reressone lnere Reressone nere Semplce Per ottenere l veloctà d un corpo s msur l su poszone vr temp. Spendo che l relzone tr l poszone del corpo s l tempo t è dt dll lee s = v t trovre con l reressone
reressone lnere Reressone nere Semplce Per ottenere l veloctà d un corpo s msur l su poszone vr temp. Spendo che l relzone tr l poszone del corpo s l tempo t è dt dll lee s = v t trovre con l reressone
Potenziali e campi di dipoli elettrici e magnetici
 Potena e camp d dpo eettc e magnetc S vuoe mostae come s puo tovae andamento de campo eettco e d queo magnetco, ne mte d gand dstane, pe caso d un dpoo eettco e d un dpoo magnetco. Dpoo eettco Schematamo
Potena e camp d dpo eettc e magnetc S vuoe mostae come s puo tovae andamento de campo eettco e d queo magnetco, ne mte d gand dstane, pe caso d un dpoo eettco e d un dpoo magnetco. Dpoo eettco Schematamo
MECCANICA STATICA CINEMATICA DINAMICA
 MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
CURRICOLO VERTICALE D ISTITUTO DI SCIENZE
 .C.Trilussa CUCOLO VETCLE D SCENZE stituto Comprensivo Statale TLUSS via Trilussa 10-20157 Milano scuola Primaria e scuola Secondaria di 1 grado Plessi dipendenti: Plessi di Scuola Primaria: via Trilussa
.C.Trilussa CUCOLO VETCLE D SCENZE stituto Comprensivo Statale TLUSS via Trilussa 10-20157 Milano scuola Primaria e scuola Secondaria di 1 grado Plessi dipendenti: Plessi di Scuola Primaria: via Trilussa
Facoltà di Ingegneria Prova scritta di Fisica II 22 Luglio Compito A
 Fcoà d gege o sc d Fsc Lugo - Compo A Fg. y ueso. musco pce d mss m possede u cc o o q. S ede, peò, che e pce es equbo, e puo (Fg. ), qudo ee soopos zoe cocome de foz peso e de foz d u eeosc gee d dsbuzoe
Fcoà d gege o sc d Fsc Lugo - Compo A Fg. y ueso. musco pce d mss m possede u cc o o q. S ede, peò, che e pce es equbo, e puo (Fg. ), qudo ee soopos zoe cocome de foz peso e de foz d u eeosc gee d dsbuzoe
Approfondimento 7.4 - Altri tipi di test di significatività del coefficiente di correlazione di Pearson
 Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
COMPARATORI. Comparatore invertente
 COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
A) Meccanica Soluzione
 A) Meccnc Un uot omogene d ggo R, mss M e momento d nez spetto l popo sse I, otol senz stsce su un pno ozzontle scbo sotto l zone d un momento motoe noto τ. S A l foz d ttto con l suolo, l ccelezone del
A) Meccnc Un uot omogene d ggo R, mss M e momento d nez spetto l popo sse I, otol senz stsce su un pno ozzontle scbo sotto l zone d un momento motoe noto τ. S A l foz d ttto con l suolo, l ccelezone del
Note sull elettrostatica
 . Mffucc: Not su ttosttc. 1. 11/1 Unstà g tu Cssno Not su ttosttc pof. ntono Mffucc www.ocnt.uncs.t/ntono_mffucc V.1. - nomb 1 1 . Mffucc: Not su ttosttc. 1. 11/1. Mffucc: Not su ttosttc. 1. 11/1 1. Conctt
. Mffucc: Not su ttosttc. 1. 11/1 Unstà g tu Cssno Not su ttosttc pof. ntono Mffucc www.ocnt.uncs.t/ntono_mffucc V.1. - nomb 1 1 . Mffucc: Not su ttosttc. 1. 11/1. Mffucc: Not su ttosttc. 1. 11/1 1. Conctt
Ministero della Salute D.G. della programmazione sanitaria --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA
 Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
IL Potenziale elettrostatico
 Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
POLITECNICO DI MILANO IV FACOLTÀ Ingegneria Aerospaziale II Verifica di Fisica Sperimentale A+B 4 Luglio 2006
 POITENIO DI MIANO IV FAOTÀ Ingegne Aeospzle II Vefc Fsc Spementle A+B 4 uglo 6 Gustfce le sposte e scvee n moo cho e leggble Sosttue vlo numec solo ll fne, opo ve cvto le espesson lettel Ince nome e cognome
POITENIO DI MIANO IV FAOTÀ Ingegne Aeospzle II Vefc Fsc Spementle A+B 4 uglo 6 Gustfce le sposte e scvee n moo cho e leggble Sosttue vlo numec solo ll fne, opo ve cvto le espesson lettel Ince nome e cognome
Fisica II - Ingegneria Biomedica - A.A. 2016/ Appello del 4/7/2017
 sc II - Ingegne omedc -.. 6/ - ppello del // ---------------------------------------------------------------------------------------------------------------------- Nome ognome N o Mtcol -----------------------------------------------------------------------------------------------------------------------
sc II - Ingegne omedc -.. 6/ - ppello del // ---------------------------------------------------------------------------------------------------------------------- Nome ognome N o Mtcol -----------------------------------------------------------------------------------------------------------------------
tramite della Segreteria della scuola), trasmissione dei verbali e degli atti al
 L verbae n"..8j... Ogg, se marzo duemaqundc, ae ore 13.00, s è runta nea sede d questa sttuzone Scoastca a commssone Eettorae così composta RBEZZO ASSUNTA Presdente; VAL SABNA Segretaro, FATORELLO GAMPETRO
L verbae n"..8j... Ogg, se marzo duemaqundc, ae ore 13.00, s è runta nea sede d questa sttuzone Scoastca a commssone Eettorae così composta RBEZZO ASSUNTA Presdente; VAL SABNA Segretaro, FATORELLO GAMPETRO
CARATTERISTICHE DEI SEGNALI RANDOM
 CARATTERISTICHE DEI SEGNALI RANDOM I segnal random o stocastc rvestono una notevole mportanza poché sono present, pù che segnal determnstc, nella maggor parte de process fsc real. Esempo d segnale random:
CARATTERISTICHE DEI SEGNALI RANDOM I segnal random o stocastc rvestono una notevole mportanza poché sono present, pù che segnal determnstc, nella maggor parte de process fsc real. Esempo d segnale random:
Fisica II. 2 Esercitazioni
 Poitecnico i Toino Fisic II Esecitzioni Esecizi svoti Esecizio. Su i un fio i unghezz infinit è istibuit un cic unifome pe unità i unghezz λ 5 nc/m. Ccoe i cmpo eettico in un punto che ist 5 cm fio. Souzione:
Poitecnico i Toino Fisic II Esecitzioni Esecizi svoti Esecizio. Su i un fio i unghezz infinit è istibuit un cic unifome pe unità i unghezz λ 5 nc/m. Ccoe i cmpo eettico in un punto che ist 5 cm fio. Souzione:
NUMERI FUZZY (a cura di Marco Buttolo (2006))
 NUMERI FUZZY ( cu di Mco Buttoo (2006)) definizione: Un numeo fuzzy un insieme fuzzy nome e convesso. Un insieme fuzzy è nome se su funzione di pptenenz possiede voi che pe foz di cose sono compesi t 0
NUMERI FUZZY ( cu di Mco Buttoo (2006)) definizione: Un numeo fuzzy un insieme fuzzy nome e convesso. Un insieme fuzzy è nome se su funzione di pptenenz possiede voi che pe foz di cose sono compesi t 0
Laboratorio: Metodi quantitativi per il calcolo del VaR. Aldo Nassigh Financial Risk Management A.A. 2011/12 Lezione 4
 Laboatoo: Metod quanttatv pe l calcolo del VaR Aldo Nassgh Fnancal Rsk Management A.A. 011/1 Lezone 4 METODO PARAMETRICO Sngolo fattoe d scho e poszone lneae Poszone l cu valoe attuale è soggetto ad un
Laboatoo: Metod quanttatv pe l calcolo del VaR Aldo Nassgh Fnancal Rsk Management A.A. 011/1 Lezone 4 METODO PARAMETRICO Sngolo fattoe d scho e poszone lneae Poszone l cu valoe attuale è soggetto ad un
MACCHINA ELEMENTARE CON UN SOLO AVVOLGIMENTO
 MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
VOLUME 2 CAPITOLO 6 MODULO D LE VENTI REGIONI ITALIANE. Golfo di Biscaglia. I b e r i. Madrid. Mulhacén 3478 M E D I T E R R A A R.
 VOLUM 2 CAPTOLO 6 MODULO D L VNT RGON TALAN LA SPAGNA Cose d spee A. Le dee mpotnt l Qudo fsco l L Spgn h qus 40 mlon d btnt che vvono sopttutto nelle cttà e sulle coste l L econom spgnol è n fote svluppo
VOLUM 2 CAPTOLO 6 MODULO D L VNT RGON TALAN LA SPAGNA Cose d spee A. Le dee mpotnt l Qudo fsco l L Spgn h qus 40 mlon d btnt che vvono sopttutto nelle cttà e sulle coste l L econom spgnol è n fote svluppo
Facoltà di Ingegneria 2 a prova in itinere di Fisica II Compito A
 Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Fisica II - Ingegneria Biomedica - A.A. 2017/ Appello del 13/2/2018
 Fsc II - Ingegne oedc - A.A. 7/8 - Appello del 3//8 ---------------------------------------------------------------------------------------------------------------------- oe: ognoe: o Mtcol: ----------------------------------------------------------------------------------------------------------------------
Fsc II - Ingegne oedc - A.A. 7/8 - Appello del 3//8 ---------------------------------------------------------------------------------------------------------------------- oe: ognoe: o Mtcol: ----------------------------------------------------------------------------------------------------------------------
Regime Permanente. (vedi Vitelli-Petternella par. VI.1,VI.1.1,VI.2)
 Regme Permanente (ve Vtell-Petternella par. VI.,VI..,VI.) Comportamento a regme permanente Clafcazone n tp Conzon a Cclo Chuo Conzon a Cclo Aperto Rpota a Regme per Dturb Cotant Dturbo ulla mura Rpota
Regme Permanente (ve Vtell-Petternella par. VI.,VI..,VI.) Comportamento a regme permanente Clafcazone n tp Conzon a Cclo Chuo Conzon a Cclo Aperto Rpota a Regme per Dturb Cotant Dturbo ulla mura Rpota
ADPF COSTONE NEWS. Newsletter dell adpf costone con risultati notizie e classifiche dalla serie A2 all U13 NEXT MATCH
 ADPF COSTONE NEWS Newette de dpf te utt te e fhe d ee A2 U13 NEXT MATCH DOMENICA 2 OTTOBRE 18.00 PALASPRINT LA SPEZIA VS um.t e tempe pe S pte! Rm vvetu dee te, gudte d Pefe Be, e ge ud de mpt d ee A/2,
ADPF COSTONE NEWS Newette de dpf te utt te e fhe d ee A2 U13 NEXT MATCH DOMENICA 2 OTTOBRE 18.00 PALASPRINT LA SPEZIA VS um.t e tempe pe S pte! Rm vvetu dee te, gudte d Pefe Be, e ge ud de mpt d ee A/2,
SCHEDA TECNICA. MISURATORE DI OSSIGENO DISCIOLTO - TEMPERATURA HD2109.1 e HD2109.2
 ecnoveo S... V agab e ed Annunz e. 039.200.60.17 fax. 039.200.60.64 web se: www.ecnoveo. ma: nfo@ecnoveo. SHEDA TENIA MISURATORE DI OSSIGENO DISIOLTO - TEMPERATURA HD2109.1 e HD2109.2 L HD2109.1 e HD2109.2
ecnoveo S... V agab e ed Annunz e. 039.200.60.17 fax. 039.200.60.64 web se: www.ecnoveo. ma: nfo@ecnoveo. SHEDA TENIA MISURATORE DI OSSIGENO DISIOLTO - TEMPERATURA HD2109.1 e HD2109.2 L HD2109.1 e HD2109.2
AF 1 RITIRATO 26,1 26 2A AL 1 18,2 RITIRATO 25,7 26 3A AL 1 30,2 30 2A AL 0 RITIRATO 23,7 24 5A
 1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
N 10 I NUMERI COMPLESSI
 Untà Ddttc N 0 I NUMERI COMPLESSI 0) Introduzone dell untà mmgnr 0) Introduzone elementre de numer compless 0) Alcune operzon su numer compless 0) Rppresentzone geometrc de numer compless 05) Rppresentzone
Untà Ddttc N 0 I NUMERI COMPLESSI 0) Introduzone dell untà mmgnr 0) Introduzone elementre de numer compless 0) Alcune operzon su numer compless 0) Rppresentzone geometrc de numer compless 05) Rppresentzone
Momento di una forza rispettto ad un punto
 Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Condizioni di equilibrio TD nelle reazioni chimiche
 Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
VOLUME 2 CAPITOLO 9 MODULO D LE VENTI REGIONI ITALIANE
 a VOLUME 2 CAPITOLO 9 GERMANIA MODULO D LE VENTI REGIONI ITALIANE Cose da sapere A. Le dee mportant Quadro fsco In Europa, a Germana è o stato con pù abtant La Germana è uno stato federae con 16 stat (Lander)
a VOLUME 2 CAPITOLO 9 GERMANIA MODULO D LE VENTI REGIONI ITALIANE Cose da sapere A. Le dee mportant Quadro fsco In Europa, a Germana è o stato con pù abtant La Germana è uno stato federae con 16 stat (Lander)
Progetto Lauree Scientifiche. La corrente elettrica
 Progetto Lauree Scentfche La corrente elettrca Conoscenze d base Forza elettromotrce Corrente Elettrca esstenza e resstvtà Legge d Ohm Crcut 2 Una spra d rame n equlbro elettrostatco In un crcuto semplce
Progetto Lauree Scentfche La corrente elettrca Conoscenze d base Forza elettromotrce Corrente Elettrca esstenza e resstvtà Legge d Ohm Crcut 2 Una spra d rame n equlbro elettrostatco In un crcuto semplce
Calcoli di campo elettrico
 Clcl d cmp elettc Il pncp d svppszne pe l cmp elettc Il cmp elettc genet dlle sgent,, è p ll smm de cp elettc,,... genet dlle sngle sgent: + +... Inftt, mltplcnd mb memb dell euzne pe, s tv ( + +...) +...
Clcl d cmp elettc Il pncp d svppszne pe l cmp elettc Il cmp elettc genet dlle sgent,, è p ll smm de cp elettc,,... genet dlle sngle sgent: + +... Inftt, mltplcnd mb memb dell euzne pe, s tv ( + +...) +...
3. Esercitazioni di Teoria delle code
 3. Eserctazon d Teora delle code Poltecnco d Torno Pagna d 33 Prevsone degl effett d una decsone S ndvduano due tpologe d problem: statc: l problema non vara nel breve perodo dnamc: l problema vara Come
3. Eserctazon d Teora delle code Poltecnco d Torno Pagna d 33 Prevsone degl effett d una decsone S ndvduano due tpologe d problem: statc: l problema non vara nel breve perodo dnamc: l problema vara Come
SICAV: LUOGHI DI VENTURA.2 REPORT OPERATIVO
 CV: UOGH D VENTU.2 EPOT OPETVO CHN - HONG KONG - TWN - KOE - JPN valori del redatto in data 1/12/217 4/12/217 e sottoscritto alle ore 12.25 da Edoardo E. Macallè Corto Maltese vs "il Monakos " Νικκαια
CV: UOGH D VENTU.2 EPOT OPETVO CHN - HONG KONG - TWN - KOE - JPN valori del redatto in data 1/12/217 4/12/217 e sottoscritto alle ore 12.25 da Edoardo E. Macallè Corto Maltese vs "il Monakos " Νικκαια
Elemento Finito (FE) per travi 2D
 Eemento Fnto (FE) per trav D Govann Formca corso d Cacoo Automatco dee Strutture AA. 9/1 Premesse a modeo modeo fsco prncp d banco e dsspazone { Pest P nt = { q u S u = P nt φ modeo smuato (dscretzzazone)
Eemento Fnto (FE) per trav D Govann Formca corso d Cacoo Automatco dee Strutture AA. 9/1 Premesse a modeo modeo fsco prncp d banco e dsspazone { Pest P nt = { q u S u = P nt φ modeo smuato (dscretzzazone)
COMUNE DI BORGETTO (Città Metropolitana di Palermo)
 OMU D BORGTTO à Mep e).y.. O, 4. V 518510821 Te. 091898109 e see. e@pe. u. e e e@ue. e.p. 2 ^ e R U.GG. U eee DTRMZO. / e,s /, /) Oe ee De e esee e Ree e essee Ree S e 5 ee201. Lue pes pe se eee. L O R
OMU D BORGTTO à Mep e).y.. O, 4. V 518510821 Te. 091898109 e see. e@pe. u. e e e@ue. e.p. 2 ^ e R U.GG. U eee DTRMZO. / e,s /, /) Oe ee De e esee e Ree e essee Ree S e 5 ee201. Lue pes pe se eee. L O R
, m = = = è la risultante delle sole forze esterne, dal momento che quella delle forze interne è nulla
 Eseczo l cento d ss () d un sste d punt tel è un punto geoetco l cu poszone spetto d un sste d feento è ndvdut dl ggo vettoe:, dove ed ppesentno spettvente le sse e vetto poszone de sngol punt tel che
Eseczo l cento d ss () d un sste d punt tel è un punto geoetco l cu poszone spetto d un sste d feento è ndvdut dl ggo vettoe:, dove ed ppesentno spettvente le sse e vetto poszone de sngol punt tel che
Richiami di modelli di utilità aleatoria
 Corso d LOGISTICA TERRITORIALE www.unroma.t/ddattca/lt DOCENTE prof. ng. Agostno Nuzzolo Rcham d modell d utltà aleatora prof. ng. Agostno Nuzzolo - Corso d Logstca Terrtorale Modell d domanda e utltà
Corso d LOGISTICA TERRITORIALE www.unroma.t/ddattca/lt DOCENTE prof. ng. Agostno Nuzzolo Rcham d modell d utltà aleatora prof. ng. Agostno Nuzzolo - Corso d Logstca Terrtorale Modell d domanda e utltà
DI SAN MARCELLIN COMUNE. Importo. Riferimento normativo. Oggetto. Fondo Contratto Decentrato ^ CCNL 22/01/04 art. 31 -c. 2
 v COMUNE Fondo Contratto Decentrato ^ D SAN MARCELLN [Data nov-13ì Oggetto Rfermento normatvo mporto Totale delle rsorse d natura stable al 22.1.2004 CCNL 22/01/04 art. 31 -c. 2 COMUNE D SAN MARCELLNO
v COMUNE Fondo Contratto Decentrato ^ D SAN MARCELLN [Data nov-13ì Oggetto Rfermento normatvo mporto Totale delle rsorse d natura stable al 22.1.2004 CCNL 22/01/04 art. 31 -c. 2 COMUNE D SAN MARCELLNO
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
I vettori. a b. 180 α B A. Un segmento orientato è un segmento su cui è stato fissato un verso. di percorrenza, da verso oppure da verso.
 I vettor B Un segmento orentto è un segmento su cu è stto fssto un verso B d percorrenz, d verso oppure d verso. A A Il segmento orentto d verso è ndcto con l smolo. Due segment orentt che hnno l stess
I vettor B Un segmento orentto è un segmento su cu è stto fssto un verso B d percorrenz, d verso oppure d verso. A A Il segmento orentto d verso è ndcto con l smolo. Due segment orentt che hnno l stess
PROPRIETÀ DEL CAMPO ELETTROSTATICO (PARTE 2) G. Pugliese 1
 PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
Lezione 19. Elementi interi ed estensioni intere.
 Lezoe 9 Peequst: Modul ftamete geeat Elemet algebc Elemet te ed esteso tee Sa A u aello commutatvo utao sa B u suo sottoaello Tutt sottoaell cosdeat coteao l utà moltplcatva d A Defzoe 9 U elemeto α A
Lezoe 9 Peequst: Modul ftamete geeat Elemet algebc Elemet te ed esteso tee Sa A u aello commutatvo utao sa B u suo sottoaello Tutt sottoaell cosdeat coteao l utà moltplcatva d A Defzoe 9 U elemeto α A
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE. (Metodo delle Osservazioni Indirette) - 1 -
 PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
Iscrizione N: MI04258 Il Presidente della Sezione regionale della Lombardia dell'albo Nazionale Gestori Ambientali
 Abo Nazonae Gesto Ambenta SEZONE REGONALE DELLA LOMBARDA sttuta pesso a Camea d Commeco ndusta Atganato e Agcotua d MLANO Va Meavg, 9/B Dss 6 sczone N: M48 Pesdente dea Sezone egonae dea Lombada de'abo
Abo Nazonae Gesto Ambenta SEZONE REGONALE DELLA LOMBARDA sttuta pesso a Camea d Commeco ndusta Atganato e Agcotua d MLANO Va Meavg, 9/B Dss 6 sczone N: M48 Pesdente dea Sezone egonae dea Lombada de'abo
TRATTATO CHE ISTITUISCE LA C.E. Allegato 1)
 TRATTATO CHE ISTITUISCE LA C.E. Ago 1) Ago 2) GIURISPRUDENZA COMUNITARIA Ago 3) BIBLIOGRAFIA Gmbno G * Cobn G. L nomv u ng mpn : 3 o 1) Obbgo d u u voo I G o n d I ng. 2 / 1 / 19 79p. 7 2
TRATTATO CHE ISTITUISCE LA C.E. Ago 1) Ago 2) GIURISPRUDENZA COMUNITARIA Ago 3) BIBLIOGRAFIA Gmbno G * Cobn G. L nomv u ng mpn : 3 o 1) Obbgo d u u voo I G o n d I ng. 2 / 1 / 19 79p. 7 2
Lezione 5: descrizione qualitativa e quantitativa dei fenomeni magnetici. VII secolo: magnetite (FeO.Fe 2 O 3 ) attira limatura di ferro:
 Lezone 5: desczone quatatva e quanttatva de fenomen magnetc enomen magnetc VII secoo: magnette (eo.e O 3 ) atta matua d feo: ápopetà non unfome ne mateae; ás manfesta n detemnate pat. campon cndc (magnet)
Lezone 5: desczone quatatva e quanttatva de fenomen magnetc enomen magnetc VII secoo: magnette (eo.e O 3 ) atta matua d feo: ápopetà non unfome ne mateae; ás manfesta n detemnate pat. campon cndc (magnet)
ECOSFERA SERVIZI. Ecosfera Servizi opera nel campo della progettazione e gestione integrata di servizi agli immobili
 ECOSFERA SERVIZI Ecofea Sevz opea ne campo dea pogeazone e geone negaa d evz ag mmob La oceà vana un epeenza conodaa e unca ne eoe pe ampezza deo peo d azone, a eeà d appocco e a compeenza pecfca S popone
ECOSFERA SERVIZI Ecofea Sevz opea ne campo dea pogeazone e geone negaa d evz ag mmob La oceà vana un epeenza conodaa e unca ne eoe pe ampezza deo peo d azone, a eeà d appocco e a compeenza pecfca S popone
IMPOSTA COMUNALE sugli IMMOBILI
 OMUNE DI EGGIO ALABIA Uffc Tut II IMPOSTA OMUNALE su IMMOBILI ------ TABELLE DEI VALOI DEI TEENI IDONEI ALLA EDIFIAZIONE O SOGGETTI AD ESPOPIO A fn d cc d Impst mun su Imm ( t. 6 d mnt mun p dscpn d II)
OMUNE DI EGGIO ALABIA Uffc Tut II IMPOSTA OMUNALE su IMMOBILI ------ TABELLE DEI VALOI DEI TEENI IDONEI ALLA EDIFIAZIONE O SOGGETTI AD ESPOPIO A fn d cc d Impst mun su Imm ( t. 6 d mnt mun p dscpn d II)
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Provincia di Terni DETERMINAZIONE DIRIGENZIALE. Repertorio Generale delle Determinazioni dirigenziali n. 114 del 27/02/2015
 Tit. SETTRE: DIRIGENTE: SERVIZI: Ambiente e Difesa de Suoo Arch. Donatea Venti Gestione amm.va contabie Repertorio U.. dee determinazioni dirigenziai n. 2 de 26/01/2015 GGETT: Piano di Azione Ambientae
Tit. SETTRE: DIRIGENTE: SERVIZI: Ambiente e Difesa de Suoo Arch. Donatea Venti Gestione amm.va contabie Repertorio U.. dee determinazioni dirigenziai n. 2 de 26/01/2015 GGETT: Piano di Azione Ambientae
MODELLI DI UTILITÀ ALEATORIA
 corso d Teora e Tecnca della Crcolazone + Trasport e Terrtoro a.a. 2012-2013 MODELLI DI UTILITÀ ALEATORIA PROF. ING. UMBERTO CRISALLI Dpartmento d Ingegnera dell Impresa crsall@ng.unroma2.t Modell d utltà
corso d Teora e Tecnca della Crcolazone + Trasport e Terrtoro a.a. 2012-2013 MODELLI DI UTILITÀ ALEATORIA PROF. ING. UMBERTO CRISALLI Dpartmento d Ingegnera dell Impresa crsall@ng.unroma2.t Modell d utltà
I equazione cardinale della dinamica
 I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
Algebra vettoriale: un breve formulario. E r
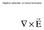 slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
~genzia ~ .l.;lntrate~ Il modello F24 "enti pubblici" (F24 EP)
 Aegato ~genza ~..;Lntrate~ I modeo F24 "ent pubbc" (F24 EP) PREMESSA modeo F24 "ent pubbc" (F24 EP) è o strumento che g ent ttoar d contabtà speca d tesorera mùca devono utzzare per esegure versament dee
Aegato ~genza ~..;Lntrate~ I modeo F24 "ent pubbc" (F24 EP) PREMESSA modeo F24 "ent pubbc" (F24 EP) è o strumento che g ent ttoar d contabtà speca d tesorera mùca devono utzzare per esegure versament dee
V Stage. Astronomia. V Stage. Astronomia. "Il cielo negli occhi, le stelle nel cuore" Gennaio-Giugno 2016
 Gennao-Gugno 2016 V Stage d Astonoma "Il celo negl occh, le stelle nel cuoe" pe student DELLA scuola secondaria superiore DELLA CLAsse IV INTEREssATI ALL astronomia CORSO DI ASTRONOMIA BASE LEZIONI DI
Gennao-Gugno 2016 V Stage d Astonoma "Il celo negl occh, le stelle nel cuoe" pe student DELLA scuola secondaria superiore DELLA CLAsse IV INTEREssATI ALL astronomia CORSO DI ASTRONOMIA BASE LEZIONI DI
Teoremi su correnti e tensioni
 Teorem su corrent e tenson 1) ombnzone lnere efnzone: n un crcuto, ogn corrente e tensone è dt un combnzone lnere d genertor: V = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... I = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... oe
Teorem su corrent e tenson 1) ombnzone lnere efnzone: n un crcuto, ogn corrente e tensone è dt un combnzone lnere d genertor: V = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... I = K 1 $ g 1 K 2 $ g 2 K 3 $ g 3... oe
Modellazione e Identificazione Dinamica della Cupola della Basilica di S. Gaudenzio in Novara
 Modellzone e Identfczone Dnmc dell Cupol dell Bslc d S. Gudenzo n Novr Ing. Slvno Erlcher Sommro Nell prm prte dell rtcolo s present un modello gl element fnt dell Cupol dell Bslc d S. Gudenzo. S mostrno
Modellzone e Identfczone Dnmc dell Cupol dell Bslc d S. Gudenzo n Novr Ing. Slvno Erlcher Sommro Nell prm prte dell rtcolo s present un modello gl element fnt dell Cupol dell Bslc d S. Gudenzo. S mostrno
Centro di massa. Coppia di forze. Condizioni di equilibrio. Statica Fisica Sc.Tecn. Natura. P.Montagna Aprile pag.1
 L EQUILIBRIO LEQU L Corpo rgdo Centro d massa Equlbro Coppa d forze Momento d una forza Condzon d equlbro Leve pag.1 Corpo esteso so e corpo rgdo Punto materale: corpo senza dmenson (approx.deale) Corpo
L EQUILIBRIO LEQU L Corpo rgdo Centro d massa Equlbro Coppa d forze Momento d una forza Condzon d equlbro Leve pag.1 Corpo esteso so e corpo rgdo Punto materale: corpo senza dmenson (approx.deale) Corpo
DIPLOMA A DISTANZA IN INGEGNERIA ELETTRICA CORSO DI ELETTRONICA INDUSTRIALE DI POTENZA II Lezione 35
 DIPOMA A DISTANZA IN INGEGNERIA EETTRICA CORSO DI EETTRONICA INDUSTRIAE DI POTENZA II ezone 35 Compensator Statc d Potenza Reattva Seconda Parte Paolo Mattavell Dpartmento d Ingegnera Elettrca Unverstá
DIPOMA A DISTANZA IN INGEGNERIA EETTRICA CORSO DI EETTRONICA INDUSTRIAE DI POTENZA II ezone 35 Compensator Statc d Potenza Reattva Seconda Parte Paolo Mattavell Dpartmento d Ingegnera Elettrca Unverstá
Vedendo amor. j œ j. j œ œ j. j œ. j œ. j œ. r œ. r œ. j œ. j œ. j œ. j œ. j œ
 Ve - den - doia - mo he pe me te - seiin - va - no, a - 3 ve - va le - sue e - ti e he, fug - gi - toia a - so di sua 5 ma - no pas - sa - vaii gio - ni miei on - ten - tiie n 7 lie - ti, ten - to die
Ve - den - doia - mo he pe me te - seiin - va - no, a - 3 ve - va le - sue e - ti e he, fug - gi - toia a - so di sua 5 ma - no pas - sa - vaii gio - ni miei on - ten - tiie n 7 lie - ti, ten - to die
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione marzo 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Unità Didattica N 5 Il riferimento cartesiano
 01 Mtemtc Lceo \ Untà Ddttc N 5 : l femento ctesno 1 Untà Ddttc N 5 Il femento ctesno 01) Coodnt scss 0) Coodnte ctesne nel pno 03) Ve spece d sstem d femento 04) Rppesentzone ctesn d un vettoe 05) Le
01 Mtemtc Lceo \ Untà Ddttc N 5 : l femento ctesno 1 Untà Ddttc N 5 Il femento ctesno 01) Coodnt scss 0) Coodnte ctesne nel pno 03) Ve spece d sstem d femento 04) Rppesentzone ctesn d un vettoe 05) Le
PREMESSA . SPAZI URBANI EDIFICI PUBBLICI
 Nuovo Rego men o U bn s co ComunedB g P ov nc dlucc S ndco:rg.m cobon n Assesso e U bn s c:avv.a be og ovnne G n ede Comun cz one:do. ssc cepogg G uppodlvo o:a easse odete o o Responsb ea ee esponsb edep
Nuovo Rego men o U bn s co ComunedB g P ov nc dlucc S ndco:rg.m cobon n Assesso e U bn s c:avv.a be og ovnne G n ede Comun cz one:do. ssc cepogg G uppodlvo o:a easse odete o o Responsb ea ee esponsb edep
RORY 140 x 70 cm 140 x 80 cm
 1 140 x 70 cm 140 x 80 cm 1 150 x 70 cm 150 x 80 cm 1 160 x 70 cm 160 x 80 cm 1 170 x 70 cm 170 x 80 cm 2 140 x 70 cm 140 x 80 cm 2 150 x 70 cm 150 x 80 cm 2 160 x 70 cm 160 x 80 cm 2 170 x 70 cm 170 x
1 140 x 70 cm 140 x 80 cm 1 150 x 70 cm 150 x 80 cm 1 160 x 70 cm 160 x 80 cm 1 170 x 70 cm 170 x 80 cm 2 140 x 70 cm 140 x 80 cm 2 150 x 70 cm 150 x 80 cm 2 160 x 70 cm 160 x 80 cm 2 170 x 70 cm 170 x
GOMITO 90 TESTA/TESTA PE 80
 GOMITO 90 TESTA/TESTA PE 80 garantita a parità di spessore fra PE diversi; PE 80 PE 100 PE 100 PE 100 PN 8 PN 10 PN 16 PN 25 20 49 75 n.d. n.d. 30 n.d. 25 61 80 n.d. n.d. 45 n.d. 32 60 81 n.d. n.d. 55
GOMITO 90 TESTA/TESTA PE 80 garantita a parità di spessore fra PE diversi; PE 80 PE 100 PE 100 PE 100 PN 8 PN 10 PN 16 PN 25 20 49 75 n.d. n.d. 30 n.d. 25 61 80 n.d. n.d. 45 n.d. 32 60 81 n.d. n.d. 55
Codice di Stoccaggio Capitolo 7 Bilanciamento e reintegrazione dello stoccaggio
 Codce d Stoccaggo Captolo 7 Blancamento e rentegrazone dello stoccaggo 7.4 Corrspettv per servz d stoccaggo L UTENTE è tenuto a corrspondere a STOGIT, per la prestazone de servz, gl mport dervant dall
Codce d Stoccaggo Captolo 7 Blancamento e rentegrazone dello stoccaggo 7.4 Corrspettv per servz d stoccaggo L UTENTE è tenuto a corrspondere a STOGIT, per la prestazone de servz, gl mport dervant dall
Insegnare oggi Perché sembra così difficile? Bologna, 28 gennaio 2015
 Insegnare oggi Perché sembra così difficile? Giancarlo Cerini Bologna, 28 gennaio 2015 1 Tutti sanno dare consigli agli insegnant Più compiti e più severità Sii comprensiv o No, stai sbagliando Più ascolto
Insegnare oggi Perché sembra così difficile? Giancarlo Cerini Bologna, 28 gennaio 2015 1 Tutti sanno dare consigli agli insegnant Più compiti e più severità Sii comprensiv o No, stai sbagliando Più ascolto
Problemi di Fisica. Principio conservazione momento angolare
 www.lceoweb.t Prnc d Conserzone Problem d Fsc Prnco conserzone momento ngolre www.lceoweb.t Prnc d Conserzone TEORIA Per un coro untorme m che ruot su un crconerenz d rggo R con eloctà costnte, l momento
www.lceoweb.t Prnc d Conserzone Problem d Fsc Prnco conserzone momento ngolre www.lceoweb.t Prnc d Conserzone TEORIA Per un coro untorme m che ruot su un crconerenz d rggo R con eloctà costnte, l momento
1 VETTORI. 1.1 Operazioni tra vettori
 1 VETTORI Ttte le gndee pe l ci definiione non concoono lti elementi l di foi dell loo mis engono dette gndee scli; sono esempi di gndee scli l intello di tempo l mss l tempet ecc Esistono ttti delle gndee
1 VETTORI Ttte le gndee pe l ci definiione non concoono lti elementi l di foi dell loo mis engono dette gndee scli; sono esempi di gndee scli l intello di tempo l mss l tempet ecc Esistono ttti delle gndee
IL RUMORE NEGLI AMPLIFICATORI
 IL RUMORE EGLI AMPLIICATORI Defnzon S defnsce rumore elettrco (electrcal nose) l'effetto delle fluttuazon d corrente e/o d tensone sempre present a termnal degl element crcutal e de dspostv elettronc.
IL RUMORE EGLI AMPLIICATORI Defnzon S defnsce rumore elettrco (electrcal nose) l'effetto delle fluttuazon d corrente e/o d tensone sempre present a termnal degl element crcutal e de dspostv elettronc.
REGIONE CODICE PROVINCIA MESE PRESENTAZIONE NUMERO DOMANDE ACCOLTE
 REGIONE CODICE PROVINCIA MESE PRESENTAZIONE NUMERO DOMANDE ACCOLTE ABRUZZO AQ mar-19 3.190 ABRUZZO AQ apr-19 608 ABRUZZO AQ mag-19 0 ABRUZZO CH mar-19 3.441 ABRUZZO CH apr-19 672 ABRUZZO CH mag-19 0 ABRUZZO
REGIONE CODICE PROVINCIA MESE PRESENTAZIONE NUMERO DOMANDE ACCOLTE ABRUZZO AQ mar-19 3.190 ABRUZZO AQ apr-19 608 ABRUZZO AQ mag-19 0 ABRUZZO CH mar-19 3.441 ABRUZZO CH apr-19 672 ABRUZZO CH mag-19 0 ABRUZZO
Modelli di utilità aleatoria
 corso d Teora de Sstem d Trasporto Modell d utltà aleatora PROF. ING. UMBERTO CRISALLI Dpartmento d Ingegnera dell Impresa crsall@ng.unroma.t Iscrzone al corso Modell d offerta ü Da effettuars anche on
corso d Teora de Sstem d Trasporto Modell d utltà aleatora PROF. ING. UMBERTO CRISALLI Dpartmento d Ingegnera dell Impresa crsall@ng.unroma.t Iscrzone al corso Modell d offerta ü Da effettuars anche on
ointroduzione operché i significati? oontologia e Social Software oblog di scuola3d otagging geografico e gerarchie rappresentate osemacode e Wiki
 U cmtà per cstre cettv d sfct Isttt pedc d s.fr@sc.t-de.t Itrde Perché sfct? Ot e Sc Sftwre d sc3d T erfc e errche rppresette Semcde e Wk Sftwre ber e Ope Srce per 'e-er: stt de'rte e svpp ftr U cmtà per
U cmtà per cstre cettv d sfct Isttt pedc d s.fr@sc.t-de.t Itrde Perché sfct? Ot e Sc Sftwre d sc3d T erfc e errche rppresette Semcde e Wk Sftwre ber e Ope Srce per 'e-er: stt de'rte e svpp ftr U cmtà per
Sviluppo dell algoritmo per l allineamento dello spettrometro magnetico di PAMELA
 Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
PIOVE DI SACCO (Padova)
 ORGNE CENTRO RESDENZE PERNZN UMBERT g» 35028 POE D SCCO (Padova) N 88 de 25/03/2014 Segetao Dettoe d questo sttuto Pen Dottssa Emanuea a sens de Dgs n 165/ 2001 dee successve dsoszon d egge n matea vgent
ORGNE CENTRO RESDENZE PERNZN UMBERT g» 35028 POE D SCCO (Padova) N 88 de 25/03/2014 Segetao Dettoe d questo sttuto Pen Dottssa Emanuea a sens de Dgs n 165/ 2001 dee successve dsoszon d egge n matea vgent

