Statistica I, Ing. Gestionale, a.a. 2009/10 Registro delle lezioni
|
|
|
- Rossana Bassi
- 5 anni fa
- Visualizzazioni
Transcript
1 Statistica I, Ig. Gestioale, a.a. 9/1 Registro delle lezioi Lezioe 1 (/3). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli, Si osserva che ci soo tre corsi a carattere statistico el percorso di Gestioale a Pisa, ovvero Statistica I alla trieale, Statistica II alla magistrale, Statistica Applicata (Prof. Lazetta) tra i facoltativi della trieale, corsi coordiati ta loro. La statistica si può grosso modo dividere i Statistica descrittiva da u lato, e Statistica basata sul Calcolo delle Probabilità dall altro. Il capitolo del Ross è dedicato al primo argometo. Si cosiglia la lettura del paragrafo. i relazioe ai temi trattati i questa lezioe. Gli altri capitoli putao alla Statistica basata sul Calcolo delle Probabilità, sempre aiutadosi comuque co le idee pratiche e gra che della statistica descrittiva. Si suggerisce u po di uso del programma di calcolo R per capire più i coceto alcui argometi del corso. Esercizio. i) Scaricare R da rete (basta cercare R stat co Google). ii) ritracciare le temperature di alcue città italiae e scriverle el comado T<-c(.,...,.) iii) eseguire i comadi mea(t), sd(t), hist(t), hist(t,k) per qualche k, hist(t,freq=true). Vegoo descritte le formule per la media x e la deviazioe stadard S di u campioe x 1 ; :::; x e la variate x = x 1 + ::: + x ; S = X jx i i=1 xj X (x k x) : (che potremmo chiamare media delle distaze dalla media ). Etrambi soo idicatori che quati cao l icertezza (la dispersioe, la casualità, l aleatorietà, la variabilità, dei dati ecc.). Viee spiegata la di ereza tra istogramma assoluto (quello di hist(t)) e relativo (quello di hist(t,freq=false)). Viee evideziato l aspetto cotigete degli istogrammi, dipedete dai dati speci ci o altri dettagli come il umero di dati o il umero di classi. 1 k=1
2 Emerge come aturale l idea che dietro agli istogrammi coi loro dettagli accidetali ci sia ua curva più regolare che descrive il feomeo sico. Questo itroduce il cocetto di desità di probabilità (pdf) (de izioe 4..). Viee itrodotta la desità gaussiaa stadard (par. 5.5). La speci ca freq=false egli istogrammi serve ad otteere area uo sotto l istogramma, i modo che sia cofrotabile co la desità, es. gaussiaa. Viee descritto (a titolo facoltativo) il calcolo co cui si veri ca che f (x) = 1 p e x è ua pdf: Z 1 e x 1 dx = Z 1 Z 1 = 1 1 Z 1 e x e y dxdy = Z e t dt = : d Z 1 e d Lezioe (3/3). Ceo di studio di fuzioe per ricooscere il gra co di f (x) = p 1 e x. Comadi di R per otteeerlo: X=-4+(1:8)/1 Y=dorm(X,,1) plot(x,y) Gaussiae qualsiasi, di parametri e : gra co, somigliaze e di ereze rispetto al caso stadard, i particolare il ruolo di (esempi gra ci), veri ca della proprietà di area uo (col cambio di variabile y = x ). La trasformazioe y = x : sigi cato gra co, stadardizzazioe. Come scegliere e a partire da u campioe sperimetale x 1 ; :::; x? L idea è che e (che immagiiamo essere i parametri veri di u modello) soo approssimati dai umeri empirici (sperimetali) x ed S. Ricooscimeto che misura la dispersioe del gra co gaussiao. Lezioe 3 (4/3). Richiamo su quato visto o ad ora: dato u campioe sperimetale x 1 ; :::; x, da esso possiamo calcolare u istogramma, x ed S, e co questi costruire ua gaussiaa. A cosa può servire? Immagiiamo ad esempio di vedere u certo prodotto e voler teere ua riserva per accotetare tutti o quasi i clieti. Quato deve essere ampia la riserva? Se dispoiamo di u campioe delle richieste passate della clietela, relative a quel prodotto, possiamo estrapolare ua desità (per ora gaussiaa) el modo detto sopra, e calcolare il umero alla cui destra sta u area di ampiezza da oi decisa a priori, es. 5%. La probabilità che le richieste superio è il 5%. Nel 95% dei casi le richeiste sarao iferiori
3 a. Questo è il valore che terremo ella riserva, se abbiamo deciso a priori di correre u rischio del 5%. Vedremo meglio più avati che tale valore si chiama quatile di ordie.95 e si calcola col comado qorm(.95,m,s). Si oti per iciso che dispoedo di u campioe di umerisotà 1, avrebbe seso evitare le gaussiae e predere come u umero alla cui destra stao gli ultimi 5 valori più gradi del campioe. Fatte le dovute proporzioi, si può usare lo stesso metodo co campioi di umerosità diversa, ma se la umerosità è troppo bassa divetao troppo pochi i valori alla destra di ed il metodo perde di sigi cato o a dabilità. Si iizia lo studio del capitolo 3, sui fodameti del calcolo delle probabilità. Dopo le de izioi di uiverso, eveti, eveti elemetari e probabilità, e l illustrazioe delle varie regole (esempli cate ituitivamete col cocetto di massa), si tora alle pdf, prededo come esempio di uiverso tutto R, come eveti gli itervalli o isiemi più geerici e come probabilità di u isieme A l area sottesa dalla pdf su A, ovvero R f (x) dx. Le regole delle probabilità A soo veri cate. L eveto le richieste superao è u esempio. Viee poi descritto il cocetto di probabilità uiforme su uo spazio ito, esempli cadolo col problema del lacio di due dadi. Si cofrotao i due esempi ( ito e cotiuo): el caso ito i sigoli eveti elemetari hao probabilità o ulla e che geera la probabilità di ogi altro eveto, per somma; el caso cotiuo ogi puto ha probabilità ulla, quidi o è sigi cativo. Si coclude co u esempio speciale di spazio ito. Si cosiderao persoe, ciascua che può scegliere ua possibilità A o B, codi cate co 1 o. Ciascua persoa sceglie 1 co probabilità p, uguale per tutte le persoe. Gli eveti elemetari di S soo le strighe di e 1. Se ua striga ha k umeri uguali a 1, la sua probabilità è p k (1 p) k : Capiremo meglio questa formula del prodotto e trarremo le cosegueze di questo calcolo. Lezioe 4 (9/3). Probabilità codizioale, iterpretazioe ituitiva e gra ca. Idipedeza tra eveti, legame co la probabilità codizioale (A e B soo idipedeti se e solo se P (AjB) = P (A), se e solo se P (BjA) = P (B), quado P (B) > e P (A) > ). Di ereza rispetto al cocetto di eveti disgiuti. Spiegazioe della formula p k (1 p) k, tramite l idipedeza. Formula di fattorizzazioe. 3
4 Esercizio: vedite di vio a F (5%) e G (5%); le vedite a F riguardao vio B per i 3/4; le vedite a G riguardao vio B per 1/4. Che probabilità c è di vedere vio B? (Soluzioe co la formula delle probabilità totali). Calcolo combiatorio: pricipio di eumerazioe, disposizioi, permutazioi e combiazioi. Lezioe 5 (1/3). Formula di Bayes. Esercizio. Se ua fotocopiatrice può fare cattive fotocopie sia per surriscaldameto (S) sia per dispersioe di toer (D), se tra i due problemi S accade il 7% delle volte e D il 3%, se quado accade S le fotocopie vegoo male il % metre se accade D l 8% delle volte, quado osserviamo ua fotocopia veuta male, è più probabile che sia a causa di S o D? Esercizio. Se ua baca ha 1 corretisti, idipedeti, ciascuo che si preseta durate u gioro co probabilità p, che probabilità c è che si presetio corretisti? Ricordado che p (1 p) 1 è la probabilità di ua be precisa vetia di corretisti, e che il umero di vetie è 1, la probabilità richiesta è 1 p (1 p) 1. Lezioe 6 (11/3). Cocetto di variabile aleatoria, esposto attraverso esempi (es. tempo di vita, quatità veduta i futuro, costo futuro di u bee). V.a. discrete e cotiue. Rappresetazioe gra ca di v.a. discrete, tramite lista dei valori e delle loro probabilità. La successioe (p k ) viee detta fuzioe massa di probabilità. Devoo essere umeri a somma 1. Gra co della massa. Esempi: Beroulli e biomiale (veri ca di somma 1 usado il biomio di Newto). Simbolo X B (; p) (Beroulli: B (1; p)). Vedremo u altro legame tra i due. Si rammetao le formule ( 1) ( k + 1)! = = k k! k! ( k)! ed i casi particolari = 1, = 1, 1 =, 1 =, usati per esempli care p ; p 1 ; p 1 ; p della biomiale. Diversi gra ci della biomiale, a secoda del valore di p. Si rammeta che il umero p k = k p k (1 p) k è la probabilità che i ua sequeza luga di e 1 ci siao k valori 1, suppoedo idipedeti i valori e probabilità p di avere 1. V.a. cotiue, fuzioe desità di probabilità (pdf), P (X I) = R f (x) dx. I Esempi: uiforme su [a; b], espoeziale di parametro. I etrambi i casi abbiamo calcolato ua certa costate impoedo area 1. Fuzioe di ripartizioe (detta ache fuzioe di distribuzioe cumulativa, cumulative distributio fuctio, cdf): F (t) = P (X t). Ha seso 4
5 sia per le discrete sia per le cotiue, cioè ui ca u po le teorie. Nel caso cotiuo si lega alla pdf f i due modi: e F (t) = Z t f (x) dx F (t) = f (t) ei puti i cui f è cotiua, e quidi F è derivabile. Lezioe 7 (16/3). De izioe di valor medio per v.a. discrete. Esempio B (1; p), esempio di variabile che vale 1; ; 1 co ugual probabilità ed altri esempi. Iterpretazioe gra ca (media pesata dei valori, baricetro, cetro di massa, comuque sull asse delle ascisse). Esempio: B (; p) co calcoli espliciti; ceo: E [X] = X k p k (1 p) k = X! k (k 1)! ( k)! pk (1 p) k = X ( 1)! (k 1)! ( k)! pk (1 p) k = p X ( 1)! (k 1)! ( k)! pk 1 (1 p) k = p (p + (1 p)) 1 = p: Richiamo sul cocetto di media aritmetica x = x 1+:::+x sperimetale. Legame tra i due cocetti: di u campioe x 1 + ::: + x ( + ::: + ) + ::: + (k + ::: + k) + ::: = = + ::: + k k + ::: dove k è il umero di elemeti x i uguali a k. Se ipotizziamo che le frequeze empiriche k (quelle degli istogrammi) siao prossime alle probabilità teoriche p k (quelle della fuzioe massa di probabilità), allora la somma precedete è circa uguale a p + ::: + p k k + ::: = E [X] : De izioe di v.a. idipedeti: P (X 1 I 1 ; :::; X I ) = Y P (X i I i ) i=1 5
6 per ogi sequeza di isiemi I 1 ; :::; I. Se soo v.a. discrete, è su ciete predere come isiemi I 1 ; :::; I i puti: P (X 1 = a 1 ; :::; X = a ) = Y P (X i = a i ) i=1 per ogi sequeza di puti a 1 ; :::; a. Teorema 1: se X 1 ; :::; X soo idipedeti B (1; p), allora S = X 1 +:::+X è ua B (; p). Dimostrazioe: si osserva che l eveto (S = k) è l uioe degli eveti che speci cao esattamete quali k delle X i soo uguali a 1. Ciascuo di tali eveti, ad es. (X 1 = 1; :::; X k = 1; X k+1 = ; :::; X = ) per l idipedeza ha probabilità data dal prodotto, ad es. P (:::) = Y P (X i = a i ) = p k (1 p) k i=1 essedoci k valori a i uguali ad 1. Il umero degli eveti di questo tipo è k. Quidi la probabilità complessiva è la somma di k valori di probabilità, tutti però uguali a p k (1 p) k, quidi k p k (1 p) k. Teorema : liearità del valor medio. Osservazioe: o richiede l ipotesi di idipedeza. Teorema 3: se X; Y soo idipedeti, allora E [XY ] = E [X] E [Y ]. Osservazioe: il viceversa o è vero: da questa sigola codizioe o si riesce a dedurre la sequeza di codizioi che de isce l idipedeza. Esempio: dimostrazioe che per X B (; p) vale E [X] = p, usado i teoremi 1 e. Lezioe 8 (17/3). Valor medio per v.a. cotiue. Esempi: uiforme, espoeziale, gaussiaa. Iterpretazioe gra ca. De izioi di mediaa e moda, osservazioi sul legame co la media. Valor medio di trasformazioi: esempio di E [X ] e E [X 3 ] i u caso discreto. Lezioe 9 (18/3). Valor medio di ua trasformazioe: E [' (X)] = X ' (a k ) p k ; E [' (X)] = Z 1 1 ' (x) f (x) dx 6
7 ei dua casi, cotiuo e discreto. Casi particolari rilevati: mometi di ordie k, E X k, e variaza V ar [X] = E (X ) dove = E [X]. E lo scarto quadratico medio. Media di ua costate: uguale alla costate. Usado questo e la liearità si trova la formula V ar [X] = E [X ]. Note: E [X ] sempre; E [X ] = solo se X è costate (quidi uguale alla sua media). Calcolo della variaza per la Beroulli. De izioe di covariaza; geeralizza la variaza; de izioe di v.a. scorrelate; teorema: idipedeti implica scorrelate (equivalete al teorema secodo cui idipedeti implica E [XY ] = E [X] E [Y ]). Formula geerale per la variaza della somma X +Y ; caso particolare quado le v.a. soo idipedeti. Utilità ella gestioe di u portfolio (diversi cazioe degli ivestimeti tra titoli idipedeti). Calcolo della variaza per la biomiale. Implicazioi per esempi co grade umero di uteti idipedeti: piccolo scarto rispetto alla media. Lezioe 1 (3/3). Esercizio 1 del compito di MMS del 6/6/7, parti i), ii), iii), iv), v). Per completare gli ultimi dettagli di alcue domade serve cooscere la variaza di espoeziali e gaussiae, la geeratrice delle espoeziali, il calcolo di probabilità gaussiae co le tavole, che vedremo. Fuzioe geeratrice dei mometi, come si calcolao i mometi, Teorema sulla geeratrice della somma di v.a. idipedeti (co dimostrazioe), esempi di Beroulli, biomiale, gaussiaa. Lezioe 11 (4/3). Teorema: X, Y gaussiae idipedeti, a; b; c umeri reali, implica ax + by + c gaussiaa (co dimostrazioe). Calcolo della sua media e variaza. Stadardizzazioe, i geerale e per le gaussiae; dalle gaussiae qualsiasi alle caoiche. Lezioe 1 (5/3). Fuzioe di ripartizioe, gra co tipico, uso per calcolare probabilità; operazioe iversa: quatili; trasformazioe el caso gaussiao, dalla F alla caoica; calcolo di probabilità e quatili tramite le tavole; esercizi. Formule del tipo q per le soglie (es. scorte di magazzio), assegato il rischio. Ceo alle V.a. di Poisso, media e variaza (per ora seza dimostrazioe e seza geeratrice). Tabella di media, variaza e geeratrice per Beroulli, biomiali, Poisso, espoeziali e gaussiae (per esercizio la variaza di queste due ultime a partire dalla geeratrice; geeratrice delle espoeziali per esercizio). 7
8 Acora da svolgere, su Poisso ed espoeziali: teorema degli eveti rari, macaza di memoria, teorema sul miimo. Esercizi suggeriti sul programma svolto o ad ora: 3/4/8: primi 5 puti secodo compitio 8: primi 3 puti 4/6/8: puti 1,,3,4,6 15/7/8: puti 1,,3,4 16/9/8: puti 1,,3,4,5,6,7,8,9 7/1/9: puti 1,,3,4,5,6,8 17//9: puti 1,,3,4,5,6,7,8 4/5/9: puti 1,3,4,5,8 1/6/9: puti 1,,3,4,5,6,7 /7/9: puti 1,,3,6,7,8,9 17/9/9: puti 1,,3 (provare),8,9,1. Lezioe 13* (8/4). Il testo delle lezioi cotrassegate co * si può trovare alla pagia Itroduzioe alla statistica, campioe, media campioaria e sue proprieta. Teorema limite cetrale co esempi. Lezioe 14* (13/4). Approssimazioe gaussiaa della v.a. biomiale co esempio, distribuzioe della media campioaria. Esempio che fa uso della distribuzioe della media campioaria. Variaza campioaria e suo valore atteso. Lezioe 15* (14/4). Variabile chi quadro e sua applicazioe per la determiazioe della legge dalla variaza campioaria. Lezioe 16* (15/4). Esercizio sull uso della variabile chi quadro. Campioameto aleatorio e sue proprieta. Trattameto statistico delle risposte biarie i u sodaggio. Esercizi vari di statistica. Lezioe 17* (/4). Stima putuale, metodo della massima verosimigliaza, applicazioe alla stima dei parametri della distribuzioe espoeziale e beroulliaa. Altri esempi di applicazioe della massima verosimigliaza per la stima dei parametri della distribuzioe di Poisso, della gaussiaa e della distribuzioe uiforme. Stima di itervalli, cocetto di itervallo di co - deza ed esempio di calcolo per la media di ua distribuzioe gaussiaa. Lezioe 18* (1/4). Itervalli di co deza per la media uilaterali e bileterali (co sigma ota) al variare della co deza e della umerosita campioaria. Lezioe 19* (/4). Utilizzo della t di Studet el calcolo degli itervalli di co deza quado ache la sigma e stimata dai dati. Itervalli di 8
9 co deza per la sigma co l uso della distribuzioe del chi quadro. Itervalli di co deza per la di ereza fra due medie sia el caso di sigma ota che el caso di sigma stimata dai dati. Lezioe * (7/4). Itervalli di co deza per la stima di ua probabilita. Esercizio di ripasso sulla variabile poissoiaa. Itroduzioe alla veri ca delle ipotesi. Ipotesi ulla, ipotesi alterativa, regioe critica, errori di prima e secoda specie, sigi cativita. Come esercizi relativi alle lezioi 13- si suggerisce di esamiare attetamete gli esercizi svolti a lezioe (vedi pdf pag. più i segueti: 3/4/8, puto. 6; 4/8, ultimi due puti; 4/6/8, puti. 5, 7, 9; 4/6/8, puti. 3, 4, 6; 15/7/8, puti. 5, 6, più puti. 1, della pagia seguete; 16/9/8, puti. 1, 11; 17//9, puti. 7, 9; 4/5/9, puto. 7; 1/6/9, puto. 1; /7/9, puti. 3, 5, 1; 17/9/9, puti. 5, 7. Lezioe 1 (8/4). L algoritmo del test (bilaterale) per la media di ua gaussiaa co variaza ota viee esempli cato col seguete esercizio. U certo sistema di servizio (si pesi ad esempio agli sportelli di ua baca) è be dimesioato se ci soo i media 1 richieste al gioro (se soo di più bisoga aumetarlo, se soo di meo si stao sprecado risorse). Forse il mercato è cambiato e le richieste o soo più 1 i media. Si registra u campioe per 9 giori: 98; 11; 13; 96; 18; 115; 1; 99; 19: Al 95%, il servizio è be dimesioato? Si suppoga, sulla base di esperieze passate, che sia = 4. Sol: z = x p 14: 1p = 9 = 3:15 4 maggiore (i valore assoluto) di q 1 = z = 1:96 (vale = :5, = :5, 1 = :975, q :975 = 1:96). Il sistema o è be dimesioato. 9
10 Nella risoluzioe si è iterpretato gra camete il test, tramite ua gaussiaa e le sue code. Si è isistito sul rischio, del 5%, ecessariamete presete. E l area totale delle code. Se o si speci ca tale rischio a priori, o ha seso cofrotare u campioe co ua media ipotizzata. La media empirica x è sempre diversa da, per la casualità del campioe e o perche sia falsa. Quidi il puto è capire se x dista da i modo eccessivo oppure o. Il grado si aomalia della distaza di x da è dato dalle code, idividuate da. Lezioe (9/4). Viee risolto u altro esercizio sul test (esercizio 1 del 7/1/9), commetado di uovo il sigi cato, la ragioevolezza, di ciò che fa il test, i termii gra ci. Se vale l ipotesi H (che i tale esercizio è il umero medio di forme è 5, o più cocisamete = 5 ), la v.a. X è ua N ;. I suoi valori cadoo molto raramete elle due piccole code di area totale.5. Quidi, se il valore empirico x cade proprio i tali code, siamo idotti a cocludere che era sbagliata l ipotesi (perche sotto di essa ua tale cosa o doveva accadere). Quidi il test si può eseguire cotrollado se x cade elle code della gaussiaa N ;. Stadardizzado, lo si può eseguire cotrollado se z = x p cade elle code della gaussiaa caoica, cioè cotrollado se jzj > q 1 : Vegoo poi mostrate alcue variati (alcue iquietati) dell idea precedete, tutte giuste: ivece di predere le due code simmetriche, si cosidera come aomala solo ua coda di ampiezza.5; oppure ua fascia cetrale di ampiezza.5. Questa osservazioe molto critica si capirà meglio più avati. No c è comuque ulla di sbagliato. E l idea geerale dei test, co cui si possoo ivetare tatissimi test validi: se vale l ipotesi H, ua certa gradezza da oi scelta (X o altre), assume valori i certe zoe molto raramete, per cui se l aaloga gradezza empirica lo fa, ri utiamo l ipotesi. Si sottoliea che u test o ri uta H, oppure o è i grado di farlo. No ha seso dire che il test coferma H. Ache questo sarà sempre più chiaro. Cocetto di p-value (valore p). E la probabilità che l idicatore da oi usato assuma valori più estremi di quello empirico. Si ra gura la desità, si disega il valore di x, da esso si trovao le due code corrispo- N ; deti: il p-value è l area di tali code. 1
11 Negli esempi precedeti: X p p = P > x p : Dopo alcui calcoli si trova p = x p : I software calcolao il p-value, o chiedoo. Se il p-value viee piccolo, sigi ca che l idicatore assume raramete valori più estremi di quello empirico. Quidi l ipotesi o è ragioevole. Se si sceglie i aticipo, e si calcola il p-value ivece di eseguire il test, si può dedurre il risultato del test per quel valore di? Sì. se > p, si ri uta H, altrimeti o. Questo viee spiegato gra camete, co la solita desità N ; e le sue code. I e, viee esamiato u esercizio u po diverso. Esercizio. U servizio ferroviario viee cacellato se il umero medio di passeggeri è iferiore a. I passeggeri che viaggiao ad ua certa ora tra Fireze e Pisa vegoo cotati, per 1 giori. I valori soo 17; 13; 9; 3; 14; 1; 16; 11; 14; 1: A livello di sigi catività 95%, c è ragioe di cacellare quel servizio serale? Soluzioe. Si può eseguire il solito test, ma questo o è aderete al problema. Meglio ragioare dall iizio. Se la media è (caso limite), X è ua N ;. Se i valori di X cadoo ella coda destra, o c è ulla di male: può sigi care che il umero medio di passeggeri è ache maggiore di, meglio acora. Il problema sussiste solo se X cade ella coda siistra, cioè assume valori troppo piccoli. Allora è solo la coda siistra che rappreseta la situazioe aomala. Prediamo quidi ua coda siistra di ampiezza.5, seza coda destra. Il test cosiste el vedere se X cade i essa, ovvero, dopo stadardizzazioe, se x p < q1 : Questo test uilaterale è più itelligete di quello solito bilaterale, vista la particolare domada dell esercizio. Questo è u esempio i cui si vede 11
12 l utilità delle variati dette sopra. Capiremo meglio tutto questo col cocetto di poteza di u test. Lezioe 3 (4/5). Approfodimeti sui test statistici. Vegoo formulati due test, uo basato sulla media X (si ri uta quado cade elle code di ua N ; ), l altro basato semplicemete su X stessa, u solo esperimeto (si ri uta quado cade elle code di ua N ( ; )). Ituitivamete, come mai pesiamo che il primo sia migliore? Se le code hao area (es..5) i etrambi i casi, i etrambi abbiamo la stessa probabilità di errore di prima specie: la probabilità che il test ri uti H quado era vera, è. Cosa li distigue? Viee itrodotto il cocetto di errore di secoda specie (accettare H quado è falsa). Viee calcolata la sua probabilità, detta. Ci si accorge che è ua fuzioe della media vera. Attraverso alcui esercizi prelimiari si trova () = p + q1 p q1 Come fuzioe della media vera stadardizzata, più precisamete di d = p la fuzioe è detta curva caratteristica operativa (curva OC). La poteza del test è, per de izioe, 1 (), cioè la probabilità di ri utare H quado è falsa. I due test visti all iizio di eriscoo i poteza. Lo si spiega attraverso l iyerpretazioe gra ca di, che risulta molto più alto per il secodo test. I e, viee cofrotato il caso uilaterale col bilaterale, sempre i termii di o di poteza. Quado si cerca di scoprire che il valor medio è uilateralmete diverso da, il test uilaterale è più potete. Lezioe 4 (5/5). Esercizio (esempio) 8.36 del libro. Svolto sia col test bilaterale sia uilaterale. Spiegazioe gra ca dettagliata del fatto che la poteza è maggiore per il test uilaterale, che quidi è il migliore tra quelli a oi oti (eppure o ha ri utato l ipotesi). Calcolo del valore p. Per tetare di far meglio, l azieda produttrice dell esercizio, el tetativo di arrivare a ri utare l ipotesi (cosa che desidera), potrebbe aumetare la umerosità campioaria. Oppure predere u meo strigete, ma dal calcolo del p- value si vede che gli uici valori di per cui si ri uterebbe l ipotesi o soo propoibili. 1 :
13 Lezioe 5 (6/5). Esercizio: calcolare la poteza del test uilaterale destro. Sol. Se il test ha come ipotesi alterativa H 1 = la media è >, la probabilità () dell errore di secoda specie se la media vera è ua certa > è (dopo alcui calcoli co ausilio del gra co) p () = + q1 : Quidi la poteza è 1 (). Come icide la umerosità sulla poteza? A livello aalitico: più grade implica p più egativo, quidi () più piccolo. Quidi poteza maggiore. Si vede ache a livello gra co, mostrado che al crescere di le gaussiae cetrate i e divetao più cocetrate, e quidi più separate, ecc. Desig Of Experimets (DOE). Si tratta di u ampia teoria che guida alla progettazioe razioale di esperimeti. Qui ci occupiamo solo di u dettaglio, però importatissimo: la scelta della umerosità del campioe da esamiare. Abbiamo visto che i uisce sulla poteza. Quidi la domada è: ssata la sigi catività, scelto il tipo di test (uilaterale, bilaterale, ecc.), quale bisoga scegliere per avere ua certa poteza? O più precisamete, per avere ua certa poteza di osservare ua certa di ereza? Caso uilaterale destro: ssati, e (), es. () = :5, si risolve l equazioe p + q1 = :5 ovvero p + q1 = q :5 da cui si trova. Nota: la soluzioe o è u itero, quidi si prede l itero immediatamete superiore (q:1 q 1 ) : Vao bee ovviamete tutti quelli acora superiori, ma quello è il più piccolo che va bee. A livello pratico, ci soo molte scelte da fare, prima di calcolare. Ua delle più critiche è. U idea possibile, ache se vaga, è che sia il primo 13
14 valore critico diverso da, cioè il primo valore che, se realizzato, provoca delle cosegueze rilevati, e che quidi deve essere rilevato dal test. Quado si eseguoo test elle aziede? Ad esempio quado si fa moitoraggio, ad esempio co le carte di cotrollo. Vegoo spiegate sommariamete le carte di cotrollo, le bade, il campioameto a tempi regolari, l allarme quado si esce dalle bade, l aalogia co l eseguire u test ad ogi istate di cotrollo. Vegoo calcolate le bade: q 1 p, come per l itervallo di co deza (ma lo scopo è u test, o la stima della media). Operativamete, pesado ad u esempio cocreto, come si realizza ua carta? Vao scelti ed, ssati ua volta per tutte. Per sceglerli si deve aver chiaro il sigi cato di ogi elemeto della teoria del test. è la probabilità di usciere dalle bade quado ivece la media è rimasta. I molti casi questo o è così grave: quado accade basta rifare il campioameto, per cotrollare meglio. va scelto per avere ua certa poteza, relativamete ad u certo. Si deve sapere, ad es. dagli esperti delle cose prodotte, quali deviazioi da redoo iservibili o pericolose le cose prodotte. corrispode a tali valori critici. A quel puto va scelto (). E la probabilità di o accorgersi di u cambiameto di, quado questo è avveuto. Questo sì che può essere periciloso: vedere cose fuori orma seza saperlo. Allora () va preso molto piccolo, e trovato i corrispodeza. Lezioe 6 (11/5). p.187 e segueti: richiamo sulla de izioe di v.a. chi quadro, gra co delle desità al variare di, media e deviazioe stadard proporzioale a p (cocetrazioe relativa). Numeri (simili a i quatili) ;, tavole relative, iterpretazioe geometrica. p. : ricordado la de izioe di S e la proprietà dimostrata E [S ] =, vale il teorema: S ( 1) ha legge 1. La dimostrazioe è di cile ma u idea si ha el seguete modo. Itroduciamo S := 1 X (X i ) : i=1 Esercizio per casa: mostrare che E S =. Si vede subito che S X = Xi i=1 14
15 cioè S è somma di quadrati di gaussiae caoiche idipedeti. Quidi S è, per de izioe. No è così strao quidi che S ( 1) possa essere ua chi quadro; meo facile da ituire è che abbia solo 1 gradi di libertà. p. 33 e segueti: test chi quadro per la variaza, caso uilaterale (destro). Esempio 8.5.1, ache proprio eseguedo il test a livello = :5, tramite le tavole. L idea ituitiva del test è la seguete: ci di chiede se S sia sigi cativamete più grade di (l ipotesi ulla è che la variaza sia, oppure ); se lo è, ri utiamo l ipotesi ulla. Il problema è cofrotare S co (o basta la semplice disuguagliaza S > ): di quato deve essere S maggiore di per ri utare? Tutto è relativo ai parametri del problema (es. ) ed al rischio che vogliamo correre. Allora, come el caso del test per la media, il metodo matematico cosiste ell itrodurre ua gradezza uiversale (es. la stadardizzazioe) associata alla gradezza statistica i oggetto. Per la media, si itrodiceva la stadardizzazioe Z = X p. Per la variaza, si itroduce S ( 1). Il problema se S sia sigi cativamete maggiore di si traduce el problema se S ( 1) sia sigi cativamete grade. Sappiamo che S ( 1) è ua 1, quado l ipotesi ulla è vera. Quidi S ( 1) supera ; 1 solo co probabilità. Preso piccolo, se per il campioe sperimetale vale S ( 1) > ; 1, giudichiamo questo icompatibile co l ipotesi ulla ( S ( 1) è troppo grade). Quidi ri utiamo l ipotesi. Viee ache calcolato il valore p: la probabilità che ua 1 superi il valore sperimetale di S ( 1). Bisoga usare le tavole della chi quadro al cotrario, cosa spesso poco agevole per via dei pochi valori. Lezioe 7 (1/5). Problema: lato prodotto correttamete: = : mm, = : mm. Spessore da evitare: :3 mm, o :1 mm. Creare carte di cotrollo. Osservazioe 1: si tratta di u processo ad alta precisioe, cioè co molto piccola. U campioe ha probabilità piccolissima di superare :3 mm per caso (servoo 5 sigma, quasi impossibile). Osservazioe : ha quidi seso teere sotto cotrollo la media, ivece che il sigolo esemplare. Ifatti il sigolo esemplare è improbabile che superi :3 mm per caso, se la media resta quella. Il pericolo o è ella causalità, ma i u peggiorameto sistematico della media. Osservazioe 3: oppure il pericolo è i u peggiorameto della variaza: 15
16 se fosse ad es. = :5 mm., basta arrivare a per raggiugere :3 mm per caso i u esemplare. Questo sarebbe frequete. Coclusioe: vao teute sotto cotrollo media e variaza. Itato si crea ua carta di cotrollo per la media, i cui UCL = + q 1 q p 1 e LCL = p. Vao scelti ed. Come già detto i ua lezioe precedete, forse può essere scelto o troppo severo, es..5, metre va scelto co lo scopo di avere ua certa poteza. Va ideti - cato u valore che o si vuole raggiugere, va scelta la relativa poteza (qui bisoga essere severi, trattadosi della probabilità di accettare del lato troppo spesso o sottile), e calcolato. Lo faremo ella prossima lezioe. Poi si deve creare ua carta di cotrollo per la variaza. Si può impostare così: l idicatore è positivo, c è u uico limite, U CL. U modo è predere come idicatore S ( 1), e UCL = ;. Di uovo vao scelti ed, co ragioameti aaloghi. Lezioe 8 (13/5). Esercizi di preparazioe al compito. Il compito coterrà alcui esercizi semplici di calcolo ed altri più articolati, da presetare co ua discussioe più ampia. Vegoo svolti quattro esercisi semplici di calcolo: Esercizio 1: se X; Y soo Poisso di parametro 5, calcolare E X e Y Y. Esercizio : se X è ua N (3; 4), trovare tale che P (X > ) = :8. Esercizio 3: se X è ua N ( 5; 9), calcolare P (X > ). Esercizio 4: se X è ua B (; :7), calcolare E X 1 X+1. Viee poi svolto u esercizio più strutturato, sulla falsariga del problema della volta precedete. la prosuzioe corretta di u lato deve avere spessore medio. mm co deviazioe stadard. mm. Se lo spessore di u esemplare raggiuge.3 mm, si ota ei tessuti; se raggiuge.1 mm, il lo si può strappare. Domada 1 : calcolare la probabilità che u esemplare superi.3 mm. Domada : a parità di, che spessore medio dovremmo avere a che u esemplare su 1 superi.3 mm? Domada 3 : alla luce del risultato appea otteuto, costruire ua carta di cotrollo per la media, esamiado criticamete le scelte da e ettuare i fase di DOE. Lezioe 9 (18/5). Esercizio. Nei mesi T = 1; ; 3; 4; 5; 6; 7; 8; 9; 1; 11; 1 16
17 soo state registrate le vedite di u prodotto, pari a X = 18; ; 3; 1; 1; 1; 1; 7; 9; 17; 13; 3: Per risparmiare calcoli, el seguito si usio i segueti risultati itermedi: X xi = 15; X x i = 115; X t i = 78; X t i = 65; X x i t i = 763: Domada 1. Tracciare u istogramma co itevalli (; 5], (5; 1], (1; 15], ecc. e sovrapporre la gaussiaa stimata. Domada. Calcolare la quatità da teere i magazzio su ciete al 9%. Sol. Dobbiamo trovare il umero q tale che P (X q) = :9. Vale q = + q :9 1: :6 1:8 = 1: 44. Domada 3. Quati mesi di osservazioe servirebbero per stimare la media co u errore pari all uità, al 95%? Che precisioe si ottiee i tre mesi? Domada 4. Sappiamo che ei mesi sopra cosiderati è peggiorata la crisi ecoomica. Questo ha i uito sulle vedite? Circa la domada 4 viee data la formula per la covariaza empirica dcov = 1 X (xi x) (y i y) 1 discusso il fatto che Cov d > corrispode a dati che crescoo o calao di pari passo, metre Cov d < corrispode a dati che si muovoo i cotrotedeza; viee poi evideziato il difetto che Cov d dipede dall ordie di gradezza dei umeri i gioco e delle loro uttuazioi, quidi si itroduce il coe ciete di correlazioe Cov r = d S X S Y che ha le stesse proprietà sul sego ma è uiversale e varia tra -1 ed 1 (si trova tutto al par..6). Nell esempio si trova r = :145, che idica sostazialmete asseza di legame tra tempo e vedite. Esercizio per casa: ripetere le stesse cose per i dati T = 1; ; 3; 4; 5; 6; 7; 8; 9; 1; 11; 1 X = 1; 13; 11; 3; 1; 4; 8; 8; 3; 1; 9; 1: 17
18 Lezioe 3 (19/5). Retta di regressioe (regressioe lieare semplice, o multipla), calcolo dei coe cieti col metodo dei miimi quadrati, par. 9.: B = r S Y S X ; A = y Bx: Calcolo e rappresetazioe gra ca el caso dell esercizio precedete. Si tora all istogramma dell esercizio precedete, dove la desità gaussiaa o sembra ua buoa approssimazioe. Si pesa di provare co le desità espoeziali. Esse dipedoo da u solo parametro. Come ricavarlo (stimarlo) dai dati? Prima idea: = 1 quidi 1 x : Poteziale cotraddizioe: ache = 1, quidi ache 1 dovrebbe essere S ua ragioevole stima, ma se S ed x di eriscoo molto, forse il modello espoeziale o è ragioevole. Note sugli esercizi assegati. Ci soo alcui errori ella risoluzioe degli esercizi dei compiti di MMS suggeriti. Ecco la lista: 7/1/9 es. 3, errore ella variaza; 16/9/8 es. 1, errore el calcolo di ; 17//9 es. 9, maca u quadrato el calcolo di ; 15/7/8, è sbagliato il valore di q :975. Lezioe 31 (/5). Toriamo ai dati dell esercizio della lezioe 9. Domada 1. Trovare la desità espoeziale associata ai dati e disegarla. Sol. Possoo esserci varie desità espoeziali, a secoda di come stimiamo. Usiamo prima di tutto 1 = 1 = :96, che poi disegeremo x 1:416 sovrapposta all istogramma. Questa stima è ache supportata dal metodo della massima verosimigliaza. U altra stima sarebbe 1 = 1 = :116. S 8:6 Più avati vedremo u altro metodo di stima più adattato al problema della coda destra. Domada. Calcolare la quatità da teere i magazzio su ciete al 9%. Sol. Dobbiamo trovare il umero q tale che P (X q) = :9. Se X Exp (), F X (t) = 1 e t, quidi dobbiamo trovare q tale che 1 e q = :9, dove è uo di quelli stimati sopra. Vale e q = :1, q = log 1, q = log 1 = 18
19 log 1 :96 = 3: 985. E maggiore di 1: 44, quidi forse più realistico alla luce del valore 3 che si è osservato el campioe. Domada 3. Che precisioe ha, approssimativamete, la stima di 1 data da x, al 95%? Come si dovrebbe ragioare se è richiesta la precisioe della stima di, ovvero se è richiesta ua valutazioe dell errore 1 x? Nota: si usao gli itervalli di co deza 1 = x q p:975, che però soo approssimati per due ragioi. La prima è che o si coosce la vera ; questo sarebbe rimediabile prededo. La secoda è che le v.a. di parteza o soo gaussiae, quidi X o è N ; e quidi gli estremi dell itervallo di co deza o adrebbero calcolati tramite i quatili gaussiai. Ma per il TLC, X è approssimativamete N ;, quidi le varie coclusioi soo circa corrette. Nota: l errore relativo, al 95%, cioè x, è circa.5, molto alto. Nota: vale 1 = jx j, quidi si possoo riportare le iformazioi x x su jx j a quelle per 1 x. Facedo i coti si vede che l errore relativo j xj 1 è di uovo circa.5. Esercizio per casa (Domada 4). Trovare i modo da avere errore relativo iferiore a /1. Domada 5 (riviata). Se o si dispoeva del campioe della lezioe 9, che di coltà c era a rispodere alla domada 4? Se avessimo ipotizzato, da aalisi di mercato, che le vedite avrebbero avuto ua media tra 5 e 15 ed ua deviazioe tra 5 e 15? Problema: come decidere razioalmete se è meglio la gaussiaa o l espoeziale? mmagiiamo di ivetare u test, i cui l ipotesi ulla H sia del tipo: la desità è la gaussiaa N (1:416; 8:6 ); oppure, la desità è espoeziale di parametro :96. Magari il test ri uta ua delle due e o l altra, permettedoci di scegliere. Ache se il test o discrimiasse, possiamo scegliere la desità che coquista il miglior valore p. Relativamete alla partizioe co cui facciamo l istogramma (o u altra, ssata), si calcolio le frequeze teoriche p i e quelle sperimetali bp i. Itediamo: p i è la probabilità (ad es. ell ipotesi gaussiaa) di cadere i quell itervallo della partizioe; se tale itervallo ha estremi [a i ; b i ] vale St( 1) :975 p p i = F (b i ) F (a i ) 19
20 che, el caso gaussiao diveta bi ai metre el caso espoeziale diveta 1 e b i 1 e a i : 4 Ivece, la frequeza sperimetale bp i è quella del campioe: ad es. per 1 l itervallo (; 5], ecc. Sia k il umero di itervallii. Se prediamo P k i=1 jbp i p i j, stiamo valutado quato distao le due desità. Però così diamo poco peso alle code (assai importati per le applicazioi), i quato elle code i valori bp i e p i soo più piccoli e quidi jbp i p i j è troppo piccolo, idipedetemete dal fatto che la desità sia ua buoa approssimazioe dell istogramma. Prededo la somma degli errori relativi kx bp i i=1 si cura questo difetto, ma si ottiee u espressioe molto istabile, molto sesibile a piccole variazioi, i quato i deomiatori p i soo troppo piccoli, proprio sulle code. U miglior equilibrio è l espressioe p i p i T = kx i=1 jbp i p i j p i : Esercizio per casa: calcolare T per la gaussiaa e per l espoeziale, cofrotadoli. Nota: la migliore è quella col T più piccolo (frequeze più vicie). Si può vedere che questo corrispode al miglior p-value e ad ua maggior possibilità di o veir ri utati dal test. Attezioe: la gradezza T che si userà el cosidetto test chi quadro è uguale a T T = T : Lezioe 3 (5/5). Esercizio 1. Data X N (5; 4), calcolare P (X > 3).
21 Esercizio. Se X rappreseta il quadago gioraliero, quale guadago è garatito al 95%? Ovvero, qual è il guadago miimo che ci si aspetta al 95%? Esercizio 3. Ed il guadago massimo, al 98%? Esercizio 4. Co che probabilità il guadago o supererà 8? Esercizio 5. Se X ed Y soo come sopra ma idipedeti, guadagi relativi a due diversi giori, co che probabilità il guadago totale dei due giori sarà maggiore di 6? Esercizio 6. Cosiderado 5 giori lavorativi i u mese ed i guadagi idipedeti ed ugualmete distribuiti, ma o più N (5; 4) besì espoeziali di media 5, calcolare approssimativamete la probabilità di guadagare più di 1. Soluzioi (cei) relative ad alcui esercizi. Esercizio. Cerchiamo il valore g tale che P (X g) = :95 (il valore miimo, superato il 95% delle volte). Dopo aver fatto u disego ed u cofroto gra co co la gaussiaa caoica, si capisce (o i altro modo) che g = 5 q :95 = ::: Esercizio 5. Il guadago totale dei due giori è X+Y, che è N (5 + 5; 4 + 4) = N (1; 8). Quidi bisoga calcolare P (X + Y > 6) = p = ::: 8 Esercizio 6. Detti X 1 ; :::; X 5 i guadagi gioralieri, vale X1 + ::: + X 5 5 P (X 1 + ::: + X 5 > 1) = P p > p 5 dove prediamo = E [X i ] = 5, = V ar [X i ] = 5. Per il TLC la v.a. X 1 +:::+X 5 5 è approssimativamete ua Z N (; 1), quidi p 5 P (X 1 + ::: + X 5 > 1) P Z > p = 1 p = ::: Esercizio. Due laboratori esamiao la percetuale di difettosità di certi pezzi prodotti. Il LabA trova p A = :45, metre il LabB trova p B = :91. 1
22 Il committete vuole capire questa discrepaza ed esamia lui stesso 1 esemplari, trovadoe uo difettoso. Quale laboratorio gli sembra migliore? Può ri utare alcue delle loro dichiarazioi? Sol. bp = 1 = :83. Quato è distate (relativamete ai parametri del 1 problema, es. 1 esemplari)? Dette X 1 ; :::; X 1 delle v.a. che valgoo 1 se il corrispodete pezzo è difettoso, co probabilità p, zero altrimeti, posto S = X 1 +:::+X 1 = umero di pezzi difettosi, S è B (1; p), quidi potremmo tetare di usare le biomiali per ragioare sul problema. Questo aprirebbe la strada ai test biomiali, test esatti, che però o trattiamo. Possiamo ivece, i virtù del TLC (ma 1 è u po bassa), pesare che S è circa gaussiaa, quidi applichiamo approssimativamete il test gaussiao per la media. Esamiado la dichiarazioe del LabA, l ipotesi ulla è (o se si vuole p ) = :45, e la media empirica è proprio S = bp = 1 1 = :83: Quidi calcoliamo :83 :45p z = 1. C è il problema di. Prediamo la del modello ipotizzato, che essedo ua B (1; p ) porta a = p (1 p ), quidi = p :45 :955 = :497: Pertato z = :635. Questo va cofrotato co u quatile preso a priori, es. q :975 = 1:96. Il test o è sigi cativo: o possiamo ri utare la dichiarazioe di LabA (a maggior ragioe quella di LabB che è più vicia al risultato sperimetale). Altro approccio. Problema dell adattameto (corrispodeza tra proporzioi empiriche e desità teorica pre ssata) e test chi quadro: si cofrota T = kx jbp i p i j i=1 (che è approssimativamete k 1, per grade) col quatile ;k 1. Lezioe 33 (6/5). Esercizio. Calcolare T per etrambi i laboratori i casi e cofrotarli. Eseguire il test chi-quadro al 95%. p i
23 Sol. bp 1 = 11 = :917, bp 1 = 1 = :83, 1 5 1:416 p A 1 = = (1: 696) = :955 8:6 p A = 1 :955 = :45: da cui p B 1 = 1 e :965 = :99 p B = 1 :99 = :91 T A = 1 j:917 :955j : j:83 :45j :45 = :43 T B = 1 j:917 :99j : j:83 :91j :91 = :9 quidi è migliore l approssimazioe espoeziale della coda. Ma :5;1 = 3:841, o superato da etrambi. No possiamo ri utare essua delle due ipotesi. Nota: il test gaussiao della lezioe precedete è idetico a quello appea svolto: i quadrati dei due umeri z = :635 e q :975 = 1:96 su cui si basava il test gaussiao, soo esattamete pari ai due umeri T A = :43 e :5;1 = 3:841 su cui si basa il test chi-quadro. Esercizio. Dividere i dati della lezioe 9 elle due classi ( 1; 5], (5; 1). Calcolare frequeze empiriche e frequeze teoriche sia gaussiae sia espoeziali, calcolare T i etrambi i casi e cofrotarli. Eseguire il test chi-quadro al 95%. Lezioe 34 (7/5). Esercizio 7 del capitolo 8. Attezioe: la domada b richiede l uso della poteza (vedi DOE, ricerca della umerosità per avere ua poteza data). Esercizio. Si predao i dati dell esempio Il programma di prevezioe illustrato i quell esempio ha avuto e etto? Sol. Come illustrato ell esempio, si traduce il problema i uo che sappiamo studiare: si calcolao le di ereze e si cosidera come uova variabile di studio la di ereza tra il valore uovo (dopo l iovazioe) e quello vecchio (prima dell iovazioe). L ipotesi ulla è (come i tutti i test fatti o 3
24 ad ora) che l iovazioe o abbia avuto e etto, cioè le cose stiao come prima, cioè = ( è la media delle di ereze tra dopo e prima). Dette w 1 ; :::; w 1 le dieci di ereze egli stabilimeti, calcoliamo w p prededo come la deviazioe S W dei dati w 1 ; :::; w 1 stessi. Vale w p = p : Eseguiamo u test uilaterale del tipo w p < q1 = 164 (al 95%). Risulta sigi cativo, l iovazioe ha avuto e etto. Si chiede poi di calcolare il p-dei-dati, che essedo al probabilità di avere valori più estremi di quello sperimetale, è dato da P Z < :15 p :15 p 1 = 1 = ::: 3 3 I e, viee richiesta la poteza di questo test di accorgersi di u calo di 3 uità. Disegadosi l itervallo i cui viee accettata l ipotesi ulla ( ; 1), = q p1 (è u test uilaterale) e la gaussiaa di W, che è ua N ; = N 3; 3 1, si deve calcolare () = ( 3), la probabilità dell errore di secoda specie, cioè la probabilità secodo la gaussiaa N 3; 3 1 di cadere ell itervallo di accettazioe ( ; 1), probabilità che vale! 1 F ( ) = 1 p p = 1 q1 3 p = 1 1 1:64 3 da cui la poteza vale 3 3p 1 1:64. 4
Statistica I, Laurea triennale in Ing. Gestionale, a.a /11 Registro delle lezioni
 Statistica I, Laurea trieale i Ig. Gestioale, a.a. 20010/11 Registro delle lezioi Lezioe 1 (27/10). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli: http://www2.ig.uipi.it/~a008484/dispstatisticagestioaletrieale.html.
Statistica I, Laurea trieale i Ig. Gestioale, a.a. 20010/11 Registro delle lezioi Lezioe 1 (27/10). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli: http://www2.ig.uipi.it/~a008484/dispstatisticagestioaletrieale.html.
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Statistica I, Laurea triennale in Ing. Gestionale, a.a /11 Registro delle lezioni
 Statistica I, Laurea trieale i Ig. Gestioale, a.a. 0010/11 Registro delle lezioi Lezioe 1 (7/10). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli: http://www.ig.uipi.it/~a008484/dispstatisticagestioaletrieale.html.
Statistica I, Laurea trieale i Ig. Gestioale, a.a. 0010/11 Registro delle lezioi Lezioe 1 (7/10). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli: http://www.ig.uipi.it/~a008484/dispstatisticagestioaletrieale.html.
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Lezione 4 Corso di Statistica. Francesco Lagona
 Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Elementi di statistica
 Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Statistica I, Laurea triennale in Ing. Gestionale, a.a. 2011/12 Registro delle lezioni
 Statistica I, Laurea trieale i Ig. Gestioale, a.a. 2011/12 Registro delle lezioi Lezioe 1 (28/9, ore 11:30). Vedere la registrazioe di Barsati, dispoibile alla pagia http://users.dma.uipi.it/barsati/statistica_2011/idex.html.
Statistica I, Laurea trieale i Ig. Gestioale, a.a. 2011/12 Registro delle lezioi Lezioe 1 (28/9, ore 11:30). Vedere la registrazioe di Barsati, dispoibile alla pagia http://users.dma.uipi.it/barsati/statistica_2011/idex.html.
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Lezioni del Corso di Fondamenti di Metrologia Meccanica
 Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Lezione 4 Corso di Statistica. Domenico Cucina
 Lezioe 4 Corso di Statistica Domeico Cucia Uiversità Roma Tre D. Cucia (domeico.cucia@uiroma3.it) 1 / 22 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Domeico Cucia Uiversità Roma Tre D. Cucia (domeico.cucia@uiroma3.it) 1 / 22 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Registro di MMS parte di Statistica a.a. 2007/08
 Registro di MMS parte di Statistica a.a. 007/08 Lezioe 1 (6//08, 1 ora). Eveti, eveti elemetari (esiti), uiverso S (spazio degli esiti). Formalizzazioe matematica: S è u isieme ambiete, gli eveti soo i
Registro di MMS parte di Statistica a.a. 007/08 Lezioe 1 (6//08, 1 ora). Eveti, eveti elemetari (esiti), uiverso S (spazio degli esiti). Formalizzazioe matematica: S è u isieme ambiete, gli eveti soo i
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Migo A.A. 019-00 Facoltà di Scieze Politiche, Sociologia, Comuicazioe Corso di laurea Magistrale i «Orgaizzazioe e marketig per la comuicazioe
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Migo A.A. 019-00 Facoltà di Scieze Politiche, Sociologia, Comuicazioe Corso di laurea Magistrale i «Orgaizzazioe e marketig per la comuicazioe
Calcolo delle Probabilità e Statistica, Ing. Informatica e dell Automazione, a.a. 2009/10 Registro delle lezioni
 Calcolo delle Probabilità e Statistica, Ig. Iformatica e dell Automazioe, a.a. 009/0 Registro delle lezioi Lezioe (4/3). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli, http://www.ig.uipi.it/~a008484/eps.html.
Calcolo delle Probabilità e Statistica, Ig. Iformatica e dell Automazioe, a.a. 009/0 Registro delle lezioi Lezioe (4/3). Itroduzioe al corso; materiale e comuicazioi alla pag. di F. Fladoli, http://www.ig.uipi.it/~a008484/eps.html.
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Titolo della lezione. Dal campione alla popolazione: stima puntuale e per intervalli
 Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
STUDIO DEL LANCIO DI 3 DADI
 Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
oggetti?, coefficiente binomiale. Dimostrazione usando i due esempi precedenti (detti
 Descrizioe sommaria degli argometi svolti a lezioe, ao accademico 006-07 Lezioe 1 (7/, ore). Itroduzioe al corso (lezioi ed esercitazioi: Fraco Fladoli e David Barbato; testo: S. Ross, Probabilità e Statistica
Descrizioe sommaria degli argometi svolti a lezioe, ao accademico 006-07 Lezioe 1 (7/, ore). Itroduzioe al corso (lezioi ed esercitazioi: Fraco Fladoli e David Barbato; testo: S. Ross, Probabilità e Statistica
N.B. Per la risoluzione dei seguenti esercizi, si fa riferimento alle Tabelle riportate alla fine del documento.
 N.B. Per la risoluzioe dei segueti esercizi, si fa riferimeto alle Tabelle riportate alla fie del documeto. Esercizio 1 I u villaggio turistico gli aimatori orgaizzao ua sfida. Vice u prazo i u ristorate
N.B. Per la risoluzioe dei segueti esercizi, si fa riferimeto alle Tabelle riportate alla fie del documeto. Esercizio 1 I u villaggio turistico gli aimatori orgaizzao ua sfida. Vice u prazo i u ristorate
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Esame di Probabilità e Statistica del 9 luglio 2007 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esame di Probabilità e Statistica del 9 luglio 27 Corso di Laurea Trieale i Matematica, Uiversità degli Studi di Padova). Cogome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto fiale Attezioe: si cosegao
Esame di Probabilità e Statistica del 9 luglio 27 Corso di Laurea Trieale i Matematica, Uiversità degli Studi di Padova). Cogome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto fiale Attezioe: si cosegao
Daniela Tondini
 Daiela Todii dtodii@uite.it Facoltà di Bioscieze e Tecologie agro-alimetari e ambietali e Facoltà di Medicia Veteriaria C.L. i Biotecologie Uiversità degli Studi di Teramo 1 La mediaa o valore mediao M
Daiela Todii dtodii@uite.it Facoltà di Bioscieze e Tecologie agro-alimetari e ambietali e Facoltà di Medicia Veteriaria C.L. i Biotecologie Uiversità degli Studi di Teramo 1 La mediaa o valore mediao M
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Migo A.A. 017-018 Facoltà di Scieze Politiche, Sociologia, Comuicazioe Corso di laurea Magistrale i «Orgaizzazioe e marketig per la comuicazioe
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Migo A.A. 017-018 Facoltà di Scieze Politiche, Sociologia, Comuicazioe Corso di laurea Magistrale i «Orgaizzazioe e marketig per la comuicazioe
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA. Prof.ssa Donatella Siepi tel:
 UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
Programma della parte introduttiva: Lezione 4
 Programma della parte itroduttiva: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
Programma della parte itroduttiva: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
Elementi di statistica descrittiva. Tabella dei dati :
 - - Elemeti di statistica descrittiva I dati riportati sotto si riferiscoo a 20 studeti uiversitari che frequetavao u corso di Statistica e soo stati raccolti facedo compilare ad ogi studete il seguete
- - Elemeti di statistica descrittiva I dati riportati sotto si riferiscoo a 20 studeti uiversitari che frequetavao u corso di Statistica e soo stati raccolti facedo compilare ad ogi studete il seguete
Y = ln X è normalmente distribuita. (y) = dg(x) dx. f Y. (x) = dy dx f Y. f X. (g(x)) & exp$ dx x - $ % ( x) DISTRIBUZIONE LOG-NORMALE.
 DISTRIBUZIONE LOG-NORMALE. La variabile si dice log-ormalmete distribuita se: l è ormalmete distribuita g( l g ( e 0 +. uzioe di desità di probabilità: f ( d d f ( dg( d f (g( dg( d f (. & ep$ - / $ %,
DISTRIBUZIONE LOG-NORMALE. La variabile si dice log-ormalmete distribuita se: l è ormalmete distribuita g( l g ( e 0 +. uzioe di desità di probabilità: f ( d d f ( dg( d f (g( dg( d f (. & ep$ - / $ %,
Scheda n.6: legame tra due variabili; correlazione e regressione
 Scheda.6: legame tra due variabili; correlazioe e regressioe October 26, 2008 Covariaza e coefficiete di correlazioe Date due v.a. X ed Y, chiamiamo covariaza il umero Cov (X, Y ) = E [(X E [X]) (Y E [Y
Scheda.6: legame tra due variabili; correlazioe e regressioe October 26, 2008 Covariaza e coefficiete di correlazioe Date due v.a. X ed Y, chiamiamo covariaza il umero Cov (X, Y ) = E [(X E [X]) (Y E [Y
Fonti e strumenti statistici per la comunicazione
 Foti e strumeti statistici per la comuicazioe Prof.ssa Isabella Migo A.A. 018-019 Idici Medi Esercizio:calcolo media soluzioe Numeri addetti xi i xi * i 10 18 180 1 15 180 14 5 350 16 10 160 18 9 5 0 18
Foti e strumeti statistici per la comuicazioe Prof.ssa Isabella Migo A.A. 018-019 Idici Medi Esercizio:calcolo media soluzioe Numeri addetti xi i xi * i 10 18 180 1 15 180 14 5 350 16 10 160 18 9 5 0 18
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
 Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
Lezione 5. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 5. A. Iodice.
 La Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 26 Outlie La 1 2 La 3 4 () Statistica 2 / 26 Trimmed mea - La aritmetica risete della preseza di valori
La Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 26 Outlie La 1 2 La 3 4 () Statistica 2 / 26 Trimmed mea - La aritmetica risete della preseza di valori
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Proposizione 1. Due sfere di R m hanno intersezione non vuota se e solo se la somma dei loro raggi e maggiore della distanza fra i loro centri.
 Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Esempio: distribuzione di frequenze. =, Pagina 90. Esempio: distribuzione di frequenze
 Esempio: distribuzioe di frequeze Distribuzioe degli studeti di SDC frequetati la facoltà ell a.a. 001/00 per Num. Corsi Frequetati 83 K 7 = + + + + + + = = Num. Corsi Freq. i 1 15 43 3 103 4 80 5 3 6
Esempio: distribuzioe di frequeze Distribuzioe degli studeti di SDC frequetati la facoltà ell a.a. 001/00 per Num. Corsi Frequetati 83 K 7 = + + + + + + = = Num. Corsi Freq. i 1 15 43 3 103 4 80 5 3 6
Programma della parte introdu0va: Lezione 4
 Programma della parte itrodu0va: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
Programma della parte itrodu0va: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Esame di Stato - Liceo Scientifico Prova scritta di Matematica - 21 giugno Problema 1 Soluzione a cura di L. Tomasi
 Esame di Stato - Liceo Scietifico Prova scritta di Matematica - giugo 8 Problema Soluzioe a cura di L. Tomasi Soluzioe Puto Co riferimeto all esempio semplice del mauale d uso della macchia che colora
Esame di Stato - Liceo Scietifico Prova scritta di Matematica - giugo 8 Problema Soluzioe a cura di L. Tomasi Soluzioe Puto Co riferimeto all esempio semplice del mauale d uso della macchia che colora
Probabilità CENNI DI PROBABILITÀ
 CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA
 UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
1 Sulla dimostrazione del TLC
 1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
Distribuzioni di probabilità
 Itroduzioe Distribuzioi di robabilità Fio ad ora abbiamo studiato ua secifica fuzioe desità di robabilità, la fuzioe di Gauss, che descrive variabili date dalla somma di molti termii idiedeti es. ua misura
Itroduzioe Distribuzioi di robabilità Fio ad ora abbiamo studiato ua secifica fuzioe desità di robabilità, la fuzioe di Gauss, che descrive variabili date dalla somma di molti termii idiedeti es. ua misura
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
ELEMENTI DI CALCOLO COMBINATORIO
 ELEMENTI DI CALCOLO COMBINATORIO 1 Elemeti di calcolo combiatorio Si tratta di ua serie di teciche per determiare il umero di elemeti di u isieme seza eumerarli direttamete. Dati elemeti distiti ci chiediamo
ELEMENTI DI CALCOLO COMBINATORIO 1 Elemeti di calcolo combiatorio Si tratta di ua serie di teciche per determiare il umero di elemeti di u isieme seza eumerarli direttamete. Dati elemeti distiti ci chiediamo
Soluzioni quarta esercitazione
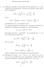 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
REGRESSIONE LINEARE E POLINOMIALE
 REGRESSIONE LINEARE E POLINOMIALE Nota ua tabella di dati relativi alle osservazioi di due gradezze X e Y, è aturale formulare ipotesi su quale possa essere ua ragioevole fuzioe che rappreseti o che approssimi
REGRESSIONE LINEARE E POLINOMIALE Nota ua tabella di dati relativi alle osservazioi di due gradezze X e Y, è aturale formulare ipotesi su quale possa essere ua ragioevole fuzioe che rappreseti o che approssimi
Formulazione del problema - 1
 Formulazioe del problema - Date due variabili aleatorie X e Y si tratta di cercare ua relazioe lieare tra esse. Sappiamo già che se il modulo del coefficiete di correlazioe o vale esattamete, le determiazioi
Formulazioe del problema - Date due variabili aleatorie X e Y si tratta di cercare ua relazioe lieare tra esse. Sappiamo già che se il modulo del coefficiete di correlazioe o vale esattamete, le determiazioi
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
