7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
|
|
|
- Lorenza Locatelli
- 4 anni fa
- Visualizzazioni
Transcript
1 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere se accettare o rifiutare la verità di questa ipotesi. i potrao verificare quattro situazioi alterative: 1. L ipotesi è vera e l accetto bee. L ipotesi è vera ma i base ai dati la rifiuto i questo caso si dice che si commette errore di prima specie 3. L ipotesi è falsa ma i base ai dati la accetto i questo caso si dice che si commette errore di secoda specie 4. L ipotesi è falsa e la rifiuto bee Per chiarirsi le idee vediamo prima u esempio. Esempio Ho { ua moeta. Voglio verificare se è bilaciata o meo. La lacio 1 se all i-esimo lacio esce testa, volte. Pogo X i =, i = 1,...,. Ho u campioe 0 se all i-esimo lacio esce croce. statistico beroulliao di umerosità e parametro p [0, 1] icogito, dove p è la probabilità che esca testa i u sigolo lacio. L ipotesi ulla che dobbiamo testare è H 0 p = 0.5. Facciamo duque laci. Otteiamo teste ed croci: { 1 se all i-esimo lacio esce testa, x 1, x,..., x dove x i = 0 se all i-esimo lacio esce croce. e duque x = 1 x i =. tabilisco ua distaza massima ε tra x e 0.5 etro la quale accettare l ipotesi p = 0.5 e oltre la quale rifiutarla. Ovvero: accetto H 0 se x 0.5 < ε e la rifiuto se x 0.5 ε. cioè se x i ε. Quato vale la probabilità di commettere errore di prima specie, ovvero di rifiutarla quado esse ivece è vera? 61
2 Commetto errore di prima specie co probabilità α := P X i ε. Poiché le v.a. X i soo idipedeti e seguoo tutte la distribuzioe di Beroulli di parametro p, la v.a. Y := X i è ua v.a. biomiale di parametri e p. e l ipotesi H 0 è vera, allora p = 0.5 duque : Y B, 0.5 e Y α := P ε = P Y + ε + P Y ε Vediamo alcui casi = 50, ε = 0.1 α = P Y P Y 5 5 = 1 F Y 9 + F Y 0. > 1 - pbiomc9, size=50, prob=0.5, lower.tail=true + pbiomc0, size=50, prob=0.5, lower.tail=true [1] = 100, ε = 0.1 α = P Y P Y = 1 F Y 59 + F Y 40. > 1 - pbiomc59, size=100, prob=0.5, lower.tail=true + pbiomc40, size=100, prob=0.5, lower.tail=true [1] = 00, ε = 0.1 α = P Y P Y = 1 F Y F Y 80. > 1 - pbiomc119, size=00, prob=0.5, lower.tail=true + pbiomc80, size=00, prob=0.5, lower.tail=true [1] = 300, ε = 0.1 α = P Y P Y = 1 F Y F Y 10. > 1 - pbiomc179, size=300, prob=0.5, lower.tail=true + pbiomc10, size=300, prob=0.5, lower.tail=true [1]
3 = 50, ε = 0.05 α = P Y P Y 5.5 = 1 F Y 7 + F Y. > 1 - pbiomc7, size=50, prob=0.5, lower.tail=true + pbiomc, size=50, prob=0.5, lower.tail=true [1] = 100, ε = 0.05 α = P Y P Y 50 5 = 1 F Y 54 + F Y 45. > 1 - pbiomc54, size=100, prob=0.5, lower.tail=true + pbiomc45, size=100, prob=0.5, lower.tail=true [1] = 00, ε = 0.05 α = P Y P Y = 1 F Y F Y 90. > 1 - pbiomc109, size=00, prob=0.5, lower.tail=true + pbiomc90, size=00, prob=0.5, lower.tail=true [1] = 300, ε = 0.05 α = P Y P Y = 1 F Y F Y 135. > 1 - pbiomc164, size=300, prob=0.5, lower.tail=true + pbiomc135, size=300, prob=0.5, lower.tail=true [1] = 400, ε = 0.05 α = P Y P Y 00 0 = 1 F Y 19 + F Y 180. > 1 - pbiomc19, size=400, prob=0.5, lower.tail=true + pbiomc180, size=400, prob=0.5, lower.tail=true [1] = 500, ε = 0.05 α = P Y P Y 50 5 = 1 F Y 64 + F Y 5. > 1 - pbiomc74, size=500, prob=0.5, lower.tail=true + pbiomc5, size=500, prob=0.5, lower.tail=true [1]
4 Figura 7.1: βp olitamete si vuole cotrollare el seso di teere bassa, iferiore a 0.1 o a 0.05 la probabilità α di commettere errore di prima specie. Tale probabilità viee detta livello di sigificatività del test. Fissato il livello di sigificatività α, la umerosità e la soglia di tolleraza ε adrao scelti di cosegueza come visto egli esempi precedeti. Ioltre, fissato α, ci chiediamo quato valga la probabilità di commettere errore di secoda specie, ovvero di accettare H 0 quad essa ivece è falsa. e H 0 è falsa, allora la probabilità di otteere testa o è 0.5 ma assume u valore p 0.5 igoto e duque Y B, p e io accetto H 0 co probabilità Y βp := P p < ε = P p Y < + ε P p Y ε i calcola βp per vari valori di p. La fuzioe βp è detta curva operativa caratteristica OC metre 1 βp cioè la probabilità di rifiutare H 0 quad essa i effetti è falsa e il parametro icogito vale p, è detta poteza del test. Esempio Cosideriamo la solita moeta e stavolta vogliamo vedere se è più probabile otteere testa che otteere croce. Vogliamo cioè testare l ipotesi ulla H 0 p 0.5 U test di questo tipo è detto test uilaterale. 64
5 tabilisco ua tolleraza massima ε etro la quale accettare l ipotesi p 0.5 e oltre la quale rifiutarla. Ovvero: accetto H 0 se x < ε e la rifiuto se x ε cioè se x i +ε. Quato vale la probabilità di commettere errore di prima specie, ovvero di rifiutarla quado essa ivece è vera? Commetto errore di prima specie co probabilità α := P Y + ε. e H 0 è vera, allora Y B, p per qualche p 0.5. Idico F p Y ripartizioe Vediamo alcui casi la sua fuzioe di = 50, ε = 0.1 α = 1 P Y < = 1 F p Y 9 sup { 1 F p Y 9} = 1 FY p [0,0.5 > 1 - pbiomc9, size=50, prob=0.5, lower.tail=true = 100, ε = 0.1 α = 1 P Y < = 1 F p Y 59 sup { 1 F p Y 59} = 1 FY p [0,0.5 > 1 - pbiomc59, size=100, prob=0.5, lower.tail=true [1] = 00, ε = 0.1 α = 1 P Y < = 1 F p Y 119 sup { 1 F p Y 119} = 1 FY p [0,0.5 > 1 - pbiomc119, size=00, prob=0.5, lower.tail=true [1] = 50, ε = 0.05 α = 1 P Y < = 1 F p Y 7 sup { 1 F p Y 7} = 1 FY p [0,0.5 > 1 - pbiomc7, size=50, prob=0.5, lower.tail=true [1] = 100, ε = 0.05 α = 1 P Y < = 1 F p Y 54 sup { 1 F p Y 54} = 1 FY p [0,0.5 65
6 > 1 - pbiomc55, size=100, prob=0.5, lower.tail=true [1] = 00, ε = 0.05 α = 1 P Y < = 1 F p Y 109 sup { 1 F p Y 109} = 1 FY p [0,0.5 > 1 - pbiomc109, size=00, prob=0.5, lower.tail=true [1] = 300, ε = 0.05 α = 1 P Y < = 1 F p Y 164 sup { 1 F p Y 164} = 1 FY p [0,0.5 > 1 - pbiomc164, size=300, prob=0.5, lower.tail=true [1] I geerale duque u test d ipotesi ha la seguete struttura: 1. i ha u campioe statistico X 1, X,..., X, X i Dθ, dove θ è u parametro reale.. i formula u ipotesi che si chiama ipotesi ulla e si idica co H 0, solitamete ella forma dove Θ 0 è u sottoisieme di R. H 0 θ Θ 0 3. i formula ua regola di decisioe per l accettazioe o il rifiuto di H 0. La regola di decisioe è di questo tipo: si sceglie ua statistica che forisce ua stima del parametro θ e u sottoisieme A R, detto regioe di accettazioe. Dopodiché se Y A, allora si accetta H 0 ; se Y / A, allora si rifiuta H 0. L isieme A c := R \ A è detto regioe di rifiuto. Come già detto, è solitamete richiesto di limitare la probabilità di commettere errore di prima specie, cioè di limitare la probabilità di rifiutare l ipotesi ulla quado essa è vera. Vediamo come questo sia possibile el caso di campioi gaussiai. 66
7 7.1. Test d ipotesi per la media di campioi gaussiai Campioe gaussiao di cui è ota la variaza Test bilaterale ia X 1, X,..., X u campioe gaussiao di media µ icogita e variaza ota. Vogliamo testare l ipotesi ulla H 0 µ = µ 0. H 0 è vera se e solo se E [ X ] = 0 duque accetto l ipotesi ulla H 0 se la media campioaria si discosta da µ 0 per meo di u valore soglia ε ovvero se x µ 0 < ε e la rifiuto altrimeti. Il livello di di sigificatività cioè la probabilità di commettere u errore di prima specie è allora α = P µ0 X µ 0 ε dove il pedice µ 0 idica che H 0 è vera, cioè che µ = µ 0. e H 0 è vera, X N µ 0, e Z := X µ 0 N 0, 1. Duque α = P µ0 X µ 0 ε X µ0 = P µ0 ε = P Z ε = P Z ε + P Z ε ε ε = 1 Φ + Φ ε = 1 Φ ε e voglio fissare a priori α, deve essere allora Φ = 1 α ε = z 1 α e duque devo scegliere cioè deve essere ε = z 1 α. Presi i dati x 1, x,..., x, sia duque x = 1 x i la loro media. Accetto H 0 se x µ 0 < z 1 α e la rifiuto altrimeti. 67
8 Test uilaterale ia X 1, X,..., X u campioe gaussiao di media µ icogita e variaza ota. Vogliamo testare l ipotesi ulla H 0 µ µ 0. Accetto l ipotesi ulla H 0 se la media campioaria è iferiore a µ 0 + ε cioè se x < µ 0 + ε. La probabilità di commettere u errore di prima specie è allora P µ µ0 X µ0 + ε. dove il pedice idica che la media del campioe è µ µ 0. Poiché X N µ, e Z := X µ N 0, 1, si ha P µ µo X µ0 + ε X µ = P µ µ0 = 1 P Z µ 0 µ + ε = 1 Φ µ 0 µ + ε = P Z µ 0 µ + ε µ0 µ + ε ε e voglio limitare superiormete P µ µ0 X > µ0 + ε, cioè se voglio 1 Φ P µ µ0 X > µ0 + ε α µ µ 0 ε scelgo ε i modo da avere 1 Φ = α cioè ε = z 1 α e duque scelgo ε = z 1 α.. Presi i dati x 1, x,..., x, sia duque x = 1 x i la loro media. Accetto H 0 se x < µ 0 + z 1 α e la rifiuto altrimeti. Test uilaterale ia X 1, X,..., X u campioe gaussiao di media µ icogita e variaza ota. Vogliamo testare l ipotesi ulla H 0 µ µ 0. Accetto l ipotesi ulla H 0 se la media campioaria è superiore a µ 0 ε cioè se x > µ 0 ε. La probabilità di commettere u errore di prima specie è allora P µ µ0 X µ0 ε. 68
9 Poiché X N µ,, e Z := X µ P µ µ0 X µ0 ε X µ = P µ µ0 µ0 µ ε ε = Φ Φ N 0, 1, si ha µ 0 µ ε = P Z µ 0 µ ε ε = 1 Φ e voglio limitare superiormete P µ µ0 X µ0 ε cioè se voglio. ε scelgo ε i modo da avere Φ P µ µ0 X µ0 ε α µ µ 0 = 1 α cioè ε ε = z 1 α. = z 1 α e duque scelgo Presi i dati x 1, x,..., x, sia duque x = 1 x i la loro media. Accetto H 0 se x > µ 0 z 1 α e la rifiuto altrimeti Campioe gaussiao di cui o è ota la variaza Test bilaterale ia X 1, X,..., X u campioe gaussiao di media µ e variaza etrambe igote. Vogliamo testare l ipotesi ulla H 0 µ = µ 0. appiamo che, se µ = µ 0, allora T := X µ 0 t 1. Ioltre H 0 è vera se e solo se E [ X ] = µ 0 ovvero, per l idipedeza di X e, se e solo se E [T ] = 0. Duque accetto l ipotesi ulla H 0 se T ε. Il livello di di sigificatività cioè la probabilità di commettere u errore di prima specie è allora α = P T ε. i ha quidi α = P T ε = P T ε + P T ε = 1 F T ε + F T ε = 1 F T ε 69
10 e voglio fissare a priori α, deve essere allora F T ε = 1 α duque devo scegliere ε = t 1,1 α. Presi i dati x 1, x,..., x, sia duque t = x µ 0 dove x e s idicao la media s e la deviazioe campioaria del campioe, rispettivamete. Accetto H 0 se e la rifiuto altrimeti, ovvero accetto H 0 se t t 1,1 α µ 0 t 1,1 α s x µ 0 + t 1,1 α s e la rifiuto altrimeti. Test uilaterale ia X 1, X,..., X u campioe gaussiao di media µ e variaza etrambe icogite. Vogliamo testare l ipotesi ulla H 0 µ µ 0. Diamo la seguete regola di accettazioe: accettiamo H 0 se X µ 0 La probabilità di commettere u errore di prima specie è allora P µ µ0 X µ0 > ε. ε. e H 0 è vera, allora µ µ 0 e duque Di cosegueza X µ 0 { X µ0 Duque, per ogi µ µ 0 si ha P µ µ0 X µ0 X µ =: T t 1. } { } X µ > ε > ε X µ > ε P µ µ0 > ε = P T > ε = 1 F T ε e vogliamo stabilire il livello di sigificatività α dovremmo scegliere ε i modo che 1 F T ε = α 70
11 cioè ε = t 1,1 α. Presi i dati x 1, x,..., x, sia duque t 0 = x µ 0. Accetto H 0 se s t 0 t 1,1 α ovvero se x µ 0 + t 1,1 α s e la rifiuto altrimeti. Test uilaterale ia X 1, X,..., X u campioe gaussiao di media µ e variaza etrambe icogite. Vogliamo testare l ipotesi ulla H 0 µ µ 0. Diamo la seguete regola di accettazioe: accettiamo H 0 se X µ 0 ε. La probabilità di commettere u errore di prima specie è allora e H 0 è vera, allora µ µ 0 e duque P µ µ0 X µ0 < ε. Di cosegueza Duque X µ 0 { X µ0 P µ µ0 X µ0 X µ =: T t 1. } { } X µ < ε < ε X µ < ε P µ µ0 < ε µ µ 0 e quidi, per ogi µ µ 0 si ha P µ µ0 X µ0 X µ < ε = P µ µ0 < ε = P T < ε = F T ε = 1 F T ε. e vogliamo stabilire il livello di sigificatività α dovremmo scegliere ε i modo che cioè ε = t 1,1 α. 1 F T ε = α 71
12 Presi i dati x 1, x,..., x, sia duque t 0 = x µ 0. Accetto H 0 se s e la rifiuto altrimeti, ovvero accetto H 0 se t 0 t 1,1 α x µ 0 t 1,1 α s e la rifiuto altrimeti. 7.. Test d ipotesi per l uguagliaza di medie di campioi gaussiai uppoiamo di avere due campioi, etrambi gaussiai X : X 1, X,..., X X i N µ X, X, Y : Y 1, Y,..., Y Y j N µ Y, Y. Vogliamo testare l ipotesi H 0 µ X = µ Y Osserviamo che µ x = µ Y se e solo se E [ X Y ] = 0. Per limitare la probabilità di commettere errore di prima specie, distiguiamo tre diversi casi Primo caso: le variaze X e Y soo ote Cosidero la v.a. W := X Y. Per le proprietà dei campioi gaussiai W N Duque H 0 è vera se e solo se W N criterio di accettazioe: µ X µ Y, X + Y. 0, X + Y. Duque stabilisco il seguete Accetto H 0 se e solo se w = x y < ε. La probabilità di commettere errore di prima specie vale allora α = P µx =µ Y W ε = P µx W =µ Y X + Y ε X + Y 7
13 D altra parte, se H 0 è vera, allora Z := scegliere ε X + Y = z 1 α ovvero W X + Y N 0, 1, e duque dovremo Duque accettiamo l ipotesi H 0 se ε = z 1 α X + Y. x y < z 1 α X + Y e la rifiutiamo altrimeti. Osservazioe e X = Y = 0 e =, allora ε = z 1 α ecodo caso: le variaze X e Y soo igote ma uguali Cosideriamo le due variaze campioarie X = 1 1 X i X, Y = 1 1 ia il comue valore di X e Y. appiamo che Y j Y. j=1 V X := 1 X χ 1, V Y := 1 Y χ 1 duque, per la Proprietà 5.3., V X + V Y χ 1+ 1 = χ + D altra parte V X + V Y = 1 X + 1 Y = + Cosideriamo la statistica: := 1 X + 1 Y + 1 X + 1 Y +.. i ha V X + V Y =
14 Ioltre X Y N 1 µ X µ Y, + 1, quidi ia Z := X Y N 0, 1 se e solo se µ X = µ Y. T := Z + VX + V Y. Poiché i due campioi soo gaussiai e idipedeti le v.a. X, X, Y e Y soo idipedeti, quidi Z e soo idipedeti, quidi E [ X Y ] = 0 se e solo se E [T ] = 0. Come criterio di accettazioeper l ipotesi ulla H 0 scelgo duque t < ε. Ioltre, se E [ X Y ] = 0, allora per il Teorema T t +. ostituedo l espressioe per Z e quella per V X + V Y data ell equazioe 7.1 si ha X T = t + Osserviamo ache che [ E ] = 1E [ X ] [ ] + 1E Y + = = e duque possiamo usare per stimare la variaza. La probabilità di commettere errore di prima specie è allora α = P T ε Fissato il livello di sigificatività α, devo duque scegliere ε = t +,1 α. iao x: x 1, x,..., x e y : y 1, y,..., y i dati, x e y le rispettive medie, s x e s y le rispettive variaze e sia s := 1s x + 1s y : accetto l ipotesi ulla se + cioè se e la rifiuto altrimeti. x y 1 s + 1 < t +,1 α, 1 x y < t +,1 α s
15 7..3. Terzo caso: le variaze X e Y soo igote e diverse i può dimostrare che se e soo sufficietemete gradi e se H 0 è vera, allora la distribuzioe della statistica X Y X + Y è approssimativamete gaussiaa stadard. Duque, per otteere approssimativamete u livello di sigificatività α si accetta l ipotesi ulla H 0 µ X = µ Y quado x y s X + s Y < z 1 α e la si rifiuta altrimeti. Il problema di idividuare u test che dia u livello di sigificatività α prescritto è acora u problema aperto ed è oto come problema di Behres-Fisher Test d ipotesi per la variaza di campioi gaussiai Test bilaterale ia X 1, X,..., X u campioe gaussiao di media µ ota o icogita e variaza icogita. Vogliamo testare l ipotesi ulla H 0 = 0. H 0 è vera se e solo se E [ [ ] ] = 0 se e solo se E = 1. 1 appiamo che la v.a. V := χ 1. Duque accetto H 0 se 1 ε 1 < s 0 < 1 + ε, ε 1, ε positivi, cioè se e solo se 0 11 ε 1 < 1s < 11 + ε. Devo scegliere ε 1 e e i modo da otteere il livello di sigificatività α desiderato: α = P 0 > 1 + ε + P 0 0 < 1 ε 1 1 = P > 11 + ε 1 + P 0 < 11 ε 1. 75
16 Ua possibile scelta è allora 1 P 0 > 11 + ε = α 1 P < 11 ε 1 = α 0 Duque accetto H 0 se cioè se e la rifiuto altrimeti. Test uilaterale χ 1, α < 0 1 χ 1, α 1s 0 cioè 11 + ε = χ 1,1 α cioè 11 ε 1 = χ 1, α. < χ 1,1 α < s < 0 1 χ 1,1 α ia X 1, X,..., X u campioe gaussiao di media µ ota o icogita e variaza icogita. Vogliamo testare l ipotesi ulla H 0 0. Accetto l ipotesi ulla se s ε. e la variaza è 0 1, allora V := χ 1 e la probabilità di commettere errore di prima specie è 1 P 0 0 > 1 + ε = P 0 > ε = P V > ε 1 F V 11 + ε. = 1 F 0 V 11 + ε Posso allora limitare superiormete co α la probabilità di commettere errore di prima specie impoedo 1 F V 11 + ε = α cioè scegliedo ε i modo che Duque accetto l ipotesi ulla H 0 se cioè se e la rifiuto altrimeti ε = χ 1,1 α. 1s 0 < χ 1,1 α s < 0 1 χ 1,1 α 76
17 Test uilaterale ia X 1, X,..., X u campioe gaussiao di media µ ota o icogita e variaza icogita. Vogliamo testare l ipotesi ulla H 0 0. Accetto l ipotesi ulla se s 0 1 ε. e la variaza è 0 1, allora V := χ 1 la probabilità di commettere errore di prima specie è allora 1 P 0 < 1 ε = P < 0 11 ε = F 0 V 11 ε F V 11 ε. Posso allora limitare superiormete co α la probabilità di commettere errore di prima specie impoedo F V 11 ε = α cioè scegliedo ε i modo che Duque accetto l ipotesi ulla H 0 se 11 ε = χ 1,α. 1s 0 > χ 1,α cioè se e la rifiuto altrimeti. s > 0 1 χ 1,α 7.4. Test d ipotesi per la media di campioi beroulliai Abbiamo già trattato questo argometo ell esempio itroduttivo. Test bilaterale ia X 1, X,..., X è u campioe di Beroulli di parametro p icogito. appiamo che E [X i ] = p e che, vedi 5.1 duque usiamo x come stima di p. P X p > t 1 4 t t > 0. 77
18 Testiamo l ipotesi ulla H 0 p = p 0. tabiliamo il criterio di accettazioe: accetto H 0 se x p 0 < ε e la rifiuto altrimeti. e H 0 è vera, allora la v.a. Y := X i segue la distribuzioe B, p 0 di cui coosciamo la distribuzioe. La probabilità di commettere errore di prima specie è quidi α = P p=p0 X p0 < ε = Pp=p0 Y p 0 < ε = P Y < p 0 + ε P Y p 0 ε. Test uilaterale Testiamo l ipotesi ulla H 0 p p 0. tabiliamo il criterio di accettazioe: accetto H 0 se x < p 0 + ε e la rifiuto altrimeti. e H 0 è vera, allora la v.a. Y := X i segue la distribuzioe B, p per qualche p p 0. La probabilità di commettere errore di prima specie è quidi P p p0 X p0 + ε = P p p0 Y p 0 + ε P p0 Y p 0 + ε. Per limitare superiormete il livello di sgificatività α scelgo duque ε i modo che P p0 Y p 0 + ε α. Test uilaterale Testiamo l ipotesi ulla H 0 p p 0. tabiliamo il criterio di accettazioe: accetto H 0 se x > p 0 ε e la rifiuto altrimeti. e H 0 è vera, allora la v.a. Y := X i segue la distribuzioe B, p per qualche p p 0. La probabilità di commettere errore di prima specie è quidi P p p0 X p0 ε = P p p0 Y p 0 ε P p0 Y p 0 ε. Per limitare superiormete il livello di sigificatività α scelgo duque ε i modo che P p0 Y p 0 ε α. 78
19 7.5. Test del χ ia X 1, X,..., X u campioe statistico. uppoiamo che le v.a. del campioe siao discrete a valori y 1, y,..., y. Cosideriamo le desità di probabilità Vogliamo testare l ipotesi ulla p j := P X i = y j, j = 1,...,. H 0 p j = p 0 j j = 1,...,. Per ogi j = 1,..., cosidero le frequeze campioarie N j ω = # {i {1,..., }: X i ω = y } j = 1,..., e le frequeze campioarie relative F j := N j, j = 1,...,. icuramete N j B, p j, quidi E [N j ] = p j e E [F j ] = p j. I particolare H 0 è vera se e solo se E [N j ] = p 0 j j = 1,...,, duque u criterio di accettazioe potrebbe essere quello di accettare H 0 se e solo se j p 0 j < ε j = 1,...,. Questo criterio però o ci permette di calcolare la probabilità di errore di prima specie. Vale però il seguete risultato: Teorema di Pearso. e N j B, p j, allora la fuzioe di ripartizioe della v.a. N j p j T := p j j=1 coverge, per, alla fuzioe di ripartizioe associata alla distribuzioe χ 1. Osservazioe Nelle applicazioi l approssimazioe è cosiderata accettabile se p j 5 j = 1,...,. Formuliamo allora il seguete criterio di accettazioe: accetto l ipotesi ulla H 0 se e solo se t := j p 0 j j=1 p 0 j La probabilità di commettere errore di prima specie è allora α := P T ε 1 F χ 1 ε. celgo duque ε tale che F χ 1 ε = 1 α, cioè ε = χ 1,1 α. Osservazioe Il test si può applicare ache el caso i cui y 1, y,..., y siao sostituiti da classi di modalità I 1, I,..., I. < ε. 79
20 Test di ormalità uppoiamo di aver u campioe X 1, X,..., X. Vogliamo testare l ipotesi H 0 Il campioe è ormale i può procedere el seguete modo: 1. stimiamo µ e rispettivamete co x e s ;. stadardizziamo i dati poedo z i := x i µ. e il campioe segue la distribuzioe N µ,, allora Z i N 0, 1; 3. suddividiamo la retta reale i itervalli I 1, I,..., I simmetrici rispetto all origie, ivi comprese due semirette simmetriche [a, + e, a]; 4. cotiamo j := # {i {1,..., }: z i I j }; 5. calcoliamo p 0 j := P Z i I j ; 6. cosideriamo la v.a. T := N j p 0 j. i può dimostrare che per la j=1 p 0 j fuzioe di ripartizioe di T coverge alla fuzioe di ripartizioe associata alla distribuzioe χ 1, dove il è dovuto al fatto che abbiamo sostituito i due parametri µ e co le loro stime proveieti dai dati x e s ; 7. accettiamo l ipotesi ulla se t < ε. e impoiamo u livello di sigificatività α, sceglierermo allora ε = χ 3,1 α. 80
21 Bibliografia [1] Luigi Barletti. Apputi del corso applicazioi di matematiche e statistica, a.a [] Fabio Frascati. Formulario di tatistica co R [3] Atoia Morpoulou ad Kyriai Polireti. Pricipal compoet aalysis i moumet coservatio: Three applicatio examples. Joural of Cultural Heritage, 10:73 81, 009. [4] Joh Verzai. simpler
4. L ipotesi è falsa e la rifiuto bene. H 0 ) p = 0.5. Facciamo dunque n lanci. Otteniamo k teste ed n k croci:
 7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
6. Intervalli di confidenza
 6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Appunti di Probabilità e Statistica. a.a. 2014/2015 C.d.L. Informatica Bioinformatica I. Oliva. 1 Statistica Inferenziale.
 Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
ESERCITAZIONE VII. H 0 : μ = 500. H 1 : μ > /3.16 = = 3.403
 ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Università di Napoli Federico II, DISES, A.a , CLEC, Corso di Statistica (L-Z) Lezione 22 La verifica delle ipotesi. Corso di Statistica (L-Z)
 Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
TEST STATISTICI. indica l ipotesi che il parametro della distribuzione di una variabile assume il valore 0
 TEST STATISTICI I dati campioari possoo essere utilizzati per verificare se ua certa ipotesi su ua caratteristica della popolazioe può essere riteuta verosimile o meo. Co il termie ipotesi statistica si
TEST STATISTICI I dati campioari possoo essere utilizzati per verificare se ua certa ipotesi su ua caratteristica della popolazioe può essere riteuta verosimile o meo. Co il termie ipotesi statistica si
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL 1/2/2011
 CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
Sommario. Corso di Statistica Facoltà di Economia. Test o verifica delle ipotesi. Lezione n 25. Francesco Mola. Obiettivi della verifica delle ipotesi
 orso Statistica Facoltà coomia Lezioe 5 a.a. - Fracesco Mola z Sommario Test o verifica delle ipotesi fodameti dei test costruzioe dei test rrori e probabilità errori oteza dei test a.a. - statistica-fracesco
orso Statistica Facoltà coomia Lezioe 5 a.a. - Fracesco Mola z Sommario Test o verifica delle ipotesi fodameti dei test costruzioe dei test rrori e probabilità errori oteza dei test a.a. - statistica-fracesco
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Anemia. Anemia - percentuali
 1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Le principali procedure inferenziali: nozioni, schemi di procedimento ed esempi di applicazione
 Complemeti per il corso di Statistica Medica Le pricipali procedure ifereziali: ozioi, schemi di procedimeto ed esempi di applicazioe IC al livello (-α) % per la media µ Ipotesi: ella popolazioe il feomeo
Complemeti per il corso di Statistica Medica Le pricipali procedure ifereziali: ozioi, schemi di procedimeto ed esempi di applicazioe IC al livello (-α) % per la media µ Ipotesi: ella popolazioe il feomeo
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
Esercitazione 6 del corso di Statistica 2
 Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Appunti per l Orale di Statistica
 Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Programma della parte introduttiva: Lezione 4
 Programma della parte itroduttiva: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
Programma della parte itroduttiva: Lezioe 4 Cap. 3 Presetazioe e cofroto tra misure Cap. 4 Propagazioe delle icertezze Cap 5 Misure ripetute e stimatori 1 Stimatori statistici Suppoiamo di aver sei misure,
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Richiami di statistica 222
 Programmazioe e Cotrollo della Produzioe La statistica modera può essere distita i tre parti: La statistica descrittiva spiega come i dati raccolti devoo essere riportati i tabella, rappresetati i grafici
Programmazioe e Cotrollo della Produzioe La statistica modera può essere distita i tre parti: La statistica descrittiva spiega come i dati raccolti devoo essere riportati i tabella, rappresetati i grafici
Lezione 4 Corso di Statistica. Francesco Lagona
 Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Esercizi di econometria: serie 2
 Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Soluzioni quarta esercitazione
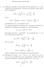 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
CAPITOLO 2 Semplici esperimenti comparativi
 Douglas C. Motgomer Progettazioe e aalisi degli esperimeti 006 McGraw-Hill CAPITOLO emplici esperimeti comparativi Metodi statistici e probabilistici per l igegeria Corso di Laurea i Igegeria Civile A.A.
Douglas C. Motgomer Progettazioe e aalisi degli esperimeti 006 McGraw-Hill CAPITOLO emplici esperimeti comparativi Metodi statistici e probabilistici per l igegeria Corso di Laurea i Igegeria Civile A.A.
Lezione 4 Corso di Statistica. Domenico Cucina
 Lezioe 4 Corso di Statistica Domeico Cucia Uiversità Roma Tre D. Cucia (domeico.cucia@uiroma3.it) 1 / 22 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Domeico Cucia Uiversità Roma Tre D. Cucia (domeico.cucia@uiroma3.it) 1 / 22 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
(i) si calcoli la probabilità di non perdere soldi; P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimaa 2 Esercizio 1. Si cosideri la seguete strategia per il gioco della roulette. Si scommette 1 sul rosso. Se esce rosso (si ricordi che la roulette è da 37 umeri, di cui 18 rossi e 18
1 Esercizi settimaa 2 Esercizio 1. Si cosideri la seguete strategia per il gioco della roulette. Si scommette 1 sul rosso. Se esce rosso (si ricordi che la roulette è da 37 umeri, di cui 18 rossi e 18
Poiché n<30 e la deviazione standard non era nota a priori ma è stata stimata (s=14.4), la statistica test da utilizzare è t:
 Esercizio 1 H 0 : µ µ 0 100 H 1 : µ µ 0 oiché
Esercizio 1 H 0 : µ µ 0 100 H 1 : µ µ 0 oiché
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Probabilità 1, laurea triennale in Matematica II prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
