Esempio 1 Determinazione modi propri e forme modali per sistema a 2 gdl 7.1
|
|
|
- Aurora Pastore
- 4 anni fa
- Visualizzazioni
Transcript
1 Esempo Detemnazone mod pop e fome modal pe sstema a gdl 7.
2
3 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
4 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
5 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Esempo 4 Detemnazone oscllazone lbea pe sstema a gdl S detemn la legge del moto pe l sstema d Fg. 7., con le seguent condzon nzal. CdL Specalstca/Magstale n Ingegnea Meccanca
6 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
7 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE L equazone d equlbo dnamco pe l sstema non smozato con fozante : Ωt [ M ]{ && x} [ K]{} x { F t } { F} e Sosttuendo nell equazone lo svluppo n base alle fome modal: { x t } [ Y ]{} q [ M ][ Y ]{ q&& } [ K][ Y ]{ q} { F t } e pe-moltplcando pe la tasposta della matce modale: [ Y ] [ M ][ Y ]{} q&& [ Y ] [ K][ Y ]{ q} [ Y ] { F t }
8 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE s ottene: []{} {} [ ] { } t n e F Y q q I Ω && { } { } t t e f e F Y q q Ω Ω && che costtusce un sstema d n equazon ndpendent dsaccoppate del tpo: [ ] [ ][ ]{} [ ] [ ][ ]{ } [ ] { } t e F Y q Y K Y q Y M Y Ω &&
9 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE S osseva che la fozante estena ha andamento nel tempo d tpo amonco: q&& q Ωt Assumendo una soluzone del tpo: S ottene: q Ω t Q Q e Ω Ωt Q f e Ωt e Q e Ωt Q Q Ω f f f e Ωt
10 Q SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE Ω f La soluzone geneale sulta qund data da: N { x t } Q { Y } Ωt e che può essee vsta come sovapposzone d N oscllato elementa ad gdl. N { } Ωt Y e Ω f
11 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE CEDEVOLEZZA DINAMICA Rsulta utle fomalzzae l compotamento geneale del sstema attaveso una matce d cedevolezza dnamca. Posto: Ωt Ωt { F t } { F} e { x t } { X} e S defnsce matce d cedevolezza dnamca la matce α : { X} [ α ]{ F} Ω Dall equazone d equlbo dnamco s ha: Pe cu: [ K ] Ω [ M ]{ X} { F} [ ] [ K] Ω [ M ] α Ω
12 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE CEDEVOLEZZA DINAMICA [ ] [ K] Ω [ M ] α Ω [ Y ] α [ Ω ] [ Y ] [ Y ] [ K] Ω [ M ] [ Y ] [ Ω ] [ Y ] dag[ Ω ] [ Y ] α [ Ω ] [ Y ] dag[ Ω ][ Y ] α [ α Ω ] [ Y ] dag[ Ω ] [ Y ] α Ω { } Y Y { } N Ω
13 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE CEDEVOLEZZA DINAMICA L espessone della matce d cedevolezza dnamca può essee ottenuta anche a pate dalle coodnate modal: Ωt Ωt { F t } { F} e { x t } { X} e { X} [ Y ]{ Q} S osseva che sulta : pe cu s ha: { Q} dag[ Ω ] [ Y ] { F} da cu s ottene mmedatamente: { X} [ Y ] dag[ Ω ] [ Y ] { F} [ α Ω ] [ Y ] dag[ Ω ] [ Y ] α Ω { } Y Y { } N Ω
14 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
15 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
16 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
17 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
18 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
19 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
20 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
21 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Foma modale CdL Specalstca/Magstale n Ingegnea Meccanca
22 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Foma modale CdL Specalstca/Magstale n Ingegnea Meccanca
23 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Foma modale CdL Specalstca/Magstale n Ingegnea Meccanca
24 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Foma modale CdL Specalstca/Magstale n Ingegnea Meccanca
25 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
26 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
27 SISEMA A MOLI G.D.L. LIBERO SMORZAO CARAERISICHE GENERALI DELLA SOLUZIONE Equazone d equlbo dnamco [ M ]{&& x} [ C]{ x& } [ K ]{ x} S dovebbeo cecae soluzon del tpo λt { x} { Z} e λt {} x& λ{ Z} e λ {} && x λ { Z} e t sosttuendo: λ λt λt λt [ M ]{ Z} e λ[ C]{ Z} e [ K ]{ Z} e da cu: λ [ M ] λ[ C] [ K] { Z}
28 λ [ M ] λ[ C] [ K] { Z} SISEMA A MOLI G.D.L. LIBERO SMORZAO CARAERISICHE GENERALI DELLA SOLUZIONE Pe avee soluzone non banale det λ [ M ] λ[ C] [ K] Da cu l polnomo caattestco: λ N N aλ. an λ a N coppe d adc autovalo λ complesse conugate, che sosttute, fonscono N coppe d autovetto compless {Z }. Poblema agl autovalo n campo complesso, solvble dettamente pe pccol N, o con metod numec pe N gand. Nel seguto saanno pesentate delle metodologe d soluzone analtca, fnalzzate pncpalmente a evdenzae le caattestche geneal del compotamento del sstema. N
29 SISEMA A MOLI G.D.L. LIBERO SMORZAO CARAERISICHE GENERALI DELLA SOLUZIONE Equazone d equlbo dnamco [ M ]{&& x} [ C]{ x& } [ K ]{ x} La pocedua d soluzone, come è lecto attendes, è fotemente nfluenzata dalla natua della matce [C]. In patcolae è oppotuno dstnguee due cas: la matce [C] vene dagonalzzata dalla matce modale [Y] del sstema non smozato Smozamento Classco o Classcal Dampng la matce [C] non vene dagonalzzata dalla matce modale [Y] Smozamento Non Classco o Non Classcal Dampng
30 SISEMA A MOLI G.D.L. LIBERO SMORZAO CLASSICAL DAMPING In geneale [ Y ] [ C][ Y ] non è una matce dagonale, pe cu le equazon del moto non possono essee dsaccoppate. Se lo smozamento è molto pccolo, dvene lecto assumee fome dagonalzzabl della matce d smozamento. In tal caso s ha Smozamento Classco o Classcal Dampng : d c d [ Y ] [ C][ Y ] [ C ]. dag[ c ] c d d Matce modale sstema non smozato c.... c nd d
31 SISEMA A MOLI G.D.L. LIBERO SMORZAO CLASSICAL DAMPING Ponendo: { x t } [ Y ]{ q t } { x & t } [ Y ]{ q& } {& x t } [ Y ]{ q& } Sosttuendo nell equazone d equlbo dnamco: [ M ][ Y ]{} q&& [ C][ Y ]{ q& } [ K ][ Y ]{ q} Pemoltplcando pe la tasposta della matce modale [ Y ][ M ][ Y ]{ q&& } [ Y ] [ C][ Y ]{ q& } [ Y ][ K][ Y ]{ q} da cu: [ ]{ } [ ]{ } [ I q&& dag q& dag ]{ q}
32 SISEMA A MOLI G.D.L. LIBERO SMORZAO CLASSICAL DAMPING []{ } [ ]{ } [ I q&& dag q& dag ]{ q} Sstema d N equazon ndpendent dsaccoppate del tpo: q&& q& q cu cospondono autovalo λ ± ± q e soluzon del tpo: [ t ] t t t e A e A e s s s
33 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I SISEMA A MOLI G.D.L. LIBERO SMORZAO CLASSICAL DAMPING CdL Specalstca/Magstale n Ingegnea Meccanca Pe quanto guada gl autovetto fome modal s dmosta che, nel caso d smozamento classco, concdono con quell del sstema non smozato. [ K] [ M ] { Y } n [ M ] λ [ C] [ K] { λ Z } Sstema non smozato Sstema smozato { } { } Ipotzzando che valga la: Z Y [ ] [ ] [ ]{ λ M λ C K Y } [ K] [ M ] { Y } n λ [ ]{ } [ ]{ M Y λ C Y } [ M ]{ Y } n Pemoltplcando pe la tasposta della foma modale {Y }: λ s ottene: { } [ ]{ } { } [ ]{ } { } Y M Y λ Y C Y Y [ M ]{ Y } n
34 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I SISEMA A MOLI G.D.L. LIBERO SMORZAO CLASSICAL DAMPING S dmosta qund che l poblema agl autovalo del sstema smozato è soddsfatto dagl autovetto del sstema non smozato e da autovalo dat dalla elazone pecedente. { } [ ]{ } { } [ ]{ } { } [ ]{ } n Y M Y Y C Y Y M Y λ λ λ λ λ ± ± [ ] [ ] [ ] { } Y K C M λ λ λ ±
35 SISEMA A MOLI G.D.L. LIBERO SMORZAO UN CASO DI CLASSICAL DAMPING SMORZAMENO PROPORZIONALE S dmosta che la matce d smozamento è dagonalzzable se: m l [ C] [ M ] α [ M ] [ K ] l l Se s pone m, s ottene l cosddetto smozamento popozonale o d Raylegh. [ C] α [ M ] β[ K]
36 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale Combnando: [ ] [ ] [ ] K M C β α { } [ ]{ } { } [ ]{ } " " " " " " " " s pe Y M Y s pe Y M Y s s { } [ ]{ } { } [ ]{ } " " " " " " " " s pe Y K Y s pe Y K Y s s con: [ ] [ ][ ][ ] [ ] [ ][ ] [ ][ ][ ] [ ] [ ] d d c dag I Y K Y Y M Y Y C Y C β α β α β α s ottene: SISEMA A MOLI G.D.L. LIBERO SMORZAO UN CASO DI CLASSICAL DAMPING SMORZAMENO PROPORZIONALE
37 SISEMA A MOLI G.D.L. LIBERO SMORZAO UN CASO DI CLASSICAL DAMPING SMORZAMENO PROPORZIONALE cd α β Combnando con : s ottene: α β α β cd
38 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING L equazone d equlbo dnamco pe l sstema smozato con fozante estena: { } [ ] { } t q Y t x Sosttuendo nell equazone d equlbo dnamco: pe-moltplcando pe la tasposta della matce modale, qualoa la matce C sa dagonalzzable, s ottene: []{} {} {} [ ] { } t F Y q q q I n n n & && { } { } t t e f e F Y q q q Ω Ω && che costtusce un sstema d n equazon ndpendent dsaccoppate del tpo: [ ]{ } [ ]{} [ ]{ } { } t F x K x C x M & &&
39 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING Assumendo una soluzone del tpo: t e f q q q Ω && t e Q t q Ω S ottene: t t t t e f Q e Q e Q e Ω Ω Ω Ω Ω Ω Ω Ω f Q
40 SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING La soluzone completa assume qund una foma del tpo: { x t } N Ω f Ω { Y } e ovveo la somma del contbuto d N oscllato ad gdl, ognuno cospondente ad uno de mod pop. Sstema fozato a gdl effetto smozamento Ωt
41 SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING Contbuto de due mod pop
42 SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING Andamento modulo e fase spostament
43 SISEMA A MOLI G.D.L. SMORZAO OSCILLAZIONI FORZAE CLASSICAL DAMPING CEDEVOLEZZA DINAMICA Rsulta utle, anche n questo caso, fomalzzae l compotamento geneale del sstema attaveso una matce d cedevolezza dnamca, defnta come : { X } [ α ]{ F} Ω Dall equazone d equlbo dnamco s ha: [ K ] Ω[ C] Ω [ M ]{ X} { F} Pe cu: [ α Ω ] [ K] Ω[ C] Ω [ M ] [ Y ] α [ Ω ] [ Y ] [ Y ] [ K] Ω[ C] Ω [ M ] [ Y ] [ Ω ] [ Y ] dag[ ] Ωdag[ ] Ω [ I ] [ Y ] α
44 SISEMA A MOLI G.D.L. NON SMORZAO OSCILLAZIONI FORZAE MEODO DI SOVRAPPOSIZIONE MODALE CEDEVOLEZZA DINAMICA α [ Y ] α [ α Ω ] [ Y ] Ω [ Ω ] [ Y ] dag[ ] Ωdag[ ] Ω [ I ] [ α Ω ] [ Y ] dag[ Ω Ω ] [ Y ] dag[ Ω Ω ][ Y ] [ α Ω ] [ Y ] dag[ Ω Ω ] [ Y ] { } Y Y { } N Ω Ω
45 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Soluzone con metodo detto
46 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
47 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
48 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
49 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I Calcolae la sposta fozata del sstema d Fg., usano dat dell eseczo pecedente CdL Specalstca/Magstale n Ingegnea Meccanca
50 Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Specalstca/Magstale n Ingegnea Meccanca
51 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Se temn fuo dagonale della matce [ ] [ ] C Y [ C][ Y ] d sono tascuabl, s può assumee pe essa una foma dagonale, nella quale lo smozamento d ogn modo vene genealmente ottenuto dettamente pe va spementale [ ] C n N d..... nn
52 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Una quantfcazone dell mpotanza elatva de temn fuo dagonale è data dal cosddetto Coeffcente d Accoppamento Ξ: [ C ] d c d c d c c d d c NNd Ξ max c c d dc d
53 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE È possble vefcae quanttatvamente l eoe commesso nel tascuae temn fuo dagonale, nel caso del sstema fozato a gdl. S assume una matce d smozamento pncpale del tpo: [ ] C d Ξ n 4 n n Ξ 4 S calcola qund la sposta del sstema, n temn d un vettoe complesso d ampezze d spostamento, tamte soluzone detta esatta delle equazon del moto: n { } [ ] [ ] X, Ω, Ξ K Ω C Ω [ M ] exact [ C] [ Y ] [ ][ ] C Y d n n { F}
54 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE S calcola qund la sposta del sstema con l MSM, utlzzando la matce d spostamento pncpale seguente nella quale sono stat tascuat temn fuo dagonale : [ ] * n C d S ottene n tal modo un alto vettoe complesso d ampezze d spostamento { X, Ω, Ξ } MSM n N Ω Ω f { Y }
55 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE S defnsce qund un eoe pecentuale massmo della soluzone ottenuta tascuando temn fuo dagonale, nella foma : E, Ω, Ξ max, Ω, Ξ X MSM,, Ω, Ξ X, Ω, Ξ X exact,, N max, N exact, nella quale l eoe assoluto vene appotato al massmo valoe d ampezza che s vefca, ta tutt gad d lbetà, pe valo dat d Ω, Ξ ed. Nel seguto s analzza l andamento dell eoe, pe un sstema a gdl, n un ange d valo d smozamento < <.5 e d fequenza < Ω < 3 Hz. Le pulsazon natual del sstema sono: n 3.6 Hz n 3.7 Hz
56 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Ξ.
57 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Ξ.5
58 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Ξ.5
59 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Ξ.
60 SISEMA A MOLI G.D.L. LIBERO SMORZAO NON CLASSICAL DAMPING EFFEO ERMINI FUORI DIAGONALE Ossevazon: l eoe pecentuale massmo commesso tascuando temn fuo dagonale appae dpendee pncpalmente dal Coeffcente d accoppamento Ξ, ducendos a poche untà pecentual su tutto l campo d fequenze e smozament analzzato pe Ξ < l eoe pecentuale massmo appae dpendente anche dal lvello geneale d smozamento, assumendo genealmente valo nfeo a poche untà pecentual pe <. esstono tuttava delle condzon Es: valo d elatvamente elevat >.-. nelle qual l eoe commesso tascuando temn fuo dagonale può sultae naccettable; n tal condzon, dventa necessao solvee dettamente le equazon del moto accoppate, coendo all Anals Modale/Amonca Non Classca, tamte la tecnca detta dello Spazo delle Vaabl d Stato o dello Spazo degl Stat.
61 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI Qualoa la matce d smozamento non sa dagonalzzable,è necessao pocedee alla soluzone detta del poblema agl autovalo n campo complesso. Nel seguto vedemo le pncpal caattestche della tecnca d soluzone detta d Anals nello Spazo degl Stat State Space Analyss, non tanto con l ntento d ottenee stument effettv d calcolo, quanto d pote evdenzae, anche pe questo caso, alcune delle caattestche salent della soluzone. Vettoe della vaabl d stato N component, nseme appesentano completamente lo stato del sstema: { u t } { x t } { x& t } S aggungono alle N equazon d equlbo, N ulteo equazon sempe vefcate: [ M ]{ && x} [ C]{} x& [ K]{ x} { F t } [ M ]{} x& [ M ]{} x&
62 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI [ M ]{ && x} [ C]{} x& [ K]{ x} { F t } [ M ]{} x& [ M ]{} x& In foma matcale [ C] [ M ] [ M ] [ ] Posto: x& && x C M [ K] [ ] [] [ M ] M x x& [ A] [ B] S ottene: [ A ]{ u& } [ B]{ u} K M
63 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI Assumendo una soluzone del tpo: { x} { X } {} x& s{ X } e st S ottene: { t } e st { X } { X } { X } { X } st u e st st {& t } s s e e { X } e { X } s { X } { X } st u e st st s e s s { U} e st s { U} e st
64 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI Sosttuendo: { t } S ottene: { X } { X } e { X } { X } st u e st st s e s st s{ X } e s{ X } u & t e { } { } st s st s X e s X { } s [ st ]{ } [ st A U e B ]{ U} e Ovveo: s[ A] [ B ]{ U} { U} e st { U} e st [ A ]{ u& } [ B]{ u} Poblema agl autovalo n foma genealzzata, che può potas a quella standad: [ A] [ B]{ U} s{ U}
65 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI La soluzone compende N coppe d autovalo compless conugat λ N coppe d autovetto assocat {Z }, anch ess compless conugat, che soddsfano la: [ A] [ B]{ Z } { } λ Z { } λ, { Z } Autovaloe autovettoe λ, Z Conugat Autovalo ed autovetto nello spazo delle vaabl d stato: λ s λ s n n n n { } { } λ λ { Z} { Z } { Z } { } Z
66 Matce modale complessa NxN SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI [ ] [{ } { } ] Popetà d otogonaltà spetto alle matc d sstema [ ][ A][ ] dag[ a ] [ ] [ B][ ] dag[ b ] b λ a Vettoe vaabl d stato come combnazone lneae autovetto compless { u t } [ ]{ q t } { u & t } [ ]{ q& t }
67 Sosttuendo nel sstema ognale: { u t } [ ]{ q t } { u & t } [ ]{ q& t } S ottene: [ A ][ ]{} q& [ B ][ ]{ q} [ A ]{ u& } [ B]{ u} Moltplcando pe la tasposta della matce modale complessa [ ][ A][ ]{ q& } [ ] [ B ][ ]{ q} enendo conto della otogonaltà, che vale anche pe queste fome modal: dag [ a ]{ q& } dag[ b ]{ q} SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI
68 dag SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI [ a ]{} q& dag[ b ]{ q} Sstema d N equazon dsaccoppate del tpo: a q & Soluzone d cascuna d esse q Soluzone complessva N { u t } { } b q λt t Q e Q e λ t
69 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI In pesenza d fozant [ A ]{ u& } [ B]{} u { p t } Dove s è posto: { p t } { F} {} e Ω t { } Ωt P e Assumendo, come al solto, una soluzone del tpo : { u t } [ ]{ q t } [ ]{ } Ωt { u& t } Ω[ ]{ Q} e Q e Ωt Sosttuendo nella equazone dello Spazo degl Stat: Ω [ ][ ]{ } Ωt [ ][ ]{ } Ωt { } Ωt A Q e B Q e P e
70 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI Ω [ ][ ]{ } Ωt [ ][ ]{ } Ωt { } Ωt A Q e B Q e P e [ A][ ]{ Q} [ B][ ]{ Q} { P} Ω Ω[ A] [ B] [ ]{ Q} { P} [ ]{ } [ ] [ ] Q Ω A B { P} Intoducendo, ancoa una volta, la matce d flessbltà: [ ]{ Q} [ α ]{ P} S ottene: [ ] α Ω[ A] [ B]
71 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI [ ] α Ω[ A] [ B] Pe e post-moltplcando pe la matce modale [ ][ α ] [ ] [ ] Ω[ A] [ B] [ ] [ ] [ ] [ ] α Ω dag a dag b [ ] α [ ] [ ] [ ] dag[ a ] Ω [ I ] dag[ λ ] [ ] [ ] α [ ] dag[ a ] dag[ Ω λ ] [ ] [ ] [ ] [ ] [ ] α dag a dag Ω λ [ ]
72 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI [ ] [ ] [ ] [ ] α dag a dag Ω λ [ ] Il sngolo temne della matce d cedevolezza dnamca è dato da: α k k Ω Ω { }{ } N k a N Ω λ { }{ } a Se s tene conto che gl autovalo/vetto compaono n coppe complesse conugate, s può poe: α k Ω λ { }{ } k a Ω λ
73 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI { }{ } { }{ } Ω Ω Ω N k k k a a α { }{ } { }{ } Ω Ω Ω N k k k a a α { }{ } { }{ } Ω Ω Ω Ω Ω N k k k a a a a α { }{ } { }{ } { }{ } { }{ } Ω Ω Ω Ω Ω N k k k k k a a a a a a α
74 CdL Specalstca/Magstale n Ingegnea Meccanca Coso d Pogettazone Assstta delle Stuttue Meccanche Pate I CdL Magstale n Ingegnea Meccanca Coso d Costuzone d Macchne Dnamca Stuttuale SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI { }{ } { }{ } Ω Ω Ω Ω N k k k a a a a Im Re α { }{ } { }{ } { }{ } Ω Ω Ω Ω N k k k k a a a a a Re Im Re α { }{ } { }{ } { }{ } Ω Ω Ω Ω N k k k k a a a a a Re Im Re α
75 SISEMA A MOLI G.D.L. LIBERO SMORZAO ANALISI NON CLASSICA SPAZIO DEGLI SAI α Il confonto ta l espessone tovata pe la matce d cedevolezza dnamca nel caso d smozamento non classco: k Ω N { }{ } { }{ } Ω Re k a Im k a Re { }{ k } a a a Ω Ω e quella tovata n pecedenza pe l caso d smozamento classco: α Ω { } Y Y { } N Ω Ω s può ossevae come la pncpale dffeenza ta le due sa che, nella pma, l numeatoe dpende da Ω. uttava, dato che sngol temn della sommatoa sono sgnfcatv sopattutto n un stetto ange d valo d Ω attono alla sonanza, l andamento effettvo atteso delle due dvese espesson saà molto smle.
ESERCITAZIONE DEL 10 MARZO 2005
ESERCITAZIONE DEL 10 MARZO 005 Poblema pano n.5 Dato l sstema composto da un asta gda vncolata con una cenea n O e un dsco gdo d aggo R vncolato all asta da un contatto blateo con puo otolamento, detemnae
MACCHINA ELEMENTARE CON UN SOLO AVVOLGIMENTO
MAHINA ELEMENTARE ON UN SOLO AVVOLGIMENTO S consde una macchna elementae avente le seguent caattestche: statoe a pol salent otoe clndco un avvolgmento sul otoe pol pp = 1 θ = θ m ω = ω m 1 La macchna può
ESERCITAZIONE 8. Esercitazioni del corso FONDAMENTI DI PROCESSI CHIMICI Prof. Gianpiero Groppi
Dpatmento d Enega oltecnco d Mlano azza eonado da nc - 01 MINO Esectazon del coso FONDMENI DI ROESSI HIMII of. Ganpeo Gopp ESERIIONE 8 alcolo della tempeatua d bolla e d ugada d una mscela n-butano/n-esano
Condizioni di equilibrio TD nelle reazioni chimiche
Condzon d equlbo TD nelle eazon chmche Voglamo studae l metodo geneale pe la detemnazone delle condzon d equlbo d un sstema fomato da N spece chmche dvese n pesenza d una eazone chmca. S utlzza una funzone
Esempio 1 Determinazione modi propri e forme modali per sistema a 2 gdl 7.1
Corso Corso di Progettazione di Costruzione Assistita di Macchine delle Strutture Dinamica Meccaniche Strutturale Parte I Esempio 1 Determinazione modi propri e forme modali per sistema a gdl CdL Specialistica/Magistrale
ESPERIMENTO CASUALE. P(X) è la funzione di probabilità secondo la quale ad ogni numero reale di X si assegna una misura di probabilità.
ESPERIMENTO CASUALE S Spazo camponao : è l nseme d event necessa e ncompatbl che s pesentano come sultat dell ESPERIMENTO CASUALE. X è l nseme de nume eal assocato ad S, n modo che ad ogn elemento (evento)
Sessione live #1 Settimana #2 dal 10 al 16 marzo. Statistica descrittiva: Indici di posizione, dispersione e forma Istogramma frequenze, box plot
Sessone lve #1 Settmana # dal 10 al 16 mazo Statstca descttva: Indc d poszone, dspesone e foma Istogamma fequenze, box plot Lezon CD: 1 - - 3 Eseczo 1 S consde la seguente dstbuzone delle nduste tessl
Approcci algoritmici. Capitolo Approccio sequenziale. y = y (che collegano il modello di trasporto a quello di
Captolo 3 Appocc algotmc In questo captolo descveemo alcun appocc algotmc mat alla soluone del poblema pesentato nel pmo captolo. C sono dves mod d pos spetto ad un poblema con un numeo così elevato d
Lezione 9. N-poli. N-poli passivi. Pilotato in tensione
Lezone 9 N-pol 4 Fn oa c samo lmtat a bpol. Esstono peò anche dspostv che non sono conducbl a bpol, nel senso che non nteagscono con l esteno attaveso due sol pol. In fgua è appesentato un quadpolo, ma
Esercizi sulle reti elettriche in corrente continua (parte 2)
Esecz sulle et elettche n coente contnua (pate ) Eseczo 3: etemnae gl equalent d Theenn e d Noton del bpolo complementae al esstoe R 5 nel ccuto n fgua e calcolae la coente che ccola attaeso l esstoe R
Momento angolare. Considero il moto di una particella di massa m lungo la traiettoria indicata e calcolo la variazione del suo momento angolare
Noe fle d:\scuola\cos\coso fsca\eccanca\oento angolae\oento angolae, d'neza e cento d assa.doc eato l 0//00 9.46 Densone fle: 48640 byte laboato l 7//00 alle oe 0.44, salvato l 5//0 7. stapato l 7//00
Economia del turismo. Prof.ssa Carla Massidda
Economa del tusmo Pof.ssa Cala Massdda Pate 2 Agoment Defnzone d domanda tustca Detemnant della domanda tustca L elastctà della domanda tustca La stma della domanda tustca Defnzone d domanda tustca Dato
Economia del turismo
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2014-2015 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 4 LA DOMANDA
CONDUZIONE NON STAZIONARIA
CONDUZIONE NON AZIONARIA Caso geneale de sstem a tempeatua unfome ebbene l pocesso d conduzone non stazonaa n un soldo sa comunemente dovuto allo sco temco convettvo dal fludo ccostante, alt pocess d sco
Sviluppo dell algoritmo per l allineamento dello spettrometro magnetico di PAMELA
Svluppo dell algotmo pe l allneamento dello spettometo magnetco d PAMELA Fancesca Gamb Unvestà degl Stud d Fenze Congesso Nazonale SIF 19 Settembe 003 Lo spettometo magnetco d PAMELA Lo spettometo magnetco
Figura 1 Geometria attuale. Figura 2 Sezione trapezia
ESERCITAZIONE N. 4 (20 aple 2005) Dmensonamento daulco d un canale apeto PROBLEMA Nel pogetto d ecupeo d un aea s ntende potae alla luce un canale che n passato è stato tombnato con tubazon pefabbcate
Economia del turismo
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc A.A. 2013-2014 Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof.ssa Cala Massdda Sezone 8 I MODELLI
Sommario. Facoltà di Economia E E2 E 5 E 4. S x1. Le Variabili Casuali o Variabili Aleatorie. francesco mola. Lezione n 13.
Coso d Statstca Facoltà d conoma a.a. - fancesco mola Sommao Le Vaabl Casual o Vaabl Aleatoe Lezone n Lez._a.a. 9- statstca-fancesco mola Vaabl Casual Vaabl Casual (cont. Una Vaable Casuale è una egola
Sommario. Corso di Statistica Facoltà di Economia. Le Variabili Casuali o Variabili Aleatorie. Lezione n 16. Francesco Mola. Variabili Casuali (cont
Coso d Statstca Facoltà d conoma Lezone n 6 z Sommao Le Vaabl Casual o Vaabl Aleatoe a.a. - Fancesco Mola a.a. - statstca-fancesco mola Vaabl Casual Vaabl Casual (cont cont.) Una Vaable Casuale è una egola
IL Potenziale elettrostatico
Ve.. d 27/5/9 IL Potenzale ettostatco ) La oza ettca è consevatva Patamo col vecae che la oza ettca è consevatva, lmtandoc nzalmente al caso d cache ettche puntom. Posta una caca +Q ema n un punto ogne,
Laboratorio: Metodi quantitativi per il calcolo del VaR. Aldo Nassigh Financial Risk Management A.A. 2011/12 Lezione 4
Laboatoo: Metod quanttatv pe l calcolo del VaR Aldo Nassgh Fnancal Rsk Management A.A. 011/1 Lezone 4 METODO PARAMETRICO Sngolo fattoe d scho e poszone lneae Poszone l cu valoe attuale è soggetto ad un
Economia del turismo
Unvestà degl Stud d Cagla Facoltà d Economa Coso d Lauea n Economa e Gest. de Sev. Tustc Economa del tusmo Pof.ssa Cala Massdda Economa del Tusmo Pof..ssa Cala Massdda Sezone 4 LA DOMANDA TURISTICA Agoment
Meccanica dei sistemi
Meccanca de sste 1. 1. Moento angolae 2. Moento d una foza 3. Foze cental 4. Sste d punt ateal 5. Foze estene e Foze ntene 6. Cento d assa d un sstea 7. Consevazone della quantta d oto 8. Teoea del oento
Calcolo del lavoro compiuto dalle forze elementari
Calcolo del lavoo computo dalle foze elementa avoo computo da una foza costante In base alla defnzone, l lavoo computo da una foza costante, l cu punto d applcazone s sposta da a, vale: F s F s F s S not
Analisi Modale. Le evoluzioni libere dei due sistemi a partire dalla condizione iniziale x(0) = x 0 sono
Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Definizione di mutua induzione
Mutua nduzone Defnzone d mutua nduzone Una nduttanza poduce un campo magnetco popozonale alla coente che v scoe. Se le lnee d foza d questo campo magnetco ntesecano una seconda nduttanza, n questo d poduce
Operatori differenziali (1)
Opeato dffeenal Gadente opea s no scalae; a come sltato n vettoe gad Φ Φ Φ Φ Φ Dvegena opea s n vettoe; a come sltato no scalae dv Rotaonale o otoe opea s n vettoe; a come sltato n vettoe ot Esectaon d
Risultati esame scritto Fisica 2-29/09/2014 orali: alle ore presso aula O
sultat esame sctto Fsca - 9/9/ oal: -- alle oe. pesso aula O gl student nteessat a vsonae lo sctto sono pegat d pesentas l gono dell'oale Nuovo odnamento matcola voto 66 9 6 ammesso 9 nc 5 9 5 56 nc 5
Metodi di integrazione numerica
Metod d ntegazone numeca Con patcolae emento agl element sopaametc ove compae anche l Jacobano, non è possble espmee analtcamente temn che compaono nell ntegale d volume dell elemento Occoe qund coee all
Ottimizzazione Combinatoria
Ottmzzazone Combnatoa Clusteng de dat Lezone Lezon a cua d Sla Canale contatto e-mal: canale@ds.unoma.t Unestà d Roma La Sapenza Dpatmento d Infomatca e Sstemstca Coso d Lauea n Ingegnea Gestonale Defnzone
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Approfondimento 7.4 - Altri tipi di test di significatività del coefficiente di correlazione di Pearson
Appofondmento 7.4 - Alt tp d test d sgnfcatvtà del coeffcente d coelazone d Peason Una delle cause pncpal della cattva ntepetazone del test d sgnfcatvtà d è che s fonda su un potes nulla pe cu ρ 0. In
CAPITOLO 6. Dunque, se il volume è costante, la variazione di temperatura si può calcolare nel seguente modo:
Intoduzone alla Temodnamca Esecz svolt CAITOO 6 Eseczo n 6 Calcolae la vaazone d tempeatua d mol d un gas ( C R ) che assobe caloe (q J): a) Se la pessone è costante; b) Se l volume è costante In quale
6. Catene di Markov a tempo continuo (CMTC)
6. Catene d Markov a tempo contnuo (CMTC) Carla Seatzu, 8 Marzo 28 Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto
Il campo magnetico prodotto da correnti continue
Leone 6: l campo magnetco podotto da coent contnue l potenale vettoe l campo magnetco podotto da coent contnue Ossevaon spemental: á Osted: coent elettche danno luogo a camp magnetc; á Legge d ot-savat:
RISPOSTA IN FREQUENZA DI UN AMPLIFICATORE
Unestà degl Stud d oma To Vegata Dpatmento d Ing. Elettonca coso d ELETTONIA APPLIATA Ing. Patck E. Longh ISPOSTA IN FEQUENZA DI UN AMPLIFIATOE II / INTODUZIONE Detemnae la sposta n fequenza d un amplfcatoe
Una semplice applicazione del metodo delle caratteristiche: la propagazione di un onda di marea all interno di un canale a sezione rettangolare.
Una semplce applcazone del metodo delle caratterstche: la propagazone d un onda d marea all nterno d un canale a sezone rettangolare. In generale la propagazone d un onda monodmensonale n una corrente
ESERCITAZIONE DEL 3 MARZO 2005
ESERCITAZIONE DEL 3 MARZO 2005 Ela lnda (on passo p ostante) Equazon dell ela: x = R os θ y = R sn θ z = p 2π θ 5 La uva appatene al lndo olae, on geneat paallele all asse z, d equazone: x 2 + y 2 = R
6. Catene di Markov a tempo continuo (CMTC)
6. Catene d Markov a tempo contnuo (CMTC) Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto numerable. L nseme de
Teorema del momento angolare. Momento angolare totale rispetto al polo P che può essere mobile F31 F13 F32. r r r r r F23. r r P1 F21.
Teoea del oento angolae F F3 3 Moento angolae totale spetto al polo che può essee oble F3 F3 F3 L ( v ) F O d v + dv + [( ) + ( )] (E) (I) v v v F F Teoea del oento angolae (E) v + + v v v F v v p M (
Controllo di Azionamenti Elettrici. Lezione n 12. Controllo ad orientamento di campo degli azionamenti con motore in corrente alternata
Contollo d Azonament Elettc Lezone n 2 Coo d Lauea n Ingegnea dell Automazone Facoltà d Ingegnea Unvetà degl Stud d Palemo Contollo ad oentamento d campo degl azonament con motoe n coente altenata Pncpo
N X Y SVOLGIMENTO.
RELAZIONE. La cenea dell pesostentatoe d un aeeo leggeo è collegata alla centna d estemtà tamte chodatua secondo le ndcazon potate n fgua. Lo sfozo d taglo massmo agente sul peno della cenea è pa a 00
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Le equazionidimaxwell 1873: Trattato sull elettricità e sul magnetismo
Lezone : quazon d Maxwell, enega e quanttà d moto del campo eletto-magnetco Le equazondmaxwell 873: Tattato sull elettctà e sul magnetsmo álegge d Gauss pe elettctà ρ ε álegge d Gauss pe l magnetsmo álegge
Cenni sulla Gravitazione Universale
Cenn sulla Gavtazone nvesale ) La oza gavtazonale Fno al 665 (anno n cu Netwon ntuì la legge della Gavtazone nvesale) pe spegae le nteazone de cop con la ea eano necessae: a) La oza peso F P mg esectata
La regione delle basse masse
La egone delle basse masse Lo studo della egone delle basse masse pemette d nvestgae fenomen legat al pstno della smmeta chale della QCD Dffeenze concettual con egone alte masse J/ Vta lunga (Γ = 93 kev)
r v i i P = m i i dt (M r cm ) = Mv r r i = d avendo definito il concetto di centro di massa (CM) del sistema ( M = m i r r r cm
6. Sstem d patcelle Legge della dnamca d taslazone pe un sstema d patcelle È possble scvee una legge pe l moto collettvo d un nseme d patcelle nteagent fa loo e con l esteno. Questo modo d fae pemette
EX 1 Calcolare la velocità di rinculo di un fucile di 4 kg che spara un proiettile di 0.05kg alla velocità di 280m/s.
SITEMI ISOLATI EX 1 Calcolae la veloctà d nculo d un ucle d 4 kg che spaa un poettle d 0.05kg alla veloctà d 80m/s. EX Un one che vagga alla veloctà d = 6*10 5 m/s colpsce un alto one emo. S osseva che
7. Proprietà dei circuiti lineari adinamici
A. Moand, Unestà d Bolona Elettotecnca T-A, A.A. 6/7 7. Popetà de ccut lnea adnamc Foma matcale del sstema solente d un ccuto lneae. Ccuto nete. Coeffcent d ete. ecpoctà de ccut lnea. Popetà d soapposzone.
Algebra vettoriale: un breve formulario. E r
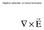slde# Geoge Stokes Ilanda 1819 1903 Olve Heavsde Inghltea 1850 195 G. Stokes dede mpotant contbut alla teoa della popagaone ondulatoa con patcolae femento a flud (equaon d Nave-Stokes) all'ottca e all
posizione, velocità, quantità di moto, energia cinetica, momento angolare, ecc.
Unvestà a Sapena FONDAMENTI DEA MECCANICA QUANTISTICA Pma delle legg ( Postulat vedamo concett Vaabl dnamce Funone d onda o d stato 3 Opeato Vaable Dnamca S tatta d una qualsas vaable ce defnsce l moto
Intorduzione alla teoria delle Catene di Markov
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Prova scritta del corso di Fisica con soluzioni
Pova sctta del coso d Fsca con soluzon Pof. F. cc-tesengh 13/02/2013 Quest 1. State ossevando una gosta d quelle con seggoln volant che ga a veloctà angolae costante. Su uno de seggoln è seduto un bambno
Realizzazione di FSM sincrone. Sommario. Introduzione. Sommario. M. Favalli
Realzzazone d FSM sncrone M. Favall Engneerng Department n Ferrara Realzzazone d FSM Anals e sntes de sstem dgtal / Introduzone Realzzazone d FSM Anals e sntes de sstem dgtal 2 / Una volta ottenuto l automa
APPENDICE 4. sono determinati imponendo che la (2) sia verificata p W M
APPENDICE 4 PROBLEA DI DIRICHLET PER L EQUAZIONE DI POISSON 2D SOLUZIONE COL ETODO DEGLI ELEENTI FINITI EDIANTE ATLAB assmlano d Aquno Fomulazone del poblema Consdeamo l seguente poblema d valo al contono:
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Fisica Generale B. Campo elettromagnetico. Scuola di Ingegneria e Architettura UNIBO Cesena Anno Accademico Maurizio Piccinini
A.A. 14 15 Fsca Geneale Campo elettomagnetco cuola d Ingegnea e Achtettua UNIO Cesena Anno Accademco 14 15 A.A. 14 15 Induzone Mchael Faaday (1791-1867). Nel 1831 studa l nteazone ta spe e magnet e l nteazone
Ingegneria Elettrica Politecnico di Torino. Luca Carlone. ControlliAutomaticiI LEZIONE III
Ingegnera Elettrca Poltecnco d Torno Luca Carlone ControllAutomatcI LEZIONE III Sommaro LEZIONE III Trasformata d Laplace Propretà e trasformate notevol Funzon d trasfermento Scomposzone n fratt semplc
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PROBLEMA 1. Soluzione. β = 64
PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
I vettori. A cura di dott. Francesca Fattori Speranza dott. Francesca Paolucci
I vetto cua d dott. Fancesca Fatto Speana (speana@fs.unoma3.t) dott. Fancesca Paolucc GRNDEZZE SLRI E VETTORILI S defnscono gandee SLRI quelle gandee caatteate solo da un valoe numeco o modulo come: tempo,
Algoritmi e Strutture di Dati
Algotm e Stuttue d Dat Quck-sot m.patgnan Nota d copyght queste sldes sono potette dalle legg sul copyght l ttolo ed l copyght elatv alle sldes (nclus, ma non lmtatamente, mmagn, foto, anmazon, vdeo, audo,
C 2. Quesiti: 1) Calcolare tutte le correnti in figura. 2) Verificare la conservazione delle potenze complesse.
UNIESITÀ DEGI STUDI DI NPOI FEDEICO II FCOTÀ DI INGEGNEI COSO DI UE IN INGEGNEI BIOMEDIC COSO DI UE IN INGEGNEI MECCNIC I COSO DI UE IN INGEGNEI PE GESTIONE DEI SISTEMI DI TSPOTO Prof. ug erolno Prova
3 Il teorema di Gauss
3 Il teoema d Gauss 3. Il flusso d un vettoe attaveso una supefce Pe una pozone d supefce che sa pana, dsposta nello spazo, c è una dezone che sulta ndvduata n modo unvoco ed è quella della pependcolae
SOLUZIONI PER IL CONTROLLO DEL RISCALDAMENTO GLOBALE
Confeenza Nazonale su Cambament Clmatc Roma / settembe 7, Palazzo FAO SOLUZIONI PER IL CONROLLO DEL RISCALDAMENO GLOBALE F. Cotana, F. Ross, M. Flppon () () CIRIAF - Cento Inteunvestao d Rceca sull Inqunamento
I Dati Volumetrici e Calorimetrici.
aptolo 4 I Dat Volumetc e alometc. Dato che nessun poblema temodnamco può essee affontato senza la conoscenza d adeguat dat spemental e dato che, come s vedà nel seguto, tamte le elazon D fondamental è
Circuiti dinamici. Circuiti del secondo ordine. (versione del ) Circuiti del secondo ordine
rcut dnamc rcut del secondo ordne www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 9-6- rcut del secondo ordne rcut del secondo ordne: crcut l cu stato è defnto da due varabl x ( e x ( Per un crcuto
PROPRIETÀ DEL CAMPO ELETTROSTATICO (PARTE 2) G. Pugliese 1
PROPRIETÀ DEL CMPO ELETTROSTTICO (PRTE 2) G. Puglese Campo elettostatco & elettco F 0 E S pala d foza elettostatca uando sa le cache che geneano l campo (elettostatco) che 0 sono fsse e costant Quando
Sistemi Intelligenti Reinforcement Learning: Evaluative Feedback
Sstem Intellgent Renfocement Leanng: Evaluatve Feedbac Albeto Boghese Unvestà degl Stud d Mlano Laboatoo d Sstem Intellgent Applcat (AIS-Lab Dpatmento d Scenze dell Infomazone boghese@ds.unm.t /9 http:\\homes.ds.unm.t\
Circuiti RLC RIASSUNTO: L(r)C serie: impedenza Z(ω) Q valore risposta in frequenza L(r)C parallelo Circuiti risonanti Circuiti anti-risonanti
icuiti R RIASSUNTO: () seie: impedenza () valoe isposta in fequenza () paallelo icuiti isonanti icuiti anti-isonanti icuito in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un
Leggi di Biot-Savart e di Ampère. Fisica II - CdL Chimica
Legg d Bot-Savat e d Ampèe d P R dl Ossevazon spemental Legge d Bot-Savat db ds espemento: X db... assumendo n fomula Legge d Bot-Savat db ds pemeabltà magnetca X db Il campo magnetco è dstbuto ntono al
Termodinamica molecolare
. Temodnamca molecolae.. Intoduzone Lo studo delle popetà d equlbo della matea, fuendo delle conoscenze sulla stuttua delle molecole e sulle loo foze d nteazone ecpoca, costtusce l oggetto della temodnamca
Teoremi dei circuiti
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-03) Teorema d Tellegen Ipotes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Dinamica del Corpo rigido
Dnamca del Copo gdo Defnzone Un copo gdo è un sstema d punt mateal n cu le dstanze elatve NON cambano ed è un oggetto esteso. Le foze ntene (foze d coesone che mantengono nvaate le dstanze fa punt) hanno
Corso di. Gasdinamica II Tommaso Astarita
Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Corso di Elettrotecnica
Unerstà degl Stud d Paa Facoltà d Ingegnera orso d orso d Elettrotecnca Teora de rcut rcut elettrc n funzonamento perturbato rcut elettrc n funzonamento perturbato I IRUITI OMPRENONO: Sorgent nterne d
Campo elettrico e campo magnetico statici
1 Campo elettco e campo magnetco statc Flusso d un campo vettoale Consdeamo una zona d spazo n cu sa pesente un ceto campo vettoale v e, n uesto spazo, una ceta supefce (apeta o chusa) Dvdamo l'ntea supefce
Il campo elettrico è conservativo. L A1B = F i l r
F = qe α l 2 Il campo elettco è consevatvo n L = F l In un campo elettco stazonao l lavoo non dpende dalla taettoa ma solo dal punto nzale e dal punto fnale. L = L 2 La foza elettca è consevatva 2 Se calcolamo
LA NORMA UNI ENV 13005:2000 E LE GUIDE ACCREDIA DT-0002 E DT-0002/3 SULLA STIMA DELL INCERTEZZA DEI RISULTATI
P.le R. Moand, - 0 MILANO LA NORMA UNI ENV 3005:000 E LE GUIDE ACCREDIA DT-000 E DT-000/3 SULLA STIMA DELL INCERTEZZA DEI RISULTATI RELATORE: N. BOTTAZZINI (UNICHIM) Coso: SISTEMA DI GESTIONE PER LA QUALITA
Corso di. Dott.ssa Donatella Cocca
Corso d Statstca medca e applcata 3 a Lezone Dott.ssa Donatella Cocca Concett prncpale della lezone I concett prncpal che sono stat presentat sono: Mede forme o analtche (Meda artmetca semplce, Meda artmetca
ω 0 =, abbiamo L = 1 H. LC 8.1 Per t il condensatore si comporta come un circuito aperto pertanto la corrente tende a zero: la R
8. Per t l condensatore s comporta come un crcuto aperto pertanto la corrente tende a zero: la funzone non può essere la (c). caando α e ω 0 s ottengono seguent alor: α 5 0 e ω 0 0. Essendo α > ω 0 l crcuto
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
6 Prodotti scalari e prodotti Hermitiani
6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
Corrente elettrica. Conduttore in equilibrio. Condutture in cui è mantenuta una differenza di potenziale (ddp) E=0 V=cost
Coente elettca Conduttoe n equlbo B E 0 E0 cost B Conduttue n cu è mantenuta una dffeenza d potenzale (ddp) > B E 0 _ B Un campo elettco all nteno d un conduttoe appesenta una stuazone d non equlbo. Un
Fisica Generale B. Campo magnetico stazionario. Scuola di Ingegneria e Architettura UNIBO Cesena Anno Accademico Maurizio Piccinini
A.A. 14 15 Fsca Geneale Campo magnetco staonao Scuola d Ingegnea e Achtettua UNIO Cesena Anno Accademco 14 15 A.A. 14 15 Il magnetsmo Fenomen magnetc not da lungo tempo (Socate, V secolo a. C.). Popetà
L elettrostatica dei sistemi macroscopici
L elettostatca de sstem macoscopc Oggett cach Tutt cop sono fatt d atom e dunue contengono moltssme cache postve e negatve. Tuttava, negl stat pù comun della matea, gl atom sono neut; oppue, fomano molecole
Leggi di Biot-Savart e di Ampère. Fisica II - CdL Chimica
Legg d ot-savat e d Ampèe q d q P R dl Ossevazon spemental d Legge d ot-savat ds q espemento: X d d d d d d d ds 1 ds 2 sen q... assumendo n fomula I ds ˆ d k m 2 d Legge d ot-savat ds q X d d k c m pemeabltà
Teoremi dei circuiti
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Workshop MatFinTN 2012
Wokshop MatFnTN 2012 Dalla Bnson Attbuton al Black&Ltteman model: anals matematche nell'asset management D.ssa Tzana Rgon Lauea n Matematca conseguta pesso l'unvestà d Tento con tes dal ttolo: Metod d
= E! Se E ha proprietà di simmetria Enorme semplificazione
pplcazon del teoema d Gauss a dstbuzon d caca smmetche Il teoema d Gauss è utle pe detemnae l campo elettco geneato da dstbuzon d caca che pesentano una qualche smmeta spazale. qn Φ ˆ E E Se E ha popetà
B - ESERCIZI: IP e TCP:
Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Circuiti LC in serie
8//00 Isidoo Feante A.A. 00/003 icuiti in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un condensatoe ed una induttanza in seie si ha: z ϕ tan ompotamento capacitivo Pe fequenze
Bipoli resistivi. (versione del ) Bipoli resistivi
Bpol resst www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 6--0) Bpol resst Bpolo ressto: componente a due termnal aente equazone caratterstca del tpo f (t), (t), t0 (f funzone generca) L equazone
δ = = ωσμ ωσμ μ 2 ωσμ SCHERMO CONDUTTORE LARGO
CHRMO CONDUTTOR LARGO e l ateale da cu è costtuto lo scheo è un buon conduttoe, è possble ulteoente specalzzae le elazon del paagafo pecedente. Rcodao che un ateale è detto un buon conduttoe se la sua
ELETTROTECNICA ED ELETTRONICA (C.I.) Modulo di Elettronica. Lezione 2. a.a
586 - EEOECNCA ED EEONCA C.. Mdul d Elettnca ezne a.a. 00-0 Funzn d ete Dat un genec sstema, S densce Funzne d ete un appt ta le tasmate d due gandezze elettche Funzne d mmettenza: appt ta / sulla stessa
ATOMI POLIELETTRONICI
Unvestà d Roma La Sapenza he- ATOMI POLILTTRONICI ATOMO DI LIO : Stato fondamentale Impostamone l Hamltonano de mot nten tascuando la enega cnetca del nucleo ( assumamo che, spetto ad me, mn,) h m e h
TEORIA ASSIOMATICA DELLA RADIAZIONE
TEORA AOMATCA DELLA RADAZONE ntoduzone alle antenne ed alla adazone elettomagnetca L appocco assomatco-deduttvo allo studo della popagazone elettomagnetca s basa sulla possbltà d pote ndagae ed analzzae
Soluzione del compito del 5 settembre 2012
del compto del 5 settembe Ottca geometca Un aggo d luce banca ncde su un psma d veto d angolo d apetua φ 6 con un angolo d ncdena 45. A causa della dspesone della luce, l aggo s sepaa n un pennello d agg
Una rendita è una somma di capitali pagabili (o esigibili) a determinate scadenze, fissate secondo intervalli regolari di tempo.
14. Le endte 14.1 Nozon geneal Una endta è una somma d captal pagabl (o esgbl) a detemnate scadenze, fssate secondo ntevall egola d tempo. Ognuno d quest captal è detto ata; gl ntevall sono dett peod e