Sui teoremi di Vitali-Hahn-Saks e di Dieudonné
|
|
|
- Gilberto Repetto
- 7 anni fa
- Visualizzazioni
Transcript
1 Sui teoremi di Vitali-Hah-Saks e di Dieudoé DOMENICO CANDELORO, GIORGIO LETTA Red.Accad.Naz.Detta XL, 9,1985,pp SUMMARY. We give a geeral versio of the well-kow Vitali-Hah-Saks theorem, cocerig coverget sequeces of measures. The we use this result to obtai a abstract form of the theorem of Dieudoé, related to coverget sequeces of regular measures. 0 Itroduzioe Sebbee sia trascorso piú di mezzo secolo dalla prima formulazioe (dovuta a Nikodým, [10] del cosiddetto teorema di Vitali-Hah-Saks, questo suggestivo risultato cotiua ad esser oggetto di ricerca; e si puó be dire che i ogua delle sue svariate formulazioi fiora ote ci sia qualcosa di sorpredete: cioé il fatto che certe proprietá cotiuio a valere, quasi isperatamete, i strutture e situazioi tato lotae da quelle origiarie. Il processo di geeralizzazioe si é sviluppato essezialmete i tre direzioi: estesioe della struttura algebricotopologica dell isieme i cui le misure i gioco predoo i loro valori; passaggio dall additivitá umerabile alla fiita additivitá; ideboeto della struttura di σ-algebra per il domiio di defiizioe delle misure. Ua ricca rassega dei risultati otteuti al riguardo si puó trovare i [4]. Tra i teoremi tradizioalmete legati a quello di Vitali-Hah-Saks, figura, oltre a u classico teorema di Nikodým sull uiforme itatezza (si veda [9], [3], [8], [11]), u teorema, assai piú profodo, dovuto a Dieudoé [5]: Se ua successioe di misure di Borel regolari, su uo spazio di Hausdorff compatto, coverge su ogi isieme aperto, essa coverge su ogi isieme boreliao. I tal caso, ioltre, le misure della successioe soo uiformemete regolari. Le estesioi di questo teorema esisteti ella letteratura sembrao alquato artificiose: e ache le dimostrazioi appaioo spesso piuttosto complicate, e comuque poco ituitive: si veda ad es. [1], [2] (recetemete il Prof. Morales ci ha comuicato di aver trovato u estesioe al caso di misure a valori i u semigruppo topologico). Nella presete ota si dimostra dapprima ua versioe assai geerale del teorema di Vitali-Hah-Saks (Teorema 2.4), valida per fuzioi fiitamete additive i u algebra A, a valori i u gruppo abeliao topologico Γ. Questo 1
2 risultato permette poi di otteere, i modo abbastaza diretto e aturale, ua formulazioe astratta del teorema di Dieudoé (teorema 4.1), la quale riguarda acora fuzioi fiitamete additive ell algebra A, a valori el gruppo topologico Γ. I questa formulazioe, il cocetto topologico di regolaritá (per ua misura di Borel su uo spazio di Hausdorff compatto) é sostituito co u cocetto astratto di regolaritá, defiito mediate ua coppia F, G di reticoli (coteuti ell algebra A e aveti rispettivamete il ruolo del reticolo degli isiemi compatti e di quello degli isiemi aperti). Ioltre il ruolo della umerabile additivitá é svolto da ua ozioe assai piú debole: quella di G-esaustivitá (v. Def. 1.1). 1 Esaustivitá I tutto il seguito, Γ desiga u gruppo abeliao topologico separato, il cui elemeto eutro viee idicato co 0. Se (B ) é ua successioe di parti di Γ, la scrittura B = 0 é u modo abbreviato per sigificare che, per ogi itoro U di 0, si ha defiitivamete B U. Ua massa (a valori i Γ) é ua fuzioe fiitamete additiva, a valori i Γ, defiita i u algebra di isiemi. Ua misura é ua massa che sia defiita su ua tribú (o σ-algebra d isiemi) e che sia umerabilmete additiva. I tutto il seguito, A desiga ua fissata algebra d isiemi, ammettete Ω come elemeto massimo, metre F, G deotao due reticoli d isiemi, etrambi coteuti i A, tali che il complemetare (rispetto a Ω) di ciascu elemeto di F appartega a G. U esempio tipico di questa situazioe si ottiee suppoedo che Ω sia uo spazio topologico, el quale A sia la tribú boreliaa, G il reticolo degli isiemi aperti, F u reticolo d isiemi chiusi (per esempio, quello degli isiemi chiusi e compatti). Se λ é ua fuzioe defiita i ua classe H d isiemi, si poe, per ogi elemeto B di H, λ + (B) = {λ(a) : A H, A B} Defiizioe 1.1 Ua massa µ sull algebra A si dice G-esaustiva se, per ogi successioe (G ) di elemeti di G, a due a due disgiuti, si ha µ(g ) = 0. (I tal caso, se si deota co λ la restrizioe di µ a G, si ha ache λ + (G ) = 0 per ogi successioe (G ) di elemeti di G, a due a due disgiuti). Defiizioe 1.2 Ua successioe (µ i ) di masse su A si dice uiformemete G- esaustiva se, per ogi successioe (G ) di elemeti di G a due a due disgiuti, si ha i λ + i (G ) = 0 dove, per ciascu i, λ i deota la restrizioe di µ i a G. 2
3 Ua massa su A, che sia A-esaustiva, si dice semplicemete esaustiva. Cosí pure ua successioe di masse su A, che sia uiformemete A-esaustiva, si dice uiformemete esaustiva. Defiizioe 1.3 Diremo che il reticolo G gode della proprietá (E) (v. [11]) se, per ogi successioe (G ) di elemeti di G, a due a due disgiuti, esiste ua sottosuccessioe (G k ) tale che G cotega tutte le uioi d isiemi del tipo G k. Il lemma elemetare che segue é utile perché permette, i certe situazioi, di ricodursi al caso i cui il gruppo Γ sia metrizzabile. Lemma 1.4 Sia U u itoro dello zero i Γ. Esistoo allora u gruppo abeliao metrizzabile Γ 1, u omomorfismo cotiuo h di Γ su Γ 1, e u itoro W dello zero di Γ 1, tali che si abbia h 1 (W ) U. Dimostrazioe. Per iduzioe si puó costruire ua successioe (U ) 1 d itori simmetrici dello zero i Γ, tale che si abbia: U 1 + U 1 U, U +1 + U +1 U per ogi 1. Deotiamo co Γ 0 il gruppo topologico (o ecessariamete separato) otteuto muedo il gruppo Γ dell uica topologia, compatibile co la sua struttura di gruppo, che ammetta (U ) 1 come sistema fodametale d itori dello zero. Poiamo poi V = 1 U. Allora V é u sottogruppo chiuso di Γ 0, e il gruppo quoziete Γ 1 = Γ 0 /V é metrizzabile. Deotiamo co h l omomorfismo caoico di Γ 0 su Γ 1, e poiamo W = h(u 1 ). Poiché la topologia di Γ 0 é meo fie di quella di Γ, h é a maggior ragioe u omomorfismo cotiuo di Γ su Γ 1. Ioltre W é u itoro dello zero i Γ 1, e si ha: Il lemma é cosí dimostrato. h 1 (W ) = U 1 + V U 1 + U 1 U. 2 Il Teorema di Vitali-Hah-Saks La seguete forma del teorema di Vitali-Hah-Saks é be ota, e facilmete dimostrabile co le teciche usuali (v.[6]): Teorema 2.1 Se ua successioe di misure (a valori i Γ), tutte assolutamete cotiue rispetto a ua medesima misura reale positiva, coverge putualmete, essa é uiformemete esaustiva. Useremo questo euciato per giugere a euciati piú geerali. Premettiamo, a questo scopo, alcui lemmi. 3
4 Lemma 2.2 Si suppoga che il reticolo G goda della proprietá (E). Sia µ ua massa G-esaustiva su A, e sia (G i ) i I ua famiglia ifiita umerabile di elemeti di G a due a due disgiuti. Sia ifie U u itoro di 0 i Γ. Esiste allora ua parte ifiita I 0 di I co la proprietá seguete: ( ) Per ogi parte H di I 0, risulta µ( G i ) U. Dimostrazioe. Seza perdita di geeralitá, possiamo supporre che G cotega tutte le uioi d isiemi del tipo G i. Sia (I k ) ua successioe di parti ifiite di I, a due a due disgiute. Se essua di esse possiede la proprietá desiderata ( ), si puó trovare, per ogi k, ua parte H k di I k verificate la relazioe µ( G i ) U c. i H k Ma ció cotraddice la supposta G-esaustivitá di µ. Il lemma é cosí dimostrato. i H Lemma 2.3 Si suppoga che il gruppo Γ sia metrizzabile e che il reticolo G possieda la proprietá (E). Sia µ ua massa G-esaustiva su A, e sia (G i ) ua famiglia ifiita umerabile di elemeti di G, a due a due disgiuti. Allora esiste ua parte ifiita J di I, tale che la restrizioe di µ alla tribú geerata dalla famiglia (G j ) j J sia ua misura. Dimostrazioe. Sia (U ) ua successioe decrescete che costituisca u sistema fodametale d itori di 0 i Γ. Sfruttado il lemma precedete, si puó costruire, per iduzioe, ua successioe decrescete (I ) di parti ifiite di I, tale che, per ogi, si abbia I +1 I e µ( G i ) U per ogi parte H di I. i H Si scelga allora, per ogi, u elemeto j di I \ I +1, e si poga J = {j : 1}. L isieme J cosí costruito possiede la proprietá desiderata. Siamo ora i grado di dimostrare il seguete euciato, piú geerale di (2.1). Teorema 2.4 Si suppoga che il reticolo G possieda la proprietá (E) (v. Def.(1.3)). Sia (µ i ) ua successioe di masse G-esaustive ell algebra A, covergete su ogi elemeto di G. Allora la successioe (µ i ) é uiformemete G-esaustiva. Dimostrazioe. Il Lemma (1.4) permette di ricodursi facilmete al caso i cui Γ sia metrizzabile. Ragioado per assurdo, eghiamo la tesi. Esistoo allora: u itoro U di 0 i Γ, ua successioe strettamete crescete (i ) d iteri e ua successioe (G ) di elemeti di G a due a due disgiuti, tali che si abbia µ i (G ) U c, per ogi. (1) 4
5 La tribú I geerata su Ω dagli isiemi G é coteuta ell algebra A e ammette come atomi gli isiemi G e il complemetare della loro riuioe. Pertato esiste su di essa ua misura reale positiva che si aulli solo sull isieme vuoto. Grazie al Lemma (2.3), si puó supporre (pur di passare a opportue sotto-successioi) che, per ogi, la restrizioe di µ i a I sia ua misura. Grazie a (2.1), queste restrizioi formao allora ua successioe uiformemete esaustiva. Ma ció cotrasta co la relazioe (1). Il teorema é cosí dimostrato. Corollario 2.5 Ua successioe di masse esaustive su ua medesima tribú, che coverga su ogi elemeto di questa, é uiformemete esaustiva. 3 Regolaritá e suoi rapporti co l esaustivitá Defiizioe 3.1 Ua massa µ sull algebra A si dice regolare se verifica le due codizioi segueti: (a) per ogi elemeto A di A, esiste ua coppia (F ), (G ) di successioi d isiemi, verificate le relazioi F F, G G, F F +1 A G +1 G (2) per ogi, e tale che si abbia µ + (G \ F ) = 0 (e quidi, i particolare, µ(a) = µ(f )); (b) per ogi elemeto B di F, esiste ua coppia (G ), (F ) di successioi d isiemi, verificate le relazioi per ogi, e tale che si abbia G G, F F, B F +1 G F (3) µ + (G \ B) = 0. Osservazioe 3.2 Si suppoga i particolare che l isieme Ω sia muito di ua topologia di spazio ormale (risp. di spazio di Hausdorff localmete compatto), che A sia la tribú boreliaa di Ω, F il reticolo degli isiemi chiusi (risp. compatti), G quello degli isiemi aperti, e che µ sia ua misura reale ella tribú boreliaa. Si vede allora che, ella defiizioe precedete, la codizioe (b) é ua cosegueza della codizioe (a), e che quest ultima si riduce semplicemete all usuale codizioe di regolaritá per la misura µ (cosistete ell imporre l approssimabilitá dall estero co isiemi aperti, e dall itero co isiemi chiusi (risp. compatti)). 5
6 Osservazioe 3.3 Sia (µ i ) ua successioe di masse regolari su A. Assegato u elemeto A di A, si puó allora costruire (usado u classico procedimeto diagoale) ua coppia (F ), (G ) di successioi d isiemi, verificate le relazioi (2) e tali che si abbia µ + i (G \ F ) = 0 per ogi i. (4) I modo aalogo, assegato u elemeto B di F, si puó costruire ua coppia (G ), (F ) di successioi d isiemi, verificate le relazioi (3) e tali che si abbia µ + i (G \ B) = 0 per ogi i. (5) Defiizioe 3.4 Ua successioe (µ i ) di masse sull algebra A si dice uiformemete regolare se verifica le due codizioi segueti: (a) per ogi elemeto A di A esiste ua coppia (F ), (G ) di successioi d isiemi, verificate le relazioi (2) e tale che si abbia i µ + i (G \ F ) = 0; (6) (b) per ogi elemeto B di F esiste ua coppia (G ), (F ) di successioi d isiemi, verificate le relazioi (3) e tale che si abbia i µ + i (G \ B) = 0; (7) Sussiste il seguete teorema: Teorema 3.5 Si suppoga che la successioe (µ i ), di masse regolari su A sia uiformemete G-esaustiva. Allora essa é uiformemete esaustiva e uiformemete regolare. Allo scopo di dimostrare il teorema sopra euciato, premettiamo alcui lemmi. Lemma 3.6 Sia µ ua massa regolare su A e si deoti co λ la sua restrizioe a G. Allora, per ogi elemeto G di G, l isieme µ + (G) é coteuto ell adereza dell isieme λ + (G) λ + (G). Dimostrazioe. Ifatti, per ogi elemeto A di A coteuto i G, µ(a) é aderete all isieme {µ(f ) : F F, F A}, il quale, essedo idetico all isieme {µ(g) µ(g \ F ) : F F, F A}, é coteuto ell isieme λ + (G) λ + (G). Lemma 3.7 Si suppoga che la successioe (µ i ) di masse regolari su A sia uiformemete G-esaustiva. Assegato u elemeto B di F, sia (G ), (F ) ua coppia di successioi d isiemi, verificate le relazioi (3),(5) (cfr.(3.3). Allora sussiste ache la relazioe (7). 6
7 Dimostrazioe. Comiciamo co l osservare che che, per ogi coppia i, d iteri e per ogi elemeto A di A, co A G \ B, risulta µ i (A) = m µ i (A F c m). (8) Per covicersee, basta scrivere, per ogi m >, l ovvia relazioe µ i (A) µ i (A F c m) = µ i (A F m ) µ + i (G m 1 \ B). Osserviamo i secodo luogo che, grazie al lemma precedete, la relazioe (7) da dimostrare é equivalete alla relazioe i λ + i (G \ B) = 0 dove, per ciascu i, λ i deota la restrizioe di µ i a G. Ragioado per assurdo, suppoiamo che quest ultima relazioe sia falsa. Esiste allora u itoro chiuso U di 0 i Γ co la proprietá seguete: per ogi itero p, esistoo u itero > p, u itero i e u elemeto A di G, tali che si abbia A G \ B, µ i (A) U c e quidi ache (i virtú di (8)) µ i (A F c m) U c per m abbastaza grade. Sfruttado questa proprietá di U, si possoo costruire, per iduzioe, tre successioi d iteri, ( k ), (i k ), (m k ), e ua successioe (A k ) di elemeti di G, i modo tale che si abbia, per ogi k, A k G k \ B, µ ik (A k F c m k 1) U c, k < m k < k+1. Poiché gli isiemi A k Fm c k appartegoo a G e soo a due a due disgiuti, ció cotraddice l ipotesi di uiforme G-esaustivitá. Se si applica il lemma ora dimostrato prededo F=G=A e B =, si ottiee il corollario seguete: Corollario 3.8 Si suppoga che la successioe (µ i ) di masse su A sia uiformemete esaustiva, e sia (A ) ua successioe decrescete di elemeti di A tale che si abbia µ + i (A ) = 0 per ogi i. Si ha allora i µ + i (A ) = 0. Siamo ora i grado di dimostrare il teorema (3.5) sopra euciato. Comiciamo col provare che la successioe (µ i ) é uiformemete esaustiva. Supposto vero il cotrario, esisterao: ua successioe (A ) di elemeti di A a due a due 7
8 disgiuti, u itoro chiuso U di 0 i Γ e ua successioe d iteri (i ), tali che si abbia: µ i (A ) U c per ogi. (9) Grazie alla codizioe (a) che figura ella defiizioe (3.1) di regolaritá, si puó supporre, seza ledere la geeralitá, che gli isiemi A appartegao a F. Poiamo allora B = A 1... A e scegliamo i Γ u itoro U di 0, co U +U U, e due successioi (U ), (V ) d itori di 0, tali che si abbia, per ogi U U, U + V U 1. Vogliamo provare che é possibile costruire ua coppia (G ), (F ) di successioi d isiemi, la quale verifichi, per ogi, le relazioi segueti: G G, F F, B G F G +1, i µ + i (F \ B ) U. (10) Si puó procedere per iduzioe: (a) sfruttado il Lemma (3.7), si puó azitutto trovare ua coppia d isiemi G 1, F 1 verificate le relazioi G 1 G, F 1 F, B 1 G 1 F 1, i µ + i (F 1 \ B 1 ) U 1 ; (b) supposta poi giá costruita la coppia d isiemi (G ), (F ), verificate le relazioi G G, F F, B G F G +1, i µ + i (F \ B ) U, si puó trovare (sempre sfruttado il lemma (3.7)) ua coppia d isiemi G +1, F +1 tale che si abbia G +1 G, F +1 F, B +1 F G +1 F +1, i µ + i (F +1\(B +1 F )) V, e quidi, per ogi i, µ + i (F +1 \ B +1 ) µ + i (F +1 \ (B +1 F )) + µ + i (F B c +1) V + µ + i (F \ B ) V + U U +1. Costruita cosí, per iduzioe, la coppia di successioi (G ), (F ) verificate le relazioi (10), osserviamo che si ha, per ogi coppia i, d iteri, µ + i (A +1) µ + i (G +1 \ F ) + µ + i (F \ B ) µ + i (G +1 \ F ) + U. (11) D altra parte, poiché gli isiemi G +1 \ F appartegoo a G e soo a due a due disgiuti, si ha i λ + i (G +1 \ F ) = 0 8
9 (dove λ i deota la restrizioe di µ i a G), e quidi ache, i virtú di (3.6), i µ + i (G +1 \ F ) = 0. Dalla relazioe (11) segue duque, per abbastaza grade, i µ + i (A +1) U + U U, e ció cotraddice l ipotesi (9). É cosí provato che la successioe (µ i ) é uiformemete esaustiva. Rimae da provare che essa é ache uiformemete regolare, ossia che soo soddisfatte le codizioi (a), (b) della defiizioe (3.4). Per quel che riguarda la codizioe (b), basta applicare il Lemma (3.7). Occupiamoci duque della codizioe (a). A questo scopo, assegato l elemeto A di A scegliamo (cfr.(3.3)) ua coppia (F ), (G ) di successioi d isiemi, verificate le relazioi (2),(4). Per provare che ha luogo ache la relazioe (6), basta applicare il Corollario (3.8) alla successioe (A ) defiita da: A = G \ F. Il teorema é cosí dimostrato. 2 4 Il teorema di Dieudoé Il teorema che segue si puó cosiderare come u estesioe del classico teorema di Dieudoé (cfr. [5]). Teorema 4.1 Si suppoga che il gruppo Γ sia completo e che il reticolo G (coteuto ell algebra A) sia stabile rispetto all uioe umerabile d isiemi disgiuti. Sia poi (µ i ) ua successioe di masse regolari e G-esaustive su A, la quale coverga su ogi elemeto di G. Allora essa coverge su ogi elemeto di A ed é uiformemete esaustiva (e quidi ache (cfr. (3.5)) uiformemete regolare). Pertato la massa ite é a sua volta esaustiva e regolare. Dimostrazioe. Grazie alla versioe (2.4) del teorema di Vitali-Hah-Saks, la successioe (µ i ) é uiformemete G-esaustiva. Dal teorema (3.5) segue allora che essa é ache uiformemete esaustiva e uiformemete regolare. Rimae soltato da provare che, per ogi elemeto A di A, la successioe (µ i (A)) é di Cauchy i Γ. A questo scopo, assegato i Γ u itoro V di 0, si determii u itoro simmetrico U di 0, verificate la relazioe U + U + U V. Sia poi (F ), (G ) ua coppia di successioi d isiemi, verificate le relazioi (2), (6), e sia u itero tale che si abbia i µ + i (G \ F ) U. Poiché la successioe (µ + i (G )) i 1 é di Cauchy, esiste u itero k tale che risulti µ i (G ) µ j (G ) U 9
10 per ogi coppia i, j d iteri maggiori di k. d iteri Si ha allora, per ua tal coppia µ i (A) µ j (A) = µ i (G ) µ j (G ) + µ j (G \ A) µ i (G \ A) U + U + U V. Ció prova che la successioe (µ i (A)) é di Cauchy. Refereces [1] J.K.BROOKS: O a theorem of Dieudoé; Advaces i Math. 36 (1980), [2] J.K.BROOKS, R.V.CHACON: Cotiuity ad compactess of measures; Advaces i Math. 37 (1980), [3] N.CONSTANTINESCU: O Nikodým s boudedess theorem; Libertas Mathematica, 1 (1981), [4] J.DIESTEL, J.J.UHL: Vector measures; A.M.S. Providece (1977). [5] J.DIEUDONNE : Sur la covergece des suites de mesures de Rado; Aais.Acad.Brasil.Ci., 23 (1951), 21-38, [6] N.DUNFORD, J.SCHWARTZ: Liear Operators, Part I, Wiley (1951). [7] B.T.FAIRES: O Vitali-Hah-Saks-Nykodým type theorems; A.Ist. Fourier, 26 (1976), [8] D.LANDERS, T.ROGGE: The Hah-Vitali-Saks ad the uiform boudedess theorem i topological groups; Mauscripta Math. 4 (1971), [9] O.NIKODYM: Sur les familles borées de foctios parfaitemet additives d esemble abstrait; Moatsch.Math.Phys. 40 (1933), [10] O.NIKODYM: Sur les suites covergetes de foctios parfaitemet additives d esemble abstrait; Moatsch.Math.Phys. 40 (1933), [11] W.SCHACHERMAYER: O some classical measure-theoretical theorems for o-sigma-complete Boolea algebras; Dissertatioes Math. 214 (1982),
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Lezione 2. . Gruppi isomorfi. Gruppi S n e A n. Sottogruppi normali. Gruppi quoziente. , ossia, equivalentemente, se x G Hx = xh.
 Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
Dinamica topologica, ultrafiltri e approssimazione diofantea
 Diamica topologica, ultrafiltri e approssimazioe diofatea Deis Nardi 2 luglio 2011 1 Prelimiari di combiatoria U sottoisieme di N è u IP -set se è della forma { } F S(X) = x F X, #F < x F per qualche X
Diamica topologica, ultrafiltri e approssimazioe diofatea Deis Nardi 2 luglio 2011 1 Prelimiari di combiatoria U sottoisieme di N è u IP -set se è della forma { } F S(X) = x F X, #F < x F per qualche X
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
9 LIMITI DI SUCCESSIONI NUMERICHE
 9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
n + 1 n + 2 = 1 n + 1 n n n Esercizio. Verificare il seguente limite a partire dalla definizione: n n 2 + n + 1 = 0 lim
 3.. Esercizio. Ricoosciuto che determiare i valori ε tali che ε : ANALISI Soluzioi del Foglio 3 + = + ε essedo ε ua prima volta e ua secoda 0.5 ε = 9 ottobre 009 + + disuguagliaza soddisfatta da ogi N,
3.. Esercizio. Ricoosciuto che determiare i valori ε tali che ε : ANALISI Soluzioi del Foglio 3 + = + ε essedo ε ua prima volta e ua secoda 0.5 ε = 9 ottobre 009 + + disuguagliaza soddisfatta da ogi N,
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
1 Congruenze. Definizione 1.1. a, b, n Z n 2, allora definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Definizione 1. Data una successione (a n ) alla scrittura formale. 1) a 1 + a a n +, si dà il nome di serie.
 SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
1 Congruenze. Definizione 1.1. Siano a, b, n Z con n 2, definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Un risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazione ad un risultato di esistenza per le equazioni differenziali ordinarie.
 U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
1 Alcune premesse sugli spazi di Hilbert
 1 Alcue premesse sugli spazi di Hilbert 1.1 Lo spazio di Hilbert Sia H uo spazio vettoriale sul corpo K, che si supporrà essere il corpo dei umeri reali R o quello dei umeri complessi C. È defiito u prodotto
1 Alcue premesse sugli spazi di Hilbert 1.1 Lo spazio di Hilbert Sia H uo spazio vettoriale sul corpo K, che si supporrà essere il corpo dei umeri reali R o quello dei umeri complessi C. È defiito u prodotto
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
1 Successioni numeriche
 Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti 1 Lorezo Freddi 1 1 Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 33100
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE
 DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
Proposizione 1. Due sfere di R m hanno intersezione non vuota se e solo se la somma dei loro raggi e maggiore della distanza fra i loro centri.
 Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI
 DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
Nozioni preliminari: sia R n lo spazio n-dimensionale dell algebra vettoriale. Un punto in R n e una n-pla di numeri reali (x 1, x 2 x n )
 SPAZI TOPOLOGICI: topologia locale (a cui siamo iteressati topologia globale (proprieta a larga scala, come quelle che distiguoo ua sfera da u coo Nozioi prelimiari: sia R lo spazio -dimesioale dell algebra
SPAZI TOPOLOGICI: topologia locale (a cui siamo iteressati topologia globale (proprieta a larga scala, come quelle che distiguoo ua sfera da u coo Nozioi prelimiari: sia R lo spazio -dimesioale dell algebra
1 Sulla dimostrazione del Teorema di Carathéodory
 Sulla dimostrazioe del Teorema di Carathéodory Ricordiamo che la dimostrazioe del Teorema di Carathéodory procede secodo diversi passi, riassuti dal seguete diagramma: (A, P ) (B, P ) (P (Ω), P ) (C, P
Sulla dimostrazioe del Teorema di Carathéodory Ricordiamo che la dimostrazioe del Teorema di Carathéodory procede secodo diversi passi, riassuti dal seguete diagramma: (A, P ) (B, P ) (P (Ω), P ) (C, P
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Il caso di coefficienti decrescenti e infinitesimi
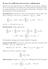 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Limiti di successioni
 Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
Esercizi sulle successioni
 Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Successioni e limiti di successioni
 Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Esercizi di approfondimento di Analisi IA
 Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Aritmetica 2016/2017 Esercizi svolti in classe Seconda lezione
 Aritmetica 06/07 Esercizi svolti i classe Secoda lezioe Dare ua formula per 3 che o coivolga sommatorie Dato che sappiamo che ( + e ( + ( + 6 vogliamo esprimere 3 mediate, e poliomi i U idea possibile
Aritmetica 06/07 Esercizi svolti i classe Secoda lezioe Dare ua formula per 3 che o coivolga sommatorie Dato che sappiamo che ( + e ( + ( + 6 vogliamo esprimere 3 mediate, e poliomi i U idea possibile
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Lezione 4. Gruppi di permutazioni
 Lezioe 4 Prerequisiti: Applicazioi tra isiemi Lezioi e Gruppi di permutazioi I questa lezioe itroduciamo ua classe ifiita di gruppi o abeliai Defiizioe 41 ia X u isieme o vuoto i dice permutazioe su X
Lezioe 4 Prerequisiti: Applicazioi tra isiemi Lezioi e Gruppi di permutazioi I questa lezioe itroduciamo ua classe ifiita di gruppi o abeliai Defiizioe 41 ia X u isieme o vuoto i dice permutazioe su X
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Esercizi Determinare il dominio di de nizione delle seguenti funzioni: a.
 Esercizi -. Determiare il domiio di deizioe delle segueti fuzioi a. () = log jj p (jj ) b. () = µ 5 c. d. e. f. g. h. i. j. () =log jj () = 4p j j! Ã () =arcsi () = log 3 + () =log(jj ) p jj () =log(jcos
Esercizi -. Determiare il domiio di deizioe delle segueti fuzioi a. () = log jj p (jj ) b. () = µ 5 c. d. e. f. g. h. i. j. () =log jj () = 4p j j! Ã () =arcsi () = log 3 + () =log(jj ) p jj () =log(jcos
Appunti per Algebra Superiore
 Apputi per Algebra Superiore Moica Idà April 29, 2009 Qui aello sigifica sempre aello commutativo uitario; A deota sempre u aello e K u campo. 1 A- algebre Defiizioe 1.1 Ua A-algebra R è u aello o ecessariamete
Apputi per Algebra Superiore Moica Idà April 29, 2009 Qui aello sigifica sempre aello commutativo uitario; A deota sempre u aello e K u campo. 1 A- algebre Defiizioe 1.1 Ua A-algebra R è u aello o ecessariamete
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
TEORIA DELLE MATRICI. dove aij K. = di ordine n, gli elementi aij con i = j (cioè gli elementi a 11
 1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
7 Il metodo variazionale
 7 Il metodo variazioale I questo capitolo itrodurremo alcue teciche variazioali, co lo scopo di otteere ulteriori risultati di esisteza di soluzioi per il problema periodico { x (P ) + g(t, x) =, x() =
7 Il metodo variazioale I questo capitolo itrodurremo alcue teciche variazioali, co lo scopo di otteere ulteriori risultati di esisteza di soluzioi per il problema periodico { x (P ) + g(t, x) =, x() =
SERIE DI POTENZE. n=0 a n z n.
 SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Consideriamo un insieme di n oggetti di natura qualsiasi. Indicheremo questi oggetti con
 Calcolo Combiatorio Adolfo Scimoe pag 1 Calcolo combiatorio Cosideriamo u isieme di oggetti di atura qualsiasi. Idicheremo questi oggetti co a1 a2... a. Co questi oggetti si voglioo formare dei gruppi
Calcolo Combiatorio Adolfo Scimoe pag 1 Calcolo combiatorio Cosideriamo u isieme di oggetti di atura qualsiasi. Idicheremo questi oggetti co a1 a2... a. Co questi oggetti si voglioo formare dei gruppi
Analisi Matematica II
 Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
2 Criteri di convergenza per serie a termini positivi
 Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
Istituzioni di Analisi Superiore Esercizi
 Istituzioi di Aalisi Superiore Esercizi G.P.Leoardi 13 aprile 2010 Nota: gli esercizi delle sezioi 2 4 soo stati tratti i buoa parte da ua raccolta di esercizi di Aalisi Fuzioale ad opera di H.Brezis e
Istituzioi di Aalisi Superiore Esercizi G.P.Leoardi 13 aprile 2010 Nota: gli esercizi delle sezioi 2 4 soo stati tratti i buoa parte da ua raccolta di esercizi di Aalisi Fuzioale ad opera di H.Brezis e
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
7 LE PROPRIETÀ DEI NUMERI NATURALI. SUCCES- SIONI
 7 LE PROPRIETÀ DEI NUMERI NATURALI. SUCCES- SIONI Abbiamo usato alcue proprietà dei umeri aturali che coviee mettere i evideza. Per prima cosa otiamo che N gode delle due proprietà (i 0 N; (ii se N allora
7 LE PROPRIETÀ DEI NUMERI NATURALI. SUCCES- SIONI Abbiamo usato alcue proprietà dei umeri aturali che coviee mettere i evideza. Per prima cosa otiamo che N gode delle due proprietà (i 0 N; (ii se N allora
Funzioni continue. Definizione di limite e di funzione continua. Esercizio 1. x 0, 1 x 2, 3
 Fuzioi cotiue Defiizioe di limite e di fuzioe cotiua Esercizio. Dire quali delle segueti fuzioi soo cotiue. f : 0,, 3, f 0,, 3 Plot Piecewise,,,,, 0, 3.0 0.8 0.6 0.4 0. f è cotiua. Ifatti, fissiamo y [0,].
Fuzioi cotiue Defiizioe di limite e di fuzioe cotiua Esercizio. Dire quali delle segueti fuzioi soo cotiue. f : 0,, 3, f 0,, 3 Plot Piecewise,,,,, 0, 3.0 0.8 0.6 0.4 0. f è cotiua. Ifatti, fissiamo y [0,].
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09, CANALE E-O)
 ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09, CANALE E-O) DISPENSA N. 1 1. Limiti superiori, iferiori ed esatti, O, Ω, Θ Defiizioe 1.1 (Limitazioe Superiore). Diciamo che g() è ua itazioe superiore
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09, CANALE E-O) DISPENSA N. 1 1. Limiti superiori, iferiori ed esatti, O, Ω, Θ Defiizioe 1.1 (Limitazioe Superiore). Diciamo che g() è ua itazioe superiore
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
F. Ricci. Appunti per il corso. Introduzione alla Teoria della Misura e all Analisi Funzionale A.A
 F. Ricci Apputi per il corso Itroduzioe alla Teoria della Misura e all Aalisi Fuzioale A.A. 2013-14 Idice Capitolo 1. σ-algebre e misure 5 1. Fuzioi di isieme additive e σ-additive 5 2. Spazi misurabili
F. Ricci Apputi per il corso Itroduzioe alla Teoria della Misura e all Aalisi Fuzioale A.A. 2013-14 Idice Capitolo 1. σ-algebre e misure 5 1. Fuzioi di isieme additive e σ-additive 5 2. Spazi misurabili
A.A CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 8.
 A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 8. Esercizio 8.1. Siao, m N due umeri aturali tali che MCD(, m) = 1; dimostrare che il gruppo Z Z m è u gruppo
A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 8. Esercizio 8.1. Siao, m N due umeri aturali tali che MCD(, m) = 1; dimostrare che il gruppo Z Z m è u gruppo
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 AA Dott.ssa Sandra Lucente Successioni numeriche
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
Esercitazione di AM310
 Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
ALTRI ESERCIZI SULL INTEGRALE DI LEBESGUE. A. Figà Talamanca
 ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
