Interazioni Elettrodeboli. Lezione n. 9. Campo di Dirac Invarianza di Gauge Globale Campi interagenti
|
|
|
- Luigina Vitale
- 7 anni fa
- Visualizzazioni
Transcript
1 Interazioni Elettrodeboli prof. Franceco Ragua Univerità di Milano Lezione n Campo di Dirac Invarianza di Gauge Globale Campi interagenti anno accademico
2 Quantizzazione del Campo di Dirac La quantizzazione del campo di Dirac i effettua in modo del tutto analogo alla quantizzazione del campo di Klein-Gordon Seguendo il notro approccio per il campo di KG Si viluppa il campo nei modi normali Si promuovono i coefficienti dello viluppo a operatori Si impongono le regole di commutazione Alternativamente i può eguire il metodo canonico Si crive la Lagrangiana del campo di Dirac Si individuano i momenti coniugati ai campi Si impongo le relazioni di di commutazioni fra campi e momenti coniugati Anticipiamo che la differenza fondamentale ta nel fatto che nelle regole di commutazione ai commutatori [A,B] i otituicono gli anticommutatori {A,B} La neceità degli anticommutatori può eere motivata alternativamente Dal principio di ecluione di Pauli che richiede l antiimmetria degli tati fermionici cotruiti con gli operatori di creazione e ditruzione Dalla neceità che l Hamiltoniana ia definita poitiva Entrambi gli approcci derivano da motivazioni fiiche Vale la pena approfondire entrambi gli apetti Interazioni Elettrodeboli Franceco Ragua 26
3 Lagrangiana del campo di Dirac La Lagrangiana del campo di Dirac è Notiamo che non contiene i campi L (,, ) ( i / m) L equazione di Dirac egue emplicemente applicando le equazioni di Eulero Lagrange ai campi e Variando i campi L L L aimmetria fra e deriva dal fatto che più Lagrangiane ono poibili Ad eempio ( ) ( φ ) Tuttavia i può dimotrare che le azioni corripondenti differicono per l integrale di una 4-divergenza che i può rendere nullo all infinito Pertanto conducono alle tee equazioni L L φ γ ( / ) ( i/ m) i m Alternativamente, variando i campi L L i m γ ( i/ + m) * ( uav ) ( uav ) L L ( / ) ( [ iγ m ) ] 1 i m ( i γ m) L1 ( i / + m) ( i m ) γ Interazioni Elettrodeboli Franceco Ragua 27
4 Hamiltoniana del campo di Dirac Poiamo a queto punto calcolare i momenti coniugati di I momenti coniugati di ono nulli per l aimmetria fra e nella Lagrangiana L π γ i ( ) L Hamiltoniana è pertanto i γγ i Dal momento che oddifa l equazione di Dirac Abbiamo una utile epreione alternativa per l Hamiltoniana H i Si potrebbe calcolare il momento del campo calcolando il tenore T ν Diamo i due riultati (il calcolo può eere un eercizio) ( i/ m) L H π L i ( i/ m) γ γ γ iγ m γ i γ m ( iα + γ m) H ( iα + mβ) 1, r P d r ( i ) H d i iα + mβ i Interazioni Elettrodeboli Franceco Ragua 28
5 Epanione del campo di Dirac L epanione del campo di Dirac in onde piane i può fare allo teo modo di quanto fatto per il campo calare d i x + i x ( x) ( a, u, e + b, v, e ) ( 2π ) 2E Anche in queto cao conviene definire delle funzioni con ben definite proprietà di ortogonalità i x + i x u, e v, e f, g, ( 2π ) 2E ( 2π ) 2E Le relazioni di ortogonalità ono Il campo diventa ± δ r, δ, r f ( x) f ( x) d Utilizzando quete relazioni i può facilmente invertire l epanione Interazioni Elettrodeboli Franceco Ragua 29 g x g x d δ δ f x g x d r p p r a f ( x) ( x) d g x f x d r,,,, ± ( x) d ( f a + g b ) p p r b g ( x) ( x) d,,
6 Quantizzazione del campo di Dirac Poiamo adeo dicutere la quantizzazione del campo di Dirac Seguendo il notro approccio promuoviamo le funzioni a e b a operatori in uno pazio atratto e fiiamo le regole di anti-commutazione { } a, a 2 π δ δ { b, b } ( 2 ) π δ δ tutte le altre nulle Con queti operatori i poono cotruire gli tati con n particelle nello pazio di Foc 11, n n 2E 2E a a Una analoga epreione i può crivere con gli operatori b (antiparticelle) Le regole di anticommutazione fra gli operatori a e b aicurano che gli tati abbiano la corretta antiimmetria ripetto alle permutazioni di due particelle 11,, jj,,,, nn ± 11,,,, jj,, nn Il egno è + o per permutazioni pari o dipari ripettivamente Nel eguito arà utile trattare eparatamente le due componenti di un campo ( x) a + b x La componente a energia poitiva a x f x a, d La componente a energia negativa 1 n 1 1 n n Interazioni Elettrodeboli Franceco Ragua 21 b ± x g x b d, ±
7 Quantizzazione del campo di Dirac Calcoliamo adeo gli anticommutatori (a tempi uguali t t ) { n x, m( x )} { n x, m ( x )} Notiamo che i campi hanno 4 componenti Dal momento che gli operatori a e b anti-commutano fra di loro avremo { } { } n x, m x an x, am x + { bn x, ( x ) bm } Cominciamo con le componenti a energia poitiva { } an x, am x d d f n x f ( x ){ a, a m } { a, a } 2 ( 2π ) d f n x f m ( x ) Ricordiamo t t 1 + i ( r r ) 1 d e u nu m ( 2π ) 2E Analogamente per le componenti a energia negativa 1 d i ( ) { bn x, ( x ) bm } e r r v nv m ( 2π ) 2E 1 + i ( r r ) 1 d e v nv m ( 2π ) 2E Interazioni Elettrodeboli Franceco Ragua 211 { n x, m( x )} π δ δ
8 Quantizzazione del campo di Dirac Sommando i due pezzi 1 i ( ) 1 + r r { n x, m( x )} d e u u + v v ( 2π ) 2E nm Oltre alle relazioni di completezza già tudiate (diapoitiva ) ne eitono altre 1 ( u u + v v ) Inm δ nm ( iiii) 2E nm In concluione otteniamo 1 { n x, m ( x )} δnm d e ( 2π ) Con una procedura imile i ottengono le altre relazioni { n x, m ( x )} δnmδ( r r ) + i ( r r ) iiii iiii iiii i i i iiii, { n x m ( x )}, { n x m ( x )} Interazioni Elettrodeboli Franceco Ragua 212
9 Hamiltoniana e regole di commutazione Veniamo adeo all epreione dell Hamiltoniana in funzione degli operatori di creazione e ditruzione È conveniente partire dalle relazioni H d i x d f a + g b r (,,,, ) ± Utilizzando l epanione di otteniamo i x d E f a g b,,,, ± Introducendo nell Hamiltoniana Eeguiamo l integrazione ul volume Utilizziamo le relazioni di ortogonalità: opravvivono olo due termini Interazioni Elettrodeboli Franceco Ragua 21 x d ( f a + g b, ) ±,,, H d i d d d f a + g b E f a g b, ' ± ( ) ( ) r r,,,,,,,,, ± H d d E d f f a a g g b b, ' ± (,,,, ) r,,,, d d E a a b b (, δ δ, δ δ ),, nel cao di Dirac c è olo una derivata d E a, a b b, ± (,, )
10 Hamiltoniana e regole di commutazione H d E a a b b,, ± (,, ) Il termine relativo ai quanti a è già otto forma di un operatore numero Per mettere anche il econdo termine otto forma di operatore numero abbiamo biogno di commutare i due operatori Se aveimo una regola di commutazione (eliminiamo il termine infinito) b,, b, c b, b, c + b, b,, H d E a, a b, b Queta Hamiltoniana non è definita poitiva ± I quanti b contribuicono con energia negativa! Al contrario, con una regola di anticommutazione b, b c b b c b b, H d E a a + b b { },,,,,, (,, ),, ± (,, ) Queta volta anche i quanti b contribuicono all energia con egno poitivo Adottare regole di anticommutazione è neceario per avere una Hamiltoniana definita poitiva Nel dettaglio del calcolo la differenza è tata introdotta dal fatto che l equazione di Dirac è di primo ordine nel tempo Interazioni Elettrodeboli Franceco Ragua 214
11 Invarianza di gauge globale Anche la Lagrangiana del campo di Dirac è invariante per traformazioni di fae cotante: traformazioni di gauge globali L ( i / m) i e α + i e α Ovviamente e la fae è cotante la Lagrangiana è invariante ( i/ m) + iα iα L e ( i/ + m) e i i e α e α ( i / m) L Calcoliamo adeo la corrente che corriponde a queta invarianza Per una traformazione infiniteima δ ( 1 iδα) δ iδα i δα δ Analogamente i δα Ricordiamo l epreione per la corrente di Noether n N L δ L δ L δ + n ( n ) δα ( ) δα ( ) δα N iγ ( i ) j γ Abbiamo ritrovato la corrente di probabilità della teoria di Dirac È una corrente conervata j L ( ) ( ) iγ L Interazioni Elettrodeboli Franceco Ragua 215
12 Invarianza di gauge globale Calcoliamo adeo la carica conervata aociata alla conervazione della corrente Q j d r ( x) γ ( x) d r x x d r Le epanioni dei campi ono x d f a + g b,,,, ± Inerendo le due epreioni nella carica,,,, ± ( x) d ( f a + g b ) Utilizzando le proprietà di ortogonalità delle funzioni f e g opravvivono olo due termini Q d d d r f f a a + g g b b Q d d d f a + g b f a + g b r,,,, (,,,, ) (,,,,,,,, ) (,, δ δ,, δ δ ) d a, a, + b, b, Q d d a a + b b Interazioni Elettrodeboli Franceco Ragua 216
13 Invarianza di gauge globale Q d a a + b b,, (,, ) Vediamo che anche in queto cao per traformare il econdo operatore in un operatore numero abbiamo biogno di regole di commutazione Vediamo adeo l effetto di avere utilizzato anticommutatori b, b c b b c b b, Q d E a a b b { },,,,,,,, ± (,, ) Con queta celta le particelle e le antiparticelle hanno cariche oppote Nei due calcoli che abbiamo fatto ( Q e H ) abbiamo cartato il contributo infinito che deriva dal commutatore Nel cao dei campi fermionici abbiamo però cambiato anche il egno degli operatori Dobbiamo preciare la definizione del prodotto normale nel cao di campi fermionici Il prodotto normale porta gli operatori di ditruzione a detra e inerice un egno + o a econda del numero pari o dipari di permutazioni : aa : a a : baa : a ba Interazioni Elettrodeboli Franceco Ragua 217
14 Invarianza di gauge globale L invarianza globale di gauge della Lagrangiana di Dirac porta alla corrente conervata L ( i / m) j γ L apetto importante, coneguenza dell invarianza di gauge, è il fatto che i campi appaiono nella forma j O Banalizzando, la preenza contemporanea di un campo hermitiano coniugato e un campo normale aicura che compaia il prodotto della fae e della ua complea coniugata il cui prodotto è 1 Meno banale: la preenza contemporanea di un campo hermitiano coniugato e un campo normale aicura che la carica ia conervata I campi contengono operatori di creazione e ditruzione:protoni e antiprotoni x d f a + g b p p (, ),,, ' ±,,,, ± ( x) d ( f a + g b ) L azione della corrente induce una variazione di carica nulla Δ Q Q p Q p Q T a a +1 1 a b b a b b 1 +1 Interazioni Elettrodeboli Franceco Ragua 218
15 Campi interagenti La teoria quantitica dei campi fin qui vita decrive l evoluzione di particelle libere Gli operatori numero Nˆ aa commutano con l Hamiltoniana Il numero delle particelle in ogni modo rimane cotante Non riolve il problema di avere una teoria capace di decrivere un numero di particelle variabile nel tempo È necearia una teoria con campi interagenti La teoria dei campi quantitici interagenti va oltre gli obbiettivi del coro Tuttavia dicutiamo brevemente alcuni apetti 1 1 Ritorniamo all ocillatore quantitico unidimenionale Hˆ mpˆ + mω qˆ 2 2 L energia potenziale ha una forma quadratica Di olito riultato di approimazioni al primo ordine Eenziale per trovare la oluzione algebrica Implica la conervazione del numero di quanti ( N commuta con H ) Per introdurre la poibilità di variazione del numero dei quanti occorre andare oltre l approimazione armonica 2 2 Interazioni Elettrodeboli Franceco Ragua 219
16 Campi interagenti Introduciamo un termine anarmonico di terzo grado Hˆ mpˆ + mω qˆ + λqˆ 2 2 Eprimendo l Hamiltoniano in funzione degli operatori a e a 1 Hˆ ( aˆˆ a + aa ˆˆ ) ω + λ( aˆ + aˆ ) Hˆ ˆ + λ H 2 Non i può riolvere con i metodi algebrici utilizzati precedentemente Si può verificare che N a a e H' non commutano Gli autovettori di H hanno un numero variabile di quanti Non eite una oluzione eatta di queto problema Si ricorre al metodo perturbativo Si tratta il termine λ H' come perturbazione Si epandono gli autovettori (e autovalori) di H in funzione degli autovettori dell Hamiltoniano imperturbato H Agli autovettori imperturbati r corripondono gli autovettori perturbati ˆ ( ) H r Er r r c Hˆ rn n r Er r n r r r r E E E E + λ + λ + r Interazioni Elettrodeboli Franceco Ragua 22
17 Campi interagenti Si trova il eguente riultato ˆ r H r E r 1 r E r H r r r r r E E E E + λ + λ + Per calcolare la correzione del econdo ordine occorre calcolare elementi di matrice del tipo È facile renderi conto che il econdo elemento di matrice è divero da zero anche per r, in particolare per r +, r + 1, r 1, r Queta emplice dicuione motra che l introduzione di un termine anarmonico porta a coniderare procei con numero di particelle non cotante In particolare allo tato r> (che ha numero definito di quanti) i otituice uno tato che ha un numero differenti di quanti di H r Nella derivazione della Lagrangiana del campo crn n n 2 il termine del potenziale era diventato q 2 n qn 1 φ τδx τ dx Δx x Prodotto di due campi L interazione è rappreentata dal prodotto di almeno tre campi Interazioni Elettrodeboli Franceco Ragua 221 E 2 r r r H H r E r E ( ˆ+ ˆ ) ( ˆ+ ˆ ) r H r r a a r r H r a a
18 Campi interagenti Abbiamo gia vito la forma di alcune interazioni Kein Gordon * * em iq φf φi φf φi j 4 Mfi i d x jem x A x Dirac em f γ i j q x x Come eempio l interazione di un fermione con il campo elettromagnetico LD iγ m 1 ν LA F F 4 ν F A A Lint eγ A L LD + LA + Lint Se l interazione non contiene derivate dei campi i momenti coniugati non cambiano ν ν ν π L ( φ) L Hamiltoniana è pertanto H HD + HA + Hint Hint Lint Interazioni Elettrodeboli Franceco Ragua 222
Introduzione. Esempio di costruzione one del contorno delle radici. Esempio... 4
 Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
Corso di Fondamenti di Automatica A.A. 2015/16. Diagrammi di Bode
 1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1. Teorema di reciprocità
 1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
16. Onde elastiche. m s
 1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
= 20 m/s in una guida verticale circolare. v A A
 Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo
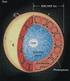 7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
Controllo di Azionamenti Elettrici. Lezione n 13
 Controllo di Azionamenti Elettrici Lezione n 1 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di Palermo CTROLLO DIRETTO DI COPPIA DI AZIAMENTI C MOTORE IN CORRENTE
Controllo di Azionamenti Elettrici Lezione n 1 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di Palermo CTROLLO DIRETTO DI COPPIA DI AZIAMENTI C MOTORE IN CORRENTE
DINAMICHE COMPLESSE NEL FERRO DI CAVALLO
 DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
DINAMICHE COMPLEE NEL FERRO DI CAVALLO La mappa a erro di cavallo L inieme invariante Dinamica imbolica Dinamiche nell inieme invariante Ferro di cavallo e cao C. Piccardi e F. Dercole Politecnico di Milano
Meccanica Applicata alle Macchine Appello del 12/01/2012
 Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
Esercitazione 16 Novembre 2012 Circuiti dinamici del secondo ordine. t come riportato in figura.
 Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
La trasformata di Fourier in Ottica
 Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
A.A MATERIALI POLIMERICI B. Capitolo 5 Calore specifico
 A.A. 2005-06 MATERIALI POLIMERICI B Capitolo 5 Calore pecifico A preione cotante il calore pecifico c p (JK -1 kg -1 ) o la capacità termica molare (JK -1 mol -1 ) ((298) = M 0 c p(298) con M 0 peo molecolare
A.A. 2005-06 MATERIALI POLIMERICI B Capitolo 5 Calore pecifico A preione cotante il calore pecifico c p (JK -1 kg -1 ) o la capacità termica molare (JK -1 mol -1 ) ((298) = M 0 c p(298) con M 0 peo molecolare
ESERCIZIO 1 L/2 C.R. D
 SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Progetto di reti correttrici e controllori PID e traduzione nel discreto con il metodo di emulazione
 Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
H = H 0 + V. { V ti t t f 0 altrove
 Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
Esercizio 1 (Regola d oro di Fermi Determinare la probabilità di transizione per unità di tempo da uno stato a ad uno stato b al primo ordine perturbativo di un sistema per cui si suppone di aver risolto
1_ Filtro passa-basso Con A(jw) si indica la funzione di trasferimento del filtro, il cui modulo A assume un valore costante
 PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 2 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 2 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE ATTENZIONE
 U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
U.21/0 UNITA' 21 SOMMARIO U.21 LE MODALITÀ DI TRASMISSIONE DEL CALORE 21.1. Introduzione 21.2. Conduzione 21.3. Convezione 21.4. Irraggiamento 21.5. Modalità imultanee di tramiione del calore ATTENZIONE
Lezione 11. Progetto del controllore
 Lezione Progetto del controllore Specifiche di progetto Conideriamo nuovamente un itema di controllo in retroazione: d y + + + y () G() + + n Fig : Sitema di controllo Supporremo aegnata la funzione di
Lezione Progetto del controllore Specifiche di progetto Conideriamo nuovamente un itema di controllo in retroazione: d y + + + y () G() + + n Fig : Sitema di controllo Supporremo aegnata la funzione di
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008
 MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
Controllo di Azionamenti Elettrici. Lezione n 3. Caratteristiche e predisposizione dei regolatori PID
 Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
ESERCIZI SVOLTI di ANALISI DEI SISTEMI
 ESERCIZI SVOLTI di ANALISI DEI SISTEMI Davide Giglio DIST - Univerità di Genova Via Opera Pia, 3 645 - Genova, Italy Tel: +39 353748 Fax: +39 35354 Davide.Giglio@unige.it Queta raccolta di eercizi volti
ESERCIZI SVOLTI di ANALISI DEI SISTEMI Davide Giglio DIST - Univerità di Genova Via Opera Pia, 3 645 - Genova, Italy Tel: +39 353748 Fax: +39 35354 Davide.Giglio@unige.it Queta raccolta di eercizi volti
Calcolo della tensione ammissibile Dovendo essere il grado di sicurezza non inferiore a 3 si ricava che il coefficiente di sicurezza γ è 3 per cui:
 Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Nel caso di molte misure e statistica gaussiana
 Dicrepanza Nella tragrande maggioranza dei cai le concluioni perimentali implicano il confronto tra due o più valori. Queti valori poono eere delle miure (e quindi con un incertezza), delle time teoriche
Dicrepanza Nella tragrande maggioranza dei cai le concluioni perimentali implicano il confronto tra due o più valori. Queti valori poono eere delle miure (e quindi con un incertezza), delle time teoriche
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA
 DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
Appello di Meccanica Quantistica I
 Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
PROBLEMI RISOLTI DI DINAMICA
 PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
Lezione XXI - 09/04/2003 ora 8:30-10:30 - Esercizi sulle perdite di carico - Originale di Berti Sara.
 Lezione XXI - 09/04/00 ora 8:0-10:0 - Eercizi ulle perdite di carico - Originale di Berti Sara. Eercizio 1 Calcolare la potenza di una pompa necearia a far correre il fluido attravero un tubo collegato
Lezione XXI - 09/04/00 ora 8:0-10:0 - Eercizi ulle perdite di carico - Originale di Berti Sara. Eercizio 1 Calcolare la potenza di una pompa necearia a far correre il fluido attravero un tubo collegato
L equazione che descrive il moto del corpo è la seconda legge della dinamica
 Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
F = 150 N F 1 =? = 3,1 s. 3,2
 ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
Stati Coerenti. Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana. p = i d.
 1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
LAVORO ED ENERGIA. 1J = 1N 1m
 ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ALCUNI SIMBOLI E FORMULE UTILI NELL ESERCIZIO 3, DOMANDE 3B, 3C, 3D (pagg. 5 e 6)
 Univerità C. Cattaneo Liuc, Coro di Statitica, Seione n., 01 Laboratorio Excel Seione n. Venerdì 101 Gruppo PZ Lunedì 7101 Gruppo AD Martedì 8101 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE N. (I) Tabella
Univerità C. Cattaneo Liuc, Coro di Statitica, Seione n., 01 Laboratorio Excel Seione n. Venerdì 101 Gruppo PZ Lunedì 7101 Gruppo AD Martedì 8101 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE N. (I) Tabella
Corso di Laurea in Ingegneria Energetica FISICA GENERALE T-A (9 Settembre 2011) Prof. Roberto Spighi
 Coro di Laurea in Ingegneria Energetica FIICA GENERALE -A (9 ettebre 0) Prof. Roberto pighi ) Uain Bolt, pritita ondiale, partecipa ad una gara di 00 etri. Partendo ovviaente da fero, decide di accelerare
Coro di Laurea in Ingegneria Energetica FIICA GENERALE -A (9 ettebre 0) Prof. Roberto pighi ) Uain Bolt, pritita ondiale, partecipa ad una gara di 00 etri. Partendo ovviaente da fero, decide di accelerare
a) Caso di rottura duttile con armatura compressa minore di quella tesa
 LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
Alessandro Scopelliti
 Aleandro Scopelliti Univerità di Reggio Calabria Univerity of Warwick aleandro.copelliti@unirc.it Robert Barro, viluppando un ragionamento inizialmente propoto da David Ricardo, otiene ulla bae della teoria
Aleandro Scopelliti Univerità di Reggio Calabria Univerity of Warwick aleandro.copelliti@unirc.it Robert Barro, viluppando un ragionamento inizialmente propoto da David Ricardo, otiene ulla bae della teoria
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. FISICA MODERNA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2013-2014 (1) Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2013-2014 (1) Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si
corso di Terminali per i Trasporti e la Logistica Umberto Crisalli
 coro di Terminali per i Traporti e la Logitica ELEMENTI DI TEORIA DELLE CODE Umberto Crialli crialli@ing.uniroma.it INTRODUZIONE Simulazione dei terminali In generale, un terminale è cotituito da un inieme
coro di Terminali per i Traporti e la Logitica ELEMENTI DI TEORIA DELLE CODE Umberto Crialli crialli@ing.uniroma.it INTRODUZIONE Simulazione dei terminali In generale, un terminale è cotituito da un inieme
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Esperienza n 6: Pendolo di Kater
 Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Modellistica dinamica di sistemi fisici
 .. MODELLISTICA - Modellitica dinamica. Modellitica dinamica di itemi fiici Nella realtà fiica eitono vari ambiti energetici, per eempio: meccanico (tralazionale e rotazionale) elettrico-magnetico idraulico
.. MODELLISTICA - Modellitica dinamica. Modellitica dinamica di itemi fiici Nella realtà fiica eitono vari ambiti energetici, per eempio: meccanico (tralazionale e rotazionale) elettrico-magnetico idraulico
Un problema di dadi. Michele Impedovo
 Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
19.12. Impianti motori con turbine a gas
 19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
Sistemi aperti E 2. E = m w. velocità w in un campo gravitazionale, con accelerazione di gravità g.
 ) Concetti di bae Sitemi aperti ) Primo principio della termodinamica 3) Secondo principio della termodinamica 4) Stati di equilibrio tabile 5) Diagramma energia-entropia 6) Lavoro, non-lavoro e calore
) Concetti di bae Sitemi aperti ) Primo principio della termodinamica 3) Secondo principio della termodinamica 4) Stati di equilibrio tabile 5) Diagramma energia-entropia 6) Lavoro, non-lavoro e calore
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 14 Gennaio 2010
 CORSO DI LURE IN SCIENZE BIOLOGICHE Prova critta di FISIC 4 Gennaio 00 ) Un bambino lancia una palla di maa m = 00 gr verticalmente vero l alto con velocità v 0 = m/, a partire da una roccia alta h 0 =
CORSO DI LURE IN SCIENZE BIOLOGICHE Prova critta di FISIC 4 Gennaio 00 ) Un bambino lancia una palla di maa m = 00 gr verticalmente vero l alto con velocità v 0 = m/, a partire da una roccia alta h 0 =
D. MR (*) 2. Il modulo dell accelerazione angolare α della carrucola vale rad A s rad B s rad C s rad D. 55.
 acoltà di Ingegneria a prova intracoro di iica I 30.0.0 Copito A (*) Eercizio n. Una carrucola, aiilabile ad un dico di aa 3.7 kg e raggio 70 c, è libera di ruotare intorno ad un ae orizzontale paante
acoltà di Ingegneria a prova intracoro di iica I 30.0.0 Copito A (*) Eercizio n. Una carrucola, aiilabile ad un dico di aa 3.7 kg e raggio 70 c, è libera di ruotare intorno ad un ae orizzontale paante
I brani della batteria MT si possono leggere tutti con la stessa velocità?
 t r u m e n t i a p p l i c a t i v i I brani della batteria MT i poono leggere tutti con la tea velocità? Norme traverali dal econdo anno della al terzo della econdaria di primo grado Patrizio E. Treoldi
t r u m e n t i a p p l i c a t i v i I brani della batteria MT i poono leggere tutti con la tea velocità? Norme traverali dal econdo anno della al terzo della econdaria di primo grado Patrizio E. Treoldi
Flessione su 4 punti. Configurazione sperimentale. Schematizzazione di calcolo. Studio delle sollecitazioni semplici. Taglio.
 Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Test 1 - Teoria dei Campi 2010
 Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Stati limite nel cemento armato Stato limite ultimo per tensioni normali: applicazioni BOZZA
 Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Controllore Processo. Le principali componenti del sistema sono: il rivelatore di errore, il controllore che ha il compito di trasformare il segnale
 CONTROLLORI DI TIO ID rincipi di funzionamento Il termine controllo definice l azione volta per portare e mantenere ad un valore prefiato un parametro fiico di un impianto o di un proceo (ad eempio, la
CONTROLLORI DI TIO ID rincipi di funzionamento Il termine controllo definice l azione volta per portare e mantenere ad un valore prefiato un parametro fiico di un impianto o di un proceo (ad eempio, la
Note su alcuni principi fondamentali di macroeconomia Versione parziale e provvisoria. Claudio Sardoni Sapienza Università di Roma
 Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Caso di A non regolare
 Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
Problema n. 2. Soluzione
 Problema n. Un auto da cora A iaia u un piano orizzontale con elocità cotante = 69 km/ i 11 km/ j ripetto ad un oeratore olidale al uolo Ox. Qual è la elocità dell auto A miurata da un oeratore olidale
Problema n. Un auto da cora A iaia u un piano orizzontale con elocità cotante = 69 km/ i 11 km/ j ripetto ad un oeratore olidale al uolo Ox. Qual è la elocità dell auto A miurata da un oeratore olidale
L induzione elettromagnetica - Legge di Faraday-Lentz
 L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
STRUTTURE IN CEMENTO ARMATO - III
 Suidi didattici per il coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STRUTTURE IN CEMENTO ARMATO - III AGGIORNAMENTO 26/09/2012 Coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STATI LIMITE
Suidi didattici per il coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STRUTTURE IN CEMENTO ARMATO - III AGGIORNAMENTO 26/09/2012 Coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STATI LIMITE
Q Flusso di calore (Joule m -2 s -1 )
 Conduzione Convezione Meccanimo Colliioni molecolari Diffuione molecolare Equazione generale ka ha T dt dx ( T ) Radiazione Evaporazione Fotoni Cambiamento di fae Fluo di calore (Joule m -2-1 ) Calore
Conduzione Convezione Meccanimo Colliioni molecolari Diffuione molecolare Equazione generale ka ha T dt dx ( T ) Radiazione Evaporazione Fotoni Cambiamento di fae Fluo di calore (Joule m -2-1 ) Calore
Modellazione e Analisi di Sistemi Idraulici
 Modellazione e Analii di Sitemi Idraulici Modellazione e Analii di Sitemi Idraulici Davide Giglio La ingola vaca Si conideri il itema rappreentato in figura. Il itema conite in una vaca contenente acqua.
Modellazione e Analii di Sitemi Idraulici Modellazione e Analii di Sitemi Idraulici Davide Giglio La ingola vaca Si conideri il itema rappreentato in figura. Il itema conite in una vaca contenente acqua.
V u = C. Funzione di rete. Cambio di punto di vista ω variabile. Il circuito simbolico è resistivo e lineare, con un solo generatore indipendente
 ambio di pnto di vita variabile Fnzione di rete X X X X l circito imbolico è reitivo e lineare, con n olo eneratore indipendente H Proporzionalità tra caa ed effetto H è na qantità complea, fnzione di
ambio di pnto di vita variabile Fnzione di rete X X X X l circito imbolico è reitivo e lineare, con n olo eneratore indipendente H Proporzionalità tra caa ed effetto H è na qantità complea, fnzione di
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
acciaio nelle condizioni di esercizio
 Analii di affidabilità di una truttura in acciaio nelle condizioni di eercizio v Dati: 6 m : N(9.5, 1) kn/m : N(3.6, 1.) kn/m : N(10000, 800) N/mm a trave è cotituita da un profilato IP 70. a funzionalità
Analii di affidabilità di una truttura in acciaio nelle condizioni di eercizio v Dati: 6 m : N(9.5, 1) kn/m : N(3.6, 1.) kn/m : N(10000, 800) N/mm a trave è cotituita da un profilato IP 70. a funzionalità
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
corso di formazione ed aggiornamento
 coro di formazione ed aggiornamento NUOVE NORME TECNICHE IN ZONA SISMICA di cui all ordinanza n. 37 del P.C.M. del 0.03.003 pubblicata ulla Gazzetta Ufficiale in data 08.05.003 ARGOMENTO DELLA LEZIONE:
coro di formazione ed aggiornamento NUOVE NORME TECNICHE IN ZONA SISMICA di cui all ordinanza n. 37 del P.C.M. del 0.03.003 pubblicata ulla Gazzetta Ufficiale in data 08.05.003 ARGOMENTO DELLA LEZIONE:
Elementi di programmazione lineare. Ottimizzazione di funzioni soggette a vincoli
 Elementi di programmazione lineare Ottimizzazione di funzioni oggette a vincoli Formulazione del problema min Z ma oggetta b c a T d Z:funzione obiettivo calare d: coto fio calare : variabile deciionale
Elementi di programmazione lineare Ottimizzazione di funzioni oggette a vincoli Formulazione del problema min Z ma oggetta b c a T d Z:funzione obiettivo calare d: coto fio calare : variabile deciionale
Esercizio: calcolo di media e deviazione standard campionaria
 Eercizio: calcolo di media e deviazione tandard campionaria Per verificare le pretazioni di un hard dik per PC, i oervano in miure ripetute i tempi di crittura T di uno teo file di grandi dimenioni. In
Eercizio: calcolo di media e deviazione tandard campionaria Per verificare le pretazioni di un hard dik per PC, i oervano in miure ripetute i tempi di crittura T di uno teo file di grandi dimenioni. In
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16)
 FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
Sistemi dinamici-parte 2 Parentesi di Poisson e trasformazioni canoniche
 Sistemi dinamici-parte 2 Parentesi di e trasformazioni AM Cherubini 11 Maggio 2007 1 / 25 Analogamente a quanto fatto per i sistemi lagrangiani occorre definire, insieme alla struttura del sistema, anche
Sistemi dinamici-parte 2 Parentesi di e trasformazioni AM Cherubini 11 Maggio 2007 1 / 25 Analogamente a quanto fatto per i sistemi lagrangiani occorre definire, insieme alla struttura del sistema, anche
La macchina sincrona
 MACCHINE E AZIONAMENTI ELETTRICI Coro di Laurea in Ingegneria Indutriale La macchina incrona Docente Prof. Franceco Benzi Univerità di Pavia e-mail: franceco.benzi@unipv.it Principio di funzionamento Nella
MACCHINE E AZIONAMENTI ELETTRICI Coro di Laurea in Ingegneria Indutriale La macchina incrona Docente Prof. Franceco Benzi Univerità di Pavia e-mail: franceco.benzi@unipv.it Principio di funzionamento Nella
Le ipotesi di base che si utilizzano sono le stesse quattro già viste con riferimento al caso della flessione semplice e cioè:
 LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
Sicché l effetto di una variazione del prezzo sulla domanda del bene può essere scisso in due componenti
 Appunti equazione di Slutk. Variazione del prezzo e quantità doandata In preenza di un auento del prezzo i conuatori reagicono a due egnali differenti a) è auentato il prezzo relativo del bene in quetione
Appunti equazione di Slutk. Variazione del prezzo e quantità doandata In preenza di un auento del prezzo i conuatori reagicono a due egnali differenti a) è auentato il prezzo relativo del bene in quetione
Sintesi tramite il luogo delle radici
 Sintei tramite il luogo delle radici Può eere utilizzata anche per progettare itemi di controllo per itemi intabili Le pecifiche devono eere ricondotte a opportuni limiti u %, ta, t di W(), oltre quelle
Sintei tramite il luogo delle radici Può eere utilizzata anche per progettare itemi di controllo per itemi intabili Le pecifiche devono eere ricondotte a opportuni limiti u %, ta, t di W(), oltre quelle
Divisori e combinatori
 Diviori e combinatori Luca Vincetti a.a. - Diviori e combinatori La combinazione lineare di egnali differenti o, all invero, la uddiviione di un unico egnale in componenti divere fa parte della normale
Diviori e combinatori Luca Vincetti a.a. - Diviori e combinatori La combinazione lineare di egnali differenti o, all invero, la uddiviione di un unico egnale in componenti divere fa parte della normale
Diffusione e membrane
 Eercizi di fiica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Diffuione e membrane 1) Calcolare il fluo avvettivo di oluto in un tubicino di ezione 0.1 mm 2 in cui corrono 0.2 ml al
Eercizi di fiica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Diffuione e membrane 1) Calcolare il fluo avvettivo di oluto in un tubicino di ezione 0.1 mm 2 in cui corrono 0.2 ml al
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17)
 FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
Annichilazione elettrone-positrone
 Annichilazione elettrone-positrone Nicola Cabibbo 23 Novembre 1999 1 Il processo e + e µ + µ Vogliamo prendere in considerazione la annichilazione e + e µ + µ per illustrare una serie di aspetti interessanti
Annichilazione elettrone-positrone Nicola Cabibbo 23 Novembre 1999 1 Il processo e + e µ + µ Vogliamo prendere in considerazione la annichilazione e + e µ + µ per illustrare una serie di aspetti interessanti
L energia rinnovabile con l antica vite di Archimede
 Vite Idrodinamica L energia rinnovabile con l antica vite di Archimede Da più di un ecolo Spaan Babcock è conociuto come il più grande fornitore al mondo di pompe a vite di Archimede. La vite idrodinamica
Vite Idrodinamica L energia rinnovabile con l antica vite di Archimede Da più di un ecolo Spaan Babcock è conociuto come il più grande fornitore al mondo di pompe a vite di Archimede. La vite idrodinamica
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Università degli Studi di Pisa. CdLS in Ingegneria dell Automazione. Attività Progettuale
 Univerità degli Studi di Pia CdLS in Ingegneria dell Automazione Attività Progettuale Simulazione del Controllo DTC per il motore aincrono dell ETR5 A cura di BABBONI QUAGLI Franceco Andrea Indice Indice
Univerità degli Studi di Pia CdLS in Ingegneria dell Automazione Attività Progettuale Simulazione del Controllo DTC per il motore aincrono dell ETR5 A cura di BABBONI QUAGLI Franceco Andrea Indice Indice
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Determinazione formula composto chimico dato dalla reazione tra due elementi. Differenza di elettronegatività tra i due elementi
 Determinazione formula comoto chimico ato alla reazione tra ue elementi Differenza i elettronegatività tra i ue elementi E. metallo + non metallo Si forma un comoto ionico Si forma un comoto covalente
Determinazione formula comoto chimico ato alla reazione tra ue elementi Differenza i elettronegatività tra i ue elementi E. metallo + non metallo Si forma un comoto ionico Si forma un comoto covalente
Forma canonica di Jordan
 Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Matematica Avanzata Per La Fisica - I accertamento,
 1 Matematica Avanzata Per La Fisica - I accertamento, 13 2 2004 1. Sia X un insieme. Sia H(X) l insieme delle trasformazioni f : X X. Sia G H(X), tale che f G sse f è unijezione. a) Dimostrare che G è
1 Matematica Avanzata Per La Fisica - I accertamento, 13 2 2004 1. Sia X un insieme. Sia H(X) l insieme delle trasformazioni f : X X. Sia G H(X), tale che f G sse f è unijezione. a) Dimostrare che G è
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
TRACCIA DI STUDIO. Tecniche di campionamento. Popolazione e campione
 TRACCIA DI STUDIO Popolazione e campione Dopo aver individuato e definito la popolazione da eaminare, che può eere finita o infinita, arebbe ideale condurre l indagine u tutti gli elementi della popolazione;
TRACCIA DI STUDIO Popolazione e campione Dopo aver individuato e definito la popolazione da eaminare, che può eere finita o infinita, arebbe ideale condurre l indagine u tutti gli elementi della popolazione;
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
CINEMATICA. determinare il vettore velocità (modulo, direzione e verso) all istante Trovare inoltre la traiettoria.
 . Data la legge oraria : CINEMATICA x( t) = at con a= m b= m c= 3 m y( t) bt c = + determinare il vettore velocità (modulo, direzione e vero) all itante Trovare inoltre la traiettoria. t=. y x 3 v ˆi ˆ
. Data la legge oraria : CINEMATICA x( t) = at con a= m b= m c= 3 m y( t) bt c = + determinare il vettore velocità (modulo, direzione e vero) all itante Trovare inoltre la traiettoria. t=. y x 3 v ˆi ˆ
2.1 Esponenziale di matrici
 ¾ ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori Esponenziale di matrici Esercizio : Data la matrice λ A λ calcolare
¾ ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori Esponenziale di matrici Esercizio : Data la matrice λ A λ calcolare
3. Catene di Misura e Funzioni di Trasferimento
 3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
8.1 Problema della diffusione in meccanica quantistica
 8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
Corso di Matematica II Anno Accademico Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori
 Esercizio 1 Corso di Matematica II Anno Accademico 29 21. Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori May 7, 21 Commenti e correzioni sono benvenuti. Mi scuso se ci fosse qualche
Esercizio 1 Corso di Matematica II Anno Accademico 29 21. Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori May 7, 21 Commenti e correzioni sono benvenuti. Mi scuso se ci fosse qualche
Lo studio dell evoluzione libera nei sistemi dinamici
 Lo studio dell evoluzione libera nei sistemi dinamici December, Un sistema lineare, dinamico, a dimensione finita e continuo (ovvero in cui il tempo t appartiene all insieme dei reali) può essere descritto
Lo studio dell evoluzione libera nei sistemi dinamici December, Un sistema lineare, dinamico, a dimensione finita e continuo (ovvero in cui il tempo t appartiene all insieme dei reali) può essere descritto
Capitolo. Semplificazioni di schemi a blocchi. 4.1 Blocchi in cascata. 4.2 Blocchi in parallelo. 4.3 Blocchi in catena chiusa (reazione negativa)
 Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
0.1 Numeri complessi C
 0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
Geotecnica e Laboratorio. Tensioni totali, neutrali e efficaci
 Coro di Laurea a ciclo Unico in Ingegneria Edile-Architettura Geotecnica e Laboratorio Tenioni totali, neutrali e efficaci Prof. Ing. Marco Favaretti e-mail: marco.favaretti@unipd.it ebite:.marcofavaretti.net
Coro di Laurea a ciclo Unico in Ingegneria Edile-Architettura Geotecnica e Laboratorio Tenioni totali, neutrali e efficaci Prof. Ing. Marco Favaretti e-mail: marco.favaretti@unipd.it ebite:.marcofavaretti.net
