Appunti ed Esercizi di Fisica Tecnica e Macchine Termiche
|
|
|
- Isabella Pizzi
- 8 anni fa
- Visualizzazioni
Transcript
1 Appun d Esrz d Fsa Tna Mahn Trmh Cap.. Sambaor d alor Nola Forgon Paolo D Maro Vrson La prsn dspnsa è rdaa ad slusvo uso ddao dgl allv d Dplom Unvrsar dl sor ndusral dll Unvrsà dgl Sud d Psa. Gl auor s n rsrvano u dr. Essa può ssr rprodoa solo oalmn d al n summnzonao, non può ssr alraa n aluna manra o ssr rvndua ad un oso supror a qullo no dlla rproduzon. Ogn alra orma d uso rproduzon dv ssr auorzzaa pr sro dall auor. Gl auor saranno gra a hunqu sgnal loro rror, nsazz o possbl mgloramn.
2 Cap.. Sambaor d alor. Tpologa dgl sambaor d alor Gl sambaor d alor sono dll apparhaur nll qual s ha rasmsson dl alor da un ludo ad un alro. Com gà annao nl Cap.5, gl sambaor d alor possono dsngurs n: sambaor a mslamno, n u du lud hanno n gnr la sssa naura s msolano ra loro; sambaor a supr, n u du lud, h possono ssr d dvrsa naura, sono spara da una supr mprmabl alla massa non s msolano. Nl sguo rarmo solo gl sambaor d alor a supr snza h d vola n vola vnga spao. In ss la rasmsson dl alor ra du lud avvn pr onvzon ra lud l rspv supr sold lamb pr onduzon aravrso la par dl ubo h l spara. Alun smp d sambaor d alor sono: l radaor d un auovolo, l vaporaor d un unà d ondzonamno, l ondnsaor d una nral rmolra,. Il pù smpl sambaor d alor è qullo osuo da du ub oassal (vd gura ). Uno d du lud lus nl ubo nrno mnr l alro lus nlla rgon anular, n quorrn o n onroorrn on l lusso dl ludo nrno; s parla rspvamn d sambaor ad quorrn (gura.a) d sambaor a onroorrn (gura.b). Nl onronar l du dsposzon, quorrn onroorrn, s può noar h solo pr lo sambaor a onroorrn la mpraura d usa dl ludo rddo può ssr maggor dlla mpraura d usa dl ludo aldo. Inolr ngl sambaor a onroorrn la drnza d mpraura ra lud ( d onsgunza l lusso rmo) s mann prssohè osan lungo ua la supr, h onsgunmn vn sruaa n manra mglor h n qull ad quorrn. Al onraro, n qus ulm la supr d sambo n prossmà dll usa (ararzzaa da un T rlavamn basso) dà un onrbuo molo mnor alla ponza rma oal sambaa. T T T, T, C >C T,u T,u T,u T,u T, T, x x (a) Sambaor ad quorrn. (b) Sambaor a onroorrn. Fgura : Andamno dll mpraur ngl sambaor d alor a ub oassal. -
3 Cap.. Sambaor d alor Un po d sambaor molo duso nll applazon ndusral è qullo a ub manllo (vd smpo mosrao n gura ) osuo da un aso d ub opporunamn rahus all nrno d un nvoluro (manllo). I ub sono mannu n poszon all nrno dl manllo mdan d daramm h svolgono anh la unzon d mgloramno dllo sambo rmo onvvo. Un ludo (gnralmn lqudo) vn ao sorrr all nrno d ub h possono ssr sagoma a pù passagg (l ludo prorr n drzon oppos l lao nrno d ub prma d usr), mnr l alro ludo (gnralmn lqudo) vn ao passar all srno d ub d all nrno dl manllo. Fgura : Sambaor d alor a ub manllo on passaggo nl manllo, orno d daramm, passagg n ub. Allorhé uno od nramb lud sono n as gassosa s ulzzano sambaor a orrn nroa (vd gura 3), n qual s ra d rdurr l o d dgradazon dllo sambo rmo, dovuo alla rlavamn bassa ondublà rma d gas, aumnando la supr d sambo rmo (mdan alaur) su una od nramb l supr d sambo (sambaor ompa). I luss nroa possono ssr: nramb pur (gura 3.a), quando du lud sono orza a prorrr ammn ra loro prpndolar; nramb msola, quando nramb lud sono lbr d muovrs anh n drzon parallla l uno all alro; uno msolao l alro puro (gura 3.b). (a) Enramb luss pur. (b) Un lusso mso d uno puro. Fgura 3: Sambaor d alor a orrn nroa. -3
4 Cap.. Sambaor d alor Un po d sambaor d alor aualmn molo usao, soprauo nl ampo dll ndusra almnar, è qullo a pasr (v. Fg.4). S raa d uno sambaor d po modular osuo da una sr d pasr mallh pan, doa d parolar rlv pr aumnar lo sambo rmo, srra ra d loro mdan ran. L avà ra l pasr sono prors alrnavamn dal ludo aldo da qullo rddo, h s sambano alor aravrso l pasr sss. S possono assmblar modularmn un numro arbraro d pasr, no a raggungr la supr d sambo dsdraa. Inolr, lo sambaor può ssr almn smonao pr sgur la pulza. Fgura 4: Shma d luss n uno sambaor a pasr. Inn, un po d sambaor h onvolg l passaggo alrnao d ludo aldo d qullo rddo aravrso una sssa szon è qullo rgnravo. Il alor vn rasro n una prma as dal ludo aldo al maral h osus l rgnraor (aumulo dl alor) sussvamn al ludo rddo quando qus ulmo rmpazza qullo aldo. Un paramro h ararzza lo sambaor è l rapporo β [m /m 3 ] ra la supr d sambo d l volum dllo sambaor. S parla d sambaor ompa quando β è supror a 700 m /m 3. Ad smpo, radaor d auomobl hanno β 000 m /m 3 ; polmon uman (n u s ralzza sambo d massa olr h d alor) arrvano al massmo valor d β 0000 m /m 3.. Il on d sambo rmo global La ponza rma sambaa ra du lud mannu a mpraura osan T (ludo aldo) T (ludo rddo), spara da una par solda, è daa da: ( T ) u A T [] dov A è la supr aravrso u avvn lo sambo d u è l osddo on d sambo rmo global o onduanza rma unara (/(m K)). Com gà sposo nl Cap., l analoga on la lgg d Ohm onsn d nrodurr la rssnza rma oal R lgaa al on d sambo rmo global aravrso la sgun ormula: R ( u A T T ) [K/] R Andamo ora a mosrar l dvrs polog h possono prsnars pr l alolo dlla rssnza rma global ( qund d u) ngl sambaor d alor. -4
5 Cap.. Sambaor d alor Caso d par d sparazon pana (vd gura 5): R R + R u A par + R s + + α A k A α A dov s è lo spssor dlla par, k è la ondublà rma dlla par α d rapprsnano, rspvamn, l on d sambo rmo onvvo nrno d srno. α R α A T, α s T, α s R par k A R α A T R R par R T Fgura 5: Rssnza rma oal nl aso d par d sparazon pana. Caso d par d sparazon lndra (vd gura 6): bsogna onsdrar h n gnral l ara d sambo rmo srna è dvrsa da qulla nrna h l ara da nrodurr all nrno dlla rssnza rma onduva è un opporuna mda (logarma) ra qus du. R u A u A dov n quso aso nrna, daa da: A A A ln A log A R α A R par s + + α A k A α A s r r d A è la mda logarma ra l ara srna qulla π ln ( r / r ) s ln k A π k L ( r r ) ( r / r ) L r r T, α T, α R α A T R R par R T Fgura 6: Rssnza rma oal nl aso d par d sparazon lndra. -5
6 Cap.. Sambaor d alor Caso d par d sparazon lndra on alaura srna (vd gura 7): n quso aso l ara da onsdrar pr lo sambo onvvo srno è un ara a, gnralmn mnor dll ara oal srna, da alolar mdan la sgun ormula: A A + η A,, non al. ala, al. dov ηala è l nza dll ala valuabl n unzon dlla orma dlla dmnson dll ala ram dagramm od appropra ormul (v. Cap., App.). Così ando s n ono dll varazon d mpraura lungo l al. Nl aso d al anular all srno d un ubo a szon rolar (vd gura 6) paramr da ulzzar pr l alolo dll ara srna a possono ssr onu ando uso dll sgun ormul: A A, non al. π r ( P ) L al al [ π ( r r ) π r ] L, al. al + al al η ala anh( bψ ) ; ( a)( 0.35log a) bψ ψ ; r r a ; al b r al α k al anh ( bψ ) [ xp( bψ ) xp( bψ )]/ [ xp( bψ ) + xp( bψ )] nll qual al sa ad ndar la rqunza dll al (al/m), mnr gl alr paramr gomr sono dn n gura 7. P al r r r al Fgura 7: Caso d par d sparazon lndra alaa. Gnralmn l prsazon d uno sambaor d alor pggorano duran l unzonamno a ausa dll aumulo d dpos d nrosazon (n ngls oulng) sull supr d sambo. In un alolo d vra s può nr ono d qusa dgradazon dllo sambo rmo aggungndo du rssnz rmh addzonal nlla sr d rssnz rmh pr l alolo dlla onduanza rma global. In as d progo è prò dl prvdr l valor d qus rssnz rmh addzonal pr u s prrs non nrn ono nl ompuo dlla onduanza rma global, ma s sgl uno sambaor ssn n ommro avn un ara d sambo maggor d qulla alolaa. -6
7 Cap.. Sambaor d alor La drmnazon dl on d sambo rmo global, u, può rsular molo rapdo allorhé s aa uso d aalogh orn dall d h ralzzano gl sambaor d alor. Ina, pr una daa pologa d sambaor, u può ssr ravao da appos dagramm n unzon dll pora dl ludo rddo dl ludo aldo. ESEMPIO Con d sambo rmo global Il lndro d un lomoor, osruo n lga d allumno (d ondublà rma 90 /(m K)), ha un alzza par a 0.6 m, un damro srno d 50 mm d uno spssor d 5 mm. In ondzon ph d unzonamno la mpraura dl gas onnuo all nrno dl lndro raggung valor d ra 00 C. Il on d sambo rmo onvvo nrno è ugual a 30 /(m K), mnr qullo srno val 40 /(m K). Il lndro è sposo all ara ambn avn una mpraura d 5 C d è doao d al anular pr aumnar lo sambo rmo vrso l srno. L al sono al 0 mm sono spss 3 mm. Qual è l aumno dllo sambo rmo dovuo alla prsnza dll al? Qual è la mpraura ragguna sulla supr nrna dl lndro qulla h s raggungrbb nl aso d assnza dll al?. Clndro snza alaura In qusa ongurazon l ara nrna l ara srna valgono: A π r L 0.00 m A π r L 0.05 m L sngol rssnz rmh sono da da: R α A.67 K/ ; R par s k ( r / r ) log A π k L K/ ; R.00 K/ α A La rssnza rma oal è daa dalla somma dll r rssnz alola n prdnza: R o R + Rpar + R.67 K/ S dspon qund d u l normazon nssar pr l alolo dlla ponza rma sambaa dall nrno dl lndro vrso l srno dlla mpraura dlla par nrna: T T 440. ; Tpar T R 465 C R o. Clndro on alaura In qusa ongurazon l ara nrna è la sssa d qulla valuaa nlla prdn ongurazon mnr l ara srna dlla zona non alaa d qulla alaa valgono, rspvamn: A π r P L 0.04 A ( ), non al. al al m [ π ( r r ) ] + π r 0.077, al. al al al L m L nza dll al alolaa mdan l apposa ormula l ara srna a valgono: -7
8 Cap.. Sambaor d alor η A ala anh bψ ( bψ ) 0.97, A, non al. + ηala A, al m A quso puno è possbl rdrmnar l valor dlla rssnza rma oal: R 0.6 K/ Ro R + Rpar + R.93 K/ α A, La ponza rma sambaa dall nrno dl lndro vrso l srno la mpraura dlla par nrna valgono: T T ; Tpar T R 83 C R o E quso l movo pr l qual l lndro non ond, pur avndo al suo nrno un ludo alla mpraura d 00 C. 3. Il dmnsonamno dgl sambaor d alor Lo sopo dl prsn paragrao è qullo d ornr l nozon nssar pr sgur sa l alolo rmo d progo h l alolo rmo d vra d uno sambaor d alor. Il alolo rmo d progo ha om sopo qullo d dmnsonar d sglr opporunamn uno sambaor h dv ralzzar l voluo sambo rmo ra du lud d u sono no: a) l pora massh b) l mpraur d ngrsso ) d u è prsra una mpraura d usa (dsdraa). Il alolo onss allora nl slzonar un po d sambaor d alor nl drmnar l ara d sambo rmo A nssara pr onr la dsdraa mpraura d usa. Il alolo rmo d vra vn sguo su uno sambaor gà ssn d u sono no a) l ara oal d sambo rmo, b) l pora massh, ) l mpraur d ngrsso d du lud. In quso aso l obvo è qullo d drmnar la ponza rma sambaa l mpraur d usa d du lud. Il alolo rmo dgl sambaor avvn normalmn ando uso dll quazon d blano dlla massa dll nrga. Com gà sposo nl Cap.5, qus quazon vngono normalmn rava onsdrando gl sambaor d alor om ssm apr a rgm, globalmn adaba. Applando l quazon d blano d massa d nrga al ludo G h, G h,u G h, Par adabaa G h,u Fgura 8: Blano d nrga n uno sambaor d alor. -8
9 Cap.. Sambaor d alor aldo d al ludo rddo (vd gura 8) s ongono l sgun ormul pr l alolo dlla ponza rma global,. In ss, pd d s rrsono rspvamn a lud aldo rddo pd d u all nraa all usa. ( h h ) G,, u ( h h ) G, u, Nll pos h du lud non subsono ambamn d as h orrspondn alor sp prsson sano osan, l quazon prdn dvngono: ( T T ) G p,,, u ( T T ) G p,, u, Nllo sudo dgl sambaor d alor è ul rrrs alla osdda poraa rma (orara), C, daa dal prodoo ra la poraa massa d l alor spo: C G p, ; C G p, [/K] In al aso l du quazon d blano prdn possono srvrs nlla sgun orma: C ( T T ) ; C ( T T ),, u, u, A qus du quazon d blano nrgo, s può assoar una quazon d sambo rmo; qus ulma assoa la ponza rma sambaa ra du lud all mpraur d ngrsso /o d usa, all pora, al on d sambo rmo global d all ara d sambo. Nl sguo, vngono spos du drn mod pr onr un quazon d sambo rmo da assoar all du quazon d blano dll nrga vs prdnmn. Il prmo è l modo dlla mda logarma dll drnz d mpraura (o MLDT) d l sondo è l modo ε-nut. Pr arn uso, s suppon nolr h la onduanza rma unara rmanga osan lungo ua la par dllo sambaor. E mporan noar h, avndo a dsposzon solo r quazon ndpndn ( blan nrg pr du lud la quazon d sambo rmo), s possono ravar al massmo r varabl nogn dllo sambaor ra: l quaro mpraur, l du pora, la ponza sambaa la supr d sambo. Modo dlla mda logarma dll drnz d mpraura (MLDT o n ngls LMTD) In quso aso la ponza rma sambaa ra du lud vn lgaa alla drnza d mpraura ra l ludo aldo d l ludo rddo, T T T, ovvro (v. Cap.) u A ( T T ) u A T Tuava, pohé T vara on la poszon all nrno dllo sambaor d alor è nssaro ulzzar una drnza d mpraura opporunamn mdaa. Nl aso dgl sambaor d alor ad quorrn o a onroorrn, s la onduanza d par non vara lungo la supr, s può dmosrar h la drnza d mpraura da ulzzar è la mda -9
10 Cap.. Sambaor d alor logarma ra l drnz ssn a mon d a vall dllo sambaor onndo osì la sgun quazon d sambo rmo: dov u A T ml T T T ml ) ln( T / T ) T T T T T T,,, u, u (samb. quorrn) T T, T, u T T, u T, (samb. onroorrn) Pr gl alr p d sambaor, l va drnza mda d mpraura da ulzzar nll quazon d sambo rmo è daa dal prodoo d qulla onua om mda logarma (om s lo sambaor oss a onroorrn) pr un aor d orrzon, F, mnor d uno: u A T ml F Il aor d orrzon dpnd dal po d sambaor dall mpraur d ngrsso d usa d du lud. Esso è qund dagrammao pr ogn sambaor d alor n unzon dll mpraur d du lud (vd gura 9). Il modo MLDT vn ulzzao pr l anals dgl sambaor d alor quando s onos, olr all mpraur d nraa all pora d du lud, almno una mpraura d usa (oppur quando s onos, olr all mpraur d nraa d usa d du lud, almno una poraa), ovvro nl aso dl problma d progo. La produra d alolo è la sgun:. s drmna la ponza rma sambaa ando uso d una dll du quazon d blano dll nrga, n u u gl alr rmn sano no.. on al valor d ponza rma, s drmna l vnual mpraura d usa (o l vnual poraa) nogna ando uso dlla sonda dll du quazon d blano dll nrga; 3. s alola la drnza d mpraura mda logarma, una vola slo l po d sambaor d alor da ulzzar, s ndvdua l valor dl aor d orrzon; 4. s drmna l valor dl on d sambo rmo global mdan abll o orrlazon d sambo rmo; 5. s alola l ara dlla supr d sambo rmo ando uso dll quazon d sambo rmo; 6. s ordna qund uno sambaor d alor dl po sablo on una supr d sambo ugual o supror a qulla alolaa. Un sondo po d alolo rmo (problma d srzo) pr gl sambaor d alor è la drmnazon dlla ponza rma sambaa dll mpraur d usa, no l mpraur d ngrsso l pora d du lud noo l po d sambaor nonhé la supr d sambo rmo (alolo rmo d vra). In quso aso s porbb anora ulzzar l modo MLDT, ma la soluzon è pù omplaa dao h, ssndov du mpraur nogn, l r quazon non possono ssr rsol una alla vola. Un modo molo smpl pr rsolvr un problma d quso po è, nv, l modo ε-nut h analzzrmo nl sguo. -0
11 Cap.. Sambaor d alor ESEMPIO Modo MLDT Uno sambaor a onroorrn è usao pr rrgrar l olo d lubrazon d una grand urbna a gas d po ndusral. L aqua usaa om rrgran aravrsa l ubo nrno on una poraa d 0. kg/s, mnr l olo vn ao passar nlla rgon anular on una poraa d 0. kg/s. L olo l aqua nrano alla mpraura d C, rspvamn. Il ubo nrno è un ubo n aao ¾ shdula 5S (ub ANSI), mnr l ubo srno ha un damro d 45 mm. Drmnar la lunghzza dl ubo anhé la mpraura d usa dll olo sa d 60 C. (Proprà: pr l olo d lubrazon ad una mpraura mda d 80 C orrspondono l sgun proprà: p 3 J/(kg K), µ (Pa s), k 0.38 /(mk); pr l aqua d rrgrazon ad una mpraura d 30 C orrspondono l sgun pora: p 478 J/(kg K), µ (Pa s), k 0.65 /(mk), Pr 4.85; dall abll ANSI s rova h l ubo n aao ha un damro srno d 6.67 mm d uno spssor d.65 mm, la sua ondublà rma è par a ra 50 /(mk)) T,u Aqua T,u T, D D D an. T, S raa d un po alolo rmo d progo. La ponza rma sambaa ra du lud può ssr onua dall quazon d blano dll nrga pr l ludo aldo: G p, ( T, T, u ) 854 La mpraura on la qual l aqua uors dallo sambaor d alor può ssr drmnao mdan l quazon d blano dll nrga pr l ludo rddo: T, u T, C G p, Pr por drmnar l ara d sambo rmo nssara, mdan l quazon d sambo MLDT, è nssaro ravar l on d sambo rmo global, u. A al n oorr nnanzuo alolar on d sambo rmo onvv lao nrno, α, lao srno, α. Pr l lusso d aqua all nrno dl ubo s ha: ρ v D 4G R 509 µ π D µ Olo Essndo l lusso d po urbolno pnamn svluppao l on d sambo rmo può ssr drmnao mdan la orrlazon d Colburn 0.8 / 3 Nu 0.03R Pr 85.5 da u: k α Nu 87 /m K D -
12 Cap.. Sambaor d alor Pr l lusso d olo nlla rgon anular dl ubo l damro draulo da ulzzar pr l alolo dl numro d Rynolds è: D Il numro d Rynolds val: ρ v Dh R µ h Dan. D ρ D µ h ρ π G 3 m ( D D ) an. 55 / 4 Il lusso anular è, qund, d po lamnar d l numro d Nussl è n qus ondzon prssohé osan d ugual a ra 4. Il on d sambo rmo lao srno val qund: k α Nu 30 /m K Dh Nl paragrao s è vso h l on d sambo rmo global può ssr drmnao mdan la sgun rlazon R R + Rpar R u A u A + dov: R α A α π D L L R R par log π k α A ( D / D ) par L L α π D L L Com s può noar la rssnza rma domnan rsula ssr qulla srna l alr possono ssr rasura. In dnva s ha: R R u α 30 /m K u A R A A quso puno samo n grado d por applar l quazon d sambo rmo pr ravar la lunghzza dl ubo: L 78.5 m u π D Tml Modo ε-nut (n ngls ε-ntu) Pr onr un sprsson dll quazon d sambo rmo h non omprnda aluna mpraura d usa s dns l nza d uno sambaor, ε, l rapporo ra la ponza rma vamn sambaa nllo sambaor la massma ponza rma sambabl: ε ( 0 < ε <),max -
13 Cap.. Sambaor d alor (a) Sambaor ad passaggo nl manllo, 4, 6, n ub. (b) Sambaor a passagg nl manllo 4, 8,, n ub. () Sambaor a luss nroa on nramb lud pur. (d) Sambaor a luss nroa on un ludo puro l alro mso. Fgura 9: Faor d orrzon pr drn polog d sambaor. -3
14 Cap.. Sambaor d alor La massma ponza rma sambabl è qulla ralzzabl n uno sambaor n u l ludo d mnor poraa rma subs l massmo salo d mpraura possbl snza volar l sondo prnpo dlla rmodnama, quso s vra quando sso s dallo sambaor ad una mpraura par a qulla d ngrsso dl sondo ludo. In alr parol ( T T ), max Cmn,, Tal ponza sarbb onbl on uno sambaor d alor n onroorrn on una supr d sambo nna; n quso sambaor la mpraura d usa dl ludo rddo uguagla qulla d ngrsso dl ludo aldo quando C > C, mnr la mpraura d usa dl ludo aldo uguagla la mpraura d ngrsso dl ludo rddo quando C < C ; n dnva s ha: ( T T ),max C,, ( C > C ( T T ), max C,, s ) ( s C < C ) L du rlazon prdn possono ssr rassun nll una rlazon sposa n prdnza. S s onosono l nza l mpraur d ngrsso dllo sambaor allora la ponza rma sambaa può ssr alolaa mdan la sgun quazon d sambo: ( T T ) ε Cmn,, Pr una daa pologa d sambaor d alor s può dmosrar h l nza è sprmbl n unzon d du paramr admnsonal: ε ( NUT C), dov NUT è hamao numro d unà d rasmsson dl alor, dno om: u A NUT C mn R T C mn mnr C è l rapporo ra l apaà rmh orar d du lud: C C C mn max L nza d uno sambaor d alor può ssr ravaa da appos dagramm (vd gur dalla 0 alla 5) n unzon d du paramr sudd. Il modo -NUT può ssr applao ndrnmn sa pr alol d progo h d vra snza rhdr prodmn rav: nl prmo aso, noa ε, s rava NUT, da u s on la supr d sambo, nl sondo, noo NUT, s rava ε, da u s drmna la ponza sambaa. -4
15 Cap.. Sambaor d alor Enza (ε ) [%] C mn /C max Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura 0: Enza d uno sambaor d alor ad quorrn. Enza (ε ) [%] C mn /C max Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura : Enza d uno sambaor d alor a onroorrn. -5
16 Cap.. Sambaor d alor Enza (ε ) [%] C mn /C max Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura : Enza d uno sambaor ad passaggo nl manllo, 4, 6, n ub. Enza (ε ) [%] C mn /C max Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura 3: Enza d uno sambaor a passagg nl manllo 4, 8,, n ub. -6
17 Cap.. Sambaor d alor Enza (ε ) [%] C mn /C max Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura 4: Enza d uno sambaor a luss nroa on nramb lud pur. Enza (ε ) [%] C mso /C puro 0, Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura 5: Enza d uno sambaor a luss nroa on un ludo puro l alro mso. -7
18 Cap.. Sambaor d alor Rlavamn all nza d uno sambaor d alor, s possono ar l ossrvazon rpora nl sguo. L nza aumna rapdamn pr pol valor dl NUT (no a NUT.5) puoso lnamn pr grand valor. Pr quso movo l uso d sambaor d alor on valor d NUT maggor d 3 qund on grand dmnson può non ssr onomamn onvnn. Pr un dao NUT C l nza maggor è qulla rlava ad uno sambaor a onroorrn sguo da vno da uno sambaor d alor a luss nroa on nramb luss pur (vd gura 6); l pù basso valor dll nza lo s on nv on uno sambaor ad quorrn. L nza è ndpndn dal rapporo dll apaà C pr valor d NUT mnor d ra 0.3 (vd gura 5). Enza (ε ) [%] A onroorrn C mn /C max Ad quorrn A luss nroa on luss pur Numro d unà d rasmsson dl alor (NUT ua /C mn ) Fgura 6: Conrono dll andamno dll nza pr r drn p d sambaor d alor. Pr un dao NUT l nza dvna massma pr C 0 mnma pr C. Il aso C 0, orrspondn ad avr C max, è ralzzao quando uno d du lud nll aravrsar lo sambaor d alor subs ambamno d as (n quso aso la dsrbuzon d mpraura è qulla mosraa n gura 7). Pr C 0 l andamno dll nza è smpr lo ssso qualsas sa la pologa dgl sambaor d alor. In parolar la rlazon pr l nza s rdu alla ε xp( NUT ) pr quano do al puno prdn, al sprsson è omunqu valda pr qualunqu sambaor s NUT <
19 Cap.. Sambaor d alor T T T, T,u T T,u T x (a) Evaporaor. (b) Condnsaor. Fgura 7: Andamno dll mpraur quando un ludo subs ambamno d as. T, x La sla d uno sambaor d alor olr a rhdr un alolo rmo può rhdr anh alr onsdrazon qual qull lga al oso (onomh), all ngombro, alla alà d mpgo, all adablà, al lvllo d rumorosà, alla rssnza mana (sollazon dovu alla prsson d lud d all dlaazon rmh drnzal),.. ESEMPIO 3 - Modo ε-nut In un lo Rankn, una poraa d vapor par a.5 kg/s lasa la urbna om vapor sauro so alla prsson d 0.08 bar. Il vapor vn ondnsao a lqudo sauro andolo passar all'srno d ub d uno sambaor a ub manllo, mnr l'aqua lquda d rrgrazon, avn una mpraura d ngrsso d 90 K vn aa passar aravrso l'nrno d ub. Il ondnsaor onn 00 ub molo sol, asuno d 0 mm d damro la poraa oal d aqua aravrso ub è ugual a 80 kg/s. Il on d sambo rmo mdo assoao on la ondnsazon sulla supr srna d ub val 5000 /(m K). S drmn:. la ponza rma sambaa ra du lud;. la mpraura d usa dll'aqua d rrgrazon; 3. la lunghzza rhsa pr ogn sngolo ubo, suppos u ugual. Pr l proprà dll'aqua d rrgrazon s assuma sgun valor: p 486 J/(kg K), µ (Pa s), k 0.68 /(m K) Pr 4.6; pr l proprà dl vapor sauro s aa uso dll abll rmodnamh. T T T,u T, A In orrspondnza d una prsson d 0.08 bar l vapor sauro possd l sgun proprà: mpraura d 34.7 K, nalpa dl lqudo sauro d J/kg d nalpa dl vapor sauro so d J/kg. La ponza rma sambaa ra du lud val qund -9
20 Cap.. Sambaor d alor ( h h ) G,, u Noa la ponza rma, s può ravar almn la mpraura d usa dll'aqua d rrgrazon: T, u T, K G Ravamo l'ara d sambo rmo on l modo ε-nut; a al n è nssaro rovars nnanzuo l nza dllo sambaor: ε 0.44 C T T G T T,max mn p ( ) ( ),, A quso puno è possbl ravar l numro d unà d rasmsson dl alor aravrso l apposa ormula (od un qualsas dagramma): NUT ln ( ε ) Prma d ravar l'ara è nssaro drmnar anh l on d sambo rmo global u: + u A α A α A dov s è rasuraa la rssnza rma onduva dlla par d ub, suppos sol. Il on d sambo rmo srno, α, è dao, mnr qullo nrno dv ssr drmnao mdan un opporuna orrlazon d sambo rmo pr onvzon. Il numro d Rynolds pr l'aqua h passa all'nrno d ub val: ρ v D 4G R 4553 µ µ π D00 Lo sambo rmo avvn all'nrno d ub pr onvzon orzaa. Adoando la orrlazon d Colburn s on l sgun valor dl numro d Nussl: Nu 0.03R Pr 56.4 Il on d sambo rmo onvvo nrno val qund: k α Nu 3430 /(m K) D A quso puno è possbl ravar l on d sambo rmo global: + u /m K u A α A α A α α Dalla dnzon dl numro d unà d rasmsson dl alor s on la sgun sprsson pr l alolo dll ara dlla supr d sambo rmo: u A NUT Cmn NUT A 7.9 m Cmn u La lunghzza d ogn sngolo ubo val qund: A L.5 m π D N p,, -0
21 Cap.. Sambaor d alor ESEMPIO 4 - Modo MLDT d ε-nut Uno sambaor d alor d un mpano hmo è usao pr rsaldar alool lo ( p, 670 J/kg C) da 5 C a 70 C ad una poraa d. kg/s. Il rsaldamno vn ao on aqua ( p, 490 J/kg C) h nra nllo sambaor a 95 C d s a 45 C. S drmn la ponza rma sambaa ra du lud la poraa d aqua nssara pr l prosso. Nll pos h l on d sambo rmo global sa par a 800 /(m C), alolar l ara dlla supr d sambo rmo n sgun du as (s us sa l modo MLDT h l modo ε-nut):. sambaor n onroorrn;. sambaor a ub manllo on passagg nl manllo d 8 n ub (l aqua nra nl manllo). T,u Aqua T,u T, Alool S raa d un po alolo rmo d progo. La ponza rma sambaa da du lud val: G p, ( T, u T, ) 535 Noa la ponza rma s può ravar almn la poraa dll'aqua: G p, ( T, T, u ) G. kg/s p, ( T, T, u ). Sambaor n onroorrn Con l modo MLDT, noa la ponza rma sambaa ra du lud, è al onr l ara dlla supr d sambo rmo on la sgun ormula: A 4. m u Tml Con l modo ε-nut è nssaro rovars nnanzuo l nza d l rapporo ra l apaà rmh orar: C ε 0.743, C mn 0. 9,max Cmn ( T, T, ) C max A quso puno è possbl ravar l numro d unà d rasmsson dl alor aravrso l apposa ormula (o l apposo dagramma): ε NUT Cmn NUT ln.3 4. m A C ε C u S no om l modo ε-nut rsul pù omplsso d qullo MLDT. Non è prò smpr possbl usar l modo MLDT n quano non è do h s onosano smpr l mpraur d usa dl ludo rddo dl ludo aldo. T, -
22 Cap.. Sambaor d alor. Sambaor a ub manllo on passagg nl manllo d 8 n ub Con l modo MLDT, noa la ponza rma sambaa ra du lud è al onr l ara dlla supr d sambo rmo on la sgun ormula: A u Tml F Il aor d orrzon F può ssr ravao dall apposo dagramma. S on un valor d F par a ra 0.8. L ara dlla supr d sambo rmo è: A u T ml F 7.4 m Con l modo ε-nut è nssaro rovars nnanzuo l nza d l rapporo ra l apaà rmh orar: Cmn ε 0.743, C 0. 9,max Cmn ( T, T, ) Cmax A quso puno è possbl ravar l numro d unà d rasmsson dl alor aravrso l apposo dagramma onndo un NUT par a ra.8. L ara dlla supr d sambo rmo val: NUT Cmn A 7.6 m u 4. Impan on sambaor d alor Rgolazon. L prsazon dgl sambaor h vngono nsalla non sono saamn par a qull d progo pr una sr d mov, ra u prnpal sono: l va supr d sambo non è saamn par a qulla alolaa n sd d progo; sono nrzz nlla drmnazon dl on d sambo rmo global; pù n gnral, l modo d alolo a uso d numros pos smplav; l prsazon dllo sambaor s dgradano nl mpo a ausa dllo sporamno dll supr (oulng); alun sambaor sono soopos a varazon d aro duran l srzo. In u qus as s pon l problma d rporar l ondzon d unzonamno dllo sambaor a qull nomnal mdan organ d rgolazon. Gnralmn, la rgolazon è dl po ad anllo huso, val a dr s ags sull organo d rgolazon (d solo una valvola, nl nosro aso) sulla bas dllo sosamno ra l valor dlla varabl d onrollo msurao da un snsor (s. la mpraura d usa d uno d du lud) d l valor d rrmno mposao d al varabl. I dsposv dda a quso ompo (onrollr) possono ssr anh molo omplss la loro raazon è oggo d ors d rgolazon o d auomaa. L pù dus soluzon mpansh pr la rgolazon dgl sambaor agsono sulla poraa d uno d du lud sono l sgun: rgolazon d poraa ram valvola a du v; rgolazon d poraa ram pompa a vloà varabl; rgolazon n drvazon a poraa osan; rgolazon n drvazon a mpraura d ngrsso osan. -
23 Cap.. Sambaor d alor Rgolazon d poraa ram valvola a du v In quso po d rgolazon (v. Fg.8-a) la poraa vn varaa ram una valvola d rgolazon a du v. S vara qund l nza dllo sambaor agndo sa sul rapporo C mn /C max, sa sul valor d NUT (s la poraa rgolaa orrspond a C mn ) sa sulla varazon dl on d sambo global dovua alla varazon d vloà d uno d du lud. Qusa rgolazon è d po dsspavo, n quano la valvola d rgolazon nrodu una prda d aro aggunva, l h ompora un aumno dlla ponza d pompaggo rspo al aso n u la sssa poraa lusa nllo sambaor snza valvola. Quso shma mpla mnor os d mpano ra u l soluzon spos, uava l ampo d rgolazon (h dpnd dall ararsh dlla valvola dlla pompa) non è n gnr molo ampo. Rgolazon d poraa ram pompa a vloà varabl. Pr onr lo ssso o dl aso prdn snza nrodurr prd d aro aggunv, s può rorrr ad una pompa a vloà varabl (v. Fg.8-b). La vloà d roazon dlla pompa, gnralmn azonaa da un moor lro asnrono monoas o ras, può ssr rgolaa n modo dsonnuo ram ru lron (qusa soluzon non è adaa pr la rgolazon ad anllo huso) od n modo onnuo ram un nvrr. I os sono gnralmn maggor rspo al aso prdn. T, T, I T,u T, T,u T, T,u T,u (a) (b) Fgura 8: Rgolazon d poraa n uno sambaor a) ram valvola a du v b) ram pompa a vloà varabl. In quso aso, la varabl rgolaa è T,u. Rgolazon n drvazon a poraa osan In qusa soluzon (v. Fg.9) s nrodu un ramo AB d drvazon (o bypass) dl ruo, s a uso d una valvola a r v mslar: qusa valvola msla du pora n ngrsso pr onr un lusso n usa l u valor s mann osan. In quso modo, lo sambaor unzona a poraa osan, ma on mpraura n ngrsso varabl a sonda dlla quanà d ludo rrolaa nl ramo AB. Rgolazon n drvazon a mpraura d ngrsso osan In qusa soluzon (Fg.0a) s a uso d una valvola a r v dvar: qusa valvola suddvd la poraa n ngrsso n du luss n usa la u somma s mann osan. In quso aso lo sambaor unzona a poraa varabl, ma on mpraura d ngrsso osan. Lo ssso shma s può ralzzar nsrndo n usa allo sambaor una valvola mslar, d mnor oso (v. Fg.0b). Qusa soluzon è prrbl quando non s vuol varar molo la mpraura mda dlla supr d sambo. S no h n ogn aso d -3
24 Cap.. Sambaor d alor rgolazon n drvazon (Fg.9 0) la pompa vn pazzaa sul ramo dl ruo ov rola la poraa oal (osan) pr non vararn l puno d unzonamno. La sla ra l una o l alra soluzon mpansa dpnd da un gran numro d aor, la u raazon sula da qus no, ra u ampzza dl ampo d rgolazon rhso, oso d mpano, layou d ru. T, B T,u T, A T,u Fgura 9: Rgolazon d poraa n drvazon n uno sambaor ram valvola a r v a poraa osan. In quso aso, la varabl rgolaa è T,u s a uso d una valvola mslar. T, T, T,u T, T,u T, T,u T,u (a) (b) Fgura 0: Rgolazon d poraa n drvazon n uno sambaor ram valvola a r v a mpraura d ngrsso osan: a) on valvola dvar; b) on valvola mslar. In quso aso, la varabl rgolaa è T,u. -4
25 Cap.. Sambaor d alor BIBLIOGRAFIA Y. A. Cngl, Trmodnama rasmsson dl alor, MGraw-Hll, Nw York, M. Kays, A. L. London, Compa Ha Exhangrs, MGraw-Hll, Nw York, 964. R. Masrullo, P. Mazz, V. Naso R. Vanol, Fondamn d rasmsson dl alor, Vol., Lguor dor, Napol, 988. F Krh, Prnp d Trasmsson dl alor, Lguor dor, Napol, 99. J.P. Holman, Ha Transr, MGraw-Hll, Nw York,
Appunti ed Esercizi di Fisica Tecnica e Macchine Termiche
 Appun d Esrz d Fsa Tna Mahn Trmh ap. 3. Sambaor d alor Nola Forgon Paolo D Maro Vrson 006.03 3.05.07. La prsn dspnsa è rdaa ad slusvo uso ddao dgl allv d Dplom Unvrsar dl sor ndusral dll Unvrsà dgl Sud
Appun d Esrz d Fsa Tna Mahn Trmh ap. 3. Sambaor d alor Nola Forgon Paolo D Maro Vrson 006.03 3.05.07. La prsn dspnsa è rdaa ad slusvo uso ddao dgl allv d Dplom Unvrsar dl sor ndusral dll Unvrsà dgl Sud
Sistemi trifase. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 30-10-2012) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Edutecnica.it Circuiti a scatto -Esercizi 1
 duna. Cru a sao -srz srzo no. Soluzon a pag.5 Nl ruo d gura, l nrruor n huso all san ; dopo un mpo 4,8µs, n rapro onmporanamn n huso. roar l andamno dlla nson a ap dl ondnsaor. 4 kω CpF roar l alor dlla
duna. Cru a sao -srz srzo no. Soluzon a pag.5 Nl ruo d gura, l nrruor n huso all san ; dopo un mpo 4,8µs, n rapro onmporanamn n huso. roar l andamno dlla nson a ap dl ondnsaor. 4 kω CpF roar l alor dlla
Diploma Universitario in Ingegneria Meccanica. Corso di Fisica Tecnica. Nicola Forgione. Paolo Di Marco. Cap. 11. Scambiatori di calore
 Sambaor d alor Dploma Unvrsaro n Inggnra Mana Corso d Fsa na Nola Forgon Paolo D Maro Cap.. Sambaor d alor Vrson. 6//.. pologa dgl sambaor d alor Gl sambaor d alor sono dll apparhar nll qal s ha rasmsson
Sambaor d alor Dploma Unvrsaro n Inggnra Mana Corso d Fsa na Nola Forgon Paolo D Maro Cap.. Sambaor d alor Vrson. 6//.. pologa dgl sambaor d alor Gl sambaor d alor sono dll apparhar nll qal s ha rasmsson
Esercitazione n 4. Meccanismi combinati Resistenze termiche e Trasmittanze termiche
 Ercazon n 4 Mccanm combna nz rmch Tramanz rmch ) Valuar l ramanz rmch dll gun polog d fnr: a) fnra a vro ngolo ( por vro L [mm]; [W/(m)]); b) fnra con dopp vr ( por vro L [mm], ε ε 0.9, nrcapdn ara L n
Ercazon n 4 Mccanm combna nz rmch Tramanz rmch ) Valuar l ramanz rmch dll gun polog d fnr: a) fnra a vro ngolo ( por vro L [mm]; [W/(m)]); b) fnra con dopp vr ( por vro L [mm], ε ε 0.9, nrcapdn ara L n
Sistemi trifase. Parte 2. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 16-12-2013) Potenza assorbita da un carico trifase (1)
 Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
EFFETTI DELLA COMPRESSIBILITA SULLA GESTIONE DI UNA DISCARICA PER RIFIUTI URBANI
 EFFETTI DELLA COMPRESSIBILITA SULLA GESTIOE DI UA DISCARICA PER RIFIUTI URBAI Gabrl D Rull Door Inggnr Dparmno DICEA d Inggnra Cvl prsso la faolà d Inggnra dll Unvrsà dgl Sud d Frnz. Pro Srn Profssor ordnaro
EFFETTI DELLA COMPRESSIBILITA SULLA GESTIOE DI UA DISCARICA PER RIFIUTI URBAI Gabrl D Rull Door Inggnr Dparmno DICEA d Inggnra Cvl prsso la faolà d Inggnra dll Unvrsà dgl Sud d Frnz. Pro Srn Profssor ordnaro
Lezione 3. F. Previdi - Automatica - Lez. 3 1
 Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Seminario: Dinamica quantistica inerziale di una particella in una dimensione
 Snaro: Dnaa quansa nrzal d una parlla n una dnson Foralso quanso Funzon d onda: pr d ' ' dnsà d probablà sulla oordnaa al po  Valor d asa al po dll opraor : d A d A A ˆ ˆ * Saro quadrao do dlla proprà:
Snaro: Dnaa quansa nrzal d una parlla n una dnson Foralso quanso Funzon d onda: pr d ' ' dnsà d probablà sulla oordnaa al po  Valor d asa al po dll opraor : d A d A A ˆ ˆ * Saro quadrao do dlla proprà:
1. Variabili casuali continue e trasformazioni di variabili casuali...3. 2. La variabile casuale normale... 14
 ESERCIZI DI CALCOLO DELLE PROBABILITÀ PARTE II Rccardo Borgon Elna Colcno Pro Quao Sara Sala INDICE. Varabl casual connu rasformazon d varabl casual....3. La varabl casual normal... 4 3. Funzon gnrarc
ESERCIZI DI CALCOLO DELLE PROBABILITÀ PARTE II Rccardo Borgon Elna Colcno Pro Quao Sara Sala INDICE. Varabl casual connu rasformazon d varabl casual....3. La varabl casual normal... 4 3. Funzon gnrarc
17. Le soluzioni dell equazione di Schrödinger approfondimento
 7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
Aspettative. In questa lezione: Discutiamo di previsioni sulle variabili future, e di aspettative. Definiamo tassi di interesse nominale e reale.
 Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Il ruolo delle aspettative in economia
 Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Il processo inverso della derivazione si chiama integrazione.
 Ingral Indinio l Anidrivaa Il prosso invrso dlla drivazion si hiama ingrazion. Noa la variazion isanana di una grandzza p.s. la vloià è nssario sapr om si ompora al grandzza isan pr isan p.s. la posizion.
Ingral Indinio l Anidrivaa Il prosso invrso dlla drivazion si hiama ingrazion. Noa la variazion isanana di una grandzza p.s. la vloià è nssario sapr om si ompora al grandzza isan pr isan p.s. la posizion.
Calcolo delle Probabilità: esercitazione 10
 Calcolo dll Probablà: srcazon 0 Argono: Dsrbuzon noral (pag. 47 sgun dl lbro d so). Valor aso, varanza (pag. sgun). Dsrbuzon bvara dscr (pag. 44 sgun) covaranza (pag 45 sgun). NB: asscurars d conoscr l
Calcolo dll Probablà: srcazon 0 Argono: Dsrbuzon noral (pag. 47 sgun dl lbro d so). Valor aso, varanza (pag. sgun). Dsrbuzon bvara dscr (pag. 44 sgun) covaranza (pag 45 sgun). NB: asscurars d conoscr l
Errore standard di misurazione. Calcolare l intervallo del punteggio vero
 Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
Lezione 21 (BAG cap. 19) Regimi di cambio. Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
 Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Laboratorio di Navigazione Laurea Specialistica in Ingegneria Informatica, Ingegneria per l Ambiente e il Territorio Politecnico di Milano Campus
 Laoraoro Navgazon Laura Spcalsca n Inggnra Inormaca, Inggnra pr l mn l Trroro Polcnco Mlano Campus Como NVIGZION INRZIL Ssm rrmno n ssma rrmno è un nsm rgol msur ch c prmono rsponr a qus: ov s rova un
Laoraoro Navgazon Laura Spcalsca n Inggnra Inormaca, Inggnra pr l mn l Trroro Polcnco Mlano Campus Como NVIGZION INRZIL Ssm rrmno n ssma rrmno è un nsm rgol msur ch c prmono rsponr a qus: ov s rova un
MERCATI FINANZIARI IN ECONOMIA APERTA (Modello IS-LM in economia aperta)
 MRATI FINANZIARI IN ONOMIA APRTA Modllo - n conoma apra Invsmn fnanzar. Scla ra: a. mona nazonal: ransazon b. mona sra: non ha nssun vanaggo dnrla c. ol nazonal: fruano nrss d. ol sr: fruano nrss sono
MRATI FINANZIARI IN ONOMIA APRTA Modllo - n conoma apra Invsmn fnanzar. Scla ra: a. mona nazonal: ransazon b. mona sra: non ha nssun vanaggo dnrla c. ol nazonal: fruano nrss d. ol sr: fruano nrss sono
Formule generali di carica e scarica dei condensatori in un circuito RC
 Formul gnrali di aria saria di ondnsaori in un iruio A ura di ugnio Amirano onnuo dll ariolo:. Inroduzion........ 2 2. aria saria di un ondnsaor..... 2 3. Formula gnral pr nsioni fiss..... 4 4. Formula
Formul gnrali di aria saria di ondnsaori in un iruio A ura di ugnio Amirano onnuo dll ariolo:. Inroduzion........ 2 2. aria saria di un ondnsaor..... 2 3. Formula gnral pr nsioni fiss..... 4 4. Formula
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 PRIMITIVE E INTEGRALI DEFINITI
 Univrsià Carlo Caano Inggnria gsional nalisi mamaia aa 7/8 PRIMITIVE E INTEGRLI DEFINITI ESERCIZI CON SOLUZIONE Calolar i sguni ingrali indfinii: ) d ; ) d ; ) d ; ) os sin d ; 6 ) d SOLUZIONI ) La funzion
Univrsià Carlo Caano Inggnria gsional nalisi mamaia aa 7/8 PRIMITIVE E INTEGRLI DEFINITI ESERCIZI CON SOLUZIONE Calolar i sguni ingrali indfinii: ) d ; ) d ; ) d ; ) os sin d ; 6 ) d SOLUZIONI ) La funzion
Simulazione del processo di essiccazione di cereali. in letto fisso. condizionamento industriale. Natalino Mandas, Francesco Cambuli
 52_TER_dc_mandas 29-11-2007 20:11 Pagna 52 condzonamno ndusral d glucd (dra d carbono), l frmnazon nrcllular, gl svlupp d bar d muff, favor dal rscaldamno naural. Nl corso dgl ulm dcnn, l procsso d ssccazon
52_TER_dc_mandas 29-11-2007 20:11 Pagna 52 condzonamno ndusral d glucd (dra d carbono), l frmnazon nrcllular, gl svlupp d bar d muff, favor dal rscaldamno naural. Nl corso dgl ulm dcnn, l procsso d ssccazon
Si possono distuguere due casi: a) molecole distinguibili: il numero di modi è dato da
 ESISTE UA OTEOLE DIFFEEA TA LE SOLUIOI DEI POLIEI E QUELLE DELLE OLECOLE PICCOLE DOUTA ALLA DIFFEEA DI DIESIOI TA LE OLECOLE POLIEICHE E QUELLE DEL SOLETE. Pr qusto motvo trattrmo l soluzon polmrch attravrso
ESISTE UA OTEOLE DIFFEEA TA LE SOLUIOI DEI POLIEI E QUELLE DELLE OLECOLE PICCOLE DOUTA ALLA DIFFEEA DI DIESIOI TA LE OLECOLE POLIEICHE E QUELLE DEL SOLETE. Pr qusto motvo trattrmo l soluzon polmrch attravrso
CIRCUITO RLC IN SERIE
 ~ ~ IUITO L IN SEIE onsdrazon gnral Il crcuo L n sr (vd fgura) è formao da una sola magla n cu sono prsn una rssnza, un nduanza L, un condnsaor d capacà un gnraor d nson alrnaa cararzzao da una forza lromorc
~ ~ IUITO L IN SEIE onsdrazon gnral Il crcuo L n sr (vd fgura) è formao da una sola magla n cu sono prsn una rssnza, un nduanza L, un condnsaor d capacà un gnraor d nson alrnaa cararzzao da una forza lromorc
I sensori di spostamento
 I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
3) DIFFUSIONE DELLA LUCE E SPETTROSCOPIA RAMAN
 DIFFUSION DLLA LU STTROSOIA RAAN La uso lla lu a pa u aomo quval al sgu posso (l aomo è l lvllo : (A Assobmo u oo quza vo oa k passaggo allo sao ao aua (sao al o msso u oo quza vo oa k. Oppu: (B msso u
DIFFUSION DLLA LU STTROSOIA RAAN La uso lla lu a pa u aomo quval al sgu posso (l aomo è l lvllo : (A Assobmo u oo quza vo oa k passaggo allo sao ao aua (sao al o msso u oo quza vo oa k. Oppu: (B msso u
Laurea triennale in BIOLOGIA A. A
 Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
La tabella presenta 4 casi ed i relativi differenziali di rendimento tra un investimento in Dollari ed uno in Euro:
 MONETA E FINANZA INTERNAZIONALE Lzion 3 ARBITRAGGIO SUI TASSI DI INTERESSE Invsimno sro domanda di valua sra Disinvsimno rischio di cambio prché rndimno ral dipnd da R La ablla prsna 4 casi d i rlaivi
MONETA E FINANZA INTERNAZIONALE Lzion 3 ARBITRAGGIO SUI TASSI DI INTERESSE Invsimno sro domanda di valua sra Disinvsimno rischio di cambio prché rndimno ral dipnd da R La ablla prsna 4 casi d i rlaivi
Teoria delle opzioni e Prodotti strutturati
 L FIME a.a. 8-9 9 oa ll ozon Poo suua Gogo Consgl gogo.onsgl@unbg. Uff 58 vmno m:.-3. Pogamma. Mao ll ozon ona va. oa ll ozon 3. nh valuazon 4. Hgng 5. Inggna fnanzaa 6. Pou numh 7. Dvavs sass Ozon Pou
L FIME a.a. 8-9 9 oa ll ozon Poo suua Gogo Consgl gogo.onsgl@unbg. Uff 58 vmno m:.-3. Pogamma. Mao ll ozon ona va. oa ll ozon 3. nh valuazon 4. Hgng 5. Inggna fnanzaa 6. Pou numh 7. Dvavs sass Ozon Pou
Parte 4 - Pag.1. Vision 2000 - obiettivi della revisione. Oltre la ISO 9000: Vision 2000. Vision 2000 - elementi innovativi
 Olr la ISO 9000: Vso 2000 G.Rass - 11 maggo 2001 1 Vso 2000 - obv dlla rvso Obv dlla rvso dlla ISO 9000: passar dalla culura dlla coformà dll vdz a qulla dl couo mgloramo, ral msurabl dal cl Il progo d
Olr la ISO 9000: Vso 2000 G.Rass - 11 maggo 2001 1 Vso 2000 - obv dlla rvso Obv dlla rvso dlla ISO 9000: passar dalla culura dlla coformà dll vdz a qulla dl couo mgloramo, ral msurabl dal cl Il progo d
Oscillazioni e onde. Oscillatore armonico. x( t) e sostituendo nell equazione originale si ha. dx dt. x cos infatti. Periodo del moto armonico T
 No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
Principi ed applicazioni del metodo degli elementi finiti. Formulazione base con approccio agli spostamenti
 Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Interferenza e diffrazione con gli esponenziali complessi. Nota
 Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Serie di Fourier a tempo continuo. La rappresentazione dei segnali nel dominio della frequenza. Jean Baptiste Joseph Fourier (1768 1830 )
 Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Misura dell anisotropia. Misura dell anisotropia. Lock-in. Lock-in = S(
 nsoropa sgnfa varazon d brllanza al varar dlla drzon d ossrvazon. L prm ur d ansoropa vnvano sgu om amponamn sas dl lo, sglndo un ro numro d drzon onfronandon la brllanza on una na d modulazond Il lok-n
nsoropa sgnfa varazon d brllanza al varar dlla drzon d ossrvazon. L prm ur d ansoropa vnvano sgu om amponamn sas dl lo, sglndo un ro numro d drzon onfronandon la brllanza on una na d modulazond Il lok-n
Corso di ELETTRONICA INDUSTRIALE
 Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
11.c Gli operatori in Meccanica Quantistica
 Gl opraor U opraor è u applazo assoa ua fuzo a ua fuzo A La drvaa è u opraor : : L ombazo lar d opraor soo opraor La molplazo pr ua fuzo è u opraor U ( ) : U L applazo rpua d u opraor è u opraor a + b
Gl opraor U opraor è u applazo assoa ua fuzo a ua fuzo A La drvaa è u opraor : : L ombazo lar d opraor soo opraor La molplazo pr ua fuzo è u opraor U ( ) : U L applazo rpua d u opraor è u opraor a + b
Macroeconomia. Laura Vici. laura.vici@unibo.it. www.lauravici.com/macroeconomia LEZIONE 22. Rimini, 19 novembre 2014
 Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Esercizi sui gas perfetti
 Eserz su gas perett Eserzo In un repente d esertata dal gas è d delle oleole d elo. 0 d sono ontenute ol d He. La pressone 5.5 Trasorao l volue n untà SI: 0d 0 Pa. Deternare la velotà quadrata eda Ravao
Eserz su gas perett Eserzo In un repente d esertata dal gas è d delle oleole d elo. 0 d sono ontenute ol d He. La pressone 5.5 Trasorao l volue n untà SI: 0d 0 Pa. Deternare la velotà quadrata eda Ravao
Capitolo III: I Regolatori
 SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
Calcolo della funzione d uscita per un generico segnale d'ingresso
 Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
Spettro di densità di potenza e rumore termico
 Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
App.Cap.II: Dettagli e sviluppi per il capitolo 2. App.Cap.II-1: Risposta di un sistema del primo ordine con ingresso a impulso.
 SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
MERCATI FINANZIARI IN ECONOMIA APERTA (Modello IS-LM in economia aperta)
 MRTI FINNZIRI IN ONOMI PRT (Modllo - n conoma apra) Invmn fnanzar. Scla ra: a. mona nazonal: ranazon b. (mona ra): non ha nun vanaggo dnrla c. ol nazonal: fruano nr d. ol r: fruano nr ono ogg a rcho d
MRTI FINNZIRI IN ONOMI PRT (Modllo - n conoma apra) Invmn fnanzar. Scla ra: a. mona nazonal: ranazon b. (mona ra): non ha nun vanaggo dnrla c. ol nazonal: fruano nr d. ol r: fruano nr ono ogg a rcho d
Lezione 15 (BAG cap. 14) Le aspettative: nozioni di base
 Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
CENNI SULL USO DEL METODO SIMBOLICO PER IL CALCOLO DELLA
 ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
Scambio Termico. il calore per la vaporizzazione del fluido non viene ceduto da un altro fluido ma per irraggiamento (fiamme)
 Scambo rmco Il modo pù smplc pr scambar calor ra du corp, n parcolar, ra du flud è qullo d porl n dro conao; quso, prò, non è smpr auabl n quano pormmo non avr pù du fas dsn. In qus cas, l rasfrmno d calor
Scambo rmco Il modo pù smplc pr scambar calor ra du corp, n parcolar, ra du flud è qullo d porl n dro conao; quso, prò, non è smpr auabl n quano pormmo non avr pù du fas dsn. In qus cas, l rasfrmno d calor
Allocazione Statica. n i
 Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Esercitazioni di Elettrotecnica: circuiti in regime stazionario
 Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Esercizi & Domande per il Compito di Elettrotecnica del 15 giugno 2004
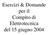 Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
La corrente i(t) che percorre l avvolgimento del trasformatore durante il transitorio è definita dalla seguente equazione: di dt
 Cosruzo Elroach Corr d coro crcuo u rasforaor Sovracorr rasforaor Esaao qus au, odo slfcao, l org l cosguz dll sovracorr ch ossoo sollcar l avvolgo d u rasforaor dura u coro crcuo a ors dl scodaro. 1 -
Cosruzo Elroach Corr d coro crcuo u rasforaor Sovracorr rasforaor Esaao qus au, odo slfcao, l org l cosguz dll sovracorr ch ossoo sollcar l avvolgo d u rasforaor dura u coro crcuo a ors dl scodaro. 1 -
IL BREVE PERIODO: MODELLO IS-LM. Mercato dei beni e curva IS
 L BREVE ERODO: ODELLO S-L rao bn urva S nvsmno: pn posvamn al ro (pù è alo, pù salgono l vn pù l mprs nvsono n mahnar, mpan,.) ngavamn al asso nrss (pù osa prnr a prso mno l mprs nvsono). ov ),, ( < >
L BREVE ERODO: ODELLO S-L rao bn urva S nvsmno: pn posvamn al ro (pù è alo, pù salgono l vn pù l mprs nvsono n mahnar, mpan,.) ngavamn al asso nrss (pù osa prnr a prso mno l mprs nvsono). ov ),, ( < >
Autovalori complessi e coniugati
 Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Tassi Equivalenti. Benedetto Matarazzo
 Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Sistemi dinamici lineari del 1 ordine
 Appuni di onrolli Auomaici Simi dinamici linari dl ordin Inroduzion... ipoa al gradino uniario... ipoa alla rampa... Empio...3 Empio...4 INTODUZIONE Si dfinic ima (lmnar) dl primo ordin un ima (linar mpo-invarian)
Appuni di onrolli Auomaici Simi dinamici linari dl ordin Inroduzion... ipoa al gradino uniario... ipoa alla rampa... Empio...3 Empio...4 INTODUZIONE Si dfinic ima (lmnar) dl primo ordin un ima (linar mpo-invarian)
 L soluzon Data la funzon ln( ) f ( ) 3 a trova l domno d f b scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c dtrmna l vntual ntrszon con gl ass d studa l
L soluzon Data la funzon ln( ) f ( ) 3 a trova l domno d f b scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c dtrmna l vntual ntrszon con gl ass d studa l
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA 7 DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO.
 DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO Sia A un apro di : sis un vor ab, al ch,, f A Prso, A si dic ch f è diffrnziabil in,, 0, 0 0 0 f f a b 0 si pon df, a, b f Si dimosra ch a, b,, quindi
DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO Sia A un apro di : sis un vor ab, al ch,, f A Prso, A si dic ch f è diffrnziabil in,, 0, 0 0 0 f f a b 0 si pon df, a, b f Si dimosra ch a, b,, quindi
FACOLTA DI INGEGNERIA. Corso di Fisica Tecnica Ambientale ESERCIZI SVOLTI CONDUZIONE
 FO DI INGEGNERI orso d Fsa a tal ESERIZI SVOI ONDUZIONE Esrzo Esrzo Dtrar l flusso tro pr utà d suprf attravrsa rg prat ua lastra paa ooga dllo spssor d 8 o l du fa atut all tpratur d 9 =.9 /..9 9 85.8
FO DI INGEGNERI orso d Fsa a tal ESERIZI SVOI ONDUZIONE Esrzo Esrzo Dtrar l flusso tro pr utà d suprf attravrsa rg prat ua lastra paa ooga dllo spssor d 8 o l du fa atut all tpratur d 9 =.9 /..9 9 85.8
Sistemi trifase. Parte 1. (versione del ) Sistemi trifase
 Ssm rfas Par www.d.ng.unbo./prs/masr/ddaca.hm rson dl -0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Ssm rfas Par www.d.ng.unbo./prs/masr/ddaca.hm rson dl -0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
CONSERVAZIONE A CALDO
 ONSERVAZIONE A ALDO prcolo azon prvnv lm crc azon corrva monoraggo rgsrazon documnazon frqunza d rgsrazon vrfca A l m n Mcrobologco (dovua alla grmnazon dll spor alla conamnazon croca ) Apparcchaura prfamn
ONSERVAZIONE A ALDO prcolo azon prvnv lm crc azon corrva monoraggo rgsrazon documnazon frqunza d rgsrazon vrfca A l m n Mcrobologco (dovua alla grmnazon dll spor alla conamnazon croca ) Apparcchaura prfamn
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 FUNZIONI INTEGRALI
 Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Esercizi riguardanti l integrazione
 Esrizi riguardanti l intgrazion. Trovar una primitiva dlla funzion f. Calolar il sgunt intgral indfinito d. Trovar una primitiva dlla funzion f. Tra tutt l primitiv dlla funzion f os sn, dtrminar qulla
Esrizi riguardanti l intgrazion. Trovar una primitiva dlla funzion f. Calolar il sgunt intgral indfinito d. Trovar una primitiva dlla funzion f. Tra tutt l primitiv dlla funzion f os sn, dtrminar qulla
8. Circuiti non lineari
 8. Crc non lnar odo dal. odo ral. nal d crc con dod mdan l modllo dal. Modllo dl dodo con cada d non. Modo rafco. nal d n crco lmaor d non mdan modo rafco. odo dodo dal = = < Cararca rafca Un dodo dal
8. Crc non lnar odo dal. odo ral. nal d crc con dod mdan l modllo dal. Modllo dl dodo con cada d non. Modo rafco. nal d n crco lmaor d non mdan modo rafco. odo dodo dal = = < Cararca rafca Un dodo dal
La popolazione in età da 0 a 2 anni residente nel comune di Bologna
 Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
SISTEMI TRIFASE B 1. i 2. i 3. Figura 1. - Schema di linea trifase
 SSTM TRFAS Dfnzon prncpal. ssm rfas sono schmazzabl com nlla fgura. Non s fa nssuna pos né sul gnraor d almnazon suao prma dlla szon A-A, né sull'ulzzaor suao dopo la szon B-B. A X B A X Fgura. - Schma
SSTM TRFAS Dfnzon prncpal. ssm rfas sono schmazzabl com nlla fgura. Non s fa nssuna pos né sul gnraor d almnazon suao prma dlla szon A-A, né sull'ulzzaor suao dopo la szon B-B. A X B A X Fgura. - Schma
Le soluzioni della prova scritta di Matematica per il corso di laurea in Chimica e Tecnologie Farmaceutiche (raggruppamento A-L)
 L soluzon dlla prova scrtta d Matmatca pr l corso d laura n Chmca Tcnolo Farmacutch raruppamnto A-L. Data la unzon a. trova l domno d b. scrv, splctamnt pr stso, qual sono l ntrvall n cu rsulta postva
L soluzon dlla prova scrtta d Matmatca pr l corso d laura n Chmca Tcnolo Farmacutch raruppamnto A-L. Data la unzon a. trova l domno d b. scrv, splctamnt pr stso, qual sono l ntrvall n cu rsulta postva
Le soluzioni della prova scritta di Matematica del 7 Febbraio 2014
 L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
LE SOLUZIONI. [Per definizione la concentrazione di una soluzione è il rapporto
 LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
Cognome e Nome: Numero di Matricola: Spazio riservato alla correzione
 Cognom Nom: Numro i Mariola: Progazion i Algorimi Anno Aamio 2016/2017 Appllo l 10/7/2017 Spazio rirao alla orrzion 1 2 3 4 Toal /20 /35 /20 /25 /100 1.Grafi a) Fornir lo puooi un algorimo riorio h in
Cognom Nom: Numro i Mariola: Progazion i Algorimi Anno Aamio 2016/2017 Appllo l 10/7/2017 Spazio rirao alla orrzion 1 2 3 4 Toal /20 /35 /20 /25 /100 1.Grafi a) Fornir lo puooi un algorimo riorio h in
La valutazione finanziaria
 STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
Università di Siena Sede di Grosseto Secondo Semestre 2010-2011. Macroeconomia. Paolo Pin ( pin3@unisi.it ) Lezione 7 2 Maggio 2011
 Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Raccolta Esercizi per il corso di Costruzione di Macchine
 Raccola Escz l coso d osuzon d Maccn Vson 0. Damno d Inggna Unvsà d Faa 9/0/0 obo.ovo@unf. Escz d osuzon d Maccn Inoduzon Qusa dsnsa accogl alcun scz la aazon dllo sco d osuzon d Maccn. Qull oa sono scz
Raccola Escz l coso d osuzon d Maccn Vson 0. Damno d Inggna Unvsà d Faa 9/0/0 obo.ovo@unf. Escz d osuzon d Maccn Inoduzon Qusa dsnsa accogl alcun scz la aazon dllo sco d osuzon d Maccn. Qull oa sono scz
SOLUZIONI. risparmio totale = D altra parte la traccia di dice anche che: e 64 L = produzione. Pertanto si ha: Quindi si ha un risparmio del 9,902%.
 SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
Determinare il dominio di una funzione
 Drminar il dominio di una funzion CHE COSA SONO LE FUNZON. Una funzion = f( è una rlazion ch lga du grandzz (variabili: la variabil vin chiamaa variabil indipndn, mnr la variabil dipndn. Pr smpio la rlazion
Drminar il dominio di una funzion CHE COSA SONO LE FUNZON. Una funzion = f( è una rlazion ch lga du grandzz (variabili: la variabil vin chiamaa variabil indipndn, mnr la variabil dipndn. Pr smpio la rlazion
Fisica Generale B. 5. Circuiti in Corrente Continua. Elementi di Circuito. Elettrodotti. Elementi di Circuito (II)
 Fsa enerale 5. ru n orrene onnua Elemen d ruo I ru eler sono osu da l onduor, generaor, ressor, ondensaor e alr elemen d ruo ollega ra loro. S suppone he gl elemen d ruo deal, se non sono ressor, abbano
Fsa enerale 5. ru n orrene onnua Elemen d ruo I ru eler sono osu da l onduor, generaor, ressor, ondensaor e alr elemen d ruo ollega ra loro. S suppone he gl elemen d ruo deal, se non sono ressor, abbano
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione
![[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione [ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione](/thumbs/92/110333272.jpg) Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Modello di Einstein. Stato eccitato. Stato fondamentale
 Modllo di Einsin Il modllo di Einsin dscriv in manira fnomnoloica d a livllo microscopico i procssi di l inrazion ra la r..m. maria ch porano ai fnomni di assorbimno d mission radiaiva. Il sisma modllo
Modllo di Einsin Il modllo di Einsin dscriv in manira fnomnoloica d a livllo microscopico i procssi di l inrazion ra la r..m. maria ch porano ai fnomni di assorbimno d mission radiaiva. Il sisma modllo
VALORE EFFICACE DEL VOLTAGGIO
 Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t
![Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t](/thumbs/24/2314935.jpg) 4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI
 RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI Da un sgnal aprdc s(), la sua rapprsnazn nl dmn dlla frqunza è frna dalla sgun dfnzn d rasfrmaa d Furr: S( ) F[s()]
RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI Da un sgnal aprdc s(), la sua rapprsnazn nl dmn dlla frqunza è frna dalla sgun dfnzn d rasfrmaa d Furr: S( ) F[s()]
Esame di Matematica e Abilità Informatiche - Settembre Le soluzioni
 Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
SVOLGIMENTO. 2 λ = b S
 RELAZIONE Dimnsionar sol d anima dl longhron d il rivsimno dl bordo di aacco, in una szion disan 4 m dalla mzzria, pr un ala monolonghron di un vlivolo avn l sguni cararisich: - pso oal W 4700 N - suprfici
RELAZIONE Dimnsionar sol d anima dl longhron d il rivsimno dl bordo di aacco, in una szion disan 4 m dalla mzzria, pr un ala monolonghron di un vlivolo avn l sguni cararisich: - pso oal W 4700 N - suprfici
Corsi di Laurea in Fisica, Fisica ed Astrofisica
 Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Apprendimento per Perceptron: esempio. Apprendimento di Reti di Perceptron. Discesa di Gradiente. gradiente
 / 3 ; J DA E F DA DA I DA $ N 45 2 dov "#$ &'#$, 9? K 9 O L M M K 9L 7 9 AC AC Sstm d Elaborazon dll Informazon 9 Sstm d Elaborazon dll Informazon Apprndmnto pr Prcptron smpo Apprndmnto d Rt d Prcptron
/ 3 ; J DA E F DA DA I DA $ N 45 2 dov "#$ &'#$, 9? K 9 O L M M K 9L 7 9 AC AC Sstm d Elaborazon dll Informazon 9 Sstm d Elaborazon dll Informazon Apprndmnto pr Prcptron smpo Apprndmnto d Rt d Prcptron
Soluzioni. 1. Data la funzione. a) trova il dominio di f
 Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
Sistemi trifase. (versione del ) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl -05-09 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl -05-09 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Alessandro Ottola matr. 208003 lezione del 11/3/2010 ora 10:30-13:30. Parete omogenea sottoposta a differenze termiche e diffusione
 Alssandro Ottola matr. 0800 lzon dl //00 ora 0:0-:0 Indc Dagramma d Glasr... Part omogna sottoosta a dffrnz trmch dffuson... Dagramma d Glasr r art omogna... 4 Dagramma d Glasr r art multstrato... 5 Esrczo
Alssandro Ottola matr. 0800 lzon dl //00 ora 0:0-:0 Indc Dagramma d Glasr... Part omogna sottoosta a dffrnz trmch dffuson... Dagramma d Glasr r art omogna... 4 Dagramma d Glasr r art multstrato... 5 Esrczo
AF 1 RITIRATO 26,1 26 2A AL 1 18,2 RITIRATO 25,7 26 3A AL 1 30,2 30 2A AL 0 RITIRATO 23,7 24 5A
 1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
Compact-1401. Compact-1401. Listino prezzi F6 Marzo 2013 MICRON
 Listino przzi F6 Marzo 013 UNI EN 1401 act-1401 UNI EN 1401 Carbonato di calcio,5 MICRON Tubi di PVC-U pr condott fognari civili d industriali costruiti scondo UNI EN 1401 GRESINTEX DALMINE RESINE Tubi
Listino przzi F6 Marzo 013 UNI EN 1401 act-1401 UNI EN 1401 Carbonato di calcio,5 MICRON Tubi di PVC-U pr condott fognari civili d industriali costruiti scondo UNI EN 1401 GRESINTEX DALMINE RESINE Tubi
Esercizi sullo studio di funzione
 Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
UNIONI BULLONATE: TAGLIO TORSIONE FLESSIONE. ESERCIZIO: Verificare il giunto a cerniera con squadrette d anima.
 UNIONI BULLONATE: TAGLIO TORSIONE FLESSIONE ESERCIZIO: Verare l guno a ernera on squadree d anma. S vuole verare l unone bullonaa allo sao lme ulmo nel aso d un guno a ernera on squadree d anma a orma
UNIONI BULLONATE: TAGLIO TORSIONE FLESSIONE ESERCIZIO: Verare l guno a ernera on squadree d anma. S vuole verare l unone bullonaa allo sao lme ulmo nel aso d un guno a ernera on squadree d anma a orma
Corso di IMPIANTI TECNICI per l EDILIZIAl. Vaso di espansione. Prof. Paolo ZAZZINI Dipartimento INGEO Università G.
 Corso di IMPIANTI TECNICI per l EDILIZIAl aso di espansione Prof. Paolo ZAZZINI Diparimeno INGEO Universià G. D Annunio Pescara www.lf.unich.i Prof. Paolo ZAZZINI Diparimeno INGEO Universià G. D Annunio
Corso di IMPIANTI TECNICI per l EDILIZIAl aso di espansione Prof. Paolo ZAZZINI Diparimeno INGEO Universià G. D Annunio Pescara www.lf.unich.i Prof. Paolo ZAZZINI Diparimeno INGEO Universià G. D Annunio
PRINCIPALI VANTAGGI:
 Ricamo-Lasr-Srass IL PRIMO PROGRAMMA AL MONDO CHE PERMETTE IN UN UNICO SOFTWARE: - La crazion di programmi Ricamo - La crazion di disgni Lasr con vari ffi (da uilizzar con ui i macchinari lasr in grado
Ricamo-Lasr-Srass IL PRIMO PROGRAMMA AL MONDO CHE PERMETTE IN UN UNICO SOFTWARE: - La crazion di programmi Ricamo - La crazion di disgni Lasr con vari ffi (da uilizzar con ui i macchinari lasr in grado
ALGORITMO FFT (Fast Fourier Transform)
 AGORITO FFT (Fast Fourr Transor) Rha sulla DFT Sa un sgnal rodo d rodo rarsntato dal vttor -dnsonal d oonnt [], [],.., [-] S dns Trasorata d Fourr Dsrta (DFT) dl sgnal la susson F: F[ ] Forula d nvrson:
AGORITO FFT (Fast Fourr Transor) Rha sulla DFT Sa un sgnal rodo d rodo rarsntato dal vttor -dnsonal d oonnt [], [],.., [-] S dns Trasorata d Fourr Dsrta (DFT) dl sgnal la susson F: F[ ] Forula d nvrson:
ESERCIZI PARTE I SOLUZIONI
 UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
ELETTROTECNICA Ingegneria Industriale
 EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
Biennio CLEM - Prof. B. Quintieri. Anno Accademico 2012-2013, I Semestre. (Tratto da: Feenstra-Taylor: International Economics)
 CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
