Sistemi trifase. (versione del ) Sistemi trifase
|
|
|
- Aloisia Giovannini
- 8 anni fa
- Visualizzazioni
Transcript
1 Ssm rfas vrson dl Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d gnraor snusodal sofrqunzal l collgamno r gnraor gl ulzzaor è ralzzao mdan ln d collgamno a r fl
2 Corrn d lna nson concana Corrn d lna Corrn n r conduor dlla lna n ogn san la LK rchd ch sa 0 0 Tnson concana Tnson ra conduor n una gnrca szon dlla lna S l mpdnza dlla lna è rascurabl l nson concana non dpndono dalla szon consdraa n ogn san la LK rchd ch sa v v v 0 0 Corrn d lna nson concana Nl pano complsso, fasor dll corrn d lna dll nson concana possono ssr rapprsna da r vor dspos a rangolo somma voral nulla 4
3 Trn d nson smmrch Una rna d nson rfas s dc smmrca s l nson hanno ugual ampzza la loro somma è nulla n ogn san Cò rchd ch lo sfasamno ra du nson conscuv sa rna smmrca dra v cos v v cos cos rna smmrca nvrsa v v v cos cos cos 4 4 cos cos 5 Trn d nson smmrch Trna dra Trna nvrsa 6
4 Trn d nson smmrch Trna dra Trna nvrsa ja ja j j j j 0 7 Trn d corrn qulbra Una rna d corrn rfas s dc qulbraa s l corrn hanno ugual ampzza la loro somma è nulla n ogn san Pr l rn d corrn qulbra valgono consdrazon analogh a qull fa pr l rn d nson smmrch Lo sfasamno r du corrn conscuv d una rna qulbraa può ssr / rna dra o / rna nvrsa Trna dra Trna nvrsa 8
5 No Nllo sudo d ssm rfas, s ulzzranno sclusvamn fasor l cu modulo concd con l valor ffcac non con l valor massmo dll nson dll corrn valor ffcac dll nson corrn saranno ndca con l lr mauscol,, L sss rn d nson concana d corrn d lna possono ssr nrpra com dr o nvrs a sconda d com sono numra conduor n sguo, s non ndcao splcamn, s consdrranno smpr rn dr daa l arbrarà dlla numrazon d conduor, quso non compora prda d gnralà 9 Trn dr nvrs Trn dr Trn nvrs 0
6 nraor rfas Schma d prncpo Par mobl roor schmazzaa con un magn prmann ch ruoa con vlocà angolar Par fssa saor r avvolgmn dnc rapprsna con una spra ruoa l uno rspo all alro d 0 fluss d nduzon magnca concana con gl avvolgmn sono funzon prodch con prodo T n cascun avvolgmno vn ndoa una f..m. prodca Dmnsonando opporunamn l ssma è possbl onr f..m. snusodal nraor rfas r avvolgmn fas dl gnraor quvalgono a r gnraor snusodal con nson sfasa ra loro d l avvolgmn vngono collga a slla o a rangolo
7 nraor a rangolo L nson concana concdono con l nson d fas j j j 4 nraor a slla j j j Tnson d fas slla Tnson concana
8 Tnson concana nson d fas Nl pano complsso, fasor dll nson concana possono ssr rapprsna da r vor dspos n modo da formar un rangolo qularo fasor dll nson slla possono ssr rapprsna da vor ch unscono vrc dl rangolo ad un puno O cnro dll nson d fas L nson slla soddsfano la rlazon 0 Qund l puno O concd con l barcnro dl rangolo = puno d nrszon dll mdan 5 Tnson concana nson d fas Con smplc consdrazon gomrch s può rconoscr ch valgono l rlazon cos 6 arg arg 6 L nson concana sono j 6 j 6 j 6 6
9 Ulzzaor rfas l ulzzaor rfas sono normalmn rapprsnabl mdan rn d mpdnz fas dll ulzzaor collga a slla o a rangolo 7 Noa collgamn a slla a rangolo vngono rapprsna anch nl modo sgun 8
10 quvalnza slla-rangolo 9 Carch rgolar Y Carco rgolar o qulbrao: l r mpdnz sono ugual Formul d rasformazon slla rangolo Y Y 0
11 Carco a rangolo L nson d fas concdono con l nson concana Corrn d fas: Corrn d lna: Carco a rangolo Nl pano complsso, fasor dll corrn d lna possono ssr rapprsna da r vor ch formano un rangolo fasor dll corrn d fas possono ssr rapprsna da r vor ch collgano vrc dl rangolo ad un puno O
12 Carco a rangolo rgolar S l carco è rgolar l nson concana cosuscono una rna smmrca, l corrn d fas cosuscono una rna qulbraa Anch l corrn d lna cosuscono una rna qulbraa l rangolo è qularo l puno O concd con l suo barcnro Con smplc consdrazon gomrch s può rconoscr ch l sprsson dll corrn d lna sono j j j arg j j 6 6 j 6 Carco a slla L corrn d fas concdono con l corrn d lna L corrn d fas possono ssr onu rsolvndo l ssma 0 La rza quazon non srv prché è consgunza dll prm du No l corrn d fas s rcavano l nson d fas 4
13 Carco a slla calcolo dll nson d fas odo alrnavo pr l calcolo dll nson d fas L sss nson a rmnal dlla slla porbbro ssr onu mdan du sol gnraor avn nson ugual a du dll nson concana com nll smpo n fgura Dalla formula d llman s on dramn Y Y Y Y Y Consdrando l alr possbl copp d gnraor s possono onr l alr nson d fas 5 Carco a slla calcolo dll nson d fas Y Y Y Y Y Y Y Y Y Y 6
14 Cnro dll nson d fas L nson d fas l nson concana sono lga dall rlazon S l nson concana cosuscono una rna smmrca, nl pano complsso possono ssr rapprsna da r vor ch formano un rangolo qularo vor ch rapprsnano l nson d fas unscono vrc dl rangolo con un puno O cnro dll nson d fas 7 Carco a slla rgolar S l carco è rgolar s ha 0 La rna dll nson d fas è smmrca l cnro dll nson d fas concd con l barcnro dl rangolo, qund l nson d fas sono j 6 j 6 j 6 8
15 Noa La rlazon ra l corrn d lna l corrn d fas d un carco a rangolo la rlazon ra l nson concana l nson d fas d un carco a slla sono sml, ma non hanno saamn la sssa forma Quso ha com consgunza ch, nl caso d rn dr, vor ch rapprsnano l corrn d fas crcolano n snso oraro vor ch rapprsnano l nson concana crcolano n snso anoraro S no, comunqu, ch l rn dll corrn d lna dll nson concana sono nramb dr 9 Noa Cascun vor s on applcando al prcdn una roazon d 0 n snso oraro rna dra 0
16 Tnson prncpal d fas L nson d fas corrspondn ad un carco a slla rgolar sono d nson prncpal d fas vrranno ndca anch con smbol 0, 0, 0 l cnro dll nson prncpal d fas corrspond al barcnro dl rangolo dll nson concana Nl caso d un carco a slla non qulbrao è possbl drmnar l nson d fas a parr dall nson prncpal d fas dalla nson O sposamno dl cnro dll nson d fas O O O Sposamno dl cnro dll nson d fas La rna d nson concana ch almna l carco a slla può ssr onua mdan r gnraor collga a slla avn nson concdn con l nson prncpal d fas La nson O può ssr calcolaa mdan la formula d llman 0Y 0Y 0Y O Y Y Y Pr un carco smmrco s ha O 0
17 R rdoa monofas pos: L nson concana cosuscono una rna smmrca carch sono rgolar smpo R rdoa monofas S sosuscono vnual gnraor a rangolo con gnraor a slla S rasformano vnual carch a rangolo n sll quvaln collgamno ra cnr dll sll Tu carch sono rgolar cnr d u l sll sono allo ssso ponzal collgandol ra loro non s alra l comporamno dl crcuo 4
18 R rdoa monofas Nl crcuo così onuo, cascuna dll fas può ssr sudaa sparaamn dall alr crcu rlav all r fas sono dnc, a par la roazon d fas d gnraor Rsola la r rlava alla prma fas r rdoa monofas è possbl drmnar l nson l corrn dll alr du fas nroducndo corrspondn sfasamn d ±/ 5 Ssm rfas con nuro Nl caso d gnraor carco a slla è possbl aggungr un quaro conduor nuro ch collga l cnro dlla slla d gnraor al nodo cnral dl carco L nson d fas dl carco concdono con l nson d gnraor qund non dpndono dall mpdnz d carco l nuro consn d garanr valor prfssa dll nson d fas n prsnza d carch squlbra 6
19 Ssm rfas con nuro l nuro è prcorso dalla corrn N N s annulla s l r mpdnz sono ugual carco rgolar n quso caso la nson ra l cnro dlla slla d gnraor l cnro dlla slla d mpdnz è nulla anch n assnza dl nuro la prsnza dl nuro è rrlvan S l carco è rrgolar nl nuro crcola una corrn la cu nnsà è ano maggor quano pù l carco è squlbrao 7 Ssm rfas con nuro ssm con nuro sono ulzza nlla dsrbuzon d nrga a bassa nson n ala l valor normalzzao dll nson d fas pr la dsrbuzon a bassa nson è d 0 ffcac, corrspondn a nson concana d 400 ffcac fno al 00 valor rano 0 80 L nson d fas sono ulzza pr almnar carch monofas ndpndn s. unz domsch normalmn l carco rsula squlbrao L nson concana sono ulzza pr carch rfas o pr carch monofas ch rchdono ponz pù lva 8
20 9 Ponza assorba da un carco rfas Un gnrco carco rfas è un rpolo Sclo un arbraramn un rmnal d rfrmno, s può sprmr la ponza assorba n funzon dll corrn dgl alr rmnal dll nson dgl alr rmnal rspo al rfrmno v v v v p 40 Ponza assorba da un carco rfas ndpndnmn dalla sruura dl carco, la ponza può ssr sprssa anch n funzon d un arbrara rna d nson slla assocaa all nson concana fssaa scglndo arbraramn l puno O n parcolar è possbl sprmr la ponza n funzon dll nson prncpal d fas v v p p
21 Ponza assorba da un carco rfas La ponza ava la ponza rava d un carco rfas sono dfn com somm dll ponz av rav assoca all r fas Qund anch la ponza complssa è daa dalla somm dll ponz assoca all r fas, può ssr sprssa nll form N * * * * * La ponza apparn l faor d ponza sono dfn convnzonalmn mdan l rlazon vald nl caso monofas S P cos Q P S cosarcg Q P n quso caso è un angolo convnzonal, n gnral, non può ssr nrprao com angolo d sfasamno ra una nson una corrn 4 Ponza n ssm smmrc d qulbra pos L nson concana cosuscono una rna smmrca l carco è rgolar S sprm la ponza assorba dal carco n funzon dll nson prncpal d fas dll corrn d lna p cos cos cos cos cos cos cos 0 valor ffcac dll nson prncpal d fas valor ffcac dll corrn d lna 0 n un ssma smmrco d qulbrao la ponza sanana è cosan rmn oscllan formano una rna smmrca la loro somma è nulla 4
22 Ponza n ssm smmrc d qulbra l valor ffcac dll nson prncpal d fas è lgao al valor dll nson concana dalla rlazon 0 l valor cosan dlla ponza sanana, concdn con la ponza ava può ssr sprsso com P cos n quso caso l angolo non è lo sfasamno ra una nson concanaa una corrn d lna, ma ra una nson prncpal d fas la corrspondn corrn d lna 4 Ponza n ssm smmrc d qulbra Nl caso d un carco a slla rgolar, l nson dll mpdnz concdono con l nson prncpal d fas rapprsna l argomno dll mpdnz Pr un carco a rangolo rgolar l nson dll mpdnz concdono con l nson concana qund sono ruoa d rspo all nson prncpal d fas l corrn dll mpdnz sono ruoa d rspo all corrn d lna anch n quso caso rapprsna l argomno dll mpdnz 44
23 Ponza n ssm smmrc d qulbra Ponza ava P 0 cos cos Ponza rava Q 0 sn sn Ponza apparn S 0 Faor d ponza cos cos pr un carco rgolar a slla o a rangolo rapprsna l argomno dll mpdnz d carco 45 Rfasamno d un carco rfas Carco rfas qulbrao ch assorb una ponza ava P S vuol porar l faor d ponza da cos a cos S mpgano r bpol rav ugual collga a slla o a rangolo al da assorbr la ponza rava P g g Q R 46
24 Rfasamno d un carco rfas l caso pù frqun nlla praca è qullo d un carco ohmco-nduvo bpol rav sono condnsaor alor ffcac dll nson d condnsaor collgamno a slla Y C valor ffcac dll nson concana collgamno a rangolo Ponz rav Q R C Y C CC CY C 47 Rfasamno d un carco rfas Capacà d rfasamno collgamno a slla P g g' CY collgamno a rangolo P g g' C C Y Nl caso dl collgamno a slla la capacà è vol maggor, mnr la nson su condnsaor è nfror d un faor Dao ch l coso d un condnsaor aumna sa con la capacà ch con la massma nson d funzonamno, la scla dl po d collgamno dpnd dal faor ch ncd n msura maggor 48
25 Prncpal vanagg d ssm rfas n un ssma smmrco d qulbrao la ponza sanana è cosan L nrga lrca è onua convrndo l nrga mccanca forna al roor n un ssma monofas la ponza sanana è varabl, s l carco non è puramn rssvo n alcun san è anch ngava Dao ch dv ssr cosan è ncssaro applcar al roor una coppa varabl n un ssma rfas smmrco d qulbrao è rchsa una coppa cosan A parà d condzon, n un ssma rfas l prd nll ln d rasporo dll nrga lrca sono nfror Un ssma d corrn rfas può ssr ulzzao pr gnrar un campo magnco roan, su cu s basa l funzonamno dll macchn lrch roan n corrn alrnaa 49 Trasmsson dll nrga lrca Confrono ra lna n corrn connua lna n corrn alrnaa monofas lna n corrn alrnaa rfas l lunghzza dlla lna P ponza assorba dal carco n corrn connua ponza ava assorba dal carco n corrn alrnaa nson sul carco n corrn connua valor ffcac dlla nson sul carco monofas valor ffcac dll nson concana dlla lna rfas 50
26 Corrn nlla lna Corrn dlla lna n corrn connua P CC alor ffcac dlla corrn dlla lna monofas P CA cos alor ffcac dll corrn dlla lna rfas P CAT cos s assum ch faor d ponza dl carco monofas dl carco rfas sano ugual 5 Ponza dsspaa nlla lna Ponza dsspaa nlla lna P D nr n numro d conduor R rssnza d un conduor l lunghzza dlla lna S szon d un conduor rssvà n l S volum oal d conduor nls n r cas CC, CA, CAT n l 5
27 Ponza dsspaa nlla lna nsrndo nll sprsson d P D l numro d conduor l sprsson dlla corrn s on n r cas P DCC l P 4K 4 CC CC P DCA l P 4K 4 cos cos CA CA P DCAT l P K cos cos CAT CAT dov K l P 5 Confrono A parà d volum d conduor L prd nlla lna rfas sono smpr nfror dl 5% rspo a qull dlla lna monofas L prd nlla lna monofas sono maggor d qull nlla lna n connua rann ch nl caso d cos, n cu sono ugual Pr cos / l prd nlla lna rfas sono mnor d qull nlla lna n connua A parà d prd La lna rfas consn d rsparmar l 5% d maral conduor rspo alla lna monofas Pr valor lva d cos, è pù convnn anch dlla lna n connua 54
28 Campo magnco roan Campo magnco roan = campo magnco avn nnsà cosan drzon ch ruoa aorno ad un ass con vlocà angolar cosan Un campo magnco roan può ssr prodoo facndo ruoar con vlocà angolar cosan un magn prmann o un solnod prcorso da corrn cosan possbl gnrar un campo magnco roan anch mdan un nsm d avvolgmn fss, opporunamn dspos prcors da corrn snusodal opporunamn sfasa ra loro 55 Camp conroroan Solnod prcorso da una corrn snusodal cos S consdra l campo n un puno P dll ass dl solnod l campo magnco ha drzon assal vara con lgg snusodal H H cos l campo magnco può ssr scomposo nlla somma d du vor d modulo H / ch ruoano, uno n snso opposo all alro, con vlocà angolar aorno al puno P n un pano passan pr l ass dl solnod H d campo dro roazon n snso oraro H campo nvrso roazon n snso anoraro 56
29 Camp conroroan Una roazon n rardo d un angolo dlla fas dlla corrn produc roazon d un angolo, n snso opposo ra loro, d camp H d H cos H 0 H cos H 0 H cos 57 Campo magnco roan prodoo da du corrn n quadraura S consdrano du solnod dnc, pos alla sssa dsanza dal puno P Agndo sull fas dll corrn sull ornamno d du solnod è possbl far n modo ch ss producano nl puno P camp dr n fas ra loro camp nvrs n opposzon d fas n praca occorr ch la corrn dl scondo solnod sa n quadraura n rardo rspo alla corrn dl prmo ch l ass dl scondo solnod sa ruoao n snso oraro d 90 rspo all ass dl prmo camp nvrs s ldono, mnr camp dr s sommano n gnrao un campo magnco roan 58
30 Campo magnco roan prodoo da du corrn n quadraura cos cos Η Η 0 59 Campo magnco roan prodoo da un ssma d corrn rfas Dsponndo d un almnazon rfas, s può onr un campo roan mdan r solnod dnc cascuno avn l ass ruoao d 0 n snso oraro rspo al prcdn prcors da una rna qulbraa dra d corrn Pr camp dr, gl ff dlla roazon dl solnod dlla roazon dlla fas dlla corrn s compnsano camp dr s sommano camp nvrs formano una rna smmrca camp nvrs s ldono 60
31 Campo magnco roan prodoo da un ssma d corrn rfas cos cos cos 6 oor a nduzon - prncpo d funzonamno S consdra una spra lbra d ruoar aorno ad un ass, posa n una rgon n cu è prsn un campo magnco roan con vlocà angolar c l flusso concanao con la spra vara nl mpo n ndoa una f..m qund nlla spra crcola corrn La spra prcorsa da corrn è sogga a forz ch la fanno ruoar n snso concord con l campo magnco La roazon dlla spra nllo ssso snso dl campo nd ad annullar la varazon dl flusso concanao n accordo con la lgg d Lnz, l forz ndono ad oppors alla causa ch l ha gnra 6
32 oor a nduzon - prncpo d funzonamno dalmn la spra ndrbb a raggungr una vlocà d roazon concdn con qulla dl campo vlocà d sncronsmo n praca la spra non può raggungr la vlocà dl campo roan prchè n qus condzon l flusso concanao sarbb cosan d consgunza la coppa agn sulla spra s annullrbb A rgm la spra ruoa ad una vlocà, nfror alla vlocà d sncronsmo, n corrspondnza dlla qual la coppa dovua al campo magnco la coppa rssn ad s. dovua all aro s blancano Da quso drva l nom macchna asncrona 6
Sistemi trifase. Parte 2. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 16-12-2013) Potenza assorbita da un carico trifase (1)
 Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
Sistemi trifase. (versione del ) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl --00 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl --00 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Sistemi trifase. (versione del ) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl -05-09 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl -05-09 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Sistemi trifase. Parte 1. (versione del ) Sistemi trifase
 Ssm rfas Par www.d.ng.unbo./prs/masr/ddaca.hm rson dl -0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Ssm rfas Par www.d.ng.unbo./prs/masr/ddaca.hm rson dl -0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Sistemi trifase. Parte 1. (versione del ) Sistemi trifase
 Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl -9-04 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl -9-04 Ssm rfas l rasporo la dsrbuzon d nrga lrca angono n pralnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn d
SISTEMI TRIFASE B 1. i 2. i 3. Figura 1. - Schema di linea trifase
 SSTM TRFAS Dfnzon prncpal. ssm rfas sono schmazzabl com nlla fgura. Non s fa nssuna pos né sul gnraor d almnazon suao prma dlla szon A-A, né sull'ulzzaor suao dopo la szon B-B. A X B A X Fgura. - Schma
SSTM TRFAS Dfnzon prncpal. ssm rfas sono schmazzabl com nlla fgura. Non s fa nssuna pos né sul gnraor d almnazon suao prma dlla szon A-A, né sull'ulzzaor suao dopo la szon B-B. A X B A X Fgura. - Schma
Lezione 3. F. Previdi - Automatica - Lez. 3 1
 Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Il ruolo delle aspettative in economia
 Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
17. Le soluzioni dell equazione di Schrödinger approfondimento
 7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
Esercitazioni di Elettrotecnica: circuiti in regime stazionario
 Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
Correnti di linea e tensioni concatenate
 Sismi Trifas Sismi rifas l rasporo la disribuzion di nrgia lrica avvngono in prvalnza pr mzzo di lin rifas Un sisma rifas è alimnao mdian gnraori a r rminali rapprsnabili mdian rn di gnraori sinusoidali
Sismi Trifas Sismi rifas l rasporo la disribuzion di nrgia lrica avvngono in prvalnza pr mzzo di lin rifas Un sisma rifas è alimnao mdian gnraori a r rminali rapprsnabili mdian rn di gnraori sinusoidali
1. Variabili casuali continue e trasformazioni di variabili casuali...3. 2. La variabile casuale normale... 14
 ESERCIZI DI CALCOLO DELLE PROBABILITÀ PARTE II Rccardo Borgon Elna Colcno Pro Quao Sara Sala INDICE. Varabl casual connu rasformazon d varabl casual....3. La varabl casual normal... 4 3. Funzon gnrarc
ESERCIZI DI CALCOLO DELLE PROBABILITÀ PARTE II Rccardo Borgon Elna Colcno Pro Quao Sara Sala INDICE. Varabl casual connu rasformazon d varabl casual....3. La varabl casual normal... 4 3. Funzon gnrarc
Appunti ed Esercizi di Fisica Tecnica e Macchine Termiche
 Appun d Esrz d Fsa Tna Mahn Trmh Cap.. Sambaor d alor Nola Forgon Paolo D Maro Vrson 0.03 0.05.0. La prsn dspnsa è rdaa ad slusvo uso ddao dgl allv d Dplom Unvrsar dl sor ndusral dll Unvrsà dgl Sud d Psa.
Appun d Esrz d Fsa Tna Mahn Trmh Cap.. Sambaor d alor Nola Forgon Paolo D Maro Vrson 0.03 0.05.0. La prsn dspnsa è rdaa ad slusvo uso ddao dgl allv d Dplom Unvrsar dl sor ndusral dll Unvrsà dgl Sud d Psa.
CIRCUITO RLC IN SERIE
 ~ ~ IUITO L IN SEIE onsdrazon gnral Il crcuo L n sr (vd fgura) è formao da una sola magla n cu sono prsn una rssnza, un nduanza L, un condnsaor d capacà un gnraor d nson alrnaa cararzzao da una forza lromorc
~ ~ IUITO L IN SEIE onsdrazon gnral Il crcuo L n sr (vd fgura) è formao da una sola magla n cu sono prsn una rssnza, un nduanza L, un condnsaor d capacà un gnraor d nson alrnaa cararzzao da una forza lromorc
Corso di ELETTRONICA INDUSTRIALE
 Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
Laurea triennale in BIOLOGIA A. A
 Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
Calcolo delle Probabilità: esercitazione 10
 Calcolo dll Probablà: srcazon 0 Argono: Dsrbuzon noral (pag. 47 sgun dl lbro d so). Valor aso, varanza (pag. sgun). Dsrbuzon bvara dscr (pag. 44 sgun) covaranza (pag 45 sgun). NB: asscurars d conoscr l
Calcolo dll Probablà: srcazon 0 Argono: Dsrbuzon noral (pag. 47 sgun dl lbro d so). Valor aso, varanza (pag. sgun). Dsrbuzon bvara dscr (pag. 44 sgun) covaranza (pag 45 sgun). NB: asscurars d conoscr l
Esercizi & Domande per il Compito di Elettrotecnica del 15 giugno 2004
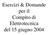 Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
MERCATI FINANZIARI IN ECONOMIA APERTA (Modello IS-LM in economia aperta)
 MRATI FINANZIARI IN ONOMIA APRTA Modllo - n conoma apra Invsmn fnanzar. Scla ra: a. mona nazonal: ransazon b. mona sra: non ha nssun vanaggo dnrla c. ol nazonal: fruano nrss d. ol sr: fruano nrss sono
MRATI FINANZIARI IN ONOMIA APRTA Modllo - n conoma apra Invsmn fnanzar. Scla ra: a. mona nazonal: ransazon b. mona sra: non ha nssun vanaggo dnrla c. ol nazonal: fruano nrss d. ol sr: fruano nrss sono
Esercitazione n 4. Meccanismi combinati Resistenze termiche e Trasmittanze termiche
 Ercazon n 4 Mccanm combna nz rmch Tramanz rmch ) Valuar l ramanz rmch dll gun polog d fnr: a) fnra a vro ngolo ( por vro L [mm]; [W/(m)]); b) fnra con dopp vr ( por vro L [mm], ε ε 0.9, nrcapdn ara L n
Ercazon n 4 Mccanm combna nz rmch Tramanz rmch ) Valuar l ramanz rmch dll gun polog d fnr: a) fnra a vro ngolo ( por vro L [mm]; [W/(m)]); b) fnra con dopp vr ( por vro L [mm], ε ε 0.9, nrcapdn ara L n
Aspettative. In questa lezione: Discutiamo di previsioni sulle variabili future, e di aspettative. Definiamo tassi di interesse nominale e reale.
 Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Serie di Fourier a tempo continuo. La rappresentazione dei segnali nel dominio della frequenza. Jean Baptiste Joseph Fourier (1768 1830 )
 Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Campi Elettromagnetici e Circuiti I Circuiti del secondo ordine
 Facolà Inggnra Unrsà gl su Paa orso Laura Trnnal n Inggnra Elronca Informaca amp Elromagnc rcu I rcu l scono orn amp Elromagnc rcu I a.a. 3/4 Prof. Luca Prrgrn rcu l scono orn, pag. ommaro Dfnzon rcuo
Facolà Inggnra Unrsà gl su Paa orso Laura Trnnal n Inggnra Elronca Informaca amp Elromagnc rcu I rcu l scono orn amp Elromagnc rcu I a.a. 3/4 Prof. Luca Prrgrn rcu l scono orn, pag. ommaro Dfnzon rcuo
Laboratorio di Navigazione Laurea Specialistica in Ingegneria Informatica, Ingegneria per l Ambiente e il Territorio Politecnico di Milano Campus
 Laoraoro Navgazon Laura Spcalsca n Inggnra Inormaca, Inggnra pr l mn l Trroro Polcnco Mlano Campus Como NVIGZION INRZIL Ssm rrmno n ssma rrmno è un nsm rgol msur ch c prmono rsponr a qus: ov s rova un
Laoraoro Navgazon Laura Spcalsca n Inggnra Inormaca, Inggnra pr l mn l Trroro Polcnco Mlano Campus Como NVIGZION INRZIL Ssm rrmno n ssma rrmno è un nsm rgol msur ch c prmono rsponr a qus: ov s rova un
Lezione 15 (BAG cap. 14) Le aspettative: nozioni di base
 Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
SOLUZIONI. risparmio totale = D altra parte la traccia di dice anche che: e 64 L = produzione. Pertanto si ha: Quindi si ha un risparmio del 9,902%.
 SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
Lezione 21 (BAG cap. 19) Regimi di cambio. Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
 Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Edutecnica.it Circuiti a scatto -Esercizi 1
 duna. Cru a sao -srz srzo no. Soluzon a pag.5 Nl ruo d gura, l nrruor n huso all san ; dopo un mpo 4,8µs, n rapro onmporanamn n huso. roar l andamno dlla nson a ap dl ondnsaor. 4 kω CpF roar l alor dlla
duna. Cru a sao -srz srzo no. Soluzon a pag.5 Nl ruo d gura, l nrruor n huso all san ; dopo un mpo 4,8µs, n rapro onmporanamn n huso. roar l andamno dlla nson a ap dl ondnsaor. 4 kω CpF roar l alor dlla
Spettro di densità di potenza e rumore termico
 Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
Simulazione del processo di essiccazione di cereali. in letto fisso. condizionamento industriale. Natalino Mandas, Francesco Cambuli
 52_TER_dc_mandas 29-11-2007 20:11 Pagna 52 condzonamno ndusral d glucd (dra d carbono), l frmnazon nrcllular, gl svlupp d bar d muff, favor dal rscaldamno naural. Nl corso dgl ulm dcnn, l procsso d ssccazon
52_TER_dc_mandas 29-11-2007 20:11 Pagna 52 condzonamno ndusral d glucd (dra d carbono), l frmnazon nrcllular, gl svlupp d bar d muff, favor dal rscaldamno naural. Nl corso dgl ulm dcnn, l procsso d ssccazon
LE SOLUZIONI. [Per definizione la concentrazione di una soluzione è il rapporto
 LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
Parte 4 - Pag.1. Vision 2000 - obiettivi della revisione. Oltre la ISO 9000: Vision 2000. Vision 2000 - elementi innovativi
 Olr la ISO 9000: Vso 2000 G.Rass - 11 maggo 2001 1 Vso 2000 - obv dlla rvso Obv dlla rvso dlla ISO 9000: passar dalla culura dlla coformà dll vdz a qulla dl couo mgloramo, ral msurabl dal cl Il progo d
Olr la ISO 9000: Vso 2000 G.Rass - 11 maggo 2001 1 Vso 2000 - obv dlla rvso Obv dlla rvso dlla ISO 9000: passar dalla culura dlla coformà dll vdz a qulla dl couo mgloramo, ral msurabl dal cl Il progo d
Principi ed applicazioni del metodo degli elementi finiti. Formulazione base con approccio agli spostamenti
 Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Prncp d applcazon dl mtodo dgl lmnt fnt Formulazon bas con approcco agl spostamnt PRINCIPIO DEI LAVORI VIRTALI Data una crta statca: sforz σ j, forz d volum F forz d suprfc f j ; s dmostra ch mporr la
Autoinduzione. 4 L: coefficiente di autoinduzione o. 4 r. Un circuito percorso da corrente genera un B (legge di Ampere-Laplace):
 S ds u r Autonduzon Un crcuto prcorso da corrnt gnra un B (lgg d Ampr-aplac): ds ur B 4 r Produc un flusso attravrso l crcuto stsso (così com attravrso una ualunu S ch abba com contorno) nds r 4 : coffcnt
S ds u r Autonduzon Un crcuto prcorso da corrnt gnra un B (lgg d Ampr-aplac): ds ur B 4 r Produc un flusso attravrso l crcuto stsso (così com attravrso una ualunu S ch abba com contorno) nds r 4 : coffcnt
Errore standard di misurazione. Calcolare l intervallo del punteggio vero
 Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
MACCHINE ELETTRICHE. Campo rotante. Stefano Pastore. Dipartimento di Ingegneria e Architettura Corso di Elettrotecnica (IN 043) a.a.
 MACCINE ELETTRICE Campo roane Sefano Pasore Diparimeno di Ingegneria e Archieura Corso di Eleroecnica (IN 043) a.a. 01-13 Inroduzione campo magneico con inensià ane che ruoa aorno ad un asse con velocià
MACCINE ELETTRICE Campo roane Sefano Pasore Diparimeno di Ingegneria e Archieura Corso di Eleroecnica (IN 043) a.a. 01-13 Inroduzione campo magneico con inensià ane che ruoa aorno ad un asse con velocià
I sensori di spostamento
 I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
0 < a < 1 a > 1. In entrambi i casi la funzione y = a x si può studiare per punti e constatare che essa presenta i seguenti andamenti y.
 INTRODUZIONE Ossrviamo, in primo luogo, ch l funzioni sponnziali sono dlla forma a con a costant positiva divrsa da (il caso a è banal pr cui non sarà oggtto dl nostro studio). Si possono allora vrificar
INTRODUZIONE Ossrviamo, in primo luogo, ch l funzioni sponnziali sono dlla forma a con a costant positiva divrsa da (il caso a è banal pr cui non sarà oggtto dl nostro studio). Si possono allora vrificar
RIFLETTOMETRIA NEL DOMINIO DEL TEMPO (TDR)
 RFLETTOMETRA NEL DOMNO DEL TEMPO (TDR) Scopo dll srctaon La rflttomtra nl domno dl tmpo è una tcnca frquntmnt utlata, mpgando prncp dll co, pr carattrar ln d comuncaon, localar guast sa nll ln d trasmsson
RFLETTOMETRA NEL DOMNO DEL TEMPO (TDR) Scopo dll srctaon La rflttomtra nl domno dl tmpo è una tcnca frquntmnt utlata, mpgando prncp dll co, pr carattrar ln d comuncaon, localar guast sa nll ln d trasmsson
Richiami su numeri complessi
 Richiami su numri complssi Insim C di numri complssi E' l'insim dll coppi ordina di numri rali = Z R j Z I ; Z R, Z I R Z = Z R, Z I j Δ = (0,1) unià immaginaria Si noi ch C conin R; in paricolar linsim
Richiami su numri complssi Insim C di numri complssi E' l'insim dll coppi ordina di numri rali = Z R j Z I ; Z R, Z I R Z = Z R, Z I j Δ = (0,1) unià immaginaria Si noi ch C conin R; in paricolar linsim
Soluzioni. 1. Data la funzione. a) trova il dominio di f
 Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
Interferenza e diffrazione con gli esponenziali complessi. Nota
 Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Intrfrnza dffrazon con gl sponnzal complss ota on s fanno commnt sul sgnfcato d rsultat ottnut, n su qullo dll pots d volta n volta assunt: lo scopo solo qullo d mostrar com funzon n pratca l formalsmo
Ripasso onde piane: riflessione e trasmissione all interfaccia piana tra due mezzi
 scaon n. 4 Rpasso ond pan: flsson asmsson all nfacca pana a du m Impao ambnal d camp lomagnc Popagaon onda pana Puno d pana p l oca gomca è, n qualch modo, lo sudo dlla popagaon dll ond pan. λ β nfa...
scaon n. 4 Rpasso ond pan: flsson asmsson all nfacca pana a du m Impao ambnal d camp lomagnc Popagaon onda pana Puno d pana p l oca gomca è, n qualch modo, lo sudo dlla popagaon dll ond pan. λ β nfa...
Attuatore: Motore in corrente continua (DC)
 Auaor: Moor in corrn coninua DC Sisma: Movimnazion monoass Modllo pr moor DC Accoppiaor oico Circuio ingrao piloa pr moor DC Sisma di piloaggio razionao Encodr incrmnal 360 impulsi/giro Moor in DC Vi snza
Auaor: Moor in corrn coninua DC Sisma: Movimnazion monoass Modllo pr moor DC Accoppiaor oico Circuio ingrao piloa pr moor DC Sisma di piloaggio razionao Encodr incrmnal 360 impulsi/giro Moor in DC Vi snza
LA COMPATIBILITA tra due misure:
 LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
 L soluzon Data la funzon ln( ) f ( ) 3 a trova l domno d f b scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c dtrmna l vntual ntrszon con gl ass d studa l
L soluzon Data la funzon ln( ) f ( ) 3 a trova l domno d f b scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c dtrmna l vntual ntrszon con gl ass d studa l
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
Esame di Matematica e Abilità Informatiche - Settembre Le soluzioni
 Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione
![[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione [ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione](/thumbs/92/110333272.jpg) Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Calcolo della funzione d uscita per un generico segnale d'ingresso
 Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
Si possono distuguere due casi: a) molecole distinguibili: il numero di modi è dato da
 ESISTE UA OTEOLE DIFFEEA TA LE SOLUIOI DEI POLIEI E QUELLE DELLE OLECOLE PICCOLE DOUTA ALLA DIFFEEA DI DIESIOI TA LE OLECOLE POLIEICHE E QUELLE DEL SOLETE. Pr qusto motvo trattrmo l soluzon polmrch attravrso
ESISTE UA OTEOLE DIFFEEA TA LE SOLUIOI DEI POLIEI E QUELLE DELLE OLECOLE PICCOLE DOUTA ALLA DIFFEEA DI DIESIOI TA LE OLECOLE POLIEICHE E QUELLE DEL SOLETE. Pr qusto motvo trattrmo l soluzon polmrch attravrso
RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI
 RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI Da un sgnal aprdc s(), la sua rapprsnazn nl dmn dlla frqunza è frna dalla sgun dfnzn d rasfrmaa d Furr: S( ) F[s()]
RAPPRESENTAZIONE DI SEGNALI NEL DOMINIO DELLA FREQUENZA: CASO DEI SEGNALI APERIODICI Da un sgnal aprdc s(), la sua rapprsnazn nl dmn dlla frqunza è frna dalla sgun dfnzn d rasfrmaa d Furr: S( ) F[s()]
La valutazione finanziaria
 STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
Sistemi trifase. Parte 1. (versione del ) Sistemi trifase
 Sistmi trifas Part www.di.ing.unibo.it/prs/mastri/didattica.htm (vrsion dl 5--08) Sistmi trifas l trasporto la distribuzion di nrgia lttrica avvngono in prvalnza pr mzzo di lin trifas Un sistma trifas
Sistmi trifas Part www.di.ing.unibo.it/prs/mastri/didattica.htm (vrsion dl 5--08) Sistmi trifas l trasporto la distribuzion di nrgia lttrica avvngono in prvalnza pr mzzo di lin trifas Un sistma trifas
CENNI SULL USO DEL METODO SIMBOLICO PER IL CALCOLO DELLA
 ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
Raccolta Esercizi per il corso di Costruzione di Macchine
 Raccola Escz l coso d osuzon d Maccn Vson 0. Damno d Inggna Unvsà d Faa 9/0/0 obo.ovo@unf. Escz d osuzon d Maccn Inoduzon Qusa dsnsa accogl alcun scz la aazon dllo sco d osuzon d Maccn. Qull oa sono scz
Raccola Escz l coso d osuzon d Maccn Vson 0. Damno d Inggna Unvsà d Faa 9/0/0 obo.ovo@unf. Escz d osuzon d Maccn Inoduzon Qusa dsnsa accogl alcun scz la aazon dllo sco d osuzon d Maccn. Qull oa sono scz
Modelli equivalenti del BJT
 Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
CARATTERISTICHE DELL INVOLUCRO EDILIZIO
 CAATTEISTICHE DELL INVOLUCO EDILIZIO Lvo d Santol, Francsco Mancn Unvrstà La Sapnza d oma lvo.dsantol@unroma1.t francsco.mancn@unroma1.t www.plus.t www.ngnrga.t Trasmttanza d una part opaca 2 La trasmttanza
CAATTEISTICHE DELL INVOLUCO EDILIZIO Lvo d Santol, Francsco Mancn Unvrstà La Sapnza d oma lvo.dsantol@unroma1.t francsco.mancn@unroma1.t www.plus.t www.ngnrga.t Trasmttanza d una part opaca 2 La trasmttanza
1. METODO DELLE EQUAZIONI DI STATO
 IUII ON MMOIA Vngono d crcu con mmora (o crcu dnamc) qull n cu è prsn almno un componn doao d mmora (com nduor condnsaor, ma non solo); n quso caso l ssma rsoln dl crcuo ssso conn l cararsch (dffrnzal)
IUII ON MMOIA Vngono d crcu con mmora (o crcu dnamc) qull n cu è prsn almno un componn doao d mmora (com nduor condnsaor, ma non solo); n quso caso l ssma rsoln dl crcuo ssso conn l cararsch (dffrnzal)
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa (3)
 Corso d Mtod Matmatc pr l Inggnra A.A. 206/207 Esrc svolt sull funon d varabl complssa 3 Marco Bramant Poltcnco d Mlano Novmbr 8, 206 Classfcaon dll sngolartà d una funon, calcolo d svlupp d Laurnt, calcolo
Corso d Mtod Matmatc pr l Inggnra A.A. 206/207 Esrc svolt sull funon d varabl complssa 3 Marco Bramant Poltcnco d Mlano Novmbr 8, 206 Classfcaon dll sngolartà d una funon, calcolo d svlupp d Laurnt, calcolo
Biennio CLEM - Prof. B. Quintieri. Anno Accademico 2012-2013, I Semestre. (Tratto da: Feenstra-Taylor: International Economics)
 CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
CONOMIA INTRNAZIONAL Bnno CLM - Prof. B. Quntr IL TASSO DI CAMBIO Anno Accadmco 2012-2013, I Smstr (Tratto da: Fnstra-Taylor: Intrnatonal conomcs) S propon, d sguto, una brv rassgna d prncp fondamntal
Induzione magnetica. Capitolo. 1. Autoinduzione
 Capiolo nduzion magnica B. Auoinduzion La forza lromoric indoa rapprsna il lavoro pr unià di carica svolo dall forz ch gnrano la corrn indoa. Essa è lgaa alla variazion dl flusso magnico F concanao al
Capiolo nduzion magnica B. Auoinduzion La forza lromoric indoa rapprsna il lavoro pr unià di carica svolo dall forz ch gnrano la corrn indoa. Essa è lgaa alla variazion dl flusso magnico F concanao al
Esercizi sullo studio di funzione
 Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
Tassi Equivalenti. Benedetto Matarazzo
 Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Macchine. 5 Esercitazione 5
 ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
Corso di Macroeconomia
 Corso di Macroconomia LE ASPETTATIVE: NOZIONI DI BASE. Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao
Corso di Macroconomia LE ASPETTATIVE: NOZIONI DI BASE. Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao
CONSERVAZIONE A CALDO
 ONSERVAZIONE A ALDO prcolo azon prvnv lm crc azon corrva monoraggo rgsrazon documnazon frqunza d rgsrazon vrfca A l m n Mcrobologco (dovua alla grmnazon dll spor alla conamnazon croca ) Apparcchaura prfamn
ONSERVAZIONE A ALDO prcolo azon prvnv lm crc azon corrva monoraggo rgsrazon documnazon frqunza d rgsrazon vrfca A l m n Mcrobologco (dovua alla grmnazon dll spor alla conamnazon croca ) Apparcchaura prfamn
Tekla Structures Guida di riferimento per le opzioni avanzate. Versione del prodotto 21.1 agosto 2015. 2015 Tekla Corporation
 Tkla Structurs Guda d rfrmnto pr l opzon avanzat Vrson dl prodotto 21.1 agosto 2015 2015 Tkla Corporaton Indc 1 Guda d rfrmnto pr l opzon avanzat... 17 1.1 Catgor nlla fnstra d dalogo Opzon avanzat...
Tkla Structurs Guda d rfrmnto pr l opzon avanzat Vrson dl prodotto 21.1 agosto 2015 2015 Tkla Corporaton Indc 1 Guda d rfrmnto pr l opzon avanzat... 17 1.1 Catgor nlla fnstra d dalogo Opzon avanzat...
Facoltà di Economia. Equazioni differenziali Lineari ed Applicazioni Economiche
 Facolà di Economia Equazioni diffrnziali Linari d Applicazioni Economich prof. EQUAZIONI DIFFERENZIALI LINEARI APPLICAZIONI ECONOMICHE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE LINEARI Quso ipo di quazioni
Facolà di Economia Equazioni diffrnziali Linari d Applicazioni Economich prof. EQUAZIONI DIFFERENZIALI LINEARI APPLICAZIONI ECONOMICHE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE LINEARI Quso ipo di quazioni
Oscillazioni e onde. Oscillatore armonico. x( t) e sostituendo nell equazione originale si ha. dx dt. x cos infatti. Periodo del moto armonico T
 No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
ELETTROTECNICA Ingegneria Industriale
 EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
La corrente i(t) che percorre l avvolgimento del trasformatore durante il transitorio è definita dalla seguente equazione: di dt
 Cosruzo Elroach Corr d coro crcuo u rasforaor Sovracorr rasforaor Esaao qus au, odo slfcao, l org l cosguz dll sovracorr ch ossoo sollcar l avvolgo d u rasforaor dura u coro crcuo a ors dl scodaro. 1 -
Cosruzo Elroach Corr d coro crcuo u rasforaor Sovracorr rasforaor Esaao qus au, odo slfcao, l org l cosguz dll sovracorr ch ossoo sollcar l avvolgo d u rasforaor dura u coro crcuo a ors dl scodaro. 1 -
ELETTROTECNICA Ingegneria Industriale
 EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
EETTROTENA nggnra ndural TRANSTOR Sfano Paor Darmno d nggnra Archura oro d Elrocnca 43N a.a. 3-4 nroduzon Sudrmo l ranoro nl domno dl mo d crcu D dl ordn con orgn coan orgn nuodal om ranoro nndamo l oluzon
La popolazione in età da 0 a 2 anni residente nel comune di Bologna
 Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
Le soluzioni della prova scritta di Matematica del 7 Febbraio 2014
 L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
LA DOMANDA DI TRASPORTO CARATTERIZZAZIONE E MODELLI (Capitolo 2)
 Fcolà d Inggnr - Unvrsà d Bologn nno ccdmco: 00/ TECNIC ED ECONOMI DEI TSPOTI Docn: Mrno Lup L DOMND DI TSPOTO CTTEIZZZIONE E MODELLI (Cpolo Modll d domnd - Modllo d domnd dscrvo (o non compormnl: non
Fcolà d Inggnr - Unvrsà d Bologn nno ccdmco: 00/ TECNIC ED ECONOMI DEI TSPOTI Docn: Mrno Lup L DOMND DI TSPOTO CTTEIZZZIONE E MODELLI (Cpolo Modll d domnd - Modllo d domnd dscrvo (o non compormnl: non
Fig. 4.1 - Struttura elementare del motore in corrente continua
 4 MACCHINA IN CORRENTE CONTINUA 4.1 Suu schm lmn P compn l pncpo funzonmno ll mcchn n con connu (m.c.c.) fccmo fmno ll suu lmn nc n Fg. 4.1. 1 A φ 2 B Fg. 4.1 - Suu lmn l moo n con connu Fg. 4.2 - Pcoso
4 MACCHINA IN CORRENTE CONTINUA 4.1 Suu schm lmn P compn l pncpo funzonmno ll mcchn n con connu (m.c.c.) fccmo fmno ll suu lmn nc n Fg. 4.1. 1 A φ 2 B Fg. 4.1 - Suu lmn l moo n con connu Fg. 4.2 - Pcoso
Corsi di Laurea in Fisica, Fisica ed Astrofisica
 Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Autovalori complessi e coniugati
 Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
ESERCIZI PARTE I SOLUZIONI
 UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
EFFETTI DELLA COMPRESSIBILITA SULLA GESTIONE DI UNA DISCARICA PER RIFIUTI URBANI
 EFFETTI DELLA COMPRESSIBILITA SULLA GESTIOE DI UA DISCARICA PER RIFIUTI URBAI Gabrl D Rull Door Inggnr Dparmno DICEA d Inggnra Cvl prsso la faolà d Inggnra dll Unvrsà dgl Sud d Frnz. Pro Srn Profssor ordnaro
EFFETTI DELLA COMPRESSIBILITA SULLA GESTIOE DI UA DISCARICA PER RIFIUTI URBAI Gabrl D Rull Door Inggnr Dparmno DICEA d Inggnra Cvl prsso la faolà d Inggnra dll Unvrsà dgl Sud d Frnz. Pro Srn Profssor ordnaro
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 FUNZIONI INTEGRALI
 Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Macroeconomia. Laura Vici. laura.vici@unibo.it. www.lauravici.com/macroeconomia LEZIONE 22. Rimini, 19 novembre 2014
 Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Processi di separazione
 6. Procss d sparazon 6.. Carattrstch d procss d sparazon La sparazon d soluzon mscl n loro sngol componnt costtusc un oprazon d grand mportanza pr l ndustra chmca, ptrolchmca ptrolfra. Quas tutt procss
6. Procss d sparazon 6.. Carattrstch d procss d sparazon La sparazon d soluzon mscl n loro sngol componnt costtusc un oprazon d grand mportanza pr l ndustra chmca, ptrolchmca ptrolfra. Quas tutt procss
2. Strutture e servizi soggetti ai requisiti minimi per l'autorizzazione.
 D.M. 21-5-2001 n. 308 Rgolamno concnn «Rqus mnm suual oganzzav p l'auozzazon all'sczo d svz dll suu a cclo sdnzal smsdnzal, a noma dll'acolo 11 dlla L. 8 novmb 2000, n. 328». Pubblcao nlla Gazz. Uff. 28
D.M. 21-5-2001 n. 308 Rgolamno concnn «Rqus mnm suual oganzzav p l'auozzazon all'sczo d svz dll suu a cclo sdnzal smsdnzal, a noma dll'acolo 11 dlla L. 8 novmb 2000, n. 328». Pubblcao nlla Gazz. Uff. 28
Compact-1401. Compact-1401. Listino prezzi F6 Marzo 2013 MICRON
 Listino przzi F6 Marzo 013 UNI EN 1401 act-1401 UNI EN 1401 Carbonato di calcio,5 MICRON Tubi di PVC-U pr condott fognari civili d industriali costruiti scondo UNI EN 1401 GRESINTEX DALMINE RESINE Tubi
Listino przzi F6 Marzo 013 UNI EN 1401 act-1401 UNI EN 1401 Carbonato di calcio,5 MICRON Tubi di PVC-U pr condott fognari civili d industriali costruiti scondo UNI EN 1401 GRESINTEX DALMINE RESINE Tubi
Esercizio 1. Costruire un esempio di variabili casuali X ed Y tali che Cov(x,y) = 0, ma X ed Y siano dipendenti.
 srcz d conomtra: sr srczo Costrur un smpo d varabl casual d tal ch Cov(,), ma d sano dpndnt. Soluzon Dobbamo vrcar l sgunt condzon: σ [ ] [ ] [ ] covaranza nulla ) ( ) ( ) dpndnza non lnar Prma cosa da
srcz d conomtra: sr srczo Costrur un smpo d varabl casual d tal ch Cov(,), ma d sano dpndnt. Soluzon Dobbamo vrcar l sgunt condzon: σ [ ] [ ] [ ] covaranza nulla ) ( ) ( ) dpndnza non lnar Prma cosa da
PROGRAMMA DI RIPASSO ESTIVO
 ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
ESERCIZI SULLA DEMODULAZIONE INCOERENTE
 Esrcitazioni dl corso di trasmissioni numrich - Lzion 4 6 Fbbraio 8 ESERCIZI SULLA DEMODULAZIONE INCOERENE I du sgnali passa basso di figura sono utilizzati pr la trasmission di simboli binari quiprobabili
Esrcitazioni dl corso di trasmissioni numrich - Lzion 4 6 Fbbraio 8 ESERCIZI SULLA DEMODULAZIONE INCOERENE I du sgnali passa basso di figura sono utilizzati pr la trasmission di simboli binari quiprobabili
Le soluzioni della prova scritta di Matematica del 24 Aprile 2014
 L soluzon dlla prova scrtta d Matmatca dl Aprl. Sa data la unzon 3 a. Trova l domno d b. Scrv, splctamnt pr stso non sono sucnt dsgnn, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l
L soluzon dlla prova scrtta d Matmatca dl Aprl. Sa data la unzon 3 a. Trova l domno d b. Scrv, splctamnt pr stso non sono sucnt dsgnn, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l
Esercizi sulla CONVOLUZIONE
 Esrcizi sulla CONVOLUZIONE 1 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x(), rali o complssi, indicaa simbolicamn com: C xy () = x() * è daa indiffrnmn dall du sprssioni: C xy () = C xy ()
Esrcizi sulla CONVOLUZIONE 1 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x(), rali o complssi, indicaa simbolicamn com: C xy () = x() * è daa indiffrnmn dall du sprssioni: C xy () = C xy ()
Valore attuale di una rendita. Valore attuale in Excel: funzione VA
 Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
Esercizi sulla CONVOLUZIONE INTRODUZIONE. x(t)y( τ - t)dt. x(τ - t)y(t)dt
 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x() y(), rali o complssi, indicaa simbolicamn com: C xy () = x() * y() è daa indiffrnmn dall du sprssioni: Esrcizi sulla CONVOLUZIONE C xy () = C
INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x() y(), rali o complssi, indicaa simbolicamn com: C xy () = x() * y() è daa indiffrnmn dall du sprssioni: Esrcizi sulla CONVOLUZIONE C xy () = C
Esercizio 1. Cov(X,Y)=E(X,Y)- E(X)E(Y).
 Esrcizi di conomtria: sri 4 Esrcizio Siano, Z variabili casuali distribuit scondo la lgg multinomial di paramtri n, p, p, p p p.. Calcolar la Covarianza tra l variabili d. Soluzion Dat du variabili dinit
Esrcizi di conomtria: sri 4 Esrcizio Siano, Z variabili casuali distribuit scondo la lgg multinomial di paramtri n, p, p, p p p.. Calcolar la Covarianza tra l variabili d. Soluzion Dat du variabili dinit
Campi Elettromagnetici e Circuiti I Potenza in regime sinusoidale
 Facolà d ngegnera Unersà degl sud d aa Corso d aurea rennale n ngegnera Eleronca e nformaca Camp Eleromagnec e Crcu oenza n regme snusodale Camp Eleromagnec e Crcu a.a. 05/6 rof. uca erregrn oenza n regme
Facolà d ngegnera Unersà degl sud d aa Corso d aurea rennale n ngegnera Eleronca e nformaca Camp Eleromagnec e Crcu oenza n regme snusodale Camp Eleromagnec e Crcu a.a. 05/6 rof. uca erregrn oenza n regme
Aspettative, produzione e politica economica
 Lzion 18 (BAG cap. 17) Aspttativ, produzion politica conomica Corso di Macroconomia Prof. Guido Ascari, Univrsità di Pavia 2 1 L aspttativ la curva IS Dividiamo il tmpo in du priodi: 1. un priodo corrnt
Lzion 18 (BAG cap. 17) Aspttativ, produzion politica conomica Corso di Macroconomia Prof. Guido Ascari, Univrsità di Pavia 2 1 L aspttativ la curva IS Dividiamo il tmpo in du priodi: 1. un priodo corrnt
