Stima dei parametri. a cura del prof. Guida
|
|
|
- Gianfranco Corradini
- 5 anni fa
- Visualizzazioni
Transcript
1 Stima dei parametri a ura del prof. Guida
2 Preedetemete soo state aalizzate le relazioi tra le statistihe ampioarie e i parametri della popolazioe: µ µ x σ 2 2 x σ σ x σ * per la distribuzioe ampioaria delle medie el aso di estrazioe beroulliaa * (errore medio di ampioameto)
3 µ µ x σ 2 x σ 2 N N 1 σ x σ N N 1 * per la distribuzioe ampioaria delle medie el aso di estrazioe i bloo * (errore medio di ampioameto) diap. 29 diap. 34 diap. 37
4 per la distribuzioe ampioaria della variaza el aso di estrazioe beroulliaa 1 µ M ( S 2 ) S 2 σ 2 per la distribuzioe ampioaria della variaza el aso di estrazioe i bloo N µ M ( S ) S N σ 2
5 per la distribuzioe ampioaria della frequeza dei suessi (el aso di ua popolazioe o distribuzioe biomiale) µ k M ( F) p σ k pq diap.. 45 diap.. 77
6 I risultati otteuti sulle statistihe ampioarie sarao utilizzati per risolvere problemi di Ifereza statistia
7 Rietrao i questa ategoria tutti i problemi he possoo riodursi a: STIMA dei parametri Verifia di IPOTESI STATISTICHE
8 Le STIME dei parametri possoo essere: STIME PUNTUALI STIME INTERVALLARI Soo stime putuali quelle defiite da u uio umero, la statistia ampioaria Soo stime itervallari le stime espresse o due umeri he idiao u itervallo etro il quale ade, o ua probabilità be defiita, u parametro della popolazioe
9 L ifereza statistia utilizza i risultati otteuti dalle idagii ampioarie per otteere STIME relative ai parametri della popolazioe dalla quale è stato estratto il ampioe
10 INDICHIAMO CON: ϑ θ (teta) o il parametro della popolazioe he deve essere stimato T (tau) o il geerio stimatore (variabile aleatoria he dipede dai dati del ampioe e possiede ua distribuzioe di probabilità be determiata) ϑˆ Diap. 50
11 AD ESEMPIO: La media ampioaria X è uo STIMATORE del parametro µ (media della popolazioe). Se si estrae u ampioe e si determia il valore x, tale valore, he varia da ampioe a ampioe, è ua STIMA di µ La frequeza ampioaria relativa è uo STIMATORE del parametro p (probabilità di suesso) di ua popolazioe o distribuzioe beroulliaa. Se si estrae u ampioe e si determia la frequeza relativa ampioaria dei suessi, tale valore, he varia da ampioe a ampioe, è ua STIMA.
12 E ituitivo ammettere he ua stima è tato migliore quato più si avviia al valore vero (iogito) del parametro da stimare. Poihé T (tau) è ua variabile aleatoria, questo equivale a hiedere he la distribuzioe di probabilità dello stimatore sia oetrata attoro al valore del parametro θ (teta) da stimare, ovvero he la dispersioe dei valori di T attoro al suo valor medio sia la miima possibile.
13 u oorrete i ua gara di tiro a bersaglio, desidera he i suoi olpi si distribuisao attoro al etro del bersaglio!!!!
14
15 aalogamete, hi effettua ua stima statistia desidera avere la massima probabilità di avviiarsi al vero valore da stimare. Questo può essere espresso i termii matematii i base alle proprietà degli stimatori; tali proprietà soo:
16 PROPRIETA DEGLI STIMATORI Correttezza Effiieza Cosisteza
17 Correttezza Uo stimatore T del parametro θ si die orretto se il suo valor medio M(T) oiide o θ per qualsiasi valore di T M(T) θ Ad esempio X è uo stimatore orretto della media µ della popolazioe: ifatti M(X) µ diap.. 45
18 ..ahe la frequeza relativa dei suessi i u ampioe estratto da ua popolazioe di tipo biomiale è uo STIMATORE orretto del parametro p della popolazioe INFATTI Essedo si ha: Si può oludere he la frequeza ampioaria è uo STIMATORE orretto del parametro p della popolazioe o distribuzioe biomiale k p k P k 0 ) ( ) ( 1 ) ( 0 0 k P k k P k k M k k p p k M 1
19 Stimatore orretto M(T)θ M(T)θ
20 La variaza ampioaria S 2 risulta, ivee, uo stimatore distorto della variaza σ 2 della popolazioe ifatti: ( ) µ S 2 σ 2 ( ) risultado: µ S σ
21 Stimatore distorto M(T) θ θ M(T)
22 Effiieza La botà di uo stimatore o può essere valutata solo i base alla orrettezza. Si osideri u parametro θ he può essere valutato mediate due stimatori orretti, T 1 e T 2 ; Tra i due risulta migliore quello o variaza miore
23 PERTANTO Uo stimatore è tato più effiiete quato miore è la sua variaza
24
25 Ad esempio la media µ di ua popolazioe può essere valutata sia mediate la media X ampioaria sia mediate la mediaa X ~ ampioaria ma tra i due stimatori la media ampioaria risulta più EFFICIENTE
26 Cosisteza Uo stimatore si die osistete quado, al resere delle dimesioi del ampioe, overge verso il parametro della popolazioe da stimare; i formula: lim P( T ϑ < ε ) 1 diap.. 45
27 Distribuzioe di T per ampioi di ampiezza diap.. 45
28 Ua volta selto lo stimatore he risulta migliore per stimare u parametro della popolazioe Si possoo effettuare due tipi di stime STIME PUNTUALI STIME INTERVALLARI
29 Le stime putuali di u parametro, soo quelle he si esprimoo o u valore umerio e soo più semplii da alolare: si assume ome stima il valore alolato dal ampioe assoiadogli lo sarto quadratio medio detto errore medio di ampioameto he idia l errore mediamete ommesso stimado, per mezzo del ampioe, il parametro iogito della popolazioe
30 Per hiarire quato detto fiora, svolgere i laboratorio la seguete attività: Si osideri ua popolazioe formata dalle misure: 130, 140, 180, 110. Ci propoiamo di stimare il parametro µ utilizzado ampioi beroulliai di dimesioe 3, mediate due stimatori: lo stimatore media e lo stimatore mediaa..fare riferimeto al file prodotto
31 Le stime itervallari di u parametro, soo quelle he si esprimoo o u itervallo (detto fiduiario) he otega o ua erta probabilità il parametro iogito della popolazioe. La stima per itervallo si applia se è ota la legge di distribuzioe dello stimatore e permette di valutare meglio l errore he si può ommettere. diap.. 50
32 STIME PUNTUALI STIMA PUNTUALE DI UNA MEDIA STIMA PUNTUALE DI UNA FREQUENZA STIME PER INTERVALLO INTERVALLO FIDUCIARIO PER LA MEDIA INTERVALLO FIDUCIARIO PER LE FREQUENZE RELATIVE
33 Per quato riguarda le STIME PUNTUALI, i rifaremo a quato preedetemete studiato riguardo alla valutazioe della media e della frequeza ampioaria uitamete alle rispettive relazioi o i parametri della popolazioe
34 Il problema della stima putuale di ua media osiste el valutare da u ampioe il valore µ della popolazioe; ome preedetemete visto tale valore (stima) orrispode alla media della popolazioe; a tale stima si dovrà assoiare lo sarto quadratio medio delle medie ampioarie (errore medio di ampioameto), he, ome preedetemete visto,, NON orrispode allo sarto quadratio medio della popolazioe
35 Per questo motivo si assume ome stimatore di σ 2 la VARIANZA CAMPIONARIA CORRETTA S ) 2 ) s 2 1 s 2 DEVIAZIONE STANDARD CAMPIONARIA CORRETTA ) s s 1 diap.. 71 (el aso di estrazioe beroulliaa)
36 Per questo motivo si assume ome stimatore di σ 2 la VARIANZA CAMPIONARIA CORRETTA sˆ 2 s 2 N 1 N 1 S ) 2 DEVIAZIONE STANDARD CAMPIONARIA CORRETTA sˆ s 1 N N 1 diap.. 71 (el aso di estrazioe seza ripetizioe) - u elemeto alla volta -
37 Per questo motivo si assume ome stimatore di σ 2 la VARIANZA CAMPIONARIA CORRETTA S ) 2 sˆ 2 N 1 s 2 N 1 DEVIAZIONE STANDARD CAMPIONARIA CORRETTA sˆ N 1 N 1 (el aso di estrazioe seza ripetizioe) - estrazioe i bloo - s diap.. 71
38 PERTANTO, el aso i ui o oosiamo σ, per determiare l errore di ampioameto sarà suffiiete sostituire a σ elle preedeti relazioi il valore di ŝ sˆ sˆ N σ x σ x N 1 estrazioe beroulliaa estrazioe i bloo Per redere miore l errore di ampioameto e avere quidi ua stima più preisa, oorre aumetare il umero degli elemeti del ampioe eserizi.
39 1 Valutare i risultati otteuti. 2 Ua popolazioe è omposta dai umeri 1,2,3,4. Estrarre tutti i possibili ampioi di dimesioe 2, dapprima seodo lo shema della estrazioe seza ripetizioe e suessivamete utilizzado lo shema della estrazioe i bloo; valutare i risultati otteuti. S
40 3 (stima putuale, ota la deviazioe stadard della popolazioe) 4 (stima putuale, seza la deviazioe stadard della popolazioe) S
41 5 Il diametro medio di alui usietti a sfera è di 0,60 m o ua deviazioe stadard di 0,01 m; effettuare ua stima putuale del diametro medio dei usietti e determiare l errore medio di ampioameto. Ioltre: a) qual è la probabilità he selezioado u ampioe asuale di 50 elemeti, si ottega u diametro medio del ampioe superiore a 0,601 m? b) qual è la probabilità he selezioado u ampioe asuale di 50 elemeti, si ottega u diametro medio del ampioe iferiore a 0,598 m? S
42 6 S
43 7 S
44 Il problema della stima putuale di ua frequeza osiste el valutare quate uità di ua popolazioe posseggoo ua erta aratteristia; ome preedetemete visto, per stimare il parametro della popolazioe (ioè la probabilità he u erto attributo della popolazioe ha di presetarsi), prederemo i osiderazioe l estrazioe beroulliaa he dà luogo ad ua distribuzioe biomiale
45 Riordado he la frequeza relativa del ampioe è: f - x umero degli elemeti del ampioe he posseggoo l attributo x - la dimesioe del ampioe e he tale stimatore oltre ad essere orretto è ahe osistete ASSOCIAMO alla stima f l errore medio di ampioameto he dalle formule preedeti è dato da: σ k pq
46 σ k pq essedo p igoto si stima l errore medio di ampioameto sostituedo a p e q rispettivamete f ed (1-f ) f ( 1 f ) s f he si può redere piolo, e quidi otteere ua stima più aurata, aumetado il umero degli elemeti del ampioe el aso di estrazioe beroulliaa
47
48 8 9 U ampioe di 40 elemeti è estratto da ua popolazioe biomiale o parametro p0,9. Determiare la probabilità he el ampioe si verifihi ua peretuale di suessi maggiore dell 88%. S
49 10 Fare riferimeto al file.xls relativamete alla sheda Distribuzioe ampioaria delle frequeze
50 Rispetto a quato detto preedetemete (diap. 10 e diap.31) idihiamo o: ϑ ε ϑˆ ϑ + ε l itervallo fiduiario α il rishio di errore o livello di sigifiatività (geeralmete prefissato) 1 α il livello fiduiario o probabilità di ofideza
51 P( ϑ PERTANTO ˆ + ) 1 ε ϑ ϑ ε α idia he il valore dello stimatore ell itervallo di ofideza ϑˆ è oteuto [ ϑ ε; ϑ + ε ] o probabilità 1 α
52 P( MENTRE ϑˆ ε ϑ ϑˆ + ε ) 1 α idia he il valore del parametro ell itervallo di ofideza ϑ è oteuto [ ] ϑ ˆ ε; ϑˆ + ε o probabilità 1 α a hiarimeto osideriamo la seguete esemplifiazioe:
53 Si osideri il aso assai riorrete i ui il parametro da stimare è la media di ua popolazioe; si vuole determiare u itervallo fiduiario attoro alla media ampioaria, tale he, o ua probabilità prefissata (pari al livello fiduiario), iluda il valore della MEDIA della popolazioe.
54 PRENDIAMO IN ESAME DUE CASI: la popolazioe è distribuita ormalmete o variaza ota la popolazioe è distribuita ormalmete o variaza iogita
55 I^ CASO: la popolazioe è distribuita ormalmete o variaza ota I questo aso la media ampioaria X è ua variabile aleatoria o distribuzioe esattamete ormale o
56 µ µ x σ 2 2 x σ σ x σ el aso di estrazioe beroulliaa µ µ x σ 2 x σ 2 N N 1 σ x σ N N 1 aso di estrazioe seza ripetizioe (i bloo)
57 Di osegueza la v.. Z X µ σ ha distribuzioe ormale stadardizzata Fissato il valore di α (o il livello di ofideza 1-α), è possibile determiare, per mezzo della tavola delle aree delle superfii sotto la urva ormale stadardizzata, i due valori z 1 e z 2 detti valori ritii, tali he: P( z Z z ) α
58 P( z Z z 1 ) α
59 α 1 ( ) z Z z P Sostituedo a Z il valore si ha: σ µ X α σ µ 1 z X z P Moltipliado iasu termie della disuguagliaza per e aggiugedo µ si ha: σ α σ µ σ µ + 1 z X z P
60 α σ µ σ µ + 1 z X z P he esprime la probabilità he la media ampioaria appartega all itervallo z X z σ µ σ µ + risolvedo la disuguagliaza i fuzioe di µ si ottiee: α σ µ σ + 1 z X z X P he esprime la probabilità he la media della popolazioe appartega all itervallo aleatorio
61 Questa figura mette i evideza he, per ogi ampioe estratto (o ostate), si ottiee ua stima X metre la probabilità he sia eslusa è α
62 Esempio 1 (ostruzioe itervalli di ofideza) Selto il livello di ofideza 1-α 0,8664, vogliamo determiare l itervallo z Z z tale he P( z Z z ) 0, 8664 f (Z ) per la simmetria di si ha: P( 0 Z z ) 0,4332 Utilizzado la tavola perveiamo al valore z 1,5 Pertato l itervallo rihiesto è: 1,5 Z 1, 5
63 Esempio 2 (ostruzioe itervalli di ofideza) Costruire l itervallo di ofideza della variabile stadardizzata Z, al livello di sigifiatività: α 31,73% ; Per quato riguarda α 31,73% ioèα 0,3173 si ha: 1-α0,6827 ioè: P( z Z z ) 0, 6827 Essedo per la simmetria di f (Z ) P( 0 Z z ) 0,34135 i orrispodeza di questo valore, sulla tavola troviamo he z 1 Per ui possiamo essere fiduiosi he il 68,27% dei valori assuti dalla v.. Z sia ompreso fra -1 e +1; parimeti i aspettiamo he il rimaete 31,73% sia estero a questi limiti
64 Esempio 3 (ostruzioe itervalli di ofideza) U ampioe asuale beroulliao di dimesioe ha ome media e proviee da ua popolazioe distribuita ormalmete o σ10. Forire ua stima della media per itervallo, o livello di ofideza del 95%. Essedo (1-α)0,95 ioè P( z Z z ) 0, 95 x Per la simmetria di f (Z ) P( 0 Z z ) 0,4750 i orrispodeza di questo valore, sulla tavola troviamo he z 1, 96
65 Quidi la probabilità he la media della popolazioe appartega all itervallo aleatorio è: P X σ σ z µ X + z 1 α P 50 1,96 µ , ,95 P( 48,04 µ 51,96) 0,95 Siamo osì fiduiosi he o probabilità del 95% il valore della media dell uiverso sia ompresa ell itervallo trovato.
66 Esempio 4 (ostruzioe itervalli di ofideza) Da u uiverso ostituito da 2500 studeti, o σ 12,25. m variaza 2 2 è stato estratto u ampioe asuale seza ripetizioe o estraz. i bloo di 150 studeti. Determiare l itervallo di ofideza per la stima dell altezza media o probabilità di ofideza pari al 98%, sapedo he la statistia assume el ampioe il valore x 169,5.m X
67 Trattadosi di ampioe estratto SENZA RIPETIZIONE (estraz. i bloo), si tratta di determiare la seguete probabilità: P X σ N σ N z µ + X z 1 α N 1 N 1 Essedo (1-α)0,98 si ha: P( z Z z ) 0, 98 Per la simmetria di (Z ) f P( 0 Z ) 0,49 i orrispodeza di questo valore, sulla tavola troviamo mediate proedimeto di iterpolazioe he z per ui: z 2,326 3, , P 169,5 2, ,5 2,326 µ + 0,
68 Cioè: P ( 168,86 µ 170,14 ) 0, 98 Possiamo oludere diedo he l altezza media dei 2500 studeti è ompresa el suddetto itervallo, osapevoli he il rishio massimo di errore è del 2%.b. proedimeto di iterpolazioe : ( 2,33 2,32) : (0,4901 0,4898) ( z 2,32) : (0,49 0,4898)
69 Eserizi (ostruzioe itervalli di ofideza) Costruire gli itervalli di ofideza della variabile stadardizzata Z, ai livelli di sigifiatività: α 4,55% ; α 0,27%
70 II^ CASO: la popolazioe è distribuita ormalmete o variaza iogita Cosa mettere, elle formule per il alolo degli estremi di u itervallo di ofideza al posto di σ?
71 Se oosiamo la variaza S 2 di u ampioe, la variaza orretta può essere alolata direttamete osì, ome si evie ahe dalle preedeti formule: 2 ŝ 1 ˆ 2 2 s s Per ampioi o ripetizioe (beroulliai) 1 1 ˆ 2 2 N N s s Per ampioi seza ripetizioe (u elemeto alla volta) 1 1 ˆ 2 2 N N s s Per ampioi seza ripetizioe (estraz. I bloo)
72 Esempio 1 (ostruzioe itervalli di ofideza) Misurado la lughezza di u tavolo 65 volte, si è trovata ua media ed uo s.q.m. x 1,853.m s 0,012. m Stimare per itervallo la lughezza reale µ del tavolo o grado di fiduia del 95%, osiderado he il ampioe sia di tipo beroulliao. Possiamo utilizzare la ota relazioe: P X σ σ z µ X + z 1 α
73 α σ µ σ + 1 z X z X P Ma o abbiamo lo s.q.m. reale (σ), oosedo soltato quello del ampioe ( ); pertato possiamo utilizzare la relazioe: Sostituedo a s.m 0,012 µ α + 1 ˆ ˆ s z X s z X P ŝ 0, ,012 1 ˆ s s
74 Essedo (1-α)0,95 ioè P( z Z z ) 0, 95 Per la simmetria di (Z ) f P( 0 Z z ) 0,4750 i orrispodeza di questo valore, sulla tavola troviamo he Pertato si avrà: z 1,96 0, ,01209 P 1,853 1,96 µ 1, , P 0,95 ( 1,85006 µ 1,85594 ) 0, 95 Possiamo oludere diedo he la lughezza del tavolo è ompresa el suddetto itervallo, osapevoli di u margie di errore pari al 5%
75 11 U ampioe di 100 lampadie, estratto da u lotto di lampadie, preseta ua durata media di 900 ore o ua deviazioe stadard di 98 ore. Calolare i limiti etro i quali è oteuta la media della popolazioe al livello di ofideza del: a) 90% b) 95% ) 99% S
76 Si osideri il aso di ua popolazioe o distribuzioe biomiale. Si vuole determiare u itervallo fiduiario per la stima del parametro p della popolazioe, ioè della probabilità he si abbiao k suessi su N osservazioi. Dalla ota relazioe P X µ z 1 α z σ
77 α σ µ 1 z X z P Dalle formule preedeti, sostituedo σ si ha: Trattadosi di distribuzioe ampioaria delle frequeze, la variabile stadardizzata Z potrà sriversi: per ui σ p f Z r f f r r ) 1 ( risolvedo la disuguagliaza i fuzioe di p si ottiee: α σ 1 r z p f z P ( ) α σ σ + 1 r r z f p z f P α + 1 ) (1 ) (1 f f z f p f f z f P r r r r r r
78 Esempio 1 (ostruzioe itervalli di ofideza) Estraedo u ampioe di 80 elemeti da ua popolazioe di tipo biomiale si soo otteuti 20 suessi; determiare ua stima itervallare del parametro p della popolazioe ad u livello fiduiario del 95%. I questo aso: f r 20/800,25 Essedo (1-α)0,95 ioè P( z Z z ) 0, 95 Per la simmetria di (Z ) f P( 0 Z z ) 0,4750 i orrispodeza di questo valore, sulla tavola troviamo he z 1,96
79 Appliado la relazioe: P f r si ha: f r (1 f r ) f r (1 f r ) z p f + z r 1 σ 0,25 0,75 0,25 0,75 P 0,25 1,96 0,25 1,96 p ,95 ioè: P ( 0,155 p 0,345) 0, 95 Possiamo oludere diedo il parametro p della popolazioe è ompreso el suddetto itervallo, osapevoli di u margie di errore pari al 5%
80 12 E stata odotta u idagie su tutte le persoe di maggiore età allo sopo di aertare la frequeza relativa dei possessori di patete. A tale sopo è stato estratto u ampioe di 2000 persoe ed è stato aertato he 1850 di esse soo i possesso di patete. Vogliamo determiare la frequeza relativa dei possessori di patete dell uiverso delle persoe di maggiore età o u livello di ofideza del 95%. 13 Su u ampioe di 1800 abboati alla televisioe la peretuale di oloro he hao dihiarato di avere seguito u dato programma è risultata pari al 27%. Etro quali valori sarà ompresa, o probabilità uguale a 99%, la peretuale di oloro he hao dihiarato di avere visto quel programma ell uiverso di tutti gli abboati? S
81 RIFERIMENTO LIBRO DI TESTO pag FINE DELLA LEZIONE prof. C. Guida
VERIFICA DI IPOTESI STATISTICHE
 VERIFICA DI IPOTESI STATISTICHE La proedura della VERIFICA DI IPOTESI STATISTICHE, o proedura dei test statistii, riguarda il problema di voler avere maggiori iformazioi sul valore di u erto parametro
VERIFICA DI IPOTESI STATISTICHE La proedura della VERIFICA DI IPOTESI STATISTICHE, o proedura dei test statistii, riguarda il problema di voler avere maggiori iformazioi sul valore di u erto parametro
VERIFICA DI IPOTESI STATISTICHE
 VERIFICA DI IPOTESI STATISTICHE La proedura della VERIFICA DI IPOTESI STATISTICHE, o proedura dei test statistii, riguarda il problema di voler avere maggiori iformazioi sul valore di u erto parametro
VERIFICA DI IPOTESI STATISTICHE La proedura della VERIFICA DI IPOTESI STATISTICHE, o proedura dei test statistii, riguarda il problema di voler avere maggiori iformazioi sul valore di u erto parametro
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Tecnica delle misurazioni applicate LS - Esame del 25 marzo 2010
 Teia delle misurazioi appliate L - Esame del 5 marzo 010 Problema 1. La Adria ablaggi pa è u impresa he produe quadri elettrii e he, per la sua attività, aquista igeti quatità di avo elettrio. U poteziale
Teia delle misurazioi appliate L - Esame del 5 marzo 010 Problema 1. La Adria ablaggi pa è u impresa he produe quadri elettrii e he, per la sua attività, aquista igeti quatità di avo elettrio. U poteziale
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Problemi sui test di ipotesi per la varianza
 Problemi sui test di ipotesi per la variaza Problema V1 Cotrolli periodii sulla produzioe di odesatori hao permesso al ostruttore di defiire ua variabile asuale X (he assume valore pari alla apaità di
Problemi sui test di ipotesi per la variaza Problema V1 Cotrolli periodii sulla produzioe di odesatori hao permesso al ostruttore di defiire ua variabile asuale X (he assume valore pari alla apaità di
INFERENZA o STATISTICA INFERENTE
 INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Inferenza statistica. Come descrivo una generica popolazione? Che tipo di di informazioni posso ottenere?
 Iereza I Fodameti della teoria della stima Campioameto beroulliao ed i blocco Problema della stima: stima e stimatore Proprietà di uo stimatore Stima putuale e per itervallo: valore atteso e variaza Iereza
Iereza I Fodameti della teoria della stima Campioameto beroulliao ed i blocco Problema della stima: stima e stimatore Proprietà di uo stimatore Stima putuale e per itervallo: valore atteso e variaza Iereza
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
Università degli Studi di Napoli Parthenope. STATISTICA per il Turismo
 Uiversità degli Studi di Napoli Partheope Corso di Laurea i Maagemet per le Imprese Turistiche STATISTICA per il Turismo Docete: Sergio Logobardi sergio.logobardi@uipartheope.it Stima itervallare Stima
Uiversità degli Studi di Napoli Partheope Corso di Laurea i Maagemet per le Imprese Turistiche STATISTICA per il Turismo Docete: Sergio Logobardi sergio.logobardi@uipartheope.it Stima itervallare Stima
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
ESERCITAZIONE N. 6 corso di statistica
 ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Titolo della lezione. Dal campione alla popolazione: stima puntuale e per intervalli
 Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezione. Campionamento e Distribuzioni Campionarie
 Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Inferenza statistica. Popolazione. Camp. Statistiche campionarie basate sulle osservazioni del campione. Estrazione casuale. Parametro e statistica
 6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
Probabilità e Statistica
 Probabilità e Statistica I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di
Probabilità e Statistica I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
STATISTICA 1- parte 1/2
 STATISTICA - parte / I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di ua
STATISTICA - parte / I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di ua
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a Esame del STATISTICA
 FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
INTRODUZIONE ALLA INFERENZA STATISTICA
 INTRODUZIONE ALLA INFERENZA STATISTICA 1) CONCETTO DI INFERENZA STATISTICA E SCOPI : L ifereza statistica è il procedimeto iduttivo che, avvaledosi del calcolo delle probabilità, cosete di estedere all
INTRODUZIONE ALLA INFERENZA STATISTICA 1) CONCETTO DI INFERENZA STATISTICA E SCOPI : L ifereza statistica è il procedimeto iduttivo che, avvaledosi del calcolo delle probabilità, cosete di estedere all
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
In linguaggio analitico parlare di tre tagli equivale ad individuare le equazioni di tre rette che intersecano il triangolo in questione.
 Tre tagli... sette parti Dividere u triagolo dato o tre tagli rettiliei i sette parti di ui quattro siao triagoli (e le rimaeti tre, petagoi). Ua delle parti triagolari è limitata dai tre tagli, iasua
Tre tagli... sette parti Dividere u triagolo dato o tre tagli rettiliei i sette parti di ui quattro siao triagoli (e le rimaeti tre, petagoi). Ua delle parti triagolari è limitata dai tre tagli, iasua
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
 Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA. Prof.ssa Donatella Siepi tel:
 UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
= ed è: n. 2 2 x. tra ns x
 0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
Elementi di statistica
 Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Test Statistici. In termini statistici, agli eventi appena indicati viene attribuita una probabilità ed una specifica definizione:
 Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
LA MISURA IN PSICOLOGIA
 Prof. Giulio Vidotto (Uiversità di Padova) Lez. 3 - Distribuzioe ormale e stadardizzazioe delle misure Argometi della lezioe Stadardizzazioe Distribuzioe Normale Distribuzioe Normale Stadard Stadardizzazioe
Prof. Giulio Vidotto (Uiversità di Padova) Lez. 3 - Distribuzioe ormale e stadardizzazioe delle misure Argometi della lezioe Stadardizzazioe Distribuzioe Normale Distribuzioe Normale Stadard Stadardizzazioe
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
1. (Punti 8) Deteminare modulo e argomento delle soluzioni della seguente equazione nel campo complesso. 1 x = 0. x 2 e 8.
 Corso di Laurea i Igegeria Biomedia ANALISI MATEMATICA Prova sritta del giugo 7 Fila. Esporre il proedimeto di risoluzioe degli eserizi i maiera ompleta e leggibile.. Puti 8) Detemiare modulo e argometo
Corso di Laurea i Igegeria Biomedia ANALISI MATEMATICA Prova sritta del giugo 7 Fila. Esporre il proedimeto di risoluzioe degli eserizi i maiera ompleta e leggibile.. Puti 8) Detemiare modulo e argometo
La stima per intervalli
 La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
Gli Indici di VARIABILITA
 Elemeti di Statistica descrittiva Gli Idici di VARIABILITA - Campo di variazioe - Scarto dalla media - Variaza - Scarto quadratico medio - Coefficiete di variazioe Idici di Variabilità I valori medi soo
Elemeti di Statistica descrittiva Gli Idici di VARIABILITA - Campo di variazioe - Scarto dalla media - Variaza - Scarto quadratico medio - Coefficiete di variazioe Idici di Variabilità I valori medi soo
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
15 Equilibri chimici in fase gassosa
 15 Equilibri himii i fase gassosa roblemi risolti A) I u oteitore del volume di L a 7 C vegoo itrodotti 85 g di NH. Si stabilise il seguete equilibrio NH N + H Sapedo he la K vale 9. 10, alolare a) la
15 Equilibri himii i fase gassosa roblemi risolti A) I u oteitore del volume di L a 7 C vegoo itrodotti 85 g di NH. Si stabilise il seguete equilibrio NH N + H Sapedo he la K vale 9. 10, alolare a) la
STATISTICA A K (63 ore)
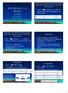 STATISTICA A K (63 ore) Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto =400 X =34.000 Km; s cor =9000 Km Calcolare l
STATISTICA A K (63 ore) Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto =400 X =34.000 Km; s cor =9000 Km Calcolare l
Daniela Tondini
 Daiela Todii dtodii@uite.it Facoltà di Bioscieze e Tecologie agro-alimetari e ambietali e Facoltà di Medicia Veteriaria C.L. i Biotecologie Uiversità degli Studi di Teramo 1 La mediaa o valore mediao M
Daiela Todii dtodii@uite.it Facoltà di Bioscieze e Tecologie agro-alimetari e ambietali e Facoltà di Medicia Veteriaria C.L. i Biotecologie Uiversità degli Studi di Teramo 1 La mediaa o valore mediao M
Tecnica delle misurazioni applicate LM - Esame del 26 febbraio 2013
 Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Lezioni del Corso di Fondamenti di Metrologia Meccanica
 Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Approfondimento 2.1 Scaling degli stimoli mediante il metodo del confronto a coppie
 Approfodimeto 2.1 Scalig degli stimoli mediate il metodo del cofroto a coppie Il metodo del cofroto a coppie di Thurstoe (Thurstoe, 1927) si basa sull assuzioe che la valutazioe di u oggetto o di uo stimolo
Approfodimeto 2.1 Scalig degli stimoli mediate il metodo del cofroto a coppie Il metodo del cofroto a coppie di Thurstoe (Thurstoe, 1927) si basa sull assuzioe che la valutazioe di u oggetto o di uo stimolo
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Statistica. Capitolo 9. Stima: Ulteriori Argomenti. Cap. 9-1
 Statitica Capitolo 9 Stima: Ulteriori Argometi Cap. 9-1 Obiettivi del Capitolo Dopo aver completato il capitolo, arete i grado di: Cotruire itervalli di cofideza per la differeza tra le medie di due popolazioi
Statitica Capitolo 9 Stima: Ulteriori Argometi Cap. 9-1 Obiettivi del Capitolo Dopo aver completato il capitolo, arete i grado di: Cotruire itervalli di cofideza per la differeza tra le medie di due popolazioi
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
Soluzione IC=[20.6,22.6]
![Soluzione IC=[20.6,22.6] Soluzione IC=[20.6,22.6]](/thumbs/96/128482049.jpg) Eercizio 1 Suppoiamo di etrarre u campioe cauale di umeroità = da ua popolazioe ormale co deviazioe tadard pari a 5.1. Sapedo che la media campioaria x è pari a 21.6, cotruire u itervallo di cofideza al
Eercizio 1 Suppoiamo di etrarre u campioe cauale di umeroità = da ua popolazioe ormale co deviazioe tadard pari a 5.1. Sapedo che la media campioaria x è pari a 21.6, cotruire u itervallo di cofideza al
Esame di Statistica A-Di Prof. M. Romanazzi
 1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
Anemia. Anemia - percentuali
 1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
STATISTICA 1 ESERCITAZIONE 5
 STATISTICA ESERCITAZIONE 5 Dott. Giuseppe Padolfo 28 Ottobre 203 VARIABILITA IN TERMINI DI DISPERSIONE DA UN CENTRO Cetro Me o μ La dispersioe viee misurata come sitesi delle distaze tra le uità statistiche
STATISTICA ESERCITAZIONE 5 Dott. Giuseppe Padolfo 28 Ottobre 203 VARIABILITA IN TERMINI DI DISPERSIONE DA UN CENTRO Cetro Me o μ La dispersioe viee misurata come sitesi delle distaze tra le uità statistiche
Università degli Studi di Roma - La Sapienza, Facoltà di Farmacia Formulario di Matematica - versione per esame
 Uiversità degli Studi di Roma - La Sapieza, Facoltà di Farmacia Formulario di Matematica - versioe per esame L equazioe lieare ax + by + c 0 elle coordiate cartesiae x e y rappreseta ua retta el piao.
Uiversità degli Studi di Roma - La Sapieza, Facoltà di Farmacia Formulario di Matematica - versioe per esame L equazioe lieare ax + by + c 0 elle coordiate cartesiae x e y rappreseta ua retta el piao.
Corso di Statistica. Stima. Prof.ssa T. Laureti a.a Corso di Statistica a.a DEIM, Univ.TUSCIA - Prof.
 Corso di Statistica Stima Prof.ssa T. Laureti a.a. 01-013 Stima putuale - Caso di studio U azieda deve teere sotto cotrollo la qualità del processo di produzioe di u macchiario che produce pezzi di ua
Corso di Statistica Stima Prof.ssa T. Laureti a.a. 01-013 Stima putuale - Caso di studio U azieda deve teere sotto cotrollo la qualità del processo di produzioe di u macchiario che produce pezzi di ua
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
ES 1.3. Data la distribuzione unitaria di una variabile quantitativa X. la media aritmetica di X è data dal rapporto tra il totale n
 ES 1.3 1 Media e variaza Data la distribuzioe uitaria di ua variabile quatitativa X x 1... x i... x, la media aritmetica di X è data dal rapporto tra il totale x i e il umero delle uità rilevate: x = 1
ES 1.3 1 Media e variaza Data la distribuzioe uitaria di ua variabile quatitativa X x 1... x i... x, la media aritmetica di X è data dal rapporto tra il totale x i e il umero delle uità rilevate: x = 1
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Argomenti. Perché una stima per intervallo? Stima per intervallo. Leonardo Grilli. Intervalli di confidenza (intervalli fiduciari)
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Itervalli di cofideza (itervalli fiduciari) Cicchitelli cap. 17 Argometi Stima per itervallo (IC: Itervalli di Cofideza): IC per
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Itervalli di cofideza (itervalli fiduciari) Cicchitelli cap. 17 Argometi Stima per itervallo (IC: Itervalli di Cofideza): IC per
Esercizio 1. Si supponga di aver assegnato ad una popolazione di N = 4 dattilografe un test e di aver ottenuto i seguenti risultati:
 Esercizio 1 Si suppoga di aver assegato ad ua popolazioe di N = 4 dattilografe u test e di aver otteuto i segueti risultati: Dattilografa N. Errori A 3 B C 1 D 4 La variabile, il umero di errori commessi
Esercizio 1 Si suppoga di aver assegato ad ua popolazioe di N = 4 dattilografe u test e di aver otteuto i segueti risultati: Dattilografa N. Errori A 3 B C 1 D 4 La variabile, il umero di errori commessi
Confronto di due misure Campioni indipendenti
 Statistica7 /11/015 Cofroto di due misure Campioi idipedeti o meglio.. rispodere al quesito Due serie di misure soo state estratte dalla stessa popolazioe (popolazioe comue o idetica) o soo state estratte
Statistica7 /11/015 Cofroto di due misure Campioi idipedeti o meglio.. rispodere al quesito Due serie di misure soo state estratte dalla stessa popolazioe (popolazioe comue o idetica) o soo state estratte
POLITECNICO DI MILANO, POLO DI CREMONA CALCOLO DELLE PROBABILITA' E STATISTICA
 POLITECNICO DI MILANO, POLO DI CREMONA 02-05-2018 CALCOLO DELLE PROBABILITA' E STATISTICA NOME MATRICOLA COGNOME FIRMA I diritti d'autore soo riservati. Ogi sfruttameto commerciale o autorizzato sarà perseguito.
POLITECNICO DI MILANO, POLO DI CREMONA 02-05-2018 CALCOLO DELLE PROBABILITA' E STATISTICA NOME MATRICOLA COGNOME FIRMA I diritti d'autore soo riservati. Ogi sfruttameto commerciale o autorizzato sarà perseguito.
SIGMA ALGEBRE RICHIAMI DI TEORIA
 SIGM LGEBRE RICHIMI DI TEORI Def.: lgebra Sia Ω uo spazio arbitrario o vuoto. Ua famiglia (lasse) F di sottoisiemei di Ω è detta algebra se e solo se: ) Ω F (la famiglia otiee lo spazio) 2) F F (la famiglia
SIGM LGEBRE RICHIMI DI TEORI Def.: lgebra Sia Ω uo spazio arbitrario o vuoto. Ua famiglia (lasse) F di sottoisiemei di Ω è detta algebra se e solo se: ) Ω F (la famiglia otiee lo spazio) 2) F F (la famiglia
