FUNZIONI. Mauro Saita Ottobre 2013.
|
|
|
- Tommaso Gallo
- 5 anni fa
- Visualizzazioni
Transcript
1 FUNZIONI Mauro Saita Ottobre Indice 1 Funzioni Deinizione 1.1 (Funzione). Una unzione da in B consiste di: 1. un insieme detto dominio della unzione; 2. un insieme B detto codominio della unzione; 3. una reola o azione che assena ad oni elemento a del dominio un unico elemento b del codominio. L elemento b si chiama immaine di a tramite e si indica con il simbolo (a) (si lee: di a ). Si scrive B (oppure : B) per denotare una unzione il cui dominio è e il cui codominio è B. Deinizione 1.2 (Immaine di una unzione). Si chiama immaine Im della unzione B il sottoinsieme del codominio Im = {y B x (x) =y} Deinizione 1.3 (Controimmaine). Si consideri la unzione B eunelementob del codominio. Si chiama controimmaine di b mediante (e si scrive 1 (b) ) il sottoinsieme di così deinito 1 (b) ={a (a) =b} L insieme 1 (b) si chiama anche ibra di sull elemento b. Esso può essere ormato da uno opiùelementi oppure coincidere con l insieme vuoto. Una unzione per la quale il dominio sia uuale al codominio, si chiama endounzione. Funzione identità. 0 Nome ile: unzioni-2013.tex 1
2 Per oni insieme, esiste una particolare endounzione, detta unzione identità di che si denota con la scrittura: 1 La unzione identità di è deinita nel modo seuente: il dominio e il codominio di 1 sono l insieme stesso e 1 (x) =x per oni elemento x in. 1.1 Composizione di unzioni Se e sono due unzioni per le quali il codominio di coincide con il dominio di, ossia allora si può costruire una nuova unzione deinendo B C C ( )(x) =((x)) per oni x in. Si può visualizzare la situazione con il seuente diaramma commutativo: B C Si noti che la unzione composta non è sempre deinita: è deinita soltanto quando il codominio di coincide con il dominio di. 1.2 Proprietà della composizione di unzioni Valono inoltre le lei seuenti: LEGGI D IDENTIT. Se Dunque commutano i diarammi: B, allora 1 = e 1 B = (1.1) 2
3 1 B B B 1 B LEGGE SSOCITIV. Se allora B C h D (h ) = h ( ) (1.2) Dunque per la lee dell associatività, il diaramma seuente commuta: B h C h D La lee associativa permette di tralasciare la parentesi e scrivere semplicemente h. 1.3 Funzioni invertibili o isomorismi Deinizione 1.4 (Funzione invertibile). Una unzione B si dice invertibile (o un isomorismo dall insieme all insieme B) se esiste una unzione B per cui risulti: =1 e =1 B Una tale unzione (se esiste) si chiama unzione inversa di. Se B è invertibile la sua inversa è unica. Vale inatti il seuente Proposizione 1.5. Sia B una unzione invertibile. Se B entrambe inverse di allora =., B sono Dimostrazione. 3
4 = 1 B (deinizione di unzione identitá) = ( ) ( è l inversa di ) = ( ) (proprietá associativa della composizione di unzioni) = 1 ( è l inversa di ) = (deinizione di unzione identitá). Se B ha inversa, allora l inversa (che è unica) si denota con il simbolo 1. Deinizione 1.6. Si dice che due insiemi e B hanno la stessa cardinalità isomori) se esiste una unzione invertibile (un isomorismo) B. (o che sono Teorema 1.7. Siano X e Y e Y Z unzioni invertibili. llora X Z è invertibile ( ) 1 = 1 1. Dimostrazione. Per deinizione di inversa, per dimostrare che ( ) 1 = 1 1 si deve provare che e Ora ( )( 1 1 )=1 Z ( 1 1 )( ) =1 X. ( ) ( 1 1 ) = ( 1 ) 1 = 1 = 1 Z. naloamente si prova ( 1 1 ) ( ) =1 X. 1.4 Funzioni iniettive, suriettive e biunivoche Deinizione 1.8 (Funzione iniettiva). Una unzione B si dice iniettiva se soddisa la seuente proprietà diunicità : oni elemento b B ha al più una controimmaine in. In altri termini, è iniettiva se vale una delle due seuenti proprietà tra loro equivalenti Quindi, una unzione distinti del codominio. (i) a 1,a 2 (a 1 )=(a 2 ) = a 1 = a 2 (ii) a 1,a 2 a 1 a 2 = (a 1 ) (a 2 ) B iniettiva associa a elementi distinti del dominio elementi 4
5 Deinizione 1.9 (Funzione suriettiva). Una unzione B si dice suriettiva se soddisa la seuente proprietà diesistenza: oni elemento di b B possiede almeno una controimmaine in, cioè In altre parole è se suriettiva se b B a (a) =b. Im () =B Deinizione 1.10 (Funzione biunivoca). Una unzione B si dice biunivoca (o biettiva) se è iniettiva e suriettiva. Proposizione Sia B una unzione da un insieme auninsiemeb. llora le due condizioni seuenti sono equivalenti: (i) è iniettiva; (ii)) ha un inversa sinistra, cioè esiste una unzione B unica) per la quale =1. Dimostrazione. (i) (ii) Si deve trovare una B nel modo seuente: (non necessariamente in modo tale che =1. Per oni b B, sideinisce(b) se b Im(), esiste, per ipotesi, esattamente un a per il quale (a) =b; si pone allora per deinizione (b) =a; se invece b/ Im(), si deinisce (b) in modo del tutto arbitrario: per esempio, si scelie un elemento a 0 ( ) e per oni b B, b/ Im(), si pone (b) =a 0. llora è acile vedere che =1. Naturalmente di inversa sinistra ne può esistere più d una. (ii) (i) Per oni a 1,a 2 Dunque è iniettiva. (a 1 )=(a 2 )= ((a 1 )) = ((a 2 )) = a 1 = a 2. Proposizione Sia B una unzione da un insieme auninsiemeb. llora le due condizioni seuenti sono equivalenti: (i) è suriettiva; (ii)) ha un inversa destra, cioè esiste una unzione B (non necessariamente unica) per la quale =1 B. 5
6 Dimostrazione. (i) (ii) Si deve trovare una B in modo tale che =1 B. Per oni b B, sideinisce(b) nel modo seuente: b Im(), perchè è suriettiva per ipotesi. Quindi esiste, almeno un a per il quale (a) =b; siponealloraperdeinizione(b) =a (per oni b in B la scelta dell elemento a può essere atta in almeno un modo). llora è acile vedere che =1 B. Naturalmente di inversa destra ne può esisterepiù d una. (ii) (i) =1 B per ipotesi. llora per oni b B ( )(b) =((b)) = b; esiste dunque un elemento a = (b) per il quale (a) =b; diconseuenza è suriettiva. Proposizione Siano, B insiemi. Una unzione B èbiunivocaseesoloseè invertibile Prima dimostrazione. B biunivoca B iniettiva e suriettiva B ha un inversa sinistra e un inversa destra Siano B 1 e B 2 rispettivamente un inversa sinistra e un inversa destra di llora 1 e 2 coincidono, inatti 1 =1 e 2 =1 B 1 = 1 ( 2 ) = ( 1 ) 2 proprietà associativa = 1 2 deinizione di inversa sinistra = 2 lee d identità Quindi esiste una unzione (= 1 = 2 )cheè contemporaneamente inversa sinistra e inversa destra di. Pertanto B è invertibile. Seconda dimostrazione. biunivoca invertibile. è suriettiva cioè per oni y B esiste almeno un x per il quale (x) =y; essendo anche iniettiva l elemento x trovato è unico. Quindi è ben deinita la unzione, chiamiamola B, che a oni y in B associa l unico x in per il quale (x) =y. Pertanto, per oni y 6
7 in B, ((y)) = y, cioè =1 B. D altra parte, per il modo stesso in cui è deinita, per oni x, vale((x)) = x, cioè =1. Quindi è invertibile. invertibile biunivoca. Per ipotesi esiste la unzione inversa di, chiamiamola B. è iniettiva. Inatti se per oni x 1,x 2 (x 1 )=(x 2 ), applicando la unzione, si ottiene ((x 1 )=((x 2 )), vale a dire x 1 = x 2 perchè è l identità di. è suriettiva. Inatti, sia y in B. Poichè =1 B,sihay =( )(y) =((y)). Posto (y) =x si ottiene y = (x). Proposizione Siano ( ),B,C insiemi e valono le seuenti proposizioni B, B C unzioni. llora (a), iniettive iniettiva. (b), suriettive suriettiva. (c) iniettiva iniettiva. (d) suriettiva suriettiva. Dimostrazione. (a) 1 a Dimostrazione. Una unzione (con dominio non vuoto) èiniettivaseesoloseha un inversa sinistra (proposizione 1.11). Siano allora B h e C k B inverse sinistre rispettivamente di e : questo siniica che h =1 e k =1 B. llora (h k) ( ) = h (k ) (proprietà associativa delle unzioni) = h 1 B (k è inversa sinistra di ) = h (lee d identità ) = 1 (h è inversa sinistra di ) Questo prova che h k è un inversa sinistra di, e quindi che è iniettiva. (a) 2 a Dimostrazione. Per oni x 1,x 2 : ( )(x 1 )=( )(x 2 ) ((x 1 )) = ((x 2 )) (deinizione di ) = (x 1 )=(x 2 ) ( è iniettiva) = x 1 = x 2 ( è iniettiva) Questo prova che è iniettiva (b) Dimostrazione. Una unzione è suriettiva se e solo se ha un inversa destra (proposizione 1.12). Siano allora B h e C k B inverse destre rispettivamente di e : questo siniica che h =1 B e k =1 C. llora 7
8 ( ) (h k) = ( h) k (proprietà associativa delle unzioni) = 1 B k (h è inversa destra di ) = k (lee d identità ) = 1 (k è inversa destra di ) Questo prova che h k è un inversa destra di, e quindi che è suriettiva. (c) 1 a Dimostrazione. Per ipotesi è iniettiva, quindi ha un inversa sinistra (Teorema 1.11). Questo siniica che esiste C h per la quale h ( ) =1. Per l associatività della composizione di unzioni: 1 = h ( ) =(h ) Ma allora h è un inversa sinistra di, epertanto è iniettiva. (c) 2 a Dimostrazione. Per oni x, x X: (x 1 ) = (x 2 ) ((x 1 )) = ((x 2 )) ( )(x 1 ) = ( )(x 2 ) x 1 = x 2 ( è iniettiva) Questo prova che è iniettiva. (d) Dimostrazione. Per ipotesi è suriettiva, quindi ha un inversa destra (Teorema 1.12). Questo siniica che esiste C h per la quale ( ) h =1 C. Per l associatività della composizione di unzioni: 1 C =( ) h = ( h) Ma allora h è un inversa destra di, epertanto è suriettiva. 1.5 Due diversi impiehi delle unzioni Le unzioni venono utilizzate im moltissime situazioni; qui si descrivono due impiehi molto requenti del concetto di unzione. Primo aspetto. Classiicare il dominio mediante una proprietà. Sia X B una unzione da un insieme X auninsiemeb. La controimmaine di b B tramite è il sottoinsieme (del dominio) deinito da 1 {b} = {x X (x) =b} La unzione X B può essere pensata come una amilia di sottoisiemi del dominio 1 {b}, b B 8
9 indiciata con li elementi del codominio. Se nessuna ibra è vuota (cioè se è suriettiva), si dice che { 1 {b}} b B è una partizione di X. Esempio. Si consideri la unzione Z {0, 1}, (z) = { 0 se z èpari 1 se z èdispari Si può pensarea come alla partizione di Z nelle due ibre 1 {0} = {numeri pari}, 1 {1} = {numeri dispari} Secondo aspetto. Nominare il codominio. Sia X una unzione da un insieme auninsiemex. La unzione X può essere pensata come unaamiliadielementidix etichettata dali elementi di. In altre termini, per oni a in si può scrivere a al posto di (a). llora la unzione X può essere pensata come una amilia { a } a di elementi del codominio indiciata dal dominio. Esempio. Una successione di numeri reali N R è una amilia (ininita) { n } n N di numeri reali indiciata da N: 0, 1, 2,..., n,... Esempio. Se = {1, 2, 3,...n} e X = {a,b,c,...,z} è l alabeto della linua italiana, allora la unzione X è una parola di lunhezza n. nche in questo caso si è portati a vedere una parola come una amilia di elementi del codominio X (vale a dire una amilia di lettere dell alabeto) indiciata da. 9
10 1.6 Funzioni da R a R. Deinizione 1.15 (Graico di una unzione). Sia B una unzione. Il raico G di è il sottoinsieme del prodotto cartesiano B G() ={(a, b) B b = (a)} Esempio. Il raico della unzione R cos R è il sottoinsieme di R R così deinito G cos = {(x, y) R R y =cosx} y +1 2π 3 2 π π π π 2 π 3 2 π 2π x Fiura 1: Graico della unzione R cos R. Sia R R una unzione non invertibile. In molti casi è possibile restrinere opportunamente dominio e codominio di in modo tale da avere una unzione invertibile (iniettiva e suriettiva). Per esempio R cos cos R non è invertibile mentre [0,π] [ 1, 1] lo è. La unzione inversa del coseno [ 1, 1] cos 1 [0,π] è la unzione arcocoseno (si scrive arcos). Fiura 2: Graico di [0,π] cos [ 1, 1] (in nero); raico di [ 1, 1] arcos [0,π] (in blu). Il raico G 1 di 1 è il simmetrico di G rispetto alla retta y = x. 10
11 Deinizione 1.16 (Zeri di una unzione). Si consideri il sottoinsieme D di R elaunzione D R, y = (x). Glizeri di sono li elementi x D per i quali risulta (x) =0 Gli zeri di sono le ascisse dei punti di intersezione del raico G di con l asse x. Deinizione 1.17 (Punti issi di una unzione). Si consideri il sottoinsieme D di R ela unzione D R, y = (x). Ipunti issi di sono li elementi x D per i quali risulta (x) =x I punti issi di sono le ascisse dei punti di intersezione del raico G di con la retta di equazione y = x (bisettrice primo-terzo quadrante). Deinizione 1.18 (Funzione pari). La unzione R R, y = (x) è pari se vale la proprietà x R ( x) =(x) Se èpariilraicog di è simmetrico rispetto alla retta x = 0 (asse y). La unzione R cos R è pari, sono unzioni pari tutte le unzioni polinomiali del tipo p(x) = a 2n x 2n +...a 2 x 2 + a 0 (cioè i polinomi in cui compaiono esclusivamente esponenti pari). Deinizione 1.19 (Funzione dispari). La unzione R proprietà R, y = (x) è dispari se vale la x R ( x) = (x) Se è dispari il raico G di è simmetrico rispetto all oriine O deli assi cartesiani. La unzione R sin R è dispari, sono unzioni dispari tutte le unzioni polinomiali del tipo p(x) =a 2n+1 x 2n a 3 x 3 +a 1 x (cioè i polinomi in cui compaiono esclusivamente esponenti dispari). Dalle simmetrie di due unzioni e si deduce la simmetria di h = (attenzione, h = indica il prodotto puntuale di unzioni e non la loro composizione) come indicato nella seuente tabella pari dispari pari pari dispari dispari dispari pari La dimostrazione di queste proposizioni è lasciata per esercizio. 11
12 1.7 Esercizi Esercizio Per onuna delle seuenti unzioni (a) si diseni il raico qualitativo; (b) si dica se la unzione è iniettiva, suriettiva, invertibile. (c) se la unzione è invertibile si determini dominio, codominio e l espressione analitica della unzione inversa. Inine, si diseni il raico della unzione inversa. 1. R R (x) =x 2 2. R 0 R 0 (x) =x 2 3. R >0 R >0 (x) = 1 x 4. R R (x) =x 3 5. R 0 R 0 6. R R 7. R R 8. R R (x) = x (x) = 3 x (x) =2cosx (x) =3sin2x 9. R R (x) =cos(x π 2 ) 10. R \{1} R{0} (x) = R R x 1 (x) = x 12. R \{1} R (x) = 2x 3 x R exp 2 R >0 exp 2 (x) =2 x 14. R exp 2 R lo 15. R 2 >0 R exp 2 (x) =2 x lo2 x = loaritmo in base 2 di x Esercizio La unzione R R, (x) =x 2 5x. è iniettiva? è suriettiva? Determinare, se esistono, li zeri di. Esercizio Si considerino le unzioni Trovare,, Im ( ), Im ( ). 1. R 0 R 0 (x) =3x R 0 R 0 (x) = x Esercizio Sia R R, (x) =ax + b per oni x in IR. 1. Determinare i valori di a e b per i quali =. 12
13 2. Determinare i valori di a e b per i quali =1 R (l identità dir). 3. Determinare i valori di a e b per i quali è invertibile. 4. Studiare, al variare di a e b, l esistenza dei punti issi di. Risposta: 1) (a =0, b IR) o (a =1,b=0),2)(a = 1, b IR) o (a =1,b=0),3)a 0, 4)a 1. Esercizio Si consideri la unzione R R, (x) =mx + q (m, q R ). Per quali valori di m, q la unzione è pari? Per quali valori èdispari? Risposta: èpariperm =0; èdispari m e q =0. Esercizio Se R R èparier R èdispari. Cosasipuò dire delle unzioni composte,,,? Sono pari, dispari, né parinédispari? Motivarelerisposte. Risposta: èpari, èpari, èpari, èdispari. Esercizio Si considerino le unzioni Trovare,, Im ( ), Im ( ). 1) R R (x) =x 1 2) R R (x) =3 x Esercizio Trovare l immaine Im e il numero di punti issi della unzione R R, (x) =x 2 3 Esercizio La unzione R sin R è iniettiva? suriettiva? Come si può restrinere opportunamente dominio e codominio in modo da ottenere una unzione invertibile? In tal caso, come si chiama l inversa? Esercizio 1.29 (Galileo). Dimostrare che l insieme dei numeri naturali N = {0, 1, 2,..., n,..} ha la stessa cardinalità dell insieme S = {0, 1, 4,..., n 2,..} dei quadrati peretti. (Si dice che due insiemi X, Y hanno la stessa cardinalità se esiste una unzione invertibile (un isomorismo) : X Y.) Esercizio La unzione [ π 2, + π 2 ] tan R è iniettiva? È suriettiva? È invertibile? Se è invertibile come come si chiama l inversa? Qual èilsuoraico? Esercizio Trovare dominio, raico qualitativo e immaine delle seuenti unzioni 13
14 1. y = sinx 2. y =2 x 1 3. y =arctanx 4. y =2 x 5. y = lo x 6. y = e x y = e x Esercizio Siano R R e R R due unzioni. Se e sono entrambe pari che cosa si può dire sulla loro somma? Se èparie èdisparichecosasipuò dire sulla loro somma? Esercizio Determinare i valori di k R per i quali la unzione R k R, k (x) =x + k x è invertibile. Tracciare un raico di k e quando esiste di ( k ) 1. 14
Funzioni Esercizi e complementi
 Funzioni Esercizi e complementi e-mail: maurosaita@tiscalinet.it Novembre 05. Indice Esercizi Insiemi ininiti 6 Suggerimenti e risposte 9 Esercizi. Scrivere la deinizione di unzione e ornire almeno un
Funzioni Esercizi e complementi e-mail: maurosaita@tiscalinet.it Novembre 05. Indice Esercizi Insiemi ininiti 6 Suggerimenti e risposte 9 Esercizi. Scrivere la deinizione di unzione e ornire almeno un
Funzioni. Mauro Saita 22 ottobre 2011.
 Funzioni Mauro Saita e-mail: maurosaita@tiscalinet.it 22 ottobre 2011. Indice 1 Funzioni 1 1.1 Esercizi............................................ 4 1.2 Composizione di unzioni..................................
Funzioni Mauro Saita e-mail: maurosaita@tiscalinet.it 22 ottobre 2011. Indice 1 Funzioni 1 1.1 Esercizi............................................ 4 1.2 Composizione di unzioni..................................
Appunti di Matematica 5 - Funzioni - Funzioni. f : A B, con A e B insiemi non vuoti, è una legge x A uno e un solo elemento y B
 Funzioni Deinizione di unzione : una unzione che associa ad ogni elemento : A B, con A e B insiemi non vuoti, è una legge A uno e un solo elemento y B y = () y viene chiamato immagine di e indicato anche
Funzioni Deinizione di unzione : una unzione che associa ad ogni elemento : A B, con A e B insiemi non vuoti, è una legge A uno e un solo elemento y B y = () y viene chiamato immagine di e indicato anche
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI A. MARTINI Castelfranco Veneto (TV) Relazioni e Funzioni n n n n
 0 ottobre 008 A. MARTINI Castelranco Veneto (TV) Relazioni e Funzioni. Insieme delle parti. Partizione di un insieme 3. Prodotto cartesiano 4. Deinizione di relazione 5. Deinizione di unzione 6. Funzioni
0 ottobre 008 A. MARTINI Castelranco Veneto (TV) Relazioni e Funzioni. Insieme delle parti. Partizione di un insieme 3. Prodotto cartesiano 4. Deinizione di relazione 5. Deinizione di unzione 6. Funzioni
05 - Funzioni di una Variabile
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 05 - Funzioni di una Variabile Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 05 - Funzioni di una Variabile Anno Accademico 2015/2016
f : A B NOTAZIONE DELLE FUNZIONI x associa A D y è l immagine di x : y = f (x) (variabile dipendente)
 Funzioni Dati due insiemi non vuoti A e B, si chiama funzione da A a B una relazione tra i due insiemi che a ogni elemento di A fa corrispondere uno e un solo elemento di B. A B NOTAZIONE DELLE FUNZIONI
Funzioni Dati due insiemi non vuoti A e B, si chiama funzione da A a B una relazione tra i due insiemi che a ogni elemento di A fa corrispondere uno e un solo elemento di B. A B NOTAZIONE DELLE FUNZIONI
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale
 Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
CENNI SUL CONCETTO DI FUNZIONE
 CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Progetto Matematica in Rete - Funzioni - FUNZIONI. f : A B, con A e B insiemi non vuoti, è una legge x A uno e un solo elemento y B
 FUNZIONI Deinizione di unzione : una unzione che associa ad ogni elemento : A B, con A e B insiemi non vuoti, è una legge A uno e un solo elemento y B y () y viene chiamato immagine di e indicato anche
FUNZIONI Deinizione di unzione : una unzione che associa ad ogni elemento : A B, con A e B insiemi non vuoti, è una legge A uno e un solo elemento y B y () y viene chiamato immagine di e indicato anche
Lezione 15. Omomorfismi di anelli e loro proprietà.
 Lezione 15 Prerequisiti: Lezioni 3, 9, 14 Rierimenti ai testi: [FdG] Sezione 54; [H] Sezioni 33-34; [PC] Sezione 44 Ricordiamo la seguente Omomorismi di anelli e loro proprietà Deinizione 151 Dati due
Lezione 15 Prerequisiti: Lezioni 3, 9, 14 Rierimenti ai testi: [FdG] Sezione 54; [H] Sezioni 33-34; [PC] Sezione 44 Ricordiamo la seguente Omomorismi di anelli e loro proprietà Deinizione 151 Dati due
Corso di Analisi Matematica Funzioni di una variabile
 Corso di Analisi Matematica Funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 24 1 Generalità 2 Funzioni reali
Corso di Analisi Matematica Funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 24 1 Generalità 2 Funzioni reali
AL220 - Gruppi, Anelli e Campi
 AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
Verso il concetto di funzione
 Verso il concetto di funzione Il termine funzione già appare in alcuni scritti del matematico Leibniz (1646-1716). Tuttavia, in un primo momento tale termine venne usato in riferimento a espressioni analitiche
Verso il concetto di funzione Il termine funzione già appare in alcuni scritti del matematico Leibniz (1646-1716). Tuttavia, in un primo momento tale termine venne usato in riferimento a espressioni analitiche
FUNZIONI E INSIEMI DI DEFINIZIONE
 FUNZIONI E INSIEMI DI DEFINIZIONE In matematica, una funzione f da X in Y consiste in: ) un insieme X detto insieme di definizione I.d.D. (o dominio) di f 2) un insieme Y detto codominio di f 3) una legge
FUNZIONI E INSIEMI DI DEFINIZIONE In matematica, una funzione f da X in Y consiste in: ) un insieme X detto insieme di definizione I.d.D. (o dominio) di f 2) un insieme Y detto codominio di f 3) una legge
MATEMATICA. a.a. 2014/15. 1a. Funzioni (II parte):
 MATEMATICA a.a. 014/15 1a. Funzioni (II parte): Funzioni iniettive, suriettive, bigettive. Funzioni reali. Campo di esistenza. Funzioni pari e dispari Funzione iniettiva y=f() 1 3 X 4 y 6 Y y y 1 y 3 y
MATEMATICA a.a. 014/15 1a. Funzioni (II parte): Funzioni iniettive, suriettive, bigettive. Funzioni reali. Campo di esistenza. Funzioni pari e dispari Funzione iniettiva y=f() 1 3 X 4 y 6 Y y y 1 y 3 y
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
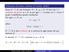 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Modello di un fenomeno
 Funzioni Modello di un fenomeno Un modello è una costruzione ideale basata su alcune caratteristiche essenziali del fenomeno, dette variabili. Un modello è ovviamente una approssimazione del fenomeno che
Funzioni Modello di un fenomeno Un modello è una costruzione ideale basata su alcune caratteristiche essenziali del fenomeno, dette variabili. Un modello è ovviamente una approssimazione del fenomeno che
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1 PROPRIETA' GENERALI DELLE FUNZIONI. FUNZIONE: Relazione tra due insiemi A e B che associa ad ogni elemento di A uno ed un solo elemento di B.
 PROPRIETA' GENERALI DELLE FUNZIONI FUNZIONE: Relazione tra due insiemi A e B che associa ad oni elemento di A uno ed un solo elemento di B. 6 C ; - - - -6 7 6 Funzione iniettiva. Una unzione - elemento
PROPRIETA' GENERALI DELLE FUNZIONI FUNZIONE: Relazione tra due insiemi A e B che associa ad oni elemento di A uno ed un solo elemento di B. 6 C ; - - - -6 7 6 Funzione iniettiva. Una unzione - elemento
Coordinate cartesiane nel piano
 Coordinate cartesiane nel piano O = (0, 0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate cartesiane nel piano O = (0, 0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Funzioni e grafici. prof. Andres Manzini
 Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione Definizione Si dice funzione (o applicazione)
Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione Definizione Si dice funzione (o applicazione)
Data le funzioni e con, e tre generici insiemi, non. x A X. , a sua volta a questo elemento corrisponde, tramite la funzione, l elemento
 Funzione composta Chiariamo prima di tutto il concetto di unzione composta: Data le unzioni e con, e tre generici insiemi, non necessariamente numerici, si ha che tramite ad ogni (x) Y l elemento : A X
Funzione composta Chiariamo prima di tutto il concetto di unzione composta: Data le unzioni e con, e tre generici insiemi, non necessariamente numerici, si ha che tramite ad ogni (x) Y l elemento : A X
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
ELEMENTI di TEORIA degli INSIEMI
 ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
ELEMENTI di TEORI degli INSIEMI & 1. Nozioni fondamentali. ssumeremo come primitivi il concetto di insieme e di elementi di un insieme. Nel seguito gli insiemi saranno indicati con lettere maiuscole (,,C,...)
FUNZIONI ELEMENTARI Funzione retta
 1 FUNZIONI ELEMENTARI Funzione retta L equazione generale della funzione retta è y = a x + b dove a, b sono numeri reali fissati. Il termine b si chiama termine noto e dà l ordinata dell intersezione tra
1 FUNZIONI ELEMENTARI Funzione retta L equazione generale della funzione retta è y = a x + b dove a, b sono numeri reali fissati. Il termine b si chiama termine noto e dà l ordinata dell intersezione tra
Metodo delle coordinate. Rette nel piano. Mauro Saita. Versione provvisoria. Novembre 2015.
 . Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
. Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
03 - Le funzioni reali di variabile reale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale ppunti del corso di Matematica 03 - Le funzioni reali di variabile reale nno ccademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale ppunti del corso di Matematica 03 - Le funzioni reali di variabile reale nno ccademico 2013/2014
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
.y 6. .y 4. .y 5. .y 2.y 3 B C C B. B f A B f -1
 Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. A x 1. x. x 3..y 1.y.y 3 B C.y 5 x 4..y
Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. A x 1. x. x 3..y 1.y.y 3 B C.y 5 x 4..y
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019. Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
5. Concetto di funzione. Dominio e codominio.
 5. Concetto di unzione. Dominio e codominio. Intro (concetto intuitivo) Che cosa e una unzione? Esempi di unzioni? Concetto di unzione Il concetto di unzione è legato all esistenza di una relazione tra
5. Concetto di unzione. Dominio e codominio. Intro (concetto intuitivo) Che cosa e una unzione? Esempi di unzioni? Concetto di unzione Il concetto di unzione è legato all esistenza di una relazione tra
ESERCITAZIONE 7 : FUNZIONI
 ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
Matematica. Funzioni. Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica
 Matematica Funzioni Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica Le Funzioni e loro caratteristiche Introduzione L analisi di diversi fenomeni della natura o la risoluzione di problemi
Matematica Funzioni Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica Le Funzioni e loro caratteristiche Introduzione L analisi di diversi fenomeni della natura o la risoluzione di problemi
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Indice. NUMERI REALI Mauro Saita Versione provvisoria. Ottobre 2017.
 NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
PREMESSE DELL ANALISI INFINETISIMALE
 PREMESSE DELL ANALISI INFINETISIMALE LE PREMESSE DELL ANALISI INFINETISIMALE Insiemi numerici e insiemi di punti Un insieme i cui elementi sono numeri reali è chiamato insieme numerico. Detto R l insieme
PREMESSE DELL ANALISI INFINETISIMALE LE PREMESSE DELL ANALISI INFINETISIMALE Insiemi numerici e insiemi di punti Un insieme i cui elementi sono numeri reali è chiamato insieme numerico. Detto R l insieme
2. I numeri reali e le funzioni di variabile reale
 . I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
. I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
Def. L unico elemento y Y associato ad un elemento x domf si dice immagine. di x attraverso f e si scrive y = f(x) (oppure f : x y = f(x)).
 FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
Richiami sugli insiemi numerici
 Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Definizione: Dato un sottoinsieme non vuoti di. Si chiama funzione identica o identità di in sé la funzione tale che.
 Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x. (ad un numero reale associo. il suo inverso). 2 2/3... e... 0.
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
Teoria degli Insiemi
 Teoria degli Insiemi Docente: Francesca Benanti Ottobre 2017 1 Teoria degli Insiemi La Teoria degli Insiemi è una branca della matematica creata alla fine del diciannovesimo secolo principalmente dal matematico
Teoria degli Insiemi Docente: Francesca Benanti Ottobre 2017 1 Teoria degli Insiemi La Teoria degli Insiemi è una branca della matematica creata alla fine del diciannovesimo secolo principalmente dal matematico
Teoria degli Insiemi
 Teoria degli Insiemi Docente: Francesca Benanti Ottobre 2015 1 Teoria degli Insiemi La Teoria degli Insiemi è una branca della matematica creata alla fine del diciannovesimo secolo principalmente dal matematico
Teoria degli Insiemi Docente: Francesca Benanti Ottobre 2015 1 Teoria degli Insiemi La Teoria degli Insiemi è una branca della matematica creata alla fine del diciannovesimo secolo principalmente dal matematico
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 31 index Proprietà elementari dei
Istituzioni di Matematiche seconda parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 31 index Proprietà elementari dei
Mauro Saita Gennaio Equazioni cartesiane di rette e equazioni parametriche di piani Esempi...
 ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
Esame di Stato di Liceo Scientifico Corso di Ordinamento. Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 2009.
 Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 9 Sommario Problema 3 Punto 3 Punto 3 Punto 3 5 Punto 4 6 Problema 7 Punto 7 Punto 7 Punto 3 8 Punto 4 8 Questionario
Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 9 Sommario Problema 3 Punto 3 Punto 3 Punto 3 5 Punto 4 6 Problema 7 Punto 7 Punto 7 Punto 3 8 Punto 4 8 Questionario
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Domande Vero/Falso (prima parte) 1. (a) Un numero complesso diverso da zero è invertibile. (b) Una successione illimitata superiormente
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Domande Vero/Falso (prima parte) 1. (a) Un numero complesso diverso da zero è invertibile. (b) Una successione illimitata superiormente
Generalità sulle funzioni
 Pagina 1 Generalità sulle funzioni Definizione: Dati due insiemi A e B, si definisce funzione una relazione che associa ad ogni elemento di A uno e un solo elemento di B. Osservazione: Dalla definizione
Pagina 1 Generalità sulle funzioni Definizione: Dati due insiemi A e B, si definisce funzione una relazione che associa ad ogni elemento di A uno e un solo elemento di B. Osservazione: Dalla definizione
Esempi di funzione...
 Funzioni Dati due insiemi non vuoti A e B, si chiama applicazione o funzione da A a B una relazione tra i due insiemi che a ogni elemento di A fa corrispondere uno e un solo elemento di B. A B Esempi di
Funzioni Dati due insiemi non vuoti A e B, si chiama applicazione o funzione da A a B una relazione tra i due insiemi che a ogni elemento di A fa corrispondere uno e un solo elemento di B. A B Esempi di
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
FUNZIONI E LORO PROPRIETÀ. V CLASSICO a. s. 2015-2016 prof. ssadelfino M. G.
 FUNZIONI E LORO PROPRIETÀ 1 V CLASSICO a. s. 2015-2016 prof. ssadelfino M. G. A1 DEFINIZIONE DI FUNZIONE 2 Diapositiva 2 A1 Autore; 08/09/2015 DEFINIZIONE DI FUNZIONE X Y E una funzione! g a b c d e f.1.2.3.4
FUNZIONI E LORO PROPRIETÀ 1 V CLASSICO a. s. 2015-2016 prof. ssadelfino M. G. A1 DEFINIZIONE DI FUNZIONE 2 Diapositiva 2 A1 Autore; 08/09/2015 DEFINIZIONE DI FUNZIONE X Y E una funzione! g a b c d e f.1.2.3.4
Esercizi svolti. g(x) = sono una l inversa dell altra. Utilizzare la rappresentazione grafica di f e f 1 per risolvere l equazione f(x) = g(x).
 Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Proprietà delle funzioni. M.Simonetta Bernabei, Horst Thaler
 Proprietà delle funzioni M.Simonetta Bernabei, Horst Thaler Funzioni crescenti e decrescenti Una funzione f è crescente (non decrescente) in un intervallo I se f ( 1 ) < f ( ) (f ( 1 ) f ( )), quando 1
Proprietà delle funzioni M.Simonetta Bernabei, Horst Thaler Funzioni crescenti e decrescenti Una funzione f è crescente (non decrescente) in un intervallo I se f ( 1 ) < f ( ) (f ( 1 ) f ( )), quando 1
FUNZIONI TRA INSIEMI. Indice
 FUNZIONI TRA INSIEMI LORENZO BRASCO Indice. Definizioni e risultati.. Introduzione.. Iniettività e suriettività.3. Composizione di funzioni 4.4. Funzioni inverse 5. Esercizi 5.. Esercizi svolti 5.. Altri
FUNZIONI TRA INSIEMI LORENZO BRASCO Indice. Definizioni e risultati.. Introduzione.. Iniettività e suriettività.3. Composizione di funzioni 4.4. Funzioni inverse 5. Esercizi 5.. Esercizi svolti 5.. Altri
Proprietà delle funzioni. M.Simonetta Bernabei & Horst Thaler
 Proprietà delle funzioni M.Simonetta Bernabei & Horst Thaler Funzioni crescenti e decrescenti Una funzione f è crescente in (a, b) se f ( 1 ) f ( ) quando 1
Proprietà delle funzioni M.Simonetta Bernabei & Horst Thaler Funzioni crescenti e decrescenti Una funzione f è crescente in (a, b) se f ( 1 ) f ( ) quando 1
Lo studio delle trasformazioni del piano in sé presuppone anche la conoscenza di alcune
 Capitolo 1 Richiami sulle funzioni 1.1 Richiami di teoria Lo studio delle trasformazioni del piano in sé presuppone anche la conoscenza di alcune nozioni sulle funzioni e sui vettori. Per tale motivo in
Capitolo 1 Richiami sulle funzioni 1.1 Richiami di teoria Lo studio delle trasformazioni del piano in sé presuppone anche la conoscenza di alcune nozioni sulle funzioni e sui vettori. Per tale motivo in
Funzioni (parte II).
 Funzioni (parte II). Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 21 ottobre 214 Paola Mannucci e Alvise Sommariva Introduzione. 1/ 55 Funzioni trigonometriche.
Funzioni (parte II). Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 21 ottobre 214 Paola Mannucci e Alvise Sommariva Introduzione. 1/ 55 Funzioni trigonometriche.
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1
 Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
Funzione Composta. Il campo di esistenza della funzione composta è costituito dai soli valori di x per i quali la composizione funzionale ha senso.
 Funzione Composta Date due funzioni g : A B e f : B C si può definire la funzione composta: f g : A C g() f(g()) notazione funzionale (f g)() = f(g()) La composizione ha senso se il valore g() appartiene
Funzione Composta Date due funzioni g : A B e f : B C si può definire la funzione composta: f g : A C g() f(g()) notazione funzionale (f g)() = f(g()) La composizione ha senso se il valore g() appartiene
Funzioni reali di variabile reale
 Funzioni reali di variabile reale Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni reali di variabile reale 1 / 50 Funzioni Definizione Sia A un sottoinsieme di R.
Funzioni reali di variabile reale Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni reali di variabile reale 1 / 50 Funzioni Definizione Sia A un sottoinsieme di R.
Analisi Matematica. Alcune funzioni elementari
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Liceo Classico Statale Vittorio Emanuele II Matematica in analisi
 Liceo Classico Statale Vittorio Emanuele II Matematica in analisi Le funzioni Definizione di funzione Dati due insiemi A e B, si definisce funzione una relazione che associa ad ogni elemento di A uno e
Liceo Classico Statale Vittorio Emanuele II Matematica in analisi Le funzioni Definizione di funzione Dati due insiemi A e B, si definisce funzione una relazione che associa ad ogni elemento di A uno e
Compito di matematica Classe III ASA 14 maggio 2015
 Compito di matematica Classe III ASA 14 maggio 015 1. Data la funzione y = f(x) rappresentata sul piano cartesiano dal grafico sottostante: a) determinare l espressione analitica di f(x) b) disegnare (su
Compito di matematica Classe III ASA 14 maggio 015 1. Data la funzione y = f(x) rappresentata sul piano cartesiano dal grafico sottostante: a) determinare l espressione analitica di f(x) b) disegnare (su
LE FUNZIONI CLASSE III D
 LE FUNZIONI CLASSE III D GENERALITÀ SULLE FUNZIONI Definizione: Dati due insiemi A e B, si definisce funzione una relazione che associa a ogni elemento di A uno e un solo elemento di B. Osservazione: Dalla
LE FUNZIONI CLASSE III D GENERALITÀ SULLE FUNZIONI Definizione: Dati due insiemi A e B, si definisce funzione una relazione che associa a ogni elemento di A uno e un solo elemento di B. Osservazione: Dalla
Esercizi di Geometria 1 - Foglio 1
 Esercizi di Geometria 1 - Foglio 1 Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso 22 dicembre 2017 Esercizio 1. Sia V uno spazio vettoriale sul
Esercizi di Geometria 1 - Foglio 1 Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso 22 dicembre 2017 Esercizio 1. Sia V uno spazio vettoriale sul
METODI MATEMATICI PER L INFORMATICA. Canale E O a.a Docente: C. Malvenuto Primo compito di esonero 26 novembre 2008
 METODI MATEMATICI PER L INFORMATICA Canale E O a.a. 2008 09 Docente: C. Malvenuto Primo compito di esonero 26 novembre 2008 Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio
METODI MATEMATICI PER L INFORMATICA Canale E O a.a. 2008 09 Docente: C. Malvenuto Primo compito di esonero 26 novembre 2008 Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio
1 Funzioni reali di una variabile reale
 1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
Indice degli argomenti
 Indice degli argomenti 1 Teoria degli insiemi 2 Numeri 3 Calcolo combinatorio 4 Approssimazioni, propagazione degli errori, percentuali 5 Funzioni reali 6 Funzioni lineari 7 Programmazione lineare 8 Funzioni
Indice degli argomenti 1 Teoria degli insiemi 2 Numeri 3 Calcolo combinatorio 4 Approssimazioni, propagazione degli errori, percentuali 5 Funzioni reali 6 Funzioni lineari 7 Programmazione lineare 8 Funzioni
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA INSIEMI
 M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA INSIEMI Assumiamo come primitivo il concetto di insieme e quello di appartenenza di un elemento a un insieme. La notazione x A indica
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA INSIEMI Assumiamo come primitivo il concetto di insieme e quello di appartenenza di un elemento a un insieme. La notazione x A indica
Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 4//206 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti.. Sia data la funzione
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 4//206 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti.. Sia data la funzione
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI A. MARTINI Castelfranco Veneto (TV) 25 novembre 2008 III A mercurio Docente: Daniele De Pieri
 A. MARTINI Castelranco Veneto (TV) novembre 8 III A mercurio Sia ( ) la unzione rappresentata in Fiura N. ) Risolvi la disequazione ( ) > ) Risolvi la disequazione < ) Risolvi la disequazione > 4) Risolvi
A. MARTINI Castelranco Veneto (TV) novembre 8 III A mercurio Sia ( ) la unzione rappresentata in Fiura N. ) Risolvi la disequazione ( ) > ) Risolvi la disequazione < ) Risolvi la disequazione > 4) Risolvi
Capitolo 3. Le funzioni elementari
 Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
FUNZIONI ELEMENTARI E LORO TRASFORMAZIONI. 4 Liceo Scientifico a.s. 2017/18
 FUNZIONI ELEMENTARI E LORO TRASFORMAZIONI 4 Liceo Scientifico a.s. 2017/18 FUNZIONI ELEMENTARI E LORO TRASFORMAZIONI Presentiamo il grafico delle funzioni elementari e delle funzioni che si ottengono trasformando
FUNZIONI ELEMENTARI E LORO TRASFORMAZIONI 4 Liceo Scientifico a.s. 2017/18 FUNZIONI ELEMENTARI E LORO TRASFORMAZIONI Presentiamo il grafico delle funzioni elementari e delle funzioni che si ottengono trasformando
Matematica ed statistica Corso di Laurea in Biotecnologie - anno acc. 2014/2015
 Matematica ed statistica Corso di Laurea in Biotecnologie - anno acc. 014/015 Esercizi sulle funzioni Esercizio 1. Determinare il dominio delle seguenti funzioni: + ; : + ; : + 1 ; : 1 ; : [, + [ 1 ; :
Matematica ed statistica Corso di Laurea in Biotecnologie - anno acc. 014/015 Esercizi sulle funzioni Esercizio 1. Determinare il dominio delle seguenti funzioni: + ; : + ; : + 1 ; : 1 ; : [, + [ 1 ; :
Analisi Matematica 1
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
Relazioni e Principio di Induzione
 Relazioni e Principio di Induzione Giovanna Carnovale October 12, 2011 1 Relazioni Dato un insieme S, un sottoinsieme fissato R del prodotto cartesiano S S definisce una relazione ρ tra gli elementi di
Relazioni e Principio di Induzione Giovanna Carnovale October 12, 2011 1 Relazioni Dato un insieme S, un sottoinsieme fissato R del prodotto cartesiano S S definisce una relazione ρ tra gli elementi di
Lezione Settembre ore (Il concetto di funzione)
 Laurea in Scienze e Tecnologie Biomolecolari, anno accademico 2014/15 Corso di Matematica e Statistica I Lezione 2. 17 Settembre 2014 2 ore (Il concetto di funzione) Il concetto di funzione Dati gli insiemi
Laurea in Scienze e Tecnologie Biomolecolari, anno accademico 2014/15 Corso di Matematica e Statistica I Lezione 2. 17 Settembre 2014 2 ore (Il concetto di funzione) Il concetto di funzione Dati gli insiemi
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Insiemistica, logica, principio di induzione ed altro
 Insiemistica, logica, principio di induzione ed altro. Data l operazione logica p q definita da (p q), scriverne la tabella di verità. Dimostrare poi che le espressioni p, p q, p q, p = q, p q possono
Insiemistica, logica, principio di induzione ed altro. Data l operazione logica p q definita da (p q), scriverne la tabella di verità. Dimostrare poi che le espressioni p, p q, p q, p = q, p q possono
4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].
![4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1]. 4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].](/thumbs/96/128120172.jpg) Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Prova scritta di Matematica Discreta del 15/2/2005
 Prova scritta di Matematica Discreta del 15/2/2005 1. a. Quante parole di 6 lettere si possono formare con un alfabeto contenente 25 lettere? b. Quante se sono proibite le doppie (ossia lettere uguali
Prova scritta di Matematica Discreta del 15/2/2005 1. a. Quante parole di 6 lettere si possono formare con un alfabeto contenente 25 lettere? b. Quante se sono proibite le doppie (ossia lettere uguali
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti
 FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
Funzioni: definizioni e tipi. Prof.ssa Maddalena Dominijanni
 Funzioni: definizioni e tipi Definizione di funzione Dati due insiemi non vuoti A e B, si dice funzione o applicazione da A a B una relazione che associa ad ogni elemento dell insieme A uno ed un solo
Funzioni: definizioni e tipi Definizione di funzione Dati due insiemi non vuoti A e B, si dice funzione o applicazione da A a B una relazione che associa ad ogni elemento dell insieme A uno ed un solo
Nozioni introduttive e notazioni
 Capitolo 1 Nozioni introduttive e notazioni 1.1 Gli insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Non daremo qui una definizione
Capitolo 1 Nozioni introduttive e notazioni 1.1 Gli insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Non daremo qui una definizione
FUNZIONI REALI DI UNA VARIABILE REALE
 FUNZIONI REALI DI UNA VARIABILE REALE Vogliamo ora limitare la nostra attenzione a quelle funzioni che hanno come insieme di partenza e di arrivo un sottoinsieme dei numeri reali, cioè A, B R. Es6. Funzione
FUNZIONI REALI DI UNA VARIABILE REALE Vogliamo ora limitare la nostra attenzione a quelle funzioni che hanno come insieme di partenza e di arrivo un sottoinsieme dei numeri reali, cioè A, B R. Es6. Funzione
3. Generalità sulle funzioni
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 3. Generalità sulle funzioni A. A. 2013-2014 1 DALLA RETTA REALE AL PIANO CARTESIANO L equivalenza tra numeri reali e punti di una retta permette
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 3. Generalità sulle funzioni A. A. 2013-2014 1 DALLA RETTA REALE AL PIANO CARTESIANO L equivalenza tra numeri reali e punti di una retta permette
Analisi Matematica per Bio-Informatici Esercitazione 03 a.a
 Analisi Matematica per Bio-Informatici Esercitazione a.a. 7-8 Dott. Simone Zuccher 6 Novembre 7 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sci.univr.it).
Analisi Matematica per Bio-Informatici Esercitazione a.a. 7-8 Dott. Simone Zuccher 6 Novembre 7 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sci.univr.it).
Funzioni funzione univocità relazione univoca variabile dipendente variabile indipendente primo insieme secondo insieme
 Funzioni Chiamiamo unzione un insieme di coppie ordinate che goda della seguente proprietà: non possono appartenere alla stessa unzione due coppie ordinate che abbiano lo stesso primo elemento e diversi
Funzioni Chiamiamo unzione un insieme di coppie ordinate che goda della seguente proprietà: non possono appartenere alla stessa unzione due coppie ordinate che abbiano lo stesso primo elemento e diversi
1. FUNZIONI IN UNA VARIABILE
 1. FUNZIONI IN UNA VARIABILE Definizione: Dati due insiemi A, B chiamiamo funzione da A in B ogni, f, applicazione (legge, corrispondenza) che associa ad ogni elemento di A uno ed uno solo elemento di
1. FUNZIONI IN UNA VARIABILE Definizione: Dati due insiemi A, B chiamiamo funzione da A in B ogni, f, applicazione (legge, corrispondenza) che associa ad ogni elemento di A uno ed uno solo elemento di
1 Funzioni derivabili. Esercizi
 Politecnico di Milano. Scuola di Ingegneria Industriale. Corso di Analisi e Geometria 1 (Docente: Federico Lastaria) Settembre 2012 1 Funzioni derivabili. Esercizi Ricordiamo alcune deinizioni. Deinizione
Politecnico di Milano. Scuola di Ingegneria Industriale. Corso di Analisi e Geometria 1 (Docente: Federico Lastaria) Settembre 2012 1 Funzioni derivabili. Esercizi Ricordiamo alcune deinizioni. Deinizione
