1. Serie Numeriche. 1.1 Serie Numeriche nel campo reale. Definizione 1.1 Data una successione {a n } R costruiamo un altra successione {s n } ponendo
|
|
|
- Romolo Battaglia
- 4 anni fa
- Visualizzazioni
Transcript
1 . Serie Numeriche. Serie Numeriche el campo reale Defiizioe. Data ua successioe {a } R costruiamo u altra successioe {s } poedo s j a j. La coppia ordiata {a }, {s }) si dice serie umerica di termie geerale {a }. Se la successioe - che chiameremo successioe delle somme parziali - {s } è regolare idicheremo co il simbolo a il suo limite che si chiamerà somma della serie. Esempio. Serie di Mègoli Studiamo la serie +). Per calcolare s otiamo che pp + ) p p +, p R, p 0, p e quidi s j j ) ) + j ) ) + +. La serie è regolare ed ha per somma. Esempio.2 Serie armoica Studiamo la serie. Proviamo che la serie è divergete a +. Notiamo che, essedo a > 0, la successioe s, quidi la serie, è regolare. Sarà allora sufficiete provare che ua estratta di s è divergete. Si ha: s ) ) ) ) Esempio.3 La serie geometrica 0 q co q R. Se q si ha s +. Sia perciò q. Ricordado la formula per la somma dei termii di ua progressioe geometrica abbiamo, s q q da cui si deduce facilmete il comportameto della serie. Precisamete si trova che la serie coverge se e solo se q < ed i tal caso la sua somma è q. Esempio.4 Studiamo la serie log + ).
2 La serie diverge positivamete. Ifatti, s log + j ) j j logj + ) log j) log + ) +. Notiamo che per determiare il carattere della serie abbiamo proceduto per via diretta. Cioè abbiamo espresso i forma chiusa il termie geerale della successioe delle somme parziali. I geerale, u tale procedimeto è da scosigliare per le difficoltà di carattere algebrico. Cerchiamo quidi delle codizioi dalle quali dedurre il carattere della serie seza essere costretti a maipolare la successioe s. Defiizioe.2 Serie resto). Data ua serie umerica a e u umero k N, diciamo serie resto di ordie k la serie otteuta da qualla data cacellado i primi k termii ovvero la serie k+ a. Teorema. Ua serie ed u suo qualsiasi resto hao lo stesso carattere. Dim. Si ha: s a + + a k + a j s k + jk+ jk+ a j Teorema.2 La successioe dei resti di ua serie covergete è ifiitesima. Dim. Usado le otazioi del teorema precedete abbiamo: R k jk+ a j lim jk+ a j lim s s k s s k da cui lim k R k lim k s s k 0. Teorema.3 Si ha: λa λ a λ 0; a + b ) a + b. trae il caso i cui si preseti la forma +. 2
3 Apputi di Aalisi Matematica I Dim. Basta passare al limite elle eguagliaze λa j λ a j, a j + b j ) a j + j j j j j b j Teorema.4 Codizioe ecessaria e sufficiete affichè la serie a sia covergete è che +p ε > 0 ν N : > ν p N a j < ε. j+ Dim. Basta applicare il criterio di covergeza per le successioi alla successioe s. Corollario. Codizioe ecessaria affichè la serie a risulti covergete è che a 0. Dim. Basta applicare il criterio precedete co p. La codizioe o è sufficiete per la covergeza. Basti pesare alla serie armoica. Ua classe particolare di serie è costituita dalle serie a termii di sego costate. La caratteristica di queste serie è di avere la successioe delle somme parziali mootoa cosicchè tali serie risultao sempre regolari. Teorema.5 cofroto) Siao a, b due serie tali che: 0 a b N. Allora:. b R a R ed i tal caso a b ; 2. a + b + Dim. Dall ipotesi si ha: a j j b j j e ricordado che le somme parziali di ciascua delle due serie soo mootoe segue la. Similmete si prova la 2. b Teorema.6 Sia a ua serie umerica covergete a termii positivi. Sia {k } ua successioe crescete di iteri e sia b a k. Allora b coverge e si ha: b a. Dim. Si ha: b j da cui la tesi per mootoia. j j a kj k a j j j a j N 3
4 Corollario.2 Siao a, b due serie a termii positivi che cotegao gli stessi termii. Allora si ha: a b. Dim. Basta applicare due volte il teorema precedete. Studiamo adesso alcue codizioi sufficieti per la covergeza delle serie a termii positivi. Teorema.7 del rapporto) Sia a ua serie a termii positivi. Suppoiamo che esistoo h [0, [ e ν N tali che a + h > ν. a Allora la serie coverge. Dim. Dall ipotesi si ha: e quidi la tesi dal teorema di cofroto. a ν+k+ ha ν+k h 2 a ν+k h k a ν+ Teorema.8 Sia a ua serie a termii positivi. Suppoiamo che esiste ν N tale che Allora la serie diverge. a + a > ν. Dim. La successioe a è mootoa crescete e quidi o può tedere a zero. Viee violata la codizioe ecessaria di covergeza. Corollario.3 criterio del rapporto) Sia a ua serie a termii positivi. Suppoiamo che a esiste lim + a l R. Allora:. Se l > la serie diverge; 2. Se l < la serie coverge; 3. Se l ulla può dirsi. La dimostrazioe è ua ovvia cosegueza del teorema precedete e del teorema della permaeza del sego. Co riferimeto al caso 3. otiamo che la serie armoica e la serie di Megoli si trovao etrambe al caso 3. ma hao carattere diverso. 4
5 Apputi di Aalisi Matematica I Teorema.9 della radice) Sia a ua serie a termii positivi. Suppoiamo che esistoo h [0, [ e ν N tali che a h > ν. Allora la serie coverge. Dim. Si ha: a h e la tesi è immediata per cofroto. Teorema.0 della radice) Sia a ua serie a termii positivi. Suppoiamo che esiste ν N tale che a > ν. Allora la serie diverge. Dim. Si ha: a e la tesi segue dalla codizioe ecessaria di covergeza. Corollario.4 criterio della radice) Sia a ua serie a termii positivi. Suppoiamo che esiste lim a Allora:. Se l > la serie diverge; 2. Se l < la serie coverge; 3. Se l ulla può dirsi. Teorema. Raabe) Sia a ua serie a termii positivi. Suppoiamo che esiste Allora:. Se l > la serie coverge; 2. Se l < la serie diverge; 3. Se l ulla può dirsi. lim ) a a + l R. Attraverso i criteri del rapporto e della radice si possoo studiare le serie il cui termie geerale preseta u tasso di decadimeto più che poliomiale. Falliscoo etrambi, ad esempio, per la serie armoica geeralizzata) α > 0. Talvolta risulta utile il criterio di Raabe. Comuque α proviamo il seguete risultato dovuto a Cauchy. 5
6 Teorema.2 di codesazioe) Sia a ua serie a termii positivi tale che 0 a + a N. Allora le serie a e 0 2 a 2 hao lo stesso carattere. Dim. Si ha: σ 2 k a 2 k a + 2 {a 2 + a 3 + a 4 ) + a a 8 ) + + a a 2 )} ovvero D altra parte a + 2s 2 a ) a + 2s 2 s s 2 2 k σ a + 2s 2 N. a k a + a 2 + a 3 ) + a 4 + a a 7 ) + + a a 2 ) a + 2a a a 2 σ e la tesi segue applicado due volte il teorema di cofroto. Usado il teorema di codesazioe è possibile studiare la serie armoica geeralizzata. Esempio.5 Studiamo la serie α α > 0. Applicado il teorema di codesazioe, è sufficiete cooscere il carattere della serie 2 α ) α > 0 0 che è ovviamete oto i quato serie geometrica. Pertato la serie armoica geeralizzata coverge se e solo se α >. Dal teorema di cofroto segue immediatamete il Teorema.3 del cofroto asitotico) Siao a e b due serie a termii positivi. a Se lim b l > 0 allora le due serie hao lo stesso carattere. Osservazioe. Il teorema si può riformulare el modo seguete: Se a o), e b o) e a l b + o) allora le due serie hao lo stesso carattere. Adesso, per mostrare l utilità dei vari criteri di covergeza, studiamo alcue serie umeriche. Esempio.6 se +. Ifatti, se + o ). 6
7 Apputi di Aalisi Matematica I Esempio.7 log ) + ha lo stesso carattere della serie armoica geeralizzata. α Ifatti, log + ) α ) α + o α. Esempio.8 se2 2 coverge. Ifatti, se o 4 ). Esempio coverge Ifatti, ) o 2. Esempio.0 log k, k N, α > 0 ha lo stesso carattere della serie armoica geeralizzata. α Ifatti, applicado il teorema di codesazioe, la serie data ha lo stesso carattere della serie k 2 α ) la quale risulta covergete per α > e divergete se α idipedetemete dal valore di k. Notiamo icidetalmete che, come cosegueza della covergeza della serie si ha: log k lim α 0. Esempio e x2 ) ; È ua serie geometrica di ragioe e x2 ) e quidi coverge se e solo se il modulo della ragioe è miore di ovvero, per x > log 2. Esempio.2 2 ) ; La serie diverge. Ifatti, aplicado il criterio del rapporto si trova + ) +) ) ) + ) + ) 2)! + )!) 2!) )! + ) + ) )2 + 2) +. Esempio.3!) 2 ; La serie coverge. Applicado il criterio del rapporto si ha: + ) + + )!) 2!)2 0. 7
8 Esempio.4! ; La serie coverge. Applicado il criterio del rapporto si ha: ) + )! + ) +)! + e <. Esempio ; Ifatti, ragioado come el caso della serie di Mègoli si ha: ), N 2 + e quidi s 2 ) 2 2. Esempio ) ; La serie coverge. Ifatti, applicado il criterio della radice si ha: 3 + ) e 3 <. Esempio.7 0 log 2 x log x ), x > 0; La serie è geometrica di ragioe q log 2 x log x) e quidi coverge se e solo se q < ovvero per x < e 5 2. Esempio.8 )) log 2 + x ; Posto q log x), applicado il criterio del rapporto si ha che la serie coverge se q <. Esempio.9 x2! + arctag ) ; Usado il criterio del cofroto asitotico si vede che la serie ha lo stesso carattere della serie. Quest ultima serie si studia poi co il criterio della radice trovado che coverge x R. x2! Esempio ) x 2 ; 2 Applichiamo il criterio del rapporto. ) ) ) x 2 2 x 2+2 +) ) x 2 x 2 e quidi la serie è covergete se e solo se x <. 8
9 Apputi di Aalisi Matematica I log ; Esempio.2 La serie coverge. Ifatti, log 2 2. Esempio.22 2 log! ; Cofrotiamo co la serie defiitivamete si ha: e quidi la serie data diverge. 2! log. Ifatti, ricordado che log log! 0 si deduce che, almeo Esempio.23 2 ; cofrota co α.).2 Serie a termii di sego o costate Prelimiarmete mostriamo la validità della seguete formula di sommazioe per parti. Lemma 2. Abel) Posto A a k, si ha: q q a b A q b q A p b p + A b b + ) p, q N 0, p q. Dim. p q a b p q q A A )b p p q A b p A b b + ) + A q b q A p b p. p q A b p q A b p q mp A m b m+ Servedoci del Lemma di Abel possiamo dimostrare il seguete teorema di Cauchy - Dirichlet. Teorema 2. Sia data la serie 0 a b. Suppoiamo che b b + 0 ed ioltre esista M : A j0 a j M N. Allora la serie 0 a b coverge. Dim. Proviamo che la serie coverge verificado il criterio di Cauchy. Ricordiamo che b 0 ovvero che ε > 0 ν N : > ν 0 < b < ε e quidi, se > ν, p N, si ha: +p a k b k A +pb +p A b + k +p k A k b k b k+ ) M b +p + b + +p k b k b k+ ) M b +p + b + b b + + b + b b +p b +p ) 2Mb < ε. ) 9
10 Teorema 2.2 Suppoiamo che la serie 0 a sia covergete. Sia ioltre b ua successioe mootoa e limitata. Allora la serie 0 a b è covergete. Dim. Suppoiamo, ad esempio, che la successioe b sia decrescete e chiamiamo l il suo limite. Applicado il teorema precedete si ha che la serie 0 a b l). Dal fatto che a b a b l) + a l la tesi si ottiee applicado il teorema precedete alla serie + 0 a b l). Come corollario si ha il seguete criterio di covergeza di Leibiz. Teorema 2.3 Sia data la serie 0 ) a tale che: 0 < a + < a, a 0. Allora la serie è covergete. Osservazioe 2. Nelle stesse ipotesi del teorema appea dimostrato si ha: s s Mb, N. Dim. Ifatti, + s s a j b j lim k j k a j b j j lim a b b + ) + a + a + )b + b +2 ) b k b k )a a k ) k +b k a a k ) Mb N. e, el caso del teorema di Leibiz la disuguagliaza prede la forma seguete s s b N. Defiizioe 2. La serie 0 a si dice Assolutamete covergete se la serie 0 a coverge. I geerale covergeza e covergeza assoluta o soo equivaleti. Ifatti, si ha: Teorema 2.4 Ua serie Assolutamete covergete è covergete. Dim. Applicado il criterio di covergeza di Cauchy si ha: +p j a j +p j a j < ε. 0
11 Apputi di Aalisi Matematica I Esempio 2. La serie ) è covergete ma o assolutamete covergete. Teorema 2.5 Sia a ua serie tale che a b + oc ) dove la serie b è covergete metre la serie c è assolutamete covergete. Allora la serie a risulta covergete. Dim. Per ipotesi si ha: a b oc ) e quidi a b ) è assolutamete covergete, quidi a a b ) + b coverge. Esempio 2.2 La serie è covergete. Ifatti, ) e! 0 N, θ ]0, [ :! e 2πe θ /2 e quidi ) e! ) θ )) 2π 2 + o ) ) ) θ 2π 2 2π + o 3/2 3/2 da cui quato affermato perché la serie ) è covergete per il teorema di Leibiz metre la serie ) θ 3/2 è assolutamete covergete..3 Proprietà associativa e commutativa Defiizioe 3. Sia data la serie a. Sia {k } ua successioe di iteri crescete. A partire dalla serie data possiamo costruire la successioe b k jk + a j e la serie b. Diciamo che la serie a gode della proprietà associativa se la serie b coverge per ogi scelta possibile della successioe {k } ed ioltre b a Esempio 3. La serie 0 ) o gode della proprietà associativa. Ifatti, + ) + ) + ) ) + ) + ) 0. 0 Teorema 3. Ogi serie regolare gode della proprietà associativa. Dim. Ifatti la successioe delle somme parziali della serie b è ua estratta della successioe delle somme parziali della serie a.
12 Defiizioe 3.2 Diciamo che la serie b è u riordiameto della serie a se esiste ua corrispodeza biuivoca j : N N tale che: b a j N. Defiizioe 3.3 Diciamo che la serie a gode della proprietà commutativa se ogi suo riordiameto è covergete e la somma di tutti i riordiameti è uguale alla somma della serie data. Teorema 3.2 Ogi serie assolutamete covergete gode della proprietà commutativa. Dim. Il teorema è stato già provato el caso delle serie a termii positivi. Sia a la serie i questioe. Poiamo a + max{a, 0}, a max{ a, 0}, e aalogamete, Si ha: b + max{b, 0}, b max{ b, 0}. 0 a + a ; 0 a a e quidi dall ipotesi segue che le serie a+, queste ultime a termii positivi possiamo dire che a soo etrambe covergeti. Essedo b + a + ; b a. Allora, per differeza, coverge ache il riordiameto e si ha: b b + b a + a a. che è la tesi. Teorema 3.3 Riema - Dii) Sia a ua serie covergete ma o assolutamete covergete. Allora assegati ad arbitrio α β, α, β R è possibile costruire u riordiameto della serie data tale che α, β siao rispettivamete massimo e miimo limite per la successioe delle somme parziali delle serie riordiata. Dim. Si ha: + 0 a a +. Siao {P j } e {Q j } rispettivamete i termii positivi ed i moduli dei termii egativi della serie data ello stesso ordie i cui si presetao i + 0 a. Naturalmete, + 0 P + 0 Q +. 2
13 Apputi di Aalisi Matematica I Adesso assegamo due successioi {α }, {β } tali che α α, β β. Sia m il miimo itero tale che P + P P m > β, e sia k il miimo itero tale che P + P P m Q + Q Q k ) < α I maiera simile si determiao i umeri m 2, k 2,..., m, k. Posto ifie x P + P P m Q + Q Q k ) + P m + + P m P m2 Q k + + Q k Q k2 ) P m + + P m P m y P + P P m Q + Q Q k ) + P m + + P m P m2 Q k + + Q k Q k2 ) P m + + P m P m Q k + + Q k Q k ) Sfruttado la miimalità dei umeri m, k si ha: { x β P m y α Q k e, passado al limite per, si ottiee la tesi..4 Serie Prodotto secodo Cauchy Defiizioe 4. Date due serie umeriche 0 a, 0 b chiamiamo serie prodotto secodo Cauchy - o prodotto di covoluzioe - la serie i cui il termie geerale è il prodotto delle rispettive somme parziali, ovvero ) a b a k b k I geerale la serie prodotto di sue serie covergeti o è covergete come mostra il seguete Esempio 4. La serie 0 ) ) o lo è. Il termie geerale della serie prodotto è: ) + è covergete per il teorema di Leibiz. Mostriamo che la serie ) k + ))k + ). 3
14 Per provare che la serie prodotto o coverge mostriamo che il valore assoluto del termie geerale o tede a zero. Ifatti, k + ))k + ) + ) +. D altra parte ci soo i segueti risultati: Teorema 4. Mertes) Se 0 a, 0 b soo due serie delle quali ua coverge e l altra assolutamete covergete allora la serie prodotto è covergete. Teorema 4.2 Se 0 a, assolutamete covergete. 0 b soo assolutamete covergeti allora la serie prodotto è Esempio 4.2 La costate di Eulero - Mascheroi Cosideriamo la serie log + ). Usado la formula di Taylor arrestata al secodo ordie si ha: e perciò la serie coverge. Ioltre log + )) o 2 ) o 2 s k k log k + H log k e quidi, chiamado γ la somma della serie, otteiamo che la ridotta della serie armoica diverge logaritmicamete. La costate γ si chiama costate di Eulero - Mascheroi. No è oto se si tratti o o di umero razioale. Possiamo studiare la serie Dal fatto che log lim lim H log ) lim H H log. H lim H log ) H. segue che la serie da studiare ha lo stesso carattere della serie vede facilmete attraverso il criterio di codesazioe. 2 log che è divergete e si 4
15 Apputi di Aalisi Matematica I Esempio 4.3 Studiamo la serie ) a dove Si ha: a + a + 2 ) + 3 2) + + k e quidi la serie data è k k k + ). ) k + + k ) H + ) H + ) A. Verifichiamo le ipotesi del teorema di Leibiz. Ricordado che H log γ segue A H + H log + log Verifichiamo adesso la decresceza di A. Co semplici calcoli si vede che la disuguagliaza A + < A è equivalete alla disuguagliaza H + ) > che è vera perché H >. La serie quidi coverge per il teorema di Leibiz. Ioltre la serie risulta assolutamete divergete perché lim H + log + H lim log 0. Esempio 4.4 Studiamo la serie se ) se ). La serie è a termii positivi. Applicado la formula di Taylor, si trova se ) 3 + o 3 quidi, da cui segue che la serie data è covergete..5 Ua osservazioe sui umeri reali se ) se ) ) o 2 5
16 Sia x 0 R, suppoiamo x 0 > 0 per fissare le idee. Poiamo C {0,,..., 9}. Come sappiamo esiste u uico umero C 0 N 0 tale che C 0 x 0 < C 0 +. Adesso cerchiamo C C tale che Portado a forma itera si trova che C 0 + C 0 x 0 < C 0 + C +. 0 x 0 0C 0 < C x 0 0C 0 e C è uico per le proprietà del umero parte itera. Abbiamo quidi Cerchiamo adesso C 2 C tale q C 0 + C 0 x 0 < C 0 + C q + 0. j0 q + C x 0 < q + C Procededo come prima si trova u uico umero co i requisiti richiesti. Cotiuado i questo modo abbiamo C j 0 j x C j 0 < 0 j + 0 N j0 da cui, passado al limite per si trova che x 0 0 C 0. I questo modo i umeri reali si possoo vedere come particolari serie umeriche. Ogi umero reale è somma di ua serie di umeri razioali, ovvero si rede cocreta l affermazioe Q R. Ioltre se si vuole costruire ua successioe di umeri razioali covergete al umero x 0 basta predere la successioe delle somme parziali della serie otteuta. I particolare, dalla serie si può spiegare la regola della frazioe geeratrice. Per esempio, vogliamo covertire i frazioe il umero 0, 3. Si ha: 0, Covertiamo i frazioe il umero 2, 34. Si ha: 2, , ) Serie a termii complessi 6
17 Apputi di Aalisi Matematica I Cocludiamo questo capitolo sulle serie umeriche co u breve ceo alle serie umeriche a termii complessi. Sia quidi {a } ua successioe a termii complessi. I modo simile a quato fatto el caso reale costruiamo la successioe delle somme parziali chiamiamo il suo limite - i C - somma della serie. Si poe duque s a lim 0 a k. È immediato il seguete Teorema 6. La serie 0 a coverge ed ha per somma il umero s se e solo se le due serie reali 0 Ra e 0 Ia soo covergeti rispettivamete a Rs, Is. I modo simile si da la ozioe di serie assolutamete covergete. Diciamo cioè ua serie assolutamete covergete quado coverge la serie dei moduli. Teorema 6.2 Ua serie assolutamete covergete è covergete e si ha: a 0 a. 0 Dim. Poichè Ra, Ia a si ha la covergeza della serie delle parti reali e della serie delle parti immagiarie da cui la covergeza della serie. Ioltre, dalle disuguagliaze j0 a j a j j0 a j N j0 e quidi, passado al limite j0 a j a j j0 Esempio 6. La serie geometrica Studiamo la serie 0 z, z C. La serie coverge assolutamete per z < e o coverge per z perchè il termie geerale o è ifiitesimo. Esempio 6.2 Studiamo la serie z, z C. La serie coverge assolutamete per z < e o coverge per z > perchè il termie geerale o è ifiitesimo. Studiamo la serie per z. Posto z e iθ, la serie da studiare diveta: eiθ. Applicado il criterio di Cauchy - Dirichlet si trova che la serie coverge qualuque sia θ 2kπ, k Z..7 L espoeziale complesso 7
18 Studiamo adesso ua delle fuzioi più importati di tutta la Matematica. La fuzioe espoeziale complessa. Defiizioe 7. La serie z! 0 è assolutamete covergete i C quidi poiamo per defiizioe e z 0 z! z C. Teorema 7. Si ha lim + z ) e z z C. Dim. Proviamo che ε > 0 ε N : > ε z k k! + z ) < ε da cui poi facilmete si deduce la tesi. Fissato z 0 C siao z C, m N : z < z 0 m. Applicado la formula di Newto, z k k! + z ) k2 k2 Per quato riguarda II abbiamo: II z k k! z k k! z m+ + z m + )! z m+ m + )! j0 ) z k k k! k)! k z k k! c, k) m k2 ) k2 z k k! z k k! c, k) + c, k) km+ z k c, k) I + II. k! m z 2 ) m + 2)m + 3) + + z m m + 2) ) j z z m+ m + 2 m + )! z m+2 z 0 m+ m + )! 0 se m. Possiamo quidi scegliere m i modo che II < ɛ 2. Per I si ha ivece: ferma restado la scelta fatta per m), II m k2 c, k) z k k! m k2 c, k) z 0 k k! se perchè, come facilmete si verifica per iduzioe su k, lim c, k)
19 Apputi di Aalisi Matematica I Teorema 7.2 Si ha:. e z+w e z e w, 2. e z e z 3. e z e Rz z, w C z C z C. Dim. Per provare la. utilizziamo il teorema pecedete ed il fatto che le serie soo tutte assolutamete covergeti. Si ha: e z+w z + w) ) z k w k!! k 0 0 z w e z e w.!! k! k)! zk w k Per provare la 2. basta passare al limite ell idetità: + z ) + z. ) Proviamo ifie la 3. da cui la tesi. e z 2 e z e z e z e z e 2Rz e Rz ) 2 Defiizioe 7.2 Poiamo cos t Re it se t Ie it ; t R. ovvero cos t eit + e it 2 se t eit e it ; t R. 2i Teorema 7.3 Per ogi t R si ha: se t ) t )! 0 cos t ) t2 2)!. 0 Dim. Ifatti, dalla defiizioe segue cos t eit + e it it) + it) 2! 0 ) 2)! t2 t R ı + )! t 9
20 Similmete, se t eit e it it) it) 2ı 2i! 2ı 0 ) 2 + )! t2+ t R. 0 ) ı t! 0 Osservazioe 7. Se t [0, [ la serie del seo soddisfa le ipotesi del teorema di Leibiz e quidi si ottiee, se t t. Teuto coto che, se t > la diseguagliaza è ovvia e della simmetria, si ottiee: se t t t R. Come ulteriore applicazioe del teorema di Leibiz, si trae ifie, t t3 3! se t t t [0, [. Procededo similmete co la serie del coseo si trova t2 2 cos t t [0, [ da cui, cos t t 2 2 t [0, [ Osservazioe 7.2 Notiamo che si ha: se t j0 ) j 2j + )! t2j+ + ot 2+ ), t 0, cos t j0 ) j 2j)! t2j + ot 2 ), t 0. Ifatti, per N, e t <, si ha: se t ) j 2j + )! t2j+ j0 + j+ + j+ ) j 2j + )! t2j+ Similmete si dimostra la formula per il coseo. 2j + )! t2j+ t j+ 2j + )! t2j ) ot 2+ ) 20
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Definizione 1. Data una successione (a n ) alla scrittura formale. 1) a 1 + a a n +, si dà il nome di serie.
 SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
SERIE NUMERICHE Defiizioe. Data ua successioe (a ) alla scrittura formale ) a + a 2 + + a +, si dà il ome di serie. I umeri a, a 2,, a, rappresetao i termii della serie, i particolare a è il termie geerale
4 - Le serie. a k = a k. S = k=1
 4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
Esercizi su serie numeriche - svolgimenti
 Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie numeriche. Esercizi
 Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Corso di Analisi Matematica 1 - professore Alberto Valli
 Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
Limiti di successioni
 Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
n 1 = n b) {( 1) n } = c) {n!} In questo caso la successione è definita per ricorrenza: a 0 = 1, a n = n a n 1 per ogni n 1.
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Successioni e limiti di successioni
 Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
2 Criteri di convergenza per serie a termini positivi
 Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Svolgimento degli esercizi del Capitolo 4
 4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
4 - Le serie Soluzioni. n + 3. n + 3. n + 2
 4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
1 Successioni numeriche
 Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
16 - Serie Numeriche
 Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Università degli Studi di Palermo Facoltà di Economia. Dip. di Scienze Statistiche e Matematiche Silvio Vianelli
 Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
Serie numeriche. Paola Rubbioni. 1 Denizione, serie notevoli e primi risultati. i=0 a i, e si indica con il simbolo +1X.
 Serie umeriche Paola Rubbioi Deizioe, serie otevoli e primi risultati Deizioe.. Data ua successioe di umeri reali (a ) 2N, si dice serie umerica la successioe delle somme parziali (S ) 2N, ove S = a +
Serie umeriche Paola Rubbioi Deizioe, serie otevoli e primi risultati Deizioe.. Data ua successioe di umeri reali (a ) 2N, si dice serie umerica la successioe delle somme parziali (S ) 2N, ove S = a +
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 AA Dott.ssa Sandra Lucente Successioni numeriche
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
Corso di laurea i Matematica Corso di Aalisi Matematica -2 AA. 0809.. Cooscere. Dott.ssa Sadra Lucete. Successioi umeriche Defiizioe di successioe, isieme degli elemeti della successioe, successioe defiita
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
9 LIMITI DI SUCCESSIONI NUMERICHE
 9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
Corso integrato di. Matematica. per le scienze naturali ed applicate. Materiale integrativo
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 3300 Udie,
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 3300 Udie,
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
Università di Trieste Facoltà d Ingegneria. Esercizi sulle serie numeriche e sulle successioni e serie di funzioni Dott.
 e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
CONFRONTO TRA SUCCESSIONI DIVERGENTI. (2) Sia a>1. Allora lim =+ per ogni β>0.
 Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
1. Converge. La serie è a segno alterno. Non possiamo usare il criterio di assoluta convergenza, perché
 Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE ANTONIO IANNIZZOTTO Sommario. Limiti di successioi e teoremi relativi. Successioi mootoe, itate, sottosuccessioi. Defiizioe di serie covergete, divergete, idetermiata. Serie
SUCCESSIONI E SERIE NUMERICHE ANTONIO IANNIZZOTTO Sommario. Limiti di successioi e teoremi relativi. Successioi mootoe, itate, sottosuccessioi. Defiizioe di serie covergete, divergete, idetermiata. Serie
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
n + 1 n + 2 = 1 n + 1 n n n Esercizio. Verificare il seguente limite a partire dalla definizione: n n 2 + n + 1 = 0 lim
 3.. Esercizio. Ricoosciuto che determiare i valori ε tali che ε : ANALISI Soluzioi del Foglio 3 + = + ε essedo ε ua prima volta e ua secoda 0.5 ε = 9 ottobre 009 + + disuguagliaza soddisfatta da ogi N,
3.. Esercizio. Ricoosciuto che determiare i valori ε tali che ε : ANALISI Soluzioi del Foglio 3 + = + ε essedo ε ua prima volta e ua secoda 0.5 ε = 9 ottobre 009 + + disuguagliaza soddisfatta da ogi N,
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Corso integrato di. Matematica. per le scienze naturali ed applicate. Materiale integrativo
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 3300 Udie,
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 06, 3300 Udie,
AM110 - ESERCITAZIONI XIII - XIV. (Per la dimostrazione discussa durante l esercitazione si veda ad esempio il libro di testo)
 AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
ANALISI MATEMATICA L-B, SERIE. n k=1. n=1
 ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SERIE NUMERICHE. Test di autovalutazione. 1+a 2
 SERIE NUMERICHE Test di autovalutazioe. E data la serie: dove a R. Allora: ( ) 3a +a (a) se a = la serie coverge a (b) se a = 3 la somma della serie vale 5 (c) se a = 5 la serie diverge a (d) se a 0 la
SERIE NUMERICHE Test di autovalutazioe. E data la serie: dove a R. Allora: ( ) 3a +a (a) se a = la serie coverge a (b) se a = 3 la somma della serie vale 5 (c) se a = 5 la serie diverge a (d) se a 0 la
Serie numeriche e di funzioni - Esercizi svolti
 Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
SOLUZIONI COMPITO del 12/01/2017 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A. ; 9 + 4α = 1
 SOLUZIONI COMPITO del /0/07 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio i Osserviamo che effettuado la divisioe si ottiee w = 9+4α iα +iα +iα = i α Poiché 9+4α 9+4α w = 9+4α + α 9+4α =, si
SOLUZIONI COMPITO del /0/07 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio i Osserviamo che effettuado la divisioe si ottiee w = 9+4α iα +iα +iα = i α Poiché 9+4α 9+4α w = 9+4α + α 9+4α =, si
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
6 - Serie numeriche. n=1
 6 - Serie umeriche Ultimo aggiorameto: 9 ottobre 09. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
6 - Serie umeriche Ultimo aggiorameto: 9 ottobre 09. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI
 DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Correzione del primo compitino di Analisi 1 e 2 A.A. 2014/2015
 Correzioe del primo compitio di Aalisi e 2 A.A. 20/205 Luca Ghidelli, Giovai Paolii, Leoardo Tolomeo 5 dicembre 20 Esercizio Testo. Calcolare, se esiste, + 3 + 5 + + (2 ). 2 + + 6 + + 2 Soluzioe. Al deomiatore
Correzioe del primo compitio di Aalisi e 2 A.A. 20/205 Luca Ghidelli, Giovai Paolii, Leoardo Tolomeo 5 dicembre 20 Esercizio Testo. Calcolare, se esiste, + 3 + 5 + + (2 ). 2 + + 6 + + 2 Soluzioe. Al deomiatore
n=0 a n(z z 0 ) n converge} è chiamato insieme di convergenza della serie; si ha sempre z 0 I e quindi I non è mai vuoto. Nasce quindi una funzione
 Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
[È ben noto che la serie geometrica converge se e solo se x <1 e che ha per somma la funzione S(x)= 1
 Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE E DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Defiizioe di serie umerica covergete, divergete, irregolare. Serie a termii di sego costate: criterio del cofroto, rapporto, radice. Serie a
SERIE NUMERICHE E DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Defiizioe di serie umerica covergete, divergete, irregolare. Serie a termii di sego costate: criterio del cofroto, rapporto, radice. Serie a
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
I appello - 11 Dicembre 2006
 Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Qualche limite e serie standard svolti.
 3 Novembre 04 Qualche ite e serie stadard svolti. Idice Successioi. Cofroti di crescita di espoeziali.................... Qualche criterio...............................3 Altri cofroti...............................
3 Novembre 04 Qualche ite e serie stadard svolti. Idice Successioi. Cofroti di crescita di espoeziali.................... Qualche criterio...............................3 Altri cofroti...............................
Michela Eleuteri ANALISI MATEMATICA. Serie numeriche (teoria ed esercizi)
 Michela Eleuteri ANALISI MATEMATICA Serie umeriche (teoria ed esercizi) A Giulia co la speraza che almeo ella matematica o assomigli al papà Idice Serie 5. Deizioe di serie e prime proprietà........................
Michela Eleuteri ANALISI MATEMATICA Serie umeriche (teoria ed esercizi) A Giulia co la speraza che almeo ella matematica o assomigli al papà Idice Serie 5. Deizioe di serie e prime proprietà........................
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
c Fabio Paronetto Serie numeriche Ultimo aggiornamento: 28 febbraio 2018
 Serie umeriche Ultimo aggiorameto: 28 febbraio 208. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
Serie umeriche Ultimo aggiorameto: 28 febbraio 208. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
LIMITI DI SUCCESSIONI
 LIMITI DI SUCCESSIONI Formalmete, ua successioe di elemeti di u dato isieme A è u'applicazioe dall'isieme N dei umeri aturali i A: L'elemeto a della successioe è quidi l'immagie a = f) del umero secodo
LIMITI DI SUCCESSIONI Formalmete, ua successioe di elemeti di u dato isieme A è u'applicazioe dall'isieme N dei umeri aturali i A: L'elemeto a della successioe è quidi l'immagie a = f) del umero secodo
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
Prova scritta di Analisi Matematica I 15/09/2010
 Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
Prova scritta del 9/1/2003
 Prova scritta del 9//00 Soluzioe degli esercizi N. Le quattro serie proposte soo a termii positivi. Per studiare la covergeza delle serie a termii positivi è possibile utilizzare uo dei segueti criteri
Prova scritta del 9//00 Soluzioe degli esercizi N. Le quattro serie proposte soo a termii positivi. Per studiare la covergeza delle serie a termii positivi è possibile utilizzare uo dei segueti criteri
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE LORENZO BRASCO Idice. Criteri di covergeza per successioi 2. Teoremi di Cesàro per successioi 4 3. Serie umeriche 9 4. Criteri di covergeza per serie umeriche a termii positivi
SUCCESSIONI E SERIE NUMERICHE LORENZO BRASCO Idice. Criteri di covergeza per successioi 2. Teoremi di Cesàro per successioi 4 3. Serie umeriche 9 4. Criteri di covergeza per serie umeriche a termii positivi
Esercizi sulle successioni
 Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Il caso di coefficienti decrescenti e infinitesimi
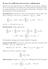 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Ottavio Serra La costante C di Eulero-Mascheroni e la funzione Gamma. 1. =
 Ottavio Serra La costate C di Eulero-Mascheroi e la fuzioe Gamma la costate C di Eulero Mascheroi è defiita come il limite della seguete successioe: [] a = +/+/3+ +/ log(+) Il termie a è la differeza tra
Ottavio Serra La costate C di Eulero-Mascheroi e la fuzioe Gamma la costate C di Eulero Mascheroi è defiita come il limite della seguete successioe: [] a = +/+/3+ +/ log(+) Il termie a è la differeza tra
SOLUZIONI COMPITO del 04/02/2016 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A
 SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
