Cammini minimi. Chapter Il problema del cammino minimo e alcuni esempi di applicazioni

Transcript

1 Chapter 7 Cammini minimi Come abbiamo vito nel capitolo precedente, il linguaggio dei grafi permette di rappreentare in modo emplice la truttura di molti problemi applicativi, conentendo, in molti cai di grande importanza, di cotruire metodi razionali di oluzione dei problemi tei. Fra i problemi più importanti, più emplici e più antichi, per la cui oluzione ono utilizzate rappreentazioni baate u grafi, vi ono i problemi di ricerca di cammini con caratteritiche prefiate. Fra le applicazioni più importanti i poono citare: - intradamento di veicoli (routing); - ottimizzazione del traffico u reti di comunicazione; - ottimizzazione del traffico u reti di traporto; - alcuni problemi di controllo degli tock; - problemi di getione dei progetti; - problemi di controllo riolti con tecniche di programmazione dinamica; - alcuni problemi di elaborazione di egnali; - problemi di codifica e decodifica di meaggi; - problemi di allocazione temporale di attivita (equenziamento o cheduling); - alcuni problemi di intelligenza artificiale; - alcuni problemi di riconocimento di immagini; - alcuni problemi di verifica di correttezza di programmi per calcolatori. Igrafi coniderati in queta unità ono, alvo divera pecificazione, grafi orientati. Nel cao della ricerca di cammini infatti è empre poibile riconduri con poca fatica a queto cao. Per fare queto èufficiente otituire ogni arco non orientato (e quindi percorribile in entrambi i veri) con due archi diretti in direzione oppota. Se eite un cammino con le caratteritiche richiete nel grafo originario, allora eite anche nel grafo traformato e vicevera. 7. Il problema del cammino minimo e alcuni eempi di applicazioni Dato un grafo orientato G =(V,E), aociamo a ciacun arco e =(u, v) E un peo p u,v IR. Per ogni cammino orientato P = {v,e,..., e p,v p },definiamo peo p(p ) del cammino P la omma dei 9

2 pei degli archi che appartengono a P,ecioè: p(p )= (u,v) P cammino con l elenco dei nodi P = {v,v,...,v p }. Il problema del cammino minimo può eere enunciato nel modo eguente: p u,v. Per emplicità peoindicheremoil Dati due nodi V e t V, trovare un cammino orientato P (, t) in G da a t che abbia peo minimo. Notiamo che: - Se non eite un cammino orientato che vada da a t in G, il problema non ha oluzioni ammiibili. - Se eite un ciclo orientato C in G, talechep(c) < 0 (peo negativo), il problema è illimitato inferiormente. Nella letteratura eitono moltiimi algoritmi per il calcolo dei cammini minimi. Ognuno di ei ha le ue peculiarità e le ue limitazioni. Per eempio alcuni algoritmi funzionano olo u determinate clai di grafi (grafi aciclici, grafi con pei non negativi, etc.), inoltre ci poono eere notevoli differenze nella efficienza degli algoritmi. In generale un algoritmo che funziona u una clae ampia di grafi arà più compleo di un algoritmo tudiato per una clae ritretta di grafi, tenendo conto delle peculiarità di quella clae. Gli algoritmi che conideriamo in queto capitolo determinano il cammino minimo da un nodo a tutti gli altri nodi i del grafo. Un generico cammino da a i è indicato con P (i) ={, v,...,v k = i}; il cammino minimo da a i è indicato con P (i). Premettiamo il eguente riultato di carattere generale che ará utile nel eguito: Lemma 7.. Sia P (i k )={, i,i,...i k } un cammino minimo dal nodo al nodo i k.allorap (i q )= {, i,...,i q } è un cammino minimo da a i q,perogniq k. Dimotrazione. Supponiamo, per aurdo, che eita un nodo i l, l<ktale che P (i l )={, i,...,i l } non ia un cammino minimo da a i l. Allora eiterà uncamminop (i l )talechep(p (i l )) <p(p (i l )). Ma allora il cammino P (i k )={P (i l ),i l+,...,i k } ètalechep(p (i k )) <p(p (i k )), che porta a una contraddizione. Per ogni nodo j V,iad(j) un etichetta che denoti il peo di un cammino P (j) (non neceariamente minimo) dal nodo ad un nodo j. Una tale etichetta i dice etichetta ditanza. Valeileguenteriultato Teorema 7.. Per ogni nodo j V,iad (j) la ua etichetta ditanza. I valori d (j), j =,..., V rappreentano i pei dei cammini minimi dal nodo ad ogni nodo j eeoloe per ogni i ω e (j). d (j) d (i)+p i,j, Dimotrazione. Sufficienza. (Se d (j) d (i) +p i,j, allora il cammino minimo P (j) da a j ha peo d (j).) Per aurdo upponiamo che eita un nodo j la cui etichetta d (j) ia trettamente maggiore del peo p(pj ) del cammino minimo P (j) ={, v,...,v z,v z,...,v q = j} da a j. Per il Lemma 7.., per qualunque k =0,...,q il ottocammino P (v k )={ = v 0,...,v k } di P (j) è un cammino minimo da a v k. Sul cammino P (j) individuiamo il primo nodo v z, a cui corriponde il cammino minimo P (v z ), per cui i abbia d (v z ) > p(p (v z )). Quindi, il nodo v z che lo precede nel cammino P (j) aràtaleche d (v z )=p(p (v z )). Ma allora i avrà p(p (v z )) = p(p (v z )) + p vz,v z = d (v z )+p vz,v z d (v z ) >p(p (v z )), che è una contraddizione. Neceità. (Se il cammino minimo P (j) da a j ha peo p(p (j)) = d (j) allorad (j) d (i)+p i,j.) Per aurdo, upponiamo che le d (j) =p(p (j)) per ogni j ma che eitano due nodi k, q per cui riulti 9

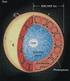
3 d (k) >d (q) +p q,k. Ovviamente eiterà l arco (q, k). Inoltre, per definizione di etichetta ditanza, deve eitere un cammino orientato P (q) da a q di peo d (q). Ma allora poo cotruire un cammino orientato da a k che paa per q, cioè P (k) =P (q) {(q,k)} di peo p(p (k)) = d (q)+p q,k.quetaè una contraddizione eendo p(p (k)) <d (k) =p(p (q)). Nella parte rimanente di queta ezione illutriamo alcuni emplici eempi di calcolo dei cammini minimi. 7.. Percoro di tempo minimo u una rete tradale Dato un grafo peato che rappreenta la rete tradale italiana in cui i pei degli archi indicano il (valore atteo del) tempo di percorrenza dell arco, il problema è quello di trovare il cammino che congiunge due particolari nodi del grafo (nodo di partenza e nodo di arrivo) con tempo di percorrenza minimo. Si noti che poono eitere più cammini con la caratteritica di eere minimi. Queto eempio, apparentemente emplice, olleva complei problemi di modellitica. Un primo problema è relativo al livello di dettaglio neceario nella rappreentazione. Se, per eempio, il percoro da effettuare parte da Milano e arriva a Brindii, il grafo dovrà contenere olo le autotrade e le principali trade di collegamento fra città divere e un intera città potrà eere rappreentata con un nodo del grafo. Un ecceo di dettaglio appeantirebbe inutilmente la rappreentazione, rendendo ogni algoritmo di oluzione lento e inefficace. Se, d altra parte, il percoro da effettuare parte da piazza San Pietro a Roma e arriva a un indirizzo di Fracati (a circa 0 km. da Roma), la rappreentazione davrà eere completamente divera, non olo perché il grafo arà divero,maancheperché il peo degli archi, per eere ignificativo, dovrà prendere in coniderazione i problemi del traffico urbano e quindi eere funzione dell ora ed eventualmente del giorno. Infatti, effettuare tale percoro alle 0 di mattina di un giorno feriale non arà ovviamente la tea coa che effettuarlo alle del mattino. Un econdo problema è relativo al tipo di obiettivi che ci i propone. Infatti, una rappreentazione può eere o può non eere adeguata, a econda del motivo per cui i vuole conocere il cammino di tempo minimo. Per eempio, per alcune applicazioni critiche (autombulanze, vigili del fuoco, polizia), non bata l informazione ul valore atteo del tempo di tranito, ma erve anche valutare la varianza di tale tempo, oia le poibili variazioni ripetto alla media. È meglio infatti utilizzare un percoro un po più lungo ma con un tempo di percorrenza prevedibile con relativa certezza, piuttoto che un percoro mediamente piu breve ma per cui vi ia il richio di retare imbottigliati nel traffico. Un terzo problema è relativo alla quantità di informazioni che è neceario inerire nell elaboratore per affrontare il problema. Per calcolare il cammino da Milano a Brindii è neceario inerire l intera carta tradale italiana, o bata una porzione? Da un lato, più informazioni vengono inerite maggiore èil tempo neceario per inerirle e il coto dell operazione; d altro canto e vengono calcolati peo percori di tempo minimo ulla rete tradale italiana fore conviene memorizzare tutto in modo organico una volta per tutte. 7.. Cotruzione di una autotrada Il problema coniderato è quello di cotruire al coto minimo una autotrada fra le citta A e B. Nel grafo riportato in figura 7. i nodi rappreentano i punti per cui l autotrada puo paare e gli archi i poibili collegamenti fra punti. Il peo degli archi rappreenta il coto di cotruzione della relativa tratta di autotrada. Si noti che in queto cao il grafo è non orientato in quanto ogni arco puo eere percoro in entrambi i eni; per riconduri al cao orientato bata otituire ogni arco con due archi orientati in eno oppoto, a ognuno dei quali viene attribuito un peo pari al peo dell arco eliminato. La celta di una autotrada tra A e B con coto compleivo di cotruzione minimo, corriponde alla celta del cammino di minimo coto dal nodo A al nodo B ul grafo. Nella figura 7. tale cammino è indicato in graetto e il coto compleivo è pari a. 9

4 A 8 Q 0 Z 7 E 9 R T 8 Y 8 6 U 0 B Figure 7.: Cammino minimo tra A e B 7.. Attraveramento di un fiume Su di una riva di un fiume vi è un patore con un cane lupo, un agnello e un ceto di cavoli. Per attraverare il fiume il patore dipone di una piccola barca che permette di traportare, oltre al patore, un olo altro paeggero (il cane lupo, l agnello o il ceto di cavoli). Se u di una riva retano oli il cane lupo e l agnello, il cane lupo puo uccidere l agnello. Se retano oli l agnello e il ceto di cavoli, l agnello puo mangiare i cavoli. Il problema è quello di tabilire e è poibile traferire tutto ull altra riva del fiume enza mai laciare oli cane lupo e agnello o agnello e ceto di cavoli. Il problema puo eere facilmente formulato come problema di eitenza di un cammino u di un opportuno grafo. Sia dato il grafo G =(V,E) dove i nodi corripondono a tutti i poibili tati ammiibili del itema patore-lupo-agnello-cavoli. I poibili tati ammiibili del itema ono i eguenti: PLAC patore, lupo,agnello e cavoli ulla riva di partenza neuno ulla riva di arrivo PLC patore, lupo e cavoli ulla riva di partenza agnello ulla riva di arrivo PAC patore, agnello e cavoli ulla riva di partenza lupo ulla riva di arrivo PLA patore,lupo e agnello ulla riva di partenza cavoli ulla riva di arrivo PA patore e agnello ulla riva di partenza lupo e cavoli ulla riva di arrivo LC lupo e cavoli ulla riva di partenza patore e agnello ulla riva di arrivo A agnello ulla riva di partenza patore lupo,e cavoli ulla riva di arrivo L lupo ulla riva di partenza patore,agnello e cavoli ulla riva di arrivo C cavoli ulla riva di partenza patore,lupo e agnello ulla riva di arrivo neuno ulla riva di partenza patore,lupo,agnello e cavoli ulla riva di arrivo Altri tati del itema non ono ammiibili; per eempio non è ammiibile lo tato PL in quanto lacerebbe agnello e cavoli oli ulla riva di arrivo. Nel grafo G eite un arco tra due nodi e è poibile paare da uno all altro dei due tati corripondenti con un olo viaggio in barca. Il grafo aociato al problema viene riportato in figura 7.. Si noti che in queto cao il grafo è immetrico in quanto, e è poibile paare dal nodo A al nodo B, allora è anche poibile paare da B a A; per emplicità quindi il grafo viene riportato come grafo non orientato. 96

5 PLAC LC PLC L C PLA PAC A PA Ø Figure 7.: Eitenza tra un cammino tra due nodi L eitenza di una oluzione equivale all eitenza di un cammino tra il nodo PLAC e il nodo. Il numero minimo di viaggi neceario per compiere l operazione è pari a 7 e corriponde al cammino con il minimo numero di archi tra il nodo PLAC e il nodo. Si noti che eitono due poibili cammini emplici tra i due nodi, entrambi con 7 archi. 7.. Controllo delle corte In una indutria manifatturiera, l ufficio acquiti ha il compito di verificare ogni trimetre lo tato delle corte e ordinare il materiale neceario per oddifare la domanda. Ogni tipo di prodotto è indipendente dagli altri; conideriamo quindi un olo prodotto. Gli elementi ui quali i può baare la deciione di acquito ono i eguenti: - la domanda del prodotto relativa a ogni trimetre ènotaconcertezzapern trimetri; ia d(i) la domanda relativa al trimetre i con i =,,...,n; - il coto di acquito per unità di prodotto in ogni trimetre è noto con certezza per n trimetri; ia c(i) il coto unitario relativo al trimetre i con i =,,...,n (nel coto i tiene conto anche degli interei); - la capacità del magazzino con riferimento al prodotto in eame è limitata; ia S il numero maimo di pezzi che è poibile immagazzinare. Il problema è quello di tabilire una politica ottima degli acquiti per n trimetri, oia quanto acquitare del prodotto al termine di ogni trimetre in modo da oddifare la domanda al coto minimo. Si uppongono dati i livelli iniziale (corripondente al trimetre 0) e finale (corripondente al trimetre n) delle corte (per eempio entrambi nulli). Il problema puo eere formulato come cammino minimo nel eguente modo. Sia G =(E,V )ungrafo in cui i nodi rappreentano tati del itema al termine dei vari trimetri. Un nodo è quindi indicato con due indici (i, j): il primo relativo allo tato del itema (numero i di pezzi del prodotto nel magazzino), il econdo relativo al trimetre coniderato (per comodità ci poniamo empre al termine del trimetre). Il numero di nodi del grafo èparia(n )(S +)+,inquanto,peritrimetridaa(n ) vi ono (S + ) poibili tati del itema (uno per ogni poibile livello delle corte), per i trimetri 0 e n lo tato è fiato (per eempio pari a 0). Nel grafo eite un arco tra due nodi (i, j) e(k,h), e h = j + e k = i d(h), oppure e h = j e k i. Il primo cao corriponde al conumo di d(k) unità del prodotto durante il trimetre k; il peo dell arco è pari a 0 in quanto i uppone che vengano utilizzati olo pezzi già preenti in magazzino; indichiamo queti archi come archi conumo. Il econdo cao corriponde all acquito di un numero di pezzi del prodotto pari a (k i); il peo dell arco èparia 97

6 c(j)(k i), corripondente al coto di acquito di un pezzo al termine del trimetre j per il numero di pezzi acquitati; indichiamo queti archi come archi acquito. Il problema può ora eere formulato come il problema di trovare il cammino minimo tra il nodo (0, 0) eilnodo(0,n). Infatti ogni cammino da (0, 0) a (0,n) ul grafo è formato da una ucceione di archi acquito e conumo che i alternano ul cammino e corripondono a una ucceione di acquiti e conumi fatta dall azienda. Il coto compleivo del cammino è dato dalla omma dei coti delle varie operazioni. Si noti che il grafo è aciclico. Se non eite cammino tra i due nodi coniderati, vuol dire che, con il vincolo di capacità del magazzino coniderato, non è poibile oddifare tutta la domanda. 7. Cammini minimi e maimi u grafi aciclici Una clae di grafi orientati di particolare interee in campo applicativo èlaclaedigrafi aciclici. Per eempio il grafo di attività di un progetto con vincoli di precedenza fra le attivitàè aciclico (vedi il capitolo Tecniche reticolari di programmazione delle attività ). La ricerca di cammini minimi o maimi u tali grafi è uno trumento di progetto di notevole importanza. Come i vedrà nel eguito, i due problemi di minimo e di maimo ono, in queto cao particolare, riolti da due algoritmi identici eccetto che per la otituzione di un maimo a un minimo nella formula ricoriva alla bae del procedimento. Nel eguito verrà prima coniderato il cao di un problema di cammino minimo. Per poter procedere con la decrizione dell algoritmo, è neceario tudiare prima una particolare tecnica di numerazione dei nodi di un grafo aciclico. 7.. Numerazione topologica dei nodi di un grafo Una caratteritica peculiare dei grafi aciclici (ia G =(V,E) ilgrafo,con V = n e E = m) conite nella poibilità di numerare i nodi del grafo con i numeri,,,...,n-,n in modo tale che: e eite un arco dal nodo i al nodo j allora j>i Tale numerazione viene detta numerazione topologica dei nodi del grafo e non è in generale unica. Non tutti i grafi poono eere numerati topologicamente. In effetti l eitenza di una numerazione topologica dei nodi di un grafo caratterizza eattamente la clae dei grafi aciclici. Vale infatti il eguente teorema. Teorema 7.. Un grafo èaciclicoeeoloeeiteunanumerazionetopologicadeiuoinodi. Dimotrazione. Sufficienza. Supponiamo che eita una numerazione topologica dei nodi e facciamo vedere che l eitenza di un ciclo porterebbe ad una contraddizione. Poiamo aumere che i nodi iano numerati topologicamente, indicheremo l i-eimo nodo di queta particolare numerazione, come v i. Seeiteun ciclo (orientato) vuol dire che eite una ucceione di nodi (v i,v j,v k,...,v r,v )taliche - eitono gli archi (v i,v j ), (v j,v k ),...,(v r,v ); - v i = v. Ma allora, da una parte, iccome la numerazione è topologica abbiamo i < j < k <... < r <,cioè i<, mentre dall altra, poiché v i = v abbiamo i =. Quetaè una contraddizione e coì il grafo deve eere aciclico. Neceità. Supponiamo che il grafo ia aciclico e motriamo che deve eitere almeno una numerazione topologica. La dimotrazione è cotruttiva, faremo cioè vedere che eite una numerazione topologica cotruendone una. 98

7 Come primo pao oerviamo che e il grafo è aciclico, deve eitere almeno un nodo che non abbia archi entranti. Infatti, e ciò non foe vero, potremmo ragionare nel modo eguente. Prendiamo un nodo qualunque, chiamiamolo v. Siccome tutti i nodi hanno archi entranti eite un nodo predeceore di v, indichiamolo con v ; notiamo che per come abbiamo celto v eite l arco (v,v ) (attenzione, queta è una numerazione non topologica). Poiamo ripetere il ragionamento con v e trovare un nodo v tale che eita l arco (v,v ). Siccome tiamo upponendo, per aurdo, che tutti gli archi abbiano degli archi entranti, poiamo ripetere il ragionamento quante volte vogliamo. Notiamo che ogni nodo generato deve eere divero dai precedenti, altrimenti avremmo trovato un ciclo, contraddicendo l aciclicità del grafo. D altra parte, arrivati a v n i nodi del grafo ono finiti e quindi il predeceore di v n che tiamo upponendo eitente per aurdo, deve per forza eere uno dei nodi già eaminati. Coì i viene a formare un ciclo. Quindi dato un grafo aciclico deve per forza eitere almeno un nodo che non ha archi entranti. Prendiamo uno di queti nodi e numeriamolo con il numero. Eliminiamo dal grafo il nodo e tutti gli archi ucenti da eo. Il nuovo grafo che otteniamo è ovviamente ancora un grafo aciclico. Quindi per lo teo ragionamento fatto prima deve eitere almeno un nodo che non ha archi entranti. Prendiamo uno di queti nodi e numeriamolo con il numero. Notiamo che ovviamente e conideriamo il grafo originario il nodo può avere archi entranti, ma olo provenienti dal nodo e quindi la condizione i<j è ripettata. Poiamo ora ripetere il procedimento n volte (quanti ono i nodi) ed ottenere coì una numerazione topologica del grafo. Il precedente teorema è importante, anche perché nella dimotrazione della neceità è otanzialmente dato un algoritmo per numerare topologicamente i nodi di un grafo. Rieponiamo qui l algoritmo per chiarezza. - Siccome il grafo è aciclico, deve eitere almeno un nodo con olo archi ucenti; - individuiamo uno di queti nodi e attribuiamogli il numero ; - cancelliamo il nodo numerato e tutti gli archi adiacenti, nel nuovo grafo ridotto individuiamo un nodo con oli archi ucenti e attribuiamogli il numero, e coì via fino ad aver numerato tutti i nodi La correttezza e validità di queta procedura è tata provata nella dimotrazione della neceità del Teorema 7... Notiamo che e ad un certo punto dell applicazione della procedura non poiamo procedere, e uccede cioè che ad un determinato pao non riuciamo a trovare un nodo enza archi entranti, queto vuol dire che il grafo coniderato contiene un ciclo. Quindi la procedura per la numerazione topologica di un grafo può anche eere utilizzata per determinare e un grafo è aciclico o meno. Come eempio conideriamo il grafo di figura 7.. Si tratta di decidere e il grafo è aciclico e, in cao, numerare i nodi topologicamente. I vari pai dell algoritmo ono riportati qui di eguito Pao Nodo enza Nodi non ancora Numerazione archi entranti numerati A B,C,D A= B C,D B= C D C= D D= Il procedimento è terminato con la numerazione di tutti i nodi. Il grafo è dunque aciclico e la numerazione trovata è topologica. Supponiamo ora che nel precedente grafo l arco (B,D) ia orientato da D a B. Ovviamente iverrebbe a creare un ciclo. Se proviamo ad applicare la procedura per la determinazione di una numerazione 99

8 B A D C Figure 7.: Numerazione dei nodi di un grafo topologica poiamo iniziare numerando il nodo A come nodo. Ma dopo non poiamo più procedere perché eliminato il nodo A e gli archi da eo ucenti ((A,B) e (A,C)) non è più poibile individuare un nodo che non abbia archi entranti. 7.. Un algoritmo per il cammino minimo u grafi aciclici La numerazione dei nodi di un grafo aciclico decritta nella ezione precedente conente di cotruire un algoritmo di oluzione per il problema di cammino minimo particolarmente emplice. Infatti, nella ricerca di un cammino tra una qualiai coppia di nodi i e j del grafo, a caua della numerazione attribuita ai nodi, i può affermare che: e j<iallora non eitono cammini da i a j; e j>iallora gli unici nodi che è neceario coniderare nella ricerca del cammino da i a j ono i nodi con indice k tale che i<k<j. Infatti, e il cammino paae per un nodo h>j, allora non potrebbe tornare u j, a caua della mancanza di archi che collegano nodi con indice maggiore a nodi con indice minore; e paae per un nodo h<i, allora dovrebbe eitere un cammino da i a h, il che comporterebbe l eitenza di archi che collegano nodi con indice maggiore a nodi con indice minore. Sulla bae di quete coniderazioni, è poibile impotare un algoritmo per il calcolo dell albero dei cammini minimi tra un nodo del grafo (per eempio il nodo ) e tutti i nodi con indice uperiore (per quelli con indice inferiore non eite icuramente un cammino; ovviamente, e il nodo di partenza èquello contraegnato con l indice, allora i tratta di calcolare l albero dei cammini minimi tra il nodo e tutti gli altri). L algoritmo per il calcolo dell albero dei cammini minimi dal nodo a tutti gli altri nodi i baaulcalcoloinequenzadeicamminiminimidalnodoalnodo,dalnodoalnodo,dalnodo al nodo, e coí via. Indichiamo con: - p i,j il peo dell arco (i, j) che parte dal nodo i earrivaalnodoj; - ω e (i) l inieme dei nodi predeceori del nodo i; - d (i) ilvaloredelcamminominimodalnodoalnodoi; - J(i) il nodo che precede i u tale cammino (nel cao il cammino minimo non ia unico, allora e ne ceglie uno qualiai fra quelli minimi). Poiamo allora illutrare l algoritmo per il calcolo dei percori minimi. 00

9 - d () := 0; J() := ; - per j =,,,...,n,n ripeti la eguente erie di operazioni d (j) :=min i ω e (j){d (i)+p i,j }; J(j) := valoredii per cui i èverificato il minimo; Si noti che una volta aegnato un peo d (i) a un nodo (cioè un valore del cammino minimo dal nodo al nodo coniderato), tale peo non viene più modificato nel coro dell algoritmo, ma indica in modo definitivo il valore del cammino. Queto è dovuto al fatto, già citato, che tutti i nodi ucceivi non devono eere coniderati per il calcolo del percoro dal nodo al nodo i. Inoltre dai valori J(i) è poibile ricotruire in modo immediato l albero (o uno dei poibili alberi) dei cammini minimi. La dimotrazione della correttezza della procedura egue immediatamente dal Teorema 7... Eempio 7.. Come eempio conideriamo il grafo di figura 7.. Figure 7.: Percoro minimo u grafi aciclici Si tratta di determinare l albero dei cammini minimi tra il nodo e tutti gli altri nodi. I vari pai dell algoritmo, corripondenti alla ucceione di nodi viitati, (i oervi che in queto cao particolare l indice del pao coincide con l indice del nodo viitato) portano alla eguente ucceione di valori d (i) e J(i) Pao Valore di d (i) Valore di J(i) d () = 0 J() = d () = J() = d () = min{, +} = J() = d () = min{+, +} = J() = Il corripondente albero dei cammini minimi è riportato in figura 7. Eempio 7.. Sia dato il grafo di Figura 7.6. Determinare l albero dei cammini minimi, utilizzando l algoritmo per grafi aciclici. Soluzione. Si deve prima numerare topologicamente il grafo. I pai ono riportati nella eguente tabella ed il grafo riultante in Figura 7.7 0

10 Figure 7.: Albero dei cammini minimi B E A C 0 F D G Figure 7.6: Grafo Eercizio 7.. 0

11 Pao Nodo enza Nodi non ancora Numerazione archi entranti numerati A B,C,D,E,F,G A= B o D B,C,E,F,G D = B C,E,F,G B= C E,F,G C= E o G F,G E= 6 G F G=6 7 F F=7 Oerviamo che la numerazione topologica in queto eempio non é unica; infatti ai pai e potevamo cegliere tra due nodi. Applichiamo ora l algoritmo. I pai ono riportati nella eguente tabella Figure 7.7: Numerazione topologica del grafo di Figura 7.6 Pao Valore di d (i) Valore di J(i) d () = 0 J() = d () = J() = d () = J() = d () = min{0+, +, +} = J() = d () = min{+, +} = J() = d (6) = min{+, +} = J(6) = d (7) = min{+0, +, +} =8 J(7) = 6 Il corripondente albero dei cammini minimi è riportato in figura Un algoritmo per il cammino maimo u grafi aciclici Se il problema di ottimo è quello della determinazione del cammino di peo maimo ul grafo, allora è facile convinceri che bata otituire nella formula ricoriva al min un max e tutte le coniderazioni fatta continuano, in queto cao particolare di grafi aciclici, a eere valide. L algoritmo per il calcolo dei cammini maimi u grafici aciclici è allora il eguente - f() := 0; J() := ; - per j =,,,...,n,n ripeti la eguente erie di operazioni f(j) :=max i ω e (j){f(i)+p i,j }; 0

12 7 8 6 Figure 7.8: Albero dei cammini minimi J(i) := valore di i per cui i èverificato il maimo; Come eempio conideriamo empre il grafo di figura 7. Si tratta di determinare l albero dei cammini maimi tra il nodo e tutti gli altri nodi. I vari pai dell algoritmo portano alla eguente ucceione di valori f(i) ej(i) Pao Valore di f(i) Valore di J(i) f() = 0 J() = f() = J() = f() = max{, +} = J() = f() = max{+, +} = J() = (oppure J() = ) 7. Cammini minimi u grafi con pei poitivi: algoritmo di Dijktra L algoritmo di Dijktra permette di riolvere il problema del cammino minimo fra due nodi qualora tutti i pei degli archi iano non negativi. Più preciamente, l algoritmo calcola il peo del cammino minimo da un nodo a tutti gli altri nodi del grafo, cotruendo conteporaneamente l albero dei cammini minimi. A ogni iterazione dell algoritmo di Dijktra, l inieme dei nodi V è partizionato in due ottoiniemi S e T. L inieme S contiene il nodo etuttiinodij per cui l etichetta ditanza aociata d (j) è ottima; in T ci ono i retanti nodi V \ S. A ogni iterazione k l algoritmo pota un nodo h da T a S, e aggiorna alcune etichette ditanza d k (i). L eecuzione termina quando T è vuoto. Ricordiamo che con ω u (i) i indica l inieme dei nodi j tali che (i, j) δ u (i) echetaleiniemeè detto intorno ucente del nodo i. L inizializzazione dell algoritmo prevede che eita empre l arco (, i), per ogni i =. Se qualche arco non è preente nel grafo originale, i può aggiungere un arco fittizio di peo pari a +. Indichiamo con J(i) il predeceore del nodo i ul cammino ottimo. ALGORITMO DI DIJKSTRA S T = V e S T = 0

13 . Inizializzazione. Poni S 0 {}, T 0 {,...,n}. d () = 0. Per ogni nodi i poni. Per k =,...n d 0 (i) = p,i e eite l arco (,i) altrimenti Aegnazione etichetta permanente Trova j T k tale che d (j) =d k (j) = min d k (i). i T k Aegnazione etichetta provvioria Per ogni i T k ω u (j) J 0 (i) =,i=,...,n. d k (j)+p j,i e d k (j)+p j,i <d k (i) d k (i) = d k (i) altrimenti i e d k (i) >d k (j)+p j,i J k (i) = J k altrimenti Aggiornamento iniemi S e T Poni T k = T k \{j}, S k = S k {j}. Eempio 7.. Vediamo, nel grafo di figura 7.9, come procede l algoritmo Figure 7.9: Eempio per l algoritmo di Dijktra Indichiamo con D k il vettore di dimenione V le cui componenti ono le ditanze (provviorie e permanenti) d k (i) per ogni nodo i. I pai dell algoritmo ono i eguenti (l evoluzione di T èomea eendo emplicemente T = V S). 0

14 Iterazione 0 Inizializzazione. (a) S = {}. I vettori delle ditanze D 0 e dei predeceori J 0 ono: D 0 = J 0 = Iterazione. j ==argmin i T 0 d 0 (i). S = {, }. ω u () T 0 = {,, 6}. E facile vedere che per ognuno dei nodi {,, 6} èverificata la condizione d(i) >d() + p,i, e quindi le etichette vanno tutte aggiornate. D = J = Iterazione. j ==argmin i T d (i). S = {,, }. ω u () T = {, }. d() = d() + =. d() = d() + = 8. e quindi D = J = Iterazione j ==argmin i T d (i). S = {,,, }. ω u () T = {, 6}. L etichetta del nodo non oddifa la condizione di decremento, per cui i aggiorna olo l etichetta (e il predeceore) del nodo 6. D = J = Iterazione. j =6. S = {,,,, 6}. ω u (6) T =. Non i aggiorna niente, D = D 06

15 Iterazione. j =. S = {,,,,, 6} e D = D. STOP. I pei dei cammini minimi aranno quindi: d() = 0. d() =. d() =. d() = 8. d() =. d(6) = 6. Una comoda rappreentazione dell evolvere dell algoritmo èlaeguenteformatabellareovelerighe rappreentano iterazioni mentre le colonne rappreentano i nodi elezionati ad ogni iterazione. Per ciacun nodo j ci ono due colonne che riportano il valore della variabile d k (j) e della J k (j) all iterazione k-eima. L elemento elezionato all iterazione k-eima è rappreentato in graetto e, nelle iterazioni ucceive, il valore della variabile corripondente non viene più riportato. La colonna corripondente al nodo è omea. nodo 6 d J d J d J d J d J It (fitt.) + (fitt.) + (fitt.) It. 6 + (fitt.) 8 It. 8 8 It. 8 6 It. 8 6 It. 8 Prima di dimotrare la correttezza dell algoritmo di Dijktra, dicuteremo alcune proprietà delle etichette ditanza calcolate dall algoritmo teo. Di eguito denoteremo con d k (j) il valore dell etichetta ditanza del nodo j all iterazione k-eima. Proprietà 7.. L etichetta provvioria d(j) aegnata a un nodo j è non crecente all aumentare delle iterazioni dell algoritmo, ovvero d k (j) d k+ (j). Queta proprietà è legata al fatto che ogni volta che l etichetta provvioria di un nodo viene aggiornata, ea decrece. Lemma 7.. L etichetta permanente d k delle iterazioni, cioè riultad k+ d k. aegnata a ogni iterazione k è non decrecente all aumentare Dimotrazione. Per cotruzione riulta d k = dk (j) =min i T k d k (i) Quindi d k = dk (j) d k (i) per ogni i T k. (7.) Poichè all iterazione k-eima è tato elezionato il nodo j, T k+ = T k \{j} e devono eere aggiornate le etichette dei nodi in T k+ ω u (j), mentre le altre rimangono invariate. In particolare l etichetta del nodo i T k+ ω u (j) vale d k (i) e d k (i) d k (j)+p j,i d k+ (i) = d k (j)+p j,i e d k (i) >d k (j)+p j,i Ricordando che p j,i 0, i ottiene che per i T k+ d k (i) d k (j) per le etichette invariate (7.) d k+ (i) = d k (j)+p j,i d k (j) per le etichette aggiornate p j,i 0 07

16 Quindi i ottiene d k+ (i) d k (j) =d k per ogni i T k+ Queto varrà in particolare anche per il valore minimo min i T k+ d k+ (i) d k e quindi riulta d k+ d k. Il eguente teorema aicura la correttezza dell algoritmo di Dijktra. Teorema 7.. Quando l algoritmo di Dijktra termina, il valore dell etichetta ditanza d(j) per j =...,n, rappreenta il peo di un cammino minimo da a j. Dimotrazione. Bata dimotrare che, alla terminazione dell algoritmo, le etichette ditanza d (i) oddifano la condizione di ottimalità del Teorema 7.., d (j) d (i)+p i,j per j ω e (i). Per aurdo upponiamo che eitano due nodi, p e q, che non la verificano: d (p) >d (q)+p q,p. Eendo i pei degli archi non negativi per ipotei p q,p 0, i ha d (p) >d (q). Quindi, per il Lemma 7.., il nodo q èentratoins in un iterazione k precedente all iterazione in cui il nodo p èentratoins. Alla fine dell iterazione k abbiamo la eguente ituazione: q S k e p T k ω u (q), e inoltre l etichetta d k (q) =d (q) è diventata permanente e non verrà piùmodificata. Per la Proprietà 7.., l etichetta provvioria del nodo p può olo decrecere all aumentare delle iterazioni, cioè d (p) d k (p). Quindi, avendo uppoto d (p) >d (q)+p q,p, poiamo crivere d k (p) d (p) >d (q)+p q,p = d k (q)+p q,p. All iterazione k-eima riulta quindi d k (p) d k (q) +p q,p epoiché p T k ω u (q), l etichetta di p viene aggiornata e pota d k+ (p) =d k (q) +p q,p ;mapoichériultaanched (p) d k+ (p) =d k (q) +p q,p = d (q) +p q,p abbiamo una contraddizione. 7. Un algoritmo per il calcolo dei cammini minimi u grafi qualunque In queta ezione preentiamo un algoritmo molto emplice ed efficiente per il calcolo contemporaneo dei cammini minimi tra tutte le coppie di nodi di un grafo G =(V,E) (con V = n e E = m). A differenza dell algoritmo tudiato nella ezione precedenza l algoritmo può lavorare con grafi aciclici e con grafi contenenti cicli. Inoltre, e eite un ciclo di lunghezza negativa (cao in cui, ricordiamo, il problema di determinare il cammino minimo non è ben poto), l algoritmo è in grado di accorgerene. L algoritmo conta eattamente di n (numero dei nodi) iterazioni (e non eitono cicli di lunghezza negativa,altrimentiilnumerodiiterazionepuò eere minore). Ad ogni iterazione l algoritmo produce due matrici quadrate n n: D h e J h. La matrice D h è chiamata matrice delle ditanze (all h-eima iterazione) mentre la matrice J h è chiamata matrice dei predeceori (all h-eima iterazione). L indice h indica l iterazione e varierà da0an. Per illutrare l algoritmo procederemo nel eguente modo: - prima daremo una definizioni delle matrici D h e J h ; - poi motreremo come, a partire dalla decrizione del grafo, ia poibile calcolare immediatamente D 0 e J 0 ; - faremo vedere quindi come, note D h e J h ia poibile calcolare D h+ e J h+ ; - infine motreremo come a partire da D n e J n i poano agevolmente ricotruire i cammini minimi tra tutti i nodi del grafo. Paiamo quindi a definire le matrici D h e J h Definizione 7.. D h è una matrice quadrata n n il cui elemento (ij), D h ij,dàilpeodelcammino minimo tra il nodo i eilnodoj che paa al più periprimih nodi. Se non eite neun cammino tra il nodo i eilnodoj che paa al più periprimih nodi, i pone convenzionalmente D h ij =. 08

17 Definizione 7.. J h èunamatricequadratan n il cui elemento (ij), Jij h dàilpredeceoredelnodo j nel cammino minimo tra il nodo i eilnodoj che paa al più periprimih nodi. Se eite più diun tale cammino, Jij h è il predeceore del nodo j lungo uno qualunque di tali cammini. Se non eite neun cammino tra il nodo i eilnodoj che paa al più periprimih nodi, i pone convenzionalmente Jij h =0. Data quete definizioni, è ora molto facile calcolare, a partire dalla decrizione del grafo, le matrici D 0 e J 0. Infatti un cammino minimo tra due nodi, i e j, che paa per i primi 0 nodi può eere cotituito olamente dall arco (i, j), e eite, altrimenti il cammino non eite. Quindi abbiamo p i,j e eite l arco (ij) conpeop i,j Dij 0 = 0 e i = j altrimenti e i e eite l arco (ij) Jij 0 = (7.) 0 altrimenti Notiamo di nuovo che abbiamo aunto la convenzione di porre pari a la lunghezza dei rami che non eitono e di porre uguale a 0 la ditanza di un nodo da e teo. Inoltre, empre per convenzione, poniamo uguale a 0 il predeceore di un nodo j e il ramo (ij) noneite. Sarà facile convinceri, eguendo le piegazione u come calcolare le varie D h e J h che quete quete convenzioni i propagano. Tutte le volte che riulterà Dij h =, quetovorràdirechenoneiteneun cammino tra il nodo i eilnodoj che pai al più oloperiprimih nodi; inoltre in corripondenza riulterà anchejij h =0. Il proimo teorema illutra come a partire dalla matrice D h i poa agevolmente calcolare la D h+. Teorema 7.. Per ogni h =0,,...,n eperognicoppia(i, j), coni =,,...n e j =,,...n, riulta D h+ ij =min{d h ij,dh i(h+) + Dh (h+)j } (7.) Dimotrazione. Dij h+ è il peo del cammino minimo tra il nodo i eilnodoj che paa al più peri primi h + nodi. Ci ono evidentemente due poibilità:. Il cammino minimo tra il nodo i eilnodoj che paa al più periprimih + nodi non paa per il nodo h +;. Il cammino minimo tra il nodo i eilnodoj che paa al più periprimih + nodi paa per il nodo h +. Le due ituazioni ono illutrate nella figura 7.0, dove gli archi ondulati rappreentano dei cammini e nonuningoloarco. Nel cao., rappreentato in figura 7.0a), è evidente che il peo del cammino minimo tra il nodo i e il nodo j che paa al più periprimih + nodi è uguale al peo del cammino minimo tra il nodo i eil nodo j che paa al più periprimih nodi. Riulta quindi (7.) D h+ ij = D h ij. (7.) Nel cao. invece, figura7.0b),ilpeodelcamminominimotrailnodoi eilnodoj che paa al più per i primi h +nodi è dato dalla omma del peo del cammino minimo dal nodo i al nodo h +che paa al più periprimih + nodi e di quello che va dal nodo h + al nodo j paando al più peri primi h + nodi, abbiamo cioè pezzato il cammino in due parti. Notando che tutte e due le parti in cui è decompoto il cammino hanno il nodo h + come etremo, e che quindi queto nodo non può anche eere nodo intermedio deduciamo ubito che il peo del cammino minimo tra il nodo i eilnodoj che 09

18 h+ h+ i j a) b) i D h+ i j j Figure 7.0: Calcolo di D h+ ij paa al più periprimih + nodi è dato anche dalla omma del peo del cammino minimo dal nodo i al nodo h + che paa al più periprimih nodi e di quello che va dal nodo h + al nodo j paando al più periprimih nodi; cioè D h+ ij = Di(h+) h + Dh (h+)j. (7.6) Tenendo conto che e qualcuno dei cammini coniderati non eite, riulta per convenzione che la ua lunghezza è, dalla (7.) e dalla (7.6) i deduce immediatamente la validità della (7.). La prova del Teorema 7.. uggerice anche il modo di calcolare J h+ apartiredaj h. Infatti, ricordando la figura 7.0, è chiaro che i poono preentare due cai. Se il cammino minimo tra il nodo i eilnodoj che paa al piùperiprimih+ nodi non paa per il nodo h+ (figura 7.0a)) allora Jij h+ = Jij h ; e invece il cammino minimo tra il nodo i eilnodoj che paa al più periprimih + nodi paa effettivamente per il nodo h+ (figura 7.0b)) allora J h+ ij = J(h+)j h. Per capire quale dei due cai i verifica, e cegliere quindi come aggiornare la matrice dei predeceori, poiamo baarci ull aggiornamento della matrice delle ditanze. In concluione riulta J h+ ij = J h ij e D h+ ij J h (h+)j e D h+ ij = D h ij = D h i(h+) + Dh (h+)j (7.7) Notiamo che in effetti nella precedente regola c è un ambiguità. Infatti, e riulta D h+ ij = Dij h = Dh i(h+) + D(h+)j h h+,la(7.7)nondefinice eattamente Jij. Notiamo che Dij h+ = Dij h = Dh i(h+) + Dh (h+)j,vuol dire che tra il nodo i eilnodoj eitono (almeno) due cammini minimi di uguale peo che paano al più periprimih + nodi: uno che non paa per h + e uno che invece paa per h +. In queto cao è ovvio che noi poiamo cegliere uno qualiai dei due cammini e quindi porre indifferentemente J h+ ij = Jij h o J h+ ij = J(h+)j h. Per emplicità noi faremo empre la prima celta. È chiaro a queto punto che, a partire da D 0 e J 0, e poibile calcolare D e J, D e J ecoí via, fino ad arrivare a D n e J n. A queto punto motriamo come ia poibile calcolare in modo molto emplice, a partire da D n e J n, un qualunque percoro di peo minimo tra una qualunque coppia di nodi. Prima di tutto notiamo che il cammino minimo tra il nodo i eilnodoj che paano al più periprimi n nodi coincide con il cammino minimo tra il nodo i eilnodoj ul grafo, vito che i nodi del grafo ono n. Quindi le matrici D n e J n rappreentano la matrice delle ditanze minime ul grafo e quella dei predeceori ui cammini minimo ripettivamente. Supponiamo allora di voler calcolare il cammino minimo tra il nodo i eilnodoj. Prima di tutto conideriamo l elemento Dij n della matrice delle ditanze. Se Dn ij = vuol dire, per le convenzioni fatte, 0

19 che non eite neun cammino tra i due nodi coniderati e quindi non i deve proeguire. Supponiamo allora che Dij n abbia un valore finito, queto valore rappreenta il peo del cammino minimo tra i e j. Per calcolare il percoro uiamo la matrice J n. Notiamo che la notra ituazione è quella illutrata nella figura 7.. i? j Figure 7.: Calcolo del percoro minimo: primo tadio Conociamo il nodo iniziale del cammino, i, e quello finale, j, e vogliamo determinare il percoro minimo che li congiunge. Queto è equivalente a determinare tutti i nodi intermedi. Conideriamo allora l elemento J n ij e upponiamo che valga k. Per la definizione di J n poiamo allora paare dalla figura 7. alla figura 7.. i? k j Figure 7.: Calcolo del percoro minimo: econdo tadio È a queto punto ovvio come proeguire. Se onideriamo l elemento Jik n abbiamo il predeceore di k lungoilpercorominimoecoì via. Poiamo quindi, utilizzando la matrice J n procedere all indietro fino ad arrivare al nodo i, ricotruendo coì il cammino minimo che ci eravamo propoti di trovare. A queto punto poiamo decrivere l algoritmo in modo intetico nel eguente modo.. Calcola la D 0 elaj 0 uando la (7.) e la (7.),. Uando ripetutamente le (7.), (7.7) calcola ucceivamente D e J, D e J..., fino ad ottenere D n e J n ;. Uando D n e J n calcola, come piegato opra, i cammini minimi tra tutte le coppie di nodi di interee. Notiamo che e durante il proceo di calcolo per paare da D 0 e J 0 a D n e J n (punto.) compareulla diagonale di una D h un elemento negativo, vorrà dire, per come ono tate definite e calcolate le D h, che eite un ciclo di peo negativo. In queto cao è inutile proeguire e il procedimento i arreta con l indicazione dell eitenza di un ciclo negativo.