Applicazioni del Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
|
|
|
- Carla Martina
- 7 anni fa
- Visualizzazioni
Transcript
1 Applicazioni del Maimo fluo Progeazione di Algorimi a.a. 0-6 Maricole congrue a Docene: Annalia De Boni
2 Maching bipario
3 Problema del max maching. Inpu: grafo non direzionao G = (V, E). M E e` un maching e ogni nodo appare in al piu` un un arco di M. Maching Max maching: rova un maching di cardinalia` maima. PROGETTAZIONE DI ALGORITMI A.A. 0-6
4 Maching bipario Problema del max maching bipario. Inpu: grafo non direzionao bipario G = (L R, E). M E e` un maching e ogni nodo appare in al piu` un arco di M. Max maching bipario: rova un maching di maima cardinalia`. ' ' ' maching -', -', -' ' L ' R PROGETTAZIONE DI ALGORITMI A.A. 0-6
5 Maching bipario ' ' ' max maching -', -', - -' ' L ' R PROGETTAZIONE DI ALGORITMI A.A. 0-6
6 Maching Bipario Formulazione in ermini del max fluo. Crea un grafo direzionao G' = (L R {, }, E' ). Oriena gli archi ra L ad R da L vero R, e aegna capacia` pari ad uno a quei archi. Aggiungi un arco con capacia` uno da a ciacun nodo di L. Aggiungi un arco con capacia` uno da ciacun nodo di R a. G' ' ' ' ' L ' R PROGETTAZIONE DI ALGORITMI A.A
7 Teorema. La cardinalia` del max maching in G = Valore del max fluo in G'. Maching Bipario Dim. Dimoriamo prima che max maching max fluo Sia M un max maching e ia k la ua cardinalia. Conideriamo la funzione fluo f che invia unia` lungo ciacuno dei k percori che paano per i k archi di G corripondeni agli archi di G in M. Per ogni arco (i,j ) in M, f aegna agli archi (,i), (i,j ), (j,) di G f oddifa le propriea` del fluo e ha valore k ' ' ' ' ' ' ' ' G ' PROGETTAZIONE DI ALGORITMI A.A. 0-6 ' G' 7
8 Maching bipario Dimoriamo che valore dimenione max maching max fluo Sia f un maimo fluo di G' e ia k il uo valore. Capacia` degli archi = k e` inero ed eie f di valore k ale che f(e) inero (0 o ) per ogni e. Conideriamo l inieme di archi M = {e=(u,v): u in L, v in R, f(e)=} Conideriamo il aglio (L, R ). Lemma del valore del aglioà M =k Ciacun nodo di L ed R e` conenuo in al piu` un arco. Se u e` in L allora in u arriva fluo 0 o da. Per la conervazione del fluo da u ece quea ea quania` di fluo e quindi c e` al piu` un arco con origine u aravero il quale fluice unia` di fluo. Se u e` in R allora da u fuoriece fluo 0 o vero. Per la conervazione del fluo in v enra quea ea quania` di fluo e quindi c e` al piu` un arco con deinazione v aravero il quale fluice unia` di fluo. ' ' ' ' ' ' ' ' G' ' ' G 8
9 Maching bipario Poiamo rovare il max maching di un grafo bipario G eeguendo Ford-Fulkeron ul grafo G oenuo a parire da G. Il max maching e` oenuo come illurao nella econda pare della dimorazione del eorema precedene. Tempo di eecuzione: O(nm) in quano la capacia` di ogni arco di G e` al piu` C= e di coneguenza O(nmC)=O(nm) PROGETTAZIONE DI ALGORITMI A.A
10 Maching perfei Def. Un maching M E e` perfeo e ciacun nodo appare eaamene in un arco di M. Domanda. Quando un grafo bipario ha un maching perfeo? Sruura dei grafi biparii con maching perfei. Ovviamene deve eere L = R. Quali alre condizioni ono necearie? Quali condizioni ono ufficieni? PROGETTAZIONE DI ALGORITMI A.A
11 Maching Perfeo Noazione. Sia S un ooinieme di nodi di L. Indichiamo con N(S) l inieme dei nodi di R adiaceni ai nodi di S. Oervazione. Se un grafo bipario G = (L R, E) ha un maching perfeo allora N(S) S per ui i ooiniemi S L. Dim. Ciacun nodo in S deve eere accoppiao ad un nodo differene in N(S). ' ' ' Neun maching perfeo: S = {,, } N(S) = { ', ' }. ' L ' R
12 Teorema dei marimoni Il eorema dei marimoni. [Frobeniu 97, Hall 9] Sia G = (L R, E) un grafo bipario con L = R. G ha un maching perfeo e e olo e N(S) S per ui i ooiniemi S L. Dim. L implicazione l abbiamo gia` dimoraa nella lide precedene. ' ' ' No perfec maching: S = {,, } N(S) = { ', ' }. ' L ' R
13 Dimoriamo l implicazione Supponiamo G non abbia un maching perfeo. Queo vuol dire che il max maching ha dimenione < L Teorema dei marimoni Coruiamo la ree di fluo G nello eo modo di prima. Sia (A, B) un minimo aglio di G. Teorema del Max Fluo-Min Taglio à cap(a,b)< L Definiamo L A = L A, L B = L B, R A = R A. Poiamo raformare (A,B) in un alro aglio minimo (Z,W) in cui N(L Z ) Z. Per far queo aggiungiamo ad A ciacun nodo di N(L A ) che i rova in B. Sia y un ale nodo. Ovviamene in G y ha un arco ucene che finice in e almeno un arco enrane che pare da un nodo x di L A. Porando y in A, la nuova capacia` del aglio e` oenua aggungendo c(y,)= e oraendo almeno c(x,y)=. Di coneguenza la capacia` del aglio non aumena. coninua
14 Teorema dei marimoni Il nuovo aglio (Z,W) e` ale che non ci ono archi uceni da Z che hanno come origine un nodo di L Z. Ne conegue che ui gli archi uceni hanno come origine e deinazione un nodo in L W oppure hanno come origine un nodo in R Z e come deinazione. Si ha quindi cap(z, W) = L W + R Z. Inolre i ha che N(L Z ) R Z per cui N(L Z ) R Z = cap(z, W) - L W < L - L W = L Z. Abbiamo rovao un inieme L Z che e` piu` grande di N(L Z ). Cio` conraddice l ipoei che ogni per ooinieme S di L i ha N(S) S PROGETTAZIONE DI ALGORITMI A.A. 0-6
15 Percori digiuni PROGETTAZIONE DI ALGORITMI A.A. 0-6
16 Percori enza archi in comune Def. Due percori vengono dei digiuni e non hanno archi in comune Il problema dei percori digiuni. Dao un grafo direzionao e due nodi e, rovare il maimo numero di percori da a enza archi in comune. Eempio: rei di comunicazione 6 7 PROGETTAZIONE DI ALGORITMI A.A
17 Percori enza archi in comune Eempio: queiono percori digiuni nell eempio precedene 6 7 PROGETTAZIONE DI ALGORITMI A.A
18 Formulazione in ermini di max fluo: aegnamo fluo pari ad ad ogni arco. Percori enza archi in comune Teorema. Sia dao un grafo direzionao G e iano e due nodi di G. Il maimo numero di percori digiuni da a in G e` uguale al valore del max fluo nella ree oenua aegnando capacia` agli archi di G. Dim. Dimoriamo Supponiamo che ci iano k percori digiuni P,..., P k. Poniamo f(e) = e e compare u qualche percoro P i ; alrimeni poniamo f(e) = 0. Siccome i percori ono digiuni allora f e` un fluo (conervazione del fluo oddifaa) e ha valore k (k diini archi e uceni da con f(e)=) PROGETTAZIONE DI ALGORITMI A.A
19 Percori digiuni Dimoriamo Supponiamo che il max fluo abbia valore k. Siccome capacia` ono ineri uguali ad eie una funzione fluo f che aegna valori ineri (0 o ) ad ogni arco e ha valore k. Conideriamo un arco (, u) con f(, u) =. Per la conervazione del fluo eie un arco (u,v) per cui f(u,v)=. Per lo eo moivo eie un arco (v,z) per cui f(v,z)=. E coi` via. In queo modo poiamo individuare un percoro da a fao di archi con flui uniari. Siccome il valore di f e` k allora da econo k archi con fluo pari ad. Quindi con il procedimeno decrio poiamo produrre k percori da a (non neceariamene emplici) che non hanno archi in comune (e li aveero non arebbe oddifaa la propriea` ulla conervazione del fluo)
20 Conneivia` di una ree Conneivia` di una ree. Dao un grafo direzionao G = (V, E) e due nodi e, rovare il minimo numero di archi la cui rimozione diconnee da. Def. Un inieme di archi F E diconnee da e ogni percoro da a ua un arco di F. 6 7 PROGETTAZIONE DI ALGORITMI A.A
21 Percori digiuni e conneivia` di una ree Teorema. [Menger 97] Sia G un grafo direzionao e iano e due nodi di G. Il max numero di percori digiuni in G da a e` uguale al minimo numero di archi la cui rimozione diconnee da. Dim. Dimoriamo Supponiamo che la rimozione di F E diconnea da e che F = k à ciacun percoro da a ua almeno un arco in F. Sia S un qualiai inieme di percori digiuni da a. Ciacun arco di F e` uao da al piu` un percoro in S à S k PROGETTAZIONE DI ALGORITMI A.A
22 Percori digiuni e conneivia` di una ree Dimoriamo Supponiamo che il max numero di percori digiuni ia k. Abbiamo dimorao che max numero percori digiuni = valore max fluo nella ree oenua aegnando capacia` agli archi di G. Quindi il valore del max fluo in quea ree e` k. Teorema Maimo Fluo & Minimo Taglio eie aglio (A, B) con cap(a,b)= k. Sia F l inieme degli archi che vanno da A vero B. Ogni arco ha capacia` e la omma delle capacia` degli archi direi da A vero B e` k à F = k Ovviamene e rimuoviamo gli archi di F diconneiamo da per cui F e` un inieme che diconnee da e ha cardinalia` k. A PROGETTAZIONE DI ALGORITMI A.A
Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Maimo fluo Progeazione di Algorimi a.a. 2016-17 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
Maimo fluo Progeazione di Algorimi a.a. 2016-17 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
2.4 Flussi di valore massimo
 .4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
.4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
Ulteriori Esercizi su Grafi. Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Problema del flusso massimo
 Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
Applicazioni del Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Applicazioni del Massimo flusso Progettazione di Algoritmi a.a. 06-7 Matricole congrue a Docente: Annalisa De Bonis Matching bipartito Problema del max matching. Input: grafo non direzionato G = (V, E).
Applicazioni del Massimo flusso Progettazione di Algoritmi a.a. 06-7 Matricole congrue a Docente: Annalisa De Bonis Matching bipartito Problema del max matching. Input: grafo non direzionato G = (V, E).
Ricerca Operativa. Facoltà di Ingegneria dell Informazione, Informatica e Statistica. (Massimo Flusso) Giovanni Fasano.
 Facolà di Ingegneria dell Informazione, Informaica e Saiica Appuni dalle lezioni di Ricerca Operaiva (Maimo Fluo) ede di Laina Giovanni Faano faano@unive.i hp://venu.unive.i/ faano anno accademico 2013-2014
Facolà di Ingegneria dell Informazione, Informaica e Saiica Appuni dalle lezioni di Ricerca Operaiva (Maimo Fluo) ede di Laina Giovanni Faano faano@unive.i hp://venu.unive.i/ faano anno accademico 2013-2014
Progetto e Ottimizzazione di Reti A. A
 Progeo e Oimizzazione di Rei A. A. 006-007 Docene Fabrizio Roi roi@di.univaq.i Orario Maredi 15-17 aula.5 Mercoledi 11.30-13.30 aula.5 Giovedi 11.30-13.30 aula.5 Orario di ricevimeno Mercoledi 17-19 Progeo
Progeo e Oimizzazione di Rei A. A. 006-007 Docene Fabrizio Roi roi@di.univaq.i Orario Maredi 15-17 aula.5 Mercoledi 11.30-13.30 aula.5 Giovedi 11.30-13.30 aula.5 Orario di ricevimeno Mercoledi 17-19 Progeo
Laboratorio di Algoritmi e Strutture Dati
 Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Massimo Flusso. Ulteriori vincoli. Descrizione del problema. Rete di flusso. Flusso in G
 Maimizzare il # di PC prodoi Maimo Flo rre dai 2 Decrizione del problema Una fabbrica (orgene) di PC dee abilire il nmero di PC da aemblare giornalmene. Ti i PC prodoi erranno endi in n negozio (deinazione).
Maimizzare il # di PC prodoi Maimo Flo rre dai 2 Decrizione del problema Una fabbrica (orgene) di PC dee abilire il nmero di PC da aemblare giornalmene. Ti i PC prodoi erranno endi in n negozio (deinazione).
Tema 3. Insiemi, elementi di logica, calcolo combinatorio, relazioni e funzioni
 Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
Dato un cammino P indichiamo con c(p ) il costo dell insieme di archi A(P ) del cammino, ovvero c(p )=c(a(p )) = uv P c uv. c 1
 Capiolo 7 Cammini minimi 7. Definizioni fondamenali Sia dao un grafo non orienao G(N,A) conneo, con coi aociai agli archi c uv R per ogni uv A. Siano anche dai due nodi peciali, N. Faremo la eguene: Aunzione
Capiolo 7 Cammini minimi 7. Definizioni fondamenali Sia dao un grafo non orienao G(N,A) conneo, con coi aociai agli archi c uv R per ogni uv A. Siano anche dai due nodi peciali, N. Faremo la eguene: Aunzione
Dispense del corso di Analisi II
 Dipene del coro di Analii II verione preliminare Paolo Tilli Diparimeno di Maemaica Poliecnico di Torino email: paolo.illi@polio.i gennaio 25 Capiolo 5 Traformaa di Laplace 5. Inroduzione Sia x() una funzione
Dipene del coro di Analii II verione preliminare Paolo Tilli Diparimeno di Maemaica Poliecnico di Torino email: paolo.illi@polio.i gennaio 25 Capiolo 5 Traformaa di Laplace 5. Inroduzione Sia x() una funzione
Cammini Minimi. Un problema molto comune. Formalizziamo. Peso di un cammino. Esempio. Ritorniamo all esempio iniziale. Input:
 Cammini Minimi Un problema molto comune i uole andare da alerno a Milano in auto percorrendo il minor numero di chilometri oluzione inefficiente: i coniderano TUTTI i percori poibili e e ne calcola la
Cammini Minimi Un problema molto comune i uole andare da alerno a Milano in auto percorrendo il minor numero di chilometri oluzione inefficiente: i coniderano TUTTI i percori poibili e e ne calcola la
PREMESSA In questa lezione verranno esposte le regole per l analisi dei sistemi continui con il metodo della Trasformata di Laplace.
 ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
Laboratorio di Algoritmi e Strutture Dati
 Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/ ~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Pr oblema: Supponiamo che
Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/ ~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Pr oblema: Supponiamo che
Lezione 5. Calcolo dell antitrasformata di Laplace. F. Previdi - Automatica - Lez. 5 1
 Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/10. Lecture 11: 13-14 Maggio 2010. Meccanismi per la Condivisione dei Costi
 Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/0 Lecture : 3-4 Maggio 200 Meccanimi per la Condiviione dei Coti Docente Paolo Penna Note redatte da: Paolo Penna Primo Eempio Vogliamo vendere
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/0 Lecture : 3-4 Maggio 200 Meccanimi per la Condiviione dei Coti Docente Paolo Penna Note redatte da: Paolo Penna Primo Eempio Vogliamo vendere
Problemi di flusso. Reti. Problemi di flusso. Problemi di flusso. Problemi di percorso. minσ (i,j) E c ij x ij. i N (i,j) E.
 Problemi di fluo Rei Problemi di percoro Fluo a coo minimo MinoFlow(G(V,E),b,l,u,c,min) Ianza: una ree G(V,E) per cui è dao un valore inero b i (fluo prodoo dal nodo) per ogni nodo v i un coo c ij per
Problemi di fluo Rei Problemi di percoro Fluo a coo minimo MinoFlow(G(V,E),b,l,u,c,min) Ianza: una ree G(V,E) per cui è dao un valore inero b i (fluo prodoo dal nodo) per ogni nodo v i un coo c ij per
4.1 Interval Scheduling. Chapter 4. Greedy Algorithms. Schedulazione intervalli. Schedulazione intervalli: Algoritmi Greedy. Schedulazione intervalli.
 Chaper.1 Inerval Scheduling Greedy Algorihm 1 Schedulazione inervalli Schedulazione inervalli: Algorimi Greedy Schedulazione inervalli.! Job j inizia a j e finice a f j.! Due job ono compaibili e non hanno
Chaper.1 Inerval Scheduling Greedy Algorihm 1 Schedulazione inervalli Schedulazione inervalli: Algorimi Greedy Schedulazione inervalli.! Job j inizia a j e finice a f j.! Due job ono compaibili e non hanno
Problema 1: Una collisione tra meteoriti
 Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Ci domandiamo allora se e sempre possibile rappresentare una funzione in questo modo.
 1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
Basi di Elettronica (1 parte)
 Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
0.0.1 Esercizio Q1, tema d esame del 10 settembre 2009, prof. Dario d Amore Testo R 3
 1 0.0.1 Esercizio Q1, ema d esame del 10 seembre 2009, prof. Dario d more 0.0.1.1 Teso E1 Il circuio di figura opera in regime sazionario. Sapendo che R 1 = 2 kω, = 4 kω, = 2 kω, = 2 kω E=12 V, =3 m Deerminare,
1 0.0.1 Esercizio Q1, ema d esame del 10 seembre 2009, prof. Dario d more 0.0.1.1 Teso E1 Il circuio di figura opera in regime sazionario. Sapendo che R 1 = 2 kω, = 4 kω, = 2 kω, = 2 kω E=12 V, =3 m Deerminare,
Università Politecnica delle Marche, Facoltà di Agraria. C.d.L. Scienze Forestali e Ambientali, A.A. 2013/2014, Fisica
 C.d.. Scienze oretali e Ambientali, A.A. 03/04, iica Seconda legge della dinamica: a forza riultante agente u un corpo è in relazione con la rapidità con cui quel corpo modifica la propria velocità (l
C.d.. Scienze oretali e Ambientali, A.A. 03/04, iica Seconda legge della dinamica: a forza riultante agente u un corpo è in relazione con la rapidità con cui quel corpo modifica la propria velocità (l
REGISTRAZIONE DEL MOTO. Lo scopo è riempire una tabella t/s (istante di tempo/posizione occupata)
 REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
Trasformazione di Laplace
 Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
Traformazione di Laplace Gabriele Sicuro. Definizioni fondamentali Sia data una funzione f : C; ea i dice originale e ono oddifatte le eguenti condizioni: () f (t) per t
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
Lezione 4. Risposte canoniche dei sistemi del primo e del secondo ordine
 Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Processi di cost management - Programmazione multiperiodale
 Processi di cost management - Programmazione multiperiodale Queste slide (scrte da Carlo Mannino) riguardano il problema di gestione delle attivà di un progetto allorché i costi di esecuzione sono legati
Processi di cost management - Programmazione multiperiodale Queste slide (scrte da Carlo Mannino) riguardano il problema di gestione delle attivà di un progetto allorché i costi di esecuzione sono legati
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Equazioni Differenziali (5)
 Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Alberi di copertura. Mauro Passacantando. Dipartimento di Informatica Largo B. Pontecorvo 3, Pisa
 Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
Fabio Peron. La trasmissione del calore: 1. conduzione termica. Le modalità di scambio del calore. L esperienza di J.B. Fourier. La conduzione termica
 Coro i Progeaione Ambienale prof. Fabio Peron Le moalià i cambio el calore Una ifferena i emperaura coiuice uno uilibrio che la naura cerca i annullare generano un fluo i calore. La ramiione el calore:.
Coro i Progeaione Ambienale prof. Fabio Peron Le moalià i cambio el calore Una ifferena i emperaura coiuice uno uilibrio che la naura cerca i annullare generano un fluo i calore. La ramiione el calore:.
Università Politecnica delle Marche, Facoltà di Agraria. C.d.L. Scienze Forestali e Ambientali, A.A. 2007/2008, Fisica 1
 Energia: Univerità Politenia delle Marhe, aoltà di Agraria C.d.. Sienze oretali e Ambientali, A.A. 007/008, iia quel bambino ha tanta energia il gioatore è rimato enza energia alla fine della partita energia
Energia: Univerità Politenia delle Marhe, aoltà di Agraria C.d.. Sienze oretali e Ambientali, A.A. 007/008, iia quel bambino ha tanta energia il gioatore è rimato enza energia alla fine della partita energia
Note su alcuni principi fondamentali di macroeconomia Versione parziale e provvisoria. Claudio Sardoni Sapienza Università di Roma
 Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Calcolo della tensione ammissibile Dovendo essere il grado di sicurezza non inferiore a 3 si ricava che il coefficiente di sicurezza γ è 3 per cui:
 Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Sintesi di circuiti sequenziali
 Sintei di circuiti equenziali Salvatore Orlando Arch. Elab. S. Orlando Circuito equenziale incrono I Circuiti combinatori I n O O m R e g Per determinare il comportamento del circuito equenziale di opra,
Sintei di circuiti equenziali Salvatore Orlando Arch. Elab. S. Orlando Circuito equenziale incrono I Circuiti combinatori I n O O m R e g Per determinare il comportamento del circuito equenziale di opra,
Velocità. s t. m = m s. Il concetto di velocità. Abbiamo rappresentato le posizioni di un oggetto nel tempo. Come rappresentare ora le sue velocità?
 Pagina 1 di 12 Verione 17/02/04 Velocià Il conceo di velocià Abbiamo rappreenao le poizioni di un oggeo nel empo. Come rappreenare ora le ue velocià? Il conceo di velocià viene uao normalmene nel linguaggio
Pagina 1 di 12 Verione 17/02/04 Velocià Il conceo di velocià Abbiamo rappreenao le poizioni di un oggeo nel empo. Come rappreenare ora le ue velocià? Il conceo di velocià viene uao normalmene nel linguaggio
a) Caso di rottura duttile con armatura compressa minore di quella tesa
 LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
Aniello Murano Altri problemi NP- Completi
 Aniello Murano Alri problemi NP- Complei 6 Leione n Parole chiave: Np-complee Corso di Laurea: Informaica Codice: Email Docene: murano@ nainfni AA 2008-2009 Perché vedere alri problemi Np- complee? Per
Aniello Murano Alri problemi NP- Complei 6 Leione n Parole chiave: Np-complee Corso di Laurea: Informaica Codice: Email Docene: murano@ nainfni AA 2008-2009 Perché vedere alri problemi Np- complee? Per
Corso di Fondamenti di Telecomunicazioni
 Coro di Fondameni di elecomunicazioni EORIA DEI SEGNALI DEERMINAI Pro. Giovanni Schembra Fondameni di LC - Pro. G. Schembra Sruura della lezione Proprieà dei egnali nel dominio del empo Valore medio, poenza,
Coro di Fondameni di elecomunicazioni EORIA DEI SEGNALI DEERMINAI Pro. Giovanni Schembra Fondameni di LC - Pro. G. Schembra Sruura della lezione Proprieà dei egnali nel dominio del empo Valore medio, poenza,
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
FISICA TECNICA AMBIENTALE
 COSO DI LUE IN SCIENZE DELL CHITETTU FISIC TECNIC MIENTLE Tramiione del calore: La conduzione I parte Prof. Gianfranco Caruo.. 03/04 Il Calore Il Calore è una forma di energia in tranito: ad eempio un
COSO DI LUE IN SCIENZE DELL CHITETTU FISIC TECNIC MIENTLE Tramiione del calore: La conduzione I parte Prof. Gianfranco Caruo.. 03/04 Il Calore Il Calore è una forma di energia in tranito: ad eempio un
Dai ponti di Königsberg al postino cinese
 Dai ponti di Königsberg al postino cinese Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/1 - Corso di Ricerca Operativa Università
Dai ponti di Königsberg al postino cinese Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/1 - Corso di Ricerca Operativa Università
LAVORO ED ENERGIA. 1J = 1N 1m
 ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
Trasformata di Laplace unilatera Teoria
 Definizione Tafomaa di Laplace unilaea Teoia L[f()] = f() $ e ($) d = F() Dove: f() = funzione eale afomabile. E nulla pe
Definizione Tafomaa di Laplace unilaea Teoia L[f()] = f() $ e ($) d = F() Dove: f() = funzione eale afomabile. E nulla pe
L induzione elettromagnetica - Legge di Faraday-Lentz
 L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo
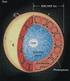 7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
PROBLEMI RISOLTI DI DINAMICA
 PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
PROBLEMI RISOLTI DI DINAMICA 1 Un autoobile di aa 100 Kg auenta in odo unifore la ua velocità di 30 / in 0 a) Quale forza agice durante i 0? b) Quale forza arebbe necearia per ipriere un accelerazione
Funzioni a valori vettoriali
 Funzioni vlori veorili Definizione. Un ppliczione defini u un inieme di numeri reli il cui codominio è un n inieme dir è per definizione un funzione vlori veorili. F è un veore che h n componeni e i crive
Funzioni vlori veorili Definizione. Un ppliczione defini u un inieme di numeri reli il cui codominio è un n inieme dir è per definizione un funzione vlori veorili. F è un veore che h n componeni e i crive
Rappresentazione del sistema. Classificazione dei sistemi di controllo
 Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
25.2. Osservazione. Siccome F(x, y, z) = 0 è un equazione e non un identità, una superficie non contiene tutti gli 3 punti dello spazio.
 . Cono e cilindro.. Definiione. Diremo superficie il luogo geomerico dei puni dello spaio le cui coordinae soddisfano un equaione del ipo F che viene dea equaione caresiana della superficie. Se F è un
. Cono e cilindro.. Definiione. Diremo superficie il luogo geomerico dei puni dello spaio le cui coordinae soddisfano un equaione del ipo F che viene dea equaione caresiana della superficie. Se F è un
Metodo della Trasformata di Laplace (mtl)
 Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008
 MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
Introduzione. Esempio di costruzione one del contorno delle radici. Esempio... 4
 Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
2. Politiche di gestione delle scorte
 deerminisica variabile nel empo Quando la domanda viaria nel empo, il problema della gesione dell invenario divena preamene dinamico. e viene deo di lo-sizing. Consideriamo il caso in cui la domanda pur
deerminisica variabile nel empo Quando la domanda viaria nel empo, il problema della gesione dell invenario divena preamene dinamico. e viene deo di lo-sizing. Consideriamo il caso in cui la domanda pur
16. Onde elastiche. m s
 1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
Capitolo IV L n-polo
 Capitolo IV L n-polo Abbiamo oervato che una qualiai rete, vita da due nodi, diventa, a tutti gli effetti eterni, un bipolo unico e queto è in qualche miura ovvio e abbiamo anche motrato come cotruire
Capitolo IV L n-polo Abbiamo oervato che una qualiai rete, vita da due nodi, diventa, a tutti gli effetti eterni, un bipolo unico e queto è in qualche miura ovvio e abbiamo anche motrato come cotruire
Analisi in frequenza di segnali campionati
 Analii in requenza di egnali campionai - 1 Analii in requenza di egnali campionai 1 Analii dei egnali nel dominio della requenza I principali meodi di analii dei egnali di miura poono eere riauni nei concei
Analii in requenza di egnali campionai - 1 Analii in requenza di egnali campionai 1 Analii dei egnali nel dominio della requenza I principali meodi di analii dei egnali di miura poono eere riauni nei concei
2.3.3 Cammini ottimi nei grafi senza circuiti
 .. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
.. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
Ricerca Operativa. G. Liuzzi. Lunedí 20 Aprile 2015
 1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33
 Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33 Ottimizzazione su grafi:massimo flusso (parte 1) p. 2/33 Reti di flusso Una rete di flusso è una
Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33 Ottimizzazione su grafi:massimo flusso (parte 1) p. 2/33 Reti di flusso Una rete di flusso è una
ANELLO DEI QUOZIENTI E LOCALIZZAZIONE
 Alma Mater Studiorum Univerità di Bologna FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI Coro di Laurea Secialitica in Matematica ANELLO DEI QUOZIENTI E LOCALIZZAZIONE Matteo Curina Lunedì, 2 Arile
Alma Mater Studiorum Univerità di Bologna FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI Coro di Laurea Secialitica in Matematica ANELLO DEI QUOZIENTI E LOCALIZZAZIONE Matteo Curina Lunedì, 2 Arile
Grafi bipartiti. Applicazioni. Matrimoni stabili: uomini = rosso, donna = blu. Scheduling: macchine = rosso, job = blu. Un grafo bipartito
 Grafi bipartiti Def. Un grafo non direzionato è bipartito se l insieme di nodi può essere partizionato in due sottoinsiemi X e Y tali che ciascun arco del grafo ha una delle due estremità in X e l altra
Grafi bipartiti Def. Un grafo non direzionato è bipartito se l insieme di nodi può essere partizionato in due sottoinsiemi X e Y tali che ciascun arco del grafo ha una delle due estremità in X e l altra
Modulo n.3 - I materiali nelle lavorazioni metalliche
 oduo n. - I maeriai nee avorazioni meaiche PROPRIETÀ ISIHE, EANIHE, TENOOGIHE (Diiazione vericae) OBIETTIVI: A) onocenza dee proprieà dei maeriai finaizzaa a oro uiizzo; B) apacià di eeguire cacoi ue principai
oduo n. - I maeriai nee avorazioni meaiche PROPRIETÀ ISIHE, EANIHE, TENOOGIHE (Diiazione vericae) OBIETTIVI: A) onocenza dee proprieà dei maeriai finaizzaa a oro uiizzo; B) apacià di eeguire cacoi ue principai
Proprietà razionali per il prezzo
 Proprieà razionali per il prezzo delle opzioni call 8/09/0 Corso di Finanza quaniaiva L aricolo di Rober Meronpubblicao nel 973, heoryofraionalopionpricing idenifica una serie di proprieà che devono valere
Proprieà razionali per il prezzo delle opzioni call 8/09/0 Corso di Finanza quaniaiva L aricolo di Rober Meronpubblicao nel 973, heoryofraionalopionpricing idenifica una serie di proprieà che devono valere
Principi di Ingegneria Chimica Anno Accademico Cognome Nome Matricola Firma
 Principi i Ingegneria Chimica Anno Accaemico 2010 2011 Cognome Nome Maricola Firma Problema 1. Uno cambiaore i calore è coiuio a ue ubi coaiali i iameri D 1 e D 2, con parei i peore racurabile e lunghezza
Principi i Ingegneria Chimica Anno Accaemico 2010 2011 Cognome Nome Maricola Firma Problema 1. Uno cambiaore i calore è coiuio a ue ubi coaiali i iameri D 1 e D 2, con parei i peore racurabile e lunghezza
Metodo della trasformata di Laplace
 Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Esercitazione 6 Ancora sul Network Flow
 Esercitazione 6 Ancora sul Network Flow Problema 14 (appello 28/09/2015) Un importante azienda di sviluppo software ha n progetti da portare a termine entro la fine dell anno. Il manager dell azienda stima
Esercitazione 6 Ancora sul Network Flow Problema 14 (appello 28/09/2015) Un importante azienda di sviluppo software ha n progetti da portare a termine entro la fine dell anno. Il manager dell azienda stima
SCELTA DI UN INNESTO A FRIZIONE
 SELTA DI UN INNESTO A FRIZIONE Si conideri l'impiano in Fig. 1, coiuio da un moore elerico aincrono riae, un inneo a rizione ad azionameno eleromagneico, un riduore ad ingranaggi ed una macchina operarice.
SELTA DI UN INNESTO A FRIZIONE Si conideri l'impiano in Fig. 1, coiuio da un moore elerico aincrono riae, un inneo a rizione ad azionameno eleromagneico, un riduore ad ingranaggi ed una macchina operarice.
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
Corso di Fondamenti di Automatica A.A. 2015/16. Diagrammi di Bode
 1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
la velocità con cui il bombardiere viaggia alla quota costante di H = 1200m
 Problema n. : Un bombardiere ola a 43 km/h alla quoa coane di m ero un puno poo ulla ericale di una nae ormeiaa in mare apero. Soo quale anolo iuale (ripeo alla direzione orizzonale) il piloa dorebbe lanciare
Problema n. : Un bombardiere ola a 43 km/h alla quoa coane di m ero un puno poo ulla ericale di una nae ormeiaa in mare apero. Soo quale anolo iuale (ripeo alla direzione orizzonale) il piloa dorebbe lanciare
ESPERIMENTO 2: ATTRITO
 ESPERIMETO 2: ATTRITO Scopo dell eperimento: tudiare l attrito tatico, dinamico e volvente. MATERIALE A DISPOSIZIOE: 1 coppia di blocchetti 1 dinamometro di preciione da 5 1 dinamometro di preciione da
ESPERIMETO 2: ATTRITO Scopo dell eperimento: tudiare l attrito tatico, dinamico e volvente. MATERIALE A DISPOSIZIOE: 1 coppia di blocchetti 1 dinamometro di preciione da 5 1 dinamometro di preciione da
Problemi di Flusso: Il modello del Trasporto
 Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Ottica. LEYBOLD Schede di fisica P Determinazione della velocità della luce con lo specchio ruotante secondo il metodo di Foucault e Michelson
 Ottica LEYBOLD Schede di fiica Velocità della luce Miura con il metodo di Foucault/Michelon LEYBOLD Schede di fiica Determinazione della velocità della luce con lo pecchio ruotante econdo il metodo di
Ottica LEYBOLD Schede di fiica Velocità della luce Miura con il metodo di Foucault/Michelon LEYBOLD Schede di fiica Determinazione della velocità della luce con lo pecchio ruotante econdo il metodo di
Differenza tra microeconomia (analisi dei comportamenti individuali) e macroeconomia (analisi dei comportamenti aggregati).
 Capitolo 2 Domana e offerta pagina 1 CAPITOLO 2 DOMANDA E OFFERTA Differenza tra microeconomia (analii ei comportamenti iniviuali) e macroeconomia (analii ei comportamenti aggregati). La prima i fona ui
Capitolo 2 Domana e offerta pagina 1 CAPITOLO 2 DOMANDA E OFFERTA Differenza tra microeconomia (analii ei comportamenti iniviuali) e macroeconomia (analii ei comportamenti aggregati). La prima i fona ui
Università di Pisa - Polo della Logistica di Livorno Corso di Laurea in Economia e Legislazione dei Sistemi Logistici. Anno Accademico: 2013/14
 Universià di isa - olo della Logisica di Livorno Corso di Laurea in Economia e Legislazione dei Sisemi Logisici Anno Accademico: 03/4 CORSO DI SISTEMI DI MOVIMENTAZIONE E STOCCAGGIO Docene: Marino Lupi
Universià di isa - olo della Logisica di Livorno Corso di Laurea in Economia e Legislazione dei Sisemi Logisici Anno Accademico: 03/4 CORSO DI SISTEMI DI MOVIMENTAZIONE E STOCCAGGIO Docene: Marino Lupi
INTRODUZIONE ALLE LEGGI FINANZIARIE
 Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Flessione su 4 punti. Configurazione sperimentale. Schematizzazione di calcolo. Studio delle sollecitazioni semplici. Taglio.
 Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Il modello di crescita deriva dalla logica del tasso di interesse semplice
 Eserciazione 7: Approfondimeni sui modelli di crescia. Crescia arimeica, geomerica, esponenziale. Calcolo del asso di crescia e del empo di raddoppio. Viviana Amai 03/06/2009 Modelli di crescia Nella prima
Eserciazione 7: Approfondimeni sui modelli di crescia. Crescia arimeica, geomerica, esponenziale. Calcolo del asso di crescia e del empo di raddoppio. Viviana Amai 03/06/2009 Modelli di crescia Nella prima
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
Ad ogni arco (i,j) del grafo e' associato un valore intero c(i,j) detto capacita' dell'arco
 6) FLUSSI Definizione di flusso Si definisce rete di flusso un grafo orientato e connesso con i) un solo vertice con esclusivamente archi uscenti ii) un solo vertice con esclusivamente archi entranti Tradizionalmente
6) FLUSSI Definizione di flusso Si definisce rete di flusso un grafo orientato e connesso con i) un solo vertice con esclusivamente archi uscenti ii) un solo vertice con esclusivamente archi entranti Tradizionalmente
Corso di Fondamenti di Telecomunicazioni
 Coro di Fondamenti di elecomunicazioni - SEGNALI E SPERI Pro. Mario Barbera [parte 3] Fondamenti di LC - Pro. M. Barbera - Segnali e pettri [parte 3] = 3 log Banda di un egnale Deinizione di banda di un
Coro di Fondamenti di elecomunicazioni - SEGNALI E SPERI Pro. Mario Barbera [parte 3] Fondamenti di LC - Pro. M. Barbera - Segnali e pettri [parte 3] = 3 log Banda di un egnale Deinizione di banda di un
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA
 DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
TERMODINAMICA E TERMOFLUIDODINAMICA. Cap. 6 CICLI TERMODINAMICI DIRETTI ED INVERSI
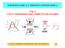 ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
ERMODINAMICA E ERMOFLUIDODINAMICA Cap. 6 CICLI ERMODINAMICI DIREI ED INVERSI max min Sorgente termica (Bruciatore) Q H = Q in a 2 Caldaia 2 L - = L in L + = L urbina out Pompa Condenatore = 2 = Q C = Q
= 20 m/s in una guida verticale circolare. v A A
 Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
A tal fine consideriamo un esempio come punto di partenza per le nostre considerazioni.
 Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
2.3 Cammini ottimi. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 . Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
. Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
PIL NOMINALE, PIL REALE E DEFLATORE
 PIL NOMINALE, PIL REALE E DEFLATORE Il PIL nominale (o a prezzi correni) Come sappiamo il PIL è il valore di ui i beni e servizi finali prodoi in un cero periodo all inerno del paese. Se per calcolare
PIL NOMINALE, PIL REALE E DEFLATORE Il PIL nominale (o a prezzi correni) Come sappiamo il PIL è il valore di ui i beni e servizi finali prodoi in un cero periodo all inerno del paese. Se per calcolare
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Si vuole trafilare una barra di acciaio di diametro pari a 10 millimetri, fino a portarla ad un diametro di 8 millimetri. D F D I
 Eercizio C. Trafilatura di una barra d acciaio Si vuole trafilare una barra di acciaio di diametro pari a millimetri, fino a portarla ad un diametro di 8 millimetri. v I v D D I ILIERA Calcolare la forza
Eercizio C. Trafilatura di una barra d acciaio Si vuole trafilare una barra di acciaio di diametro pari a millimetri, fino a portarla ad un diametro di 8 millimetri. v I v D D I ILIERA Calcolare la forza
1. Teorema di reciprocità
 1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
3. La coppia di avviamento [Nm] La coppia massima [Nm] 5
![3. La coppia di avviamento [Nm] La coppia massima [Nm] 5 3. La coppia di avviamento [Nm] La coppia massima [Nm] 5](/thumbs/71/65755864.jpg) UNESÀ D OMA LA SAPENZA FACOLÀ D NGEGNEA - COSO D LAUEA N NGEGNEA ENEGECA AA 8-9 DSCPLNA D MACCHNE E CONEO D ENEGA ELECA POA SCA D ESAME DEL 5 GUGNO 9.. Sono dai due raformaori rifae della ea oenza nominale
UNESÀ D OMA LA SAPENZA FACOLÀ D NGEGNEA - COSO D LAUEA N NGEGNEA ENEGECA AA 8-9 DSCPLNA D MACCHNE E CONEO D ENEGA ELECA POA SCA D ESAME DEL 5 GUGNO 9.. Sono dai due raformaori rifae della ea oenza nominale
Parte V: Rilassamento Lagrangiano
 Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Raggio di tentativo Le caratteristiche geometriche dell'imbocco sono determinate con le formule di Lazzeri: x o := h + y o
 Sfioratori a calice Gli fioratori a calice ono dei manufatti particolari che poono funzionare come luce a tramazzo e come luce a battente a econda dei carichi al di opra della oglia. Il paaggio da un tipo
Sfioratori a calice Gli fioratori a calice ono dei manufatti particolari che poono funzionare come luce a tramazzo e come luce a battente a econda dei carichi al di opra della oglia. Il paaggio da un tipo
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
1. Introduzione Il convertitore a semplice semionda Il sistema di controllo... 5
 . Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
. Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
Grafi (non orientati e connessi): minimo albero ricoprente
 .. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
.. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
velocità angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un intervallo di tempo)
 V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
