PREMESSA In questa lezione verranno esposte le regole per l analisi dei sistemi continui con il metodo della Trasformata di Laplace.
|
|
|
- Ilaria Rita Martini
- 6 anni fa
- Visualizzazioni
Transcript
1 ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario coruire un modello maemaico, ovvero occorre deerminare le equazioni maemaiche che permeono di deerminare l andameno nel empo delle ucie noi quelli degli ingrei Il modello può eere aico o dinamico Il modello aico decrive la relazione ra i valori degli ingrei (uppoi coani) e quelli delle ucie una vola che il iema abbia raggiuno la condizione di regime azionario Quea modellizzazione non dà alcuna inormazione ul regime raniorio e quindi ull andameno delle ucie durane il paaggio da uno ao di regime ad un alro Il modello dinamico permee, invece, di deerminare l andameno del egnale di ucia corripondene ad un precio egnale di ingreo e quindi di deerminare la ripoa del iema ad una ecciazione noa Il modello dinamico arà coiuio da una o più equazioni dierenziali che legano le variabili di ingreo, le variabili di ucia e le loro derivae ripeo al empo I iemi dinamici poono eere caraerizzai nel empo in empo-coninui, empo-dicrei e a eveni dicrei Nei primi la variabile empo ha un andameno coninuo, nei econdi l evoluzione del iema avviene ad iani diini nel empo e negli ulimi l evoluzione non dipende dal empo ma dal veriicari di deerminae condizioni (eveni) Lo udio dei iemi di conrollo avviene ipoizzando che il iema ia lineare, ovvero ia applicabile il principio di ovrappoizione degli eei Quea empliicazione, quai empre realizzabile purché i valori delle variabili non ecano da deerminai campi, permee di poer decrivere i enomeni iici con equazioni dierenziali a coeicieni coani TRASFORMATA DI LAPLACE Per eeuare l analii di un iema coninuo lineare occorre: ) individuare gli elemeni che compongono il iema e la unzione che volgono ) deerminare la unzione caraeriica di ogni elemeno 3) deerminare la unzione caraeriica dell inero iema uilizzando le regole dell algebra degli chemi a blocchi 4) analizzare la ripoa del iema nel empo daa una deerminaa olleciazione Un eempio di procedura può eere vio analizzando un pariore di enione come quello nella igura: Dove con Vi( è ao indicao il valore nel empo della enione di ingreo, con Vu( il valore nel Wih he uppor o he Lielong Learning Programme o he European Union Thi projec ha been unded wih uppor rom he European Commiion
2 ITIS G CARDANO empo della enione di ucia e con R e R i uoi elemeni caraeriici coruivi Le unzioni caraeriiche dei due elemeni ono: V R R I( ) e V R R I( ) ( ( Uilizzando il eorema di Kirchho alla maglia i oiene il modello maemaico dell inero iema: dalla quale è anche poibile ricavare l equazione: Vi V ( V ( ( R R ) I( ), ( R R Vi( I( R R Il egnale di ucia è pari alla cadua di poenziale ai capi della reienza R e quindi i oiene dalla relazione: Vu VR ( R I( ) ( E oiuendo a I( l equazione ricavaa precedenemene i oiene l equazione che decrive la ripoa del iema ad una deerminaa olleciazione: R Vu( Vi( R R Gli elemeni del iema poono eere a econda dei cai di ipo: meccanici, elerici, ermici, pneumaici, idraulici Per rovare il loro modello maemaico i può uilizzare una delle re caegorie di leggi della iica: - congruenza degli poameni (i ua nei iemi rigidi) - equilibrio (rierio a orze, momeni, dierenze di poenziale elerico, emperaure, preioni) - bilancio (rierio a energia, quanià di calore, mae, quanià di cariche eleriche) Le unzioni caraeriiche ono peo epree da equazioni dierenziali e ciò rende più diicile la rioluzione del problema dal puno di via maemaico Con la raormazione è, però, poibile raormare operazioni complee in alre più emplici agendo ulle variabili Un emplice eempio del conceo di raormazione può eere vio nella rioluzione di una equazione del quaro grado del ipo: 4 5x x 3 Se oiuiamo x y l equazione verrà raormaa nell epreione: 5y y 3 molo più emplice della precedene eendo di econdo grado Una vola ricavae le due oluzioni y e y occorrerà riraormarle uando la ea legge precedenemene adoaa in: x y e x y per ricavare ue e quaro le oluzione del iema Quea ulima ae è denominaa ani-raormazione Wih he uppor o he Lielong Learning Programme o he European Union Thi projec ha been unded wih uppor rom he European Commiion
3 ITIS G CARDANO Nei iemi di regolazione e conrollo in paricolare i ua la ecnica della raormaa di Laplace, grazie alla quale: - l inegrale divena una diviione e la derivaa una moliplicazione - l equazione dierenziale divena una equazione algebrica Come vio nell eempio precedene l applicazione di queo meodo richiede quaro ai: ) ricavare l equazione dierenziale nel dominio del empo ) arne la raormaa di Laplace 3) riolvere l equazione algebrica nel dominio di 4) arne l ani-raormaa di Laplace Il dominio di uao nella raormaa di Laplace è di ipo arao non eendo poibile aribuire ad eo neun igniicao iico La raormazione avviene in una variabile complea: a ib I imboli maemaici per indicare la raormaa e l ani-raormaa ono ripeivamene: 5) L[ ] 6) L [ ] Alcune delle raormazioni di Laplace più uilizzae ono: TRASFORMATA h e e h ( ) en co en ( a) e h e h co ANTITRASFORMATA ( a) ( a) Wih he uppor o he Lielong Learning Programme o he European Union Thi projec ha been unded wih uppor rom he European Commiion 3
4 ITIS G CARDANO Nella raormazione ove neceario è poibile uilizzare anche alcune regole: L[ a bg( ] a bg( L[ F'( ] ) L ) d e e non i individua ubio l ani-raormazione occorre ricordare che l ani-raormaa di una omma di unzioni è pari alla omma delle ani-raormae delle ingole unzioni Vediamo un eempio di applicazione delle raormae di Laplace nella rioluzione dell equazione dierenziale: y '( y( con condizione iniziale: y ( ) Traormando i oerrà: L[ y'( ] L[ y( ] L[] Traormando i oerrà quindi: dalla quale raccogliendo y(: Ani-raormando i oerrà: y( y( y ( ( ) y( L [ y( ] L e ( ) y ( y( y() y ( La unzione caraeriica di un iema o di un uo elemeno prende il nome di unzione di raerimeno (FDT) ed è rieria al dominio di : U( I( FDT E RISPOSTA ALLE SOLLECITAZIONI DI UN ELEMENTO MECCANICO Vediamo una applicazione praica di uo il procedimeno ad un iema meccanico e prendiamo come eempio una maa m con velocià v al empo Applicando una orza variabile nel empo ( (leera minucola per non cononderla con la ) dopo l inervallo di empo - il corpo avrà ubio una variazione di velocià v -v Con gli chemi a blocchi i decriverà il enomeno con: v( ( v( ( Wih he uppor o he Lielong Learning Programme o he European Union Thi projec ha been unded wih uppor rom he European Commiion 4
5 ITIS G CARDANO Dalla econda legge della dinamica appiamo che: ( m a( v( ma eendo l accelerazione da deinizione: a( v'( oiuendo nell epreione precedene i oiene: ( mv'( Facendo la raormaa di Laplace i ricava la FDT: Se al empo la v ( ) i ha: Quindi la FDT arà: ( m v( v() ( m v( v( v( ( ( m m Fiao l andameno nel empo di ( e calcolaa la ua raormaa di Laplace (() i deerminerà la ripoa nel dominio di (v() eeuando emplicemene il prodoo ra la FDT e la raormaa dell ingreo Per avere la ripoa nel dominio del empo i dovrà are l ani-raormaa di Laplace FDT Se nel noro cao ad eempio ipoizziamo la orza coane: ( co allora: ( L[ ( ] L[ ] e di coneguenza l ucia arà: v( ( m m Per avere la ripoa nel empo i dovrà are l ani-raormaa, e i oerrà: v( m Poiché iica: m è l accelerazione coane che avrà la maa, è aa coì oenua la noa legge della v a Wih he uppor o he Lielong Learning Programme o he European Union Thi projec ha been unded wih uppor rom he European Commiion 5
3. MODELLI MATEMATICI
 3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
Lezione 5. Calcolo dell antitrasformata di Laplace. F. Previdi - Automatica - Lez. 5 1
 Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Basi di Elettronica (1 parte)
 Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 25 Settembre y=x 2 =i L
 .9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
.9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
campionatore - converte un segnale a tempo continuo in una sequenza sono quindi presenti sia variabili a tempo discreto sia variabili a tempo
 Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
Lezione 9. Calcolo dell antitrasformata di Laplace. F. Previdi - Fondamenti di Automatica - Lez. 9 1
 ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A )
 Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
Esercizi & Domande per il Compito di Elettrotecnica del 24 giugno 2002
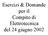 Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
Rappresentazione del sistema. Classificazione dei sistemi di controllo
 Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Problema 1: Una collisione tra meteoriti
 Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Esercizio 1. Sia L : R 3 R 2 l'applicazione lineare rappresentata, rispetto alle basi canoniche, dalla matrice : A =
 Tuoraggio di Algebra Lineare e Geomeria Eercii di ripao ulle applicaioni lineari Eerciio Sia L : R R 2 l'applicaione lineare rappreenaa, ripeo alle bai canoniche, dalla marice : A ( 2 2 Deerminare la marice
Tuoraggio di Algebra Lineare e Geomeria Eercii di ripao ulle applicaioni lineari Eerciio Sia L : R R 2 l'applicaione lineare rappreenaa, ripeo alle bai canoniche, dalla marice : A ( 2 2 Deerminare la marice
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 21 Luglio 2008
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI
 CAMPIONAMENO E RICOSRUZIONE DI SEGNALI CAMPIONAMENO E RICOSRUZIONE Numerizzazione dei egnali Nei Nei moderni iemi di di memorizzazione e ramiione i i egnali in in ingreo ono ono di di ipo ipo numerio,
CAMPIONAMENO E RICOSRUZIONE DI SEGNALI CAMPIONAMENO E RICOSRUZIONE Numerizzazione dei egnali Nei Nei moderni iemi di di memorizzazione e ramiione i i egnali in in ingreo ono ono di di ipo ipo numerio,
ALGEBRA DEGLI SCHEMI A BLOCCHI. La figura seguente rappresenta una relazione ingresso/uscita in forma grafica.
 Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
SisElnB3 12/19/ Dec SisElnB DDC. Antenna. Transmit Signal Generation. 19-Dec SisElnB DDC
 SiElnB3 2/9/ Ingegneria dell Informazione Obieivi del gruppo di lezioni B Modulo SISTEMI ELETTRONICI B - AMPLIFICATORI E DOPPI BIPOLI B.3 - Tipologie di amplificaori» Comporameno dinamico di amplificaori»
SiElnB3 2/9/ Ingegneria dell Informazione Obieivi del gruppo di lezioni B Modulo SISTEMI ELETTRONICI B - AMPLIFICATORI E DOPPI BIPOLI B.3 - Tipologie di amplificaori» Comporameno dinamico di amplificaori»
Lezione 4. Risposte canoniche dei sistemi del primo e del secondo ordine
 Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Metodo della Trasformata di Laplace (mtl)
 Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
Esercizi di supporto al modulo di Comunicazioni Elettriche
 Eercizi di upporo al modulo di Comunicazioni Eleriche Diplomi Univeriari eledidaici Dario Farina A.A. 3/4 Indirizzo per corripondenza: Dario Farina Dip. di Eleronica Poliecnico di orino Coro Duca degli
Eercizi di upporo al modulo di Comunicazioni Eleriche Diplomi Univeriari eledidaici Dario Farina A.A. 3/4 Indirizzo per corripondenza: Dario Farina Dip. di Eleronica Poliecnico di orino Coro Duca degli
Applicazioni del Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Applicazioni del Maimo fluo Progeazione di Algorimi a.a. 0-6 Maricole congrue a Docene: Annalia De Boni Maching bipario Problema del max maching. Inpu: grafo non direzionao G = (V, E). M E e` un maching
Applicazioni del Maimo fluo Progeazione di Algorimi a.a. 0-6 Maricole congrue a Docene: Annalia De Boni Maching bipario Problema del max maching. Inpu: grafo non direzionao G = (V, E). M E e` un maching
Dispense del corso di Analisi II
 Dipene del coro di Analii II verione preliminare Paolo Tilli Diparimeno di Maemaica Poliecnico di Torino email: paolo.illi@polio.i gennaio 25 Capiolo 5 Traformaa di Laplace 5. Inroduzione Sia x() una funzione
Dipene del coro di Analii II verione preliminare Paolo Tilli Diparimeno di Maemaica Poliecnico di Torino email: paolo.illi@polio.i gennaio 25 Capiolo 5 Traformaa di Laplace 5. Inroduzione Sia x() una funzione
Istituzioni di Probabilità Laurea magistrale in Matematica prova scritta del 20/6/2013
 Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
L attrito. coefficiente d attrito statico. f s s N = f smax. forza normale. f d = d N. coefficiente d attrito dinamico
 L aio coefficiene d aio aico f N = f ma foza nomale f d = d N coefficiene d aio dinamico e d dipendono dalla upeficie ma poco dall aea di conao in geneale > d e d = d () 0.05 1.5 Foze iadani b b dipende
L aio coefficiene d aio aico f N = f ma foza nomale f d = d N coefficiene d aio dinamico e d dipendono dalla upeficie ma poco dall aea di conao in geneale > d e d = d () 0.05 1.5 Foze iadani b b dipende
Titolo unità. Dalla serie alla trasformata di Fourier Proprietà della trasformata di Fourier Uguaglianza di Parseval e principio di indeterminazione
 Inroduzione ai segnali deerminai iolo unià Dalla serie alla rasormaa di ourier Proprieà della rasormaa di ourier Uguaglianza di Parseval e principio di indeerminazione 005 Poliecnico di orino 1 Dalla serie
Inroduzione ai segnali deerminai iolo unià Dalla serie alla rasormaa di ourier Proprieà della rasormaa di ourier Uguaglianza di Parseval e principio di indeerminazione 005 Poliecnico di orino 1 Dalla serie
Dispositivi e Sistemi Meccanici. 11 Esercizi. Politecnico di Torino CeTeM. Esercizio 11
 Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Metodo della trasformata di Laplace
 Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Analisi Matematica 3/Analisi 4 - SOLUZIONI (19/01/2015)
 Corso di Laurea in Maemaica Docene: Claudia Anedda Analisi Maemaica 3/Analisi 4 - SOLUZIONI (19/1/215) 1) Daa la serie x b e nx [(n + 1) 2 e x n 2 ], n1 b N +, b pari: i) dimosrare che essa è una serie
Corso di Laurea in Maemaica Docene: Claudia Anedda Analisi Maemaica 3/Analisi 4 - SOLUZIONI (19/1/215) 1) Daa la serie x b e nx [(n + 1) 2 e x n 2 ], n1 b N +, b pari: i) dimosrare che essa è una serie
Teoria dei segnali terza edizione
 eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
SCELTA DI UN INNESTO A FRIZIONE
 SELTA DI UN INNESTO A FRIZIONE Si conideri l'impiano in Fig. 1, coiuio da un moore elerico aincrono riae, un inneo a rizione ad azionameno eleromagneico, un riduore ad ingranaggi ed una macchina operarice.
SELTA DI UN INNESTO A FRIZIONE Si conideri l'impiano in Fig. 1, coiuio da un moore elerico aincrono riae, un inneo a rizione ad azionameno eleromagneico, un riduore ad ingranaggi ed una macchina operarice.
n 1 Un esempio di sistema rappresentabile con equazioni differenziali lineari del tipo (1) è illustrato in Appendice.
 RICHIAMI SULLE FUNZIONI DI TRASFERIMENTO, TRASFORMATE DI FOURIER E LAPLACE E DIAGRAMMI DI BODE Univerià di Padova Facolà di Ingegneria Coro di Fondameni di Eleronica A.A.4/5 Padova, 4//5 Le noe egueni
RICHIAMI SULLE FUNZIONI DI TRASFERIMENTO, TRASFORMATE DI FOURIER E LAPLACE E DIAGRAMMI DI BODE Univerià di Padova Facolà di Ingegneria Coro di Fondameni di Eleronica A.A.4/5 Padova, 4//5 Le noe egueni
Analisi in frequenza di segnali campionati
 Analii in requenza di egnali campionai - 1 Analii in requenza di egnali campionai 1 Analii dei egnali nel dominio della requenza I principali meodi di analii dei egnali di miura poono eere riauni nei concei
Analii in requenza di egnali campionai - 1 Analii in requenza di egnali campionai 1 Analii dei egnali nel dominio della requenza I principali meodi di analii dei egnali di miura poono eere riauni nei concei
Algebra vettoriale. risultante. B modulo, direzione e verso A punto di applicazione. Somma e differenza di vettori: a + b = c
 Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Tab. 1 - modulo elastico e resistenza a trazione del calcestruzzo
 18 Capiolo 5 Tab. 1 - modulo elaico e reienza a razione del calceruzzo clae C2/25 C25/ C28/5 C2/4 ck 2 MPa 25 MPa 28 MPa 2 MPa Ecm MPa 15 MPa 2 MPa MPa cm 2.21 MPa 2.57 MPa 2.77 MPa.2 MPa ck 1.55 MPa 1.8
18 Capiolo 5 Tab. 1 - modulo elaico e reienza a razione del calceruzzo clae C2/25 C25/ C28/5 C2/4 ck 2 MPa 25 MPa 28 MPa 2 MPa Ecm MPa 15 MPa 2 MPa MPa cm 2.21 MPa 2.57 MPa 2.77 MPa.2 MPa ck 1.55 MPa 1.8
Modelli circuitali per le linee di trasmissione
 Modelli circuiali per le linee di ramiione prof. Anonio Maffucci A. Maffucci, Modelli circuiali per le linee di ramiione [pag. 1/73] Inerconneioni eleriche A vari livelli Board Package hip A. Maffucci,
Modelli circuiali per le linee di ramiione prof. Anonio Maffucci A. Maffucci, Modelli circuiali per le linee di ramiione [pag. 1/73] Inerconneioni eleriche A vari livelli Board Package hip A. Maffucci,
Laboratorio di Algoritmi e Strutture Dati
 Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Corso di Fondamenti di Telecomunicazioni
 Coro di Fondameni di elecomunicazioni EORIA DEI SEGNALI DEERMINAI Pro. Giovanni Schembra Fondameni di LC - Pro. G. Schembra Sruura della lezione Proprieà dei egnali nel dominio del empo Valore medio, poenza,
Coro di Fondameni di elecomunicazioni EORIA DEI SEGNALI DEERMINAI Pro. Giovanni Schembra Fondameni di LC - Pro. G. Schembra Sruura della lezione Proprieà dei egnali nel dominio del empo Valore medio, poenza,
CAPITOLO 9 - RETI DINAMICHE NEL DOMINIO DELLA FREQUENZA
 G. SUPT FUGA MT D TOA D T ovembre CAPTOO 9 - T DAMCH DOMO DA FQUZA pag. / CAPTOO 9 - T DAMCH DOMO DA FQUZA TODUZO l meodo della raformaa di aplace, chiamao anche analii nel dominio della frequenza, è una
G. SUPT FUGA MT D TOA D T ovembre CAPTOO 9 - T DAMCH DOMO DA FQUZA pag. / CAPTOO 9 - T DAMCH DOMO DA FQUZA TODUZO l meodo della raformaa di aplace, chiamao anche analii nel dominio della frequenza, è una
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI
 DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine egnale i indica una funzione, generalmene del empo, che rappreena la legge di variazione di una grandezza fiica, (acuica, elerica, oica ec.) la preione
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine egnale i indica una funzione, generalmene del empo, che rappreena la legge di variazione di una grandezza fiica, (acuica, elerica, oica ec.) la preione
Vin(t) c) Si assuma per l operazionale una risposta in frequenza ad anello aperto A(s)=A o /(1+sτ ο
 Eercizio Fondameni di Eleronica - ngegneria Auomaica - AA 3/4 a rova in iinere- 5 ebbraio 4 ndicare chiaramene la domanda a cui i a riondendo. Ad eemio a) ou() in() - µ µ 3 6 µ µ kω 8kΩ C 3F in() C a)
Eercizio Fondameni di Eleronica - ngegneria Auomaica - AA 3/4 a rova in iinere- 5 ebbraio 4 ndicare chiaramene la domanda a cui i a riondendo. Ad eemio a) ou() in() - µ µ 3 6 µ µ kω 8kΩ C 3F in() C a)
Esercizi & Domande per il Compito di Elettrotecnica del 1 giugno 2004
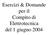 Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
= 1. Le equazioni della trave su suolo elastico considerata illimitata, in presenza di uno spostamento relativo imposto y 0 (Figura 1.
 STUDIO TEORICO DEL COMPORTAMENTO DELLE GIUNZIONI Appendice A: Valuazione eorica della rigidezza della conneione. Vengono ucceivamene riporai i paaggi maemaici che porano alla formulazione della rigidezza
STUDIO TEORICO DEL COMPORTAMENTO DELLE GIUNZIONI Appendice A: Valuazione eorica della rigidezza della conneione. Vengono ucceivamene riporai i paaggi maemaici che porano alla formulazione della rigidezza
Esercizi riassuntivi sugli argomenti del corso in preparazione alla prova d esame:
 8 apiolo Eercizi riaunivi ugli argomeni del coro in preparazione alla prova d eame: Influenza delle funzioni aenuarici ul valore del empo di aeameno. Volendo fare un dicoro qualiaivo, e non formale e rigoroo
8 apiolo Eercizi riaunivi ugli argomeni del coro in preparazione alla prova d eame: Influenza delle funzioni aenuarici ul valore del empo di aeameno. Volendo fare un dicoro qualiaivo, e non formale e rigoroo
Vediamo come si sviluppa la soluzione esplicita del problema. ( t)
 Analisi ransioria L'analisi dinamica ransioria (dea anche analisi emporale) è una ecnica che consene di deerminare la risposa dinamica di una sruura soggea ad una generica ecciazione emporale Gli effei
Analisi ransioria L'analisi dinamica ransioria (dea anche analisi emporale) è una ecnica che consene di deerminare la risposa dinamica di una sruura soggea ad una generica ecciazione emporale Gli effei
Proprietà della Trasformata. Funzioni trasformabili (1/3) L {af(t) + bg(t)} (s) = (af(t) + bg(t))e st dt. Tabella 1. = a f(t)e st dt + b g(t)e st dt
 Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 27/28 (aggiornaa al 8//27) 2 Proprieà della rasformaa
Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 27/28 (aggiornaa al 8//27) 2 Proprieà della rasformaa
Corso di SEGNALI a.a
 Coro di SEGNALI anno accademico 008-009 Appunti u: Teorema del Campionamento Introduzione Il proceo di campionamento è di enorme importanza ai ini della realizzazione dei dipoitivi digitali per le telecomunicazioni.
Coro di SEGNALI anno accademico 008-009 Appunti u: Teorema del Campionamento Introduzione Il proceo di campionamento è di enorme importanza ai ini della realizzazione dei dipoitivi digitali per le telecomunicazioni.
Volume FISICA. Elementi di teoria ed applicazioni. Fisica 1
 Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Outline. La trasformata di Laplace. (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi
 Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
2.4 Flussi di valore massimo
 .4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
.4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
INTRODUZIONE ALLE LEGGI FINANZIARIE
 Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Equazioni differenziali lineari
 0.0. 2. Equazioni differenziali lineari Da un puno di visa dinamico, i sisemi lineari sazionari sono descrii da equazioni differenziali ordinarie lineari a coefficieni cosani: a n d n y d n + a n d n y
0.0. 2. Equazioni differenziali lineari Da un puno di visa dinamico, i sisemi lineari sazionari sono descrii da equazioni differenziali ordinarie lineari a coefficieni cosani: a n d n y d n + a n d n y
Trasformata di Laplace
 Traformata di Laplace In matematica e in particolare nell'analii funzionale la traformata di Laplace di una funzione f (t ) (definita per tutti i numeri reali e localmente integrabile) è la funzione F
Traformata di Laplace In matematica e in particolare nell'analii funzionale la traformata di Laplace di una funzione f (t ) (definita per tutti i numeri reali e localmente integrabile) è la funzione F
FUNZIONI DI TRASFERIMENTO
 FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
Circuito Simbolico. Trasformazione dei componenti
 Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
RICERCA OPERATIVA GRUPPO A prova scritta del 5 luglio 2010
 RICERCA OPERATIVA GRUPPO A prova cria del luglio 00. Dao il problema di programmazione lineare P) min z = x +x +x max y + y x x x = y +y < x + x x y + y < x, x, x 0 y y < y > 0 a) coruirne il duale D;
RICERCA OPERATIVA GRUPPO A prova cria del luglio 00. Dao il problema di programmazione lineare P) min z = x +x +x max y + y x x x = y +y < x + x x y + y < x, x, x 0 y y < y > 0 a) coruirne il duale D;
Nome: Nr. Mat. Firma:
 Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Progettazione di Algoritmi Anno Accademico Esercizi su Grafi: Parte Seconda
 Progeazione di Algorimi Anno Accademico 0 09 Eercizi Ugo Vaccaro Eercizi u Grafi: Pare Seconda N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu
Progeazione di Algorimi Anno Accademico 0 09 Eercizi Ugo Vaccaro Eercizi u Grafi: Pare Seconda N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu
Equazioni Differenziali (5)
 Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
3. La coppia di avviamento [Nm] La coppia massima [Nm] 5
![3. La coppia di avviamento [Nm] La coppia massima [Nm] 5 3. La coppia di avviamento [Nm] La coppia massima [Nm] 5](/thumbs/71/65755864.jpg) UNESÀ D OMA LA SAPENZA FACOLÀ D NGEGNEA - COSO D LAUEA N NGEGNEA ENEGECA AA 8-9 DSCPLNA D MACCHNE E CONEO D ENEGA ELECA POA SCA D ESAME DEL 5 GUGNO 9.. Sono dai due raformaori rifae della ea oenza nominale
UNESÀ D OMA LA SAPENZA FACOLÀ D NGEGNEA - COSO D LAUEA N NGEGNEA ENEGECA AA 8-9 DSCPLNA D MACCHNE E CONEO D ENEGA ELECA POA SCA D ESAME DEL 5 GUGNO 9.. Sono dai due raformaori rifae della ea oenza nominale
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO Problematiche di controllo digitale
 INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO Problemaiche di conrollo digiale Prof. Carlo Roi DEIS - Univerià di Bologna Tel: 051 2093020 email: croi@dei.unibo.i Progeo di un conrollore digiale Due
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO Problemaiche di conrollo digiale Prof. Carlo Roi DEIS - Univerià di Bologna Tel: 051 2093020 email: croi@dei.unibo.i Progeo di un conrollore digiale Due
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
REGISTRAZIONE DEL MOTO. Lo scopo è riempire una tabella t/s (istante di tempo/posizione occupata)
 REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
Note per la Lezione 33 Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 208 209 Noe per la Lezione 33 Ugo Vaccaro In quea lezione vedremo alcune applicazioni dei riulai ul calcolo del fluo maimo, derivai nelle lezioni precedeni. Prima
Progeazione di Algorimi Anno Accademico 208 209 Noe per la Lezione 33 Ugo Vaccaro In quea lezione vedremo alcune applicazioni dei riulai ul calcolo del fluo maimo, derivai nelle lezioni precedeni. Prima
APPENDICE. L-trasformazione dei componenti R, L,C Esempi di risoluzione di equazioni differenziali con la T.d.L.
 APPENDICE Modelli matematici dei componenti R, L, C Ripota di un circuito nel dominio del tempo con il metodo delle equazioni differenziali Traformata di Laplace L-traformazione dei componenti R, L,C Eempi
APPENDICE Modelli matematici dei componenti R, L, C Ripota di un circuito nel dominio del tempo con il metodo delle equazioni differenziali Traformata di Laplace L-traformazione dei componenti R, L,C Eempi
PARTE 4: CINEMATICA DEL PUNTO MATERIALE
 PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1. Docente: Annalisa De Bonis
 Maimo fluo Progeazione di Algorimi a.a. 2017-18 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
Maimo fluo Progeazione di Algorimi a.a. 2017-18 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
intervalli di tempo. Esempio di sistema oscillante: Fig. 1 Massa m che può traslare in una sola direzione x, legata ad una molla di rigidezza k.
 Sudio delle vibrazioni raa ogni oscillazione di una grandezza inorno ad una posizione di equilibrio. La forma piu semplice di oscillazione e il moo armonico che puo i essere descrio da un veore roane Ae
Sudio delle vibrazioni raa ogni oscillazione di una grandezza inorno ad una posizione di equilibrio. La forma piu semplice di oscillazione e il moo armonico che puo i essere descrio da un veore roane Ae
K c s h. P(s) 1/K d. U(s) + Y(s)
 Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
Eame di Fondamenti di Automatica Coro di Laurea Vecchio Ordinamento in Ingegneria Elettronica febbraio 3 Compito A Cognome: Nome Matricola: Email:. Ricavare la funzione di traferimento tra u ed y nel eguente
Ulteriori Esercizi su Grafi. Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Uso della trasformata di Laplace per il calcolo della risposta
 Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
Uo della traformata di Laplace per il calcolo della ripota Conigli generali (Aggiornato 7//) ) Si vuole qui richiamare l attenzione ul fatto che la preenza di zeri o di una truttura triangolare a blocchi
Note per la Lezione 29 Ugo Vaccaro
 Progeaione di Algorimi Anno Accademico 1 1 Noe per la Leione Ugo Vaccaro In quea leione coninueremo lo udio di cammini minimin grafi in cui vi poono eere archi di coo negaivo. Ricordiamo l algorimo baao
Progeaione di Algorimi Anno Accademico 1 1 Noe per la Leione Ugo Vaccaro In quea leione coninueremo lo udio di cammini minimin grafi in cui vi poono eere archi di coo negaivo. Ricordiamo l algorimo baao
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1- soluzioni - Leggi finanziarie, rendite ed ammortamenti
 Esercizi di Maemaica Finanziaria - Corso Par Time scheda - soluzioni - Leggi finanziarie, rendie ed ammorameni. Le soluzioni sono: (a) M 3 = 00 ( + 3) = 5, M 8 = 5 ( + 5) = 43.75. (b) Va risola l equazione
Esercizi di Maemaica Finanziaria - Corso Par Time scheda - soluzioni - Leggi finanziarie, rendie ed ammorameni. Le soluzioni sono: (a) M 3 = 00 ( + 3) = 5, M 8 = 5 ( + 5) = 43.75. (b) Va risola l equazione
Esempi Calcolo Antitrasformate
 Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Maimo fluo Progeazione di Algorimi a.a. 2016-17 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
Maimo fluo Progeazione di Algorimi a.a. 2016-17 Maricole congrue a 1 Docene: Annalia De Boni 1 Maimizzare il # di PC prodoi 2 Decrizione del problema Una fabbrica (orgene) di PC deve abilire il numero
Università degli Studi di Napoli. Federico II. Appunti di METODI MATEMATICI PER L INGEGNERIA INDUSTRIALE
 Carlo Colella Davide Formiano Univerià degli Sudi di Napoli Federico II Diparimeno di Ingegneria Navale Appuni di METODI MATEMATICI PER INGEGNERIA INDUSTRIAE A.A. 8/9 INDICE Capiolo I A TRASFORMAZIONE
Carlo Colella Davide Formiano Univerià degli Sudi di Napoli Federico II Diparimeno di Ingegneria Navale Appuni di METODI MATEMATICI PER INGEGNERIA INDUSTRIAE A.A. 8/9 INDICE Capiolo I A TRASFORMAZIONE
Teoria dei segnali. Unità 2 Sistemi lineari. Sistemi lineari: definizioni e concetti di base. Concetti avanzati Politecnico di Torino 1
 Sisemi lineari: deinizioni e concei di base Teoria dei segnali Unià 2 Sisemi lineari Sisemi lineari Deinizioni e concei di base Concei avanzai 2 25 Poliecnico di Torino Sisemi lineari: deinizioni e concei
Sisemi lineari: deinizioni e concei di base Teoria dei segnali Unià 2 Sisemi lineari Sisemi lineari Deinizioni e concei di base Concei avanzai 2 25 Poliecnico di Torino Sisemi lineari: deinizioni e concei
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
LA PUNTA ELICOIDALE. ϕ angolo dei taglienti; è l angolo formato dai due taglienti principali. γ angolo di spoglia superiore. β angolo di taglio
 1 LA PUNTA ELICOIDALE È l uenile più emplice per l eecuzione di fori cilindrici, generalmene dal pieno. La puna elicoidale è coiuia: da un codolo cilindrico o conico per il cenraggio ul mandrino della
1 LA PUNTA ELICOIDALE È l uenile più emplice per l eecuzione di fori cilindrici, generalmene dal pieno. La puna elicoidale è coiuia: da un codolo cilindrico o conico per il cenraggio ul mandrino della
IL METODO FISHER-LANGE
 IL METODO FISHER-LANGE Maeriale didaico a cura di Domenico Giorgio Auario Danni di Gruppo Socieà Caolica di Aicurazioni Domenico Giorgio Il meodo Fiher-Lange METODO FISHER-LANGE Il meodo Fiher-Lange (di
IL METODO FISHER-LANGE Maeriale didaico a cura di Domenico Giorgio Auario Danni di Gruppo Socieà Caolica di Aicurazioni Domenico Giorgio Il meodo Fiher-Lange METODO FISHER-LANGE Il meodo Fiher-Lange (di
Circuiti dinamici. Circuiti del primo ordine. (versione del ) Circuiti del primo ordine
 ircuii dinamici ircuii del primo ordine www.die.ing.unibo.i/pers/masri/didaica.hm (versione del 4-5- ircuii del primo ordine ircuii del primo ordine: circuii il cui sao è definio da una sola variabile
ircuii dinamici ircuii del primo ordine www.die.ing.unibo.i/pers/masri/didaica.hm (versione del 4-5- ircuii del primo ordine ircuii del primo ordine: circuii il cui sao è definio da una sola variabile
Note per la Lezione 28 Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 2017 2018 Noe per la Lezione 28 Ugo Vaccaro In quea lezione udieremo ancora problemi u cammini minimi, ma in grafi in cui vi poono eere archi di coo negaivo. Quindi,
Progeazione di Algorimi Anno Accademico 2017 2018 Noe per la Lezione 28 Ugo Vaccaro In quea lezione udieremo ancora problemi u cammini minimi, ma in grafi in cui vi poono eere archi di coo negaivo. Quindi,
CRESCITA. Modello di Solow
 CRESCITA Modello di Solow Modello di Solow (956) Idea: la crecia è dovua all accumulo di capiale. Capiale fiico () Y S I ecc. (idea di circolarià, ma aenzione a rendimeni decreceni di Ipoei: Economia chiua
CRESCITA Modello di Solow Modello di Solow (956) Idea: la crecia è dovua all accumulo di capiale. Capiale fiico () Y S I ecc. (idea di circolarià, ma aenzione a rendimeni decreceni di Ipoei: Economia chiua
LABORATORIO di ELETTRONICA SEGNALI ELETTRICI PERIODICI
 LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
LA TRASFORMATA DI LAPLACE
 LA RASFORMAA DI LAPLACE Per decrivere l evoluzione di un itema in regime tranitorio, oia durante il paaggio delle ucite da un regime tazionario ad un altro, è neceario ricorrere ad un modello più generale
LA RASFORMAA DI LAPLACE Per decrivere l evoluzione di un itema in regime tranitorio, oia durante il paaggio delle ucite da un regime tazionario ad un altro, è neceario ricorrere ad un modello più generale
( ) ( ) Esempio di Prova di MATEMATICA E FISICA - MIUR PROBLEMA 1 (traccia di soluzione di S. De Stefani)
 Esempio di Prova di MATEMATICA E FISICA - MIUR - 8..9 PROBLEMA (raccia di soluzione di S. De Sefani) Assegnae due cosani reali a e (con >), si consideri la funzione ) così definia: )=. A seconda dei possiili
Esempio di Prova di MATEMATICA E FISICA - MIUR - 8..9 PROBLEMA (raccia di soluzione di S. De Sefani) Assegnae due cosani reali a e (con >), si consideri la funzione ) così definia: )=. A seconda dei possiili
Analisi nei domini del tempo e della frequenza
 Elaborazione digiale dei egnali di miura - 1 Analii nei domini del empo e della requenza Ogni egnale reale può eere prodoo aggiungendo onde inuoidali a) Coordinae ridimenionali: empo, requenza ed ampiezza.
Elaborazione digiale dei egnali di miura - 1 Analii nei domini del empo e della requenza Ogni egnale reale può eere prodoo aggiungendo onde inuoidali a) Coordinae ridimenionali: empo, requenza ed ampiezza.
Soluzioni degli esercizi di Analisi Matematica I
 Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Il Luogo delle Radici
 Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
Il Luogo delle Radici Il luogo delle radici è un procedimento, otanzialmente grafico, che permette di analizzare come varia il poizionamento dei poli di un itema di controllo in retroazione al variare
LA CONDUZIONE TERMICA IN PARETE (SERIE E PARALLELO)
 L CONDUZIONE ERMIC IN PREE (SERIE E PRLLELO Capiolo quino La conduzione 5. Inroduzione Il meccanimo conduivo fa riferimeno al raferimeno di energia ermica in un mezzo o ra più mezzi in conao fiico, unicamene
L CONDUZIONE ERMIC IN PREE (SERIE E PRLLELO Capiolo quino La conduzione 5. Inroduzione Il meccanimo conduivo fa riferimeno al raferimeno di energia ermica in un mezzo o ra più mezzi in conao fiico, unicamene
Analisi Matematica II Corso di Ingegneria Gestionale Compito del log 1 + x2 y 2
 Analisi Maemaica II Corso di Ingegneria Gesionale Compio del 5-7-7 - È obbligaorio consegnare ui i fogli, anche la brua e il eso. - Le rispose senza giusificazione sono considerae nulle. Esercizio. puni
Analisi Maemaica II Corso di Ingegneria Gesionale Compio del 5-7-7 - È obbligaorio consegnare ui i fogli, anche la brua e il eso. - Le rispose senza giusificazione sono considerae nulle. Esercizio. puni
Claudio Arbib Università dell Aquila. Ricerca Operativa. Problemi di cammino ottimo
 Claudio Arbib Univerià dell Aquila Ricerca Operaiva Problemi di cammino oimo Sommario Il problema del cammino più breve Il problema del cammino più icuro Una formulazione come PL 0- Proprieà della formulazione
Claudio Arbib Univerià dell Aquila Ricerca Operaiva Problemi di cammino oimo Sommario Il problema del cammino più breve Il problema del cammino più icuro Una formulazione come PL 0- Proprieà della formulazione
Linea guida raccomandata per la valutazione della vita residua di componenti esercìti in regime di scorrimento viscoso
 ISPESL Linea guida raccomandaa per la valuazione della via residua di componeni esercìi in regime di scorrimeno viscoso Calcolo della frazione di via consumaa per scorrimeno viscoso Sezione 2 LG v. 1 Nella
ISPESL Linea guida raccomandaa per la valuazione della via residua di componeni esercìi in regime di scorrimeno viscoso Calcolo della frazione di via consumaa per scorrimeno viscoso Sezione 2 LG v. 1 Nella
Lezione 9. Schemi di controllo avanzati parte prima. F. Previdi - Controlli Automatici - Lez. 9 1
 Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
Lezione 9. Schemi di controllo avanzati parte prima F. Previdi - Controlli Automatici - Lez. 9 Schema. Regolatori in anello aperto Controllo multivariabile:. Regolatori di diaccoppiamento 3. Controllo
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
Circuiti del I ordine
 ircuii del I ordine 9 Un circuio è deo del I ordine se coniene un solo elemeno dinamico, condensaore o induore, e per il reso è cosiuio da componeni elerici di ipo algebrico privi di memoria, ovvero generaori
ircuii del I ordine 9 Un circuio è deo del I ordine se coniene un solo elemeno dinamico, condensaore o induore, e per il reso è cosiuio da componeni elerici di ipo algebrico privi di memoria, ovvero generaori
Simulare un sistema dinamico
 Simulare un sisema dinamico Serie di Taylor Daa una unzione, ed un puno 0 in cui la unzione sia noa assieme alle sue derivae, è possibile approssimare la unzione ramie serie di Taylor: 0 + ' 0 0 + '' 0
Simulare un sisema dinamico Serie di Taylor Daa una unzione, ed un puno 0 in cui la unzione sia noa assieme alle sue derivae, è possibile approssimare la unzione ramie serie di Taylor: 0 + ' 0 0 + '' 0
