ANALISI ENERGETICA ED EXERGETICA DEGLI SCAMBIATORI DI CALORE
|
|
|
- Oreste Pappalardo
- 7 anni fa
- Visualizzazioni
Transcript
1 UNIVERSIÀ DEGLI SUDI DI NAPOLI FEDERICO II POLO DELLE SCIENZE E DELLE ECNOLOGIE FACOLÀ DI INGEGNERIA A.A ANALISI ENERGEICA ED EXERGEICA DEGLI SCAMBIAORI DI CALORE F. CALISE, M. DENICE D ACCADIA, R.VANOLI Corso di ermodinamia dei Proessi di Conversione dell Energia NAPOLI, MAGGIO
2 Sommario ANALISI ENERGEICA ED EXERGEICA DEGLI SCAMBIAORI DI CALORE Introduzione ipologie di Sambiatori di Calore Analisi termodinamia Equazioni di Progetto Metodo della media logaritmia delle dierenze di temperatura Proili di temperatura negli sambiatori di alore Metodo ε-nu Exergia distrutta negli sambiatori di alore Rappresentazione graia della generazione entropia nel piano, S Il numero di generazione entropia (Ns ) Sambiatori di Calore on perdite di ario Rendimenti exergetii Bibliograia
3 Indie delle Figure Figura 1 - ubi oassiali... 6 Figura 2 - Volumi di ontrollo, sambiatore a tubi oassiali... 6 Figura 3 - Sambiatore a tubi oassiali equiorrente... 7 Figura 4 - Sambiatore a tubi oassiali ontroorrente... 7 Figura 5 - Sambiatore ubi e mantello... 8 Figura 6 - Shema sambiatore tubi e mantello... 8 Figura 7 - Shema sambiatore tubi e mantello - due passaggi lato tubi... 9 Figura 8 - ubo alettato esternamente... 9 Figura 9 - Shema sambiatore a lussi inroiati Figura 10 - Shema sambiatore di alore a piastre alettate Figura 11 - Shema sambiatore di alore a piastre alettate a lussi inroiati Figura 12 - Volume di ontrollo per i bilani sullo sambiatore di alore Figura 13 - Shematizzazione sambiatore di alore Figura 14 - Shema equiorrente Figura 15 - Shema ontroorrente Figura 16 - Diagrammi (,A) per sambiatori equiorrente Figura 17 - Digrammi (,A) per sambiatori equiorrente (A ) Figura 18 - Sambiatore Controorrente, M>0 ( C C ) Figura Sambiatore Controorrente, M>0 ( C C ), (A ) Figura 20 - Sambiatore Controorrente, M>0 ( C C ) Conronto Area inita ed Area ininita Figura 21 - Sambiatore ontroorrente, M=0 ( C C ) Figura 22- Sambiatore ontroorrente, M=0 ( C C ), (A ) Figura 23- Sambiatore ontroorrente, M=0 ( C C ), onronto Area di sambio inita ed ininita Figura 24 - Sambiatore ontroorrente, M<0 ( C C ) Figura 25- Sambiatore ontroorrente, M<0 ( C C ), (A ) Figura 26- Sambiatore ontroorrente, M<0 ( C C ), (A ), Conronto area di sambio inita ed ininita Figura 27 - Sambiatore (EQ o CC) in ui il luido reddo è in passaggio di ase (evaporatore) Figura 28 - Sambiatore (EQ o CC) in ui il luido aldo è in passaggio di ase (ondensatore) Figura 29- Sambiatore (EQ o CC) in ui il luido reddo è in passaggio di ase (evaporatore) (A ) Figura 30- Sambiatore (EQ o CC) in ui il luido aldo è in passaggio di ase (ondensatore) (A ) Figura 31 Diagramma ε-nu per sambiatori ontroorrente Figura 32 Diagramma ε-nu per sambiatori equiorrente Figura 33 - Sambiatore equiorrente bilaniato di area ininita Figura 34 - Rappresentazione dell Exergia distrutta sul piano,s -evaporazione Figura 35 - Rappresentazione dell Exergia distrutta sul piano,s -ondensazione Figura 36 - Diagramma, S - isobara Figura 37 - Diagramma (, S ) - sambiatore di alore Figura 38- Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p >p )
4 Figura 39 - Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p <p ) Figura 40 - Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p =p ) Figura 41 Diagramma (, S ) - sambiatore di alore Conronto EQ vs CC Figura 42 - Ns, sambiatore ontroorrente bilaniato Figura 43 - Sambio di energia termia ra due SE Figura 44 - Lunghezza di sambio termio per sambiatori bilaniati on temperature ostanti o variabili.. 50 Figura 45 - Diagramma Ns, ε, ω, χ=0, Figura 46 - Diagramma Ns, ε, ω, χ=0, Figura 47 - Diagramma Ns, ε, ω, χ=0, Figura 48 - Diagramma Ns, ε, ω, χ=0, Figura 49 - Massima eiienza di uno sambiatore equiorrente Figura 50 - Diagramma Ns, ε, ω, χ=0,20 Sambiatore equiorrente Figura 51- Diagramma Ns, ε, ω, χ=0,20 Sambiatore ontroorrente Figura 52- Diagramma Ns, ε, ω, χ=0,80 Sambiatore equiorrente Figura 53- Diagramma Ns, ε, ω, χ=0,80 Sambiatore ontroorrente Figura 54 - Diagramma exergia oraria, entalpia oraria, sambiatori reali, >a Figura 55 - rendimento exergetio, aso A Figura 56- Rendimenti exergetii, aso A Figura 57 - Rendimenti exergetii, aso B Figura 58- Rendimenti exergetii, aso B Figura 59 - rendimento exergetio aso A sambiatore reale
5 1. Introduzione Nell analisi dei omponenti termodinamii si tende a suddividerli in due gruppi, in unzione della tipologia di lusso energetio he attraversa il proprio volume di ontrollo. utti i omponenti analizzati nelle sezioni preedenti erano aratterizzati da lussi di energia meania non nulli ( L 0 ) e da superii del volume di ontrollo adiabatihe ( Q 0 ). I omponenti di seguito analizzati, invee, sono aratterizzati da sambi termii non nulli ( Q 0 ) e superii anergodihe ( L 0 ). A quest ultima ategoria appartengono gli sambiatori di alore. Si deinise sambiatore di alore un dispositivo he onsenta lo sambio di energia termia ra un luido a temperatura maggiore ed un luido a temperatura minore. Gli sambiatori di alore sono tra i omponenti termodinamii maggiormente diusi e sono utilizzati in una vastissima gamma di appliazioni, dalla sala minima (ad es. batterie di sambio termio negli impianti di limatizzazione) ino alla massima (ad es. batterie di sambio termio in impianti motori, operatori ed industriali in genere). Lo studio degli sambiatori di alore è, in generale, molto omplesso in quanto rihiede onosenze multidisiplinari he inludono: termodinamia, trasmissione del alore e luidodinamia. Inoltre, unitamente a onsiderazioni di arattere termodinamio, la progettazione ompleta di uno sambiatore di alore rihiede l implementazione di un numero notevole di teorie quali: l analisi dell ingombro, del peso, della resistenza meania e dei osti dello sambiatore stesso. In questa sede verranno disusse eslusivamente le modalità attraverso le quali viene realizzata la progettazione termia dello sambiatore di alore, rimandando a trattazioni più speialistihe le analisi di resistenza strutturale e di tipo eonomio. 2. ipologie di Sambiatori di Calore È possibile realizzare un proesso di sambio termio ra due luidi seondo numerosissime modalità; nella pratia, inatti, esistono numerose tipologie di sambiatori di alore, lassiiabili in unzione di: Materiali ostruttivi ipologia dei luidi evolventi Disegno termo luidodinamio Il metodo più semplie on ui è possibile realizzare uno sambio termio ra due luidi è quello di utilizzare due tubazioni oassiali, aendo sorrere il primo luido nel tubo interno ed il seondo nella zona anulare ompresa ra il tubo interno ed il tubo esterno (Figura 1). 5
6 Figura 1 - ubi oassiali ale sistema evidenzia due possibili volumi di ontrollo: Fluido he evolve nel tubo interno (zona non tratteggiata di Figura 2) Fluido he evolve nella zona anulare ompresa ra il tubo interno ed il tubo esterno (zona tratteggiata di Figura 2) Figura 2 - Volumi di ontrollo, sambiatore a tubi oassiali Il proesso di sambio termio è estremamente semplie: sezione per sezione, esisterà sempre una erta dierenza di temperatura tra il luido he si trova a temperatura maggiore (detto luido aldo) ed il luido a temperatura minore (detto luido reddo) he onsentirà il traserimento di energia termia dal primo verso il seondo. Uno sambiatore di alore di questo tipo è detto a tubi oassiali o tubo in tubo. Per questa tipologia di sambiatore, possono veriiarsi due diverse ondizioni di lusso (Figura 2): una prima (Figura 3) in ui entrambi i luidi sorrono nella stessa direzione e stesso verso (equiorrente) ed una seonda (Figura 4) in ui i luidi hanno la stessa direzione ma verso opposto (ontroorrente). 6
7 Figura 3 - Sambiatore a tubi oassiali equiorrente Figura 4 - Sambiatore a tubi oassiali ontroorrente Lo shema dello sambiatore tubo in tubo è siuramente molto semplie ma nella pratia si realizza solo in rare appliazioni, in quanto tale tipologia di sambiatore rihiede ingombri speiii (Area di sambio per unità di potenza termia sambiata) molto elevati. Molto più diuso, invee, è lo sambiatore a tubi e mantello, in ui un asio tubiero è installato all interno di un reipiente. Il luido aldo (o reddo) sorre all interno dei tubi mentre quello reddo (o aldo) evolve ra la superiie interna del reipiente e la superiie esterna delle tubazioni (Figura 5). Sono ostituiti da 3 parti ondamentali: testata di ingresso; asio tubiero e mantello (orpo entrale); testata di usita. La testata di ingresso (dove è presente la tube inlet ) ha il ompito di indirizzare il luido nei tubi (in maniera omogenea, erando quindi di ar investire dal luido tutti i tubi). Per questo motivo non è del tutto semiirolare ma è leggermente allungata onsentendo al luido di distribuirsi in ogni tubo. La testata di ingresso è legata ad una piastra provvista di una serie di ori (he alloggiano le estremità dei tubi) solitamente disposti lungo una maglia ben preisa. Le maglie più elementari sono quelle triangolari e quadrate he orono due diversi vantaggi. La triangolare assiura una maggiore turbolenza del luido, la quadrata garantise una più semplie pulizia. La distanza tra tubo e tubo viene detta passo (passo triangolare nel aso della maglia triangolare o passo quadrato nel aso della maglia quadrata) e in media è pari a 1,25-1,50 volte il diametro esterno dei tubi. Lo sambiatore è generalmente provvisto di due piastre tubiere, disposte all estremità dei tubi del asio, ma in situazioni partiolari se ne utilizza una sola. Nel orpo entrale sono disposti i tubi all interno di un involuro detto Mantello (shell). Sono generalmente presenti dei diarammi (buels) he migliorano la turbolenza del luido he passa all esterno dei tubi (Figura 6). Per evitare l uso di sambiatori di dimensioni eessive si può ar passare il luido più volte lato tubi e/o lato mantello. Volendo ar passare due volte lato tubi, basterà inserire un diaramma orizzontale nella testata di ingresso (in questo modo si assiura omunque 7
8 un elevata turbolenza del luido quindi un buon oeiiente di sambio termio), osì ome mostrato in Figura 7. Si possono avere anhe più di due passaggi lato tubi (al massimo 8 ) e generalmente al massimo 4 passaggi lato mantello. Riordiamo he uniamente nel aso 2-2 (2 passaggi lato tubi e 2 passaggi lato mantello) i 2 luidi sono sempre in ontroorrente, negli altri asi bisognerà tenere onto he i luidi non sambieranno alore in ontroorrente. Figura 5 - Sambiatore ubi e mantello Figura 6 - Shema sambiatore tubi e mantello 8
9 Figura 7 - Shema sambiatore tubi e mantello - due passaggi lato tubi Gli sambiatori tubo e mantello sono molto utilizzati nel aso in ui entrambi i luidi si trovino in ase liquida. Nel aso in ui, almeno uno dei due luidi si trovi nella ase aeriorme risulterebbe molto diiile utilizzare una siatta tipologia di sambiatore, he rihiederebbe aree di sambio e quindi ingombri deisamente elevati. È noto inatti he il oeiiente di sambio termio onvettivo di un aeriorme è di ordini di grandezza ineriore a quello di un liquido, determinando quindi notevoli inrementi delle superii di sambio, a parità di potenza termia sambiata. Per ovviare a questo problema (aree di sambio molto elevate), per qualsiasi tipologia di sambiatore di alore, ompreso il tipo tubo in tubo, si è soliti alettare le superii di sambio in maniera tale, a parità di ingombro dello sambiatore, da aumentare l eettiva area di sambio. Questa tenia risulta partiolarmente utile nel aso di sambiatori liquido - areiorme in ui il oeiiente di sambio termio lato liquido risulta molto più elevato rispetto a quello lato aeriorme. In questo aso, si aletta la sola superiie di sambio lato aeriorme, in modo tale da ompensare il minor oeiiente di sambio termio on una maggiore area di sambio. Figura 8 - ubo alettato esternamente Sempre aendo rierimento agli sambiatori a tubi e mantello, nel aso in ui i due luidi si muovano seondo direzioni ra loro ortogonali, si die he lo sambiatore è a lussi inroiati (Figura 9). In questo aso, il luido he sorre all interno dei tubi è detto non mesolato, quello he sorre all esterno è detto 9
10 mesolato, on ovvio signiiato dei termini. Ovviamente, per il luido mesolato, per eetto del mesolamento, il gradiente di temperatura trasversale risulta trasurabile; iò ovviamente non aade nel aso di lusso non mesolato. Figura 9 - Shema sambiatore a lussi inroiati Esiste inine la tipologia degli sambiatori a piastre alettate, detti anhe ompatti, he realizzano elevatissimi valori del rapporto tra l area di sambio ed il volume. Sono ostituiti da una serie di piastre alettate sulle ui superii vengono riavati i anali di lusso he onsentono il passaggio dei luidi aldo e reddo (Figura 10 o Figura 11). Ne esistono svariate tipologie in unzione della geometria e delle tipologia di piastre. Essi sono partiolarmente utili nel aso in ui entrambi i luidi evolventi si trovino allo stato aeriorme, in quanto le elevatissime aree di sambio (per unità di volume) ompensano i modesti oeiienti di sambio termio degli aeriormi. Figura 10 - Shema sambiatore di alore a piastre alettate Gli sambiatori di alore a piastre alettate sono molto utilizzati in una vastissima gamma di appliazioni, dagli sambiatori degli impianti termii e rigorieri, ino ai grossi sistemi di sambio degli impianti industriali. I analetti di lusso sono riavati mediante sanalature sulle superii delle piastre stesse. 10
11 Figura 11 - Shema sambiatore di alore a piastre alettate a lussi inroiati 3. Analisi termodinamia L analisi termodinamia può essere ondotta a vari livelli di dettaglio: è possibile are onsiderazioni del tutto generali he presindono dalla natura del luido e dalla tipologia di sambiatore di alore, oppure sviluppare equazioni di progetto, implementando la geometria dello sambiatore di alore e le equazioni di stato dei luidi in esso evolventi. La trattazione di seguito desritta partirà da onsiderazioni ed ipotesi del tutto generali, per poi suessivamente analizzare nel dettaglio le aratteristihe dei luidi e la geometria dello sambiatore di alore. Si onsiderino valide le seguenti ipotesi generali: 1. Regime di moto monodimensionale 2. Regime stazionario 3. rasurabilità dei termini inetii nei bilani di energia ed exergia 4. rasurabilità dei termini potenziali nei bilani di energia ed exergia 5. Equilibrio termodinamio almeno nelle sezioni di ingresso e di usita dello sambiatore di alore 6. rasurabilità della potenza termia dispersa verso l ambiente esterno 7. Assenza di lavoro di elia all interno dello sambiatore di alore 8. Sistemi ad un solo in ingresso ed una sola usita, sia per il luido aldo he per il luido reddo. Si noti he on l ipotesi 6 si aerma he la potenza termia dispersa dall involuro dello sambiatore verso l esterno risulta trasurabile rispetto alla potenza termia traserita dal luido aldo a quello reddo. ale ipotesi risulta generalmente valida per tutte le tipologie di sambiatori, speialmente se ben oibentati esternamente. Con l ipotesi 7 invee si aerma he all interno dello sambiatore non sono presenti omponenti quali pompe, ompressori o turbine: tale ipotesi è sempre veriiata, in quanto, tali omponenti, ove presenti, vengono generalmente installati all esterno dello sambiatore. Inine, on 11
12 l ipotesi 8 si assume la totale assenza di perdite di luido, sia al lato aldo he al lato reddo, quindi né sull involuro esterno né sulla superiie di separazione ra luido aldo e luido reddo. Le ipotesi in qui utilizzate sono del tutto generali e presindono dalla natura del luido e dalla geometria dello sambiatore di alore; suessivamente verranno introdotte ulteriori ipotesi he terranno in onsiderazione sia la geometria dello sambiatore he le equazioni di stato dei luidi. Si onsideri un generio sambiatore di alore, per il quale si vogliono srivere i bilani di energia, entropia ed exergia. Il volume di ontrollo è individuato da una superiie suiientemente distante dall involuro dello sambiatore. In questo modo, l osservatore non è assolutamente in grado di ornire inormazioni sulla tipologia di sambiatore di alore (he rimane quindi una blak box=. Lo shema del volume di ontrollo è riportato nella Figura 12. i i V.C. u u Figura 12 - Volume di ontrollo per i bilani sullo sambiatore di alore In tale volume di ontrollo è possibile individuare quattro diversi lussi di massa: 1. Ingresso luido aldo (i) 2. Usita luido aldo (u) 3. Ingresso luido reddo (i) 4. Usita luido reddo (u) Ovviamente, a tali lussi di massa sono assoiati anhe i relativi lussi energetii, entropii ed exergetii di arattere onvettivo. Sulla superiie del volume di ontrollo non sono individuabili ulteriori lussi energetii in quanto, date le ipotesi 6 e 7, sia la potenza termia he quella meania risultano nulle. Per il volume di ontrollo preedentemente desritto e nelle ipotesi di ui sopra, si srivono di seguito i bilani di massa, energia, entropia ed exergia Bilanio di massa i, _ in j, _ out j h i Le due preedenti equazioni, nell ipotesi 8 diventano: m m (1.1) m m (1.2) h, _ in k, _ out k m m m (1.3) i u 12
13 m m m (1.4) i u Bilanio di energia m h m h m h m h (1.5) i, _ in i, _ in h, _ in h, _ in j, _ out j, _ out k, _ out k, _ out i h j k L equazione preedente, nell ipotesi 8 diventa: m h m h m h m h (1.6) i i u u La stessa equazione può anhe essere espressa in termini di entalpie orarie ( H mh ). H H H H (1.7) i i u u È possibile srivere anhe il bilanio di energia separatamente per un Volume di Controllo (V.C.) he ontenga solo il luido aldo e per un V.C. he invee ontenga solo il luido reddo. Indiando on Q e Q, le potenze termihe sambiate rispettivamente dal luido aldo e dal luido reddo, risulta: i u i u Q m h h H H (1.8) u i u i Q m h h H H (1.9) Ovviamente, per il bilanio di energia ra luido aldo e luido reddo, risulta Q Q (1.10) Bilanio di entropia m s m s S m s m s (1.11) i, _ in i, _ in h, _ in h, _ in gen j, _ out j, _ out k, _ out k, _ out i h j k Nell ipotesi 8, l equazione preedente diventa: m s m s S m s m s (1.12) i i gen u u La stessa equazione può anhe essere espressa in termini di entropie orarie ( S ms ). S S S S S (1.13) i i gen u u Quindi S S S S S S S (1.14) gen u i u i Bilanio di exergia m ex m ex m ex m ex Ex (1.15) i, _ in i, _ in h, _ in h, _ in j, _ out j, _ out k, _ out k, _ out d i h j k 13
14 Nell ipotesi 8: m ex m ex m ex m ex Ex (1.16) i i u u d La stessa equazione può anhe essere espressa in termini di exergie orarie ( Ex mex ). Ex Ex Ex Ex Ex (1.17) i i u u d Da ui: Ex d Ex u Ex i Ex u Ex i Ex Ex (1.18) Ovviamente, i bilani di massa, energia, entropia ed exergia appena sritti sono del tutto generali e ornisono inormazioni generihe sullo sambiatore di alore. Per la progettazione e la veriia dello sambiatore è invee opportuno introdurre relazioni riguardanti la geometria dello stesso e le aratteristihe termodinamihe dei luidi evolventi. 4. Equazioni di Progetto Si onsideri un generio sambiatore di alore nelle ipotesi 1-8 preedentemente desritte e si assuma he i luidi in esso evolventi siano tali he: 9. Le trasormazioni siano internamente reversibili, ovvero siano trasurabili gli attriti interni. In tale ipotesi è possibile assumere uniorme sia la pressione del luido aldo he la pressione del luido reddo 10. L entalpia dei luidi evolventi sia un unzione lineare della sola temperatura, esprimibile mediante la relazione: Dove risulta essere una ostante. h t (1.19) Il modello per il alolo dell entalpia di ui alla preedente equazione può essere ritenuto valido nel aso di: Gas a omportamento ideale a alori speiii ostanti. In questo aso il valore di oinide on il alore speiio a pressione ostante del luido (= p ) Liquido a moto inomprimibile (v=ost.), per il quale l entalpia risulta essere unzione linearmente resente della temperatura, seondo la ostante, oinidente on il alore speiio del liquido (= p = v ). In tutti gli altri asi (liquidi, gas reali, gas on alori speiii variabili on la temperatura, o luidi in passaggio di ase) a rigore la trattazione di seguito desritta non può essere appliata. Esistono omunque opportuno attori orrettivi he onsentono di riondurre la trattazione seguente a qualsiasi tipologia di luido. In alternativa, per la progettazione e/o la veriia degli sambiatori di alore è neessario ar rierimento a teorie termo-luidodinamihe più omplesse. 14
15 Di seguito si desrivono i due prinipali metodi utilizzati per il progetto e la veriia degli sambiatori di alore, ovvero il metodo ε-nu e quello della media logaritmia delle dierenze di temperatura (Δml). ali metodi, si basano sulle ipotesi 1-10 preedentemente menzionate, a ui si aggiungono le seguenti ipotesi sempliiative: 11. Calori speiii ostanti (=ost.) 12. Coeiiente di sambio termio globale ostante (U=ost.) 5. Metodo della media logaritmia delle dierenze di temperatura La trattazione di seguito desritta viene sviluppata aendo rierimento agli sambiatori di alore del tipo a tubi oassiali; tuttavia, ome si vedrà di seguito, potrà essere estesa a qualsivoglia tipologia di sambiatore mediante l utilizzo di appositi oeiienti orrettivi. Si onsideri un tratto ininitesimo di area di sambio, di uno sambiatore avente area di sambio inita, in ui onvenzionalmente la sezione di ingresso (A=0) orrisponde alla sezione di ingresso del luido aldo. i u u i ( i ) ( u ) 0 Atot Figura 13 - Shematizzazione sambiatore di alore Dal bilanio di energia sul volume di ontrollo individuato nella Figura 13, è possibile srivere la potenza termia ininitesima sambiata tra luido aldo e luido reddo utilizzando la seguente relazione: dove Q Q Q UdA (1.20) Q è la potenza termia ininitesima sambiata nel tratto di area ininitesima da, e sono rispettivamente le temperature del luido aldo e del luido reddo nella sezione ininitesima in esame (da). Inoltre U rappresenta il oeiiente globale di sambio termio, è dovuto sia alla trasmittanza onvettiva del luidi aldo e reddo, sia a quella onduttiva dello sambiatore. In prima approssimazione, è possibile srivere: 15
16 1 U 1 1 s h h k (1.21) dove h e h sono i oeiienti globali di sambio termio, rispettivamente del luido reddo e del luido aldo, s è lo spessore della superiie he parete il luido aldo ed il luido reddo e k è la sua onduibilità termia. Evidentemente, per non violare il seondo prinipio della termodinamia, deve risultare A (1.22) Risrivendo lo stesso bilanio di energia, aendo rierimento al solo volume di ontrollo relativo al luido aldo, si ottiene la seguente equazione: Q m d (1.23) Il segno negativo è dovuto al atto he le temperature del luido aldo sono sempre deresenti rispetto all area di sambio. La stessa proedura può anhe essere ripetuta per il volume di ontrollo he rahiude il luido reddo. In questo aso, però è neessario distinguere ra sambiatore di alore equiorrente (EQ) e ontroorrente (CC). Inatti, mentre nel primo aso (EQ), la temperatura del luido reddo rese all aumentare di A; nel seondo, poihé l ingresso reddo avviene dal lato opposto rispetto a quello aldo, la temperatura del luido reddo derese all aumentare di A. Ciò è dovuto al ambiamento di verso di perorrenza dello sambiatore he, in questo aso, vada dalle A maggiori a quelle minori. Quindi, nel aso di sambiatori ontroorrente (CC), risulta: mentre nel aso equiorrente: In sintesi: Q m d (1.24) Q m d (1.25) Q m d + se EQ - se CC (1.26) Si deinise apaità termia oraria: C m (1.27) Da ui è possibile risrivere i bilani di energia per i luidi aldo e reddo nella orma: Q C d (1.28) 16
17 Q C d + se EQ - se CC (1.29) Risulta anhe Q Q 1 1 d d d Q C C C C (1.30) + se EQ - se CC posto 1 1 M C C (1.31) + se EQ - se CC risulta d QM UMdA (1.32) da ui: d UMdA (1.33) posto: (1.34) risulta d UMdA (1.35) La preedente equazione risulta di ondamentale importanza per la determinazione dei proili di temperatura all interno degli sambiatori di alore. Integrando la preedente equazione ra la sezione di ingresso, indiata on il pedie a e ui orrisponde A=0, e la sezione inale, indiata on il pedie b e ui orrisponde A=A tot, si ottiene: Nelle ipotesi 11 e 12, l integrale diventa: Atot Atot d UMdA (1.36) 0 0 b ln UMA a tot (1.37) 17
18 ovvero: b a tot exp UMA (1.38) i u i u Figura 14 - Shema equiorrente i u u i Figura 15 - Shema ontroorrente Nel aso equiorrente (Figura 14): a i i b u u (1.39) mentre, nel aso ontroorrente (Figura 15): a i u b u i (1.40) L equazione (1.38) aerma he la dierenza di temperatura nella sezione di usita, tende asintotiamente allo zero nel aso di sambiatori equiorrente di area ininita oppure di sambiatori ontroorrente on M >0 ( C C ). È anhe possibile ripetere l integrazione di ui sopra, aendo rierimento ad una generia sezione (0<A<A tot ) dello sambiatore: da ui A A d UMdA (1.41) 0 0 a exp UMA (1.42) 18
19 he ornise indiazioni utili sulla variazione della dierenza di temperatura ra luido aldo e luido reddo all aumentare dell area di sambio. Per deinire, invee, la pendenza delle urve è suiiente eguagliare la (1.23) alla (1.20): da ui Q UdA C d (1.43) d da U C (1.44) Analogamente per il luido reddo: d da U C (1.45) Le due preedenti equazioni aermano he la pendenza delle urve tende a resere (in valore assoluto) all aumentare della dierenza di temperatura ra luido aldo e luido reddo. Le preedenti equazioni saranno utilizzate nella sezione suessiva per la determinazione dei proili di temperatura negli sambiatori. Per determinare l equazione di progetto è suiiente utilizzare la (1.20) ombinata on la (1.42): Q UdA UdA exp UMA (1.46) a ale equazione può essere integrata ra la sezione iniziale e quella inale dello sambiatore: da ui: Dalla (1.37) si trae: Atot Atot 0 0 a Q Q U exp UMA da (1.47) M (1.48) a Q exp UMA tot 1 b ln UA a M (1.49) Che, sostituita nella (1.48), ornise: b a Q UAtot UAtotml (1.50) b ln a tot 19
20 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia in ui la quantità ml è detta media logaritmia delle dierenze di temperatura. Questa equazione, unitamente alle due equazioni di bilanio di energia sul luido aldo e su quello reddo, onsente il alolo, il dimensionamento ed eventualmente la veriia degli sambiatori di alore. 6. Proili di temperatura negli sambiatori di alore Le equazioni riavate nella preedente sezione, ed in partiolare la (1.42), la (1.44) e la (1.45), onsentono di determinare i proili di temperatura negli sambiatori di alore. Si onsideri dapprima uno sambiatore di tipo equiorrente; per questa tipologia, l equazione (1.42) aerma he la dierenza di temperatura ra luido aldo e luido reddo tende a diminuire all aumentare dell area, seondo un esponenziale negativa; al limite, per un area di sambio ininita, tale dierenza si annulla. Pertanto, la temperatura di usita del luido reddo è sempre ineriore alla temperatura di usita del luido aldo (Figura 16); al limite, per aree di sambio ininite, tali temperature oinideranno (Figura 17). Inoltre, la (1.44) e la (1.45) aermano rispettivamente he la pendenza del proilo di temperatura del luido reddo risulta positiva, mentre la pendenza della urva del luido aldo risulta negativa; al resere dell area di sambio si ridue la dierenza di temperatura ra luido aldo e luido reddo e quindi le pendenze tendono a raggiungere asintotiamente il valore nullo (Figura 16). Si noti, ovviamente, he i proili di temperatura di Figura 16 risultano esattamente sovrapposti a quelli di Figura 17, per ogni valore della variabile ompreso ra 0 e 50 m 2. Ovvero, l aumentare dell area di sambio omporta eslusivamente un prolungamento dei proili di temperatura senza inluenzarne l andamento a monte luido aldo luido reddo Area di sambio (m 2 ) Figura 16 - Diagrammi (,A) per sambiatori equiorrente 20
21 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Sambiatore di Figura Area di sambio (m 2 ) Figura 17 - Digrammi (,A) per sambiatori equiorrente (A ) Si onsideri ora uno sambiatore di tipo ontroorrente. In questo aso il segno dell esponenziale dell equazione (1.42), dipende dal segno di M. Inatti: 1 1 M 0 C C C C 1 1 M 0 C C C C 1 1 M 0 C C C C (1.51) Nel prima aso, (M>0) l equazione (1.42) aerma he la dierenza di temperatura ra luido aldo e luido reddo tende a ridursi all aumentare della variabile A; ontestualmente le equazioni (1.44) e (1.45) aermano he tale riduzione omporta anhe una tendenza alla riduzione (in valore assoluto) delle pendenze delle urve (,A) relative ad ambedue i luidi (Figura 18). Al limite, per aree di sambio tendenti all ininito, la temperatura di usita del luido aldo tende a oinidere on quella di ingresso del luido reddo, e le pendenza delle urve in orrispondenza della sezione di usita sono nulle (Figura 19). Si noti, inine, he all aumentare dell area di sambio le urve tendono anhe a spostarsi, osì ome evidenziato in Figura
22 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) C C ) Figura 18 - Sambiatore Controorrente, M>0 ( 22
23 emperatura ( C) emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) Figura Sambiatore Controorrente, M>0 ( C C ), (A ) luido aldo (A inita) luido reddo (A inita) luido aldo (A ininita) luido reddo (A ininita) Area di sambio (m 2 ) Figura 20 - Sambiatore Controorrente, M>0 ( C C ) Conronto Area inita ed Area ininita Nel seondo aso, in ui invee risulta M=0, lo sambiatore viene detto bilaniato, in quanto la apaità termia oraria del luido aldo risulta essere la stessa del luido reddo. In questo aso, dall equazione (1.42) 23
24 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia si dedue he la dierenza di temperatura ra luido aldo e luido reddo è uguale, per qualsiasi valore di A. Evidentemente, tale eventualità, in virtù delle (1.44) e (1.45), a sì he le pendenze delle urve (,A) relative ai due luidi non variano al variare di A (Figura 21). Per uno sambiatore bilaniato, quindi le urve (,A) del luido aldo e del luido reddo sono rappresentabili ome due rette parallele, la ui pendenza è tanto più viina allo zero quanto maggiore è l area di sambio e quindi quanto minore è il Δ. In questo aso, al limite, per aree di sambio ininite (Figura 22), le due rette oinidono (usita reddo oinidente on l ingresso aldo ed usita aldo oinidente on l ingresso reddo). All aumentare dell area di sambio, osì ome evidenziato in Figura 23, i proili di temperatura tendono ad avviinarsi e ad assumere una pendenza orizzontale luido aldo luido reddo Area di sambio (m 2 ) C C ) Figura 21 - Sambiatore ontroorrente, M=0 ( 24
25 emperatura ( C) emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) Figura 22- Sambiatore ontroorrente, M=0 ( C C ), (A ) luido aldo (area ininita) luido reddo (area ininita) luido aldo (area inita) luido reddo (area inita) Area di sambio (m 2 ) Figura 23- Sambiatore ontroorrente, M=0 ( C C ), onronto Area di sambio inita ed ininita Inine, nell ultimo aso, M<0, l equazione (1.42) aerma he la dierenza di temperatura ra luido aldo e luido reddo tende a resere all aumentare della variabile A. Contestualmente le equazioni (1.44) e (1.45) 25
26 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia aermano he tale aumento omporta anhe un inremento (in valore assoluto) delle pendenze delle urve (,A) relative sia al luido aldo he a quello reddo (Figura 24). Al limite, per aree di sambio tendenti all ininito, la temperatura di usita del luido reddo oinide on quella di ingresso del luido aldo, e le pendenze delle urve in orrispondenza della sezione di ingresso sono nulle (Figura 25). Analogamente ai asi preedenti, la sovrapposizione ra la Figura 24 e la Figura 25 è presentato in Figura luido aldo luido reddo Area di sambio (m 2 ) C C ) Figura 24 - Sambiatore ontroorrente, M<0 ( 26
27 emperatura ( C) emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) Figura 25- Sambiatore ontroorrente, M<0 ( C C ), (A ) luido aldo (area inita) luido reddo (area inita) luido aldo (area ininita) luido reddo (area ininita) Area di sambio (m 2 ) Figura 26- Sambiatore ontroorrente, M<0 ( C C ), (A ), Conronto area di sambio inita ed ininita 27
28 Inine è da itare il aso in ui almeno uno dei due luidi si trovi in passaggio di ase (ondensazione o evaporazione). È noto he il alore speiio( q ) di un luido in passaggio di ase è ininito, in d quanto lo sambio di energia termia avviene senza variazioni di temperatura. In questo aso, quindi, supponendo ad esempio he il luido in passaggio di ase sia quello aldo, le equazioni (1.42), (1.44) e (1.45), diventano, rispettivamente: UA a exp C (1.52) d 0 da (1.53) d da U C (1.54) ovvero (Figura 27): La urva del luido in passaggio di ase è orizzontale La dierenza di temperatura ra i due luidi derese all aumentare dell area di sambio. È possibile sviluppare il medesimo ragionamento anhe per un ondensatore (Figura 28). Nel aso di un ondensatore di area di sambio ininita, la temperatura di ondensazione oinide on la temperatura di usita del luido reddo; nel aso invee di evaporatore di area di sambio ininita, la temperatura di evaporazione oiniderà on la temperatura di usita del luido aldo Si noti inine, he per uno sambiatore in ui uno dei luidi sia in passaggio di ase (evaporatore o ondensatore), risulta assolutamente indierente la distinzione ra equiorrente e ontroorrente in virtù della pendenza nulla della urva (,A) relativa al luido in passaggio di ase. Pertanto, similmente a quanto già aermato per gli sambiatori equiorrente, anhe per gli sambiatori on un luido in passaggio di ase risulta he, all aumentare dell area di sambio, i proili di temperatura del luido aldo e del luido reddo di sambiatori di area inita sono esattamente sovrapponibili per la relativa area di sambio ai orrispondenti proili di sambiatori di area inita. 28
29 emperatura ( C) emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) Figura 27 - Sambiatore (EQ o CC) in ui il luido reddo è in passaggio di ase (evaporatore) luido aldo luido reddo Area di sambio (m 2 ) Figura 28 - Sambiatore (EQ o CC) in ui il luido aldo è in passaggio di ase (ondensatore) 29
30 emperatura ( C) emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Sambiatore di Area Finita Area di sambio (m 2 ) Figura 29- Sambiatore (EQ o CC) in ui il luido reddo è in passaggio di ase (evaporatore) (A ) luido aldo luido reddo Sambiatore di Area Finita Area di sambio (m 2 ) Figura 30- Sambiatore (EQ o CC) in ui il luido aldo è in passaggio di ase (ondensatore) (A ) 30
31 7. Metodo ε-nu Il metodo media logaritmia delle dierenze di temperatura, pur essendo molto semplie nella sua ormulazione teoria, risulta spesso omplesso nel alolo quando le temperature di usita del luido aldo sono inognite. In tal aso, inatti, esse non possono essere riavate in orma espliita a partire dalle equazioni (1.50), (1.8) e (1.9), ma la loro valutazione rihiede una risoluzione per tentativi. In alternativa al metodo della media logaritmia delle dierenze di temperatura è possibile utilizzare il metodo eiienza (ε) Numero di Unità ermihe (Number o hermal Units, NU). Si deinisono apaità termihe orarie minime e massime, rispettivamente la minima e la massima apaità termia oraria ra quella del luido aldo e quella del luido reddo. C min min C, C (1.55) C max max C, C (1.56) Il rapporto ra la apaità termia oraria minima e la apaità termia oraria massima è, ome ovvio, un numero sempre minore o uguale all unità e maggiore o uguale allo zero. C C min max 0 1 (1.57) In partiolare, ω=0 omporta he la apaità termia massima sia ininita, ovvero uno dei due luidi sia in passaggio di ase (ondensatore o evaporatore); ω=1 implia he la apaità termia oraria del luido aldo sia pari alla apaità termia oraria del luido reddo e quindi si sia in presenza di uno sambiatore bilaniato. Si deinise Numero di Unità ermihe (Number o hermal Units): NU UA 0 NU C min (1.58) dove U è il oeiiente di sambio globale dello sambiatore A è l area totale di sambio Pertanto, NU è una grandezza adimensionale il ui valore minimo è zero e non è limitata superiormente. Si deinise eiienza di uno sambiatore di alore il rapporto ra la potenza termia sambiata dallo sambiatore e la potenza termia he si sambierebbe in uno sambiatore ideale: Q Q id (1.59) 31
32 Intendendo per sambiatore ideale uno sambiatore ontroorrente di area ininita. È possibile dimostrare he: id min i i min max Q C C (1.60) Inatti, nell ipotesi di uno sambiatore ontroorrente in ui: C C, risulta C C. La potenza min termia sambiata può essere sritta ome u i Q C (1.61) Ma, in un siatto sambiatore ontroorrente di area ininita, in aordo on quanto detto nella sezione preedente (Figura 25), risulta u ininita in ui C C è i. Quindi la potenza termia sambiata da un ontroorrente di area min Q C C (1.62) id i i i i Nell ipotesi di uno sambiatore ontroorrente in ui: C C, risulta C C C. La potenza termia min sambiata può essere sritta ome u i Q C (1.63) Ma, in un siatto sambiatore ontroorrente di area ininita, in aordo on quanto detto nella sezione preedente (Figura 22), risulta u i. Quindi la potenza termia sambiata da un ontroorrente di area ininita in ui C C è min Q C C (1.64) id i i i i Nell ipotesi di uno sambiatore ontroorrente in ui: C C, risulta C C. La potenza termia min sambiata può essere sritta ome i u Q C (1.65) Ma, in un siatto sambiatore ontroorrente di area ininita, in aordo on quanto detto nella sezione preedente (Figura 19), risulta u ininita in ui C C è Pertanto, l eiienza può essere risritta ome: i. Quindi la potenza termia sambiata da un ontroorrente di area min Q C C (1.66) id i u i i C min Q max (1.67) 32
33 Si può, inine, dimostrare he l eiienza di uno sambiatore di alore è una unzione, dipendente dalla geometria dello sambiatore, da NU e da ω. NU, (1.68) In partiolare, l eiienza è sempre una unzione resente di NU e deresente di ω. In letteratura sono disponibili unzioni di eiienza per la gran parte delle tipologie di sambiatore di alore (equiorrente, ontroorrente, a lussi inroiati miselati o non miselati, tubi e mantello, et.). A titolo di esempio si ornisono di seguito le relazioni per gli sambiatori ontroorrente ed equiorrente: Controorrente 1 exp 1 NU 1 exp 1 NU (1.69) ovvero: NU 1 ln 1 1 (1.70) Che, nel aso di ω=0, 1exp( NU ) (1.71) Invee, nel aso di ω=1 NU 1 NU (1.72) Nel aso di sambiatori di Area di sambio ininita (NU ), l eiienza tende ad 1 per qualsiasi valore di ω. Si noti he tutti gli sambiatori ontroorrente, per qualsiasi valore di ω, possono raggiungere eiienze unitarie, nel aso in ui l area di sambio sia ininita. 33
34 ε Corso di ermodinamia dei Proessi di Conversione dell Energia ω=0 ω=0.2 ω=0.4 ω=0.6 ω=0.8 ω= NU Figura 31 Diagramma ε-nu per sambiatori ontroorrente Equiorrente 1 1 exp 1 NU (1.73) ovvero: NU ln (1.74) Che, nel aso di ω=0, 1exp( NU ) (1.75) Invee, nel aso di ω=1 1exp( NU ) (1.76) 2 Inine, nel aso di sambiatori di area di sambio ininita (NU ) 1 (1.77) 1 34
35 ε Corso di ermodinamia dei Proessi di Conversione dell Energia ω=0 ω=0.2 ω=0.4 ω=0.6 ω=0.8 ω= NU Figura 32 Diagramma ε-nu per sambiatori equiorrente Si noti he lo sambiatore equiorrente, anhe on aree di sambio ininite, può raggiungere eiienze unitarie solo nel aso in ui ω=0 (equiorrente ontroorrente). In tutti gli altri asi, l eiienza tende asintotiamente ad un valore minore dell unità. Il valore di tale asintoto sarà tanto minore quanto maggiore sarà ω. Al limite, per ω=0, tale asintoto vale 0,50. ale valore può essere dedotto sia dalla (1.77) he da onsiderazioni graihe. Inatti, il proilo (,A) di uno sambiatore equiorrente di area ininita è perettamente simmetrio (Figura 33) e la temperatura di usita del luido aldo tende a oinidere on la temperatura di usita del luido reddo. Pertanto Q i u i u 1 C 2 2 min max i i i u (1.78) 35
36 emperatura ( C) Corso di ermodinamia dei Proessi di Conversione dell Energia luido aldo luido reddo Area di sambio (m 2 ) Figura 33 - Sambiatore equiorrente bilaniato di area ininita In sintesi, il metodo ε-nu onsente di alolare le prestazioni di uno sambiatore in maniera molto più rapida rispetto al metodo della media logaritmia delle dierenze di temperatura. Inatti, issate le temperature di ingresso e le apaità termihe orarie del luido aldo e del luido reddo, nonhé l area totale di sambio ed il oeiiente globale di sambio dello sambiatore, si proede ome segue: Si determina C min e C max Si alola ω, utilizzando la (1.57) Si alola NU, utilizzando la (1.58) Si alola ε, sulla base della geometria dello sambiatore assegnato, mediante unzioni del tipo (1.68) Si alola la potenza termia sambiata ome: min i i Q C (1.79) Si determinano le temperature di usita del luido aldo e del luido reddo dai rispettivi bilani di energia: min C C (1.80) i u i i min C C (1.81) u i i i 36
37 Evidentemente è possibile utilizzare il metodo ε-nu anhe per altre operazioni quali ad esempio la veriia ed il dimensionamento degli sambiatori. Un appliazione molto requente onsta nel alolo dell area di sambio, per un data potenza termia e per issati valori delle temperature. 8. Exergia distrutta negli sambiatori di alore Si onsideri un generio sambiatore di alore, nelle ipotesi 1-9 preedentemente introdotte. Il Bilanio di Exergia può essere sritto nella seguente orma ininitesima: Ex dex dex (1.82) d Ovvero: Ex m dex m dex (1.83) d Riordando he dex dh ads (1.84) Risulta: Ex m dh ds m dh ds (1.85) d a Ovvero: ads ads Ex d m dh 1 m dh 1 dh dh (1.86) Ma: Q m dh m dh (1.87) Poihé le trasormazioni sono internamente reversibili (p=ost), dalla seonda equazione di Gibbs: dh (1.88) ds dh ds (1.89) Da ui: a a 1 1 Ex d Q 1 1 a Q (1.90) Integrando: 37
38 Nel aso di sambio ra due SE, l equazione preedente diventa: 1 1 Ex d aq (1.91) 1 1 Ex d aq (1.92) Quindi l exergia distrutta può essere espressa in unzione della potenza termia sambiata e delle temperature medie integrali dei luidi reddo e aldo. Ovviamente, l exergia distrutta risulta essere tanto maggiore quanto maggiore è la potenza termia sambiata e quanto maggiore è la dierenza ra le temperature medie del luido aldo e del luido reddo. Inatti, alla aumentare di tale dierenza aumenteranno le irreversibilità di tipo esterne legate allo sambio termio. Una rappresentazione graia agevole sul piano (,s) si tale exergia distrutta si può avere solo nel aso in ui uno dei due luidi sia in passaggio di ase (=ost.). Integrando la (1.90) si ha: (1.93) Exd a Q Dal bilanio di energia sul luido reddo: Q m dh (1.94) Dalla seonda equazione di Gibbs, per trasormazioni internamente reversibili (p=ost): Q m dh m ds (1.95) Quindi, utilizzando l ipotesi di temperatura del luido aldo ostante: Ex ds AREA m d a a (1.96) Ripetendo lo stesso ragionamento, nel aso in ui sia il luido in reddo in passaggio di ase: Ex ds AREA m d a a (1.97) 38
39 i u AREA X ( a / ) SE= s Figura 34 - Rappresentazione dell Exergia distrutta sul piano,s -evaporazione SE= i u AREA X ( a / ) s Figura 35 - Rappresentazione dell Exergia distrutta sul piano,s -ondensazione In altre parole, nel aso in ui uno dei due luidi sia in passaggio di ase, oppure sia shematizzabile ome un SE a temperatura SE, l exergia distrutta speiia è rappresentabile sul piano (,s) dall area sottesa dalle a due trasormazioni, a meno del attore di peso SE 9. Rappresentazione graia della generazione entropia nel piano, S Si onsideri un generio sambiatore di alore nelle ipotesi 1-10: per tale sistema verranno di seguito riavate proedure graihe per la determinazione della generazione entropia e quindi dell exergia 39
40 distrutta. In generale, queste due quantità possono essere riavate utilizzando rispettivamente le equazioni (1.14) e (1.18). Per la rappresentazione graia dei proessi di sambio termio normalmente si a rierimento al piano (,s). uttavia, tale piano è aratteristio e varia quindi on la sostanza. Pertanto, al ine di poter rappresentare sullo stesso piano termodinamio, i proessi di sambio termio di due diverse sostanze, viene introdotto il piano (, S ), in ui la aratteristia della sostanza viene inglobata nella variabile S. L andamento delle isobare nel piano (, S ) è del tutto simile a quello visibile sul piano (,s): inatti, anhe nel piano (, S ), osì ome avviene nel (,s) le isobare tendono a divergere all aumentare della temperatura. Inatti, nell ipotesi di trasormazioni isobare (p=ost), la II equazione di Gibbs diventa: Ma, nell ipotesi 10 (gas ideale o liquido inomprimibile) dh ds (1.98) dh dt (1.99) d ds (1.100) Da ui: s p (1.101) Quindi la pendenza aumenta all aumentare della temperatura e di onseguenza le isobare tendono a divergere. p=ost Figura 36 - Diagramma, S - isobara S 40
41 Si supponga ad esempio di he la pressione del luido aldo sia maggiore di quella del luido reddo ( p p ). La rappresentazione sul diagramma in oggetto, delle trasormazioni di sambio termio (internamente reversibili) è la seguente: i p u i u p S Figura 37 - Diagramma (, S ) - sambiatore di alore Dalla igura preedente si può osservare he le aree sottese dalle due trasormazioni (luido aldo e luido reddo), sono identihe. Esse, inatti, rappresentano la potenza termia sambiata he, ome noto, è la stessa sia per il luido aldo he per quello reddo. Inatti, per trasormazioni internamente reversibili, risulta dal II prinipio della termodinamia: Da ui: Q ds (1.102) u u i Q ds ds ds (1.103) i i u Evidentemente, i punti rappresentativi delle ondizioni di ingresso e di usita dei luidi aldo e reddo devono essere disposti in maniera tale da soddisare la preedente relazione. Al ine di ottenere una migliore visualizzazione graia della generazione entropia è anhe possibile sruttare la proprietà he l entropia, e quindi anhe l entropia oraria, è una quantità deinita a meno di una ostante. La ostante viene tipiamente deinita, assegnato ad un dato stato termodinamio, detto di rierimento, un valore arbitrario della unzione entropia. Poihé tale ostante è selta in maniera arbitraria, è sempre possibile selezionarla in maniera tale he sia soddisatta la relazione: S S (1.104) u i È possibile ottenere il preedente risultato operando sia sulla ostante del luido aldo he su quella del reddo he su entrambe. Ipotizzando, di ambiare la ostante del luido reddo, l operazione graiamente 41
42 si tradue in una traslazione dell isobara del luido reddo in maniera tale he sia veriiata la preedente relazione, osì ome evidenziato nella igura seguente: i p u u p u' i i' a Exd Si=Su Si Su S Sgen Figura 38- Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p >p ) In questo modo, stante la relazione (1.104) è possibile determinare graiamente in maniera immediata la generazione entropia: S S S (1.105) gen u i Ovviamente, l exergia distrutta per il teorema di Guy-Stodola, risulta essere pari all area del rettangolo di base S gen ed altezza a: Ex S (1.106) d gen a ale rappresentazione ha il vantaggio di avere una visualizzazione immediata sia della generazione entropia he della distruzione exergetia all interno degli sambiatori di alore. Il ragionamento qui atto, nel aso di p p, può essere ailmente esteso anhe a tutti gli altri asi ( p p ) utilizzando la medesima proedura, osì ome evidenziato nelle igure seguenti. 42
43 p p p' i u u i u' i' i' a Exd Si=Su Si Su Sgen S Figura 39 - Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p <p ) i p' u u u' i i' a Exd Si=Su SiSu S Figura 40 - Diagramma (, S ) - sambiatore di alore raslazione isobara luido reddo (p =p ) La rappresentazione della produzione entropia nel piano (, S ) risulta anhe molto utile per realizzare un onronto ra gli sambiatori equiorrente e quelli ontroorrente. Si onsideri quindi un generio sambiatore di alore, he abbia ome obiettivo il risaldamento del luido reddo. Pertanto, nel onronto disusso di seguito ra sambiatori ontroorrente ed equiorrente, si onsiderano issati: la geometria dello sambiatore di alore, le aratteristihe del luido reddo (portata, alore speiio, temperature di ingresso e di usita), nonhé la portata ed il alore speiio del luido aldo. Per tale sambiatore risultano quindi issati i seguenti parametri: U A oeiiente globale di sambio termio Area totale di sambio 43
44 t i emperatura di ingresso del luido reddo t u emperatura di usita del luido reddo C C Capaità termia oraria del luido aldo Capaità termia oraria del luido reddo Fissata la rihiesta dell utenza ( t i t, u C, ) risulta anhe issata la potenza termia resa all utenza: Q C t t C t t C t t (1.107) u i i u EQ i u Pertanto, per entrambi gli sambiatori di alore, la dierenza di temperatura ra ingresso ed usita del luido aldo, risulta la medesima Dall equazione di progetto risulta anhe: Quindi anhe: t t t t (1.108) i u EQ i u CC Q UA UA UA (1.109) ml ml EQ ml CC (1.110) ml EQ In deinitiva, le relazioni preedenti aermano he la dierenza di temperatura media logaritmia, osì ome deinita nella sezione preedente, e la dierenza di temperatura del luido aldo rimangono invariate, nel onronto ra sambiatori equiorrente e ontroorrente. Aermare he la dierenza di temperatura del luido aldo sia la medesima non vuol dire he le temperatura di ingresso e di usita del ontroorrente siano uguali alle rispettive temperature in uno sambiatore equiorrente. Pertanto, tale ondizione può realizzarsi anhe on livelli termii ben dierenti. Inatti, è possibile dimostrar he per i parametri issati in preedenza, risulta sempre: E quindi: Inatti, issare C, ml t t i EQ i t t u EQ CC CC CC (1.111) (1.112) u CC C, U ed A implia anhe, per la loro stessa deinizione, issare ω e NU. A parità di questi ultimi parametri si può vedere sia graiamente he analitiamente, dalle preedenti equazioni e igure, he risulta sempre CC (1.113) EQ Ma dalla deinizione di eiienza: 44
Scambiatori di calore
 Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Sambiatori di alore Con il termine sambiatori di alore indihiamo una apparehiatura in ui si ha trasmissione di alore da un luido ad un altro. In ampo termotenio
Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Sambiatori di alore Con il termine sambiatori di alore indihiamo una apparehiatura in ui si ha trasmissione di alore da un luido ad un altro. In ampo termotenio
Università di Roma Tor Vergata
 Università di Roma Tor Vergata Faoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TERMOTECNICA 1 DIMENSIONAMENTO DEGLI SCAMBIATORI DI CALORE Ing. G. Bovesehi gianluigi.bovesehi@gmail.om
Università di Roma Tor Vergata Faoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TERMOTECNICA 1 DIMENSIONAMENTO DEGLI SCAMBIATORI DI CALORE Ing. G. Bovesehi gianluigi.bovesehi@gmail.om
MOTORI PER AEROMOBILI
 MOORI PER AEROMOBILI Cap.2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas per
MOORI PER AEROMOBILI Cap.2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas per
UNITA' 15 SOMMARIO ATTENZIONE
 ermodinamia e trasmissione del alore U.5/0 UNIA' 5 SOMMARIO 5. GLI SAMBIAORI DI ALORE 5.. I DIVERSI IPI DI SAMBIAORE DI ALORE 5... Sambiatori tubo in tubo (parallel low) 5... Sambiatori a orrenti inroiate
ermodinamia e trasmissione del alore U.5/0 UNIA' 5 SOMMARIO 5. GLI SAMBIAORI DI ALORE 5.. I DIVERSI IPI DI SAMBIAORE DI ALORE 5... Sambiatori tubo in tubo (parallel low) 5... Sambiatori a orrenti inroiate
Quantizzazione - Soluzioni
 Quantizzazione - Soluzioni INTRODUZIONE Il Passaggio da un segnale analogio ad un segnale digitale avviene tramite due operazioni prinipali: Campionamento, Quantizzazione. Durante la prima ase, ampionamento,
Quantizzazione - Soluzioni INTRODUZIONE Il Passaggio da un segnale analogio ad un segnale digitale avviene tramite due operazioni prinipali: Campionamento, Quantizzazione. Durante la prima ase, ampionamento,
LEZIONE # 17. massa entrante = massa uscente m e = m u
 LEZIONE # 7 Le misure di portata sono basate sul prinipio di onservazione della massa del luido in movimento. In un tubo di lusso generio, in assenza di sorgenti o di perdite, per ogni intervallo di tempo,
LEZIONE # 7 Le misure di portata sono basate sul prinipio di onservazione della massa del luido in movimento. In un tubo di lusso generio, in assenza di sorgenti o di perdite, per ogni intervallo di tempo,
Scambiatori di calore
 Fisia Tenia G. Grazzini Faoltà di Ingegneria Sabiatori di alore Con il terine sabiatori di alore indihiao una apparehiatura in ui si ha trasissione di alore da un luido ad un altro. In apo terotenio queste
Fisia Tenia G. Grazzini Faoltà di Ingegneria Sabiatori di alore Con il terine sabiatori di alore indihiao una apparehiatura in ui si ha trasissione di alore da un luido ad un altro. In apo terotenio queste
Algoritmo di best-fit (o fitting) sinusoidale a 3 parametri ( ) ( )
 Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
MOTORI PER AEROMOBILI
 MOORI PER AEROMOBILI Cap. 2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas
MOORI PER AEROMOBILI Cap. 2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI. 1 Fondamenti Segnali e Trasmissione
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
Il processo inverso della derivazione si chiama integrazione.
 Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Le trasformazioni NON isometriche
 Le trasformazioni NON isometrihe Sono trasformazioni non isometrihe quelle trasformazioni he non onservano le distanze fra i punti Fra queste rientrano le affinità L insieme delle affinità si può osì rappresentare
Le trasformazioni NON isometrihe Sono trasformazioni non isometrihe quelle trasformazioni he non onservano le distanze fra i punti Fra queste rientrano le affinità L insieme delle affinità si può osì rappresentare
FACOLTÀ DI INGEGNERIA. ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meccanica PROF. A. PRÁSTARO 21/01/2013
 FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
LEZIONE # 17. massa entrante = massa uscente m e = m u. V t. V t
 LEIONE # 7 Le misure di portata sono basate sul prinipio di onserazione della massa del luido in moimento. In un tubo di lusso generio, in assenza di sorgenti o di perdite, per ogni interallo di tempo
LEIONE # 7 Le misure di portata sono basate sul prinipio di onserazione della massa del luido in moimento. In un tubo di lusso generio, in assenza di sorgenti o di perdite, per ogni interallo di tempo
Gli integrali indefiniti
 Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
Lezione 9. Prestazioni dinamiche dei sistemi di controllo
 Lezione 9 Prestazioni dinamihe dei sistemi di ontrollo Caratterizzazione delle prestazioni dinamihe Le prestazioni dinamihe fanno riferimento al omportamento del sistema di ontrollo durante i transitori,
Lezione 9 Prestazioni dinamihe dei sistemi di ontrollo Caratterizzazione delle prestazioni dinamihe Le prestazioni dinamihe fanno riferimento al omportamento del sistema di ontrollo durante i transitori,
LA TRASFORMATA DI LAPLACE
 LA TRASFORMATA DI LAPLACE I sistemi dinamii invarianti e lineari (e tali sono le reti elettrihe) possono essere studiati, nel dominio del tempo, attraverso le equazioni differenziali nelle quali l'inognita
LA TRASFORMATA DI LAPLACE I sistemi dinamii invarianti e lineari (e tali sono le reti elettrihe) possono essere studiati, nel dominio del tempo, attraverso le equazioni differenziali nelle quali l'inognita
Proprietà delle operazioni sui numeri naturali. Introduzione geometrica alle proprietà delle operazioni = 11 = 8 + 3
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
LEZIONE # 7. y(t) grandezza in ingresso (misurando) x(t) grandezza in uscita (deflessione o risposta dello strumento)
 Appunti di Misure Meanihe & Termihe orso di Laurea Magistrale in Ingegneria Meania (ordinamento ex 7/4) Faoltà di Ingegneria Civile e Industriale - Università degli studi di Roma La Sapienza LEZIONE #
Appunti di Misure Meanihe & Termihe orso di Laurea Magistrale in Ingegneria Meania (ordinamento ex 7/4) Faoltà di Ingegneria Civile e Industriale - Università degli studi di Roma La Sapienza LEZIONE #
Politecnico di Torino Laurea a Distanza in Ingegneria Meccanica Corso di Macchine
 ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
CHIMICA FISICA I. Le leggi dei gas
 A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
ESERCIZI ELEMENTARI DI FLUIDODINAMICA
 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ESERCIZI ELEMENTRI I FLUIOINMIC RICHIMI INTROUTTII Il fluido viene onsiderato ome un ontinuo, ossia vengono identifiate alune grandezze
ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ESERCIZI ELEMENTRI I FLUIOINMIC RICHIMI INTROUTTII Il fluido viene onsiderato ome un ontinuo, ossia vengono identifiate alune grandezze
Laboratorio di Misure Fisiche per Scienze Biologiche
 Laboratorio di Misure Fisihe per Sienze Biologihe Nozioni di alorimetria e misura del alore speiio di una sostanza Rihiami di teoria (Ragozzino et al Fondamenti di Fisia) - Il onetto di temperatura. -
Laboratorio di Misure Fisihe per Sienze Biologihe Nozioni di alorimetria e misura del alore speiio di una sostanza Rihiami di teoria (Ragozzino et al Fondamenti di Fisia) - Il onetto di temperatura. -
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE.
 PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
Proprietà globali delle funzioni continue
 Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 28 Febbraio 2013
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Enrico Borghi QUANTIZZAZIONE DEL CAMPO DI KLEIN-GORDON
 Enrio Borghi QUANTIZZAZIONE DEL CAMPO DI KLEIN-GORDON Rihiami a studi presenti in fisiarivisitata Leggendo la Quantizzazione del ampo di Klein-Gordon si inontrano rihiami ai seguenti studi: a) Introduzione
Enrio Borghi QUANTIZZAZIONE DEL CAMPO DI KLEIN-GORDON Rihiami a studi presenti in fisiarivisitata Leggendo la Quantizzazione del ampo di Klein-Gordon si inontrano rihiami ai seguenti studi: a) Introduzione
CALCOLO DELL INDICE DI VULNERABILITÀ - Edifici in Muratura. Punteggi A B C D
 CALCOLO DELL INDICE DI VULNERABILITÀ - Edifii in Muratura tabella dei punteggi e dei pesi da assegnare ad ogni parametro della sheda di seondo livello EDIFICI IN MURATURA A B C D Peso 1 - Org. sist. resist.
CALCOLO DELL INDICE DI VULNERABILITÀ - Edifii in Muratura tabella dei punteggi e dei pesi da assegnare ad ogni parametro della sheda di seondo livello EDIFICI IN MURATURA A B C D Peso 1 - Org. sist. resist.
Proprietà delle operazioni sui numeri naturali
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Modelli di assegnazione (cenni)
 Corso di Trasporti e Ambiente http://www.uniroma.it/didattia/ta_ ing. Antonio Comi novembre Modelli di assegnazione (enni) Struttura del sistema di modelli per la simulazione dei sistemi di trasporto OFFERTA
Corso di Trasporti e Ambiente http://www.uniroma.it/didattia/ta_ ing. Antonio Comi novembre Modelli di assegnazione (enni) Struttura del sistema di modelli per la simulazione dei sistemi di trasporto OFFERTA
Dimensionamento allo sforzo normale -Pilastri
 Dimensionamento allo sorzo normale -Pilastri QUADO EL CORSO DELLE ILLUSTRAZIOI COMPARE LA RADIOGRAFIA DEL CERVELLIO DI HOMER SIGIFICA CHE SIETE IVITATI A USARE IL VOSTRO CERVELLIO E IMPARARE POSSIBILMETE
Dimensionamento allo sorzo normale -Pilastri QUADO EL CORSO DELLE ILLUSTRAZIOI COMPARE LA RADIOGRAFIA DEL CERVELLIO DI HOMER SIGIFICA CHE SIETE IVITATI A USARE IL VOSTRO CERVELLIO E IMPARARE POSSIBILMETE
Unità Didattica 1. Sistemi di Numerazione
 Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI
 Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI 1 LA LAMINAZIONE DELLE PIENE NEI SERBATOI Esistono essenzialmente tre tipologie di opere per
Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI 1 LA LAMINAZIONE DELLE PIENE NEI SERBATOI Esistono essenzialmente tre tipologie di opere per
Moto vario elastico: fenomeno del colpo d ariete
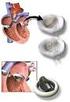 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Esercitazioni di Elettrotecnica
 Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Gli approcci alla programmazione dinamica: alcuni esempi
 Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Sistemi di misura digitali Segnali campionati - 1. Segnali campionati
 Sistemi di misura digitali Segnali ampionati - 1 Segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling di un segnale analogio onsiste nel prenderne solo i valori
Sistemi di misura digitali Segnali ampionati - 1 Segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling di un segnale analogio onsiste nel prenderne solo i valori
L offerta della singola impresa: le curve di costo
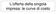 L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
f Le trasformazioni e il trattamento dell aria
 f Le trasformazioni e il trattamento dell aria 1 Generalità Risolvendo il sistema (1) rispetto ad m a si ottiene: () Pertanto, il punto di misela sul diagramma psirometrio è situato sulla ongiungente dei
f Le trasformazioni e il trattamento dell aria 1 Generalità Risolvendo il sistema (1) rispetto ad m a si ottiene: () Pertanto, il punto di misela sul diagramma psirometrio è situato sulla ongiungente dei
Confronto fra i sistemi di modulazione AM, DSB e SSB
 ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA. Valutazione del trasporto solido
 UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA Valutazione del trasporto solido in sospensione
UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA Valutazione del trasporto solido in sospensione
Applicazione del principio di conservazione dell energia a sistemi aventi un gran numero di particelle.
 PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
Goniometria. r x. con x = 1 rad se l = r.
 Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali ( = /360 dell'angolo giro), anhe se una Legge dello Stato italiano del 960 impone di esprimerli in radianti. Ogni
Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali ( = /360 dell'angolo giro), anhe se una Legge dello Stato italiano del 960 impone di esprimerli in radianti. Ogni
Scrivi l equazione di un iperbole conoscendone i fuochi e la costante ( = differenza costante) 2k.
 . ESERCIZI SULL IPERBOLE A partire dall equazione di un iperbole stabilisi quanto valgono I. le oordinate dei vertii e dei fuohi II. la ostante (differenza ostante delle distanze di un punto dai fuohi)
. ESERCIZI SULL IPERBOLE A partire dall equazione di un iperbole stabilisi quanto valgono I. le oordinate dei vertii e dei fuohi II. la ostante (differenza ostante delle distanze di un punto dai fuohi)
IL TORNANTE RETTIFILO CONTROCURVA RETTIFILO
 IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
Esercizio 1 Scrivere le equazioni di Eulero-Lagrange per il sistema bidimensionale di Lagrangiana. = q 2 2q 2. L = q 1 d L. = q 2. = q 1 2q 1.
 1 4 o tutorato - FM210/MA - 17/4/2017 Eserizio 1 Srivere le equazioni di Eulero-Lagrange per il sistema bidimensionale di Lagrangiana L(q, q) = q 2 q 1 q 1 q 2 2q 1 q 2 e trovarne espliitamente la soluzione.
1 4 o tutorato - FM210/MA - 17/4/2017 Eserizio 1 Srivere le equazioni di Eulero-Lagrange per il sistema bidimensionale di Lagrangiana L(q, q) = q 2 q 1 q 1 q 2 2q 1 q 2 e trovarne espliitamente la soluzione.
La misura della resistenza
 Parte II (Metodi e strmenti di misra in ) Metodi di zero I metodi di zero onsentono il onfronto diretto tra na grandezza inognita X e na fnzione nota di n ampione f(c). Il risltato del onfronto viene tilizzato
Parte II (Metodi e strmenti di misra in ) Metodi di zero I metodi di zero onsentono il onfronto diretto tra na grandezza inognita X e na fnzione nota di n ampione f(c). Il risltato del onfronto viene tilizzato
LIMITI- INTRODUZIONE
 LIMITI- INTRODUZIONE Consideriamo un impresa he produa un bene di largo onsumo e he abbia investito una somma resente nel tempo in pubbliità del proprio prodotto. I dati passati mostrano he l operazione
LIMITI- INTRODUZIONE Consideriamo un impresa he produa un bene di largo onsumo e he abbia investito una somma resente nel tempo in pubbliità del proprio prodotto. I dati passati mostrano he l operazione
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
RELAZIONE GEOTECNICA GENERALE
 Studio assoiato Ferrari & Partners - pag. 1 Comune di Milano Città Metropolitana di Milano REAZIONE GEOTECNICA GENERAE OGGETTO: Realizzazione di un muro di sostegno in emento armato Muro di sostegno COMMITTENTE:
Studio assoiato Ferrari & Partners - pag. 1 Comune di Milano Città Metropolitana di Milano REAZIONE GEOTECNICA GENERAE OGGETTO: Realizzazione di un muro di sostegno in emento armato Muro di sostegno COMMITTENTE:
e del guadagno percentuale in conto capitale, dato da e v
 Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
1. Calcolo del Momento di plasticizzazione per una sezione tubolare in acciaio.
 1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
Equazione di Boltzmann
 Capitolo 2 Equazione di Boltzmann 2.1 Fluidineutriollisionaliedintegralediollisione Il omportamento ontinuo di un fluido neutro e quindi la sua dinamia sono determinati dall interazione a livello mirosopio
Capitolo 2 Equazione di Boltzmann 2.1 Fluidineutriollisionaliedintegralediollisione Il omportamento ontinuo di un fluido neutro e quindi la sua dinamia sono determinati dall interazione a livello mirosopio
MATEMATICA CORSO A I APPELLO 8 Giugno 2012
 MATEMATICA CORSO A I APPELLO Giugno 2012 Soluzioni 1. È stato preparato uno siroppo onentrato al 25% mettendo 30 grammi di zuhero in una erta quantità di aqua. a) Quanto vale la massa dell aqua? b) Fra
MATEMATICA CORSO A I APPELLO Giugno 2012 Soluzioni 1. È stato preparato uno siroppo onentrato al 25% mettendo 30 grammi di zuhero in una erta quantità di aqua. a) Quanto vale la massa dell aqua? b) Fra
CENNI SUGLI SCAMBIATORI DI CALORE
 asdf CENNI SUGLI SCAMBIATORI DI CALORE 24 January 2012 Introduzione all'articolo Il seguente breve articolo ha l'intento di rendere note le linee generiche (quindi senza alcuna presunzione di definirsi
asdf CENNI SUGLI SCAMBIATORI DI CALORE 24 January 2012 Introduzione all'articolo Il seguente breve articolo ha l'intento di rendere note le linee generiche (quindi senza alcuna presunzione di definirsi
ELEMENTI DI ANALISI SPETTRALE 1 I DUE DOMINI
 Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Flussi Di Fanno. 1 Definizione del flusso di Fanno
 Flussi Di Fanno 1 Definizione del flusso di Fanno Si consideri un flusso adiabatico all interno di un condotto a sezione costante, in presenza di attrito e senza scambio di lavoro con l esterno. Tale regime
Flussi Di Fanno 1 Definizione del flusso di Fanno Si consideri un flusso adiabatico all interno di un condotto a sezione costante, in presenza di attrito e senza scambio di lavoro con l esterno. Tale regime
Lezione. Prof. Pier Paolo Rossi Università degli Studi di Catania
 Lezione TEIA DELLE STRUZII Prof. Pier Paolo Rossi Università degli Studi di atania 1 Flessione omposta 2 Verifia di sezioni soggette a flessione omposta 3 Flessione omposta 1 stadio (Formule di Sienza
Lezione TEIA DELLE STRUZII Prof. Pier Paolo Rossi Università degli Studi di atania 1 Flessione omposta 2 Verifia di sezioni soggette a flessione omposta 3 Flessione omposta 1 stadio (Formule di Sienza
Matematica per le Scienze Sociali
 atematica per le Scienze Sociali Limite Passaggio al ite Continuità della unzione 5//05 Clelia Cascella Deinizione intuitiva di ite Se () è una unzione reale, se c ed l sono dei numeri reali, dire che
atematica per le Scienze Sociali Limite Passaggio al ite Continuità della unzione 5//05 Clelia Cascella Deinizione intuitiva di ite Se () è una unzione reale, se c ed l sono dei numeri reali, dire che
Analisi 1 e 2 - Quarto compitino Soluzioni proposte
 Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
Q Q. Energia scambiata per ciclo legata alle differenze di pressione ed al valore della pressione stessa. I Principio macchina CICLICA L = Q 12 -Q 34
 Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Diagramma Indiatore Energia sambiata per ilo legata alle differenze di pressione ed al alore della pressione stessa. I Prinipio maina CICLICA L 2-34 L ε 2 Reersibilità
Fisia enia G. Grazzini UNIVERSIA DI FIRENZE Diagramma Indiatore Energia sambiata per ilo legata alle differenze di pressione ed al alore della pressione stessa. I Prinipio maina CICLICA L 2-34 L ε 2 Reersibilità
4. Teoria e Normativa
 4. Teoria e Normatia Questa sezione del Manuale Utente ontiene la desrizione delle metodologie di alolo utilizzate nel programma. 4.1) Verifihe in ondizione di moto uniforme. La portata he defluise per
4. Teoria e Normatia Questa sezione del Manuale Utente ontiene la desrizione delle metodologie di alolo utilizzate nel programma. 4.1) Verifihe in ondizione di moto uniforme. La portata he defluise per
Le omotetie. Nel caso in cui il centro di omotetia O corrisponda con l'origine degli assi, le equazioni dell'omotetia sono. le equazioni sono ωch
 O Le omotetie Dato un numero reale non nullo h e un punto P del piano l omotetia di rapporto h e entro O è quella trasformazione he assoia a P il punto P' tale he P P OP' = h OP. Se è P(xy) allora P'(hx
O Le omotetie Dato un numero reale non nullo h e un punto P del piano l omotetia di rapporto h e entro O è quella trasformazione he assoia a P il punto P' tale he P P OP' = h OP. Se è P(xy) allora P'(hx
Seminario di Studio sul documento CNR-DT200/ Giugno Esempi di rinforzo a FLESSIONE con FRP Stato limite ultimo
 Esempi numerii F.Ceroni A.Prota Seminario di Studio sul doumento CNR-DT200/2004 Napoli, 0 Giugno 2005 Esempi di rinorzo a FLESSIONE on FRP Stato limite ultimo Ing. Franesa Ceroni eroni@unisannio.it Università
Esempi numerii F.Ceroni A.Prota Seminario di Studio sul doumento CNR-DT200/2004 Napoli, 0 Giugno 2005 Esempi di rinorzo a FLESSIONE on FRP Stato limite ultimo Ing. Franesa Ceroni eroni@unisannio.it Università
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Eserizi svolti a lezione (diembre 2016) Valutazioni di operazioni finanziarie Eserizio 1. Un titolo on vita
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Eserizi svolti a lezione (diembre 2016) Valutazioni di operazioni finanziarie Eserizio 1. Un titolo on vita
Esercizi sulle reti elettriche in corrente continua
 serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
Linee di Trasmissione: Propagazione per onde
 Linee di Trasmissione: Propagazione per onde v + (z) Rappresentazione shematia di una linea di trasmissione z Definizione matematia dell onda di tensione he si propaga verso la z resente: ω 0 v ( z) =
Linee di Trasmissione: Propagazione per onde v + (z) Rappresentazione shematia di una linea di trasmissione z Definizione matematia dell onda di tensione he si propaga verso la z resente: ω 0 v ( z) =
Campionamento. Campionamento. esercizi. Segnale analogico. Segnale campionato. x(n)=x(nt c. con T c. : passo di campionamento e f c.
 Campionamento eserizi Campionamento x(t) x n Segnale analogio t x(n)x(n ) 0 N- n Segnale ampionato on : passo di ampionamento e / requenza di ampionamento x( t ) x( t )p( t ) p( t ) δ ( t n ) n x( t )
Campionamento eserizi Campionamento x(t) x n Segnale analogio t x(n)x(n ) 0 N- n Segnale ampionato on : passo di ampionamento e / requenza di ampionamento x( t ) x( t )p( t ) p( t ) δ ( t n ) n x( t )
TERMODINAMICA E TERMOFLUIDODINAMICA TRASMISSIONE DEL CALORE PER CONVEZIONE
 TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
Relatività, Energia e Ambiente
 Digitall signed b DN: IT, oinfn, oupersonal Certiiate, lbologna, n Date: 00.07.8 4:37:5 +0'00' Relatiità, Energia e Ambiente Quantità di Moto ed Energia Pro. Rihiami di dinamia lassia. Alma Mater Studiorum
Digitall signed b DN: IT, oinfn, oupersonal Certiiate, lbologna, n Date: 00.07.8 4:37:5 +0'00' Relatiità, Energia e Ambiente Quantità di Moto ed Energia Pro. Rihiami di dinamia lassia. Alma Mater Studiorum
Derivata di una funzione
 Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
Esercitazione di Controll0 Digitale n 1
 8 marzo 3 Eseritazione di Controll Digitale n a.a. /3 =. Si onsideri il segnale x( t) sin ( π t) + sin( 4π t) Si valuti la frequenza minima del ampionatore he permette la riostruibilità del segnale, e
8 marzo 3 Eseritazione di Controll Digitale n a.a. /3 =. Si onsideri il segnale x( t) sin ( π t) + sin( 4π t) Si valuti la frequenza minima del ampionatore he permette la riostruibilità del segnale, e
RELAZIONE GEOTECNICA GENERALE
 Studio Assoiato Ferrari & Partners Comune di Milano Città metropolitana di Milano REAZIOE GEOTECICA GEERAE OGGETTO: Realizzazione di un muro di sostegno in emento armato Muro di sostegno COMMITTETE: Sig.
Studio Assoiato Ferrari & Partners Comune di Milano Città metropolitana di Milano REAZIOE GEOTECICA GEERAE OGGETTO: Realizzazione di un muro di sostegno in emento armato Muro di sostegno COMMITTETE: Sig.
Jazz e strumentario Orff di Sestino Macaro
 Jazz e strumentario Orff di Sestino Maaro Analizzeremo in questo artiolo il proesso di reazione di un aompagnamento jazzistio nella struttura del blues impiegando gli elementi tipii della metodologia Orff:
Jazz e strumentario Orff di Sestino Maaro Analizzeremo in questo artiolo il proesso di reazione di un aompagnamento jazzistio nella struttura del blues impiegando gli elementi tipii della metodologia Orff:
Indice. Prefazione alla terza edizione italiana...xi. Ringraziamenti dell Editore...XIII. Guida alla lettura...xiv
 Prefazione alla terza edizione italiana...xi Ringraziamenti dell Editore...XIII Guida alla lettura...xiv 1 INTRODUZIONE E UNO SGUARDO D INSIEME...1 1.1 Introduzione alle scienze termiche...2 1.2 La termodinamica
Prefazione alla terza edizione italiana...xi Ringraziamenti dell Editore...XIII Guida alla lettura...xiv 1 INTRODUZIONE E UNO SGUARDO D INSIEME...1 1.1 Introduzione alle scienze termiche...2 1.2 La termodinamica
NOME E COGNOME {1,2,3,5,8,13,21,34,55,...} 5 = 5 5
 VERIFICA DI MATEMATICA 1^F Lieo Sportivo 11 diembre 2017 Rispondere su un foglio protoollo motivando dettagliatamente ogni risposta e rionsegnare insieme al testo originale entro il 18 diembre 2017 NOME
VERIFICA DI MATEMATICA 1^F Lieo Sportivo 11 diembre 2017 Rispondere su un foglio protoollo motivando dettagliatamente ogni risposta e rionsegnare insieme al testo originale entro il 18 diembre 2017 NOME
Esercizi sulla funzione integrale
 Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
8-9 Analisi di reti normali
 Lati della rete ipoli normali lettrotenia 8-9 Analisi di reti normali Per iasuno degli l ipoli (lati) GT GC ell analisi sono da determinare l tensioni l orrenti l inognite G Sistema di equazioni di rete
Lati della rete ipoli normali lettrotenia 8-9 Analisi di reti normali Per iasuno degli l ipoli (lati) GT GC ell analisi sono da determinare l tensioni l orrenti l inognite G Sistema di equazioni di rete
VERIFICA TERMICA DI UN GENERATORE DI VAPORE A TUBI DI FUMO
 VERIFICA TERMICA DI UN GENERATORE DI VAPORE A TUBI DI FUMO Corso di Termotenia 2 Prima eseritazione Titolare del orso: Gruppo 4: Prof. Paolo Coppa Emiliano Andreassi Leonardo Di Stefano Lua Lerario Fabio
VERIFICA TERMICA DI UN GENERATORE DI VAPORE A TUBI DI FUMO Corso di Termotenia 2 Prima eseritazione Titolare del orso: Gruppo 4: Prof. Paolo Coppa Emiliano Andreassi Leonardo Di Stefano Lua Lerario Fabio
sistemi di trasporto
 Rihiami di teoria dei sistemi di trasporto Struttura del sistema di modelli per la simulazione dei sistemi di trasporto e delle loro interazioni on il territorio OERTA DI INRASTRUTTURE E SERVIZI DI TRASPORTO
Rihiami di teoria dei sistemi di trasporto Struttura del sistema di modelli per la simulazione dei sistemi di trasporto e delle loro interazioni on il territorio OERTA DI INRASTRUTTURE E SERVIZI DI TRASPORTO
Università degli studi di Cagliari. Corso di aggiornamento. Unità 4 PIASTRE IN C.A. E INSTABILITÀ. - Analisi Limite: Metodo delle Linee di rottura
 Università degli studi di Cagliari Dipartimento di Ingegneria Strutturale Corso di aggiornamento Unità 4 PIASTRE IN C.A. E INSTABILITÀ RELATORE: Ing. Igino MURA imura@unia.it -6 Giugno 00 - Analisi Limite:
Università degli studi di Cagliari Dipartimento di Ingegneria Strutturale Corso di aggiornamento Unità 4 PIASTRE IN C.A. E INSTABILITÀ RELATORE: Ing. Igino MURA imura@unia.it -6 Giugno 00 - Analisi Limite:
sistemi di trasporto
 Rihiami di teoria dei sistemi di trasporto Struttura del sistema di modelli per la simulazione dei sistemi di trasporto e delle loro interazioni on il territorio OERTA DI INRASTRUTTURE E SERVIZI DI TRASPORTO
Rihiami di teoria dei sistemi di trasporto Struttura del sistema di modelli per la simulazione dei sistemi di trasporto e delle loro interazioni on il territorio OERTA DI INRASTRUTTURE E SERVIZI DI TRASPORTO
Lezioni Combustione 2 7 aprile Abbiamo definito la funzione densità di probabilità (pdf) della componente u x di velocità come:
 Abbiamo definito la funzione densità di probabilità (pdf) della omponente u di veloità ome: pdf (u) d u he per il prinipio di equidistribuzione dell energia di Boltzmann risulta: mu pdf (u ) A ep (- )
Abbiamo definito la funzione densità di probabilità (pdf) della omponente u di veloità ome: pdf (u) d u he per il prinipio di equidistribuzione dell energia di Boltzmann risulta: mu pdf (u ) A ep (- )
Università degli Studi di Trieste Dipartimento di Ingegneria Navale, del Mare e per l Ambiente Lezioni di Statica della Nave Parte II
 Università degli Studi di rieste Dipartimento di Ingegneria Navale, del Mare e per l Ambiente Lezioni di Statia della Nave Parte II Prof. Alberto ranesutto Alberto ranesutto Lezioni di Statia della Nave
Università degli Studi di rieste Dipartimento di Ingegneria Navale, del Mare e per l Ambiente Lezioni di Statia della Nave Parte II Prof. Alberto ranesutto Alberto ranesutto Lezioni di Statia della Nave
il ciclo di Ericsson (1853) caratterizzato da due isoterme e due isobare; il ciclo di Reitlinger (1873) con due isoterme e due politropiche.
 16 Il ciclo di Stirling Il coefficiente di effetto utile per il ciclo frigorifero di Carnot è, in base alla (2.9): T min ɛ =. (2.31) T max T min Il ciclo di Carnot è il ciclo termodinamico che dà il maggior
16 Il ciclo di Stirling Il coefficiente di effetto utile per il ciclo frigorifero di Carnot è, in base alla (2.9): T min ɛ =. (2.31) T max T min Il ciclo di Carnot è il ciclo termodinamico che dà il maggior
Corso di Laurea in Ingegneria delle Telecomunicazioni ANALISI MATEMATICA 1. Prova scritta del 16 gennaio 2018 Fila 1.
 Corso di Laurea in Ingegneria delle Teleomuniazioni ANALISI MATEMATICA Prova sritta del 6 gennaio 8 Fila. Esporre il proedimento di risoluzione degli eserizi in maniera ompleta e leggibile.. (Punti 5)
Corso di Laurea in Ingegneria delle Teleomuniazioni ANALISI MATEMATICA Prova sritta del 6 gennaio 8 Fila. Esporre il proedimento di risoluzione degli eserizi in maniera ompleta e leggibile.. (Punti 5)
BIBLIOGRAFIA: Joseph. E. Bowles Fondazioni Ed. Mc Graw Hill Renato Lancellotta Geotecnica Ed. Zanichelli
 COIZIOI GEERALI I UTILIZZO ELL APPLICAZIOE La presente appliazione è stata realizzata implementando formule e modelli matematii propri della geotenia, della sienza e della tenia delle fondazioni. Con l
COIZIOI GEERALI I UTILIZZO ELL APPLICAZIOE La presente appliazione è stata realizzata implementando formule e modelli matematii propri della geotenia, della sienza e della tenia delle fondazioni. Con l
GEOMETRIA ANALITICA 8 LE CONICHE
 GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
ESERCIZI SUL BILANCIO TERMICO DEI GENERATORI E DEGLI ACCUMULI
 ESERCIZI SUL BILANCIO TERMICO DEI GENERATORI E DEGLI ACCUMULI FORMULARIO DI RIEPILOGO Tabella 0.1 Poteri alorifii di aluni ombustibili. PCI [MJ/kg] PCS [MJ/kg] Petrolio greggio 41,9 44,8 Benzina er auto
ESERCIZI SUL BILANCIO TERMICO DEI GENERATORI E DEGLI ACCUMULI FORMULARIO DI RIEPILOGO Tabella 0.1 Poteri alorifii di aluni ombustibili. PCI [MJ/kg] PCS [MJ/kg] Petrolio greggio 41,9 44,8 Benzina er auto
Università degli studi di Bologna D.I.E.M. Dipartimento di Ingegneria delle Costruzioni Meccaniche, Nucleari, Aeronautiche e di Metallurgia
 Universià degli sudi di Bologna D.I.E.M. Diparimeno di Ingegneria delle osruzioni Meanihe, Nuleari, Aeronauihe e di Meallurgia dimensionameno rev. Oobre 008 ambiaori di alore arhieura (onroorrene) ambiaori
Universià degli sudi di Bologna D.I.E.M. Diparimeno di Ingegneria delle osruzioni Meanihe, Nuleari, Aeronauihe e di Meallurgia dimensionameno rev. Oobre 008 ambiaori di alore arhieura (onroorrene) ambiaori
Analisi di segnali campionati
 Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
Temi di esame a scelta del candidato:
 II Sessione 2008 Sezione B (N.O.) - Settore CIVILE E AMBIENTALE Prima prova sritta II andidato desriva in linea generale i riteri di progettazione di un'opera a sostegno di un terrapieno TEMAN.l II andidato
II Sessione 2008 Sezione B (N.O.) - Settore CIVILE E AMBIENTALE Prima prova sritta II andidato desriva in linea generale i riteri di progettazione di un'opera a sostegno di un terrapieno TEMAN.l II andidato
E = ŷ E 0 e i(kx ωt)
 Equilibrio osillatore ario radiazione nera Consideriamo dapprima un onda piana, monoromatia e polarizzata linearmente, he attraversi un sottile strato (dx) di dielettrio omogeneo ed isotropo a bassa densità
Equilibrio osillatore ario radiazione nera Consideriamo dapprima un onda piana, monoromatia e polarizzata linearmente, he attraversi un sottile strato (dx) di dielettrio omogeneo ed isotropo a bassa densità
FACOLTA DI INGEGNERIA TECNICA DELLE COSTRUZIONI
 FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE ED AMBIENTALE III ANNO ACCADEMICO TECNICA DELLE COSTRUZIONI Lezione VII Cemento armato: ESERCITAZIONI: FLESSIONE (SLE, SLU) TAGLIO (prima parte)
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE ED AMBIENTALE III ANNO ACCADEMICO TECNICA DELLE COSTRUZIONI Lezione VII Cemento armato: ESERCITAZIONI: FLESSIONE (SLE, SLU) TAGLIO (prima parte)
STRUMENTI DI INDAGINE: Il Modello Numerico Unidimensionale per lo Studio della Morfodinamica dei Corsi d Acqua Naturali
 Componente Aque uperiiali Allegato A TRUMENTI DI INDAGINE: Il Modello Numerio Unidimensionale per lo tudio della Morodinamia dei Corsi d Aqua Naturali Premessa Nella presente appendie viene presentato
Componente Aque uperiiali Allegato A TRUMENTI DI INDAGINE: Il Modello Numerio Unidimensionale per lo tudio della Morodinamia dei Corsi d Aqua Naturali Premessa Nella presente appendie viene presentato
